Transfer Learning in Large-scale Gaussian Graphical Models with False Discovery Rate Control

Abstract

Transfer learning for high-dimensional Gaussian graphical models (GGMs) is studied. The target GGM is estimated by incorporating the data from similar and related auxiliary studies, where the similarity between the target graph and each auxiliary graph is characterized by the sparsity of a divergence matrix. An estimation algorithm, Trans-CLIME, is proposed and shown to attain a faster convergence rate than the minimax rate in the single-task setting. Furthermore, we introduce a universal debiasing method that can be coupled with a range of initial graph estimators and can be analytically computed in one step. A debiased Trans-CLIME estimator is then constructed and is shown to be element-wise asymptotically normal. This fact is used to construct a multiple testing procedure for edge detection with false discovery rate control. The proposed estimation and multiple testing procedures demonstrate superior numerical performance in simulations and are applied to infer the gene networks in a target brain tissue by leveraging the gene expressions from multiple other brain tissues. A significant decrease in prediction errors and a significant increase in power for link detection are observed.

1. Introduction

Gaussian graphical models (GGMs), which represent the dependence structure among a set of random variables, have been widely used to model the conditional dependence relationships in many applications, including gene regulatory networks and brain connectivity maps (Drton and Maathuis, 2017; Varoquaux et al., 2010; Zhao et al., 2014; Glymour et al., 2019). In the classical setting with data from a single study, the estimation of high-dimensional GGMs has been well studied in a series of papers, including penalized likelihood methods (Yuan and Lin, 2007; Lam and Fan, 2009; Friedman et al., 2008; Rothman et al., 2008), convex optimization-based methods (Cai et al., 2011, 2016; Liu and Wang, 2017), and penalized ℓ₁ log-determinant divergence (Ravikumar et al., 2011). Model selection has been considered in Ravikumar et al. (2008). The minimax optimal rates are studied in Cai et al. (2016). Ren et al. (2015) studies the estimation optimality and inference for individual entries. A survey of optimal estimation of the structured high-dimensional GGMs can be found in Cai et al. (2016). Liu (2013) considers the inference for GGMs based on a node-wise regression approach and introduces a multiple testing procedure for the partial correlations with the FDP and FDR control and Xia et al. (2015) studies simultaneous testing for the differential networks.

Methods for estimating a single GGM have also been extended to simultaneously estimating multiple graphs when data from multiple studies are available. For example, Guo et al. (2011), Chiquet et al. (2011), Danaher et al. (2014), and Cai et al. (2016) consider jointly estimating multiple GGMs by employing some penalties in order to induce common structures among different graphs. This problem falls in the category of multi-task learning (Lounici et al., 2009; Agarwal et al., 2012), whose goal is to jointly estimate several related graphs.

Due to high dimensionality and relatively small sample sizes in many modern applications, estimation of GGMs based on a single study often has large uncertainty and low power in link detection. However, the blessing is that samples from some different but related studies can be abundant. Particularly, for a given target study, there might be other studies where we expect some similar dependence structures among the same set of variables. One example is to infer the gene regulatory networks among a set of genes for a given issue. Although gene regulatory networks are expected to vary from tissue to tissue, certain shared regulatory structures are expected and have indeed been observed (Pierson et al., 2015; Fagny et al., 2017). This paper introduces a transfer learning approach to improve the estimation and inference accuracy for the gene regulatory network in one target tissue by incorporating the data in other tissues.

Transfer learning techniques have been developed in a range of applications, including pattern recognition, natural language processing, and drug discovery (Pan and Yang, 2009; Turki et al., 2017; Bastani, 2021). Transfer learning has been studied in different settings with various similarity measures, but only a few of them offer statistical guarantees. Cai and Wei (2021) investigates nonparametric classification in transfer learning and proposes minimax and adaptive classifiers. In linear regression models, Li et al. (2021) considers the estimation of high-dimensional regression coefficient vectors when the difference between the auxiliary model and the target model is sufficiently sparse and proves the minimax optimal rate. Tripuraneni et al. (2021) proposes an algorithm that assumes all the auxiliary studies and the target study share a common, low-dimensional linear representation. Transfer learning in general functional classes has been studied in Tripuraneni et al. (2020) and Hanneke and Kpotufe (2020). Loosely speaking, transfer learning aims to improve the learning accuracy for the target study by transferring information from multiple related studies. This is different from the multi-task learning outlined above, where the goal is to simultaneously estimate multiple graphs. In terms of theoretical results, the error criteria for these two learning frameworks are different and are incomparable in general. The convergence rate for estimating the target graph in transfer learning can be faster than the corresponding rate in multi-task learning.

1.1. Model set-up

Suppose that we observe independent and identically distributed (i.i.d.) samples $x_i\in {ℝ}^p$ generated from N(μ,Σ), i = 1,…,n, and the parameter of interest is the precision matrix Ω = Σ⁻¹. Indeed, Ω uniquely determines the conditional dependence structure and the corresponding graph. If the i-th and j-th variables are conditionally dependent in the target study, there is an undirected edge between the i-th and j-th nodes in the Gaussian graph and, equivalently, the (i, j)-th and (j, i)-th entries of Ω are nonzero. Our focus is on the estimation and inference for high-dimensional sparse Gaussian graphs where p can be much larger than n and Ω is sparse such that each column of Ω has at most s nonzero elements with s ≪ p.

In the transfer learning setting, besides the observations {x₁,…,x_n} from the target distribution N(μ,Σ), we also observe samples from K auxiliary studies. For k = 1,…,K, the observations $x_i^{(k)}\in {ℝ}^p$ are independently generated from N(μ^(k),Σ^(k)),i = 1,…,n_k. Let Ω^(k) = {Σ^(k)}⁻¹ be the precision matrix of the k-th study, k = 1,…,K. If some knowledge can be transferred to the target study, a certain level of similarity needs to be possessed by the auxiliary models and the target one.

To motivate our proposed similarity measure, consider the relative entropy, or equivalently the Kullback-Leibler (KL) divergence, between the k-th auxiliary model and the target model. That is,

$${\mathcal{D}}_{KL}\left(N_{{\mathrm{\Sigma }}^{(k)}}\Vert N_{\mathrm{\Sigma }}\right)=\frac{1}{2}\mathrm{Tr}\left({\mathrm{\Delta }}^{(k)}\right)-\frac{1}{2}\log \det \left(I_p+{\mathrm{\Delta }}^{(k)}\right)\text{for}{\mathrm{\Delta }}^{(k)}=\mathrm{\Omega }{\mathrm{\Sigma }}^{(k)}-I_p,$$ (1)

where $N_{{\mathrm{\Sigma }}^{(k)}}$ and N_Σ denote the normal distributions with mean zero and covariance matrix Σ^(k) and Σ, respectively. The KL-divergence is parametrized by the matrix Δ^(k) and we call Δ^(k) the k-th divergence matrix. We characterize the difference between Ω and Ω^(k) via

$${\mathcal{D}}_q\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)={\max }_{1\le j\le p}{\Vert {\mathrm{\Delta }}_{j,.}^{(k)}\Vert }_q+{\max }_{1\le j\le p}{\Vert {\mathrm{\Delta }}_{.,j}^{(k)}\Vert }_q$$ (2)

for some fixed q ∈[0,1]. In words, ${\mathcal{D}}_q\left(\mathrm{\Omega },{\mathrm{\Omega }}^{(k)}\right)$ is the maximum row-wise ℓ_q-sparsity of Δ^(k) plus the maximum column-wise ℓ_q-sparsity of Δ^(k). Both the row-wise and column-wise norms are taken into account because Δ^(k) is non-symmetric. The quantity ${\mathcal{D}}_q\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)$ measures the “relative distance” between Ω and Ω^(k) in the sense that ${\mathcal{D}}_q\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)={\mathcal{D}}_q\left(c{\mathrm{\Omega }}^{(k)},c\mathrm{\Omega }\right)$ for any constant c > 0. Notice that the spectral norm of Δ^(k) is upper bounded by ${\mathcal{D}}_1\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)$, which further provides an upper bound on the KL-divergence.

In this work, we develop estimation and inference procedures for GGMs under the similarity characterization (2) for any fixed q ∈[0,1]. We focus on the methods and theory when q = 1 in the main paper and provide matching minimax upper and lower bounds for q ∈[0,1] in the Supplemental Materials.

1.2. Our contributions

A transfer learning algorithm, called Trans-CLIME, is proposed for estimating the target GGM. Inspired by the CLIME in the single-task setting (Cai et al., 2011), the proposed algorithm includes additional steps to incorporate auxiliary information. Furthermore, edge detection with uncertainty quantification is considered. We introduce a universal debiasing method that can be coupled with many initial graph estimators, including both the single-task and the transfer learning estimators. The debiasing step can be analytically computed in one step. We demonstrate the asymptotic normality under certain conditions. Applying this procedure, we construct the confidence interval for an edge of interest and propose a multiple testing procedure for all the edges with false discovery rate (FDR) control.

Theoretically, we establish the minimax optimal rate of convergence for estimating the GGMs with transfer learning in the Frobenius norm by providing matching minimax upper and lower bounds. We also establish the optimal rate of convergence for estimating individual entries in the graph. These convergence rates are faster than the corresponding minimax rates in the classical single-task setting, where no auxiliary samples are available or used. Our proposed Trans-CLIME and debiased Trans-CLIME are shown to be rate optimal for different error criteria under proper conditions.

1.3. Organization and notation

The rest of this paper is organized as follows. In Section 2, we propose an algorithm for graph estimation with transfer learning given q = 1 in the similarity characterization. In Section 3, we study statistical inference for each edge of the graph. In Section 4, we consider multiple testing of all the edges in the graph with false discovery rate guarantee. In Section 5, we establish the minimax lower bounds for any fixed q ∈[0,1]. In Section 6, we study the numerical performance of Trans-CLIME in comparison to some other relevant methods. We then present an application of the proposed methods to estimate gene regulatory graphs based on data from multiple brain tissues in Section 7. Section 8 concludes the paper. The proofs and other supporting information are given in the Supplementary Materials.

For a matrix $A\in {ℝ}^{p\times p}$, let A_j denote the j-th column of A. For any fixed j ≤ p, we call ∥ A_j ∥₂ the column-wise ℓ₂ -norm of A. Let ∥ A ∥_∞,q = max_j≤q ∥ A_j ∥_q for q > 0 and ∥ A ∥_∞,∞ = max_i,j≤p | A_i,j |, and $\Vert A{\Vert }_1=\sum _{j=1}^p{\Vert A_j\Vert }_1$. Let ∥ A∥₂ denote the spectral norm of A and ∥ A ∥_F denote the Frobenius norm of A. For a vector $v\in {ℝ}^p$, let ∥ v ∥₀ denote the number of nonzero elements of v. For a symmetric matrix A, let Λ_max (A) and Λ_min (A) denote the largest and smallest eigenvalues of A, respectively. Let Φ(t) denote the standard normal probability function. Let z_q denote the q-th quantile of standard normal distribution. We use c₀,c₁,… and C₀,C₁,… as generic constants which can be different at different places.

2. GGM estimation with transfer learning

In this section, we study GGM estimation based on transfer learning. In Section 2.1, we introduce the rationale for the proposed algorithm. The proposal is introduced in Section 2.2 and its theoretical properties are studied in Section 2.3.

2.1. Rationale and moment equations

Moment equations provide a powerful tool for deriving estimation methods in parametric models. By the definition of Ω, it is natural to consider the following moment equation:

$$\mathrm{\Sigma }\mathrm{\Omega }-I_p=0.$$ (3)

The idea of CLIME (Cai et al., 2011) is to solve an empirical version of (3) and to encourage the sparsity of the estimator. In the context of transfer learning, we re-express the moment equation (3) to incorporate auxiliary information. Specifically, for k = 1,…,K,

$$I_p={\mathrm{\Sigma }}^{(k)}{\mathrm{\Omega }}^{(k)}={\mathrm{\Sigma }}^{(k)}\mathrm{\Omega }-{\left({\mathrm{\Delta }}^{(k)}\right)}^{\top },$$ (4)

where Δ^(k) is the divergence matrix defined in (1). We see from (4) that Δ^(k) corresponds to the bias in the moment equations when we try to identify Ω based on the k-th study. To simultaneously leverage all the auxiliary studies, we further define the weighted average of the covariance and divergence matrices

$${\mathrm{\Sigma }}^{\mathcal{K}}=\sum _{k=1}^K{\alpha }_k{\mathrm{\Sigma }}^{(k)}\text{and}{\mathrm{\Delta }}^{\mathcal{K}}=\sum _{k=1}^K{\alpha }_k{\mathrm{\Delta }}^{(k)},$$ (5)

where α = n_k / N and $N=\sum _{k=1}^K{n}_k$. For knowledge transfer, the moment equation considered for Ω is

$${\mathrm{\Sigma }}^{\mathcal{K}}\mathrm{\Omega }-{\left({\mathrm{\Delta }}^{\mathcal{K}}\right)}^{\top }-I_p=0,$$ (6)

where ${\mathrm{\Sigma }}^{\mathcal{K}}$ is an average parameter over the K source studies and it incorporates the auxiliary information. The moment equation (6) motivates our procedure. First, we will estimate ${\mathrm{\Delta }}^{\mathcal{K}}$ based on the following moment equation:

$$\mathrm{\Sigma }{\mathrm{\Delta }}^{\mathcal{K}}-\left({\mathrm{\Sigma }}^{\mathcal{K}}-\mathrm{\Sigma }\right)=0.$$ (7)

Once ${\mathrm{\Delta }}^{\mathcal{K}}$ is identified, we can estimate our target Ω via (6).

In some practical scenarios, the similarity between Ω^(k) and Ω can be weak, for some 1 ≤ k ≤ K, i.e. ${\mathcal{D}}_q\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)$ can be large. In fact, the similarity is often unknown a priori in practice. In this case, information transfer may negatively affect the learning performance of the target problem, which is also known as the “negative transfer” (Hanneke and Kpotufe, 2020). To address this issue, we will further perform an aggregation step. The aggregation methods and theory have been extensively studied in the existing literature in regression problems, to name a few, Rigollet and Tsybakov (2011); Tsybakov (2014); Lecué and Rigollet (2014). This type of methods can guarantee that, loosely speaking, the aggregated estimator has prediction performance comparable to the best prediction performance which could be achieved by the initial estimators.

2.2. Trans-CLIME algorithm

We introduce our proposed transfer learning algorithm, Trans-CLIME. We randomly split the data from the target study into two disjoint folds. Specifically, let $\mathcal{I}$ be a random subset of {1,…,n} such that $|\mathcal{I}|=cn$ for some constant 0 < c < 1. Let ${\mathcal{I}}^c$ denote the complement of $\mathcal{I}$. Let $\overline{x}=\frac{1}{|\mathcal{I}|}\sum _{i\in \mathcal{I}}{x}_i,\tilde{x}=\frac{1}{\left|{\mathcal{I}}^c\right|}\sum _{i\in {\mathcal{I}}^c}{x}_i$,

$$\widehat{\mathrm{\Sigma }}=\frac{1}{\left|\mathcal{I}\right|}\sum _{i\in \mathcal{I}}{x}_i{x}_i^{\top }-{\overline{xx}}^{\top }\text{and}\tilde{\mathrm{\Sigma }}=\frac{1}{\left|{\mathcal{I}}^c\right|}\sum _{i\in {\mathcal{I}}^c}{x}_i{x}_i^{\top }-\tilde{x}{\tilde{x}}^{\top }.$$ (8)

We will use $\widehat{\mathrm{\Sigma }}$ for constructing estimators and will use $\tilde{\mathrm{\Sigma }}$ for aggregation. Let $\tilde{n}=\left|{\mathcal{I}}^c\right|$. Let ${\overline{x}}^{\mathcal{K}}=\sum _{k=1}^K\sum _{i=1}^{n_k}{x}_i^{(k)}/N$ denote the sample mean and ${\widehat{\mathrm{\Sigma }}}^{\mathcal{K}}=\sum _{k=1}^K\sum _{i=1}^{n_k}{x}_i^{(k)}{\left(x_i^{(k)}\right)}^{\top }/N-{\overline{x}}^{\mathcal{K}}{\left({\overline{x}}^{\mathcal{K}}\right)}^{\top }$ denote the sample covariance based on the auxiliary samples. To begin with, we compute the single-task CLIME ${\widehat{\mathrm{\Omega }}}^{(\text{CL})}$ such that

$$\begin{array}{l}{\widehat{\mathrm{\Omega }}}^{(\text{CL})}=\arg {\min }_{\mathrm{\Omega }\in {ℝ}^{p\times p}}\Vert \mathrm{\Omega }{\Vert }_1\\ \text{subject}\text{to}{\Vert (\widehat{\mathrm{\Sigma }}+|\mathcal{I}{|}^{-1}{I}_p)\mathrm{\Omega }-I_p\Vert }_{\infty ,\infty }\le {\lambda }_{\text{CL}}\text{,}\end{array}$$ (9)

Where $\widehat{\mathrm{\Sigma }}$ is defined in (8) and λ_CL > 0 is a tuning parameter. A diagonal matrix $|\mathcal{I}{|}^{-1}{I}_p$ is added to $\widehat{\mathrm{\Sigma }}$ for making the sample covariance matrix positive definite. This modification has been considered in a refined version of the CLIME (Cai et al., 2016).

Step 1.

We estimate ${\mathrm{\Delta }}^{\mathcal{K}}$ based on the moment equation (7). Compute

$$\begin{array}{l}{\widehat{\mathrm{\Delta }}}^{\mathcal{K}}=\arg {\min }_{\mathrm{\Delta }\in {ℝ}^{p\times p}}\Vert \mathrm{\Delta }{\Vert }_1\\ \text{subject}\text{to}{\Vert \mathrm{\Delta }-\{({\widehat{\mathrm{\Omega }}}^{(\text{CL})}{)}^{\top }{\widehat{\mathrm{\Sigma }}}^{\mathcal{K}}-I_p\}\Vert }_{\infty ,\infty }\le {\lambda }_{\mathrm{\Delta }}\text{.}\end{array}$$ (10)

The optimization (10) can be understood as an adaptive thresholding of an initial estimate ${\mathrm{\Delta }}^{\mathcal{K}}$,$({\widehat{\mathrm{\Omega }}}^{(\text{CL})}{)}^{\top }{\widehat{\mathrm{\Sigma }}}^{\mathcal{K}}-I_p$. This initial estimate is inspired by the moment equation (7). We further explain that the CLIME estimator ${\widehat{\mathrm{\Omega }}}^{(\mathrm{C}\mathrm{L})}$ is not necessarily symmetric and we use $({\widehat{\mathrm{\Omega }}}^{(\mathrm{C}\mathrm{L})}{)}^{\top }$ in step 1 to directly leverage the constraints in the CLIME optimization. The optimization in (10) is a more sophisticated version of hard thresholding and it is designed for the approximate sparse parameter ${\mathrm{\Delta }}^{\mathcal{K}}$. The estimate ${\widehat{\mathrm{\Delta }}}^{\mathcal{K}}$ is row-wise and column-wise ℓ₁-sparse and will be used in the next step.

Step 2.

For ${\widehat{\mathrm{\Delta }}}^{\mathcal{K}}$ defined in (10), compute

$$\begin{array}{l}\widehat{\mathrm{\Theta }}=\arg {\min }_{\mathrm{\Theta }\in {ℝ}^{p\times p}}\Vert \mathrm{\Theta }{\Vert }_1\\ \text{subject}\text{to}||\left({\widehat{\mathrm{\Sigma }}}^{\mathcal{K}}+N^{-1}{I}_p\right)\mathrm{\Theta }-{\left({\widehat{\mathrm{\Delta }}}^{\mathcal{K}}+I_p\right)}^{\top }|{|}_{\infty ,\infty }\le {\lambda }_{\mathrm{\Theta }}\text{.}\end{array}$$ (11)

This step is a CLIME-type optimization based on the moment equation (6) and it outputs an estimator of the target graph Ω. When the similarities between auxiliary studies and the target study are sufficiently high, $\widehat{\mathrm{\Theta }}$ is a desirable transfer learning estimator of Ω.

As we have discussed in Section 2.1, $\widehat{\mathrm{\Theta }}$ may not be as good as the single-task estimator if the similarity is weak. Hence, we perform a model selection aggregation in Step 3 based on the single-task CLIME estimator and $\widehat{\mathrm{\Theta }}$ to produce a final graph estimator. Loosely speaking, we compute a weight vector ${\widehat{v}}_j$ motivated by the moment equation

$$\tilde{\mathrm{\Sigma }}\left({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})},{\widehat{\mathrm{\Theta }}}_j\right)v_j-e_j\approx 0.$$

Notice that the sample splitting step guarantees that both $\widehat{\mathrm{\Theta }}$ and ${\widehat{\mathrm{\Omega }}}^{(CL)}$ are independent of the samples used for aggregation,$\tilde{\mathrm{\Sigma }}$.

Step 3.

For j = 1,…, p, compute

$$\widehat{W}(j)=\left(\begin{array}{cc}{\left({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})}\right)}^{\top }\tilde{\mathrm{\Sigma }}{\widehat{\mathrm{\Omega }}}_j^{(\text{CL})}& {\left({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})}\right)}^{\top }\tilde{\mathrm{\Sigma }}{\widehat{\mathrm{\Theta }}}_j\\ {\left({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})}\right)}^{\top }\tilde{\mathrm{\Sigma }}{\widehat{\mathrm{\Theta }}}_j& {\widehat{\mathrm{\Theta }}}_j^{\top }\tilde{\mathrm{\Sigma }}{\widehat{\mathrm{\Theta }}}_j\end{array}\right)$$

and

$${\widehat{v}}_j=\arg {\min }_{v\in \left\{{(0,1)}^{\top },{(1,0)}^{\top }\right\}}{v}^{\top }\widehat{W}(j)v-2v^{\top }({\widehat{\mathrm{\Omega }}}_{j,j}^{(\text{CL})},{\widehat{\mathrm{\Theta }}}_{j,j})$$

where ${\widehat{\mathrm{\Omega }}}^{(\mathrm{C}\mathrm{L})}$ is defined in (9) and $\widehat{\mathrm{\Theta }}$ is defined in (11). For j = 1,…, p, let

$${\widehat{\mathrm{\Omega }}}_j=({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})},{\widehat{\mathrm{\Theta }}}_j){\widehat{v}}_j.$$ (12)

We summarize the formal algorithm as follows.

Algorithm 1: Trans-CLIME algorithm

Input : Target data (after a random sample splitting) $\{\widehat{\mathrm{\Sigma }},\tilde{\mathrm{\Sigma }}\}$ and auxiliary samples ${\widehat{\mathrm{\Sigma }}}^{\mathcal{K}}$.

Output: $\widehat{\mathrm{\Omega }}$.

Step 1. Compute ${\widehat{\mathrm{\Delta }}}^{\mathcal{K}}$ via (10).

Step 2. Compute $\widehat{\mathrm{\Theta }}$ via (11).

Step 3. Aggregation for positive transfer: For j = 1,…, p, compute ${\widehat{\mathrm{\Omega }}}_j$ via (12).

Computationally, all the optimizations in these three steps can be separated into p independent optimizations, analogous to the original CLIME algorithm. This makes the computation scalable. While $\widehat{\mathrm{\Omega }}$ is not symmetric in general, one can use $\left(\widehat{\mathrm{\Omega }}+{\widehat{\mathrm{\Omega }}}^{\top }\right)/2$ as a symmetric estimate for Ω. It is not hard to show that $\left(\widehat{\mathrm{\Omega }}+{\widehat{\mathrm{\Omega }}}^{\top }\right)/2$ has the same convergence rate as $\widehat{\mathrm{\Omega }}$ in Frobenius norm.

2.3. Convergence rate of Trans-CLIME

In this subsection, we provide theoretical guarantees for the Trans-CLIME algorithm. We assume the following condition in our theoretical analysis.

Condition 2.1 (Gaussian graphs).

For i = 1,…, n, $x_i\in {ℝ}^p$ are i.i.d. distributed as N(μ,Σ). For each 1 ≤ k ≤ K, $x_i^{(k)}$ are i.i.d. distributed as N(μ^(k),Σ^(k)) for i = 1,…,n_k. It holds that 1/C ≤ Λ_min (Σ) ≤ Λ_max (Σ) ≤ C and 1/C ≤ min_1≤k≤K Λ_min (Σ^(k)) ≤ max_1≤k≤K Λ_max (Σ^(k)) ≤ C for some constant C > 0.

The Gaussian assumption facilitates the justification of the restricted eigenvalue conditions of the empirical covariance matrices. The Gaussian distribution of the target data also simplifies the limiting distribution of our proposed estimator for inference.

The parameter space we consider is

$${\mathbb{G}}_q(s,h)=\left\{\left(\mathrm{\Omega },{\mathrm{\Omega }}^{(1)},\dots ,{\mathrm{\Omega }}^{(K)}\right):{\max }_{1\le j\le p}{\Vert {\mathrm{\Omega }}_j\Vert }_0\le s,{\max }_{1\le k\le K}{\mathcal{D}}_q\left(\mathrm{\Omega },{\mathrm{\Omega }}^{(k)}\right)\le h\right\}.$$ (13)

We mention that the parameter space for GGMs in the single-task setting (Ren et al., 2015) can be written as ${\mathbb{G}}_q(s,\infty )$ under Condition 2.1 for any q ∈[0,1]. This is because ${\mathbb{G}}_q(s,\infty )$ allows the auxiliary studies to be arbitrarily far away from the target study and the worst-case scenario is equivalent to the setting where only the target data is available.

In the following, we demonstrate the convergence rate of Trans-CLIME under Condition 2.1. Let ${\delta }_{h,\mathrm{\Omega }}=\left\{\left(\Vert \mathrm{\Omega }{\Vert }_{\infty ,1}+h\right)h\sqrt{\log p/n}\right\}\wedge h^2$ and ${\delta }_h=h\sqrt{\log p/n}\wedge h^2$. We see that δ_h,Ω ≳ δ_h as ∥Ω∥_∞,1 ≥ c > 0. If max{∥Ω∥_∞,1, h} is finite, then δ_h,Ω ≍ δ_h.

Theorem 2.1 (Convergence rate of Trans-CLIME).

Assume Condition 2.1. Let the Trans-CLIME estimator $\widehat{\mathrm{\Omega }}$ be computed with

$${\lambda }_{\mathrm{\Delta }}=c_1\left(\Vert \mathrm{\Omega }{\Vert }_{\infty ,1}+h\right)\sqrt{\frac{\log p}{n}}\text{and}{\lambda }_{\mathrm{\Theta }}=c_1\sqrt{\frac{\log p}{N}},$$

where c₁ is a large enough constant. If p ≥ c₂N for some positive constant c₂ and s log p / N + δ_h,Ω ˄ s log p / n = o(1), then for any true models in ${\mathbb{G}}_1(s,h)$, we have

$$\mathbb{E}\left[\frac{1}{p}\Vert \widehat{\mathrm{\Omega }}-\mathrm{\Omega }{\Vert }_F^2\vee \Vert {\widehat{\mathrm{\Omega }}}_j-{\mathrm{\Omega }}_j{\Vert }_2^2\right]\le C\left(\frac{s\log p}{N+n}+{\delta }_{h,\mathrm{\Omega }}\wedge \frac{s\log p}{n}+\frac{1}{n}\right)$$ (14)

for any fixed 1 ≤ j ≤ p and some positive constant C.

Theorem 2.1 demonstrates that under a proper choice of the tuning parameters, the upper bounds can be obtained in Frobenius norm and in column-wise ℓ₂ -norm. We first illustrate the convergence rate of $\widehat{\mathrm{\Omega }}$ in column-wise ℓ₂ -norm. As all the Ω^(k), k = 1,…, K, share the column-wise s-sparse matrix Ω, the term s log p / (N + n) comes from estimating Ω based on N + n independent samples. The term δ_h,Ω comes from the errors of estimating ${\mathrm{\Delta }}^{\mathcal{K}}$ in row-wise ℓ₂ -norm. It goes to zero as the target sample size n goes to infinity. The term δ_h,Ω is determined by the target sample size because the divergence matrix is defined and can only be identified based on the target samples. Nevertheless, δ_h,Ω can still be a fast rate when the similarity among these studies is high, i.e., h is small. The minimal term δ_h,Ω ˄ s log p / n is a consequence of the aggregation performed in Step 3, where s log p / n is the single-task convergence rate under the same distance measure. However, there is a mild cost of aggregation, which is of order n⁻¹ shown in the last term in (14), and it is negligible in most parameter spaces of interest.

To understand the gain of transfer learning, we compare the current results with the convergence rate of CLIME in the single-task setting.

Remark 2.1 (Convergence rate of single-task CLIME).

Assume Condition 2.1, s² _{log p = o(n) and p} ≥ c₁n for some positive constant c₁. For the CLIME estimator ${\widehat{\mathrm{\Omega }}}^{(\mathrm{C}\mathrm{L})}$ defined in (9) with ${\lambda }_{\text{CL}}=c_2\sqrt{\log p/n}$ with large enough constant c2, then for any true models in ${\mathbb{G}}_1(s,\infty )$,

$$\mathbb{E}\left[\frac{1}{p}{\Vert {\widehat{\mathrm{\Omega }}}^{(\text{CL})}-\mathrm{\Omega }\Vert }_F^2\vee \Vert {\widehat{\mathrm{\Omega }}}_j^{(\text{CL})}-{\mathrm{\Omega }}_j{\Vert }_2^2\right]\le \frac{Cs\log p}{n}$$

for any fixed 1 ≤ j ≤ p and some positive constant C.

We see that the convergence rate of Trans-CLIME is no worse than CLIME in Frobenius norm for any s ≥ 1, which is a consequence of aggregation. Furthermore, Trans-CLIME has faster convergence rate when N ≫ n and ${\delta }_{h,\mathrm{\Omega }}\ll s\sqrt{\log p/n}$. That is, if the total auxiliary sample size is dominant and the similarity is sufficiently strong (h is sufficiently small), then the learning performance can be significantly improved using Trans-CLIME. This demonstrates the gain of transfer learning in estimating the graphical models.

Remark 2.2 (Faster convergence rate in a restricted regime).

Assume Condition 2.1. Let the Trans-CLIME estimator $\widehat{\mathrm{\Omega }}$ be computed with

$${\lambda }_{\mathrm{\Delta }}=c_1\sqrt{\frac{\log p}{n}}\text{and}{\lambda }_{\mathrm{\Theta }}=c_1\sqrt{\frac{\log p}{N}},$$

where c₁ is a large enough constant. If p ≥ c₂N and s² log p ≤ c₃n for some positive constants c₂ and c₃, then for any true models in ${\mathbb{G}}_1(s,h)$, we have

$$\mathbb{E}\left[\frac{1}{p}\Vert \widehat{\mathrm{\Omega }}-\mathrm{\Omega }{\Vert }_F^2\vee \Vert {\widehat{\mathrm{\Omega }}}_j-{\mathrm{\Omega }}_j{\Vert }_2^2\right]\le C\left(\frac{s\log p}{N+n}+{\delta }_h\wedge \frac{s\log p}{n}+\frac{1}{n}\right)$$ (15)

for any fixed 1 ≤ j ≤ p and some positive constant C.

In Remark 2.2, we prove another convergence rate of Trans-CLIME when s² log p ≲ n. Its difference from (14) is that δ_h,Ω is replaced by δ_h in (15). Hence, the convergence rate in (15) is sharper than the rate in (14) when max{∥Ω∥_∞,1, h} grows to infinity and is of the same order of the rate in (14) when max{∥Ω∥_∞,1, h} is finite. However, the condition on s in Remark 2.2 is stronger than the one assumed in Theorem 2.1 and it is indeed the same as the requirement in the single-task problems (Cai et al., 2016; Liu and Wang, 2017). In fact, we will show in Section 5.1 that the minimax lower bound in Frobenius norm is s log p / (N + n) + δ_h ˄ (s log p / n) for the current parameter space. The convergence rate of Trans-CLIME in (15) has one more term 1 / n, which is the cost when the relative magnitude of h and s is unknown a priori. In most nontrivial parameter spaces, Trans-CLIME enjoys minimax optimality when s² log p ≤ c₀n or when max{∥Ω∥_∞,1, h} is finite.

3. Entry-wise inference

We propose in this section a debiasing procedure for inference of individual entries in the graph. The main features of our proposal are its flexibility to couple with a broad range of initial graph estimators and its computational efficiency. We first introduce a universal debiasing method and study its theoretical guarantees in Section 3.1. We will then use it for the construction of confidence intervals in the transfer learning setting in Section 3.2.

3.1. A universal debiasing method

Our procedure on inference for Ω_i,j is inspired by the idea of debiasing quadratic forms. We begin by expressing Ω_i,j as a quadratic form:

$${\mathrm{\Omega }}_{i,j}={\mathrm{\Omega }}_i^{\top }\mathrm{\Sigma }{\mathrm{\Omega }}_j={\mathrm{\Omega }}_i^{\top }\mathbb{E}\left[{\mathrm{\Sigma }}^n\right]{\mathrm{\Omega }}_j,$$ (16)

where Σⁿ denotes the sample covariance matrix based on the target data. In many occasions, Σⁿ can be computed based on all the target data. Sometimes for a sharp theoretical analysis, sample splitting is performed and Σⁿ can be computed based on a constant proportion of the target data. We call the samples involved in Σⁿ the debiasing samples. Equation (16) holds for any inverse covariance matrix Ω not restricting to Gaussian random graphs.

Leveraging (16), we are able to use the idea of debiasing quadratic forms (Cai and Guo, 2020) to make inference for Ω_i,j. Specifically, Ω_i,j takes the same format as the co-heritability if we view Ω_i and Ω_j as the regression coefficient vectors for two different outcomes and view X as the measurements of genetic variants. Motivated by this observation, we arrive at the following debiased estimator of Ω_i,j. Let ${\widehat{\mathrm{\Omega }}}^{(init)}$ be any initial estimator of Ω. The corresponding debiased estimator is

$$\begin{array}{l}{\stackrel{\circ }{\mathrm{\Omega }}}_{i,j}^{(db)}={({\widehat{\mathrm{\Omega }}}_i^{(init)})}^{\top }{\mathrm{\Sigma }}^n{\widehat{\mathrm{\Omega }}}_j^{(init)}+{({\widehat{\mathrm{\Omega }}}_i^{(init)})}^{\top }(e_j-{\mathrm{\Sigma }}^n{\widehat{\mathrm{\Omega }}}_j^{(init)})+{({\widehat{\mathrm{\Omega }}}_j^{(init)})}^{\top }(e_i-{\mathrm{\Sigma }}^n{\widehat{\mathrm{\Omega }}}_i^{(init)})\\ ={\widehat{\mathrm{\Omega }}}_{j,i}^{(init)}+{\widehat{\mathrm{\Omega }}}_{i,j}^{(init)}-{({\widehat{\mathrm{\Omega }}}_j^{(init)})}^{\top }{\mathrm{\Sigma }}^n{\widehat{\mathrm{\Omega }}}_i^{(init)}.\end{array}$$ (17)

We mention that ${\widehat{\mathrm{\Omega }}}^{(init)}$ is not necessarily symmetric and hence we distinguish ${\widehat{\mathrm{\Omega }}}_{i,j}^{(init)}$ and ${\widehat{\mathrm{\Omega }}}_{i,j}^{(init)}$. It is easy to see that the above debiasing procedure can be coupled with any ${\widehat{\mathrm{\Omega }}}^{(init)}$ which has a sufficiently fast convergence rate in column-wise ℓ₂-norm. Hence, the candidate estimators for debiasing include, say, graphical Lasso (Friedman et al., 2008), CLIME (Cai et al., 2011), multi-task graph estimators (Guo et al., 2011; Danaher et al., 2014; Cai et al., 2016), and our proposed Trans-CLIME. In comparison to Liu (2013) and Ren et al. (2015), where the debiased estimators are constructed using ℓ₁ -penalized node-wise regression, our proposal in (17) is more flexible in incorporating various types of initial estimators under different structural assumptions. To the best of our knowledge, ${\stackrel{\circ }{\mathrm{\Omega }}}^{(db)}$ is the first universal debiasing method for graph estimators.

Besides the general applicability, our debiased estimator for the whole graph can be analytically computed in one step given the initial graph estimator ${\widehat{\mathrm{\Omega }}}^{(init)}$. Specifically, the debaised estimator in (17) can be re-expressed as

$${\stackrel{°}{\mathrm{\Omega }}}^{(db)}={\widehat{\mathrm{\Omega }}}^{(init)}+{({\widehat{\mathrm{\Omega }}}^{(init)})}^{\top }-{({\widehat{\mathrm{\Omega }}}^{(init)})}^{\top }{\mathrm{\Sigma }}^n{\widehat{\mathrm{\Omega }}}^{(init)}.$$

To demonstrate the power of this universal debiasing method, we first prove the asymptotic normality for the debiased single-task CLIME estimator, which is

$${\widehat{\mathrm{\Omega }}}_{i,j}^{(\text{db}-\text{CL})}={\widehat{\mathrm{\Omega }}}_{j,i}^{(\text{CL})}+{\widehat{\mathrm{\Omega }}}_{i,j}^{(\text{CL})}-{({\widehat{\mathrm{\Omega }}}_j^{(\text{CL})})}^{\top }\widehat{\mathrm{\Sigma }}{\widehat{\mathrm{\Omega }}}_i^{(\text{CL})},$$

where $\widehat{\mathrm{\Sigma }}$ is defined in (8).

Proposition 3.1 (Asymptotic normality for debiased CLIME).

Assume Condition 2.1 and $s\log p\ll \sqrt{n}$. For any fixed i ≠ j,

$$\frac{\sqrt{n}\left({\widehat{\mathrm{\Omega }}}_{i,j}^{(\text{db}-\text{CL})}-{\mathrm{\Omega }}_{i,j}\right)}{\sqrt{V_{i,j}}}\stackrel{D}{\to }N(0,1)$$

for $V_{i,j}={\mathrm{\Omega }}_{i,i}{\mathrm{\Omega }}_{j,j}+{\mathrm{\Omega }}_{i,j}^2$.

The asymptotic normality of ${\widehat{\mathrm{\Omega }}}_{i,j}^{(\text{db}-\text{CL})}$ requires that $s\log p\ll \sqrt{n}$. The condition and the asymptotic distribution in Proposition 3.1 recover the results in Ren et al. (2015) and ${\widehat{\mathrm{\Omega }}}_{i,j}^{(\text{db}-\text{CL})}$ is indeed minimax optimal in ${\mathbb{G}}_q(s,\infty )$ for estimating Ω_i,j. This demonstrates the optimality of this universal debiasing method.

3.2. Entry-wise confidence intervals based on transfer learning

Applying the universal debiasing scheme to the Trans-CLIME estimator $\widehat{\mathrm{\Omega }}$, we arrive at the following debiased Trans-CLIME estimator for Ω_i,j

$${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}={\widehat{\mathrm{\Omega }}}_{j,i}+{\widehat{\mathrm{\Omega }}}_{i,j}-{\widehat{\mathrm{\Omega }}}_j^{\top }\tilde{\mathrm{\Sigma }}{\widehat{\mathrm{\Omega }}}_i.$$ (18)

In (18), we only use a proportion of target data, i.e., those involved in $\tilde{\mathrm{\Sigma }}$, as debiasing samples, while the realization of $\widehat{\mathrm{\Omega }}$ involves both target and auxiliary samples. This is because first, only the target data are known to be unbiased; second, the samples involved in $\tilde{\mathrm{\Sigma }}$ has mild dependence on $\widehat{\mathrm{\Omega }}$ which is induced by the aggregation step and it allows us to prove the desirable convergence rate. Ideally, one can use some debiasing samples independent of $\widehat{\mathrm{\Omega }}$, which can be achieved through another sample splitting. In practice, sample splitting always leads to sub-optimal empirical performance and hence we analyze (18) and take care of the dependence through careful analysis.

Theorem 3.1 (Asymptotic normality for debiased Trans-CLIME).

Assume Condition 2.1 and the sample size condition stated in (20). For any true models in G₁(s,h) and any fixed 1 ≤ i, j ≤ p the debiased Trans-CLIME satisfies

$$\frac{\sqrt{\tilde{n}}\left({\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}-{\mathrm{\Omega }}_{i,j}\right)}{\sqrt{V_{i,j}}}\stackrel{D}{\to }N(0,1).$$ (19)

In Theorem 3.1, we establish the asymptotic normality of ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$. We now discuss the improvement in the convergence rates with transfer learning. For the asymptotic normality to hold, one requires the sparsity condition that

$$\{\begin{array}{ll}s\log p=o(N/\sqrt{n})\text{and}{\delta }_{h,\mathrm{\Omega }}=o\left(n^{-1/2}\right)\hfill & \text{if}{\delta }_{h,\mathrm{\Omega }}\le s\log p/n\hfill \\ s\log p=o(\sqrt{n})\hfill & \text{otherwise}.\hfill \end{array}$$ (20)

In comparison, the sparsity condition given by the minimax rate in single-task setting is $s\log p=o(\sqrt{n})$ (Proposition 3.1). We see that the sparsity condition in (20) is weaker when δ_h,Ω ≪ s log p / n and N ≫ n. Specifically, if the similarity is sufficiently high, i.e., δ_h,Ω ≤ s log p / n, then transfer learning relaxes the sparsity condition for asymptotic normality from $s\log p\ll \sqrt{n}$ to $s\log p\ll N/\sqrt{n}$. This relaxation is significant as the regime $s\log p\ll \sqrt{n}$ is known as the “ultra-sparse” regime and is very restrictive when n is small. When N ≫ n, which is not hard to satisfy in many applications, the condition on s is largely relaxed for valid inference. Another way of interpreting (20) is that inference based on Trans-CLIME requires weaker sparsity conditions as long as $\widehat{\mathrm{\Omega }}$ has a smaller estimation error than the single-task CLIME. The minimax optimality of debiased Trans-CLIME is studied in Section 5.2.

Next, we introduce an estimator for the variance of ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$, which is

$${\widehat{V}}_{i,j}={\widehat{\mathrm{\Omega }}}_{i,i}{\widehat{\mathrm{\Omega }}}_{j,j}+{\widehat{\mathrm{\Omega }}}_{i,j}{\widehat{\mathrm{\Omega }}}_{j,i}.$$ (21)

The variance estimator ${\widehat{V}}_{i,j}$ is based on the limiting distribution of ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ given that the observations are Gaussian distributed.

Lemma 3.1 (Consistency of variance estimator).

Under the conditions of Theorem 3.1, the variance estimator defined in (21) satisfies

$$\left|{\widehat{V}}_{i,j}-V_{i,j}\right|=o_P(1)$$

and hence

$$\frac{\sqrt{\tilde{n}}\left({\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}-{\mathrm{\Omega }}_{i,j}\right)}{\sqrt{{\widehat{V}}_{i,j}}}\stackrel{D}{\to }N(0,1).$$ (22)

Based on Lemma 3.1, a 100 × (1 − α)% two-sided confidence interval for Ω_i,j is ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}\pm z_{1-\alpha /2}{\left({\widehat{V}}_{i,j}/\tilde{n}\right)}^{1/2}$.

We examine the empirical performance of this inference method in Section 6.

4. Edge detection with FDR control

An important task regarding the graphical models is edge detection with uncertainty quantification. That is, we consider testing (H₀)_i,j :Ω_i,j = 0 1 ≤ i < j ≤ p. This is a multiple testing problem with m = p(p−1)/2 hypotheses to test in total. For the uncertainty quantification, we consider the false discovery proportion (FDP) and false discovery rate (FDR). Let $\mathcal{R}$ denote the set of rejected null hypotheses. The FDP and FDR are defined as, respectively,

$$\mathrm{FDP}(\mathcal{R})=\frac{\sum _{(i,j)\in \mathcal{R}}1\left((i,j)\in {\mathcal{H}}_0\right)}{\left|\mathcal{R}\right|\vee 1}\text{and}\mathrm{FDR}(\mathcal{R})=\mathbb{E}[\mathrm{FDP}(\mathcal{R})],$$

where ${\mathcal{H}}_0$ is the set of true nulls. Many algorithms have been proposed and studied for FDR and FDP control in various settings. Especially, Liu (2013) proposes an FDR control algorithm for GGMs that can be easily combined with our proposed debiased estimator. The procedure is presented as Algorithm 2.

Algorithm 2: Edge detection with FDR control at level α

Input : ${\left\{{\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}\right\}}_{i<j}$, ${\left\{{\widehat{V}}_{i,j}\right\}}_{i<j}$ and FDR level α

Output: A set of selected edges $\mathcal{R}$

Step 1. For 1 ≤ i < j ≤ p, let ${\widehat{z}}_{i,j}={\widehat{V}}_{i,j}^{-1/2}\sqrt{\tilde{n}}{\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$, where ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ and ${\widehat{V}}_{i,j}$ are defined in (18) and (21), respectively.

Step 2.

$$\widehat{t}=\inf \left\{t\in [0,\sqrt{2\log m-2\log \log m}]:\frac{2m(1-\text{Φ}(t))}{\max \{\sum _{1\le i<j\le p}1\left(\left|{\widehat{z}}_{i,j}\right|\ge t\right),1\}}\le \alpha \right\}.$$ (23)

If (23) does not exist, we set $\widehat{t}=\sqrt{2\log m}$.

Step 3. The rejected hypotheses are

$$\mathcal{R}=\left\{(i,j):\left|{\widehat{z}}_{i,j}\right|\ge \widehat{t},1\le i<j\le p\right\}.$$

Let $m_0=\left|{\mathcal{H}}_0\right|$ denote the cardinality of ${\mathcal{H}}_0$ and m = (p² − p) / 2 denote the total number of hypotheses to test. Define a subset of random variables “highly” correlated with the i-th variable ${\mathcal{C}}_i(\gamma )=\left\{j:1\le j\le p,j\ne i,\left|{\mathrm{\Omega }}_{i,j}\right|\ge {(\log p)}^{-2-\gamma }\right\}$.

Theorem 4.1 (FDR control).

Let p ≤ n^r for some r > 0 and m₀ ≥ cp² for some c > 0. Assume that Condition 2.1 holds and the true model is in G₁ (s, h). Suppose that

$$s{(\log p)}^{3/2}\ll N/\sqrt{n},{\delta }_{h,\mathrm{\Omega }}\wedge s\log p/n\ll {(n\log p)}^{-1/2},$$

and ${\max }_{1\le i\le p}\left|{\mathcal{C}}_i(\gamma )\right|=O\left(p^{\rho }\right)$ for some ρ < 1 / 2 and γ > 0. We have $\underset{(n,p)\to \infty }{\lim }\frac{\mathrm{FDR}(\mathcal{R})}{\alpha m_0/m}=1$ and $\frac{\text{FDP}(\mathcal{R})}{\alpha m_0/m}\to 1$ in probability as (n, p) → ∞.

Theorem 4.1 implies that Algorithm 2 can asymptotically control FDR and FDP at nominal level under certain conditions. The sample size condition in Theorem 4.1 guarantees that the remaining bias of ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ is uniformly o_P ((nlog p)^−1/2). The condition on the cardinality of ${\mathcal{C}}_i(\gamma )$ guarantees that the z-statistics have mild correlations such that the FDR control is asymptotically valid.

5. Minimax optimal rates for q ∈[0,1]

In this section, we establish the minimax lower bounds for estimation and inference of GGMs in the parameter space ${\mathbb{G}}_q(s,h)$ for any fixed q ∈[0,1]. We provide matching minimax upper bounds in the supplements (Section C.3 and Section C.4).

5.1. Optimal rates under Frobenius norm

Theorem 5.1 (Minimax lower bounds under Frobenius norm).

Assume Condition 2.1 and 3 < s log p < c₁N for some small constant c₁. (i) For q = 0, if h log p ≤ c₂n for some small enough constant c₂, then for some positive constant C₁,

$$\underset{\widehat{\mathrm{\Omega }}}{\inf }\underset{{\mathbb{G}}_0(s,h)}{\sup }\mathbb{E}\left[\frac{1}{p}\Vert \widehat{\mathrm{\Omega }}-\mathrm{\Omega }{\Vert }_F^2\right]\ge C_1\left\{\frac{s\log p}{N+n}+(h\wedge s)\frac{\log p}{n}\right\}.$$

(ii) For any fixed q ∈(0,1], if h^q(log p / n)^1−q/2 ≤ c₃ for some small enough constant c₃, then there are some positive constants C₂ such that

$$\underset{\widehat{\mathrm{\Omega }}}{\inf }\underset{{\mathbb{G}}_q(s,h)}{\sup }\mathbb{E}\left[\frac{1}{p}\Vert \widehat{\mathrm{\Omega }}-\mathrm{\Omega }{\Vert }_F^2\right]\ge C_2\left\{\frac{s\log p}{N+n}+h^q{\left(\frac{\log p}{n}\right)}^{1-q/2}\wedge h^2\wedge \frac{s\log p}{n}\right\}.$$

Theorem 5.1 establishes the minimax optimal rates under Frobenius norm. These lower bounds generalize the existing lower bound in ${\mathbb{G}}_q(s,\infty )$ (Cai et al., 2016) to allow for arbitrarily small h. According to the discussion at the end of Section 2, the Trans-CLIME is minimax optimal with respect to Frobenius norm in most parameter spaces of interest when s² log p ≤ c₀n or when max{∥Ω∥_∞,1, h} is finite. In fact, the only difference of the rate in (15) and the minimax lower bound is the cost of aggregation, which is of order 1 / n. We mention that the estimator which achieves the minimax upper bounds depends on the relative magnitude of h and s and hence is not adaptive. In comparison, the Trans-CLIME estimator does not depends on the unknown parameters and only has a small inflation term.

5.2. Optimal rates for estimating Ω_i,j

Theorem 5.2 (Minimax lower bounds for estimating [INEQ-START). Ω_i,j] Assume Condition 2.1 and 3 < s < c₁ min{p^v, N / log p} for some small constant c₁ > 0 and v < 1/ 2. (i) For q = 0, if 1 ≤ h log p ≤ c₂n for some small enough constant c2, then for some constant C₁ > 0,

$$\underset{\widehat{\mathrm{\Omega }}}{\inf }\underset{{\mathbb{G}}_0(s,h)}{\sup }\mathbb{P}\left(\left|{\widehat{\mathrm{\Omega }}}_{i,j}-{\mathrm{\Omega }}_{i,j}\right|\ge C_1\left\{n^{-1/2}+\frac{s\log p}{N+n}+(h\wedge s)\frac{\log p}{n}\right\}\right)>1/4.$$

(ii) For any fixed q ∈(0,1], if h^q (log p / n)^1−q/2 <c3 for some small enough constant c₃, then

$$\underset{\widehat{\mathrm{\Omega }}}{\inf }\underset{{\mathbb{G}}_q(s,h)}{\sup }\mathbb{P}\left(\left|{\widehat{\mathrm{\Omega }}}_{i,j}-{\mathrm{\Omega }}_{i,j}\right|\ge C_3\left\{R_q+\frac{s\log p}{N+n}+h^q{\left(\frac{\log p}{n}\right)}^{1-q/2}\wedge h^2\wedge \frac{s\log p}{n}\right\}\right)>1/4,$$

where C₃ is a positive constant and R_q = (N + n)^−1/2 + n^−1/2 ⋀ h.

Theorem 5.2 establishes the minimax lower bound for estimating each entry in the graph. These lower bounds are related to the sparsity conditions in Theorem 3.1. They generalize the existing lower bound in ${\mathbb{G}}_q(s,\infty )$ (Ren et al., 2015) to allow for finite h. When q = 0, the parametric rate is n^−1/2, which is the same as in the single-task setting. When q ∈(0,1], the parametric rate is R_q and the rest terms are the remaining bias. We now illustrate this bound in detail with q = 1.

For q = 1, the minimax optimal rate can be achieved by ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ when max{h,∥Ω∥_∞,1} ≤ C and h ≳ n^−1/2. See (15) in the supplements for more details. When h ≪ n^−1/2, a minimax optimal estimator is debiased (single-task) CLIME using X and X^(k),1 ≤ k ≤ K, as debiasing samples. In the scenario h ≪ n^−1/2, the auxiliary studies are very similar to the target study and using N + n debiasing samples can have faster parametric rate, (n + N)^−1/2, with bias no larger than h. However, the central limit theory may not hold for the rate optimal estimator when h ≪ n^−1/2. This is because the parametric rate is dominated by the bias h when (n + N)^−1/2 ≲ h ≲ n^−1/2. In contrast, ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ has parametric rate n^−1/2 and its asymptotic normality holds for arbitrarily small h under the conditions of Theorem 3.1. Hence, ${\widehat{\mathrm{\Omega }}}_{i,j}^{(db)}$ is a proper choice for statistical inference.

6. Numerical experiments

We evaluate the numerical performance of our proposal and other comparable methods. We set n = 150, p = 200, K = 5, and n_k = 300 for k = 1,…,K. We consider three types of target graph Ω.

1. Banded matrix with bandwidth 8. For 1 ≤ i, j ≤ p, Ω_i,j = 2 × 0.6^|i−j|1 (|i−j|≤ 7).

2. Block diagonal matrix with block size 4, where each block is Toeplitz (1.2,0.9,0.6,0.3).

3. Define ${\stackrel{\circ }{\mathrm{\Omega }}}_{i,j}=1(i=j)+u_{i,j}/\sqrt{|i-j|+1}$, where μ_i,j are independently generated from a uniform distribution with range [0, 0.8]. We threshold $\left(\stackrel{°}{\mathrm{\Omega }}+{\stackrel{°}{\mathrm{\Omega }}}^{\top }\right)/2$ such that only the first s largest values in each column and each row of $\left(\stackrel{°}{\mathrm{\Omega }}+{\stackrel{°}{\mathrm{\Omega }}}^{\top }\right)/2$ are kept. A diagonal matrix is added to guarantee that the minimum eigenvalue of the target graph is at least 0.1.

To accommodate the practical setting that some auxiliary studies can be very far from the target study, we define a set $\mathcal{A}\subseteq \{1,\dots ,K\}$ to be the set of informative studies. Specifically, for each setting in (i) or (ii), we generate Δ^(k) in two ways. For $k\in \mathcal{A}$, ${\mathrm{\Delta }}_{i,j}^{(k)}$ is zero with probability 0.9 and is nonzero with probability 0.1. If an entry is nonzero, it is randomly generated from U[−r / p, r / p] for r ∈{10,20,30}. For Ω^(k), $k\notin \mathcal{A}$, we generate ${\mathrm{\Delta }}_{i,j}^{(k)}=0.51(i=j)+{\xi }_{i,j}$, where ξ_i,j is zero with probability 0.7 and is 0.4 with probability 0.3. In fact, ${\mathcal{D}}_1\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)\approx 15$ for $k\in \mathcal{A}$ and ${\mathcal{D}}_1\left({\mathrm{\Omega }}^{(k)},\mathrm{\Omega }\right)\approx 80$ for $k\notin \mathcal{A}$ and hence the studies not in $\mathcal{A}$ are relatively far away from the target Ω. For k = 1,…,K, we symmetrize Ω^(k) and if Ω^(k) is not positive definite, we redefine Ω^(k) to be its positive definite projection.

We compare four methods in each experiment. The first one is the proposed Trans-CLIME. The second one is the single-task CLIME that only uses the data from the target study. The third one applies Trans-CLIME to the target study and informative auxiliary studies, denoted by “oracle Trans-CLIME”. Here “oracle” indicates that it leverages the knowledge of oracle $\mathcal{A}$. The fourth one is multi-task graphical lasso (Guo et al., 2011), shorthanded as “MT-Glasso”. For the choice of tuning parameters, we consider ${\lambda }_{\text{CL}}=2c_n\sqrt{\log p/n}$ for CLIME. We pick c_n to minimize the prediction error defined in (24) based on five fold cross-validation. For the Trans-CLIME, we set ${\lambda }_{\mathrm{\Delta }}=2{\Vert {\widehat{\mathrm{\Omega }}}^{(\text{CL})}\Vert }_1\sqrt{\log p/n}$ and ${\lambda }_{\mathrm{\Theta }}=2c_n\sqrt{\log p/N}$ where c_n is the same as in the CLIME optimization. For the oracle Trans-CLIME, the tuning parameters are set in the same way as in Trans-CLIME except that N is replaced by $\sum _{k\in \mathcal{A}}{n}_k$. For Trans-CLIME-based methods, we split the target data into two folds such that ${\widehat{\mathrm{\Omega }}}^{(\text{CL})}$ and $\widehat{\mathrm{\Theta }}$ are computed based on 4n / 5 samples and the aggregation step (Step 3) is based on the rest n / 5 samples. For the debiased Trans-CLIME, we use all the target data as debiasing samples as it has a better empirical performance. For “MT-Glasso”, we implement and choose the tuning parameter based on Bayesian information criterion according to Section 2.3 and Section 2.4 of Guo et al. (2011). The R code for the four methods is available at https://github.com/saili0103/TransCLIME.

6.1. Estimation and prediction results

We evaluate the estimation performance in Frobenius norm and prediction performance based on the negative log-likelihood. Specifically, we generate $x_i^{(test)}~N(0,\mathrm{\Sigma })$ for i = 1,…,n_test = 100 and $x_i^{(test)}$ are independent of the samples for estimation. We evaluate the out-of-sample prediction error of an arbitrary graph estimator ${\widehat{\mathrm{\Omega }}}^{(init)}$ in the following way. We symmetrize ${\widehat{\mathrm{\Omega }}}^{(init)}$ and compute the positive definite projection of the symmetrized ${\widehat{\mathrm{\Omega }}}^{(init)}$, denoted by ${\widehat{\mathrm{\Omega }}}_{+}^{(init)}$. The prediction error of ${\widehat{\mathrm{\Omega }}}^{(init)}$ is evaluated via

$$\widehat{Q}({\widehat{\mathrm{\Omega }}}^{(init)})=\frac{1}{p}\left\{\frac{1}{2n_{\text{test}}}\sum _{i=1}^{n_{\text{test}}}\mathrm{Tr}(x_i^{(test)}{(x_i^{(test)})}^{\top }{\widehat{\mathrm{\Omega }}}_{+}^{(init)})-\frac{1}{2}\log det({\widehat{\mathrm{\Omega }}}_{+}^{(init)})\right\}.$$ (24)

In Figure 1, we report the estimation and prediction performance in setting (i). As the number of informative auxiliary studies increases, the estimation errors of two Trans-CLIME-based methods decrease. As r increases, the estimation errors of two Trans-CLIME-based methods increase. The oracle Trans-CLIME has a faster convergence rate than the Trans-CLIME. This is because $K-|\mathcal{A}|$ non-informative studies are used in the Trans-CLIME, which affects the convergence rates. Nevertheless, we see that the Trans-CLIME algorithm is robust to the non-informative auxiliary studies as its performance is always not much worse than the single-task CLIME. The estimation and prediction results for settings (ii) and (iii) are reported in the supplements (Section E.2). We have observed similar patterns in those settings.

Fig. 1.

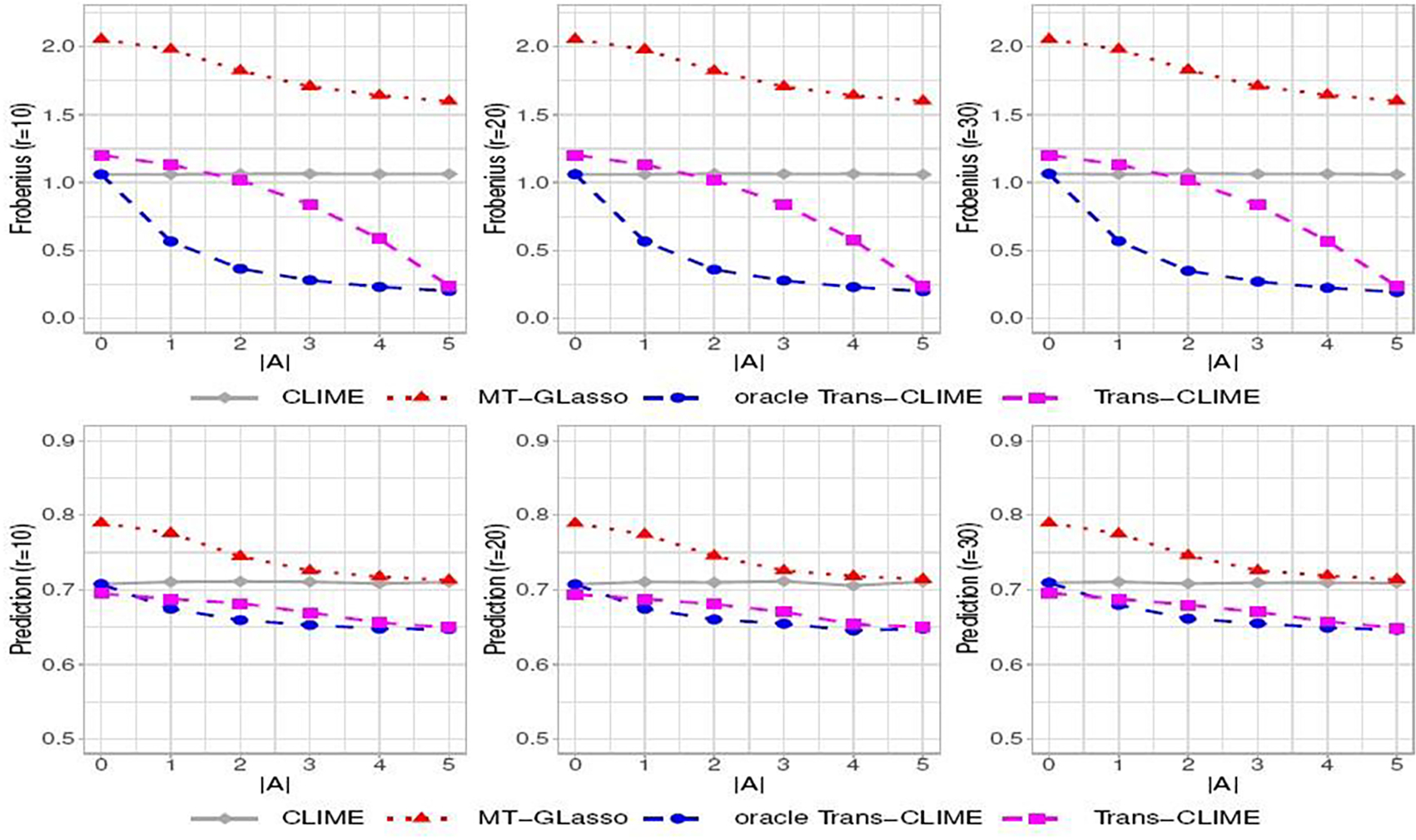
Estimation errors in Frobenius norm (first row) and negative log-likelihood (second row) for banded Ω (i) as a function of the number of informative studies (out of a total of K = 5 studies) for different values of r.

6.2. Sample complexity

We further evaluate the dependence of the estimation errors in Frobenius norm on the target sample size n, the total auxiliary sample size N, and the sparsity s. We consider the random graph (iii) that has more flexibility in varying s and present the results in Figure 2. We see that the estimation errors of single-task CLIME decrease fast as the target sample size increases. The errors of oracle Trans-CLIME, and Trans-CLIME also decrease as the target sample size increases but not in a large amount. In other words, the improvement of transfer learning becomes smaller as n increases when auxiliary samples are informative. This aligns with our theoretical results as we demonstrate the significant gain of transfer learning when N ≫ n. As the total auxiliary sample size N increases, errors of the oracle Trans-CLIME and Trans-CLIME decrease linearly but the errors of CLIME do not change (middle plot of Figure 2). This agrees with our theoretical findings in Theorem 2.1 and Remark 2.1. Finally, all the methods have estimation errors increase with the sparsity parameter s with an approximately linear trend.

Fig. 2.

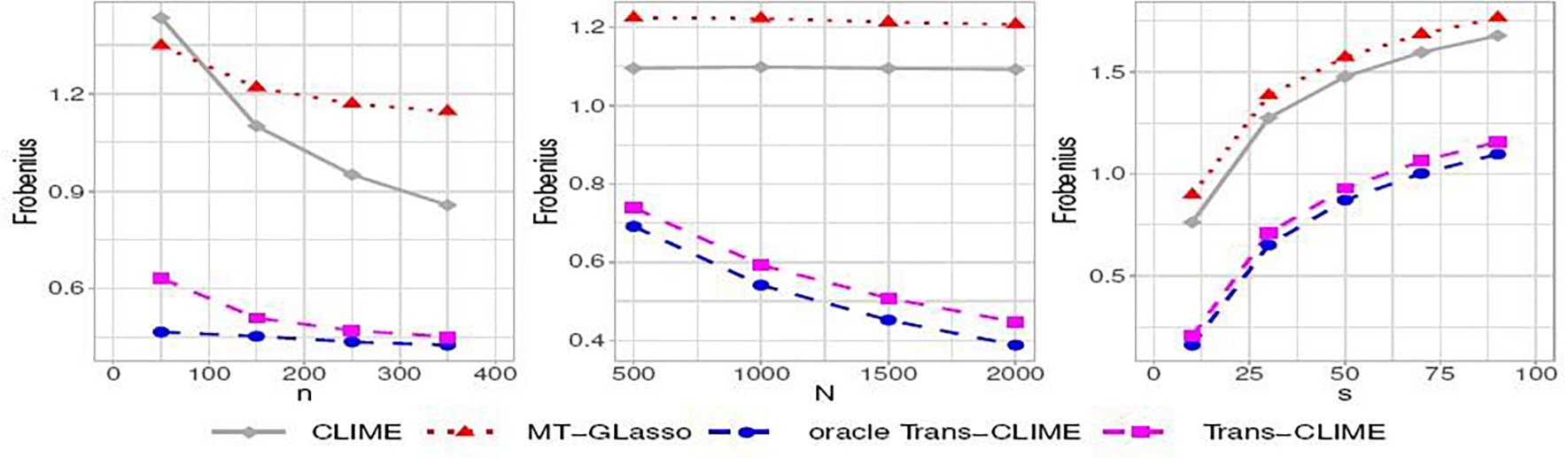
Estimation errors in Frobenius norm for random Ω (iii) with varying target sample size n (left), total auxiliary sample size N (middle), and the sparsity s (right). The default setting is p = 200, n = 150, N = 1500, s = 20, r = 20, and $\mathcal{A}=\{1,\dots ,K\}$. In each plot, all the parameters are fixed at default values except the parameter indexed by the x-axis.

6.3. FDR control

We then consider FDR control at level α = 0.1 based on the debiasing method introduced in Section 3. From Figure 3, we see that all three debiased estimators have empirical FDR no larger than the nominal level in setting (i). In terms of power, the Trans-CLIME and oracle Trans-CLIME have higher power when $\mathcal{A}$ is nonempty. We observe the robustness of Trans-CLIME in the sense that the FDR is under control even if non-informative studies are included. The multiple testing results for settings (ii) and (iii) are reported in the supplements (Section D.2). We observe that the power curves in setting (ii) are the highest in comparison to the other two settings. This is because the nonzero entries in the target graph have the largest magnitude in setting (ii).

Fig. 3.

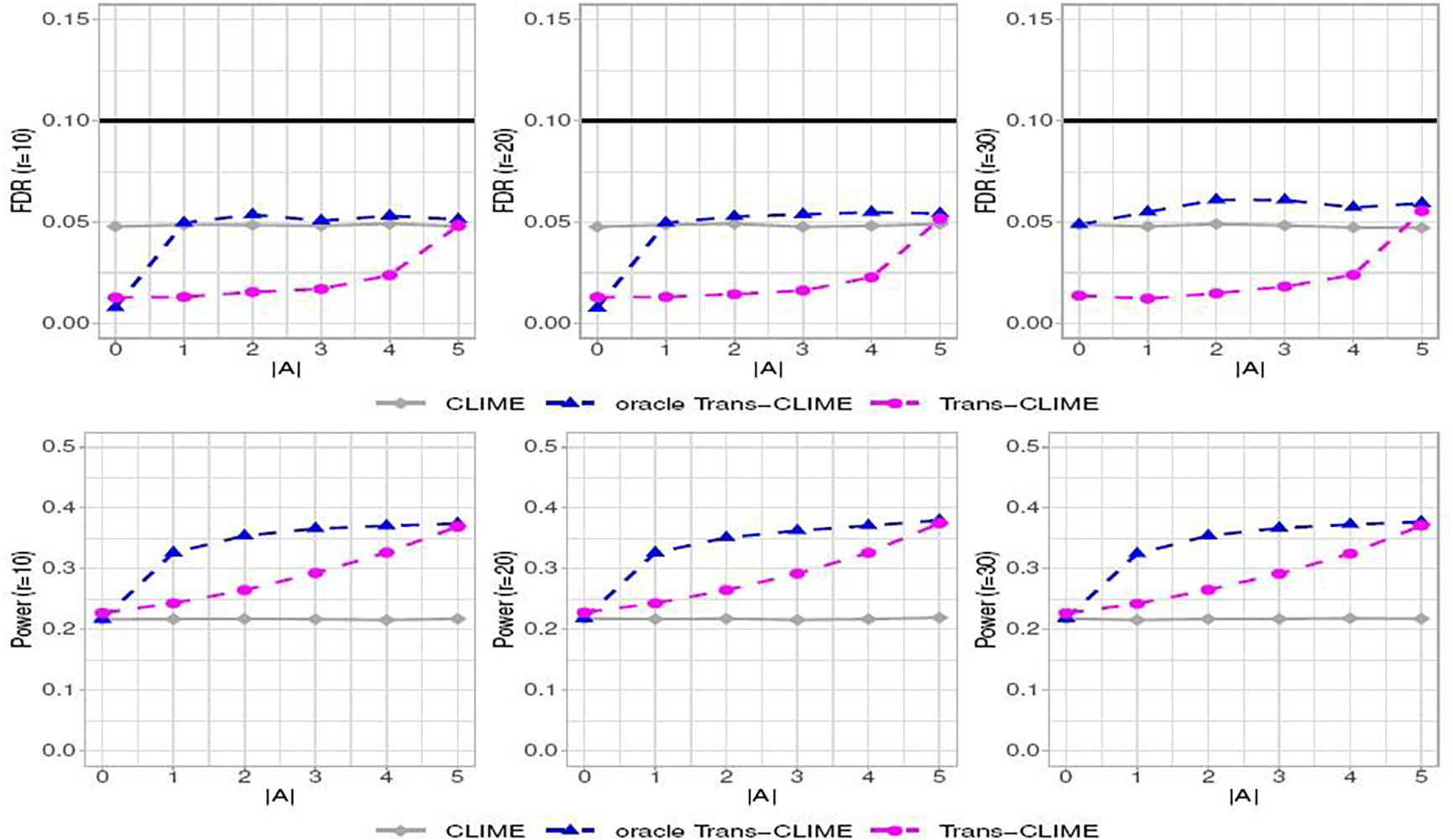
The FDR and power at nominal level 0.1 as a function of the number of informative studies (out of K = 5) and r for banded Ω (i). The methods in comparison are debiased as in Section 3.

7. Gene network estimation in multiple tissues

In this section, we apply our proposed algorithms to detect gene networks in different tissues using the Genotype-Tissue Expression (GTEx) data (https://gtexportal.org/). Overall, the data sets measure gene expression levels in 49 tissues from 838 human donors, comprising a total of 1,207,976 observations of 38,187 genes. We focus on genes related to central nervous system neuron differentiation, annotated as GO:0021953. This gene set includes a total of 184 genes. A complete list of the genes can be found at https://www.gsea-msigdb.org/gsea/msigdb/cards/GO_CENTRAL_NERVOUS_SYSTEM_NEURON_DIFFERENTIATION.

Our goal is to estimate and detect the gene network in a target brain tissue. Since we use 20% of the samples to compute test errors, the sample size for the target tissue should not be too small. We therefore consider each brain tissue with at least 100 samples as the target in each experiment. We use the data from multiple other brain tissues as auxiliary samples with K = 12. We remove the genes that have missing values in these 13 tissues, resulting in a total of 141 genes for the graph construction. The average sample size in each tissue is 115. A complete list of tissues and their sample sizes are given in the Supplementary Materials.

We apply CLIME and Trans-CLIME to estimate the graph among these 141 genes in multiple target brain tissues. We first compare the prediction performance of CLIME and Trans-CLIME, where we randomly split the samples of the target tissue into five folds. We fit the model with four folds of the samples and compute the prediction error with the rest of the samples. We report the mean of the prediction errors, each based on a different fold of the samples. The prediction errors are measured by the negative log-likelihood defined in (24).

The prediction results are reported in the left panel of Figure 4. We see that the prediction errors based on Trans-CLIME are significantly lower than those based on CLIME in many cases, indicating that the brain tissues in GTEx possess relatively high similarities in gene associations. On the other hand, these brain tissues are also heterogeneous in the sense that the improvements with transfer learning are significant in some tissues (e.g., A.C. cortex and F. cortex) and they are relatively mild in others (e.g., C. hemisphere and Cerebellum). We then apply Algorithm 2 with α = 0.1 to identify the connections among these genes. The proportion of detected edges are reported in the right panel of Figure 4. We see that the proportion of detected edges are relatively low, implying that the networks are sparse. The Trans-CLIME has more discoveries than CLIME in almost all the tissues in detecting the gene-gene links, agreeing with our simulation results. In Figure 5, we evaluate the similarities among the tissues based on the constructed graphs. Specifically, we examine the degrees of nodes in A.C. cortex in comparison to the degrees of nodes in the other nine tissues, all estimated using Trans-CLIME. We see that the degree distribution in A.C. cortex is relatively similar to the degree distributions in Cortex and F. cortex.

Fig. 4.

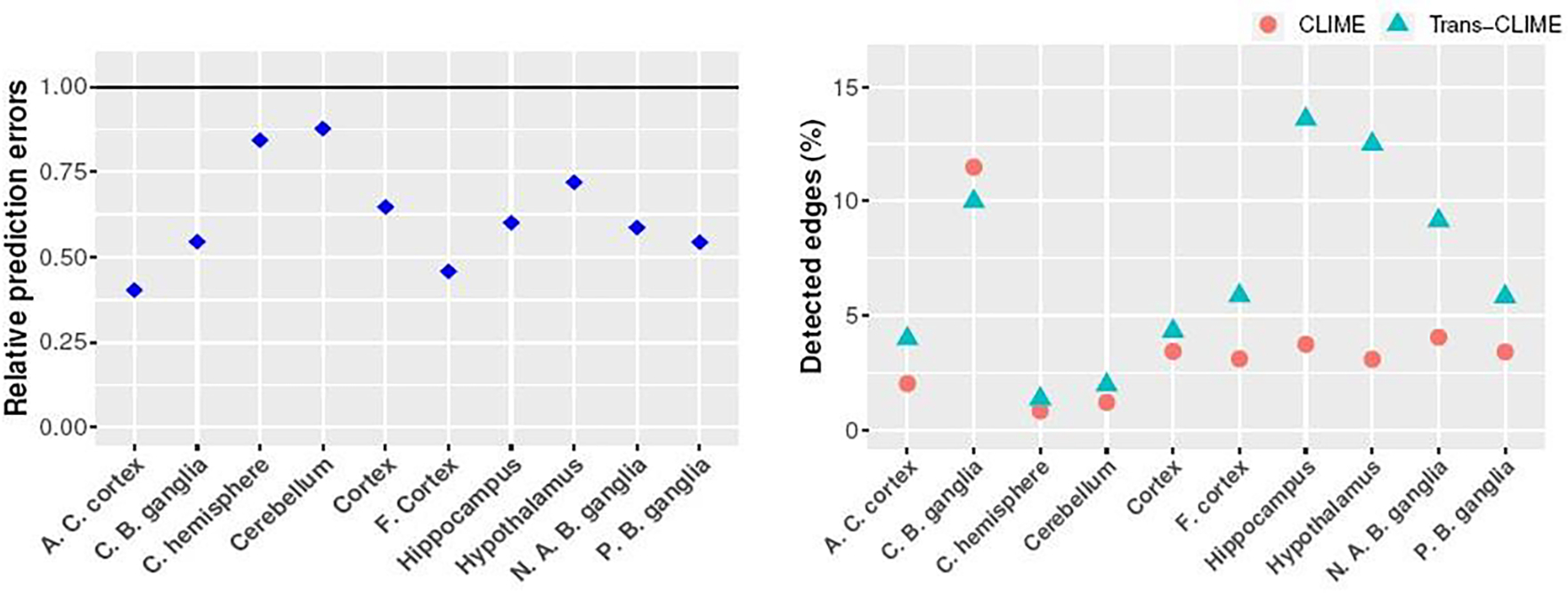
The left panel presents the prediction errors of Trans-CLIME relative to the prediction errors of CLIME for ten different target tissues. The right panel presents the number of detected edges divided by p(1 − p) using CLIME and Trans-CLIME with FDR=0.1. The full names of the target tissues are given in the supplementary files.

Fig. 5.

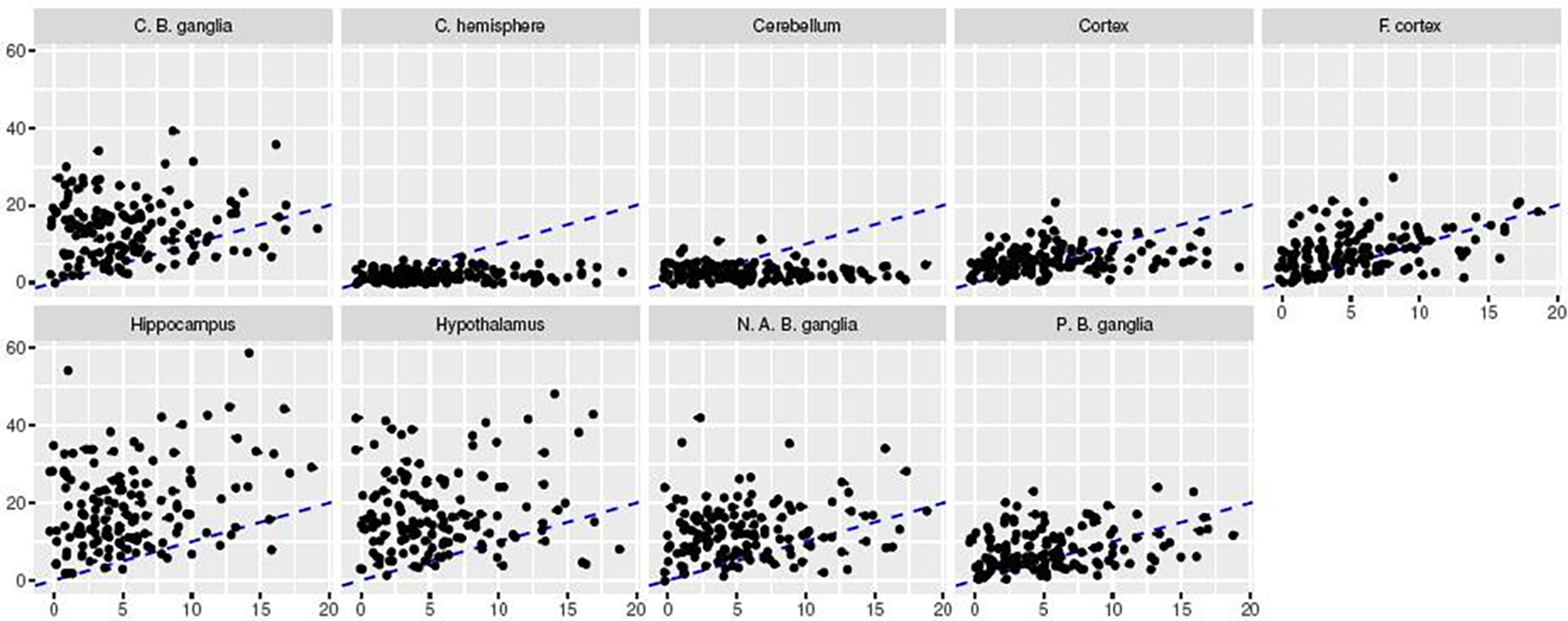
Comparison of the node degree distribution based on the graph estimated by Trans-CLIME for each of the tissue at FDR level of 10%. The x-axis represents the degrees of the nodes in A. C. cortex and the y-axis represents the degrees of the nodes in nine other tissues. The dashed line is diagonal.

In the Supplementary Material (Section E.1), we report the hubs detected by these two methods in different tissues and observe that many hubs appear more than once in different tissues based on the results of debiased Trans-CLIME, further demonstrating a certain level of similarity in gene regulatory networks among different brain tissues. For example, for A.C Cortex with Trans-CLIME, we are able to identify the hub genes SOX1, SHANK3, ATF5, and SEMA3A. These genes are either the known transcriptional factors (SOX1, ATF5) and have been shown to be related to neurological diseases, including the leading autism gene SHANK3 (Lutz et al., 2020) and gene-related to motor neurons in ALS patients (Sema3A) (Birger et al., 2018). In comparison, the graphs estimated using CLIME in single tissue are too sparse and do not reveal any of these hub genes.

8. Discussion

In this paper, we have studied the estimation and inference of Gaussian graphical models with transfer learning. Our proposed algorithm Trans-CLIME admits a faster convergence rate than the minimax rate in the single-task setting under mild conditions. The Trans-CLIME estimator can be further debiased for statistical inference.

We have seen in the numerical experiments that including some non-informative auxiliary studies can weaken the improvement of transfer learning. While our proposal is guaranteed to be no worse than the single-task minimax estimator, it may not be the most efficient way to use the auxiliary studies. A practical challenge in transfer learning is to find the best set of auxiliary studies such that the algorithm can gain the most from the auxiliary tasks. In the high-dimensional regression problem, Li et al. (2021) proposes to first rank all the auxiliary studies according to their similarities to the target and then perform a model selection aggregation. They prove that the aggregated estimator can be adapted to the informative set under certain conditions. In a more recent paper, Hanneke and Kpotufe (2020) proves that, loosely speaking, if the ranks of the auxiliary studies can be recovered, then performing empirical risk minimization in a cross-fitting manner can achieve adaptation to the informative set to some extent in some functional classes. For the high-dimensional GMMs, heuristic rank estimators can also be derived using their connections to linear models, based on which one can perform aggregation towards an adaptive estimator. However, theoretical analysis for such rank estimators may require strong conditions, especially in the high-dimensional setting. Hence, finding the best subset of auxiliary studies is an important topic for future research.