Estimating SARS-CoV-2 seroprevalence

Abstract

Governments and public health authorities use seroprevalence studies to guide responses to the COVID-19 pandemic. Seroprevalence surveys estimate the proportion of individuals who have detectable SARS-CoV-2 antibodies. However, serologic assays are prone to misclassification error, and non-probability sampling may induce selection bias. In this paper, non-parametric and parametric seroprevalence estimators are considered that address both challenges by leveraging validation data and assuming equal probabilities of sample inclusion within covariate-defined strata. Both estimators are shown to be consistent and asymptotically normal, and consistent variance estimators are derived. Simulation studies are presented comparing the estimators over a range of scenarios. The methods are used to estimate severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) seroprevalence in New York City, Belgium, and North Carolina.

1. Introduction

Estimating the proportion of people who have antibodies to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is useful for tracking the pandemic’s severity and informing public health decisions (Arora et al., 2021). Individuals may have detectable antibodies for different reasons, including prior infection or vaccination. Antibody levels within a person are dynamic, typically increasing after an infection or vaccination, and then eventually decreasing (waning) over time. Thus, individuals may not have detectable antibodies if never (or very recently) infected or vaccinated, or if their antibody levels have waned below the limit of detection of the assay being employed. To the extent that antibody levels are associated with protection from infection with SARS-CoV-2 or COVID-19 disease (Earle et al., 2021; Khoury et al., 2021), seroprevalence estimates may be helpful in modelling the fraction of a population which may be immune or less susceptible to COVID-19. Likewise, cross-sectional seroprevalence estimates, combined with certain modelling assumptions and other data, may permit inference about other parameters such as the cumulative incidence of previous SARS-CoV-2 infection, infection fatality rate, or attack rate (Brazeau et al., 2020; Buss et al., 2021; Perez-Saez et al., 2021; Shioda et al., 2021; Takahashi et al., 2021).

Unfortunately, seroprevalence studies often suffer from at least two sources of bias: measurement error due to false positives and negatives, and selection bias due to non-probability sampling designs. Typically, blood tests for antibodies result in a continuous measure of a particular antibody response, such as that of immunoglobulin G, M, or A (IgG, IgM, or IgA). Dichotomizing antibody responses using a cut-off value almost always produces misclassification bias in the form of false positives and false negatives (Bouman et al., 2021). The following example from Sempos and Tian (2021) demonstrates how this measurement error can lead to biased seroprevalence estimates. Suppose that true seroprevalence is 1% and antibody tests are performed using an assay which perfectly identifies true positives as positive, so with 100% sensitivity, and nearly perfectly identifies true negatives as negative, with 99% specificity. Despite this assay’s high sensitivity and specificity, it is straightforward to show that naively using the sample proportion of positive test results as a seroprevalence estimator would, in expectation, lead to a seroprevalence estimate of nearly 2% rather than 1%. To account for measurement error, sensitivity and specificity can be estimated and incorporated into the seroprevalence estimator, e.g. using the method popularized by Rogan and Gladen (1978) (see also Levy & Kass, 1970; Marchevsky, 1979).

Many seroprevalence studies are conducted by non-probability sampling methods, which may lead to selection bias when characteristics that drive participation in the study are also risk factors for SARS-CoV-2 infection. Probability-based sampling studies are ideal because they are representative by design and often lead to less biased estimates than non-probability samples with post-hoc statistical adjustments (Accorsi et al., 2021; Shook-Sa et al., 2020). However, probability-based sampling may not always be feasible due to time and cost constraints. For this reason, seroprevalence studies often utilize convenience sampling by, for example, drawing blood samples from routine clinic visitors (e.g. Barzin et al., 2020; Stadlbauer et al., 2021) or using residual sera from blood donors (e.g. Uyoga et al., 2021) or commercial laboratories (e.g. Bajema et al., 2021). Convenience sample-based estimators often assume that each person in a covariate-defined stratum has an equal probability of being in the sample (Elliott & Valliant, 2017). Under this assumption, population seroprevalence of SARS-CoV-2 can be estimated with direct standardization (Barzin et al., 2020; Cai et al., 2022; Havers et al., 2020), though weighting methods such as calibration can be used (e.g. Bajema et al., 2021).

In this paper, methods are considered which combine standardization and the Rogan–Gladen adjustment to account for both measurement error and selection bias. The article is organized as follows. Section 2 reviews prevalence estimation under measurement error. Non-parametric and parametric standardized prevalence estimators and their large-sample properties are described in Section 3. Section 4 presents simulation studies to evaluate the empirical bias and 95% confidence interval (CI) coverage of the standardized estimators across a range of assay characteristics and bias scenarios. The methods are then applied in Section 5 to three studies that estimate seroprevalence of SARS-CoV-2 in 2020 among all residents of New York City (NYC), all residents of Belgium, and asymptomatic residents of North Carolina. Section 6 concludes with a discussion. Proofs are in the appendices in the online supplementary material.

2. Seroprevalence estimation under measurement error

2.1. Problem set-up

Let the true serology status for an individual in the target population be denoted by Y, with $Y=1$ if the individual has antibodies against SARS-CoV-2 and $Y=0$ otherwise. Our goal is to draw inference about the population seroprevalence $\pi =P(Y=1)$. Because of error in the serology assay, Y is not observed directly. Let the result of the serology assay be denoted by X, with $X=1$ if the individual tests positive (according to the antibody assay used) and $X=0$ otherwise. Three key quantities are sensitivity, the probability that a true positive tests positive, denoted by ${\sigma }_e=P(X=1\mid Y=1)$; specificity, the probability that a true negative tests negative, denoted by ${\sigma }_p=P(X=0\mid Y=0)$; and the population expectation of the serology assay outcome, denoted by $\rho =\mathbb{E}(X)=P(X=1)$. Unless the assay has perfect sensitivity and specificity with ${\sigma }_e={\sigma }_p=1$, $\rho$ typically will not equal π and X will be a misclassified version of Y.

The sensitivity and specificity of a diagnostic test are commonly estimated by performing the assay on ‘validation’ samples of known true positives and true negatives, respectively. Specifically, measurements are taken on $n_1$ independent and identically distributed (iid) units from strata of the population where $Y=1$ and on $n_2$ iid units from strata where $Y=0$. Thus, $n_1$ copies of X are observed to estimate sensitivity and $n_2$ copies of X are observed to estimate specificity. In the COVID-19 setting, samples from patients who had a case confirmed with reverse transcription polymerase chain reaction (PCR) testing are often assumed to be true positives. Remnant blood samples that were drawn in 2019 or earlier are often assumed to be true negatives. To estimate seroprevalence in a target population, a ‘main’ study with $n_3$ iid copies of X is then conducted, among which true infection status is unknown.

Assume, as is realistic in many SARS-CoV-2 studies, that there is no overlap between the units in each of the three studies. Let ${\delta }_i$ be an indicator of which study the ith individual’s sample $X_i$ is from, with ${\delta }_i=1$ for the sensitivity study, ${\delta }_i=2$ for the specificity study, and ${\delta }_i=3$ for the main study. Note that $\sum I({\delta }_i=j)=n_j$ for $j=1,2,3$, where $n=n_1+n_2+n_3$ and here and throughout summations are taken from $i=1$ to n unless otherwise specified. Assume $n_j/n\to c_j\in (0,1)$ as $n\to \mathrm{\infty }$.

2.2. Estimators and statistical properties

Let $\theta =({\sigma }_e,{\sigma }_p,\rho ,\pi {)}^T$. Consider the estimator $\hat{\theta }=({\hat{\sigma }}_e,{\hat{\sigma }}_p,\hat{\rho },{\hat{\pi }}_{RG}{)}^T$, where ${\hat{\sigma }}_e=n_1^{-1}\sum I({\delta }_i=1)X_i$, ${\hat{\sigma }}_p=n_2^{-1}\sum I({\delta }_i=2)(1-X_i)$, $\hat{\rho }=n_3^{-1}\sum I({\delta }_i=3)X_i$, and ${\hat{\pi }}_{RG}=(\hat{\rho }+{\hat{\sigma }}_p-1)/({\hat{\sigma }}_e+{\hat{\sigma }}_p-1)$. The prevalence estimator ${\hat{\pi }}_{RG}$ is motivated by rearranging the identity that $\rho =\pi {\sigma }_e+(1-\pi )(1-{\sigma }_p)$ and is sometimes referred to as the Rogan–Gladen (1978) estimator. Note the sample proportions ${\hat{\sigma }}_e$, ${\hat{\sigma }}_p$, and $\hat{\rho }$ are maximum likelihood estimators (MLEs) for ${\sigma }_e$, ${\sigma }_p$, and $\rho$, respectively, so ${\hat{\pi }}_{RG}$ is a function of the MLE of $({\sigma }_e,{\sigma }_p,\rho )$ (see online supplementary Appendix A for details).

The estimator $\hat{\theta }$ can be expressed as the solution (for $\theta$) to the estimating equation vector

$$\sum \psi (X_i;{\delta }_i,\theta )=\left(\begin{array}{c}\sum {\psi }_e(X_i;{\delta }_i,\theta )\\ \sum {\psi }_p(X_i;{\delta }_i,\theta )\\ \sum {\psi }_{\rho }(X_i;{\delta }_i,\theta )\\ {\psi }_{\pi }(X_i;{\delta }_i,\theta )\end{array}\right)=\left(\begin{array}{c}\sum I({\delta }_i=1)(X_i-{\sigma }_e)\\ \sum I({\delta }_i=2)\{(1-X_i)-{\sigma }_p\}\\ \sum I({\delta }_i=3)(X_i-\rho )\\ (\rho +{\sigma }_p-1)-\pi ({\sigma }_e+{\sigma }_p-1)\end{array}\right)=0$$

where here and below 0 denotes a column vector of zeros. Since the samples were selected from three different populations, the data $X_1,\dots ,X_n$ are not identically distributed and care must be taken to derive the large-sample properties of $\hat{\theta }$. In the online supplementary Appendix B, the estimator $\hat{\theta }$ is shown to be consistent and asymptotically normal. Specifically, as $n\to \mathrm{\infty }$, $\sqrt{n}(\hat{\theta }-\theta ){\to }_d\mathcal{N}(0,\mathbb{A}(\theta {)}^{-1}\mathbb{B}(\theta )\mathbb{A}(\theta {)}^{-T})$ and $\sqrt{n}(\hat{\pi }-\pi ){\to }_d\mathcal{N}(0,V_{\pi ,RG})$ assuming ${\sigma }_e>1-{\sigma }_p$ (as discussed below), where $\mathbb{A}(\theta {)}^{-1}\mathbb{B}(\theta )\mathbb{A}(\theta {)}^{-T}$ is a covariance matrix with bottom right element

$$V_{\pi ,RG}=\{\frac{{\pi }^2{\sigma }_e(1-{\sigma }_e)}{c_1}+\frac{(1-\pi {)}^2{\sigma }_p(1-{\sigma }_p)}{c_2}+\frac{\rho (1-\rho )}{c_3}\}({\sigma }_e+{\sigma }_p-1{)}^{-2}.$$ (1)

The proof of consistency and asymptotic normality is similar to proofs from standard estimating equation theory (e.g. Boos & Stefanski, 2013, Equation 7.10), but because the data are not identically distributed the Lindeberg-Feller Central Limit Theorem (CLT) is used in place of the classical Lindeberg-Lévy CLT. Note that the asymptotic variance (1) consists of three components corresponding to the sensitivity, specificity, and main studies. In some circumstances, investigators may be able to decrease the variance of ${\hat{\pi }}_{RG}$ by increasing the sample sizes of the sensitivity or specificity studies compared to the main study (Larremore et al., 2020).

Let ${\hat{V}}_{\pi ,RG}$ denote the plug-in estimator defined by replacing ${\sigma }_e,{\sigma }_p,\rho ,\pi$, and $c_j$ in Equation (1) with ${\hat{\sigma }}_e,{\hat{\sigma }}_p,\hat{\rho },{\hat{\pi }}_{RG}$, and $n_j/n$ for $j=1,2,3$, and note that ${\hat{V}}_{\pi ,RG}/n$ is the variance estimator proposed by Rogan and Gladen (1978). By the continuous mapping theorem, ${\hat{V}}_{\pi ,RG}$ is consistent for the asymptotic variance assuming ${\sigma }_e>1-{\sigma }_p$ and can be used to construct Wald-type CIs that asymptotically attain nominal coverage probabilities. In finite samples, Wald-type CIs can sometimes have erratic coverage properties when estimating a single binomial parameter (Brown et al., 2001; Dean & Pagano, 2015). In Section 4, simulations are conducted to assess the performance of the Wald-type CIs in seroprevalence estimation scenarios. Alternative approaches for constructing CIs are discussed in Section 6.

2.3. Truncation into $[0,1]$

In finite samples, ${\hat{\pi }}_{RG}$ sometimes yields estimates outside of $[0,1]$ when (i) ${\hat{\sigma }}_e<1-{\hat{\sigma }}_p$, (ii) $\hat{\rho }<1-{\hat{\sigma }}_p$, or (iii) $\hat{\rho }>{\hat{\sigma }}_e$. Indeed, (ii) occurred in the ScreenNC study discussed in Section 5.3. Estimates are typically truncated to be inside $[0,1]$ because the true population prevalence must exist in $[0,1]$ (Hilden, 1979). In this article, all point estimates and bounds of interval estimates are so truncated. Note, though, that as the three sample sizes grow large, the estimator ${\hat{\pi }}_{RG}$ yields estimates inside $[0,1]$ almost surely unless ${\sigma }_e<1-{\sigma }_p$. In practice, settings where ${\sigma }_e<1-{\sigma }_p$ may be very unlikely; in such scenarios, the probability of a positive test result is higher for seronegative persons than for seropositive persons, so such a measurement instrument performs worse in expectation than random guessing. Throughout this manuscript, it is assumed that ${\sigma }_e>1-{\sigma }_p$.

3. Standardized seroprevalence estimation

3.1. Problem set-up

In some settings it may not be reasonable to assume the $n_3$ copies of X from the main study constitute a random sample from the target population. Suppose instead that for each copy of X a vector of discrete covariates Z is observed, with Z taking on k possible values $z_1,\dots ,z_k$. The covariates Z are of interest because seroprevalence may differ between the strata; for instance, Z might include demographic variables such as age group, race, or gender. Denote the mean of X in the jth stratum as ${\rho }_j=P(X=1\mid Z=z_j)$ and the sample size for the jth stratum as $n_{z_j}=\sum I({\delta }_i=3,Z_i=z_j)$, so $\sum _{j=1}^k{n}_{z_j}=n_3$.

The distribution of strata in the target population, if known, can be used to standardize estimates so they are reflective of the target population [for a review of direct standardization, see van Belle et al. (2004, Chapter 15)]. Denote the proportion of the target population comprised by the jth stratum as ${\gamma }_j=P(Z=z_j)$ and suppose that these stratum proportions are known with each ${\gamma }_j>0$ and $\sum _{j=1}^k{\gamma }_j=1$. The stratum proportions are commonly treated as known based on census data or large probability-based surveys (Lohr, 2010, Ch. 4.4; Korn & Graubard, 1999, Ch. 2.6). Alternatively, ${\gamma }_1,\dots ,{\gamma }_k$ could be estimated, e.g. from a random sample of the target population, and the estimator of the seroprevalence estimator’s variance could be appropriately adjusted to reflect the uncertainty in these estimated proportions.

Assume that all persons in a covariate stratum defined by Z have the same probability of inclusion in the sample. Then the covariates Z in the main study sample have a multinomial distribution with k categories, sample size $n_3$, and an unknown sampling probability vector $(s_1,\dots ,s_k{)}^T$ where $\sum _{j=1}^k{s}_j=1$. For $j=1,\dots ,k$, the probability $s_j$ indicates the chance of a sampled individual being in stratum j. Note that if the main study were a simple random sample from the target population, then the sampling probabilities would be equal to the stratum proportions (with $s_j={\gamma }_j$ for $j=1,\dots ,k$).

3.2. Non-parametric standardization

First, consider a seroprevalence estimator which combines non-parametric standardization and the Rogan–Gladen adjustment to account for both selection bias and measurement error. Note that $\rho$ is a weighted average of the stratum-conditional means ${\rho }_j$, where each weight is a known stratum proportion ${\gamma }_j$, i.e. $\rho =\sum _{j=1}^k{\rho }_j{\gamma }_j$. A non-parametric standardization estimator for $\rho$ using the sample stratum-conditional prevalences ${\hat{\rho }}_j=n_{z_j}^{-1}\sum I(Z_i=z_j,{\delta }_i=3)X_i$ for $j=1,\dots ,k$ is ${\hat{\rho }}_{SRG}=\sum _{j=1}^k{\hat{\rho }}_j{\gamma }_j$. A standardized prevalence estimator accounting for measurement error is ${\hat{\pi }}_{SRG}=({\hat{\rho }}_{SRG}+{\hat{\sigma }}_p-1)/({\hat{\sigma }}_e+{\hat{\sigma }}_p-1)$, which has been used in SARS-CoV-2 seroprevalence studies (Barzin et al., 2020; Cai et al., 2022; Havers et al., 2020).

Let ${\theta }_s=({\sigma }_e,{\sigma }_p,{\rho }_1,\dots ,{\rho }_k,\rho ,\pi {)}^T$. The estimator ${\hat{\theta }}_s=({\hat{\sigma }}_e,{\hat{\sigma }}_p,{\hat{\rho }}_1,\dots ,{\hat{\rho }}_k,{\hat{\rho }}_{SRG},{\hat{\pi }}_{SRG}{)}^T$ solves the vector $\sum \psi (X_i,Z_i;{\delta }_i,{\theta }_s)=(\sum {\psi }_e,\sum {\psi }_p,\sum {\mathit{\psi }}_{\mathit{\rho }},{\psi }_{\rho },{\psi }_{\pi }{)}^T=0$ of estimating equations, where $\sum {\psi }_e,\sum {\psi }_p$, and ${\psi }_{\pi }$ are defined in Section 2; $\sum {\mathit{\psi }}_{\mathit{\rho }}$ is a k-vector with jth element $\sum {\psi }_{{\rho }_j}=\sum I(Z_i=z_j,{\delta }_i=3)(X_i-{\rho }_j)$; and ${\psi }_{\rho }=\sum _{j=1}^k{\rho }_j{\gamma }_j-\rho$. It follows that ${\hat{\theta }}_s$ is consistent and asymptotically normal and that $\sqrt{n}({\hat{\pi }}_{SRG}-\pi ){\to }_d\mathcal{N}(0,V_{\pi ,SRG})$ where

$$V_{\pi ,SRG}=\{\frac{{\pi }^2{\sigma }_e(1-{\sigma }_e)}{c_1}+\frac{(1-\pi {)}^2{\sigma }_p(1-{\sigma }_p)}{c_2}+{\displaystyle \sum _{j=1}^k}\frac{{\gamma }_j^2{\rho }_j(1-{\rho }_j)}{c_3{s}_j}\}({\sigma }_e+{\sigma }_p-1{)}^{-2}.$$ (2)

The asymptotic variance $V_{\pi ,SRG}$ can be consistently estimated by the plug-in estimator ${\hat{V}}_{\pi ,SRG}$ defined by replacing ${\sigma }_e,{\sigma }_p,{\rho }_j,s_j,\pi$, and $c_l$ in Equation (2) with ${\hat{\sigma }}_e,{\hat{\sigma }}_p,{\hat{\rho }}_j,n_{z_j}/n_3,{\hat{\pi }}_{SRG}$, and $n_l/n$ for $j=1,\dots ,k$ and $l=1,2,3$. Consistency of ${\hat{V}}_{\pi ,SRG}$ holds by continuous mapping, and a proof of asymptotic normality and justification of Equation (2) are in the online supplementary Appendix C.

Standardization requires estimating the stratum-conditional mean of X, ${\rho }_j=P(X=1\mid Z=z_j)$. However, when $n_{z_j}=0$ for some strata j, the corresponding estimator ${\hat{\rho }}_j$ is undefined, and ${\hat{\rho }}_{SRG}$ is then undefined as well. Values of $n_{z_j}$ may equal zero for two reasons. First, the study design may exclude these strata ($s_j=0$), a situation referred to as deterministic or structural non-positivity (Westreich & Cole, 2010). Second, even if $s_j>0$, random non-positivity can occur if no individuals with $Z=z_j$ are sampled, which may occur if $s_j$ is small or if $n_3$ is relatively small. When non-positivity arises, an analytical approach often employed entails ‘restriction’ (Westreich & Cole, 2010), where the target population is redefined to consist only of strata j for which $n_{z_j}>0$. However, this redefined target population may be less relevant from a public health or policy perspective.

3.3. Parametric standardization

Rather than redefining the target population, an alternative strategy for combatting positivity violations is to fit a parametric model to estimate all stratum-conditional means ${\rho }_j$. Such parametric models allow inference to the original target population and, when they are correctly specified, typically outperform non-parametric approaches (Petersen et al., 2012; Rudolph et al., 2018; Zivich et al., 2022). Assume the binary regression model $g({\rho }_j)=\beta h(z_j)$ holds, where g is an appropriate link function for a binary outcome like the logit or probit function; β is a row vector of p regression coefficients with intercept ${\beta }_1$; and $h(z_j)$ is a user-specified p-vector function of the jth stratum’s covariate values that may include main effects and interaction terms, with lth element denoted $h_l(z_j)$ and $h_1(z_j)$ set equal to one to correspond to an intercept. Let $\text{supp}(z)$ be the covariate support in the sample, i.e. $\text{supp}(z)=\{z_j:n_{z_j}>0\}$ with dimension $\text{dim}\{\text{supp}(z)\}=\sum _{j=1}^{k}I(n_{z_j}>0)$, and assume $p\le \text{dim}\{\text{supp}(z)\}\le k$. (Note that $\text{dim}\{\text{supp}(z)\}=k$ only when there is positivity, and in that case ${\hat{\pi }}_{SRG}$ can be used with no restriction needed.)

Under the assumed binary regression model, each ${\rho }_j$ is a function of the parameters β and the covariates $z_j$ that define the jth stratum, denoted ${\rho }_j(\beta ,z_j)=g^{-1}\{\beta h(z_j)\}$. A model-based standardized Rogan–Gladen estimator of π is ${\hat{\pi }}_{SRGM}=({\hat{\rho }}_{SRGM}+{\hat{\sigma }}_p-1)/({\hat{\sigma }}_e+{\hat{\sigma }}_p-1)$, where ${\hat{\rho }}_{SRGM}=\sum _{j=1}^k{\hat{\rho }}_j(\hat{\beta },z_j){\gamma }_j$ and $\hat{\beta }$ is the MLE of β. Estimating equation theory can again be used to derive large-sample properties by replacing the k equations for ${\rho }_1,\dots ,{\rho }_k$ from Section 3.2 with p equations for ${\beta }_1,\dots ,{\beta }_p$ corresponding to the score equations from the binary regression.

Let ${\theta }_m=({\sigma }_e,{\sigma }_p,{\beta }_1,\dots ,{\beta }_p,\rho ,\pi {)}^T$ and ${\hat{\theta }}_m=({\hat{\sigma }}_e,{\hat{\sigma }}_p,{\hat{\beta }}_1,\dots ,{\hat{\beta }}_p,{\hat{\rho }}_{SRGM},{\hat{\pi }}_{SRGM}{)}^T$. The estimator ${\hat{\theta }}_m$ solves the vector $\sum \psi (X_i,Z_i;{\delta }_i,{\theta }_m)=(\sum {\psi }_e,\sum {\psi }_p,\sum {\psi }_{\beta },{\psi }_{\rho },{\psi }_{\pi }{)}^T=0$ of estimating equations, where $\sum {\psi }_e,\sum {\psi }_p$, and ${\psi }_{\pi }$ are as in Section 2; $\sum {\psi }_{\beta }$ is a p-vector with jth element $\sum {\psi }_{{\beta }_j}=\sum I({\delta }_i=3)[X_i-g^{-1}\{\beta h(Z_i)\}]h_j(Z_i)$; and ${\psi }_{\rho }=\sum _{j=1}^k{g}^{-1}\{\beta h(Z_j)\}{\gamma }_j-\rho$. It follows that ${\hat{\theta }}_m$ is consistent and asymptotically normal and $\sqrt{n}({\hat{\pi }}_{SRGM}-\pi ){\to }_d\mathcal{N}(0,V_{\pi ,SRGM})$. The asymptotic variance $V_{\pi ,SRGM}$ can be consistently estimated by ${\hat{V}}_{\pi ,SRGM}$, the lower right element of the empirical sandwich variance estimator of the asymptotic variance of ${\hat{\theta }}_m$. A proof of asymptotic normality and the empirical sandwich variance estimator are given in the online supplementary Appendix D. An R package for computing ${\hat{\pi }}_{SRG}$, ${\hat{\pi }}_{SRGM}$, and their corresponding variance estimators is available at https://github.com/samrosin/rgStandardized.

4. Simulation study

Simulation studies were conducted to compare ${\hat{\pi }}_{RG}$, ${\hat{\pi }}_{SRG}$, and ${\hat{\pi }}_{SRGM}$. Four data generating processes (DGPs) were considered, within which different scenarios were defined through full factorial designs that varied simulation parameters $\pi ,{\sigma }_e,{\sigma }_p,n_1,n_2$, and $n_3$. These DGPs featured no selection bias (DGP 1), selection bias with two strata (DGP 2), and more realistic selection bias with 40 strata and 80 strata (DGPs 3 and 4).

For each DGP and set of simulation parameters, sensitivity and specificity validation samples of size $n_1$ and $n_2$ were generated with X distributed Bernoulli with a mean of ${\sigma }_e$ or $1-{\sigma }_p$, respectively. In DGPs 1 and 2, a main study of size $n_3$ was then generated, where Y was Bernoulli with mean π and $X\mid Y$ was Bernoulli with mean ${\sigma }_{e}Y+(1-{\sigma }_p)(1-Y)$; in DGPs 3 and 4, X was generated from the distribution of $X\mid Z$, as described below. Simulation parameter values were selected based on the seroprevalence studies described in Section 5. Sensitivity was varied in ${\sigma }_e\in \{.8,.99\}$, specificity in ${\sigma }_p\in \{.8,.95,.99\}$, and prevalence in $\pi \in \{.01,.02,\dots ,.20\}$. Sample sizes were $n_1=40$, $n_2=250$, and $n_3=2500$. The full factorial design led to 120 scenarios per DGP, and within each scenario 1,000 simulations were conducted unless otherwise specified. Performance was measured by: (a) mean bias, computed as the mean of $\hat{\pi }-\pi$ for each estimator $\hat{\pi }$; (b) empirical coverage, i.e. whether the 95% Wald-type CIs based on each variance estimator ${\hat{V}}_{\pi }$ contained the true prevalence; (c) mean squared error (MSE), computed as the mean of $(\hat{\pi }-\pi {)}^2$ for each estimator $\hat{\pi }$. R code implementing the simulations is available at https://github.com/samrosin/rgStandardized˙ms.

4.1. No selection bias

For DGP 1, 10,000 simulations were conducted to assess the performance of ${\hat{\pi }}_{RG}$ when no selection bias was present. The estimator ${\hat{\pi }}_{RG}$ was generally unbiased, as seen in the online supplementary Figure 1. Performance improved as ${\sigma }_e$ and ${\sigma }_p$ tended toward 1, with ${\sigma }_p$ being a stronger determinant of bias. An exception to these results occurred when $\pi \le 0.05$ and ${\sigma }_p\le 0.95$, in which case ${\hat{\pi }}_{RG}$ overestimated the true prevalence. The Rogan–Gladen estimator without truncation was also evaluated in this DGP to determine if truncation caused the bias. While the non-truncated estimator was slightly biased, the magnitude of the bias was $<0.002$ in all scenarios, suggesting the bias of ${\hat{\pi }}_{RG}$ in low prevalence, low specificity settings is due largely to truncation.

Wald CIs based on ${\hat{V}}_{\pi ,RG}$ attained nominal coverage in almost every scenario, as seen in the online supplementary Figure 2. However, when some parameters were near their boundaries, coverage did not reach the nominal level. For instance, when π was 0.01 and ${\sigma }_p$ was 0.99, 95% CIs covered in 90% and 91% of simulations for two values of ${\sigma }_e$. These variable CI coverage results concord with previous simulation studies evaluating ${\hat{V}}_{\pi ,RG}$ (Lang & Reiczigel, 2014). The MSE of ${\hat{\pi }}_{RG}$, shown in the online supplementary Figure 3, tended to increase with π and decrease as ${\sigma }_e$ and ${\sigma }_p$ approached 1.

4.2. Low-dimensional selection bias

In DGP 2, the target population was comprised of two strata defined by a covariate $Z\in \{z_1,z_2\}$ with proportions ${\gamma }_1={\gamma }_2=.5$. Within the main study, Z was generated from a binomial distribution of sample size $n_3$ and sampling probabilities $(.2,.8)$. Individuals’ serostatuses were generated from the conditional distribution $Y\mid Z$, which was such that $P(Y=1\mid Z=z_1)=1.5\pi$ and $P(Y=1\mid Z=z_2)=0.5\pi$ for each value of π. In each simulation, ${\hat{\pi }}_{RG}$ and ${\hat{\pi }}_{SRG}$ and their corresponding 95% CIs were computed.

The non-parametric standardized estimator ${\hat{\pi }}_{SRG}$ was empirically unbiased for true prevalences $\pi \ge 0.05$, as seen in the online supplementary Figure 4, and 95% CIs based on ${\hat{V}}_{\pi ,SRG}$ attained nominal coverage in almost every scenario, as seen in the online supplementary Figure 5. As with ${\hat{\pi }}_{RG}$ in DGP 1, CI coverage for ${\hat{\pi }}_{SRG}$ was slightly less than the nominal level for very low π and for ${\sigma }_p$ near the boundary, e.g. coverage was 91% for $\pi =.01$ and ${\sigma }_e={\sigma }_p=.99$. MSE trends for ${\hat{\pi }}_{SRG}$ were similar to those of ${\hat{\pi }}_{RG}$ in DGP 1, as seen in the online supplementary Figure 6. Online supplementary Figures 4, 5, and 6 show that ${\hat{\pi }}_{RG}$ performed poorly under selection bias, with large negative bias, CI coverage far less than the nominal level in most cases, and much greater MSE than ${\hat{\pi }}_{SRG}$.

4.3. More realistic selection bias

4.3.1. DGP 3

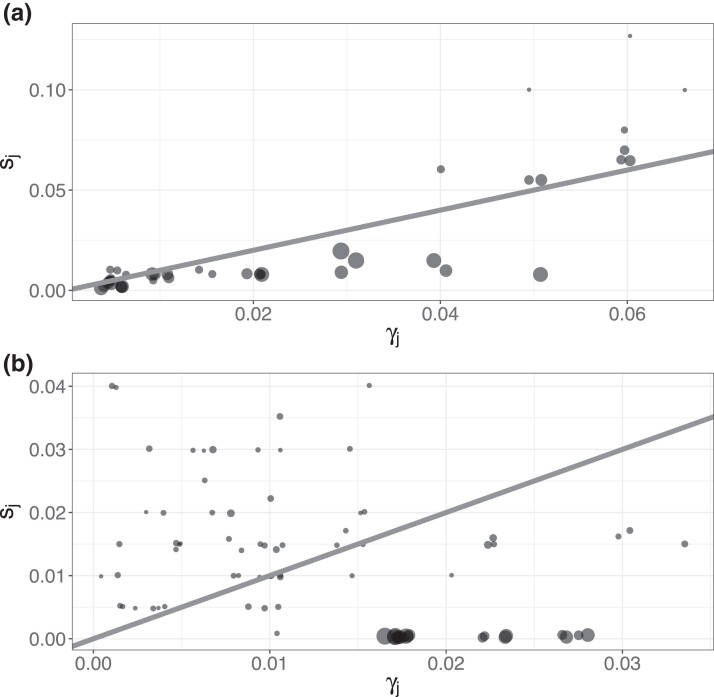
DGPs 3 and 4 compared ${\hat{\pi }}_{SRG}$ and ${\hat{\pi }}_{SRGM}$ in scenarios with larger numbers of strata. In DGP 3, three covariates were defined as $Z_1\in \{z_{10},z_{11}\}$, $Z_2\in \{z_{20},z_{21},z_{22},z_{23}\}$, and $Z_3\in \{z_{30},z_{31},z_{32},z_{33},z_{34}\}$, leading to $k=40$ strata with proportions $({\gamma }_1,\dots ,{\gamma }_{40})$. Within the main study, Z was generated as multinomial with size $n_3$ and known sampling probabilities. Figure 1a shows the structure of selection bias in DGP 3 by comparing the stratum proportions and sampling probabilities. Some low-prevalence strata that frequently occur in the population were oversampled, while most remaining strata were undersampled. Individuals’ test results were generated from the conditional distribution $X\mid Z$, where

Figure 1.

Panels (a) and (b) represent selection bias in the simulation studies of data generating processes 3 and 4, described in Sections 4.3.1 and 4.3.2, respectively. Circle size is proportional to prevalence. Points are jittered slightly for legibility, and the diagonal lines denote equality between ${\gamma }_j$ (stratum proportion) and $s_j$ (sampling probability).

$$\begin{array}{rl}\text{logit}\{P(X=1\mid Z)\}& ={\beta }_0+{\beta }_{1}I(Z_1=z_{11})+{\beta }_{2}I(Z_2=z_{20})+{\beta }_{3}I(Z_2=z_{21})\\ & +{\beta }_{4}I(Z_3=z_{30})+{\beta }_{5}I(Z_3=z_{31}).\end{array}$$

The parameters ${\beta }_1=-1,{\beta }_2=-.6,{\beta }_3=.8,{\beta }_4=.6,$ and ${\beta }_5=.4$ were set to reflect differential prevalences by stratum, while a ‘balancing intercept’ ${\beta }_0$ (Rudolph et al., 2021) was set to different values so that π equalled (approximately) $\{.01,.02,\dots ,.20\}$. The non-parametric estimator ${\hat{\pi }}_{SRG}$ and corresponding CI were computed using a restricted target population when random non-positivity arose; the values of π used to compute bias and coverage were based on the total (unrestricted) population, which is the parameter of interest. The parametric estimator ${\hat{\pi }}_{SRGM}$ was computed with a correctly specified logistic regression model, with parameters estimated using maximum likelihood.

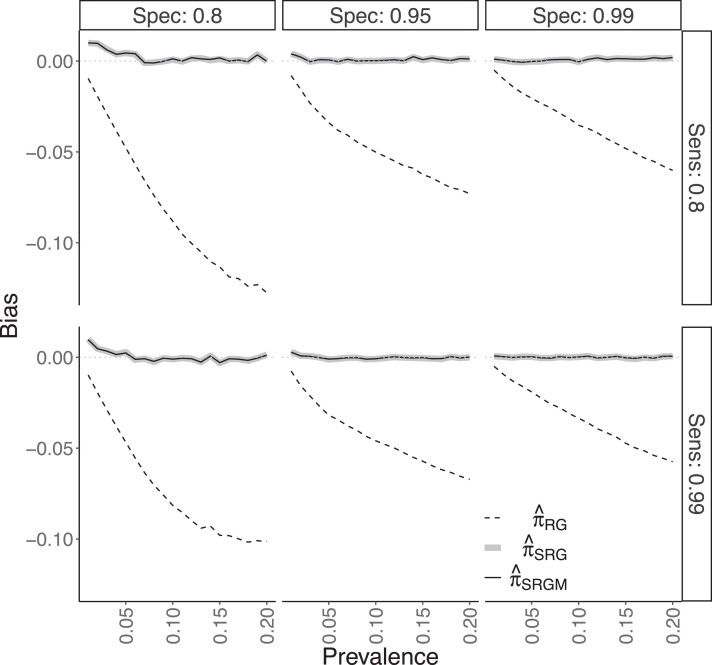
Both ${\hat{\pi }}_{SRG}$ and ${\hat{\pi }}_{SRGM}$ performed well in this scenario. Figure 2 shows that the estimators were generally empirically unbiased, though modest bias occurred when ${\sigma }_p=0.8$ and π was low. As in DGP 2, ${\hat{\pi }}_{RG}$ exhibited substantial bias and the CIs based on ${\hat{\pi }}_{RG}$ did not attain nominal coverage. Online supplementary Figure 7 shows 95% CIs based on either ${\hat{V}}_{\pi ,SRG}$ or ${\hat{V}}_{\pi ,SRGM}$ attained nominal coverage, with slight under-coverage for $\pi <0.05$, similar to the results from DGPs 1 and 2. For $\pi =.01$ and ${\sigma }_p=.99$, coverage was 92% and 90% based on ${\hat{V}}_{\pi ,SRG}$ and 91% and 90% based on ${\hat{V}}_{\pi ,SRGM}$ for ${\sigma }_e\in \{.8,.99\}$, respectively. The two standardized estimators had roughly equivalent MSE (online supplementary Figure 8). On average across all 120 scenarios, positivity was present in 89% (range of 86%–92%) of simulated data sets, i.e. these data sets included all strata in the target population.

Figure 2.

Empirical bias of the Rogan–Gladen (${\hat{\pi }}_{RG}$), non-parametric standardized (${\hat{\pi }}_{SRG}$), and logistic regression standardized (${\hat{\pi }}_{SRGM}$) estimators from simulation study for data generating process 3, described in Section 4.3.1. The six facets correspond to a given combination of sensitivity (‘Sens’) and specificity (‘Spec’).

4.3.2. DGP 4

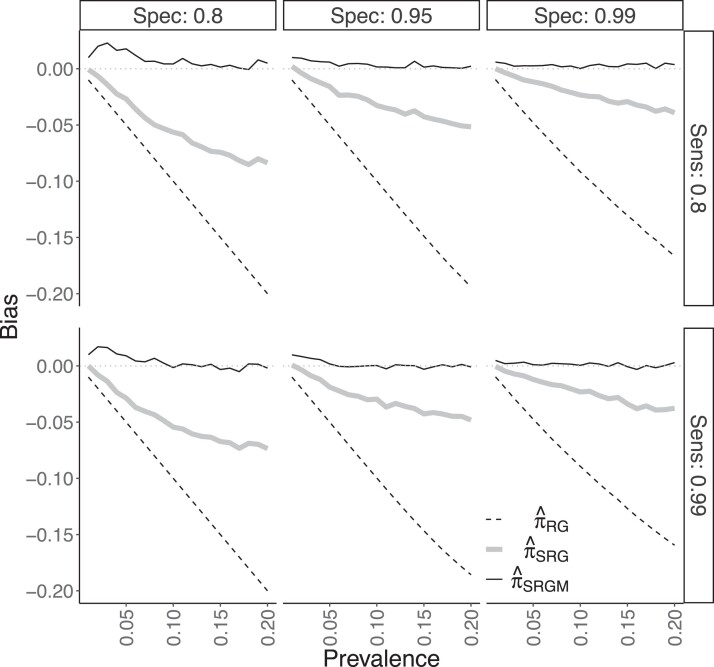
Data were generated as in DGP 3, but the inclusion of a fourth covariate $Z_4\in \{z_{40},z_{41}\}$ led to 80 strata. The conditional distribution $X\mid Z$ was such that $\text{logit}\{P(X=1\mid Z)\}=\nu h(Z)$, where $h(Z)$ here contains the same terms as in DGP 3 plus a main effect for $I(Z_4=z_{41})$ with corresponding coefficient ${\nu }_6$. Regression parameters were a balancing intercept ${\nu }_0$, ${\nu }_1=-1$, ${\nu }_2=3.25$, ${\nu }_3=.8$, ${\nu }_4=.6$, ${\nu }_5=.4$, and ${\nu }_6=.1$. The larger value for ${\nu }_2$, as compared to ${\beta }_2$, led to a stronger relationship between X and Z than was present in DGP 3. Figure 1b displays selection bias in DGP 4. Some of the highest-prevalence and most commonly occurring strata were undersampled to a greater degree than occurred in DGP 3, so in this sense there was more selection bias in DGP 4. The parametric estimator ${\hat{\pi }}_{SRGM}$ was again computed with a correctly specified logistic regression model using maximum likelihood for parameter estimation.

Results for the DGP 4 simulations are shown in Figure 3 and online supplementary Figures 9–11. Figure 3 shows that only ${\hat{\pi }}_{SRGM}$ was generally unbiased under DGP 4, although there was positive bias when ${\sigma }_p=.8$ and $\pi <.1$. The non-parametric ${\hat{\pi }}_{SRG}$ typically had a moderately negative bias. Non-positivity almost always occurred (in either all or all but one of the simulations, for each of the 120 scenarios). The worse bias of ${\hat{\pi }}_{SRG}$ may be explained by restriction leading to bias under non-positivity. CIs based on ${\hat{V}}_{\pi ,SRGM}$ typically attained nominal or close-to-nominal coverage, unlike those based on ${\hat{V}}_{\pi ,SRG}$ or ${\hat{V}}_{\pi ,RG}$, as seen in the online supplementary Figure 9. For instance, when ${\sigma }_p=0.8$, the lowest coverage for CIs based on ${\hat{V}}_{\pi ,SRGM}$ was 92% across all 40 combinations of ${\sigma }_e$ and π. However, the ${\hat{V}}_{\pi ,SRGM}$-based CIs exhibited under-coverage when ${\sigma }_p=.99$ and prevalence π was low. For example, coverage of these CIs was only 59% when $\pi =0.01$ and ${\sigma }_e={\sigma }_p=.99$; online supplementary Figure 10 shows this undercoverage is due to 39% of the ${\hat{\pi }}_{SRGM}$ estimates being truncated to 0 with corresponding CIs which were overly narrow. Note that ${\hat{V}}_{\pi ,SRGM}$ was negative for two simulations in a single scenario, and these ‘Heywood cases’ (Kolenikov & Bollen, 2012) were ignored in the coverage calculation for that scenario. The MSE of ${\hat{\pi }}_{SRGM}$ tended to be less than that of ${\hat{\pi }}_{SRG}$ (online supplementary Figure 11).

Figure 3.

Bias results from simulation study on data generating process 4, described in Section 4.3.2. Figure layout is as in Figure 2.

In summary, both the non-parametric and parametric standardized estimators ${\hat{\pi }}_{SRG}$ and ${\hat{\pi }}_{SRGM}$ had low empirical bias and close-to-nominal 95% CI coverage when there was positivity or near positivity. As the number of covariates, amount of selection bias, and potential for non-positivity increased, the (correctly specified) parametric ${\hat{\pi }}_{SRGM}$ generally maintained its performance, while ${\hat{\pi }}_{SRG}$ had greater empirical bias and the intervals based on ${\hat{V}}_{\pi ,SRG}$ did not attain nominal coverage levels.

4.4. Model misspecification

The performance of ${\hat{\pi }}_{SRGM}$ was assessed in scenarios similar to DGPs 3 and 4, but under model misspecification. Here, the true conditional distributions of $Y\mid Z$ were $\text{logit}\{P(Y=1\mid Z)\}=\beta h(Z)$ and $\text{logit}\{P(Y=1\mid Z)\}=\nu h(Z)$, where $\beta h(Z)$ and $\nu h(Z)$ are the specifications used in the models for $\text{logit}\{P(X=1\mid Z)\}$ in DGPs 3 and 4, respectively. The test results X were generated from $X\mid Y$ as in DGPs 1 and 2. The results shown in the online supplementary Figures 12–17 demonstrate that, in terms of bias, 95% CI coverage, and MSE, inferences based on ${\hat{\pi }}_{SRGM}$ were generally robust to this misspecification. For DGP 3, the true $X\mid Z$ distribution was $\text{Pr}(X=1\mid Z)=[{\text{logit}}^{-1}\{\beta h(Z)\}+{\sigma }_p-1]/[{\sigma }_e+{\sigma }_p-1]$, while the model-based estimator incorrectly assumed $\text{Pr}(X=1\mid Z)={\text{logit}}^{-1}\{\beta h(Z)\}$, and likewise for DGP 4 with $\nu h(Z)$ replacing $\beta h(Z)$. Thus, the degree of misspecification was determined by ${\sigma }_e$ and ${\sigma }_p$, with values farther from 1 leading to greater misspecification. For all simulation scenarios ${\sigma }_e\ge 0.8$ and ${\sigma }_p\ge 0.8$ such that the overall degree of misspecification was generally mild, potentially explaining the robustness of ${\hat{\pi }}_{SRGM}$ to model misspecification in these simulations.

Robustness of the model-based estimator ${\hat{\pi }}_{SRGM}$ was also assessed when the model was misspecified by omitting a variable. Under DGP 3, ${\hat{\pi }}_{SRGM}$ was estimated based on three misspecified logistic regression models, each omitting one of the three variables $Z_1$, $Z_2$, or $Z_3$ (i.e. omitting all indicator variables that included the variable). Results displayed in the online supplementary Figure 18 show the empirical bias of ${\hat{\pi }}_{SRGM}$ depended on which variable was omitted, with substantial bias when $Z_2$ was not included in the model. These results demonstrate that ${\hat{\pi }}_{SRGM}$ may not be robust to model misspecification due to variable omission.

5. Applications

5.1. NYC seroprevalence study

The methods were applied to a seroprevalence study in NYC that sampled patients at Mount Sinai Hospital from 9 February to 5 July 2020 (Stadlbauer et al., 2021). Patients were sampled from two groups: (a) a ‘routine care’ group visiting the hospital for reasons unrelated to COVID-19, including obstetric, gynaecologic, oncologic, surgical, outpatient, cardiologic, and other regular visits; (b) an ‘urgent care’ group of patients seen in the emergency department or admitted to the hospital for urgent care. Analyses were stratified by these two care groups. The urgent care group may have included individuals seeking care for moderate-to-severe COVID-19 (Stadlbauer et al., 2021); this would potentially violate the assumption of equal sampling probabilities within strata, but standardized analysis of the urgent care group is included here to demonstrate the methods. The routine care group was thought to be more similar to the general population (Stadlbauer et al., 2021). Serostatus was assessed using a two-step enzyme-linked immunosorbent assay (ELISA) with estimated sensitivity of ${\hat{\sigma }}_e=0.95$ from $n_1=40$ PCR-confirmed positive samples and estimated specificity of ${\hat{\sigma }}_p=1$ from $n_2=74$ negative controls, 56 of which were pre-pandemic and 18 of which did not have confirmed SARS-CoV-2 infection.

In this analysis, the samples were grouped into five collection rounds of approximately equal length of time. The demographics considered were sex, age group, and race. Sex was categorized as male/female, with one individual of indeterminate sex excluded. Five age groups were $[0,20),[20,40),[40,60),[60,80)$, and $[80,103]$. Race was coded as Asian, Black or African-American, Other, and White, with 446 individuals of unknown race excluded. After exclusions, the sample size ranged from $n_3=937$ to 1,576 in the routine care group and $n_3=622$ to 955 in the urgent care group across the collection rounds. The target population for standardization was NYC (8,336,044 persons), with stratum proportions and population size obtained from the 2019 American Community Survey (US Census Bureau, 2019). Table 1 compares the distributions of sex, age group, and race in the routine and urgent care groups to the NYC population. Women were over-represented in the routine care group relative to the general population of NYC. Persons aged 0–19 were under-represented in both groups, and persons aged 60 and older were over-represented. Persons with race classified as Other were over-represented in both groups relative to the NYC population. There was slight non-positivity in four of the five collection rounds for the routine group and five of the five rounds for the urgent care group, and ${\hat{\pi }}_{SRG}$ made inference to restricted target populations. The model-based estimators ${\hat{\pi }}_{SRGM}$ included main effects for sex, age group, and race and an interaction term between sex and age group.

Table 1.

Demographic comparisons of the New York City (NYC) seroprevalence study (9 Feb–5 July 2020) routine and urgent care group samples with the NYC population

		Routine care		Urgent care		NYC
		n	%	n	%	n	%
		6,348	100	3,898	100	8,336,044	100
Sex	Female	4,274	67	1,789	46	4,349,715	52
	Male	2,074	33	2,109	54	3,986,329	48
Age	0–19	238	4	93	2	1,887,268	23
	20–39	2,624	41	551	14	2,608,394	31
	40–59	1,396	22	1,065	27	2,080,599	25
	60–79	1,780	28	1,633	42	1,426,301	17
	80+	310	5	556	14	333,482	4
Race	Asian	562	9	217	6	1,202,530	14
	Black or African-American	1,287	20	1,051	27	2,057,795	25
	Other	1,774	28	1,514	39	1,528,503	18
	White	2,725	43	1,116	29	3,547,216	43

Note. Data on the NYC population are from the 2019 American Community Survey (US Census Bureau, 2019). Sample size is denoted by n. Some column totals do not sum to 100% because of rounding.

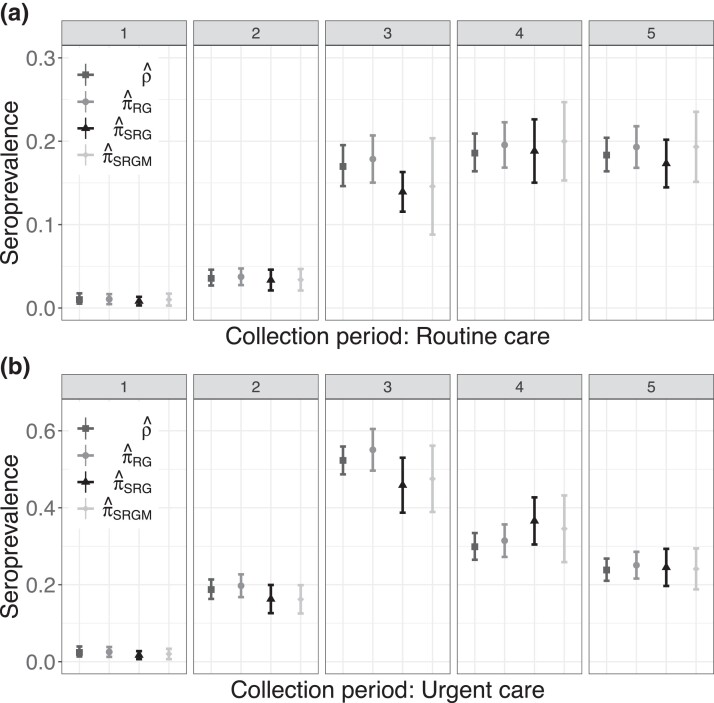
Seroprevalence estimates are presented in Figure 4. Adjusting for assay sensitivity and specificity resulted in slightly higher estimates and slightly wider CIs than the naive estimator $\hat{\rho }$. Standardization had the largest impact on the estimates in the third round, when ${\hat{\pi }}_{RG}$ and the standardized estimators differed by as much as 9 percentage points. The standardized estimates were accompanied by wider CIs relative to $\hat{\rho }$ and ${\hat{\pi }}_{RG}$, reflecting greater uncertainty associated with estimating seroprevalence when not assuming the main study data constitute a random sample from the target population.

Figure 4.

Estimates and corresponding 95% confidence intervals for each of five collection rounds for the New York City seroprevalence study (Stadlbauer et al., 2021), stratified by routine and urgent care groups, described in Section 5.1.

5.2. Belgium seroprevalence study

The standardized Rogan–Gladen methods were applied to a nation-wide SARS-CoV-2 seroprevalence study in Belgium conducted across seven week-long collection rounds between March and October 2020 (Herzog et al., 2022). The final collection round took place before the first vaccine authorization in the European Union in December 2020. Residual sera were collected in a stratified random sample from private laboratories encompassing a wide geographical network, with stratification by age group (10-year groups from 0–9, 10–19, …, 90+), sex (male or female), and region (Wallonia, Flanders, or Brussels). The presence of SARS-CoV-2 IgG antibodies was determined using a semi-quantitative EuroImmun ELISA. Based on validation studies of $n_1=181$ reverse transcription PCR-confirmed COVID-19 cases and $n_2=326$ pre-pandemic negative controls, sensitivity and specificity were estimated to be ${\hat{\sigma }}_e=.851$ and ${\hat{\sigma }}_p=.988$ (Herzog et al., 2022, Table S1.1). The number of samples for assessing seroprevalence varied between $n_3=2,960$ and $n_3=3,910$ across the seven collection rounds.

In this analysis, nation-wide seroprevalence in Belgium was estimated during each collection round standardized by age group, sex, and province (11 total), using 2020 stratum proportion data from the Belgian Federal Planning Bureau (2021). Province was used rather than region to match the covariates selected for weighting in Herzog et al. (2022). Table 2 compares the sex, age group, and province distributions in collection rounds 1 and 7 to the Belgian population as a whole. The seroprevalence study samples were similar to the population, although the study over-represented older persons and under-represented younger persons relative to the population. In six of the seven collection rounds non-positivity arose, with between 2 and 15 of the 220 strata not sampled, so restricted target populations were used for computation of ${\hat{\pi }}_{SRG}$. For ${\hat{\pi }}_{SRGM}$, each logistic regression model had main effects for age group, sex, and province, as well as an interaction term between age group and sex.

Table 2.

Demographic comparisons of the 2020 Belgium seroprevalence study sample participants in collection rounds 1 (30 March–5 Apr) and 7 (9–12 Sept) with the Belgium population

		Round 1		Round 7		Belgium
		n	%	n	%	n	%
		3,910	100	2,966	100	11,492,641	100
Sex	Female	2,111	54	1,589	54	5,832,577	51
	Male	1,799	46	1,377	46	5,660,064	49
Age	0–9	36	1	68	2	1,269,068	11
	10–19	294	8	405	14	1,300,254	11
	20–29	436	11	402	14	1,407,645	12
	30–39	461	12	397	13	1,492,290	13
	40–49	468	12	397	13	1,504,539	13
	50–59	498	13	400	13	1,590,628	14
	60–69	507	13	406	14	1,347,139	12
	70–79	506	13	204	7	924,291	8
	80–89	493	13	160	5	539,390	5
	90+	211	5	127	4	117,397	1
Province	Antwerp	819	21	473	16	1,869,730	16
	Brussels	204	5	288	10	1,218,255	11
	East Flanders	388	10	392	13	1,525,255	13
	Flemish Brabant	261	7	317	11	1,155,843	10
	Hainaut	245	6	271	9	1,346,840	12
	Liege	515	13	425	14	1,109,800	10
	Limburg	318	8	280	9	877,370	8
	Luxembourg	254	7	177	6	286,752	3
	Namur	352	9	170	6	495,832	4
	Walloon Brabant	145	4	101	3	406,019	4
	West Flanders	409	10	72	2	1,200,945	10

Note. Data on the Belgium population are from the Federal Planning Bureau (2021). Sample size is denoted by n. Some column totals do not sum to 100% because of rounding.

Figure 5 displays point estimates and CIs for ${\hat{\pi }}_{RG}$, ${\hat{\pi }}_{SRG}$, and ${\hat{\pi }}_{SRGM}$ alongside those for the unadjusted, or naive, sample prevalence $\hat{\rho }$ for each collection round (with exact Clopper-Pearson 95% CIs). The naive estimates $\hat{\rho }$ were typically greater than the other three estimates and had narrower CIs. The greatest differences were between $\hat{\rho }$ and ${\hat{\pi }}_{RG}$, which can be attributed to (estimated) measurement error in the assay. Both standardized estimates ${\hat{\pi }}_{SRG}$ and ${\hat{\pi }}_{SRGM}$ were similar in value to ${\hat{\pi }}_{RG}$ in most collection periods. These estimates, in combination with the stratified random sampling design, suggest that the magnitude of measurement error in this study may have been larger than that of selection bias.

Figure 5.

Estimates and corresponding 95% confidence intervals for each of seven collection rounds for the 2020 Belgian seroprevalence study (Herzog et al., 2022), described in Section 5.2.

5.3. North Carolina seroprevalence study

The standardization methods of Section 3 were also applied to ScreenNC, which tested a convenience sample of $n_3=2,973$ asymptomatic patients age 20 and older in North Carolina (NC) for antibodies to SARS-CoV-2 between April and June 2020 (Barzin et al., 2020), before the authorization of vaccines in the United States. These patients were seeking unrelated medical care at 11 sites in NC associated with the University of North Carolina (UNC) Health Network. The presence of antibodies was determined with the Abbott Architect SARS-CoV-2 IgG assay. Based on validation studies of $n_1=40$, reverse transcription PCR confirmed positive patients and $n_2=277$ pre-pandemic serum samples assumed to be negative, sensitivity was estimated as ${\hat{\sigma }}_e=1$ and specificity as ${\hat{\sigma }}_p=0.989$.

In our analysis, seroprevalence was estimated in two relevant target populations. First, standardization was made to the population patients accessing the UNC Health Network during a similar timeframe (21,901 patients from February to June 2020). The main study sample differed from this UNC target population in terms of age group, race, and sex characteristics, as seen in Table 3, and meta-analyses suggested that prevalence of COVID-19 infections differed between levels of these covariates in some populations (Mackey et al., 2021; Pijls et al., 2021), supporting the covariates’ use in standardization. Note that several racial classifications, including patient refused and unknown, were reclassified as ‘Other’. Second, standardization was made to the 2019 NC population over the age of 20 (7,873,971 persons) using covariate data from the American Community Survey (US Census Bureau, 2019). The assumption of equal sampling probabilities may be less reasonable for this target population because not all NC residents are in the UNC Health Network and because there were some geographic areas where no patients in the study sample were from. There was no sample data in the main study for two covariate strata that existed in the UNC Health Network, so restriction was used for ${\hat{\pi }}_{SRG}$. Logistic regression models with main effects for sex, race, and age group were used to compute ${\hat{\pi }}_{SRGM}$; interaction effects were not included, as the small number of positive test results could have led to model overfit.

Table 3.

Demographic comparisons of the ScreenNC study sample, UNC hospitals patient population, and North Carolina population aged 20+

		ScreenNC		UNC hospitals		NC
		n	%	n	%	n	%
		2,973	100	21,901	100	7,873,971	100
Sex	Female	1,955	66	13,926	64	4,108,603	52
	Male	1,018	34	7,975	36	3,765,368	48
Race	Asian	67	2	460	2	230,759	3
	Black or Af.-Am.	395	13	5,109	23	1,640,311	21
	Other	311	10	1,799	8	455,600	6
	White or Cauc.	2,200	74	14,533	66	5,547,301	70
Age	20–29	342	12	2060	9	1,400,918	18
	30–39	599	20	2,763	13	1,344,647	17
	40–49	518	18	3,382	15	1,351,156	17
	50–59	602	20	4,200	19	1,360,357	17
	60–69	489	17	4,548	21	1,228,123	16
	70–79	310	11	3,325	15	806,002	10
	80+	77	3	1,623	7	382,768	5

Note. Data on the NC population are from the 2019 American Community Survey (US Census Bureau, 2019). Several racial classifications including Patient Refused and Unknown were reclassified as Other. Sample size is denoted by n. Some column totals do not sum to 100% because of rounding. NC = North Carolina; UNC = University of North Carolina.

The sample proportion of positive tests was $\hat{\rho }=24/2973=0.81\mathrm{\%}$. The sample false positive rate was $1-{\hat{\sigma }}_p=1.08\mathrm{\%}$, so the data are, at first appearance, consistent with a population prevalence of 0%. Indeed, the Rogan–Gladen seroprevalence estimate was ${\hat{\pi }}_{RG}=0$% (95% CI 0%, 1.00%). Likewise, the UNC target population had non-parametric and parametric standardized estimates of ${\hat{\pi }}_{SRG}=0$% (0%, 1.11%) and ${\hat{\pi }}_{SRGM}=0$% (0%, 1.13%), and the NC target population had corresponding estimates of 0% (0%, 1.10%) and 0% (0%, 1.11%). All estimates were truncated into $[0,1]$. The closeness of the standardized and unstandardized results may be due to the small number of positive test results and similarities between the sample and the target populations. Note that the limited violations of positivity and modest demographic differences (Table 3) make this application more similar to DGP 3 than DGP 4. Simulation results suggest the standardized estimators and corresponding CIs may perform well in settings similar to DGP 3, even if the true prevalence is low; e.g. see the lower right facets of Figure 2 and online supplementary Figure 7, where ${\sigma }_e={\sigma }_p=.99$.

6. Discussion

Non-parametric and model-based standardized Rogan–Gladen estimators were examined, and their large-sample properties and consistent variance estimators were derived. While motivated by SARS-CoV-2 seroprevalence studies, the methods considered are also applicable to prevalence estimation of any binary variable for settings where validation data can be used to estimate the measurement instrument’s sensitivity and specificity and covariate data can be used for standardization. Simulation studies demonstrated that both standardized Rogan–Gladen methods had low empirical bias and nominal CI coverage in the majority of practical settings. The empirical results in Section 4 highlight the trade-offs inherent in choosing which method to use for a seroprevalence study. The parametric standardized estimator ${\hat{\pi }}_{SRGM}$ was empirically unbiased even when the number of strata and covariates, and with them the potential for random non-positivity, increased. A drawback to ${\hat{\pi }}_{SRGM}$ is the need to correctly specify the form of a regression model. On the other hand, the non-parametric standardized estimator ${\hat{\pi }}_{SRG}$ does not require model specification and performed well in scenarios with lower amounts of selection bias and non-positivity. As the number of strata and covariates grew, however, ${\hat{\pi }}_{SRG}$ was empirically biased and its corresponding 95% CIs did not attain nominal coverage.

For practical use of either method, careful choice of covariates is necessary. Including additional covariates may make the assumption of equal probability of sampling within strata more reasonable. However, such inclusion also makes covariate-defined strata smaller and random non-positivity more likely. An alternative strategy is to collapse smaller strata with few or no persons to create larger strata, which may make random non-positivity less likely. However, if strata with sufficiently different sampling probabilities were collapsed together, then the assumption of equal probability of sampling within strata would be violated.

Throughout this paper it was assumed that the validation samples constitute random samples from the population strata of true positives and true negatives. Extensions could be considered which allow for possible ‘spectrum bias’, which can occur if the $n_1$ individuals in the validation sample of true positives are not representative of the general population of seropositive individuals; for instance, a validation sample might be based on hospitalized patients who on average have more severe disease than the general population of seropositive individuals. Spectrum bias can lead to overestimates of sensitivity and underestimates of seroprevalence, but can be overcome using Bayesian mixture modelling of continuous antibody response data (Bottomley et al., 2021) or longitudinal modelling of antibody kinetic and epidemic data (Takahashi et al., 2021).

The limitations of Wald-type confidence intervals as they relate to parameters near their boundary values are mentioned in Sections 2.2 and 4. Alternative confidence intervals could be considered based on the bootstrap (Cai et al., 2022), Bayesian posterior intervals (Gelman & Carpenter, 2020), test inversion (DiCiccio et al., 2022), or fiducial confidence distributions (Bayer et al., in press). In particular, extensions of CIs designed to guarantee coverage at or above the nominal levels (Bayer et al., in press; Lang & Reiczigel, 2014) could be developed to accommodate potential selection bias due to unknown sampling probabilities.

Other topics for future research and broader issues in SARS-CoV-2 seroprevalence studies merit mention. While the approaches here estimate seroprevalence at a fixed point in time, seroprevalence is a dynamic parameter. For analysis of studies with lengthier data collection periods, extensions of the estimators in this paper could be considered which make additional assumptions (e.g. smoothness, monotonicity) about the longitudinal nature of seroprevalence. Another possible extension could consider variations in assay sensitivity, which may depend on a variety of factors such as the type of assay used; the recency of infection or vaccination of an individual; disease severity in infected individuals; the type and dose of vaccine for vaccinated individuals; and so forth. Where additional data are available related to these factors, then extensions of the standardized Rogan–Gladen estimators which incorporate these additional data could be developed. As an alternative to standardization, inverse probability of sampling weights (Lesko et al., 2017) or inverse odds of sampling weights (Westreich et al., 2017) could be considered. Standardization and weighting methods may possibly be combined to create a doubly robust Rogan–Gladen estimator.

Funding

This research was supported by the NIH (Grant R01 AI085073), the UNC Chapel Hill Center for AIDS Research (Grants P30 AI050410 and R01 AI157758), and the NSF (Grant GRFP DGE-1650116). The content is solely the responsibility of the authors and does not represent the official views of the NIH.

Data availability

Data and R code supporting the Belgium and North Carolina seroprevalence study findings in Section 5 are available at https://github.com/samrosin/rgStandardized˙ms. Data supporting the New York City seroprevalence study findings include both data available from Stadlbauer et al. (2021) and individual demographic data shared by the authors of that study.

Supplementary material

Supplementary material is available online at Journal of the Royal Statistical Society: Series A.