Abstract
Recently, MAX phases have attained considerable technological interest owing to their two inherent properties metallic and ceramic properties. This study extensively examined Nb2ScAC2 MAX phases using DFT, to assess the structural, mechanical, electronic, and Thermal characteristics. Firstly, the stability of these two compounds was confirmed through the formation energy, elastic constants (Cij), and phonon band structure, which confirmed their thermodynamic, mechanical, and dynamical stability. The optimized lattice parameters of these compounds were examined and then utilized to calculate the physical properties of the Nb2ScAC2 compound. Our compounds are brittle due to their Pugh’s ratio of less than 1.75. The covalent bonding of the structure revealed by the Poisson ratio is less than 0.25 for the two compounds. The Nb2ScAC2 material is anisotropic, and Nb2ScAlC2 is harder than Nb2ScSiC2.The metallic character of the materials was affirmed by the electronic band structure analysis. Calculated thermal properties such as Debye temperature and minimum and lattice thermal conductivity reveal that both compounds have the potential to enhance their deployment in thermal barrier coating materials. On the other hand, the high melting temperatures indicate that our compounds could potentially be utilized in demanding or severe conditions. Finally, the thermodynamic characteristics, comprising the isochoric heat capacity (Cv) and Debye temperature (ϴD) were analyzed subjected to high temperatures and pressures. The optical constants such as real and imaginary parts of the dielectric function, refractive index and reflectivity, are investigated. The current study recognizes these two compounds as promising candidates for utilization in modern technologies and diverse industries.
Subject terms: Materials science, Physics
Introduction
Recently, the MAX phase has garnered significant interest in the cutting-edge world due to its excellent mechanical and thermal properties of these compounds at elevated temperatures, exhibiting characteristics of both metals and ceramics1–3. Consequently, it has found extensive applications in diverse industrial fields, including machinable refractories, ductile heating elements operating at elevated temperatures, coatings for electrical contacts, and nuclear-resistant components for neutron irradiation. Recently, certain materials have exhibited potential as Thermal Barrier Coatings (TBCs)4–7. The MAX phases are an ideal option for high-temperature TBC applications8, Ta2AlC and Cr2AlC have been identified significant potential for use as thermal barrier coatings due to their low minimum thermal conductivity, which can be at a minimum value of 0.855 W/(m–K) and 0.963 W/(m–K) respectively. In addition, Ta4AlC3 has a lattice thermal conductivity of 5 W/m–K and an experimental value of 6 W/m–K at 1300 K, while Nb4AlC3 has a lattice thermal conductivity of 7 W/m–K at 1300 K9. Efforts to develop improved TBC materials are hindered by the inadequate information on the thermal and mechanical properties of MAX phases. Comprehending the transfer of properties within the MAX phase oxide family and establishing an effective screening method are essential to accelerate the creation and identification of TBC materials based on MAX phases10–12. Materials containing Niobium (Nb) are attracting attention due to their demonstrated usefulness in various modern technologies, diverse industries, and structural transitions. They also enable the application of exceptionally high-temperature Thermal Barrier Coatings (TBC)13. One notable example is the incorporation of Nb on the M-site, which provides an opportunity to synthesize metallic-based nano-lamellar materials with desirable electronic properties14. A study by M.A. Ali et al. the physical properties of the new MAX phase borides Nb2SB were studied, and they showcased the best combination of mechanical properties in bulk crystal form15. In the current year, P. Das et al. published a report on the physical properties of the Nb2AC (A = Ga, Ge, Tl, Zn, P, In, Cd, and Al) 211-MAX phase compound. Their findings indicated that this compound has potential suitability for applications as solar radiation-protecting coatings and thermal barrier coating (TBC) materials16. Furthermore, M. R. Rana et al. discovered that MAX phase borides, specifically M2GaB (M = Sc, V, Nb, Ta) compounds, have the potential to serve as coating materials for the purpose of reducing solar heating17. In the aforementioned applications of MAX phases, several specific materials have been studied. Some of the notable materials investigated include: (Ti1-xMox)2AlC (0 ≤ x ≤ 0.20)18, Ti-based M2AX phases 314-MAX phase boride Zr3CdB419, 27 S-based M2SX (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W; X = B, C, N)20, Te-containing layered ternary Hf2TeB MAX phase21. MAX phases are a large family of materials; they are more than one hundred and fifty various compositions have been studied and researched, over the past 25 years22–26. They are structured in layers and present a unique combination of properties. Despite their excellent properties, their industrial utilization is limited by the main factors: (i) it takes a significant amount of time to obtain licenses for products in industries. (ii) Large and complex family of materials. (iii) Higher pure commercial powders are unavailable27. Actually, MAX phases are structured in atomic layers forming both metallic and covalent bonding responsible of their ceramic and metallic character. Their structure consists of « Mn+1Xn » ceramic layers where n = 1, 2, and 3 intercalated layers of metallic "A-group elements" that are separated by layers that are only about one atom thick. The M-X bonds in MAX phases are robust, whereas the M-A bonds are comparatively weaker. All MAX phases exhibit a hexagonal crystal structure characterized by the space group P63/mmc (N° 194)28. The MAX phases are distinguished by a close-packed arrangement of “M” atoms interpolated with A-group atomic laminae, with “X” atoms occupying the octahedral positions between the M layers. Because of this arrangement, the MAX phases possess laminated layered structure, which qualifies them as nano-laminates. The researchers have suggested that the chemical, physical, and mechanical properties of MAX phase Mn+1AXn can be improved by introducing double transition metal. As a result, MAX phase compounds hold the potential for enhancing the characteristics exhibited by this category of materials for future engineering applications by adding double transition metal on “M” sites29. MAX phase compounds have recently gained significant attention from the scientific community due to the potential to customize their physical properties by adding a fourth element to the M-site. As a result, the expansion of their research has resulted in the establishment of a new research wing and the broadening of their field of applications. The compounds have demonstrated significant improvements in essential properties including oxidation resistance, fracture toughness, strength, and self-healing capabilities. Furthermore, both theoretical and experimental efforts have been undertaken to enhance the hardness and strength of quaternary MAX phases. For instance, new products such as Cr2TiAlC230,31, Mo2ScAlC2 and Mo2TiAlC232,33 have been synthesized. A recent study by Ouadha et al. presented a comprehensive theoretical analysis of a new ferromagnetic quaternary Mn2VSnC2 compound, which demonstrated both mechanical and thermodynamic stability in the α-polymorph ferromagnetic arrangement. The study also revealed that the compound has potential applications in harsh environmental conditions34,35. Benjemai et al. pursued a similar approach in their study of V2ScSnC2 and Nb2ScSnC2 compounds, examining several of their physical properties and proposing potential applications in modern contexts, such as high-energy applications36. Therefore, conducting theoretical research on other materials is of great significance. The present study aims to explore the structural, electronic, mechanical, lattice dynamic and optical properties and verify the stability of V2ScSnC2 and Nb2ScSnC2 compounds for the first time. Based on these properties it can be decided whether Nb2ScAC2 be a suitable candidate material for high energy applications. The following sections are arranged as: Section "Details of computational methodology" describes the method of calculations; the results are described with implications in Section "Results and discussions". Finally, in Section "Conclusions", concluding remarks are presented.
Details of computational methodology
The FP-LAPW scheme has been utilized all over this study37–39, coded within WIEN2K40. We adopted the (GGA-PBE) for the exchange–correlation functional41. Therefore, the input parameters must be chosen in the sake of obtaining good precisions of the results. An R × Kmax value of 8 has been utilized. Similarly, the maximum values of lmax = 10 and Gmax = 14 have been chosen for the largest G-vector in charge density Fourier expansion and for the magnitude of “l” for the partial waves within atomic spheres, respectively. For the RMT radii for Niobium (Nb), Scandium (Sc), Aluminium (Al), Silicon (Si) and carbon (C) we have chosen 1.97, 2.2, 2.5, 2.2 and 1.62 respectively. The SCF-cycles are performed iteratively until convergence energy reached 10–5 Ry and the same for charge convergence. We have used the Monkhorst–pack method to sample the irreducible Brillouin zone of our predicted compounds, with 9 × 9x2 special k-points. The cut-off energy of -6 Ry was selected to establish the separation of valence and core states. The thermodynamic properties were computed using the quasi-harmonic Debye model approximation, which was executed in the Gibbs2 software42.
The elastic parameters were determined using the measured elastic constants and the Voigt-Reuss-Hill approximations43. The following relations define these elastic parameters:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
The following equations can be used to derive Young's modulus (E) and Poisson's ratio from the bulk and shear moduli;
| 7 |
| 8 |
The Cauchy pressure for hexagonal structured materials can be approximated along two distinct orientations44.
| 9 |
| 10 |
The elastic moduli are further used to estimate the hardness of both compounds by using the following expressions45:
| 11 |
For a material with a hexagonal structure, the shear anisotropy factor can be determined for three different crystallographic planes: (1,0,0), (0,1,0), and (0,0,1), using the following equations46:
| 12 |
| 13 |
| 14 |
The following equation can be used to obtain the linear compressibility coefficient (kc/ka)47:
| 15 |
Results and discussions
This study represents the first comprehensive investigation into the equilibrium ground-state properties, as well as the thermodynamic and dynamical stability, of the quaternary Nb2ScAC2 (A = Al or Si) MAX phases. Furthermore, this study investigates the mechanical, thermal, and electronic characteristics of these compounds to enhance our understanding of their potential applications. Using the methods described above, the results for these MAX phases are presented in detail in this section, with each physical characteristic analyzed separately.
Structural properties
The hexagonal structure of space group P63/mmc (No.194) is shared by both Nb2ScAlC2 and Nb2ScSiC2, which are MAX phase compounds. The unit cell of these MAX phase compounds is conventionally composed of 12 atoms, as depicted in Fig. 1. Table 1 presents the Wyckoff positions of Nb2ScAC2 (A = Al or Si), where ZM and ZC refer to the internal parameters of “Nb” and “C” atoms, respectively. In this study, the internal parameter c/a ratio and the (a, c) parameters were relaxed for each structure that was analyzed. The equilibrium cell volume was determined by optimizing the cell geometry using the conjugate gradient approach for total energy minimization. The energy vs. volume data for each structure was plotted and fitted using the Birch-Murnaghan EOS to determine the equilibrium ground state. The graphical representation of the overall energy with respect to volume for their two feasible configurations (α- and β-polymorph) is illustrated in Fig. 2. The lower total energy of the α-polymorph ensures that it is more stable for both Nb2ScAlC2 and Nb2ScSiC2 compounds. In order to assess the stability of our compounds and gain insights into their thermodynamic behavior, the calculation of formation energies is employed as the most reliable indicator. The formation energies of both compounds are determined using the following equation48:
| 16 |
where is the formation energy of Nb2ScAC2 with (M = V and Nb), Etot. is the total energy per unit cell of the bulk compounds , and finally ‘a’, ‘b’, ‘c’ and ‘d’ indicates a number of Nb , Sc, (Al/Si) and C atoms in a unit cell of in the cell respectively. From Table 2 summarizes the lattice parameters, formation energies, and comparison studies for the two compounds, indicates that the Nb2ScAC2 compounds have negative formation energy, indicating their thermodynamic stability. It is noteworthy that Nb2ScSiC2 has particularly negative formation energy, indicating that it is more stable than Nb2ScAlC2. It should be noted that, as far as we know, no previous measurements or calculations have been conducted to determine the formation energy of Nb2ScAC2 compounds. Thus, our results can be regarded as a precise theoretical forecast.
Figure 1.
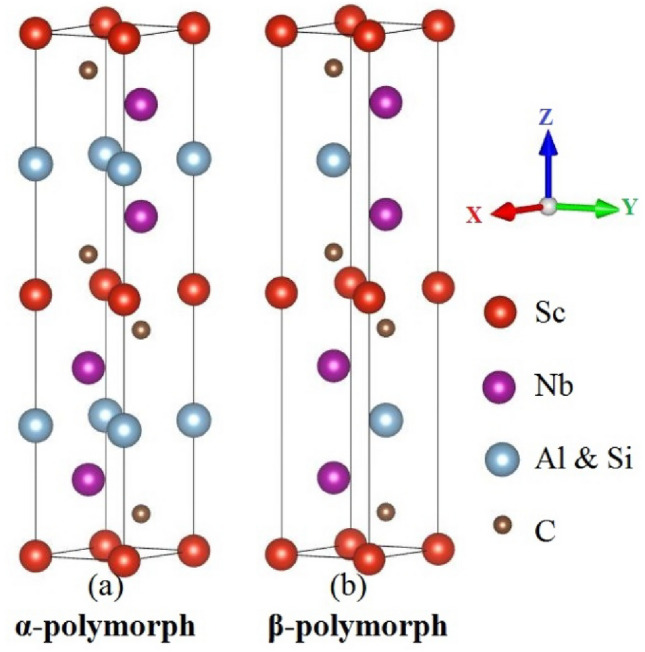
An illustration of the crystal structure of the MAX phases Nb2ScAC2 (A = Al & Si).
Table 1.
The Wyckoff positions of the polymorphs.
| Atom | Site | Coordinates | |||
|---|---|---|---|---|---|
| Wyckoff | X | y | Z | Zi-range | |
| α-polymorph | |||||
| MI(Sc) | 4f. | 0 | 0 | 0 | – |
| MII(Nb) | 2a | ZM | 0.1272771/0.1401692 | ||
| A(Al/Si) | 2d | 0 | 0 | – | |
| X(C) | 4f. | ZC | 0.071231/0.078092 | ||
| β-polymorph | |||||
| MI(Sc) | 4f. | 0 | 0 | 0 | – |
| MII(Nb) | 2a | ZM | 0.120231/0.123022 | ||
| A(Al/Si) | 2d | – | |||
| X(C) | 4f. | ZC | 0.069541/0.072292 | ||
1Nb2ScAlC2, 2Nb2ScSiC2.
Figure 2.
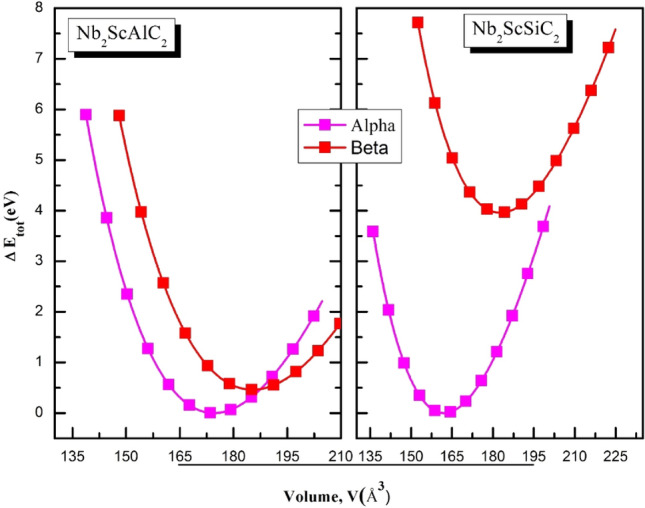
Changes in the energy with respect to volume for the quaternary Nb2ScAC2 compounds.
Table 2.
Computed structural parameters for both the compounds.
| Compounds | Phase | a (Å) | c (Å) | c/a | B (GPa) | B’ | Energy (eV) | Eform (eV/atom) | |
|---|---|---|---|---|---|---|---|---|---|
| Nb2ScAlC2 | Our work | Alpha | 3.2369 | 19.2271 | 5.9398 | 175.9247 | 4.0254 | − 474,799.4163 | − 4.062 |
| Beta | 3.1427 | 21.6585 | 6.8915 | 159.2836 | 4.0267 | − 474,798.9553 | − 4.023 | ||
| Nb2ScSiC2 | Alpha | 3.2000 | 18.2819 | 5.7129 | 203.4167 | 4.0204 | − 477,372.4966 | − 3.164 | |
| Beta | 3.2232 | 20.3093 | 6.3009 | 172.4173 | 4.3757 | − 477,368.54063 | − 2.931 | ||
| Mo2ScAlC2 | 32 | Alpha | 3.0524 | 19.0638 | – | – | – | – | – |
To verify the dynamic stability of the quaternary Nb2ScAC2 (A = Al or Si) MAX phases, we employed the finite displacement method, coded in the WIEN2K package, to calculate the phonon band structures of the compounds in the frequency interval of 0 THz to 30 THz. The hexagonal crystal structure of Nb2ScAC2 consists of 12 atoms per unit cell, while the phonon dispersion graph contains 36 branches consisting of 12 acoustic and 24 optic branched. The resulting phonon dispersion curves are displayed in Fig. 3. Notably, the dispersion relations for both substances exhibit only positive values, with the absence of negative values, which are an indication of imaginary phonon frequencies. This positive dispersion confirms the dynamical stability of the phonon modes in both compounds, providing further evidence for their overall thermodynamic stability. Moreover, the acoustic mode frequency is zero at the center zone point (Γ), robustly indicates that the Nb2ScAC2 is dynamically stable. So far, in our knowledge, phonon dispersion of both compounds has not been investigated theoretically or experimentally yet.
Figure 3.
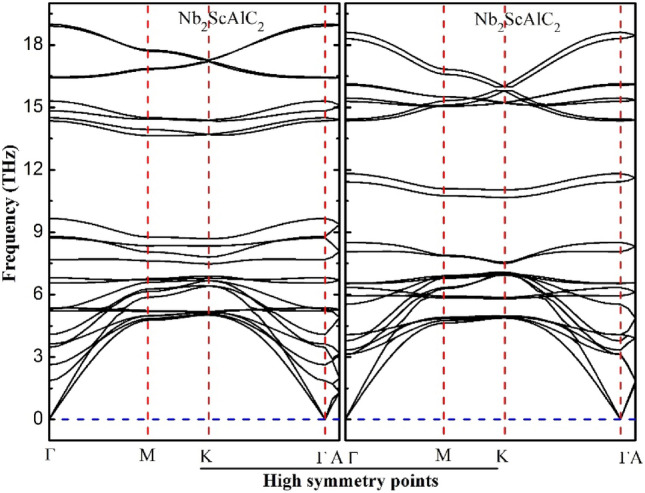
Calculated phonons dispersion for Nb2ScAC2 (A = Al, Si) compounds within the high symmetry directions of the initial Brillouin zone.
Mechanical properties
The elastic constants can be employed to comprehend the mechanical characteristics of a material (Cij), which determine its response to external forces and provide insights into its mechanical properties. The mechanical stability and toughness of a material can be determined by these constants. To calculate elastic constants for a hexagonal crystal, the IR-elast package is used, which requires only five independent elastic constants. When a material is subjected to deformation within an elastic range, these constants can be used to link the mechanical response to the material's strength or weakness.
Elastic moduli and hardness
The elastic constants (Cij) can reveal information about the type of bonding between atoms, as they are the derivatives of the internal energy. The hexagonal structure of MAX phases results in only five independent Cij, namely C11, C12, C13, C33, and C44, subject to ensuring the subsequent requirements49:
| 17 |
Table 3 shows the elastic constants obtained from our calculations and compared with other theoretical studies. Our compounds satisfy the Born stability criteria, suggesting that they are mechanically stable against small elastic deformations. In order to evaluate the resilience of linear compression along the crystallographic a- and c-axes, the elastic constants C11 and C33 are calculated accordingly. Analysis of the elastic tensor indicates that for the compounds under study, C11 is higher than C33. This difference can be explained by the fact that along the a- and b-axes, the material exhibits higher resistance to compression along the a-axis compared to the c-axis. By analyzing the shear elastic constants C12 and C13, it was found that the maximum values were observed in the compounds under study in comparison to other compounds of the MAX phase, suggesting that both compounds are more effective in resisting shear deformation along the crystallographic c-direction than along the crystallographic a- and b-directions under certain stresses.
Table 3.
Calculated elastic constants (Cij) (in GPa).
The stiffness of the material under investigation can be evaluated using the B, G, and E values obtained from the study. Table 4 presents the estimated values of B, E, and G. It is remarkable from Table 4 that Nb2ScAlC2 is less stiff than Nb2ScSiC2 which themselves are less stiff than the quaternary compound Mo3TiAlC2. However, compared to the same quaternary compound Mo2ScAlC2 (the Pugh’s ratio = 1.72) they are more brittle than this one. It should be noted that the Pugh's ductility index50,51, υ52 and the C11-C44 are the three conformist criteria used to assess the ductility and brittleness of the compounds. Nevertheless, the Pugh ratio carries greater significance as a criterion for determining the brittle or ductile nature of materials. The covalent or ionic bonding nature of a material can be determined based on the sign of the Cauchy pressure. Negative Cauchy pressure indicates a covalent bond, though positive Cauchy pressure indicates an ionic bond. A decisive value of 0.25 is assigned to Poisson's ratio53,54. Furthermore, an ionic bond is typically associated with a high value of Poisson's ratio, while a value below 0.25 is indicative of a covalent bond. Table 4 shows that both compounds have a Poisson's ratio below 0.25, indicating their covalent character, but the Nb2ScSiC2 compound will have a value close to 0.25 and this indicates the appearance of an ionic character, and it will appear clearly in the charge density, also through the Cauchy pressure for the two compounds.
Table 4.
The following parameters were calculated for our compounds in two distinct orientations.
By using the Vicker’s formula, where K = G/B, we estimated the hardness of the compounds. It is apparent from the results that Nb2ScAlC2 has a higher hardness than Nb2ScSiC2. However, the values for both compounds fall within the range of hardness typically observed for MAX phases55.
Anisotropy factor
Evaluating the shear anisotropy factor of materials is crucial to gain insight into the extent of anisotropy in various physical occurrences. The kc/ka can be determined from the equation mentioned earlier. A kc/ka value of 1 signifies that the material is isotropic, while kc/ka > 1 indicates that the compressibility along the a-axis is less than that of the c-axis. Similarly, kc/ka < 1 indicates that the compressibility along the c-axis is less than that of the a-axis. Table 5 displays the anisotropy factors and compressibility coefficients. The value of the kc/ka coefficient is higher than “1” for Nb2ScAlC2, whereas for Nb2ScSiC2 it is lower than 1 (0.90), indicating that the crystals exhibit higher compressibility along the c-axis than the a-axis for Nb2ScAlC2 and vice versa for Nb2ScSiC2. The distinction arises when replacing Al with Si, as Al forms a covalent bond while Si leads to the appearance of an ionic bond, creating a hybrid between covalent and ionic bonding. The results obtained for the electronic and mechanical properties are highly consistent with these findings.
Table 5.
Shear anisotropic parameters were computed for three different shear planes () and .
Thermal properties
The Debye temperature (θD) is often used as a means of correlating physical properties such as thermal conductivity, thermal expansion, melting temperature, specific heat, and lattice vibrations of materials. This papers contain the final details for calculating these parameters and Table 6, presents the calculated values along with the sound wave velocities , , and , as well as their corresponding literature values. The high Debye temperature of our compounds suggests that they may be a promising candidate for use as a thermal barrier coating (TBC) material when compared to other Mo2ScAlC2 and Nb2ScSnC2 compounds. Furthermore, the melting temperature of our compounds has also been calculated and is listed in Table 6. It is evident that our compounds exhibit a higher melting point than the compounds used for comparison, likely due to their associated elastic constants. Notably, our compounds have higher theoretical values than the comparison compound, the results suggest that these materials could potentially be useful in harsh environments.
Table 6.
The properties that were computed include density, longitudinal and transverse elastic wave velocities, average elastic wave velocity (in units of g/cm3 and m/s), Debye temperatures (in Kelvin), melting temperature (in Kelvin), as well as minimum and lattice thermal conductivity at 300K (in units of W/m–K).
| Compounds | ρ(g/cm3) | θD | kmin | kph | |||||
|---|---|---|---|---|---|---|---|---|---|
| Nb2ScAlC2 | Our work | 5.3637 | 8060.67 | 4901.51 | 5415.06 | 660.547 | 1842.642 | 1.256 | 46.03 |
| Nb2ScSiC2 | 5.7943 | 7924.56 | 4633.73 | 5138.49 | 642.316 | 1863.012 | 1.251 | 34.49 | |
| Mo2ScAlC2 | 32 | 6.375 | 12,136 | 4058 | 4617 | 592.7 | – | – | – |
One of the most crucial parameters is the minimum thermal conductivity (κmin). For our investigation, we employed the Clark's model56:
| 18 |
Table 6 displays the calculated values of the minimum thermal conductivity (κmin) for the Nb2ScAlC2 and Nb2ScSiC2 solid solutions. It is noteworthy that both of our compounds exhibit the same minimum thermal conductivity values (0.603 W/m–K and 0.601 W/m–K, respectively). For thermal barrier coatings, a maximum limit of κmin less than 1.25 W/m–K is considered appropriate. Consequently, we can conclude that both compounds may be utilized as materials for thermal barrier coating (TBC) applications57. The obtained result is highly favorable, as MAX phases possess an exceptionally symmetric crystal structure. The unique layered arrangement confers a remarkable degree of symmetry to the crystal lattice, making these materials extremely attractive for a wide array of applications, particularly as coating materials. On the other hand, we have employed Slack's model to calculate the lattice thermal conductivity (kph)58.
Slack's model is an empirical formula, derived as follows:
| 19 |
One of the variables in the equation is the dimensionless Grüneisen parameter, γ, which is obtained from the expression of Poisson's ratio:
| 20 |
The factor A( due to julian is calculated as:
| 21 |
Table 6 displays the calculated kph values at room temperature (300 K) for the materials under investigation. Figure 4 illustrates the dependence of kph on temperature within the range of (100-2000K). Lattice thermal conductivity is extremely susceptible to the Debye temperature. The credibility of the Slack model has been proven for MAX phases because their calculated lattice thermal conductivity matches fairly well with the experimental values. For example, the calculated (experimental) lattice thermal conductivity at 1300 K for Ta4AlC3 and Nb4AlC3 are 5 (6) W/m–K and 7 (7) W/m–K, respectively9. Notably, the replacement of Al with Si results in a disparity ratio of zero, indicating that the two compounds possess the same property. This feature also suggests that the material has potential as a thermal barrier coating (TBC)59.
Figure 4.
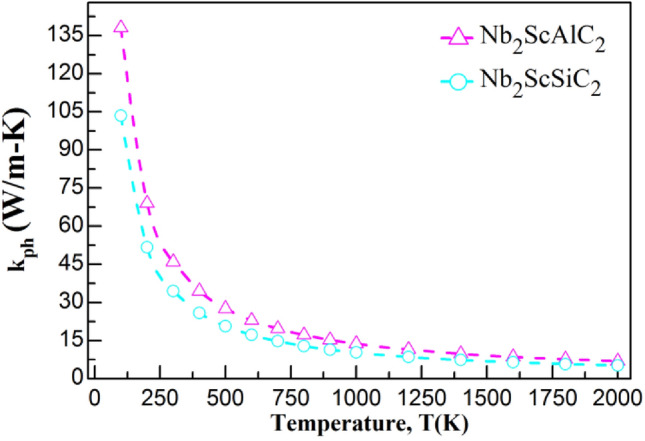
Temperature dependence of the lattice thermal conductivity of the Nb2ScAC2 (A = Al, Si) compounds.
To verify the suitability of studied compounds for TBC application their relevant properties are compared with those of promising TBC materials including MAX phases that are predicted as candidate materials for TBC application in the following Table 7.
Table 7.
The properties that were computed include minimum thermal conductivity Debye temperatures, melting temperature, lattice thermal conductivity, as well as young modulus.
| Compounds | Ref | kmin (W/m–K) | θD (K) | Tm (K) | kph (W/m–K) | E (GPa) |
|---|---|---|---|---|---|---|
| Nb2ScAlC2 | Our work | 1.256 | 660.5 | 1842.6 | 46.03 | 311.0 |
| Nb2ScSiC2 | 1.251 | 642.3 | 1863.0 | 34.49 | 308.6 | |
| Y4Al2O9 | 60 | 1.12 | 564 | 191 | ||
| Al2O3 | 59 | 2323 | ||||
| Ti3ZnC2 | 61 | 1.229 | 617.9 | 1718.9 | 22.84 | 238 |
| Ti3GaC2 | 1.399 | 702.1 | 1872.0 | 45.59 | 305 | |
| Ti3GeC2 | 1.420 | 707.0 | 1913.1 | 41.91 | 319 | |
| Ti3AlC2 | 1.550 | 780.7 | 1866.5 | 53.74 | 307 | |
| Ti3SiC2 | 1.631 | 806.4 | 1975.9 | 52.12 | 340 | |
| Ti3InC2 | 1.208 | 620.6 | 1782.2 | 36.31 | 279 | |
| Ti3SnC2 | 1.230 | 629.3 | 1808.8 | 36.24 | 294 |
Electronic properties
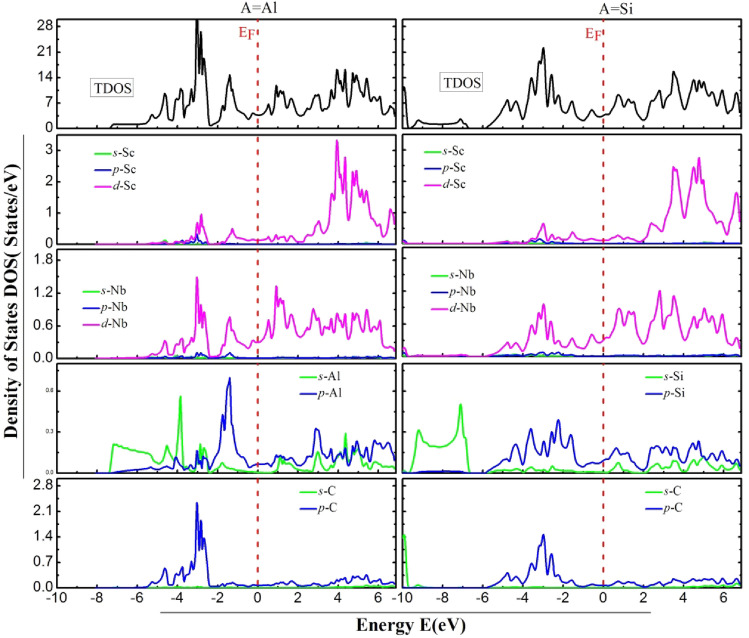
Studying the electronic properties of MAX phases is essential to gain a comprehensive understanding of them. These electronic properties, and the types of bonding that occur between their constituent elements along with the gap energies, are determined by their electronic band structure (EBS) and density of states (DOS). Hence, the analysis of EBS and TDOS is crucial to understand the electronic properties of these materials is depicted in Fig. 5, and Fig. 6, at first sight, we remark that the EBS, TDOS and partial density of states (PDOS) reveals the metallic character of the two compounds. It can be observed that multiple VBs intersect with the Fermi level and coincide with CBs. The (TDOS) and (PDOS) are calculated and plotted in Fig. 6. We can divide the spectrum into three regions founded on the analysis of the Partial Density of States (PDOS). For the Nb2 ScAlC2 we have the following:
Figure 5.
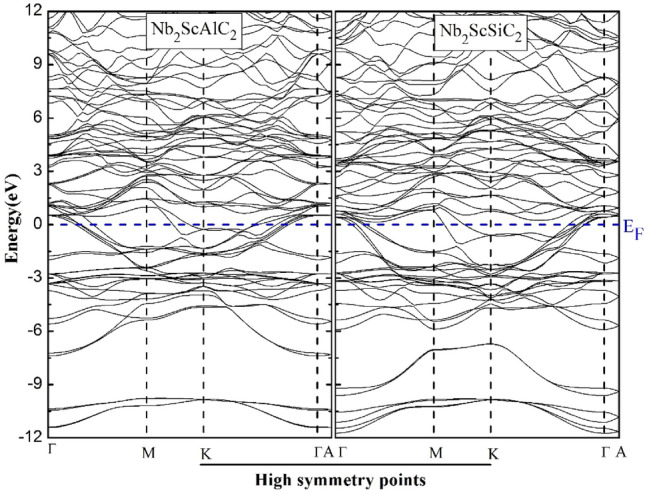
Band structure of the Nb2ScAC2 compounds within the high-symmetry directions of the initial Brillouin zone.
Figure 6.
Electronic densities of states of Nb2ScAlC2 and Nb2ScSiC2.
From − 10 eV to –7eV is the VB dominated by the s states of silicon, the second region (− 7 eV to – 2.5 eV) a strong hybridization between the d(Nb) states and p(C) states and d(Sc) states. (-2.5 eV to EF = 0 eV), the hybridization between the p(Al) states and the d(Nb) states. For the CB it is dominated by the d(Sc, Nb) states. For the Nb2 ScSiC2 compound, the lower VB is dominated by the s(Si) states. From (− 6 Ev to 0 eV) there is a hybridization between p(C) states d(Nb) states and a partial hybridization between the p(Si) states and d(Nb) states. Moreover, the CB is dominated by the d(Nb, Sc) states. This strong pd covalent bonding is mainly origin of the metallicity of our compounds. While the observed results in mechanical properties further substantiate this conclusion.
The Figure demonstrates the calculated electron charge density mapping (in units of e/Å3) along the (110) crystallographic plane, aiming to provide a more detailed description of the chemical bonding nature in Nb2ScAC2. Figure 7 clearly reveals that the positions of C atoms and Nb atoms exhibit the highest accumulation of charge. This observation indicates the presence of strong covalent bonding between Nb and C atoms. The analysis of electronic properties indicates the presence of another covalent bonding between Nb and Si atoms, albeit with a comparatively weaker strength. This finding aligns with the results obtained from elastic constants, hardness measurements, and the density of states (DOS) analysis. It is worth highlighting that in both compounds, the covalent bonding between Nb and C is significantly stronger than that between Nb and Al for Nb2ScAlC2 but for Nb2ScSiC2 the covalent bonding between Nb and C is considered to be similar to the covalent bonding between Nb and Si. This observation is commonly observed in MAX phases, where the stacking of "hard" M-X bonds and "soft" M-A bonds along the c-direction contributes to this difference4. This finding is consistent with the correlation observed between the shear modulus, bulk modulus, and hardness.
Figure 7.
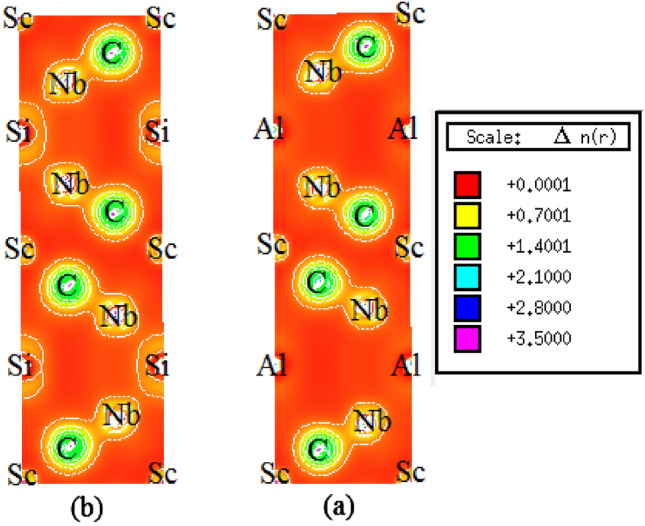
Charge density mapping image of (a) Nb2ScAlC2 and (b) Nb2ScSiC2.
Optical properties
Optical properties of materials have gained significant importance in the current age of information technology62,63. They are also important from the point of view of fundamental physics. The optical properties including dielectric constant, reflectivity and refractive index are calculated for the new layered semiconductor Nb2ScAC2 and their description with implications are given below:
The Fig. 8 shows the real and imaginary parts of the dielectric functions. The real part of the dielectric function ε1(ω) calculated for photon energy of 15 eV is shown in Fig. 8a. It can be said that the solid solutions exhibit highly anisotropic nature at the low energy region from 0 to ~ 4 eV. It is seen that the real part ε1(ω) goes through zero in the low energy range, indicating the metallic nature for all compositions of both compounds. The imaginary part of the dielectric function ε2(ω) represents the optical absorption of a material and is linked with the real part of the optical conductivity. The calculated ε2(ω) for Nb2ScAC2 is shown in Fig. 8b, For both polarization directions it approaches zero from above, indicating the metallic nature of all compositions. At the IR and visible light regions, the spectral features are different for the two polarization directions, highlighting the anisotropic nature in optical properties. At the high energy region the spectra for both polarizations are almost identical for all compositions. The electronic structure of a material is mostly accountable for optical spectra. For this reason, the origin of the peaks in the spectra can be explained from the DOS plot of the relevant material.
Figure 8.
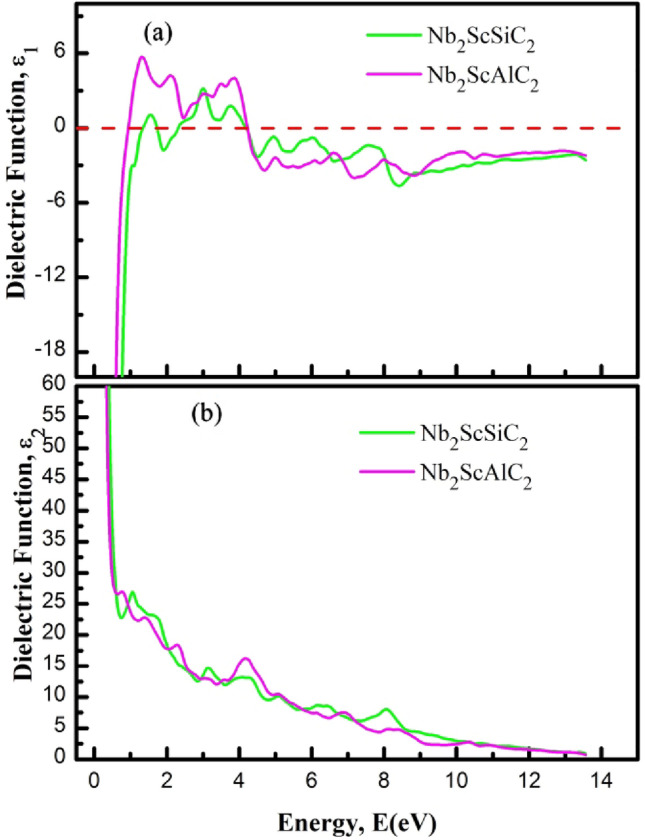
The (a) real of dielectric function (ε1), and (b) imaginary part of dielectric function (ε2) of Nb2ScAC2 (A = Al, Si) compounds.
One of the significant applications of MAX phase materials is their use as coating materials to mitigate solar heating. The evaluation of this capability can be done by studying the reflectivity of the target materials. In our study, we have calculated the reflectivity spectrum of Nb2ScAC2 (A = Al, Si) compounds, illustrated in Fig. 9a. Previous research conducted by M. A. Ali et al. and Li et al.64,65 predicted that MAX phase materials with a reflectivity greater than 44% would effectively reduce solar heating. Based on the obtained reflectivity spectrum, it can be concluded that Nb2ScAC2 (A = Al, Si) compounds meet the criterion with a reflectivity greater than 44%. As a result, these materials have the potential to be utilized as effective coating materials for reducing solar heating.
Figure 9.
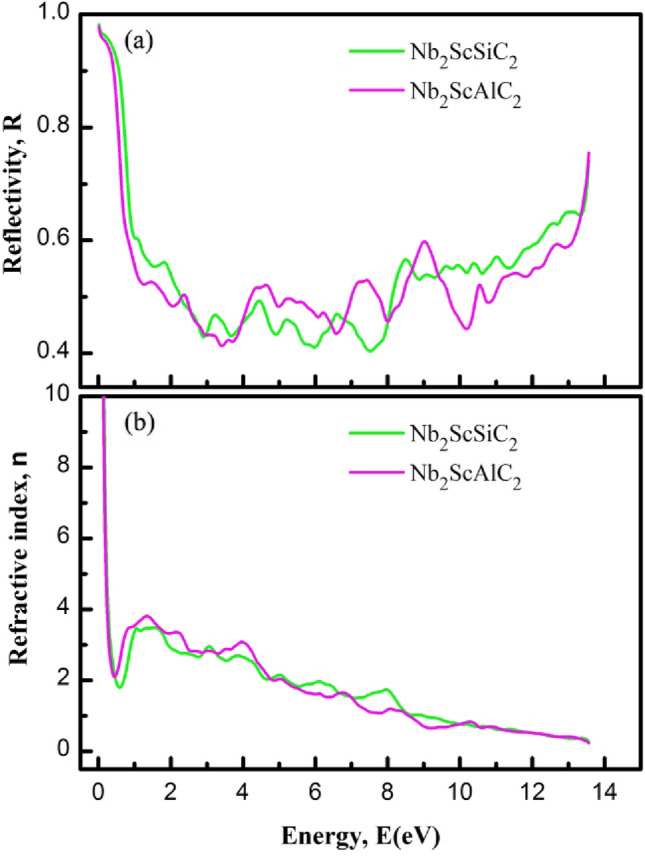
The (a) refractive index (n), and (b) reflectivity (R) of Nb2ScAC2 (A = Al, Si) compounds.
The exact knowledge of the refractive index n(ω) of a material serves as a guide for perfect design of electronic devices. The refractive index is plotted in Fig. 9b. The static values of n(0) for Nb2ScAC2 (A = Al, Si) compounds are 5.91, and 6.64, respectively. These values represent the refractive index, indicating the phase velocity of incident radiation, and are specific to the mentioned compounds.
Thermodynamic properties
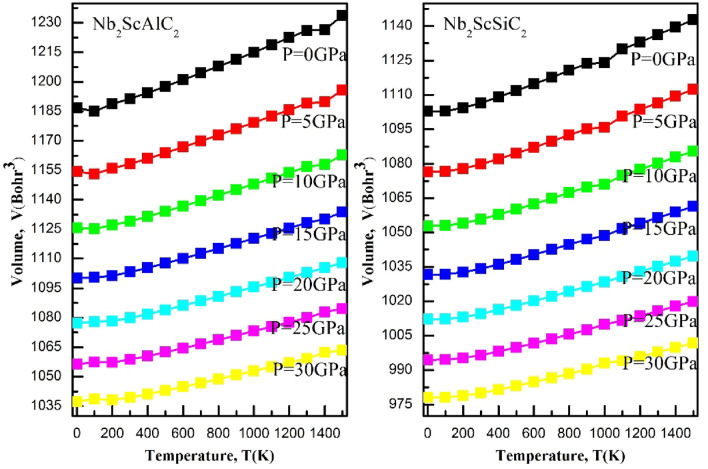
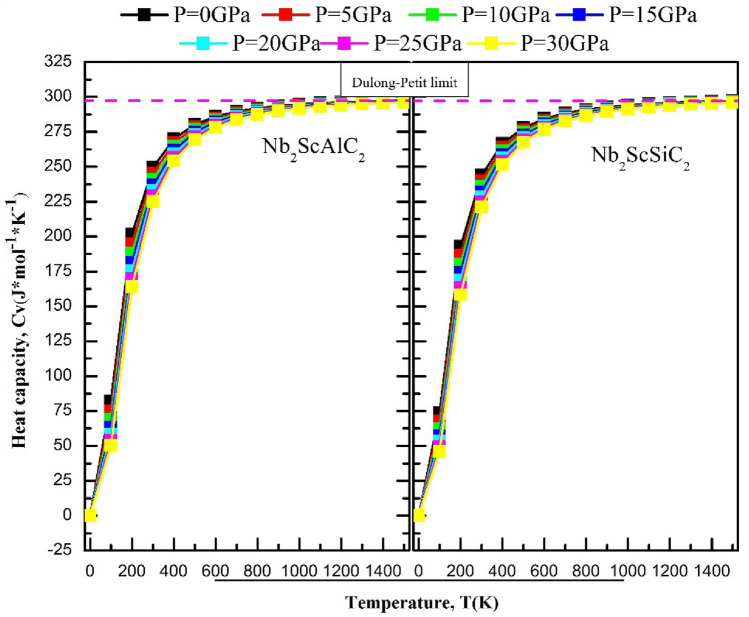
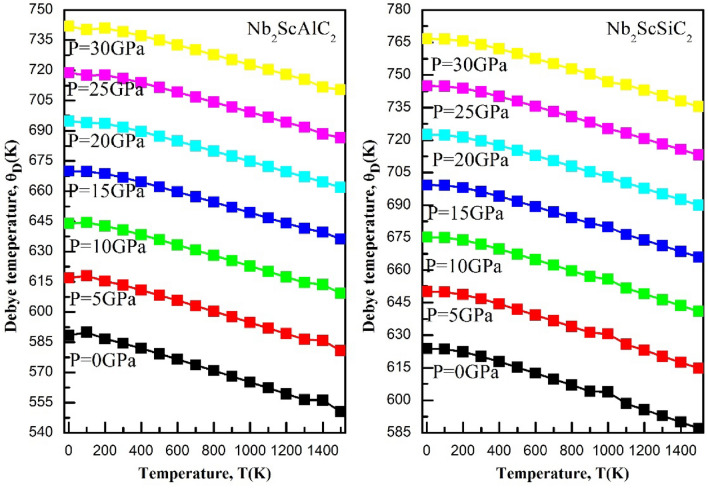
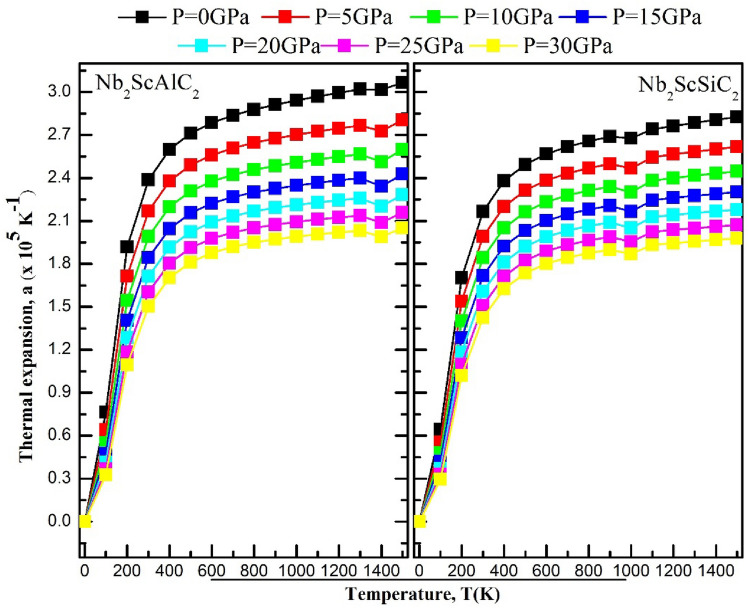
A range of temperatures from 0 to 1500 K and a range of pressures from 0 to 30 GPa are explored to study the thermodynamic properties. The quasi-harmonic Debye model was employed in conjunction with the Gibbs package. The Debye model involves connecting a solid's elastic properties to its acoustic vibrations located at the center of the first Brillouin zone. Figure 10 illustrates the changes in volume for both compounds with respect to temperature and pressure. It is evident that, at a given temperature, the volume experiences a significant reduction with increasing pressure. On the other hand, as the temperature increases, the volume also increases. Therefore, the aforementioned findings strongly establish that alterations in temperature and pressure substantially impact the volume of the α-polymorph of both compounds. Figure 11 illustrates the changes in heat capacity at a constant volume with varying temperature at different pressures. For both compounds, the heat capacity at a constant volume approaches the Dulong-Petit classical limit at high temperatures. They exhibit a similar behavior to that of the ternary compounds V3SnC2 and the quaternary compound Mn2VSnC2. Within the temperature range of 0 K to 300° K, the heat capacity at constant volume cv, exhibits a rapid increase proportional to T3 and eventually attains a constant value at higher temperatures, adhering to the classical Dulong-Petit asymptotic limit. Figure 12 shows the Debye temperature, ƟD, as a function of temperature and pressure, the Debye temperature serves as an indicator of the strength of bonding in crystals. As temperature rises, atomic vibrations weaken the interatomic bonds, causing a decrease in ƟD. It can be observed that, at a given pressure, ƟD decreases as the temperature increases. As the pressure increases up to 30 GPa, the Debye temperature experiences a significant increase. The thermal expansion coefficient α has been studied with varying temperature and pressure, their effects are shown in Fig. 13. Below 200K, the coefficients augment almost linearly. Exceeding 300K, its intensity reduces to 70% as the pressure increases similarly as the Mn2VSnC2 compound.
Figure 10.
Volume as a function of the temperature at different pressures for the Nb2ScAC2 (A = Al, Si) compounds.
Figure 11.
The graph shows the variation of heat capacity (CV) with temperature at different pressures for the Nb2ScAC2 (A = Al, Si) compounds.
Figure 12.
The variation of the Debye temperature (ƟD) with temperature at different pressures for the Nb2ScAC2 (A = Al, Si) compounds.
Figure 13.
The thermal expansion coefficient as a function of temperature at various pressures for the Nb2ScAC2 (A = Al, Si) compounds.
Conclusions
A new MAX phase compounds based on Niobium has been predicted by using ab-initio calculations and study of their stability for their future use in smart coating. The Nb2ScAC2 (A = Al, Si) compounds, were stable in the α-polymorph structure. We calculated their formation energies which are negative ensuring the thermodynamic stability of the two compounds. The electronic band structure of the two compounds shows their metallic behavior. From the point of view of the elastic constants of the structure, the compounds are mechanically stable against elastic deformations. Thermodynamic analysis indicated that the effect of temperature escort the effect of the pressure on the Debye temperature whereas, the coefficient expansion exhibits the opposite effect of both temperature and pressure. The results revealed that these compounds are promising for smart coating and in harsh environment due to their high melting and Debye temperatures compared to quaternary compound like Mo2ScAlC2. Finally, we hope that this report will inspire experimentalists to synthesize these compounds in order to use them in future applications.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the Small Groups Project under grant number RGP.1/427/44. The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [GRANT5,260]. One of the Authors (Ahmed AZZOUZ RACHED) is thankful to Prof Abdallah ZEDJADJ for his friendship and the helpful discussions I had with him all these years. The author, Ahmed AZZOUZ RACHED, dedicates this work to all salaried doctors in Algeria, acknowledging their enduring commitment despite facing various challenges and exposure to exclusion.
Author contributions
A.A-R., M.B. and M.H. designed the project, made the calculation and analysis, and wrote the manuscript. A.B., H.R-D., V.T., A.A., T.A-M. and A.H.A., analyzed the results, plotted the graphs, and reviewed the manuscript. H.A. and N.R. contributed to designing the project, analysis and manuscript.
Funding
Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia Small Groups Project under grant number RGP.1/427/44. Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Kingdom of Saudi Arabia under the annual funding track [GRANT5,260].
Data availability
Data can be provided on request made to the first author, Ahmed Azzouz-Rached.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ahmed Azzouz-Rached, Email: a.azzouzrached@univ-chlef.dz.
Mudasser Husain, Email: mudasserhusain01@gmail.com.
Nasir Rahman, Email: nasir@ulm.edu.pk.
References
- 1.Azzouz-Rached A, Qureshi MW, Ouadha I, Rached H, Hadji T, Rekab-Djabri H. DFT analysis of physical properties of quaternary MAX phase nitrides:(Fe0. 5M0. 5) 2SiN (M= Cr & Mn) Comput. Condens. Matter. 2022;33:e00748. doi: 10.1016/j.cocom.2022.e00748. [DOI] [Google Scholar]
- 2.Ouadha I, Rached H, Azzouz-Rached A, Reggad A, Rached D. Study of the structural, mechanical and thermodynamic properties of the new MAX phase compounds (Zr1-xTix) 3AlC2. Comput. Condens. Matter. 2020;23:e00468. doi: 10.1016/j.cocom.2020.e00468. [DOI] [Google Scholar]
- 3.Ma G, et al. Promoting bonding strength between internal Al-Si based gradient coating and aluminum alloy cylinder bore by forming homo-epitaxial growth interface. Mater. Des. 2023;227:111764. doi: 10.1016/j.matdes.2023.111764. [DOI] [Google Scholar]
- 4.Barsoum MW. MAX Phases: Properties of Machinable Ternary Carbides and Nitrides. John Wiley & Sons; 2013. [Google Scholar]
- 5.Katoh Y, et al. Radiation-tolerant joining technologies for silicon carbide ceramics and composites. J. Nucl. Mater. 2014;448(1–3):497–511. doi: 10.1016/j.jnucmat.2013.10.002. [DOI] [Google Scholar]
- 6.Azzouz-Rached A, Hadi MA, Rached H, Hadji T, Rached D, Bouhemadou A. Pressure effects on the structural, elastic, magnetic and thermodynamic properties of Mn2AlC and Mn2SiC MAX phases. J. Alloys Compd. 2021;885:160998. doi: 10.1016/j.jallcom.2021.160998. [DOI] [Google Scholar]
- 7.Zhu T, et al. Parameters calibration of the GISSMO failure model for SUS301L-MT. Chinese J. Mech. Eng. 2023;36(1):20. doi: 10.1186/s10033-023-00844-2. [DOI] [Google Scholar]
- 8.Gonzalez-Julian J, Go T, Mack DE, Vaßen R. Thermal cycling testing of TBCs on Cr2AlC MAX phase substrates. Surf. coatings Technol. 2018;340:17–24. doi: 10.1016/j.surfcoat.2018.02.035. [DOI] [Google Scholar]
- 9.Dhakal C, Aryal S, Sakidja R, Ching W-Y. Approximate lattice thermal conductivity of MAX phases at high temperature. J. Eur. Ceram. Soc. 2015;35(12):3203–3212. doi: 10.1016/j.jeurceramsoc.2015.04.013. [DOI] [Google Scholar]
- 10.Azzouz-Rached A, Rached H, Babu MH, Hadji T, Rached D. Prediction of double transition metal (Cr1− xZrx) 2AlC MAX phases as thermal barrier coatings: Insight from density functional theory. Int. J. Quantum Chem. 2021;121(20):e26770. doi: 10.1002/qua.26770. [DOI] [Google Scholar]
- 11.Chen D, Wang Q, Li Y, Li Y, Zhou H, Fan Y. A general linear free energy relationship for predicting partition coefficients of neutral organic compounds. Chemosphere. 2020;247:125869. doi: 10.1016/j.chemosphere.2020.125869. [DOI] [PubMed] [Google Scholar]
- 12.Zhang X, Tang Y, Zhang F, Lee C. A novel aluminum–graphite dual-ion battery. Adv. energy Mater. 2016;6(11):1502588. doi: 10.1002/aenm.201502588. [DOI] [Google Scholar]
- 13.Hadi MA, Ali MS, Naqib SH, Islam A. Band structure, hardness, thermodynamic and optical properties of superconducting Nb 2 AsC, Nb 2 InC and Mo 2 GaC. Int. J. Comput. Mater. Sci. Eng. 2013;2(02):1350007. [Google Scholar]
- 14.Wang X-M, et al. Enantioselective synthesis of nitrogen–nitrogen biaryl atropisomers via copper-catalyzed Friedel-Crafts alkylation reaction. J. Am. Chem. Soc. 2021;143(37):15005–15010. doi: 10.1021/jacs.1c07741. [DOI] [PubMed] [Google Scholar]
- 15.Ali MA, Hossain MM, Uddin MM, Islam A, Naqib SH. Understanding the improvement of thermo-mechanical and optical properties of 212 MAX phase borides Zr2AB2 (A= In, Tl) J. Mater. Res. Technol. 2021;15:2227–2241. doi: 10.1016/j.jmrt.2021.09.042. [DOI] [Google Scholar]
- 16.Das P, Jahan N, Ali MA. DFT insights into Nb-based 211 MAX phase carbides: Nb2AC (A= Ga, Ge, Tl, Zn, P, In, and Cd) RSC Adv. 2023;13(8):5538–5556. doi: 10.1039/D2RA07468K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rana MR, et al. DFT prediction of the stability and physical properties of M2GaB (M= Sc, V, Nb, Ta) J. Mater. Res. Technol. 2023;24:7795–7815. doi: 10.1016/j.jmrt.2023.05.008. [DOI] [Google Scholar]
- 18.Ali MA, Naqib SH. Recently synthesized (Ti 1–x Mo x) 2 AlC (0≤ x≤ 0.20) solid solutions: deciphering the structural, electronic, mechanical and thermodynamic properties via ab initio simulations. RSC Adv. 2020;10(52):31535–31546. doi: 10.1039/D0RA06435A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qureshi MW, Ali MA, Ma X. Screen the thermomechanical and optical properties of the new ductile 314 MAX phase boride Zr3CdB4: A DFT insight. J. Alloys Compd. 2021;877:160248. doi: 10.1016/j.jallcom.2021.160248. [DOI] [Google Scholar]
- 20.Tan W, et al. Trends in mechanical, anisotropic, electronic, and thermal properties of MAX phases: a DFT study on M2SX phases. Mater. Today Commun. 2023;35:105759. doi: 10.1016/j.mtcomm.2023.105759. [DOI] [Google Scholar]
- 21.Miao N, et al. Computational prediction of boron-based MAX phases and MXene derivatives. Chem. Mater. 2020;32(16):6947–6957. doi: 10.1021/acs.chemmater.0c02139. [DOI] [Google Scholar]
- 22.Nowotny VH. Strukturchemie einiger verbindungen der übergangsmetalle mit den elementen C, Si, Ge, Sn. Prog. Solid State Chem. 1971;5:27–70. doi: 10.1016/0079-6786(71)90016-1. [DOI] [Google Scholar]
- 23.Zhang P, et al. Enantioselective synthesis of atropisomeric biaryls by Pd-catalyzed asymmetric Buchwald-hartwig amination. Angew. Chemie. 2021;133(40):21886–21890. doi: 10.1002/ange.202108747. [DOI] [PubMed] [Google Scholar]
- 24.Barsoum MW, El-Raghy T. Synthesis and characterization of a remarkable ceramic: Ti3SiC2. J. Am. Ceram. Soc. 1996;79(7):1953–1956. doi: 10.1111/j.1151-2916.1996.tb08018.x. [DOI] [Google Scholar]
- 25.Barsoum MW, Brodkin D, El-Raghy T. Layered machinable ceramics for high temperature applications. Scr. Mater. 1997;36(5):4566. doi: 10.1016/S1359-6462(96)00418-6. [DOI] [Google Scholar]
- 26.Barsoum MW, Farber L, Levin I, Procopio A, El-Raghy T, Berner A. High-resolution transmission electron microscopy of Ti4AlN3, or Ti3Al2N2 revisited. J. Am. Ceram. Soc. 1999;82(9):2545–2547. doi: 10.1111/j.1151-2916.1999.tb02117.x. [DOI] [Google Scholar]
- 27.Gao S, Li H, Huang H, Kang R. Grinding and lapping induced surface integrity of silicon wafers and its effect on chemical mechanical polishing. Appl. Surf. Sci. 2022;599:153982. doi: 10.1016/j.apsusc.2022.153982. [DOI] [Google Scholar]
- 28.Barsoum MW. The MN+ 1AXN phases: A new class of solids: Thermodynamically stable nanolaminates. Prog. Solid State Chem. 2000;28(1–4):201–281. doi: 10.1016/S0079-6786(00)00006-6. [DOI] [Google Scholar]
- 29.Tao Q, et al. Two-dimensional Mo1. 33C MXene with divacancy ordering prepared from parent 3D laminate with in-plane chemical ordering. Nat. Commun. 2017;8(1):4949. doi: 10.1038/ncomms14949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ze-Jin Y, et al. Magnetic moment collapse induced axial alternative compressibility of Cr2TiAlC2 at 420 GPa from first principle. Sci. Rep. 2016;6(1):34092. doi: 10.1038/srep34092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li YF, Ding YC, Xiao B, Cheng YH. Anisotropic electrical and lattice transport properties of ordered quaternary phases Cr2TiAlC2 and Mo2TiAlC2: A first principles study. Phys. Lett. A. 2016;380(44):3748–3755. doi: 10.1016/j.physleta.2016.09.015. [DOI] [Google Scholar]
- 32.Hadi MA, Naqib SH, Christopoulos S-R, Chroneos A, Islam A. Mechanical behavior, bonding nature and defect processes of Mo2ScAlC2: A new ordered MAX phase. J. Alloys Compd. 2017;724:1167–1175. doi: 10.1016/j.jallcom.2017.07.110. [DOI] [Google Scholar]
- 33.Meshkian R, Tao Q, Dahlqvist M, Lu J, Hultman L, Rosen J. Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo2ScAlC2, and its two-dimensional derivate Mo2ScC2 MXene. Acta Mater. 2017;125:476–480. doi: 10.1016/j.actamat.2016.12.008. [DOI] [Google Scholar]
- 34.Husain M, et al. Structural, electronic, elastic, and magnetic properties of NaQF3 (Q= ag, Pb, Rh, and Ru) flouroperovskites: A first-principle outcomes. Int. J. Energy Res. 2022;46(3):2446–2453. doi: 10.1002/er.7319. [DOI] [Google Scholar]
- 35.Husain M, et al. Exploring the exemplary structural, electronic, optical, and elastic nature of inorganic ternary cubic XBaF3 (X= Al and Tl) employing the accurate TB-mBJ approach. Semicond. Sci. Technol. 2022;37(7):75004. doi: 10.1088/1361-6641/ac6d00. [DOI] [Google Scholar]
- 36.Bendjemai M, et al. First-principles calculations to investigate structural, elastic and thermodynamic properties of new M2ScSnC2 (M= V or Nb) quaternary compounds for 312 MAX phases. J. Mater. Res. Technol. 2023;24:3211–3221. doi: 10.1016/j.jmrt.2023.03.212. [DOI] [Google Scholar]
- 37.Hadji T, Khalfoun H, Rached H, Guermit Y, Azzouz-Rached A, Rached D. DFT study with different exchange-correlation potentials of physical properties of the new synthesized alkali-metal based Heusler alloy. Eur. Phys. J. B. 2020;93:1–10. doi: 10.1140/epjb/e2020-10204-5. [DOI] [Google Scholar]
- 38.Bentouaf, A., Rached, H. & Azzouz Rached, A. “Theoretical study of thermal and magneto‐electronic properties of YbX2 (X= Co and Fe) intermetallic compounds,” Energy Storage, e455.
- 39.Husain M, et al. Insight into the physical properties of the inter-metallic titanium-based binary compounds. Eur. Phys. J. Plus. 2021;136(6):1–10. doi: 10.1140/epjp/s13360-021-01590-x. [DOI] [Google Scholar]
- 40.Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, D., & Luitz, J. “wien2k,” An Augment. Pl. wave+ local Orb. Progr. Calc. Cryst. Prop.60(1), 302 (2001).
- 41.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77(18):3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 42.Otero-de-la-Roza A, Abbasi-Pérez D, Luaña V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011;182(10):2232–2248. doi: 10.1016/j.cpc.2011.05.009. [DOI] [Google Scholar]
- 43.Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM J. Appl. Math. Mech. für Angew. Math. Mech.9(1), 49–58 (1929).
- 44.Yang A, Bao L, Peng M, Duan Y. Explorations of elastic anisotropies and thermal properties of the hexagonal TMSi2 (TM= Cr, Mo, W) silicides from first-principles calculations. Mater. Today Commun. 2021;27:102474. doi: 10.1016/j.mtcomm.2021.102474. [DOI] [Google Scholar]
- 45.Jiang X, Zhao J, Jiang X. Correlation between hardness and elastic moduli of the covalent crystals. Comput. Mater. Sci. 2011;50(7):2287–2290. doi: 10.1016/j.commatsci.2011.01.043. [DOI] [Google Scholar]
- 46.Ledbetter HM. Elastic properties of zinc: A compilation and a review. J. Phys. Chem. Ref. Data. 1977;6(4):1181–1203. doi: 10.1063/1.555564. [DOI] [Google Scholar]
- 47.Wang J, Zhou Y, Liao T, Lin Z. First-principles prediction of low shear-strain resistance of Al3BC3: A metal borocarbide containing short linear BC2 units. Appl. Phys. Lett. 2006;89(2):4566614. doi: 10.1063/1.2220549. [DOI] [Google Scholar]
- 48.Zhang Z, Duan X, Jia D, Zhou Y, van der Zwaag S. On the formation mechanisms and properties of MAX phases: A review. J. Eur. Ceram. Soc. 2021;41(7):3851–3878. doi: 10.1016/j.jeurceramsoc.2021.02.002. [DOI] [Google Scholar]
- 49.Mouhat F, Coudert F-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B. 2014;90(22):224104. doi: 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
- 50.Pugh SF. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin. Philos. Mag. J. Sci. 1954;45(367):823–843. doi: 10.1080/14786440808520496. [DOI] [Google Scholar]
- 51.Rached AA, et al. First-principles calculations to investigate physical properties of orthorhombic perovskite YBO 3 (B= Ti & Fe) for high energy applications. RSC Adv. 2023;13(7):4138–4149. doi: 10.1039/D2RA07727B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Savin A, Flad H, Flad J, Preuss H, von Schnering HG. On the bonding in carbosilanes. Angew. Chem. Int. Ed. Engl. 1992;31(2):185–187. doi: 10.1002/anie.199201851. [DOI] [Google Scholar]
- 53.Greaves GN, Greer AL, Lakes RS, Rouxel T. Poisson’s ratio and modern materials. Nat. Mater. 2011;10(11):823–837. doi: 10.1038/nmat3134. [DOI] [PubMed] [Google Scholar]
- 54.Husain M, et al. Examining computationally the structural, elastic, optical, and electronic properties of CaQCl 3 (Q= Li and K) chloroperovskites using DFT framework. RSC Adv. 2022;12(50):32338–32349. doi: 10.1039/D2RA05602J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sokol M, Natu V, Kota S, Barsoum MW. On the chemical diversity of the MAX phases. Trends Chem. 2019;1(2):210–223. doi: 10.1016/j.trechm.2019.02.016. [DOI] [Google Scholar]
- 56.Clarke DR. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003;163:67–74. doi: 10.1016/S0257-8972(02)00593-5. [DOI] [Google Scholar]
- 57.Liu Y, et al. Discovery of AB O3 perovskites as thermal barrier coatings through high-throughput first principles calculations. Mater. Res. Lett. 2019;7(4):145–151. doi: 10.1080/21663831.2019.1566183. [DOI] [Google Scholar]
- 58.Qin G, et al. High-throughput computational evaluation of lattice thermal conductivity using an optimized Slack model. Mater. Adv. 2022;3(17):6826–6830. doi: 10.1039/D2MA00694D. [DOI] [Google Scholar]
- 59.Clarke DR, Phillpot SR. Thermal barrier coating materials. Mater. Today. 2005;8(6):22–29. doi: 10.1016/S1369-7021(05)70934-2. [DOI] [Google Scholar]
- 60.Zhou Y, Xiang H, Lu X, Feng Z, Li Z. Theoretical prediction on mechanical and thermal properties of a promising thermal barrier material: Y4Al2O9. J. Adv. Ceram. 2015;4:83–93. doi: 10.1007/s40145-015-0140-6. [DOI] [Google Scholar]
- 61.Hadi MA, Ahmed I, Ali MA, Hossain MM, Nasir MT, Ali ML, Naqib SH, Islam AKMA. A comparative DFT exploration on M- and A-site double transition metal MAX phase, Ti3ZnC2. Open Ceram. 2022;12:100308. doi: 10.1016/j.oceram.2022.100308. [DOI] [Google Scholar]
- 62.Hadi MA, Panayiotatos Y, Chroneos A. Structural and optical properties of the recently synthesized (Zr 3–x Ti x) AlC 2 MAX phases. J. Mater. Sci. Mater. Electron. 2017;28:3386–3393. doi: 10.1007/s10854-016-5933-z. [DOI] [Google Scholar]
- 63.Peng B, Zhang H, Shao H, Xu Y, Zhang R, Zhu H. The electronic, optical, and thermodynamic properties of borophene from first-principles calculations. J. Mater. Chem. C. 2016;4(16):3592–3598. doi: 10.1039/C6TC00115G. [DOI] [Google Scholar]
- 64.Ali MA, Hossain MM, Uddin MM, Islam A, Jana D, Naqib SH. DFT insights into new B-containing 212 MAX phases: Hf2AB2 (A= In, Sn) J. Alloys Compd. 2021;860:158408. doi: 10.1016/j.jallcom.2020.158408. [DOI] [Google Scholar]
- 65.Li S, Ahuja R, Barsoum MW, Jena P, Johansson B. Optical properties of Ti3SiC2 and Ti4AlN3. Appl. Phys. Lett. 2008;92:22. doi: 10.1063/1.2938862. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data can be provided on request made to the first author, Ahmed Azzouz-Rached.