Abstract
Mitral regurgitation (MR) is the most common type of valvular heart disease, affecting over 2% of the world population, and the gold-standard treatment is surgical mitral valve repair/replacement. Compared to open-heart surgeries, minimally invasive surgeries (MIS) using transcatheter approaches have become popular because of their notable benefits such as less postoperative pain, shorter hospital stay, and faster recovery time. However, commercially available catheters are manually actuated, causing over-exposure of clinical staff to radiation and increased risk of human error during medical interventions. To tackle this problem, in this letter, we propose a telerobotic transcatheter delivery system, which consists of a robotic catheter (5.7 mm OD), a reinforced guide tube (1.11m length), and an actuation system. We present the robotic system design, fabrication of key components, and static model of reinforced quadlumen tube. The robot interface design enables the user to intuitively control the robot. We demonstrate the effectiveness of the telerobotic transcatheter delivery system and reinforced quadlumen tube in a realistic human cardiovascular phantom for preclinical evaluation.
Keywords: Medical robots and systems, telerobotics and teleoperation, steerable catheters, mitral valve, preclinical evaluation
I. Introduction
MITRAL regurgitation (MR) is defined as systolic retrograde flow from the left ventricle (LV) into the left atrium (LA) through the mitral valve (MV) [1], MR is the most common type of valvular heart disease, affecting over 2% of the world population and the prevalence increases with age [2], Open-heart surgery can provide immediate relief through MV repair or replacement, while medications can only reduce the symptoms. However, 50 % of the patients suffering from MR are not recommended an open-heart surgery due to their age and high possibility of post-operative complications [3]. Also, most patients with severe MR are over the age of 75, which mostly makes open-heart surgery unfeasible. Compared to open-heart surgeries, minimally invasive surgeries (MIS) using transcatheter approaches have become popular because of their notable benefits such as less postoperative pain, shorter hospital stay, and faster recovery time [4]—[6]. A review of literature in [7], [8] also shows that minimally invasive MV surgery using a right mini-thoracotomy has long-term outcomes compared to the conventional gold standard MV surgery, but transcatheter mitral valve repair (TMVR) therapy is preferred in patients who are judged inoperable as it does not require a cardiopulmonary bypass. The existing transcatheter systems, such as MitraClip G4 (Abbott, IL) and PASCAL (Edwards Lifesciences, CA), can be used for MV repair [9], [10]. However, these commercially available catheters are manually actuated, cause over-exposure to radiation and increased risk of human error during medical interventions. They also have limited torsion capabilities at the distal end of the catheter, i.e., remote torquing causes torque transmission loss [11].
Using robotic catheters guided by imaging, provides an effective way that can reduce the radiation exposure to users and patients [12]–[14], could potentially require lesser personnel in the operating room, and would be highly repeatable [13]. However, the design of a robotic catheter system is challenging because it requires miniaturization, agility, large workspace envelope, and high stiffness to navigate in tortuous vasculature and dynamic environment (blood flow through the heart). Loschak et al. [15] demonstrated automatic cardiac catheter navigation in-vivo, but they used a commercial ultrasound imaging catheter. Kim et al. [16] developed a teleoperated robotic neurointerventional platform with magnetic manipulation and demonstrated the system’s capability of navigating in narrow and winding pathways. However, their system is designed for neurovascular interventions and is not able to deliver MV implants because the steerable guidewire is very thin and flexible. In our preliminary work [17]-[19], we developed steerable robots to manipulate the MV implant, but the design proposed in this letter is closer to clinical feasibility.
In this letter, we propose a telerobotic transcatheter delivery system (see Fig. 1), including a robotic catheter, a reinforced guide tube, and an actuation system with stabilizer. We discuss the design and fabrication of the robotic system design and the deflection model of reinforced quadlumen tube. Moreover, we develop a telerobotic control method which can help the user operate the robot intuitively. For preclinical evaluation, we demonstrate our system’s capability to navigate pathways and deliver an MV implant in a realistic human cardiovascular phantom while discussing the advantages of using a reinforced quadlumen tube. Also, the features that bring the current robot closer to clinical feasibility over those in [17]–[20] are as follows: 1) reinforced guide tube that can be introduced into a 24Fr commercially steerable outer sheath, 2) actuation system with larger torque outputs and motion ranges, 3) delivery system waterproofed with three-way stopcocks for saline introduction, 4) stabilizer on which the actuation system is mounted, to accurately introduce the catheter into the vasculature, 5) wireless joystick, for easy and intuitive control of the robotic end tip by the surgeon, and 6) demonstration of the procedure in a realistic human cardiovascular phantom.
Fig. 1:
Overview of the telerobotic transcatheter delivery system in a realistic human cardiovascular phantom for preclinical evaluation.
This letter is organized as follows: Sec. II describes the robotic system design, Sec. III presents fabrication, modeling, and the control method used, and Sec. IV and Sec. V explain the experimental validation and discussion, respectively. Finally, conclusions and future work are summarized in Sec. VI.
II. SYSTEM DESIGN
The proposed robotic catheter system, as shown in Fig. 2, consists of three units: a robotic catheter (5.7mm OD), a reinforced guide tube (1.11m length), and an actuation system with stabilizer. The robotic catheter has four joints: two perpendicular bending joints (proximal bending and distal bending), a prismatic joint, and a distal torsion joint. In this letter, we use two perpendicular bending joints, instead of the combination of a proximal torsion joint and a bending joint [18], [19], to strength the catheter’s 3D steering capability. The proximal bending joint is used to align the implant to the MR jet by sweeping the implant along the MV annulus plane in the anterior-posterior direction. This joint contains three concentric 3D printed segments with a total steerable length of 8.52mm and can achieve bending up to ±90°, beyond the clinical required range of ±45°. The distal bending joint is used to align the implant perpendicular to the MV plane. This joint is composed of six concentric 3D printed segments with a total steerable length of 15.66mm and can achieve up to ±120°, beyond the clinical required range of ±90°. Also, the minimum radii of curvature of proximal and distal bending joints are 10mm and 5.95mm, respectively. The prismatic joint can be advanced up to 60mm to deploy the implant under the MV leaflet. The distal torsion joint, similar as the design shown in [19], is used to rotate the implant to align the MV leaflet for effective grasping. This joint can achieve up to ±75° torsion, which exceeds the ±45° motion required for the clinical application.
Fig. 2:
Telerobotic transcatheter delivery system.
The reinforced guide tube (1.11m length) that connects the robotic catheter and the actuation system (see Fig. 2), is designed for tendon and prismatic tube routing. This tube has high axial stiffness to oppose to the tendon forces (maximum ~20N) for bending joints actuation and low bending stiffness to comply with an outer steerable sheath. Sec. III–A details the fabrication of a reinforced guide tube.
The actuation system is used to actuate four joints of the robotic catheter (see Fig. 2), where the bending and distal torsion joints are respectively actuated by two antagonistic tendons. The two antagonistic tendons from each joint (the topmost ring of each bending joint or bottom of the implant), routed through the reinforced guide tube, are attached to the bearing holder and lead screw holder of their joint actuators in the actuation system, respectively. We choose polyethylene (PE) braided line (Hercules, CA) as the tendon because it is made from ultra-high-molecular-weight polyethylene, which has low friction, high strength, great abrasion resistance, small diameter, and high flexibility. Each bending joint actuator and distal torsion joint actuator has a bearing holder, a lead screw holder, and a pulley structure. The lead screw holder is actuated by a DC motor (0.5W, 8mm, Maxon Precision Motors, MA) with a gearbox of gear ratio 64:1 (bending joints) or 16:1 (distal torsion joint). The connection in between the bearing holder and the lead screw holder is held in tension using a pulley and a compression spring (4.75mm OD, spring rate 0.5079N/cm, WB Jones, KY). Hence, the bending joints or distal torsion joint can be actuated by pulling one tendon and releasing the other one. Furthermore, the prismatic joint is advanced by translating a variable stiffness quadlumen tube attached to the motor bracket of the distal joint actuator. This motor bracket, mounted on a linear guide, is advanced by a DC gearmotor (HPCB 6V dual-shaft, gear ratio 100:1, Pololu Corp., NV) through a lead screw mechanism. The prismatic joint can be actuated to 70mm, but we restrict the motion to 60mm for this application which is the clinical requirement. Moreover, we employ a miniature clamp (clamp ID range 7mm to 8.2mm), a washer, and a screw nut (M3×10) to brace each bending joint actuation motor in the actuation system. The tendon stroke of each bending joint is in the range of [−35mm, 35mm] while that of the distal torsion joint is [15mm, 15mm]. For the bending joint actuators, the lead screw holder moves on a M3 lead screw attached to the gearbox of the DC motor (64:1) through a flexible shaft coupler. For the distal torsion joint, the lead screw holder moves on the lead screw directly attached to the 16:1 gearbox of the DC motor. A stabilizer, the support structure for the entire system, is designed to change the robotic catheter’s introduction angle and advancement displacement of the catheter, by adjusting a knob and sleeve bearing carriage on the linear guide rail (igus, Inc., RI), respectively. Also, the actuation system is waterproofed with two three-way stopcocks for saline introduction.
Additionally, the control cabinet (see Fig. 2) consists of an Arduino board (Arduino Due) and four small-sized servo motor drivers (ESCON Module 24/2) for the DC motors. The Arduino Due, connected to a real-time control platform via Ethernet and four motor drivers, is used to convert the position signals from the real-time control platform into PWM signals to actuate the DC motors (through motor drivers), read the position signals from the corresponding motor encoders, and transmit them to the real-time control platform. The proposed robot is being actuated using a model in Simulink Real-Time (MATLAB® R2021a, The Mathworks Inc., MA) designed to control the individual joint of the robot. The user can intuitively send desired position command to the Simulink program and control the individual motor by a wireless joystick. The joystick knob (see Fig. 2) is employed for steering control (proximal bending (PB) up, PB down, distal bending (DB) left, and DB right), and four buttons are employed for prismatic motion control (advance and retract), and distal torsion motion control (counterclockwise rotation and clockwise rotation). The Simulink program includes four DC motor feedback controllers (proportional-derivative (PD) controller with a disturbance observer) and a telerobotic control algorithm (see Sec. III–D).
III. FABRICATION, MODELING, AND CONTROL
In Fig. 2, the robotic catheter’s joints, motor brackets, lead screw holders, bearing holders, connectors on either sides of the reinforced guide tube, the actuation system and the three-way stopcocks inlets are printed using a high-resolution 3D printer (ProJet MJP 5600, 3D Systems, SC) because of their complex designs and miniature features. The base mount of the actuation system (Acrylic, 6.5mm thickness) connected to the carriage, and stabilizer base (Acrylic, 13.0mm thickness) are machined using a laser cutting platform (PLS6.150D, Universal Laser Systems, Inc., AZ). The connectors among the stabilizer base, linear guide rail, and knob are fabricated using a low-resolution 3D printer (Form 3, Formlabs, Inc., MA). The ends of lead screws and shafts in the actuation system are machined using a lathe for assembling and fastening. Also, thin stainless steel sheets (0.25mm thickness), included in the lead screw holder, bearing holder, and pulley bracket for strengthening their structure, are micromachined using a femtosecond laser (Optec Laser S.A., Frameries, Belgium). In this letter, we detail the fabrication of reinforced guide tube and variable stiffness quadlumen tube in Sec. III–A and Sec. III–B, respectively.
A. Fabrication of Reinforced Guide Tube
The proposed reinforced guide tube includes two segments (see Fig. 3): a semi-flexible segment (6.0mm OD and ~1312mm length) and a flexible segment (5.6mm OD and ~88mm length), connected to the actuation system via a tube connector and robotic catheter, respectively. As shown in Fig. 3, the semi-flexible segment consists of several layers as follows: (i) PET medical heat shrink (0.2mm wall, TE Connectivity) to increase axial and torsional stiffness of the straight section; (ii) PVC outer jacket (3.97mm ID, 5.56mm OD, and a durometer of 70A) to waterproof and connect the robotic catheter and the actuation system; (iii) stainless steel spring (0.3mm wire diameter and 4.0mm OD, MiSUMi USA, Inc., IL) to increase axial stiffness; (iv) braided PTFE liner with PebaSLIX™ 72D jacket (2.31mm OD, 1.98mm ID, Duke Extrusion, CA) to protect the quadlumen tube from kinking and reduce friction for advancing and retracing the quadlumen tube; (v) four PTFE liners (0.381mm ID, 0.838mm OD, Scientific Commodities, Inc., AZ) to route four tendons for the bending joints and reduce friction for pulling the tendons. Additionally, the flexible segment is composed of layers (ii)~(v). However, one can adjust its stiffness by attaching multiple rings of heat shrink through the flexible segment (e.g., each ring with a height of ~7.0mm and ~7.0mm gap between two rings, see Fig. 7(b)).
Fig. 3:
Schematic of reinforced guide tube.
Fig. 7:
Experimental setup for telerobotic implant delivery. (a) main view of the experimental setup, (b) robotic catheter, (c) side view of the realistic human cardiovascular phantom, and (d) top view of the realistic human cardiovascular phantom.
A reinforced guide tube is fabricated by the following steps:
Step 1: Inset a length of 1.11m stainless steel spring (iii) into a PVC tube (ii);
Step 2: Glue the braided PTFE liner with PebaSLIX™ 72D jacket (iv) and four PTFE liners (v). As shown schematically in Fig. 3, the four PTFE liners are aligned together on one side of the stainless steel spring;
Step 3: Inset the bonded PTFE lines (Step 2) into the tube in Step 1;
Step 4: Attach the tubes in Step 3 to the robotic catheter’s base and tube connector (see Fig.2). They include threads that are fit for the spring and barbs that can create a smooth clamping surface for tight connections and minimize leaks.
Step 5: Reinforce the semi-flexible segment by sliding a length of ~1312mm PET heat shrink (i) onto the PVC jacket (Step 4) from the tip of the robotic catheter and aligning with the tube connector, and then use a heat gun to make it shrink until it is tight against the PVC jacket.
B. Fabrication of Variable Stiffness Quadlumen Tube
The variable stiffness quadlumen tube (1.41m) is made up of two segments: a ~1.31m long semi-flexible quadlumen tube (Pebax 72D, Spectrum Plastics Group, GA) attached to the motor bracket of the distal joint actuator (see Fig. 2(a)) and a reinforced quadlumen tube (~100mm) attached to the distal joint module of the robotic catheter (see Fig. 2 and Fig. 3). We introduce miniature Nitinol tubes (0.4mm ID, 0.48mm OD, Edgetech Industries LLC, FL) into the quadlumen tube (Pebax 55D, Spectrum Plastics Group, GA), namely, reinforced quadlumen tube, to increase the robot’s bending stiffness and simultaneously reduce its tip deflection. Here we propose a simple yet effective method, without using a commercial fabrication process, to fabricate a variable stiffness quadlumen tube (see Fig. 4):
Fig. 4:
Steps to fabricate a variable stiffness quadlumen tube.
Step 1: Inset four Nitinol tubes (0.4mm ID, 0.48mm OD, and ~120mm length) into two quadlumen tubes, Pebax 55D and 72D, with a gap of ~5mm between them (see Fig.4(a)). The Nitinol tubes are used to align the lumens of two quadlumen tubes;
Step 2: Melt two ends of the quadlumen tubes and then push them together (see Fig. 4(b));
Step 3: Cut off unnecessary surface pieces after solidifying (< 1min) (see Fig. 4(c));
Step 4: Remove two diagonal Nitinol tubes (see Fig.4(d)). Note that these two Nitinol tubes can be replaced by other metal tubes or wires.
C. Static Model of Reinforced Quadlumen Tube
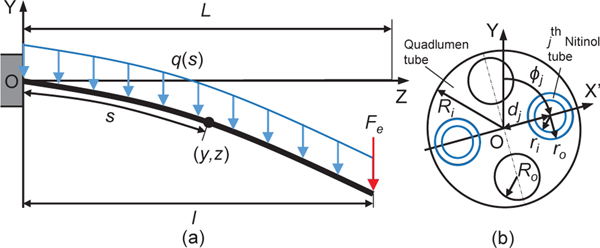
The reinforced quadlumen tube (Sec. III–B) plays a key role in the mitral valve implant delivery. For proper delivery of the implant onto the mitral vave, the quadlumen tube must have appropriate stiffness to minimize deflection due to external forces (e.g., gravity and pulsatile blood flow in the heart) and flexibility to achieve a large bending angle (≥ 90°). Here, we propose a model to evaluate the deflection of Nitinol tubes with a plastic sleeve to guide the designing process of the reinforced quadlumen tube. We assume that the reinforced quadlumen tube consists of Nitinol tubes and a quadlumen tube. For simplification, in this letter, we focus on deriving static governing equations projected onto the YZ plane (see Fig.5), because the tube deflection, under combined uniformly distributed and tip concentrated load, mainly occurs in the Y direction, and the prismatic joint is configured to move along the Z direction. The deflection model of the reinforced quadlumen tube is derived as follows: Considering an individual tube under a uniformly distributed load (gravity), which is given by:
| (1) |
where and represent the outer and lumen radii of the quadlumen tube, respectively, is the density of Pebax 55D, and are the outer and inner radii of each Nitinol tube, respectively, denotes the density of Nitinol, and .
Fig. 5:
Deflection of reinforced quadlumen tube. (a) front view and (b) cross-sectional view.
Using the parallel axis theorem, the projection of the area moment of inertia (or second moments of area) onto the YZ plane is described as:
| (2) |
where , with axis passing through the center of the quadlumen tube and the center of the Nitinol tube, as shown in Fig. 5(b), and is the distance between these two centers.
Remark 1:
The area moment of inertia of the quadlumen in (2) can be extended to a multilumen tube, and is given by:
| (3) |
where is the number of lumen, is the radius of the lumen, denotes the angle between axis Y and the axis passing through the center of the quadlumen tube and the center of the lumen, and represents the distance between these two centers.
When the individual tube is under uniformly distributed load and tip concentrated load , the bending moment is given by:
| (4) |
where is the projected tube length onto the Z axis. Then, the curvature of the tube can be described as:
| (5) |
where is the modulus of elasticity of the tube material and is the pre-curvature. Substituting (4) into (5) and integrating (5), we can get:
| (6) |
Here we assume that the initial condition is . The tube governing equation can be obtained by substituting (6) into the general expressions [21]:
| (7) |
| (8) |
Given a projected tube length (on to the Z axis), the total length of the tube, , can be obtained by integrating (7). The final length , namely , is given by:
| (9) |
where denotes 2-norm of , is the set of all real numbers in the feasible region . Subsequently, Eqns. (4)–(8) are solved with the obtained value of (replaced by and substituted into (4)–(8)), where the curvature of individual tube is computed using (5).
Finally, we use the method in [22], [23] to determine the final curvature of the combined tube:
| (10) |
where represents the number of tubes and the individual curvature, , is computed using (5)–(9). and are the moduli of elasticity of the Nitinol and Pebax 55D, respectively. Also, for simplification, we assume that the tip concentrated load, , in (4) and (6) is equal to .
To validate our reinforced quadlumen tube model (Eqns. (1)–(10)), we assume that the initial curvature, , is equal to zero and use 12 configurations as shown in Table I, where the configuration index, , represents an element of set . In each case, we calculate the mean curvature of , namely,. The numerical solution of (1)–(10) is computed in MATLAB® R2021a, where each load step in (7) is set as and . We then validate our model with finite element simulations (finite element method (FEM)) in ANSYS® 18.2 (static structural analysis workbench), where the contacts between the quadlumen and Nitinol tubes are defined as bonded. Also, the parameters “Physics Reference”, ”Element Order”, “Size Function”, “Relevance Center”, “Mesh Defeaturing”, “Transition”, “Initial Size Seed”, “Span Angle Center”, “Check Mesh Quality”, “Error Limits”, “Smoothing”, and “Mesh Metric” are set as Mechanical, Program Controlled, Adaptive, Fine, Yes, Fast, Assembly, Coarse, Yes, Standard Mechanical, Medium, and None, respectively. All other parameters are set to their default values. The moduli of elasticity of the Nitinol and Pebax 55D are the same as those used in (10).
TABLE I:
Verification of proposed model.
| FEM (mm−1) | Expt. (mm−1) | Model (mm−1) | FEM (mm) | Expt. (mm) | Model (mm) | |
|---|---|---|---|---|---|---|
| 1 | 9.74e 6 | 7.19e 5 | 9.95e 6 | 0.02 | 0.13 | 0.02 |
| 2 | 2.21e 5 | 1.57e 4 | 2.24e 5 | 0.09 | 0.64 | 0.09 |
| 3 | 3.95e 5 | 1.73e 4 | 3.98e 5 | 0.28 | 1.25 | 0.29 |
| 4 | 1.67e 4 | 1.05e 3 | 1.67e 4 | 0.30 | 1.89 | 0.30 |
| 5 | 2.58e 4 | 1.49e 3 | 2.58e 4 | 1.04 | 6.03 | 1.04 |
| 6 | 3.53e 4 | 1.98e 3 | 3.54e 4 | 2.54 | 14.19 | 2.55 |
| 7 | 5.65e 5 | 3.16e 4 | 5.68e 5 | 0.10 | 0.57 | 0.10 |
| 8 | 1.27e 4 | 2.16e 4 | 1.28e 4 | 0.51 | 0.87 | 0.52 |
| 9 | 2.27e 4 | 2.60e 4 | 2.27e 4 | 1.63 | 1.87 | 1.63 |
| 10 | 9.52e 4 | 9.10e 4 | 9.51e 4 | 1.71 | 1.64 | 1.71 |
| 11 | 1.46e 3 | 1.49e 3 | 1.46e 3 | 5.90 | 6.03 | 5.90 |
| 12 | 1.99e 3 | 1.97e 3 | 1.99e 3 | 14.26 | 14.12 | 14.26 |
In each configuration, we observe that the model accurately predicts the shape of the combined tubes (see Table I). Additionally, we use a CMOS camera (CS165MU/M - Zelux®, Thorlabs, Inc., Newton, NJ) with a lens (MVL8M1, Navitar, Rochester, NY) to experimentally test the combined tube under gravity loading and with the addition of a concentrated tip load , as shown in Figs. 6(a) and 6(b), respectively. The weight of the implant and distal torsion joint assembly is 6.63mN. In this experiment, we first obtain tube binary images and then calculate the shape of the deformed tube using the Image Processing Toolbox (MATLAB® R2021a) and third-order polynomial fitting algorithm (polyfit in MATLAB® R2021a). Compared to the FEM results shown in Table I, the model successfully estimates all deflections of the combined tube. Compared to the experimental results shown in Table I, the model successfully estimates large deflections of the combined tube. We also observe that the model deviates from the experimental results for small deflections. We hypothesize that this may be due to the machining tolerances of the quadlumen tube (e.g., four small lumens are slightly twisted) and assembly error of the combined tube. Also, since the prismatic joint is required to advanced up to 60mm, then the maximum deflection of the proposed reinforced quadlumen tube occurs when equals . In this condition, substituting the corresponding values (, ,, and , see Table I) into gives tip deflections in the Y and Z directions: (1.71mm, 0.03mm), (1.64mm, 0.03mm), and (1.71mm, 0.03mm). These tip deflection values are considered negligible in MR implant delivery application. Additionally, all tip deflections in the Z direction are given in Table I.
Fig. 6:
Experimental setup for verification of proposed model. (a) Under gravity loading (Fe = 0N) and (b) with the addition of a concentrated tip load (Fe = 6.63mN), where the weight of the implant and distal torsion joint assembly is 6.63mN.
D. Telerobotic Control
Telerobotic control is an effective way that can help the user operate the robot intuitively. In this letter, we employ a wireless joystick (Xbox 360 Wireless Controller, Microsoft, WA) to actuate the robot joints and the input to the joint is given by:
| (11) |
where is the tendon length or displacement, i.e., , , and represent tendon lengths of the proximal bending, distal bending, and distal torsion joints, respectively, denotes the displacement of the prismatic joint, represents the normalized voltage signal, getting form the joystick, and are the lower and upper limits of the dead zone, respectively, is the scaling factor, and means the initial condition. Considering the output constraints of (11), the final input to the robot is given by:
| (12) |
where and are lower and upper saturation limits of , respectively.
IV. EXPERIMENT
A. Telerobotic Implant Delivery
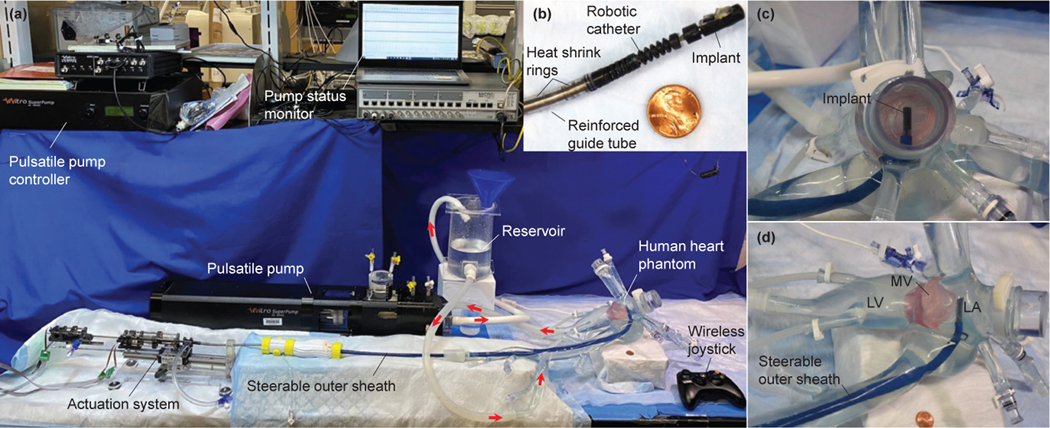
In this section, we demonstrate the telerobotic implant delivery in a realistic human cardiovascular phantom. The experimental setup is shown in Fig. 7, where a customized outer sheath (VERGO® Steerable Access Sheath, Duke Extrusion, CA), with a dimension of 6.6mm ID, 8.3mm OD, and 990.6mm length, is used to guide the robotic catheter from the femoral vein to the left atrium within the realistic cardiovascular phantom (United Biologics, Inc., CA), as shown in Fig. 7(a). A pulsatile pump (ViVitro Labs, Inc., Victoria, BC, Canada) is used to create physiological cardiac flows for in vitro testing. In Fig. 7(a), the left atrium is attached to a reservoir, and the reservoir is provided water periodically from the output of the pulsatile pump. The left ventricle (at the apex of the heart) is connected to the input of the pulsatile pump. This configuration achieves water circulation. Also, the pulsatile pump is set as 63.1ml/stroke and 70beat/min heart rate to ensure the MV opening during diastole. The parameters in (11) and (12) are set as: , , , , , and .
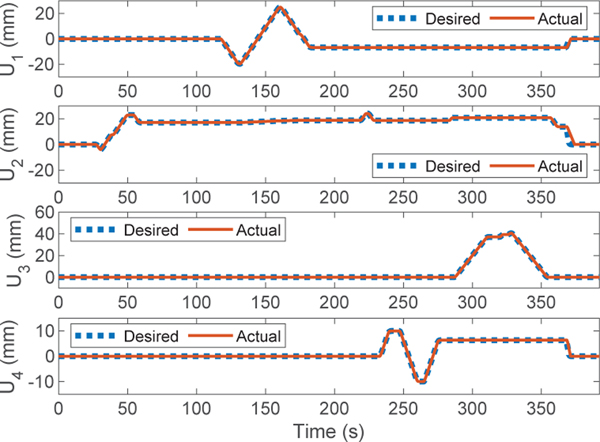
We demonstrate the telerobotic implant delivery in the realistic human cardiovascular phantom as follows (see Fig.8): First, the robotic transcatheter is manually introduced into (by moving the linear guide block attached to the actuation system, see Fig.2) the left atrium of phantom through the customized outer sheath (Fig. 8 (00:00)). Then, the distal bending joint bends about 90° (Fig. 8 (0:59)) to let the robot tip to be close to the MV opening. Afterwards, the proximal bending joint is actuated about −45° ~ 45° (Fig. 8 (02:11~02:41)) to sweep the implant along the MV annulus plane in the anterior-posterior direction. Then, the distal torsion joint is rotated about 45° (Fig.8 (03:53~04:25)) to align the implant with the MV opening. Subsequently, the prismatic joint is advanced 40mm and successfully deliver the implant getting under the MV leaflet (Fig.8 (05:10~05:28)). After the implant delivery, the prismatic joint is retracted 40mm to its home position, followed by the bending and distal torsion joints (Fig. 8 (05:54~06:11)). Finally, robotic transcatheter is manually retracted to its home configuration (Fig.8 (06:11)). Additionally, Fig.9 shows the tracking performance of the telerobotic control with a PD controller for each joint (, , , and ), where the desired commands are given in (12) and the actual joint trajectories are obtained from the encoder of the corresponding DC motor. The tracking errors (RMSE values) are 0.20mm, 0.74mm, 0.02mm, and 0.17mm. In summary, we observe from the demonstration in Fig. 8 and Fig. 9, the implant can be successfully delivered in the realistic human cardiovascular phantom and the telerobotic control has a good tracking performance (RMSE values are small).
Fig. 8:

Demonstration of telerobotic implant delivery in the realistic human cardiovascular phantom.
Fig. 9:
Tracking performance of telerobotic implant delivery.
B. Validation of Reinforced Quadlumen Tube
To evaluate the effectiveness of the reinforced quadlumen tube designed in Sec. III, we evaluate two scenarios in the realistic human cardiovascular phantom, as shown in Fig. 10. We use the same experimental setup as in Fig. 8 and add a stationary millimeter ruler mounted on the laboratory table to evaluate the deflection of the robot tip. In Fig. 10(a), we first manually introduce the robotic catheter into the left atrium of phantom through the outer sheath and then advance the bending joints to steer the robot end-tip close to the MV opening (the robot tip is aligned with the center of the MV, Fig.10(a) (00:00)). Then, we only advance the prismatic joint until the implant is delivered under the MV leaflet (Fig. 10(a) (00:15~00:25)), and the robot stops moving for 15 seconds (Fig. 10(a) (00:25~00:40)) so that we can observe deflections of the robot tip. During 00:25~00:40, we observe that the maximal deflection is about 2mm (from point to point , see Fig. 10(a)(inset)), which is negligible. Finally, the prismatic joint is retracted to its initial position (Fig. 10(a) (00:50~01:04)). Fig. 10(a) shows the implant is not in contact with the leaflet during diastole, where the robot tip concentrates on the movement to the MV.
Fig. 10:

Demonstration and validation of the reinforced quadlumen tube in the realistic human cardiovascular phantom. (a) Implant is not in contact with the leaflet during diastole and (b) implant is in contact with the leaflet during diastole.
In Fig.10(b), we demonstrate the implant is in contact with the leaflet during diastole. Same as Fig. 10(a) (00:00), we advance the robot implant to be close to the MV opening (Fig. 10(b) (00:00)), and then, we advance the prismatic and bending joints to enable the robot tip close to the edge of leaflet (Fig. 10(b) (00:10)). We continually advance the prismatic joint until the implant is delivered under the MV leaflet (Fig. 10(b) (00:15~00:25)), and then the robot stops moving (Fig.10(a) (00:25~00:35)). Finally, we retract the the prismatic joint to its initial position (Fig.10(a) (00:45~01:25)). During 00:25~00:35, we observe that the implant is in contact with the leaflet and moves with it. This performance shows the compliance property of the quadlumen tube which can prevent soft tissue from injuries.
V. DISCUSSION
In this letter, we use a wireless user interface to control the robotic catheter. It is an intuitive and reliable way so that the user can operate the robotic catheter with minimal training. They can control the robot speed by adjusting the gain (using buttons on the joystick), , in (11), i.e., a larger gain results in a higher movement speed. The hysteresis modeling (e.g., Bouc-Wen [24], Preisach [25], and Prandtl-Ishlinskii (PI) [26]) and tendon elongation modeling were done in our prior work [19], [20], and have not been included in this letter for system simplification, reliability, and robustness.
VI. CONCLUSIONS AND FUTURE WORK
This letter proposed a telerobotic transcatheter delivery system, including an actuation system with stabilizer, a reinforced guide tube, and a robotic catheter. We presented the robotic system design, fabrication of various components, and a deflection model to guide the design of reinforced quadlumen tube. This model is verified by commercial FEA software (ANSYS®) and experiments. Also, we propose a telerobotic control method such that the user can operate the robot intuitively. Finally, we demonstrate the effectiveness of the telerobotic transcatheter delivery system and reinforced quadlumen tube in the realistic human cardiovascular phantom for preclinical evaluation. We observed that the implant can be successfully delivered in the human cardiovascular phantom using the telerobotic control and with a good tracking performance (joint tracking errors are 0.20mm, 0.74mm, 0.02mm, and 0.17mm). The maximal deflection of the reinforced quadlumen tube was negligible during the implant delivery, and the proposed reinforced quadlumen tube also demonstrated compliance which can prevent soft tissue injuries. In the future, we plan to evaluate the proposed telerobotic transcatheter delivery system in an animal study.
Supplementary Material
ACKNOWLEDGMENT
We thank Dr. Muralidhar Padala, Associate Professor, Division of Cardiothoracic Surgery, Emory University, for providing us with suggestions to improve the robotic system, an experimental environment with a pulsatile pump system and realistic human cardiovascular phantom, and guidance to setup parameters for the pulsatile pump.
This paper was recommended for publication by Editor Jessica Burgner-Kahrs upon evaluation of the Associate Editor and Reviewers’ comments. This work was supported in part by the National Heart, Lung, And Blood Institute of the National Institutes of Health under Award Number R01HL140325. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
REFERENCES
- [1].Enriquez-Sarano M, Akins CW, and Vahanian A, “Mitral regurgitation,” The Lancet, vol. 373, no. 9672, pp. 1382–1394, 2009. [DOI] [PubMed] [Google Scholar]
- [2].Douedi S and Douedi H, “Mitral regurgitation,” In: StatPearls [Internet], 2022, PMID: 31985928. [PubMed] [Google Scholar]
- [3].Mirabel M, Iung B et al. , “What are the characteristics of patients with severe, symptomatic, mitral regurgitation who are denied surgery?” Eur. Heart J, vol. 28, no. 11, pp. 1358–1365, 2007. [DOI] [PubMed] [Google Scholar]
- [4].Goldstone AB, Atluri P et al. , “Minimally invasive approach provides at least equivalent results for surgical correction of mitral regurgitation: a propensity-matched comparison,” J. Thorac. Cardiovasc. Surg, vol. 145, no. 3, pp. 748–756, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Meier S, Seeburger J, and Borger MA, “Advances in mitral valve surgery,” Curr. Treat. Options Cardio. Med, vol. 20, 2018. [DOI] [PubMed] [Google Scholar]
- [6].Van Praet KM, Stamm C et al. , “Minimally invasive surgical mitral valve repair: State of the art review,” Interv. Cardiol. Rev, vol. 13, no. 1, pp. 14–19, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Nishimura RA, Otto CM et al. , “2017 aha/acc focused update of the 2014 aha/acc guideline for the management of patients with valvular heart disease: A report of the american college of cardiology/american heart association task force on clinical practice guidelines,” Circulation, vol. 135(20), 2017, PMID: 33620807. [DOI] [PubMed] [Google Scholar]
- [8].Yandrapalli S, Biswas M, and Kaplan J, “Mitral valve minimally invasive surgical treatment,” In: StatPearls [Internet], 2021, PMID: 33620807. [Google Scholar]
- [9].Chen M and Sun L, “What is the next generation of transcatheter mitral valve repair devices?” Front. Cardiovasc. Med, vol. 8, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Corpataux N, Winkel M, Kassar M et al. , “The pascal device–early experience with a leaflet approximation device: What are the benefits/limitations compared with the mitraclip?” Curr. Cardiol. Rep, vol. 22, pp. 74:1–74:7, 2020. [DOI] [PubMed] [Google Scholar]
- [11].Abbott Laboratories. (2013) MitraClip® Clip Delivery System. [Accessed: August 5, 2022]. [Online]. Available: https://www.accessdata.fda.gov/cdrh docs/pdf10/P100009c.pdf.
- [12].Lanfranco AR DJ, Castellanos AE and M WC, “Robotic surgery: a current perspective,” Ann. Surg, vol. 239, no. 1, pp. 14–21, Jan 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].M R and KP S, “Robotic-Assisted Percutaneous Coronary Intervention: Rationale, Implementation, Case Selection and Limitations of Current Technology,” J. Clin. Med, vol. 7, no. 3, Jan 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Godzik J, Mastorakos GM et al. , “Surgeon and staff radiation exposure in minimally invasive spinal surgery: prospective series using a personal dosimeter,” J. Neurosurg.: Spine, Feb 2020. [DOI] [PubMed] [Google Scholar]
- [15].Loschak PM, Degirmenci A et al. , “Automatically steering cardiac catheters in vivo with respiratory motion compensation,” Int. J. Robot. Res, vol. 39, no. 5, pp. 586–597, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Kim Y, Genevriere E et al. , “Telerobotic neurovascular interventions with magnetic manipulation,” Sci. Robot, vol. 7, no. 65, p. eabg9907, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Nayar N, Jeong S, and Desai JP, “Towards the development of a robotic transcatheter delivery system for mitral valve implant,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst, 2020, pp. 3172–3177. [Google Scholar]
- [18].Nayar N, Jeong S, and Desai JP, “Design and control of 5DoF robotically steerable catheter for the delivery of the mitral valve implant,” in Proc. IEEE Int. Conf. Robot. Autom., 2021, pp. 12268–12274. [Google Scholar]
- [19].Nayar NU, Qi R, and Desai JP, “Toward the design and development of a robotic transcatheter delivery system for mitral valve implant,” IEEE Trans. Med. Robot. Bionics, pp. 1–12, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Nayar NU, Qi R, and Desai JP, “Modeling of a robotic transcatheter delivery system,” in Proc. IEEE Int. Conf. Robot. Autom, 2023, (accepted). [Google Scholar]
- [21].Chen L, “An integral approach for large deflection cantilever beams,” Int. J. Non-Linear Mech, vol. 45, no. 3, pp. 301–305, 2010. [Google Scholar]
- [22].Robert J I. Webster and B. A. Jones, “Design and kinematic modeling of constant curvature continuum robots: A review,” Int. J. Robot. Res, vol. 29, no. 13, pp. 1661–1683, 2010. [Google Scholar]
- [23].Dupont PE, Lock J, Itkowitz B, and Butler E, “Design and control of concentric-tube robots,” IEEE Trans. Robot, vol. 26, no. 2, pp. 209–225, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Ikhouane F and Rodellar J, Systems with Hysteresis: Analysis, Identification and Control using the Bouc—Wen Model. John Wiley & Sons Ltd, Chichester, West Sussex, England, 2007. [Google Scholar]
- [25].Liu L and Yang Y, Modeling and Precision Control of Systems with Hysteresis. Waltham, MA, USA: Elsevier Inc., 2016. [Google Scholar]
- [26].Kuhnen K, “Modeling, identification and compensation of complex hysteretic nonlinearities: A modified prandtl-ishlinskii approach,” Eur. J. Control, vol. 9, no. 4, pp. 407–418, 2003. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.