Abstract
The SSRMP recommendations on reference dosimetry in kilovolt beams as used in radiation therapy were revised to establish current practice in Switzerland.
The recommendations specify the dosimetry formalism, reference class dosimeter systems and conditions used for the calibration of low and medium energy x-ray beams. Practical guidance is provided on the determination of the beam quality specifier and all corrections required for converting instrument readings to absorbed dose to water. Guidance is also provided on the determination of relative dose under non-reference conditions and on the cross calibration of instruments.
The effect of lack of electron equilibrium and influence of contaminant electrons when using thin window plane parallel chambers at x-ray tube potentials higher than 50 kV is elaborated in an appendix. In Switzerland the calibration of the reference system used for dosimetry is regulated by law. METAS and IRA are the authorities providing this calibration service to the radiotherapy departments. The last appendix of these recommendations summarise this calibration chain.
Keywords: Dose determination in kilovolt beams
1. Introduction
1.1. Scope
1.1.1. Dosimetry recommentation
This document is a revision of recommendations number 9 by the Swiss Society of Radiobiology and Medical Physics (SSRMP) on the determination of absorbed dose to water under reference conditions in kilovoltage x-ray beams for accelerating potentials between 10 kV and 300 kV as applied in radiotherapy and radiobiology [1]. This revision was considered necessary because the recommendations from 2001 no longer described clinical practice on reference dosimetry in the medium energy x-ray range. It was also considered appropriate to provide clarification on the use of absorber foils in the low energy x-ray range and additional guidance on relative dosimetry.
Its scope is to provide concise and practical guidance to the medical physicist for carrying out reference dosimetry in kV beams. Reference dosimetry is based on the DIN 6809-4:2020-04 and IAEA TRS-398 dosimetry codes of practice [2], [3]. The reader is encouraged to read and be familiar with these dosimetry codes of practice for in depth understanding of the fundamental concepts and data requirements relevant to the determination of absorbed dose to water in kV x-ray beams.
It is not in the scope of these recommendations to provide guidance for dosimetry in kV beams used in diagnostic radiology.
1.1.2. Dosimetry of low and medium energy x-rays
The kV beams in use for radiation therapy and radiobiology in Switzerland [10] are classified into two groups [3], [11]:
-
•
low-energy x-ray beams; energies from tube potentials between 10 and 100 kV
-
•
medium-energy x-ray beams; energies from tube potentials between 100 and 300 kV
The reference class dosimeter system (abbreviated to reference system in this document) comprises of the ionisation chamber and its sheath, if appropriate, an electrometer with a calibration traceable to a primary standard and an associated radioactive check source. The legislative details on the calibration and verification of the reference dosimeter system are given in the Ordinance for Measuring Instruments for Ionizing Radiation (SR 941.210.5,[8]). Accordingly, the calibrated reference dosimeter system must be verified every 4 years at the beam qualities at which it is used. From the verification the calibration coefficients of the instrument are determined and recorded on its calibration certificate. Reference systems must be calibrated and verified with an uncertainty of ± 3% (medium energy x-rays) and 4% (low energy x-rays) and at a confidence level of 95%. It is important to note that reference systems (electrometer and ionization chamber) must be instruments which have a type test approval. Only such instruments can be issued with a calibration certificate. The competent authority for this approval is the Federal Institute of Metrology (METAS). For new equipment it must be demonstrated that they meet the requirements as stated in the Ordinance for Measuring Instruments for Ionizing Radiation. A list of approved dosimetrer systems and components can be found through the certsearch database of METAS1. Currently, verifcation of reference systems in Switzerland in the low kV energy range are provided by METAS and in medium kV energy range by the Institut de Radiophysique (IRA/CHUV). At present both calibrations are traceable to primary standards at the Physikalisch-Technische Bundesanstalt (PTB, Germany).
The formalism for the determination of absorbed dose to water in the low energy x-ray range is presented in Section 2, and in the medium energy x-ray range in Section 3. Section 4 reports on the estimated uncertainties in reference dose. Section 5 describes the practical implementation of these recommendations in terms of choice of dosimetry instruments, and the methodology for the experimental determination of the beam quality specifier or beam quality index. The determination of dose away from reference conditions is not in the main scope of these recommendations. However, it was considered important and necessary in this revision to provide guidance on the measurement of relative dose in kV beams and in particular the determination of the percentage depth dose (PDD) and relative output factors. Therefore, Section 5 includes recommendations of good practice on relative dosimetry. Appendix A elaborates on two effects that need to be considered in the calibration of the reference system. Appendix B contains a brief summary on the calibration of reference systems at the standards laboratories (PTB, METAS and IRA).
1.2. Legislative aspects
The relevant legislation on which the present recommendations are based is:
-
•
Radiological Protection Act (StSG) of 22nd March 1991 (version 1st May 2017, SR 814.50) [4]
-
•
Radiological Protection Ordinance (StSV) of 26th April 2017 (online version 1st January 2021, SR 814.501) [5]
-
•
Radiological Protection Ordinance for Medical X-ray Equipment (RöV) of 26th April 2017 (online version 6th February 2018, SR 814.542.1) [6]
-
•
Measuring Instruments Ordinance (MessMV) of 15th February 2006 (online version 20th April 2016, SR 941.210) [7]
-
•
Ordinance for Measuring Instruments for Ionizing Radiation (StMmV) of 7th December 2012 (online version 1st January 2013, SR 941.210.5) [8]
-
•
Ordinance for Units of 23rd November 1994 (online version 20th May 2019) [9]
The medical physicist may specifically consider the relevant articles in these documents prior to the implementation of the recommendations. The above list should not be considered exhaustive, as there might be other resources defining legislative aspects and common practice in the context of reference dosimetry in low and medium x-ray beams.
It is the responsibility of the qualified medical physicist to implement the present recommendations appropriately and to perform accurate reference dosimetry in compliance with Swiss legislation. It is the task of medical physicists practicing elsewhere to consider the legislative aspects relevant to their country.
2. Reference dosimetry in the low energy range: 10 kV - 100 kV
2.1. Beam quality specification
The beam quality index is the Half-Value-Layer (HVL). This is defined as the thickness of an absorber which reduces the air kerma rate of a narrow x-ray beam at a reference point distant from the absorbing layer to 50% compared with the air kerma rate for the non-attenuated beam [11]. For beams with accelerating potentials between 10 kV and 100 kV, the HVL is reported in millimetres of aluminium (mm Al). Beams are usually referred to by both their accelerating potential in kV and the HVL in mm Al. The experimental determination of HVL is described in Section 5.2.
2.2. Reference dosimety system
The recommended detectors for the determination of absorbed dose in the low energy range are air-filled plane-parallel ionisation chambers with cavity volume not greater than 0.2 cm3 and a thin entrance window (soft x-ray chambers) [11], [12]. Their entrance window must be extremely thin (between 2-3 mg cm-2) in order to minimise photon attenuation [13]. Chambers should have a flat response with beam energy (less than 5% over the energy range used [3]) and field size. It is recommended to use chambers with a field size dependence less than 1%. Examples of recommended reference chambers suitable for dose determination in low energy kV beams are given in Table 1. The response of the PTW 23344 chamber is known to vary more than 5% with field size in comparison to the PTW 23342 [12] (further details in Section 5.3.5).
Table 1.
Characteristics of recommended plane-parallel ionisation chambers for reference dosimetry in low energy x-rays.
| Chamber type | Volume (cm3) | Window material | Window thickness (mg cm-2) | Manufacturer |
|---|---|---|---|---|
| 23342 | 0.02 | Polyethylene | 2.76 | PTW1 |
| 23344 | 0.2 | Polyethylene | 2.76 | PTW1 |
| 34013 | 0.005 | Polyethylene | 2.76 | PTW1 |
PTW-Freiburg GmbH, Freiburg, Germany.
Suitable reference electrometers must pass the type test approval by METAS (see Section 1 above). Guidance on the specification of reference class electrometers can also be found in the literature [14], [15].
The reference system must be used in beam qualities similar to those at which it has been calibrated. At the time of writing, the beam qualities of the radiation beams available for calibration in the low kV energy range are: 10 kV / 0.03 mm Al, 15 kV / 0.071 mm Al, 20 kV / 0.113 mm Al, 30 kV / 0.359 mm Al, 40 kV / 0.741 mm Al, 50 kV / 0.940 mm Al, 70 kV / 2.94 mm Al and 100 kV / 4.41 mm Al [2].
2.3. Reference conditions
The reference medium is water, but in the low kV energy range the use of water-equivalent plastics, and even PMMA phantom materials is acceptable [3], [11]. This is because the combination of reference system and phantom as a unit is calibrated in terms of absorbed dose to water at the surface and no further corrections are needed irrespective of the type of plastic material used. The dimensions of the phantom should extend in the direction of the beam by at least 5 g cm-2 and in the lateral direction at least far enough to ensure that the entire primary beam exits from the rear face of the phantom.
Because the entrance window of the reference chambers in Table 1 is not sufficiently thick to absorb contaminant electrons originating from applicator walls, for beams above 50 kV collimated with open-end applicators, it is recommended to use a foil of about 0.1 mm water-equivalent thickness during the determination of reference dose and subsequently during patient treatment (see discussion in Sections 6 and Appendix B.1.2).
Table 2 lists the reference irradiation conditions for the determination of absorbed dose to water. These are the same irradiation conditions listed on the calibration certificate provided by METAS.
Table 2.
Reference irradiation conditions for low energy x-rays.
| Influence quantity | Reference characteristics or value |
|---|---|
| Phantom material | Water-equivalent plastic or PMMA |
| Chamber type | Plane-parallel for low-energy x-rays |
| Reference point of chamber | At the centre of the outside surface of the chamber window (or additional foil, if this is used for beams above 50 kV) |
| Measurement depth | Phantom surface |
| SSD | 30 cm |
| Field size at SSD | 3 cm diameter or the closest field size to this that will be used clinically |
| Reference air pressure | 1013.25 hPa |
| Reference air temperature | 20 °C |
| Humidity | 50% |
2.4. Dose determination under reference conditions
The formalism for the determination of absorbed dose to water at the surface of the phantom is:
| (1) |
with
| (2) |
where:
| Absorbed dose to water at the surface of the phantom; in Gy | |
| Reading of the dosimeter, with the chamber’s reference point at the measurement depth, in beam quality Q corrected for all influence quantities; in C | |
| Absorbed dose to water calibration coefficient for the reference beam quality Qo and under reference conditions; in units of Gy/C | |
| Beam quality correction factor for beam quality Q | |
| Reading of dosimeter, with the chamber’s reference point at the measurement depth, in beam quality Q corrected for time-end effect errors; in C | |
| Correction for deviations from reference ambient conditions: air density | |
| Correction for deviations from reference relative humidity | |
| Correction to dosimeter reading to account for ion recombination effects | |
| Correction to dosimeter reading to account for polarity effects | |
| Correction to account for the change in chamber response as a result of changes in field size and/or SSD from the field size and SSD at which the calibration coefficient was determined |
3. Reference dosimetry in the medium energy range: 100 kV - 300 kV
3.1. Beam quality specification
The beam quality index is the Half-Value-Layer (HVL). This is defined as the thickness of an absorber, which reduces the air kerma rate of a narrow x-ray beam at a reference point distant from the absorbing layer to 50% compared with the air kerma rate for the non-attenuated beam [3]. For beams with accelerating potentials between 100 kV and 300 kV the HVL is reported in millimetres of copper (mm Cu). Beams are usually referred to by both their accelerating potential in kV and the HVL in mm Cu. The experimental determination of HVL is described in Section 5.2.
3.2. Reference dosimeter system
The recommended reference detectors for the determination of absorbed dose in the medium energy range are air-filled cylindrical ionisation chambers with cavity volume not greater than 1.0 cm3. For chambers that are non-waterproof a water-proofing sleeve must be used. This should be made of PMMA and not be thicker than 1.0 mm. The waterproofing sleeve used for the calibration of the ionisation chamber at the standards laboratory becomes part of the reference system and should also be used for any subsequent measurements of absorbed dose. Chambers should have a flat response with beam energy (less than 5% over the energy range used [3]). It is recommended to use chambers with field size dependence of less than 1% within the range of field sizes being used. Recommended chambers suitable for reference dose determination in medium energy kV beams are listed in Table 3.
Table 3.
Characteristics of some recommended cylindrical ionisation chambers for reference dosimetry in medium energy x-rays.
| Chamber type | Volume (cm3) | Wall material | Central electrode | Wall thickness (mg cm-2) | Waterproof? | Manufacturer |
|---|---|---|---|---|---|---|
| 30010 | 0.6 | graphite & PMMA | aluminium | 56.5 | no | PTW1 |
| 30012 | 0.6 | graphite | aluminium | 79 | no | PTW1 |
| 30013 | 0.6 | graphite & PMMA | aluminium | 56.5 | yes | PTW1 |
| 30015 / 23331 | 1.0 | graphite & PMMA | aluminium | 73 | no | PTW1 |
| 30016 / 23332 | 0.3 | graphite & PMMA | aluminium | 67 | no | PTW1 |
| 31013 | 0.125 | graphite & PMMA | aluminium | 78 | yes | PTW1 |
| 2561 | 0.325 | graphite | aluminium | 90 | no | NE2 |
| 2611 | 0.325 | graphite | aluminium | 90 | no | NE2 |
| 2571 | 0.6 | graphite | aluminium | 65 | no | NE2 |
PTW: PTW-Freiburg GmbH, Freiburg, Germany.
Bicron-NE Ltd, Beenham, Reading, United Kingdom.
Suitable reference electrometers must conform to the specifications by METAS (see Section 1 above). The reference system must be used in beam qualities similar to those at which it has been calibrated. At the time of writing, the beam qualities of the radiation beams available for calibration in the medium kV energy range at IRA are: 94 kV / 0.15 mmCu, 104 kV / 0.20 mmCu, 129 kV / 0.5 mmCu, 170 kV / 1.0 mmCu, 212 kV / 2.0 mmCu and 276 kV / 4 mmCu.
3.3. Reference conditions
The reference medium is water. The phantom should extend to at least 5 cm beyond all four sides of the largest field size employed at the depth of measurement. There should also be a margin of at least 10 g cm-2 beyond the maximum depth of measurement. When horizontal beams are used, the window of the phantom should be made of plastic with thickness not more than 0.5 cm. The water-equivalent thickness (in g cm-2) of the phantom window should be taken into account when evaluating the depth in water at which the chamber is to be positioned. For PMMA and polystyrene the mass densities of 1.19 g cm-3 and 1.06 g cm-3, respectively, can be used in the calculation of water-equivalent thickness of the window of the phantom [3].
Table 4 lists the reference irradiation conditions for the determination of absorbed dose to water. These are the same irradiation conditions listed on the calibration certificate provided by the dosimetry standards laboratory (IRA).
Table 4.
Reference conditions for medium energy x-rays.
| Influence quantity | Reference characteristics or value |
|---|---|
| Phantom material | Water |
| Reference point of chamber | On the central axis at the centre of the cavity volume |
| Measurement depth | 2 g cm-2 |
| SSD | 100 cm or the applicator with the greatest SSD |
| Field size at SSD | 10 cm × 10 cm or the closest field size to this used clinically |
| Reference air pressure | 1013.25 hPa |
| Reference air temperature | 20 °C |
| Humidity | 50% |
3.4. Dose determination under reference conditions
The formalism for the determination of absorbed dose to water at the depth of 2 cm in water is:
| (3) |
with
| (4) |
where
| Absorbed dose to water at the surface of the phantom in Gy | |
| Reading of the dosimeter, with the chamber’s reference point at the measurement depth, in beam quality Q corrected for all influence quantities; in C | |
| Absorbed dose to water calibration coefficient for the reference beam quality Qo and under reference conditions; in units of Gy/C | |
| Beam quality correction factor for beam quality Q | |
| Reading of dosimeter, with the chamber’s reference point at the measurement depth, in beam quality Q, corrected for time-end effect errors; in C | |
| Correction for deviations from reference ambient conditions: air density | |
| Correction for deviations from reference relative humidity | |
| Correction to dosimeter reading to account for ion recombination effects | |
| Correction to dosimeter reading to account for polarity effects | |
| Correction to account for the change in chamber response as a result of changes in field size and/or SSD from the field size and SSD at which the calibration coefficient was determined |
4. Uncertainties in dose determination
The evaluation of uncertainties in dose determination is carried out in accordance with the ISO guidance (GUM) [16]. The standard uncertainty in the determination of absorbed dose under reference conditions is derived by combining the standard uncertainties from two steps. The first step (step 1) includes the uncertainties related to the calibration of the reference system at the standards laboratory. The second step (step 2) includes the evaluation of the uncertainty in dose determination in the user's beam. The overall standard uncertainty is obtained from the square root of the combination in quadrature of the values from each step. The verification certificates by METAS and IRA provide calibration coefficients with an expanded standard uncertainty (U95%, coverage factor k = 2).
Table 5 provides an example of an uncertainty budget. The values in this table are relative standard uncertainties at a confidence level of 68% (coverage factor k = 1). The uncertainties associated with the calibration of the user's reference system (step 1) include, in addition to the uncertainty of the secondary standard itself, contributions of uncertainties from chamber positioning in water, pressure and temperature, fluctuations in dosimeter readings during cross calibration against the secondary standard.
Table 5.
Example of estimated relative standard uncertainty (coverage factor k = 1) of Dw,Q under reference conditions in low and medium kV x-rays.
| Example of uncertainty budget (in%) | Low energy | Medium energy |
|---|---|---|
| Step 1: Calibration of the reference dosimeter at SSDL (METAS, IRA) | ||
| Calibration of the secondary standard at the primary laboratory | 1.40 | 1.10 |
| Long term stability of the secondary standard | 0.10 | 0.10 |
| Cross-calibration procedure of the reference dosimeter | 1.00 | 0.60 |
| Combined standard uncertainty (k = 1) | 1.72 | 1.26 |
| Step 2: Absorbed dose measurement in the user's beam | ||
| Long term stability of the user's reference dosimeter | 0.30 | 0.20 |
| Establishment of the reference conditions | 1.00 | 0.54 |
| Positioning of the chamber at the reference depth (± 0.5 mm, 1% / mm) | n.a | 0.50 |
| Positioning of the chamber at SSD (1 mm) | 1.00 | 0.20 |
| Dosimeter reading MQ (including all influence quantities) | 2.01 | 0.55 |
| Temperature and pressure in reference chamber, kPT (±0.3 K, 1 hPa) | 0.10 | 0.10 |
| Humidity in reference chamber, kh | 0.10 | 0.10 |
| Correction for recombination effect, ks | 0.10 | 0.10 |
| Correction for polarity effect, kpol | 0.10 | 0.10 |
| Correction for field size and SSD (if different from that at reference calibration conditions) | 2.00 | 0.5 |
| Stability in dosimeter reading (relative to external monitor) | 0.10 | 0.10 |
| Differences in beam quality between calibration and measurement in users' beam | 1.50 | 1.00 |
| Combined standard uncertainty (k = 1) | 2.72 | 1.28 |
| Step 1: Calibration of the reference dosimeter | 1.72 | 1.26 |
| Step 2: Dose determination in the user's beam | 2.72 | 1.28 |
| Combined standard uncertainty from steps 1 and 2 (k = 1) | 3.22 | 1.79 |
For the evaluation of the uncertainty associated in the measurement of absorbed dose by the user (step 2), the uncertainty on long term stability of the reference system is taken from [2].
No uncertainty on positioning the chamber at the reference depth is considered in the case of the low energy range. The positioning uncertainty at the reference depth at the medium energy range is estimated to be 0.5 mm. For a dose gradient of 1% / mm, the associated uncertainty is taken to be 0.5%. In the medium energy range positioning to the correct SSD is estimated to be within 1 mm and a relative standard uncertainty of 0.2% is assigned to this [2]. The uncertainties associated to air density, humidity, recombination and polarity effects are taken from [2].
The rationale for the 2% relative standard uncertainty considered for the correction for field size and SSD in the low energy range is discussed in Section 5.3.5.1. In the medium energy range, when the field size is not very different from the reference field, no correction is applied because the effect remains below 1% (see 5.3.5.2). For this reason an uncertainty of 0.5% is considered in this case.
The uncertainty on the dosimeter reading relative to an external beam monitor chamber or timer is estimated to be 0.1%. The effect of differences in beam-quality between that used for calibration and that of the users' beam can lead to non-negligible differences in the response of the dosimeter. Namely the combination of generating potential and HVL could result in different absorbed dose to water coefficient and an uncertainty of 1.5% and 1% is associated with this at the low and medium energy range, respectively [3].
5. Implementation
5.1. Stability checks on measurement instruments
Radioactive check source measurements are performed to control the stability in the response of a measurement system (the combination of chamber and electrometer). It is recommended to perform such a quality control check at frequent intervals as part of a quality assurance programme on dosimetry equipment.
A stability check source usually consists of one or more radioactive sources (often foils) which are situated in a shielded container. The radionuclide usually used is 90Sr (with a half-life of 28.79 years). The design of a check source depends on the type of chamber (whether cylindrical or of plane parallel design). If the ionisation current varies as the chamber is rotated within the source housing it is recommended that the check is carried out with the chamber and its adaptor in a reproducible position with respect to the source (marks engraved on chambers by the manufacturer can be aligned with a marks on the source housing to ensure reproducibility in position).
If the check source has recently been in temperature conditions different from those in the place of measurement, then sufficient time should be allowed for it to reach the new temperature before taking readings; this may take several hours. To monitor its temperature, a check source should be provided with a thermometer that can be inserted into a hole in the container. Time should also be allowed after inserting a chamber in the source, for it to stabilise and to achieve temperature equilibrium with the source; about 2 to 3 min per degree. Before measurement the chamber must always be pre-irradiated in the check source with a dose between 2 – 5 Gy for the measurement instrument to reach charge equilibrium.
The check on stability of the measurement instrument also involves the investigation of any leakage current. This is the current measured in absence of radiation and it could be also induced after radiation [3]. Leakage current should be small in comparison to the current measured during radiation (less than approximately 0.1% of the measurement current). If leakage current is measured to be more than 1% of the measurement current, the chamber should not be used.
The calibration of the reference dosimeter is no longer valid if the current measured during a stability check differs by more than 1.5% and 0.5% from the reference value on the calibration certificate of the instrument for reference dosimetry in low kV beams and medium kV beams respectively. If the cause of the discrepancy cannot be resolved, the dosimeter must be re-calibrated, as its response can no longer be related to that at calibration.
5.2. Determination of beam quality index
It is recommended that HVLs are measured in scatter-free narrow beam geometry with the ionisation chamber at about 1 meter from the x-ray source, floor and surrounding walls. Beam attenuators (filters) made of Al or Cu (materials of 99.9% high purity and with thickness known to be within 0.05 mm [11]) must be placed half-way in-between. The ionisation chamber used should have an energy response that does not vary by more than 2% over the range of beam qualities measured [3]. The x-ray beam must be collimated using the smallest applicator together with additional collimators made of lead such that the ionisation chamber is fully exposed at the distance of one meter from the beam source. The position of the chamber within the narrow beam should be checked with film placed behind the chamber. The recommended experimental set-up is shown in Figure 1.
Figure 1.
(a) Irradiation geometry for the measurement of HVLs. SCD: source to chamber distance; SFD: source to filter distance; FCD: filter to chamber distance; with SFD ≈ FCD ≈ SCD/2 ≈ 50 cm. (b) Example of HVL measurement setup; (c) setup with film to check the position of the chamber with respect to the narrow beam aperture.
The thickness of filter that generates a beam with HVLQ, should be such, so that the ratio R of readings with and without the filter is exactly 0.5. If it is not possible to obtain exactly this correspondence, then for the ratio R with an attenuation of thickness , the HVLQ is derived from:
| (5) |
5.3. Corrections to instrument readings
5.3.1. Air density correction
This correction accounts for differences between the air density in the chamber at the time of measurement and the ambient conditions at which the calibration coefficient applies. The factor kTP is given by:
| (6) |
where T is the temperature of the air in the chamber cavity in oC and P is the ambient air pressure in hPa (or mbar). The reference ambient conditions are Po = 1013.25 hPa and To = 20°C. The calibration of the thermometer and barometer used for the determination of air density corrections should be traceable to primary standards [7].
5.3.2. Humidity
It is difficult to determine the relative humidity of the air in a chamber particularly when it is immersed in a water phantom. However, the correction for any difference between the humidity at the time of measurement and 50% relative humidity, for which the calibration coefficient applies, is small (<0.1%) for a relative humidity between 20% and 80% and a temperature between 15°C and 25°C [17]. For this reason the correction factor for changes in humidity is assumed to be unity:
| (7) |
5.3.3. Polarity effect
In the low energy range and for the recommended plane-parallel chambers it is difficult to experimentally determine corrections for polarity and ion recombination due to electrostatic distortion of the chamber window [3]. It is recommended to always apply the same polarization voltage as that used for calibration. In the medium energy range it is also recommended to always use the cylindrical chamber with the same polarity. In both energy ranges and for the recommended chambers the value of a correction for polarity effects is therefore set to unity:
| (8) |
5.3.4. Ion recombination effects
A correction for ion recombination accounts for possible inefficiency of the measurement system in collecting the charge in the ionisation chamber cavity. A detailed description of the effect can be found in textbooks [18], [19] and in dosimetry codes of practice [3], [11], [20].
In the low kV energy range and for the recommended plane parallel ionisation chambers it is not necessary that ion recombination correction is measured. When using the chamber at the same polarity as at calibration and at absorbed dose rates less than a few Gray per second ion recombination is normally negligible and changing the polarization voltage may distort the chambers' window and result in a false assessment of the ion recombination effect [3]. In the medium kV energy range and for the recommended cylindrical ionisation chambers ion recombination is negligible when the absorbed dose rates is less than a few Gray per minute [3], [11]. Thus, it is recommended to use:
| (9) |
It is recommended to investigate the magnitude of the ion recombination correction only at high absorbed dose rates (of the order of 10 Gy/s and 10 Gy/min at low and medium energies respectively) or at small SSDs.
5.3.5. Correction for changes in field size
5.3.5.1. Low- energy range: 10 kV - 100 kV
For the first two plane parallel ionisation chambers listed in Table 1, field size correction factors for radiation fields ranging between 2 cm and 20 cm and SSDs of 20 cm and 30 cm were determined by Engelke and Grosswendt [21]. At field sizes less than the reference field (3 cm) the correction is greater than unity as less of the chamber housing is being irradiated in comparison to the reference field. At field sizes larger than the reference field, the correction is less than unity to account for the overresponse of the chamber as more of its housing and cable are being exposed to the primary beam. Engelke and Grosswendt [21] warn that the uncertainty associated with the determination of such correction factors can be large at increasing field sizes and SSD. From their data it can be concluded that for field sizes between 2 cm and 5 cm and at SSDs between 20 cm and 30 cm, correction factors are of the order of 2% whereas for field sizes larger than 5 cm they can be up to 10%.
Because of the limited published data available on this correction for the plane parallel ionisation chambers listed in Table 1, it is recommended to use:
-
•
kFS/SSD = 1 for dose determination under reference conditions and at irradiation conditions close to these (field sizes between 2 cm and 5 cm and SSDs less than 30 cm). A relative standard uncertainty of 2% should be associated to this value [21] (see Section 4);
-
•
At fields and SSD greater than those under reference conditions absorbed dose determination is carried out through the application of output factors measured with detectors whose response does not exhibit a dependence on field size and SSD (see Section 5.7.2). Under non-reference irradiation conditions, it is not recommended to use the detectors listed in Table 1 directly.
5.3.5.2. Medium- energy range: 100 kV - 300 kV
Seuntjens and Verhaegen have investigated the change in response of the cylindrical chamber NE2571 with field size and depth in medium energy x-ray beams [22]. Specifically, they have investigated how the chambers’ response varies with changes in photon fluence at the point of measurement in the water phantom with respect to an in-air irradiation. The overall effect comprises three components: a displacement effect accounting for the presence of the air cavity in water, a stem effect responsible for different amounts of photon scatter from the stem of the chamber when this is irradiated by different field sizes, and a field size effect as a result of the change in chamber response due to differences between radiation fields. For beam energies with HVL between 0.17 mm Cu (about 100 kV) and 3.41 mm Cu (about 280 kV), field diameters between 5 cm and 16 cm and at the depth of 2 cm in water the overall correction factor to the chamber response from that in a field of 10 cm diameter varies by at most 1%. Thus, assuming that chambers of similar design respond in an analogous way as the NE2571, the correction factor to the chamber response due to differences in field size alone can be considered negligible. The field size correction factor kFS/SSD in equation (3) for the recommended chambers listed in Table 3 is set to unity:
| (10) |
A relative standard uncertainty of 0.5% should be associated to this value [22] (see Section 4).
5.4. Beam quality correction factor
It is recommended that the reference system is calibrated at the standard laboratory at beam qualities that cover the range of beam qualities at which the instrument is to be used. If the beam quality Q of the user beam (of beam quality index HVLQ) is not identical to a beam quality at which the reference system was calibrated, the calibration coefficient provided on the calibration certificate by METAS or IRA must be corrected. The beam quality correction factor is simply derived by linear interpolation from the coefficients provided on the certificate for the range of beams qualities (at corresponding HVLs) at which the reference system was calibrated.
5.5. Time-end effect
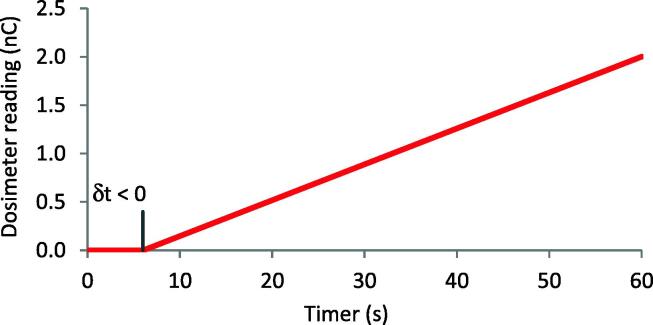
The time-end effect or error δt is the amount of time not accounted for by the machine timer mechanism during the x-ray beam delivery. It is the difference between the elapsed time indicated by the machine timer and the time when the desired kVp and mA have been reached [11], [23]. At a negative δt, the timer starts early, resulting in a dose deficit and thus would need to be added to the treatment time, whereas a positive value indicates the timer starts late and thus would need to be subtracted from to the treatment time. Ma et al. [11] recommend that a graphical extrapolation method be used for accurate determination of δt. The graphical solution of zero exposure on a plot of exposure versus exposure-timer yields the time-end error (see Figure 2).
Figure 2.
Plot of exposure versus timer for the determination of the time-end error δt. In this example the timer starts early.
The error can also be approximated using the equation proposed by Attix [18]
| (11) |
where M1 and M2 are the readings of the ionisation chamber at exposure times Δt1 and Δt2 respectively and Δt2 = 4 × Δt1. A small time-end effect (0.5 – 3s) may need to be considered in the calibration of the kV beam output at small doses (short treatment times).
5.6. Cross calibration of field instruments
For the cross calibration of a field dosimeter against a reference dosimeter the following needs to be taken into consideration:
-
(1)
The recommended medium for the inter-comparison is water or water-equivalent solid plastic.
-
(2)
The same waterproof sleeve or foil is to be used with the reference chamber, if these were included in its calibration at the standards laboratory.
-
(3)
The reference dosimeter and the field dosimeter can be irradiated either simultaneously or sequentially. The irradiation geometry should be the same as the reference calibration conditions at which the calibration coefficient of the reference system was determined. If the chambers are irradiated simultaneously there should be a separation of the chamber centres of 3 cm and with each chamber equidistant from the beam’s central axis. If the chambers are irradiated sequentially, the geometric centre of each chamber should be placed on axis at the measurement depth.
-
(4)
All readings should be corrected for influence quantities as described in Section 5.3.
-
(5)
In the case of simultaneous irradiation, in order to account for possible non-uniformity in the beam profile the positions of the chambers should be reversed and the readings repeated. At least three readings are to be acquired at each position. Thus, at the first position of chambers (series A) the following ratio of at least two corrected readings M is calculated:
| (12) |
After the chambers are inter-changed the ratio of readings (series B) is:
| (13) |
From the two series of measurements, the true inter-comparison ratio is calculated from the geometric mean of the mean of ratios from each series, and , respectively [24], [25]:
| (14) |
where superscripts R and F indicate the reference and field dosimeter, respectively.
5.7. Relative dosimetry measurements
5.7.1. Percentage depth dose (PDD)
The experimental determination of PDD data in kV beams is challenging due to the choice of appropriate detector for the measurement [26], [27], [28]. It is desirable that an ionisation chamber with a flat energy response (better than ±5%) and suitable shape and size is used that would allow measurements at shallow depths and at the surface for the range of field sizes as defined by the applicators [3], [11], [26], [27].
5.7.1.1. Use of published data
If an experimental determination of the PDD is not possible, Ma et al. [11] recommended interpolating from published data [29], [30]. These data however tend to be averages from measurements on older treatment units obtained using a variety of (unspecified) ionisation chambers and phantom materials (both liquid water and solid plastics). It has been observed that in low kV beams, PDDs interpolated from data in BJR Supplement 25 [29] do not agree with the PDDs measured in liquid water, possibly due to differences in the irradiation medium and type of detector used [31].
5.7.1.2. Measurement: recommendations on phantom
Since the reference medium for dosimetry in radiotherapy is liquid water, the measurement of PDDs in kV beams ideally should be carried out in water or, at least, in a water-equivalent medium [27]. The use of non-water equivalent plastics however has not been discouraged [2], [3], [32]. Commercially available solid phantoms have been reported to be water-equivalent within ±2% in kV beams, and PDDs measured in some other plastics can differ from those measured in water by up to 7% and this depends on beam quality and field size [27], [33]. Hill et al. [33] calculated depth doses, dose profiles, and surface doses for kV photon beams ranging between 50.kV / 0.16.mmAl HVL and 280 kV / 3.3.mmCu HVL in several commercial solid plastics and water using the Monte Carlo method and have found relative dose parameters to vary significantly from those in water. Differences were smaller with increasing x-ray beam energy. This was attributed to decreased influence of the photoelectric effect due to the reduced dependence on the atomic number of the material with increased energy [33].
Based in these findings, it is not recommended to measure relative dose in kV beams using the following commercial solid plastics: Plastic Water (CIRS®, Norfolk, Virginia USA), RW3 (PTW-Freiburg, Germany), PRESAGE (Heuris Pharma, Skillman, NJ), PMMA and polystyrene. Recommended solid plastics for relative dosimetry in kV beams are: A150, PAGAT, Plastic Water DT (CIRS®, Norfolk, Virginia USA), RMI457 Solid Water (Gammex-RMI, Middleton, WI) and Virtual Water (Med-Cal, Verona, WI) [27], [33], [34], [35].
5.7.1.3. Measurement: recommendations on detectors
Farmer-type, thimble-type cylindrical ionisation chambers and chambers with an aluminium central electrode exhibit a relatively flat energy response in kV beams from tube potentials ranging between 20.kV / 0.148.mmAl HVL and 250.kV / 18.5 mmAl HVL and with these chambers depth doses are measured with an uncertainty less than 3% [28], [36], [37]. In the case of Farmer and thimble-type chambers, their cylindrical geometry does not allow the measurement at and within the first 5 mm below the surface. One approach is to determine relative dose values at shallower depths from a curve fit (up to fifth-order polynomial fitting) to data measured with these chambers at greater depths but care must be taken that no erroneous values are derived in the first millimetres below the surface in the case of medium kV beam energies where a build-up in the PDD may be present [31]. Thus, this approach is recommended for kV energies up to about 100 kV.
Alternatively PDDs can be determined using a plane-parallel ionisation chamber exhibiting a flat energy response in the kV energy range and with changes in field size and depth. The thin window plane parallel ionisation chambers specifically designed for reference dosimetry in the low kV energy range (such as those listed in Table 1) may not have a flat energy response at depth in a phantom and may require a depth dependent correction factor leading into an increased uncertainty in the determination of the PDD. Thus, it is not recommended to use thin window plane parallel ionisation chambers for the measurement of PDD in low kV beams [11].
The suitability of other plane parallel ionisation chambers, frequently used in megavolt and electron beam dosimetry, for relative dosimetry in beams ranging between 50.kV / 0.16 mm Al HVL and 280 kV / 3.3 mm Cu HVL has been investigated by Hill et al. [28]. Based on their findings the following plane-parallel ionisation chambers are suitable for the measurement of depth dose with an uncertainty within 3% and without the requirement of a depth dependent correction: Scanditronix NACP (IBA), Markus, Advanced Markus, Roos (PTW Freiburg).
There is limited information in the literature on the measurement of PDDs in kV beams using solid state detectors, such as diode and diamond detectors. A natural diamond detector (PTW 60003) was found to require up to 12% corrections in x-ray beams up to 100 kVp to account for energy and dose rate responses in comparison to ionisation chamber readings [38], whereas at higher beam potentials relatively small depth-dependent correction factors were reported [39]. PDDs measured with a synthetic chemical vapour deposited (CVD) diamond detector (PTW TW60019 microDiamond) in kV beams (40 kVp / 0.73 mmAl – 280 kVp / 3.33 mmCu) and for radiation fields ranging between 7 mm and 12 cm × 12 cm, were in good agreement (within 3%) with those measured with ionisation chambers (PTW Advanced Markus, PTW 31014 PinPoint) and calculated data with the Monte Carlo method [40], [41].
Daniel et al. compared PDDs measured both in low and medium energy range kV beams (60 kVp / 1.3 mmAl – 300 kVp / 3.1 mmCu) and field sizes between 2 cm and 20 cm × 20 cm with shielded and unshielded diodes, the PTW microDiamond, small thimble chambers, and the PTW Advanced Markus chamber [42]. Their findings are in agreement with those by Kahn et al. who reported the PTW 60017 unshielded diode to overrespond by 10% in a 50 kVp / 0.85 mmAl beam [41] and by Damodar who investigated the PTW 60012 unshielded diode [40]. As both shielded and unshielded diodes exhibit an overresponding behaviour with increasing beam potential these detectors should not be used for the measurement of PDDs in the medium energy range.
Thus, the use of the PTW TW60019 microDiamond for the measument of PDDs is recommended in the both low and medium energy ranges, whereas shielded or unshielded diodes could be used in the low energy range. In any case it is strongly advised to corroborate measurements with solid state detectors against measurements with ionisation chambers.
There is limited information in the literature on the energy response and suitability of radiochromic EBT3 film for dosimetric measurements in the kilovoltage range. Brown et al. [43] reported small energy dependence in low energy mono-energetic photon beams (25 – 35 keV); whereas in contrast Villarreal-Barajas et al. [44] reported under-response relative to a 60Co of the order of 20% at beams of 3.0 mm Al HVL and of the order of 5% at 4 mm Cu HVL. PDDs measured with EBT3 in a water-equivalent solid phantom (Plastic Water DT, (PWDT)) were in good agreement with measurements in water and in PWDT using cylindrical and plane-parallel ionisation chambers for 50 kV / 1.2 mm Al HVL and 150 kV / 0.69 mm Cu HVL [31], [45], [46]. The experimental determination of PDDs in kV beams using radiochromic film necessitates expertise, care in handling, it is laborious and time consuming and for this reason it is not encouraged [47], [48].
5.7.2. Relative output factors
Relative output factors are ratios of the dose with a particular applicator with or without a cut-out to the dose with the reference applicator [19], [36], [49]. These are usually defined at the surface for low kV beams, or at the reference depth of 2 cm for beams from generating potentials greater than 100 kVp [36], [50].
Relative output factors can be measured directly at the surface or at depth in water or a water-equivalent plastic phantom [51], [52]. Alternatively, they could be obtained from measurements in air together with experimentally derived or published backscatter factors (BSF) in order to determine dose at the surface of water [51]. For the latter approach, the use of ratios of published BSF has been reported to lead to significant uncertainties in the determination of dose [11], [53]. The measurement or calculation (using Monte Carlo modelling) of BSF is not a straightforward task and therefore it is not recommended to determine these directly [36].
Daniel et al. reported on a comparison of relative output factors measured with solid state detectors against measurements with the PTW Advanced Markus and concluded that solid state detectors exhibit an energy dependence and overresponce greater than 2% with decreasing field size and increasing beam energy in beam potentials up to 150 kVp / 0.3 mmCu. Contrary to this trend, at 300 kVp / 3.1 mmCu and in a field size of 20 cm × 20 cm the PTW shielded diode overestimated the beam output by 3%, whereas the PTW microDiamond underestimated this by 2% [42]. Relative output factors measured with solid state detectors ought to be compared against measurements with ionisation chambers as currently there is insufficient evidence supporting their use for the determination of relative output factors in kV beams.
It is therefore recommended that relative output factors are measured in water or water-equivalent plastic phantoms using thimble and plane parallel ionistation chambers. An important consideration when using the PTW Advanced Markus is that this detector was shown to exhibit a non-negligible polarity effect which increases with field size and beam quality and its readings must be corrected for this effect [50], [54].
Table 6 summarises recommendations on detectors for relative dosimetry in kV beams.
Table 6.
Examples and recommendations of detectors appropriate for relative dosimetry in kV beams (compiled in July 2022).
| Detectors for relative dosimetry in kV beams |
Relative depth dose | Relative output factor | ||||||
|---|---|---|---|---|---|---|---|---|
| Characteristics on sensitive volume |
||||||||
| Detector type | Examples with references | volume | radius (mm) | length or thickness (mm) | position of effective point of measurement | |||
| Cylindrical ionisation chambers with aluminium central electrode |
Farmer-type | NE2571, PTW 30013 [28] | 0.6 cm3 | 3.05 | 23 | on chamber axis, 13 mm from chamber tip | ✓ | ✓ |
| Scanning thimble-type | PTW 31010 [28], [42], [41] | 0.125 cm3 | 2.75 | 6.5 | on chamber axis, 4.5 mm from chamber tip | |||
| PTW 31013 [28] | 0.3 cm3 | on chamber axis, 9.5 mm from chamber tip | Not suitable close to the surface |
|||||
| Small volume |
PTW 31014 [28], [40], [41] | 0.015 cm3 | 1 | 5 | on chamber axis 3.4 mm from chamber tip | |||
| PTW 31016 [42] | 0.016 cm3 | 1.45 | 2.9 | on chamber axis 2.4 mm from chamber tip | ||||
| Plane parallel ionisation chambers |
PTW 34045 Advanced Markus [28], [42], [40], [54] | 0.02 cm3 | 2.5 | 1 | 1.3 mm below surface of protection cap | ✓ | ✓ | |
| PTW Markus [28], [40] | 0.055 cm3 | 2.65 | 2 | ✓ | Polarity correction needed [54] | |||
| PTW Roos [28], [54] | 0.35 cm3 | 7.8 | 2 | 1.13 mm below surface | ✓ | ✓ | ||
| NACP [28] | 0.16 cm3 | 5 | 2 | 0.6 mm below surface | ✓ | Check for polarity effects! |
||
| Exradin A11 [41] | 0.62 cm3 | 10 | 2 | 1 mm below surface | ✓ | |||
| Solid state detectors | Shielded silicon diode | PTW 60016 [41] | 0.03 mm3 | 0.6 | 0.027 | 2.21 mm on axis below tip | ✓ | ✗ |
| Unshielded silicon diode | PTW 60017 [41] | 0.03 mm3 | 0.6 | 0.027 | 1.33 mm on axis below tip | ✗ | ||
| PTW 60012 [40] | 0.0025 mm3 | 0.56 | 0.0025 | 0.6 mm on axis below tip | Only in low energy range | ✗ | ||
| Stereotactic SRS diode | PTW 60018 [41] | 0.3 mm3 | 0.56 | 0.25 | 1.31 mm on axis below tip | ✗ | ||
| Synthetic CVD diamond | PTW 60019 microdiamond [40], [41], [42] | 0.004 mm3 | 1.1 | 0.001 | 1 mm on axis below tip | ✓ | ✗ | |
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The useful and constructive input of SSRMP members to the final draft of these recommendations is gratefully acknowledged.
Footnotes
http://legnet.metas.ch/legnet2/Eichaemter/certsearch
Appendix A. Use of additional absorber foils in low energy x-ray dosimetry
For accurate determination and delivery of dose in low kV x-ray therapy, there are two effects that need to be considered. These influence and relate to how the reference system is used for calibrating the user’s beam and how kV beams are used for patient treatment.
A.1. Electron equilibrium
In order to achieve full build-up of the secondary electron fluence that enters the active volume of the ionization chamber, it has to be ensured that the entrance window is thick enough. This is in general the case if the total thickness of the entrance window exceeds the maximum range of secondary electrons. According to the specifications of the ionization chambers to be used for the dosimetry of low energy X-ray beams (see Table 1, Section 2.2) the thickness of the native window (2.76 mg cm-2) is sufficiently thick to achieve full build-up for kV beams with potentials below 50 kV [55].
At kV beams with potentials equal and greater than 50 kV the native window would need to be complemented by an additional foil in order to enable full build-up. Consequently, an additional foil becomes a part of the ionization chamber (that is, the reference detector comprises of the ionization chamber and the additional foil) and should be included at calibration at the standards laboratory and during the determination of reference dose in the clinical beam. However, because the energy spectrum of secondary electrons under charged-particle equilibrium in air is quite comparable to the one in polyethylene, the use of additional foil at beams above 50 kV is omitted during the instruments’ calibration at the standards laboratory (see Appendix B.1.2).
A.2. Electron contamination of the x-ray field
At calibration of the clinical beam, secondary electrons may originate from scattering of the x-rays on the applicator walls. In low energy x-ray beams at and above 50 kV, these scattered electrons could reach the active volume of the ionization chamber during calibration of the clinical beam and contribute to the ionization current and this would strongly depend on the specific material and geometry of the applicator [2]. Consequently, if in the user’s beam there is additional electron contamination present in comparison to that during calibration of the instrument at the standards laboratory then, this would lead to erroneous determination of absorbed dose [2].
Electron contamination in low-energy x-ray beams at and above 50 kV becomes an issue particularly with applicators with open ends. To address this an absorber foil can be used during the calibration of the clinical beam (that is at the determination of reference dose) as well as during the treatment of patients using such applicators. The foil has to be thick enough to fully stop contaminant electrons. As discussed in the previous section the thickness of the appropriate foil can be defined equal to the maximum range of secondary electrons, which is derived from the maximum kinetic energy at the generating potential for each beam based on continuous-slowing-down-approximation (CSDA) (according to ICRU report 37 [55]. Table 7 provides thicknesses of foils which could be used at and above 50 kV to this purpose. Alternatively and for simplicity a foil of 0.1 mm would suffice, as recommended in the DIN-6809-4 [2]. The same type and thickness of foil needs to be used at calibration of the clinical beam and for patient treatments.
Table 7.
Thicknesses of additional foils for an ionisation chamber with an entrance window of 2.76 mg cm-2 when this is used in kV x-ray beams at and above 50 kV. These values were derived using the maximum secondary electron ranges tabulated in ICRU report 37 [55] based on continuous-slowing-down-approximation (CSDA) for the maximum kinetic energy at the generating potential. The thicknesses in μm are approximate values for foils of different materials.
| Potential |
Maximum secondary electron range |
Additional thickness required for build-up |
Polyethylene (0.94 g cm-3) |
PMMA* (1.19 g cm-3) |
Mylar (1.4 g cm-3) |
|---|---|---|---|---|---|
| Thickness of additional foil | |||||
| kV | mg cm-2 | μm | |||
| 50 | 4.025 | 1.3 | 15 | 15 | 10 |
| 60 | 5.541 | 2.8 | 30 | 25 | 20 |
| 70 | 7.249 | 4.5 | 50 | 40 | 35 |
| 80 | 9.134 | 6.4 | 70 | 60 | 50 |
| 90 | 11.18 | 8.4 | 90 | 80 | 60 |
| 100 | 13.39 | 10.6 | 120 | 90 | 80 |
Polymethyl Methacrylate also known as acrylic. Trade names are: Perspex, Lucite, and Plexiglas.
Appendix B. Calibration of reference dosimeter systems at METAS and IRA
B.1. Derivation of a calibration coefficient in low energy x-rays (10 kV – 100 kV) – METAS
B.1.1. The PTB primary standard
In the low kV energy range the primary standard at PTB is a free-air plane-parallel ionisation chamber (known as PTB standard PK100) [56], [57], [58]. The determination of absorbed dose at the surface of a water phantom is based on the measurement of air kerma free-in-air (in the absence of the phantom), :
where is the ratio of mass energy absorption coefficients of water and air averaged over the spectral energy fluence free-in-air at the point of measurement [11], [59]. The product of this with the air kerma free in-air results to water kerma to a mass of water, small enough not to perturb the primary photon fluence. is the backscatter factor for the reference field size and beam quality and accounts for the presence of scatter from the phantom. The backscatter factor is defined as the ratio of water kerma at the surface of a semi-infinite water phantom to water kerma at that point in the absence of the phantom for the reference field size and SSD. Values for backscatter factors, tabulated against beam quality in terms of HVL, are taken from [60] and values of ratios of mass energy absorption coefficients are from [61], [62]. The change in response of the PK100 chamber in radiation field sizes ranging between 2 cm and 20 cm as a result of the effect of changes in photon scatter from its stem [11] is very close to unity [58].
B.1.2. Calibration of reference dosimeter system in low energy x-rays
The calibration of the user's reference system in the low energy range is carried out at PTB with the reference chamber placed at the surface of a water-equivalent solid phantom. The reference calibration conditions are those indicated on the calibration certificate of the reference system (see Table 2). The user’s reference system is a secondary standard instrument because it is cross-calibrated directly against the primary standard at PTB. The calibration coefficient at each beam quality is defined as the ratio of the dose determined by the primary standard instrument PK100 to the reading by the reference system corrected for influence quantities.
At cross-calibration at PTB no additional foil is placed at the entrance window of the reference chamber. Investigations have shown that the presence of a foil has a negligible influence on the calibration coefficient; namely it appears that the air volume above the chamber results in full build-up in the chamber. [2], [63].
The use of the reference system in a beam with field size and/or SSD that differ from those at reference conditions may necessitate a correction to its reading, if the response of the reference chamber is dependent on field size [12]. For reference ionisation chambers in this energy range such correction factors have been determined experimentally [21] (for chambers listed in Table 1; see paragraph 5.3.5 above).
B.2. Derivation of a calibration coefficient in medium energy x-rays (100 – 300 kV) – IRA
B.2.1. The PTB Primary Standard
In the medium kV energy range the primary standard at PTB is a water calorimeter. Two transfer ionisation chambers (types NE2561 and Farmer type TM30013) are calibrated in terms of absorbed dose to water in the phantom of the calorimeter for a range of beam qualities and field sizes. The readings of the chambers are corrected for influence quantities but not for ion recombination, as the maximum dose rate at which the calibrations are carried out is less than 3 mGy/s [64].
B.2.2. Calibration of reference dosimeter system in medium energy x-rays
IRAs secondary standard instrument, comprises of a cylindrical ionisation chamber of type NE2611A, with a sleeve made of Plexiglas, and a Keithley 6517A electrometer. This instrument is calibrated against the transfer ionisation chambers of PTB.
The calibration of the user's reference system in the medium energy range is carried out through an intercomparison with IRAs secondary standard reference system in a range of beam qualities requested by the user. This cross-calibration is carried out in water under successive irradiations with a horizontal beam at the reference depth of 2 cm. A transmission chamber is used to monitor the beam and to normalize the dosimeter readings. The reference calibration conditions are quoted on the calibration certificate of the user's instrument (see Table 4). The readings of chambers are corrected for influence quantities but not for ion recombination.
References
- 1.SSRMP-09, Dosimetrie von Röntgenstrahlen im niederen und mittleren Energiebereich 2001, Schweizerische Gesellschaft für Strahlenbiologie und Medizinische Physik.
- 2.DIN-6809-4, Klinische Dosimetrie - Teil 4: Röntgentherapie mit Röntgenröhrenspannungen zwischen 10 kV und 300 kV. 2020, DIN e.V.
- 3.IAEA-TRS-398, Absorbed dose determination in external beam radiotherapy: An international code of practice for dosimetry based on standards of absorbed dose to water. 2000, IAEA: Vienna
- 4.StSG-814.50, Radiological Protection Act of 22 March 1991 (RPA). 1991, Federal Office of Public Health: Bern, Switzerland.
- 5.StSV-814.501, Radiological Protection Ordinance of 26 April 2017. 2021, Federal Office of Public Health: Bern, Switzerland.
- 6.RöV-814.542.1, Verordnung des EDI über den Strahlenschutz bei medizinischen Röntgensystemen (Stand am Februar 2018). 2017, Federal Office of Public Health: Bern, Switzerland.
- 7.MessMV-941.210, Messmittelverordnung (Stand am 20. April 2016). 2006, Federal Office of Public Health: Bern, Switzerland.
- 8.StMmV-941.210.5, Verordnung des EJPD über Messmittel für ionisierende Strahlung. 2012, Federal Office of Public Health: Bern, Switzerland.
- 9.SR-941.202, Einheitenverordnung (Stand am 20. Mai 2019). 1994, Federal Office of Public Health: Bern, Switzerland.
- 10.Nemec H.W., Elmer E. Gemeinsame Wissenschaftliche Tagung der SGSMP und SGBT. Paul Scherrer Institut; Villingen: 1993. Qualitätskontrollen an Röntgentherapieanlagen in der Schweiz. [Google Scholar]
- 11.Ma C.M., et al. AAPM protocol for 40–300 kV x-ray beam dosimetry in radiotherapy and radiobiology. Med Phys. 2001;28(6):868–893. doi: 10.1118/1.1374247. [DOI] [PubMed] [Google Scholar]
- 12.NCS-10, Dosimetry of low and medium energy x-rays. 1997, Netherlands Commission on Radiation Dosimetry.
- 13.Andreo P., Nahum A.E., Thwaites D.I. In: Handbook of Radiotherapy Physics. Mayles P., Nahum A., Rosenwald J.C., editors. Taylor & Francis Group; 2007. Ionisation Chambers. ISBN: 978-0-7503-0860-1. [Google Scholar]
- 14.IAEA-TRS-469, Calibration of Reference Dosimeters for External Beam Radiotherapy. 2009, IAEA: Vienna
- 15.Morgan A.M., et al. IPEM guidelines on dosimeter systems for use as transfer instruments between the UK primary dosimetry standards laboratory (NPL) and radiotherapy centres. Phys Med Biol. 2000;45(9):2445–2457. doi: 10.1088/0031-9155/45/9/301. [DOI] [PubMed] [Google Scholar]
- 16.JCGM100:2008, Evaluation of measurement data - Guide to the expression of uncertainty in measurement (GUM 1995). 2008: BIPM
- 17.CCEMRI(I), Comité consultatif pour les étalons de mesure des rayonnements ionisants. 1977, Bureau International des poids et Mesures: Sèvres, France.
- 18.Attix F.A. John Wiley & Sons Inc; New York, USA: 1986. Introduction to Radiological Physics and Radiation Dosimetry. ISBN: 9780471011460. [Google Scholar]
- 19.Mayles P. In: Handbook of Radiotherapy Physics, Theory and Practice. Mayles P., Nahum A., Rosenwald J.C., editors. Taylor & Francis; New York London: 2007. Kilovoltage X-rays; pp. 439–449. ISBN: 978-0-7503-0860-1. [Google Scholar]
- 20.IAEA-TRS-381, The Use of Plane Parallel Ionisation Chambers in High Energy Electron and Photon Beams. 1997, IAEA: Vienna
- 21.Engelke B.-A., Grosswendt B. Zur Bestimmung der Wasser-Energiedosis für Röntgenstrahlungen mit Erzeugerspannung bis 100kV, PTB-Mitteilungen. Editor. 1989:163–167. [Google Scholar]
- 22.Seuntjens J., Verhaegen F. Dependence of overall correction factor of a cylindrical ionization chamber on field size and depth in medium-energy x-ray beams. Med Phys. 1996;23(10):1789–1796. doi: 10.1118/1.597833. [DOI] [PubMed] [Google Scholar]
- 23.NCRP-69, Dosimetry of X-Ray and Gamma-Ray Beams for Radiation Therapy in the Energy Range 10 keV to 50 MeV. 1981: Bethesda, MD.
- 24.Abdel-Rahman W., et al. Clinic based transfer of the N(D, W)(60Co) calibration coefficient using a linear accelerator. Med Phys. 2009;36(3):929–938. doi: 10.1118/1.3075822. [DOI] [PubMed] [Google Scholar]
- 25.Armitag P., Berry G., Matthews J.N.S. Wiley-Blackwell Scientific Publications; 2001. Statistical Methods in Medical Research. ISBN: 9780632052578. [Google Scholar]
- 26.Li X.A., Ma C.M., Salhani D. Measurement of percentage depth dose and lateral beam profile for kilovoltage x-ray therapy beams. Phys Med Biol. 1997;42(12):2561–2568. doi: 10.1088/0031-9155/42/12/019. [DOI] [PubMed] [Google Scholar]
- 27.Aukett R.J., et al. Addendum to the IPEMB code of practice for the determination of absorbed dose for x-rays below 300 kV generating potential (0.035 mm Al-4 mm Cu HVL) Phys Med Biol. 2005;50(12):2739–2748. doi: 10.1088/0031-9155/50/12/001. [DOI] [PubMed] [Google Scholar]
- 28.Hill R., et al. An evaluation of ionization chambers for the relative dosimetry of kilovoltage x-ray beams. Med Phys. 2009;36(9):3971–3981. doi: 10.1118/1.3183820. [DOI] [PubMed] [Google Scholar]
- 29.BJR-Suppl25, Central Axis Depth Dose Data for Use in Radiotherapy, in British Journal of Radiology. 1996, British Institute of Radiology: London.
- 30.Wachsmann F., Drexler G. Spinger-Verlag; Berlin, Heidelberg, New York: 1976. Graphs and Tables for Use in Radiology. ISBN: 978-3-642-67898-1. [Google Scholar]
- 31.Aspradakis M.M., Zucchetti P. Acceptance, commissioning and clinical use of the WOmed T-200 kilovoltage X-ray therapy unit. Br J Radiol. 2015;88(1055):20150001. doi: 10.1259/bjr.20150001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ma C.M., Seuntjens J.P. Mass-energy absorption coefficient and backscatter factor ratios for kilovoltage x-ray beams. Phys Med Biol. 1999;44(1):131–143. doi: 10.1088/0031-9155/44/1/011. [DOI] [PubMed] [Google Scholar]
- 33.Hill R., Kuncic Z., Baldock C. The water equivalence of solid phantoms for low energy photon beams. Med Phys. 2010;37(8):4355–4363. doi: 10.1118/1.3462558. [DOI] [PubMed] [Google Scholar]
- 34.Hill R., Holloway L., Baldock C. A dosimetric evaluation of water equivalent phantoms for kilovoltage x-ray beams. Phys Med Biol. 2005;50(21):N331–N344. doi: 10.1088/0031-9155/50/21/N06. [DOI] [PubMed] [Google Scholar]
- 35.Ramaseshan R., et al. Dosimetric evaluation of Plastic Water Diagnostic Therapy. J Appl Clin Med Phys. 2008;9(2):2761. doi: 10.1120/jacmp.v9i2.2761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hill R., et al. Advances in kilovoltage x-ray beam dosimetry. Phys Med Biol. 2014;59(6):R183–R231. doi: 10.1088/0031-9155/59/6/R183. [DOI] [PubMed] [Google Scholar]
- 37.Snow J.R., Micka J.A., DeWerd L.A. Microionization chamber air-kerma calibration coefficients as a function of photon energy for x-ray spectra in the range of 20–250 kVp relative to 60Co. Med Phys. 2013;40(4) doi: 10.1118/1.4794491. [DOI] [PubMed] [Google Scholar]
- 38.Hugtenburg R.P., et al. Application of diamond detectors to the dosimetry of 45 and 100 kVp therapy beams: comparison with a parallel-plate ionization chamber and Monte Carlo. Phys Med Biol. 2001;46(9):2489–2501. doi: 10.1088/0031-9155/46/9/317. [DOI] [PubMed] [Google Scholar]
- 39.Ma C.M., Seuntjens J.P. Workshop on Kilovoltage X-Ray Beam Dosimetry for Radiotherapy and Radiobiology. Medical Physics Publishing; Standford, California, USA: 1997. Kilovoltage X-ray Beam Dosimetry for Radiotherapy and Radiobiology. [Google Scholar]
- 40.Damodar J., et al. A study on the suitability of the PTW microDiamond detector for kilovoltage x-ray beam dosimetry. Appl Radiat Isot. 2018;135:104–109. doi: 10.1016/j.apradiso.2018.01.025. [DOI] [PubMed] [Google Scholar]
- 41.Khan A.U., Culberson W.S., DeWerd L.A. Characterizing a PTW microDiamond detector in kilovoltage radiation beams. Med Phys. 2020;47(9):4553–4562. doi: 10.1002/mp.14330. [DOI] [PubMed] [Google Scholar]
- 42.Daniel J., et al. An evaluation of solid state detectors for the relative dosimetry of kilovoltage X-ray beams. Med Phys. 2022;49(6):4082–4091. doi: 10.1002/mp.15543. [DOI] [PubMed] [Google Scholar]
- 43.Brown T.A., et al. Dose-response curve of EBT, EBT2, and EBT3 radiochromic films to synchrotron-produced monochromatic x-ray beams. Med Phys. 2012;39(12):7412–7417. doi: 10.1118/1.4767770. [DOI] [PubMed] [Google Scholar]
- 44.Villarreal-Barajas J.E., Khan R.F. Energy response of EBT3 radiochromic films: implications for dosimetry in kilovoltage range. J Appl Clin Med Phys. 2014;15(1):4439. doi: 10.1120/jacmp.v15i1.4439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ma C.-M. In: Clinical Dosimetry Measurements in Radiotherapy. Rogers D.W.O., Cygler J.E., editors. Medical Physics Publishing; Madison, Wisconsin, US: 2009. Kilovoltage X-Ray Dosimetry for Radiation Therapy. ISBN: 978-1-888340-84-6. [Google Scholar]
- 46.Zucchetti P et al. The determination of relative depth doses in kilovoltage beams. In: Klöck S, editor. Joint Conference of the SSRMP, DGMP, ÖGMP: Zurich; 2014. p. 306–7. ISBN: 987-3-9816508-5-3.
- 47.Niroomand-Rad A., et al. Radiochromic film dosimetry: recommendations of AAPM Radiation Therapy Committee Task Group 55. American Association of Physicists in Medicine. Med Phys. 1998;25(11):2093–2115. doi: 10.1118/1.598407. [DOI] [PubMed] [Google Scholar]
- 48.Niroomand-Rad A., et al. Report of AAPM Task Group 235 Radiochromic Film Dosimetry: An Update to TG-55. Med Phys. 2020;47(12):5986–6025. doi: 10.1002/mp.14497. [DOI] [PubMed] [Google Scholar]
- 49.Williams J.R., Thwaites D.I. Oxford University Press; 1993. Radiotherapy Physics in Practice. ISBN: 0199633150. [Google Scholar]
- 50.Hill R., et al. Australasian recommendations for quality assurance in kilovoltage radiation therapy from the Kilovoltage Dosimetry Working Group of the Australasian College of Physical Scientists and Engineers in Medicine. Australas Phys Eng Sci Med. 2018;41(4):781–808. doi: 10.1007/s13246-018-0692-1. [DOI] [PubMed] [Google Scholar]
- 51.Evans P.A., Moloney A.J., Mountford P.J. Performance assessment of the Gulmay D3300 kilovoltage X-ray therapy unit. Br J Radiol. 2001;74(882):537–547. doi: 10.1259/bjr.74.882.740537. [DOI] [PubMed] [Google Scholar]
- 52.Jurado D., et al. Pantak Therapax SXT 150: performance assessment and dose determination using IAEA TRS-398 protocol. Br J Radiol. 2005;78(932):721–732. doi: 10.1259/bjr/15782649. [DOI] [PubMed] [Google Scholar]
- 53.Healy B.J., et al. Output factor measurements for a kilovoltage X-ray therapy unit. Australas Phys Eng Sci Med. 2005;28(2):115–121. doi: 10.1007/BF03178702. [DOI] [PubMed] [Google Scholar]
- 54.Dowdell S., et al. Potential errors in relative dose measurements in kilovoltage photon beams due to polarity effects in plane-parallel ionisation chambers. Phys Med Biol. 2016;61(23):8395–8407. doi: 10.1088/0031-9155/61/23/8395. [DOI] [PubMed] [Google Scholar]
- 55.ICRU37, Section 12. Main Tables: Stopping Powers, Ranges, and Radiation Yields, in ICRU Report 37: Stopping Powers for Electrons and Positrons. 1984, International Commission on Radiation Units and Measurements: Bethesda, MD, 20814, USA. ISBN: 0-913394-31-9
- 56.BIPM-01/08, R., Comparison of the air-kerma standards of the PTB and the BIPM in the low-energy x-ray range. In: Burns DT et al., editors. Bureau International des Poids et Mesurs: Pavillon de Breteuil, F-92312 Sèvres Cedex; 2001.
- 57.Burns D.T., Kessler C., Büermann L. Key comparison BIPM.RI(I)-K2 of the air-kerma standards of the PTB and the BIPM in the low-energy x-rays. Metrologia. 2014;51(Tech. Suppl. 06011) doi: 10.1088/0026-1394/49/1A/06006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Engelke B.-A., Oetzmann W., Struppek G. Die Messeinrichtungen der Physikalisch-Technischen Bundesanstalt zur Darstellung der Einheiten der Standard-Ionendosis. Photonen-Äquivalentdosis und Luftkerma. 1988:PTB. [Google Scholar]
- 59.IPEMB-1996 The IPEMB code of practice for the determination of absorbed dose for x-rays below 300 kV generating potential (0.035 mm Al-4 mm Cu HVL; 10–300 kV generating potential) Phys Med Biol. 1996;41:2605–2625. doi: 10.1088/0031-9155/41/12/002. [DOI] [PubMed] [Google Scholar]
- 60.Grosswendt B. Dependence of the photon backscatter factor for water on source-to-phantom distance and irradiation field size. Phys Med Biol. 1990;35(9):1233–1245. [Google Scholar]
- 61.DIN-6809-4, Klinische Dosimetrie - Teil 4: Röntgentherapie mit Röntgenröhrenspannungen zwischen 10 kV und 300 kV. 2016, DIN e.V.
- 62.Hubbell J.H. Review of photon interaction cross section data in the medical and biological context. Phys Med Biol. 1999;44(1):R1–R. doi: 10.1088/0031-9155/44/1/001. [DOI] [PubMed] [Google Scholar]
- 63.Büermann L. PTB; Braunschweig, Germany: 2017. Personal communication: Interpretation der Messungen mit der METAS M23342 Kammer mit und ohne zusätzliche Polyethylenfolie. [Google Scholar]
- 64.Krauss A., et al. Calorimetric determination of the absorbed dose to water for medium-energy x-rays with generating voltages from 70 to 280 kV. Phys Med Biol. 2012;57(19):6245–6268. doi: 10.1088/0031-9155/57/19/6245. [DOI] [PubMed] [Google Scholar]