A life off the beaten track in biomechanics: Imperfect elasticity, cytoskeletal glassiness, and epithelial unjamming

Abstract

Textbook descriptions of elasticity, viscosity, and viscoelasticity fail to account for certain mechanical behaviors that typify soft living matter. Here, we consider three examples. First, strong empirical evidence suggests that within lung parenchymal tissues, the frictional stresses expressed at the microscale are fundamentally not of viscous origin. Second, the cytoskeleton (CSK) of the airway smooth muscle cell, as well as that of all eukaryotic cells, is more solid-like than fluid-like, yet its elastic modulus is softer than the softest of soft rubbers by a factor of 10⁴–10⁵. Moreover, the eukaryotic CSK expresses power law rheology, innate malleability, and fluidization when sheared. For these reasons, taken together, the CSK of the living eukaryotic cell is reminiscent of the class of materials called soft glasses, thus likening it to inert materials such as clays, pastes slurries, emulsions, and foams. Third, the cellular collective comprising a confluent epithelial layer can become solid-like and jammed, fluid-like and unjammed, or something in between. Esoteric though each may seem, these discoveries are consequential insofar as they impact our understanding of bronchospasm and wound healing as well as cancer cell invasion and embryonic development. Moreover, there are reasons to suspect that certain of these phenomena first arose in the early protist as a result of evolutionary pressures exerted by the primordial microenvironment. We have hypothesized, further, that each then became passed down virtually unchanged to the present day as a conserved core process. These topics are addressed here not only because they are interesting but also because they track the journey of one laboratory along a path less traveled by.

I. INTRODUCTION

E.L. Doctorow is reported to have said that writing a novel is like driving a car at night: You can see only as far as your headlights but you can make the whole trip that way. This article describes a similar journey although in a different domain. One of us (Fredberg) has been invited to write a personal retrospective of a life lived and lessons learned at the interface between the physical sciences and the life sciences. In this journey, the preeminent recurring theme has been the trainees themselves—the cavalcade of outstanding young scientists who have passed through the lab and from whom we have learned so much. Among the most recent, Atia has agreed to serve in the capacity of a proxy for some 60 others who are, de facto, very much the co-authors of this report. This story is their story. As the legendary pulmonologist Nicholas Anthonisen once related, you are only as good as your trainees. In our experience, Nick's assertion held true.

To make expectations clear, for any given topic addressed here, we do not attempt to present an objective or comprehensive review. Rather, we present a narrative—an odyssey as it were—from the perspective of the characters who passed through one particular laboratory.

A. A long corridor with many doors

We followed our data wherever they might lead. This approach brought us into topics far from our initial comfort zone (Text Box 1). These topics included tumor cell invasion in cancer, cell migration during wound healing and in embryonic development, and the discovery of the epithelial unjamming transition (UJT), which is not to be confused with the epithelial-to-mesenchymal transition (EMT). Nevertheless, bronchospasm in asthma is the thread that holds our story together. The recurring theme was the study of mechanical factors that determine function of the healthy lung but go awry in the asthmatic lung. Although it was not at all our plan, again and again in these efforts we stumbled into the lurking problem of the unexplained material properties that typify soft biological matter. Even though we were focused narrowly on mechanics of the lung and asthma, it became increasingly clear that our research on these topics impinged upon deeper questions not only in biology but also in soft matter physics, and even touched upon new questions wherein biomechanics intersects with evolution.^1–3 An early mentor, Frederic Hoppin, Jr., advised us to stay basic. So we did.

1: A path less traveled by

Our team invented useful technologies, the foremost being magnetic twisting cytometry,⁴ Fourier transform traction microscopy,^5,6 monolayer traction microscopy,⁷ and monolayer stress microscopy (MSM).⁸ Each in its own way, these technologies opened windows allowing us to report eight consequential discoveries in basic biophysical sciences:

• (1) Frictional stress expressed within lung parenchymal tissues is tied directly to the tissue elastic stress, and not to the overwhelmingly fashionable—but nonetheless mistaken—notion of a tissue viscous stress.^9,10

• (2) Frictional stress expressed within activated airway smooth muscle (ASM) precisely tracks—and, thus, comprises a window into—acto-myosin cycling rate, hydrolysis of adenosine triphosphate (ATP) by acto-myosin cycling, and unloaded shortening velocity.¹¹

• (3) Activated ASM in the healthy lung attains a length that is equilibrated not by a balance of static forces, but rather becomes lengthened dynamically in response to load fluctuations associated with the act of ordinary spontaneous breathing. Breathing is good for breathing. But during a spontaneous asthmatic attack, ASM can become excessively shortened, stiffened, and frozen into a solid-like, static muscle state called latch.^12–14

• (4) The cytoskeleton (CSK) of the living cell expresses certain universal features—including small stiffness, power law rheology, and innate malleability—reminiscent of the class of materials called “soft glasses.”^4,15

• (5) In response to transient stretch-and-hold, the cytoskeleton of the living cell expresses prompt nonlinear strain stiffening followed by slow stress relaxation.¹⁶ But in response to transient stretch-and-unstretch (with zero residual strain), the cytoskeleton reveals a simple universal response, namely, fluidization.^16,17 CSK fluidization is attributable in part to the severing of actin filaments by the action of cofilin, which occurs predominantly during the unstretch phase.¹⁸

• (6) Cells comprising a confluent epithelial layer tend to migrate collectively along orientations that minimize local in-plane intercellular shear stresses—plithotaxis⁸—and tend to exert tractions pulling toward any nearby cell-free void—kenotaxis.¹⁹

• (7) The confluent epithelial layer, when mature and unperturbed, tends toward a solid-like collective cellular phase that is jammed. In such a jammed phase, cells are crowded and trapped by their neighbors, and thereby become immobilized and stuck in place. But by a variety of means, such a layer can undergo an unjamming transition (UJT) wherein the cellular collective fluidizes and migrates much as a flowing fluid.²⁰ In doing so, cell shapes become systematically more elongated and more variable.²¹ Moreover, cells within the unjammed layer retain a purely epithelial phenotype including intact cell–cell junctions, intact barrier function, and no evidence of mesenchymal markers.²² The UJT is, therefore, distinct from the epithelial-to-mesenchymal transition (EMT).

• (8) The confluent epithelial layer ordinarily stands poised in a disordered state that is just at the brink of unjamming, ready to unjam, and migrate in response to cues associated with wound healing, embryonic development, tissue remodeling, or cancer progression.^3,23 Proximity to jamming can be quantified by cell shape and shape variability.^20,21

II. IMPERFECT ELASTICITY OF LUNG PARENCHYMAL TISSUES

A. Who cares about tissue friction, anyways?

For reasons described below, the story begins with what may seem at first an obscure topic. That topic is the mechanical friction expressed by lung parenchymal tissues and, consequently, the mechanical work that must be expended to accomplish one complete cycle of lung inflation and deflation, as occurs, for example, with every breath that we take.^9,24,25 There is the closely related issue of lung tissue hysteresis, i.e., the pressure that is required to sustain a given state of lung inflation depends not only upon instantaneous lung volume but also upon the history of lung volume changes. As a result, when tracing the relationship between lung volume and distending stress (i.e., transpulmonary pressure) during an exceedingly slow or quasi-static full lung inflation, the path during inflation dramatically departs from the path during deflation (Fig. 1, left panel). An inspiratory pause reveals slow stress relaxation, and a deflationary pause shows slow stress recovery, thus displaying an appreciable degree of rate dependence (Fig. 1, right panel). Nevertheless, the loop stays open and virtually unchanged even when imposed volume changes are infinitesimally slow. The area inside the closed loop corresponds to mechanical work expended by respiratory muscles on the lung and, therefore, mechanical energy dissipated.²⁶ Simply put, no combination of elastic and viscous elements, no matter how elaborate that arrangement, can account for energy dissipation that is insensitive to rate. As described below, this inconvenient fact seems not to have impeded ongoing misapplication of purely viscoelastic models to the case of lung tissues.

FIG. 1.

Left: Quasistatic pressure–volume curve for an air-filled control lung (solid lines) or a lung filled with test liquids of graded but constant interfacial tension, γ (dashed lines). Right: Pressure volume relationship for stepwise filling and emptying of an air-filled lung reveals transient stress relaxation when inflation is halted, and stress recovery when deflation is halted. Arrows denote results with a test fluid of constant interfacial tension (γ = 28 dynes/cm). Quasistatic lung tissue hysteresis (dashed line) is attributable mainly to hysteretic adsorption–desorption dynamics of surface-active molecules.^44,244 Reproduced with permission from Smith and Stamenovic, J. Appl. Physiol. 60(4), 1341–1350 (1986). Copyright 1986 American Physiological Society.

When we first launched into the study of this topic, we were warned away by no less than two of the greatest minds in respiratory physiology of the 20th century. Jere Mead, who was Fredberg's unofficial mentor at Harvard, told us that insofar as lung tissue hysteresis dominates the pulmonary pressure vs volume relationship, it was well recognized as being important physiologically,^27–29 but up to that time, underlying mechanism had remained an intellectual quagmire. So he cautioned us to stay away. Similarly, Solbert Permutt at Johns Hopkins related that he doubted that any progress could be made on this topic, but—paraphrasing the English poet Robert Blake—he suggested that perhaps one would be able to see a world in this obscure grain of sand. More about sand grains is presented in Sec. VIII. On the other hand, Peter Macklem at McGill—another giant of the field—urged us on. After all, he argued, Roland Ingram, Jr., who was our collaborator and teacher at Harvard, and others before him had demonstrated that we all sigh roughly ten times per hour,³⁰ and that such deep inspirations (DIs) are little appreciated but nonetheless are among the most potent of all known bronchodilating agencies.^13,31–36 Indeed, a single DI is known ablate the contractile tone of airway smooth muscle and thereby dilate the constricted airway, which then remains dilated for up to several minutes thereafter.³⁵ Moreover, respiratory control ensures that we make an involuntary DI roughly once every 6 min, thus not only recruiting pulmonary surfactant from type 2 alveolar epithelial cells but also promoting and maintaining airway patency. However, for reasons that had remained obscure, during a spontaneous asthmatic attack, this potent protective mechanism not only fails to dilate the constricted airway but also sometimes acts to narrow it even more.³¹ As described below, Ingram had attributed the failure of this salutary mechanism in asthma to increased hysteresis of lung tissues.^14,22 Hence, our keen interest in that topic.

Subsequently—and almost but not quite on a straight line—our narrow interest in lung tissue hysteresis led in time to discoveries concerning the question of the mechanics of the cytoskeleton (CSK) of the adherent eukaryotic cell and its abilities to contract, deform, remodel, and migrate. Such cellular properties in turn have proven to be the key to the much more general topics of bronchospasm, tissue remodeling, wound healing, developmental biology, collective cancer cell invasion, and even, as described below, evolutionary adaptation. As usual, Permutt was right.

B. Classical descriptions

Before 1938, a wide class of experiments could be interpreted adequately based on the concept that there exists within biological tissues a frictional stress analogous to that which results from the flow of a viscous fluid. As such, the classical equation of motion used to describe small cyclic changes of lung volume, V(t), holds that: P(t) = EV(t) + R dV(t)/dt. For periodic volume changes, we can, therefore, write

$$\mathrm{P}(\omega )=(\mathrm{E}+\mathrm{j}\omega \mathrm{R})\mathrm{V}(\omega ),$$ (1)

where P denotes the pressure difference that distends lung tissues, specifically the pressure difference from alveolar gas to pleural space. To focus on lung tissues, here we have set aside the resistance to gas flow in the airways, which is an important topic but a different one.^26,37–39 The dynamic elastance E describes the tissue elastic stress associated with cyclic energy storage within the expanding lung. The resistance R had been attributed to viscous stresses within lung tissues. ω is the radian frequency, 2πf, of cyclic lung expansion, and the symbol j is the unit imaginary number denoting the fact that during cyclic lung expansion viscous stress vs elastic stress are out of phase by 90°.

C. Some ideas take much killing

Hill in the case of skeletal muscle⁴⁰ and Bayliss and Robertson in the case of lung tissue²⁴ upset this physical picture by demonstrating that frictional behavior within tissue is fundamentally incompatible with Eq. (1). That is to say, there surely exists within lung tissues substantial internal frictional stress. However, to explain such frictional stress solely by a viscous molecular mechanism, or for that matter by any combination of viscous and elastic processes as in the theory of viscoelasticity, is not only overly simplistic but on mechanistic grounds is fundamentally mistaken. For example, Bayliss and Robertson reported that the greater part of energy dissipation associated with cyclic lung expansion depends upon the amount of lung expansion but not upon the rate of expansion. Further characterization of this behavior came largely from the pioneering work of Hildebrandt and co-workers^25,41,42 and proved to be rather complicated. In the range of frequencies corresponding to spontaneous breathing, for example, these and other studies showed that when friction is expressed by the resistance parameter, R, that parameter becomes characterized not only by responsiveness to constrictor stimuli, as expected, but also by strong inverse dependence on frequency (close to 1/ω). R is also characterized by negative dependence on tidal volume and strong sensitivities to changes of lung volume and volume history. Together, this constellation of complex behaviors had remained unexplained. As such, much of what we had learned about mechanics of materials in graduate studies in engineering materials seemed curiously inapplicable to lung tissues.

D. Concept of the tissue hysteresivity

For those reasons, we teamed up with Dimitrije Stamenovic at Boston University and, together, suggested a radical departure.⁹ We reasoned that Eq. (1), by virtue of its mathematical form, embeds from the outset two implicit assumptions that we found to be questionable. First, Eq. (1) implies that frictional stress within lung tissues is of viscous origin, at least to a first approximation. A viscous framing is built-in from the beginning. Second, Eq. (1) also implies that the frictional stress and the elastic stress correspond to distinct and independent molecular processes. Instead, we proposed that the frictional stress within lung parenchymal tissue is somehow tied innately to the elastic stress, not to a viscous stress. In other words, at the molecular scale, the frictional stress and the elastic stress reside within the very same stress-bearing element. If so, the equation of motion described by Eq. (1) could become replaced by

$$\mathbf{P}(\omega )=(\mathrm{E}+\mathrm{j}\eta \mathrm{E})\mathbf{V}(\omega )$$ (2)

or simply, P(ω) = (1 + j η) Ε V(ω). Such a description leads naturally to consideration of a readily measured phenomenological attribute of frictional (dissipative) behavior that we called lung tissue hysteresivity, η. η is a non-dimensional measure of the fatness of a closed P–V loop (or length-tension loop) and can be defined even in nonlinear systems in which the loop is sigmoidal, as in Fig. 1. As such, η of a frictionless spring is zero even if the spring is nonlinear. It follows from Eq. (2) that for every joule of elastic energy, ε, stored in lung tissues at peak lung volume expansion, the amount of energy dissipated over one complete inflation–deflation cycle is simply ηε. That is to say, frictional energy dissipation in lung tissues acts as a tax on the peak elastic energy stored, with a simple tax rate per cycle of η. This perspective leads to a stunning empirical simplification.

For example, when lung pressure–volume data are interpreted through Eq. (1), the resistance parameter R is found to vary strongly not only with frequency but also with lung size, lung volume history, lung growth, body mass, and across species. However, when these very same data are reinterpreted through Eq. (2), the parameter η is found to be nearly invariant.⁹ In inflated lung tissue, η almost always falls close to 0.2 and typically within the limited range 0.1–0.3. (The case of η in isolated airway smooth muscle is an interesting departure, as described below.) Such simple conserved behavior is consistent with the notion that within lung tissue the elastic energy storage and dissipative energy loss reside within the very same stress-bearing element and, moreover, that those processes within the stress-bearing element bear an approximately fixed relationship.

These alternative empirical descriptions of the lung tissue frictional stress [i.e., Eq. (1) vs Eq. 2], when taken together, lead to a disarmingly simple relationship and a deep insight as follows:

$$\omega \mathrm{R}\hspace{0.17em}=\eta \mathrm{E}.$$ (3)

We emphasize that Eq. (3) is an empirical statement, not a mechanistic one. Nevertheless, to the extent that the tax rate, η, is found to vary little, Eq. (3) would, therefore, account for why any empirical descriptions of a lung tissue resistance, R, must always change in tandem with any change in lung tissue elastance. That is to say, the dependence of R on multiple factors is embedded within and largely accounted for by the dependence of E on those same factors. Equation (3) would also account for why lung tissue resistance—looked at within the physiological frequency range—must vary with frequency very nearly as 1/ω. In other words, if one knows the lung tissue elastance, then to a first approximation the lung tissue resistance is determined as well.

Specific molecular mechanisms that might couple dissipation to elasticity in this manner remain unclear⁹ but are illustrated in detachment of a stretched molecular bond. As in snapping a stretched rubber band, mechanical energy dissipated in a microscale detachment event depends directly on the elastic energy imparted to the bond during the preceding stretch. For example, consider the case of the myosin molecule bound to and detaching from the actin filament in smooth muscle. In that system, there exist spontaneous myosin detachment events as well as stretch-induced detachment events, and these events have mechanical and metabolic implications as well, as described below.^11,43 Similarly, the mechanical work done to adsorb an amphiphilic surface active molecule from the alveolar sub-phase to the gas–liquid interface during the lung expansion becomes lost when that molecule desorbs irreversibly into an solid-like phase during deflation.⁴⁴ These and other possibilities have been addressed elsewhere.⁹

As a practical matter, as in testing of pulmonary mechanics in mouse models of lung disease, Eq. (2) has come into wide use as embedded into the similar but somewhat more elaborate “constant phase model.”⁴⁵ Tissue hysteresivity is closely related to the parameter K used by Bachofen and Hildebrandt⁴¹ to describe energy dissipation per cycle, and both lend themselves directly to interpretation based on processes ongoing at the levels of microstructure and molecule. Surprisingly, Eq. (2) had appeared previously in the physical sciences in the context of structural vibration and geophysics.^9,46,47 In those fields, η is sometimes referred to as the loss tangent, the loss factor, or the structural damping factor.

III. HYSTERESIVITY, SMOOTH MUSCLE CONTRACTION, AND ACTO-MYOSIN CYCLING

There exists no known disease entity or physiological deficit associated with loss of airway smooth muscle contractility. It has been debated, therefore, whether airway smooth muscle serves any useful physiologic function at all or rather is a vestigial tissue capable only of mean-spirited mischief, as in asthma.^48–50 Accordingly, it has been called by Wayne Mitzner the appendix of the lung.^49,51,52

Airway smooth muscle (ASM) contractility and associated mechanical hysteresis are interesting for at least three reasons. Perhaps the least of these is that the extensive airway branching tree of the lung comprises tens of thousands small intraparenchymal airways, along with their embedded ASM, which contribute somewhat to overall lung elastic recoil.⁵³ Perhaps more important is that the relative hysteresis of airway vs lung parenchyma in which it is embedded strongly impacts the effect of lung volume history upon current airway caliber.^{14,31,54–56} However, the most compelling may be that if airway inflammation did not cause airway smooth muscle contraction and resulting bronchospasm, then asthma would be a tolerable disease.⁵⁷ However, asthma is most certainly not a tolerable disease. It is not tolerable mainly because the effects of ASM contraction become amplified by those of mucus hypersecretion and progressive airway remodeling, and thereby drive asthma morbidity and mortality. Therefore, the lab pivoted from studying the mechanics of lung parenchymal tissue to that of airway smooth muscle. As described in Sec. VIII, emerging evidence now suggests that smooth muscle contraction causes airway epithelial injury which, in turn, is permissive of the inflammatory response.

In smooth muscle, the active contractile force, F, and stiffness, E, are roughly proportional to numbers of actin–myosin crossbridges.⁵⁸ With onset of electrical field stimulation (EFS), for example, the parameters E and F are seen to rise rapidly and in tandem with each forming a stable plateau (Fig. 2). The time course of hysteresivity, by contrast, follows a biphasic pattern, spiking upward initially and then diminishing rapidly even as force and stiffness continue to increase. Steady state isometric contraction of ASM is, therefore, seen to be a high-stiffness low-friction state.

FIG. 2.

Mechanics of a representative isolated canine tracheal smooth muscle subjected to electrical field stimulation (EFS). (a) Force (tension), F. (b) Elastance (stiffness), E. (c) Hysteresivity, η. The off-transient of η has never been investigated but is suggestive of a transition from slowly cycling latch bridges during isometric stimulation to an avalanche of detachment events upon cessation of that stimulation.¹¹ Reproduced with permission from Fredberg et al., J. Appl. Physiol. 81(6), 2703–2712 (1996). Copyright 1996 American Physiological Society.

For reasons hinted at above, we suspected that this time-dependence of hysteresivity in activated airway smooth muscle might be linked to the rate of cross bridge detachment, and we tested that idea in isolated canine ASM.¹¹ As shown below, we found that the notion that η is linked directly to the rate of acto-myosin crossbridge cycling is supported by three independent lines of evidence: mechanical (Vmax), metabolic (myosin ATPase activity), and computational.

A. Maximal unloaded shortening velocity

Using a similar preparation as in Fig. 2, we tracked time-dependence of unloaded shortening velocity, Vmax (Fig. 3).¹¹ Vmax is a well-studied and direct index of underlying bridge cycling rate; as described by Huxley, for purely kinematic reasons, the unloaded velocity of shortening must be proportional to the rate of bridge cycling.⁵⁹ Vmax is measured by setting muscle to its optimal length and then subjecting it to electrical field stimulation (EFS) in isometric conditions. After some defined time after EFS onset, the muscle is then suddenly released, unloaded, and allowed to shorten. Resulting Vmax is then measured and this experiment is then repeated at a series of different defined times of unloading.

FIG. 3.

Maximal velocity of shortening, V_max, in optimal lengths (L_o) per second, measured as function of time after onset of EFS in canine trachealis. Inset: regression line, η vs V_max, r² = 0.98, P < 0.0001 (Fisher's z transform).¹¹ Reproduced with permission from Fredberg et al., J. Appl. Physiol. 81(6), 2703–2712 (1996). Copyright 1996 American Physiological Society.

As distinct from behavior of striated muscle, a cardinal feature of smooth muscle is time-dependence of Vmax. The longer one waits after stimulus onset to perform the quick release the greater is the tension but, paradoxically, the slower is the subsequent unloaded shortening velocity, Vmax (Fig. 3). Murphy and co-workers at the University of Virginia attributed this time-dependence of Vmax in smooth muscle to cycling rate regulation, namely, the progressive transition from rapidly cycling cross bridges early in the contraction event to slowly cycling latch bridges later in the contraction.^60–62 Others have suggested the alternative ideas that it is cytoskeletal remodeling and/or increasing internal mechanical load that act to slow the rate of cross-bridge cycling.^63,64

However, whatever the underlying mechanism of cycling rate regulation might be, we found that time-dependence of η tracks that of Vmax rather precisely (Fig. 3).¹¹ They peak at the same instant and decay at precisely the same rate. The simplest explanation, and the one that we favor, is that both η and Vmax represent the shadow of the very same underlying molecular process, namely, the rate of acto-myosin cycling and its changes in time.^43,58,59

B. ATP metabolism

Murphy argued further that striated muscle evolved to optimize efficiency.^61,65,66 Optimizing efficiency allows for extraction of maximal mechanical work from each unit of metabolic energy expended, and thereby facilitates kinetic acts such as running, walking, pulling, or lifting. Muscle efficiency is, therefore, defined as mechanical work performed per unit chemical energy (i.e., metabolic energy) expended. Efficiency of striated muscle falls in the range 15%–35% and is, therefore, comparable to that of the internal combustion engine. In striated muscle, myosin cycling is on–off and controlled by a steric tropomyosin switch.

By contrast with the concept of muscle efficiency, Murphy argued that smooth muscle evolved to optimize muscle economy. Muscle economy is defined as isometric tension maintained per unit metabolic energy expended. Optimizing economy allows for maintaining isometric tone in hollow organs at minimal metabolic cost and thereby facilitates isometric tone maintenance in systems such as bladder detrusor, iris dilator, and vascular smooth muscle. Unlike the case of striated muscle, myosin cycling in smooth muscle is graded and regulated. How do economies of striated vs smooth muscle compare? Smooth muscle can generate just as high a muscle tension as does striated muscle but does so with only 25% of the myosin content and while metabolizing a scant 300-fold smaller rate of ATP utilization.

As such, our second line of evidence focused upon the rate of ATP utilization. With the help of Gary Sieck at Mayo Clinic, we used skinned ASM fibers, NADH fluorimetry, and calcium activation to measure simultaneously the changes in the frictional stress (ηE) and the rate of actomyosin ATP utilization. Remarkably, we found that time dependence of the frictional stress, ηE, closely tracks ATPase activity (Fig. 4).¹¹

FIG. 4.

Simultaneous measurement of muscle mechanics and ATPase activity. Left y-axis (filled circles) is frictional stress per unit strain. Right y-axis (open squares) is rate of ATP utilization. Inset: cross plot of same data with regression line, r² = 0.86, P < 0.0007 (Fisher's z transform).¹¹ Reproduced with permission from Fredberg et al., J. Appl. Physiol. 81(6), 2703–2712 (1996). Copyright 1996 American Physiological Society.

C. The HHM computational model

Finally, Srba Mijailovich developed a computational model that embedded in a partial differential equation Huxley's famous sliding filament model⁵⁹ together with the cycling rate regulation model for smooth muscle that had been postulated by Hai and Murphy.^65,66 We called this the HHM model.^43,58 The HHM computational model became a useful tool for thought and, in doing so, confirmed much—but not all—of the physical picture described above (data not shown). However, as described below, HHM failed to account for ASM fluidization with stretch, ASM plasticity, and dependency of the ASM contractile state upon the history of contraction.⁶⁷

These lines of evidence, taken together, show, first, that like shortening velocity and the rate of actomyosin ATP utilization, mechanical friction in airway smooth muscle is also governed by the rate of cross-bridge detachment. Second, they show that changes in ASM hysteresivity represent the shadow of changes in acto-myosin cycling rate. Third, they show that that steady-state isometric force maintenance in smooth muscle is a low-friction contractile state.

IV. PERTURBED EQUILIBRIUM OF MYOSIN BINDING

A. Dynamically equilibrated contractile states

Quiet tidal breathing causes peak-to-peak tidal linear strains in lung parenchymal tissue of approximately 4%–6%, and a DI approximately 20%–40%. To a first approximation, relaxed small intraparenchymal airways and their ASM follow close to the same strains as do the lung parenchymal tissues in which they are embedded.^53,54,68 We were interested, therefore, that the HHM theory predicted that cyclic tissue strains such as these would perturb the binding of myosin to actin in a major way.^12,43 Indeed, experiments confirmed that imposed tidal stretches in the physiological ranges of amplitude and frequency suppress both ASM active force and stiffness while increasing hysteresivity (Fig. 5). As such, imposed tidal stretches drive what could be thought of as a phase change from a stiff, low-friction, solid-like phase at low cyclic strains to a compliant, high-friction liquid-like phase at high strains.^12–14 In concert with this picture, Hoppin and co-workers showed that large cyclic strain of activated ASM engenders appreciable mechanical hysteresis.^14,54

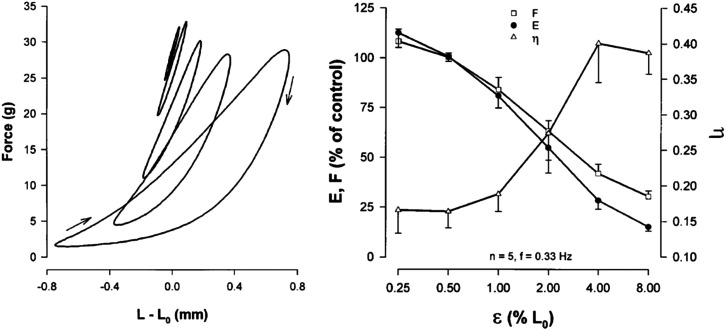
FIG. 5.

Left: Steady-state loops showing force vs length for six amplitudes of tidal stretch, ε = 0.25%, 0.5%, 1%, 2%, 4%, or 8% of Lo, in fully activated bovine tracheal smooth muscle set to mean length of Lo. As ε was increased, the loops became banana-shaped, more hysteretic, the chord slope became less steep, and the mean value of the active force fell.⁷⁹ Right: Plateau values (t = 900 s) of F and E during tidal stretch expressed as a percentage of control (values measured at t = 400 s with ε = 0.25%). The provocative stretch amplitude required to cause F or E to fall by half, or η to double, was close to 2%, whereas quiet tidal breathing at rest corresponds to 4%–6%. On this relationship describing ASM dynamics, therefore, we ordinarily live well out on the dynamically determined tail.^43,58,79 Reproduced with permission from Fredberg et al., Am. J. Respir. Crit. Care Med. 156(6), 1752–1759 (1997). Copyright 1997 American Thoracic Society.

Instead of imposing controlled length fluctuations, as in Fig. 5, imposing controlled force fluctuation causes fluctuation-induced ASM lengthening.^12,13 Imposing physiological fluctuations in load yields not only a more complete picture still but also points to increases of smooth muscle mass as being the main culprit responsible for airway hyper-responsiveness (AHR).⁶⁹ However, it turned out that there was more to the story than perturbed acto-myosin interactions.

1. Breathing is good for breathing

As described above, spontaneous deep inspirations serve as the first line of defense against excessive airway narrowing.^13,31–36 The failure of a DI to dilate the constricted asthmatic airway represents the loss of this potent homeostatic mechanism of bronchodilation. Using an argument that was impeccably logical but rather difficult to follow, Ingram and co-workers attributed this failure of a DI to dilate the asthmatic airway to excessive lung tissue hysteresis, thus stimulating our interest in that topic.^9,24,25 However, to the contrary, working together with Julian Solway at the University of Chicago and William Gerthoffer at University of Nevada, Reno, we later showed that the bronchodilation caused by a DI has little to do with lung tissue hysteresis.

The mechanism underlying the bronchodilatory effect of a DI remains in dispute.^70–72 Nevertheless, the preponderance of evidence points to the ability of a DI to stretch the cytoskeleton (CSK) of the activated airway smooth muscle cell and thereby cause it to fluidize and relax. This evidence includes force measurements obtained at the level of isolate airway smooth muscle (ASM) tissue in a muscle bath, traction measurements obtained at the level of the single isolated ASM cell in culture (Fig. 9), and direct observation of airway caliber in intraparenchymal airways embedded within the precision cut lung slice ex vivo.^{13,43,69,73–77} Molecular mechanisms that underlie fluidization and its converse—solidification—are described in Sec. VI. However, before resolidification can be completed and contractile force fully restored, along comes another DI just in time to knock down contractile force and muscle stiffness yet again and so on. That is to say, in the healthy lung during spontaneous breathing, the length of contracted ASM becomes systematically lengthened and softened by force fluctuations driven by the very act of breathing itself and is, therefore, dynamically determined.^78–80 Breathing is good for breathing.

FIG. 9.

Traction dynamics in ASM following a biaxial isotropic stretch. (a) Tractions as represented by the contractile moment T relative to the unstretched baseline value T₀ vs time, after stretch cessation. The greater was the applied stretch, the greater were the reductions in cell traction, and the faster were the recoveries. Peak strains of 0 (blue; n = 9), 2.5 (green; n = 12), 5.0 (yellow; n = 11), and 10.0% (red; n = 14). (b) When traction data from (a) are plotted not vs time, but rather vs the instantaneous value of the cell stiffness (G′), all data collapse. Following a transient cell stretch, cell stiffness (x axis) and cell tractions (y axis) evolve in concert. Similar strong associations between stiffness and tractions have been measured previously in response to graded concentrations of relaxing or contracting agonists, but exclusively under static steady-state conditions (black).¹⁷ Reproduced with permission from Krishnan et al., PLoS One 4(5), e5486 (2009). Copyright 2009 authors, licensed under a Creative Commons Attribution License.

2. Frozen objects

However, as the asthmatic airway becomes progressively remodeled and the ASM, whether through hypertrophy and/or proliferation, becomes more thickened and more massive, the ASM becomes progressively harder and harder to stretch.⁶⁹ The stiffer it becomes the less it stretches, and the less it stretches the stiffer it becomes and so on. Indeed, the ASM can become so stiff that it fails to stretch with a DI and, therefore, fails to fluidize. It, therefore, remains stiff, frozen, and stuck in a shortened, solid-like, static muscle state called latch.^{11,13,60,79,80} That is to say, in the asthmatic lung during a severe and spontaneous asthmatic attack, the dynamically equilibrated length of contracted ASM can collapse to become statically equilibrated and so stiff that it becomes refractory to a DI, like a frozen object. By refraining from spontaneous DIs for an extended period of time, similar frozen behavior of the ASM has been demonstrated even in the lungs of healthy human volunteers.⁸¹

These observations, taken together, dovetail with the early observations reported by Salter in 1859:⁸²

[Bronchial] spasm may be broken through, and the respiration for the time rendered perfectly free and easy, by taking a long, deep, full inspiration. In severe asthmatic breathing this cannot be done; but in the slight bronchial spasm that characterizes hay asthma I have frequently witnessed it. It seems as if the deep inspiration overcame and broke through the contracted state of the air-tubes, which was not immediately re-established.

V. A HARD DAY IN THE LIFE OF A SOFT CELL

A. New tools beget new questions

Up to this time, our laboratory had focused upon the levels of organ and tissue. However, in rapid succession, we invented four technologies that gave us a window into biomechanics of bronchospasm at the single cell level, and even the sub-cellular level. And if we could probe biomechanics of the isolated ASM cell, we could do so with any cell type. So the lab undertook its second major pivot, reinventing itself to address mechanics of the cytoskeleton (CSK). We were accompanied in this pivot by Daniel Navajas and his co-workers at the University of Barcelona.

First came magnetic twisting cytometry—MTC.⁸³ In a project led by Ning Wang and guided by James P. Butler, we used ligand-coated ferrimagnetic microbeads (diameter 4 μm), each of which was bound to integrin β₁ receptors on the cell surface (Fig. 6). Once magnetized, each bead acts like a compass needle. Just as the earth's magnetic field causes a compass needle to rotate into alignment, we imposed a uniform magnetic field that imparted to each bead a known mechanical torque. We then used magnetometers to measure the amount of resulting bead rotation. By knowing the imposed torque and measuring the resulting amount and pace of resulting bead rotations, we could measure the mechanical properties of the CSK. Using MTC, Wang demonstrated mechano-transduction through β₁ integrins across the cell surface and deep into the cytoskeleton.^83,84

FIG. 6.

Magnetic twisting cytometry (MTC). (a) Scanning electron microscopy image of a bead bound to the surface of a human ASM cell. (b) A ferrimagnetic bead coated with RGD-containing peptide binds avidly to cell adhesion molecules (integrins) and thereby connects mechanically to the actin cytoskeleton (stained with fluorescently labeled phalloidin). (c) A magnetic twisting field induces a torque, which causes the bead to rotate and to displace. Assuming a continuum model, the computed von Mises stress is color coded (Pa). (d) Large arrows indicate the direction of the bead's magnetic moment before (black) and after (gray) twisting. If the twisting field is varied sinusoidally in time, then the microbead wobbles to and fro, resulting in lateral oscillatory displacements, d, that can be measured.^4,15,245 Reproduced with permission from Mijailovich et al., J. Appl. Physiol. 93, 1429 (2002). Copyright 2002 American Physiological Society.

MTC had its drawbacks, however. The MTC apparatus was not only exceedingly sensitive but also exceedingly complex, even requiring elaborate measures to suppress the effects of the earth's magnetic field. Maksym showed that the experiments were cumbersome, moreover, and that the bandwidth of MTC was limited to frequencies less than 1 Hz.⁸⁵ Moreover, data provided only average values over many cells for behavior that were shown subsequently to be highly variable from cell-to-cell.^85–87 Even though the bandwidth was severely limited, Geoffrey Maksym noted in his data strong hints of CSK dynamics that are glassy, as we elaborated subsequently using optical magnetic twisting cytometry (OMTC) and discuss below.

All these shortcomings were remedied in one stroke in a technical advance led by Ben Fabry. We called this new method optical magnetic twisting cytometry—OMTC.^4,15 Fabry showed that we could avoid all those limitations and, in doing so, could dramatically simplify the apparatus and increase its throughput, by detecting bead motions not by magnetometers measuring bead rotations on an ensemble basis, but rather by using optical microscopy to measure bead displacements on a bead-by-bead cell-by-cell basis in thousands of cells simultaneously. In doing so, the bandwidth of measurements jumped from the Hz range to the kHz range. As such, we could measure the complex elastic modulus G^*(ω) = G′(ω) +j G″(ω) over five decades of frequency. As alluded to above and described below, the findings surprised us and disrupted the field.

Third, these advances were complemented by our development of Fourier transform traction microscopy—FTTM.^5,6,88 Here, James P. Butler built upon the pioneering traction method of Dembo and Wang.⁸⁹ Dembo had kept a tight grip on his traction code, however, and, for that reason, his method was much admired but not widely available. Moreover, Dembo reported that to obtain one traction image, his code required hours of computation on a supercomputer.

Butler democratized traction microscopy in the following way. The basic idea of traction microscopy begins with seeding a cell on a flat, linearly elastic substrate. Within that substrate are embedded sub-micron fluorescent particles, which act as fiducial markers. As the cell applies traction forces, the substrate deforms in response, and displacements of the fiducial markers are tracked with respect to a stress-free state. From these displacements, the traction field can be computed, but this calculation requires solution of a so-called inverse problem that turns out to be computationally expensive.⁸⁹ Butler overcame this hurdle by solving the elastic equations in the Fourier domain and then using the convolution theorem to easily handle the inverse problem.⁵ Moreover, in the Fourier domain, his code could be executed on a desktop computer in milliseconds. Butler made his code widely available, and from that point onward, his seminal work provided the foundation for an easy and direct method to calculate maps of traction forces applied on the substrate by a single cell in isolation.

By combining measurements of the complex modulus of the CSK by OMTC with simultaneous measurement of traction forces by FTTM, we were able to establish a clear relationship between the cytoskeletal elastic modulus and the cytoskeletal tension^88,90 and also show that in the adherent cell, the microtubule network balances only a small part of the tensile prestress.⁹¹ Chan Young Park et al. advanced traction microscopy further by adapting it to 96-well format suitable for high throughput drug screening⁹² and Ramaswamy Krishnan et al. by adapting traction microscopy to study the effects of cell stretch on CSK fluidization and reinforcement.^17,93

Fourth, by combining measurements of forced bead motions using microbeads and OMTC with measurements of the spontaneous unforced random motions of these same beads, Bursac worked together with our colleague David Weitz to demonstrate that the generalized Stokes–Einstein (GSE) relationship is not applicable to the CSK of the living adherent cell.^94–97 These studies showed anomalous slow dynamics associated with ATP-dependent non-equilibrium behavior whereas GSE applies only to equilibrium systems.^95–97 More about this below.

These technologies developed in our own lab were complemented by those developed by our collaborators David Weitz and Ming Guo, especially Force Spectrum Microscopy (FSM), which characterizes the active forces within the cytoplasm and thereby probes stochastic motor activity,⁹⁸ and optical tweezers to probe cytoskeletal nonlinearities.⁹⁹ Together, these and other new technologies transformed understanding of cytoskeletal mechanics, answered some old questions, and provoked several new ones.

B. The CSK in vitro vs airway hyperresponsiveness in vivo

Simultaneously, in the same cell, Steven An et al. used OMTC to measure cell stiffness and traction microscopy to measure contractile forces.^100–102 To measure remodeling dynamics, he quantified spontaneous nanoscale motions of a microbead tightly anchored to the CSK. In response to a panel of contractile and relaxing agonists, ASM cells obtained from the relatively hyperresponsive Fisher rat showed greater stiffening, bigger contractile forces, and faster CSK remodeling compared with those obtained from the relatively hyporesponsive Lewis rat; they also exhibited higher “effective temperature” of the CSK matrix, as described below. These physical differences measured at the level of the single cell in vitro were consistent with differences in airway responsiveness in vivo. As such, comprehensive biophysical characterizations of CSK dynamics at the level of the cell in culture provided novel perspectives on the ASM and its contributions to the excessive airway narrowing in asthma.

C. Cytoskeleton and soft glasses

With the novel capabilities of OMTC in hand, our hypothesis had held that the complex elastic modulus of the cytoskeleton of the ASM cell would reveal one or more well-defined relaxation times as predicted by classical ideas of cell viscoelasticity and/or acto-myosin molecular attachment and detachment dynamics. However, as shown in Fig. 7, using OMTC, we found no such thing.^4,15 We found instead weak power laws, which show no peaks, knees, or inflections that might be indicative of some internal sale of time. Such behavior is, therefore, called “scale-free.” With the exception of the red blood cell,¹⁰³ scale-free power-law behavior held true for every bead ligand that we used¹⁰⁴ and every cell type that we studied.^4,15 These features and others, taken together, showed that the CSK of the eukaryotic cell is strongly reminiscent of, and arguably belongs within, the class of materials called soft glasses (Text Box 2).

FIG. 7.

For CSK, power law rheology is universal: OMTC data for g′ and g″ vs frequency in five different cell types: Human airway smooth muscle cells (HASM); mouse embryonic carcinoma cells (F9); human bronchial epithelial cells (HBE); mouse pulmonary macrophages (J774A.1); and human neutrophils. Control conditions (■), and after 10 min treatment with histamine (10⁻⁴ M) (◊), DBcAMP (10⁻³ M) (♦), cytochalasin D (2 × 10⁻⁶ M) (◻), or FMLP (10⁻⁸ M). Solid lines are fit to the structural damping equation^4,15,86 g″ approaches a universal exponent of ¾ at high frequencies, which behavior is of entropic origin and is attributable to fluctuations in semiflexible polymers driven by thermal forces.^95,109 If specific torque is torque per unit bead volume, then g^* is specific torque per unit bead displacement.^4,15 Reproduced from Fabry et al., Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 68(4 Pt 1), 041914 (2003). Copyright 2003 Copyright American Physical Society.

2: Soft glassy materials (SGMs)

As defined below, this class is now understood to include foams, pastes, emulsions, colloids, slurries, and, arguably, cytoskeleton.^78,105,106

1. 1. Soft: All materials of this class display a Young's modulus of order 10²–10³ Pa (Fig. 8). This range is softer than a typical hard material by 8–10 orders of magnitude and even softer than the softest of soft rubbers by 4–6 orders of magnitude.⁷⁸

2. 2. Solid-like: All SGMs have an elastic modulus G′ that is larger than the loss modulus G″ by roughly 10 fold, in which case they are seen to be mainly solid-like rather than fluid-like (Fig. 7).

3. 3. Malleable: Although solid-like, when they are subjected to shear stress they fluidize and transition readily from an elastic-like solid to a flowing fluid.^16,105–107 But when shear is halted, they transition back to a solid-like phase. As such, they demonstrate remarkable malleability and mechanical plasticity.

4. 4. Scale-free: Over at least five decades of frequency, f, both G′ and G″ vary as a weak power law f^α, where the exponent α typically falls in the range 0.1–0.2 (Fig. 7). As such, in SGMs, there exists no special frequency or relaxation time scale that stands out. The dynamics are, therefore, said to be scale-free. Sollich attributed scale-free dynamics of SGMs to trapping of constituent particles in energy wells with an exponential distribution of well depths, with some being so deep that thermal fluctuations, k_BT, by themselves are insufficient to drive escape from the well.^105–107

5. 5. Disordered: Although recent evidence suggests intermediate-range order in certain systems,¹⁰⁸ SGMs are generally considered to be structurally disordered and amorphous.

Linhong Deng was at first frustrated with his observations that G″ at high frequencies departed from pure power law behavior, suspecting a technical artifact in these data. We became excited, however, when we realized that G″ at high frequencies exhibits an additive term that approaches a frequency exponent of ¾. This additive frictional behavior at higher frequencies is of entropic origin and is attributable to fluctuations in semiflexible polymers driven by thermal forces.^95,109

D. How soft is the cytoskeleton, anyways?

Consider the following thought experiment. If you could shrink down to the scale of an adherent eukaryotic cell and could poke that cell with your finger, what would it feel like? Rubbery like a toy balloon? Viscous like petroleum jelly? Based upon our own measurements of cell rheology,^4,15 and widely confirmed by others,^110,111 the correct answer is rather surprising. It would feel a lot like shaving foam. Foams like shaving foam, or pastes like tooth paste, emulsions like mayonnaise, or slurries like tomato ketchup—as well as the cytoskeleton of the living eukaryotic cell—when taken together share several characteristic features.^78,105,106 (Text Box 2).

Nevertheless, the material properties of the CSK and their determinants are hardly a settled issue. Clearly, there exist important differences between these passive inert systems, which are called soft glassy materials (SGMs), and the CSK of the living metabolically active eukaryotic cell, but these differences proved to be instructive.^{4,15,105–107,110,112,113} The discovery that the CSK exhibits glassy dynamics seems to have become well-accepted, but whether CSK truly belongs to the class of SGMs, as we have asserted here and elsewhere, has been disputed. We refer the reader to our commentary on alternative frameworks that have been suggested.^114–117 We generalize some of these notions below.

E. Soft, large, and trapped

What physics might account for the curious constellation of mechanical properties that defines SGMs, in general, and CSK, in particular? Although the answer remains unclear, an insight comes from our colleague Weitz, who offers the following dimensional argument:²

Soft: The units of Young's modulus are the Pascal. However, the Pascal, being force per unit area, N/m², is the same as Nm/m³, or simply J/vol. In other words, the Young's modulus of any material can be thought of as the energy density of cohesive bonds. The first conclusion, therefore, is that the energy density of cohesive bonds in the CSK—and in all SGMs more generally—must be quite small. Soft materials imply small energy density of cohesive bonds.

Large: Furthermore, an energy density logically comprises two factors: an energy and a characteristic volume. Consider first energy. Compared with thermal energy, k_BT, the binding energy of a covalent bond is larger by at most only two orders of magnitude, i.e., of order 100 k_BT. However, a range of two decades for binding energy is hardly enough to account for a range of ten decades for the Young's modulus, as in Fig. 8.⁷⁸ Logically, the rest must be attributable to differences in some characteristic volume over which that binding energy acts. The second conclusion, therefore, is that soft materials imply rather large internal scales of length.²

FIG. 8.

The Young's modulus of common materials spans at least 10 orders of magnitude.

Trapped: Finally, a large scale of length implies not only large structures but also trapping of those structures in deep energy wells, wells too deep for thermal fluctuations, which are of order k_BT, to drive a structural rearrangement. These systems are, therefore, athermal and can become trapped away from thermodynamic equilibrium. However, if thermal agitation by itself cannot drive internal structural rearrangements, what can? In an active system such as the CSK, hydrolysis of an ATP molecule by a motor protein releases about 20–25 k_BT per event, and hundreds or thousands of motor proteins working cooperatively can agitate that much more. However, to explain dynamics in passive inert SGMs is problematic. The concept of a fictive or effective temperature, or so-called “noise” temperature, has been postulated but its nature remains unclear. Ambiguous though it is, the noise temperature remains a useful concept because it is (1) readily measured and (2) easily manipulated.^{105–107,118}

F. CSK plasticity and malleability, remodeling, and adaptation

Structural proteins such as the actin lattice, the myosin filament, and the focal adhesion plaque are all evanescent structures that can be spontaneously demolished in some circumstances and then reconfigured and stabilized in others.^{48,64,119–124} For example, within a timeframe of 1 h or less, ASM has the ability to adapt its optimal length (L₀) over a threefold range.^{67,122,124–127} This remarkable malleability is not shared by striated muscle and has been called length adaptation or plastic adaptation. As a practical matter, it has been suggested that progressive plastic adaptations of ASM to shorter and shorter working muscle lengths may play an important role in airway hyperresponsiveness (AHR). In that connection, a striking contrast between smooth muscle vs striated muscle is that the former is capable to shorten down to as little 15% of its optimal length whereas the latter can shorten only to 65%.¹²⁸

G. Fragile objects^129,130

The structural basis of the remarkable shortening capacity and plastic adaptation of smooth muscle has been investigated in depth at the level of scanning electron microscopy by Seow and co-workers, who demonstrated ongoing series-to-parallel rearrangements within the ASM filament lattice.^{64,77,122,131,132} However, how can we get some better sense how CSK adaptation and remodeling work as a dynamic biophysical process? An important clue comes from looking at the appreciable effects of imposed cyclic strains, as occur, for example, during breathing. Madhavi Oliver et al.¹³³ showed that during slow imposed deformations, cytoskeletal rearrangements are continuously ongoing. The cytoskeleton is at every instant remodeling so as to adapt to the current muscle length—a dynamic process called length adaptation as discussed above. However, length is continually changing and as such remodeling dynamics never quite catch up. To probe this process the dynamics, such as the complex elastic modulus G^*, can be measured as cyclic amplitude is held constant as cyclic frequency is varied, or as frequency is held constant as cyclic amplitude is varied. Such data show families of curves indicative of strong mechanical nonlinearities. However, remarkably, all data collapse onto a unified relationship when considered not in terms of the frequency or the amplitude of those cyclic strains, but rather in terms of their product, namely, the strain rate.¹³³ Note that since strain is dimensionless the strain rate has dimensions of inverse time, 1/s.

Centrality of the rate of strain rate to CSK remodeling fits neatly within the framework of SGM dynamics.¹³⁴ Following Sollich^105,106 and Wyss et al.,¹³⁴ we picture structural rearrangements within the CSK as being governed by long-lived but fragile micro-configurations wherein stress-bearing structures become trapped in energy wells much deeper than thermal energy, k_BT. Structural rearrangements might become forced, nevertheless, provided that agitation of non-thermal origin becomes large enough. When the level of non-thermal agitation is very small, the relaxation time must remain close to its natural (slow) time scale. However, when the level of non-thermal agitation becomes appreciable another time scale enters the problem, namely, the strain rate itself. The rate of structural rearrangements at a given strain rate is then determined by the sum of the rate of unforced slow rearrangements and the rate of forced (fragile) rearrangements.¹³³

I. How much does water matter?

The cell interior is not the ideal dilute space we learned about while studying college chemistry.^135–138 Because of molecular crowding, not only does the volume fraction of water come into play, as might be expected, but perhaps also the dynamics of the water molecule itself.¹³⁹ As regards dynamics of the CSK, we considered the role of water at three levels: at the level of the cell, at the level of the multicellular organoid, and at the level of the water molecule itself.

At the level of the cell, we found that hyperosmotic stress causes the CSK dynamics to slow dramatically and CSK stiffness to increase exponentially¹⁴⁰ as later confirmed by others.^141–143 Small decreases in cell volume cause exponentially large changes in cell mechanics, and, as described below, water efflux comprises a major mechano-biological modulatory mechanism. Working with Guo and his team at MIT, we found that as a cell spreads on its substrate, or as substrate stiffness is changed, cell volume decreases while cell stiffness increases.¹⁴⁴ These cell volume changes occur through water efflux and are also found to direct stem cell fate. These increases in stiffness combined with the slowing of relaxation processes are reminiscent of a glass transition of colloidal suspensions.

At the level of the multicellular mammary cancer spheroid model,¹⁴⁵ together with Guo, we found that compared with cells in the spheroid core, cells at the periphery and the invasive front are systematically softer, larger, and more dynamic. These mechanical changes were shown to arise from supracellular fluid flow through gap junctions, the suppression of which delays the transition to an invasive phenotype.

Guillaume Lenormand et al. considered the role of the water molecule itself.¹³⁹ The effects of the hydration shell on protein dynamics had been studied extensively but mainly in the contexts of isolated protein crystals or dilute idealized solutions. The role of water in the dynamics of the integrated living cytoskeleton (CSK) had remained obscure. We were particularly interested because the cell interior features extensive molecular crowding. Water within a living cell is, therefore, highly confined, and mechanical properties of water are known to undergo solidification when confined to a few molecular layers.^142,146,147 Therefore, we asked the question: In the dynamics of the living cytoskeleton, how much does the water molecule itself actually matter? At the suggestion of H. Eugene Stanley at Boston University, we designed a study based upon the fact that H₂O water vs deuterium oxide D2O—heavy water—are similar chemically but the addition of a neutron to H₂O to form D₂O increases bulk density by about 11%, increases viscosity by about 25%, and increases the energy of hydrogen bonds by about 20%. Previously, we had shown that dynamics of the CSK are scale-free (see Text Box 2 and Fig. 7) and, furthermore, that extrapolation of scale-free trajectories of stiffness vs frequency converge and ultimately intersect at a very high frequency, f_0, that falls close to the dielectric relaxation frequency of H₂O molecules interacting with proteins in solution. Replacing H₂O acutely with D₂O caused no short-term toxicity and preserved scale-free (power law) CSK dynamics. However, D₂O slowed CSK remodeling appreciably and, for reasons that remain unclear, lowered f₀ by four orders of magnitude. Although these observations do not distinguish contributions of bulk water solvent vs hydration shell, they suggested the unifying hypothesis that dynamics of integrated CSK networks are tied in direct fashion to fluctuations arising in intracellular water.

VI. STRETCH FLUIDIZES THE CSK

With every beat of the heart, inflation of the lung or peristalsis of the gut, cell types of diverse function are subjected to substantial stretch. Stretch is known to be a potent stimulus for growth, differentiation, migration, remodeling, and gene expression. We have reported that in response to transient stretch the cytoskeleton fluidizes in such a way as to define a universal response class (Fig. 9).^16–18 The universality of this finding implicates mechanisms mediated not only by specific molecular intermediates, as described below, but also by nonspecific actions of a slowly evolving network of long-lived but fragile microconfigurations.^16,95,96 These results support the idea that the cell interior is at once a crowded chemical space and also a fragile soft material in which the effects of biochemistry, molecular crowding, and physical forces conspire to yield a remarkably general fluidization response to stretch. Moreover, the existence of a great many microconfigurations with comparable energy well depths is typical of all glassy systems and, thus, might account for the nonspecific and universal nature of the fluidization response to transient stretch–unstretch, as occurs during a deep inspiration. Recurrent episodes of stretch-induced fluidization and subsequent resolidification¹⁴⁸ provide a mechanism for the cell to reorganize and adapt contractile units, stress fibers, and adhesions in response to mechanical stress.

As mentioned above, the bronchodilatory effect of a DI is now understood to be attributable mainly to the ability of a DI to stretch and fluidize activated airway smooth muscle (ASM), but can we now say more about molecular mechanism? Like a triangle, this issue has three sides. First, stretch perturbs binding of myosin to actin, as suggested above (Fig. 5).^13,43 Second, stretch fluidizes the solid-like cytoskeleton in two ways: actin filaments become severed by the action of the protein cofilin;¹⁸ also other molecular bonds and fragile microstructures get pulled out of the energy wells in which they are trapped, thereby causing the nearly total—but transient—loss of ASM contractile force.^{16,18,69,77,80,133} Third, with the help of Mary Beckerle at the University of Utah and Peter D. Paré at the University of British Columbia, we showed that contractile force in ASM can then become restored at least in part through the repair and reinforcement action of the protein zyxin.^148–151

VII. MAPPING PHYSICAL FORCES THAT DRIVE COLLECTIVE CELLULAR MIGRATION

In 2004, Xavier Trepat came into the lab expressing his desire to study mechanics of the pulmonary epithelium. Fredberg explained to him that the lab at that time had no experience in epithelium, no expertise, and little interest. The lab was focused instead on airway smooth muscle (ASM), its cytoskeleton (CSK), its contraction, and its cytoskeletal remodeling as they pertain to excessive airway narrowing as occurs during an asthmatic attack. Reluctantly, Trepat agreed to study ASM. In short order, he then went on to publish a seminal paper in Nature demonstrating that the CSK of ASM, as well as other cell types, fluidizes when subjected to a transient stretch simulating a DI, i.e., a transient shear deformation.¹⁶ This discovery was not only important in the context of bronchospasm but also, as described below, demonstrated that the CSK expresses one of the hallmarks of soft glassy materials—fluidization in response to shear.^4,106 On the very day that his publication was accepted for publication at Nature, Trepat insisted yet again that he wanted to study mechanics of the pulmonary epithelium. So the lab undertook yet another pivot, now focusing on mechanics of the cellular collective.

Biophysical understanding of the single cell migrating in isolation was relatively well developed at that time, with the reductionist notion being that one needed to understand the simplified system first, i.e., understanding the single cell migrating in isolation before going on to understand the more complex case of the multicellular collective migrating as an integrated confluent epithelium.⁸⁹ The case of collective cellular migration was far more relevant developmentally, physiologically, and pathophysiologically, but remained rather poorly understood mechanistically. In fact, for those reasons basic questions concerning collective cellular migration had been intensely debated for almost 100 years.^152,153 However, without the benefit of primary data measuring physical forces exerted by and acting within the confluent layer, conflicting opinions and diverse mathematical models grew in number, thus leaving a rather confusing physical picture. Communities studying epithelial injury and wound healing, for example, emphasized the idea that leader cells at the advancing front edge of a wound must be the main drivers of locomotion; the physical picture was that these leader cells appear to be structurally specialized for pulling, and together act like a locomotive to tug the epithelial sheet forward. In such a physical picture, the follower cells within the epithelial sheet would be dragged along passively in a state of mechanical tension.^154,155 To the contrary, communities studying developmental biology and organ formation emphasized a physical picture in which cell proliferation well behind the advancing front tended to expand the cell colony and thereby push the advancing front edge of the cell sheet forward. However, in such a physical picture, the epithelial sheet would be in a state of mechanical compression. Remarkably, therefore, the various schools of thought could not agree even on the sign of the mechanical stress within the layer, i.e., tension or compression (Fig. 10).

FIG. 10.

Making forces visible: Traction forces exerted by cells upon the substrate in a collectively migrating MDCK cell sheet. (a) Phase contrast. (b) Traction forces normal to leading edge. (c) Traction forces parallel to leading edge. Field of view 750 × 750 μm.⁷ Reproduced with permission from Trepat et al., Nat. Phys. 5(6), 426–430 (2009). Copyright 2009 Springer Nature.

Concerning mechanical stresses and their distribution within the epithelial layer, conflicting hypotheses such as these could not be resolved because there were no primary data. The central question became, what is the spatiotemporal distribution of physical forces that propels an epithelial sheet so as to close a cell-free void, such as a wound? As described below, Trepat et al.—and later extended by Tambe et al. and by Kim et al.—cracked this problem and showed rather surprising experimental findings.^7,8,19,156

A. Monolayer traction microscopy

To adapt Butler's single cell traction method to the confluent epithelial layer, we needed to overcome three technical hurdles. The first was image registration due to the microscope stage drift which, in the case of the single cell in isolation, is a trivial problem. In the case of the single cell in isolation, Newton's second law requires that vectorial forces exerted by the cell on the substrate must be in balance and, therefore, sum to zero. As such, image registration is simply achieved by setting the average bead displacements to zero. However, in the case of a multicellular tissue sheet that extends out of the microscope field of view, the forces at the optical field boundary are nonzero and unknown. Therefore, the force balance approach is no longer applicable. Instead, we resolved stage drift by embedding a second layer of large fluorescent particles to the inferior side of the flexible substrate and using those particles as fiducial markers for image registration. The second hurdle was spatial resolution. Resolution was enhanced by localizing the fluorescent beads used for displacement measurements to the top plane of the gel by centrifugation during the gelation process. The third hurdle concerned extension of the Boussinesq solution, which lies at the heart of the method. The Boussinesq solution as had been used in single cell traction measurements assumes that the cell sits atop an elastic substrate whose depth relative to cell diameter is semi-infinite. This assumption holds approximately true for the case of a single cell in isolation with a cell diameter much smaller than the depth of the substrate. However, for the multicelluar epithelial sheet whose lateral extent might encompass hundreds or even thousands of cells, the assumption of a semi-infinite depth becomes problematic. To overcome this problem, Trepat and Butler generalized the Boussinesq solution to the case of finite substrate thickness by solving the full elastic equations in Fourier space. This technology for a multicellular collective became what is now commonly known as Fourier transform traction force microscopy (FT-TFM).^7,157

These traction maps led to three findings. First, pulling tractions are not at all restricted to the close proximity of the advancing leader cells. Rather, data showed that large pulling tractions persist not only a great many cell rows behind the leading edge but also everywhere within the advancing cell sheet. Second, the traction field is chaotic in space, with nearby cells pulling this way and that. Third, local tractions fluctuate dramatically in time, pulling in one direction at one moment and in the opposite direction the next. In fact, the traction field in the advancing cell sheet is dominated by spatiotemporal fluctuations that show fat-tailed non-Gaussian distributions. Such behavior, even when constituent cells themselves are homogeneous, is called dynamic heterogeneity.¹⁵⁸ Despite these fluctuations, summing all tractions using a simple tug-of-war argument showed that tension borne by the layer is dominated by the traction forces exerted well behind the leader cells. Although these traction maps were illuminating, a mapping of the internal stresses borne by the CSK of each cell, and transmitted from across junctions from cell-to-cell, remained a blind spot.

B. Monolayer stress microscopy (MSM)

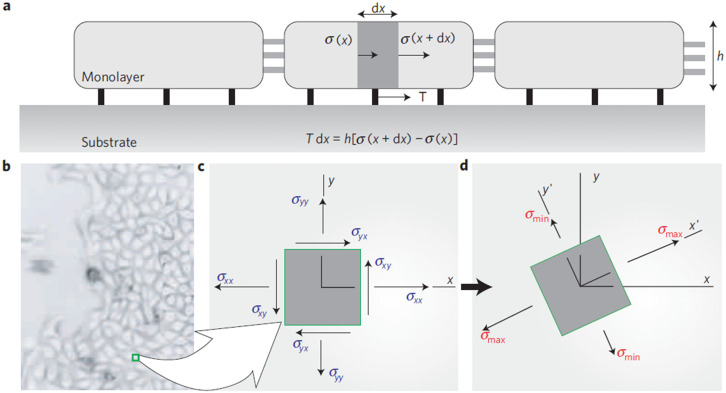
Around that time a new postdoctoral trainee arrived in the lab. Dhananjay T. Tambe had experience in continuum mechanics and computation. In an extension of the efforts by Trepat and Butler,⁷ Tambe suggested further assumptions—later validated^8,10—through which the two-dimensional distribution of in-plane intercellular stresses could be measured, i.e., the complete 2D stress tensor σ(x,y). A local force balance for each infinitesimal element in two dimensions leads to a set of partial differential equations that govern the stress tensor within the epithelial monolayer. Solution of these equations required a finite element numerical scheme but results were shown to be insensitive to the Poisson ratio. Assuming no out-of-plane contributions, he focused upon the in-plane stresses (Fig. 11). This approach was called monolayer stress microscopy (MSM).⁸ Using MSM, we discovered kenotaxis and plithotaxis, waves of epithelial polarization (Text Box 2).

FIG. 11.

Principal intercellular stresses. (a) Simplified transverse representation of the relationship between cell–substrate tractions, T(x) and stresses borne by the cells and their cell–cell junctions, σ(x). (b) Local traction forces acting over some distance, dx, must be balanced by a local difference in intercellular stress, σ(x+dx) – σ(x). (c) In-plane normal stress and shear stress components in the laboratory frame of reference. (d) By simple rotation of the coordinate system, a new frame of orientation can be found, called the principal orientation, in which shear stresses vanish and the resulting normal stresses are called principal stresses, σmax and σmin.⁸ Reproduced with permission from Tambe et al., Nat. Mater. 10(6), 469–475 (2011). Copyright 2011 Springer Nature.

To visualize stress anisotropy within the monolayer, Tambe et al. plotted ellipses for which the major stress axis corresponds to the local σ_max and the minor axis corresponds to the local σ_min, with each ellipse aligned with the corresponding principal stress orientations (Fig. 12). The shear stress at a point within a material varies with orientation and attains its maximal value, μ = (σ_max − σ_min)/2, at 45° from the principal orientations. In regions where σ_max = σ_min, the stress field is isotropic, the ellipse becomes a circle, μ is zero, and there exists no preferred stress orientation. However, in regions where σ_max ≫ σ_min, the local stress field is highly anisotropic, the ellipse becomes spindle-like, μ is nonzero, and there exists a strongly preferred and well-defined stress orientation.

FIG. 12.

In a migrating sheet of rat pulmonary microvascular endothelial cells, the local stress-tensor is depicted by blue ellipses and the local migration velocity is depicted by red arrows. The stress field is disordered but with strong local correlations. Within that stress landscape, local cellular migrations tend to follow local orientations of maximal principal stress. Equivalently, cells migrate in a direction that minimizes intercellular shear stress (plithotaxis). Inset: For the highest quintile of in-plane shear stress, the angle, ϕ, between the major axis of the principal stress ellipse and the direction of the cellular migration becomes well aligned.⁸ See text. Reproduced with permission from Tambe et al., Nat. Mater. 10(6), 469–475 (2011). Copyright 2011 Springer Nature.

Tambe et al. found that from region-to-region, the ellipse size, the ellipse shape, and the ellipse orientation varied extensively but with strong spatial correlations that spanned many cell bodies, thus suggesting appreciable cooperativity within any given cell pack (Fig. 12). Furthermore, because the major principal orientation corresponds to the local axis of highest normal stresses and zero shear stress, these results suggested that the cell–cell junction, as well as the cell body, supports high normal stresses, which are overwhelmingly tensile, but support only minimal shear stresses. These observations regarding the stress tensor together with the observations of the local migration velocity led to the discovery of plithotaxis⁸ (Text Box 3).

3: Propulsion and navigation, fluctuations, and cooperativity within the epithelial sheet

As a wound heals, a body plan forms, or a tumor invades, observed cellular motions within the advancing cell swarm had been thought to stem from yet to be observed physical stresses that act in some direct and causal mechanical fashion. Monolayer stress microscopy revealed that such a relationship between motion and stress is far from direct. For example, the most striking features are disorder and “chaos.” Stress fields are dominated by stochastic spatiotemporal fluctuations, but buried within that chaos there emerge strong and systematic behaviors.

Kenotaxis: Kim et al.¹⁹ probed migration velocities, cellular tractions and intercellular stresses in an epithelial cell sheet advancing toward an island on which cells cannot adhere, i.e., a cell free void. They found that cells located near the island boundary exert tractions that pull systematically toward the void regardless of whether the cells are approaching the island, migrating tangentially along its edge, or even receding from it. This unanticipated cell-patterning motif they called kenotaxis, where “keno” derives from the Greek for void, thus, literally, pulling toward the void. Kenotaxis represents the robust and systematic mechanical drive of the cellular collective to fill unfilled space.

Plithotaxis: Tambe et al.⁸ developed MSM and the first two-dimensional maps of the internal tensorial stress distributions within the migrating epithelial monolayer. These maps revealed an unanticipated but unifying physiological principle: each cell within the layer tends to migrate and remodel so as to minimize the local intercellular shear stress (inset: shear stress indicated by blue arrow and normal stress by red arrows). In other words, within that stress landscape, local cellular migrations tend to follow local orientations of maximal principal stress. Migrations of both endothelial and epithelial monolayers conform to this behavior, as do breast cancer cell lines before but not after the epithelial–mesenchymal transition. By analogy to the well-known guidance mechanisms of chemotaxis, durotaxis, and haptotaxis, they called this innately collective mechanism plithotaxis from the Greek “plithos” denoting crowd, swarm, or throng.

Polarization and effective inertia: Notbohm et al.¹⁵⁹ studied forces and motions in a confined epithelial monolayer and noted oscillating waves of cellular motion that arise spontaneously. Based on these observations, they proposed a theory that connects forces and motions using two internal state variables, one of which generates an effective cellular polarization, and the other, through contractile forces, an effective cellular inertia. In agreement with theoretical predictions, drugs that inhibit contractility reduce both the cellular effective elastic modulus and the frequency of oscillations. Together, theory and experiment provided evidence suggesting that collective cellular motion is driven by at least two internal variables that serve to sustain waves and to polarize local cellular traction in a direction that deviates systematically from local cellular velocity.

C. Discovery of epithelial jamming and the unjamming transition (UJT)

Epithelial cell packing and cell shape had been linked to stress percolation and epithelial layer rigidity by the pioneering work Lewis,¹⁶⁰ Gibson et al.,¹⁶¹ and Farhadafar et al.¹⁶² However, the connection to glassy dynamics and “cell jamming” had yet to be discovered. In our laboratory, the notions of cooperativity, fluctuations, and glassiness became appreciated due to the influence of our long-standing collaboration with David A. Weitz and his trainees, especially Angelini.¹⁶³ As noted above, Trepat and Angelini et al.⁷ observed that traction forces exerted on its substrate by an epithelial cell layer exhibited dynamic heterogeneity characterized by distribution functions that were non-Gaussian with fat tails.^158,163 Curiously, similar force distribution functions had been observed in inanimate granular systems close to a jamming transition.¹⁶⁴ For that reason and others, Trepat et al. proposed the radical hypothesis that we called cell jamming. Soon thereafter we speculated further how cell jamming and unjamming, if true, might provide a useful physical picture and perhaps even play a fundamental role in understanding embryonic development, wound repair, regeneration, and collective cancer cell invasion.¹⁶⁵ As described below, Park et al. then published definitive evidence establishing the discovery of epithelial cell jamming and the unjamming transition, UJT.²⁰ Jennifer Mitchel et al. then went on to show that the epithelial UJT is distinct from—and not to be confused with—the epithelial-to-mesenchymal transition, EMT.²² Both the EMT and the UJT comprise gateways to collective epithelial cellular migration, plasticity, and remodeling, but UJT can exist in the complete absence of EMT. EMT and UJT are, therefore, distinct pathways to epithelial migration.

1. And I hope you like jammin' too¹⁶⁶

With attribution to reggae music of the same title by Bob Marley, here we offer a word of caution regarding nomenclature. When we first reported the UJT, we were aware that this collective cellular phenomenon may more properly correspond to a glass transition rather than to a jamming transition.^20,163 Nevertheless, we adopted the nomenclature of jamming mainly because the jamming concept is intuitive. Also, the contrast between the jamming transition in inert granular systems vs the glass transition in confluent epithelial systems proved to be instructive.^21,23 The distinction between the jamming transition and the glass transition have since been clarified.^117,167 Rigorously, the jamming transition is purely a geometric phenomenon that is devoid of dynamics and, thus, represents a zero-activity limit. The glass transition, by contrast, reflects the competition between crowding and adhesion dynamics on the one hand vs agitation and propulsion dynamics on the other. While this distinction is clear in principle, it is less clear in practice. For example, a common feature of granular materials such as a sand-pile, as well as SGMs such as foams, colloids, and CSK (Text Box 3), is that such systems unjam and flow as does a fluid if agitated sufficiently (i.e., shaken) but jam and solidify as agitation intensity is lowered.^16,164 In these systems, thermal energy by itself is insufficient to change the packing of grains, bubbles, droplets, or intercellular organelles. Moreover, disorder in packing geometry is a common feature in all these systems, and disorder by itself plays a role in driving such systems through phase transitions.^168–173 However, for whatever reason, the jamming nomenclature has stuck.

Here is how the discovery of the epithelial UJT happened. Trainees in our lab had the privilege to interact with several distinguished investigators. For example, Jeffrey M. Drazen at that time served not only as Editor-in-Chief of the New England Journal of Medicine (NEJM) but also ran an active laboratory on the same floor as our own. It so happens that Fredberg and Drazen had been undergraduates together studying engineering at Tufts University and enjoyed long-standing collaborations thereafter. Drazen's laboratory had developed a model system to study the effects of mechanical squeezing applied to the airway epithelium as occurs during asthmatic bronchospasm.¹⁷⁴ Using finite element modeling of how ASM contraction squeezes the airway epithelium, Drazen's team estimated that stress levels in the vicinity of the lamina propria and epithelium can easily attain values of 3 kPa, which is sufficient to produce local cellular mechanical strains of order 1 as well as ample stimulus for mechanotransduction.^174,175 Although we did not know it at the time, recent evidence from the laboratory of Jody Rosenblatt now supports the proposition that bronchoconstriction by itself and the resulting epithelial squeeze—even in the absence of inflammatory stimuli—injures airway epithelia by means of crowding-induced epithelial extrusion.^176,177 Reversing traditional notions of cause vs effect, this squeeze-induced epithelial injury triggers inflammation and mucus secretion, whereas inhibition of epithelial extrusion during bronchoconstriction prevents such symptoms.

As we became immersed in epithelial dynamics and migration, our interest and those of Drazen converged. A major component of asthma pathobiology is thought to be injury of the airway epithelium followed by aberrant wound repair.^178,179 Accordingly, our hypothesis held that (1) mechanical squeeze alone, even in the absence of inflammation, might be sufficient to trigger in the airway epithelium an aberrant wound repair response; and (2) such a wound repair response would, in turn, trigger the epithelial unjamming transition and resulting epithelial migration. Although we had no way to know at that time, this reasoning later proved close to being accurate. We, therefore, asked Drazen and his trainee at that time, Park, if mechanical squeeze triggers migration in their culture system of primary human bronchial epithelial cells (HBECs) in air–liquid-interface (ALI) culture. The short answer was that no one in asthma biology had ever considered such notions. Rather, dogma held that each HBEC sits at a fixed locus like a tile embedded in grout on a tile floor. There it maintains a tight barrier at cell–cell junctions. However, in disease, the crucial response is that the grout fails, so to speak, and these barriers become compromised and leaky. Since no one had previously studied migration in primary HBECs, Park proposed that we do so.

2. Early evidence for the epithelial unjamming transition

Park collaborated with Jae H. Kim and Jennifer A. Mitchel, two trainees in our lab, to make time-lapse video imaging of a confluent layer of primary HBECs derived from non-asthmatic vs asthmatic human donors.²⁰ These data provided evidence showing that the mature non-asthmatic HBEC layer was non-migratory. However, when they applied an apical-to-basal pressure difference so as to emulate roughly the squeezing of the asthmatic epithelium, as occurs during bronchospasm, they found a strong migratory phenotype and striking changes in cell shapes.²⁰ Cell shapes became more elongated and more variable, and cellular migration became chaotic and cooperative in a manner reminiscent of turbulent fluid flow. Importantly, a closely similar migratory phenotype was observed in HBECs that were not compressed but were derived from asthmatic donors [Fig. 12(a)].

Thinking in the lab at that time was that increased cellular migration must be a hallmark of decreased mutual cell–cell adhesive stresses. Paradoxically, data showed just the opposite [Fig. 13(b)].

FIG. 13.

Multicellular dynamics and intercellular tension are abrogated in jammed HBECs that are derived from non-asthmatic donors. (a) Speed color maps (left) and velocity vector maps (right) show how HBECs derived from asthmatic donor were hypermobile as opposed to non-asthmatic counterparts. Shown are representative samples from ALI day 6. (b) Color maps of intercellular tension show how in HBECs derived from asthmatic donor intercellular stresses are greater but the spatial correlation of tension decays faster. Reproduced with permission from Park et al., Nat. Mater. 14(10), 1040–1048 (2015). Copyright 2015 Springer Nature.

3. Missing pieces

If the UJT hypothesis were thought of as a stool, at this time it was still missing its three legs. It was missing: (1) a theory that was mechanistic, quantitative, and testable; (2) evidence for existence and relevance in vivo; and (3) genomic signatures. The first of these legs was put into place with the help of the theoretical physicists M. Lisa Manning, M. Cristina Marchetti, and Dapeng Bi at Syracuse University; the second with help from Jeffrey M. Drazen, Jin-Ah Park, Lior Atia in our group and Adam C. Martin from MIT; and the third with help from Scott T. Weiss at Brigham and Women's Hospital.

4. Theory: UJT, cell shape, and the vertex model

At about the same time, M. Lisa Manning and Dapeng (Max) Bi visited our lab. Building upon earlier work of others,^162,180,181 they showed us a new computational framework that not only helped to explain our findings but also provided testable predictions. Called the vertex model, this approach focused upon a non-dimensional index of cell shape,

$$\mathrm{q}=\frac{\mathit{Cell}\hspace{0.17em}\mathit{\text{perimeter}}}{\sqrt{\mathit{Cell}\hspace{0.17em}\mathit{\text{area}}}}.$$

As cells become more elongated, q increases (Fig. 14). For all cases, the theory predicted that as a fluid-like (unjammed) layer approaches a rigidity transition (jamming) cell shape, q, must decrease so as to approach a universal critical numerical value of 3.81. Just as transition to turbulent flow for all Newtonian fluids in a straight pipe occurs at a critical universal value of the Reynolds number, so too the transition to jamming was predicted to occur at a critical universal value of cell shape, q. As a physical picture, the model predicted that unjamming happens when cell–cell adhesive forces that describe how strongly cells wet one another exceed contractile forces that describe how cells contract against one another.

FIG. 14.

ZO-1 staining of tight junctions in jammed (top) and unjammed (bottom) human bronchial epithelial layers (courtesy of Jennifer Mitchel, Wesleyan University). As the layer unjams, cell shapes become more elongated and more variable, and they do so in a very particular way.^20,21

We immediately recognized that we already had in hand images together with cell migration data from which we could put this quantitative prediction to the test. Specifically, Jennifer Mitchel had observed that HBECs from non-asthmatic donors migrate vigorously during early days in air–liquid-interface (ALI) culture, but their migration progressively slows as the layer matures. By day 8 of maturation, migration arrests altogether. However, from the point of view of mechanism, did this migratory arrest correspond to a jamming transition? The short answer was yes. When plotted against days in culture, and just as migration ceased, cell shape q approached the predicted critical value of 3.81 (Figs. 14 and 15). Just as the asthmatic HBECs failed to show migration arrest up to 18 days in ALI culture, so too their shapes were consistently more elongated. In a stunning confirmation, the vertex model had explained our data.²⁰

FIG. 15.

With increasing maturation of HBECs in ALI culture, the median of cell shape, as quantified by the normalized perimeter, decreases systematically toward the critical value 3.81. This is predicted to occur at multicellular jamming by the vertex mode. Reproduced with permission from Park et al., Nat. Mater. 14(10), 1040–1048 (2015). Copyright 2015 Springer Nature.

D. One person's noise is another person's signal

We were struck at the success of the vertex model in quantitatively predicting median cell shape at the jamming limit. Because the statistics were highly confirmatory, we had dismissed in a cavalier fashion the rather appreciable cell-to-cell variability; we attributed this variability merely to measurement error and innate biological noise (Fig. 15). This interpretation was in keeping literature which had emphasized cell shape as regulator of other cell behaviors.^{161,182–189} We were also reassured by the knowledge that biology is innately messy, about which we say, more below.

Lior Atia came into the lab with quite a different perspective. Having a background in engineering and statistical physics, he called attention to this variability. To better study that variability he set about to measure a dataset that was far more accurate and an order of magnitude larger.²¹ As a metric of cell shape, he switched from the parameter q to the cell length-to-width aspect ratio, AR, which he showed exhibits similar qualities but greater dynamic range than does q.

We first plotted the standard deviation of AR vs the mean, $\overline{\mathrm{AR}}$, for all data combined (i.e., for both asthmatic and non-asthmatic donors and for all days of maturation). We were surprised to find that all data collapsed onto one linear relationship, with data at the upper right corresponding to markedly migratory (unjammed) systems and those at the lower left approaching a jamming transition (Fig. 16). With maturation, these HBEC systems progressed toward jamming, but HBECs from asthmatic donors lagged those from non-asthmatic donors [Fig. 16(b), inset].

FIG. 16.

Cell shape and shape variability in vitro are mutually constrained. (a) The apical actin ring was used to measure projected cell length-to-width aspect ratio, AR. With ongoing layer maturation, the AR of both non-asthmatic and asthmatic cells became progressively smaller and less variable (corresponding color maps). (b) AR from all donors and all days of maturation defined a clear relationship between the mean of AR ( $\overline{AR}$) and the standard deviation (s.d.) of AR (each datum represents a different field of view). Top left inset: With increasing days of maturation, $\overline{AR}$ and s.d. (AR) decreased in tandem (each datum pools all cells for a given day of maturation), but were systematically increased in asthmatic compared with non-asthmatic controls. Bottom right inset: to rule out the possibility that this relationship might reflect an idiosyncrasy of layer maturation, we studied changes in cell shape and shape variability that occur acutely in response to an imposed mechanical perturbation. Application of an apical-to-basal pressure difference causes the mature, jammed, HBEC layer to unjam, and for cell shape to track in the opposite direction with time. To complement results from HBEC compression, we applied sequential stretches to the mature MDCK layer plated on a deformable substrate. Immediately after stretch cessation, cell shapes became elongated, but within 60 min, these changes relaxed back to pre-stretch values. The dark continuous lines in (b) are not regression lines, but rather the prediction given by vertex model. The light continuous line in (b) represents a linear regression.²¹ Reproduced with permission from Atia et al., Nat. Phys. 14, 613 (2018). Copyright 2018 Springer Nature.

We were even more surprised to see the strong a priori prediction that the vertex model made about cell shape variability, which neatly accounted for all observations [solid dark lines in Fig. 16(b)]. Altogether, these data showed that as the epithelial layer becomes more jammed cell shapes become less elongated and less variable, and conversely. Rather than representing mere random noise, cell shape variability was a signal. Specifically, this signal was the signature of a collective cellular system approaching a jamming transition. Jamming dynamics, therefore, accounted not only for changes of cell shape but also for cell shape variability.

E. To see a world in a grain of sand

Using powders as a model of granular systems, Edwards and Oakeshott proposed that among the immense number of packing geometries possible within a granular collective, all jammed configurations are equally likely; this notion became known as the Edwards conjecture.^190,191 This appealing idea was by no means obvious but later was proven.¹⁹² Aste and DeMatteo¹⁹¹ then showed that free space (free volume) surrounding each grain follows a k-gamma distribution. Because k-gamma is a one-parameter family, the mean and the standard deviation of the distribution of cell shapes are, therefore, linked through the single parameter k.

However, how did these ideas about behavior of inanimate granular systems, wherein free volume is the central control parameter, relate to the confluent epithelia layer wherein free volume is nil? After all, in the two dimensions defined by the confluent epithelial plane the areal packing fraction is always unity.

Atia's insight was to generalize the Edwards conjecture in the following way. Atia reasoned that the packing, fluctuations, and dynamic heterogeneity associated with any of these collective systems must depend upon the micro-configurations and associated statistics of constituent particles. In the case of a thermal system such as a gas, as described by Gibbs and Boltzmann, those statistics are set by temperature. In the case of an athermal granular system, such as a powder, Edwards and Oakeshott proposed that the role of temperature is taken by free volume, thus implying that free volume acts as an effective temperature.^190,191 In the case of the confluent epithelial layer, Atia proposed that the role of free volume is taken by cell shape.²¹ As regards micro-configurations, therefore, this reasoning points to cell shapes and their statistics as defining proximity to a jamming transition and, therefore, an effective epithelial temperature. Confirming this analogy, when Atia examined his data for cell shapes, all confluent epithelial systems were found to conform to a k-gamma distribution,²¹ as did cancer cell lines studied by Kim et al.¹⁹³ However, for reasons that remain unclear, across all these epithelial systems k is nearly constant and close to 2.5; also unclear is why k in granular matter is far greater.^21,191

1. UJT in the fruit fly embryo

To establish relevance in an in vivo system, Atia joined efforts with Yasha Sharma, a postdoctoral fellow in the lab, and Adam Martin, a developmental biologist at MIT. Together they explored cell shape dynamics during gastrulation in the Drosophila embryo. Using multiple embryos and various genetic manipulations, they demonstrated cellular jamming and unjamming in an in vivo system.²¹ Soon thereafter, the laboratory of Otger Campas showed how body axis elongation during zebrafish development was in concordance with the notion of mesoderm tissue unjamming.¹⁹⁴ Celeste Nelson and her team then went on to link cellular unjamming to airway epithelial branching in the embryonic avian lung.¹⁹⁵ Through these studies and others subsequently, jamming and unjamming in living systems became well established.

2. Genomics of the UJT

In studies led by De Marzio and co-workers, we combined RNA sequencing with protein interaction networks.^196,197 These studies identified distinct transcriptional hubs triggered by squeeze-induced unjamming of HBECs and led directly to the genes and their genetic programming that encode the UJT. We were struck by the finding that squeezing of HBECs causes a genomic profile that is closely similar to that measured in HBECs that are not compressed but are derived from asthmatic donors (Fig. 17). These results established that mechanical squeeze as occurs during bronchospasm is sufficient to induce asthma-like signatures at both biophysical and genomic levels, even in the absence of inflammatory stimuli. Moreover, just as the epithelial-to-mesenchymal transition (EMT) arises in many contexts and cannot be defined by any limited set of molecular markers,^198–200 so too with the UJT.^196,197

FIG. 17.

Pathways enriched in the three transcriptional regimes triggered in compression-induced UJT. Each node represents a pathway, and edges between pairs of nodes represent common differentially expressed (DE) genes annotated to both pathways. For visualization purposes, we showed only edges with more than three common DE genes. Node size and color are based on the number of DE genes annotated to the pathway and its adjusted P value, respectively. (a) Enriched in the transient response, (b) enriched in the long-term response, and (c) enriched in the increasing response.^196,197 Reproduced with permission from De Marzio et al., Sci. Adv. 7(30), eabf1088 (2021). Copyright 2021 authors, licensed under a Creative Commons Attribution License.

3. UJT in cancer progression

Carcinoma invasion and metastasis have long been thought to require the EMT, the associated loss of intercellular adhesion protein E-cadherin, and resulting cellular migration.²⁰¹ However, to the contrary, Padmanaban et al. used mouse and human models of both luminal and basal invasive ductal carcinomas to show that E-cadherin is required for metastasis.²⁰² If not via partial or complete EMT and resulting loss of E-cadherin, what mechanism accounts for cell motility in these cases? In the absence of complete or partial EMT, the extent to which UJT might account cellular motility in cancer progression remains to be determined.

Nevertheless, recent studies are suggestive. Cell jamming and unjamming transitions have now been identified as key processes in certain breast cancer models.^{23,193,195,203–208} Using derivatives of MCF10A cell lines with diverse levels of invasiveness, Jae H. Kim showed that cell shape and its variability conformed to the same geometric constraint as is associated with epithelial unjamming, but higher migratory speeds were associated with enhanced size of cooperative migratory cell packs.¹⁹³ Further studies in other laboratories have used MCF10A cells to show how RAB5A, a key endocytic protein, promotes unjamming.^203,204 Perhaps most persuasively, using solid tumor explants derived from 1380 breast cancer patients, the team of Josef A. Käs demonstrated that the state of cell unjamming and resulting tissue fluidity in the explant is predictive of distant metastasis.^206,209,210

VIII. SOFT MATTER PHYSICS IN EUKARYOTIC EVOLUTION

The biophysicist now lives in a world dominated by modern molecular genetics and systems biology. In such a world, should soft glassy behavior of the CSK be regarded merely as a downstream epiphenomenon, an inconsequential biophysical by-product of upstream molecular genetics? Similarly, what about jamming and the UJT behavior of the epithelial cellular collective? As regards the direction of the arrow of causality, we wondered: Might not causality also work in precisely the opposite direction? Specifically, might the physics of soft matter have been an overlooked but nonetheless robust selective pressure driving evolution of the eukaryote and its molecular genetics?

A. The cytoskeleton as a soft glass

Ample evidence now points to soft glassy dynamics of the CSK as being conserved across all eukaryotic cells.^{4,16,17,67,78,96,97,110,211–213} From the perspective of natural selection in evolution, it would be logical to presume that this would hold true as well for the last common ancestor (LCA). However, universality of such behavior prompts the question of what selective evolutionary pressure might have caused this to be so. For example, why does the eukaryotic CSK exhibit a stiffness always of order 10²–10³ Pa? Why not orders of magnitude more stiff, like a rubber? Or orders of magnitude less stiff, like a fluid? What is so special about that particular range of stiffness, and SGM behavior overall (Text Box 2; Fig. 8)? Working with Andrew H. Knoll in our Department of Evolutionary Biology, we speculated about how these conserved mechanical behaviors might have been driven through the agency of selective evolutionary pressures exerted by the primordial cellular microenvironment.¹⁷

B. Rigid or soft

Relatively quickly after the earth formed and its surface cooled, the Bacteria and Archaea first appeared, roughly 3 × 10⁹ years ago. Modern day prokaryotic descendants now feature a relatively rigid cell wall that supports a turgor pressure as large as 0.5–50 atmospheres, or about 10⁵–10⁷ Pa, and exhibits effective elastic shear moduli in roughly the same range.²¹⁴ Stem group eukaryotes likely expanded only much later, after the initial oxygenation of the atmosphere and ocean surface about 2.4 × 10⁹ years ago.^215,216 As such, the prokaryote is stiffer than the eukaryote by three to four orders of magnitude,^4,212 and this stiff cell wall, therefore, precludes uptake of microscale particulate nutrients by phagocytosis, and instead allows uptake of nutrients by diffusion alone.²¹⁷

C. Advantages of being soft

Reasons precipitating the catastrophic loss of the rigid prokaryotic cell wall and, thereby, the resulting creation of the earliest eukaryote, remain obscure.²¹⁷ However, once that catastrophic event transpired, and having lost its rigid wall, the earliest eukaryote could secure shape stability only through the agency of its cytoskeletal machinery. However, by virtue of the loss of the rigid cell wall, and by development of a soft cytoskeleton, the earliest eukaryotes were conferred with the novel abilities to capture microscale particulate nutrients using flexible cell modifications, such as pseudopodia, and to ingest these particulates via phagocytosis.^218,219 The last common ancestor of all modern-day eukaryotes was, thus, a motile heterotroph able to ingest particulate organic matter.^216,220 Moreover, the presence in the LCA of a mitochondrion acquired via endosymbiosis indicates that slow remodeling of cytoplasm is a primitive attribute within the domain and may have arisen as early as the cytoskeleton itself.^96,97,211 In this way, dynamics of the eukaryotic CSK may have facilitated the spread and diversification of eukaryotes by endowing early protists with functional capabilities not shared by the prokaryotes that dominated earth's earliest ecosystems.

D. Soft ecosystems, strong selective pressures

Such ecosystems often feature soft uncompacted microbial mats that accumulated over eons on the seafloor or lake bottom, and such primordial mats would have elastic shear moduli that are quite small, as would be characteristic of any SGM (Text Box 2; Fig. 8).^78,105,106 For the earliest eukaryote, such a primordial mat would have represented a nutrient-rich environmental niche. However, what mechanical factors would favor the ability of the eukaryotic cell to invade such a niche, migrate within it, and ingest constituent organic particles? On the one hand, had the early eukaryotic CSK been substantially less stiff than such sediments, and able to develop tractions that are at most small compared with shear moduli of those sediments, invasion into that sediment would have been mechanically impossible. However, on the other hand, what if the primitive eukaryotic CSK had been much stiffer than such sediments? In such a case, developing adequate traction forces and cellular deformations would become inordinately expensive from the point of view of the requisite cellular energy metabolism. Logically, therefore, cytoskeletal mechanics that might optimize the capacity of the cell to invade, migrate, and ingest must lie in a sweet spot intermediate between these mechanical extremes. Accordingly, we suggest the eukaryotic LCA may have been the end result of a selective pressure that favored a rough matching of traction stresses and elastic moduli of the LCA to the mechanical properties of its soft glassy microenvironment.

E. Cytoskeletal SGM as a conserved core process

With this in mind, the striking convergence between mechanical properties of CSK and soft sediment might be seen not so much a matter of a happenstance as much as a matter of a selective pressure that acted to drive internal scales of traction, stiffness, and friction for the primitive eukaryotic cytoskeleton and its molecular machinery. If so, then these features can be reasoned to have been passed down virtually unchanged to all eukaryotic descendants that followed. In the nomenclature of Kirschner and Gerhart,²²¹ soft glassy dynamics of the CSK would, therefore, represent a conserved core process.

F. Why is biology innately messy?³

1. Plasticity, malleability, and remodeling

Well before the discovery of cell jamming and unjamming, Kauffman proposed the general biological principle that living systems exist in a solid-like regime but near the edge of chaos, and that natural selection achieves and sustains such a poised state.^222–224 In his book, Investigations, Kaufman goes on to emphasize that by the terms “order” and chaos he is not referring to classical concepts of entropy as framed by Boltzmann and Gibbs in the context of statistical thermodynamics of systems at thermodynamic equilibrium.²²⁵ Instead, he deals with the open dissipative system far from thermodynamic equilibrium, such as the living cell. His suggestion is that within the fluid-like chaotic regime, the system can, and does, sample a wide range of micro-configurations, whereas in the solid-like regime, the system can settle and freeze into one quasi-stable micro-configuration. In such a way, the system can push its way into novelty, be that novelty molecular, morphological, behavioral, or organizational.

Macklem suggested, further, that disorder may be a prerequisite of such evolutionary processes.^226,227 In that connection, the disordered aggregate of cells that comprises a tissue often expresses some of the same glass-like/jamming properties as does the disordered aggregate of molecules that comprises the CSK itself. Inherent at both levels are disorder, rigidity, malleability, fluidity. Accordingly, glass-like/jamming dynamics may provide a fundamental mechanism by which plasticity, malleability, and remodeling may be initiated in the individual cell and then propagate within the cellular collective to effect tissue formation, growth, and repair.

2. Poised on the edge

Kauffman's framework is so general as to be innately abstract, vague. and qualitative. By contrast, our knowledge of cell jamming and unjamming, while still incomplete, is concrete, specific and quantitative. For example, we now know that as epithelial cells progressively unjam, and thus transition from a solid-like to a fluid-like collective phase, their cell stiffnesses and migration velocities tend to increase, their cell shapes become more elongated and more variable, and their propulsive forces exerted on the substrate, and junctional forces exerted on immediate neighbors, tend to increase.^{20,21,145,193} In addition, the size of cooperative swirls tends to decrease.^20,163

So the question arises, do the solid-like and fluid-like phases associated with jamming and unjamming fit as a subset within Kauffman's generalized concept³? Or should his framework be regarded merely as analogy or metaphor? Certainly, this framework can address none of the experimental findings associated with cell jamming/unjamming in concrete or specific terms and, as he points out, can make no specific predictions. The best that it can do, he says, is to tell stories describing events as they unfold.²²⁵ Based upon available evidence, perhaps the strongest statement that can be made at this time is that the jammed solid-like phase of the multicellular collective—poised just at the brink of unjamming—is strongly reminiscent of Kauffman's generalized solid-like regime poised at the edge of chaos.^3,222 A similar situation may be recapitulated at a subcellular scale of organization.^4,223,228

3. A few loose ends

The journey of our laboratory as described here necessarily leaves out several topics. These include the invention of medical devices such as acoustic rhinometry, acoustic pharyngometry, as well as a device for determination of absolute lung volumes without the need of a body plethysmograph.^229–233 Other topics include physiological studies such as development of the earliest methods to compute and to measure the distributions of pressures and flows throughout the complex asymmetrically branching airway tree of the lung,^39,234–238 gas dynamics in the airways, gas transport including the first description augmented diffusion during high frequency ventilation,^239,240 and flow limitation and nonuniform lung emptying during maximum expiratory flow.^241,242

IX. THE TAKE HOME: GRATITUDE, GRIT, RADICAL OPENNESS

A. Openness

A benefit of basic research is that if one takes care of the short term, then the long term tends to take care of itself. As such, we would venture no useful insight as to where our line of research might eventually lead. However, looking back at our research experience spanning more than 50 years, we can distill certain guiding values that may be timeless. For example, from Peter Macklem we learned that if you are not having fun in the lab, then you are in the wrong business. From Joseph R. Rodarte and Theodore Wilson, who took us under their wings, we came not only to appreciate an exemplary model of the exciting things that can happen when biology meets physics, but also learned that in dealing with administration, it is oftentimes better to ask for forgiveness than to ask for permission. From Jere Mead and Mary Ellen B. Wohl we learned, above all, to trust all scientists and, when asked to do so, to provide assistance unstintingly. We also learned from Mead and Wohl the benefits of radical openness. Yes, certain others occasionally took advantage to scoop us at our own game, but we were hardly acting out of naïveté. Getting scooped occasionally is a small price to pay for trusting the best in others. Rather, we understood that openness most often begets long-standing collaborations, gratifying creativity, and mutual benefit. As Jeffrey Drazen taught us, you have a hammer, I have a saw, together we can build a house. From Mary Ellen Avery, we learned that when truly difficult or even painful decisions need to be made, whether regarding personnel, money, or laboratory space, every consideration—including history, tradition, and even friendship—must be subordinated to what is in the best interest of the science.

B. Grit

Perhaps most important of all, we learned from Solbert Permutt the core concept of how to deal with failure. In science, failure is a daily occurrence, after all. The experiment failed. Our data undermined our central hypothesis. The paper was rejected. The grant application was not funded. Perhaps most devastatingly, the desired job never materialized. Sol taught us that failure, especially early in life, is the best teacher. One then has no choice but to pick yourself up, dust yourself off, and forge ahead. As such, Sol was at once both vulnerable and tough. Or to paraphrase the psychologist Brené Brown, Sol exemplified the qualities of strong back, soft front. While offering to those with whom he disagreed openness, engagement and vulnerability, Sol staunchly defended his own ideas. Tough and tender, brave and afraid, all at the same time.

In that connection, a word about the central importance of communication. Trainees sometimes shy away from publishing controversial data or ideas. As such, in our lab, we modeled the following. First, do not compound the error of possibly being wrong with the further error of being inaudible. In clear unmuddled fashion, every scientist needs to be ready to put their ideas out there, with suitable qualifications of course, and then be ready to be proven wrong. However, as Ramon y Cajal teaches, in the end your data will defend you.²⁴³

C. Gratitude

We would be remiss if we did not recognize our de facto mentor and role model, Jere Mead. Someone once said that Jere is like the side-view mirror of an automobile: people working with Jere are less bright than they may appear. We also acknowledge with great appreciation Joseph D. Brain, without whom it would have been impossible for us to establish a laboratory at Harvard. Even in his retirement, Joe continues to be an unending source of encouragement, support, and inspiration. People frequently ask what a biophysics lab like ours is doing in a school of public health. The short answer is simple: Jere Mead and Joe Brain.

We extend special thanks to James P. Butler, with whom we have worked with great pleasure for more than 50 years. On everything good that we ever accomplished, Jim's fingerprints can be found aplenty. With Jim, we continue to have had great disagreements, up to an including the contents of this very manuscript. However, the only way to displease Jim is to agree with him! We also extend special thanks to Stephanie A. Shore, who provided critique of grants and manuscripts that was always fierce and unfailingly helpful.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

Lior Atia: Conceptualization (equal); Data curation (equal); Funding acquisition (equal); Investigation (equal); Methodology (equal); Writing – original draft (equal); Writing – review & editing (equal). Jeffrey Fredberg: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Funding acquisition (equal); Investigation (equal); Writing – original draft (equal); Writing – review & editing (equal).

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.