Abstract
Objective.
PRIMA, the photovoltaic subretinal prosthesis, restores central vision in patients blinded by atrophic age-related macular degeneration (AMD), with a resolution closely matching the 100 μm pixel size of the implant. Improvement in resolution requires smaller pixels, but the resultant electric field may not provide sufficient stimulation strength in the inner nuclear layer (INL) or may lead to excessive crosstalk between neighboring electrodes, resulting in low contrast stimulation patterns. We study the approaches to electric field shaping in the retina for prosthetic vision with higher resolution and improved contrast.
Approach.
We present a new computational framework, Retinal Prosthesis Simulator (RPSim), that efficiently computes the electric field in the retina generated by a photovoltaic implant with thousands of electrodes. Leveraging the PRIMA clinical results as a benchmark, we use RPSim to predict the stimulus strength and contrast of the electric field in the retina with various pixel designs and stimulation patterns.
Main results.
We demonstrate that by utilizing monopolar pixels as both anodes and cathodes to suppress crosstalk, most patients may achieve resolution no worse than 48 μm. Closer proximity between the electrodes and the INL, achieved with pillar electrodes, enhances the stimulus strength and contrast and may enable 24 μm resolution with 20 μm pixels, at least in some patients.
Significance.
A resolution of 24 μm on the retina corresponds to a visual acuity of 20/100, which is over 4 times higher than the current best prosthetic acuity of 20/438, promising a significant improvement of central vision for many AMD patients.
Keywords: retinal prosthesis, neural stimulation, current steering, 3D electrode, resolution, modeling, circuit simulation
1. Introduction
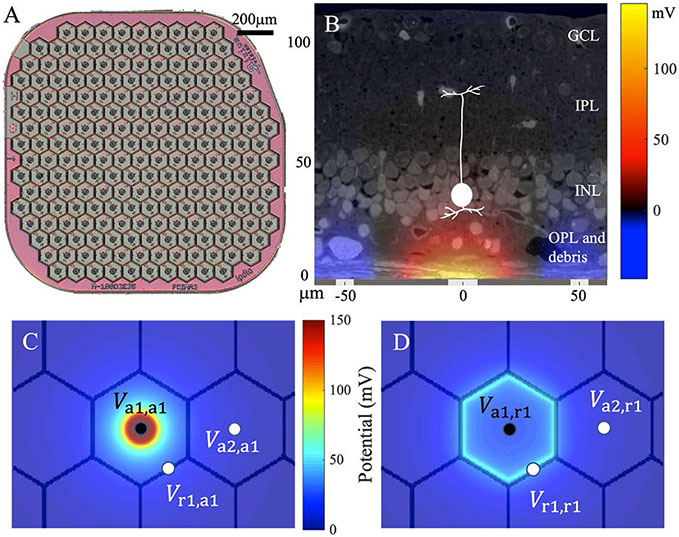
Recent years has seen the development of retinal prostheses to treat retinal degenerative diseases, including the atrophic age-related macular degeneration (AMD) and retinitis pigmentosa, for which there is no other cure. The first clinical trial of the subretinal implant PRIMA (Pixium Vision, Paris, France) with 100 μm pixels demonstrated the highest prosthetic acuity of 20/438, corresponding to 1.04 times the pixel pitch. The average visual acuity was 20/490 (20/438 to 20/564 range), corresponding to 1.17 ± 0.13 of the pixel size [1]. The close match of the prosthetic acuity to the fundamental sampling limit set by the pixel size indicates that smaller pixels may provide higher resolution. Prosthetic visual acuity can also be limited by electrical crosstalk between the neighboring pixels. In the PRIMA system, such crosstalk is suppressed by the return electrodes located around the active electrode in each pixel, connected in a hexagonal mesh (figure 1(A)).
Figure 1.
(A) The PRIMA subretinal implant with 100 μm photovoltaic bipolar pixels. (B) Electric potential generated by the 100 μm pixel injecting 1 μA of current, overlaid with a histological representation of the retina with a debris layer and a bipolar cell highlighted. (C) Elementary field of the active electrode (a1) of a bipolar pixel. Va1, a1, Va2, a1 and Vr1, a1 are the potentials at the active, the return (r1) and the active electrode of an adjacent pixel (a2), which define the corresponding mutual resistances. (D) Elementary field of the return electrode (r1) of a bipolar pixel with potentials labeled similarly to (C).
To stimulate the retina, the active electrode injects electric current into the tissue to generate a voltage drop between the dendritic end of the bipolar cell (BC) in the inner nuclear layer (INL) and its axonal arbor in the inner plexiform layer (IPL, figure 1(B)). Depolarization of the axonal terminals leads to opening of the voltage-sensitive calcium channels in the axonal terminals, which increases the release rate of glutamate into the retinal ganglion cell synapses [2]. With bipolar pixels, the penetration depth of the electric field (E-field) in tissue is constrained by the distance between the active and the return electrodes. With bipolar pixels smaller than 40 μm, retinal stimulation, even in rats, requires prohibitively high current, exceeding the charge injection limit of one of the best electrode materials - sputtered iridium oxide films (SIROFs) [3]. In human patients, where an additional debris layer of about 35 μm in thickness separates the INL from the implant [4], the stimulation threshold is even higher. Multiple designs have been proposed to increase the penetration depth of electric field into the retina, including pillars [5-7], honeycomb wells [3], and current steering with monopolar pixels for E-field shaping [8-10].
Studies of such designs involve modeling the dynamic E-field in the retina, which should include simulation of the circuit dynamics in each pixel, combined with calculation of the E-field in electrolyte for a specific current configuration. With a few pixels, it can be accomplished using the finite element method (FEM), e.g. COMSOL. However, such an approach is computationally intractable with a large number of electrodes and multiple levels of current injection at each electrode.
Here we present the Retinal Prosthesis Simulator (RPSim), a framework capable of efficient computation of the dynamic E-field in the retina generated by an implant with thousands of photovoltaic pixels coupled via a common electrolyte. We use RPSim to relate the clinical results with the PRIMA system to the electrical stimulation threshold and contrast performance in the presence of a 35 μm debris layer. With the PRIMA clinical data as a benchmark, we then model the performance of subretinal implants with 40 μm and 20 μm monopolar pixels, where current steering via transient returns (figure 6(A)) and the pillar electrodes (figure 6(B)) are utilized to further improve the contrast and the stimulation strength. The modeling results show the expected limits of resolution and contrast with a photovoltaic subretinal prosthesis. This computational framework can also be adapted to model other retinal prosthetic systems, or a general neural stimulation with large multi-electrode arrays (MEAs).
Figure 6.
(A) Schematic of the 40 μm flat monopolar pixels (top) and the electric field they generate, overlaid with a histological micrograph of the retina and two bipolar cell diagrams illustrating the best case on the left and the worst on the right (bottom). (B) 40 μm monopolar pixels with pillars penetrating through the debris layer. (C) Pre-charging the dark pixels around the illumination pattern with 35% of the stimulation irradiance (top) to enhance their conductance during the stimulation phase (bottom).
2. Methods
2.1. E-field modeling from elementary fields
Volume conduction of electric current in biological tissues is described by Poisson’s equation, the linearity of which enables synthesizing the E-field by a basis of elementary fields, each of which is generated by one electrode injecting a unitary current individually. The resulting E-field in the medium can be computed efficiently by superposing all the elementary fields weighted by the currents at their corresponding electrodes [10]. In the monopolar configuration, the current is injected from an active electrode and sinks into the common global return. In the bipolar configuration, the return electrode of each pixel (a hexagonal segment of the return mesh) also corresponds to an elementary field to account for the non- uniform current distribution across the return mesh (figures 1(C) and (D)), where the nominal ground is set at infinity. Note that by the Kirchhoff’s Current Law, after superposing the elementary fields according to the circuit dynamics, the net current to the infinity is always zero. All elementary fields are computed with FEM in COMSOL Multiphysics 5.6 (COMSOL, Inc. Burlington, MA) using the AC/DC module. The boundary condition of the current density on a capacitive electro-electrolyte interface transitions from equipotential (EP) to uniform current density (UCD) on a scale of approximately the RC time constant of the electrode [11], which is no more than a few milliseconds for the active electrode or the return segment of a pixel. Because the pulse widths we modeled are as long as 9.8 ms, the UCD (Dirichlet) boundary conditions were applied to bipolar pixels and the active electrodes in the monopolar array. However, since the global return of the monopolar array has a much larger RC time constant due to its vast area, the EP (Neumann) boundary conditions were specified there.
To further improve the computational efficiency, we exploit the spatial invariance of the elementary fields in the bipolar configuration, based on the observation that the elementary fields are laterally translated versions of each other. Therefore, we only need to compute two elementary fields with FEM - one for the active electrode and one for the return - instead of 410 fields (2 for each of the 205 pixels in figure 1(A)). In addition, the elementary field for the active electrode is axially symmetric, making the computation, data storage, and synthesis of the elementary fields very efficient. The elementary fields above the pillars are found to be isomorphic to those with flat pixels (r = 0.9936), subject to a scaling difference of 0.92. For convenience of exploring various pillar heights, we use the elementary fields of the flat pixels shifted up by the height and scaled by 0.92, as a proxy for the elementary fields of pillars.
2.2. Circuit model of the implant
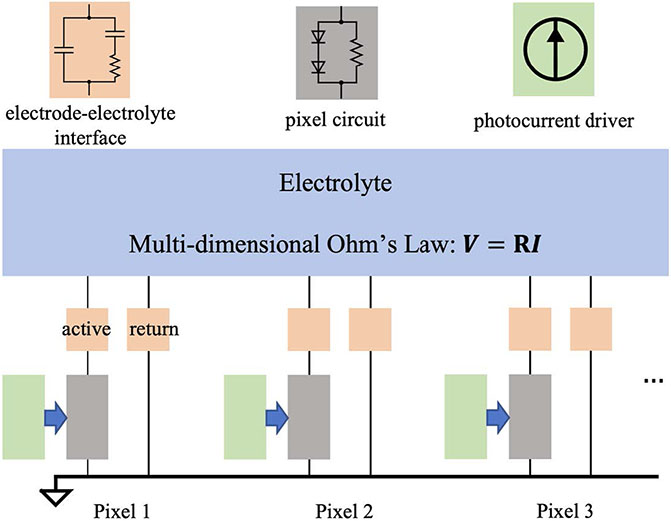
To compute the circuit dynamics with up to thousands of interrelated pixels in the implant, RPSim uses Xyce, a SPICE-compatible circuit simulator designed for extremely large circuit problems, as its kernel solver [12]. RPSim provides users with an interface in Python to configure the circuit, and calls Xyce through the PySpice module [13]. Our code is open-source on Github, together with the data necessary for simulating the devices studied in this paper [14]. As illustrated in figure 2, RPSim comprises four major components: the electrolyte, the electrodeelectrolyte interface, the pixel and the photocurrent driver.
Figure 2.
Diagram of the RPSim framework for modeling the dynamic E-field in the retina generated by an implant with up to thousands of photovoltaic pixels. The sub-circuit in each block can be adjusted independently. Current generated by an illuminated photovoltaic pixel is represented by a current source (green) in parallel with the pixel circuit in the dark (gray).
The coupling of pixels in an array through the electrolyte is quantified by the resistance matrix and the multi-dimensional Ohm’s Law , where and are vectors consisting of the potential and current at all electrodes, respectively. The entry Rm,n in is the mutual resistance between electrodes m and n, defined by , the potential at in the elementary field of n [15]. For example, in figure 1(C), Va1,a1, Va2,a1 and Vr1,a1 are the potentials induced by active electrode 1 (a1) at itself, active electrode 2 (a2) and return electrode 1 (r1), respectively. Figure 1(D) shows the elementary field of r1 with similar labeling. RPSim converts the resistance matrix to an equivalent mesh of resistors to comply with available features in Xyce, as described in the appendix. The electrodeelectrolyte interface is modeled by a surface capacitance of 6 mF cm−2, based on our previous characterization of SIROF [16]. The circuit consists of two diodes and a shunt resistor of 720 kΩ for the PRIMA bipolar 100 μm pixels, and one diode with 750 kΩ or 1.75 MΩ shunt resistor for monopolar 40 μm and 20 μm pixels, respectively. The photocurrent driver, which is a current pulse generator with an output proportional to irradiance on each pixel, is in parallel with the diodes, and together they mimic the current injection of the photodiodes under illumination [17]. Each component can be independently substituted, and for non-photovoltaic implants, the pixel and the photocurrent driver can be replaced by circuits corresponding to the power mechanism (amplifiers, for example).
2.3. In-vitro validation of the model
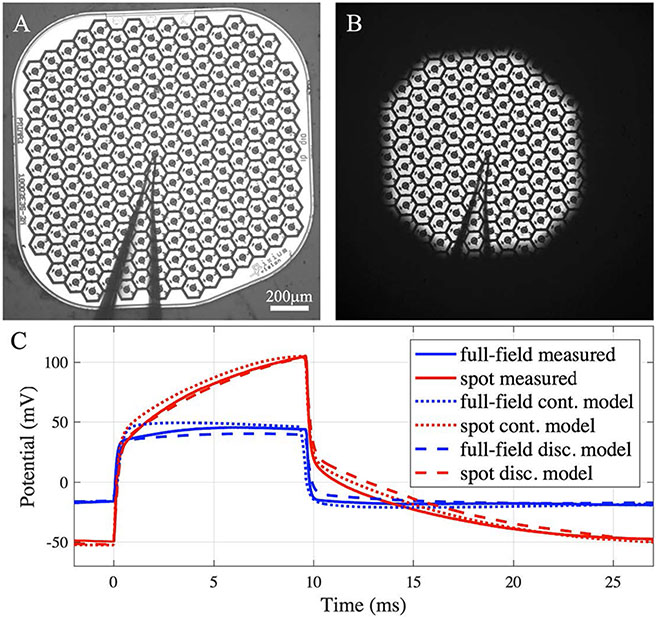
The modeling framework has been validated previously for the monopolar pixels array [15]. To validate the bipolar configuration, we compared the RPSim modeling result with in-vitro measurement and with an FEM model in COMSOL. For the measurement, we placed a PRIMA implant with 100 μm pixels in a Petri dish filled to a depth of 4 mm with NaCl solution of 1.52 mS cm−1 conductivity. A micro-pipette, with an opening of approximately 5 μm, was placed 17 μm above the center pixel (figure 3(A)). The 880 nm laser beam was projected at 3 mW mm−2 irradiance with 9.6 ms pulses repeated at 30 Hz, over the whole array (full field) or a spot covering about half of the pixels (figure 3(B)). The potential waveform shown in figure 3(C) was averaged over 100 measurements to reduce the noise. For the FEM model, we constructed the geometry of the in-vitro measurement in COMSOL and used the electrochemistry module and the electric circuits interface from the AC/DC module to calculate the voltage waveform with the same circuit parameters as RPSim. Unlike the discretized return electrodes in RPSim, where an UCD is assumed in each segment, the COMSOL model treats the return mesh as a continuous surface, where current distribution is governed by the dynamics of the electrodeelectrolyte interface.
Figure 3.
In-vitro validation of the model. (A), (B) A PRIMA implant tested in (A) full-field and (B) spot illumination, both at 3 mW mm−2, using 9.6 ms pulses at 30 Hz repetition rate. The outline of the micro-pipette, placed above the center pixel, can be seen. (C) The potential waveform measured 17 μm above the center pixel under the two illumination patterns (solid lines). Modeling results by (dotted lines) FEM in COMSOL, where the return mesh is a continuous domain, and (dash lines) by RPSim, where the return mesh is discretized into pixels.
2.4. Modeling E-field in the retina
We model the degenerate retina (including the INL, IPL and GCL, as shown in figure 1(B) as a 100 μm-thick layer with a conductivity of 1 mS cm−1 [18]. In RCS rats, the BC bodies are separated from the implant by only about 5 μm [19], while in humans, the INL is separated from electrodes by a debris layer of about 35 μm in thickness. We assume all the retinal layers have the same conductivity. A large volume representing the vitreous humor is placed above the retina, with a conductivity of 15 mS cm−1 [20, 21]. The voltage drop between the somatic and the axonal ends of a BC governs its neural response [2], and we assume that the axonal terminals are located in the middle of IPL, at 87 μm above the implant surface (figure 1(B)). The potential at the somatic end of a BC is defined by the average potential across its cross section, which is assumed to be 10 μm in diameter. To account for the probabilistic BC layout, in which the potential maximum may be anywhere relative to the cell, we estimate the stimulation strength of an image by convolving the potential map with a 20 μm-diameter ‘electrical receptive field’ and finding the maximum after convolution. We also assume that the BCs located closest to the implant will be activated first since they experience the highest potential. Their cell bodies are located in the INL, but the dendrites might reside below - in the outer plexiform layer (OPL), as discussed in section 3.2.
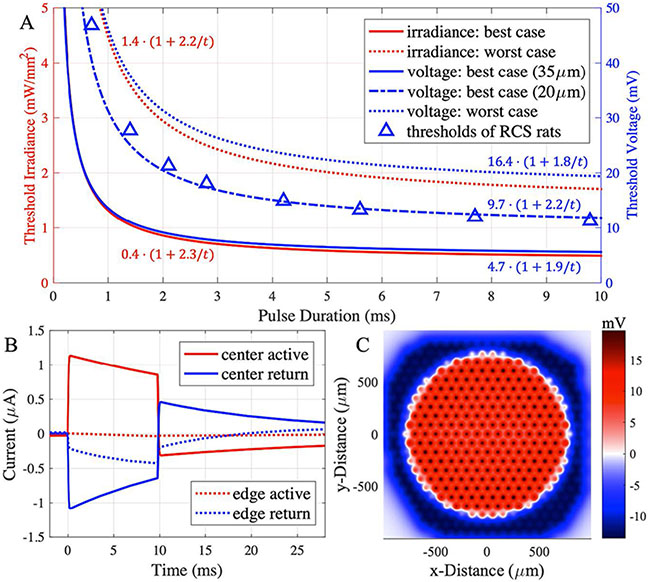
Following the PRIMA clinical protocol, we model the stimulation threshold by projecting a 1.6 mm spot on the implant at 10 Hz repetition rate, with pulse width and irradiance drawn from the clinical strength-duration (S-D) curves shown in figure 4(A) [4]. RPSim calculates the current injection of each pixel as a function of time (figure 4(B)), and the voltage drop across the BCs is computed by superimposing the elementary fields (figure 4(C)). We average the voltage drop over the pulse width and the electrical receptive field to find the maximum stimulation strength of an image, which we define as the threshold. Then, we model the electric field for an acuity test using the Landolt C with 120 μm gap width (1.2× pixel size) projected at 3 mW mm−2 irradiance with 9.8 ms pulses repeated at 30 Hz. The voltage contrast is defined by 1 − Vgap/Vstroke, where Vgap is the average voltage drop in the middle of the gap, and Vstroke - over the semicircle opposite to the gap. Next, the PRIMA implant is replaced by a monopolar array with 821 40 μm pixels or 2806 20 μm pixels. Each type was modeled with and without pillars of 30 μm height. The pillar height is designed to bring the electrodes sufficiently close to the BCs (as close as in RCS rats - 5 μm) through the debris layer. The Landolt C test is repeated with these pixels, using the gap width of 1.2 times the pixel sizes (48 μm and 24 μm) and the same irradiance and pulse duration. The stimulation strength (voltage drop across BCs) and contrast are compared to those with the PRIMA implant.
Figure 4.
(A) The S-D curves of the best-case (lowest) and the worst-case (highest) irradiance thresholds in the first clinical trial (red lines) [1]. The voltage S-D curves (blue lines) are computed for the best-case at the electrophysiologically realistic position of the dentrites at 20 μm, or the ‘naive’ one at 35 μm. For the worst case, voltage threshold is calculated for 35 μm separation of the INL. Voltage thresholds in RCS rats are shown for comparison [22]. (B) Current injection waveforms of two pixels under the 1.6 mm illumination spot in the PRIMA clinical threshold test, calculated by RPSim for the worst-case with 9.8 ms pulse duration at 1.71 mW mm−2 irradiance. (C) Potential across the BCs corresponding to the stimulus in (B).
3. Results
3.1. In-vitro validation of the model
In figure 3(C), the voltage waveform measured under full-field illumination resembles the square pulse of light, and the amplitude is well matched by both (RPSim and COMSOL) models. Under the spot illumination, however, the potential increases during the pulse, which is the result of transition from the EP boundary condition at the beginning of the pulse to an UCD on the return mesh [11]. At the onset of the pulse, current from the active electrode in illuminated pixel follows the path of least resistance and sinks to the nearby return segments. As charge accumulates and voltage on the return electrode rises in the illuminated region, current is driven to the more remote segments in the non-illuminated area, leading to deeper penetration of the E-field into the electrolyte and hence higher potential, as measured via the pipette. The COMSOL FEM computes the dynamics of the continuous current distribution on the return mesh, which accurately captures the characteristic ramp up, but takes 12 min to simulate each pulse cycle of 33 ms on a desktop computer (Intel Core i7-8700K, 3.7 GHz, 64 GB memory). In contrast, RPSim divides the return mesh into hexagonal segments of single pixels, assuming an UCD in each segment, and the circuit solver determines the current distribution among the segments. Such discrete approximation achieves similar agreement with the measurement, yet the simulation takes less than 10 s per pulse cycle, improving the computational efficiency by almost two orders of magnitude.
3.2. Stimulation threshold and contrast with the PRIMA implants
Clinical trials with the PRIMA implants demonstrated variability in the stimulation thresholds among patients by a factor of about 3.5 [4]. Figure 4(A) shows the lowest and the highest S-D curves among them (rheobase of 0.4 and 1.4 mW mm−2), which we use as the best- and the worst-case benchmarks, respectively, to estimate the range of responses with the future implants. We convert the two S-D curves from irradiance into voltage across BCs by first computing the current injection of each pixel with RPSim (figure 4(B)) and then finding the maximum voltage drop across the BCs above the implant (figure 4(C)). The resulting voltage S-D curves of the best- and the worst-case patients yield rheobases of 4.7 mV and 16.4 mV, respectively, assuming the BCs extend from 35 μm to 87 μm above the implant.
The rheobase in the worst-case patient is about twice the rodent rheobase [22], which may result from reduced neural excitability in the badly degenerate retina. However, the best-case rheobase, 4.7 mV, appears to be too low to stimulate the BCs. Literature indicates that the BC threshold is closer to 10 mV [18, 23, 24], which is consistent with the dynamics of the L-type Ca2+ channel [2], the dominant voltage-gated ion channel at the axonal terminal [25]. Such discrepancy may be reconciled by assuming the BC dendrites extend below the INL into the debris layer, thereby reducing the distance to the implant and leading to a higher voltage drop. If we assume a BC stimulation threshold at about 10 mV, the dendrites should be separated from the implant by about 20 μm. This refined S-D curve in figure 4(A) yields a rheobase of 9.7 mV. This curve matches very well the voltage thresholds in rats [22], shown by triangles in figure 4(B).
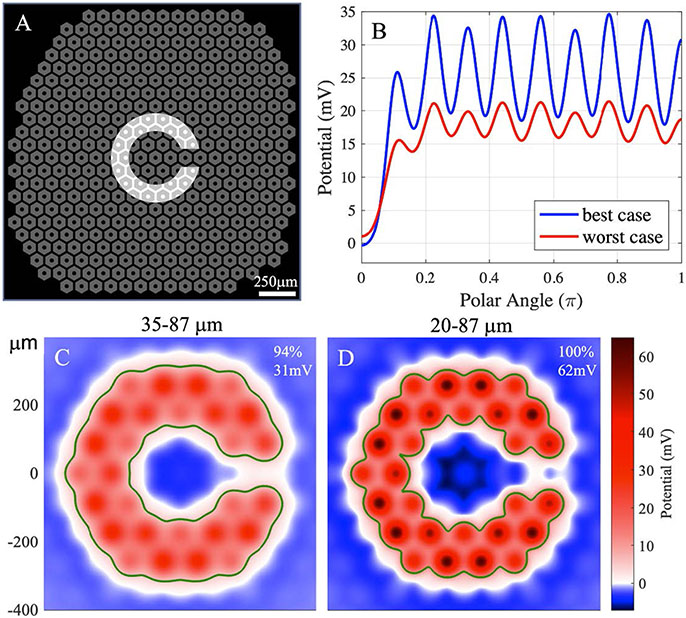
Another figure of merit to consider is the resolution of the Landolt C font used in the clinical trials for assessment of the visual acuity. Patients with the PRIMA 100 μm pixels, on average, were able to resolve the Landolt C with a 120 μm gap (1.2× pixel size) [1]. The corresponding projection pattern is shown in figure 5(A), and the voltage drop across BCs for the starting height of 35 μm and 20 μm - in figures 5(C) and (D), respectively. The stimulation strengths are found to be 31 mV and 62 mV for the two cases, exceeding the stimulation threshold of even for the worst case (19.7 mV). The contours in figures 5(C) and (D) outline the corresponding stimulation thresholds for 10 ms pulses in the best case, using the ‘naive’ (5.7 mV) and the ‘electrophysiologically realistic’ (11.7 mV) assumptions for 10 ms pulses, respectively. The two resulting contours are very similar, demonstrating that the model predictions regarding visibility of the letter do not depend strongly on this assumption. To illustrate the contrast of the letter, we plot the BC voltage drop averaged over the stroke of the C, as a function of the polar angle Θ (figure 5(B)), where Θ = 0 corresponds to the gap. The contrast is shown by the ratio between the average over the semicircle opposite to the gap (θ (Ξ [0.5π, π]) and the minimum of the plot inside the gap (Θ = 0). The worst case yields a contrast of 94%, and the best case - 100%, highlighting the well-confined electric field with 100 μm bipolar pixels.
Figure 5.
(A) The 100 μm PRIMA array overlaid with the average minimal resolvable Landolt C, having a 120 μm-wide gap (1.2× pixel size) illuminated by 3 mW mm−2, 9.8 ms pulses at 30 Hz repetition rate. (B) Potential averaged across the stroke width of the C, as a function of the polar angle about the center, where the gap is at 0°. (C), (D) Potential across the BCs for the worst (C) and the best (D) cases. Labels in the top-right corner show the contrast and the stimulation strength of each figure. The green contours outline the area above the stimulation threshold in the best case, calculated by the ‘naive’ conversion (35 μm height, 5.7 mV) in (C) and the electrophysiologically realistic one (20 μm height, 11.7 mV) in (D).
3.3. Stimulation strategies with small pixels
Flat bipolar pixels smaller than 40 μm cannot effectively stimulate the BCs even in RCS rats, where there is no debris layer [3], and even less so in the human retina. Therefore, a different electrode configuration should be used to enable on one hand, deep enough penetration of electric field into the INL, while on the other hand, sufficient field confinement to avoid excessive interference (crosstalk) from the neighboring pixels, thereby preserving high contrast of the stimulation pattern. Here, we model the performance of the 40 μm and 20 μm monopolar pixels with two strategies - current steering (figure 6(A)), and pillar electrodes (figure 6(B)), wherein the current steering is enabled by either the shunt resistors only, or enhanced by optical pre-charging, as described below.
The current steering strategy with monopolar pixels is based on the use of the active electrodes as both the anodes and cathodes, i.e. current is injected into electrolyte from the illuminated pixels and collected via the dark pixels. Conductance of the dark pixels is provided by two mechanisms: through the shunt resistor in parallel with the photodiode (figure 2), and through the diodes under forward voltage bias. For the first mechanism, the shunt resistor should be conductive enough to sink the cathodal current, but not too conductive so the photocurrent is primarily injected into the electrolyte rather than shorted via the shunt during stimulation. The shunt resistor also speeds-up the discharge of the electrodes between pulses, thereby increasing the charge injection at higher repetition rates [26]. For 0.7 ms and 9.8 ms pulses at 30 Hz, the shunt resistors that maximize the charge injection were found to be about 10 and 3 times the access resistance of a single pixel, respectively, although the maximum charge injection is not very sensitive to the shunt value. Since long pulses are more voltage-limited by the photodiodes, and a smaller shunt resistance is more favorable for the field confinement, the optimal shunt was determined to be about 3 times the access resistance - 750 kΩ and 1.75 MΩ for 40 μm and 20 μm pixels, respectively.
Conduction through photodiodes can be enhanced by pre-charging the designated pixels prior to stimulation with relatively dim light projection. Charge accumulation at the capacitive electrodeelectrolyte interface creates a forward bias across the diode, which increases its conductance and hence the return current in the stimulation phase. Stronger return current on the neighboring pixels enhances the field confinement and the associated contrast of the electrical pattern [15]. Pre-charging should be performed below the stimulation threshold, so that by itself it will not elicit neural responses. With a 30 Hz frame rate and a 9.8 ms stimulus pulse, 23.5 ms is available within each frame for pre-charging. For confinement of electric field in a pattern, a rim of pixels around the stimulation pattern can be exposed to light at a sub-threshold irradiance level between the stimulation pulses, so they become forward-biased prior to the stimulation phase. Such a pre-charging pattern can be produced by widening the stimulation pattern by 1 pixel and subtracting the stimulation pattern, as shown in figure 6(C). During the stimulation pulse, these pixels are not exposed to light, so they serve as enhanced transient returns for the illuminated pixels, which emit the photocurrent.
Another approach to enhance penetration of electric field into the retina is to use pillars that penetrate through the debris layer and bring the electrodes closer to the INL, due to the tissue migration [27]. In modeling this approach, we assume a 5 μm distance between the electrodes and BCs, as observed in RCS rats [19]. The two strategies (current steering and pillars) can be combined.
3.4. Stimulation strength and contrast with monopolar pixels
We model the voltage drop across BC with 40 μm and 20 μm monopolar pixels in a Landolt C pattern, where the gap is set at 48 μm and 24 μm, respectively, corresponding to the achievable resolution of 1.2× pixel size in PRIMA patients [1]. Figure 7 shows the potential maps with 40 μm flat pixels for the worst and the best cases, and of pillars, with and without the pre-charged transient returns. The contrast and the stimulation strength are shown in the top-right corner of each map. With flat pixels and without optically-enhanced current steering, both cases exhibit contrast below 50%. Pre-charging the edge pixels improves the contrast to a level comparable to that with PRIMA 100 μm pixels, at the price of reduced stimulation strength. As a result, the stimulation strength for the worst case, 26 mV, is close to the stimulation threshold of 19.7 mV from the clinical data. With pillars, the stimulus is much stronger and the contrast is high (75%), even without the enhanced current steering, while with the optical pre-charging it reaches 100%.
Figure 7.
Voltage drop across the BCs generated by the 40 μm monopolar pixels, with the Landolt C of 48 μm gap projected by 3 mW mm−2, 9.8 ms pulses at 30 Hz repetition rate. Results are shown for the worst and the best cases with flat pixels, and for pillars, with and without the pre-charging.
A similar set of field maps is shown in figure 8 for 20 μm pixels and the corresponding Landolt C size. In the worst case, the stimulation strength with flat pixels is below the threshold, even without the optical current steering. In the best case, only pre-charging provides a satisfactory contrast, but the stimulation strength, 15 mV, is close to the threshold of 11.7 mV. With pillars and without optical current steering, the contrast is mediocre (68%), but it can reach 100% with pre-charging, although the stimulation is rather weak (24 mV).
Figure 8.
Voltage drop across the BCs generated by the 20 μm monopolar pixels, with the Landolt C of 24 μm gap projected by 3 mW mm−2, 9.8 ms pulses at 30 Hz repetition rate. Results are shown for the worst and the best cases with flat pixels, and for pillars, with and without the pre-charging.
Table 1 summaries the contrast and stimulation strength of all the configurations mentioned above, while the gap of the Landolt C is always 1.2 times the pixel size. As expected, pillars yield stronger stimulation and better contrast than flat pixels under the same conditions.
Table 1.
Contrast and amplitude (voltage/threshold) generated by 100 μm, 40 μm and 20 μm pixels for the smallest resolvable C (gap width = 1.2× pixel size) under 3 mW mm−2 irradiance, with 9.8 ms pulses at 30 Hz repetition rate. Stimulation thresholds are 11.7 mV and 19.7 mV in the best and the worst cases, respectively.
| 100 μm PRIMA |
40 μm pixels |
20 μm pixels |
|||||
|---|---|---|---|---|---|---|---|
| Bipolar |
Monopolar |
||||||
| Contrast (%) |
Voltage/ Threshold |
Contrast (%) |
Voltage/ Threshold |
Contrast (%) |
Voltage/ Threshold |
||
| Flat, worst | Basic | 94 | 1.6 | 38 | 2.2 | 36 | 0.83 |
| Pre-charged | 92 | 1.3 | 75 | 0.45 | |||
| Flat, best | Basic | 100 | 5.3 | 48 | 5.6 | 44 | 2.2 |
| Pre-charged | 100 | 3.7 | 87 | 1.3 | |||
| Pillars, worst | Basic | 75 | 4.3 | 68 | 1.6 | ||
| Pre-charged | 100 | 3.6 | 100 | 1.2 | |||
| Pillars, best | Basic | 75 | 7.9 | 68 | 3.0 | ||
| Pre-charged | 100 | 6.8 | 100 | 2.2 | |||
3.5. 20 μm pixels with optimal shunt as a universal hardware
According to table 1, the 1.2× pixel size resolution with 40 μm pixels may be achieved in all patients, while achieving 24 μm resolution with 20 μm pixels is difficult due to rather low amplitude and contrast even with pillars, which maybe sufficient only for the best case. However, the question remains what is the best implant configuration for the 40 μm resolution? Figure 9 shows the optimal configurations for resolving 48 μm gap of Landolt C in the worst-case patient. With 40 μm pixels, sufficient contrast is achieved only with pre-charging the edge pixels. With 20 μm pixels, however, similar stimulation strength and contrast levels are achieved with only the basic current steering through the shunt resistors. The 20 μm pixel array provides a better contrast than the 40 μm pixels under the basic current steering, due to the shorter distance between the illuminated pixels injecting the current and the dark neighbors, which serve as returns. Pillars enhance the stimulus strength to a similar extent in both cases. Avoiding the need for pre-charging greatly simplifies the device operation. All configurations yield sufficient stimulation strength and contrast even for the worst case, as demonstrated by the contours for the worst-case stimulation threshold of 19.7 mV. Contrast with flat 20 μm pixels and no precharging (72%) is a little lower than with 40 μm and optical current steering (92%). The remedy, however, can be a weaker pre-charging to improve the contrast without sacrificing too much in stimulation strength. Therefore, implants with 20 μm monopolar pixels and pillars may serve as a universal hardware for all patients, which can support resolution of no worse than 48 μm, and in some patients may be as good as 24 μm, corresponding to the visual acuity of 20/100.
Figure 9.
(A)–(D) Voltage drop across the BCs in the worst case, generated by the Landolt C pattern of 48 μm gap at 3 mW mm−2, 9.8 ms pulses at 30 Hz repetition rate. (A) Flat 40 μm pixels with pre-charging; (B) 40 μm pillars with pre-charging; (C) flat 20 μm pixels without pre-charging; (D) 20 μm pillars without pre-charging. (E) Potential in (A)–(D) averaged across the stroke width of the C as a function of the polar angle about the center, where the gap is at 0°. Horizontal dash and dotted lines show the stimulation thresholds for the best and the worst cases, respectively. Green contours outline the worst-case threshold.
4. Discussion
The RPSim tool we developed is a highly efficient approach to modeling the electric field in electrolyte generated by a large-scale MEA, at the core of which is the superposition of the elementary fields. Although the FEM is still required to generate the elementary fields, they only need to be computed once, and any E-field in the medium can be obtained by simple scaling and summation of them. Furthermore, if only some linear metrics of the electric field are of interest, for example, the voltage between the two ends of the BCs in our case, we can store just these metrics in each elementary field, instead of the potential in the entire 3-dimensional (3D) volume, which further improves the computational efficiency. The only premise of this framework is the linear volume conduction of electric current in the medium, which is valid for the retina modeled as a multi-layered structure, or even biological tissues with anisotropic conductivity [28-30], and is not affected by nonlinearity of the electrode dynamics or other parts of the MEA circuitry. RPSim is modularized by design and hence can be easily adapted for modeling other retinal prosthetic systems or other neural modulators.
The boundary condition for the current on a capacitive electrode-electrolyte interface transitions from EP at the beginning of the pulse to a current density proportional to the capacitance per unit area in the steady state [11]. With a homogeneous electrode surface, this means an UCD. Such a transition can be described as a family of eigenmodes of charge and current distribution, each decaying with its own time constant. The eigenmodes with stronger spatial variation decay faster due to the less resistive pathway for the charge to equilibrate in the local vicinity. RPSim assumes an UCD within the return segment of each pixel, which is less precise than the complete FEM, where the return mesh is modeled as a continuous surface. However, such discretization only results in omitting the fast-decaying eigenmodes, while the current redistribution on the array scale is governed by the slowest ones. Therefore, RPSim was able to achieve a similar accuracy as the FEM, but in less than 2% of the computation time. In addition, if the distances between the active electrodes and BCs are larger than the electrodes themselves, the precise boundary conditions on the electrode-electrolyte interfaces are less critical to modeling the neural stimulation, which is the case for subretinal arrays with small electrodes.
To verify whether the voltage drop across BCs determines the retinal stimulation threshold, and hence our assumption that the best-case patient’s dendrites start in the debris layer, we measured the irradiance thresholds in RCS rats with the PRIMA implants of 100 μm and 75 μm pixels and converted the irradiances into voltages across BCs. Despite the 2.5-fold difference in the irradiance thresholds with these two pixel sizes, the voltage drop across BCs was very similar [22], supporting the view that they indeed determine the stimulation threshold. More details regarding the rodent experiments are described in the companion paper [22]. Despite the difference between the electrophysiologically realistic conversion assuming the dendrites at 20 μm, and the ‘naive’ conversion at 35 μm, their predictions about the irradiance thresholds and visibility contours with 75 μm bipolar pixels were also very similar, because the threshold derived from either assumption applies likewise to predictive conversions under the same assumption. Such similarity indicates that our model is not very sensitive to this paired assumption about the BC location and stimulation threshold, and hence the prediction is robust.
High-resolution neural stimulation requires both stimulation strength and lateral confinement of E-field to suppress the crosstalk between neighboring electrodes. With a flat monopolar array, where all electrodes inject current of the same polarity, field confinement is very limited. On the other end of the spectrum, bipolar pixels with a return electrode inside each pixel over-confine the field and may not reach the stimulation threshold for neurons located further away from the implant than the distance between the active and the return electrodes. Current steering in monopolar arrays provides a configurable middle ground between the two extremes, depending on the amount of current sunk to the transient returns. The basic current steering through the shunts in our system provides a baseline confinement, which is sufficient in some cases (figures 9(C) and (D), for example), while providing a simple operation of the device. Contrast can be further enhanced by a software-controlled pre-charging, if stronger field confinement is desired for higher resolution. However, development of a universal precharging algorithm for gray-scale images requires further research, and may be affected by the eye movements between the pre-charging and the stimulation phases. One approach to shaping a gray-scale E-field in the retina is by the real-time optimization-based current steering [10].
Nevertheless, current steering alone does not solve the fundamental antagonism between the stimulation strength and field confinement for remote cells because the lateral confinement also limits the vertical span of the E-fields in the retina. Analogously, current steering trades the stimulation strength for more contrast, which would not work if the stimulation is not strong enough. The fundamental solution is 3D electrodes, such as the pillars demonstrated in this work that bring the electrodes closer to the target cells, and the honeycombs that decouple the field penetration depth from the pixel size, while maximizing the stimulation efficiency by vertical alignment of electric field [3]. On the other hand, 3D electrodes require more complex fabrication and the issues of the retinal integration with the 3D implant require further study.
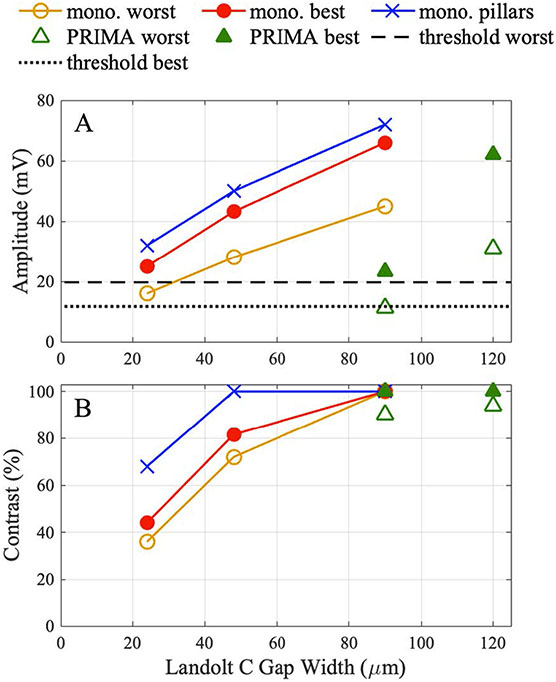
To provide a simplified overview of the findings, we plotted in figure 10 the stimulus strength (voltage across BCs) and contrast of the Landolt C patterns for various settings. All the calculations were performed with 3 mW mm−2, 9.8 ms pulse length at 30 Hz repetition rate. With the PRIMA implants of 75 μm pixel size, the stimulus amplitude is about 2.7 times lower than with 100 μm pixels for both the best and the worst patients. This is largely due to decrease of the photosensitive area per pixel by a similar amount. Such a drop could be compensated by increasing the irradiance up to the thermal safety limit of approximately 8 mW mm−2 [22]. Crosstalk between the bipolar PRIMA pixels is so small that the stimulus strength does not vary with the size of the projected Landolt C. With monopolar pixels, however, the crosstalk is very significant, and therefore the stimulus amplitude decreases with the decreasing size of the projected letter. To match the stimulus strength as in PRIMA 100 using flat monopolar pixels of 20 μm, Landolt C size can be decreased by a third for the best patients and by more than half for the worst patients. With pillar electrodes, it can be decreased further since the stimulus amplitude exceeds that with PRIMA 100 μm for the worst patient even with the Landolt C gap of 24 μm. Benefit of the pillars might be even higher if the visual perception is defined by the peak values of the electric potential rather than the average over the receptive field of a cell. Contrast also decreases with the decreasing pixel size in monopolar arrays, but with pillars, it remains at 100% with a 48 μm gap in Landolt C.
Figure 10.
(A) Potential across the BCs and (B) contrast of the Landolt C pattern generated with 3 mW mm−2 irradiance by 9.8 ms pulses at 30 Hz repetition rate and the following settings: (a) PRIMA with 100 μm and 75 μm pixels and Landolt C with a gap of 1.2× pixel size, corresponding to 120 μm and 90 μm, respectively. (b) Monopolar array of 20 μm pixels with Landolt C scaled to the gap size of 90, 48 and 24 μm, plotted for the worst patient (35 μm debris layer), best patient (20 μm debris layer) and pillars (5 μm debris layer).
With the demise of photoreceptors in retinal degeneration, horizontal cells, which regulate their terminals, become disconnected from the retinal network. This is likely a contributing factor to a reduced contrast sensitivity in prosthetic vision we observed earlier [31]. However, the antagonistic center-surround structure of the electric receptive fields is preserved, likely due to the remaining lateral inhibition by the amacrine cells [32]. Reduced contrast sensitivity can be compensated by a contrast enhancement between the camera and the ocular projector in our system, so it is hard to predict if and how the loss of horizontal cells will affect the spatial resolution.
5. Conclusions
RPSim enables efficient modeling of electric field in the retina generated by thousands of photovoltaic pixels. Using the clinical stimulation thresholds with 100 μm bipolar pixels and the corresponding Landolt C acuity test as a benchmark, such modeling can predict the stimulus strength and contrast with various pixel designs and stimulation patterns. A resolution of 48 μm can be achieved with 40 μm flat monopolar pixels using shunt resistors to sink the current via dark pixels for crosstalk suppression. Optically-controlled pre-charging can further enhance the field confinement by increasing the conductance of the diodes in transient returns. Pillars penetrating through the debris layer reduce the distance between the electrodes and the INL, and hence improve both the stimulation strength and contrast. The modeling indicates that a resolution of 24 μm may be achievable with 20 μm pixels and pillar electrodes.
Supplementary Material
Acknowledgment
The authors would like to thank Pixium Vision for providing the PRIMA implants used in this study. Studies were supported by the National Institutes of Health (Grants R01-EY-027786 and P30-EY-026877), the Department of Defense (Grant W81XWH-19-1-0738), AFOSR (Grant FA9550-19-1-0402), Wu Tsai Institute of Neurosciences at Stanford, and unrestricted grant from Research to Prevent Blindness. K M was supported by a Royal Academy of Engineering Chair in Emerging Technology, UK. E B was partially supported by the Rhona Reid Charitable Trust.
Appendix. Converting resistance matrix to resistor mesh
Electrodes in an array are coupled via the common electrolyte, and their collective current–voltage (I–V) relationship is described by the resistance matrix , of which the entry at the row and column, is the mutual resistance from electrode to electrode :
| (1) |
where is the average potential on electrode when electrode injects current individually [15]. However, the resistance matrix is not naturally supported by Xyce or Spice, where the relevant z-parameter network is compatible with neither time-domain analysis nor thousands of ports. Here we show the equivalent conversion from resistance matrix to a mesh of resistors connecting every pair of electrodes.
Let there be electrodes, where is the current injection of the mth electrode, and where is the potential at the mth electrode, for all . By the linearity of volume conduction and equation (1), we have:
| (2) |
or equivalently,
| (3) |
where . Let , be the entry in the mth row and nth column of .
Instead of the electrolyte, consider a resistor mesh connected between every pair of the electrodes, where is the resistor connecting electrode and electrode , and is the direct connection between electrode and the ground. Note that such definition requires a symmetric , which stems from the reciprocity of electromagnetism. The electric current from electrode to electrode through is given by
| (4) |
where and . Let be the current directly from electrode to the ground, which is given by . Therefore, by the linearity of a resistor network, we have:
| (5) |
Define
| (6) |
and we have:
| (7) |
Comparing equations (3) and (7), the resistor mesh is equivalent to , if
| (8) |
for all . Let us convert the conductance by
| (9) |
and equation (8) is satisfied. Equivalently, the conversion can be given in resistance:
| (10) |
where denotes the entry at the mth row and nth column of .
Data availability statement
The data that support the findings of this study are openly available at the following URL/DOI: doi.org/10.5281/ZENODO.6774591.
References
- [1].Palanker D, Le Mer Y, Mohand-Said S and Sahel J-A 2022. Simultaneous perception of prosthetic and natural vision in AMD patients Nat. Commun 13 1–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Werginz P, Wang B-Y, Chen ZC and Palanker D 2020. On optimal coupling of the ‘electronic photoreceptors’ into the degenerate retina J. Neural Eng 17 045008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Flores T, Huang T, Bhuckory M, Ho E, Chen Z, Dalal R, Galambos L, Kamins T, Mathieson K and Palanker D 2019. Honeycomb-shaped electro-neural interface enables cellular-scale pixels in subretinal prosthesis Sci. Rep 9 1–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Palanker D, Yannick LM, Mohand-Said S, Muqit M and Sahel JA 2020. Photovoltaic restoration of central vision in atrophic age-related macular degeneration Ophthalmology 127 1097–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Kim ET, Seo J-M, Woo SJ, Zhou JA, Chung H and Kim SJ 2008. Fabrication of pillar shaped electrode arrays for artificial retinal implants Sensors 8 5845–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Butterwick A, Huie P, Jones BW, Marc RE, Marmor M and Palanker D 2009. Effect of shape and coating of a subretinal prosthesis on its integration with the retina Exp. Eye Res 88 22–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Koo K, Lee S, Ban J, Jeong H, Park H, Ha S, Seo J-M, Chung H and Cho D 2009. Arrowhead-shaped micro-electrode array on polyimide substrate for retinal prostheses enabling close approach to target cells TRANSDUCERS 2009—2009 Int. Solid-State Sensors, Actuators and Microsystems Conf. (IEEE; ) pp 342–5 [Google Scholar]
- [8].Spencer TC, Fallon JB, Abbott CJ, Allen PJ, Brandli A, Luu CD, Epp SB and Shivdasani MN 2018. Electrical field shaping techniques in a feline model of retinal degeneration 2018 40th Annual Int. Conf. IEEE Engineering in Medicine and Biology Society (EMBC) (IEEE; ) pp 1222–5 [DOI] [PubMed] [Google Scholar]
- [9].Chung-Yu W, Tseng C-K, Liao J-H, Chiao C-C, Chu F-L, Tsai Y-C, Ohta J and Noda T 2020. Cmos 256-pixel/480-pixel photovoltaic-powered subretinal prosthetic chips with wide image dynamic range and bi/four-directional sharing electrodes and their exvivo experimental validations with mice IEEE Trans. Circuits Systems I 67 3273–83 [Google Scholar]
- [10].Chen ZC, Wang B-Y and Palanker D 2021. Real-time optimization of the current steering for visual prosthesis 2021 10th Int. IEEE/EMBS Conf. on Neural Engineering (NER) (IEEE; ) pp 592–6 [Google Scholar]
- [11].Chen Z, Ryzhik L and Palanker D 2020. Current distribution on capacitive electrode-electrolyte interfaces Phys. Rev. Appl 13 014004 [Google Scholar]
- [12].Keiter E, Russo T, Schiek R, Thornquist H, Mei T, Verley J, Aadithya K and Schickling J 2022. Xyce parallel electronic simulator users’ guide version 7.5 (available at: www.osti.gov/biblio/1866027) [Google Scholar]
- [13].Salvaire F 2020. PySpice 1.4.0 (available at: https://pyspice.fabrice-salvaire.fr) [Google Scholar]
- [14].Chen ZC, Goldstein AK and Palanker D 2022. RPsim v1.0.0 ( 10.5281/zenodo.6774591) [DOI] [Google Scholar]
- [15].Wang B-Y et al. 2021. Electronic “photoreceptors” enable prosthetic vision with acuity matching the natural resolution in rats bioRxiv Preprint ( 10.1101/2021.07.12.452093) (posted online 22 July 2021, accessed 25 July 2021) [DOI] [Google Scholar]
- [16].Huang TW. et al. Vertical-junction photodiode for smaller pixels in retinal prostheses. J. Neural Eng. 2021;18:036015. doi: 10.1088/1741-2552/abe6b8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Chen ZC, Wang B-Y and Palanker D 2020. Harmonic-balance circuit analysis for electro-neural interfaces J. Neural Eng 17 035001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Werginz P, Benav H, Zrenner E and Rattay F 2015. Modeling the response of ON and OFF retinal bipolar cells during electric stimulation Vis. Res 111 170–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Flores T, Goetz G, Lei X and Palanker D 2016. Optimization of return electrodes in neurostimulating arrays J. Neural Eng 13 036010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Jürgens I, Rosell J and Riu PJ 1996. Electrical impedance tomography of the eye: invitro measurements of the cornea and the lens Physiol. Meas 17 A187. [DOI] [PubMed] [Google Scholar]
- [21].Lindenblatt G and Silny J 2001. A model of the electrical volume conductor in the region of the eye in the ELF range Phys. Med. Biol 46 3051. [DOI] [PubMed] [Google Scholar]
- [22].Wang B-Y, Chen ZC, Bhuckory M, Goldstein AK and Palanker D 2022. Pixel size limit of the PRIMA implants: from humans to rodents and back J. Neural Eng 19 055003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Protti DA and Llano I 1998. Calcium currents and calcium signaling in rod bipolar cells of rat retinal slices J. Neurosci 18 3715–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Benav H 2012. Modeling effects of extracellular stimulation on retinal bipolar cells PhD Thesis Universitätsbibliothek Tübingen [Google Scholar]
- [25].Euler T, Haverkamp S, Schubert T and Baden T 2014. Retinal bipolar cells: elementary building blocks of vision Nat. Rev. Neurosci 15 507–19 [DOI] [PubMed] [Google Scholar]
- [26].Boinagrov D, Lei X, Goetz G, Kamins TI, Mathieson K, Galambos L, Harris JS and Palanker D 2015. Photovoltaic pixels for neural stimulation: circuit models and performance IEEE Trans. Biomed. Circuits Syst 10 85–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Elton H, Lei X, Flores T, Lorach H, Huang T, Galambos L, Kamins T, Harris J, Mathieson K and Palanker D 2019. Characteristics of prosthetic vision in rats with subretinal flat and pillar electrode arrays J. Neural Eng 16 066027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Dokos S, Suaning GJ and Lovell NH 2005. A bidomain model of epiretinal stimulation IEEE Trans. Neural Syst. Rehabil. Eng 13 137–46 [DOI] [PubMed] [Google Scholar]
- [29].Åström M, Lemaire J-J and Wårdell K 2012. Influence of heterogeneous and anisotropic tissue conductivity on electric field distribution in deep brain stimulation Med. Biol. Eng. Comput 50 23–32 [DOI] [PubMed] [Google Scholar]
- [30].Shahid SS, Bikson M, Salman H, Wen P and Ahfock T 2014. The value and cost of complexity in predictive modelling: role of tissue anisotropic conductivity and fibre tracts in neuromodulation J. Neural Eng 11 036002. [DOI] [PubMed] [Google Scholar]
- [31].Elton H, Lorach H, Goetz G, Laszlo F, Lei X, Kamins T, Mariani J-C, Sher A and Palanker D 2018. Temporal structure in spiking patterns of ganglion cells defines perceptual thresholds in rodents with subretinal prosthesis Sci. Rep 8 1–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Elton H, Smith R, Goetz G, Lei X, Galambos L, Kamins TI, Harris J, Mathieson K, Palanker D and Sher A 2018. Spatiotemporal characteristics of retinal response to network-mediated photovoltaic stimulation J. Neurophysiol 119 389–400 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are openly available at the following URL/DOI: doi.org/10.5281/ZENODO.6774591.