Abstract
In this issue of Cell Reports Methods, Roudot et al. present u-track 3D, a package geared toward improving the workflow of offline widefield multi-molecule tracking. The package is tailored for visualization of tracks, tracking, and assessment of trackability in tracking particles in biological systems.
In this issue of Cell Reports Methods, Roudot et al. present u-track 3D, a package geared toward improving the workflow of offline widefield multi-molecule tracking. The package is tailored for visualization of tracks, tracking, and assessment of trackability in tracking particles in biological systems.
Main text
Particle tracking, which involves determining the number of particles and their spatial trajectories, is an open problem whose relevance extends across a spectrum of disciplines from tracing the path of elementary particles through cloud chambers at the smallest scales to monitoring the movements of celestial bodies at the largest scales. Equally interesting is tracking of biological systems from the single molecule to the cellular scale. Each biological scale, and each setup from which tracking data are derived, presents its unique challenges from image registration across multiple frames or z-stacks, to particle detection (localization), to optical aberrations, detector noise, shot noise, and beyond. Indeed, under the broadest of scenarios, it is difficult to imagine an ambitious tracking tool working across all scales escaping Wolpert’s famed “no free lunch” theorem.1
One common simplifying approach is to track one single particle in real time and thereby avoid counting particles and linking across frames. Recent examples of this approach include real-time particle tracking tools such as MINFLUX2 and 3D-SMART,3 though tracking one particle is not suitable to all applications. Specific scenarios, such as intracellular transport studies,4 demand approaches with higher throughout (multi-particle tracking).
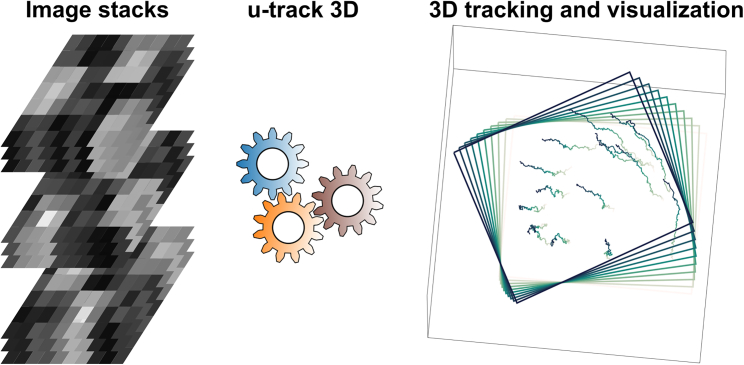
While an easy-to-use tracking tool with higher throughout (multi-particle tracking) would be helpful to the community, equally helpful are tools facilitating data visualization and even statistical assessments of the reliability of tracks. Enter u-track 3D by Roudot et al., (Figure 1).
Figure 1.
u-track 3D's simplified analysis pipeline
From the provided image stacks, u-track 3D can execute offline multi-particle tracking while automatically adjusting the region of interest (ROI, depicted by the boxes in the figure).
Here we focus, in that order, on data visualization, the underlying tracking method, and the trackability score of u-track 3D.
Data visualization is a key feature of u-track 3D. Besides addressing challenges pertaining to visual occlusions, 3D perception on a flat screen, more importantly, u-track 3D considers difficulties arising from the fact that the environment in which particles are moving is not always fixed in the lab frame. For instance, tracking proteins in a living cell, i.e., where viewing particle trajectories in the cell reference frame instead of the lab frame is often preferred. u-track 3D tackles this problem by introducing the concept of a dynamic region of interest (dynROI), which automatically defines the ROI on each frame. More concretely, to achieve this, an ROI on a frame is defined and found. Assuming that an ROI coincides with a recognizable shape, segmentation algorithms are applied to draw a cell mask. To then reduce computational cost, the mask on each frame is downsampled to a point cloud enclosed in a bounding box. Finally, these point clouds are associated to each other through rigid transformations (rotation and translation), telling us how ROIs change frame to frame (Figure 1). Although the procedure described here is general, each step requires experiment-specific adaptation for which Roudot et al.5 have equipped their tool with interactive features. For example, instead of obtaining point clouds by downsampling cell masks, dependent upon the experiment, these points can also be spindle poles or kinetochores. For cases where a bounding box is not appropriate, dynROI also allows users to switch to more appropriate shapes such as a sphere, a tube, or a cone.
In terms of the underlying tracking method, u-track 3D is built upon the mathematical core of the original 2D u-track4 platform, and hence maintains both its computational advantages and its regime of applicability.
As hinted above, the particle tracking problem issue poses a highly complex mathematical challenge. Even under dramatically simplified assumptions, concentrating only on identifying the best point estimates for both the number of particles to be tracked and their paths in space, and ignoring the uncertainty estimates, the problem remains a high-dimensional, nonlinear global optimization challenge. It includes both discrete elements (like links of particle positions across frames and particle counts in each frame) and continuous elements (such as spatial localization of particles in each frame), making it known as a “mixed-integer nonlinear problem” in the field of mathematical optimization. For the limiting case of point emitters (like fluorescently labeled single molecules), one may simultaneously and self-consistently determine the number of particles in each frame, localize each particle, and link them across frames.6 This full global optimization, leveraging information across all pixels in space and all pixels across time, introduces computational cost.
Efficient approximations can be invoked, as demonstrated by Roudot et al., which are valid in reasonably dilute and bright conditions. In such scenarios, shot noise, amongst other complexities, can be neglected. For instance, the number of particles of interest to be tracked and their localization in each frame can be independently estimated without propagating error of how many particles are present into errors on localization or linking. Similarly, exemplified by most offline particle tracking methods including u-track, another approximation is to treat particle localization and linking as two distinct steps. By doing so, particle localization on each frame can be performed independently through techniques such as single-molecule localization microscopy. Therefore, this approach necessarily requires each frame to contain sufficient information to localize particles. Fortunately, this requirement can be satisfied thanks to the development of experimental tools including super-resolution microscopy and quantum dot.
As for the linking step, it can be tackled using methods such as multiple-hypothesis tracking,7 the linear assignment problem,4 or even neural networks.8 Although the localization-then-linking approach is intuitive and widely used, it remains an approximation invoked for computational reasons. Fundamentally, tracking through separating particle localization and linking is a greedy algorithm, as intra-frame optimal particle positions are obtained then fed into the search for optimal inter-frame links. As the greedy algorithm is not guaranteed to find the global optima, this tracking approach is optimized for relatively high signal-to-noise. For the sake of an objective performance comparison to other methods, Roudot et al. closely followed the methodology established by Chenouard et al.9 Their comparison highlights u-track 3D’s competitiveness with respect to both conventional and deep-learning-based approaches.
The trickiest step in the workflow presented by Roudot et al. is the linking step. The authors provide working solutions to predict the risk of linking errors, captured in a trackability score. For synthetic data sets, where ground truth tracks are known, a widely applied approach is to evaluate the similarity between the ground truth tracks and the output of a tracking tool through the Jaccard index, also used in the work from Chenouard et al.9 Apparently, the Jaccard index cannot be applied to real experiments directly as ground truths are usually inaccessible. In order to tackle this issue, Roudot et al. define trackability based on the probability of associating the particle detections at time t to the track segments at t−1 calculated with stochastic filtering. Impressively, as shown in the paper, this trackability score aligns well with the Jaccard index for systems with various particle densities, velocities, and heterogeneities of motion types.
Together, trackability scores, alongside other features of u-track 3D, equip the biological community with a helpful tool and also serve as a reminder that tracking is a broad and open challenge to which different areas of science can contribute and mutually benefit.
Acknowledgments
Declaration of interests
The authors declare no competing interests.
References
- 1.Wolpert D., Macready W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. [Google Scholar]
- 2.Balzarotti F., Eilers Y., Gwosch K.C., Gynnå A.H., Westphal V., Stefani F.D., Elf J., Hell S.W. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science. 2017;355:606–612. doi: 10.1126/science.aak9913. [DOI] [PubMed] [Google Scholar]
- 3.Hou S., Exell J., Welsher K. Real-time 3D single molecule tracking. Nat. Commun. 2020;11:3607. doi: 10.1038/s41467-020-17444-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jaqaman K., Loerke D., Mettlen M., Kuwata H., Grinstein S., Schmid S.L., Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nat. Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roudot P., Legant W., Zou Q., Fiolka R., Betzig E., Danuser G. u-track3D: Measuring, navigating, and validating dense particle trajectories in three dimensions. Cell Reports Methods. 2023;3 doi: 10.1016/j.crmeth.2023.100655. [DOI] [PubMed] [Google Scholar]
- 6.Sgouralis I., Xu L.W., Jalihal A.P., Walter N.G., Pressé S.B.N.P.-T. 2023. A Framework for Superresolved Tracking.https://www.biorxiv.org/content/early/2023/06/13/2023.04.03.535459.full.pdf bioRxiv. eprint: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chenouard N., Bloch I., Olivo-Marin J.-C. Multiple Hypothesis Tracking for Cluttered Biological Image Sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2013;35:2736–3750. doi: 10.1109/TPAMI.2013.97. [DOI] [PubMed] [Google Scholar]
- 8.Wang Q., He H., Zhang Q., Feng Z., Li J., Chen X., Liu L., Wang X., Ge B., Yu D., et al. Deep-Learning-Assisted Single-Molecule Tracking on a Live Cell Membrane. Anal. Chem. 2021;93:8810–8816. doi: 10.1021/acs.analchem.1c00547. [DOI] [PubMed] [Google Scholar]
- 9.Chenouard N., Smal I., de Chaumont F., Maška M., Sbalzarini I.F., Gong Y., Cardinale J., Carthel C., Coraluppi S., Winter M., et al. Objective comparison of particle tracking methods. Nat. Methods. 2014;11:281–289. doi: 10.1038/nmeth.2808. [DOI] [PMC free article] [PubMed] [Google Scholar]