General Equation to Estimate the Physicochemical Properties of Aliphatic Amines

Abstract

Changes in various physicochemical properties (P_(n)) of aliphatic amines (including primary, secondary, and tertiary amines) can be roughly divided into nonlinear (P_(n)) and linear (P_LC(n)) changes. In our previous paper, nonlinear and linear change properties of noncyclic alkanes all were correlated with four parameters, n, S_CNE, ΔAOEI, and ΔAIMPI, indicating number of carbon atoms, sum of carbon number effects, average odd–even index difference, and average inner molecular polarizability index difference, respectively. To date, there has been no general equation to express changes in the properties of substituted alkanes. This work, based on the molecular structure characteristics of aliphatic amine molecules, proposes a general equation to express nonlinear changes in their physicochemical properties, named as the “NPAA equation” (eq 12), ln(P_(n)) = a + b(n) + c(S_CNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(G_N), and proposes a general equation to express linear changes in the physicochemical properties of them, named as the “LPAA equation” (eq 13), P_LC(n) = a + b(n) + c(S_CNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(G_N). In NPAA and LPAA equations, a, b, c, d, e, f, and g are coefficients, and PEI, APEI, and G_N represent the polarizability effect index, average polarizability effect index, and N atomic influence factor, respectively. The results show that nonlinear and linear change properties of aliphatic amines all can be correlated with six parameters, n, S_CNE, ΔAOEI, PEI, APEI, and G_N. NPAA and LPAA equations have the advantages of uniform expression, high estimation accuracy, and usage of fewer parameters. Further, by employing the above six parameters, a quantitative correlation equation can be established between any two properties of aliphatic amines. Using the obtained equations as model equations, the property data of aliphatic amines were predicted, involving 107 normal boiling points, 10 refractive indexes, 11 liquid densities, 54 critical temperatures, 54 critical pressures, 62 liquid thermal conductivities, 59 surface tensions, 56 heat capacities, 55 critical volumes, 54 gas enthalpies of formation, and 57 gas Gibbs energies of formation, a total of 579 values, which have not been experimentally determined yet. This work not only provides a simple and convenient method for estimating or predicting the properties of aliphatic amines but can also provide new perspectives for quantitative structure–property relationships of substituted alkanes.

1. Introduction

Physicochemical property data of organic compounds are indispensable in scientific research, chemical production, and practical application. Due to the huge number of organic compounds, it is an impossible task to determine the physicochemical properties of all organic compounds experimentally. So establishing a quantitative structure–property relationship (QSPR) method for organic compounds is very meaningful.^1,2 In 2021, Kontogeorgis et al.,³ after investigating the industrial requirements for thermodynamic and transport properties, reported that “In terms of models, companies ideally wish for a single universal model for all/many applications, but there is understanding that this is possibly utopian. The second major wish is the need for predictive models validated on extensive experimental databases and not only on just a few available experimental data points.” In fact, they proposed a challenging topic for molecular modeling: How to establish a single universal model for the property estimation of organic compounds, which can be expressed in Figure 1.

Figure 1.

Ideal QSPR model

The ultimate aim in Figure 1 is a fantastic topic and also a very difficult goal to achieve owing to the complexity of molecular structures and diversity of properties of organic compounds. However, compared to the ultimate aim, the secondary aim in Figure 1 may be relatively easier to achieve. In order to investigate this challenge, Cao et al.⁴ recently proposed a model (named the “NPOH equation”) to express various nonlinear (P_(n), eq 1) and linear (P_LC(n), eq 2) changes in the properties, of homologues, in which only two variables, carbon atom number n and the “sum of carbon number effects”, S_CNE, were used, and 14 properties, including boiling point, viscosity, ionization potential, vapor pressure, etc., were involved.

1

2

On the basis of eqs 1 and 2, a modified NPOH equation (as shown in eq 3) was proposed to express the boiling points (T_b) of 15 homologues RX (X = F, Cl, Br, I, OH, CN, NH₂, CO₂H, CHO, SH, C₆H₅, CH=CH₂, C≡CH, c-C₅H₉, and c-C₆H₁₁).⁵ It is a meaningful attempt to establish a general equation for various molecular structures, the same kind of property.

3

In eq 3, C_g is characteristic of group X and is calculated with the boiling point T_b difference between CH₃CH₂X and CH₃CH₃. I_tg is the terminal effect, and its attenuation coefficient is 1/n. μ_ind is an intramolecular charge-induced dipole, calculated with the product of parameters χ_X and PEI(R), as shown in eq 4.

4

In eq 4, χ_X and PEI(R) are the electronegativity of group X and the polarizability effect index of alkyl group R, respectively. χ_X is calculated by using the valence electron equalized electronegativity method.^6,7 PEI(R) is calculated by using the method of Cao and Li.⁸

In 2023, Cao et al.⁹ further proposed a general equation to express nonlinear changes in the physicochemical properties of noncyclic alkanes, including a total of 12 properties, named the “NPNA equation”, as shown in eq 5.

5

In eq 5, a, b, c, and f are coefficients and P_(n) represents the nonlinear change property of the alkane with n carbon atom number. ΔAOEI and ΔAIMPI are average odd–even index difference and average inner molecular polarizability index difference, respectively.

Linear changes in the physicochemical properties P_LC(n) of noncyclic alkanes can be expressed by eq 6.

6

Equations 5 and 6 show that nonlinear and linear change properties of noncyclic alkanes can all be correlated with four parameters, n, S_CNE, ΔAOEI, and ΔAIMPI, which indicates that it may be possible to establish a general model for the same kind of molecular structure-various properties.

It should be noted that eq 3 expresses the boiling point changes of homologous RX containing different functional groups, while eq 5 expresses various property changes of alkanes (including isomers) without functional groups. We want to know if a universal equation can be established for the various property changes of some substituted alkanes RX (including isomers).

In this work, we choose aliphatic amines as model compounds to investigate the general estimation model for the structure and properties of aliphatic amines. It is known that aliphatic amines have high demand and are widely used in various fields, such as chemical, daily chemical products, and medicine. Recently, Tran et al.¹⁰ even investigated the carbon dioxide absorption of amines. On the other hand, amines are also important atmospheric environmental monitoring compounds.¹¹ However, it should be noted that the property data measured experimentally are severely insufficient and cannot meet the needs of scientific research and practical applications. For example, in the famous book “CRC Handbook of Chemistry and Physics”, there are only less than 90 records of the boiling point of aliphatic amines and only less than 10 records of the enthalpy of formation.¹² In the “Chemical Properties Handbook”, there are only less than 30 records of critical properties of aliphatic amines,¹³ which indicates that estimating the property estimation aliphatic amines is a very meaningful work.

2. Results and Discussion

2.1. Theoretical Analysis of Factors Affecting the Property of Aliphatic Amines

Compared to the noncyclic alkane molecules, aliphatic amine molecules have the following characteristics: (i) aliphatic amine molecules have polarity due to having a polar amino group. (ii) On the same alkyl chain, amine groups can adhere to different positions in the alkyl chain to form positional isomers. In addition, when the number of carbon atoms in molecules is greater than or equal to 3, aliphatic amines can form three kinds of isomers, i.e., primary, secondary, and tertiary amines. Take C₃H₈ and C₃H₉N for examples, their molecular structures are shown in Figure 2.

Figure 2.

Comparison of the molecular structure of C₃H₈ versus C₃H₉N: (a) propane, (b) propylamine, (c) 2-propylamine, (d) N-methyl-ethylamine, and (e) trimethylamine.

Since the electronegativity of the nitrogen atom (N) is greater than that of the carbon atom (C), there is an intramolecular polarizability effect in the aliphatic amine molecule, and the intramolecular polarizability effect is not equal in primary amine, secondary amine, and tertiary amine with the same carbon atom number. Therefore, the factors affecting the property of aliphatic amines should involve the number of carbon atoms (descriptors n and S_CNE), the terminal effect, molecular skeleton differences, polarizability of N atom to the alkyl groups attached to the N, etc. That is, the property expression of aliphatic amines should involve the main parameters in eqs 3 and 5.

2.1.1. Calculation of Molecular Structure Descriptors of Aliphatic Amines

Here, the calculation of molecular structure descriptors mainly includes the parameters related to the number of carbon atoms (carbon atom number n and the “sum of carbon number effects,” S_CNE), average odd–even index difference (ΔAOEI), polarizability effect index (PEI), average polarizability effect index (APEI), and N atomic influence factor (G_N).

2.1.2. Calculation of Descriptors Related to the Number of Carbon Atoms

The general formula of aliphatic amines is C_nH_2n+3N. According to Cao et al.’s⁴ report, here, carbon atom number n and the sum of carbon number effects S_CNE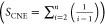 are employed to express the effect of carbon atoms on the property of aliphatic amines.

2.1.3. Calculation of Average Odd–Even Index Difference (ΔAOEI)

Take butylamine, 2-methyl-1-propylamine, and trimethylamine as examples; they all have the same molecular formula C₄H₁₁N, but have different molecular structures, as shown in Figure 3. The calculations of their OEI, AOEI, and ΔAOEI values are re-stated briefly as follows.

Figure 3.

Molecular skeleton diagram of (a) butylamine, (b) 2-methyl-1-propylamine, and (c) trimethylamine (numbers indicate the numbering of atoms). Molecular graphs of (d) butylamine, (e) 2-methyl-1-propylamine, and (f) trimethylamine (numbers indicate the numbering of vertexes).

2.1.3.1. Odd–Even Index (OEI)

According to the report of Yuan et al.,¹⁴ the OEI value of a molecular graph is calculated by eq 7.

7

In eq 7, m is the number of vertices (a total of carbon and nitrogen atoms) in the molecular graph and S indicates the derivative matrix from the distance matrix D. For the elements of S, they are the squares of the reciprocal distances (D_ij)⁻², that is, S_ij = 1/D_ij² (when i = j, let 1/D_ij² = 0).

Following are the distance matrices D(d), D(e), and D(f) of (d), (e), and (f) in Figure 3, and their derivative matrices S(d), S(e), and S(f), respectively.

Employing eq 7, the OEI values of (d), (e), and (f) in Figure 3 are calculated. Their values are as follows. OEI(d) is 6.8194 [i.e., (−1/16) × 2 + (−1/4) × 6 + (1/9) × 4 + 1 × 8], OEI(e) is 6.4444 [i.e., (1/9) × 4 + (−1/4) × 8 + 1 × 8], and OEI(f) is 5.0000 [i.e., (−1/4) × 12 + 1 × 8].

The calculated results show that the OEI values of butylamine, 2-methyl-1-propylamine, and trimethylamine are 6.8194, 6.4444, and 5.0000, respectively.

2.1.3.2. Average Odd–Even Index AOEI and Average Odd–Even Index Differences ΔAOEI

The above calculation results show that the vertex numbers of butylamine, 2-methyl-1-propylamine, and trimethylamine are equal, while their OEI values are different from each other. Their OEI value order is butylamine (6.8194) > trimethylamine (6.4444) > 2,2-dimethylpropane (5.0000). Thus, we can employ the differences of OEI values between linear and branched aliphatic amines to express the molecular skeleton differences.

Since the OEI value is affected by vertex number of aliphatic amine, here, we use eqs 8 and 9 to calculate the average value AOEI and its difference ΔAOEI between linear and branched molecular graphs, and use AOEI and ΔAOEI to express the molecular skeleton differences.

8

9

In eqs 8 and 9, m is the number of vertices (a total of carbon and nitrogen atoms) in molecular graphs and the subscripts br and lin represent branched molecular graph and linear molecular graph, which have equal number of vertexes, respectively. Equation 9 implies that the ΔAOEI values of aliphatic amines with linear molecular graph all are zero.

Take the calculations of the AOEI values of Figure 3d–f for example. The 3 molecular graphs all have 5 vertexes (4 carbon atoms and 1 nitrogen atom, m = 5); thus, their AOEI values are calculated. That is, AOEI(d) is 1.3639 [i.e., OEI(a)/m = 6.8194/5], AOEI(e) is 1.2889 [i.e., OEI(b)/m = 6.4444/5], and AOEI(f) is 1.0000 [i.e., OEI(c)/m = 5.0000/5].

Using the values of AOEI, we can calculate the ΔAOEI. It is known that AOEI value of butylamine is AOEI(d) = 1.3639; therefore, ΔAOEI(d) is 0.0000 [i.e., AOEI(d) – AOEI(d) = 1.3639–1.3639], ΔAOEI(e) is −0.0750 [i.e., AOEI(e) – AOEI(d) = 1.2889–1.3639], and ΔAOEI(f) is −0.3639 [i.e., AOEI(f) – AOEI(d) = 1.0000–1.3639].

The results show the ΔAOEI values of butylamine, 2-methyl-1-propylamine, and trimethylamine are 0.0000, – 0.0750, and −0.3639, respectively.

In this work, the parameter ΔAOEI is used to express the molecular skeleton difference between linear and branched molecular graphs of aliphatic amines.

2.1.4. Calculation of Polarizability Effect Index (PEI)

2.1.4.1. Polarizability Effect Index PEI of Alkyl Groups Attached to the N Atom

Aliphatic amines are polar molecules due to the electronegativity of the N atom being greater than that of the C atom. An intramolecular charge-induced dipole μ_ind will be generated between N atom and alkyl R, which can be expressed by eq 4.⁵ In aliphatic amines, the χ_N of N atom is fixed, thus their μ_ind values can be expressed by only using PEI(R) values of alkyl groups R.

The PEI(R) values are calculated by using the method of Cao et al.⁸ That is, PEI(R) = ΣΔPEI(i), in which the ΔPEI(i) value is the PEI increment of the ith carbon atom in the alkyl R. Table 1 lists the PEI values of some normal alkyl R.

Table 1. PEI Values of Normal Alkyl H(CH₂)_n and the ΔPEI Values of the ith Carbon Atom (n_i) in Alkyl.

n	PEI	ni	ΔPEI	n	PEI	ni	ΔPEI	n	PEI	ni	ΔPEI	n	PEI	ni	ΔPEI
1	1.0000	1	1.00000	6	1.2350	6	0.00905	11	1.2551	11	0.00238	16	1.2625	16	0.00107
2	1.1405	2	0.14053	7	1.2414	7	0.00639	12	1.2571	12	0.00197	17	1.2634	17	0.00094
3	1.1887	3	0.04813	8	1.2461	8	0.00475	13	1.2587	13	0.00166	18	1.2642	18	0.00084
4	1.2122	4	0.02350	9	1.2498	9	0.00367	14	1.2602	14	0.00142	19	1.2650	19	0.00075
5	1.2260	5	0.01380	10	1.2527	10	0.00292	15	1.2614	15	0.00123	20	1.2657	20	0.00067

Take Figure 3a-c for example; they are butylamine, 2-methyl-1-propylamine, and trimethylamine, respectively, and their molecules have one butyl, one 2-methyl-propyl, and three methyl attached to the N atom, respectively. Thus, their PEI(R) values are calculated. The obtained values are as follows. PEI(R)(a) is 1.2122, PEI(R)(b) is 1.2368 (i.e., 1.1887 + 0.04813), and PEI(R)(d) is 3.0000 (i.e., 1.0000 × 3).

2.1.4.2. Average Polarization Effect Index (APEI)

The average polarizability effect index (APEI) represents the proportion of intramolecular charge-induced dipole μ_ind in the whole aliphatic amine molecules, which can be calculated by eq 10.

10

where n is the carbon atom number in aliphatic amine molecules.

Take Figure 3a-c for example; their carbon atom numbers n all are 5, and PEI(R)(a) = 1.2122, PEI(R)(b) = 1.2368, and PEI(R)(d) = 3.0000. Thus, APEI(a), APEI(b), and APEI(d) are 1.2122/5 = 0.2442, 1.2368/5 = 0.2474, and 3.0000/5 = 0.6000, respectively.

In this work, parameters PEI(R) and APEI are used to express intramolecular charge-induced dipole differences in aliphatic amine molecules.

2.1.5. Calculation of N Atomic Influence Factor (G_N)

The N atomic influence factor (G_N) is like the terminal effect (I_tg).⁵ It means that the influence of the N atom on the property of aliphatic amine gradually decreases with the increase of the number of carbon atoms, resulting in the property of aliphatic amine being close to that of alkane. Therefore, the influence of N atom on the property of aliphatic amine also is considered to be related to the number of carbon atom (n), as shown in eq 11.

11

Take 3-methyl-1-hexylamine for example, its carbon atom number n = 7, thus its G_N = 1/n = 1/7 = 0.1429.

2.1.6. General Equation Expressing the Properties of Aliphatic Amines

Based on eqs 1 and 3 and employing the molecular descriptors calculated in Section 2.1.1, we propose eq 12 to express nonlinear changes in the properties of aliphatic amines and use eq 13 to express linear changes in the properties of aliphatic amines. For convenience, eqs 12 and 13 are named the “NPAA equation” and “LPAA equation”, respectively (i.e., the abbreviations of “Nonlinear Properties of Aliphatic Amines equation” and “Linear Properties of Aliphatic Amines equation” respectively).

12

13

In eqs 12 and 13, a, b, c, d, e, f, and g are coefficients.

2.2. Applicability of NPAA and LPAA Equations

2.2.1. Correlation with the Properties of Aliphatic Amines

In order to test the applicability of NPAA and LPAA eqs 12 and 13, quantitative correlation analysis was conducted using various physicochemical properties of aliphatic amines. First, the ΔAOEI, PEI, APEI, and G_N values were calculated with the methods described in Section 2.1.1, and the S_CNE values were taken from Cao et al. report.⁴ Then, using eqs 12 and 13 as model equations, we performed regression analysis of the nonlinear change properties P_(n) and linear change properties P_LC(n) of aliphatic amines. The results are given in Table 2. These properties, P_(n) and P_LC(n), used in Table 2 are experimental data collected from the literature,^12,13,15,16 and the detailed data can be seen in the Supporting Information.

Table 2. Correlation Equations of Nonlinear Change and Linear Change Properties for Aliphatic Amines (C_nH_2n+3N) (Model Equations: ln(P_(n)) = a + b(n) + c(S_CNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(G_N); P_LC(n) = a + b(n) + c(S_CNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(G_N)).

			ln(P(n)) = a + b(n) + c(SCNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(GN)
no.	propertya	range of nb	a	b	c	d	e	f	g	Nc	Rc	Sc	Fc	AAEd	AAPE %d
1	Tb	1–30	4.76335	–0.00356	0.50313	0.29125	–0.02906	–0.05750	0.42771	80	0.9979	0.01614	2924.25	5.35	1.17
2	nD	1–36	0.25395	–0.00146	0.04137	0.03189	0.00050	–0.04297	0.06009	72	0.9906	0.00263	567.23	0.0027	0.19
3	D	1–18	–0.44532	–0.0032	0.08709	0.11489	0.00235	–0.17358	0.10237	71	0.9902	0.00847	533.81	0.0041	0.56
4	TC	1–16	5.63571	–0.0018	0.31149	0.24972	–0.03081	–0.06859	0.21747	28	0.9979	0.01125	829.61	4.77	0.83
5	PC	1–16	1.83078	–0.08403	–0.0681	0.26213	–0.00361	–0.14656	0.50374	28	0.9932	0.05285	255.11	0.095	3.09
6	λ	1–12	–0.93989	0.05581	–0.46478	0.54339	–0.08985	–0.12948	–0.04426	20	0.9818	0.03234	57.93	0.0031	2.19
7	ST	1–12	2.16252	–0.03528	0.52359	0.85165	–0.02943	–0.41817	0.74650	23	0.9961	0.01853	344.13	0.26	1.27
8	CP	1–24	3.88041	0.02343	0.58990	0.02996	–0.00529	–0.12763	0.29125	26	0.9951	0.05039	324.15	7.89	3.45

			PLC(n) = a + b(n) + c(SCNE) + d(ΔAOEI) + e(PEI) + f(APEI) + g(GN))
			a	b	c	d	e	f	g	N	R	S	F	AAE	AAPE%
9	Vc	1–14	84.62657	59.24207	–12.7078	–0.20054	–5.96167	36.59312	–25.8733	27	0.9983	12.28	1002.70	8.32	2.16
10	Hf	1–24	–44.731	–20.3317	6.65019	98.86474	6.62091	68.09713	–39.3626	28	0.9994	3.99	2834.76	2.71	3.60
11	Gf	1–14	–52.9695	6.8301	23.1459	64.3322	7.5584	81.0863	–33.6568	25	0.9940	4.37	249.00	2.64	3.91

^aT_b, normal boiling point (K); n_D, refractive index (293.15 K); D, liquid density (g·cm^–3, 293.15 K); T_c, critical temperature (K); P_c, critical pressure (MPa); λ, liquid thermal conductivity (W·m^–1·K^–1, 298.15 K); S_T, surface tension (mN·m^–1, 298.15 K); C_p, liquid heat capacity (J·mol^–1·K^–1, 298.15 K); V_c, critical volume (cm³·mol^–1); H_f, gas enthalpy of formation (kJ·mol^–1, 298.15 K); G_f, gas Gibbs energy of formation (kJ·mol^–1, 298.15 K). These properties data are listed in Table S1 in the Supporting Information.

^bCarbon atom number range.

^cR, S, N, and F are correlation coefficient, standard error, number of data points and Fisher test, respectively.

^dAAE and AAPE % are average absolute error and average absolute percentage error between the experimental value (P_exp.) and calculated value (P_cal.), respectively.

In Table 2, the 10 correlation coefficients (R) (except for λ property) are above 0.99 for the 11 properties of aliphatic amines, indicating that eqs 12 and 13 can be used to express the regularity of nonlinear change and linear change properties of aliphatic amines respectively. The correlation coefficient R is 0.9818 for λ (eq 6 of Table 2), being still good. Since the data distribution ranges of λ (liquid thermal conductivity, W·m^–1·K^–1, 298.15 K) are narrow, in 0.1140 to 0.1997, in addition, only 20 experimental data are collected for regression, and the data are less so that the correlation coefficient of the equation is less than 0.99. However, its calculation accuracy is good, in which the average absolute percentage error (AAPE) of λ is only 2.19% for 20 compounds used in eq 6 of Table 2. The results of Table 2 show that all AAPEs are less than 4.0%, and nonlinear change and linear change properties of aliphatic amines (including primary, secondary, and tertiary amines) all can be correlated with the six parameters n, S_CNE, ΔAOEI, PEI, APEI, and G_N. Figures 4 and 5 are plots of experimental versus calculated values of T_b and H_f of aliphatic amines, respectively.

Figure 4.

Plot of experimental T_b,exp versus calculated T_b,cal values of aliphatic amines.

Figure 5.

Plot of experimental H_f,exp versus calculated H_f,cal values of aliphatic amines.

In the model eqs 12 and 13, the parameters n and S_CNE express the influence of carbon atoms in molecules on the property of aliphatic amines, ΔAOEI expresses the influence of molecular skeleton differences on the property, PEI and APEI express the influence of intramolecular charge-induced dipole differences on the property, and G_N expresses the influence of nitrogen atom in molecules on the property.

2.2.2. Relationship between Properties of Aliphatic Amines

Equations 12 and 13 indicate that both nonlinear and linear change properties of aliphatic amines can be correlated with the six parameters n, S_CNE, ΔAOEI, PEI, APEI, and G_N, which means that, using the parameters n, S_CNE, ΔAOEI, PEI, APEI, and G_N, we can link the change regularities of different properties of aliphatic amines.

2.2.2.1. Relationship between Nonlinear Change Properties of Aliphatic Amines

Let one property of aliphatic amines be P_(n) (e.g., boiling point T_b) and the other be P′_(n) (e.g., critical temperature T_c), basing on eq 12, we can theoretically deduce eqs 14 and 15.

14

15

In eq 14, a_r = a – a′, b_r = b – b′, c_r = c – c′, d_r = d – d′, e_r = e – e′, f_r = f – f′, and g_r = g – g′, while in eq 15, a_s = a + a′, b_s = b + b′, c_s = c + c′, d_s = d + d′, d_s = e + e′, f_s = f + f′, and g_s = g + g′. For the two given physicochemical properties, P_(n) and P′_(n), of aliphatic amines, coefficients a_r, b_r, c_r, d_r, e_r, f_r, g_r, a_s, b_s, c_s, d_s, e_s, f_s, and g_s can be obtained employing the regression method.

Take critical temperature T_c for example, the relationship between T_c and boiling point T_b of aliphatic amines can be expressed by eq 16.

16

Taking eq 16 as a model equation and using the experimental T_b values to calculate the critical temperature T_c of aliphatic amines, we obtained the AAE and AAPE % at 4.49 K and 0.78% for the 28 compounds used in eq 16, respectively.

2.2.2.2. Relationship between Nonlinear and Linear Change Properties of Aliphatic Amines

By combining eqs 12 and 13 and using the method described in Section 2.2.2.1, we can obtain eqs 17 and 18.

17

18

In eqs 17 and 18, for the two given physicochemical properties, P_LC(n) and P′_(n), of aliphatic amines, coefficients a_r, b_r, c_r, d_r, e_r, f_r, g_r, a_s, b_s, c_s, d_s, e_s, and g_s can be obtained employing the regression method.

Take critical volume V_c for example, the relationship between V_c and boiling point T_b of aliphatic amines can be expressed by eq 19.

19

Taking eq 19 as a model equation and using the experimental T_b values to calculate the critical volume V_c of aliphatic amines, we obtained the AAE and AAPE % at 8.11 cm³ mol^–1 and 2.16% for the 27 compounds used in eq 19, respectively.

2.2.3. Prediction of Properties of Aliphatic Amines

It should be pointed out that due to the lack of experimental data on the properties of aliphatic amines, there is less research on quantitative structure–property relationship (QSPR) via only employing aliphatic amines. Therefore, it is difficult to compare the results of this work with those reported in other works because the data sets and number of variables employed in the various works were different. For example, Cordes and Rarey¹⁷ compared some group contribution methods for predicting the boiling points of acyclic alkanes and observed the average absolute errors ranging from 6.5 to 26.7 K in the mentioned methods. In this work, the average absolute error is 5.53 K for the boiling points of aliphatic amines. We also noticed that, in some reports, the QSPR involves the property of amines. Here, we make a rough comparison. He et al.¹⁸ predicted the critical properties of organic compounds based on group contribution theory. The experimental critical temperatures T_c of 169 compounds as well as experimental critical pressures P_c of 152 compounds were predicted, and AAPE values of 0.54% for T_c and 2.19% for P_c were obtained, in which 44 first-level group contribution parameters and 11 s-level group contribution parameters were employed. In this work, the AAPE values are 0.83% for T_c and 3.09% for P_c, respectively. Zhou et al.¹⁹ applied a support vector machine (SVM) combined with genetic algorithm method to build the models for predicting gas–liquid critical temperatures T_c of organic compounds (including hydrocarbons, aldehydes, alcohols, acids, amines, benzenes, sulfur compounds) and obtained S = 0.027 (log unit, 10^0.027 = 1.064). In this work, S = 0.01125 (ln unit, e^0.01125 = 1.011). Therefore, the model equations in Table 2 are reliable.

Employing the correlation equations in Table 2, we can predict the properties of aliphatic amines. The predicted results are listed in the Supporting Information. These properties involve 107 normal boiling points (105 primary amines,1 secondary amine, and 1 tertiary amine), 10 refractive indexes, 11 liquid densities, 54 critical temperatures, 54 critical pressures, 62 liquid thermal conductivities, 59 surface tensions, 56 heat capacities, 55 critical volumes, 54 gas enthalpies of formation, and 57 gas Gibbs energies of formation for primary, secondary, and tertiary amines (a total of 579 values), which have not been experimentally determined yet.

Take primary amines as an example, their normal boiling points are predicted as follows.

First, the molecular structures of the primary amines are constructed. Lu et al.²⁰ investigated QSPR of 138 alcohols. Here, we take the alcohols reported by Lu²⁰ as model molecules and obtain primary amine molecules by replacing group OH with group NH₂ (total of 141 samples).

Second, the molecular descriptors, n, S_CNE, ΔAOEI, PEI, APEI, and G_N, are calculated with the methods described in Section 2.1.1.

And then the boiling points of primary amines are predicted by using eq 1 in Table 2, as shown in eq 20. The predicted results are listed in Table S2 in the Supporting Information.

20

For the 141 primary amines, only 36 samples have experimental T_b values, the T_b values of the other 105 samples have not been experimentally determined yet. As for the 36 primary amines with experimental values, the average absolute error between the predicted and experimental values is 3.47 K, indicating that the predicted values are reasonable. To further test the reliability of the predicted T_b values, we compare the T_b values of primary amines to that of alcohols. The molecular structure of primary amines is similar to that of aliphatic alcohols, so their boiling points have a linear relationship theoretically. Figure 6 is the plot of experimental boiling points of 32 primary amines versus that of 32 aliphatic alcohols (carbon atom number range, C₄–C₂₀), indicating an excellent linear relationship.

Figure 6.

Plot of experimental boiling points T_b of 32 primary amines (RNH₂) versus that of 32 aliphatic alcohols (ROH) (carbon atom number range C₄–C₂₀).

When we plotted the predicted boiling point (T_b, pred) values of primary amines against the experimental boiling point values (T_b, exp) of aliphatic alcohols,²⁰ we still obtained a good linear relationship (as shown in Figure 7). From the slopes and intercepts of Figures 6 and 7, it can be seen that the predicted boiling point values of primary amines in this article are reliable.

Figure 7.

Plot of predicted boiling points T_b, pred of primary amines (RNH₂) versus experimental boiling points T_b,exp of aliphatic alcohols (ROH) (carbon atom number range C₄–C₂₀).

We noticed that the experimental boiling points of dioctadecanamine (C₃₆H₇₅N) and tridodecylamine (C₃₆H₇₅N) are 541.15 K (2 mmHg) and 493.15 K (0.03 mmHg) in the literature,¹² respectively, which are the boiling point values under reduced pressure. Their normal boiling points, calculated by this work, are 788.42 and 757.44 K, respectively.

Additionally, we also noticed that the liquid densities (g cm^–3, 293.15 K) of heptadecanamine (C₁₇H₃₇N) and octadecanamine (C₁₈H₃₉N), reported in the literature,¹² are 0.8510 and 0.8618, respectively. However, the calculated values in this work are 0.8154 and 0.8171, respectively. To verify the rationality of the calculated values, we plotted the experimental and calculated densities of n-alkyl primary amines against the carbon atom numbers respectively, and obtained Figure 8. It is observed, from Figure 8, that the experimental densities of n-alkyl primary amines (C₁–C₁₆) steadily increase with the increase of carbon atom number, while the densities of heptadecanamine (C₁₇) and octadecanamine (C₁₈) suddenly increase, which is not reasonable. However, the calculated densities of n-alkyl primary amines steadily increase going from carbon atom C₁ to C₁₈, showing a regular change, which is reasonable, that is, the liquid densities of heptadecanamine and octadecanamine should be 0.8154 and 0.8171, respectively. Maybe the values of 0.8510 and 0.8618 were entered incorrectly by the editor of the literature.¹²

Figure 8.

Plot of densities versus carbon atom number of n-alkyl primary amines (O represents the experimental value, and Δ represents the calculated value).

3. Conclusions

The above research results show that the various nonlinear change properties of aliphatic amines (involving primary, secondary, and tertiary amines) can be expressed by using the general NPAA eq (eq 12), while the various linear change properties of aliphatic amines (involving primary, secondary, and tertiary amines) can be expressed by using the general LPAA eq (eq 13). Both NPAA and LPAA equations all have the same parameters, n, S_CNE, ΔAOEI, PEI, APEI, and G_N, which can be directly calculated with molecular structures. The parameters n and S_CNE express the influence of carbon atoms in molecules on the property of aliphatic amines, ΔAOEI expresses the influence of molecular skeleton differences on their property, PEI and APEI express the influence of intramolecular charge-induced dipole differences on their property, and G_N expresses the influence of nitrogen atom in molecules on their property. Furthermore, employing the six parameters n, S_CNE, ΔAOEI, PEI, APEI, and G_N, a quantitative correlation equation can be established between any two properties of aliphatic amines.

This work established a general equation to express changes in the physicochemical properties of aliphatic amines and provided a simple and convenient prediction method for the properties of aliphatic amines. Maybe this method can provide a reference for the establishment of property estimation for other substituted alkanes.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c06992.

• Physicochemical properties of aliphatic amines and the predicted values of aliphatic amines (Tables S1 and S2) (PDF)

The authors declare no competing financial interest.