Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Dec 7;5(12):6603–6610. doi: 10.1021/acsaelm.3c01141

Charge Stability and Charge-State-Based Spin Readout of Shallow Nitrogen-Vacancy Centers in Diamond

Rakshyakar Giri †,*, Rasmus Ho̷y Jensen †, Deepak Khurana †, Juanita Bocquel †, Ilya P Radko †, Johannes Lang ‡, Christian Osterkamp ‡, Fedor Jelezko ‡, Kirstine Berg-So̷rensen §, Ulrik L Andersen †, Alexander Huck †,*
PMCID: PMC10753810  PMID: 38162528

Abstract

graphic file with name el3c01141_0006.jpg

Spin-based applications of the negatively charged nitrogen-vacancy (NV) center in diamonds require an efficient spin readout. One approach is the spin-to-charge conversion (SCC), relying on mapping the spin states onto the neutral (NV0) and negative (NV–) charge states followed by a subsequent charge readout. With high charge-state stability, SCC enables extended measurement times, increasing precision and minimizing noise in the readout compared to the commonly used fluorescence detection. Nanoscale sensing applications, however, require shallow NV centers within a few nanometers distance from the surface where surface related effects might degrade the NV charge state. In this article, we investigate the charge state initialization and stability of single NV centers implanted ≈5 nm below the surface of a flat diamond plate. We demonstrate the SCC protocol on four shallow NV centers suitable for nanoscale sensing, obtaining a reduced readout noise of 5–6 times the spin-projection noise limit. We investigate the general applicability of the SCC for shallow NV centers and observe a correlation between the NV charge-state stability and readout noise. Coating the diamond with glycerol improves both the charge initialization and stability. Our results reveal the influence of the surface-related charge environment on the NV charge properties and motivate further investigations to functionalize the diamond surface with glycerol or other materials for charge-state stabilization and efficient spin-state readout of shallow NV centers suitable for nanoscale sensing.

Keywords: shallow NV centers, spin-to-charge conversion, charge-state dynamics, glycerol coating, surface effects

Introduction

The negatively charged nitrogen-vacancy (NV–) center in diamond has excellent spin properties at room temperature with a long lifetime and coherence, enabling a broad range of applications. These include the sensing of magnetic and electric fields with high sensitivity and nanometer-scale spatial resolution.1−3 Central to any NV– center sensing task is the ability to initialize and read out the spin state optically. The most common approach to read out the spin state is via the fluorescence rate, enabled by spin-dependent intersystem crossing from the triplet excited to a singlet state.4 The intersystem crossing mechanism sets a lower limit on the spin readout duration to around 300 ns as determined by the singlet-state lifetime5 that together with low photon counts in the order of 0.1 per readout hinders the efficient measurement of the spin state. In the context of sensing, it is thus required to repeat the scheme multiple times in order to build up sufficient photon statistics to determine the spin state.5,6 Nanopillars7 or solid immersion lenses8 might be used to increase the photon collection efficiency and improve the readout signal-to-noise ratio (SNR), but yet the attainable photon count rates are not sufficient to measure the spin state in a single shot.

In addition to photoelectrical readout,9 another approach for spin readout involves the charge degree of freedom of the NV center that in addition to NV– may also exist in the neutral charge state NV0. Deep in the bulk, the charge state ratio between the two is highly stable in the dark or under weak optical excitation.10−12 With zero-phonon lines at 575 and 637 nm for NV0 and NV–, respectively, and therefore different absorption spectra, the charge states are distinguishable via selective illumination that excites NV– but not NV0.13 In the spin-to-charge conversion (SCC) protocol,14 population of the ms = 0 spin state is transferred to NV0 via a photoionization process,13,15 while the population of the ms = ±1 spin state remains in the NV– charge state. The subsequent charge-state readout may be long and efficient provided sufficient photon counts and charge-state stability are attained within the readout duration. Using this approach, >1 photon per readout may be detected when the system is in ms = ±1, significantly increasing SNR per readout at the cost of significantly increased integration time as compared to standard fluorescence detection.

Applying the SCC protocol to an NV center in a diamond nanobeam with significantly improved photon collection efficiency compared to bulk diamond, Shields et al.14 demonstrated an SNR ≈ 0.55 per readout corresponding to a noise factor of ≈3σp, where σp is the spin-projection noise limit.16 More recently, the SCC readout has been demonstrated for NV center ensembles in nanodiamonds17 and bulk diamonds,18 and for single NV centers deep in the bulk,19 and applied in covariance magnetometry.20 Nanoscale sensing tasks including nuclear magnetic resonance (NMR)21,22 or sensing of free radicals,23 however, require single NV centers within a few nanometers from the diamond surface where the sensing signal is sufficiently strong.24 In the vicinity of the surface, effects including upward energy band bending25 and electron tunneling to nearby surface traps11 are known to cause ionization of NV– to NV0 at rates on the order of the inverse readout time or even faster. Although it has been demonstrated that SCC can work for NV centers implanted within a few nanometers from the surface in diamond nanopillars,26 the general applicability of the SCC protocol to near-surface NV centers as well as the possible detrimental impact of surface-related effects remains unexplored as of yet.

In this article, we explore the charge-state stability and the SCC protocol on single NV centers implanted ≈5 nm below the surface of a flat diamond plate. The implanted side of the diamond is accessible to apply a solution bath or nano-objects, an experimental configuration relevant for nanoscale sensing and spin mechanical coupling. We use a simplified experimental approach with only two lasers: one at 532 nm for NV charge and spin initialization and another at 594 nm for spin-state selective ionization and charge-state readout. From the detailed characterization of 33 single NV centers, we observe a strong variability of the probability to initialize into NV–. We present data of four NV centers labeled NVA–NVD that are representative of the distribution. We show that after coating the diamond with deuterated glycerol, the initialization probability into NV– increases while simultaneously the ionization rate from NV– to NV0 decreases as compared to the pristine surface. Furthermore, we demonstrate the general applicability of the SCC protocol on four near-surface NV centers. Our investigations indicate the importance of the local charge environment for the NV charge-state stability as well as the overall performance of the SCC protocol. We obtain a noise level as low as ≈5σp corresponding to a single-shot SNR ≈ 0.3, a result comparable to that obtained with NV centers in the bulk or nanostructures with higher attainable photon count rates.

Experimental Methods

All measurements reported in this article were conducted on a 50 μm thin electronic-grade diamond plate (Element Six) with (100) surface orientation. The sample was overgrown with a 100 nm thick and 12C-enriched (<0.05% 13C) layer of diamond using chemical vapor deposition. NV centers were created via implantation of 15N+ ions with an energy of 2.5 keV and a dose of 5 × 108 cm–2 (process pressure <1 × 10–7 mbar).27 Subsequent annealing in an ultrahigh vacuum at 1000 °C for 3 h heals radiation damage due to the ion bombardment, mobilizes vacancies, and, through capture of an implanted nitrogen, yields a Gaussian-like distribution of single NV centers with a mean depth ≈5 nm below the surface. The diamond was cleaned in a boiling acid mixture consisting in equal parts of nitric, perchloric, and sulfuric acid (triacid cleaning) to remove surface contaminants28 and creating a hydrophilic surface with partial oxygen termination.29,30 With these near-surface NV centers and using a Hahn-echo sequence, we measured T2 coherence times in the range from 3 to 15 μs, in good agreement with values obtained for a different sample fabricated using the same equipment and process parameters.31

We used a home-built scanning confocal microscope setup with an NA = 1.4 immersion-oil objective to investigate the NV charge state and implement the SCC protocol. The power of each laser, 532 and 594 nm, was controlled using acousto-optic modulators in a double-pass configuration to generate pulses for charge and spin initialization, shelving, ionization, and readout. After long-pass filtering with a cut-on at 650 nm, the NV fluorescence signal was detected with a single-photon-sensitive avalanche photodiode with dark counts <200 per second. Together with the selective excitation at 594 nm, this configuration ensures, to a very high degree, that the signal stems from the NV– emission. With a motorized 3-axis translation stage, we controlled the position of a permanent magnet to produce a bias magnetic field of ≈7 mT along one of the four [111] crystal axes that all NV centers investigated here are aligned along. The diamond plate was horizontally mounted on a 170 μm thick cover glass with the NV layer on the top side, exposed to either air or solution and suitable for nanoscale sensing (Figure 1a). The excitation lasers pass from below through the cover glass and the diamond, and the fluorescence is collected from the same side (Supporting Information). Measurements on all the NV centers with a pristine surface and with a glycerol-coated surface were performed without removing the diamond sample from the setup. To passivate the diamond surface, we carefully put a small droplet of deuterated glycerol (glycerol-d8 from Sigma-Aldrich) with a micropipette at the amount sufficient to cover the investigated region of diamond. No special procedure has been used to ensure spreading of glycerol through the surface, so the thickness of the layer was given by the glycerol surface tension and was of the order of 100 μm.

Figure 1.

Figure 1

Open in a new tab

Surface-related effects and charge-state stability of shallow NV centers. (a) Illustration of ≈5 nm shallow NV centers and their interaction with the local charge environment with glycerol passivating surface charges and traps. (b) Pulse sequence to measure the NV– charge-initialization probability P0(NV–), applying 532 nm initialization and 594 nm readout pulses. (c) Illustration of the energy levels of NV0 and NV– together with allowed transition rates. The 594 nm laser ideally excites only NV–. For strong excitation, it can ionize (Γ–0) NV– to NV0 and induce recombination (Γ0–) from NV0 to NV–. The charge-state switching is suppressed for weak excitation, and the NV0 center remains dark under 594 nm excitation. (d) Fluorescence evolution of NVA during the readout pulse, showing a reduced relaxation rate after adding glycerol (Γr,G) as compared to the relaxation with the pristine surface (Γr,P). (e, f) Photon-number distribution P(n) of NVA with the pristine (e) and the glycerol-coated (f) surface. The gray and red-shaded areas illustrate the respective contributions of NV0 and NV–.

Results

Charge-State Initialization and Stability

We begin our investigations by characterizing the charge states of 33 near-surface NV centers by applying the protocol illustrated in Figure 1b. The 2 μs short 532 nm pulse (power ≈ 400 μW; all laser powers specified herein are measured at the entrance to the objective) has the purpose to initialize the NV center into NV–, followed by a weak 10 ms long 594 nm pulse (power ≈ 3.5 μW) to selectively read out the charge state. The 594 nm readout laser mainly excites NV– as illustrated on the energy level diagrams in Figure 1c, which leads to a charge-state-dependent fluorescence intensity. During the readout, the NV center can ionize from NV– to NV0 and recombine from NV0 to NV– with the rates Γ–0 and Γ0–, respectively. The charge-state switching rates increase with increasing optical excitation power. The stability of the normalized fluorescence intensity during a readout pulse for NVA is shown in Figure 1d. The photon-number distribution P(n) obtained from NVA with the pristine diamond surface is plotted in Figure 1e, where the gray- and red-shaded areas illustrate the contributions of NV0 and NV–, respectively. We fitted the temporal evolution of P(n) with a model11,14,32 (100 μs resolution) to extract the photon detection rates γ0 and γ– from NV0 and NV–, respectively, as well as Γ–0, Γ0–, and the NV– population P0(NV–) at the start of the readout pulse. With the pristine diamond surface, we obtain P0(NV–) = 0.56 and Γ–0 = 101 Hz, while Γ0– ≈ 6 Hz (note that due to a limited measurement time and a relatively high stability of the NV0 charge state, it is not possible to quantify Γ0– with high accuracy within the measurement time). Afterward, we coated the diamond surface with glycerol, resulting in a significant change of P(n) as presented in Figure 1f. The value of P0(NV–) substantially increases to 0.75 and is now comparable to results from NV centers deeper in the bulk.13,33 Furthermore, Γ–0 substantially decreases to 9 Hz, demonstrating improved charge-state stability during the readout after coating the diamond surface with glycerol.

The increased charge-state stability of NVA after application of glycerol is also directly seen in the average fluorescence during the readout pulse as shown in Figure 1d. With the pristine surface, the fluorescence level reduces with a rate Γr,P ≈ Γ–0 + Γ0– ≈ 107 Hz, while after application of glycerol the reduction is lower with a rate Γr,G ≈ 25 Hz.

In Figure 2a, we plot the NV– initialization probability P0(NV–) versus the ionization rate Γ–0 for 33 single NV centers both with the pristine diamond surface and after the application of glycerol. The histogram for P0(NV–) is shown in Figure 2b. We observe an anticorrelation between P0(NV–) and Γ–0 irrespective of the surface condition. Upon the application of glycerol, P0(NV–) increases for all NV centers (see Figure 2c for NVA–NVD) and correspondingly Γ–0 reduces (see Figure 2d for NVA–NVD).

Figure 2.

Figure 2

Open in a new tab

(a) NV– charge initialization probability P0(NV–) versus ionization rate Γ–0 for 33 NV centers with the pristine and the glycerol-coated surfaces. (b) Histogram of P0(NV–). (c, d) Comparison of P0(NV–) and Γ–0 for pristine (P) and glycerol-coated (G) surface for emitters NVA–NVD.

Our results show that the application of glycerol generally increases the charge-initialization probability of the ≈5 nm shallow NV centers into the NV– state with a maximum probability ≈75% comparable to that of NV centers in the bulk. However, for some NV centers, including NVB, the charge-initialization probability (ionization rate) remains low (high) and only marginally improves compared to the pristine surface.

SCC Protocol

In the next step, we implement the SCC protocol (Figure 3a) on four NV centers (NVA–NVD) that have different P0(NV–), and we benchmark the performance of SCC by estimating the spin-readout noise σR.14,16 Besides initialization into NV–, the initial 2 μs, 532 nm pulse (power ≈ 400 μW) also prepares the spin state into ms = 0, which subsequently can be transferred to ms = −1 with a π pulse. The following short 594 nm pulse (power ≈ 4.4 mW) then likely shelves the NV– center into the singlet state when in ms = −1 or leaves the population in the triplet state with a higher probability when in ms = 0. Applied immediately after the shelving pulse, the triplet state of the NV center is ionized with a 29 mW (maximum available) and a 594 nm pulse of duration tion, thus effectively mapping the NV center spin states onto the distribution of charge states. Finally, the charge state is read out using a weak 15 ms long (power 3.5 μW) 594 nm pulse. The optimal duration and power of each pulse have been determined separately (see the Supporting Information). As an example, in Figure 3b we plot the integrated photon counts αms acquired during the first 2 ms readout window for the initial spin states ms = 0 and ms = −1 as a function of the ionization-pulse duration tion. The SCC readout contrast C = 1 – α0/α–1 is plotted in Figure 3c. The maximum contrast Cmax ≈ 32% is found with an optimal tion ≈ 50 ns. Similar to the mechanism of standard photoluminescence-based (PL) readout (Supporting Information), the achievable contrast in SCC is limited by the spin-dependent intersystem crossing rates (Supporting Information). With further increasing tion, the spin contrast decreases due to the relaxation of the singlet-state population back to the ground state and vanishes at tion ≈ 300 ns, the approximate singlet-state lifetime. The spin-readout contrast with the glycerol-coated surface is similar to the value obtained with the pristine surface condition.

Figure 3.

Figure 3

Open in a new tab

SCC protocol and effects of surface condition. (a) Illustration of the pulse sequence to implement the SCC protocol, where the height of the orange (594 nm) pulses indicates the strength. (b) Photon counts integrated in 2 ms of the readout pulse for initial ms = 0 and ms = −1 spin states. (c) Contrast as a function of ionization-pulse duration tion. (d, e) Photon number distributions P(n) of NVA for the initial spin states ms = 0 and ms = −1 with the pristine (d) and the glycerol-coated surface (e). The optimal threshold photon number, nth, for the distributions is indicated.

The ms-dependent photon-number distributions for NVA are plotted in Figure 3d,e for the pristine (d) and the glycerol-coated (e) surface, from which we extracted the respective NV– population p̃ms.11,14 While for the pristine surface, the difference p̃–1 – p̃0 ≈ 0.145, the value increases to ≈0.19 after adding glycerol, which is a direct result of the charge-state stability improved with glycerol. However, in the SCC-based spin readout, the final charge state is determined by counting photons and assigning the charge/spin states based on a threshold photon number nth.16 The precision of assigning the correct charge and thus spin state depends on the distinguishability of the photon number distributions Pms(n) for the initial spin states ms. In order to quantify the improved distinguishability of Pms(n) after coating the surface with glycerol, we performed a Kolmogorov–Smirnov test that measures the maximum difference between the ms-dependent cumulative photon distributions. The test yields values of 0.145 for the pristine surface and 0.174 for the glycerol-coated surface, an improvement of ≈20%. We note that no postselection of the data was applied to discard for example events executed in the NV0 state.19

The improvement in distinguishability arises due to better mapping of the spin-states onto the charges state. We quantify the mapping efficiency as the population transfer from the initial spin state, which is P0(NV–) assuming an ideal π pulse, to the population in the charge states p̃–,0:

graphic file with name el3c01141_m001.jpg 1

The mapping efficiencies for NVA to NVD are shown in Figure 4. For mapping ms = 0 to NV0, a modest improvement is seen when glycerol is applied (Figure 4a). The mapping efficiency for ms = −1 to NV– (Figure 4b) increases drastically when glycerol is applied to the surface and is around 50% for NVA. The difference in improving the mapping efficiency for different spin states is not obvious, and an understanding of this observation requires further investigation that involves time dynamics and transition rates between various states. One can also see from the plots in Figure 4 that for NVD, which was already stable with the pristine surface, addition of glycerol does not change much its charge-state mapping, while the efficiency for emitters with unstable charge environment benefits from surface passivation. Thus, different NV centers might experience different effects of adding glycerol coating, which is eventually determined by the overall charge environment of the center.

Figure 4.

Figure 4

Open in a new tab

Effect of diamond surface termination on the efficiency of spin-state-dependent charge state mapping. The mapping efficiency for ms = 0 to NV0 (a) and ms = −1 to NV– (b). Glycerol coating improves the spin-to-charge conversion efficiency, irrespective of the initial spin state of the NV– center.

For a set nth the spin-readout noise can be calculated via14

graphic file with name el3c01141_m002.jpg 2

where p0 and p–1 are the probabilities for the initial spin states ms = 0 and ms = −1 to measure NV– at time tR during the readout step, respectively. Extracted from the distributions Pms(n), in Figure 5a we plot σSCCR(tR) for NVA for both the pristine and the glycerol-coated surface. With increasing tR, more photons are accumulated, and the confidence for assigning the correct spin state improves. Hence, σSCCR(tR) decreases to an optimal value. For longer tR, charge-state switching occurs, thus causing uncertainty in determining the correct spin state and increasing σSCCR(tR). With the glycerol-covered surface, σSCCR(tR) is higher initially due to generally lower photon counts, and the optimal σSCCR(tR) is obtained at later times as a result of the improved charge-state stability.

Figure 5.

Figure 5

Open in a new tab

Charge-initialization probability and spin-readout noise. (a) Measured spin-readout noise σSCCR for NVA versus readout duration tR. The symbols are calculated from the measured distributions (cf. Figures 3d and 3e), and the solid lines are calculated from the extracted rates. (b) Optimal σSCCR obtained within tR < 15 ms readout time versus charge-initialization probability P0(NV–) for NVA–NVD. The green and blue symbols represent measured values with the pristine and glycerol-coated surface, respectively. The impact of glycerol coating on σSCCR is substantial for the charge-unstable NV center, NVB, while others show no improvement within tR < 15 ms as a result of lower photon counts. The optimal values of σSCCR together with the corresponding tR values obtained via simulation of the readout process for the glycerol-coated surface are summarized in Table 1.

Figure 5b illustrates the optimal σSCCR(tR) versus the charge initialization probability for NVA–NVD obtained within a maximum readout time tR = 15 ms. It is evident that the readout noise improves with increasing P0(NV–), decreasing Γ–0 (see Figure 2a) irrespective of the surface condition. The readout noise is higher for the charge-unstable NV centers (e.g., NVB), and the improvement upon application of glycerol is significant. The influence of glycerol on σSCCR is minimal for the NV centers that are charge stable already with the pristine surface (e.g., NVC and NVD). All key parameters for NVA–NVD are summarized in Table 1, for both the pristine (P) and the glycerol-covered (G) surface. In the experiments, the maximum readout duration tR was 15 ms. However, the significantly reduced Γ–0 after adding glycerol enables extended measurement times tR > 15 ms. We thus simulated the measurement process (see the Supporting Information) to extract the optimal tR and nth that minimizes σSCCR globally. It is clear that for all four NV centers and due to decreased Γ–0, glycerol allows for extended measurement times tR > 15 ms as compared to the pristine surface. The minimum readout noise we obtain is ≈5 σp at tR ≈ 12.8 ms for NVD with P0(NV–) ≈ 0.75 and the pristine surface. This result is comparable to the readout noise previously obtained with a shallow NV center in a nanopillar26 with significantly higher photon counts. We note that with the diamond sample turned over and the NV centers adjacent to the immersion oil with higher photon counts, we obtain a readout noise as low as ≈3.5σp. The relation between σR, tR, and bandwidth normalized sensitivity will be addressed in the following section.

Table 1. Summary of the Key Parameters Measured and Simulated for NVA–NVD for the Pristine (P) and the Glycerol-Coated (G) Surface Conditiona.

  P0(NV–)
 Γ–0 (Hz)
 σSCCR (σp) (measured)
 σSCCR (σp) (simulated)
 nth (measured)
 nth (simulated)
 tR (ms)(measured)
 tR (ms) (simulated)
  P G P G P G P G P G P G P G P G
NVA 0.56 0.75 101 9 6.0 5.6 6.1 4.6 7 4 6 11 10.4 14.9 8.7 55.9
NVB 0.42 0.52 157 104 10.7 8.2 10.6 4.8 3 3 3 16 4.3 14.9 3.8 138
NVC 0.60 0.66 74 16 5.8 6.1 5.8 6.2 7 5 8 6 10.9 15 12.6 21.3
NVD 0.72 0.74 23 8 5.2 5.4 5.2 4.8 8 4 7 9 12.8 15 11.2 49.4
Open in a new tab
a

The uncertainty in σR is around 0.1σp.

Discussion

Deuterated glycerol not only increases the spin coherence of near-surface NV centers as shown previously,34 but it generally improves the initialization probability P0(NV–) into the negative charge state and reduces the ionization rate Γ–0 from NV– to NV0. Our sample preparation routine with triacid cleaning only yields a partial surface termination with oxygen. Hence, the general improvement of the NV charge properties with glycerol could be assigned to the passivation of surface-related charges and traps.10,11 It is, however, also possible that glycerol lowers the Fermi level outside the diamond, reducing the effect of energy-band bending and thus improving the charge stability of NV–.25,35 Irrespective of the physical mechanism, our findings highlight the influence of the surface-related charge environment on P0(NV–) as well as Γ–0 during the readout with a weakly selective 594 nm laser.

In the following, we discuss the application of SCC in the context of a realistic sensing sequence and compare it to the standard PL readout. The flat sample geometry, although practical, in our case limits the photon counts to approximately 65K counts/s with 532 nm excitation at saturation. With PL spin readout in a 1 μs window, we thus obtain σPLR ≈ 30σp, a factor of 6 higher than the lowest σSCCR ≈ 5.2σp we obtained for NVD. Our results demonstrate that even with a pristine surface, it is feasible to locate charge-stable NV centers, implanted ≈5 nm deep, for which σSCCR,min is comparable to values previously only obtained from NV centers in nanobeams or deep inside bulk diamonds. However, the flat sample geometry as applied here and, although practical, limits the attainable photon count rate. To minimize σSCCR, the tR is thus required to be of the order of several milliseconds to collect a sufficient number of photons. These optimal times are even longer with the glycerol-coated surface, as the photon collection efficiency is further reduced. To account for the variability in the measurement overhead, we estimate the sensitivity to magnetic fields Inline graphic,14 where τ, tI, and tR are the interrogation, the initialization, and the readout times, respectively. Considering a similar initialization-pulse duration of 1 μs, and an optimal readout duration for PL (1 μs) and SCC (12 ms for NVA with the pristine surface) minimizing σR, we obtain ηSCC < ηPL for τ > 500 μs. Despite the improved charge stability, for the glycerol-covered surface the required τ would even be longer due to the further increased tR as a result of decreased photon counts compared to the pristine surface. The increased distance to the potential sensing medium due to the glycerol layer thickness currently poses an additional challenge. For relaxometry measurements that are conducted on time scales T1 ≈ 1 ms, with our system parameters, SCC thus would have an advantage compared to PL readout. The interrogation times τ > 500 μs required for SCC to be beneficial are much longer than the T2 coherence times (3–15 μs) measured for the shallow NV centers in our sample. Increasing T2 beyond 500 μs by applying higher-order dynamical-decoupling sequences,36 by coherently driving bath spins in the NV environment,37,38 or via application of a concatenated driving schemes39,40 is challenging and remains to be explored experimentally. We thus anticipate that for the implementation of T1-relaxometry sensing schemes on shallow NV centers with the pristine surface, it is advantageous to use the SCC instead of the PL readout. The minimum interrogation time beyond which SCC is beneficial can be further decreased by improving the photon collection via application of suitable photonic structures7,8 increasing the photon count rate.

The spin-to-charge readout may also be applied in the context of quantum information processing with NV centers in diamonds at room temperature. In combination with a photoelectric readout, the spin-to-charge mapping with charge state readout has the potential of NV center spin state readout with high spatial resolution.9 Here a figure of merit is the single spin readout fidelity 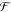Inline graphic, which should be >0.79 for single-shot readout with SNR > 1.16 In our experiment, for NVD the readout fidelity is ∼0.58 and ∼0.61 with the pristine and glycerol-coated surface, respectively.

Conclusion and Outlook

In summary, in this article we investigated the charge-state stability of single NV centers implanted with a mean depth ≈5 nm below the surface of a flat diamond sample. Applying standard processing and surface preparation by means of triacid cleaning,28 we observe a strong variation in the probability for initializing the NV centers into the negative charge state. The NV– charge-state initialization probability increases for all investigated NV centers after coating the diamond surface with glycerol and reaches up to ≈75% which is comparable to NV centers deep in the bulk. Our observations thus demonstrate that deuterated glycerol does not only enhance the coherence time of near-surface NV centers34 but also improves the initialization probability and stability of the negative-charge state NV–. While the role of surface electron traps on charge-state stability10,11,41 and their detrimental effects on spin-based measurement protocols are recognized,11,42 the exact physical mechanism of our observations is not entirely clear. We hypothesize that the observations may also be explained by a reduction of the effect of energy-band bending via a change of the local electric-field potential. Further investigations are thus required, including surface electron spectroscopy,43 electrical manipulation via application of a gate voltage,44 and variation of different oxygen and hydrogen surface terminations.25

We demonstrate the SCC protocol for shallow NV centers, obtaining a minimum readout-noise figure σSCCR in the range 5σp to 6σp, a substantial reduction compared to standard PL readout with σPLR ≈ 35σp. However, the reduction in σR is achieved at the cost of substantially increased readout times. Previously, SCC has only been achieved with NV centers located far from the diamond surface where surface-related charge instabilities are insignificant or in nanobeams with higher photon collection efficiency. For NV centers where glycerol significantly lowers the ionization rate, thus improving charge stability during readout, we observe an improvement of σSCCR as prolonged readout times are allowed. However, the low photon count rate, limited by our sample configuration, requires extended readout times with the optimum tR > 4 ms. With our configuration presented here, an improvement in terms of sensitivity is thus achieved for measurement sequences with an interrogation time τ > 500 μs, currently comprising relaxometry. The achievable interrogation times with dynamical decoupling and concatenated driving schemes remain to be explored. We expect that the optimal readout times can substantially be lowered by increasing the photon collection efficiency, reducing tR and yielding a benefit of SCC for interrogation times <500 μs.

We envision our findings will motivate further investigations on the surface functionalization and charge state dynamics of shallow NV centers and potentially the application of the SCC protocol for near-surface NV centers with improved noise figures compared to standard PL readout. Structuring the diamond with, for example, nanopillars will enhance the photon collection efficiency, thus improving the sensitivity even further for shorter interrogation times. Finally, we would like to note that despite the long readout times, SCC can be the enabling technique such as in recently demonstrated covariance magnetometry.20

Acknowledgments

We acknowledge financial support from the Novo Nordisk Foundation through the projects bioQ, biomag, and QuantBioEng, the Danish National Research Foundation (DNRF) through the center for Macroscopic Quantum States (bigQ, Grant DNRF0142), the Villum Foundation through the project bioCompass, and the EMPIR program cofinanced by the Participating States and from the European Union’s Horizon 2020 research and innovation programme via the QADeT project (Grant 20IND05).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsaelm.3c01141.

  • Details of the experimental protocols, optimization of the laser pulses for the SCC protocol, estimation of the optimal readout duration to minimize the SCC-based spin-readout noise

    (PDF)

Author Contributions

R.G. and R.H.J. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

el3c01141_si_001.pdf (3MB, pdf)

References

  1. Taylor J. M.; Cappellaro P.; Childress L.; Jiang L.; Budker D.; Hemmer P. R.; Yacoby A.; Walsworth R.; Lukin M. D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. 10.1038/nphys1075. [DOI] [Google Scholar]
  2. Balasubramanian G.; Chan I. Y.; Kolesov R.; Al-Hmoud M.; Tisler J.; Shin C.; Kim C.; Wojcik A.; Hemmer P. R.; Krueger A.; Hanke T.; Leitenstorfer A.; Bratschitsch R.; Jelezko F.; Wrachtrup J. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. 10.1038/nature07278. [DOI] [PubMed] [Google Scholar]
  3. Dolde F.; Fedder H.; Doherty M. W.; Nöbauer T.; Rempp F.; Balasubramanian G.; Wolf T.; Reinhard F.; Hollenberg L. C. L.; Jelezko F.; Wrachtrup J. Electric-field sensing using single diamond spins. Nat. Phys. 2011, 7, 459–463. 10.1038/nphys1969. [DOI] [Google Scholar]
  4. Doherty M. W.; Manson N. B.; Delaney P.; Jelezko F.; Wrachtrup J.; Hollenberg L. C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. 10.1016/j.physrep.2013.02.001. [DOI] [Google Scholar]
  5. Steiner M.; Neumann P.; Beck J.; Jelezko F.; Wrachtrup J. Universal enhancement of the optical readout fidelity of single electron spins at nitrogen-vacancy centers in diamond. Phys. Rev. B 2010, 81, 035205 10.1103/PhysRevB.81.035205. [DOI] [Google Scholar]
  6. Jiang L.; Hodges J. S.; Maze J. R.; Maurer P.; Taylor J. M.; Cory D. G.; Hemmer P. R.; Walsworth R. L.; Yacoby A.; Zibrov A. S.; Lukin M. D. Repetitive Readout of a Single Electronic Spin via Quantum Logic with Nuclear Spin Ancillae. Science 2009, 326, 267–272. 10.1126/science.1176496. [DOI] [PubMed] [Google Scholar]
  7. Hedrich N.; Rohner D.; Batzer M.; Maletinsky P.; Shields B. J. Parabolic Diamond Scanning Probes for Single-Spin Magnetic Field Imaging. Phys. Rev. Applied 2020, 14, 064007 10.1103/PhysRevApplied.14.064007. [DOI] [Google Scholar]
  8. Wildanger D.; Patton B. R.; Schill H.; Marseglia L.; Hadden J. P.; Knauer S.; Schönle A.; Rarity J. G.; O’Brien J. L.; Hell S. W.; Smith J. M. Solid Immersion Facilitates Fluorescence Microscopy with Nanometer Resolution and Sub-Angstrom Emitter Localization. Adv. Mater. 2012, 24, OP309–OP313. 10.1002/adma.201203033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Siyushev P.; Nesladek M.; Bourgeois E.; Gulka M.; Hruby J.; Yamamoto T.; Trupke M.; Teraji T.; Isoya J.; Jelezko F. Photoelectrical imaging and coherent spin-state readout of single nitrogen-vacancy centers in diamond. Science 2019, 363, 728–731. 10.1126/science.aav2789. [DOI] [PubMed] [Google Scholar]
  10. Dhomkar S.; Jayakumar H.; Zangara P. R.; Meriles C. A. Charge Dynamics in near-Surface, Variable-Density Ensembles of Nitrogen-Vacancy Centers in Diamond. Nano Lett. 2018, 18, 4046–4052. 10.1021/acs.nanolett.8b01739. [DOI] [PubMed] [Google Scholar]
  11. Bluvstein D.; Zhang Z.; Jayich A. C. B. Identifying and Mitigating Charge Instabilities in Shallow Diamond Nitrogen-Vacancy Centers. Phys. Rev. Lett. 2019, 122, 076101 10.1103/PhysRevLett.122.076101. [DOI] [PubMed] [Google Scholar]
  12. Gorrini F.; Dorigoni C.; Olivares-Postigo D.; Giri R.; Aprà P.; Picollo F.; Bifone A. Long-Lived Ensembles of Shallow NV–Centers in Flat and Nanostructured Diamonds by Photoconversion. ACS Appl. Mater. Interfaces 2021, 13, 43221–43232. 10.1021/acsami.1c09825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Aslam N.; Waldherr G.; Neumann P.; Jelezko F.; Wrachtrup J. Photo-induced ionization dynamics of the nitrogen vacancy defect in diamond investigated by single-shot charge state detection. New J. Phys. 2013, 15, 013064 10.1088/1367-2630/15/1/013064. [DOI] [Google Scholar]
  14. Shields B. J.; Unterreithmeier Q. P.; de Leon N. P.; Park H.; Lukin M. D. Efficient readout of a single spin state in diamond via spin-to-charge conversion. Phys. Rev. Lett. 2015, 114, 136402. 10.1103/PhysRevLett.114.136402. [DOI] [PubMed] [Google Scholar]
  15. Manson N.; Harrison J. Photo-ionization of the nitrogen-vacancy center in diamond. Diamond Relat. Mater. 2005, 14, 1705–1710. 10.1016/j.diamond.2005.06.027. [DOI] [Google Scholar]
  16. Hopper D. A.; Shulevitz H. J.; Bassett L. C. Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond. Micromachines (Basel) 2018, 9, 437. 10.3390/mi9090437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hopper D. A.; Grote R. R.; Parks S. M.; Bassett L. C. Amplified Sensitivity of Nitrogen-Vacancy Spins in Nanodiamonds Using All-Optical Charge Readout. ACS Nano 2018, 12, 4678. 10.1021/acsnano.8b01265. [DOI] [PubMed] [Google Scholar]
  18. Jayakumar H.; Dhomkar S.; Henshaw J.; Meriles C. A. Spin readout via spin-to-charge conversion in bulk diamond nitrogen-vacancy ensembles. Appl. Phys. Lett. 2018, 113, 122404. 10.1063/1.5040261. [DOI] [Google Scholar]
  19. Jaskula J. C.; Shields B. J.; Bauch E.; Lukin M. D.; Trifonov A. S.; Walsworth R. L. Improved Quantum Sensing with a Single Solid-State Spin via Spin-to-Charge Conversion. Physical Review Applied 2019, 11, 064003 10.1103/PhysRevApplied.11.064003. [DOI] [Google Scholar]
  20. Rovny J.; Yuan Z.; Fitzpatrick M.; Abdalla A. I.; Futamura L.; Fox C.; Cambria M. C.; Kolkowitz S.; de Leon N. P. Nanoscale covariance magnetometry with diamond quantum sensors. Science 2022, 378, 1301–1305. 10.1126/science.ade9858. [DOI] [PubMed] [Google Scholar]
  21. Mamin H. J.; Kim M.; Sherwood M. H.; Rettner C. T.; Ohno K.; Awschalom D. D.; Rugar D. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 2013, 339, 557–60. 10.1126/science.1231540. [DOI] [PubMed] [Google Scholar]
  22. Staudacher T.; Shi F.; Pezzagna S.; Meijer J.; Du J.; Meriles C. A.; Reinhard F.; Wrachtrup J. Nuclear Magnetic Resonance Spectroscopy on a (5-Nanometer)3 Sample Volume. Science 2013, 339, 561–563. 10.1126/science.1231675. [DOI] [PubMed] [Google Scholar]
  23. Perona Martinez F.; Nusantara A. C.; Chipaux M.; Padamati S. K.; Schirhagl R. Nanodiamond Relaxometry-Based Detection of Free-Radical Species When Produced in Chemical Reactions in Biologically Relevant Conditions. ACS Sens. 2020, 5, 3862–3869. 10.1021/acssensors.0c01037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Muller C.; Kong X.; Cai J. M.; Melentijevic K.; Stacey A.; Markham M.; Twitchen D.; Isoya J.; Pezzagna S.; Meijer J.; Du J. F.; Plenio M. B.; Naydenov B.; McGuinness L. P.; Jelezko F. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 2014, 5, 4703. 10.1038/ncomms5703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hauf M. V.; Grotz B.; Naydenov B.; Dankerl M.; Pezzagna S.; Meijer J.; Jelezko F.; Wrachtrup J.; Stutzmann M.; Reinhard F.; Garrido J. A. Chemical control of the charge state of nitrogen-vacancy centers in diamond. Phys. Rev. B 2011, 83, 081304 10.1103/PhysRevB.83.081304. [DOI] [Google Scholar]
  26. Ariyaratne A.; Bluvstein D.; Myers B. A.; Jayich A. C. B. Nanoscale electrical conductivity imaging using a nitrogen-vacancy center in diamond. Nat. Commun. 2018, 9, 2406. 10.1038/s41467-018-04798-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lang J.; Häußler S.; Fuhrmann J.; Waltrich R.; Laddha S.; Scharpf J.; Kubanek A.; Naydenov B.; Jelezko F. Long optical coherence times of shallow-implanted, negatively charged silicon vacancy centers in diamond. Appl. Phys. Lett. 2020, 116, 064001 10.1063/1.5143014. [DOI] [Google Scholar]
  28. Brown K. J.; Chartier E.; Sweet E. M.; Hopper D. A.; Bassett L. C. Cleaning diamond surfaces using boiling acid treatment in a standard laboratory chemical hood. Journal of Chemical Health & Safety 2019, 26, 40–44. 10.1016/j.jchas.2019.06.001. [DOI] [Google Scholar]
  29. Salvadori M.; Araújo W.; Teixeira F.; Cattani M.; Pasquarelli A.; Oks E.; Brown I. Termination of diamond surfaces with hydrogen, oxygen and fluorine using a small, simple plasma gun. Diamond Relat. Mater. 2010, 19, 324–328. 10.1016/j.diamond.2010.01.002. [DOI] [Google Scholar]
  30. Cui S.; Hu E. L. Increased negatively charged nitrogen-vacancy centers in fluorinated diamond. Appl. Phys. Lett. 2013, 103, 051603 10.1063/1.4817651. [DOI] [Google Scholar]
  31. Findler C.; Lang J.; Osterkamp C.; Nesládek M.; Jelezko F. Indirect overgrowth as a synthesis route for superior diamond nano sensors. Sci. Rep. 2020, 10, 22404. 10.1038/s41598-020-79943-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hacquebard L.; Childress L. Charge-state dynamics during excitation and depletion of the nitrogen-vacancy center in diamond. Phys. Rev. A 2018, 97, 063408 10.1103/PhysRevA.97.063408. [DOI] [Google Scholar]
  33. Waldherr G.; Beck J.; Steiner M.; Neumann P.; Gali A.; Frauenheim T.; Jelezko F.; Wrachtrup J. Dark States of Single Nitrogen-Vacancy Centers in Diamond Unraveled by Single Shot NMR. Phys. Rev. Lett. 2011, 106, 157601. 10.1103/PhysRevLett.106.157601. [DOI] [PubMed] [Google Scholar]
  34. Kim M.; Mamin H. J.; Sherwood M. H.; Ohno K.; Awschalom D. D.; Rugar D. Decoherence of Near-Surface Nitrogen-Vacancy Centers Due to Electric Field Noise. Phys. Rev. Lett. 2015, 115, 087602 10.1103/PhysRevLett.115.087602. [DOI] [PubMed] [Google Scholar]
  35. Karaveli S.; Gaathon O.; Wolcott A.; Sakakibara R.; Shemesh O. A.; Peterka D. S.; Boyden E. S.; Owen J. S.; Yuste R.; Englund D. Modulation of nitrogen vacancy charge state and fluorescence in nanodiamonds using electrochemical potential. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 3938–3943. 10.1073/pnas.1504451113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Viola L.; Knill E.; Lloyd S. Dynamical Decoupling of Open Quantum Systems. Phys. Rev. Lett. 1999, 82, 2417–2421. 10.1103/PhysRevLett.82.2417. [DOI] [Google Scholar]
  37. Bluvstein D.; Zhang Z.; McLellan C. A.; Williams N. R.; Jayich A. C. B. Extending the Quantum Coherence of a Near-Surface Qubit by Coherently Driving the Paramagnetic Surface Environment. Phys. Rev. Lett. 2019, 123, 146804. 10.1103/PhysRevLett.123.146804. [DOI] [PubMed] [Google Scholar]
  38. Bauch E.; Hart C. A.; Schloss J. M.; Turner M. J.; Barry J. F.; Kehayias P.; Singh S.; Walsworth R. L. Ultralong Dephasing Times in Solid-State Spin Ensembles via Quantum Control. Phys. Rev. X 2018, 8, 031025 10.1103/PhysRevX.8.031025. [DOI] [Google Scholar]
  39. Cai J.-M.; Naydenov B.; Pfeiffer R.; McGuinness L. P.; Jahnke K. D.; Jelezko F.; Plenio M. B.; Retzker A. Robust dynamical decoupling with concatenated continuous driving. New J. Phys. 2012, 14, 113023. 10.1088/1367-2630/14/11/113023. [DOI] [Google Scholar]
  40. Stark A.; Aharon N.; Unden T.; Louzon D.; Huck A.; Retzker A.; Andersen U. L.; Jelezko F. Narrow-bandwidth sensing of high-frequency fields with continuous dynamical decoupling. Nat. Commun. 2017, 8, 1105. 10.1038/s41467-017-01159-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Stacey A.; Dontschuk N.; Chou J.-P.; Broadway D. A.; Schenk A. K.; Sear M. J.; Tetienne J.-P.; Hoffman A.; Prawer S.; Pakes C. I.; Tadich A.; de Leon N. P.; Gali A.; Hollenberg L. C. L. Evidence for Primal sp2 Defects at the Diamond Surface: Candidates for Electron Trapping and Noise Sources. Advanced Materials Interfaces 2019, 6, 1801449. 10.1002/admi.201801449. [DOI] [Google Scholar]
  42. Giri R.; Gorrini F.; Dorigoni C.; Avalos C. E.; Cazzanelli M.; Tambalo S.; Bifone A. Coupled charge and spin dynamics in high-density ensembles of nitrogen-vacancy centers in diamond. Phys. Rev. B 2018, 98, 045401 10.1103/PhysRevB.98.045401. [DOI] [Google Scholar]
  43. Sangtawesin S.; et al. Origins of Diamond Surface Noise Probed by Correlating Single-Spin Measurements with Surface Spectroscopy. Phys. Rev. X 2019, 9, 031052 10.1103/PhysRevX.9.031052. [DOI] [Google Scholar]
  44. Grotz B.; Hauf M. V.; Dankerl M.; Naydenov B.; Pezzagna S.; Meijer J.; Jelezko F.; Wrachtrup J.; Stutzmann M.; Reinhard F.; Garrido J. A. Charge state manipulation of qubits in diamond. Nat. Commun. 2012, 3, 729. 10.1038/ncomms1729. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

el3c01141_si_001.pdf (3MB, pdf)

Articles from ACS Applied Electronic Materials are provided here courtesy of American Chemical Society

RESOURCES