Design, proof-of-concept of single robotic hair transplant mechanisms for both harvest and implant of hair grafts

Abstract

The design and development of a prototype for a singular robotic hair transplant system capable of harvesting and implanting hair grafts were executed in this study. To establish a proof-of-concept for hair transplant procedures involving harvesting and implantation, a test system using a spherical phantom of the scalp was selected. The developed prototype of the robotic hair transplant system demonstrates the potential to reduce the duration that grafts remain without a blood supply, thereby minimizing hair graft damage. Additionally, the overall operation time for follicular unit extraction is comparatively shorter than that of conventional systems. Results from the robot vision tests indicate an 89.6% accuracy for hair graft detection with a 4 mm hair length phantom and 97.4% for a 2 mm hair length phantom. In the robot position control test, the root mean square error was found to be 1.268°, with a standard error of the mean of 0.203°. These outcomes suggest that the proposed system performs effectively under the conditions of a spherical phantom with a 2 mm hair length and a 5 mm distance between harvests.

Graphical Abstract

Single Robotic Hair Transplant Mechanisms for Both Harvest and Implant of Hair Grafts.

1. Introduction

In the medical and cosmetic industries, hair restoration has experienced significant growth over time, substantially impacting hair loss and baldness in recent years [1], [2]. Hair loss and baldness pose significant challenges for both males and females, particularly as they reach adulthood. These issues can be attributed to various factors, including hormones and genetics [3], [4]. Many individuals express negative sentiments about hair loss, using terms such as feeling less attractive, self-conscious, older, and less confident [5], [6]. Consequently, millions of individuals seek optimal treatments, aiming for the most natural look possible.

Currently, a variety of treatments for hair loss exist, ranging from surgical procedures and medications to camouflage agents like creams or lotions, shampoos, hair care products, nutrition, vitamins, and even unproven treatments and scams on the market [7], [8], [9], [10], [11]. With these technological advances, researchers and developers have introduced innovative ideas for new treatments to address hair loss and baldness issues. Among these options, hair transplantation emerges as the best choice for many patients [12], [13]. Hair transplantation involves two main techniques based on the characteristics of harvesting hair follicular units. The first conventional procedure employs strip harvesting or extraction, using a scalpel to excise a strip from the donor area, typically located at the occipital and parietal sites of the scalp [14], [15], [16]. This results in a scar in the lines at the donor spot. Another method is follicular unit extraction (FUE) or Follicular Unit Excision [17], [18]. This slightly invasive surgical treatment leaves scars as dotted hypopigmented macules. The fundamental concept of FUE techniques involves detecting a follicular unit at the donor zone and extracting it using a punch device with a diameter ranging from 0.8 to 1.5 mm [19]. Moreover, the FUE method has gained popularity because its follicular unit transplantation over the recipient range appears more natural when compared to the first method. Additionally, the FUE method offers a shorter recovery time after the operation.

Evidently, the fashionable technique for hair restoration in the industrial sector is the FUE method, owing to the advantages. Therefore, it is not surprising that most patients prefer the FUE to strip procedures. In 2009, the FDA approved NeoGraft Solutions, Inc., Texas, USA, as the first robotic surgical device for hair restoration with the FUE procedure [20]. The ARTAS System of Restoration Robotics, Inc., California, USA, was approved in 2011 for harvesting follicular units (FUs) from the scalp of black or brown straight haired-men with androgenetic alopecia (male pattern hair loss) [21], [22], [23]. ARTAS System uses the FUE technique to conduct the procedure via a computer-assisted, physician-controlled robotic system to harvest FUs directly from the scalp [24], [25], [26], [27]. Owing to the demand and trend of hair restoration today, hair transplantation technology is a crucial opportunity to regrow healthy hair to society worldwide.

Performing FUE surgery presents difficulties and places a significant mental burden on the surgeon. The duration of the surgery varies between 3 and 5 and 9–10 h. Additionally, operations requiring substantially longer operating hours, including non-shaven FUE and long hair FUE, are being executed, as are mega sessions with more than 3000–4000 grafts [28], [29], [30]. Lower graft quality and higher follicular damage may result from lengthy surgical procedures [31]. Therefore, it is crucial to enhance ergonomics and shorten operating times for patients, physicians, and supporting staff [32], [33]. Moreover, this procedure requires highly skilled surgeons. Despite the high impact of the FUE procedures after hair transplantation, there are significant problems during the period between the harvest and implantation phases. Between times, the grafts are stored in media such as unbuffered normal saline without blood supply and out of the body for several hours to be trimmed and selected before implantation. This causes follicular unit (FUs) cell damage, such as ischemia, reperfusion injury, and lack of subsistence nutrients [34]. Moreover, oxygen deficiency in cells from the blood supply changes cellular respiration from aerobic respiration to anaerobic respiration. Reperfusion injury occurs when the FUs are implanted in the recipient area. Afterwards, free radicals or reactive oxygen species (ROS) are increased through the respiratory chain that damaging the transplanted grafts.

Additionally, there are several technical limitations associated with the use of commercially available robotic devices for hair transplantation. These limitations include high initial and maintenance costs, requirement for skilled human operators, potentially slower procedure times, challenges in graft selection, limitations in patient suitability, potential difficulties in efficient hair follicle harvesting, limited customization options, maintenance and downtime requirements, spatial constraints, and potential concerns related to the patient experience [35], [36], [37], [38]. It's crucial to note that technological advancements often address some of these limitations, and clinics and surgeons may have developed strategies to overcome these challenges through experience and innovation. Therefore, the purpose of this study is to reduce the total operation time and the time that grafts stay without blood supply, which causes to FUs damaging. In order to reach this goal, a prototype of robotic hair transplant system with the mechanisms in both harvest and implant, which is the prime limitation of recent commercial robots, has been designed.

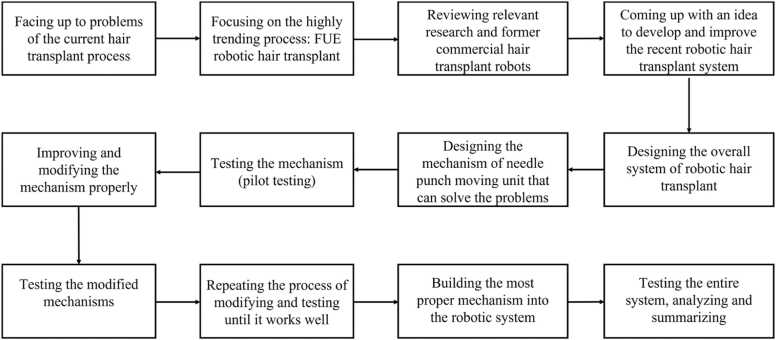
The step-by-step process to get back the complete system of robotic hair transplantation, which includes harvest and implant mechanisms within the same system is shown in Fig. 1.

Fig. 1.

Step-by-step process of robotic hair transplantation.

2. Materials and methods

2.1. Follicular unit excision (FUE) procedures

In the manual FUE technique, a doctor uses a manual punch handle with an FUE needle to perform this step by himself. However, many types of needles can support this step and help the doctor perform it more easily [22], [23], [39]. The motorized FUE technique uses the concept of oscillating the needle to facilitate graft extraction. This device has speed control of rotation and oscillation and degree control of oscillation. In robot-assisted FUE, its punch mechanism has double needles to harvest grafts [16], [23], [40]. The outer needle was blunted, whereas the inner needle was multipronged [41]. Graft extraction is normally performed using forceps along with manual FUE and robot-assisted FUE, such as ARTAS. Another way is using suction such as NeoGraft [20], [42]. After each hair graft was extracted, it was placed in a collecting medium that was a non-cytotoxic solution, that is normal saline solution [43]. The implant process includes two steps: the harvest process, namely manual punching by a hollow needle or implanter, and performing by a robot. Each graft was implanted into a recipient hole using an implanter. However, a graft must be inserted at the tip of the implanter individually before implanting each graft. In this process, a doctor usually has several assistants to help him insert each single graft into each implanter to reduce the process time.

In this study, a simplified model is employed as an initial proof of concept to establish the fundamental principles and feasibility of the proposed system. This simplified model allowed us to isolate and investigate key variables in a controlled environment before transitioning to more complex and realistic scenarios in future research. While the real human scalp exhibits greater geometric variability and three-dimensional intricacies during hair harvesting and implantation, the simplified model serves as a valuable starting point for conceptual development and proof-of-concept validation.

2.2. Design approach

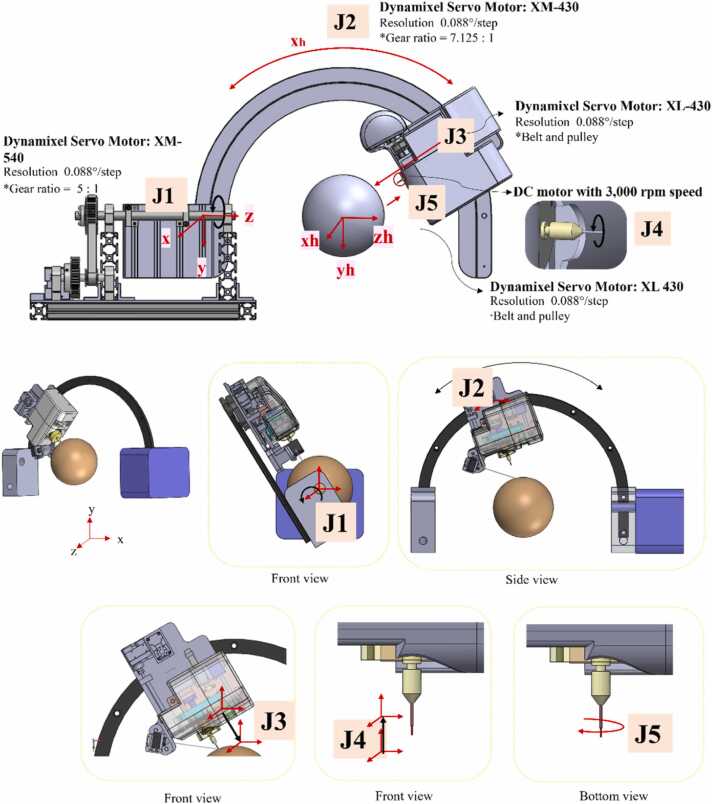
After understanding the problem of current hair transplant methods, the idea of developing a robotic hair transplant system that can solve the hair fall issue is proposed. The conceptual design of the entire system and some mechanical parts of the system are shown in Fig. 2.

Fig. 2.

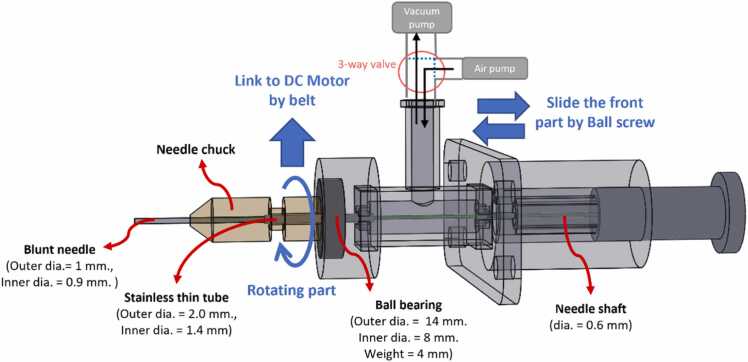
Overview of the developed robotic hair transplant system. (J1) First joint rotates about z-axis of machine frame (J2) second joint rotate about x-axis of spherical head frame, (J3) third joint penetrate skin using belt and pulley, (J4) forth joint for rotating needle tip, (J5) fifth joint for double step punching in implant phase.

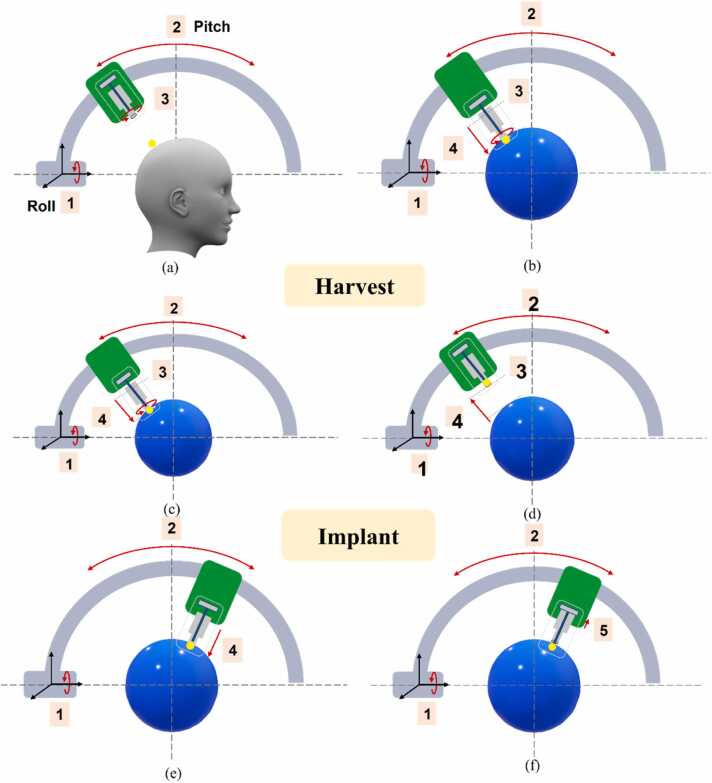
To accomplish this objective, the design consists of five joints in the system. The first joint (J1) rotated about the z-axis of the machine frame. In the spherical head frame, the second joint (J2) rotated about the X-axis. Both previous joints were used to adjust the position of the needle punch moving unit on the curved rail. The first process is illustrated in Fig. 3 (a). The mechanical idea for the harvest phase is to use a third joint (J3) to penetrate the target hair graft along the radius of the spherical head phantom. The fourth joint (J4) was also used in the harvest phase by rotating the needle tip while simultaneously penetrating the target. This phase is illustrated in Fig. 3 (b). After harvesting the target graft, it was collected at the end of the needle tip. Then J3 would retract the needle to the home position of the needle punch moving unit in a linear motion. Fig. 3 (c) illustrates this process. To perform the next phase, the needle punch moving unit is transferred to the other side of the implant area using J2 (Fig. 3 (d)). For the implant, the needle penetrated again to implant the graft at the target point on the spherical surface by J3 (Fig. 3 (e)).

Fig. 3.

(a) Preparation process using Joint 1 and Joint 2, (b) Needle penetrates to skin at target point using Joint 3 and Joint 4, (c) Target graft was harvested in phase, (d) Transferring of needle moving unit along curved rail, (e) Implant phase using joint 3 to insert graft to skin, (f) Last step, needle retracted by Joint 5 to finish one loop.

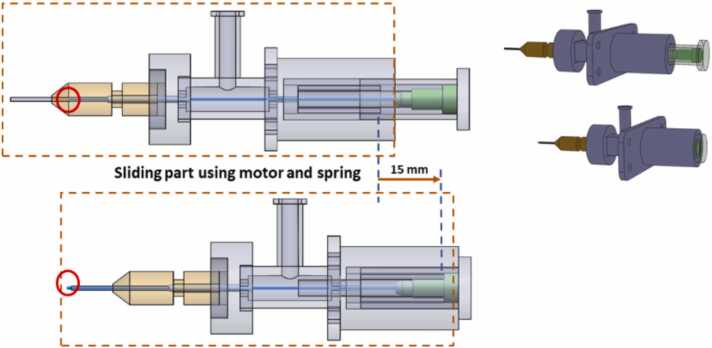
To complete the implant phase, a meticulous two-step process was employed, as illustrated in Fig. 3 (f) by (J3). The second step, crucial to the technique used in handheld implanters, involved the intricate functioning of the fifth joint (J5). In this phase, the fifth joint (J5) played a pivotal role by executing a series of precise movements that facilitated the smooth insertion of grafts into the skin. Fig. 4, Fig. 5 offer an in-depth exploration of the 3D design and internal mechanism governing both the harvest and implantation processes within a single needle. Of particular significance is the depiction of the fifth joint (J5) in action, elucidating its critical role in the retraction of the hollow needle. This movement creates the necessary space for the stylet (the implement inside the needle) to delicately push the graft into the targeted skin region.

Fig. 4.

3D design and inside mechanism of harvest and implant in single needle.

Fig. 5.

Mechanism of sliding needle shaft for implant process.

The mechanism of the sliding needle shaft during the implant process is also detailed in Fig. 4, Fig. 5, highlighting its synchronized coordination with the fifth joint (J5). This synergy is essential for the success of the autonomous implantation process, where precision is paramount. It is crucial to emphasize that this system's design represents a groundbreaking approach to FUE hair transplants, enabling automated harvesting and implantation without the need for storing hair grafts in a collecting medium. To validate the efficacy of the design, rigorous testing was conducted using medical-grade silicon to simulate a scalp phantom. The robot demonstrated its capability to autonomously harvest hair grafts from the donor site and precisely implant each graft into the designated recipient site. The intricate interplay of the fifth joint (J5) in this process underscores its significance in achieving the system's overall functionality.

The specification of motorized needle punch is with speed 3000 RPM [44], depth of needle tip insertion into the scalp phantom is about 4–5 mm [45], 10 s per hair graft in operating time (counting from harvest until implant), hemispherical shape as working space (Diameter = 145 mm, referring average human head breadth [46] with step penetrate 45 mm. the limitations are the phantom used for testing must be spherical shape and the hair style must be short haircut. The decision to employ multiphase technology in robotic hair transplant mechanisms for graft extraction is rooted in the enhancement of the precision and efficiency of the hair harvesting process. Although a rotation-only movement can be used to perform the task, oscillating the needle in a multiphase manner offers distinct advantages. First, it enables more controlled penetration into the scalp, minimizes tissue damage, and reduces the risk of follicle transection. Second, multiphase movement facilitates graft extraction by creating microincisions that closely match the size and shape of individual hair follicular units. This tailored approach optimizes graft retrieval and ensures the highest graft quality for transplantation. These aspects have been meticulously considered to maximize the efficacy of the hair transplant procedure in terms of punch diameter selection and the morphological characteristics of the internal and external bevels. The chosen punch diameter strikes a balance between minimizing donor site scarring and ensuring efficient graft extraction. Furthermore, the specific morphological characteristics of the internal and external bevels were designed to reduce tissue trauma during the harvesting process. The internal bevel was engineered to facilitate smooth and precise cutting motion, whereas the external bevel minimized friction as the punch moved through the skin.

2.3. Kinematics model

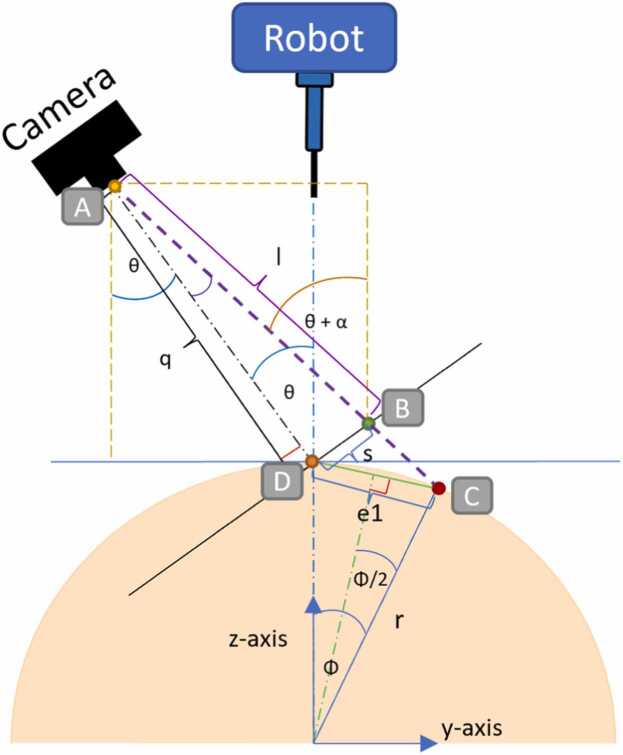
The simplest way to design a kinematic model of a hair transplant robot is to use the geometric approach to find the angles of motion in each joint. Even if the robot has 5DOF, the significant joints that will be used to find the position of the target are only the first and second joints (J1 and J2). The main reason is that the model of the phantom has a symmetric spherical shape, and the alignment of the centre of both the phantom and the workspace of the robot are at the same place. Thus, the translation of the robot in the third joint (J3) and fourth joint (J4) will be the same in every turn of a single hair graft transplant, and the geometric archetypal signifies the association between the robot and camera vision, which can be referred to as the kinematic approach of the robot after knowing some information from the camera shown in Fig. 6.

Fig. 6.

The geometric model, illustrating the relationship between the robot and camera vision, references the kinematic approach of the robot based on information acquired from the camera, where Point C signifies the target point for needle injection denoted by "Φ".

Kinematic model of the first joint (J1): The captured image from the camera at distance q can be seen in the image 2D plane. The target point, that is, point C in the real world, is recognized as point B in the image frame, as shown in Fig. 6. The aim of this approach is to determine e₁. The expected angle (or “Φ”) for J1 can then be calculated. Assume that the needle and camera were set up perfectly, as shown in Fig. 6 (main point: the centre of the camera points to the position of the needle at the phantom’s surface). The equation for the expected angle Φ can be derived in the following steps.

Given the middle point at the front of camera is point A, were,

A (y, z) = (−q sin θ, r + q cos θ) (1)

Let the distance between point A and B is l, where l = √q ² + s ².

Then α = tan− 1 $\left(\frac{s}{q}\right)$.

B (y, z) = (Ay + l sin (α + θ), Az − l cos (α + θ)) (2)

From circle equation: y² + z² = r² (3)

$$\mathrm{From\; linear\; equation\; of}\stackrel{\circledR }{\mathit{AB}}\mathrm{then},\mathrm{z}-\mathrm{Az}=\mathrm{m}1(\mathrm{y}-\mathrm{Ay})$$ (4)

where m₁ = $\frac{A_z-B_z}{A_y-B_y}$.

From (3), (4), we obtain,

$$y=\frac{{-n}_1\pm \sqrt{n_1^2-{4p}_1{k}_1}}{{2p}_1}$$ (5)

where n₁ = 2m₁(A_z − m₁Ay), p₁ = 1 + $m_1^2$, k₁ = (A_z − m₁Ay) ² − r^{2 *} Select a minus sign to be the y value for point C.

Finding z from Eqs. (3) and (5), then we will get the coordinate of point C (y, z) on y − z plane. ^** C (y, z) is the target point and D (y, z) = (0, r)

$$\stackrel{\circledR }{\mathit{DC}}=e_1=\sqrt{{(D_y-C_y)}^2+}{(D_z-C_z)}^2$$ (6)

$$\mathrm{Then\; the\; expected\; angle}\mathit{\phi }=\mathit{2}{\mathit{sin}}^{-\mathit{1}}(\frac{{\mathit{e}}_{\mathit{2}}/\mathit{2}}{\mathit{r}})$$ (7)

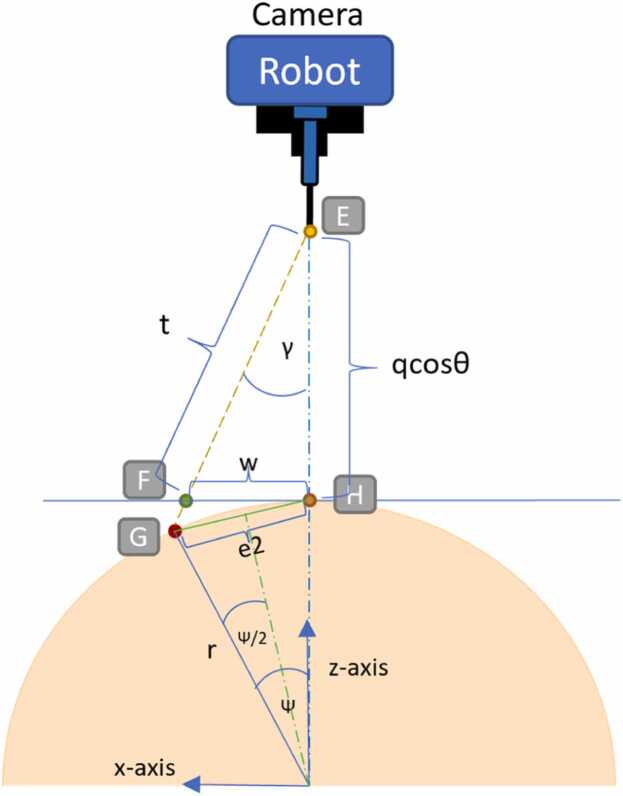
Kinematic model of the second joint (J2): The captured image from the camera at distance t can be seen in the image 2D plane. The target point, point G in the real world, is recognized as point F in the image frame. The aim of this approach was to find a e₂. The expected angle (or “Ψ”) for J2 can then be calculated. Assume that the needle and camera were set up perfectly, as shown in Fig. 7 (the centre of the camera is pointed out to the position of the needle at the phantom’s surface). The equation for the expected angle Ψ can be derived in the following steps.

Fig. 7.

The geometric model establishes a connection between the robot and camera vision, referencing the kinematic approach of the robot based on information obtained from the camera, where Point G denotes the target point for needle injection, denoted by "Ψ".

Given the middle point at the front of camera is point E, where E (x, z) = (0, r + qcosθ) and the target point in image frame is given as point F, were F (x, z) = (w, r).

From circle equation: x² + z² = r² (8)

$$\mathrm{The\; linear\; equation\; of}\stackrel{\circledR }{\mathit{AB}}\mathrm{will\; be}\mathrm{z}-\mathrm{E}\mathrm{z}=\mathrm{m}2(\mathrm{x}-\mathrm{Ex})$$ (9)

where m₂ = $\frac{A_z-B_z}{A_y-B_y}$.

From (8), (9), we obtain,

$$x=\frac{{-n}_2\pm \sqrt{n_2^2-{4p}_2{k}_2}}{{2p}_2}$$ (10)

where n₂ = 2m₂(E_z – m₂E_x), P₂ = 1 + $m_2^2$, k₂ = (E_z – m₂E_x) ² − r^{2 *} Select a minus sign to be the x value for point C.

Finding z from Eqs. (8) and (10), the coordinate of point G (x, z) on x − z plane will be identified. * * G (x, z) is the target point and H (x, z) = (0, r)

$$\stackrel{\circledR }{\mathit{HG}}=e_2=\sqrt{{(H_x-G_x)}^2+}{(H_z-G_z)}^2$$ (11)

$$\mathrm{Then\; the\; expected\; angle}\Psi =\mathbf{2}{\mathit{sin}}^{-\mathbf{1}}(\frac{{\mathit{e}}_{\mathbf{1}}/\mathbf{2}}{\mathit{r}})$$ (12)

The kinematic models represented (Fig. 6, Fig. 7) for both the first joint (J1) and the second joint (J2) involve capturing images at distances q and t, respectively. In J1, the target point C in the real world corresponds to point B in the image frame, initiating complex geometric calculations for the derivation of the expected angle Φ. The y-z plane coordinates of point C are determined through equations related to the circle equation and linear equation of (AB). The quadratic equation's root yields the y-coordinate, allowing the computation of the distance e1 using Euclidean distance. The expected angle φ is then calculated based on e1 and the radius. The kinematic model for J2 follows a similar procedure, capturing images at distance t and determining the expected angle Ψ. The coordinates of point G on the x-z plane are obtained through equations involving the circle equation and linear equation of (AB), with the distance e2 calculated using Euclidean distance. The expected angle Ψ is determined based on e2 and the radius.

2.4. Robot Vision: Feature detection and description

To identify key points, two essential parameters detector and descriptor are considered, elucidating key point detection and orientation, respectively. Numerous techniques exist for this purpose [47], with Scale-Invariant Feature Transform (SIFT) [48] being a popular example known for its high accuracy albeit slow computational speed. To address this limitation, alternative methods such as Speeded-Up Robust Features (SURF) [49], FAST, and BRIEF (Binary Robust Independent Elementary Features) [50] have been developed, each with its own trade-offs in accuracy, time, and cost. Notably, some techniques, like FAST (an effective detector) and BRIEF (an efficient descriptor), lack the ability to provide both detection and orientation. In 2011, Rublee et al. introduced a promising technique, Oriented FAST and Rotated BRIEF (ORB), capable of achieving high performance in both aspects [51]. Numerous studies have corroborated ORB's superiority over other techniques in terms of accuracy and computational time [52], [53], and it is cost-effective due to its non-patented status.

The robotic system, comprising five joints in alignment with the initial design, is depicted in Fig. 2, illustrating the components and details of each part. Following the robot's design, its assembly and control were implemented through a computer connected to all the motors, as depicted in Fig. 8, showcasing the camera and assembled robot.

Fig. 8.

The overview of developed robotic hair transplant system with sensors.

2.5. System Architecture

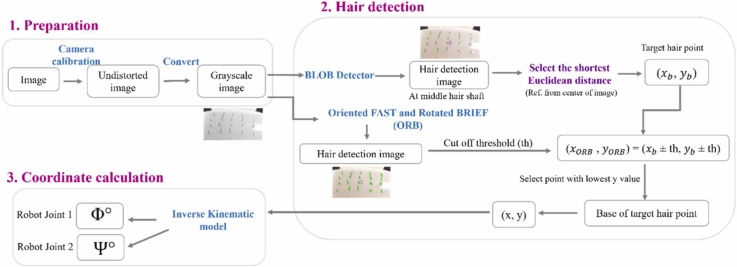
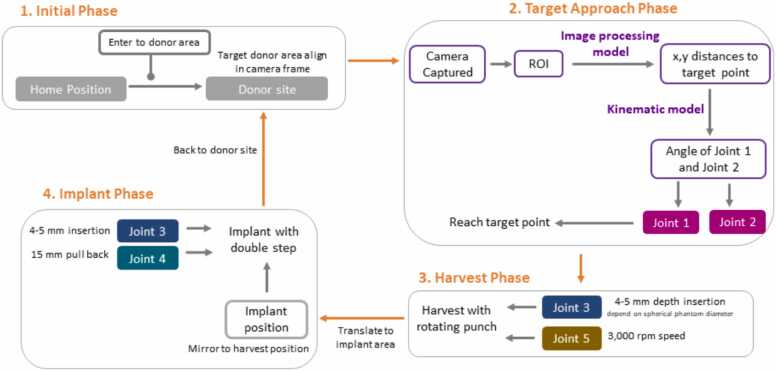
The overall robotic system, depicted in the architecture presented in Fig. 9, consists of four main phases. The initial phase involves setting the robot's position to the target donor area within the camera frame. Following this, the camera captures the Region of Interest (ROI), and an image-processing model calculates the (x, y) distance to the target point. The kinematic model is then utilized to determine the parameters of the robot joints, preparing the robot for the subsequent harvest phase. In this phase, the harvested graft is transferred to the implant area. The implant phase involves a double-step process where the needle implants the graft. To complete the grafting process, the robot repeats all phases without experiencing fatigue, providing efficiency comparable to a human surgeon. Fig. 10 further details the processes within the second phase, focusing on the target approach. This architecture summarizes the primary processes of the target approach phase, providing clarity to the entire algorithm.

Fig. 9.

The system architecture for robotic hair transplant system including 4 main phases.

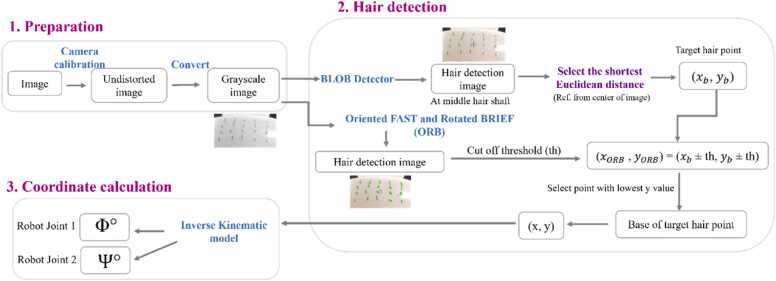
Fig. 10.

The target approach phase including 3 main processes.

The process of finding the target point, which is the hair base of the target graft, can be started by opening the camera, and then performing calibration to correct the distortion of the image and convert the size of the image from pixel units to millimetres in the real world [54]. Subsequently, the image was cropped to retain only the region of interest (ROI), which is the region we used to detect hair grafts on the testing phantom (the shape of the image ROI depends on the size of the phantom). In Fig. 10 the formulas for Φ and Ψ originate from the geometric relationships between captured images, target points, and desired joint angles, allowing precise calculations within the robotic system. This relationship is crucial for ensuring accurate robotic control, establishing a direct link between the (x, y) coordinates of the target points and the corresponding joint angles Φ and Ψ.

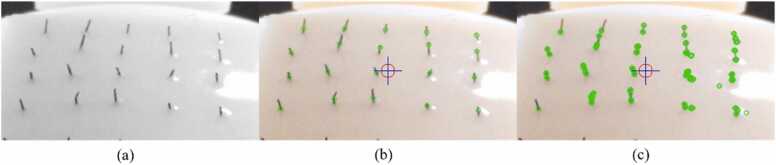
For hair detection and hair selection, the RGB image is first converted to a grayscale image (Fig. 11 (a)). Then, the feature detectors were obtained from the OpenCV library, which is an open source. The first technique used to determine the position of each hair is a simple band detector (Blob) because it usually detects a single hair graft as only a single key point (Fig. 11 (b)). Subsequently, an algorithm for selecting the target point was generated (represented on the hair graft), and the target point was nearest to the needle position on the x-y plane. Using the ORB feature detector, more key points for each single hairline were found, as shown in figure (Fig. 11 (c)) re executed.

Fig. 11.

(a) Gray scale image (scalp phantom with 2 mm hair, (b) Result image after using Blob detector (scalp phantom with 2 mm hair length), (c) Result image after using ORB detector (scalp phantom with 2 mm hair length).

To find the point that represents the hair base of the target graft, the threshold of hair length in pixel units was set such that the other key points outside the threshold length were ignored. This maintains the key points within the threshold length in an array. Thus, the array will have only all the detected points of a target hair. In selecting the hair base point, which is the lowest point of the hair graft, we created an algorithm by finding the point that gives the highest value on the y-axis. Finally, the output part is the target point, which is the hair base point, for injecting the needle at the x- and y-distances from the insertion point.

3. Results

3.1. Robot Vision Test

To evaluate the efficiency of the robot vision, we designed experiments for each process in this section. The first experiment was hair graft detection testing to estimate the accuracy of a keypoint detector (Blob detector), which is a feature from the OpenCV library [55]. Hair base selection was the next process in the robot vision part; therefore, the second experiment aimed to evaluate its capability. The scalp phantoms used in both the experiments were made of Silicone Rubber series 3. The properties of silicone provided by the manufacturer are summarized in Table 1.

Table 1.

Silicon Rubber properties.

Silicon Rubber RA-320 Properties	Value
Catalyst ratio	1%
Shore A	20
Viscosity	20,000 cps
Working time	30 min
Curing time	4 hr.
Tear Strength	28 N/mm
Tensile Strength	≥ 0.460 MPa
Shrinkage	≤ 0.28%

The comparison of silicon rubber phantoms, depicted in Fig. 12, with varying percentages of silicone oil reveals their limited significance in this research, and the test pieces derived from an appropriately selected phantom are presented in the same figure. Therefore, 5% silicone oil was the best option for conducting the experiment. To make a hairy testing phantom, dark plastic fibres were used as pseudo-hair shafts. Because the experiment required the use of two types of phantoms, which represent the donor area (hairy skin) and recipient area (non-hairy skin), plastic fibres were added to a group of silicon phantoms that will be used as donor areas, while another group was made without adding any plastic fibres as recipient areas, as shown in Fig. 13. Furthermore, the hairy skin phantom was made with two hair lengths: 2 mm haircut and 4 mm haircut [56], [57], [58]. The intentional selection of two specific hair lengths—2 mm and 4 mm haircuts—in constructing the hairy skin phantom served a precise purpose in examining a crucial parameter within the developed algorithm's functionality. This experiment's primary goal was a systematic evaluation of how varying hair lengths impact the algorithm's precision in selecting target points during the hair transplant process.

Fig. 12.

Silicone rubber varied by percent of silicone oil.

Fig. 13.

Two types of silicone phantom, non-hairy silicone phantoms (represent recipient area) and hairy silicone phantoms (represent donor areas).

The choice of 2 mm and 4 mm hair lengths was informed by the wide-ranging variations observed in clinical scenarios, where hair lengths exhibit considerable diversity. This experiment aimed to mimic real-world situations, with 2 mm representing shorter post-haircut scenarios and 4 mm simulating longer hair conditions. By incorporating these diverse lengths, the objective was a comprehensive assessment of the algorithm's resilience and adaptability across different clinical scenarios. The collected data offers valuable insights into the algorithm's response to varying hair lengths, illuminating its potential effectiveness in real-world applications. Importantly, the deliberate inclusion of 2 mm and 4 mm lengths in our experimental design ensures the algorithm's relevance to a broad spectrum of patient characteristics, transcending specific hair conditions and enhancing its clinical applicability.

Table 2 and Table 3 present experimental results for an image processing model utilizing Blob and ORB detectors to detect target points for needle insertion on 4 mm and 2 mm hair length skin phantoms, respectively. These tables detail measured and exact point coordinates, Euclidean distances, errors, precision percentages, and counts of true positive instances where the Euclidean error is less than 2. The data showcases varying degrees of success and failure in detecting and selecting target points, with instances of both true positive and false positive results. Techniques such as Scale-Invariant Feature Transform (SIFT), Speeded-Up Robust Features (SURF), FAST, and BRIEF are discussed, highlighting their strengths and weaknesses in terms of accuracy, time, and cost. Notably, the introduction of the Oriented FAST and Rotated BRIEF (ORB) technique in 2011 is recognized for its superior performance in accuracy and computational time, making it a cost-effective alternative. Both tables capture the coordinates and details of 30 experimental points, illustrating the model's efficacy in real-world applications and providing insights into its accuracy and reliability in detecting target points for needle insertion on both 4 mm and 2 mm hair length scenarios.

Table 2.

Experimental results of image processing model (using Blob and ORB detectors in detecting the target point for needle insertion) on 4 mm hair length skin phantom. (Point values are shown in pixel unit).

Hair graft and target point selection (BLOB&ORB result): Short haircut 4 mm range
No.	Measured Point		Exact Point			Error			Precision (TP/ (TP+FP))
	x axis	y axis	x axis	y axis	Euclidian distance	x axis	y axis	Euclidean Distance	%Eu_error	TP (%er<2)	Count (TP)
1	175.7743225	130.7589417	186.613	102.609	212.9624818	-10.8387	28.14994165	30.16448482	14.16422488	FALSE	0
2	187.6710053	98.4940033	187.634	99.5456	212.4049068	0.037005	-1.0515967	1.052247598	0.495397029	TRUE	1
3	171.4871368	130.7589417	178.48	113.987	211.7738099	-6.99286	16.77194165	18.17135553	8.580549001	FALSE	0
4	183	128	189.008	91.427	209.9593303	-6.008	36.573	37.06319459	17.65255896	FALSE	0
5	167.1999664	111.4666443	170.96	121.508	209.7415449	-3.76003	-10.04135571	10.72225149	5.112125731	FALSE	0
6	157.3000031	107.8000031	158.927	107.971	192.1341411	-1.627	-0.17099695	1.635958139	0.851466652	TRUE	1
7	211.2000122	100.0999985	210.065	99.6992	232.5236218	1.135012	0.40079847	1.203699352	0.517667557	TRUE	1
8	171.6000061	83.59999847	170.96	83.9069	190.4407768	0.640006	-0.30690153	0.709786135	0.372707015	TRUE	1
9	179.0800018	100.4300003	179.232	101.203	205.8304084	-0.152	-0.77299969	0.787801983	0.382743244	TRUE	1
10	160.6000061	100.0999985	159.679	99.6992	188.2480107	0.921006	0.40079847	1.004435986	0.533570571	TRUE	1
11	173.6307373	132.9025269	195.776	97.4431	218.6856189	-22.1453	35.45942686	41.80650205	19.11717024	FALSE	0
12	174.9000092	128.699997	174.72	128.276	216.752879	0.180009	0.42399695	0.460626434	0.212512256	TRUE	1
13	151.8000031	133.1000061	163.44	110.227	197.1360574	-11.64	22.8730061	25.66444889	13.01864775	FALSE	0
14	171.6000061	81.40000153	170.96	81.6508	189.4575803	0.640006	-0.25079847	0.687391941	0.362821028	TRUE	1
15	176	106	174.72	105.715	204.2124865	1.28	0.285	1.31134473	0.642147183	TRUE	1
16	188	93	186	91.427	207.2556304	2	1.573	2.544470279	1.227696576	TRUE	1
17	179	123	178.48	122.26	216.3391273	0.52	0.74	0.904433524	0.418062851	TRUE	1
18	131.7690125	142.4170075	154.415	106.467	187.5612282	-22.646	35.95000745	42.48816056	22.65295497	FALSE	0
19	210.0717468	124.3281784	200.288	96.6911	222.4060515	9.783747	27.63707841	29.31773874	13.1820778	FALSE	0
20	191.1800079	159.7200012	204.048	127.904	240.8215512	-12.868	31.81600122	34.3197196	14.2510998	FALSE	0
21	199.1000061	151.8000031	199.536	152.34	251.0420102	-0.43599	-0.53999695	0.694037021	0.276462501	TRUE	1
22	156.4820099	130.7589417	166.448	104.211	196.3794012	-9.96599	26.54794165	28.35690683	14.43985808	FALSE	0
23	152.1948395	117.8974075	162.688	93.6831	187.7336107	-10.4932	24.21430753	26.39013276	14.05722324	FALSE	0
24	157.9825134	103.7497177	168.704	79.3948	186.4526049	-10.7215	24.35491771	26.61037938	14.27192685	FALSE	0
25	209	122	207.808	91.427	227.0309697	1.192	30.573	30.59622841	13.47667609	FALSE	0
26	166.1000061	122.1000061	167.2	121.508	206.6882533	-1.09999	0.5920061	1.249182854	0.604380188	TRUE	1
27	180.0614929	124.3281784	186.752	98.1952	210.9943289	-6.69051	26.13297841	26.97583077	12.78509755	FALSE	0
28	189.199997	145.199997	189.008	145.572	238.5691331	0.191997	-0.37200305	0.418627636	0.17547435	TRUE	1
29	199.7032623	143.3354034	189.76	115.492	222.142431	9.943262	27.84340344	29.56558102	13.3092903	FALSE	0
30	202.4000092	133.1000061	205.552	101.955	229.4481352	-3.15199	31.1450061	31.3040964	13.64321239	FALSE	0

Table 3.

Experimental results of image processing model (using Blob and ORB detectors in detecting the target point for needle insertion) on 2 mm hair length skin phantom. (Point values are shown in pixel unit).

Hair graft and target point selection (BLOB&ORB result): Short haircut 1.5–2 mm range
No.	Measured Point		Exact Point			Error			Precision (TP/ (TP+FP))
	x axis	y axis	x axis	y axis	Euclidian distance	x axis	y axis	Euclidean Distance	%Eu_error	TP (%er<2)	Count (TP)
1	184.8000031	95.70000458	184.496	97.4431	208.6478654	0.304003	-1.74309542	1.769406538	0.848034814	TRUE	1
2	166.3750153	114.4660111	162.688	113.987	198.6464737	3.687015	0.47901105	3.718001226	1.871667368	TRUE	1
3	169.4000092	117.3700028	169.456	118.5	206.7790752	-0.05599	-1.12999725	1.13138356	0.547146059	TRUE	1
4	214.5732727	122.6132965	220.593	100.451	242.3874482	-6.01973	22.16229651	22.9652891	9.474619773	FALSE	0
5	181	120	172.464	117.748	208.8262982	8.536	2.252	8.828068872	4.227469887	FALSE	0
6	166	108	165.696	108.723	198.1813693	0.304	-0.723	0.7843118	0.395754557	TRUE	1
7	201.3000031	106.7000046	201.04	107.219	227.8442353	0.260003	-0.51899542	0.58048069	0.254770848	TRUE	1
8	154.3384247	115.7538223	163.44	94.4351	188.7607526	-9.10158	21.31872233	23.18030619	12.28025735	FALSE	0
9	203.640976	126.4717636	202.544	107.219	229.1723934	1.096976	19.25276361	19.28398981	8.414621639	FALSE	0
10	183	84	182.992	83.9069	201.3117978	0.008	0.0931	0.093443084	0.046417093	TRUE	1
11	171.6000061	96.80000305	171.712	97.4431	197.4339603	-0.11199	-0.64309695	0.652775858	0.330629977	TRUE	1
12	161.0510101	106.480011	161.183	107.219	193.5868628	-0.13199	-0.73898901	0.750683743	0.387776181	TRUE	1
13	204.6000061	116.6000061	204.048	117.748	235.5847572	0.552006	-1.1479939	1.273813459	0.540702834	TRUE	1
14	177.1000061	111.1000061	174.72	110.979	206.9865137	2.380006	0.1210061	2.383080257	1.151321511	TRUE	1
15	159.5	93.5	158.927	94.4351	184.8669236	0.573	-0.9351	1.096695496	0.593235109	TRUE	1
16	156.199997	118.8000031	155.919	117.748	195.3850712	0.280997	1.05200305	1.088884614	0.557301849	TRUE	1
17	198.3190155	106.480011	197.28	107.971	224.8936087	1.039016	-1.49098901	1.817306093	0.808073695	TRUE	1
18	160	107	158.927	107.971	192.1341411	1.073	-0.971	1.447124735	0.753184586	TRUE	1
19	200	131	198.784	132.78	239.0514737	1.216	-1.78	2.155703134	0.901773622	TRUE	1
20	169.4000092	112.2000046	168.704	111.731	202.348353	0.696009	0.46900458	0.839281864	0.414770791	TRUE	1
21	176.6600037	87.12000275	174.72	86.9149	195.1442498	1.940004	0.20510275	1.950815557	0.999678729	TRUE	1
22	174.9000092	94.59999847	173.968	95.1871	198.3064523	0.932009	-0.58710153	1.10151227	0.555459622	TRUE	1
23	203.2799988	90.75	195.776	89.923	215.4399872	7.503999	0.827	7.54943221	3.504192655	FALSE	0
24	161.699997	95.70000458	161.935	94.4351	187.4591484	-0.235	1.26490458	1.286549661	0.686309349	TRUE	1
25	165.8825531	119.1777573	165.696	119.252	204.1475053	0.186553	-0.07424274	0.200783574	0.098352206	TRUE	1
26	202	93	194.272	92.179	215.0315745	7.728	0.821	7.771487953	3.614114798	FALSE	0
27	186	121	185.248	122.26	221.9556918	0.752	-1.26	1.467345903	0.66109857	TRUE	1
28	170.3680115	105.1490097	170.96	106.467	201.4014491	-0.59199	-1.3179903	1.444835233	0.717390684	TRUE	1
29	182.7100067	100.4300003	176.224	98.9472	202.1025645	6.486007	1.48280031	6.653343505	3.292062881	FALSE	0
30	211.2000122	119.9000015	210.065	120.004	241.9261545	1.135012	-0.10399847	1.139766818	0.471121785	TRUE	1

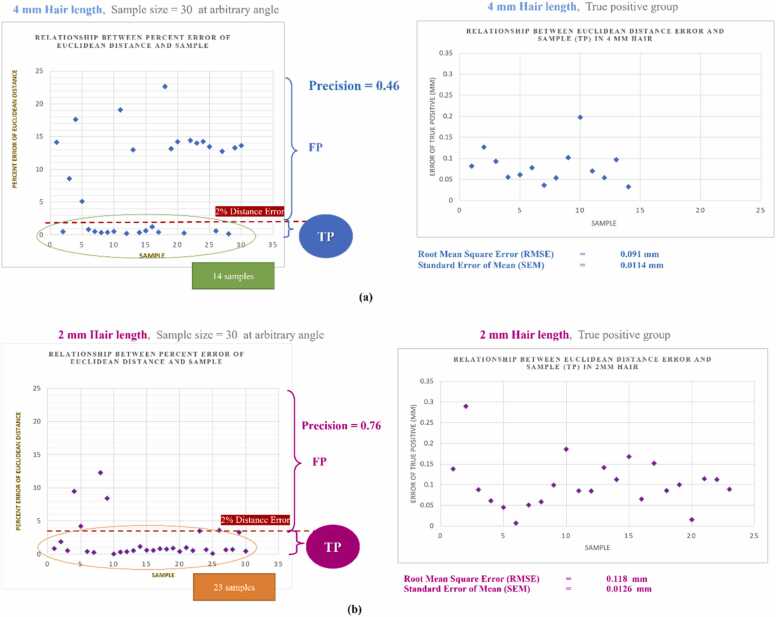
From Table 2, Table 3, the data can be analysed by calculating the root mean square error of the Euclidean distance, which was computed using the straight-line distance between the measured point and the exact point. The choice of using the root mean square error (RMSE) of the Euclidean distance for analysing the experimental results in Table 2, Table 3 was deliberate and serves as a robust method to assess the accuracy of the robot in detecting target points for needle insertion on both 4 mm and 2 mm hair length skin phantoms. The RMSE provides a comprehensive measure by considering the straight-line distance between the measured point and the exact point for each data point. This method is particularly suitable for assessing accuracy as it considers both systematic and random errors in the measurements. In Table 2, the RMSE of the Euclidean distance for the 4 mm hair length is computed as 22.15373989 pixels, with a standard error of 2.818100211. Converting this error to millimeter units using the calibration factor of 0.0778682780208998 yields a root mean square error of 2.818100211 mm and a standard error of 0.219440611. Similarly, for the 2 mm hair length in Table 3, the RMSE of the Euclidean distance is calculated as 7.591821238 pixels, with a standard error of 1.172705593. Converting to millimeter units results in a root mean square error of 0.591162047 mm and a standard error of 0.091316565.

The use of RMSE provides a clear and quantitative assessment of the accuracy of the robot across different hair lengths. However, to ensure the validity of the data, it is advisable to explore other assessment methods as well. Alternative methods such as Mean Absolute Error (MAE) or Maximum Absolute Error could be considered to complement the RMSE analysis. These methods may offer additional perspectives on the accuracy of the robot and provide a more comprehensive evaluation of its performance. Incorporating multiple assessment methods enhances the robustness of the analysis and strengthens the validity of the experimental data. Fig. 14 (a) and (b) further visualize the relationship between Euclidean distance error (mm) and samples, contributing to a holistic understanding of the robot's performance.

Fig. 14.

Relationship between error and count of sample in (a) 4 mm hair length (b) 2 mm hair length.

The initial testing phase aimed to establish a foundational performance benchmark for the image-processing algorithms under idealized conditions. These conditions, featuring a white background and black hairs, facilitated the achievement of notably high accuracy levels due to the sharp contrast aiding in hair graft detection. However, this study acknowledges the technical limitations posed by the greater intricacies encountered in real-world scenarios. Firstly, the variability in skin tone across the human scalp presents a challenge, as the proposed method, in its initial development, is not explicitly trained to contend with these variations. Skin tone differences can significantly impact the contrast between hair grafts and the scalp, potentially affecting the algorithm's precision in accurately identifying and isolating grafts. Secondly, real-world environments introduce challenges related to specular reflections and varied lighting conditions, especially in close-up images, which may lead to glare or uneven illumination, posing obstacles for consistent hair graft detection. Thirdly, the considerable diversity in hair texture and colour within individuals adds complexity, as the algorithm's performance with black hair against a white background may not directly extend to scenarios involving different hair colours or textures. Distinguishing grafts becomes challenging when the contrast between the hair and the background is less pronounced. Lastly, the diverse stages of hair growth, ranging from fine vellus hairs to thicker terminal hairs, introduce another layer of complexity, causing fluctuations in the algorithm's efficacy based on specific stages of hair growth in real-world implementations.

3.2. Robot Position Control Test

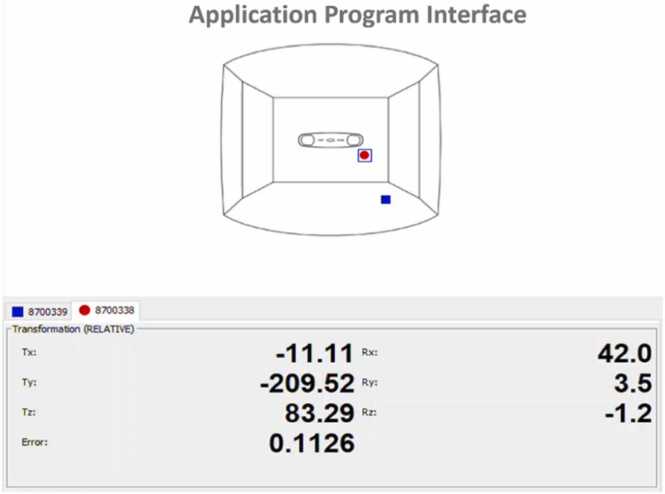
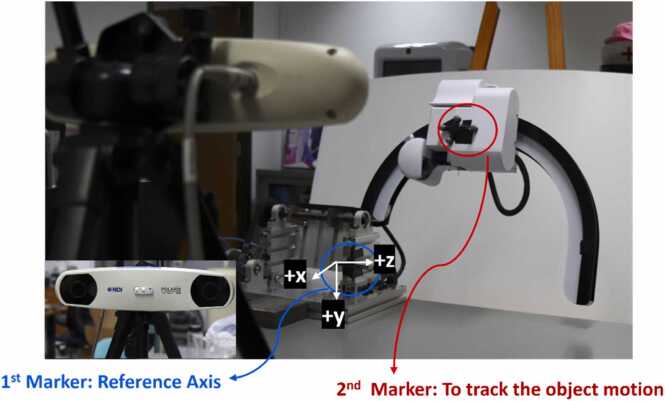
Using the optical tracking system, NDI Poralis Vicra Optical Measurement system, the motion of each joint (joints 1, 2, and 3) was tracked. The program interface from the poralis vicra system, known as the Application Program Interface (Fig. 15), was used to obtain the transformation matrix of the robot motion. The output from the tracking system was the rotation and translation of each axis (x-axis). In the experiment, the process to track the object used two markers. The first marker performed as a reference axis in the frame shown in (Fig. 16) with a blue circle. Another marker was an object tracker attached to an object that rotated with a red circle.

Fig. 15.

The window of application program interface while collecting the data in experiment.

Fig. 16.

The robot position evaluation using NDI poralis vicra optical tracking system.

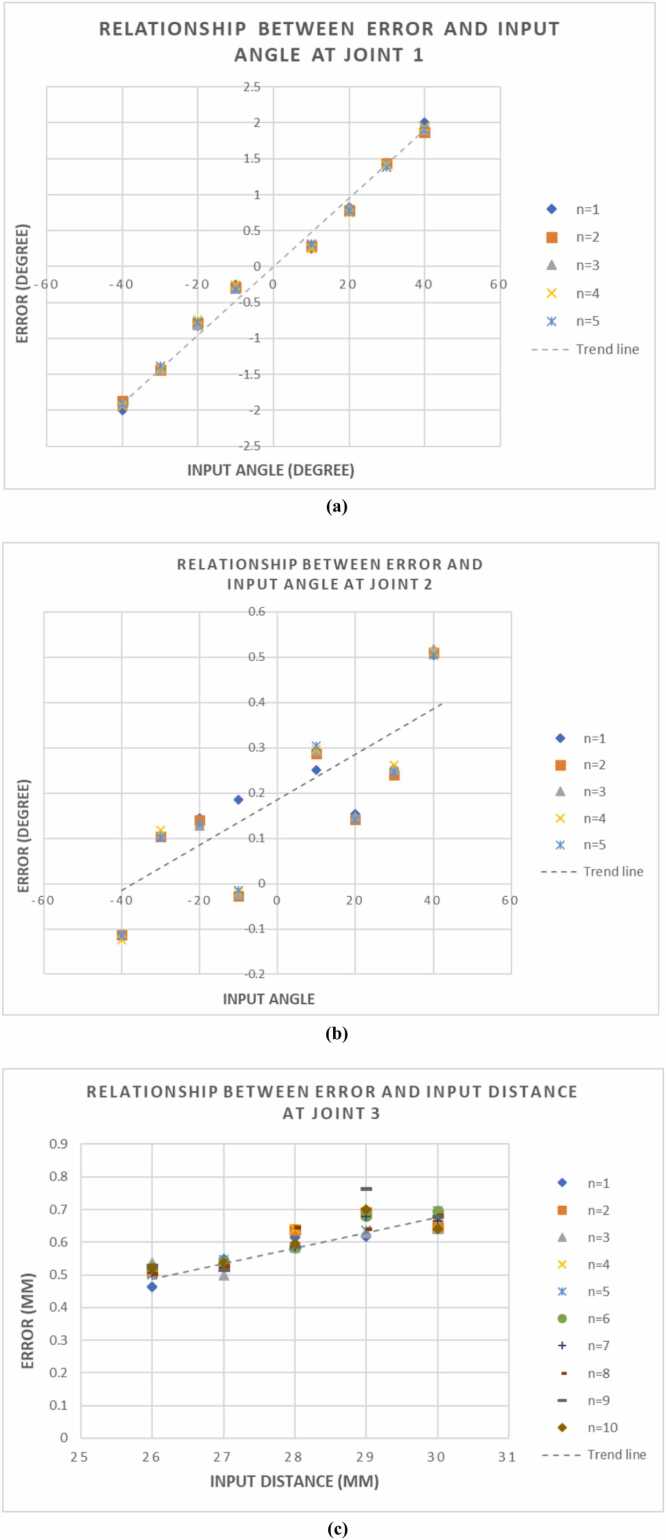
The rotation of J1 around z-axis; J2 around x-axis and J3 around y-axis of reference axis from the first marker as shown in Fig. 16 the angle error of each input angle from Table 4, Table 5 was calculated and showed in Table 6, Table 7. The root mean square error of J1 motion is 1.26779 degrees; J2 motion around x axis is 0.244179 degrees and J3 motion around y-axis is 0.60126 degrees. The standard error is 0.203009 for J1; 0.028471 for J2 and 0.01032 for J3. Fig. 17 (a)-(c) shows the trend characteristic of error of each joint (J1 to J3).

Table 4.

The actual angle experiment data from the Joint (J1) and Joint (J2).

		Joint (J1) Input Angle (degree)
		40° CCW	30° CCW	20° CCW	10° CCW	40° CW	30° CW	20° CW	10° CW
		-40	-30	-20	-10	40	30	20	10
Actual Angle	n = 1	-41.9999	-31.4469	-20.8212	-10.2582	41.99987	31.44686	20.82119	10.25822
	n = 2	-41.8665	-31.4329	-20.7801	-10.2888	41.86653	31.43286	20.78011	10.28883
	n = 3	-41.904	-31.4278	-20.8122	-10.3018	41.90399	31.42784	20.81218	10.30183
	n = 4	-41.9411	-31.417	-20.7461	-10.2515	41.94111	31.41702	20.74613	10.25153
	n = 5	-41.9149	-31.3828	-20.7711	-10.3141	41.91491	31.38282	20.77114	10.31414
	Joint (J2) Input Angle (degree)
		40° CCW	30° CCW	20° CCW	10° CCW	40° CW	30° CW	20° CW	10° CW
		-40	-30	-20	-10	40	30	20	10
	n = 1	-40.1139	-29.8947	-19.8549	-9.8152	40.50454	30.25476	20.15378	10.25168
	n = 2	-40.1138	-29.8967	-19.8605	-10.0271	40.50981	30.24063	20.14188	10.28623
	n = 3	-40.1121	-29.8918	-19.8727	-10.0245	40.51798	30.25274	20.14768	10.29344
	n = 4	-40.1249	-29.8827	-19.8679	-10.0182	40.51187	30.26154	20.14103	10.29668
	n = 5	-40.1151	-29.8985	-19.8682	-10.015	40.50454	30.24565	20.14174	10.30457

Table 5.

The actual angle experiment data from the Joint (J3).

		J3 Input Distance (mm)
		26	27	28	29	30
Actual Distance	n = 1	26.4624	27.548	28.6138	29.6166	30.6638
	n = 2	26.5114	27.5268	28.6392	29.6914	30.6462
	n = 3	26.5362	27.5112	28.5838	29.6292	30.6414
	n = 4	26.5022	27.5360	28.6402	29.6824	30.6578
	n = 5	26.5022	27.5462	28.5868	29.6366	30.696
	n = 6	26.5216	27.5402	28.585	29.68	30.6962
	n = 7	26.5068	27.5232	28.5858	29.679	30.6634
	n = 8	26.5036	27.5266	28.6466	29.6414	30.6836
	n = 9	26.5308	27.5166	28.5864	29.7644	30.6794
	n = 10	26.5202	27.5356	28.5956	29.7008	30.6416

Table 6.

The calculated angle error data from the Joint (J1) and Joint (J2).

		J1 Input Angle (degree)
		40° CCW	30° CCW	20° CCW	10° CCW	40° CW	30° CW	20° CW	10° CW
		-40	-30	-20	-10	40	30	20	10
Error	n=1	-1.99987	-1.44686	-0.82119	-0.25822	1.999872	1.446857	0.821192	0.258224
	n=2	-1.86653	-1.43286	-0.78011	-0.28883	1.866532	1.432856	0.780114	0.288826
	n=3	-1.90399	-1.42784	-0.81218	-0.30183	1.903987	1.427838	0.812179	0.301826
	n=4	-1.94111	-1.41702	-0.74613	-0.25153	1.941113	1.417022	0.746129	0.25153
	n=5	-1.91491	-1.38282	-0.77114	-0.31414	1.914914	1.382821	0.771144	0.314143
	J2Input Angle (degree)
		40° CCW	30° CCW	20° CCW	10° CCW	40° CW	30° CW	20° CW	10° CW
		-40	-30	-20	-10	40	30	20	10
	n=1	-0.11392	0.105275	0.145089	0.184803	0.504538	0.25476	0.153777	0.25168
	n=2	-0.11377	0.103314	0.139505	-0.02708	0.509808	0.240631	0.14188	0.286226
	n=3	-0.11208	0.10822	0.127301	-0.02452	0.517983	0.252744	0.147684	0.293437
	n=4	-0.12486	0.117329	0.132089	-0.01815	0.51187	0.261535	0.141033	0.296676
	n=5	-0.11514	0.101498	0.131815	-0.01503	0.504538	0.245653	0.141735	0.304567

Table 7.

The calculated angle error data from the Joint (J3).

		J3 Input Distance (mm)
		26	27	28	29	30
Error	n=1	0.4624	0.548	0.6138	0.6166	0.6638
	n=2	0.5114	0.5268	0.6392	0.6914	0.6462
	n=3	0.5362	0.5	0.5838	0.6292	0.6414
	n=4	0.5022	0.53	0.6402	0.6824	0.6578
	n=5	0.5022	0.5462	0.5868	0.6366	0.696
	n=6	0.5216	0.5402	0.585	0.68	0.6962
	n=7	0.5068	0.5232	0.5858	0.679	0.6634
	n=8	0.5036	0.5266	0.6466	0.6414	0.6836
	n=9	0.5308	0.5166	0.5864	0.7644	0.6794
	n=10	0.5202	0.5356	0.5956	0.7008	0.6416

Fig. 17.

The relationship between input distance and error in millimetre unit (a) Joint J1 (b) Joint J2 (c) Joint J3.

For the robot position control test presented in Fig. 16, the root mean square error (RMSE) of J1 was 1.268°and the standard error of mean (SEM) was 0.203°. For J2, the RMSE was 0.244°and the SEM was 0.028°. The results from J1 and J2 can be calculated as the total error of the needle position around the hemisphere surface, which was ± 1.6 mm. In addition, the total theoretical resolutions of robots J1 and J2, which were obtained from calculation, were 0.9 mm. Moreover, the results for robot J3 were 0.601 mm RMSE and 0.010 mm SEM. Thus, the error of penetration of the needle punch moving unit was ± 0.6 mm with a theoretical resolution 0.02 mm. The results indicate that the developed system performs well in a spherical phantom with a hair length of 2 mm and 5 mm between harvests. However, there is an error from the mechanical parts, especially custom parts, which affects the accuracy of the robot.

3.3. Limitations

During the harvesting process, a punch needle was used to puncture and implant the fibres into the silicone phantom skin. However, during the experiment, it was observed that while some of the fibres successfully embedded themselves in the phantom skin, many others adhered to the punch needle. Some became entirely embedded within the silicone, whereas others protruded and subsequently detached from the silicone phantom. The primary reason for the observed failure was the bending of the fibres, which increased their likelihood of becoming entangled with the needle. Furthermore, variations in puncture depth influenced by robot vision led to a significant drop in performance. To address these issues, an air vacuum pump along with a punch was employed to extract the fibres from the silicone phantom during the harvesting process. An experiment was conducted to evaluate the suction functionality, but all attempts were unsuccessful, indicating that the air vacuum pump could not effectively harvest dissected fibres from the silicone phantom. To proceed with implantation, the fibres were manually loaded into the implant needle owing to the ineffectiveness of the suction pump for harvesting. Subsequently, the servo motor was activated to compress the spring and facilitate the insertion of the fibres into the implanter tip. These fibres were successfully implanted into a silicone phantom. The results of this study demonstrated a significant success rate, suggesting the feasibility of the hair implantation process. However, it is worth noting that several samples remained unplanted, which is attributed to variations in punching depth, material properties, and operator experience. To address these technical challenges of image processing, ongoing research and development efforts have focused on advancing the proposed image-processing techniques toward real-world implementation (real shaved heads). This includes training the algorithms using diverse datasets that simulate real-world conditions, integrating machine-learning models capable of adaptability to varying contexts, and refining the algorithms to enhance resilience against factors such as skin tone and specular reflections. The objective was to elevate the robustness and precision of our image processing algorithms, rendering them suitable for the multifaceted scenarios encountered in real-world hair transplant procedures. Moreover, the innovative creative arc slide implemented in the robot design mechanism of this study stands out in the field, being a rarity among medical robots. Although it offers a wide coverage range, it is accompanied by the trade-off of either diminished accuracy or slower speed when contrasted with conventional mainstream robot arms.

4. Conclusions

The design and development of the prototype for a single robotic hair transplant system were successfully executed. The developed prototype is expected to reduce time, enhance graft retention with improved blood supply, and minimize hair graft damage. In the robot vision test, the results indicate an 89.6% accuracy for hair graft detection in the 4 mm hair length phantom and a 97.4% accuracy for the 2 mm hair length phantom. Regarding hair base selection, which pertains to the target point of the needle punch moving unit, the precision was measured at 46% for a 4 mm hair length and 76% for a 2 mm hair length. The resulting errors for correct points were a root mean square error of 0.091 mm and a standard error of mean of 0.0114 mm for the 4 mm hair length. For the 2 mm hair length, the corresponding results were 0.118 mm and 0.0126 mm, respectively. Based on these findings, the proposed system demonstrates effective performance under the conditions of a spherical phantom with a 2 mm hair length and a 5 mm distance between harvests.

Funding

This work was supported by the Reinventing System through Mahidol University, Mahidol Medical Robotics Platform IO 864102063000.

CRediT authorship contribution statement

Methodology, R.T., and J.S.; Collection of the data, R.T., and J.S.; code, R.T., and J.S.; Formal analysis, R.T., and J.S.; investigation, R.T., and J.S.; Resources, R.T., and J.S.; Plot, R.T., and J.S.; Writing—original draft preparation, R.T., and J.S.; Writing—review and editing, R.T., and J.S.; Visualization, R.T., and J.S.; Supervision, J.S.; Project administration, R.T., and J.S.; Funding acquisition J.S. All authors have read and agreed to the published version of the manuscript.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.