Strong enhancement of magnetic ordering temperature and structural/valence transitions in EuPd₃S₄ under high pressure

Significance

The complexities of Ce- and Yb-based systems have been explored extensively and continue to attract attention. By contrast, the rich phenomenology of Eu-based systems remains largely understudied, despite the same potential for coupled valence, volume, electronic, and magnetic contributions. As we show here, the inhomogeneous mixed-valence EuPd₃S₄ under hydrostatic pressure exhibits an eightfold increase of the Néel temperature followed by a structural transition to a lower symmetry structure that coincides with a transition to a fully nonmagnetic state. Our derived phase diagram differs significantly from the proposed global phase diagram for Eu compounds further emphasizing both the need for broader study and the opportunities Eu-based compounds present for developing insights into, and examples of, mixed-valent behavior.

Abstract

We present a comprehensive study of the inhomogeneous mixed-valence compound, EuPd₃S₄, by electrical transport, X-ray diffraction, time-domain ¹⁵¹Eu synchrotron Mössbauer spectroscopy, and X-ray absorption spectroscopy measurements under high pressure. Electrical transport measurements show that the antiferromagnetic ordering temperature, T_N, increases rapidly from 2.8 K at ambient pressure to 23.5 K at ~19 GPa and plateaus between ~19 and ~29 GPa after which no anomaly associated with T_N is detected. A pressure-induced first-order structural transition from cubic to tetragonal is observed, with a rather broad coexistence region (~20 GPa to ~30 GPa) that corresponds to the T_N plateau. Mössbauer spectroscopy measurements show a clear valence transition from approximately 50:50 Eu²⁺:Eu³⁺ to fully Eu³⁺ at ~28 GPa, consistent with the vanishing of the magnetic order at the same pressure. X-ray absorption data show a transition to a fully trivalent state at a similar pressure. Our results show that pressure first greatly enhances T_N, most likely via enhanced hybridization between the Eu 4f states and the conduction band, and then, second, causes a structural phase transition that coincides with the conversion of the europium to a fully trivalent state.

In general, mixed valency in f-electron systems occurs when the more localized f-orbitals of rare-earth elements hybridize with s, p, and/or d electrons. In the presence of a small energy difference between competing valence states (even smaller than f-electron bandwidth), the system can fluctuate among these nearly degenerate states with different degrees of orbital valences. This phenomenon is commonly referred to as a fluctuating valence state (1). The onset of mixed-valence behavior under external pressure, chemical substitutions, or thermal contraction has dramatic consequences on the macroscopic properties of f-electron systems including lattice collapse (2), quenched magnetism (3), superconductivity (4, 5), Kondo behavior (6), and quantum criticality (4, 5). Despite being central to f-electron physics, the underlying mechanism of mixed-valence phenomena is still not fully understood due both to experimental limitations and to the lack of an adequate diversity of ideal materials.

That said, the inhomogeneous mixed-valence behavior of europium in EuPd₃S₄ is rather special and offers the opportunity to study Eu mixed valency in a novel limit. The rare-earth palladium bronzes, RPd₃S₄, were reported to crystallize in the cubic NaPt₃O₄ structure [Pm$\overline{3}$ n, space group (SG) #223] with the rare earth occupying the 2a site and forming a bcc sublattice (7). Whereas the RPd₃S₄ compounds exist for all the trivalent rare earths, they do not appear to form with the divalent alkaline earths (Ca, Sr, …). Interestingly, when prepared with europium (7) or ytterbium (8) a roughly 50:50 mix of divalent and trivalent rare earth was found, which makes the intermediate valence in these two compounds distinct from the more general fluctuating valence phenomenon case. In EuPd₃S₄, 50% Eu²⁺ makes the material magnetic as observed in Mössbauer spectroscopy and thermodynamic measurements (7, 9). By chemical substitution, smaller Y³⁺ ions tend to replace Eu³⁺ sites first and make the valence of Eu more divalent; however, substitution with bigger La³⁺ ions on the other hand, promotes the electron hopping between Eu²⁺ and Eu³⁺, leading to an intermediate Eu valence until 60% of Eu have been replaced, above which, Eu becomes more trivalent. The chemical substitution work suggests that preservation of the unit cell volume size is a dominant factor controlling the Eu²⁺: Eu³⁺ valence ratio (9). Very recently, it was found that rather than adopting the Pm$\overline{3}$n structure with a single, crystallographic Eu site (2a) hosting the two Eu valences, EuPd₃S₄ was found to take the more reasonable cubic Pm$\overline{3}$ (SG #200) structure with two distinct Eu sites (1a and 1b) below 340 K at ambient pressure (10). As such then, EuPd₃S₄ allows for the study of valence changes in an inhomogeneously mixed-valence system.

We considering that chemical substitution and the associated changes in unit cell were shown to profoundly impact the mixed-valence state in EuPd₃S₄, it is worthwhile to appreciate that the effect of external pressure has proven to be an effective way to tune the atomic distances and thus may be used to increase the degree of orbital hybridization, and is considered to be a cleaner and more powerful tool for modifying the valence state than chemical doping. Here, we report the systematic high-pressure investigation of EuPd₃S₄ using a combined experimental approach including electrical transport measurements, X-ray diffraction (XRD), time-domain synchrotron Mössbauer spectroscopy (SMS) (11), and partial fluorescence-yield X-ray absorption spectroscopy (PFY-XAS). A significant, about eightfold, enhancement in antiferromagnetic transition temperature, (T_N) from ~2.8 K at ambient pressure (7) to ~3.5 K at ~19 GPa is observed. Subsequently, in a pressure window from ~19 GPa to ~29 GPa, T_N is almost pressure independent, whereas the size of the resistance drop below T_N is gradually suppressed with increasing pressure. The sample in this pressure window is found to be in a mixed phase of cubic and tetragonal structures with the ratio of cubic/tetragonal decreasing with increasing pressure. Above ~29 GPa, an abrupt disappearance of antiferromagnetic (AFM) order is observed. In the same pressure range, both SMS and XAS measurements show a clear change from 50:50 Eu²⁺:Eu³⁺ to fully Eu³⁺ and is coincident with the complete disappearance of the lower pressure, cubic phase, resulting in a single phase of the non-moment-bearing tetragonal structure. This comprehensive study beautifully illustrates the interplay of crystal structure, magnetic ground state, and the associated valence state tuned by high pressure and suggests that EuPd₃S₄ provides a clean and simple system for the detailed study of how magnetism, valence, and structure are intertwined and should serve as a benchmark for theoretical efforts to model and understand mixed-valence behavior.

Results

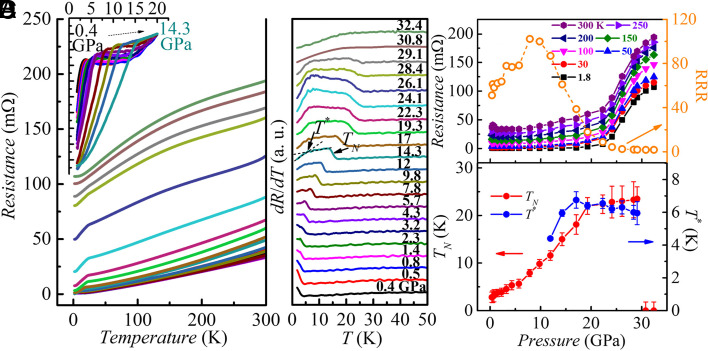
Fig. 1A presents the temperature dependence of the resistance, $R\left(T\right)$  , of single crystalline EuPd₃S₄ under pressure up to ~32 GPa. The overall $R\left(T\right)$  behavior is metallic over the whole temperature and pressure ranges covered here. A clear resistance drop is seen below 2.8 K at 0.4 GPa, reflecting the loss of spin disorder scattering as antiferromagnetic (AFM) ordering occurs. We define the Néel temperature, T_N, as the mid-point of the step in the temperature derivative of resistance ( $dR/dT$  ), with the uncertainty taken as half of the step width, as shown in Fig. 1B. T_N at 0.4 GPa is consistent with the ambient pressure heat capacity and magnetization results reported previously (7, 9). Increasing the pressure from 0.4 GPa to ~19 GPa leads to a marked rise in T_N from 2.8 K to 23.5 K, Fig. 1D. Above 20 GPa, there is a sharp increase in resistance; the position of the T_N step remains essentially unchanged, but the size of the step-like feature in $dR/dT$  becomes progressively smaller and is lost by ~29 GPa (Fig. 1B). As will be shown below, when we examine the powder X-ray data, these changes are consistent with the observation that for ~19 to 29 GPa, the system passes through a crystallographic two-phase region as the increasing pressure progressively converts the AFM-ordering Eu²⁺-containing phase into a fully trivalent nonmagnetic phase. Above ~29 GPa, the features marking loss of spin-disorder scattering in the resistance, associated with the step like feature in $dR/dT$  are gone, and no further evidence for magnetic ordering (at least above 1.8 K, our lowest measurement temperature) is observed, suggesting that the conversion is now complete. In addition to the step like feature that is related to T_N, a slope change in $dR/dT$  at lower temperature (marked as T*, in Fig. 1B) is also observable at and above 12 GPa and becomes clearer as pressure increases to ~19 GPa (Fig. 1B). Similar features in $dR/dT$  are common in rare-earth-bearing compounds and are often associated with incommensurate-to-commensurate transitions or spin reorientations (12, 13). Of note is that the shape of the higher temperature $R\left(T\right)$ curve clearly changes from concave-like at low pressures to convex-like at high pressures, indicating possible change of band structure and/or paramagnetic and phonon scattering.

Fig. 1.

Pressure dependence of electrical resistance and T_N. Temperature dependencies of the (A) electrical resistance and (B) temperature derivatives of the resistance for single crystal EuPd₃S₄, measured at different pressures. (A) and (B) share the same legend. The Inset in (A) shows the zoomed-in resistance curves normalized at 20 K from 0.4 GPa to 14.3 GPa so as to better show the evolution of T_N below 14.3 GPa. In (B), curves at various pressures are offset from each other so as to better show the evolution of T_N. T_N is determined as the midpoint of the dR/dT shoulder, and T* is defined as the intersection of two black dashed lines drawn from high temperature and low temperature. (C) Resistance at various temperatures and the residual resistivity ratio (RRR) as functions of pressure. (D) T_N and T* as functions of pressure.

The Néel temperature, T_N, and anomaly, T*, as functions of the pressure for EuPd₃S₄ are presented in Fig. 1D. We can see that with increasing pressure, T_N has an approximately eightfold enhancement from 2.8 K at 0.4 GPa to around 23.5 K at ~19 GPa with an average increasing rate of ~1.1 K/GPa, then T_N remains essentially constant from ~19 GPa to ~29 GPa, above which signatures of antiferromagnetic ordering are not observed. Meanwhile, resistance versus pressure (Fig. 1C) at all temperatures shows an abrupt increase starting from ~22 GPa. This is most likely due to the onset of a crystallographic two-phase region (as will be discussed below) but may also be associated with the commensurate change in valence and therefore band structure. As will be discussed further below, the flat T_N versus P region between ~19 GPa and ~29 GPa is most likely the result of entering a region of mixed crystallographic phases with increasing pressure leading to a larger fraction of the smaller volume, purely Eu³⁺ phase. As a result of this two-phase nature, we speculate that the strain on the remaining Eu²⁺ phase remains effectively constant over this pressure range, leading to an effectively constant T_N value. Remarkably, T* exhibits very similar behavior, rising with T_N and then becoming constant through the two-phase region, reinforcing the idea that in the two-phase region, there is relatively little change in strain on the Eu²⁺ fraction of the sample.

It is notable that the residual resistance ratio [RRR = R (300 K)/R (1.8 K)] as a function of the pressure shows a different behavior compared with the resistance as a function of the pressure, as shown in Fig. 1C. The RRR first increases from ~40 at 0.4 GPa to ~100 at ~10 GPa and then rapidly decreases to less than 2 at ~22 GPa, above which the resistance at all temperatures shows a sharp increase with the pressure, which might indicate a structural transition. Fig. 1C also presents the pressure-dependent resistance of the sample at representative temperatures ranging from 1.8 K to 300 K. Each dataset shows a marked increase in resistance at ~24 GPa indicating that in the temperature range we measured, if there is any structural/valence transition under pressure, the transition temperature should be above 300 K and its phase line is (almost) vertical in temperature–pressure (T–P) plot.

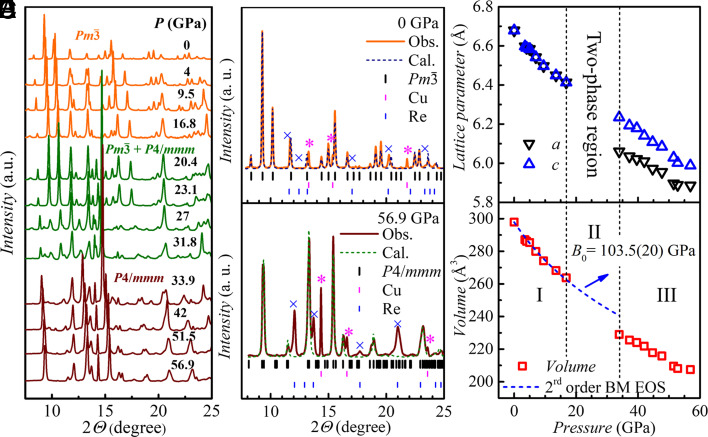
To explicitly explore the structural stability of EuPd₃S₄ under pressure, synchrotron powder X-ray diffraction (PXRD) experiments were performed on a sintered powder (polycrystalline) sample up to ~57 GPa. Fig. 2 A–C demonstrates the outcomes. Peaks from copper (calibrant) and rhenium (gasket) are indexed in Fig. 2 B and C and are marked with pink stars and blue crosses, respectively, in SI Appendix, Fig. S1 to illustrate their systematic shift with pressure. Three distinct pressure regions were detected, as shown in Fig. 2A: zone I (ambient to ~17 GPa), zone II (~20 GPa to ~32 GPa), and zone III (~34 GPa to ~57 GPa), respectively. The diffraction patterns in zone I can be indexed to the cubic space group Pm$\overline{3}$  (SG #200), as shown in Fig. 2B, which is consistent with the structure of the specimen at ambient pressure (10). In zone III, the patterns are resolvably different and could be assigned to a tetragonal space group, $P4/mmm$  (SG #123), as depicted in Fig. 2C. The pressure dependencies of the lattice parameters and unit cell volume EuPd₃S₄ are shown in Fig. 2 D and E. Clear discontinuous changes in both lattice parameters (a and c) and the unit cell volume (V) are observed. Considering that $P4/mmm$  (SG #123) is not a translationengleiche subgroup of Pm$\overline{3}$  (SG #200), which is actually a translationengleiche subgroup of Pm$\overline{3}$ n (SG #223), we expect that the structural transition under pressure to be first order according to Hermann’s theory (14, 15). The pressure–volume, $P\left(V\right)$ curve in zone I was analyzed using a second-order Birch-Murnaghan equation of state (BM EOS) as shown in Fig. 2E. For pressures up to ~18 GPa (zone I), the elastic parameters yield a zero-pressure bulk modulus B₀ of 103.5(2.0) GPa and a zero-pressure unit-cell volume V₀ of 297.89 ų at ambient conditions which is consistent with the reported value (9). The unit cell volume in zone III shows a clear deviation from the fitted curve based on the data points in zone I with the unit cell volume at ~34 GPa decreasing by ~4.8%, which is intricately linked to the structural transition and the substantial change in the valence of Eu ions. It is worth mentioning that the fitted parameters in zone I were also obtained from a larger volume of data taken from multiple experimental runs, as shown in SI Appendix, Fig. S5.

Fig. 2.

Pressure induced structural phase transition. (A) Selective powder X-ray diffraction (PXRD) patterns of EuPd₃S₄ at various pressures from 0 GPa to 56.9 GPa. The synchrotron X-ray wavelength λ is 0.4833 Å. The data were collected at room temperature. The full set is shown in SI Appendix, Fig. S1. (B) Rietveld refinement of the PXRD pattern at ambient pressure. (C) Le Bail fit to the high-pressure P4/mmm structure at 56.9 GPa. The pink stars and blue crosses in (B) and (C) represent the clear extra peaks in the PXRD spectra of copper (pressure manometer) and rhenium (gasket), respectively. (D) Pressure dependences of the refined lattice constants a and c. (E) Pressure dependence of the unit cell volume. The blue dashed curve shows the fitting by second-order Birch–Murnaghan equation of state (BM EOS). Several sets of independent PXRD measurements in zone I have been performed and show the same evolution of volume with the pressure. A more detailed plot is shown in SI Appendix, Fig. S5.

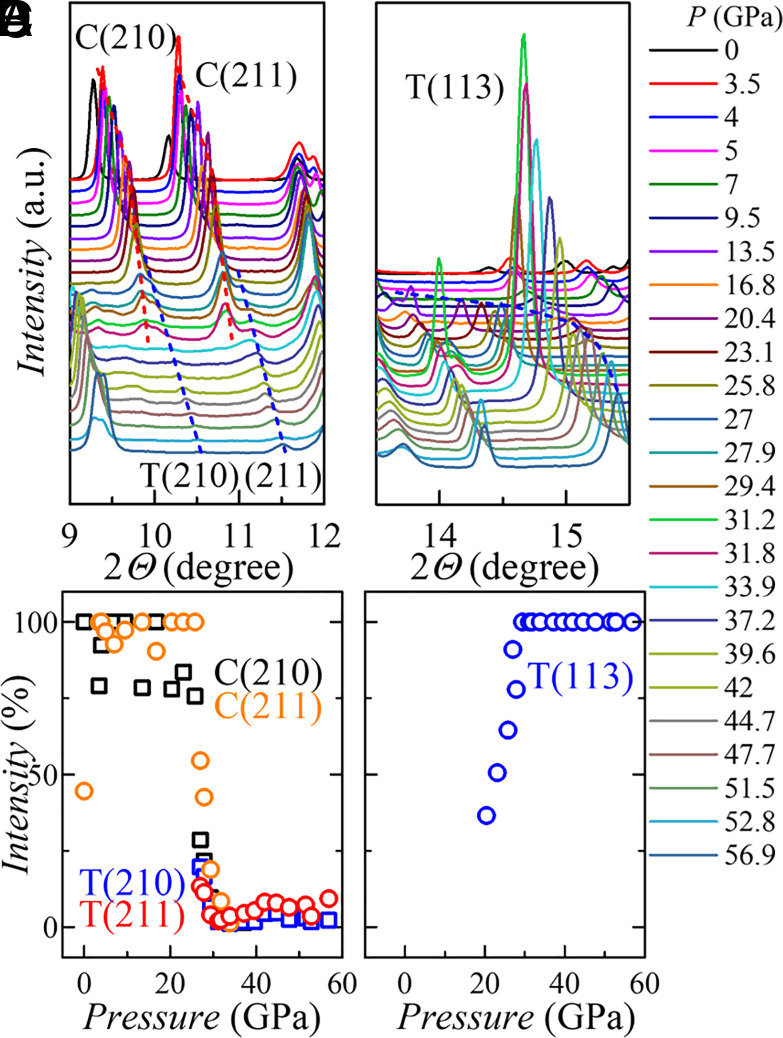
As diffraction peaks from both the cubic and tetragonal phases are observed in zone II, a two-phase scenario is a reasonable interpretation. The gradual disappearance of the cubic phase and the appearance and growth of the tetragonal phase can be seen clearly despite the increasing difficulty of indexing the diffraction patterns within zone II. Fig. 3 shows the changes of the specific diffraction peaks in detail, highlighting the disappearance of the cubic (210) and (211) Bragg peaks and the sudden emergence of the tetragonal (113) peak at ~20 GPa. SI Appendix, Figs. S2–S4 show more detail.

Fig. 3.

The evolution of diffraction peaks with the pressure in selected 2θ ranges. (A), (B) the cubic phase (210) and (211) (“cubic” is identified by “C”) to tetragonal (210) and (211) (“tetragonal” is identified by “T”); (C), (D) the emergence of T(113). (A) and (C) share the same legend. The red and blue dashed curves in (A) and (C) are the smooth guides to the eye of the position change of diffraction peaks. The percentage of the intensities in (B) and (D) are estimated by: (intensity of peak)/(maximum peak intensity in the spectrum).

A first-order structural phase transition typically involves a sudden change in lattice parameters and unit cell volume, and the presence of a two-phase region in the intermediate pressure zone. Fig. 2 D and E illustrate all these features clearly. However, the large two-phase window, more than 10 GPa, cannot simply be attributed to pressure gradients within the pressure transmitting medium since the pressure gradient in neon at 20 GPa is only 0.15 GPa (16), which is almost two orders of magnitude smaller than the observed two-phase pressure range. The broad two-phase region must therefore be considered to be an intrinsic feature associated with the valence change in EuPd₃S₄ under these conditions. An analogous large two-phase pressure range has also been reported in SmSe, SmTe (17), and CaFe₂As₂ (18, 19), possibly as a result of anharmonic strain effects caused by the significant volume mismatch between the various phases (20). Noteworthy, the Néel temperature plateau in Fig. 1D, where T_N (and T*) are almost independent of pressure, coincides well with the two-phase pressure region that has a mixed phase with shifting phase ratio. In other words, the behavior of the T_N plateau and the gradual loss of magnetic moment in the T_N plateau region are likewise intrinsic and may be closely related to the gradual increase in the relative amount of the tetragonal phase, and as will be shown below, nonmagnetic-Eu³⁺.

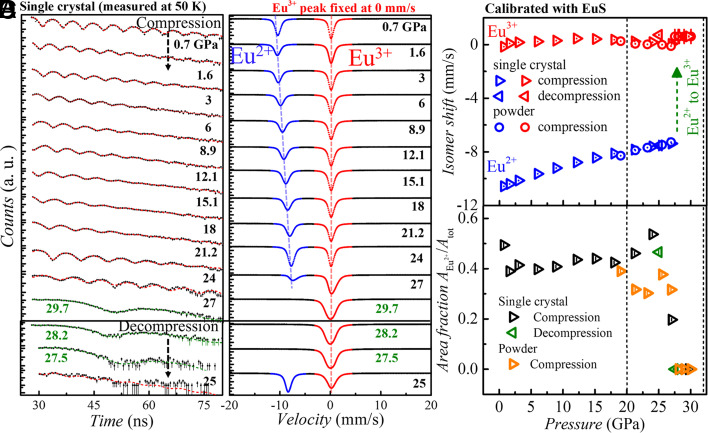
The conventional, energy-domain, ¹⁵¹Eu Mössbauer spectrum of EuPd₃S₄ shows two, roughly equal-area, well-separated lines from the Eu²⁺ and Eu³⁺ present (7, 9). These two lines reflect the two different transition energies (i.e., isomer shifts), and hence photon frequencies, associated with the two europium valence states. In the time-domain synchrotron Mössbauer spectroscopy (SMS) (11) spectra we observe a simple beat pattern between these two photon frequencies (see Fig. 4A at 0.7 GPa) with the beat frequency set by the fractional difference in photon energies (or frequencies), and the amplitude set largely by the relative populations of the two valence states. A visual inspection of Fig. 4A reveals that both change with increasing pressure: the beat frequency decreases, and the amplitude modulation generally becomes less distinct. The evolution in beat frequency indicates that the isomer shift difference between the two components is becoming smaller. Finally, there is an abrupt change in the curves above 27 GPa to a relatively very long beat period (rather than the simple exponential decay that we would associate with a single trivalent line) suggesting that the system is not just a cubic crystallographic phase with pure Eu³⁺.

Fig. 4.

Pressure-induced Eu valence transition from the isomer shift measurements. (A) The time domain 151Eu Synchrotron Mössbauer spectroscopy spectra (SMS) of EuPd₃S₄ at 50 K under various pressures taken using a single crystal sample with helium as the pressure transmitting medium. The pressure was measured at 50 K. Pressure was first increased from 0.7 GPa to 29.7 GPa, and then decreased to 25 GPa, in order to assess the reversibility of the pressure and the valence transition. The red dotted curves are fit to the SMS spectra using CONUSS (21). (B) Simulated energy-domain Mössbauer spectra based on the fitting results from each corresponding SMS spectrum. For these simulated patterns, the isomer shift of the Eu3+ peak was fixed to zero and only changes in the isomer shift and weight of the Eu2+ peaks are apparent. In (B), the blue and red dashed lines serve as visual aids to illustrate the evolution of Eu2+ isomer shift while Eu3+ remains fixed. The calibrated (using the EuS standard) pressure dependence of the absolute isomer shifts for the Eu2+ and Eu3+ peaks are shown for both samples in (C), while (D) shows the pressure dependence of the Eu2+ area fraction. The absolute value of isomer shift is calibrated by moving a reference sample (EuS, at room temperature and ambient pressure, with known isomer shift of Eu2+ at −11.496 mm/s) on the beam line. The detailed calibration process is explained in SI Appendix, Figs. S8 and S9.

More intuitive energy-domain spectra generated by CONUSS (21) by fitting the time-domain data are shown in Fig. 4B. Within the pressure range of 0.7 GPa to 27 GPa, two distinct peaks are observed, representing the isomer shifts of Eu²⁺ and Eu³⁺ at low pressures. For clarity, these two peaks are referred to as the Eu²⁺ and Eu³⁺ peaks, although it should be noted that the oxidation state of the Eu²⁺ peak tends to approach that of Eu³⁺ under pressure. The intensity of the Eu²⁺ peak weakens around 27 GPa and vanishes at 29.7 GPa, resulting in the sole presence of the Eu³⁺ peak, thereby indicating a complete transition from an initial nearly 50:50 Eu²⁺: Eu³⁺ state to a fully Eu³⁺ state. Concurrently, the linewidth of Eu³⁺ peak exhibits a clear broadening at 29.7 GPa compared to lower pressures. This can be attributed to the presence of a quadrupole interaction, $∆E\left(Q\right)$ , of 2.16(5) mm/s. This observation is consistent with the structural transition from a cubic to a tetragonal phase, where an electric field gradient develops as a result of the reduced symmetry. However, due to the crowded arrangement of multiple components split by the quadrupole interaction within the line width of ~2.3 mm/s, the absorption spectrum is not resolved. Furthermore, the quadrupole interaction, $∆E\left(Q\right)$ , increases within the pressure range of approximately 28 to 30 GPa, as shown in SI Appendix, Fig. S6. This increase can be attributed to the increase of structural anisotropy. The observed enhancement in the quadrupole interaction may correspond to the transition from a two-phase region, characterized by the presence of strain between the two phases, to a fully tetragonal phase. Upon decompression, the absorption peak corresponding to Eu²⁺ recovers at ~25 GPa, indicating the reversibility of the pressure-driven transition.

The isomer shift exhibited the same evolution with pressure in a second experimental run on a sintered powder sample (SMS data are shown in SI Appendix, Fig. S7) as it did for a single crystal sample. Absolute calibration of the isomer shifts of the two components was achieved by measuring SMS spectra at several pressures after introducing a standard (EuS) with a known isomer shift (−11.496 mm/s) in the beam after the pressure cell (detailed explanation of calibration of absolute values of isomer shifts is shown in SI Appendix, Figs. S8 and S9). These corrected measurements allowed us to show that most of the isomer shift change is due to the Eu²⁺ line moving to more positive values (Fig. 4C) with increasing pressure.

The pressure dependence of the area fraction of the Eu²⁺ peak is plotted in Fig. 4D. There are some differences between the powder and single crystal data in the ~21 to 27 GPa pressure range which are not surprising given their different microstructures and internal strain distributions. The pressure dependence of the mean Eu valence was estimated by assuming that the area of each component in the SMS spectrum was proportional to the number of ions associated with the corresponding valence state. The detailed calculation is shown in SI Appendix, Fig. S10, and the result is summarized in Fig. 5D, shown below.

Fig. 5.

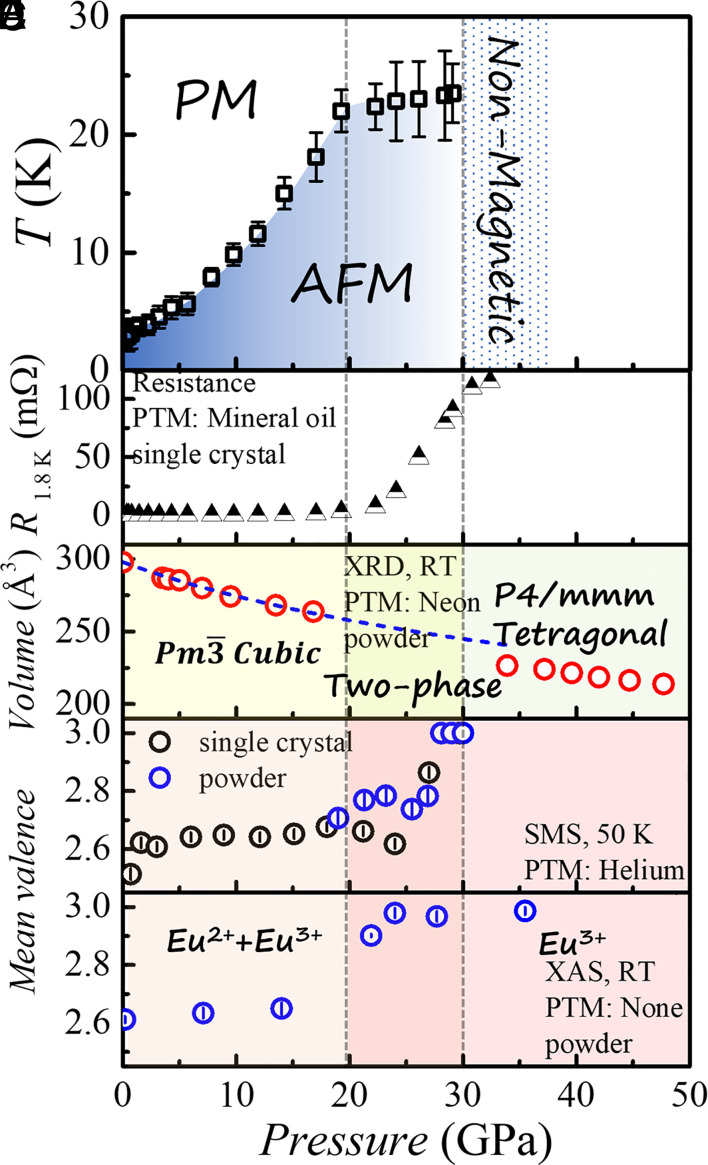
Pressure dependence of electronic, magnetic, and structural properties of EuPd₃S₄. The pressure dependence of (A) AFM transition temperature T_N, (B) resistance at 1.8 K, (C) unit cell volume estimated from the high-pressure X-ray diffraction measurement, (D) mean valence estimated from the Synchrotron Mössbauer spectroscopy (SMS) spectra, and (E) mean valence estimated from the partial fluorescence-yield X-ray absorption spectroscopy (PFY-XAS) spectra. PTM: pressure transmitting medium. RT: room temperature. The blue dashed curve in (C) is the second-order BM EOS fitted curve that shows the clear difference in the unit cell volume between zone I and zone III. The vertical dashed lines crossing all panels mark the lower and upper boundaries of the two-phase region determined from X-ray diffraction.

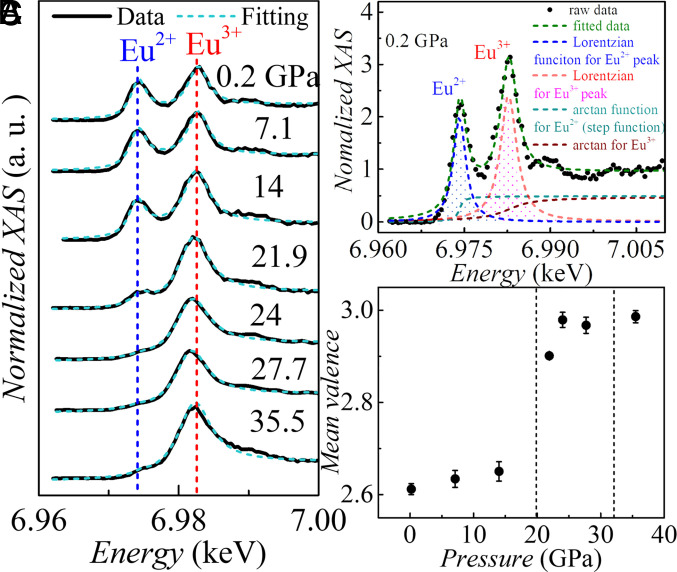
Partial fluorescence-yield X-ray absorption spectroscopy (PFY-XAS) measurements were performed to provide independent confirmation of the valence change. As shown in Fig. 6A, the absorption peak corresponding to Eu²⁺ gradually weakens as the pressure increases to 14 GPa, then becomes much weaker at ~22 GPa, and remains as a small bump for higher pressures, clearly demonstrating a transition from 50:50 Eu²⁺:Eu³⁺ to essentially Eu³⁺. The valence transition appears at a somewhat lower pressure in the PFY-XAS measurements than in the SMS results. Such a shift may be associated with nonhydrostaticity due to the lack of a pressure transmitting medium (PTM) in the PFY-XAS measurement. The persistence of a tiny Eu²⁺ peak at higher pressures may be attributed to pressure inhomogeneity. Furthermore, a small, but discernible shift toward slightly lower energy of the absorption peak corresponding to Eu³⁺ is noted at and above ~22 GPa. The possible reasons for this tiny shift in the absorption peak position, aside from experimental factors such as energy resolution and XAS instrument calibration, could be a change in the crystal field, which splits the 4f electronic state into different energy levels. This shift could be closely related to the structural transition that begins to occur between ~20 GPa and ~32 GPa. To fully comprehend the mechanism behind the absorption peak shift, additional research, such as DFT calculation based on the more accurate structure, is required.

Fig. 6.

Pressure induced valence transition from absorption spectra. (A) Partial fluorescenceyield X-ray absorption spectroscopy (PFY-XAS) data at Eu L3 absorption edge in EuPd₃S₄ at room temperature at pressures from 0.2 GPa to 35.5 GPa showing the valence transition from roughly 50:50 Eu2+:Eu3+ to essentially Eu3+. The blue and red vertical dashed lines are guides to the eye showing the absorption peak energies for Eu2+ and Eu3+, respectively. (B) Fits to the 0.2 GPa PFY-XAS data (described in the text). The red dashed line represents the total summation of two arctangent step functions and two Lorentzian peaks. (C) Mean Eu valence as a function of the pressure. The mean valence is estimated by from the ratio of the areas of fitted Lorentzian peaks.

Modeling the PFY-XAS data using a series of Lorentzian and arctangent functions for each absorption peak, as seen in Fig. 6B, yields the mean valence of the Eu ion. The average valence is estimated using the following formula:

$$v=\frac{2\times A_{{\text{Eu}}^{2+}}+3\times A_{{\text{Eu}}^{3+}}}{A_{{\text{Eu}}^{2+}}+A_{{\text{Eu}}^{3+}}},$$ [1]

where $A_{{\text{Eu}}^{2+}}$  and $A_{{\text{Eu}}^{3+}}$  are the areas of absorption peaks for Eu²⁺ and Eu³⁺, respectively. The estimated mean Eu valence as a function of pressure as measured by SMS and XAS are depicted in Fig. 5D and (Figs. 5E and 6C), respectively. Both measurements demonstrate a clear valence change from Eu²⁺ to Eu³⁺. The shift is abrupt and occurs at higher pressure (>~27 GPa) in the SMS measurements with He as the PTM. Due to the low data density and the fact that the high-pressure XAS measurement is conducted without PTM, it is not possible to determine the width of the valence transition; however, it is clear that the mean valence is very close to 3+ at and above 24 GPa.

Discussion

The pressure dependence of the AFM transition temperature T_N, resistance at 1.8 K, the volume of the unit cell, and the mean valences estimated from SMS and PTM data is presented in Fig. 5. Two vertical lines at ~20 and 30 GPa mark the lower and upper boundaries of the two-phase region and are shown crossing all the datasets. Although the use of different PTMs and manometers for different high-pressure measurements made at different temperatures may cause some inconsistency in the critical pressures and possible smearing of the first-order transition, a clear picture still can be obtained: There are three distinct pressure regions associated with i) the low-pressure cubic phase, ii) an intermediate pressure two-phase region where both cubic and tetragonal phases are present, and finally iii) the high-pressure tetragonal phase (Fig. 5C). Two pressures (~20 GPa and ~30 GPa) separate the changes we see in the T–P phase diagram shown in Fig. 5A as well as the $R\left(1.8\mathrm{K}\right)$ data shown in Fig. 5B. Fig. 5A shows that T_N rises rapidly in the low-pressure region, is essentially constant in the intermediate pressure region, and is not detectable (due to the loss of moment-bearing Eu²⁺) in the high-pressure region. Fig. 5B shows that the 1.8 K resistance of the low-pressure phase is relatively low and essentially unchanging in the low-pressure phase. In the intermediate pressure region, $R(1.8\mathrm{K})$ rises substantially in a near linear manner before appearing to saturate above 30 GPa. The unit cell volumes for the low-pressure and high-pressure phases are shown in Fig. 5C. In the two-phase region, there is an increasing amount of tetragonal phase as pressure increases. The estimated mean valence derived from SMS results is shown in Fig. 5D. The mean valence is nearly constant up to ~20 GPa, increases in a nonmonotonic manner, depending upon the run and sample, over the next 10 GPa and is fully trivalent at and above 30 GPa. The mean valence derived from XAS data in Fig. 5E is fully consistent with the SMS data but suffers from two problems. First, the XAS data is the only dataset collected without pressure medium and as such represents very different pressure conditions; second, the XAS dataset is too sparse to accurately detect an onset to valence change. All of this said, the XAS dataset is qualitatively similar to the SMS data, showing a change from roughly 50: 50 Eu²⁺: Eu³⁺ to essentially Eu³⁺ by ~25 GPa. The fact that this pressure is lower than any seen in the other measurements is most likely associated with the less hydrostatic conditions. Taken all together, then, our diverse datasets are consistent with EuPd₃S₄ being in the low-pressure cubic phase up to ~20 GPa. In this pressure range there is a large increase in T_N that we associated with an increasing coupling (or hybridization) between the Eu 4f shell and the conduction electrons. Whereas such large $d{T}_{\mathit{N}}/dP$ values are rather uncommon for rare-earth compounds, similarly large values have been found for some Eu-based intermetallics, such as EnIn₂As₂ (22), EuSn₂As₂ (23), EuSn₂P₂. (24), and EuMnBi₂ (25).

Ultimately, when the coupling (or hybridization) between the conduction electrons and the Eu-4f-shell becomes sufficiently strong, EuPd₃S₄ starts transforming into the high pressure, Eu³⁺-tetragonal phase and enters the two-phase region of the T–P phase diagram. As more and more of the sample transforms into the smaller volume, tetragonal phase, the residual cubic EuPd₃S₄ remains at a more or less constant strain and constant T_N and T*. The pressure range of this two-phase region, ~20 to 30 GPa, is fully consistent with change in volume of the unit cells (between cubic and tetragonal) and their pressure derivatives (Fig. 2E). Finally, near 30 GPa, the conversion is complete, and the sample becomes fully tetragonal and fully nonmagnetic Eu³⁺.

The EuPd₃S₄ T–P phase diagram differs from the putative “global phase diagram” (26, 27) for Eu-based compounds in several ways. Qualitatively the size of the increase in T_N for EuPd₃S₄ is remarkable, over 800% increase by ~20 GPa; this is much larger than seen for other Eu compounds. Quantitatively, the global phase diagram has the second order T_N line ending in an isostructural, first-order structural phase transition line that has a finite slope and terminates in a critical end point. Whereas, EuPd₃S₄ has a structural phase transition from a low-pressure cubic phase to a high-pressure, trivalent, tetragonal phase with an experimentally vertical phase line and an approximately 10 GPa wide, two phase coexistence region. As such, then, a critical end point is impossible. In this sense, EuPd₃S₄ is a particularly clean, stable, and well-behaved system that even at ambient conditions exhibits a rare, possibly unique, inhomogeneous mixed-valence state, making it a convenient and powerful test bed for models of mixed-valent behavior. In addition, the significant departures from the predicted global phase diagrams (26, 27) mean that EuPd₃S₄ presents a unique example of pressure-induced, valence collapse. Despite the extensive exploration and continued attention given to Ce- and Yb-based systems, the rich phenomenology of Eu-based systems has remained largely uncharted. Our finding provides a significant prototype within the Eu-based system, revealing distinct behaviors under high pressure, thereby igniting the potential for further in-depth investigations.

Materials and Methods

Crystal Growth.

High-quality single crystals of EuPd₃S₄ were grown by a two-step solution growth method by adding Eu to a Pd-S melt (28). First, a nominal composition of Eu₅Pd₅₈S₃₇ was loaded into a fritted alumina crucible set (29, 30) and sealed in a fused silica tube. The tube was heated to 1150 °C, held for 8 h, and cooled over 36 h to 1,050 °C, after which the liquid was decanted. The tube was opened, all solidified sulfides and oxides were discarded, and the captured decanted liquid reused in a new crucible set. The second crucible set was again sealed and then warmed to 1,075 °C. After holding for 8 h, the furnace was slowly cooled over 150 h to 900 °C, at which point the remaining solution was decanted. After cooling to room temperature, the crucibles were opened to reveal large, mirror-faceted crystals (28).

The polycrystal samples (used for synchrotron X-ray diffraction, Mössbauer spectroscopy, and X-ray absorption spectroscopy measurements) were prepared by a direct solid-state reaction from a stoichiometric mixture of EuS (99.9%), Pd (99.95%), and S (99.95%) powders (9). The mixture was pressed into a pellet, loaded in an alumina crucible, and sealed in a fused silica tube with a partial pressure of helium gas. The tube was heated to 650 °C over 3 h, held for an hour and then heated to 900 °C over 3 h, and held for 90 h before furnace cooling. The resulting, sintered pellets were checked for phase purity by powder X-ray diffraction and then, as needed, ground, repressed into a pellet, and heated again to 900 °C for further reaction (9).

High-Pressure Measurements.

Electrical transport.

Linear four-terminal electrical resistivity measurements were performed in a Diamond Anvil cell (DAC) [Bjscistar (31)], with 500-μm culet-size standard cut-type Ia diamonds. EuPd₃S₄ single crystals were cleaved into 20-μm-thick flakes and cut and polished into 100 μm × 40 μm plates. A single plate was loaded together with a tiny ruby sphere (<10 μm in diameter) into an apertured stainless-steel gasket covered by cubic-BN. Platinum foil was used to create electrodes to connect to the sample. Nujol mineral oil was used as pressure transmitting medium (PTM), since 1) this fluid medium can maintain a quasi-hydrostatic pressure environment with a small pressure gradient below its liquid/glass transition (16, 32, 33), and 2) the use of a fluid medium helps to minimize direct contact between the sample and diamond culet which could lead to an uniaxial pressure component. Pressure was determined by ruby fluorescence (34) at room temperature. Low-temperature resistance measurements down to 1.8 K were conducted in the Quantum Design Physical Property Measurement System (PPMS).

X-ray Diffraction (XRD).

Two room-temperature high-pressure powder XRD (PXRD) runs were carried out at the GSECARS 13-BM-D and XSD 3-ID-B Beamlines of the Advanced Photon Source (APS), at Argonne National Laboratory (ANL). X-rays with a wavelength of 0.29521 Å and 0.4833 Å were focused to a 15 µm (vertical) × 15 µm (horizontal) spot size at both beamlines. The sintered powder sample and manometer (ruby spheres for runs 1 and 2, Cu powder for run 3) were loaded into a wide opening SSDAC-70 DAC, diamond anvils with 300 µm and 500 µm diameter culets and Re gaskets were used to contain the sample. Neon was loaded as the PTM. Pressures were determined in situ using the ruby scale (34) or the equation of state of the Cu standard (JCPDS 04-0836) at the same position where the PXRD data were taken on the sample. The two-dimensional diffraction images were integrated using the DIOPTAS software (35) and Rietveld and Le Bail refinements were performed in GSAS-II (36). PXRD data shown in the main text are all from run 3.

Synchrotron Mössbauer Spectroscopy (SMS).

High-pressure ¹⁵¹Eu SMS (11) experiments were carried out at 3-ID-B Beamline of the APS, at ANL. SMS, also known as nuclear forward scattering (NFS), utilizes a pulsed synchrotron X-ray source to probe nuclear hyperfine interactions in the time domain rather than the energy domain used for conventional Mössbauer spectroscopy. The SMS experiments were performed in the 24-bunch timing mode with a 153 ns separation between successive electron bunches. A specially designed helium-flow cryostat cooled the sample to 50 K while high pressures were generated using a membrane-driven miniature panoramic DAC (37). Five hundred micrometer culet size diamonds were used as anvils and a laser drilled Re gasket formed the sample chamber. The SMS spectra were fitted using the CONUSS software package (21).

Both single crystal and sintered powder samples were measured by SMS. All the SMS measurements were performed at 50 K. This temperature was chosen for operational convenience: low enough to benefit from a factor of two increase in the recoil-free fraction (f-factor) compared with ambient temperatures (9) but high enough to remain above the expected pressure-driven increase in T_N. Helium was used as PTM to promote hydrostatic conditions at high pressure. After gas loading at room temperature, all subsequent pressure changes were made by the gas membrane at 50 K. Using an online system, laser-excited ruby fluorescence spectra were collected for the determination of pressure using the ruby scale (34). Pressure-induced changes in the europium valence, as well as structure, have been detected through either a change in the isomer shifts of the two preexisting components (Eu²⁺ and Eu³⁺) or changes in their relative proportions. Absolute isomer shift values were obtained at several pressures by adding a reference sample (EuS) with a known isomer shift (−11.496 mm/s relative to EuF₃) in the X-ray beam (38–40).

Partial Fluorescence-Yield X-ray Absorption Spectroscopy (PFY-XAS).

PFY-XAS experiments were carried out at the 16ID-D Beamline of the APS, at ANL, to provide direct information about the europium valence state and corroborate any possible changes suggested by the isomer shift measurements. The XAS experiment was carried out at Eu L₃ edge (6.97 keV, 2p_3/2 → 5d transition) at pressures up to ~36 GPa. A pair of 300-μm culet diamonds were used as anvils. The sintered powder sample (a small piece in ~50 μm size) was loaded together with a tiny ruby sphere into the aperture of the laser-drilled beryllium gasket and an insert formed by cubic boron nitride and epoxy. No PTM was added with the sample serving as its own transmission medium. As a result, the PFY-XAS measurements are expected to suffer the most from potentially nonhydrostatic effects. Pressures were measured in situ using ruby fluorescence (34). To avoid heavy absorption by the diamond anvils at these low (~7 keV) X-ray energies, the XAS data were taken with the incident beam going through the beryllium gasket and the absorption signal being taken in fluorescence geometry (90° to the incident beam) using a Pilatus detector. The X-rays were focused to 5 µm [the Full Width Half Maximum (FWHM)]. The beam spot location was carefully determined by scanning the sample position to minimize self-absorption.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.