Genomic loci influence patterns of structural covariance in the human brain

Significance

The coordinated patterns of changes in the human brain throughout life, driven by brain development, aging, and diseases, remain largely unexplored regarding their underlying genetic determinants. This study delineates 2,003 multi-scale patterns of structural covariance (PSCs) and identifies 617 newly identified genomic loci, with the mapped genes enriched in biological pathways implicated in reelin signaling, apoptosis, neurogenesis, and appendage development. Overall, the 2,003 PSCs provide genetic insights into understanding human brain morphological changes and demonstrate great potential in predicting various neurologic conditions.

Abstract

Normal and pathologic neurobiological processes influence brain morphology in coordinated ways that give rise to patterns of structural covariance (PSC) across brain regions and individuals during brain aging and diseases. The genetic underpinnings of these patterns remain largely unknown. We apply a stochastic multivariate factorization method to a diverse population of 50,699 individuals (12 studies and 130 sites) and derive data-driven, multi-scale PSCs of regional brain size. PSCs were significantly correlated with 915 genomic loci in the discovery set, 617 of which are newly identified, and 72% were independently replicated. Key pathways influencing PSCs involve reelin signaling, apoptosis, neurogenesis, and appendage development, while pathways of breast cancer indicate potential interplays between brain metastasis and PSCs associated with neurodegeneration and dementia. Using support vector machines, multi-scale PSCs effectively derive imaging signatures of several brain diseases. Our results elucidate genetic and biological underpinnings that influence structural covariance patterns in the human brain.

Brain structure and function are interrelated via complex networks that operate at multiple scales, ranging from cellular and synaptic processes, such as neural migration, synapse formation, and axon development, to local and broadly connected circuits (1). Due to a fundamental relationship between activity and structure, many normal and pathologic neurobiological processes, driven by genetic and environmental factors, collectively cause coordinated changes in brain morphology. Structural covariance analyses investigate such coordinated changes by seeking patterns of structural covariation (PSC) across brain regions and individuals (1). For example, during adolescence, PSCs derived from MRI have been considered to reflect a coordinated cortical remodeling as the brain establishes mature networks of functional specialization (2). Structural covariance is not only related to normal brain development or aging processes but can also reflect coordinated brain change due to disease. For example, individuals with motor speech dysfunction may develop brain atrophy in Broca's inferior frontal cortex and co-occurring brain atrophy in Wernicke’s area of the superior temporal cortex (3). Refer to Fig. 1C for an illustrative depiction.

Fig. 1.

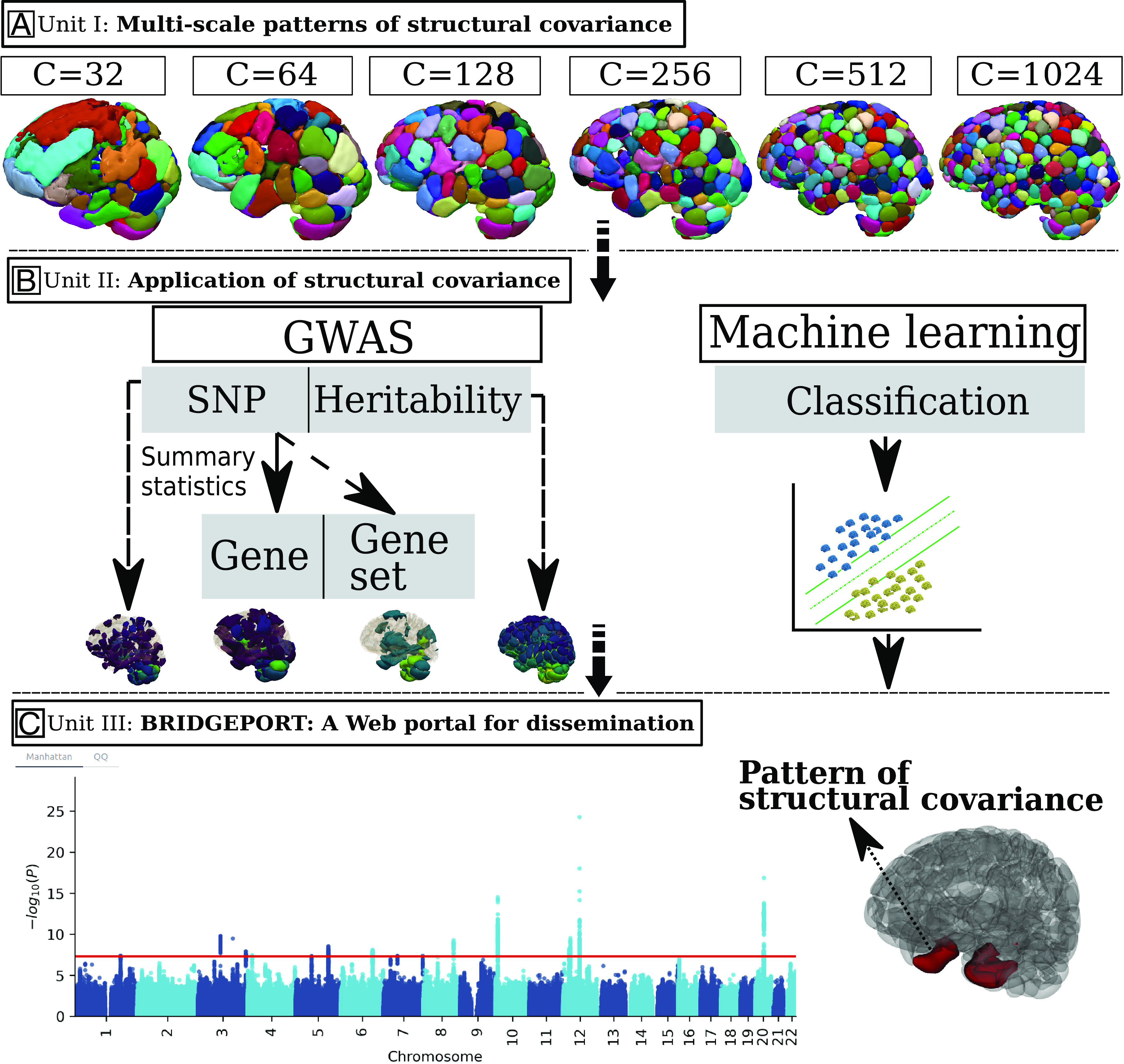
Study workflow. (A) Unit I: The stochastic orthogonally projective non-negative matrix factorization (sopNMF) algorithm was applied to a large, disease-diverse population to derive multi-scale patterns of structural covariance (PSC) at different scales (C = 32, 64, 128, 256, 512, and 1,024; C represents the number of PSCs). (B) Unit II: Two types of analyses were performed in this study: Genome-wide association studies (GWAS) relate each of the PSCs (N = 2,003) to common genetic variants; pattern analysis via machine learning demonstrates the utility of the multi-scale PSCs in deriving individualized imaging signatures of various brain pathologies. (C) Unit III: BRIDGEPORT is a web portal that makes all resources publicly available for dissemination. As an illustration, a Manhattan plot for PSC (C64-3, the third PSC of the C64 atlas) and its 3D brain map are displayed.

The human brain develops, matures, and degenerates in coordinated patterns of structural covariance at the macrostructural level of brain morphology (1). However, the mechanisms underlying structural covariance are still unclear, and their genetic underpinnings are largely unknown. We hypothesized that brain morphology was driven by multiple genes (i.e., polygenic) collectively operating on different brain areas (i.e., pleiotropic), resulting in connected networks covaried by normal aging and various disease-related processes. Along the causal pathway from underlying genetics to brain morphological changes, we sought to elucidate which genetic underpinnings (e.g., genes), biological processes (e.g., neurogenesis), cellular components (e.g., nuclear membrane), molecular functions (e.g., nucleic acid binding), and neuropathological processes (e.g., Alzheimer's disease) might influence the formation, development, and changes of structural covariance patterns in the human brain.

Previous neuroimaging genome-wide association studies (GWAS) (4, 5) have partially investigated the abovementioned questions and expanded our understanding of the genetic architecture of the human brain. However, they focused on conventional neuroanatomical regions of interest (ROI) instead of data-driven PSCs. In brain imaging research, prior studies have applied structural covariance analysis to elucidate underlying coordinated morphological changes in brain aging and various brain diseases (1) but have had several limitations. They often relied on pre-defined neuroanatomical ROIs to construct inter- and intra-individual structural covariance networks. These a priori ROIs might not optimally reflect the molecular-functional characteristics of the brain. In addition, most population-based studies have investigated brain structural covariance within a relatively limited scope, such as within relatively small samples, over a relatively narrow age window [e.g., adolescence (2)], within a single disease [e.g., Parkinson’s disease (6)], or within datasets lacking sufficient diversity in cohort characteristics or MRI scanner protocols. These have been imposed, in part, by limitations in both available cohort size and in the algorithmic implementation of structural covariance analysis, which has been computationally restricted to modest sample sizes when investigated at full image resolution. Last, prior studies have examined brain structural covariance at a single fixed ROI resolution/scale/granularity. While the optimal scale is unknown and may differ by the question of interest, the highly complex organization of the human brain may demonstrate structural covariance patterns that span multiple scales (7, 8).

To address this gap, we modified our previously proposed orthogonally projective non-negative matrix factorization [opNMF (9)] to its stochastic counterpart, sopNMF. This adaptation allowed us to train the model iteratively on large-scale neuroimaging datasets with a pre-defined number of PSCs (C). Non-negative matrix factorization has gained significant attention in neuroimaging due to its ability to reduce complex data into a sparse, part-based brain representation by projection onto a relatively small number of components (the PSCs). NMF has been shown to substantially improve interpretability and reproducibility compared to other unsupervised methods, such as PCA and ICA, thanks to the non-negative constraint that produces parcellation-like decompositions of complex signals. Our opNMF/sopNMF approach imposed an additional orthonormality constraint (9) (Eq. 1 in Method 1), further enhancing sparsity and facilitating clinical interpretability. In our previous work, we applied the opNMF method to 934 youths ages 8 to 20 to depict the coordinated growth of structural brain networks during adolescence—a period characterized by extensive remodeling of the human cortex to accommodate the rapid expansion of the behavioral repertoire (2). Remarkably, this study revealed PSCs that exhibited a cortical organization closely aligned with established functional brain networks, such as the well-known 7-network functional parcellation proposed by Yeo et al. (10). Notably, this alignment emerged without prior assumptions, was data driven, and hypothesis-free, and potentially reflected underlying neurobiological processes related to brain development and aging. Herein, we used large-scale neuroimaging data to investigate the underlying genetic determinant influencing such changes in structural covariance patterns in the human brain.

We examined structural covariance of regional cortical and subcortical volume in the human brain using MRI from a diverse population of 50,699 people from 12 studies, 130 sites, and 12 countries, comprised of cognitively healthy individuals, as well as participants with various diseases/conditions over their lifespan (ages 5 through 97). Herein, we present results from coarse to fine scales corresponding to C = 32, 64, 128, 256, 512, and 1,024. We hypothesized that PSCs at multiple scales could delineate the human brain's multi-factorial and multi-faceted morphological landscape and genetic architecture in healthy and diseased individuals. We examined the associations between these multi-scale PSCs and common genetic variants at different levels (N = 8,469,833 SNPs). In total, 617 newly identified genomic loci were identified; key pathways (e.g., neurogenesis and reelin signaling) contributed to shaping structural covariance patterns in the human brain. In addition, we leveraged PSCs at multiple scales to better derive individualized imaging signatures of several diseases than any single-scale PSCs using support vector machines. All experimental results and the multi-scale PSCs were integrated into the MuSIC (Multi-scale Structural Imaging Covariance) atlas and made publicly accessible through the BRIDGEPORT (BRaIn knowleDGE PORTal) web portal: https://www.cbica.upenn.edu/bridgeport/. Table 1 provides an overview of the abbreviations used in the present study.

Table 1.

Abbreviations used in the present study

Item	Abbreviation	Item	Abbreviation
Pattern of structural covariation	PSC	Independent component analysis	ICA
Genome-wide association study	GWAS	BRaIn knowleDGE PORTal	BRIDGEPORT
Orthogonal projective non-negative matrix factorization	opNMF	Multi-scale Structural Imaging Covariance	MuSIC
Stochastic orthogonal projective non-negative matrix factorization	sopNMF	Machine learning	ML
Principal component analysis	PCA	UK Biobank	UKBB
Imaging-based coordinate SysTem for AGing and NeurodeGenerative diseases	iSTAGING	Psychosis heterogeneity evaluated via dimensional neuroimaging	PHENOM
Single nucleotide polymorphism	SNP	Region of interest	ROI
MRI	MRI	Automated anatomical labeling	AAL
MUlti-atlas region Segmentation utilizing Ensembles	MUSE	Alzheimer’s disease	AD
Spatial PAtterns for REcognition	SPARE	Support vector machine	SVM

Results

We summarize this work in three units (I to III) outlined in Fig. 1. In Unit I (Fig. 1A), we present the stochastic orthogonally projective non-negative matrix factorization (sopNMF) algorithm (Method 1), optimized for large-scale multivariate structural covariance analysis. The sopNMF algorithm decomposes large-scale imaging data through online learning to overcome the memory limitations of opNMF. A subgroup of participants with multiple disease diagnoses and healthy controls (ages 5 to 97, training population, N = 4,000, Method 2) were sampled from the discovery set (N = 32,440, Method 2); their MRI underwent a standard imaging processing pipeline (Method 3A). The processed images were then fit to sopNMF to derive the multi-scale PSCs (N = 2,003) from the loadings of the factorization (Method 1). We incorporate participants with various disease conditions because previous studies have demonstrated that inter-regional correlated patterns (i.e., depicting a network) show variations in healthy and diseased populations, albeit to a differing degree (11). Multi-scale PSCs were extracted across the entire population and statistically harmonized (12) (Method 3B). Unit II (Fig. 1B) investigates the harmonized data for 2,003 PSCs (13 PSCs have vanished in this process for C = 1,024; see Method 1) in two brain structural covariance analyses. Specifically, we performed i) GWAS (Method 4) that sought to discover associations of PSCs at single nucleotide polymorphism (SNP), gene, or gene set-level; and ii) pattern analysis via support vector machine (Method 5) to derive individualized imaging signatures of several brain diseases and conditions. Unit III (Fig. 1C) presents BRIDGEPORT, making these massive analytic resources publicly available to the imaging, genomics, and machine learning communities.

Patterns of Structural Covariance via Stochastic Orthogonally Projective Non-Negative Matrix Factorization.

We first validated the sopNMF algorithm by showing that it converged to the global minimum of the factorization problem using the comparison population (N = 800, Method 2). The sopNMF algorithm achieved similar reconstruction loss and sparsity as opNMF but at reduced memory demand (SI Appendix, eFigure 1). The lower memory requirements of sopNMF made it possible to generate multi-scale PSCs by jointly factorizing 4,000 MRIs in the training population. The results of the algorithm were robust and obtained a high reproducibility index (RI) (SI Appendix, eMethod 2) in several reproducibility analyses: split-sample analysis (RI = 0.76 $\pm$ 0.27), split-sex analysis (RI = 0.79 $\pm$ 0.27), and leave-one-site-out analysis (RI = 0.65 to 0.78 for C32 PSCs) (SI Appendix, eFigure 2). We then extracted the multi-scale PSCs in the discovery set (N = 32,440) and the replication set (N = 18,259, Method 2) for Unit II. These PSCs succinctly capture underlying neurobiological processes across the lifespan, including the effects of typical aging processes and various brain diseases. In addition, the multi-scale representation constructs a hierarchy of brain structure networks (e.g., PSCs in cerebellum regions), which models the human brain in a multi-scale topology (7, 13).

Patterns of Structural Covariance Are Highly Heritable.

The multi-scale PSCs are highly heritable (0.05 < h² < 0.78), showing high SNP-based heritability estimates (h²) (Method 4B) for the discovery set (Fig. 2). Specifically, the h² estimate was 0.49 $\pm$ 0.10, 0.39 $\pm$ 0.14, 0.29 $\pm$ 0.15, 0.25 $\pm$ 0.15, 0.27 $\pm$ 0.15, and 0.31 $\pm$ 0.15 for scales C = 32, 64, 128, 256, 512, and 1024 of the PSCs, respectively. The Pearson correlation coefficient between the two independent estimates of h² was r = 0.94 (P-value < 10^–6, between the discovery and replication sets) in the UK Biobank (UKBB) data. The scatter plot of the two sets of h² estimates is shown in SI Appendix, eFigure 3. The h²estimates and P-values for all PSCs are detailed in Dataset S1 (discovery set) and Dataset S2 (replication set). Our results confirm that brain structure is heritable to a large extent and identify the spatial distribution of the most highly heritable regions of the brain (e.g., subcortical gray matter structures and cerebellum regions) (14).

Fig. 2.

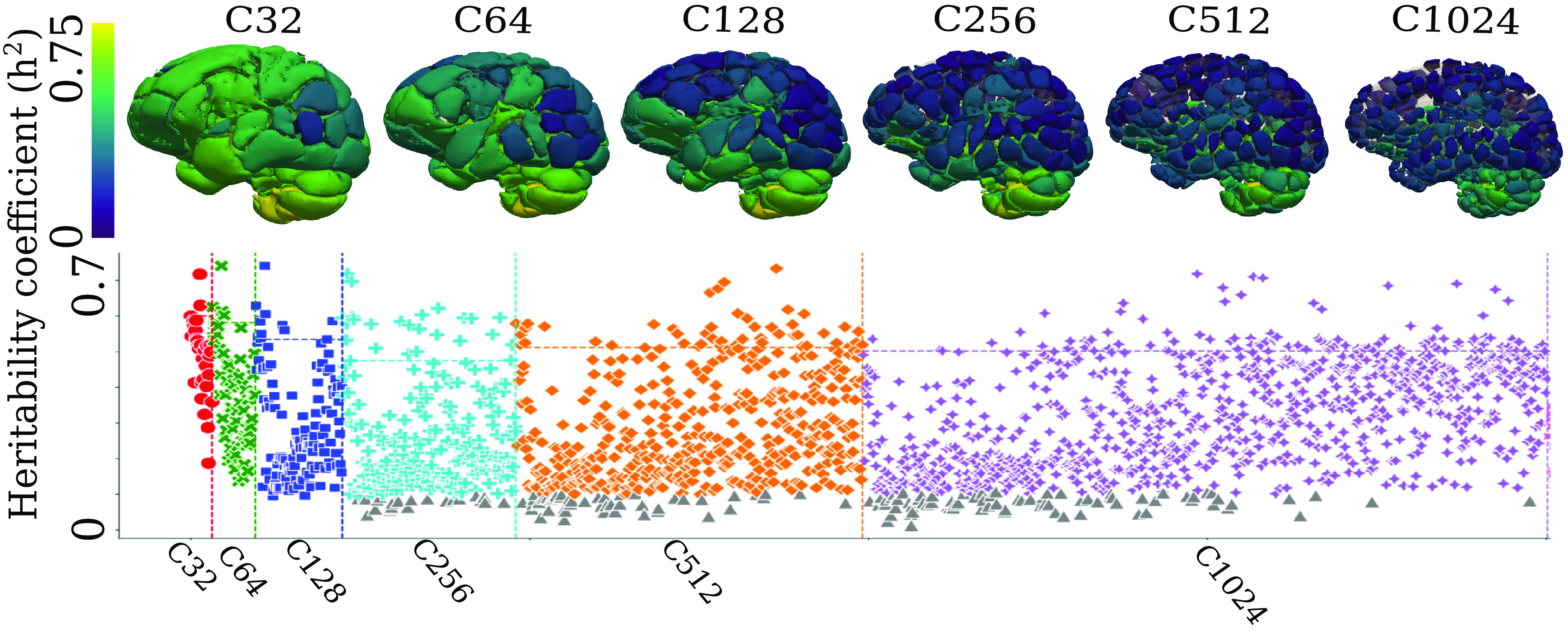
Patterns of structural covariance are highly heritable in the human brain. The SNP-based heritability estimates are calculated for the multi-scale PSCs at different scales (C). PSCs surviving Bonferroni correction for multiple comparisons are depicted in color in the Manhattan plots (gray otherwise). Each PSC’s heritability estimate (h2) was projected onto the 3D image space to show a statistical map of the brain at each scale C. The dotted line indicates each scale’s top 10% of most heritable PSCs.

617 Newly Identified Genomic Loci of Patterns of Structural Covariance.

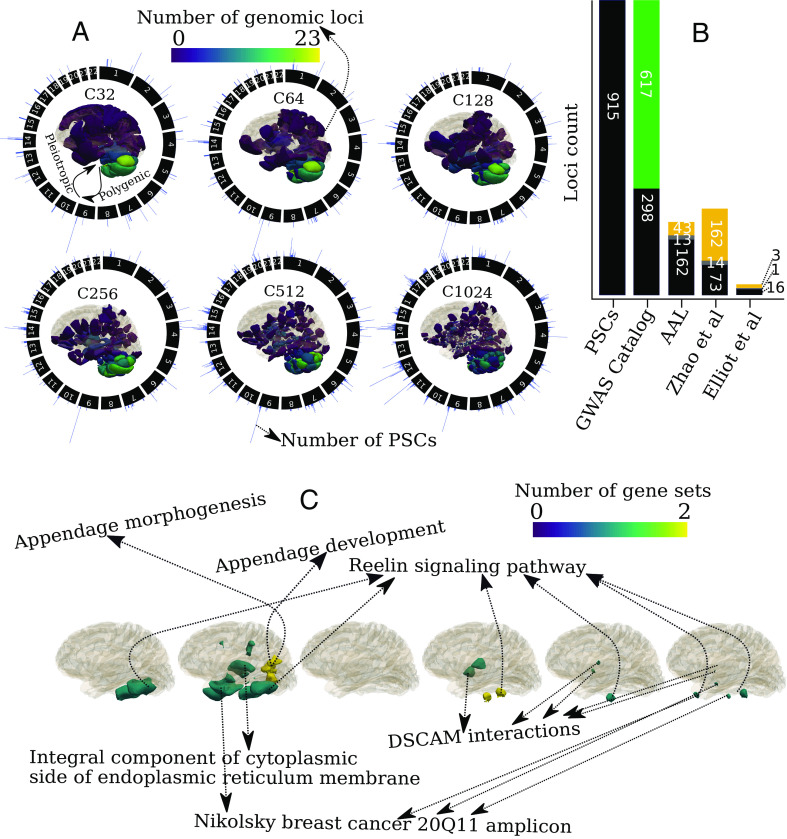
We found genomic locus–PSC pairwise associations (Method 4C, SI Appendix, eMethod 5) within the discovery set and then independently replicated these associations on the replication set. We found that 915 genomic loci had 3,791 loci–PSC pairwise significant associations with 924 PSCs after Bonferroni correction (Method 4G) for the number of PSCs (P-value threshold per scale: 10.3 > −log₁₀[P-value] > 8.8) (Dataset S3 and Fig. 3A). Our results showed that the formation of these PSCs is largely polygenic; the associated SNPs might play a pleiotropic role in shaping these networks.

Fig. 3.

Patterns of structural covariance highlight newly identified genomic loci and pathways that shape the human brain. (A) Patterns of structural covariance (PSC) in the human brain are polygenic: The number of genomic loci of each PSC is projected onto the image space to show a statistical brain map characterized by the number (C) of PSCs. In addition, common genetic variants exert pleiotropic effects on the PSCs: circular plots showed the number of associated PSCs (histograms in blue color) of each genomic loci over the entire autosomal chromosome (1 to 22). The histogram was plotted for the number of PSCs for each genomic locus in the circular plots. (B) Newly identified genomic loci revealed by the multi-scale PSCs compared to previous findings from the GWAS Catalog (15), T1-weighted MRI GWAS (4, 5), and the AAL atlas regions of interest. The green bar indicates the 617 newly identified genomic loci not previously associated with any clinical traits in GWAS Catalog; the black bar presents the loci identified in other studies that overlap (gray bar for loci in linkage disequilibrium) with the loci from our results; the yellow bar indicates the unique loci in other studies. (C) Pathway enrichment analysis highlights six unique biological pathways and functional categories (after Bonferroni correction for 16,768 gene sets and the number of PSCs) that might influence the changes of PSCs. DSCAM: Down syndrome cell adhesion molecule.

Compared to previous literature, out of the 915 genomic loci, the multi-scale PSCs identified 617 newly identified genomic loci not previously associated with any traits or phenotypes in the GWAS Catalog (15) (Dataset S4 and Fig. 3B, query date: April 5th, 2023). These associations might indicate subtle neurobiological processes that are captured thanks to the biologically relevant structural covariance expressed by sopNMF. The multi-scale PSCs identified many associations by constraining this comparison to previous neuroimaging GWAS (12, 13) using T1w MRI-derived phenotypes (e.g., regions of interest from conventional brain atlases) (Fig. 3B and SI Appendix, eTable 3 and Datasets S5–S7).

Our UKBB replication set analysis (Method 4H) demonstrated that 3,638 (96%) exact genomic locus–PSC associations were replicated at nominal significance (−log₁₀[P-value] > 1.31), 2,705 (72%) of which were significant after correction for multiple comparisons (Method 4G, −log₁₀[P-value] > 4.27). We present this validation in Dataset S8 from the replication set. The summary statistics, Manhattan, and QQ plots derived from the combined population (N = 33,541) are presented in BRIDGEPORT. In addition to the abovementioned replication analyses, we also performed several sensitivity analyses (SI Appendix, eFigure 4A). Our findings revealed the robustness of GWAS signals across both the discovery and replication sets, even when considering four additional brain-related covariates. However, the generalizability of these signals was limited in non-European ancestry populations and independent disease-specific populations (SI Appendix, eText 1 and eFigure 4).

Gene Set Enrichment Analysis Highlights Pathways That Shape Patterns of Structural Covariance.

For gene-level associations (Method 4D), we found that 164 genes had 2,489 gene-PSC pairwise associations with 445 PSCs after Bonferroni correction for the number of genes and PSCs (P-value threshold: 8.6 > −log₁₀[P-value] > 7.1) (Dataset S9).

Based on these gene-level P-values, we performed hypothesis-free gene set pathway analysis using MAGMA (16) (Method 4E): a more stringent correction for multiple comparisons was performed than the prioritized gene set enrichment analysis using GENE2FUN from FUMA (Method 4F and Fig. 4). We identified that six gene set pathways had 18 gene set-PSC pairwise associations with 17 PSCs after Bonferroni correction for the number of gene sets and PSCs (N = 16,768 and C from 32 to 1,024, P-value threshold: 8.54 > −log₁₀[P-value] > 7.03) (Fig. 3C and Dataset S10). These gene sets imply critical biological and molecular pathways that might shape brain morphological changes and development. The reelin signaling pathway regulates neuronal migration, dendritic growth, branching, spine formation, synaptogenesis, and synaptic plasticity (17). The appendage morphogenesis and development pathways indicate how the anatomical structures of appendages are generated, organized, and progressed over time, often related to the cell adhesion pathway. These pathways elucidate how cells or tissues can be organized to create a complex structure like the human brain. In addition, the integral component of the cytoplasmic side of the endoplasmic reticulum membrane is thought to form a continuous network of tubules and cisternae extending throughout neuronal dendrites and axons (18). The DSCAM (Down syndrome cell adhesion molecule) pathway likely functions as a cell surface receptor mediating axon pathfinding. Related proteins are involved in hemophilic intercellular interactions (19). Last, Nikolsky et al. (20) defined genes from the breast cancer 20Q11 amplicon pathway that were involved in the brain might indicate the brain metastasis of breast cancer, which is usually a late event with deleterious effects on the prognosis (21). In addition, previous findings (22, 23) revealed an inverse relationship between Alzheimer’s disease and breast cancer, which might indicate a close genetic relationship between the disease and brain morphological changes mainly affecting the entorhinal cortex and hippocampus (PSC: C128_3 in Fig. 4).

Fig. 4.

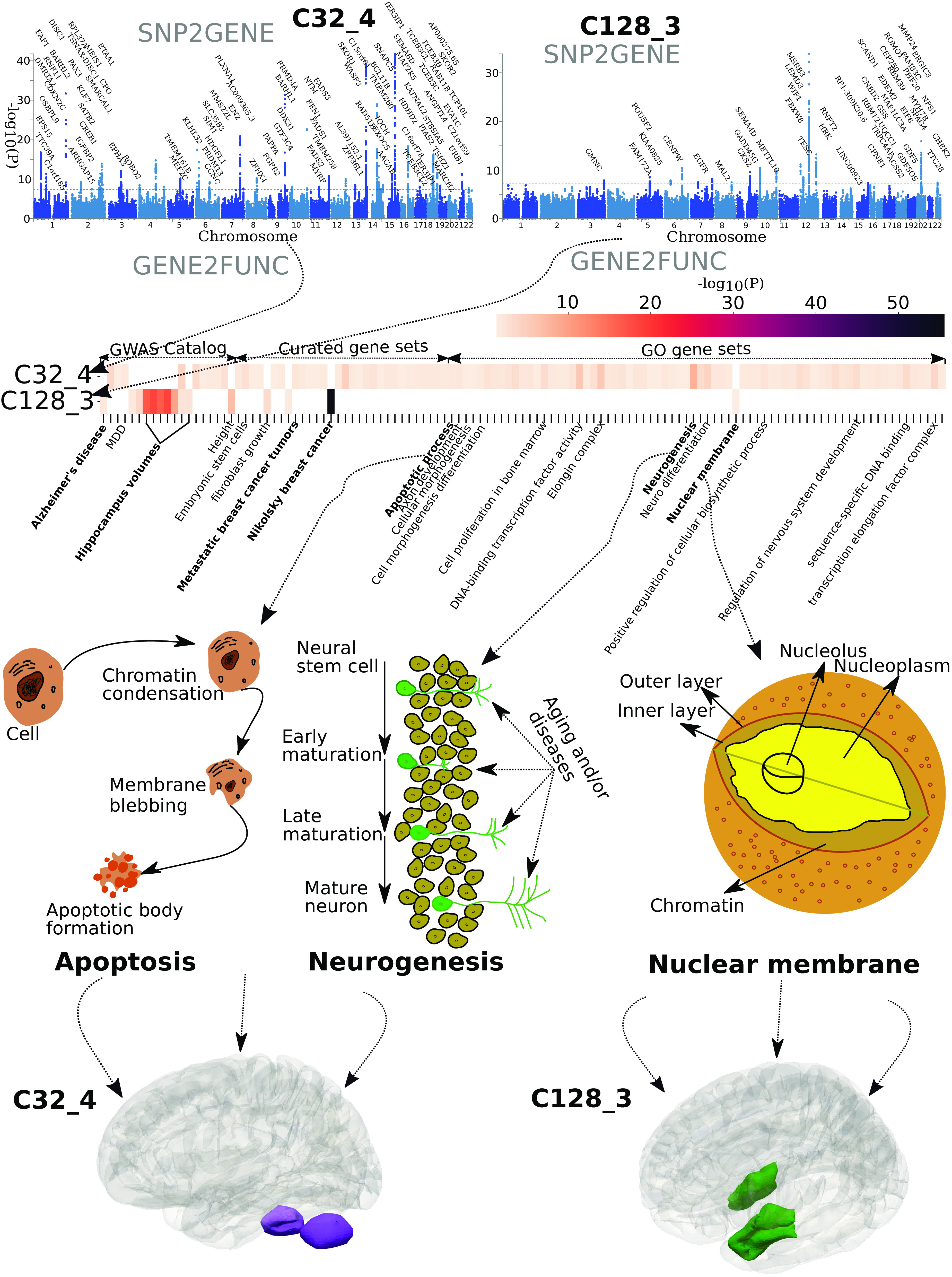
Illustrations of multiple genetic loci and pathways shaping specific patterns of structural covariance. We demonstrate how underlying genomic loci and biological pathways might influence the formation, development, and changes of two specific PSCs: the fourth PSC of the C32 PSCs (C32_4) that resides in the superior part of the cerebellum and the third PSC of the C128 PSCs (C128_3) that includes the bilateral hippocampus and entorhinal cortex. We first performed SNP2GENE to annotate the mapped genes in the Manhattan plots and then ran GENE2FUNC for the prioritized gene set enrichment analysis (Method 4F). The mapped genes are input genes for prioritized gene set enrichment analyses. The heat map shows the significant gene sets from the GWAS Catalog, curated genes, and gene ontology (GO) that survived the correction for multiple comparisons. We selectively present the schematics for three pathways: apoptosis, neurogenesis, and nuclear membrane function. Several other key pathways are highlighted in bold, and the 3D maps of the two PSCs are presented.

Illustrations of Genetic Loci and Pathways Forming Two Patterns of Structural Covariance.

To illustrate how underlying genetic underpinnings might form a specific PSC, we showcased two PSCs: C32_4 for the superior cerebellum and C128_3 for the hippocampus-entorhinal cortex. The two PSCs were highly heritable and polygenic in our GWAS using the entire UKBB data (Fig. 4, N = 33,541). We used the FUMA (24) online platform to perform SNP2GENE for annotating the mapped genes and GENE2FUNC for prioritized gene set enrichment analyses (Method 4F). The superior cerebellum PSC was associated with genomic loci that can be mapped to 85 genes, which were enriched in many biological pathways, including psychiatric disorders, biological processes, molecular functions, and cellular components (e.g., apoptotic process, axon development, cellular morphogenesis, neurogenesis, and neuro differentiation). For example, apoptosis—the regulated cell destruction—is a complicated process that is highly involved in the development and maturation of the human brain and neurodegenerative diseases (25). Neurogenesis—new neuron formation—is crucial when an embryo develops and continues in specific brain regions throughout the lifespan (26). All significant results of this prioritized gene set enrichment analysis are presented in Dataset S11.

For the hippocampus-entorhinal cortex PSC, we mapped 45 genes enriched in gene sets defined from GWAS Catalog, including Alzheimer’s disease and brain volume derived from hippocampal regions. The hippocampus and medial temporal lobe have been robust hallmarks of Alzheimer’s disease (27). In addition, these genes were enriched in the breast cancer 20Q11 amplicon pathway (20) and the pathway of metastatic breast cancer tumors (28), which might indicate a specific distribution of brain metastases: the vulnerability of medial temporal lobe regions to breast cancer (21), or highlight an inverse association between Alzheimer’s disease and breast cancer (22). Last, the nuclear membrane encloses the cell’s nucleus—the chromosomes reside inside—which is critical in cell formation activities related to gene expression and regulation. To further support the overlapping genetic underpinnings between this PSC and Alzheimer’s disease, we calculated the genetic correlation (r_g = −0.28; P-value = 0.01) using GWAS summary statistics from the hippocampus-entorhinal cortex PSC (i.e., 33,541 people of European ancestry) and a previous independent study of Alzheimer’s disease (29) (i.e., 63,926 people of European ancestry) using LDSC (30). All significant results of this prioritized gene set enrichment analysis are presented in Dataset S12.

Multi-Scale Patterns of Structural Covariance Derive Disease-Related Imaging Signatures.

We investigate the added value of the multi-scale PSCs as building blocks of imaging signatures for several brain diseases and risk conditions using linear support vector machines (SVM) (Method 5) (31). The aim is to harness machine learning to drive a clinically interpretable metric for quantifying an individual-level risk to each disease category. To this end, we define the signatures as SPARE-X (Spatial PAtterns for REcognition) indices, where X is the disease. For instance, SPARE-AD captures the degree of expression of an imaging signature of AD-related brain atrophy, which has been shown to offer diagnostic and prognostic value in prior studies (32).

The most discriminative indices in our samples were SPARE-AD and SPARE-MCI (Fig. 5 and SI Appendix, eTable 4a and eFigure 5). C = 1,024 achieved the best performance for the single-scale analysis (e.g., AD vs. controls; balanced accuracy: 0.90 $\pm$ 0.02; Cohen’s d: 2.50). Multi-scale representations derived imaging signatures that showed the largest effect sizes to classify the patients from the controls (Fig. 5) (e.g., AD vs. controls; balanced accuracy: 0.92 $\pm$ 0.02; Cohen’s d: 2.61). PSCs obtained better classification performance than both AAL (e.g., AD vs. controls; balanced accuracy: 0.82 $\pm$ 0.02; Cohen’s d: 1.81) and voxel-wise regional volumetric maps (RAVENS) (33) (e.g., AD vs. controls; balanced accuracy: 0.85 $\pm$ 0.02; Cohen’s d: 2.04) (SI Appendix, eTable 4a and eFigure 5). Our classification results were higher than previous baseline studies (34, 35), which provided an open-source framework to objectively and reproducibly evaluate AD classification. Using the same cross-validation procedure and evaluation metric, they reported the highest balanced accuracy of 0.87 $\pm$ 0.02 to classify AD from healthy controls. Notably, our experiments followed good practices, employed rigorous cross-validation procedures, and avoided critical methodological flaws, such as data leakage or double-dipping [refer to critical reviews on this topic elsewhere (34, 36)].

Fig. 5.

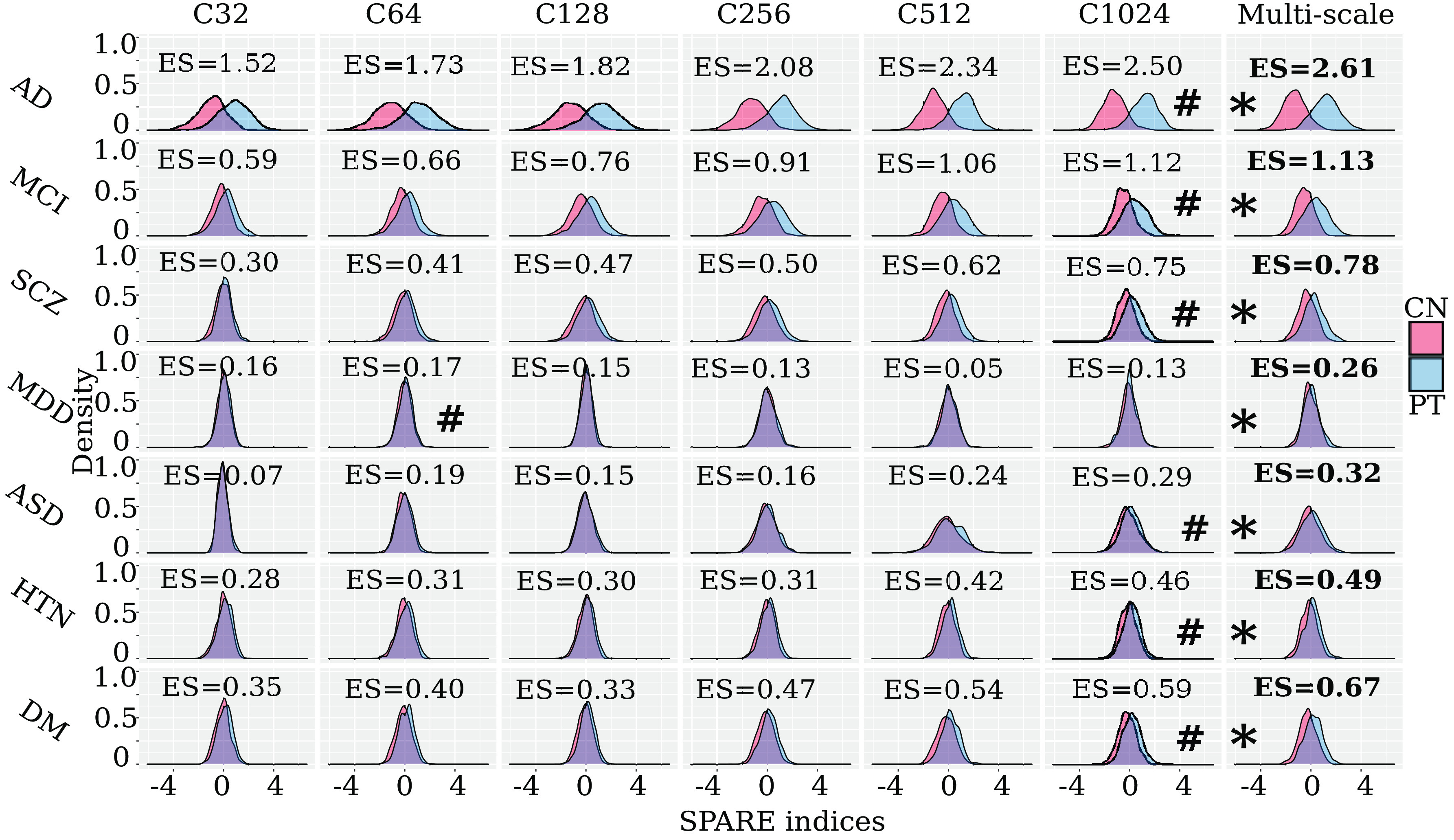
Individualized imaging signatures based on pattern analysis via machine learning. Imaging signatures (SPARE indices) of brain diseases, derived via supervised machine learning models, are more distinctive when formed from multi-scale PSCs than single-scale PSCs. The kernel density estimate plot depicts the distribution of the patient group (blue) in comparison to the healthy control group (red), reflecting the discriminative power of the diagnosis-specific SPARE (imaging signature) indices. We computed Cohen’s d for each SPARE index between groups to present the effect size of its discrimination power. * represents the model with the largest Cohen’s d for each SPARE index to separate the control vs. patient groups; # represents the model with the best performance with single-scale PSCs. Our results demonstrate that the multi-scale PSCs generally achieve the largest discriminative effect sizes (ES) (SI Appendix, eTable 4a). As a reference, Cohen’s d of $\ge$0.2, $\ge$0.5, and $\ge$0.8, respectively, refer to small, moderate, and large effect sizes.

To test the robustness of these SPARE indices, we performed leave-one-site-out analyses for SPARE-AD using the combined 2,003 PSCs from all scales (SI Appendix, eTable 4b). Overall, holding the ADNI data out as independent test data resulted in a lower balanced accuracy (0.88 $\pm$ 0.02) compared to the other cases for AIBL (0.95 $\pm$ 0.02) and PENN data (0.95 $\pm$ 0.02). The mean balanced accuracy (0.91 $\pm$ 0.02) aligns with the nested cross-validated results using the full sample (Fig. 5).

BRIDGEPORT: Bridging Knowledge across Patterns of Structural Covariance, Genetics, and Clinical Phenotypes.

We integrated our experimental results and the MuSIC atlas into the BRIDGEPORT online web portal. This online tool allows researchers to interactively browse the MuSIC atlas in 3D, query our experimental results via variants or PSCs, and download the GWAS summary statistics for further analyses. In addition, we allow users to search via conventional brain anatomical terms (e.g., the right thalamus proper) by automatically annotating traditional anatomic atlas ROIs, specifically from the MUSE atlas (37) (SI Appendix, eTable 5), to MuSIC PSCs based on their degree of overlaps (SI Appendix, eFigure 6). Open-source software dedicated to image processing (37) genetic quality check protocols, MuSIC generation with sopNMF, and machine learning (34) is also publicly available (see Data, Materials, and Software Availability for details).

Discussion

The current study investigates patterns of structural covariance in the human brain at multiple scales from a large population of 50,699 people and, importantly, a very diverse cohort allowing us to capture patterns of structural covariance emanating from normal and abnormal brain development and aging, as well as from several brain diseases. Through extensive examination of the genetic architecture of these multi-scale PSCs, we confirmed genetic hits from previous T1-weighted MRI GWAS and, more importantly, identified 617 newly identified genomic loci and molecular and biological pathways that collectively influence brain morphological changes and development over the lifespan. Using a hypothesis-free, data-driven approach to first derive these PSCs using brain MRIs, we then uncovered their genetic underpinnings and further showed their potential as building blocks to predict various diseases. All experimental results and code are encapsulated and publicly available in BRIDGEPORT for dissemination: https://www.cbica.upenn.edu/bridgeport/, to enable various neuroscience studies to investigate these structural covariance patterns in diverse contexts. Together, the current study highlighted the adoption of machine learning methods in brain imaging genomics and deepened our understanding of the genetic architecture of the human brain.

Our findings reveal valuable insights into genetic underpinnings that influence structural covariance patterns in the human brain. Brain morphological development and changes are largely polygenic and heritable, and previous neuroimaging GWAS has not fully uncovered this genetic landscape. In contrast, genetic variants, as well as environmental, aging, and disease effects, exert pleiotropic effects in shaping morphological changes in different brain regions through specific biological pathways. The mechanisms underlying brain structural covariance are not yet fully understood. They may involve an interplay between common underlying genetic factors, shared susceptibility to aging, and various brain pathologies, which affect brain growth or degeneration in coordinated brain morphological changes (1). Our data-driven, multi-scale PSCs identify the hierarchical structure of the brain under the principle of structural covariance and are associated with genetic factors at different levels, including SNPs, genes, and gene set pathways. These 617 newly identified genomic loci, as well as those previously identified, collectively shape brain morphological changes through many key biological and molecular pathways. These pathways are widely involved in reelin signaling, apoptotic processes, axonal development, cellular morphogenesis, neurogenesis, and neuro differentiation (25, 26), which may collectively influence the formation of structural covariance patterns in the brain. Strikingly, pathways involved in breast cancer shared overlapping genetic underpinnings evidenced in our MAGMA-based and prioritized (GENE2FUNC) gene set enrichment analyses (Figs. 3C and 4), which included specific pathways involved in breast cancer and metastatic breast cancer tumors. One previous study showed that common genes might mediate breast cancer metastasis to the brain (21), and a later study further corroborated that the metastatic spread of breast cancer to other organs (including the brain) accelerated during sleep in both mouse and human models (38). We further showcased that this brain metastasis of breast cancer might be associated with specific neuropathologic processes, which were captured by PSCs data driven by Alzheimer’s disease-related neuropathology. For example, the hippocampus-entorhinal cortex PSC (C128_3, Fig. 4) connected the bilateral hippocampus and medial temporal lobe— the salient hallmark of Alzheimer’s disease. Our gene set enrichment analysis results further support this claim: the genes were enriched in the gene sets of Alzheimer’s disease and breast cancer (Fig. 4). Previous research (22, 23) also found an inverse association between Alzheimer’s disease and breast cancer. In addition, PSCs from the cerebellum were the most genetically influenced brain regions, consistent with previous neuroimaging GWAS (4, 5). The cerebral cortex has been thought to largely contribute to the unique mental abilities of humans. However, the cerebellum may also be associated with a much more comprehensive range of complex cognitive functions and brain diseases than initially thought (39). Our results confirmed that many genetic substrates might support different molecular pathways, resulting in cerebellar functional organization, high-order functions, and dysfunctions in various brain disorders.

The current work demonstrates that appropriate machine learning analytics can be used to shed light on brain imaging genetics. Previous neuroimaging GWAS leveraged multimodal imaging-derived phenotypes from conventional brain atlases (4, 5) (e.g., the AAL atlas). In contrast, multi-scale PSCs are purely data-driven and likely to reflect the dynamics of underlying normal and pathological neurobiological processes giving rise to structural covariance. The diverse training sample from which the PSCs were derived, including healthy and diseased individuals of a wide age range, enriched the diversity of such neurobiological processes influencing the PSCs. In addition, modeling structural covariance at multiple scales (i.e., multi-scale PSCs) indicated that disease effects could be robustly and complementarily identified across scales (Fig. 5), concordant with the paradigm of multi-scale brain modeling (13). Imaging signatures of brain diseases, derived via supervised machine learning models, were consistently more distinctive when formed from multi-scale PSCs than single-scale PSCs. Multivariate learning techniques have gained significant prominence in neuroimaging and have recently attracted considerable attention in the domain of imaging genomics. These methods have proven valuable for analyzing complex and high-dimensional data, facilitating the exploration of relationships between imaging features and genetic factors. For instance, the MOSTest, a multivariate GWAS approach, preserves correlation structure among phenotypes via permutation on each SNP and derives a genotype vector for testing the association across all phenotypes (40). A separate study by Soheili-Nezhad et al. demonstrated that genetic components obtained through PCA or ICA applied to neuroimaging GWAS summary statistics exhibited greater reproducibility than raw univariate GWAS effect sizes (41). A recent study utilized a CNN-based autoencoder to discover new phenotypes and identify numerous newly identified genetic signals (42). Despite the effectiveness of these multivariate approaches in GWAS, they typically conduct phenotype engineering before performing GWAS without explicitly incorporating imaging genetic associations during the modeling process. Yang et al. recently conducted a study that employed generative adversarial networks [termed GeneSGAN (43)] to integrate imaging and genetic variations within the modeling framework to address this limitation. By incorporating both modalities, their approach aimed to capture the complexity and heterogeneity of disease manifestations.

MuSIC—with the strengths of being data-driven, multi-scale, and disease-effect informative—contributes to the century-old quest for a “universal” atlas in brain cartography (44) and is highly complementary to previously proposed brain atlases. For instance, Chen et al. (45) used a semi-automated fuzzy clustering technique with MRI data from 406 twins and parcellated the cortical surface area into a genetic covariance-informative brain atlas; MuSIC was data-driven by structural covariance. Glasser et al. (46) adopted a semi-automated parcellation procedure to create a multimodal cortex atlas from 210 healthy individuals. Although this method successfully integrates multimodal information from cortical folding, myelination, and functional connectivity, this semi-automatic approach requires significant resources, some with limited resolution. MuSIC allows flexible, multiple scales for delineating macroscopic brain topology; including patient samples exposes the model to sources of variability that may not be visible in healthy controls. Another pioneering endeavor is the Allen Brain Atlas project (47), whose overarching goals of mapping the human brain to gene expression data via existing conventional atlases, identifying local gene expression patterns across the brain in a few individuals, and deepening our understanding of the human brain’s differential genetic architecture, are complementary to ours—characterizing the global genetic architecture of the human brain, emphasizing pathogenic variability and morphological heterogeneity.

Bridging knowledge across the brain imaging, genomics, and machine learning communities is another pivotal contribution of this work. BRIDGEPORT provides a platform to lower the entry barrier for whole-brain genetic-structural analyses, foster interdisciplinary communication, and advocate for research reproducibility (34, 48–51). The current study demonstrates the broad applicability of this large-scale, multi-omics platform across a spectrum of neurodegenerative and neuropsychiatric diseases.

The present study has certain limitations. First, the sopNMF method utilized in brain parcellation considers only imaging structural covariance and overlooks the genetic determinants contributing to forming these structural networks, as indicated by our GWAS findings. Consequently, further investigations are needed to integrate imaging and genetics into brain parcellation. Additionally, it is important to note that our GWAS analyses primarily involved participants of European ancestry. To enhance genetic findings for underrepresented ethnic groups, future studies should prioritize the inclusion of diverse ancestral backgrounds, thereby promoting a more comprehensive understanding of the genetic underpinnings across different populations.

Methods

Method 1: Structural Covariance Patterns via Stochastic Orthogonally Projective Non-Negative Matrix Factorization.

The sopNMF algorithm is a stochastic approximation built and extended based on opNMF (9, 52). We consider a dataset of $n$ MR images and $d$ voxels per image. We represent the data as a matrix X where each column corresponds to a flattened image: $\mathit{X}= \left[x_1,x_2,\dots ,x_n\right],\mathit{X}\in {\mathrm{ℝ}}_{\ge 0}^{d\times n}$. The sopNMF algorithm factorizes X into two low-rank ($r$) matrices $\mathit{W}\in {\mathrm{ℝ}}_{\ge 0}^{d\times r}$ and $\mathit{H}\in {\mathrm{ℝ}}_{\ge 0}^{r\times n}$ under the constraints of non-negativity and column-orthonormality. Using the Frobenius norm, the loss of this factorization problem can be formulated as

$$\begin{array}{c}{\mathbf{\Vert }\mathit{X}\mathbf{-}\mathit{W}\mathit{H}\mathbf{\Vert }}_F^2\\ \text{subject} \text{to} \mathit{H}={\mathit{W}}^{\mathit{T}}\mathit{X}, \mathit{W}\ge 0 \text{and} {\mathit{W}}^{\mathit{T}}\mathit{W}=\mathit{I}\end{array},$$ [1]

where I stands for the identity matrix. The columns$w_i\in {\mathrm{ℝ}}^d, {‖w_i‖}^2=1,$$\forall i\in \{1\dots r\}$ of the so-called component matrix $\mathit{W}= \left[w_1,w_2,\dots ,w_r\right]$ are part-based representations promoting sparsity in data in this lower-dimensional subspace. From this perspective, the loading coefficient matrix $\mathit{H}$ represents the importance (weights) of each feature above for a given image. Instead of optimizing the non-convex problem in a batch learning paradigm (i.e., reading all images into memory) as opNMF (9), sopNMF subsamples the number of images at each iteration, thereby significantly reducing its memory demand by randomly drawing data batches ${\mathit{X}}_{\mathit{b}}\in {\mathrm{ℝ}}_{\ge 0}^{d\times b}$ of $b\le n$ images (b is the batch size; b = 32 was used in the current analyses); this is done without replacement so that all data goes through the model once ($⌈n/b⌉$). In this case, the updating rule can be rewritten as

$${\mathit{W}}_{t+1}={\mathit{W}}_t\frac{{\left({\mathit{X}}_{\mathit{b}}{\mathit{X}}_{\mathit{b}}^{\mathit{T}}\mathit{W}\right)}_t}{{\left(\mathit{W}{\mathit{W}}^T{\mathit{X}}_{\mathit{b}}{\mathit{X}}_{\mathit{b}}^{\mathit{T}}\mathit{W}\right)}_t}.$$ [2]

We calculate the loss on the entire dataset at the end of each epoch (i.e., the loss is incremental across all batches) with the following expression:

$${\displaystyle \sum _{i=1}^{⌈n/b⌉}}{∥{\mathit{X}}_{\mathit{b}\_\mathit{i}}-{\mathit{WW}}^{\mathit{T}}{\mathit{X}}_{\mathit{b}\_\mathit{i}}∥}_F^2.$$ [3]

We evaluated the training loss and the sparsity of W at the end of each iteration. Moreover, early stopping was implemented to improve training efficiency and alleviate overfitting. We summarize the sopNMF algorithm in SI Appendix, Algorithm 1. An empirical comparison between sopNMF and opNMF is detailed in SI Appendix, eMethod 1.

We applied sopNMF to the training population (N = 4,000). The component matrix W was sparse after the algorithm converged with a pre-defined maximum number of epochs (100 by default) with an early stopping criterion. To build the MuSIC atlas, we clustered each voxel (row-wise) into one of the $r$ features/PSCs as follows:

$${\mathit{M}}_j={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_k\left({\mathit{W}}_{j,k}\right),$$ [4]

where M is a d-dimensional vector and $j\in \{1\dots d\}$. The j-th element of M equals k if ${\mathit{W}}_{j,k}$ is the maximum value of the j-th row. Intuitively, M indicates which of the r PSCs each voxel belongs to. We finally projected the vector $\mathit{M}\in {\mathrm{ℝ}}_{\ge 0}^d$ into the original image space to visualize each PSC of the MuSIC atlas (Fig. 1). Of note, 13 PSCs have vanished in this process for C = 1,024: all 0 for these 13 vectors.

Method 2: Study Population.

We consolidated a large-scale multimodal consortium (N = 50,699) consisting of imaging, cognition, and genetic data from 12 studies, 130 sites, and 12 countries. We present the detailed demographic information of the population under study in SI Appendix, eTable 1. All individual studies were approved by their local corresponding Institutional Review Boards (IRB) (SI Appendix, eText 2). This large-scale consortium reflects the diversity of MRI scans over different races, disease conditions, and ages over the lifespan. To be concise, we defined four populations or datasets per analysis across the paper: i) discovery set, ii) replication set, iii) training population, and iv) comparison population (refer to SI Appendix, eText 3 for details).

Method 3: Image Processing and Statistical Harmonization.

(A): Image processing: Images that passed the quality check (SI Appendix, eMethod 4) were first corrected for magnetic field intensity inhomogeneity (53). Voxel-wise regional volumetric maps (RAVENS) (33) for each tissue volume were then generated by using a registration method to spatially align the skull-stripped images to a template in MNI-space (54). We applied sopNMF to the RAVENS maps to derive MuSIC.

(B): Statistical harmonization of MuSIC PSCs: We applied MuSIC to the entire population (N = 50,699) to extract the multi-scale PSCs. Specifically, MuSIC was applied to each individual’s RAVENS gray matter map to extract the sum of brain volume in each PSC. Subsequently, the PSCs were statistically harmonized by an extensively validated approach, i.e., ComBat-GAM (12) (SI Appendix, eMethod 3) to account for site-related differences in the imaging data. After harmonization, the PSCs were normally distributed (skewness = 0.11 $\pm$ 0.17, and kurtosis = 0.67 $\pm$ 0.68) (SI Appendix, eFigure 7 A and B). To alleviate the potential violation of normal distribution in downstream statistical learning, we quantile-transformed all PSCs. In agreement with the literature (55, 56), males were found to have larger brain volumes than females on average (SI Appendix, eFigure 7C). Overall, the Combat-GAM model slightly improved data normality across sites (SI Appendix, eFigure 7 E–H). The AAL ROIs underwent the same statistical harmonization procedure.

Method 4: Genetic Analyses.

Genetic analyses were restricted to the discovery and replication set from UKBB (Method 2). We processed the array genotyping and imputed genetic data (SNPs). The two datasets went through a “best-practice” imaging-genetics quality check (QC) protocol (Method 4A) and were restricted to participants of European ancestry. This resulted in 18,052 participants and 8,430,655 SNPs for the discovery set and 15,243 participants and 8,470,709 SNPs for the replication set. We reperformed the genetic QC and genetic analyses for the combined populations for BRIDGEPORT, resulting in 33,541 participants and 8,469,833 SNPs. Method 4G details the correction for multiple comparisons throughout our analyses.

(A): Genetic data quality check protocol: First, we excluded related individuals (up to second-degree) from the complete UKBB sample (N = 488,377) using the KING software for family relationship inference (57). We then removed duplicated variants from all 22 autosomal chromosomes. We also excluded individuals for whom either imaging or genetic data were not available. Individuals whose genetically identified sex did not match their self-acknowledged sex were removed. Other excluding criteria were i) individuals with more than 3% of missing genotypes; ii) variants with minor allele frequency (MAF) of less than 1%; iii) variants with larger than 3% missing genotyping rate; iv) variants that failed the Hardy–Weinberg test at 1 × 10⁻¹⁰. To adjust for population stratification (58), we derived the first 40 genetic principle components (PC) using FlashPCA software (59). The genetic pipeline was also described elsewhere (60, 61).

(B): Heritability estimates and genome-wide association analysis: We estimated the SNP-based heritability explained by all autosomal genetic variants using GCTA-GREML (62). We adjusted for confounders of age (at imaging), age-squared, sex, age–sex interaction, age-squared-sex interaction, ICV, and the first 40 genetic principal components (PC), guided by a previous neuroimaging GWAS (4). In addition, Elliot et al. (5) investigated more than 200 confounders in another study. Therefore, our sensitivity analyses included four additional imaging-related covariates (i.e., brain positions and head motion). One-side likelihood ratio tests were performed to derive the heritability estimates. In GWAS, we performed a linear regression for each PSC and included the same covariates as in the heritability estimates using PLINK (63).

(C): Identification of newly identified genomic loci: Using PLINK, we clumped the GWAS summary statistics based on their linkage disequilibrium to identify the genomic loci (see SI Appendix, eMethod 5 for the definition of the index, candidate, independent significant, lead SNP, and genomic locus). In particular, the threshold for significance was set to 5 $\times$ 10⁻⁸ (clump-p1) for the index SNPs and 0.05 (clump-p2) for the candidate SNPs. The threshold for linkage disequilibrium-based clumping was set to 0.60 (clump-r2) for independent significant SNPs and 0.10 for lead SNPs. The linkage disequilibrium physical-distance threshold was 250 kb (clump-kb). Genomic loci consider linkage disequilibrium (within 250 kb) when interpreting the association results. The GWASRAPIDD (64) package (version: 0.99.14) was then used to query the genomic loci for any previously reported associations with clinical phenotypes documented in the NHGRI-EBI GWAS Catalog (15) (P-value < 1.0 $\times$ 10⁻⁵, default inclusion value of GWAS Catalog). We defined a genomic locus as newly identified when it was not present in GWAS Catalog (query date: April 5th, 2023).

(D): Gene-level associations with MAGMA: We performed gene-level association analysis using MAGMA (16). First, gene annotation was performed to map the SNPs (reference variant location from Phase 3 of 1,000 Genomes for European ancestry) to genes (human genome Build 37) according to their physical positions. The second step was to perform the gene analysis based on the GWAS summary statistics to obtain gene-level P-values between the pairwise 2,003 PSCs and the 18,097 protein-encoding genes containing valid SNPs.

(E): Hypothesis-free gene set enrichment analysis with MAGMA: Using the gene-level association P-values, we performed gene set enrichment analysis using MAGMA. Gene sets were obtained from Molecular Signatures Database (MsigDB, v7.5.1) (65), including 6,366 curated gene sets and 10,402 Gene Ontology (GO) terms. All other parameters were set by default for MAGMA. This hypothesis-free analysis resulted in a more stringent correction for multiple comparisons (i.e., by the total number of tested genes and PSCs) than the FUMA-prioritized gene set enrichment analysis (see below FUMA Analyses for the Illustrations of Specific PSCs).

(F): FUMA analyses for the illustrations of specific PSCs: In SNP2GENE, three different methods were used to map the SNPs to genes. First, positional mapping maps SNPs to genes if the SNPs are physically located inside a gene (a 10-kb window by default). Second, expression quantitative trait loci (eQTL) mapping maps SNPs to genes showing a significant eQTL association. Last, chromatin interaction mapping maps SNPs to genes when there is a significant chromatin interaction between the disease-associated regions and nearby or distant genes (24). In addition, GENE2FUNC studies the expression of prioritized genes and tests for the enrichment of the set of genes in pre-defined pathways. We used the mapped genes as prioritized genes. The background genes were specified as all genes in FUMA, and all other parameters were set by default. We only reported gene sets with adjusted P-value < 0.05.

(G): Correction for multiple comparisons: We practiced a conservative procedure to control for the multiple comparisons. In the case of GWAS, we chose the default genome-wide significant threshold (5.0 × 10⁻⁸ and 0.05 for all other analyses) and independently adjusted for multiple comparisons (Bonferroni methods) at each scale by the number of PSCs. We corrected the P-values for the number of phenotypes (N = 6) for genetic correlation analyses. We adjusted the P-values for the number of PSCs at each scale for heritability estimates. For gene analyses, we controlled for both the number of PSCs at each scale and the number of genes. We adopted these strategies per analysis to correct the multiple comparisons because PSCs of different scales are likely hierarchical and correlated—avoiding the potential of “overcorrection.”

(H): Replication analysis for genome-wide association studies: We performed GWAS by fitting the same linear regressing models as the discovery set. Also, following the same procedure for consistency, we corrected the multiple comparisons using the Bonferroni method. We corrected it for the number of genomic loci (N = 915) found in the discovery set with a nominal P-value of 0.05, which thereby resulted in a stringent test with an equivalent P-value threshold of 3.1 × 10⁻⁵ (i.e., (−log₁₀[P-value] = 4.27). We performed a replication for the 915 genomic loci, but, in reality, SNPs in linkage disequilibrium with the genomic loci are likely highly significant.

Method 5: Pattern Analysis via Machine Learning for Individualized Imaging Signatures.

SPARE-AD captures the degree of expression of an imaging signature of AD, and prior studies have shown its diagnostic and prognostic values (32). Here, we extended the concept of the SPARE imaging signature to multiple diseases (SPARE-X, X represents disease diagnoses). Following our reproducible open-source framework (35), we performed nested cross-validation (SI Appendix, eMethod 6) for the machine learning models and derived imaging signatures to quantify individualized disease vulnerability.

SPARE indices.

MuSIC PSCs were fit into a linear support vector machine (SVM) to derive SPARE-AD, MCI, SCZ, DM, HTN, MDD, and ASD. Specifically, the SVM aims to classify the patient group (e.g., AD) from the control group and outputs a continuous variable (i.e., the SPARE indices), which indicates the proximity of each participant to the hyperplane in either the patient or control space. We compared the classification performance using different sets of features: i) the single-scale PSC from 32 to 1024, ii) the multi-scale PSCs by combining all features (with and without feature selections embedded in the CV); iii) the ROIs from the AAL atlas; and iv) voxel-wise RAVENS maps. The samples selected for each task are presented in SI Appendix, eTable 2.

No statistical methods were used to predetermine the sample size. The experiments were not randomized, and the investigators were not blinded to allocation during experiments and outcome assessment.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (XLSX)

Dataset S02 (XLSX)

Dataset S03 (XLSX)

Dataset S04 (XLSX)

Dataset S05 (XLSX)

Dataset S06 (XLSX)

Dataset S07 (XLSX)

Dataset S08 (XLSX)

Dataset S09 (XLSX)

Dataset S10 (XLSX)

Dataset S11 (XLSX)

Dataset S12 (XLSX)

Data, Materials, and Software Availability

The GWAS summary statistics corresponding to this study are publicly available on the BRIDGEPORT web portal (https://www.cbica.upenn.edu/bridgeport/) and the MEDICINE web portal (https://labs.loni.usc.edu/medicine/). The software and resources used in this study are all publicly available: sopNMF: https://pypi.org/project/sopnmf/, MuSIC, and sopNMF (developed for this study); BRIDGEPORT: https://www.cbica.upenn.edu/bridgeport/, (developed for this study); MLNI: https://pypi.org/project/mlni/, machine learning (developed for this study); MUSE: https://www.med.upenn.edu/sbia/muse.html, image preprocessing; PLINK: https://www.cog-genomics.org/plink/, GWAS; GCTA: https://yanglab.westlake.edu.cn/software/gcta/#Overview, heritability estimates; LDSC: https://github.com/bulik/ldsc, genetic correlation estimates; MAGMA: https://ctg.cncr.nl/software/magma, gene analysis; GWASRAPIDD: https://rmagno.eu/gwasrapidd/articles/gwasrapidd.html, GWAS Catalog query; and MsigDB: https://www.gsea-msigdb.org/gsea/msigdb/, gene sets database.