Effectiveness of non-pharmaceutical interventions to reduce SARS-CoV-2 transmission in Canada and their association with COVID-19 hospitalization rates

Abstract

Background

Non-pharmaceutical interventions (NPIs) aim to reduce the incidence of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections mostly by limiting contacts between people where virus transmission can occur. However, NPIs limit social interactions and have negative impacts on economic, physical, mental and social well-being. It is, therefore, important to assess the impact of NPIs on reducing the number of coronavirus disease 2019 (COVID-19) cases and hospitalizations to justify their use.

Methods

Dynamic regression models accounting for autocorrelation in time series data were used with data from six Canadian provinces (British Columbia, Alberta, Saskatchewan, Manitoba, Ontario, Québec) to assess 1) the effect of NPIs (measured using a stringency index) on SARS-CoV-2 transmission (measured by the effective reproduction number), and 2) the effect of the number of hospitalized COVID-19 patients on the stringency index.

Results

Increasing stringency index was associated with a statistically significant decrease in the transmission of SARS-CoV-2 in Alberta, Saskatchewan, Manitoba, Ontario and Québec. The effect of stringency on transmission was time-lagged in all of these provinces except for Ontario. In all provinces except for Saskatchewan, increasing hospitalization rates were associated with a statistically significant increase in the stringency index. The effect of hospitalization on stringency was time-lagged.

Conclusion

These results suggest that NPIs have been effective in Canadian provinces, and that their implementation has been, in part, a response to increasing hospitalization rates of COVID-19 patients.

Introduction

Non-pharmaceutical interventions (NPIs) were implemented globally to reduce the transmission of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and the resulting levels of coronavirus disease 2019 (COVID-19) illnesses, hospitalizations and deaths. Non-pharmaceutical interventions were used before vaccines became widely available, and at the time of writing, continue to complement vaccination efforts. Non-pharmaceutical interventions include case detection and isolation, contact tracing and quarantine, travel restrictions, restrictive closures (gathering restrictions, nonessential business closures and school closures), curfews and personal measures including physical distancing and wearing masks. Non-pharmaceutical interventions act by reducing the rate of contacts among individuals (e.g. closure of nonessential businesses) and reducing the probability of transmission when contacts do occur (e.g. masking and physical distancing). Both contact rates and transmission probability are determinants of the effective reproductive number, R_t, (i.e. the average number of secondary cases generated by a typical infectious individual at time t in a population with atypical mixing resulting from some immunity and/or NPIs) ( ((1))). The very nature of NPIs, which aims at reducing social interactions, has been shown to negatively impact economies and the physical, mental and social well-being of the underlying population ( ((2–4))); therefore, assessment on the impact of NPIs to reduce the transmission of SARS-CoV-2 is important to justify and validate their implementation. A clearer understanding of the effectiveness of NPIs will also support future public health decisions regarding their use in response to potential successive waves of COVID-19 and potential future pandemics with similar modes of transmission.

Previous articles report evidence for and against the effectiveness of NPIs. Non-pharmaceutical interventions are associated with reducing confirmed case rates ( ((5–7))), and the strength of their effectiveness increases with earlier rather than later implementation ( ((8))). A recent review suggests that most studies report evidence for NPIs being effective ( ((9))). Evidence against the effectiveness of NPIs is largely centred on the types of NPIs measures and how they vary in their effectiveness ( ((10–12))). For example, restrictions to movement were not found to be associated with a reduction in the incidence ( ((13))). Also, lockdowns were not associated with a reduction in COVID-19 prevalence and mortality ( ((14))).

Even within Canada, there is varying evidence for the effectiveness of NPIs. Provinces and territories implemented NPIs differently through time in response to their COVID-19 situation. The predominant measures included school and workplace closures, public events cancellations, gathering restrictions, stay-at-home requirements, internal and interprovincial movement restrictions, testing policies and masking. Two recent articles assessing the effectiveness of NPIs used a standardized series of indicators and composite indices developed by the University of Oxford’s Blavatnik School of Government to quantify provincial-level government NPIs over the duration of the COVID-19 pandemic ( ((15))). In one study, the stringency index was found to be associated with decreasing prevalence of COVID-19 over the first three waves in addition to the impact of vaccination but could not disentangle these effects ( ((16))). Another study focused largely on the pre-vaccination period of the pandemic and found that the effect of stringency to associate with a reduction in the daily case growth of COVID-19 was minimal to non-existent, over the first and second waves ( ((17))).

Here we aim to enhance understanding of the effectiveness—or not—of NPIs in Canada by assessing data from six provinces individually, given regional variations in the COVID-19 waves in Canada. We focused on the first and second waves of the pandemic. We accounted for possible confounding effects that might have arisen from the rollout of the first dose of vaccines and the first variant of concern during the latter months of the study period. We assessed associations with NPIs, as measured using a stringency index, from two perspectives. First, we expected 1) NPIs to reduce the frequency of infectious contacts, as measured by R_t, and 2) that the impact of NPIs should be time-lagged given the duration of the incubation period and surveillance activities (testing and reporting). Secondly, we assessed evidence that the strengthening of NPIs was in response to increasing hospitalization rates, with the intention of preventing healthcare systems from being overwhelmed. Hence, the objectives of this study were to measure the associations, at the provincial level, between 1) the stringency index of NPIs, stringency index (sidx), and transmission of SARS-CoV-2 (as measured by the effective reproduction number, R_t), and 2) the number of hospitalized COVID-19 patients and the intensity of the NPIs implemented, as measured by sidx.

Methods

Study design and population

This is an ecological study using the province as the unit of analysis. The study period was April 1, 2020, to March 31, 2021. This period excludes the first three months of 2020, before the World Health Organization declared global pandemic, when provincial health authorities were still establishing surveillance protocols. Furthermore, the study period includes the time period when NPIs were the main method of COVID-19 control—before vaccination may have had a significant impact on SARS-CoV-2 transmission in Canada (fewer than 2% of the population were fully vaccinated by March 31, 2021), though we do account for this effect as discussed below. The study period also contained the first two waves of the epidemic in Canada, and a significant part of the third wave. In this analysis, data from British Columbia (BC), Alberta (AB), Saskatchewan (SK), Manitoba (MB), Ontario (ON) and Québec (QC) were used because these provinces had the majority of cases ( ((18))).

Measurement and definition of SARS-CoV-2 transmission

Transmission of SARS-CoV-2 was estimated using the effective reproduction number R_t. The R_t is the average number of secondary infections generated by one case in a population in which some individuals are immune, and control measures may be in place ( ((1))). The lower bound of R_t is 0 with R_t<1 indicating decreasing transmission (i.e. the daily number of new cases is decreasing), R_t=1 indicating a stable rate of transmission (i.e. the infection is endemic), and R_t>1 indicating increasing transmission (i.e. the infection is spreading). The R_t was calculated from the number of new SARS-CoV-2 infections detected and reported by the provinces as temporally referenced by the date of reporting. The R library EpiEstim (version 2.2.3), with a 10-day sliding window on the reported infections, was used to estimate R_t ( ((19))). The serial interval was set at a mean of four days and a standard deviation of 4.75 days ( ((20))).

Measurement and definition of the stringency index

An adapted version of the methodology developed at the Blavatnik School of Government was used to generate a Canadian subnational dataset for NPIs implemented in response to COVID-19. Data were collected from publicly available sources, such as news articles and government press releases and briefings. These sources were identified and then coded using the indicators and codebook developed by Oxford Covid-19 Government Response Tracker, with an additional indicator being developed and coded to capture interprovincial travel restrictions: 0—No restrictions; 1—Recommend not to travel between provinces or territories; 2—Entrance into the province/territory from some provinces or territories is restricted (includes required quarantine period); 3—Entrance into the province/territory from all provinces or territories is restricted (includes required quarantine period). On a weekly basis, two team members independently coded the NPIs for each province and territory. The coded data from the two coders were then compared and any discrepancies were resolved by a third team member.

The Canadian subnational version of the Oxford’s Stringency Index included the following modifications. First, indicators that did not vary in time or between provinces (i.e. international travel restrictions, federal public health information campaigns, public transport closures) were removed. Second, indicators that may influence infection transmission in Canada (interprovincial travel restrictions, testing policy, and masking policy) were added. The modified sidx was calculated using the same formula developed to calculate Oxford’s Stringency Index but with a different set of indicators (Table 1).

Table 1. Comparison of modified stringency index and Oxford’s stringency index.

Indicator name	Oxford’s stringency index	Modified stringency index
C1_School closing	Yes	Yes
C2_Workplace closing	Yes	Yes
C3_Cancel public events	Yes	Yes
C4_Restrictions on gatherings	Yes	Yes
C5_Close public transport	Yes	No
C6_Stay at home requirements	Yes	Yes
C7_Restrictions on internal movement	Yes	Yes
C8_International travel controls	Yes	No
H1_Public information campaigns	Yes	No
H2_Testing policy	No	Yes
H6_Facial coverings	No	Yes
X1: Interprovincial travel restriction	No	Yes

Note: Yes, included in the indicated stringency Index; No, not included in the indicated stringency index

Measurement and definition of the number of hospitalized COVID-19 patients

The number of hospitalized COVID-19 patients, H, was the daily number reported publicly by the provinces: Ontario, Alberta, Québec, British Columbia, Saskatchewan, and Manitoba.

Statistical model

A dynamic regression approach was used to measure the associations between sidx and R_t (i.e. study objective 1) and sidx and H (i.e. study objective 2). The outcomes, R_t or sidx, were modelled by non-stationary processes with time-dependent mean and variance and information from past observations. Given that classical regression analysis of non-stationary data can result in spurious model parameter estimates, this study used an autoregressive integrated moving average (ARIMA) modelling approach ( ((21))). More specifically, an extended version of the ARIMA model (ARIMAX) was used such that the outcome time series, y_t, was modelled as a function of k explanatory variables (x_1t,…x_kt) by taking into account information from the past observation:

∇^dy_{t =} ∇^dy_t-1 * θ₁ + ∇^dy_t-2 * θ₂ + … +∇^dy_t-p * θ_p + β₁ * x_1t + β₂ * x_2t +…+ β_k * x_kt + ε_t + α₁ * ε_t-1 +…+ α_q * ε_t-q,

where the noise term ε_t is Gaussian with mean 0 and variance σ², and ∇^d is the differentiation operator and d is the degree of differencing. When d=1, the model is ∇¹y_{t =} y_t – y_t-1 and when d=2, ∇²y_t = ∇¹(∇¹y_t) = ∇¹(y_t – y_t-1) = (y_t – y_t-1) – (y_t-1 – y_t-2) = y_t – 2 * y_t-1+ y_t-2. Also, p is the number of the autoregressive (AR) terms of ∇^dy_t and q is the number of the moving average (MA) terms. Finally, θ₁, θ₂,…,θ_p, β₁,…, β_kt,α₁,…, α_q,σ are the model parameters. Overall, the model is denoted by ARIMAX (p, d, q), respectively. The ARIMAX models were built using the auto.arima function from the forecast package for R statistical software ( ((22–24))). This function finds the best fitting model while accounting for autocorrelation using AR terms, differencing terms and MA terms. The auto.arima function selects a best fitting model among candidate models with differing in their number of AR and MA terms by minimising Akaike’s information criterion for small sample sizes.

Model building and selection

After time-lagging the explanatory data variables (i.e. sidx and H; see below), the data were averaged at seven-day non-overlapping periods. This reduces noise that can occur in health data for social factors (e.g. organization of surveillance and hospital) at the weekly level as observed in our data and does not inject more autocorrelation by using a moving average approach with overlapping periods ( ((25))). The statistical analysis was performed at the provincial level. The general formulation of candidate models for objective 1 was: R_t ~ sidx, and for objective 2 was: sidx ~ H. In both cases, the explanatory variable effects were also assessed with time lags at seven, and 14 days. Varying the length of the time lags enables a determination for how much time a change in sidx has a stronger impact on R_t (model for objective 1) or how much time a change in hospitalizations most influences the strength of NPI (model for objective 2). Varying the length of the time lags also allows accounting for likely differences among jurisdictions in the speed with which cases and hospitalizations are reported. Fitted models were disregarded if autoregressive conditional heteroscedasticity remained in the residuals, as tested using the McLeod-Li test, and allowing up to two violations for an assessment over five time-lag periods ( ((26))).

In our model building, we also consider the possibility of confounding effects of the more highly transmissible Alpha variant of concern (B.1.1.7), the winter months resulting in closer contacts as people spend more time indoors ( ((27))) as well as the introduction of vaccination which can all be associated with the exposures of interest (sidx or H) and the outcomes (R_t and sidx). Indeed, an increase in both R_t and H were observed during the end of our study period. Our study period was not long enough to disentangle the potential confounding effects which are not fully overlapping (i.e. vaccination from January to March 2021, and alpha increasing in dominance mostly in March 2021), and the study period only contains one winter from the end of December 2020 to March 2021. We therefore decide to use a period of time as a proxy combining all three effects and dichotomized time into a pre-vaccination/Alpha variant/winter (April–December 2020; coded as C = 0) and the period when vaccination, the Alpha variant and winter were present (January–March 2021; coded as C = 1). We tested for confounding by assessing if the change in the beta coefficient of sidx was greater than 10% between model formulations R_t ~ sidx and R_t ~ sidx + C, for each time lag of sidx. If confounding existed, we retained the model with C, otherwise we retained the univariable model with sidx. We then ranked the retained models across the time lags, and no time lag, by the decreasing size of the beta coefficient for sidx, representing the variable effect size on the outcome variable. Final models were selected if the effect of sidx was significant at a p-value of 0.05 (Figure 1). For the second objective, we use the same approach given model formulations of sidx ~ H and sidx ~ H + C. In the model results from both objectives, we report the Bayesian Information Criterion (BIC), which was calculated based on the maximum likelihood for each model, to enable comparisons among multiple models of the same province ( ((28))). Lower values of BIC indicate a more parsimonious model fit to the data. A difference in BIC (∆BIC) of two or less indicates that the two models are equally effective in support of being the best model ( ((29))).

Figure 1.

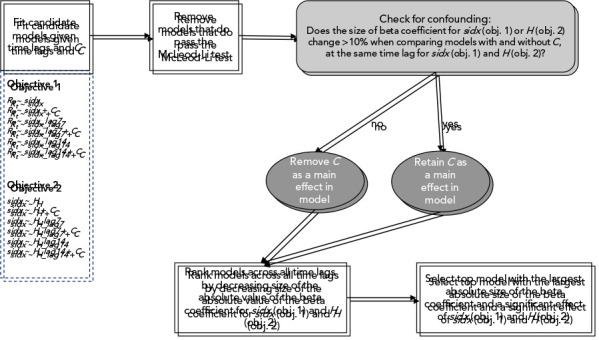
Summary of the model building and model selection approaches run separately for each province and objective

Abbreviations: C, period of time with combined effects of vaccination, Alpha variant and winter; H, number of hospitalized COVID-19 patients; lag7, time lags at seven days; lag14, time lags at 14 days; obj, objective; R_t, transmission rate; sidx, stringency index

Results

Temporal variation in R_t, sidx, and H were similar among the provinces during the study period (Figure 2). Visually, sidx and R_t were negatively associated (Figure 3), while H and sidx appeared positively associated (Figure 4). For objective 1, we found that sidx was significantly and negatively associated with R_t in all provinces except for BC. Alberta, SK, ON and QC had one final top selected model, while MB had three, with the top selected model having a lag of seven days for sidx. For the other provinces, the effects of sidx were lagged at 14 days for AB and QC, seven days for SK, but with no lag for ON (Table 2).

Figure 2.

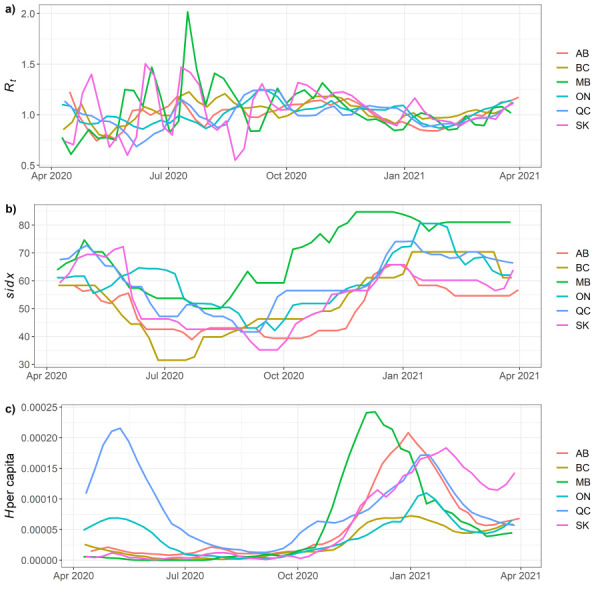
Study period time series at provincial level^a

Abbreviations: AB, Alberta; BC, British Columbia; H, number of hospitalized COVID-19 patients; MB, Manitoba; ON, Ontario; QC, Québec; R_t, transmission rate; SK, Saskatchewan

^a Study period time series at provincial level for a) transmission rate, R_t, b) stringency of NPIs, sidx, and c) number of hospitalized COVID-19 patients, H, per capita, for visual comparison. Data are averaged per week

Figure 3.

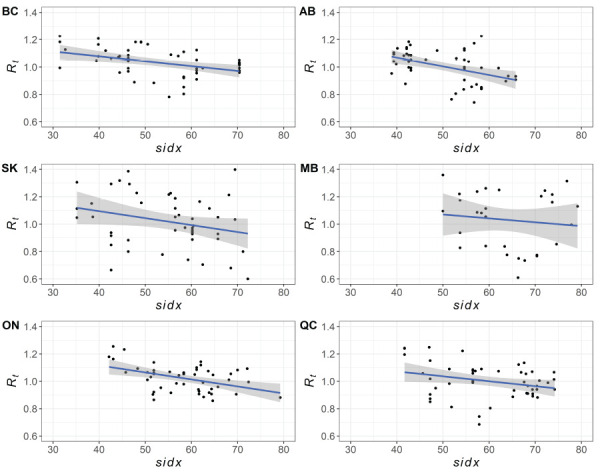
Scatter plot of stringency of non-pharmaceutical interventions against the transmission rate for six provinces in Canada^a

Abbreviations: AB, Alberta; BC, British Columbia; MB, Manitoba; ON, Ontario; QC, Québec; R_t, transmission rate; sidx, stringency index; SK, Saskatchewan

^a Data are averaged per week. A linear fitted line between sidx and R_t with standard errors are included to highlight the trend between the two variables

Figure 4.

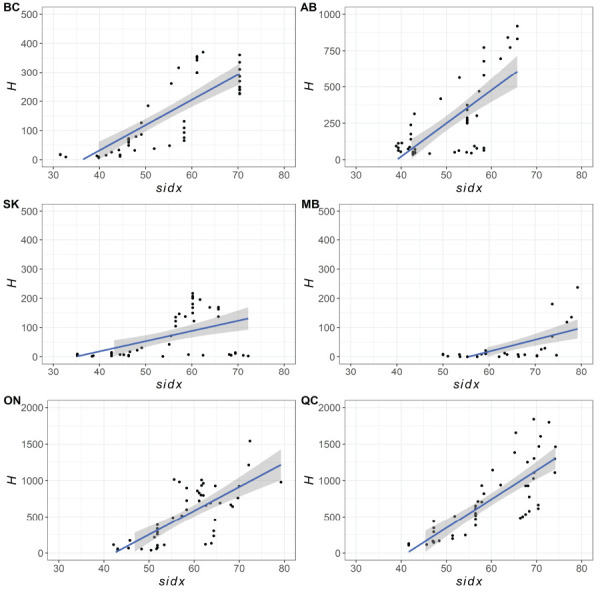
Scatter plot of stringency of non-pharmaceutical interventions against the number of hospitalized COVID-19 patients for six provinces in Canada^a

Abbreviations: AB, Alberta; BC, British Columbia; H, number of hospitalized COVID-19 patients; MB, Manitoba; ON, Ontario; QC, Québec; sidx, stringency index; SK, Saskatchewan

^a Data are averaged per week. A linear fitted line between sidx and H with standard errors are included to highlight the trend between the two variables

Table 2. Results from the final selected models at the provincial level for study objective 1^a,b.

Province	Model variables	BIC	M-Li	nV	sidx				C				nObs
					β	CI low	CI high	p-value	β	CI low	CI high	p-value
BC	sidx_lag14	-116.8	0	5	-6.06E-03	-1.37E-02	1.54E-03	1.18E-01	N/A	N/A	N/A	N/A	50
	sidx_lag7	-115.6	1	2	-3.83E-03	-1.07E-02	3.02E-03	2.73E-01	N/A	N/A	N/A	N/A	50
	sidx	-115.2	1	1	-3.23E-03	-1.02E-02	3.70E-03	3.61E-01	N/A	N/A	N/A	N/A	50
AB	sidx + C	-114.9	1	2	-9.16E-04	-7.94E-03	6.11E-03	7.98E-01	-2.80E-02	-1.27E-01	7.08E-02	5.78E-01	51
	sidx_lag14	-125.2	1	0	-7.30E-03	-1.19E-02	-2.66E-03	2.04E-03	N/A	N/A	N/A	N/A	51
	sidx_lag7 + C	-115.1	1	0	2.70E-03	-6.74E-03	1.21E-02	5.75E-01	-4.04E-02	-1.42E-01	6.10E-02	4.34E-01	51
SK	sidx_lag14	-17.1	1	2	-2.78E-03	-1.06E-02	5.03E-03	4.85E-01	N/A	N/A	N/A	N/A	51
	sidx	-18.24	1	1	-4.98E-03	-1.25E-02	2.55E-03	1.95E-01	N/A	N/A	N/A	N/A	51
	sidx_lag7	-20.61	1	0	-7.83E-03	-1.55E-02	-1.80E-04	4.48E-02	N/A	N/A	N/A	N/A	51
MB	sidx_lag7	-8.776	1	0	-8.14E-03	-1.49E-02	-1.40E-03	1.80E-02	N/A	N/A	N/A	N/A	51
	sidx	-8.04	1	0	-7.62E-03	-1.44E-02	-8.74E-04	2.68E-02	N/A	N/A	N/A	N/A	51
	sidx_lag14	-7.489	1	0	-7.12E-03	-1.40E-02	-2.86E-04	4.11E-02	N/A	N/A	N/A	N/A	51
ON	sidx + C	-148.5	1	0	-4.30E-03	-8.51E-03	-8.79E-05	4.54E-02	-9.67E-02	-1.92E-01	-1.18E-03	4.72E-02	51
	sidx_lag7 + C	-149.6	1	0	-2.20E-03	-6.25E-03	1.84E-03	2.86E-01	-3.72E-02	-1.20E-01	4.53E-02	3.77E-01	51
	sidx_lag14 + C	-145.5	1	0	-1.01E-03	-5.32E-03	3.30E-03	6.46E-01	-4.83E-02	-1.33E-01	3.66E-02	2.65E-01	51
QC	sidx_lag14	-149.2	1	0	-7.66E-03	-1.30E-02	-2.29E-03	5.20E-03	N/A	N/A	N/A	N/A	51
	sidx_lag7 + C	-138.6	1	0	-2.42E-03	-8.34E-03	3.50E-03	4.22E-01	-1.63E-02	-8.34E-02	5.08E-02	6.33E-01	51
	sidx	-141.9	1	0	-2.15E-03	-7.75E-03	3.46E-03	4.53E-01	N/A	N/A	N/A	N/A	51

Abbreviations: AB, Alberta; β, beta coefficient; BC, British Columbia; BIC, Bayesian Information Criterion; C, period of time with combined effects of vaccination, Alpha variant and winter; CI, 95% confidence interval; lag7, time lags at seven days; lag14, time lags at 14 days; MB, Manitoba; M-Li, McLeod-Li test; N/A, not applicable; nObs, number of observations for model fitting; nV, number of violations in the McLeod-Li test; ON, Ontario; QC, Québec; R_t, transmission rate; sidx, stringency index; SK, Saskatchewan

^a Results from the final selected models at the provincial level for study objective 1 of general model formulation: R_t ~ sidx and assessing for confounding from vaccination, the Alpha variant and winter

^b Models highlighted in grey were significant at p-value ≤0.05 and pass the McLeod-Li test with two or fewer violations. The models are ordered by the absolute value of the beta coefficient for sidx. Model estimates are shown for the beta coefficients, 95% confidence intervals and the p-value

For objective 2, we found that H was significant and positively associated with sidx in all provinces except for SK. In BC, two models had effectively equal support for lagged effects of H at seven and 14 days, though the effect size of H was greater at 14 days. Alberta also had two models with equally effective support with H at 0 and seven days. The effect size was larger at seven days. For MB, there was only one model with a significant effect of H, which was lagged at seven days. Ontario and QC both had two models with significant effects of H. For ON, H was lagged at seven and 14 days, with the effect size being greater at 14 days. In QC, the effect size was greatest in the model with no time lag of H, as compared to a model a seven-day lag (Table 3).

Table 3. Results from the final selected models at the provincial level for study objective 2^a,b.

Province	Model variables	BIC	M-Li	nV	H				C				nObs
					β	CI low	CI high	p-value	β	CI low	CI high	p-value
BC	H_lag14	260.3	1	0	6.44E-02	1.41E-02	1.15E-01	1.21E-02	N/A	N/A	N/A	N/A	51
	H_lag7	261.9	1	0	5.41E-02	1.87E-03	1.06E-01	4.23E-02	N/A	N/A	N/A	N/A	51
	H	265.2	1	0	2.34E-02	-2.73E-02	7.40E-02	3.66E-01	N/A	N/A	N/A	N/A	51
AB	H_lag7 + C	233.8	1	0	2.70E-02	1.50E-02	3.90E-02	1.02E-05	-4.48	-8.97	1.17E-02	5.06E-02	50
	H	231.1	1	0	2.60E-02	1.42E-02	3.78E-02	1.58E-05	N/A	N/A	N/A	N/A	50
	H_lag14	242.5	1	0	1.45E-02	1.26E-03	2.77E-02	3.18E-02	N/A	N/A	N/A	N/A	50
SK	H_lag7 + C	278.7	1	0	2.35E-02	-7.84E-02	1.25E-01	6.51E-01	2.12	-3.93	8.18	4.91E-01	50
	H + C	278.8	1	0	1.88E-02	-7.87E-02	1.16E-01	7.05E-01	2.68	-3.26	8.63	3.76E-01	50
	H_lag14 + C	278.9	1	0	1.63E-03	-1.01E-01	1.04E-01	9.75E-01	2.47E	-3.49	8.43	4.16E-01	50
MB	H_lag7	233.4	1	0	2.88E-02	2.70E-04	5.73E-02	4.79E-02	N/A	N/A	N/A	N/A	51
	H_lag14	236.1	1	0	1.49E-02	-1.45E-02	4.42E-02	3.20E-01	N/A	N/A	N/A	N/A	51
	H + C	254	1	0	7.63E-03	-2.26E-02	3.79E-02	6.21E-01	-2.04	-5.96	1.88	3.08E-01	51
ON	H_lag14	266	1	0	1.55E-02	7.74E-03	2.32E-02	8.77E-05	N/A	N/A	N/A	N/A	51
	H_lag7	269.1	1	0	1.40E-02	5.78E-03	2.23E-02	8.52E-04	N/A	N/A	N/A	N/A	51
	H	273.8	1	0	1.02E-02	-4.22E-04	2.08E-02	5.98E-02	N/A	N/A	N/A	N/A	51
QC	H + C	243.5	1	0	8.36E-03	1.29E-03	1.54E-02	2.05E-02	-2.48	-5.29	3.36E-01	8.44E-02	51
	H_lag7	229.9	1	0	6.90E-03	4.02E-04	1.34E-02	3.74E-02	N/A	N/A	N/A	N/A	51
	H_lag14 + C	247.5	1	0	3.13E-03	-3.51E-03	9.77E-03	3.55E-01	-2.34	-4.84	1.68E-01	6.75E-02	51

Abbreviations: AB, Alberta; β, beta coefficient of the variable; BC, British Columbia; BIC, Bayesian Information Criterion; C, period of time with combined effects of vaccination, Alpha variant and winter; CI, 95% confidence interval; H, number of hospitalized COVID-19 patients; lag7, time lags at seven days; lag14, time lags at 14 days; MB, Manitoba; M-Li, McLeod-Li test; N/A, not applicable; nObs, number of observations for model fitting; nV, number of violations in the McLeod-Li test; ON, Ontario; QC, Québec; sidx, stringency index; SK, Saskatchewan

^a Results from the final selected models at the provincial level for study objective 2 of general model formulation: sidx ~ H and assessing for confounding from vaccination, the Alpha variant and winter

^b Models highlighted in grey were significant at p-value ≤0.05 and pass the McLeod-Li test with two or fewer violations (nV). The models are ordered by the absolute value of the beta coefficient for the number of hospitalized COVID-19 patients. Also shown are the 95% confidence intervals for beta

Our analysis suggests there was limited evidence for confounding effects of vaccination, the Alpha variant and winter, as modelled by C, on the outcome variables. For objective 1, there was only one model, as found for ON, with a significant effect sidx on R_t that also included a significant effect of C. All other models with significant effects of sidx did not retain C (Table 2). For objective 2, there were only two models, as found for AB and QC, that had a significant effect of H on sidx and retained the variable for C (Table 3). However, in both cases, the effect of C was not significant.

The full model results, with the AR and MA terms, are provided in the supplementary material for final models that contain a significant effect of sidx on R_t for objective 1, and of H on sidx for objective 2, at a p-value ≤0.05 (Appendix).

Discussion

This study used a dynamic regression approach to assess the impact of NPIs as measured by the Canadian subnational stringency index, sidx, to reduce the transmission of SARS-CoV-2 as measured by R_t and explore the potential for the number of hospitalized COVID-19 patients, H, to drive the level of sidx. Our results provide empirical evidence for the associations that sidx has with R_t and H at the provincial level in Canada. There already exists empirical evidence for the effect of NPIs to reduce the burden of COVID-19 in other countries ( ((5–7,9))), but at the time of writing, this effect was less understood in Canada, with studies reporting varying to non-effects of NPIs ( ((16,17,30,31))).

Stratifying the analysis by province facilitated the interpretation of the effects of sidx and H given interprovincial differences in testing activities and mitigation strategies. At the provincial level, statistical results suggest that for most provinces, increasing sidx had a significant and time-lagged effect to decrease R_t. Though the effect of sidx was negative, it was not significantly associated with R_t for BC (where sidx and R_t showed a broadly negative relationship for all provinces [Figure 3]). For the second objective, increasing H was significantly associated with increasing sidx, with a time-lagged effect, in all provinces except for SK. For SK, the effect of H on sidx was positive, but not significant (where sidx and H showed a broadly positive association for all provinces [Figure 4]). For both objectives, there were interprovincial inconsistencies in the length of the lagged effects of sidx (objective 1) and H (objective 2). It is possible that the inconsistencies relate to provincial differences in reporting and compliance to NPIs. The proportion of cases reported can vary within and among provinces ( ((32))). This may be caused by 1) differences in testing criteria and rates and 2) underreporting due to socio-demographic factors that influence both willingness to be tested and access to provincial testing centres ( ((33,34))). Testing criteria changed over time and differed among the provinces. Proportionally few asymptomatic people were likely to be tested, except in healthcare, long-term care and at certain times when resources enabled a wider population testing criteria through contact tracing ( ((32))). Reporting inconsistencies would decrease the accuracy of R_t to represent the true level of transmission and thus reduce the ability to detect an association between sidx and R_t. The absence of a detectable effect of H on sidx for SK may relate to interprovincial variation in the epidemics, in that, the actual numbers of cases were mostly lower in SK, for the study period, compared to the other, larger provinces.

Interpretation of time-lagged effects of sidx on R_t also requires consideration of the calculation of R_t, which used the date of case reporting. The combined incubation period of infection ( ((35))), time from symptom onset to obtaining a positive polymerase chain reaction result, and then time lag from case detection to reporting of the case has been internally estimated by the Public Health Agency of Canada at up to 14 days. This means that the R_t used in this study is a delayed measure of the transmission rate for a particular day. Therefore, the time-lagged effects of sidx on R_t found in this study, at seven to 14 days, may in fact be identifying more rapid effects of public health measures on transmission.

Modelling studies suggest that early implementation of restrictive NPIs is optimal to maximize their effect and minimize their duration ( ((36))). However, the time-lagged effect of H on sidx suggests that the provinces implemented and strengthened NPIs in response to a growing number of hospitalized COVID-19 patients rather than preventively.

Modelling studies initially suggested that restrictive closures would not be needed to control the COVID-19 epidemic in Canada with case detection and isolation and contact tracing and quarantine (test-and-trace), combined with physical distancing measures ( ((37–39))). Clearly, repeated resurgence of the epidemic, combined with the findings here suggest that test-and-trace capacity has not been sufficient and restrictive closures (which comprise most of the components of the sidx) have had to be implemented to control the epidemic.

We did not find strong evidence for confounding. This may be in part due to our proxy variable combining effects that were expected to differ in the direction of their association, such that, vaccination should reduce R_t, while the alpha variant and more time spent indoors during the winter should associate with an increase in R_t. The analysis occurred using data prior to significant vaccination of the Canadian population so it is likely that the elucidated relationships provide evidence of genuine associations between cases, hospitalizations and NPIs.

Study strengths and limitations

The strength of our study largely centres on our statistical approach and model structure. A similar study assessing for the impact of NPIs using stringency as a composite measure on the daily growth rate of cases did not identify a significant association over a similar study period from February 2020 to February 2021 ( ((17))). We argue that our model structure is better suited to model non-stationary time-dependent data by accounting for complex temporal dynamics of the time series using the MA and AR terms ( ((40))). Vickers et al. ( ((17))) used a random effect that can only account for the autocorrelation within defined time periods. By using autoregressive functions, we were able to account for any serial dependence in the data throughout the study time period. The McLeod-Li test validated the effectiveness of the model structure ( ((26))). Furthermore, through this model structure, we could use fixed effects to assess for time-lagged effects of sidx, unlike the approach by Vickers et al. ( ((17))). Finally, this is the first study that explicitly tests for the effect that H may have on the implementation of sidx in strength and timing.

An important limitation in our study is that the stringency indices, as developed by the Blavatnik School of Government, and as adapted for this study, do not account for public compliance ( ((15))), upon which the success of NPIs to reduce the burden of COVID-19 depends. Interprovincial differences in the level of public compliance to NPIs were present during the study period. Analysis of survey data during the time period of this study indicates that compliance to NPIs tends to be lower in AB and SK, and higher in ON and QC ( ((41,42))). Furthermore, the level of public compliance is influenced by the ability of governments to clearly communicate the importance of having NPIs, the timeliness of implementation, clarity and consistency of enforcement, and public understanding and attitudes towards NPIs ( ((43–46))). In Canada, public healthcare is the mandate of the provincial governments, and sociodemographics varies among the provinces, therefore accounting for reporting differences and compliance at the provincial level should strengthen the associations of sidx with R_t, and sidx with H.

Another limitation arises from sidx being a composite index derived from multiple NPIs without weighting the strength of their contribution to limit infectious contacts. Analysis of Canadian data provides evidence that the effectiveness of NPIs depends on the type of measure ( ((30,31))). A greater understanding of the NPI measures at the individual level would benefit future policy development and implementation for using any one measure against COVID-19 or other respiratory illnesses with similar or great public health impacts.

Conclusion

Results from this study provide evidence that NPIs, as measured by a composite stringency index, are associated with reducing cases in Canada; while the strength of the stringency of NPIs was driven, in part, by the number of hospitalized COVID-19 patients. The timing of NPIs, as measured by lagging sidx at 0, 7 and 14 days, to reduce SARS-CoV-2 transmission, as measured by the effective reproduction number, was not consistent across the studied provinces. This may be caused by interprovincial differences in reporting of COVID-19 and the level of population compliance to NPIs. Future work should focus on these factors, particularly the effect of NPIs to reduce SARS-CoV-2 transmission as modified by measures of compliance and assessing for varying effects of individual NPIs.

Appendix.

This document provides the full model parameter estimates for the top ranked models, per province and objective, for models containing a significant effect of sidx (objective 1) or H (objective 2).

Table A1. Model formulation and ARIMAX (p, d, q) for provinces.

Province	Model formulation	ARIMAX (p, d, q)a	Parameter	Beta coefficient		p-value
				n	95% CI
British Columbia	sidx ~ H_lag14	ARIMAX (2, 0, 0)	ar1	1.22	0.969 to 1.48	4.86e-21
			ar2	-0.352	-0.647 to -0.057	1.93e-02
			intercept	44.6	35.3 to 53.9	7.71e-21
			H_lag14	0.0644	0.0141 to 0.115	1.21e-02
Alberta	Rt ~ sidx_lag14	ARIMAX (2, 0, 0)	ar1	1.19	0.917 to 1.45	5.06e-18
			ar2	-0.567	-0.841 to -0.294	4.79e-05
			intercept	1.38	1.15 to 1.61	6.19e-31
			sidx_lag14	-0.0073	-0.0119 to -0.00266	2.04e-03
	sidx ~ H_lag7 + C	ARIMAX (0, 1, 0)	H_lag7	0.027	0.015 to 0.039	1.02e-05
			C	-4.48	-8.97 to 0.0117	5.06e-02
Saskatchewan	Rt ~ sidx_lag7	ARIMAX (0, 0, 1)	ma1	0.76	0.55 to 0.97	1.32e-12
			intercept	1.46	1.04 to 1.88	1.00e-11
			sidx_lag7	-0.00783	-0.0155 to -0.00018	4.48e-02
Manitoba	Rt ~ sidx_lag7	ARIMAX (0, 0, 1)	ma1	0.584	0.361 to 0.806	2.65e-07
			intercept	1.61	1.14 to 2.08	2.71e-11
			sidx_lag7	-0.00814	-0.0149 to -0.0014	1.80e-02
	sidx ~ H_lag7	ARIMAX (0, 1, 1)	ma1	0.456	0.181 to 0.731	0.00115
			H_lag7	0.0288	0.00027 to 0.0573	0.04790
Ontario	Rt ~ sidx + C	ARIMAX (0, 1, 0)	sidx	-0.0043	-0.00851 to -8.79e-05	0.0454
			C	-0.0967	-0.192 to -0.00118	0.0472
	sidx ~ H_lag14	ARIMAX (1, 0, 1)	ar1	0.698	0.413 to 0.982	1.59e-06
			ma1	0.487	0.156 to 0.818	3.96e-03
			intercept	51.4	45.7 to 57.1	1.05e-70
			H_lag14	0.0155	0.00774 to 0.0232	8.77e-05
Québec	Rt ~ sidx_lag14	ARIMAX (1, 0, 1)	ar1	0.744	0.527 to 0.962	2.02e-11
			ma1	0.775	0.566 to 0.984	3.88e-13
			intercept	1.48	1.14 to 1.83	2.11e-17
			sidx_lag14	-0.00766	-0.013 to -0.00229	5.20e-03
	sidx ~ H + C	ARIMAX (1, 0, 1)	ar1	0.899	0.778 to 1.02	6.17e-48
			ma1	0.75	0.48 to 1.02	5.15e-08
			intercept	56.6	46.4 to 66.8	1.52e-27
			H	0.00836	0.00129 to 0.0154	2.05e-02
			C	-2.48	-5.29 to 0.336	8.44e-02

Abbreviations: ar, autoregressive term; ARIMAX, autoregressive integrated moving average extended; C, period of time with combined effects of vaccination, Alpha variant and winter; CI, 95% confidence interval; lag7, time lags at seven days; lag14, time lags at 14 days; MA, moving average; R_t, transmission rate; sidx, stringency index

^a ARIMAX (p,d,q) denotes the number of autoregressive terms, p, degree of differencing, d, and number of moving average terms, q