Multi-Institutional Assessment and Crowdsourcing Evaluation of Deep Learning for Automated Classification of Breast Density

Abstract

Objective:

We developed deep learning algorithms to automatically assess Breast Imaging Reporting and Data System breast density.

Methods:

Using a large multi-institution patient cohort of 108,230 digital screening mammograms from the Digital Mammographic Imaging Screening Trial, we investigated the effect of data, model, and training parameters on overall model performance and provided crowdsourcing evaluation from the attendees of the American College of Radiology 2019 Annual Meeting.

Results:

Our best performing algorithm achieved good agreement with radiologists who were qualified interpreters of mammograms, with a 4-class κ of 0.667. When training was performed with randomly sampled images from the dataset versus sampling equal number of images from each density category, the model predictions were biased away from the low-prevalence categories such as extremely dense breasts. The net result was an increase in sensitivity and a decrease in specificity for predicting dense breasts for equal class compared to random sampling. We also found that the performance of the model degrades when we evaluate on digital mammography data formats that differ from the one that we trained on, emphasizing the importance of multi-institutional training sets. Lastly, we showed that crowdsourced annotations, including those from attendees who routinely read mammograms, had higher agreement with our algorithm than with the original interpreting radiologists.

Conclusion:

We demonstrated the possible parameters that can influence the performance of the model and how crowdsourcing can be used for evaluation. This study was performed in tandem with the development of the ACR AI-LAB, a platform for democratizing Artificial Intelligence.

Introduction

Breast cancer is one of the leading causes of death among women in the US, with the expected number of deaths to be over 41,000 in 2019. [1] Early mammographic screening has resulted in a decrease in breast cancer mortality. [2,3] The correct mammographic interpretation of breast density, which measures extent of fibroglandular tissue, is important in the assessment of breast cancer risk as there is increased risk with increased density. [4,5] Furthermore, the identification of dense breast may stratify patients who may have masked cancers and may benefit from additional ultrasound and/or MR imaging. As such, there is now legislation in many states that patients must be notified of their breast density after mammography. [6]

Qualitative assessment by means of the widely used Breast Imaging Reporting and Data System (BI-RADS) include four categories: a) almost entirely fatty, b) scattered fibroglandular densities, c) heterogeneously dense, or d) extremely dense. [7] These criteria are subjective, resulting in inter-rater variability among radiologists. A study by Sprague et al. showed that the likelihood of any given mammogram being rated as dense (heterogeneously dense and extremely dense) is highly dependent on the interpreting radiologist, with the percentage ranging from 6.3%−84.5%. [8] Other studies have reported intra-reader variability to be κ = 0.58 (among 34 community radiologists) and the inter-rater variability to be κ = 0.643 (between a consensus of 5 breast radiologists and the original interpreting breast radiologist). [6,9] Similarly, commercially available software shows a wide range of agreement with clinical experts and the probability of dense classification is dependent on the specific software used. [10,11] This intra- and inter-rater variability, and even inter-software variability, may confer undue patient anxiety and potential harm to the patient, i.e. possible unnecessary supplemental screening examinations.

As such, there has been interest in using automated approaches to improve accuracy and consistency of breast density assessment. Commercial software utilize quantitative imaging features to assess breast density, with mixed agreement with radiologist interpretation. [11] Deep learning methods have yielded state-of-the-art results in a wide range of computer vision tasks without the need for domain-inspired hand-crafted imaging features. Moreover, recent studies have shown the potential of deep learning in medical fields such as dermatology, ophthalmology, and radiology. [12–14] A recent study from Lehman et al. demonstrates the utility of deep learning for mammographic density assessment in clinical practice at a single institution/mammography system. [6] Here, we further this work by validating the deep learning approach on a multi-institutional imaging cohort with a variety of digital-mammography systems. Furthermore, we provide an in-depth analysis of how choice of data, model, and training parameters affects algorithm performance. In addition to that, we investigate the generalizability of models across different digital-mammography data formats. Lastly, we deploy our system at the American College of Radiology (ACR) 2019 Annual Meeting for a crowdsourced evaluation.

Materials and Methods

Patient Cohort

Digital screening mammograms from 33 clinical sites were retrospectively obtained through the Digital Mammographic Imaging Screening Trial (DMIST), the details of which were previously published. [15] Each examination was interpreted by a single radiologist from a cohort of radiologists using ACR BI-RADS breast density lexicon (Category a: fatty, Category b: scattered, Category c: heterogeneously dense, Category d: extremely dense). [7] There were a total of 92 radiologists reading the exams. Readers in the United States were all qualified interpreters of mammograms under federal law. Canadian readers met equivalent standards. Each site’s lead radiologist received training to read for DMIST and in turn trained the site’s other readers. All images were previously de-identified before this study. The mammograms were saved in DICOM format with 4 different image data formats, corresponding to different digital-mammography systems or different versions of the same system (Table 1): 12 bit Monochrome 1 (30.3%), 12 bit Monochrome 2 (11.2%), 14 bit Monochrome 1 (58.0%), and 14-bit Monochrome 2 (0.5%). 14-bit Monochrome 2 images were excluded to ensure that each image data format included in our study had adequate representation for training of our deep learning model. Our final patient cohort consisted of 108,230 digital screening images from 21,759 patients (Table 2), which was divided into training, validation, and testing sets on the patient level. The training set was used to develop the model and the validation set was used to assess model performance during training to prevent overfitting. The test set was unseen until the model training was complete.

Table 1.

Breakdown of data format by digital mammograph system.

12 Bit Monochrome 1	12 Bit Monochrome 2	14 Bit Monochrome 1
Senoscan (99.9%) Kodak Lumiscan 75 (.1%)	Senograph (93.8%) Other (6.1%) Mammo-Clinical (.1%)	Senograph (94.1%) Mammo-Clinical (5.9%)

Table 2.

Summary of demographics in the patient cohort with regard to age, sex, race, and breast density.

	Training (n = 62316)	Validation (n = 6978)	Testing (n = 38936)
Age (median years, IQR)	46 (53–61)	46 (53–61)	47 (53–61)
Female (%)	100	100	100
Race
White	50414	5622	30845
Black or African American	8389	925	5733
Hispanic or Latino	2273	289	1416
Asian	819	62	633
American Indian or Alaska	63	8	19
Other or Unknown	358	72	290
Radiologist-assessed breast density
Fatty	6980 (11.2%)	873 (12.5%)	4575 (11.8%)
Scattered	27733 (44.5%)	2985 (42.8%)	17191 (44.2%)
Heterogeneously dense	23987 (38.5%)	2753 (39.5%)	14585 (37.5%)
Extremely dense	3616 (5.8%)	367 (5.3%)	2585 (6.6%)

Experiments on Data, Model, and Training Parameters

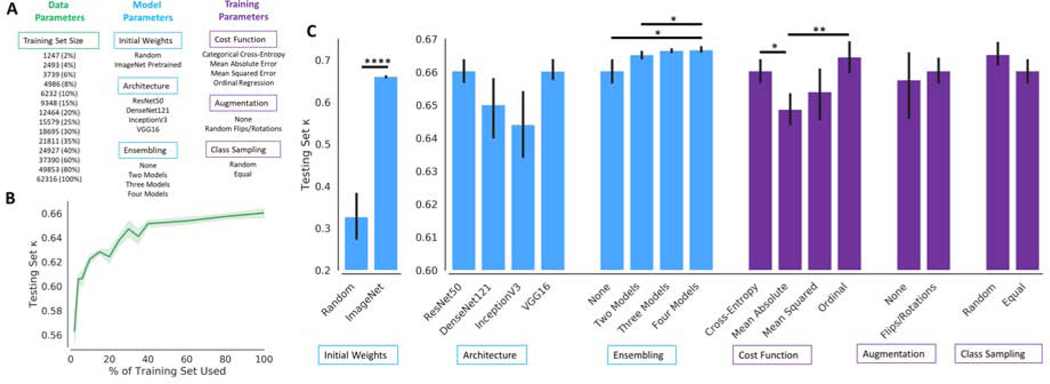
Neural network models were implemented in DeepNeuro with Keras/TensorFlow backend. [16] We investigated the effect of data, model, and training parameters on algorithm performance. A schematic of the various experiments investigating data, model, and training parameters are summarized in Fig. 1A. To investigate the effect of training set size, we utilized various different training set sizes and assessed the resulting performance on the test set. We tested four commonly used neural network architectures, each of which differ in number of layers and design: ResNet50, DenseNet121, InceptionV3, and VGG16. [17–21] We also investigated the benefit of pretraining by comparing ImageNet (a large computer vision dataset of natural images) pretrained versus random initialization. [22] A variety of cost-functions were also utilized (categorical cross-entropy, mean absolute error, mean squared error, and ordinal regression) in order to assess the effect of objective function (and their underlying assumptions of the nature of the labels) on performance. [23] The training set was augmented in real time by means of random horizontal/vertical flips (50% probability of each) and random rotations (0–45°). At each mini-batch, images from each breast density class were sampled with either random (weighting in the empirical density class distribution) or equal class (weighting each density class equally) probability to assess the effect of class weighting on performance. We also evaluated the effect of model ensembling by averaging the output of 2–4 trained models of the same architecture (ResNet50). Model ensembling describes the process by which several independently trained models are combined to improve performance. [24] The default model utilized 100% of the training set, ImageNet pretrained weights, ResNet50 architecture, no ensembling, categorical cross-entropy loss function, augmentation, and equal class sampling. Only one parameter was modified at a time in the experiments, keeping all other parameters the same as the default model (ceteris paribus).

Figure 1.

(A) A summary of all the data, model, and training parameter experiments performed. (B) Performance on the testing set (measured by 4-class κ agreement with radiologist interpretation) increased as the percentage of training set used. The 95% confidence interval is plotted in light green. (C) Effect of model and training parameters on testing set 4-class κ agreement with radiologist interpretation. Black lines denote 95% confidence interval. P-values are denoted by *p < .05, **p < .01, ****p < .001

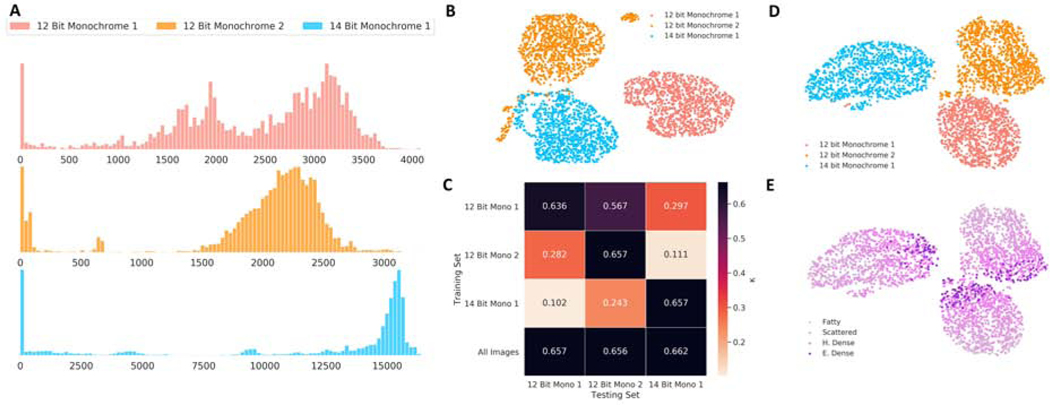
Experiments on Image Data Formats

To visualize the differences in intensity distributions across image formats, histograms of preprocessed images from the testing set were generated. The dimensionality of histograms were then reduced to a 2-dimensional projection and plotted to inspect for similarity across image formats. [25] The effect of image format of training images on generalizability of models was investigated. We trained ResNet50 models using 12 bit Monochrome 1 images only, 12 bit Monochrome 2 images only, 14 bit Monochrome 1 images only, and all images. The performance of these models for each image format was then assessed. Projections of the intermediate output of the penultimate layer of the neural network were also plotted for images in the testing set using a model trained on all images to evaluate the learned features learned by the deep learning model. Further information about the patient cohort and experiments is available in the Supplementary Information.

Crowdsourcing Assessment

As further evaluation of our breast density algorithm, we deployed an annotation workstation at the ACR 2019 Annual Meeting. Attendees of all levels (researchers, medical students, residents, radiologists) were invited to perform annotations on a subset of images within our patient cohort. Representative images of all breast density classifications from the BI-RADS manual were provided to attendees during annotation. Attendees were able to inspect all images (all views available) from a given patient study and were asked to provide a BI-RADS breast density assessment. In total, 3,649 annotations were performed on 1083 patient studies by 17 raters (Demographics summarized in Table 3). On average, there were 3 annotations per patient study and each rater performed 215 annotations. Consensus of the crowd was determined by majority vote, with random tiebreak. In our analysis, we looked at agreement between crowd and original interpreting radiologist annotation as well as crowd and algorithm (ResNet50). The ResNet50 model was chosen because it was the best performing architecture among those tested. Only a single model (as opposed to an ensembled model) was used to reflect the common scenario where only a single model is deployed for computation efficiency.

Table 3.

Demographics of participants of the crowdsourcing assessment.

	N
Experience
Radiologist (Breast)	3
Radiologist (Other)	10
Resident	2
Student	2
Read Mammograms
No	10
Yes	7

Statistical Analysis

Agreement between raters was assessed via linear κ coefficient across the four breast density categories in the testing set (4-class κ). For reference, a κ of 0.21–.40, 0.41–0.60, and 0.61–0.80 represents fair, moderate, and substantial agreement, respectively. [26]

Results

Effect of Data Parameters on Performance

The performance of training set size on testing set performance was investigated, showing that κ coefficient increases as the training set size increases. When 2% (n = 1247 images) of the training set was used, the mean 4-class κ was 0.563 (95% Confidence Interval, CI, 0.551–0.576). In contrast, when using 100% (n = 62,316 images) of the training set, the mean 4-class κ was 0.660 (95% CI 0.657–0.664) (Fig. 1B). There was a statistically significant difference between the performance of using 2%−60% and 100% of the training set (t-test p < .05). There was no difference in the performance of using 80% and 100% of the training set (p = 0.291).

Effect of Model Parameters on Performance

The mean 4-class κ of models with randomly initialized weights was 0.327 (95% CI 0.273–0.384), compared to ImageNet pretrained weights 0.660 (95% CI 0.657–0.664, p < .001) when using the full training set (Fig. 1C). In the experiments assessing model architecture, the mean 4-class κ of ResNet50, DenseNet121, InceptionV3, and VGG16 was 0.660 (95% CI 0.657–0.664), 0.650 (95% CI 0.640–0.659), 0.644 (95% CI 0.635–0.652), and 0.660 (95% CI 0.658–0.664), respectively. There was no statistically significant difference between the performance of the various architectures. The mean 4-class κ of no ensembling, ensembling two models, ensembling three models, and ensembling four models was 0.660 (95% CI 0.657–0.664), 0.665 (95% CI 0.664–0.666), 0.666 (95% CI 0.666–0.667), 0.667 (95% CI 0.666–0.668), respectively. The performance of ensembling four models and three models was greater than that of no ensembling (p = 0.041 and 0.036, respectively).

Effect of Training Parameters on Performance

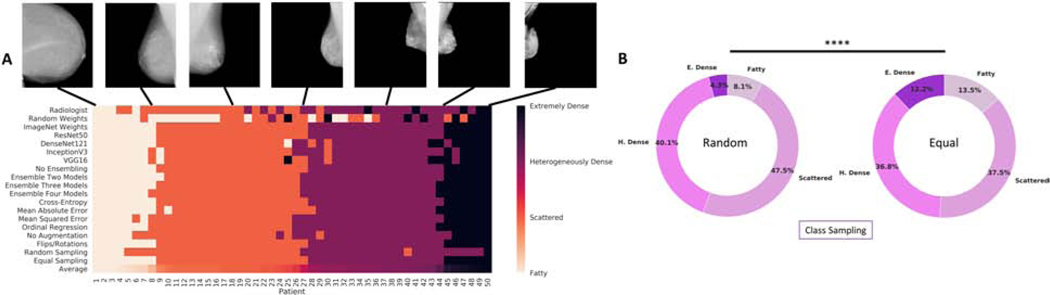
For categorical cross-entropy, mean absolute error, mean squared error, and ordinal regression, the mean 4-class κ was 0.660 (95% CI 0.657–0.664), 0.649 (95% CI 0.644–0.653), 0.654 (95% CI 0.646–0.661), and 0.664 (95% CI 0.659–0.669), respectively. The performance of categorical cross-entropy and ordinal regression was significantly greater than mean absolute error (p = 0.011 and p = 0.004, respectively). The mean 4-class κ with no augmentation was 0.658 (95% CI 0.646–0.666), compared to with augmentation 0.660 (95% CI 0.657–0.664) (p = 0.675). The mean 4-class κ with random and equal class sampling at each mini-batch was 0.665 (95% CI 0.662–0.669) and 0.660 (95% CI 0.657–0.664), respectively (p = 0.135). For random class sampling, the predicted distribution of labels on the test set was 8.1% fatty, 47.5% scattered, 40.1% heterogeneously dense, and 4.3% extremely dense. This differed from the predicted distribution of labels on the test set with equal class sampling, which was 13.5% fatty, 37.5% scattered, 36.8% heterogeneously dense, and 12.2% extremely dense (p < 0.001, Fig. 2B). The predicted binary distribution for random (44.4% dense) and equal sampling (49.0% dense) also differed (p < 0.001). For random class sampling, the mean sensitivity and specificity for classifying dense breast was 0.833 (95% CI 0.803–0.856) and 0.888 (95% CI 0.872–0.905), respectively. Comparatively, for equal class sampling, there was an increase in sensitivity (0.880, 95% CI 0.869–0.890, p < .05) with a decrease in specificity (0.842, 95% CI 0.828–0.857, p < 0.001). A display of the range of classifications for models trained with different model and training parameters for 50 patients in the testing set is shown in Fig. 2A.

Figure 2.

(A) A visual display of the range of classifications for models trained with different model and training parameters for 50 patients in the testing set. The radiologist interpretation is displayed in the first row. The average breast density rating across all models and radiologist interpretation is displayed in the last row and was used to order the patients from least dense (left) to most dense (right). (B) The distribution of predicted breast density labels in the testing set differed for experiments with random class sampling (left) compared to equal class sampling (right) at each mini-batch. P-values are denoted by ****p < .001

Effect of Digital-Mammography Data Format on Model Generalizability

A plot of projections of intensity distributions of preprocessed images showed clustering within image format, delineating differences between image formats (Fig. 3B). Clustering by intensity distribution was preserved even after passing the images through a trained neural network, as shown by projections of the output of the penultimate layer, with the grouping by breast density occurring within the respective image format cluster (Fig. 3D-E). For all image format specific models, testing set performance was decreased for other image formats compared to the image format the model was trained on (p < 0.001). In contrast, a model trained on all images showed no differences in performance across image formats (p > 0.05, Fig. 3C).

Figure 3.

(A) Intensity distribution histogram (Frequency vs Intensity Value) of 100 randomly selected images of each pixel format. (B) Visualization of the histogram of intensities of 3000 preprocessed images from the testing set demonstrating clustering of images by image format. (C) Performance of models trained on specific image formats as well as all images, showing that for image format specific models, testing set performance was decreased for other image formats compared to the image format the model was trained on. (D-E) Visualization of an intermediate layer of the trained neural network for 3000 images in the testing set, color-coded by image format and radiologist interpretation of breast density.

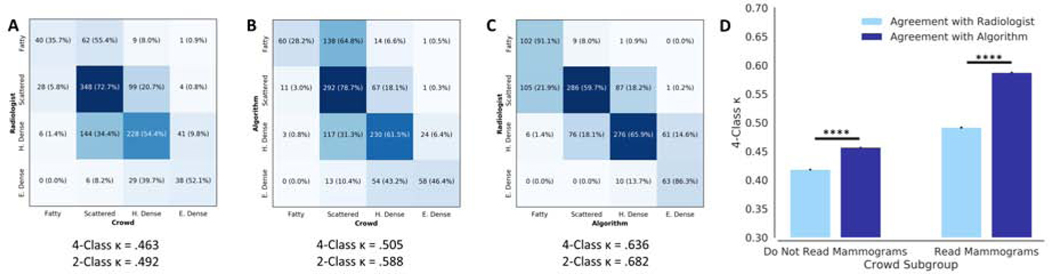
Crowdsourcing Assessment

The 4-class κ between the crowd and algorithm (0.505, 95% CI .503–.506) was greater than agreement between crowd and original interpreting radiologist (0.463, 95% CI 0.461–0.464, p < .001). Agreement with the algorithm was greater than agreement with the original interpreting radiologist for both crowd participants who regularly read mammograms and those who do not (Fig. 4D). As a reference, the 4-class κ between algorithm and radiologist was 0.636 (95% CI 0.635–0.637) for the same patient studies (Fig. 4A-C).

Figure 4.

Confusion matrices showing the agreement between original interpreting radiologist, algorithm, and crowd. The agreement between the algorithm and crowd (B) was greater than the agreement between crowd and original interpreting radiologist (A). The agreement between algorithm and original interpreting radiologist for the same patient studies (C) shown for reference. (D) There was higher agreement, in terms of 4-class κ, with the algorithm than with the original interpreting radiologist from the DMIST trial for both crowdsourcing participants who read mammograms and those who do not. P-values are denoted by *p < .001

Discussion

In this study, we investigated the performance of deep learning models in a large multi-institution and multi-mammography system patient cohort. Our best performing model achieved a κ of 0.667, equivalent to the agreement observed by Lehman et al., which only utilized mammograms from a single institution/mammography system. [6]

One challenge of training robust deep learning models is the availability of large annotated imaging datasets. [27] In this study, we provide empirical evidence that the size of the training set is a key determinant in the performance of neural networks, consistent with another study on abnormality classification in chest radiographs. [28] In accordance with deep learning studies in other domains, tens of thousands of annotated images are needed before model performance begins to plateau in diverse imaging cohorts, supporting the need for collaborative efforts among medical institutions. [28–30]

In our investigation of model parameters, pretraining and ensembling led to improvements in performance. Pretraining neural networks followed by fine-tuning in the target domain (also known as transfer learning) has become a well-established paradigm for medical imaging applications to achieve high performance. [12,29] In our study, we noted that pretraining on ImageNet improved performance for the breast density classification task. Further improvement in performance was seen with ensembling of independently trained models which is analogous to how a consensus of experts is more likely to be correct than any single expert. [31] Interestingly, neural network architecture did not have a significant effect on performance despite differences in model complexity and design.

One important consideration when training a model is the objective function used to optimize the algorithm, also known as a cost function. Our experiments have shown that the choice of cost function had a significant effect on model performance, mainly because each cost-function makes different assumptions about the nature of the labels. Specifically, mean absolute error, mean squared error, and ordinal regression assume that the categories are ordered while categorical cross-entropy does not. Furthermore, mean absolute error and mean squared error assume the distance between adjacent classes is equal whereas ordinal regression does not. In our application, breast density is classified on an ordered scale with undefined distances between adjacent classes (i.e. the distances between Fatty and Scattered compared to heterogeneously dense and extremely dense cannot be quantified), making ordinal regression the most appropriate cost function. This is validated in our experiments, where we find that ordinal regression exhibited the highest performance, although this was significantly different to only mean absolute error.

We also did not notice significant difference between random and equal class sampling on model performance in terms of κ coefficient. Class sampling is an important consideration in cases where there are differences in the number of patient samples from each class (i.e. when the majority class significantly outnumbers the minority class). In our study, we have more patients with scattered and heterogeneously dense breast (44.2% and 37.5% respectively) than with fatty and extremely dense breast (11.8% and 6.6%, respectively), which is the expected distribution as breast density has a normal distribution. Under random class sampling, the neural network would be exposed to more training examples of scattered and heterogeneously dense breast than of fatty and extremely dense breast. Equal class sampling can be used to mitigate this inherent class imbalance by ensuring that the neural network is adequately exposed to all classes. [32] However, it is also important to note that with equal class sampling, the distribution of predicted labels changes – specifically, minority classes are predicted with higher frequency and majority classes are predicted with lower frequency, as shown by our experimental results. The net result of this is that the sensitivity of predicting dense breast improves with equal class sampling. Moreover, equal class sampling leads to lower specificity for classification of dense breast. From a policy perspective, this can lead to more patients being notified that they have dense breast. If additional imaging is performed on these patients, this may lead to increases in the number of false positives. This is a key example of how the manner in which deep learning models are trained can have implications for clinical care.

One critical hurdle that prevents the deployment of deep learning models in the clinical work environment is their relatively poor generalizability across institutional differences, such as patient demographics, disease prevalence, scanners, and acquisition settings. In fact, other deep learning studies that have shown poor generalizability of deep learning models when applied to data from different institutions than the one they were trained on. [33,34] In our study, we found that models trained on specific digital-mammography data formats do not generalize to other data formats, and it was only after training on images from all digital-mammography data formats did our model high performance on all data formats. Indeed, several deep learning studies for mammographic breast density assessment were only validated on patient cohorts from a single institution and/or digital-mammography systems. [6,35,36] Some possible differences between different digital-mammography systems or versions of systems include the x-ray tube target, filter, digital detector technology, and control of automatic exposure. [37] Our results add to the growing body of literature that states that deep learning models do not necessarily generalize when applied to data that differs from that which the model was trained with.

Various studies have shown the utility of crowdsourcing and citizen science in biological and medical image annotation. [38–41] Crowdsourcing for annotation and evaluation is advantageous because it is scalable, high-throughput, cost-efficient, and accurate.[42–44] As such, we performed a crowdsourcing assessment of our algorithm. Notably, there was a diversity of experience of the participants in crowdsourcing, with its inclusion of students, residents, and radiologists who do not routinely read mammograms. As such, it is unsurprising that the agreement between the crowd and algorithm was lower than the agreement between the original interpreting radiologist and algorithm. Interestingly, the crowd (both participants who routinely read mammograms and those who did not) had higher agreement with the algorithm than with the original interpreting radiologist. This may reflect the consistency of the algorithm in its assessment compared to the various interpreting radiologists from different sites in the DMIST study. In other words, a single algorithm may allow for greater consistency than having different human radiologists rate each imaging study.

There are several limitations to our study. The first is that we only had one radiologist, from a cohort of radiologists, perform interpretation for each patient study. Future studies will incorporate multiple readers for each patient study. In addition, for models initialized with random weights, we did not optimize training hyperparameters such as the learning rate schedule or the duration of training. [45] It is possible that optimization would improve the performance of the randomly initialized model, but in this study, we show the performance advantage of pretrained neural networks with minimal hyperparameter tuning. Furthermore, in our investigation of augmentation, we only explored random flips and rotations, though future work will explore other augmentation techniques such as intensity scaling and elastic deformations. [46] Lastly, our algorithm was only developed to assess mammographic breast density. Future work can extend our algorithm and crowdsourcing evaluation for more complex tasks such as assigning BI-RADS categories.

This study was developed in conjunction with the ACR AI-LAB, a framework for democratization of Artificial Intelligence (AI). The goal of the ACR AI-LAB is to provide an interface for clinicians and scientists to work together to develop deep learning models. We highlight several fundamental features needed for AI democratization: First, we demonstrate the possible data, model, and training parameters that can influence the performance of the model. These parameters will be available as options in AI-LAB. We also show importance of diverse training data for model generalizability, supporting collaborative development of algorithms across institutions which the AI-LAB will facilitate. Lastly, we show how a crowdsourced annotations can be used to evaluate algorithm performance, which users will be able to do on the AI-LAB platform.

We demonstrate the effect of various parameters on the performance of the mammographic breast density classification model, the lack of generalizability across data formats, and how crowdsourcing can be used for evaluation.

Take-Home Points.

• The choice of data, model, and training parameters can impact deep learning model performance for evaluation of mammographic breast density. Notably, when training was performed with randomly sampled images from the dataset versus sampling equal number of images from each density category, the model predictions were biased away from the low-prevalence categories such as extremely dense breasts.

• The performance of the model degrades when evaluated on data formats that differ from the one that we trained on, emphasizing the importance of multi-institutional training sets.

• Crowdsourcing can be an effective means of evaluating model performance.

• These options for model training and evaluation will be made available in the ACR AI-LAB, a platform for democratizing Artificial Intelligence that was developed in tandem with this study.

Implications.

We showcase the various data, training, and model parameters that can influence model performance, highlighting pretraining, cost-function, and sampling approach as important parameters. Furthermore, we found that model performance deteriorates when training and testing on different imaging data formats. In performing this study in tandem with the development of the ACR AI-LAB, we demonstrate important principles and pitfalls that radiologists and data scientists have to consider when training neural network models. Our hope is that radiologists who use the AI-LAB can refer to this study as an educational tool when utilizing the AI-LAB to train their own deep learning models.