Modular geodesics and wedge domains in non-compactly causal symmetric spaces

Abstract

We continue our investigation of the interplay between causal structures on symmetric spaces and geometric aspects of Algebraic Quantum Field Theory. We adopt the perspective that the geometric implementation of the modular group is given by the flow generated by an Euler element of the Lie algebra (an element defining a 3-grading). Since any Euler element of a semisimple Lie algebra specifies a canonical non-compactly causal symmetric space $M=G/H$, we turn in this paper to the geometry of this flow. Our main results concern the positivity region W of the flow (the corresponding wedge region): If G has trivial center, then W is connected, it coincides with the so-called observer domain, specified by a trajectory of the modular flow which at the same time is a causal geodesic. It can also be characterized in terms of a geometric KMS condition, and it has a natural structure of an equivariant fiber bundle over a Riemannian symmetric space that exhibits it as a real form of the crown domain of G/K. Among the tools that we need for these results are two observations of independent interest: a polar decomposition of the positivity domain and a convexity theorem for G-translates of open H-orbits in the minimal flag manifold specified by the 3-grading.

Introduction

A new Lie theoretical approach to localization on spacetimes involved in Algebraic Quantum Field Theory (AQFT) has been introduced in the recent years by the authors and collaborators in a series of works, see [38, 41, 49–52, 54]. In the current paper, we continue the investigation of the structure of wedge regions in non-compactly causal symmetric spaces, started in [52]. First we briefly recall the motivation form AQFT, and then, we introduce tools and details to formulate our results.

Symmetric spaces are quotients $M=G/H$, where G is a Lie group, $\tau$ is an involutive automorphism of G and $H\subseteq G^{\tau }$ is an open subgroup (cf. [36]). A causal symmetric space carries a G-invariant field of pointed generating closed convex cones $C_m\subseteq T_m(M)$ in their tangent spaces. Typical examples are de Sitter space ${\text{dS}}^d\cong {\text{SO}}_{1,d}{(\mathbb{R})}_e/{\text{SO}}_{1,d-1}{(\mathbb{R})}_e$ and anti-de Sitter space ${\text{AdS}}^d\cong {\text{SO}}_{2,d-1}{(\mathbb{R})}_e/{\text{SO}}_{1,d-1}{(\mathbb{R})}_e$ as well as products ${\text{dS}}^d\times {\mathbb{S}}^k$ and ${\text{AdS}}^d\times {\mathbb{H}}^k$ with spheres and hyperbolic spaces, respectively. These are Lorentzian, but we do not require our causal structure to come from a Lorentzian metric, which creates much more flexibility and a richer variety of geometries. Causal symmetric spaces permit to study causality aspects of spacetimes in a highly symmetric environment. Here we shall always assume that M is non-compactly causal in the sense that the causal curves define a global order structure with compact order intervals (they are called globally hyperbolic), and in this context one can also prove the existence of a global “time function” with group theoretic methods (see [46]). We refer to the monograph [26] for more details and a complete exposition of the classification of irreducible causal symmetric spaces. A new perspective on the classification has been developed in [41].

Recent interest in causal symmetric spaces in relation to representation theory arose from their role as analogs of spacetime manifolds in the context of Algebraic Quantum Field Theory in the sense of Haag–Kastler. A model in AQFT is specified by a net of von Neumann algebras $\mathcal{M}(\mathcal{O})$ acting on a fixed Hilbert space indexed by open subsets $\mathcal{O}$ of the chosen spacetime M [20]. The hermitian elements of the algebra $\mathcal{M}(\mathcal{O})$ represent observables that can be measured in the “laboratory” $\mathcal{O}$. These nets are supposed to satisfy fundamental quantum and relativistic assumptions:

• (I)Isotony: ${\mathcal{O}}_1\subseteq {\mathcal{O}}_2$ implies $\mathcal{M}({\mathcal{O}}_1)\subseteq \mathcal{M}({\mathcal{O}}_2).$
• (L)Locality: ${\mathcal{O}}_1\subseteq {\mathcal{O}}_2^{\prime }$ implies $\mathcal{M}({\mathcal{O}}_1)\subseteq \mathcal{M}{({\mathcal{O}}_2)}^{\prime }$, where ${\mathcal{O}}^{\prime }$ is the “causal complement” of $\mathcal{O}$, i.e., the maximal open subset that cannot be connected to $\mathcal{O}$ by causal curves.
• (RS)Reeh–Schlieder property: There exists a unit vector $\mathrm{\Omega }\in \mathcal{H}$ that is cyclic for $\mathcal{M}(\mathcal{O})$ if $\mathcal{O}\ne \mathrm{\varnothing }$.
• (Cov)Covariance: There is a Lie group G acting on M and a unitary representation $U:G\to \text{U}(\mathcal{H})$ such that $U_g\mathcal{M}(\mathcal{O})U_g^{-1}=\mathcal{M}(g\mathcal{O})$ for $g\in G$.
• (BW)Bisognano–Wichmann property: $\mathrm{\Omega }$ is separating for some “wedge region” $W\subseteq M$ and there exists an element $h\in \mathfrak{g}$ with ${\mathrm{\Delta }}^{-it/2\pi }=U(expth)$ for $t\in \mathbb{R}$, where $\mathrm{\Delta }$ is the modular operator corresponding to $(\mathcal{M}(W),\mathrm{\Omega })$ in the sense of the Tomita–Takesaki Theorem ([4, Thm. 2.5.14]).
• (Vac)Invariance of the vacuum: $U(g)\mathrm{\Omega }=\mathrm{\Omega }$ for every $g\in G$.

The (BW) property gives a geometrical meaning to the dynamics provided by the modular group ${({\mathrm{\Delta }}^{\mathit{it}})}_{t\in \mathbb{R}}$ of the von Neumann algebra $\mathcal{M}(W)$ associated with wedge regions with respect to the vacuum state specified by $\mathrm{\Omega }$. On Minkowski/de Sitter spacetime, it provides an identification of the one-parameter group ${({\mathrm{\Lambda }}_W(t))}_{t\in \mathbb{R}}$ of boosts in the Poincaré/Lorentz group with the Tomita–Takesaki modular operator:

$$\begin{array}{c}\hfill U({\mathrm{\Lambda }}_W(t))={\mathrm{\Delta }}^{-it/2\pi }.\end{array}$$

Here ${\mathrm{\Lambda }}_W=g{\mathrm{\Lambda }}_{W_1}{g}^{-1}$ is a one-parameter group of boosts associated with $W=g.W_1$, where $W_1=\{x\in M:|x_0|<x_1\}$ is the standard right wedge and

$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{W_1}(t)=(cosh(t)x_0+sinh(t)x_1,cosh(t)x_1+sinh(t)x_0,x_2,\dots ,x_d)\end{array}$$

describes the boosts associated with $W_1$.

The homogeneous spacetimes occurring naturally in AQFT are causal symmetric spaces associated with their symmetry groups (Minkowski spacetime for the Poincaré group, de Sitter space for the Lorentz group and anti-de Sitter space for ${\text{SO}}_{2,d}(\mathbb{R})$), and the localization in wedge regions is ruled by the acting group. The rich interplay between the geometric and algebraic objects in AQFT allowed a generalization of fundamental localization properties and the subsequent definition of fundamental models (second quantization fields), having as initial data a general Lie group with distinguished elements (Euler elements) in the Lie algebra. Given an AQFT on Minkowski spacetime $M={\mathbb{R}}^{1,d}$ (or de Sitter spacetime ${\text{dS}}^d\subseteq {\mathbb{R}}^{1,d}$), the Bisognano–Wichmann (BW) property allows an identification of geometric and algebraic objects in both free and interacting theories in all dimensions [3, 13, 44]. This plays a central role in many results in AQFT and is a building block of our discussion.

One can generalize the picture we get from these explicit AQFT models and construct nets of von Neumann algebras on causal symmetric spaces with representation theoretical methods. We start with a unitary representation $U:G\to \text{U}(\mathcal{H})$ of a reductive Lie group G whose Lie algebra contains Euler elements. Then, one constructs so-called one-particle nets on causal symmetric spaces. These are isotonous, G-covariant maps that associate to non-empty open subsets of the causal symmetric space standard subspaces1 of the “one-particle space” $\mathcal{H}$. For positive energy representations, we refer to [50] for left invariant nets on reductive Lie groups, to [55] for left invariant nets on non-reductive Lie groups, and to [51] for nets on compactly causal symmetric spaces. For general unitary representation, nets on non-compactly causal symmetric spaces have been constructed in [17] and on abstract wedge families in [38]; see also [40]. These constructions have the (BW) property as a fundamental input. Bosonic second quantization associates to a one-particle net an isotonous, G-covariant net of von Neumann algebras acting on the bosonic Fock space [5, 38].

These constructions naturally generalize the AQFT framework, re-construct the free second quantization AQFT models on the chiral conformal circle, on de Sitter and anti-de Sitter space, and provide several new models [17, 38, 50]. One can also recover free AQFT models on Minkowski spacetime as addressed in [38–40]. If Z(G) is non-trivial, then a proper second quantization scheme to provide a (twisted-)local net of von Neumann algebras remains to be determined (cf. [11, 19]). We stress that our setting provides a general framework to study properties of AQFT that is not restricted to second quantization theories. It also provides results on the type of von Neumann algebras and on properties of wedge symmetries appearing in these models (see, e.g., [40]).

We know from [40] that, in the general context, the potential generators $h\in \mathfrak{g}$ of the modular groups in (BW) are Euler elements, i.e., $\text{ad}h$ defines a 3-grading

$$\begin{array}{c}\hfill \mathfrak{g}={\mathfrak{g}}_1(h)\oplus {\mathfrak{g}}_0(h)\oplus {\mathfrak{g}}_{-1}(h),\text{where}{\mathfrak{g}}_{\lambda }(h)=ker(\text{ad}h-\lambda \mathbf{1}).\end{array}$$

This leads to the question how the existence and the choice of the Euler element affect the geometry of the associated symmetric space. The (BW) property establishes a one-to-one correspondence between “wedge regions” $W\subseteq M$ and the associated Euler elements. So these fundamental localization regions can be determined in terms of Euler elements. This allowed the following generalization of nets of von Neumann algebras on Minkowski/de Sitter spacetime:

• Given a Lie group G with Lie algebra $\mathfrak{g}$, then the couples $(h,{\tau }_h)$, where $h\in \mathfrak{g}$ is an Euler element and ${\tau }_h$ an involutive automorphism of G, inducing on $\mathfrak{g}$ the involution ${\tau }_h=e^{\pi i\text{ad}h}$, allow the definition of an ordered, G-covariant set of “abstract wedge regions” carrying also some locality information [38]. In particular, they encode the commutation relation property of the Tomita operators (modular operator and modular conjugation).

• Causal symmetric spaces provide manifolds and a causal structure supporting nets of algebras. Here the wedge regions can be defined as open subsets in several ways. The equivalence of various characterizations has been shown in [51, 52]; see also the discussion below.

The whole picture complies with Minkowski, de Sitter and anti-de Sitter spacetimes and the associated free fields. A generalization of wedge regions of the Minkowski or de Sitter spacetime on general curved spacetimes has been proposed by many authors, see for instance [12] and references therein. In our framework, on non-compactly causal symmetric spaces, the rich geometric symmetries allow different characterizations of wedge regions, in particular in terms of positivity of the modular flow, or geometric KMS conditions and in terms of polar decompositions as described in [52]. Some of them directly accord with the literature, for instance for positivity of the modular flow, see [9, Defin. 3.1] and in particular [45] for the connection to thermodynamics on de Sitter space. To see how these definitions apply to wedges in de Sitter space, cf. [52, App. D.3] and [6]. For causal symmetric spaces all definitions of wedge regions discussed in [41, 52] specify the same regions, up to choosing connected components (cf. [52, Thm. 7.1]). In Theorem 7.1, we prove that the identification is actually complete for the adjoint groups since the wedge region defined in terms of positivity of the modular flow is connected. This contrasts the situation for compactly causal symmetric spaces, where wedge regions are in general not connected, as for anti-de Sitter space ([52, Lemma 11.2]).

To formulate our results, we recall some basic terminology concerning symmetric Lie algebras (see [52] for more details).

• A symmetric Lie algebra is a pair $(\mathfrak{g},\tau )$, where $\mathfrak{g}$ is a finite-dimensional real Lie algebra and $\tau$ an involutive automorphism of $\mathfrak{g}$. We write $\mathfrak{h}={\mathfrak{g}}^{\tau }=ker(\mathbf{1}-\tau )$ and $\mathfrak{q}={\mathfrak{g}}^{-\tau }=ker(\mathbf{1}+\tau )$ for the $\tau$-eigenspaces.

• A causal symmetric Lie algebra is a triple $(\mathfrak{g},\tau ,C)$, where $(\mathfrak{g},\tau )$ is a symmetric Lie algebra and $C\subseteq \mathfrak{q}$ is a pointed generating closed convex cone invariant under the group ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})=⟨e^{\text{ad}\mathfrak{h}}⟩$ acting in $\mathfrak{q}$. We call $(\mathfrak{g},\tau ,C)$ compactly causal (cc) if C is elliptic in the sense that, for $x\in C^{\circ }$ (the interior of C in $\mathfrak{q}$), the operator $\text{ad}x$ is semisimple with purely imaginary spectrum. We call $(\mathfrak{g},\tau ,C)$ non-compactly causal (ncc) if C is hyperbolic in the sense that, for $x\in C^{\circ }$, the operator $\text{ad}x$ is diagonalizable.

As explained in detail in [41], Euler elements in reductive Lie algebras $\mathfrak{g}$ lead naturally to ncc symmetric Lie algebras: For an Euler element $h\in \mathfrak{g}$, choose a Cartan involution $\theta$ of $\mathfrak{g}$ with $\mathfrak{z}(\mathfrak{g})\subseteq {\mathfrak{g}}^{-\theta }$ such that $\theta (h)=-h$. Then ${\tau }_h:=e^{\pi i\text{ad}h}$ is an involutive automorphism of $\mathfrak{g}$ commuting with $\theta$, so that $\tau :={\tau }_h\theta$ defines a symmetric Lie algebra $(\mathfrak{g},\tau )$ and there exists a pointed generating ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant hyperbolic cone C with $h\in C^{\circ }$. Under the assumption that $\mathfrak{h}={\mathfrak{g}}^{\tau }$ contains no non-zero ideal of $\mathfrak{g}$, there is a unique minimal cone $C_{\mathfrak{q}}^{\text{min}}(h)$ with this property. It is generated by the orbit ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})h\subseteq \mathfrak{q}$.

Let $(\mathfrak{g},\tau ,C)$ be an ncc symmetric Lie algebra and $(G,{\tau }^G,H)$ a corresponding symmetric Lie group, i.e., G is a connected Lie group, ${\tau }^G$ an involutive automorphism of G integrating $\tau$, and $H\subseteq G^G$ an open subgroup. If, in addition, $\text{Ad}(H)C=C$, then we call the quadruple $(G,{\tau }^G,H,C)$ a causal symmetric Lie group. On $M=G/H$, we then obtain the structure of a causal symmetric space, specified by the G-invariant field of open convex cones2

$$\begin{array}{c}\hfill V_{+}(gH):=g.C^{\circ }\subseteq T_{\mathit{gH}}(M){.}^2\end{array}$$ 1.1

We further assume that

$$\begin{array}{c}\hfill S:=Hexp(C)=exp(C)H\subseteq G\end{array}$$

is a closed subsemigroup for which the polar map $H\times C\to S,(h,x)\mapsto hexpx$ is a homeomorphism. Then

$$\begin{array}{c}\hfill g_{1}H\le g_{2}H\text{if}{g}_2^{-1}{g}_1\in S\end{array}$$ 1.2

defines on M a partial order, called the causal order on M. According to Lawson’s Theorem [30] and Theorem C.1), this is always the case if $\mathfrak{z}(\mathfrak{g})\subseteq \mathfrak{q}$ and ${exp|}_{\mathfrak{z}(\mathfrak{g})}$ is injective. The second condition is always satisfied if G is simply connected.

For an Euler element $h\in \mathfrak{g}$, we consider the associated modular flow on $M=G/H$, defined by

$$\begin{array}{c}\hfill {\alpha }_t(gH)=exp(th)gH.\end{array}$$ 1.3

We study orbits of this flow which are geodesics $\gamma :\mathbb{R}\to M$ with respect to the symmetric space structure and causal in the sense that ${\gamma }^{\prime }(t)\in V_{+}(\gamma (t))$ for $t\in \mathbb{R}$. We call them h-modular geodesics. All these are contained in the positivity domain

$$\begin{array}{c}\hfill W_M^{+}(h):=\{m\in M:X_h^M(m)\in V_{+}(m)\}\end{array}$$ 1.4

of the vector field $X_h^M$ generating the modular flow. We refer to [52] for a detailed analysis of the latter domain in the special situations where the modular flow on M has fixed points, which is equivalent to the adjoint orbit ${\mathcal{O}}_h=\text{Inn}(\mathfrak{g})h$ intersecting $\mathfrak{h}$.

We show for ncc symmetric Lie algebras, which are direct sums of irreducible ones, that:

• Causal modular geodesics exist if and only if the adjoint orbit ${\mathcal{O}}_h=\text{Ad}(G)h\subseteq \mathfrak{g}$ intersects the interior of the cone $C\subseteq \mathfrak{q}$, and then the centralizer $G^h=\{g\in G:\text{Ad}(g)h=h\}$ of h acts transitively on the union of the corresponding curves (Proposition 3.2(c)).

• Suppose that the cone is maximal, i.e., $C_{\mathfrak{q}}=C_{\mathfrak{q}}^{\text{max}}$ (see (2.3) and [41, §3.5.2] for details). Let ${\mathfrak{q}}_{\mathfrak{k}}=\mathfrak{q}\cap \mathfrak{k}$ for a Cartan decomposition $\mathfrak{g}=\mathfrak{k}\oplus \mathfrak{p}$ with $h\in {\mathfrak{q}}_{\mathfrak{p}}$ and consider the domain

  $$\begin{array}{c}\hfill {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}=\{x\in {\mathfrak{q}}_{\mathfrak{k}}:\rho (\text{ad}x)<\frac{\pi }{2}\},\end{array}$$

  where $\rho (\text{ad}x)$ is the spectral radius of $\text{ad}x$. Then, the connected component $W:=W_M^{+}{(h)}_{\mathit{eH}}$ of the base point eH in the positivity domain is

  $$\begin{array}{c}\hfill W=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\end{array}$$

  (Theorem 3.6).

• We associate to any modular geodesic a connected open subset $W(\gamma )\subseteq M$; the corresponding observer domain. For de Sitter space ${\text{dS}}^d$, we thus obtain the familiar wedge domain obtained by intersecting ${\text{dS}}^d$ with a Rindler wedge in Minkowski space ${\mathbb{R}}^{1,d}$ (Example 5.3). In Theorem 5.7, we show that it coincides with W, provided that $H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$ and $C_{\mathfrak{q}}=C_{\mathfrak{q}}^{\text{max}}$.

• A key step in the proof of Theorem 5.7 is the following Convexity Theorem. Let

  $$\begin{array}{c}\hfill P^{-}:=exp({\mathfrak{g}}_{-1}(h))G^h\subseteq G\end{array}$$

  be the “negative” parabolic subgroup of G specified by h and identity ${\mathfrak{g}}_1(h)$ with the open subset $\mathcal{B}:=exp({\mathfrak{g}}_1(h)).e{P}^{-}\subseteq G/P^{-}$. Then $\mathcal{D}:=H.0\subseteq \mathcal{B}$ is an open convex subset, and for any $g\in G$ with $g.\mathcal{D}\subseteq \mathcal{B}$, the subset $g.\mathcal{D}\subseteq \mathcal{B}$ is convex (Theorem 4.5).

• In Sect. 6 we further show that, for $C=C_{\mathfrak{q}}^{\text{max}}$ and $\mathfrak{g}$ simple, that the real tube domain $\mathfrak{h}+C^{\circ }$ intersects the set $\mathcal{E}(\mathfrak{g})$ of Euler elements in a connected subset (Theorem 6.1). As a consequence, we derive that $W_M^{+}(h^{\prime })\ne \mathrm{\varnothing }$ if and only if $h^{\prime }\in {\mathcal{O}}_h$ (Corollary 6.3). In particular, only one conjugacy class of Euler elements possesses non-empty positivity regions. This is of particular relevance for locality properties of nets of local algebras. We plan to investigate this in subsequent work.

• In Theorem 7.1 we show that the positivity domain $W_M^{+}(h)$ is connected for $G=\text{Inn}(\mathfrak{g})$ and $\mathfrak{g}$ simple, and this implies that

  $$\begin{array}{c}\hfill W(\gamma )=W=W_M^{+}(h).\end{array}$$

  From this in turn we derive that the stabilizer group $G_W=\{g\in G:g.W=W\}$ coincides with $G^h$ (Proposition 7.3), so that the wedge space $\mathcal{W}(M):=\{g.W:g\in G\}$ of wedge regions in M can be identified, as a homogeneous G-space, with the adjoint orbit ${\mathcal{O}}_h=\text{Ad}(G)h\cong G/G^h$. In particular $\mathcal{W}(M)$ also is a symmetric space.
• Finally, we show in Theorem 8.2 that W coincides with the KMS wedge domain

  $$\begin{array}{c}\hfill W^{\text{KMS}}=\{m\in M:{\alpha }_{\mathit{it}}(m)\in \mathrm{\Xi }\text{for}0<t<\pi \},\end{array}$$

  where $\mathrm{\Xi }$ is the crown domain of the Riemannian symmetric space G/K.

We conclude this introduction with some more motivation from AQFT. The analysis of the properties of the modular flow on symmetric spaces is also motivated by the investigation of energy inequalities in quantum and relativistic theories. In General Relativity, there exist many solutions to the Einstein equation that, for various reasons, may not be physical. Energy conditions such as the pointwise non-negativity of the energy density, which ensures that the gravity force is attractive, can be required to discard non-physical models [14, 62]. In quantum and relativistic theories, the energy conditions need to be rewritten. For instance, it is well known that the energy density at individual spacetime points is unbounded from below, even if the energy density integrated over a Cauchy surface is non-negative (see [14, 15] and references therein).

Families of inequalities have been discussed in several models, employing different mathematical and physical approaches (see for instance [14, 16, 27, 29, 42, 61]). In recent years, operator algebraic techniques have been very fruitful for the study of the energy inequalities because of the central role played by the modular hamiltonian in some of these energy conditions. This object corresponds to the logarithm of the modular operator of a local algebra of a specific region, which in some cases can be identified with the generator of a one-parameter group of spacetime symmetries by the Bisognano–Wichmann property. In this regard, we mention the ANEC (Averaged Null Energy Condition) and the QNEC (Quantum Null Energy Condition) and their relation with the Araki relative entropy, an important quantum-information quantity, defined in terms of relative modular operators (see, for instance, [1, 9, 10, 32–35, 43]). We stress that, in this analysis, the study of the modular flow on the manifold can be particularly relevant. Moreover, in order to find regions where energy inequalities hold, one may also need to deform the modular flow [8, 43]. In our abstract context, the Euler element specifies the flow that can be implemented by the modular operator, hence the modular Hamiltonian, when the Bisognano–Wichmann property holds. In particular, the identification of specific flows on symmetric spaces (modular flows), the characterization in terms of modular operators of covariant local subspaces attached to specific regions (wedges) motivate an analysis of modular flows on non-compactly causal symmetric spaces pursued in our project.

In this respect, the wedge regions are the first fundamental open subsets of spacetime to be studied in detail. Following General Relativity (see, for instance, [9, 12] and references therein), one can define them as an open connected, causally convex subregion W of a spacetime M, associated with a Killing flow $\mathrm{\Lambda }$ preserving W, which is timelike and time-oriented on W. On Minkowski spacetime the flow $\mathrm{\Lambda }$, a one-parameter group of boosts, corresponds to the time-evolution of a uniformly accelerated observer moving within W. Then, W is a horizon for this observer: he cannot send a signal outside W and receive it back. Then the vacuum state becomes a thermal state for the algebra of observables inside the wedge region W by the Bisognano–Wichmann property [18, 21, 31]. In our general context, we recover the definition (and equivalent ones) of wedge regions. Then, by the Bisognano–Wichmann property, the thermal property of the vacuum state holds when nets of algebras or standard subspaces are considered [38, 41, 52]. In this paper, we focus on the related properties of the wedge regions in non-compactly causal symmetric spaces.

Notation

• If M is a topological space and $m\in M$, then $M_m$ denotes the connected component of M containing m. In particular, we write $e\in G$ for the identity element in the Lie group G and $G_e$ for its identity component.

• Involutive automorphisms of G are typically denoted ${\tau }^G$, and $\tau$ is the corresponding automorphism of the Lie algebra $\mathfrak{g}=\mathbf{L}(G)$. We write ${\mathfrak{g}}^{\tau }=ker(\mathbf{1}-\tau )$ and ${\mathfrak{g}}^{-\tau }=ker(\mathbf{1}+\tau )$.

• For $x\in \mathfrak{g}$, we write $G^x:=\{g\in G:\text{Ad}(g)x=x\}$ for the stabilizer of x in the adjoint representation and $G_e^x={(G^x)}_e$ for its identity component.

• For $h\in \mathfrak{g}$ and $\lambda \in \mathbb{R}$, we write ${\mathfrak{g}}_{\lambda }(h):=ker(\text{ad}h-\lambda \mathbf{1})$ for the corresponding eigenspace in the adjoint representation.

• If $\mathfrak{g}$ is a Lie algebra, we write $\mathcal{E}(\mathfrak{g})$ for the set of Euler elements $h\in \mathfrak{g}$, i.e., $\text{ad}h$ is non-zero and diagonalizable with $\text{Spec}(\text{ad}h)\subseteq \{-1,0,1\}$. The corresponding involution is denoted ${\tau }_h=e^{\pi i\text{ad}h}$.

• For a Lie subalgebra $\mathfrak{s}\subseteq \mathfrak{g}$, we write ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{s})=⟨e^{\text{ad}\mathfrak{s}}⟩\subseteq \text{Aut}(\mathfrak{g})$ for the subgroup generated by $e^{\text{ad}\mathfrak{s}}$.

• For a convex cone C in a vector space V, we write $C^{\circ }:={\text{int}}_{C-C}(C)$ for the relative interior of C in its span.

• We use the notation

  $$\begin{array}{c}\hfill \rho (A):=sup\{|\lambda |:\lambda \in \text{Spec}(A)\}\end{array}$$ 1.5

  for the spectral radius of a linear operator A.

Causal Euler elements and ncc symmetric spaces

In this section, we recall some basic results on Euler elements and their relation with non-compactly causal symmetric spaces. Most of these statements are discussed in detail in [41].

Recall from above that an Euler element in a Lie algebra $\mathfrak{g}$ is an element h defining a 3-grading of $\mathfrak{g}$ by $\mathfrak{g}={\mathfrak{g}}_{-1}\oplus {\mathfrak{g}}_0\oplus {\mathfrak{g}}_{+1}$ with ${\mathfrak{g}}_j=ker(\text{ad}h-j\mathbf{1})$, $j=-1,0,1$. We write $\mathcal{E}(\mathfrak{g})$ for the set of Euler elements in $\mathfrak{g}$. In this section, we recall some results on from [41] on Euler elements that are crucially used in the following.

Definition 2.1

Let $\mathfrak{g}$ be a reductive Lie algebra.

1. A Cartan involution of $\mathfrak{g}$ is an involutive automorphism $\theta$ for which $\mathfrak{z}(\mathfrak{g})\subseteq {\mathfrak{g}}^{-\theta }$ and ${\mathfrak{g}}^{\theta }$ is maximal compactly embedded in the commutator algebra $[\mathfrak{g},\mathfrak{g}]$. We then write, using the notation from the introduction,

   $$\begin{array}{c}\hfill \mathfrak{g}=\mathfrak{k}\oplus \mathfrak{p}\text{with}\mathfrak{k}={\mathfrak{g}}^{\theta }\text{and}\mathfrak{p}={\mathfrak{g}}^{-\theta }\end{array}$$
2. If $\tau$ is another involution on $\mathfrak{g}$ commuting with $\theta$, $\mathfrak{h}:={\mathfrak{g}}^{\tau }$ and $\mathfrak{q}:={\mathfrak{g}}^{-\tau }$, then we have

   $$\begin{array}{c}\hfill \mathfrak{h}={\mathfrak{h}}_{\mathfrak{k}}\oplus {\mathfrak{h}}_{\mathfrak{p}},\mathfrak{q}={\mathfrak{q}}_{\mathfrak{k}}\oplus {\mathfrak{q}}_{\mathfrak{p}}\text{with}{\mathfrak{h}}_{\mathfrak{k}}=\mathfrak{h}\cap \mathfrak{k},{\mathfrak{h}}_{\mathfrak{p}}=\mathfrak{h}\cap \mathfrak{p},{\mathfrak{q}}_{\mathfrak{k}}=\mathfrak{q}\cap \mathfrak{k},{\mathfrak{q}}_{\mathfrak{p}}=\mathfrak{q}\cap \mathfrak{p}.\end{array}$$
3. The Cartan dual of the symmetric Lie algebra $(\mathfrak{g},\tau )$ is the symmetric Lie algebra $({\mathfrak{g}}^c,{\tau }^c)$ with

   $$\begin{array}{c}\hfill {\mathfrak{g}}^c=\mathfrak{h}+i\mathfrak{q}\text{and}{\tau }^c(x+iy)=x-iy\text{for}x\in \mathfrak{h},y\in \mathfrak{q}.\end{array}$$

   Note that ${\mathfrak{g}}^c={({\mathfrak{g}}_{\mathbb{C}})}^{\overline{\tau }}$ where $\overline{\tau }$ is the conjugate-linear extension of $\tau$ to ${\mathfrak{g}}_{\mathbb{C}}$; in particular ${\mathfrak{g}}^c$ is a real form of ${\mathfrak{g}}_{\mathbb{C}}$.

Definition 2.2

Let $(\mathfrak{g},\tau )$ be a symmetric Lie algebra and $h\in \mathcal{E}(\mathfrak{g})\cap \mathfrak{q}$. We say that h is causal if there exists an ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant closed pointed generating convex cone C in $\mathfrak{q}$ with $h\in C^{\circ }$. We write ${\mathcal{E}}_c(\mathfrak{q})\subseteq \mathcal{E}(\mathfrak{g})\cap \mathfrak{q}$ for the set of causal Euler elements in $\mathfrak{q}$. Recall that the triple $(\mathfrak{g},\tau ,C)$ is ncc if C is hyperbolic.

Lemma 2.3

Let $(\mathfrak{g},\tau ,C)$ be a simple ncc symmetric Lie algebra and $h\in \mathfrak{q}$ be a causal Euler element. Then, the following assertions hold:

1. There exist closed convex pointed generating ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant cones

   $$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{min}}(h)\subseteq C_{\mathfrak{q}}^{\text{max}}(h)\end{array}$$

   such that $h\in C_{\mathfrak{q}}^{\text{min}}{(h)}^{\circ }$ and either

   $$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{min}}(h)\subseteq C\subseteq C_{\mathfrak{q}}^{\text{max}}(h)\text{or}{C}_{\mathfrak{q}}^{\text{min}}(h)\subseteq -C\subseteq C_{\mathfrak{q}}^{\text{max}}(h).\end{array}$$
2. If $(G,{\tau }^G,H)$ is a connected symmetric Lie group with symmetric Lie algebra $(\mathfrak{g},\tau )$, then two mutually exclusive cases occur:

   • $\text{Ad}(H)h=\text{Ad}(H_e)h$ and G/H is causal.
   • $-h\in \text{Ad}(H)h$ and G/H is not causal.

Proof

(a) follows from [41, Sect. 3.5.2] and (b) from [41, Prop. 4.18]. $\square$

If h is an Euler element in the reductive Lie algebra $\mathfrak{g}$ and $\theta$ a Cartan involution with $\theta (h)=-h$, $\tau :=\theta {\tau }_h$ and $\mathfrak{z}(\mathfrak{g})\subseteq {\mathfrak{g}}^{-\theta }$, then [41, Thm. 4.2] implies that there exists an ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant pointed closed convex cone $C\subseteq \mathfrak{q}$ with $h\in C^{\circ }$, so that $(\mathfrak{g},\tau ,C)$ is ncc. Further, all ideals of $\mathfrak{g}$ contained in ${\mathfrak{g}}^{\tau }=\mathfrak{h}$ are compact. We have a decomposition

$$\begin{array}{c}\hfill \mathfrak{g}={\mathfrak{g}}_k\oplus {\mathfrak{g}}_r\oplus {\mathfrak{g}}_s,\end{array}$$ 2.1

where ${\mathfrak{g}}_s$ is the sum of all simple ideals not commuting with h (the strictly ncc part), ${\mathfrak{g}}_r$ is the sum of the center $\mathfrak{z}(\mathfrak{g})$ and all non-compact simple ideals commuting with h on which $\tau =\theta$ (the non-compact Riemannian part), and ${\mathfrak{g}}_k$ is the sum of all simple compact ideals (they commute with h). All these ideals are invariant under $\theta$ and $\tau ={\tau }_h\theta$, so that we obtain decompositions

$$\begin{array}{c}\hfill {\mathfrak{g}}_s={\mathfrak{h}}_s\oplus {\mathfrak{q}}_s,{\mathfrak{g}}_r={\mathfrak{h}}_r\oplus {\mathfrak{q}}_r\text{and}{\mathfrak{g}}_k={\mathfrak{h}}_k,\end{array}$$ 2.2

where ${\mathfrak{h}}_r\oplus {\mathfrak{h}}_k$ is a compact ideal of $\mathfrak{h}$, ${\mathfrak{g}}_r={\mathfrak{h}}_r\oplus {\mathfrak{q}}_r$ is a Cartan decomposition and ${\mathfrak{q}}_{\mathfrak{p}}={\mathfrak{q}}_{\mathfrak{p},s}\oplus {\mathfrak{q}}_r$. In particular $\mathfrak{q}={\mathfrak{q}}_s\oplus {\mathfrak{q}}_r$. Let $p_s:\mathfrak{q}\to {\mathfrak{q}}_s$ be the projection onto ${\mathfrak{q}}_s$ with kernel ${\mathfrak{q}}_r$. Then, [41, Prop. B.4] implies that every ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant closed convex cone C satisfies

$$\begin{array}{c}\hfill C_s:=p_s(C)=C\cap {\mathfrak{q}}_s\text{and}{C}_s^{\circ }=C^{\circ }\cap {\mathfrak{q}}_s.\end{array}$$

By Lemma 2.3(a), we obtain a pointed ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant cone $C_{{\mathfrak{q}}_s}^{\text{min}}(h)\subseteq {\mathfrak{q}}_s$, adapted to the decomposition into irreducible summands, whose dual cone $C_{{\mathfrak{q}}_s}^{\text{max}}(h)$ with respect to the Cartan–Killing form $\kappa (x,y)=\text{tr}(\text{ad}x\text{ad}y)$ satisfies $C_{{\mathfrak{q}}_s}^{\text{min}}(h)\subseteq C_{{\mathfrak{q}}_s}^{\text{max}}(h)$. Put

$$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{min}}(h):=C_{{\mathfrak{q}}_s}^{\text{min}}(h)\subseteq C_{\mathfrak{q}}^{\text{max}}(h):=C_{{\mathfrak{q}}_s}^{\text{max}}(h)+{\mathfrak{q}}_r.\end{array}$$ 2.3

Both cones are adapted to the decomposition of $(\mathfrak{g},\tau )$ into irreducible summands. Further, each pointed generating ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant cone C containing h satisfies

$$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{min}}(h)\subseteq C\subseteq C_{\mathfrak{q}}^{\text{max}}(h).\end{array}$$ 2.4

Here the first inclusion is obvious, and the second one follows from the fact that h is also contained in the dual cone

$$\begin{array}{c}\hfill C^{\star }=\{y\in \mathfrak{q}:(\forall x\in C)\kappa (x,y)\ge 0\}.\end{array}$$

This leads to $C_{\mathfrak{q}}^{\text{min}}(h)\subseteq C^{\star }$, and thus to $C\subseteq C_{\mathfrak{q}}^{\text{min}}{(h)}^{\star }=C_{\mathfrak{q}}^{\text{max}}(h)$ (cf. [41, §3.5] for more details).

Lemma 2.4

If $x\in {(C_{\mathfrak{q}}^{\text{max}})}^{\circ }$, then the centralizer ${\mathfrak{z}}_{\mathfrak{h}}(x)=\mathfrak{h}\cap ker(\text{ad}x)$ is compactly embedded in $\mathfrak{g}$, i.e., consists of elliptic elements.

Proof

First we observe that the cone $C_{\mathfrak{q}}^{\text{max}}$ is adapted to the decomposition $\mathfrak{g}=({\mathfrak{g}}_k+{\mathfrak{g}}_r)+{\mathfrak{g}}_s$ and so is the centralizer of $x=x_r+x_s$ in $\mathfrak{h}=({\mathfrak{g}}_{\mathfrak{k}}+{\mathfrak{k}}_r)+{\mathfrak{h}}_s$. Hence the assertion follows from the fact that ${\mathfrak{g}}_k+{\mathfrak{k}}_r$ is compactly embedded and ${\mathfrak{z}}_{{\mathfrak{h}}_s}(x)={\mathfrak{z}}_{{\mathfrak{h}}_s}(x_s)$ is compactly embedded because the cone $C_{{\mathfrak{q}}_s}^{\text{max}}$ is pointed ([47, Prop. V.5.11]). $\square$

Theorem 2.5

(Uniqueness of the causal involution) ([41, Thm. 4.5]) Let $(\mathfrak{g},\tau ,C)$ be a semisimple ncc symmetric Lie algebra for which all ideals of $\mathfrak{g}$ contained in $\mathfrak{h}$ are compact, ${\mathfrak{g}}_s$ the sum of all non-Riemannian ideals, ${\mathfrak{q}}_s:={\mathfrak{g}}_s\cap \mathfrak{q}$, $C_s:=C\cap {\mathfrak{q}}_s$, and $\theta$ a Cartan involution commuting with $\tau$. Then the following assertions hold:

1. $C_s^{\circ }\cap {\mathfrak{q}}_{\mathfrak{p}}$ contains a unique Euler element h, and this Euler element satisfies $\tau ={\tau }_h\theta$.

2. ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$ acts transitively on $C_s^{\circ }\cap \mathcal{E}(\mathfrak{g})$.

3. For every Euler element $h\in C_s^{\circ }$, the involution $\tau {\tau }_h$ is Cartan.

Proposition 2.6

Let $(G,{\tau }^G,H,C)$ be a connected semisimple ncc symmetric Lie group for which $\mathfrak{h}={\mathfrak{g}}^{\tau }$ contains no non-compact ideal of $\mathfrak{g}$ ($\mathfrak{g}={\mathfrak{g}}_r+{\mathfrak{g}}_s$) and let $h\in C_s^{\circ }$ (cf. Theorem 2.5) be a causal Euler element. Then the following assertions hold:

1. $H=H_e{H}^h$, i.e., every connected component of H meets $H^h$.

2. $\text{Ad}(H^h)=\text{Ad}{(H)}^h$ is a maximal compact subgroup of $\text{Ad}(H)$.

3. $\text{Ad}{(H)}^h=\text{Ad}{(H)}^{{\tau }_h}$ and ${\tau }_h:=e^{\pi i\text{ad}h}$ induces a Cartan involution on $\text{Ad}(H)$.

4. $\tau$ induces a Cartan involution on $\text{Ad}{(H)}^h$ for which $\text{Ad}{(H_e^h)}^{\tau }=e^{\text{ad}{\mathfrak{h}}_{\mathfrak{k}}}$ is connected.

Proof

The statements on the adjoint group $\text{Ad}(G)=\text{Inn}(\mathfrak{g})$ follow from [41, Cor. 4.6] because $\text{Ad}(H)\subseteq \text{Inn}{(\mathfrak{g})}^{\tau }$ preserves C. Further, $\text{Ad}{(H)}^h=\text{Ad}(H^h)$ and $H^h={\text{Ad}}^{-1}(\text{Ad}{(H)}^h)$ imply with (a) (for $\text{Ad}(G)$) that $H=H_e{H}^h$. $\square$

Definition 2.7

If $\mathfrak{g}$ is a simple hermitian Lie algebra, $\theta$ a Cartan involution of $\mathfrak{g}$ and $\mathfrak{a}\subseteq \mathfrak{p}$ maximal abelian, then the restricted root system $\mathrm{\Sigma }(\mathfrak{g},\mathfrak{a})$ is either of type $C_r$ or $B{C}_r$. In the first case, we say that $\mathfrak{g}$ is of tube type.

Recall that if $(\mathfrak{g},\tau )$ is simple ncc, then either ${\mathfrak{g}}^c$ is simple hermitian or ${\mathfrak{g}}^c\cong {\mathfrak{h}}_{\mathbb{C}}$, where $\mathfrak{h}={\mathfrak{g}}^{\tau }$ is simple hermitian ([41, Rem. 4.24]).

Proposition 2.8

([41, Lemma 5.1, Prop. 5.2]) Let $(\mathfrak{g},\tau ,C)$ be a simple ncc symmetric Lie algebra. Pick a causal Euler element $h\in C^{\circ }$ and ${\mathfrak{t}}_{\mathfrak{q}}\subseteq {\mathfrak{q}}_{\mathfrak{k}}$ maximal abelian and set $s:=\text{dim}{\mathfrak{t}}_{\mathfrak{q}}$. Then, the following assertions hold:

1. The Lie algebra $\mathfrak{l}$ generated by h and ${\mathfrak{t}}_{\mathfrak{q}}$ is reductive.

2. The commutator algebra $[\mathfrak{l},\mathfrak{l}]$ is isomorphic to ${\mathfrak{sl}}_2{(\mathbb{R})}^s$

3. $\mathfrak{z}(\mathfrak{l})=\mathbb{R}{h}_0$ for some hyperbolic element $h_0$ satisfying $\tau (h_0)=-h_0=\theta (h_0)$ which is zero if and only if ${\mathfrak{g}}^c$ is of tube type.

4. The Lie algebra $\mathfrak{l}$ is $\tau$-invariant and ${\mathfrak{l}}^{\tau }\cong {\mathfrak{so}}_{1,1}{(\mathbb{R})}^s$.

5. For $x\in {\mathfrak{t}}_{\mathfrak{q}}$, we have $\rho (\text{ad}x)=\rho (\text{ad}x{|}_{\mathfrak{s}}),$ where $\rho$ denotes the spectral radius. With the basis

   $$\begin{array}{c}\hfill z^j=(0,\dots ,0,\frac{1}{2}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right),0,\cdots ,0),j=1,\dots ,s,\end{array}$$

   in ${\mathfrak{so}}_2{(\mathbb{R})}^s$ we have for $x={\sum }_{j=1}^s{x}_j{z}^j$

   $$\begin{array}{c}\hfill \rho (\text{ad}x)=max\{|x_j|:j=1,\dots ,s\}.\end{array}$$ 2.5

Note that (c) implies that $\mathfrak{l}$ is semisimple, i.e., $h\in [\mathfrak{l},\mathfrak{l}]$, if and only if ${\mathfrak{g}}^c$ is of tube type.

Proposition 2.9

([41, Prop. 7.10]) Let $(\mathfrak{g},\tau ,C)$ be a semisimple modular non-compactly causal semisimple symmetric Lie algebra, where $\tau ={\tau }_h\theta$, $h\in {\mathfrak{q}}_{\mathfrak{p}}\cap C$ a causal Euler element,

$$\begin{array}{c}\hfill G:={\text{Inn}}_{{\mathfrak{g}}_{\mathbb{C}}}(\mathfrak{g})\cong \text{Inn}(\mathfrak{g}),K:=G^{\theta }={\text{Inn}}_{\mathfrak{g}}(\mathfrak{k}),\text{and}{G}^c:={\text{Inn}}_{{\mathfrak{g}}_{\mathbb{C}}}({\mathfrak{g}}^c).\end{array}$$

Then $H:=G\cap G^c$ satisfies

$$\begin{array}{c}\hfill H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})\text{and}H\cap K=K^h.\end{array}$$

In particular $K^h\subseteq K^{{\tau }_h}=K^{\tau }$ implies $H\subseteq G^{\tau }$.

The positivity domain and modular geodesics

Let $(G,{\tau }^G,H,C)$ be a connected semisimple causal symmetric Lie group with ncc symmetric Lie algebra $(\mathfrak{g},\tau ,C)$. We fix a causal Euler element $h\in C^{\circ }$ (Theorem 2.5) and write $M=G/H$ for the associated symmetric space.

One of our goals in this paper is to describe the structure of the positivity domain

$$\begin{array}{c}\hfill W_M^{+}(h):=\{m\in M:X_h^M(m)\in V_{+}(m)\}\end{array}$$

of the vector field $X_h^M$ generating the modular flow. Our first major result is the identification of the connected component W of the base point eH in the positivity domain $W_M^{+}(h)$ as

$$\begin{array}{c}\hfill W:=W_M^{+}{(h)}_{\mathit{eH}}=G_e^h{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\end{array}$$ 3.1

(Theorem 3.6).

Some of the results in this section had been obtained in [52] for the special case of ncc symmetric Lie algebras for which $\mathfrak{h}$ contains an Euler element, whereas here we are dealing with general non-compactly causal symmetric Lie algebras.

Modular geodesics

In this subsection, we introduce the concept of an h-modular geodesic in a non-compactly causal symmetric space M and discuss some of its immediate properties. We also show that, in compactly causal spaces, non-trivial causal modular geodesics do not exist.

Definition 3.1

(Geodesics and causality) Let $M=G/H$ as above.

• We call a geodesic $\gamma :\mathbb{R}\to M$ causal if ${\gamma }^{\prime }(t)\in V_{+}(\gamma (t))$ for every $t\in \mathbb{R}$ (see (1.1)).

• Let $h\in \mathfrak{g}$ be an Euler element. The flow on M defined by

  $$\begin{array}{c}\hfill {\alpha }_t(gH)=exp(th)gH=gexp(\text{Ad}(g^{-1})h)H\end{array}$$ 3.2

  is called the modular flow (associated to h). Its infinitesimal generator is denoted $X_h^M\in \mathcal{V}(M)$.

• A geodesic $\gamma :\mathbb{R}\to M$ is called h-modular if $\gamma (t)={\alpha }_t(\gamma (0))$ holds for all $t\in \mathbb{R}$, i.e., $\gamma$ is an integral curve of $X_h^M$.

Proposition 3.2

Suppose that $(\mathfrak{g},\tau )$ is a direct sum of irreducible ncc symmetric Lie algebras ($\mathfrak{g}={\mathfrak{g}}_s$). The following assertions hold for any Euler element $h\in \mathcal{E}(\mathfrak{g})$ and the corresponding modular flow ${\alpha }_t(m)=exp(th).m$ on $M=G/H$:

1. The orbit under the modular flow is a causal geodesic if and only if m is contained in

   $$\begin{array}{c}\hfill M_C^h=\{gH\in G/H:\text{Ad}{(g)}^{-1}h\in C^{\circ }\}.\end{array}$$ 3.3
2. All connected components of $M_C^h$ are Riemannian symmetric space of non-compact type: For every $m\in M_C^h$, the exponential map

   $$\begin{array}{c}\hfill {\text{Exp}}_m:T_m(M_C^h)\to {(M^h)}_m\end{array}$$

   is a diffeomorphism.

3. h-modular causal geodesics exist if and only if ${\mathcal{O}}_h=\text{Ad}(G)h$ intersects $C^{\circ }$. In this case $G^h$ acts transitively on $M_C^h$.

Proof

(a) Assume first that $\text{Ad}{(g)}^{-1}h\in \mathfrak{q}$. Then (3.2) implies that the orbit of $m=gH$ under the modular flow is a geodesic. The causality is by definition equivalent to $\text{Ad}{(g)}^{-1}h\in C^{\circ }$.

Suppose, conversely, that $t\mapsto {\alpha }_t(gH)$ is a causal geodesic. Lemma B.1 implies that $\text{Ad}{(g)}^{-1}h=x_{\mathfrak{h}}+x_{\mathfrak{q}}$, where $[x_{\mathfrak{h}},x_{\mathfrak{q}}]=0$ and $x_{\mathfrak{q}}\in C^{\circ }$. By Lemma 2.4, $x_{\mathfrak{h}}$ is elliptic and $x_{\mathfrak{q}}$ is hyperbolic because it is contained in $C^{\circ }$. Therefore, $\text{ad}{x}_{\mathfrak{h}}+\text{ad}{x}_{\mathfrak{q}}$ is the unique Jordan decomposition of $\text{ad}x$ into elliptic and hyperbolic summand. As $\text{Ad}{(g)}^{-1}h$ is an Euler element, the elliptic summand vanishes, and thus, $\text{ad}{x}_{\mathfrak{h}}=0$, i.e., $x_{\mathfrak{h}}\in \mathfrak{z}(\mathfrak{g})\cap \mathfrak{h}=\{0\}$ (recall that $\mathfrak{z}(\mathfrak{g})\subseteq \mathfrak{q}$). This shows that $\text{Ad}{(g)}^{-1}h\in \mathfrak{q}$, so that $gH\in M_C^h$.

(b) Choosing m as a base point, we may assume that $m=eH$, so that (a) implies that $h\in C^{\circ }\subseteq \mathfrak{q}$ is a causal Euler element. Pick a Cartan involution $\theta$ commuting $\tau$ which satisfies $\theta (h)=-h$ (cf. [28]), i.e., $h\in {\mathfrak{q}}_{\mathfrak{p}}$. Then $\tau ={\tau }_h\theta$ follows from Theorem 2.5(a). As ${(M_C^c)}_m=G_e^h.m$ by Lemma B.2, the assertion now follows from ${\mathfrak{g}}^h={\mathfrak{h}}_{\mathfrak{k}}\oplus {\mathfrak{q}}_{\mathfrak{p}}$.

(c) The first assertion follows immediately from (a). For the second assertion, suppose that $m_0=g_{0}H\in M_C^h$. As $M_C^h$ is $G^h$-invariant, $G^h.m_0\subseteq M_C^h$. Let $h_c:=\text{Ad}{(g_0)}^{-1}h$, so that $\mathcal{E}(\mathfrak{g})\cap C^{\circ }={\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})h_c$ by Theorem 2.5(b) (recall that $C=C_s$). If $gH\in M_C^h$, i.e.,

$$\begin{array}{c}\hfill \text{Ad}{(g)}^{-1}h\in C^{\circ }\cap \mathcal{E}(\mathfrak{g})\stackrel{2.5}{=}{\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})h_c={\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})\text{Ad}{(g_0)}^{-1}h,\end{array}$$

then there exists an element $g_1\in {\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$ with $g{g}_1{g}_0^{-1}\in G^h$, so that $g\in G^h{g}_0{g}_1^{-1}\in G^h{g}_{0}H$, and therefore $gH\in G^h.m_0$. $\square$

We record the following consequence of (3.2):

Lemma 3.3

For any causal Euler element $h\in C^{\circ }$, we have

$$\begin{array}{c}\hfill W_M^{+}(h)=\{gH\in G/H:\text{Ad}{(g)}^{-1}h\in {\mathcal{T}}_C\},\text{where}{\mathcal{T}}_C:=\mathfrak{h}+C^{\circ }.\end{array}$$

Due to the hyperbolicity of Euler elements, modular causal geodesics do not exist for compactly causal symmetric spaces:

Proposition 3.4

If $M=G/H$ is a compactly causal symmetric space, then non-trivial causal modular geodesics do not exist.

Proof

If there exists a modular causal geodesic and $(\mathfrak{g},\tau ,C)$ is the infinitesimal data of M, then there exists a $g\in G$ such that the Euler element h satisfies $\text{Ad}{(g)}^{-1}h=x_{\mathfrak{h}}+x_{\mathfrak{q}}$ with $x_{\mathfrak{q}}\in C^{\circ }$ and $[x_{\mathfrak{h}},x_{\mathfrak{q}}]=0$ (Lemma B.1). As C is elliptic, $x_{\mathfrak{q}}$ is elliptic. Further the pointedness of C implies that $x_{\mathfrak{h}}\in ker(\text{ad}{x}_{\mathfrak{q}})$ is elliptic. This implies that the Euler element $\text{Ad}{(g)}^{-1}h$ is elliptic, a contradiction. $\square$

The fiber bundle structure of the positivity domain

The main result of this section is Theorem 3.6 in which we exhibit a natural bundle structure on the wedge domain $W\subseteq M$ that is equivariant with respect to the connected group $G_e^h$, the base is the Riemannian symmetric space of this group, and the fiber is a bounded convex subset of ${\mathfrak{q}}_{\mathfrak{k}}$.

Definition 3.5

Let $h\in {\mathfrak{q}}_{\mathfrak{p}}\cap C^{\circ }$ be a causal Euler element, so that $\tau ={\tau }_h\theta$. Then ${\mathfrak{z}}_{\mathfrak{h}}(h)={\mathfrak{h}}^{{\tau }_h}={\mathfrak{h}}_{\mathfrak{k}}$ implies that

$$\begin{array}{c}\hfill {\mathcal{O}}_h^{\mathfrak{q}}:={\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})h=e^{\text{ad}{\mathfrak{h}}_{\mathfrak{p}}}h\end{array}$$

is the non-compact Riemannian symmetric space associated with the symmetric Lie algebra $(\mathfrak{h},\theta )$.

Theorem 3.6

(Positivity Domain Theorem) Suppose that $(G,{\tau }^G,C,H)$ is a connected semisimple non-compactly causal Lie group for which $(\mathfrak{g},\tau )$ contains no $\tau$-invariant Riemannian ideals ($\mathfrak{g}={\mathfrak{g}}_s$) and that h is a causal Euler element. Suppose that $C:=C_{\mathfrak{q}}^{\text{max}}(h)$ is the maximal ${\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})$-invariant cone with $h\in C^{\circ }$. Then, the following assertions hold:

1. The connected component $W=W_M^{+}{(h)}_{\mathit{eH}}$ of eH in the positivity domain $W_M^{+}(h)$ is given by

   $$\begin{array}{c}\hfill W=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}),\text{where}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}=\{x\in {\mathfrak{q}}_{\mathfrak{k}}:\rho (\text{ad}x)<\frac{\pi }{2}\}.\end{array}$$ 3.4

2. The polar map $\mathrm{\Psi }:G_e^h{\times }_{G_e^h\cap H}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}\to W,[g,x]\mapsto g.{\text{Exp}}_{\mathit{eH}}(x)$ is a diffeomorphism

3. W is contractible, hence in particular simply connected.

4. $G_e^h\cap H=K_e^h$.

Proof

(a) Recall from [41, Thm. 6.7] that the connected component of h in the open subset ${\mathcal{O}}_h\cap {\mathcal{T}}_C$ of ${\mathcal{O}}_h$ is

$$\begin{array}{c}\hfill {\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})e^{\text{ad}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}}h=\text{Ad}(H_e)e^{\text{ad}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}}h\subseteq {\mathcal{T}}_C.\end{array}$$ 3.5

If $x\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$, then $\rho (\text{ad}x)<\pi /2$, so that (3.5) implies that $g=expx$ satisfies

$$\begin{array}{c}\hfill \text{Ad}{(g)}^{-1}h=e^{-\text{ad}x}h\in {\mathcal{T}}_C=\mathfrak{h}+C^{\circ }.\end{array}$$ 3.6

By Lemma 3.3

$$\begin{array}{c}\hfill {\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq W_M^{+}(h),\text{and}\text{thus}{G}_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq W\end{array}$$ 3.7

by $G^h$-invariance of $W_M^{+}(h)$.

Conversely, for $gH\in W$, the element $\text{Ad}{(g)}^{-1}h\in {\mathcal{O}}_h\cap {\mathcal{T}}_C$ is contained in the connected component of h, so that (3.5) implies that it is contained in $\text{Ad}(H_e)e^{\text{ad}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}}h$. Therefore

$$\begin{array}{c}\hfill g{H}_{e}exp({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\cap G^h\ne \mathrm{\varnothing }.\end{array}$$

This is equivalent to $g{H}_e\cap G^{h}exp({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\ne \mathrm{\varnothing },$ which implies

$$\begin{array}{c}\hfill gH\in G^{h}exp({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}).eH=G^h{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\end{array}$$

and thus

$$\begin{array}{c}\hfill W\subseteq G^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}).\end{array}$$ 3.8

If $g\in G^h$ satisfies $g{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\cap W\ne \mathrm{\varnothing },$ then $g.W=W$ follows from (3.7) and the fact that g permutes the connected components of $W_M^{+}(h)$. Therefore, (3.8), combined with (3.7), leads with $G_W^h:=\{g\in G^h:g.W=W\}$ to

$$\begin{array}{c}\hfill W\subseteq G_W^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq G_W^h.W=W,\end{array}$$

and this entails

$$\begin{array}{c}\hfill W=G_W^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}).\end{array}$$ 3.9

Next we observe that the exponential map ${\text{Exp}}_{\mathit{eH}}:{\mathfrak{q}}_{\mathfrak{k}}\to M$ is regular in every $x\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$ because $\rho (\text{ad}x)<\pi /2<\pi$ ([52, Lemma C.3(b)]). Thus [52, loc.cit.] further implies that the map

$$\begin{array}{c}\hfill \mathrm{\Phi }:G^h\times {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}\to M,(g,x)\mapsto g.{\text{Exp}}_{\mathit{eH}}(x)\end{array}$$

is regular in (g, x) because $\text{Spec}(\text{ad}x)\subseteq (-\pi /2,\pi /2)i$ does not intersect $(\frac{\pi }{2}+\mathbb{Z}\pi )i$ for $x\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$. This implies that the differential of $\mathrm{\Phi }$ is surjective in each point of $G^h\times {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$; hence, the image of every connected component is open. Now the connectedness of W implies that $W\subseteq G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}),$ and this completes the proof.

(b)–(d): The surjectivity of $\mathrm{\Psi }$ follows from Theorem 3.6. As ${\mathfrak{g}}^h={\mathfrak{h}}_{\mathfrak{k}}\oplus {\mathfrak{q}}_{\mathfrak{p}}$ is a Cartan decomposition of ${\mathfrak{g}}^h$, the polar map $K_e^h\times {\mathfrak{q}}_{\mathfrak{p}}\to G_e^h,(k,x)\mapsto kexpx$ is a diffeomorphism. In particular,

$$\begin{array}{c}\hfill G_e^h\cap H\subseteq G_e^h\cap G^G=K_e^h\subseteq H\end{array}$$

implies $G_e^h\cap H=K_e^h$ and thus (b).

The space $G_e^h{\times }_{G_e^h\cap H}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$ is a fiber bundle over $G_e^h/K_e^h$ whose fiber is the convex set ${\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$. Therefore, it is homotopy equivalent to the base $G_e^h/K_e^h$, which is also contractible because the exponential map ${\text{Exp}}_{\mathit{eH}}:{\mathfrak{q}}_{\mathfrak{p}}\to G_e^h/K_e^h$ is a diffeomorphism.

It therefore suffices to show that $\mathrm{\Psi }$ is a diffeomorphism. The proof of (a) shows already that its differential is everywhere surjective, hence invertible by equality of the dimensions of both spaces. So it suffices to check injectivity, i.e., that $\text{Exp}:={\text{Exp}}_{\mathit{eH}}:\mathfrak{q}\to M$ satisfies

$$\begin{array}{c}\hfill g_1.\text{Exp}(x_1)=g_2.\text{Exp}(x_2)\Rightarrow g_2^{-1}{g}_1\in K_e^h,x_2=\text{Ad}(g_2^{-1}{g}_1)x_1.\end{array}$$ 3.10

Step 1: ${\text{Exp}|}_{{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}}$ is injective. If $\text{Exp}(x_1)=\text{Exp}(x_2)$, then applying the quadratic representation implies $exp(2x_1)=exp(2x_2)$ in G. As $x_1$ and $x_2$ are both $exp$-regular, [25, Lemma 9.2.31] implies that

$$\begin{array}{c}\hfill [x_1,x_2]=0\text{and}exp(2x_1-2x_2)=e.\end{array}$$

We conclude that $e^{2\text{ad}(x_1-x_2)}={\text{id}}_{\mathfrak{g}}$, and since the spectral radius of $2\text{ad}(x_1-x_2)$ is less than $2\pi$, it follows that $\text{ad}(x_1-x_2)=0$, so that $x_1=x_2$.

Step 2: $g.\text{Exp}(x_1)=\text{Exp}(x_2)$ with $g\in G_e^h$ and $x_1,x_2\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$ implies $g\in K_e^h$. Applying the involution ${\theta }^M$, we see that $g.\text{Exp}(x_1)$ is a fixed point, so that

$$\begin{array}{c}\hfill g.\text{Exp}(x_1)=\theta (g).\text{Exp}(x_1)\end{array}$$

entails that $\theta {(g)}^{-1}g$ fixes $m_1:=\text{Exp}(x_1)$. We now write $g=kexpz$ in terms of the polar decomposition of $G_e^h$ and obtain

$$\begin{array}{c}\hfill \theta {(g)}^{-1}g=exp(2z)\in G^{m_1}.\end{array}$$

Applying the quadratic representation, we get

$$\begin{array}{c}\hfill exp(2z)exp(2x_1)exp(2z)=exp(2x_1),\end{array}$$ 3.11

which can be rewritten as

$$\begin{array}{c}\hfill exp(e^{2\text{ad}{x}_1}2z)=exp(-2z).\end{array}$$

Since $\text{ad}z$ has real spectrum, so has $e^{2\text{ad}{x}_1}z$. Therefore the same arguments as in Step 1 above imply that

$$\begin{array}{c}\hfill [z,e^{2\text{ad}{x}_1}z]=0\text{and}exp(2e^{2\text{ad}{x}_1}z+2z)=e,\end{array}$$

and $e^{2\text{ad}{x}_1}z=-z$. The vanishing $\mathfrak{h}$-component of this element is $sinh(2\text{ad}{x}_1)z$, and since $\rho (2\text{ad}{x}_1)<\pi$, it follows that $[x_1,z]=0$. Now (3.11) leads to $exp(4z)=e$, and further to $z=0$, because the exponential function on ${\mathfrak{q}}_{\mathfrak{p}}$ is injective. This proves that $g=k\in K_e^h$.

Step 3: From (3.10), we derive

$$\begin{array}{c}\hfill g_2^{-1}{g}_1.\text{Exp}(x_1)=\text{Exp}(x_2),\end{array}$$

so that Step 2 shows that $k:=g_2^{-1}{g}_1\in K_e^h$. We thus obtain

$$\begin{array}{c}\hfill \text{Exp}(x_2)=k.\text{Exp}(x_1)=\text{Exp}(\text{Ad}(k)x_1),\end{array}$$

and since $\text{Ad}(k)x_1\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$, we infer from Step 1 that $\text{Ad}(k)x_1=x_2$. This completes the proof. $\square$

The following corollary identifies the connected component of $M_C^h$ containing eH as a submanifold (cf. Lemma B.2) of the wedge domain W.

Corollary 6.4

Assume that ${\tau }_h^G$ exists and leaves H invariant, so that ${\tau }_h^M$ exists and leaves the base point $eH\in M$ invariant. Then ${\tau }_h^M(W)=W$ and the fixed point set of ${\tau }_h^M$ in W is the Riemannian symmetric space

$$\begin{array}{c}\hfill W^{{\tau }_h^M}=M_{\mathit{eH}}^h=G_e^h.eH={\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}}).\end{array}$$

Proof

For $g\in G^h$ and $x\in {\mathfrak{q}}_{\mathfrak{k}}$:

$$\begin{array}{c}\hfill {\tau }_h^M(g{\text{Exp}}_{\mathit{eH}}(x))=g{\text{Exp}}_{\mathit{eH}}({\tau }_h(x))=g{\text{Exp}}_{\mathit{eH}}(\tau (x))=g{\text{Exp}}_{\mathit{eH}}(-x).\end{array}$$

So $g{\text{Exp}}_{\mathit{eH}}(x)$ is a fixed point if and only if ${\text{Exp}}_{\mathit{eH}}(-x)={\text{Exp}}_{\mathit{eH}}(x),$ which is equivalent to $exp(2x)\in H$. Now $\tau (x)=-x$ implies $exp(2x)=exp(-2x)$. As $\rho (2\text{ad}x)<\pi$, [52, Lemma C.3] further shows that $x-(-x)=2x\in \mathfrak{z}(\mathfrak{g})=\{0\}$. Therefore, $g{\text{Exp}}_{\mathit{eH}}(x)$ is a fixed point if and only if $x=0$.

From $W=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})$ and the polar decomposition $G_e^h=K_e^{h}exp({\mathfrak{q}}_{\mathfrak{p}})=exp({\mathfrak{q}}_{\mathfrak{p}}){(H_K)}_e$ (Theorem3.6(b)), we derive that the fixed point set is

$$\begin{array}{c}\hfill W^{{\tau }_h^M}=G_e^h.eH={\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}})=M_{\mathit{eH}}^h.\end{array}$$

The preceding corollary shows that the wedge domain $W\subseteq M=G/H$ contains the symmetric subspace $M_{\mathit{eH}}^h={\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}})$ as the fixed point set of an involution. Hence, the description of W from Theorem 3.6 as

$$\begin{array}{c}\hfill W=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\end{array}$$

suggest to consider W as a real “crown domain” of the Riemannian symmetric space $M_{\mathit{eH}}^h\cong G^h/H^h$.

Remark 3.8

Theorem 3.6 has a trivial generalization to semisimple non-compactly causal Lie algebras of the form $\mathfrak{g}={\mathfrak{g}}_k\oplus {\mathfrak{g}}_r\oplus {\mathfrak{g}}_s$ because then

$$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{max}}={\mathfrak{q}}_r\oplus C_{{\mathfrak{q}}_s}^{\text{max}}\text{and}{\mathcal{T}}_{C_{\mathfrak{q}}^{\text{max}}}={\mathfrak{g}}_k+{\mathfrak{g}}_r+{\mathcal{T}}_{C_{{\mathfrak{q}}_s}^{\text{max}}}.\end{array}$$

For $h=h_r+h_s$ with $h_s\in C_{{\mathfrak{q}}_s}^{\circ }$ the relation $\text{Ad}{(g)}^{-1}h\in {\mathcal{T}}_{C_{\mathfrak{q}}^{\text{max}}}$ is therefore equivalent to $\text{Ad}{(g)}^{-1}{h}_s\in {\mathcal{T}}_{C_{{\mathfrak{q}}_s}^{\text{max}}}$. If $M=\text{Inn}(\mathfrak{g})/\text{Inn}{(\mathfrak{g})}^{\tau }\cong M_r\times M_s$ is the corresponding product decomposition, we obtain

$$\begin{array}{c}\hfill W_M^{+}(h)=M_r\times W_{M_s}^{+}(h_s)\text{for}C=C_{\mathfrak{q}}^{\text{max}}.\end{array}$$

However, if ${\mathfrak{g}}_r\ne \{0\}$, then $C_{\mathfrak{q}}^{\text{max}}$ is not pointed, and there are many pointed invariant cones C, which are not maximal, for which the domain $W_M^{+}(h)$ may have a more complicated structure.

Example 3.9

We consider the reductive Lie algebra

$$\begin{array}{c}\hfill \mathfrak{g}={\mathfrak{gl}}_2(\mathbb{R})=\mathbb{R}\mathbf{1}\oplus {\mathfrak{sl}}_2(\mathbb{R}).\end{array}$$

Any Euler element in $\mathfrak{g}$ is conjugate to some

$$\begin{array}{c}\hfill h=\left(\begin{array}{cc}\lambda & 0\\ 0& \mu \end{array}\right)\text{with}\lambda -\mu =1.\end{array}$$

The Cartan involution $\theta (x)=-x^{\top }$ on $\mathfrak{g}$ then satisfies $\theta (h)=-h$ and $\tau :=\theta {\tau }_h$ acts by

$$\begin{array}{c}\hfill \tau \left(\begin{array}{cc}a& b\\ c& d\end{array}\right)=\left(\begin{array}{cc}-a& c\\ b& -d\end{array}\right).\end{array}$$

With the Euler element

$$\begin{array}{c}\hfill h_0:=\frac{1}{2}\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),\end{array}$$

we then have

$$\begin{array}{c}\hfill \mathfrak{h}=\mathbb{R}{h}_0={\mathfrak{so}}_{1,1}(\mathbb{R})\text{and}\mathfrak{q}=\mathbb{R}\mathbf{1}+\underset{{\mathfrak{q}}_s}{\underbrace{\mathbb{R}h+\mathbb{R}z}}\text{with}z:=\frac{1}{2}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right).\end{array}$$

The group $G:={\text{GL}}_2{(\mathbb{R})}_e$ acts by $g.A:=gA{g}^{\top }$ on the 3-dimensional space ${\text{Sym}}_2(\mathbb{R})$ of symmetric matrices and the stabilizer of $I_{1,-1}:=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$ is the subgroup $H:={\text{SO}}_{1,1}(\mathbb{R})$ with Lie algebra $\mathfrak{h}$. Therefore $M:=G.I_{1,1}\cong G/H$ can be identified with the subspace ${\text{Sym}}_{1,1}(\mathbb{R})$ of indefinite symmetric matrices. Note that ${\mathbb{R}}_e^{\times }\mathbf{1}=Z{(G)}_e$ acts by multiplication with ${\lambda }^2$ and that ${\mathbb{R}}_{+}^{\times }\times M_1\to M,(\lambda ,A)\mapsto \lambda A$ is a diffeomorphism, where

$$\begin{array}{c}\hfill M_1:=\{A\in M:det(A)=-1\}\cong {\text{SL}}_2(\mathbb{R})/{\text{SO}}_{1,1}(\mathbb{R})\cong {\text{dS}}^2\end{array}$$

is a realization of 2-dimensional de Sitter space. Note that the determinant defines a quadratic form of signature (1, 2) on ${\text{Sym}}_2(\mathbb{R})$ which is invariant under the action of the subgroup

$$\begin{array}{c}\hfill \{g\in {\text{GL}}_2(\mathbb{R}):|det(g)|=1\}\supseteq {\text{SL}}_2(\mathbb{R})\end{array}$$

which acts as ${\text{SO}}_{1,2}{(\mathbb{R})}^{\uparrow }$.

For the Euler element $h_s:=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$, we have

$$\begin{array}{c}\hfill [h_0,h_s]=z,[z,h_s]=h_0\text{and}[h_0,z]=h_s.\end{array}$$

According to [53, Ex. 3.1(c)], all $\text{Ad}(H)$-invariant cones in $\mathfrak{q}$ are Lorentzian of the form

$$\begin{array}{c}\hfill C_m=\{x_0\mathbf{1}+x_1(h_s+z)+x_{-1}(h_s-z):x_1{x}_{-1}-m{x}_0^2\ge 0,x_{\pm 1}\ge 0\}\text{for}\text{some}m>0.\end{array}$$

Actually $C_0=C_{\mathfrak{q}}^{\text{max}}$ contains $\mathbb{R}\mathbf{1}$ and is not pointed.

(a) We write

$$\begin{array}{c}\hfill h=\frac{\lambda +\mu }{2}\mathbf{1}+h_s\end{array}$$

to see that $h\in C_m$ is equivalent to

$$\begin{array}{c}\hfill m{(\lambda +\mu )}^2\le 1.\end{array}$$

We also note that the “semisimple part” of $C_m$ is

$$\begin{array}{c}\hfill C_{m,s}=C_m\cap {\mathfrak{q}}_s=C_m\cap (\mathbb{R}h+\mathbb{R}z)=\text{cone}(h_s\pm z)\end{array}$$

coincides with the projection of $C_m$ to ${\mathfrak{q}}_s$, so that $C_{m,s}^{\circ }=C_m^{\circ }\cap {\mathfrak{q}}_s$.

Write $W(C_m,h)$ for the positivity domain of the Euler element h with respect to the causal structure specified by the cone $C_m$. Then Theorem 3.6 implies that

$$\begin{array}{c}\hfill W(C_0,h_s)=G_e^s.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}),\text{where}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}=(-\frac{\pi }{2},\frac{\pi }{2})z.\end{array}$$

For $x\in {\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}$ we have

$$\begin{array}{c}\hfill e^{-\text{ad}x}.h_s\in C_s+\mathfrak{h}\subseteq C_m+\mathfrak{h}\end{array}$$

(see (3.6)) and $G^h=G^{h_s}$, so that we have

$$\begin{array}{c}\hfill W(C_0,h_s)=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq W(C_m,h_s)\subseteq W(C_0,h_s)\end{array}$$

implies the equality

$$\begin{array}{c}\hfill W(C_m,h_s)=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\text{for}\text{all}m>0.\end{array}$$

We also note that

$$\begin{array}{c}\hfill W(C_m,h)\subseteq W(C_0,h)=W(C_0,h_s)=G_e^h.{\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\end{array}$$

because $\text{Ad}{(g)}^{-1}h=h_z+\text{Ad}{(g)}^{-1}{h}_s\in C_0^{\circ }$ if and only if $\text{Ad}{(g)}^{-1}{h}_s\in C_s^{\circ }$.

To determine the domain $W(C_m,h)$ in general, we write

$$\begin{array}{c}\hfill h=h_z+h_s=\frac{\lambda +\mu }{2}\mathbf{1}+\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).\end{array}$$

By $G_e^h$-invariance, we have to determine when ${\text{Exp}}_{\mathit{eH}}(tz)$, $|t|<\frac{\pi }{2}$, is contained in $W(C_m,h)$. For $g=exp(tz)$, we have

$$\begin{array}{c}\hfill \text{Ad}{(g)}^{-1}h=h_z+e^{-t\text{ad}z}{h}_s=h_z+cos(t)h_s-sin(t)h_0,\end{array}$$

and

$$\begin{array}{c}\hfill p_{\mathfrak{q}}(\text{Ad}{(g)}^{-1}h)=h_z+cos(t)h_s=\frac{\lambda +\mu }{2}\mathbf{1}+\frac{cos(t)}{2}(h_s+z)+\frac{cos(t)}{2}(h_s-z).\end{array}$$

We then have

$$\begin{array}{c}\hfill x_0=\frac{\lambda +\mu }{2}\text{and}{x}_{\pm 1}=\frac{cos(t)}{2}.\end{array}$$

We conclude that, for $|t|<\frac{\pi }{2}$, the inclusion $h_z+cos(t)h_s\in {(C_m)}^{\circ }$ is equivalent to

$$\begin{array}{c}\hfill x_1{x}_{-1}-m{x}_0^2=\frac{1}{4}({cos}^2(t)-m{(\lambda +\mu )}^2)>0.\end{array}$$

We thus obtain the condition

$$\begin{array}{c}\hfill |t|<arccos(\sqrt{m}|\lambda +\mu |).\end{array}$$

For $m>0$ and $h\ne h_s$, this is specifies a proper subinterval of $(-\frac{\pi }{2},\frac{\pi }{2})$.

(b) To determine which cone $C_m$ corresponds to the canonical order on the space ${\text{Sym}}_{1,1}(\mathbb{R})$, induced from the natural order of ${\text{Sym}}_2(\mathbb{R})$ (which is also Lorentzian), we evaluate the tangent map $\mathfrak{q}\to {\text{Sym}}_2(\mathbb{R}),x\mapsto x{I}_{11}+I_{11}{x}^{\top }$ to

$$\begin{array}{c}\hfill \mathbf{1}.I_{1,1}=2I_{1,1},h_s.I_{1,1}=\mathbf{1},z.I_{1,1}=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right).\end{array}$$

We thus obtain for $x=x_0\mathbf{1}+x_1(h_s+z)+x_{-1}(h_s-z)$ that

$$\begin{array}{c}\hfill x.I_{1,1}=x{I}_{11}+I_{11}{x}^{\top }=\left(\begin{array}{cc}2x_0+x_1+x_{-1}& x_1-x_{-1}\\ x_1-x_{-1}& -2x_0+x_1+x_{-1}\end{array}\right).\end{array}$$

By the Hurwitz criterion, this matrix is positive semidefinite if and only if

$$\begin{array}{c}\hfill x_1+x_{-1}\ge |2x_0|\end{array}$$

and

$$\begin{array}{c}\hfill {(x_1+x_{-1})}^2-4x_0^2-{(x_1-x_{-1})}^2=4(x_1{x}_{-1}-x_0^2)\ge 0.\end{array}$$

Is $x_1+x_{-1}\ge 0$, then these two inequalities are equivalent to $x_1{x}_{-1}-x_0^2\ge 0$. As these two conditions imply that $x_{\pm 1}\ge 0$, we see that the canonical order on M corresponds to the cone $C^1$, i.e., to $m=1$.

(c) For the modular vector field $X_h$, we have

$$\begin{array}{c}\hfill X_h\left(\begin{array}{cc}a& b\\ b& d\end{array}\right)=\left(\begin{array}{cc}2\lambda a& (\lambda +\mu )b\\ (\lambda +\mu )b& 2\mu d\end{array}\right).\end{array}$$

The positivity domain of $X_h$ depends on $\lambda$, and with this formula one can also determine the positivity domain quite directly for $m=1$, where $C^1$ corresponds to the canonical order.

Example 3.10

(cf. [52, Exs. 2.11, 2.25]) Let $G:={\text{GL}}_n{(\mathbb{R})}_{+}$ and $K:={\text{SO}}_n(\mathbb{R})$. We consider the Riemannian symmetric space

$$\begin{array}{c}\hfill M_r:={\text{Sym}}_n{(\mathbb{R})}_{+}\cong {\text{GL}}_n(\mathbb{R})/{\text{SO}}_n(\mathbb{R})\end{array}$$

and the corresponding irreducible subspace

$$\begin{array}{c}\hfill M_{r,s}:=\{A\in M:det(A)=1\}\cong {\text{SL}}_n(\mathbb{R})/{\text{SO}}_n(\mathbb{R})\end{array}$$

(here the index s refers to “semisimple”). On $\mathfrak{g}={\mathfrak{gl}}_n(\mathbb{R})$, we consider the Cartan involution given by $\theta (x)=-x^{\top }$ and write $n=p+q$ with $p,q>0$. Then

$$\begin{array}{c}\hfill h_s^p:=\frac{1}{n}\left(\begin{array}{cc}q{\mathbf{1}}_p& 0\\ 0& -p{\mathbf{1}}_q\end{array}\right)\in {\mathfrak{sl}}_n(\mathbb{R})\text{and}{h}^p:=h_s^p-\frac{q}{n}\mathbf{1}=\left(\begin{array}{cc}0& 0\\ 0& {\mathbf{1}}_q\end{array}\right)\in \mathfrak{g}\end{array}$$ 3.12

are Euler elements and $\tau :={\tau }_{h^p}\theta$ leads to a non-compactly causal symmetric Lie algebra $(\mathfrak{g},\tau ,C)$, where

$$\begin{array}{c}\hfill \mathfrak{h}={\mathfrak{so}}_{p,q}(\mathbb{R})\text{and}\mathfrak{q}=\{\left(\begin{array}{cc}a& b\\ -b^{\top }& d\end{array}\right):a^{\top }=a,d^{\top }=d\}\end{array}$$

To identify G/H in the boundary of the crown domain in $G_{\mathbb{C}}/K_{\mathbb{C}}\cong G_{\mathbb{C}}.\mathbf{1}\cong {\text{Sym}}_n{(\mathbb{C})}^{\times }$, where $G_{\mathbb{C}}$ acts on ${\text{Sym}}_n(\mathbb{C})$ by $g.A:=gA{g}^{\top }$ ([52, Thm. 5.4]), we observe that

$$\begin{array}{c}\hfill exp(it{h}^p).\mathbf{1}=e^{2it{h}^p}=cos(2t{h}^p)+isin(2t{h}^p)=\left(\begin{array}{cc}{\mathbf{1}}_p& 0\\ 0& (cos(2t)+isin(2t)){\mathbf{1}}_q\end{array}\right),\end{array}$$

so that we obtain for $t=\frac{\pi }{2}$ the matrix

$$\begin{array}{c}\hfill exp(\frac{\pi i}{2}{h}^p).\mathbf{1}=I_{p,q}.\end{array}$$

The G-orbit of this matrix is the open subset

$$\begin{array}{c}\hfill M:=G.I_{p,q}=\{g{I}_{p,q}{g}^{\top }:g\in {\text{GL}}_n{(\mathbb{R})}_{+}\}={\text{Sym}}_{p,q}(\mathbb{R})\end{array}$$

of symmetric matrices of signature (p, q). We have

$$\begin{array}{c}\hfill X_{h^p}\left(\begin{array}{cc}a& b\\ b^{\top }& d\end{array}\right)=h^p\left(\begin{array}{cc}a& b\\ b^{\top }& d\end{array}\right)+\left(\begin{array}{cc}a& b\\ b^{\top }& d\end{array}\right)h^p=\left(\begin{array}{cc}0& b\\ b^{\top }& 2d\end{array}\right).\end{array}$$

These matrices are never positive definite. So we have to take $h_s$ instead to find non-trivial positivity domains.

For the case $p=q=1$ and $n=2$, this has been carried out in Example 3.9. We also write

$$\begin{array}{c}\hfill h=\left(\begin{array}{cc}\lambda {\mathbf{1}}_p& 0\\ 0& \mu {\mathbf{1}}_q\end{array}\right)\text{with}\lambda -\mu =1.\end{array}$$

Then

$$\begin{array}{c}\hfill X_h\left(\begin{array}{cc}a& b\\ b^{\top }& d\end{array}\right)=\left(\begin{array}{cc}2\lambda a& (\lambda +\mu )b\\ (\lambda +\mu )b^{\top }& 2\mu d\end{array}\right),\end{array}$$

so that

$$\begin{array}{c}\hfill X_h(I_{p,q})=2\left(\begin{array}{cc}\lambda {\mathbf{1}}_p& 0\\ 0& -\mu {\mathbf{1}}_q\end{array}\right)>>0\text{if}0<\lambda <1,\end{array}$$

which is equivalent to $\lambda \mu <0$.

The connected components of $M_C^h$

The main result in this section is Proposition 3.11 on the subgroup $H_K$ of $K^h$. We then discuss several examples to clarify the situation.

Proposition 3.11

(Connected components of $M_C^h$) If $G=\text{Inn}(\mathfrak{g})$ and $(\mathfrak{g},\tau )$ is irreducible ncc with causal Euler element h, then ${\pi }_0(M_C^h)\cong K^h/H_K$ contains at most two elements.

Proof

We recall from Proposition 3.2(c) that $M_C^h=G^h.eH$. With [36, Thm. IV.3.5] we see that the symmetric space $G^h.eH\cong G^h/H^h$ is a vector bundle over $K^h/H_K^h$, hence in particular homotopy equivalent to $K^h.eH\cong K^h/H_K^h$. In view of Proposition 2.6(c), we have for $G=\text{Inn}(\mathfrak{g})$ that $H^h=H^{{\tau }_h}=H_K\subseteq G^{\tau }$ is a maximal compact subgroup of H. It follows in particular that $H^h=H_K^h\subseteq K^h$. We conclude that ${\pi }_0(M_C^h)\cong {\pi }_0(K^h/H_K)$. From [41, §7], we know that ${\pi }_0(G^h)\cong {\pi }_0(K^h)$ has at most two elements. $\square$

Example 3.12

(The inclusion $H_K\subseteq K^h$ may be proper) We have $G^h=K^{h}exp({\mathfrak{q}}_{\mathfrak{p}})$ and $K^G=K^{{\tau }_h^G}$ because $K=G^{\theta }$. Further $H_K\subseteq K^h$ by Proposition 2.6(a), so that the equality $H_K=K^h$ is equivalent to $K^h\subseteq H_K$. This may fail for two reasons. One is failure in the adjoint group $\text{Inn}(\mathfrak{g})$ (Proposition 3.11), and the other reason is that Z(G) may be non-trivial.

Assume that $\mathfrak{g}$ is semisimple and $(\mathfrak{g},\tau ,C)$ ncc. Let G be a corresponding connected Lie group on which ${\tau }^G$ exists (for $\tau ={\tau }_h\theta$) and $H:=G_e^G$. For the connected group $K:=G^{\theta }$, the intersection $H_K:=H\cap K=⟨exp{\mathfrak{h}}_{\mathfrak{k}}⟩$ is connected but $K^h\supseteq Z(G)H_K$ is in general not connected because Z(G) need not be contained in $H_K$.

This can be seen easily for $\mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})$. For

$$\begin{array}{c}\hfill h=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),\theta (x)=-x^{\top },\text{we}\text{have}\tau =\theta {\tau }_h,\left(\begin{array}{cc}a& b\\ c& -a\end{array}\right)\mapsto \left(\begin{array}{cc}-a& c\\ b& a\end{array}\right).\\ \hfill \end{array}$$ 3.13

For any connected Lie group G with Lie algebra $\mathfrak{g}$, the group $K=G^{\theta }$ is connected 1-dimensional and $\tau (k)=k^{-1}$ for $k\in K$. Moreover, $K^h=Z(G)$ is a discrete subgroup which intersects $H=exp\mathfrak{h}\cong \mathbb{R}$ trivially. Even the inclusion $K^h\subseteq G^G$ fails if $|Z(G)|\ge 3$, i.e., if $\tau$ acts non-trivially on Z(G). Note that Z(G) is infinite if G is simply connected.

Example 3.13

(a) For $\mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})$, we consider again the Euler element h from (3.13) and the Cartan involution $\theta (x)=-x^{\top }$. By Lemma B.1, the $\alpha$-orbit of gH is a geodesic if and only if $\text{Ad}{(g)}^{-1}h$ commutes with $\tau (\text{Ad}{(g)}^{-1}h)=-\text{Ad}{(\tau (g))}^{-1}h$, i.e., if

$$\begin{array}{c}\hfill \text{Ad}(g\tau {(g)}^{-1})h\in {\mathfrak{z}}_{\mathfrak{g}}(h)=\mathbb{R}h.\end{array}$$

As ${\mathcal{O}}_h\cap \mathbb{R}h=\{\pm h\}$, this leaves two possibilities:

1. If $\text{Ad}(g\tau {(g)}^{-1})h=h$, then $\text{Ad}{(\tau (g))}^{-1}h=\text{Ad}{(g)}^{-1}h$ implies $\text{Ad}{(g)}^{-1}h\in \mathfrak{q}$.

2. If $\text{Ad}(g\tau {(g)}^{-1})h=-h$, then $-\text{Ad}{(\tau (g))}^{-1}h=\text{Ad}{(g)}^{-1}h$ implies $\text{Ad}{(g)}^{-1}h\in \mathfrak{h}$. In this case gH is a fixed point of the modular flow.

(b) For $\mathfrak{g}={\mathfrak{sl}}_{2k}(\mathbb{R})$ with the Cartan involution $\theta (x)=-x^{\top }$ and the causal Euler element

$$\begin{array}{c}\hfill h=\frac{1}{2}\left(\begin{array}{cc}{\mathbf{1}}_k& 0\\ 0& -{\mathbf{1}}_k\end{array}\right),\end{array}$$

we obtain $\mathfrak{h}={\mathfrak{so}}_{k,k}(\mathbb{R})$ for $\tau =\theta {\tau }_h$. There exists a subalgebra $\mathfrak{s}\cong {\mathfrak{sl}}_2{(\mathbb{R})}^k$, where the ${\mathfrak{sl}}_2$-factors correspond to the coordinates $x_j$ and $x_{j+k}$ for $1\le j\le k$. Accordingly, $h={\sum }_{j=1}^k{h}_j$, where the Euler elements $h_j$ in the ${\mathfrak{sl}}_2$-factors are conjugate to Euler elements $h_j^{\prime }$ in $\mathfrak{h}$. Therefore, the “geodesic condition” is satisfied by all elements ${\sum }_{j=1}^k{\tilde{h}}_j\in {\mathcal{O}}_h$, where ${\tilde{h}}_j$ is either $h_j$ or $h_j^{\prime }$.

The following example shows that modular geodesics also exist in symmetric spaces without causal structure. They can be “space-like” rather than “time-like”, resp., causal.

Example 3.14

The d-dimensional hyperbolic space

$$\begin{array}{c}\hfill {\mathbb{H}}^d:=\{x=(x_0,\mathbf{x})\in {\mathbb{R}}^{1,d}:x_0^2-{\mathbf{x}}^2=1,x_0>0\}\cong {\text{SO}}_{1,d}^{\uparrow }(\mathbb{R})/{\text{SO}}_d(\mathbb{R})\end{array}$$

carries a modular flow specified by any Euler element $h\in \mathfrak{q}\subseteq {\mathfrak{so}}_{1,d}(\mathbb{R})$ (corresponding to a tangent vector of length 1). Every geodesic of ${\mathbb{H}}^d$ is an orbit of the flow generated by an Euler element of ${\mathfrak{so}}_{1,d}(\mathbb{R})$.

Remark 3.15

Let $(\mathfrak{g},\tau ,C)$ be a simple ncc symmetric Lie algebra. In general, we have for a causal Euler element $h\in \mathcal{E}(\mathfrak{g})\cap C^{\circ }$ a proper inclusion

$$\begin{array}{c}\hfill {\text{Inn}}_{\mathfrak{g}}(\mathfrak{h})h={\mathcal{O}}_h\cap C^{\circ }\subseteq {\mathcal{O}}_h\cap \mathfrak{q}.\end{array}$$

By Lemma B.4, this implies that $M^h$ is not connected and $M_C^h\ne M^h$.

For instance, if $\mathfrak{g}={\mathfrak{h}}_{\mathbb{C}}$ and $\mathfrak{h}$ is simple hermitian of tube type, then we obtain for any pointed generating invariant cone $C_{\mathfrak{h}}\subseteq \mathfrak{h}$ a hyperbolic cone $C:=i{C}_{\mathfrak{h}}\subseteq \mathfrak{q}=i\mathfrak{h}$. If $h\in \mathcal{E}(\mathfrak{g})\cap C^{\circ }$ is a causal Euler element, then $-h\in \text{Ad}(G)h$ follows from [38, Thm. 3.10] and the subsequent discussion, but $-h\notin C^{\circ }$; see also [41, Thm. 5.4].

Example 3.16

(a) For de Sitter space $M={\text{dS}}^d$ (cf. Example 4.6 and Appendix D), the subspace $M_{\mathit{eH}}^h={\text{Exp}}_{\mathit{eH}}(\mathbb{R}h)$ is a single geodesic, hence in particular 1-dimensional. Note that $\text{dim}{\mathfrak{q}}_{\mathfrak{p}}=1$ in this case. The modular flow on M has the fixed point set $M^{\alpha }\cong {\mathbb{S}}^{d-2}$.

(b) For $M=G_{\mathbb{C}}/G$, $\mathfrak{g}$ hermitian, we have $M_{\mathit{eG}}^h={\text{Exp}}_e(i\mathfrak{k})$ with dual symmetric space the group K, considered as a symmetric space.

Open H-orbits in flag manifolds and a convexity theorem

In this section, we prove a convexity theorem that is vital to derive the equality $W=W(\gamma )$ in the next section. Here, as above, $W=W_M^{+}{(h)}_{\mathit{eH}}$.

Let $P^{-}:=exp({\mathfrak{g}}_{-1}(h))G^h\subseteq G$ be the “negative” parabolic subgroup of G specified by h and identity ${\mathfrak{g}}_1(h)$ with the open subset $\mathcal{B}:=exp({\mathfrak{g}}_1(h)).e{P}^{-}\subseteq G/P^{-}$. Then $\mathcal{D}:=H.0\subseteq \mathcal{B}$ is an open convex subset, and our convexity theorem (Theorem 4.5) asserts that, for any $g\in G$ with $g.\mathcal{D}\subseteq \mathcal{B}$, the subset $g.\mathcal{D}\subseteq \mathcal{B}$ is convex.

We consider a connected semisimple Lie group G with Lie algebra $\mathfrak{g}$ and an Euler element $h\in \mathfrak{g}$. We put

$$\begin{array}{c}\hfill {\mathfrak{n}}^{\pm }:={\mathfrak{g}}_{\pm 1}(h)\text{and}{N}^{\pm }:=exp({\mathfrak{n}}^{\pm }),\end{array}$$

and write

$$\begin{array}{c}\hfill P^{\pm }:=\{g\in G:\text{Ad}(g){\mathfrak{g}}_{\pm 1}(h)={\mathfrak{g}}_{\pm 1}(h)\}=N^{\pm }{G}^h\cong N^{\pm }⋊G^h\end{array}$$

(see [2, Thm. 1.12] for the equality) for the corresponding maximal parabolic subgroups. We write

$$\begin{array}{c}\hfill {\mathcal{M}}_{\pm }:=G/P^{\mp }\end{array}$$

for the corresponding flag manifold. The abelian subgroup $N^{+}$ has an open orbit $\mathcal{B}:=N^{+}.e{P}^{-}\subseteq {\mathcal{M}}_{+}$, which we call the open Bruhat cell. It carries a natural affine structure because the map

$$\begin{array}{c}\hfill \phi :{\mathfrak{n}}^{+}\to \mathcal{B}:=N^{+}.e{P}^{-},x\mapsto exp(x)P^{-}\end{array}$$

defines an open embedding. Below we shall always use these coordinates on $\mathcal{B}$.

Choose a Cartan involution $\theta$ with $\theta (h)=-h$ and consider the involution $\tau :=\theta e^{\pi i\text{ad}h}$. We write

$$\begin{array}{c}\hfill H:=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})\text{for}{\mathfrak{h}}_{\mathfrak{p}}={\mathfrak{g}}^{\tau }\cap \mathfrak{p}\text{and}{H}_K:=K^h.\end{array}$$

Then

$$\begin{array}{c}\hfill P^{\pm }\cap H=G^h\cap H=K^h,\end{array}$$

so that

$$\begin{array}{c}\hfill {\mathcal{D}}_{+}:=H.e{P}^{-}\cong H/H_K\end{array}$$ 4.1

is an open H-orbit in $\mathcal{B}\subseteq G/P^{-}$. It is a real bounded symmetric domain ([26, Thm. 5.1.8]) and coincides with the unit ball in the positive real Jordan triple

$$\begin{array}{c}\hfill V:=\mathfrak{n}\text{with}\{x,y,z\}:=x\square y.z=-\frac{1}{2}[[x,\theta (y)],z]\end{array}$$ 4.2

(cf. [2, (4.6)])

The open H-orbits in $G/P^{\pm }$

Lemma 4.1

([2, Cor. 1.10]) For $y\in {\mathfrak{g}}_{-1}(h)$ and $x\in {\mathfrak{g}}_1(h)$, we have $exp(y).exp(x)P^{-}\in \mathcal{B}$ if and only if the Bergman operators

$$\begin{array}{c}\hfill B_{+}(x,y):=\mathbf{1}+\text{ad}(x)\text{ad}(y)+\frac{1}{4}{(\text{ad}x)}^2{(\text{ad}y)}^2\in \text{End}({\mathfrak{g}}_1(h))\end{array}$$

and

$$\begin{array}{c}\hfill B_{-}(y,x):=\mathbf{1}+\text{ad}(y)\text{ad}(x)+\frac{1}{4}{(\text{ad}y)}^2{(\text{ad}x)}^2\in \text{End}({\mathfrak{g}}_{-1}(h))\end{array}$$

are both invertible.

Remark 4.2

Note that

$$\begin{array}{c}\hfill \theta B_{-}(y,x)\theta =\mathbf{1}+\text{ad}(\theta (y))\text{ad}(\theta (x))+\frac{1}{4}{(\text{ad}\theta (y))}^2{(\text{ad}\theta (x))}^2=B_{+}(\theta (y),\theta (x)).\end{array}$$

Example 4.3

We consider the group $G={\text{SL}}_2(\mathbb{R})$ with Lie algebra $\mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})$ and the linear basis

$$\begin{array}{c}\hfill h:=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),e=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),f=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right),\end{array}$$ 4.3

satisfying

$$\begin{array}{c}\hfill [h,e]=e,[h,f]=-f,[e,f]=2h.\end{array}$$

Then,

$$\begin{array}{c}\hfill N^{+}=\left(\begin{array}{cc}1& \mathbb{R}\\ 0& 1\end{array}\right),N^{-}=\left(\begin{array}{cc}1& 0\\ \mathbb{R}& 1\end{array}\right),\text{and}{G}^h=\{\left(\begin{array}{cc}a& 0\\ 0& a^{-1}\end{array}\right):a\in {\mathbb{R}}^{\times }\},\end{array}$$

so that

$$\begin{array}{c}\hfill P^{-}=\{\left(\begin{array}{cc}a& 0\\ c& a^{-1}\end{array}\right):a\in {\mathbb{R}}^{\times },c\in \mathbb{R}\}=\{g\in G:g{e}_2\in \mathbb{R}{e}_2\}.\end{array}$$

For $K={\text{SO}}_2(\mathbb{R})$, we have $K^h=\{\pm \mathbf{1}\}$. Identifying $G/P^{-}$ with the projective space $\mathbb{P}({\mathbb{R}}^2)=G.[e_2]$, the Bruhat cell is

$$\begin{array}{c}\hfill \mathcal{B}=\{[x:1]:x\in \mathbb{R}\}\cong \mathbb{R},\end{array}$$

and G acts by

$$\begin{array}{c}\hfill g.x=\frac{ax+b}{cx+d}\text{for}ax+b\ne 0.\end{array}$$

In particular, we have

$$\begin{array}{c}\hfill exp(yf).x=\frac{x}{1+xy}.\end{array}$$ 4.4

We consider the Cartan involution $\theta (x)=-x^{\top }$, so that $\tau :=\theta e^{\pi i\text{ad}h}$ acts by

$$\begin{array}{c}\hfill \tau \left(\begin{array}{cc}a& b\\ c& -a\end{array}\right)=\left(\begin{array}{cc}-a& c\\ b& a\end{array}\right)\text{and}{\tau }^G\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)=\left(\begin{array}{cc}d& c\\ b& a\end{array}\right).\end{array}$$

Then

$$\begin{array}{c}\hfill H={\text{SL}}_2{(\mathbb{R})}^G=\{\left(\begin{array}{cc}a& b\\ b& a\end{array}\right):a^2-b^2=1\}={\text{SO}}_{1,1}(\mathbb{R}),\end{array}$$

so that

$$\begin{array}{c}\hfill {\mathcal{D}}_{+}=H.0=\{b{a}^{-1}:a^2-b^2=1\}=(-1,1).\end{array}$$ 4.5

Note that $\text{Ad}(H)\cong H/\{\pm \mathbf{1}\}$ is connected.

The Jordan triple product satisfies

$$\begin{array}{c}\hfill \{e,e,e\}=-\frac{1}{2}[[e,\theta (e)],e]=-\frac{1}{2}[[e,-f],e]=\frac{1}{2}[2h,e]=e,\end{array}$$

so that

$$\begin{array}{c}\hfill \{xe,ye,ze\}=xyz·e\text{for}x,y,z\in \mathbb{R}.\end{array}$$

Further

$$\begin{array}{c}\hfill (\text{ad}f)e=-2h,{(\text{ad}f)}^{2}e=-2[f,h]=-2f,(\text{ad}e)f=2h,{(\text{ad}e)}^{2}f=-2e\end{array}$$

implies

$$\begin{array}{cc}\hfill B_{+}(xe,yf)e& =e+xy\text{ad}(e)\text{ad}(f)e+\frac{x^2{y}^2}{4}{(\text{ad}e)}^2{(\text{ad}f)}^{2}e\hfill \\ \hfill & =e+xy\text{ad}(e)(-h)+\frac{x^2{y}^2}{4}{(\text{ad}e)}^2(-2f)\hfill \\ \hfill & =e+xy2e+\frac{x^2{y}^2}{4}4e=(1+2xy+x^2{y}^2)e={(1+xy)}^{2}e.\hfill \end{array}$$

Moreover,

$$\begin{array}{c}\hfill B_{+}(\theta (yf),\theta (xe))e=B_{+}(-ye,-xf)e={(1+(-y)(-x))}^{2}e.=B_{+}(xe,yf)e.\end{array}$$

As $1+xy$ is invertible for all x with $|x|<1$ if and only if $|y|\le 1$, it follows that

$$\begin{array}{c}\hfill exp(y).{\mathcal{D}}_{+}\subseteq \mathcal{B}\iff |y|\le 1.\end{array}$$

Now back to the general case. In the following we write $\Vert ·\Vert$ for the spectral norm on the Jordan triple system ${\mathfrak{g}}_1(h)={\mathfrak{n}}^{+}$. If $x={\sum }_{j=1}^k{x}_j{c}_j$ with pairwise orthogonal tripotents $c_j$, then

$$\begin{array}{c}\hfill \Vert x\Vert =max\{|x_1|,\dots ,|x_k|\}.\end{array}$$ 4.6

If

$$\begin{array}{c}\hfill {\mathcal{D}}_{\mathfrak{g}}:=\{x\in {\mathfrak{g}}_1(h):\Vert x\Vert <1\},\end{array}$$ 4.7

then we have

$$\begin{array}{c}\hfill {\mathcal{D}}_{+}=exp({\mathcal{D}}_{\mathfrak{g}})P^{-}\subseteq G/P^{-}\end{array}$$ 4.8

([26, Thm. 5.1.8]).

Proposition 4.4

The following assertions hold:

1. $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is equivalent to $g\in P^{+}exp(y)$ for $y\in {\mathfrak{n}}^{-}$ with $\Vert y\Vert \le 1$.

2. $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is relatively compact if and only if $g\in P^{+}exp(y)$ for $y\in {\mathfrak{n}}^{-}$ with $\Vert y\Vert <1$.

Proof

The condition $g.e{P}^{-}\in \mathcal{B}$ is equivalent to $g\in N^{+}{P}^{-}=N^{+}{G}^h{N}^{-}=P^{+}{N}^{-}.$ Let $y\in {\mathfrak{n}}^{-}$ with $g\in P^{+}exp(y)$. Then the invariance of $\mathcal{B}$ under $P^{+}$ implies that $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is equivalent to $exp(y).{\mathcal{D}}_{+}\subseteq \mathcal{B}$.

(a) Suppose first that $exp(y).{\mathcal{D}}_{+}\subseteq \mathcal{B}$. By the Spectral Theorem for positive Jordan triples ([59, Thm. VI.2.3]3), there exist pairwise orthogonal tripotents $c_1,\dots ,c_k$ and ${\beta }_1,\dots ,{\beta }_k\in \mathbb{R}$ with

$$\begin{array}{c}\hfill y=\sum _{j=1}^k{\beta }_j\theta (c_j)\end{array}$$

([59, Thm. VI.2.3]). For $x={\sum }_j{\alpha }_j{c}_j$ and $z={\sum }_j{\gamma }_j{c}_j$, we then have

$$\begin{array}{c}\hfill \{x,\theta (y),z\}=\sum _{j=1}^k{\alpha }_j{\beta }_j{\gamma }_j·c_j\end{array}$$

([59, Prop. V.3.1]). As $x\in {\mathcal{D}}_{\mathfrak{g}}$ is equivalent to

$$\begin{array}{c}\hfill \Vert x\Vert =max\{|{\alpha }_j|:j=1,\dots ,k\}<1,\end{array}$$

the calculations in Example 4.3 show that $exp(y).{\mathcal{D}}_{+}\subseteq \mathcal{B}$ implies $\Vert y\Vert \le 1$.4

To prove the converse, suppose first that $\Vert y\Vert <1$. Then

$$\begin{array}{c}\hfill exp(-y)=\theta (exp(-\theta (y))\in \theta (H{P}^{-})=H{P}^{+}\end{array}$$

implies $exp(y)\in P^{+}H,$ so that

$$\begin{array}{c}\hfill exp(y).{\mathcal{D}}_{+}\in P^{+}H.{\mathcal{D}}_{+}=P^{+}.{\mathcal{D}}_{+}\subseteq \mathcal{B}.\end{array}$$

Now we assume that $\Vert y\Vert =1$. We observe that

$$\begin{array}{c}\hfill exp(y).x=exp(-th)exp(th)exp(y).x=exp(-th)exp(e^{-t}y).(e^{t}x),\end{array}$$

so that, for $r>0$, $exp(y).x\in \mathcal{B}$ is equivalent to $exp(r^{-1}y).(rx)\in \mathcal{B}$. For $x\in {\mathcal{D}}_{\mathfrak{g}}$, we pick $r>1$ with $rx\in {\mathcal{D}}_{\mathfrak{g}}$. Then $\Vert r^{-1}y\Vert <1$ implies $exp(r^{-1}.y).exp(rx)\in \mathcal{B},$ and thus $exp(y).exp(x)\in \mathcal{B}$. This shows that $exp(y).{\mathcal{D}}_{+}\subseteq \mathcal{B}$.

(b) If $\Vert y\Vert <1$, then the argument under (a) shows that $exp(y).{\mathcal{D}}_{+}\subseteq P^{+}.{\mathcal{D}}_{+}$ is relatively compact.

Now we assume that $\Vert y\Vert =1$. We show that this implies that $exp(y).{\mathcal{D}}_{+}$ is unbounded. As above, we use the Spectral Theorem to write

$$\begin{array}{c}\hfill y=\sum _{j=1}^k{\beta }_j\theta (c_j)\end{array}$$

and observe that there exists an $\ell \in \{1,\dots ,k\}$ with $|b_{\ell }|=1$. For $x={\sum }_j{\alpha }_j{c}_j\in {\mathcal{D}}_{\mathfrak{g}}$, we then obtain with (4.4)

$$\begin{array}{c}\hfill exp(y).x=\sum _{j=1}^k\frac{{\alpha }_j}{1+{\alpha }_j{\beta }_j}{c}_j.\end{array}$$

For $x=\alpha c_{\ell }$ we get in particular

$$\begin{array}{c}\hfill exp(y).x=\frac{\alpha }{1+\alpha {\beta }_{\ell }}{c}_{\ell }.\end{array}$$

For $\alpha \to -\text{sgn}({\beta }_{\ell })$ these element leave every compact subset of $\mathcal{B}$. Therefore, $exp(y).{\mathcal{D}}_{+}$ is unbounded. $\square$

Theorem 4.5

(Convexity theorem for conformal balls) If $g\in G$ is such that $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$, then $g{\mathcal{D}}_{+}$ is convex. If $g.{\mathcal{D}}_{+}$ is relatively compact in $\mathcal{B}$, then there exists an element $p\in P^{+}$ with $g.{\mathcal{D}}_{+}=p.{\mathcal{D}}_{+}$, so that $g.{\mathcal{D}}_{+}$ is an affine image of ${\mathcal{D}}_{+}$.

Proof

If $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is relatively compact, then Proposition 4.4(b) and its proof imply the existence of $p\in P^{+}$ with $g.{\mathcal{D}}_{+}=p.{\mathcal{D}}_{+}$. In particular $g.{\mathcal{D}}_{+}$ is an affine image of ${\mathcal{D}}_{+}$ and therefore convex.

If $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is not relatively compact, then we put $r_n:=1-\frac{1}{n}$. Now

$$\begin{array}{c}\hfill expy.{\mathcal{D}}_{+}=\bigcup _{n\in \mathbb{N}}expyexp(r_n{\mathcal{D}}_{\mathfrak{g}})P^{-}\end{array}$$

is an increasing union. Therefore it suffices to show that the subsets $expyexp(r_n{\mathcal{D}}_{\mathfrak{g}})P^{-}$ are convex. For $r_n=e^t$ we have

$$\begin{array}{cc}\hfill e^{-t}·(expyexp(r_n{\mathcal{D}}_{\mathfrak{g}})P^{-})& =exp(-th).(exp(y)exp(r_n{\mathcal{D}}_{\mathfrak{g}})P^{-})\hfill \\ \hfill & =exp(e^{t}y).exp(e^{-t}{r}_n{\mathcal{D}}_{\mathfrak{g}})P^{-}=exp(r_{n}y).{\mathcal{D}}_{+},\hfill \end{array}$$

and these sets are convex by the preceding argument. $\square$

Example 4.6

We consider $G={\text{SO}}_{1,d}{(\mathbb{R})}_e$ as the identity component of the conformal group of the Euclidean space ${\mathbb{R}}^{d-1}$, $H=G_{{\mathbf{e}}_1}={\text{SO}}_{1,d-1}(\mathbb{R})$, and the Euler element $h\in {\mathfrak{so}}_{1,1}(\mathbb{R})$ with $h.{\mathbf{e}}_0={\mathbf{e}}_1$ and $h.{\mathbf{e}}_1={\mathbf{e}}_0$. As $Z({\text{SO}}_{1,d-1}(\mathbb{R}))\subseteq \{\pm \mathbf{1}\}$ and G preserves the positive light cone, the center of G is trivial.

The symmetric space $M=G/H\cong G.{\mathbf{e}}_1\cong {\text{dS}}^d$ is d-dimensional de Sitter space, $P=N^{-}⋊G^h$ is the stabilizer of the positive light ray ${\mathbb{R}}_{+}({\mathbf{e}}_0-{\mathbf{e}}_1)$, and $G/P\cong {\mathbb{S}}^{d-1}$ is the sphere of positive light rays. On the sphere ${\mathbb{S}}^{d-1}$, the subgroup H has two open orbits which are positive half-spheres separated by the sphere ${\mathbb{S}}^{d-2}$ of positive light rays in the subspace ${\mathbf{e}}_1^{\perp }$.

In the sphere the Bruhat cells are the point complements and if $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}\cong {\mathbb{R}}^{d-1}$, then the convexity of $g.{\mathcal{D}}_{+}$ is well-known from conformal geometry because conformal images of balls are balls or half spaces.

The subset realization of the ordered space $M=G/H$

As before G is assumed to be a connected semisimple Lie group. To simplify the notation, we write $\mathcal{M}$ for ${\mathcal{M}}_{+}=G/P^{-}$. Recall the following fact about the compression semigroup of the H-orbit ${\mathcal{D}}_{+}=H.e{P}^{-}\subseteq {\mathcal{M}}_{+}$, which is the Riemannian symmetric space $H/H\cap K$.

Lemma 4.7

The compression semigroup of the open H-orbit ${\mathcal{D}}_{+}=H.e{P}^{-}\subseteq G/P^{-}$ is

$$\begin{array}{c}\hfill \text{comp}({\mathcal{D}}_{+})=\{g\in G:g.{\mathcal{D}}_{+}\subseteq {\mathcal{D}}_{+}\}=Hexp(-C_{\mathfrak{q}}^{\text{max}}(h)),\end{array}$$ 4.9

Proof

This result was announced in [57, 58], and a detailed proof was given in [24, Thm. VI.11] for the case where $G\subseteq G_{\mathbb{C}}$, $G_{\mathbb{C}}$ is simply connected and $H=G^{\tau }$. In this case $\text{Ad}(G^{\tau })$ preserves $C_{\mathfrak{q}}^{\text{max}}(h)$, so that $G^{\tau }\subseteq K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$. Conversely, $K^h$ leaves ${\mathcal{D}}_{+}$ invariant, so that we obtain $G^{\tau }=H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$ in this particular case.

To see that the lemma also holds in the general case, note that the center of G acts trivially on $G/P^{-}$ and that $Z(G)\subseteq K^h\subseteq H$. Therefore, the general assertion follows if the equality (4.9) holds at least for one connected Lie group G with Lie algebra $\mathfrak{g}$. Hence, it follows from the special case discussed above. $\square$

We now use this to realize G/H as an ordered symmetric space as a set of subsets of $\mathcal{M}$ and describe the ordering in that realization.

Proposition 4.8

(The subset realization of ncc symmetric spaces) Let G be a connected semisimple Lie group, $h\in \mathfrak{g}$ an Euler element, $\theta$ a Cartan involution with $\theta (h)=-h$ and $\tau :=\theta {\tau }_h$, so that $(\mathfrak{g},\tau )$ is a ncc symmetric Lie algebras with $\mathfrak{g}={\mathfrak{g}}_s$. Let ${\mathcal{D}}_{+}\subseteq G/P^{-}$ be the open orbit of the base point under $H:=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$. We endow the homogeneous space

$$\begin{array}{c}\hfill M_{{\mathcal{D}}_{+}}:=\{g.{\mathcal{D}}_{+}:g\in G\},\end{array}$$

consisting of subsets of $\mathcal{M}$, with the inclusion order. Then the stabilizer subgroup $G^{{\mathcal{D}}_{+}}$ of the base point is H. The map $gH\mapsto g.{\mathcal{D}}_{+}$ induces an isomorphism

$$\begin{array}{c}\hfill (M_{{\mathcal{D}}_{+}},\subseteq )\cong (G/H,C_{\mathfrak{q}}^{\text{max}}(h))\end{array}$$

of ncc symmetric spaces, where $C_{\mathfrak{q}}^{\text{max}}(h)$ is the unique maximal $\text{Ad}(H)$-invariant cone in $\mathfrak{q}$ containing h in its interior.

In this identification, the set $\{x\in G/H:x\ge eH\}$ is mapped to $\{s^{-1}{\mathcal{D}}_{+}:s\in \text{comp}({\mathcal{D}}_{+})\}$ and $\{x\in G/H:x\le eH\}$ is mapped to $\{s{\mathcal{D}}_{+}:s\in \text{comp}({\mathcal{D}}_{+})\}$. In particular, $gH\ge eH$ is equivalent to ${\mathcal{D}}_{+}\subset g.{\mathcal{D}}_{+}$ and $eH\ge gH$ to $g.{\mathcal{D}}_{+}\subset {\mathcal{D}}_{+}$.

Proof

This follows from Lemma 4.7. $\square$

Remark 4.9

(The Riemannian case) Let $(\mathfrak{g},\theta )$ be a Riemannian symmetric Lie algebra, i.e., $\mathfrak{g}={\mathfrak{g}}_r$. Then $H=K$, $M=G/K$ and $h=0$. Thus $G=P^{-}$ and $G/P^{-}$ is a single point. Hence $\text{comp}({\mathcal{D}}_{+})=G$ and ${\mathcal{M}}_{{\mathcal{D}}_{+}}$ is a single point. Therefore, Riemannian summands cannot be permitted in Proposition 4.8.

Example 4.10

Let $G={\text{SL}}_2(\mathbb{R})$ and $h=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$. Then, the canonical action of G on ${\mathbb{P}}_1(\mathbb{R})=\mathbb{P}({\mathbb{R}}^2)\cong {\mathbb{S}}^1=\mathbb{R}\cup \{\infty \}$ is given by

$$\begin{array}{c}\hfill \left(\begin{array}{cc}a& b\\ c& d\end{array}\right).x=\frac{ax+b}{cx+d}\end{array}$$

and the stabilizer of 0 is

$$\begin{array}{c}\hfill P^{-}=\{\left(\begin{array}{cc}a& 0\\ c& a^{-1}\end{array}\right):a\ne 0,c\in \mathbb{R}\}=exp({\mathfrak{g}}_{-1}(h))⋊G^h,G^h=\{\left(\begin{array}{cc}a& 0\\ 0& a^{-1}\end{array}\right)\}\cong {\mathbb{R}}^{\times }.\end{array}$$

The 1-parameter group

$$\begin{array}{c}\hfill a_t=\left(\begin{array}{cc}cosht& sinht\\ sinht& cosht\end{array}\right)\end{array}$$

fixes $\pm 1$ and the orbit ${\mathcal{D}}_{+}=H.0$ of $H=\{\pm a_t:t\in \mathbb{R}\}$ is the open unit interval ${\mathcal{D}}_{+}=(-1,1)$. The maximal cone in $\mathfrak{q}$ is generated by $\text{Ad}(H){\mathbb{R}}_{+}h$.

Since elements of ${\mathbb{P}}_1(\mathbb{R})$ represent one-dimensional linear subspaces of ${\mathbb{R}}^2$ and ${\text{SL}}_2(\mathbb{R})$ acts transitively on triples of such subspaces, it follows easily that it acts transitively on the set of non-dense open intervals $I\subseteq {\mathbb{S}}^1$, the ordered space G/H can be identified with the ordered set of open non-dense intervals in ${\mathbb{S}}^1$.

Example 4.11

A special case of the above construction is the “complex case” where H is a connected semisimple Lie group of hermitian type contained in a complex Lie group G with Lie algebra ${\mathfrak{h}}_{\mathbb{C}}=\mathfrak{h}\oplus i\mathfrak{h}$. Then, G/H is a ncc symmetric space. Let ${\theta }_H$ be a Cartan involution on H. Then ${\theta }_H$ extends to a Cartan involution $\theta$ on G. Denote the corresponding maximal compact subgroup of G by K. Then $H\cap K$ is a maximal compact subgroup of H and the Riemannian symmetric space $H/H\cap K$ can be realized as complex symmetric bounded domain ${\mathcal{D}}_{+}\subseteq G/P^{-}$. Let $z_0\in \mathfrak{z}(\mathfrak{h}\cap \mathfrak{k})$ be the element determining the complex structure on $H/H\cap K$. Then $h=-i{z}_0$ is an Euler element in $\mathfrak{q}=i\mathfrak{h}$. Now (4.1) is the Harish–Chandra realization of $H/H\cap K$ as ${\mathcal{D}}_{+}$ in $G/P^{-}$ (see [60, p. 58] or [22, Ch. VII] for details).

Suppose that the complex conjugation $\tau$ of $\mathfrak{g}$ with respect to $\mathfrak{h}$ integrates to an involution ${\tau }^G$ on G. This is the case if G is simply connected or if $G=\text{Inn}\mathfrak{g}$. We then assume that $H=G_e^G$. If G is simply connected, then $H=G^G$ is connected and [24, Thm. VI.11] implies that $H=G^{{\mathcal{D}}_{+}}$, where $G^{{\mathcal{D}}_{+}}$ is the stabilizer of the base point ${\mathcal{D}}_{+}$.

But in general, if G is not simply connected, then $G^{{\mathcal{D}}_{+}}$ and $G^G$ may differ.

As an example, consider $H={\text{PSL}}_2(\mathbb{R})\subseteq G={\text{PSL}}_2(\mathbb{C})\cong \text{Inn}(\mathfrak{g})$ and note that ${\tau }^G(g)=\tau g\tau$ in this case. Then

$$\begin{array}{c}\hfill G^G={\text{PSL}}_2{(\mathbb{C})}^G\cong {\text{PGL}}_2(\mathbb{R})\cong \text{Aut}({\mathfrak{sl}}_2(\mathbb{R})),\end{array}$$

which is not connected because it also contains the image of $\left(\begin{array}{cc}i& 0\\ 0& -i\end{array}\right)$. The domain ${\mathcal{D}}_{+}=H.i\subseteq {\mathbb{C}}_{\infty }$ (the Riemann sphere) is the upper half plane and the stabilizer subgroup of ${\mathcal{D}}_{+}$ is

$$\begin{array}{c}\hfill G^{{\mathcal{D}}_{+}}={\text{PSL}}_2(\mathbb{R})\ne {\text{PGL}}_2(\mathbb{R})=G^G.\end{array}$$

The reflections in ${\text{GL}}_2(\mathbb{R})$ exchange the two open H-orbits.

Remark 4.12

The flag manifolds $\mathcal{M}=G/P^{-}\cong K/K^h$ appearing in this section are compact symmetric spaces on which the maximal compactly embedded subgroup $K\subseteq G$ acts by automorphisms. These spaces are called symmetric R-spaces.

Defining a symmetric R-space as a compact symmetric space $\mathcal{M}$ which is a real flag manifold, Loos shows in [37, Satz 1] that this implies the existence of an Euler element $h\in \mathcal{E}(\mathfrak{g})$ such that $\mathcal{M}\cong G/P^{-}$, so that $\mathcal{M}\cong K/K\cap P^{-}=K/K^h$ as a Riemannian symmetric space (see [41, §7.2] for more details).

If G is hermitian of tube type, then $\mathcal{M}\cong K/K^h$ can be identified with the Šhilov boundary of the corresponding bounded symmetric domain ${\mathcal{D}}_G\cong G/K$, and this leads to a G-invariant causal structure on $\mathcal{M}$. As $\text{dim}Z(K)=1$, with respect to the K-action, we have a natural 1-parameter family of K-invariant Lorentzian structures on $\mathcal{M}$. They correspond to $K^h$-invariant Lorentzian forms on $T_{e{K}^h}(\mathcal{M})\cong {\mathfrak{q}}_{\mathfrak{k}}=\mathfrak{z}(\mathfrak{k})\oplus [{\mathfrak{h}}_{\mathfrak{k}},{\mathfrak{q}}_{\mathfrak{k}}]$ which are positive definite on $\mathfrak{z}(\mathfrak{k})$ and negative definite on its orthogonal space $[{\mathfrak{h}}_{\mathfrak{k}},{\mathfrak{q}}_{\mathfrak{k}}]$.

Observer domains associated with modular geodesics

In this section, we associate to any modular causal geodesic $\gamma$ in an ncc semisimple symmetric space $M=G/H$ an observer domain $W(\gamma )$. It is an open connected subset of M invariant under the centralizer $G^h$ of the corresponding causal Euler element h. We then show that, for $h\in C^{\circ }$, the domain $W(\gamma )$ coincides with the connected component $W\subseteq W_M^{+}(h)$ of the base point eH of the corresponding positivity domain. In Sect. 6, we show that $W_M^{+}(h)$ is connected for $G=\text{Inn}(\mathfrak{g})$, which implies that $W=W_M^{+}(h)$ in this case.

Definition 5.1

Let $(G,{\tau }^G,H,C)$ be a non-compactly causal symmetric Lie group and $M=G/H$ be the corresponding ncc symmetric space. We assume that $\mathfrak{g}={\mathfrak{g}}_s$, i.e., that $(\mathfrak{g},\tau )$ is a direct sum of irreducible ncc symmetric Lie algebras.

(a) We write $\le$ for the order on M defined by the closed Olshanski semigroup $S=Hexp(C)=exp(C)H$ which always exists because $\mathfrak{z}(\mathfrak{g})=\{0\}$ ([30, Thm. 3.1] or Theorem C.1in Appendix C) via

$$\begin{array}{c}\hfill g_{1}H\le g_{2}H\text{if}{g}_1^{-1}{g}_2\in SH/H={\text{Exp}}_{\mathit{eH}}(C)\end{array}$$

and write order intervals as

$$\begin{array}{c}\hfill [x,y]=\{z\in M:x\le z\le y\}=\uparrow x\cap \downarrow y,\end{array}$$

where

$$\begin{array}{c}\hfill \uparrow x=\{z\in M:x\le z\}\text{and}\downarrow y=\{z\in M:z\le y\}.\end{array}$$

(b) A subset $X\subseteq M$ is called order convex if

$$\begin{array}{c}\hfill [a,b]\subseteq X\text{for}a,b\in X.\end{array}$$

As the intersection of order convex subsets is order convex, we can defined the order convex hull

$$\begin{array}{c}\hfill \text{oconv}(D):=\bigcap \{D^{\prime }\subseteq M:D\subseteq D^{\prime },D^{\prime }\text{order}\text{convex}\}.\end{array}$$

Clearly $\text{oconv}(D)$ is the smallest order convex subset of X containing D.

(c) For a modular geodesic $\gamma :\mathbb{R}\to M$, we call

$$\begin{array}{c}\hfill W(\gamma ):=\downarrow \gamma (\mathbb{R})\cap \uparrow \gamma (\mathbb{R})=\bigcup _{t<s}[\gamma (t),\gamma (s)]\end{array}$$

the observer domain associated to $\gamma$. Note that this domain depends on the cone $C\subseteq \mathfrak{q}$ specifying the order on M.

Lemma 5.2

The subset $W(\gamma )$ has the following properties:

1. $W(\gamma )\subseteq M$ is open and connected.

2. $W(\gamma )=\text{oconv}(M_{\mathit{eH}}^h)$ for $M_{\mathit{eH}}^h={\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}})$.

3. Suppose that $H_K=K^h$ and $C=C_{\mathfrak{q}}^{\text{max}}$ and identify $M=G/H$ with $M_{{\mathcal{D}}_{+}}$ (Proposition 4.8). Then

   $$\begin{array}{c}\hfill W(\gamma )=\{g.{\mathcal{D}}_{+}:0\in g.{\mathcal{D}}_{+},g.{\mathcal{D}}_{+}\text{bounded}\}\end{array}$$ 5.1

   and this domain is $G^h$-invariant.

Proof

(a) To see that $W(\gamma )$ is open, we first observe that $\gamma (s)\in {(\uparrow \gamma (t))}^{\circ }$ for $t<s$. For real numbers $t_j\in \mathbb{R}$ with $t_1<t_2<t_3<t_4$, this implies that

$$\begin{array}{c}\hfill [\gamma (t_2),\gamma (t_3)]\subseteq {[\gamma (t_1),\gamma (t_4)]}^{\circ }.\end{array}$$

This shows that $W(\gamma )$ is open.

To see that $W(\gamma )$ is connected, we recall that the order on M is globally hyperbolic, in particular all order intervals [x, y] are compact. As all elements $z\in [x,y]$ lie on causal curves from x to y ([23, Thm. 4.29]), the order intervals are pathwise connected. As an increasing union of the order intervals $[\gamma (-n),\gamma (n)]$, the wedge domain $W(\gamma )$ is connected.

(b) Order intervals are convex and directed unions of convex sets of convex. Therefore,

$$\begin{array}{c}\hfill W(\gamma )=\bigcup _{t<s}[\gamma (t),\gamma (s)]\end{array}$$

is convex, whence $W(\gamma )=\text{oconv}(\gamma (\mathbb{R})).$

From the fact that h is central in ${\mathfrak{h}}_{\mathfrak{k}}+{\mathfrak{q}}_{\mathfrak{p}}$, it easily follows that, in the symmetric space $M_{\mathit{eH}}^h={\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}})$ the geodesic line $\gamma (\mathbb{R})$ is cofinal in both directions because we have in $\mathfrak{q}$:

$$\begin{array}{c}\hfill \bigcup _{s<t}(sh+C)\cap (th-C)\supseteq \mathfrak{q}.\end{array}$$

For $x\in {\mathfrak{q}}_{\mathfrak{p}}$, we thus find $s,t\in \mathbb{R}$ with $x\in sh+C^{\circ }$ and $x\in st-C^{\circ }$. Then

$$\begin{array}{c}\hfill \text{Exp}(sh)<\text{Exp}(x)<\text{Exp}(th)\end{array}$$

in $M_e^h$. This implies that

$$\begin{array}{c}\hfill W(\gamma )\supseteq {\text{Exp}}_{\mathit{eH}}({\mathfrak{q}}_{\mathfrak{p}})=M_{\mathit{eH}}^h=G_e^h.eH\supseteq \gamma (\mathbb{R}).\end{array}$$

This completes the proof.

(c) The modular group acts on $\mathcal{B}\cong N^{+}.e{P}^{-}\subseteq G/P^{-}$ by $exp(th).x=e^{t}x$. Therefore $\gamma (t)=e^t{\mathcal{D}}_{+}$ enlarges ${\mathcal{D}}_{+}$ for $t>0$ and shrinks ${\mathcal{D}}_{+}$ for $t<0$ (Theorem 4.5). As $\gamma$ is strictly increasing, this implies that

$$\begin{array}{c}\hfill \downarrow \gamma (\mathbb{R})=\{g.{\mathcal{D}}_{+}:(\exists t\in \mathbb{R})g.{\mathcal{D}}_{+}\subseteq e^t{\mathcal{D}}_{+}\}=\{g.{\mathcal{D}}_{+}:g.{\mathcal{D}}_{+}\text{bounded}\text{in}\mathcal{B}\}.\end{array}$$

Further

$$\begin{array}{c}\hfill \uparrow \gamma (\mathbb{R})=\{g.{\mathcal{D}}_{+}:(\exists t\in \mathbb{R})g.{\mathcal{D}}_{+}\supseteq e^t{\mathcal{D}}_{+}\}=\{g.{\mathcal{D}}_{+}:0\in g.{\mathcal{D}}_{+}\},\end{array}$$

so that (5.1) follows. As any $g\in G^h=P^{+}\cap P^{-}$ acts by linear maps on the Bruhat cell $\mathcal{B}\cong {\mathfrak{g}}_1(h)$, (5.1) implies that $G^h$ leaves the set $W(\gamma )$ of all bounded domains $g.{\mathcal{D}}_{+}$ containing 0 invariant. $\square$

Example 5.3

(de Sitter space) We consider de Sitter space

$$\begin{array}{c}\hfill M={\text{dS}}^d=\{(x_0,\mathbf{x})\in {\mathbb{R}}^{1,d}:\beta (x,x)=-1\},\text{where}\beta (x,y)=x_0{y}_0-\mathbf{x}\mathbf{y}\end{array}$$

is the canonical Lorentzian form on ${\mathbb{R}}^{1,d}$ (cf. Sect. D). Here

$$\begin{array}{c}\hfill G={\text{SO}}_{1,d}{(\mathbb{R})}^{\uparrow }={\text{SO}}_{1,d}{(\mathbb{R})}_e,H=G_{{\mathbf{e}}_1}={\text{SO}}_{1,d-1}{(\mathbb{R})}^{\uparrow }\end{array}$$

and

$$\begin{array}{c}\hfill C\subseteq T_{{\mathbf{e}}_1}(M)={\mathbf{e}}_1^{\perp }\text{given}\text{by}C=\{(x_0,\mathbf{x}):x_1=0,x_0\ge 0,x_0^2\ge {\mathbf{x}}^2\}.\end{array}$$

We claim that, for the modular geodesic

$$\begin{array}{c}\hfill \gamma (t)=cosh(t){\mathbf{e}}_1+sinh(t){\mathbf{e}}_0=e^{\mathit{th}}{\mathbf{e}}_1,\end{array}$$

we have

$$\begin{array}{c}\hfill W(\gamma )=W_{{\text{dS}}^d}(h)=\{x\in {\text{dS}}^d:x_1>|x_0|\}=W_R\cap {\text{dS}}^d,\end{array}$$ 5.2

where $W_R=\{(x_0,\mathbf{x}):x_1>|x_0|\}$ (cf. Appendix D in [52]). As the right wedge $W_R\subseteq {\mathbb{R}}^{1,d}$ is causally complete, we clearly have $W(\gamma )\subseteq W_R\cap {\text{dS}}^d=W_{{\text{dS}}^d}(h)$. For the converse inclusion, let $x\in W_R$. We have to find a $t\in \mathbb{R}$ with $x\le \gamma (t)$, i.e.,

$$\begin{array}{c}\hfill x_0<\gamma {(t)}_0=sinh(t)\end{array}$$

and

$$\begin{array}{c}\hfill 0<\beta (\gamma (t)-x,\gamma (t)-x)={(sinh(t)-x_0)}^2-{(cosh(t)-x_1)}^2-x_2^2-\cdots -x_d^2.\end{array}$$

Since $\beta (\gamma (t),\gamma (t))=-1$, we obtain for the right hand side

$$\begin{array}{cc}\hfill \beta (\gamma (t)-x,\gamma (t)-x)=& \beta (\gamma (t),\gamma (t))-2\beta (\gamma (t),x)+\beta (x,x)\hfill \\ \hfill =& -1-2\beta (\gamma (t),x)+\beta (x,x).\hfill \end{array}$$

Further

$$\begin{array}{c}\hfill -2\beta (\gamma (t),x)=2x_{1}cosh(t)-2x_{0}sinh(t)\approx e^t(x_1-x_0)\text{for}t>>0,\end{array}$$

and if $x_1>|x_0|$, this expression is arbitrarily large for $t\to \infty$. This shows that $W_R\subseteq \downarrow \gamma (\mathbb{R})$, and we likewise see that $W_R\subseteq \uparrow \gamma (\mathbb{R})$.

Proposition 5.4

If $H_K=K^h$ and $C=C_{\mathfrak{q}}^{\text{max}}$, then

1. $W(\gamma )\subseteq W=W_M^{+}{(h)}_{\mathit{eH}}$.

2. $h+{\mathcal{D}}_{\mathfrak{g}}\subseteq \mathfrak{h}+C^{\circ }$.

Proof

If $gH\in W(\gamma )\subseteq G/H$, then the corresponding subset $g.{\mathcal{D}}_{+}\subseteq \mathcal{B}$ is convex by Theorem 4.5, and it contains 0 by (5.1). Therefore the curve

$$\begin{array}{c}\hfill \eta :\mathbb{R}\to M,\eta (t):=exp(th)gH\end{array}$$

is increasing because $t\mapsto e^{t}g.{\mathcal{D}}_{+}$ is an increasing family of subsets of $\mathcal{B}$. The invariance of the order thus implies that

$$\begin{array}{c}\hfill g^{-1}.{\eta }^{\prime }(0)=p_{\mathfrak{q}}(\text{Ad}{(g)}^{-1}h)\in C_{\mathfrak{q}}^{\text{max}}.\end{array}$$

We also know that $g.{\mathcal{D}}_{+}\in P^{+}.{\mathcal{D}}_{+}$ (Theorem 4.5 and Lemma 5.2(c)), so that there exist $g_1\in G^h$ and $y\in {\mathfrak{g}}_1(h)$ with $g.H=g_{1}exp(y).H$. Thus

$$\begin{array}{c}\hfill \text{Ad}{(g)}^{-1}h\in \text{Ad}(H)e^{-\text{ad}y}h\in \mathfrak{h}+C_{\mathfrak{q}}^{\text{max}},\end{array}$$ 5.3

and therefore

$$\begin{array}{c}\hfill e^{-\text{ad}y}h=h-[y,h]=h+y\in \mathfrak{h}+C_{\mathfrak{q}}^{\text{max}}.\end{array}$$

Recall the definition of ${\mathcal{D}}_{\mathfrak{g}}$ in (4.7). The condition

$$\begin{array}{c}\hfill e{P}^{-}\in g.{\mathcal{D}}_{+}=g_{1}exp(y).{\mathcal{D}}_{+}=g_1.exp(y+{\mathcal{D}}_{\mathfrak{g}})P^{-}\end{array}$$

is equivalent to $-y\in {\mathcal{D}}_{\mathfrak{g}}=-{\mathcal{D}}_{\mathfrak{g}}$, showing that

$$\begin{array}{c}\hfill W(\gamma )=G^{h}exp({\mathcal{D}}_{\mathfrak{g}}).{\mathcal{D}}_{+}\subseteq M_{{\mathcal{D}}_{+}}\end{array}$$ 5.4

(cf. Lemma 5.2(c)). We therefore derive from (5.3) that $h+{\mathcal{D}}_{\mathfrak{g}}\subseteq \mathfrak{h}+C_{\mathfrak{q}}^{\text{max}},$ and since $h\in C_{\mathfrak{q}}^{\max ,\circ }$ and ${\mathcal{D}}_{+}$ is starlike with respect to 0, we obtain

$$\begin{array}{c}\hfill h+{\mathcal{D}}_{\mathfrak{g}}\subseteq \mathfrak{h}+C_{\mathfrak{q}}^{\max ,\circ }.\end{array}$$ 5.5

We thus obtain $\text{Ad}{(g)}^{-1}.h\in \mathfrak{h}+C_{\mathfrak{q}}^{\max ,\circ }$, i.e., $gH\in W_M^{+}(h)$. This shows that $W(\gamma )\subseteq W_M^{+}(h)$, and the connectedness of $W(\gamma )$ (Lemma 5.2(a)) yields $W(\gamma )\subseteq W$. $\square$

Remark 5.5

From (5.4) it follows that, as a subset of M,

$$\begin{array}{c}\hfill W(\gamma )=G^{h}exp({\mathcal{D}}_{\mathfrak{g}}).H=G_e^{h}exp({\mathcal{D}}_{\mathfrak{g}}).H.\end{array}$$ 5.6

For the quotient map $q:G\to G/H$, this means that

$$\begin{array}{c}\hfill q^{-1}(W(\gamma ))=G^{h}exp({\mathcal{D}}_{\mathfrak{g}})H\subseteq G.\end{array}$$

This is a $G^h\times H$-invariant domain in G specified by its intersection with the abelian subgroup $N^{+}=exp({\mathfrak{g}}_1(h))$; see [41, Rem. 6.2].

Combined with Theorem 7.1, that asserts the connectedness of $W_M^{+}(h)$, the following result implies that $W_M^{+}(h)\subseteq W(\gamma )$.

Proposition 5.6

If $H_K=K^h$ and $C=C_{\mathfrak{q}}^{\text{max}}$, then $W\subseteq W(\gamma )$.

Proof

As both sides are $G_e^h$-invariant (Lemma 5.2), the Positivity Domain Theorem (Theorem 3.6) implies that we have to verify the inclusion

$$\begin{array}{c}\hfill {\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq W(\gamma ).\end{array}$$

Invariance of both sides under ${(H_K)}_e$ and $\text{Ad}({(H_K)}_e){\mathfrak{t}}_{\mathfrak{q}}={\mathfrak{q}}_{\mathfrak{k}}$ further reduce the problem to the inclusion

$$\begin{array}{c}\hfill {\text{Exp}}_{\mathit{eH}}({\mathrm{\Omega }}_{{\mathfrak{t}}_{\mathfrak{q}}})\subseteq W(\gamma ).\end{array}$$ 5.7

To this end, we use the Lie subalgebra $\mathfrak{l}\subseteq \mathfrak{g}$ generated by h and ${\mathfrak{t}}_{\mathfrak{q}}$ (Proposition 2.8). Then $[\mathfrak{l},\mathfrak{l}]\cong {\mathfrak{sl}}_2{(\mathbb{R})}^s$ and ${\mathfrak{t}}_{\mathfrak{q}}\cong {\mathfrak{so}}_2{(\mathbb{R})}^s$. This reduces the verification of the inclusion (5.7) to the case where $\mathfrak{g}={\mathfrak{sl}}_2{(\mathbb{R})}^s$, $\mathfrak{h}={\mathfrak{so}}_{1,1}{(\mathbb{R})}^s$ and ${\mathfrak{t}}_{\mathfrak{q}}\cong {\mathfrak{so}}_2{(\mathbb{R})}^s$.

As this is a product situation, it suffices to consider the case where

$$\begin{array}{c}\hfill \mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})\supseteq \mathfrak{h}={\mathfrak{so}}_{1,1}(\mathbb{R}),{\mathfrak{t}}_{\mathfrak{q}}={\mathfrak{so}}_2(\mathbb{R})\text{and}h=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).\end{array}$$

By (5.6), we have to show that

$$\begin{array}{c}\hfill exp(tx)\in G_e^{h}exp({\mathcal{D}}_{\mathfrak{g}})H\text{for}|t|<\pi /2\text{and}x=\frac{1}{2}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right).\end{array}$$ 5.8

We identify ${\mathfrak{sl}}_2(\mathbb{R})$ with 3-dimensional Minkowski space ${\mathbb{R}}^{1,2}$, via

$$\begin{array}{c}\hfill {\mathbf{e}}_0:=\frac{1}{2}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right),{\mathbf{e}}_1:=\frac{1}{2}\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\mathbf{e}}_2:=h=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).\end{array}$$

In the centerfree group $G:=\text{Inn}(\mathfrak{g})\cong {\text{SO}}_{1,2}{(\mathbb{R})}_e$, we have

$$\begin{array}{c}\hfill K:=G_{{\mathbf{e}}_0}\cong {\text{SO}}_2(\mathbb{R})\text{and}{K}^h=\{e\}=H_K,\end{array}$$

so that $H:=G_{{\mathbf{e}}_1}=exp({\mathfrak{h}}_{\mathfrak{p}})={\text{SO}}_{1,1}{(\mathbb{R})}_e$ is connected. Therefore, $G/H\cong G.{\mathbf{e}}_1={\text{dS}}^2$ (de Sitter space) and $exp(tx)H$ corresponds to

$$\begin{array}{c}\hfill exp(tx).{\mathbf{e}}_1=cos(t){\mathbf{e}}_1+sin(t){\mathbf{e}}_2.\end{array}$$

Now $|t|<\pi /2$ implies $cos(t)>0$, hence that

$$\begin{array}{c}\hfill exp(tx).{\mathbf{e}}_1\in W_{{\text{dS}}^2}(\gamma )\text{for}\gamma (t)=cos(t){\mathbf{e}}_1+sin(t){\mathbf{e}}_0\end{array}$$ 5.9

(Example 5.3). We write elements of ${\mathcal{D}}_{+}$ as $y=se$, $|s|<1$ (see Example 4.3). Then $exp(y).{\mathbf{e}}_1$ corresponds to

$$\begin{array}{cc}\hfill e^{\text{ad}y}.\frac{1}{2}(e+f)& =\frac{1}{2}{e}^{\text{ad}se}(e+f)=\frac{1}{2}(e+e^{\text{ad}se}f)=\frac{1}{2}(e+f+s[e,f]+\frac{s^2}{2}[e,[e,f]])\hfill \\ \hfill & =\frac{1}{2}(e+f)+sh+\frac{s^2}{2}[e,h]=\frac{1}{2}(e+f)+sh-\frac{s^2}{2}e,\hfill \end{array}$$

so that

$$\begin{array}{c}\hfill exp(y).{\mathbf{e}}_1={\mathbf{e}}_1+s{\mathbf{e}}_2-\frac{s^2}{2}({\mathbf{e}}_1-{\mathbf{e}}_0)=(\frac{s^2}{2},1-\frac{s^2}{2},s).\end{array}$$

This element lies in the wedge domain $W_{{\text{dS}}^2}(h)$ if and only if $1-s^2/2>s^2/2$ (Example 5.3), which is equivalent to $|s|<1$. Then its $G_e^h$-orbit contains the element $(0,\sqrt{1-s^2},s)$. For $|t|<\pi /2$, the element $exp(tx).{\mathbf{e}}_1$ is of this form, showing that $exp(tx)\in G^{h}exp(y)H$. This completes the proof. $\square$

Combining the preceding two propositions, we get the main result of this section. It shows that the observer domain $W(\gamma )$ coincides with a connected component of the positivity domain $W_M^{+}(h)$. This result provides two complementary perspectives on this domain.

Theorem 5.7

(Observer Domain Theorem) Let $(\mathfrak{g},\tau ,C)$ be a non-compactly causal semisimple symmetric Lie algebra with causal Euler element $h\in C^{\circ }\cap {\mathfrak{q}}_{\mathfrak{p}}$ with $\tau ={\tau }_h\theta$ and let G be a connected Lie group with Lie algebra $\mathfrak{g}$ and $H:=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$. If $C=C_{\mathfrak{q}}^{\text{max}}$, then $W=W(\gamma )$.

We can even extend this result to coverings:

Corollary 7.2

If $H^{\prime }\subseteq H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$ is an open subgroup and $C=C_{\mathfrak{q}}^{\text{max}}$, then $W^{\prime }:=W_{M^{\prime }}^{+}{(h)}_{e{H}^{\prime }}=W(\tilde{\gamma })$ holds in $M^{\prime }=G/H^{\prime }$ for $\tilde{\gamma }(t):={\text{Exp}}_{e{H}^{\prime }}(th)$.

Proof

Let $q:M^{\prime }=G/H^{\prime }\to G/H\cong M_{{\mathcal{D}}_{+}}$ be the canonical equivariant covering from [41, Lemma 7.11].

First we show that $W^{\prime }\subseteq M^{\prime }$ is order convex. So let $x\le y\le z$ in $M^{\prime }$ with $x,z\in W^{\prime }$ and let $\eta :[0,2]\to M^{\prime }$ be a causal curve with

$$\begin{array}{c}\hfill \eta (0)=x,\eta (1)=y,\eta (2)=z.\end{array}$$

Then $q(\eta (t))\in [q(x),q(z)]\subseteq W$ for $t\in [0,2]$ holds because $W=W(\gamma )$ is order convex in M.

As W is contractible by Theorem3.6(b), it is in particular simply connected. Therefore, $q^{-1}(W)$ is a disjoint union of open subsets ${(W_j^{\prime })}_{j\in J}$ mapped by q diffeomorphically onto W. By definition, $W^{\prime }$ is one such connected component, so that

$$\begin{array}{c}\hfill q_W{:=q|}_{W^{\prime }}:W^{\prime }\to W\end{array}$$

is a diffeomorphism. Therefore $\eta$ is the unique continuous lift of $q\circ \eta$ in $M^{\prime }$, hence contained in $W^{\prime }$. This implies that $y\in W^{\prime }$, so that $W^{\prime }$ is order convex.

As $q_W:W^{\prime }\to W$ is an isomorphism of causal manifolds, it also is an order isomorphism. Finally $W(\gamma )=\text{oconv}(\gamma (\mathbb{R}))=W$ implies that $W^{\prime }(\gamma )=\text{oconv}(\tilde{\gamma }(\mathbb{R}))=W^{\prime }$. $\square$

Remark 5.9

It is not clear to which extent $W(\gamma )$ depends on the specific cone C. In particular it would be interesting to see if the minimal and maximal cones lead to the same domain $W(\gamma )$. We have already seen that the positivity domain $W_M^{+}(h)$ depends non-trivially on the cone C ([41, Ex. 6.8]) so one may expect that this is also the case for $W(\gamma )$.

Lemma 5.10

The involution ${\tau }_M$ on M defined by ${\tau }_M(gH)={\tau }^G(g)H$ satisfies

$$\begin{array}{c}\hfill {\tau }_M(W_M^{+}(h))=W_M^{+}(h)\text{and}{\tau }_M(W(\gamma ))=W(\gamma ).\end{array}$$ 5.10

Proof

(a) The condition $gH\in W_M^{+}(h)$ is equivalent to $\text{Ad}{(g)}^{-1}h\in {\mathcal{T}}_C$ by (5.10), and this implies that

$$\begin{array}{c}\hfill \text{Ad}{(\tau (g))}^{-1}(-h)=\tau (\text{Ad}{(g)}^{-1}h)\in \tau ({\mathcal{T}}_C)=-{\mathcal{T}}_C,\end{array}$$

so that $\text{Ad}{(\tau (g))}^{-1}h\in {\mathcal{T}}_C$, i.e., ${\tau }_M(gH)\in W_M^{+}(h)$. As ${\tau }_M$ is an involution, it follows that ${\tau }_M(W_M^{+}(h))=W_M^{+}(h)$.

(b) As $\tau (C)=-C$, the involution ${\tau }_M$ reverses the causal structure on M. Moreover, ${\tau }_M(\gamma (t))=\gamma (-t)$, so that

$$\begin{array}{c}\hfill {\tau }_M(W(\gamma ))=\bigcup _{t<s}[{\tau }_M(\gamma (s)),{\tau }_M(\gamma (t))]=\bigcup _{t<s}[\gamma (-s),\gamma (-t)]=W(\gamma ).\end{array}$$

$\square$

We have seen above that, for the modular geodesic $\gamma (t)={\text{Exp}}_{\mathit{eH}}(th)$ in M, we have $W(\gamma )=W$. The modular geodesic $\gamma$ is a specific orbit of the modular flow inside W. Now we show that all other $\alpha$-orbits in W lead to the same “observer domain”.

Proposition 5.11

Let $m\in W$ and consider the curve

$$\begin{array}{c}\hfill \beta :\mathbb{R}\to W,\beta (t)={\alpha }_t(m)=exp(th).m.\end{array}$$

Then

$$\begin{array}{c}\hfill W=W(\beta )=\bigcup _{s<t}[\beta (s),\beta (t)].\end{array}$$ 5.11

Proof

Using the subset realization of $M=G/H$ as $M_{{\mathcal{D}}_{+}}=\{g.{\mathcal{D}}_{+}:g\in G\}$ from Proposition 4.8, we have

$$\begin{array}{c}\hfill W(\gamma )=\{g{\mathcal{D}}_{+}:0\in g.{\mathcal{D}}_{+},g.{\mathcal{D}}_{+}\text{bounded}\text{in}exp({\mathfrak{g}}_1(h)).P^{-}\}\end{array}$$

(Lemma 5.2(c)) and $W=W(\gamma )$ by Theorem 5.7. So we can write

$$\begin{array}{c}\hfill \beta (t)=e^t.{\mathcal{D}}^{\prime }\text{for}\text{some}{\mathcal{D}}^{\prime }\in W(\gamma ).\end{array}$$

As $\beta (\mathbb{R})\subseteq W(\gamma )$, the order convex hull $W(\beta )$ of $\beta (\mathbb{R})$ is contained in $W(\gamma )=W$. To verify the converse inclusion, let ${\mathcal{D}}^{\prime \prime }\in W$. Then $0\in {\mathcal{D}}^{\prime \prime }$, and since ${\mathcal{D}}^{\prime }$ is bounded, there exists a $t\in \mathbb{R}$ with $\beta (t)\subseteq {\mathcal{D}}^{\prime \prime }$. Likewise the boundedness of ${\mathcal{D}}^{\prime \prime }$ implies the existence of some $s\in \mathbb{R}$ with ${\mathcal{D}}^{\prime \prime }\subseteq \beta (s)$. Hence, ${\mathcal{D}}^{\prime \prime }\in [\beta (t),\beta (s)]\subseteq W(\beta )$. This shows that $W\subseteq W(\beta )$, and hence equality in (5.11). $\square$

Remark 5.12

A similar result also holds in Minkowski space. If

$$\mathbf{x}\in W_R=\{\mathbf{y}\in {\mathbb{R}}^{1,d}:y_1>|y_0|\}$$

and

$$\begin{array}{c}\hfill \beta (t)=e^{\mathit{th}}\mathbf{x}=(cosh(t)x_0+sinh(t)x_1,cosh(t)x_1+sinh(t)x_0,x_2,\dots ,x_d),\end{array}$$

then any other element $\mathbf{y}\in W_R$ satisfies $\mathbf{y}\in [\beta (t),\beta (s)]$ for suitable $t<s$, i.e., $\mathbf{y}-\beta (t)\in V_{+}$ and $\beta (s)-\mathbf{y}\in V_{+}$. In fact, $\beta {(t)}_0\sim e^t(x_0+x_1)\to \infty$ for $t\in \infty$ and $\beta (t_0)\sim e^{-t}(x_0-x_1)\to -\infty$ for $t\to -\infty$. Moreover, for $s\to \infty$

$$\begin{array}{cc}& {(cosh(s)x_0+sinh(s)x_1-y_0)}^2-{(cosh(s)x_1+sinh(s)x_0-y_1)}^2\hfill \\ \hfill & \sim (e^s\frac{x_0+x_1}{2}-y_0{)}^2-(e^s\frac{x_0+x_1}{2}-y_1{)}^2\sim e^s(x_0+x_1)(y_1-y_0)\to \infty \hfill \end{array}$$

and, for $t\to -\infty$,

$$\begin{array}{cc}& {(cosh(t)x_0+sinh(t)x_1-y_0)}^2-{(cosh(t)x_1+sinh(t)x_0-y_1)}^2\hfill \\ \hfill & \sim (e^{-t}\frac{x_0-x_1}{2}-y_0{)}^2-(e^{-t}\frac{x_1-x_0}{2}-y_1{)}^2\sim e^{-t}(x_0-x_1)(-y_0)-e^{-t}(x_1-x_0)(-y_1)\hfill \\ \hfill & =e^{-t}(x_1-x_0)(y_0+y_1)\to \infty .\hfill \end{array}$$

This shows that $W(\beta )=W_R$ for all integral curves of the modular flow in $W_R$.

Remark 5.13

On the de Sitter space $M={\text{dS}}^d\subseteq {\mathbb{R}}^{1.d}$, the involution ${\tau }_h$ can be implemented naturally by

$$\begin{array}{c}\hfill {\tau }_{h,M}(x)=(-x_0,-x_1,x_2,\dots ,x_d).\end{array}$$

This involution does not fix the base point ${\mathbf{e}}_1$, it reverses the causal structure and it commutes with modular flow. Accordingly, we have the relation

$$\begin{array}{c}\hfill {\tau }_{h,M}(W^{+}(h))=W^{+}(-h).\end{array}$$

As we shall see in the next section, such a relation can only be realized because $-h\in \text{Ad}(G)h$, i.e., the direction of the boost can be reversed by an element of G. If $-h\notin \text{Ad}(G)$ (h is not symmetric), then we shall see in Corollary 6.3 below that $W^{+}(-h)=\mathrm{\varnothing }$, so that there is no involution on M mapping $W^{+}(h)$ to $W^{+}(-h)$.

However, as ${\tau }_h=\tau \theta$ (as involutions on $\mathfrak{g}$), and there are natural implementations ${\tau }_M$ and ${\theta }_M$ on $M=G/H$, both fixing the base points, the involution ${\tau }_M{\theta }_M$ implements the involution ${\tau }_h$ on M and fixes the base point, but it also fixes the wedge region

$$\begin{array}{c}\hfill {\tau }_M{\theta }_M(W^{+}(h))=W^{+}(h)\end{array}$$

because it preserves h and the causal structure. This is not desirable because we would prefer that ${\tau }_h$ maps $W^{+}(h)$ to some “opposite” wedge region (cf. [38]). Possible ways to resolve this problem and ideas how to implement locality conditions on non-compactly causal symmetric spaces are briefly discussed in [41, §4.3].

Existence of positivity domains for Euler elements

In this section, we show that, for the maximal cone $C=C_{\mathfrak{q}}^{\text{max}}$ and a simple Lie algebra $\mathfrak{g}$, the real tube domain ${\mathcal{T}}_C=\mathfrak{h}+C^{\circ }$ intersects the set $\mathcal{E}(\mathfrak{g})$ of Euler elements in a connected subset (Theorem 6.1). This implies that, for an Euler element $h^{\prime }\in \mathfrak{g}$, the positivity domain $W_M^{+}(h^{\prime })$ is non-empty if and only if $h^{\prime }$ and h are conjugate (Corollary 6.3).

Theorem 6.1

Suppose that $(\mathfrak{g},\tau ,C)$ is an irreducible simple ncc symmetric Lie algebra with $C=C_{\mathfrak{q}}^{\text{max}}$, ${\mathcal{T}}_C:=\mathfrak{h}+C^{\circ }$, $G=\text{Inn}(\mathfrak{g})$, $H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$ and $M=G/H$. Then $\mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_C$ is connected and a subset of ${\mathcal{O}}_h$. More precisely,

$$\begin{array}{c}\hfill \mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_C={\mathcal{O}}_h\cap {\mathcal{T}}_C=\text{Ad}(H_e)(h+{\mathcal{D}}_{\mathfrak{g}}),\end{array}$$ 6.1

where ${\mathcal{D}}_{\mathfrak{g}}=\{u\in {\mathfrak{g}}_1(h):\Vert u\Vert <1\}$ is the open unit ball for which $exp({\mathcal{D}}_{\mathfrak{g}})P^{-}=H.P^{-}\subseteq G/P^{-}.$

Proof

We recall from Proposition 4.8 the open subsets ${\mathcal{D}}_{\pm }:=H.e{P}^{\mp }\subseteq G/P^{\mp }$ which are the open orbits of the base point under $H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$. Then

$$\begin{array}{c}\hfill \text{comp}({\mathcal{D}}_{\pm })=Hexp(\mp C)\end{array}$$

follows from Proposition 4.8, applied to the causal Euler element h and its negative. These semigroups have the Lie wedges

$$\begin{array}{c}\hfill \mathbf{L}(\text{comp}({\mathcal{D}}_{\pm }))=\mathfrak{h}\mp C.\end{array}$$

Let $x\in \mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_C$ for ${\mathcal{T}}_C=\mathfrak{h}+C^{\circ }=\mathbf{L}{(\text{comp}({\mathcal{D}}_{-}))}^{\circ }$. We then have $s_t:=exp(tx)\in \text{comp}{({\mathcal{D}}_{-})}^{\circ }$ for $t>0$. We conclude that $s_t(\overline{{\mathcal{D}}_{-}})\subseteq {\mathcal{D}}_{-}$ and that there exists a complete metric on ${\mathcal{D}}_{-}$ for which each $s_t$ is a strict contraction (cf. [48, Thm. II.4]),5 so that the Banach Fixed Point Theorem implies the existence of a unique attracting fixed point $m_{-}\in {\mathcal{D}}_{-}$ for the vector field $X_x^{G/P^{+}}\in \mathcal{V}(G/P^{+})$ defined by x. We now have

$$\begin{array}{c}\hfill m_{-}\in {\mathcal{D}}_{-}=H.e{P}^{+}=H_e.e{P}^{+}.\end{array}$$

Hence there exists $g_1\in H_e$ with $g_1.m_{-}=e{P}^{+}$, and thus

$$\begin{array}{c}\hfill y:=\text{Ad}(g_1)x\in {\mathfrak{p}}^{+}={\mathfrak{g}}_1(h)⋊{\mathfrak{g}}_0(h).\end{array}$$ 6.2

Then $y\in {\mathcal{T}}_C\cap {\mathfrak{p}}^{+}$ is an Euler element, and a similar argument shows that the vector field $X_y^{G/P^{-}}$ has a unique repelling fixed point $m_{+}\in {\mathcal{D}}_{+}$. So $m_{+}=exp(-z)P^{-}$ for some $z\in {\mathfrak{g}}_1(h)$, and $exp(z).m_{+}=e{P}^{-}$. Hence the base point $e{P}^{-}\in G/P^{-}$ is a repelling fixed point of the Euler element $y^{\prime }:=e^{\text{ad}z}y\in {\mathfrak{g}}_0(h)$, and $e{P}^{+}$ is an attracting fixed point in $G/P^{+}$. The attracting and repelling properties of the fixed points imply that

$$\begin{array}{c}\hfill {\mathfrak{g}}_1(h)\subseteq {\mathfrak{g}}_1(y^{\prime })\text{and}{\mathfrak{g}}_{-1}(h)\subseteq {\mathfrak{g}}_{-1}(y^{\prime }),\end{array}$$

so that we also have

$$\begin{array}{c}\hfill {\mathfrak{g}}_0(h)=[{\mathfrak{g}}_1(h),{\mathfrak{g}}_{-1}(h)]\subseteq {\mathfrak{g}}_0(y^{\prime }).\end{array}$$

As h and $y^{\prime }$ are Euler elements, this entails that ${\mathfrak{g}}_{\lambda }(h)={\mathfrak{g}}_{\lambda }(y^{\prime })$ for $\lambda =-1,0,1$. This shows that $\text{ad}h=\text{ad}{y}^{\prime }$ and hence that $y^{\prime }=h$ because $\mathfrak{z}(\mathfrak{g})=\{0\}$.

We conclude that

$$\begin{array}{c}\hfill x=\text{Ad}{(g_1)}^{-1}y=\text{Ad}{(g_1)}^{-1}{e}^{-\text{ad}z}h\text{with}{g}_1\in H_e,z\in {\mathcal{D}}_{\mathfrak{g}}.\end{array}$$

Conversely, we have seen in Proposition 5.4 that

$$\begin{array}{c}\hfill e^{\text{ad}{\mathcal{D}}_{\mathfrak{g}}}h=h+{\mathcal{D}}_{\mathfrak{g}}\subseteq {\mathcal{T}}_C.\end{array}$$ 6.3

We finally obtain (6.1). $\square$

Remark 6.2

Note that the preceding proof is based on the natural embedding

$$\begin{array}{c}\hfill {\mathcal{O}}_h\cong G/G_h\to G/P^{-}\times G/P^{+}\end{array}$$

which maps the Euler element $\text{Ad}(g)H$ to $(m_{+},m_{-})$, where $m_{+}$ is the unique repelling fixed point of the flow defined by h in $G/P^{-}$ and $m_{-}\in G/P^{+}$ is the unique attracting fixed point.

Corollary 8.3

(The set of positivity domains in M) If $h_1\in \mathcal{E}(\mathfrak{g})$ is an Euler element for which the positivity domain

$$\begin{array}{c}\hfill W_M^{+}(h_1)=\{m\in M=G/H:X_1^M(m)\in C_m^{\circ }\}\end{array}$$

is non-empty, then there exists a $g\in G$ with $h_1=\text{Ad}(g)h$ and

$$\begin{array}{c}\hfill W_M^{+}(h_1)=g.W_M^{+}(h).\end{array}$$

Proof

As $X_1^M(g_{1}H)\in C_{g_{1}H}^{\circ }$ is equivalent to $\text{Ad}{(g_1)}^{-1}{h}_1\in \mathfrak{h}+C^{\circ }$ by (see Lemma 3.3), Theorem 6.1 implies that $h_1=\text{Ad}(g)h\in {\mathcal{O}}_h$ for some $g\in G$. The relation $W_M^{+}(h_1)=g.W_M^{+}(h)$ now follows directly from the definitions. $\square$

The preceding corollary shows that any wedge domain of the type $W_M^{+}(h_1)\subseteq M$, $h_1\in \mathcal{E}(\mathfrak{g})$, is a G-translate of the wedge domain $W_M^{+}(h)$, where $h\in C^{\circ }\cap {\mathfrak{q}}_{\mathfrak{p}}$ is a causal Euler element. So the action of G on the “wedge space” $\mathcal{W}(M)$ of M is transitive.

Corollary 8.4

If the causal Euler element h is not symmetric, then $W_M^{+}(-h)=\mathrm{\varnothing }$.

Remark 6.5

(Extensions to the non-simple case) If $(\mathfrak{g},\tau )$ is a direct sum of irreducible ncc symmetric Lie algebra $({\mathfrak{g}}_j,{\tau }_j)$ and $h={\sum }_j{h}_j$ accordingly, then

$$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{max}}(h)=\prod _j{C}_{{\mathfrak{q}}_j}^{\text{max}}(h_j)\end{array}$$

(cf. (2.3)). Projecting to the ideals ${\mathfrak{g}}_j$, we obtain with Theorem 6.1 for $C=C_{\mathfrak{q}}^{\text{max}}(h)$ and $C_j=C_{{\mathfrak{q}}_j}^{\text{max}}(h_j)$ the relation

$$\begin{array}{c}\hfill \mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_C\subseteq \prod _j\mathcal{E}({\mathfrak{g}}_j)\cap {\mathcal{T}}_{C_j}\subseteq \prod _j{\mathcal{O}}_{h_j}={\mathcal{O}}_h.\end{array}$$ 6.4

Further,

$$\begin{array}{c}\hfill {\mathcal{O}}_h\cap {\mathcal{T}}_C=\prod _j{\mathcal{O}}_{h_j}\cap {\mathcal{T}}_{C_j}\end{array}$$

and ${\mathcal{D}}_{\mathfrak{g}}={\prod }_j{\mathcal{D}}_{{\mathfrak{g}}_j}$ imply (6.1) for this case.

Note that the situation corresponds to $\mathfrak{g}={\mathfrak{g}}_s$ (see (2.2)). In the general situation, where we assume only that all ideals of $\mathfrak{g}$ contained in $\mathfrak{h}$ are compact, we have

$$\begin{array}{c}\hfill \mathfrak{g}={\mathfrak{g}}_k\oplus {\mathfrak{g}}_r\oplus {\mathfrak{g}}_s,\end{array}$$

where ${\mathfrak{g}}_k\subseteq \mathfrak{h}$ is compact, ${\mathfrak{g}}_r$ is a direct sum of Riemannian symmetric Lie algebras and ${\mathfrak{g}}_s$ is a direct sum of irreducible ncc symmetric Lie algebras. All Euler elements are contained in ${\mathfrak{g}}_r+{\mathfrak{g}}_s$. If $\mathfrak{g}$ is only reductive, we assume $\mathfrak{z}(\mathfrak{g})\subseteq {\mathfrak{g}}^{-\theta }$, so that $\mathfrak{z}(\mathfrak{g})\subseteq {\mathfrak{g}}_r$. Then $h=h_r+h_s$ and

$$\begin{array}{c}\hfill C_{\mathfrak{q}}^{\text{max}}(h)={\mathfrak{q}}_r\oplus C_{{\mathfrak{q}}_s}^{\text{max}}(h_s).\end{array}$$

We conclude that

$$\begin{array}{c}\hfill \mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_C\subseteq \mathcal{E}(\mathfrak{g})\cap {\mathcal{T}}_{C_{\mathfrak{q}}^{\text{max}}(h)}=((\mathcal{E}({\mathfrak{g}}_r)\cup \{0\})\times \mathcal{E}({\mathfrak{g}}_s))\cap {\mathcal{T}}_{C_{{\mathfrak{q}}_s}^{\text{max}}(h_s)}\subseteq (\mathcal{E}({\mathfrak{g}}_r)\cup \{0\})\times {\mathcal{O}}_{h_s}.\end{array}$$

This shows that, for any Euler element $k\in \mathfrak{g}$ with $W_M^{+}(k)\ne \mathrm{\varnothing }$ we must have $k_s\in {\mathcal{O}}_{h_s}$, but there is no restriction on the Riemannian component $k_r\in \mathcal{E}({\mathfrak{g}}_r)$.

Connectedness of the positivity domain

In this section, we show that if $G\cong \text{Inn}(\mathfrak{g})$ is the adjoint group, then the positivity domain $W_M^{+}(h)$ is connected. This contrasts the situation for compactly causal symmetric spaces, where wedge regions are in general not connected. A typical example is anti-de Sitter spacetime (cf. [52, Lemma 11.2]).

Theorem 7.1

(Connectedness of positivity domains) Suppose that $(\mathfrak{g},\tau ,C)$ is an irreducible simple ncc symmetric Lie algebra with $C=C_{\mathfrak{q}}^{\text{max}}$ and the causal Euler element $h\in C^{\circ }\cap {\mathfrak{q}}_{\mathfrak{p}}$. Let $M=G/H$ for $G=\text{Inn}(\mathfrak{g})$ and $H=K^{h}exp({\mathfrak{h}}_{\mathfrak{p}})$. Then the positivity domain $W_M^{+}(h)$ is connected.

Proof

From Theorem 6.1 we derive that

$$\begin{array}{c}\hfill G^{+}(h):=\{g\in G:\text{Ad}{(g)}^{-1}h\in {\mathcal{T}}_C\}=G^{h}exp({\mathcal{D}}_{\mathfrak{g}})H_e,\end{array}$$

and this leads with Lemma 3.3 to

$$\begin{array}{c}\hfill W_M^{+}(h)=G^{+}(h).eH=G^{h}exp({\mathcal{D}}_{\mathfrak{g}}).eH.\end{array}$$

Since $G^h$ has at most two connected components, this set is either connected or has two connected components ([41, Thm. 7.8]). As $G^h=K^{h}exp({\mathfrak{q}}_{\mathfrak{p}})$, we have $G^h=K^h{G}_e^h$, and $\text{Ad}(K^h)$ preserves the open unit ball in ${\mathfrak{g}}_1(h)$. We thus derive from $K^h=H_K$:

$$\begin{array}{cc}\hfill W_M^{+}(h)& =G^{h}exp({\mathcal{D}}_{\mathfrak{g}}).eH=G_e^h{K}^{h}exp({\mathcal{D}}_{\mathfrak{g}}).eH=G_e^{h}exp({\mathcal{D}}_{\mathfrak{g}})K^h.eH=G_e^{h}exp({\mathcal{D}}_{\mathfrak{g}}).eH,\hfill \end{array}$$

which is connected. $\square$

Corollary 3.7

$W(\gamma )=W_M^{+}(h)$.

Proposition 7.3

(The stabilizer group of the observer domain) If $\mathfrak{g}={\mathfrak{g}}_s$, then $G^h$ coincides with the stabilizer group

$$\begin{array}{c}\hfill G_{W(\gamma )}:=\{g\in G:gW(\gamma )=W(\gamma )\}\end{array}$$

of the observer domain $W(\gamma )\subseteq M=G/H$.

Proof

We work with the subset realization of $M=G/H$ as $M_{{\mathcal{D}}_{+}}=\{g.{\mathcal{D}}_{+}:g\in G\}$ from Proposition 4.8. Then

$$\begin{array}{c}\hfill W(\gamma )=\{g{\mathcal{D}}_{+}:0\in g.{\mathcal{D}}_{+},g.{\mathcal{D}}_{+}\text{bounded}\text{in}exp({\mathfrak{g}}_1(h)).P^{-}\}\end{array}$$

(Lemma 5.2(c)). Since $exp(\mathbb{R}h)$ acts on $exp({\mathfrak{g}}_1(h))$ by dilations, it follows that

$$\begin{array}{c}\hfill \bigcap _{g{\mathcal{D}}_{+}\in W(\gamma )}g{\mathcal{D}}_{+}=\bigcap _{t\in \mathbb{R}}{e}^t{\mathcal{D}}_{+}=\{e{P}^{-}\}.\end{array}$$ 7.1

Therefore, $gW(\gamma )=W(\gamma )$ for the action of g on $G/H\subseteq \mathbb{P}(G/P^{-})$ implies that g preserves the intersection $\{e{P}^{-}\}$ of all subsets contained in $W(\gamma )$. This shows that g fixes $e{P}^{-}$, so that $g\in P^{-}$.

Next we recall that the involution ${\tau }_M$ on M defined by ${\tau }_M(gH)=\tau (g)H$ leaves $W(\gamma )$ invariant (Lemma 5.10), and this leads to

$$\begin{array}{c}\hfill G_{W(\gamma )}=\tau (G_{W(\gamma )})\subseteq P^{-}\cap \tau (P^{-})=P^{-}\cap P^{+}=G^h.\end{array}$$

$\square$

The preceding proposition shows that the set $\mathcal{W}=\mathcal{W}(M)$ of wedge domains in $M=G/H$ coincides with

$$\begin{array}{c}\hfill \mathcal{W}=G.W(\gamma )\cong G/G^h\cong {\mathcal{O}}_h.\end{array}$$ 7.2

In particular, it is a symmetric space. Recall that, by Corollary 7.2, the observer domain coincides with the positivity domain $W_M^{+}(h)$.

KMS wedge regions

With the structural results obtained so far, we have good control over the positivity domains $W_M^{+}(h)$ in ncc symmetric spaces $M=G/H$. So one may wonder if they also have an interpretation in terms of a KMS like condition. In [52], this has been shown for modular flows with fixed points, using such a fixed point as a base point. In this section we extend the characterization of the wedge domain W in terms of a geometric KMS condition to general ncc spaces.

To simplify references, we list our assumptions and the relevant notation below:

• $\mathfrak{g}$ is simple,

• $G=\text{Inn}(\mathfrak{g})\subseteq G_{\mathbb{C}}=\text{Inn}{({\mathfrak{g}}_{\mathbb{C}})}_e$ (by (GP) and (Eff), [52, Lemma 2.12])

• $\sigma :G_{\mathbb{C}}\to G_{\mathbb{C}}$ denotes the complex conjugation with respect to G.

• $H=G^c\cap G$, where $G^c={(G_{\mathbb{C}}^{\overline{\tau }})}_e$ and $K_{\mathbb{C}}\subseteq G_{\mathbb{C}}^{\theta }$ is an open subgroup. Note that $H\subseteq G^{\tau }$.

• $\mathrm{\Xi }=G.{\text{Exp}}_{\mathit{eK}}(i{\mathrm{\Omega }}_{\mathfrak{p}})\subseteq G_{\mathbb{C}}/K_{\mathbb{C}}$.

• $H_{\mathbb{C}}\subseteq G_{\mathbb{C}}^{\tau }$ is open with $G\cap H_{\mathbb{C}}=H$ (see §5), so that $M=G/H\hookrightarrow G_{\mathbb{C}}/H_{\mathbb{C}}$.

• ${\tau }_h^G(H_{\mathbb{C}})=H_{\mathbb{C}}$ for the holomorphic involution of $G_{\mathbb{C}}$ integrating the complex linear extension of $\tau$.

• $\sigma (H_{\mathbb{C}})=H_{\mathbb{C}}$ for the conjugation of $G_{\mathbb{C}}$ with respect to G.

• ${\kappa }_h=e^{-\frac{\pi i}{2}\text{ad}h}$ integrates to the automorphism ${\kappa }_h^G(g)=exp(-\frac{\pi i}{2}h)gexp(\frac{\pi i}{2}h)$ of $G_{\mathbb{C}}$.

Note that

$$\begin{array}{c}\hfill {\tau }_h^G:={({\kappa }_h^G)}^2\end{array}$$ 8.1

is a holomorphic involutive automorphism of $G_{\mathbb{C}}$ inducing ${\tau }_h$ on the Lie algebra $\mathfrak{g}$.

Let

$$\begin{array}{c}\hfill \mathrm{\Xi }:=G.{\text{Exp}}_{\mathit{eK}}(i{\mathrm{\Omega }}_{\mathfrak{p}})\subseteq G_{\mathbb{C}}/K_{\mathbb{C}}\end{array}$$

be the crown of G/K. The involution ${\tau }_h$ on G preserves K, hence induces an involution on G/K, and we extend it to an antiholomorphic involution ${\overline{\tau }}_h$ on $G_{\mathbb{C}}/K_{\mathbb{C}}$. The canonical map $G{\times }_{K}i{\mathrm{\Omega }}_{\mathfrak{p}}\to \mathrm{\Xi }$ is a diffeomorphism ([52, Prop. 4.7]) and

$$\begin{array}{c}\hfill {\overline{\tau }}_h(g.\text{Exp}(ix))={\tau }_h(g).\text{Exp}(-i{\tau }_h(x))\end{array}$$

implies that

$$\begin{array}{c}\hfill {\mathrm{\Xi }}^{{\overline{\tau }}_h}=G^{{\tau }_h}.\text{Exp}(i{\mathrm{\Omega }}_{\mathfrak{p}}^{-{\tau }_h})=exp({\mathfrak{q}}_{\mathfrak{p}}).\text{Exp}(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}})\cong G_e^h{\times }_{K_e^h}i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}.\end{array}$$ 8.2

(see the proof of [52, Thm. 6.1] for details). This describes the fixed point as a “real crown domain” of the Riemannian symmetric space ${(G/K)}^{{\tau }_h}=\text{Exp}({\mathfrak{q}}_{\mathfrak{p}})$.

For an open subgroup $H_{\mathbb{C}}\subseteq G_{\mathbb{C}}^{\tau }$ (where $\tau$ denotes the holomorphic involution) with $G\cap H_{\mathbb{C}}=H$, we obtain an embedding $M=G/H\hookrightarrow G_{\mathbb{C}}/H_{\mathbb{C}}$. Then the stabilizer of

$$\begin{array}{c}\hfill m_K:={\text{Exp}}_{\mathit{eH}}(\frac{\pi i}{2}h)=exp(\frac{\pi i}{2}h)H_{\mathbb{C}}\in G_{\mathbb{C}}/H_{\mathbb{C}}\end{array}$$

coincides with K, so that $G.m_K\cong G/K$ ([52, Thm. 5.4]). Accordingly,

$$\begin{array}{c}\hfill K_{\mathbb{C}}:={({\kappa }_h^G)}^{-1}(H_{\mathbb{C}})\end{array}$$

is an open subgroup of $G_{\mathbb{C}}^{\theta }$ that coincides with the stabilizer $G_{\mathbb{C}}^K$. In this sense $G_{\mathbb{C}}/H_{\mathbb{C}}\cong G_{\mathbb{C}}/K_{\mathbb{C}}$, but with different base points $m_H:=e{H}_{\mathbb{C}}$ and $m_K$. Recall that $\tau =e^{\pi i\text{ad}h}\theta =e^{\frac{\pi i}{2}\text{ad}h}\theta e^{-\frac{\pi i}{2}\text{ad}h}$ implies $\theta ={({\kappa }_h^G)}^{-1}\tau {\kappa }_h^G$. The invariance of $H_{\mathbb{C}}$ under ${\tau }_h^G$ implies that

$$\begin{array}{c}\hfill H_{\mathbb{C}}={({\kappa }_h^G)}^{-1}(K_{\mathbb{C}}),\end{array}$$

so that $K_{\mathbb{C}}$ and $H_{\mathbb{C}}$ are exchanged by the order-4 automorphism ${\kappa }_h^G$ and invariant under ${\tau }_h^G$.

As ${\tau }_h^G$ commutes with ${\kappa }_h^G$, it also leaves $K_{\mathbb{C}}$ invariant. Moreover, $\sigma {\kappa }_h^G\sigma ={({\kappa }_h^G)}^{-1}$ entails

$$\begin{array}{c}\hfill \sigma (K_{\mathbb{C}})={\kappa }_h^G(\sigma (H_{\mathbb{C}}))={\kappa }_h^G(H_{\mathbb{C}})=K_{\mathbb{C}}.\end{array}$$

Therefore, the antiholomorphic extension ${\overline{\tau }}_h^G$ also preserves $K_{\mathbb{C}}$ and induces on $G_{\mathbb{C}}/K_{\mathbb{C}}\cong G_{\mathbb{C}}/H_{\mathbb{C}}$ an antiholomorphic involution ${\overline{\tau }}_h$ fixing the base point $m_K$ with stabilizer $K_{\mathbb{C}}$. Then

$$\begin{array}{c}\hfill m_H^{\prime }:={\overline{\tau }}_h(m_H)={\overline{\tau }}_h(exp(-\frac{\pi i}{2}h).m_K)=exp(\frac{\pi i}{2}h).m_K=exp(\pi ih).m_H,\end{array}$$

may be different from $m_H$.

Remark 8.1

The condition $m_H=m_H^{\prime }$ is equivalent to $exp(\pi ih)\in H_{\mathbb{C}}$. Note that $e^{\pi i\text{ad}h}={\tau }_h\in \text{Aut}({\mathfrak{g}}_{\mathbb{C}})$ is an involution that commutes with $\tau$, so that the choice of $H_{\mathbb{C}}$ determines whether $exp(\pi ih)$ is contained in $H_{\mathbb{C}}$ or not.

For $\mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})$, $G=\text{Inn}(\mathfrak{g})$, and $h=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$, we obtain on ${\text{SL}}_2(\mathbb{R})\subseteq {\text{SL}}_2(\mathbb{C})$ the involution

$$\begin{array}{c}\hfill \tau \left(\begin{array}{cc}a& b\\ c& d\end{array}\right)=\left(\begin{array}{cc}d& c\\ b& a\end{array}\right).\end{array}$$

For $g\in {\text{SL}}_2(\mathbb{C})$, the condition $\tau \text{Ad}(g)\tau =\text{Ad}(g)$ is equivalent to $\tau (g)g^{-1}\in ker(\text{Ad})=\{\pm \mathbf{1}\}$. As

$$\begin{array}{c}\hfill e^{\pi i\text{ad}h}=\text{Ad}(exp\pi ih)=\text{Ad}\left(\begin{array}{cc}i& 0\\ 0& -i\end{array}\right)\text{and}\tau \left(\begin{array}{cc}i& 0\\ 0& -i\end{array}\right){\left(\begin{array}{cc}i& 0\\ 0& -i\end{array}\right)}^{-1}=-\mathbf{1},\end{array}$$

it follows that

$$\begin{array}{c}\hfill {\tau }_h=e^{\pi i\text{ad}h}\in G_{\mathbb{C}}^{\tau }\backslash {(G_{\mathbb{C}}^{\tau })}_e.\end{array}$$

In particular, $K_{\mathbb{C}}$ and $H_{\mathbb{C}}$ have two connected components in $G_{\mathbb{C}}\cong {\text{PSL}}_2(\mathbb{C})$.

In $G\cong {\text{PSL}}_2(\mathbb{R})$, a similar argument shows that $\theta =\text{Ad}\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\in G^{\tau }\backslash G_e^{\tau }$. So $G^{\tau }$ also has two connected components, but only its identity component $G_e^{\tau }$ acts causally on $\mathfrak{q}$. Therefore, $H=G_e^{\tau }$, but for $H_{\mathbb{C}}$ we have two choices, $G_{\mathbb{C}}^{\tau }$, or its identity component.

Comparing with the arguments in [52, Lemma 6.3], where ${\alpha }_{\pi i}={\tau }_h$ on M, we have to be more careful in the present context. Here ${\overline{\tau }}_h$ restricts to a map

$$\begin{array}{c}\hfill M=G.m_H\to M^{\prime }:=G.m_H^{\prime }=exp(\pi ih).M,\end{array}$$

and these two copies of G/H may not be identical. However, the antiholomorphic map

$$\begin{array}{c}\hfill {\sigma }_M:={\alpha }_{\pi i}\circ {\overline{\tau }}_h\end{array}$$

maps M to itself, fixes the base point $m_H$ and commutes with the G-action. Hence it fixes M pointwise and describes a “complex conjugation” with respect to M. In particular, the two maps

$$\begin{array}{c}\hfill {\overline{\tau }}_h:M\to M^{\prime }\text{and}{\alpha }_{\pi i}:M\to M^{\prime }\end{array}$$

coincide on M.

We define the KMS wedge domain

$$\begin{array}{c}\hfill W^{\text{KMS}}:=\{m\in M:{\alpha }_{\mathit{it}}(m)\in \mathrm{\Xi }\text{for}0<t<\pi \}.\end{array}$$ 8.3

Theorem 8.2

$W^{\text{KMS}}=W_M^{+}{(h)}_{\mathit{eH}}$.

Proof

“$\subseteq$”: For $z\in \mathbb{C}$ and $p\in M$, we first observe that

$$\begin{array}{c}\hfill {\overline{\tau }}_h({\alpha }_z(p))={\alpha }_{\overline{z}}({\overline{\tau }}_h(p))={\alpha }_{\overline{z}}{\alpha }_{\pi i}(p)={\alpha }_{\pi i+\overline{z}}(p).\end{array}$$

For $z=\frac{\pi i}{2}$, we thus obtain ${\alpha }_{\pi i/2}(p)\in M_{\mathbb{C}}^h$. We conclude that

$$\begin{array}{c}\hfill {\alpha }_{\frac{\pi i}{2}}(W^{\text{KMS}})\subseteq {\mathrm{\Xi }}^{{\overline{\tau }}_h}=exp({\mathfrak{q}}_{\mathfrak{p}}).\text{Exp}(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}).\end{array}$$ 8.4

Hence,

$$\begin{array}{c}\hfill W^{\text{KMS}}\subseteq {\kappa }_h({\mathrm{\Xi }}^{{\overline{\tau }}_h})=G_e^h.{\text{Exp}}_{\mathit{eH}}({\kappa }_h(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}})),\end{array}$$

where

$$\begin{array}{c}\hfill {\kappa }_h(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}})=\{x\in {\mathfrak{q}}_{\mathfrak{k}}:\Vert \text{ad}x\Vert <\frac{\pi }{2}\}=:{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}.\end{array}$$

This suggest to define a “polar wedge domain” as

$$\begin{array}{c}\hfill W_M^{\text{pol}}(h):=G_e^h.\text{Exp}({\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}})\subseteq M.\end{array}$$

We actually know from Theorem 3.6 that this is the connected component $W=W_M^{+}{(h)}_{\mathit{eH}}\subseteq W_M^{+}(h)$ containing the base point. We thus obtain

$$\begin{array}{c}\hfill W^{\text{KMS}}\subseteq W=W_M^{+}{(h)}_{\mathit{eH}}.\end{array}$$ 8.5

“$\supseteq$”: To see that $W_M^{+}{(h)}_{\mathit{eH}}\subseteq W^{\text{KMS}}$, we first recall from the first part of the proof that

$$\begin{array}{c}\hfill W_M^{+}{(h)}_{\mathit{eH}}={\kappa }_h({\mathrm{\Xi }}^{{\overline{\tau }}_h})=G_e^h.{\text{Exp}}_{\mathit{eH}}({\kappa }_h(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}))=G_e^h.{\alpha }_{-\pi i/2}({\text{Exp}}_{\mathit{eK}}(i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}})).\end{array}$$

To see that this domain is contained in the $G_e^h$-invariant domain $W^{\text{KMS}}\subseteq M$, we thus have to show that, for $x\in {\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}$, we have

$$\begin{array}{c}\hfill {\alpha }_{\mathit{it}}.{\text{Exp}}_{\mathit{eK}}(ix)\in \mathrm{\Xi }\text{for}|t|<\pi /2.\end{array}$$

Let ${\mathfrak{t}}_{\mathfrak{q}}\subseteq {\mathfrak{q}}_{\mathfrak{k}}$ is a maximal abelian subspace (they are all conjugate under ${(H_K)}_e$). Then, ${\mathfrak{a}}_{\mathfrak{h}}:=i{\kappa }_h({\mathfrak{t}}_{\mathfrak{q}})\subseteq {\mathfrak{h}}_{\mathfrak{p}}$ is also maximal abelian and ${\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}=e^{\text{ad}{\mathfrak{h}}_{\mathfrak{k}}}.{\mathrm{\Omega }}_{{\mathfrak{a}}_{\mathfrak{h}}}$. So it suffices to show that, for $x\in {\mathrm{\Omega }}_{{\mathfrak{a}}_{\mathfrak{h}}}$ and $|t|<\pi /2$, we have ${\alpha }_{\mathit{it}}.{\text{Exp}}_{\mathit{eK}}(ix)\in \mathrm{\Xi }.$ By Proposition 2.8, ${\mathfrak{t}}_{\mathfrak{q}}$ is contained in a $\tau$-invariant subalgebra $\mathfrak{s}\cong {\mathfrak{sl}}_2{(\mathbb{R})}^s$, where $\mathbb{R}h+\mathfrak{s}$ is generated by h and ${\mathfrak{t}}_{\mathfrak{q}}$ and $h=h_0+h_1+\cdots +h_s$, where $h_j$, $j=1,\dots ,s$, is an Euler element in a simple ideal ${\mathfrak{s}}_j\cong {\mathfrak{sl}}_2(\mathbb{R})$ of $\mathfrak{s}$. Then ${\mathfrak{a}}_{\mathfrak{h}}=i{\kappa }_h({\mathfrak{t}}_{\mathfrak{q}})\subseteq \mathfrak{a}$ is spanned by s Euler elements $x_1,\dots ,x_s$ and

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{{\mathfrak{a}}_{\mathfrak{h}}}=\{\sum _{j=1}^s{t}_j{x}_j:(\forall j)|t_j|<\pi /2\}.\end{array}$$

Let $S:=⟨exp\mathfrak{s}⟩$ and ${\mathrm{\Xi }}_S:=S.\text{Exp}(i({\mathrm{\Omega }}_{\mathfrak{p}}\cap \mathfrak{s}))\subseteq \mathrm{\Xi }$. Then the discussion in Remark D.1 implies that, for $|t|<\pi /2$ and $x={\sum }_j{t}_j{x}_j\in {\mathrm{\Omega }}_{{\mathfrak{a}}_{\mathfrak{h}}}$, we have ${\alpha }_{\mathit{it}}({\text{Exp}}_{\mathit{eK}}(ix))\in {\mathrm{\Xi }}_S\subseteq \mathrm{\Xi }.$ $\square$

The preceding proof implies in particular the following interesting observation:

Corollary 5.8

For every $m\in {\mathrm{\Xi }}^{{\overline{\tau }}_h}$, we have ${\alpha }_{\mathit{it}}(m)\in \mathrm{\Xi }$ for $|t|<\pi /2$, so that the orbit map ${\alpha }^m$ extends to a holomorphic map ${\mathcal{S}}_{\pm \pi /2}\to \mathrm{\Xi }$.

Corollary 6.3

${\alpha }_{\frac{\pi i}{2}}:W^{\text{KMS}}\to {\mathrm{\Xi }}^{{\overline{\tau }}_h}$ is a diffeomorphism that induces an equivalence of fiber bundles

$$\begin{array}{c}\hfill W^{\text{KMS}}\cong G_e^h{\times }_{K_e^h}{\mathrm{\Omega }}_{{\mathfrak{q}}_{\mathfrak{k}}}\to G_e^h{\times }_{K_e^h}i{\mathrm{\Omega }}_{{\mathfrak{h}}_{\mathfrak{p}}}\cong {\mathrm{\Xi }}^{{\overline{\tau }}_h}.\end{array}$$

Proof

Theorem 8.2 implies in particular that ${\alpha }_{\frac{\pi i}{2}}:W^{\text{KMS}}\to {\mathrm{\Xi }}^{{\overline{\tau }}_h}$ is bijective. Since $W^{\text{KMS}}=W_M^{+}{(h)}_{\mathit{eH}}$ is an open subset of M and ${\mathrm{\Xi }}^{{\overline{\tau }}_h}$ an open subset of $M_{\mathbb{C}}^h$, it actually is a diffeomorphism. The second assertion follows from the fact that it commutes with the action of the subgroup $G_e^h$. $\square$

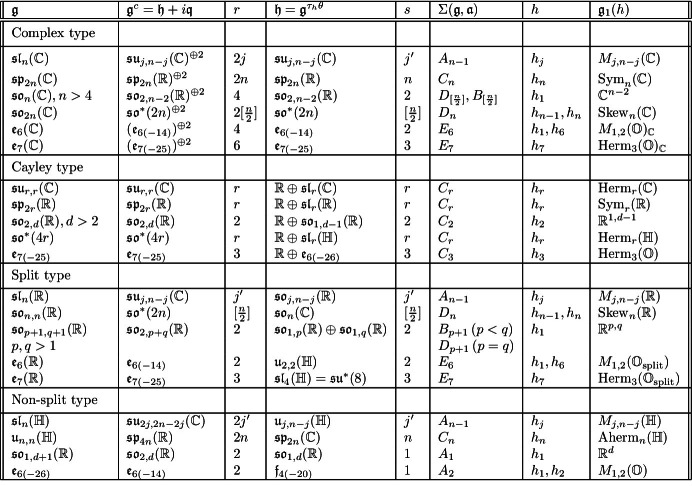
Irreducible ncc symmetric Lie algebras

The following table lists all irreducible non-compactly causal symmetric Lie algebras $(\mathfrak{g},\tau )$ according to the following types:

• Complex type: $\mathfrak{g}={\mathfrak{h}}_{\mathbb{C}}$ and $\tau$ is complex conjugation with respect to $\mathfrak{h}$. In this case ${\mathfrak{g}}^c\cong {\mathfrak{h}}^{\oplus 2}$, so that ${\text{rk}}_{\mathbb{R}}({\mathfrak{g}}^c)=2{\text{rk}}_{\mathbb{R}}(\mathfrak{h})$.

• Cayley type (CT): $\tau ={\tau }_{h_1}$ for an Euler element $h_1\in \mathfrak{h}$. Then ${\text{rk}}_{\mathbb{R}}({\mathfrak{g}}^c)={\text{rk}}_{\mathbb{R}}(\mathfrak{g})={\text{rk}}_{\mathbb{R}}(\mathfrak{h})$.

• Split type (ST): $\tau \ne {\tau }_{h_1}$ for all $h_1\in \mathfrak{h}\cap \mathcal{E}(\mathfrak{g})$ and ${\text{rk}}_{\mathbb{R}}\mathfrak{h}={\text{rk}}_{\mathbb{R}}{\mathfrak{g}}^c$:

• Non-split type (NST): $\tau \ne {\tau }_{h_1}$ for all $h_1\in \mathfrak{h}\cap \mathcal{E}(\mathfrak{g})$ and ${\text{rk}}_{\mathbb{R}}\mathfrak{h}=\frac{{\text{rk}}_{\mathbb{R}}{\mathfrak{g}}^c}{2}$:

In Table 1, we write $r={\text{rk}}_{\mathbb{R}}({\mathfrak{g}}^c)$ and $s={\text{rk}}_{\mathbb{R}}(\mathfrak{h})$. Further $\mathfrak{a}\subseteq \mathfrak{p}$ is maximal abelian of dimension r. For root systems $\mathrm{\Sigma }(\mathfrak{g},\mathfrak{a})$ of type $A_{n-1}$, there are $n-1$ Euler elements $h_1,\dots ,h_{n-1}$, but for the other root systems there are less; see [38, Thm. 3.10] for the concrete list. For $1\le j<n$ we write $j^{\prime }:=min(j,n-j)$.

Table 1.

Irreducible ncc symmetric Lie algebras with corresponding causal Euler elements $h\in \mathfrak{a}$

Geodesics in symmetric spaces

This appendix contains some elementary observations concerning geodesics in symmetric spaces.

Lemma B.1

Let $M=G/H$ be a symmetric space with symmetric Lie algebra $(\mathfrak{g},\tau )$, $x\in \mathfrak{g}$ and $y\in \mathfrak{q}$. Then

$$\begin{array}{c}\hfill exp(tx)H=exp(ty)H\text{for}\text{all}t\in \mathbb{R}\end{array}$$ B.1

holds if and only if $p_{\mathfrak{q}}(x)=y$ and $[x,y]=0$.

In particular, $\gamma (t):=exp(tx)H$ is a geodesic in M if and only if $[x,\tau (x)]=0$.

Proof

The relation (B.1) is equivalent to

$$\begin{array}{c}\hfill exp(-ty)exp(tx)\in H\subseteq G^G\text{for}\text{all}t\in \mathbb{R}.\end{array}$$

Applying ${\tau }^G$, we obtain

$$\begin{array}{c}\hfill exp(ty)exp(t\tau (x))=exp(-ty)exp(tx),\end{array}$$

which leads to $exp(2ty)=exp(tx)exp(-t\tau (x)).$ Evaluating the derivative of this curve in the right trivialization of T(G), we get

$$\begin{array}{c}\hfill 2y=x+e^{tadx}(-\tau (x))=x-e^{tadx}(\tau (x))\text{for}\text{all}t\in \mathbb{R}.\end{array}$$

For $t=0$ we get $p_{\mathfrak{q}}(x)=y$, and taking derivatives in 0 shows that $[x,\tau (x)]=0.$

If, conversely, this condition is satisfied, then $x=x_{\mathfrak{h}}+x_{\mathfrak{q}}$ with $x_{\mathfrak{h}}\in \mathfrak{h}$ and $x_{\mathfrak{q}}\in \mathfrak{q}$, where

$$\begin{array}{c}\hfill 0=[x,\tau (x)]=2[x_{\mathfrak{h}},x_{\mathfrak{q}}].\end{array}$$

Therefore,

$$\begin{array}{c}\hfill exp(tx)H=exp(t{x}_{\mathfrak{q}})exp(t{x}_{\mathfrak{h}})H=exp(t{x}_{\mathfrak{q}})H={\text{Exp}}_{\mathit{eH}}(t{x}_{\mathfrak{q}})\end{array}$$

is a geodesic in M. $\square$

The following lemma provides important information on the subset $M^x$.

Lemma B.2

Let $x\in \mathfrak{g}$ and write

$$\begin{array}{c}\hfill M^x:=\{gH\in M:\text{Ad}{(g)}^{-1}x\in \mathfrak{q}\}.\end{array}$$

Then $M^x$ is a submanifold of M which is invariant under the action of $G^x$, and the orbits or $G_e^x$ are the connected components of $M^x$.

Proof

Let $m_0=g_{0}H\in M^x$ and $x_c:=\text{Ad}{(g_0)}^{-1}x$. For $y\in \mathfrak{q}$ we have

$$\begin{array}{c}\hfill {\text{Exp}}_{m_0}(g_0.y)=g_0.{\text{Exp}}_{\mathit{eH}}(y)=g_0(expy)H=exp(\text{Ad}(g_0)y).m_0\end{array}$$

and

$$\begin{array}{cc}\hfill \text{Ad}{(g_{0}exp(y))}^{-1}x=& e^{-\text{ad}y}{x}_c=cosh(\text{ad}y)x_c-sinh(\text{ad}y)x_c\hfill \\ \hfill =& \underset{\in \mathfrak{q}}{\underbrace{cosh(\text{ad}y)x_c}}-\underset{\in \mathfrak{h}}{\underbrace{\frac{sinh(\text{ad}y)}{\text{ad}y}[y,x_c]}}.\hfill \end{array}$$

Let $U\subseteq \mathfrak{q}$ be a 0-neighborhood for which ${\text{Exp}}_{\mathit{eH}}{|}_U$ is a diffeomorphism onto an open subset of M and the spectral radius of $\text{ad}y$ is smaller than $\pi$ for $y\in U$. Then $\frac{sinh(\text{ad}y)}{\text{ad}y}:\mathfrak{h}\to \mathfrak{h}$ is invertible. With the above formula, we thus conclude for $y\in U$ that ${\text{Exp}}_{m_0}(g_0.y)\in M^x$ is equivalent to $[y,x_c]=0$, which is equivalent to $\text{Ad}(g_0)y\in {\mathfrak{g}}^x$. This shows that $M^x$ is a submanifold of M.

As ${\text{Exp}}_{m_0}(g_0.y)=exp(\text{Ad}(g_0)y).m_0\in exp({\mathfrak{g}}^x).m_0$, it further follows that the orbit of $m_0$ under the connected group $G_e^x$ contains a neighborhood of $m_0$. This shows that the orbits of $G_e^x$ in $M^x$ are connected open subsets, hence coinciding with its connected components. $\square$

Remark B.3

For $x\in \mathfrak{q}$ the centralizer ${\mathfrak{g}}^x$ is $\tau$-invariant, so that ${\mathfrak{g}}^x={\mathfrak{h}}^x\oplus {\mathfrak{q}}^x$ and the dimension of the $G_e^x$-orbit through eH is $\text{dim}{\mathfrak{q}}^x$. We have

$$\begin{array}{c}\hfill M_{\mathit{eH}}^x\cong G_e^x/(H\cap G_e^x),\end{array}$$

and Lemma B.2 shows that the geodesic ${\text{Exp}}_{\mathit{eH}}(\mathbb{R}x)$ is central in the symmetric space $M_{\mathit{eH}}^x$ in the sense that its tangent space $\mathbb{R}x$ is central in the Lie algebra ${\mathfrak{g}}^x$ (cf. [36]).

Lemma B.4

For $y\in \mathfrak{q}$, the equality $M^y=G^y.eH$ is equivalent to

$$\begin{array}{c}\hfill {\mathcal{O}}_y\cap \mathfrak{q}=\text{Ad}(H)y.\end{array}$$ B.2

Proof

As $y\in \mathfrak{q}$, the base point eH is contained in $M^y$, and thus $G^y.eH\subseteq M^y$. So the equality $M^y=G^y.eH$ means that $M^y\subseteq G^y.eH$, i.e., $\text{Ad}{(g)}^{-1}y\in \mathfrak{q}$ implies $gH\in G^y.eH$, resp., $g\in G^{y}H$. This in turn is equivalent to $\text{Ad}{(g)}^{-1}y\in \text{Ad}(H)y$. $\square$

Lawson’s Theorem

Let $(G,{\tau }^G,H,C)$ be a causal symmetric Lie group, i.e., ${\tau }^G$ is an involutive automorphism of G, $H\subseteq G^G$ an open subgroup and $C\subseteq \mathfrak{q}$ a hyperbolic pointed generating $\text{Ad}(H)$-invariant closed convex cone. We write $\mathfrak{g}=\mathfrak{h}\oplus \mathfrak{q}$ for the corresponding decomposition of $\mathfrak{g}=\mathbf{L}(G)$.

According to [30, Lemma 2.3], ${exp|}_C$ is injective if and only if ${\mathrm{\Gamma }}_Z:=\mathfrak{z}(\mathfrak{g})\cap {exp}_G^{-1}(e)$ satisfies

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_Z\cap \mathfrak{q}={\mathrm{\Gamma }}_Z\cap (C-C)=\{0\}.\end{array}$$

If $\mathfrak{z}(\mathfrak{g})\subseteq \mathfrak{q}$, this condition is satisfied if and only if ${exp|}_{\mathfrak{z}(\mathfrak{g})}$ is injective. This condition is always satisfied if $\mathfrak{g}$ is semisimple because $\mathfrak{z}(\mathfrak{g})=\{0\}$ in this case.

Suppose that ${\mathrm{\Gamma }}_Z=\{0\}$. By [30, Lemma 2.4], ${exp|}_C$ is a homeomorphism onto a closed subset of G if and only if, for no non-zero $x\in C\cap \mathfrak{z}(\mathfrak{g})$, the subgroup $\overline{exp(\mathbb{R}x)}$ is compact. By [30, Thm. 3.1], this in turn is equivalent to the polar map

$$\begin{array}{c}\hfill \mathrm{\Phi }:C\times G^G\to exp(C)G^G\end{array}$$

being a homeomorphism onto a closed subset of G. [30, Thm. 3.1] further shows that $exp(C)G^G$ is a subsemigroup of G. If G is 1-connected, then the subgroup $G^G$ is connected and Z(G) is simply connected, so that all requirements from above are satisfied ([30, Cor. 3.2]).

Theorem C.1

(Lawson’s Theorem) Let $(G,{\tau }^G,H,C)$ be a non-compactly causal reductive symmetric Lie group. Suppose that $\mathfrak{z}(\mathfrak{g})\subseteq \mathfrak{q}$ and that ${\mathrm{\Gamma }}_Z=\{0\}$. Then $S:=exp(C)H$ is a closed subsemigroup of G with Lie wedge $\mathbf{L}(S)=\mathfrak{h}+C$.

Proof

Our assumption implies that ${exp|}_{\mathfrak{z}(\mathfrak{g})}:\mathfrak{z}(\mathfrak{g})\to Z{(G)}_e$ is bijective, hence a diffeomorphism onto the closed subgroup $Z{(G)}_e$. It follows in particular that $exp(\mathbb{R}x)\cong \mathbb{R}$ is non-compact for each non-zero $x\in \mathfrak{z}(\mathfrak{g})$. Therefore the polar map $\mathrm{\Phi }$ is a homeomorphism onto a closed subset and the remaining assertions follow from [30, Thm. 3.1]. $\square$

Remark C.2

(a) If G is reductive, then $G={(G,G)}_{e}Z{(G)}_e$ and if $x\in \mathfrak{z}(\mathfrak{g})$ satisfies $expz\in {(G,G)}_e$, then $expz\in Z{({(G,G)}_e)}^{-{\tau }^G}$, which is a discrete group. We shall see below that this group may be infinite, even if ${\mathrm{\Gamma }}_Z=\{0\}$.

(b) If $M=G_{\mathbb{C}}/G$ is of complex type and G is hermitian, then $Z(G_{\mathbb{C}})$ is finite.

(c) If M is of non-complex type and irreducible, then ${\mathfrak{g}}^c$ is simple hermitian with $\mathfrak{z}({\mathfrak{k}}^c)=\mathbb{R}ih$, where $h\in \mathcal{E}(\mathfrak{g})$ is a causal Euler element. If Z(G) is infinite, then $\mathfrak{g}$ is also hermitian, hence of tube type because it contains an Euler element [38]. Then all Euler elements in $\mathfrak{g}$ are conjugate and this implies that $(\mathfrak{g},\tau )$ is of Cayley type. So $\mathfrak{z}(\mathfrak{k})\subseteq {\mathfrak{q}}_{\mathfrak{k}}$ and thus $Z{(G)}^{-\tau }$ is infinite if G is simply connected. This shows that it is possible that ${(G,G)}_e\cap Z{(G)}_e$ is infinite.

A concrete example is the group

$$\begin{array}{c}\hfill G:=({\widetilde{\text{SL}}}_2(\mathbb{R})\times \mathbb{R})/D,\end{array}$$

where $D\subseteq Z({\widetilde{\text{SL}}}_2(\mathbb{R}))\times \mathbb{R}\cong \mathbb{Z}\times \mathbb{R}$ is the graph of a non-zero homomorphism $\gamma :Z({\widetilde{\text{SL}}}_2(\mathbb{R}))\to \mathbb{R}$. Then $Z(G)\cong \mathbb{R}$ and $Z(G)\cap (G,G)\cong Z({\widetilde{\text{SL}}}_2(\mathbb{R}))\cong \mathbb{Z}$.

Remark C.3

Suppose that $h_0\in \mathfrak{h}\cap \mathcal{E}(\mathfrak{g})$ is such that $-{\tau }_{h_0}(C)=C$, then $C\cap \mathfrak{z}(\mathfrak{g})$ is contained in $C\cap -C=\{0\}$. Therefore the condition on $C\cap \mathfrak{z}(\mathfrak{g})$ in Lawson’s Theorem (cf. Appendix C) is satisfied.

de Sitter space

In this appendix we collect some concrete observations concerning de Sitter space ${\text{dS}}^d$, which is an important example of a non-compactly causal symmetric space. Some facts on 2-dimensional de Sitter space are used in particular in some of our proofs to verify the corresponding assertions for $\mathfrak{g}={\mathfrak{sl}}_2(\mathbb{R})$.

In $(d+1)$-dimensional Minkowski space ${\mathbb{R}}^{1,d}$, we write the Lorentzian form as

$$\begin{array}{c}\hfill \beta (x,y)=x_0{y}_0-\mathbf{x}\mathbf{y}\text{for}x=(x_0,\mathbf{x}),y=(y_0,\mathbf{y}).\end{array}$$

We consider d-dimensional de Sitter space

$$\begin{array}{c}\hfill M:={\text{dS}}^d:=\{x=(x_0,\mathbf{x})\in {\mathbb{R}}^{1,d}:x_0^2-{\mathbf{x}}^2=-1\},\end{array}$$

$G={\text{SO}}_{1,d}{(\mathbb{R})}_e$ and the Euler element $h\in {\mathfrak{so}}_{1,d}(\mathbb{R})$, defined by

$$\begin{array}{c}\hfill h.(x_0,\dots ,x_d)=(x_1,x_0,0,\dots ,0).\end{array}$$

It generates the Lorentz boost in the $x_0$-$x_1$-plane. The fixed point set of the modular flow in $M={\text{dS}}^d$ is

$$\begin{array}{c}\hfill M^{\alpha }=M\cap \text{span}\{{\mathbf{e}}_2,\dots ,{\mathbf{e}}_d\}=\{(0,0,x_2,\dots ,x_d):x_2^2+\cdots +x_d^2=1\}\cong {\mathbb{S}}^{d-2}.\end{array}$$

This submanifold is connected for $d>2$ and consists of two points for $d=2$. The corresponding wedge domain is the connected subset

$$\begin{array}{c}\hfill W_M^{+}(h)=M\cap W_R=\{x\in {\text{dS}}^d:x_1>|x_0|\}.\end{array}$$

By [52, Prop. D.3], the timelike geodesics of M of velocity 1 take the form

$$\begin{array}{c}\hfill \gamma (t)={\text{Exp}}_x(tv)=cosh(t)x+sinh(t)v,\beta (v,v)=1,\beta (x,v)=0,\beta (x,x)=1\end{array}$$

whereas the trajectories of the modular flow are

$$\begin{array}{c}\hfill {\alpha }_t(x)=e^{\mathit{th}}x=(cosh(t)x_0+sinh(t)x_1,cosh(t)x_1+sinh(t)x_0,x_2,\dots ,x_d).\end{array}$$

Comparing both expressions leads for h-modular geodesics to the conditions

$$\begin{array}{c}\hfill x_2=\cdots =x_d=0\text{and}v=h.x=(x_1,x_0,0,\dots ,0).\end{array}$$

Therefore exactly two orbits of the modular flow are timelike geodesics. If we also ask for the geodesic to be positive with respect to the causal structure, then $x_1>0$ determines the geodesic uniquely.

We infer from [52, Prop. D.3] that

$$\begin{array}{c}\hfill {\text{Exp}}_{{\mathbf{e}}_2}(t{\mathbf{e}}_1)=cos(t){\mathbf{e}}_2+sin(t){\mathbf{e}}_1\end{array}$$

is a closed space-like geodesics. For $0<t<\pi$, its values are contained in $W_M^{+}(h)$, and this geodesic arc connects the two fixed points ${\mathbf{e}}_2$ to $-{\mathbf{e}}_2$ of the modular flow.

Remark D.1

In addition to h, we also consider the Euler elements defined by

$$\begin{array}{c}\hfill h_d(x_0,\dots ,x_d)=(x_d,0,\dots ,0,x_0).\end{array}$$

The involution corresponding to h acts on ${\mathbb{R}}^{1+d}$ by

$$\begin{array}{c}\hfill {\tau }_h(x_0,x_1,\dots ,x_d)=(-x_0,-x_1,x_2,\dots ,x_d),\end{array}$$

and its antilinear extension acts on ${\mathbb{C}}^{1+d}$ by

$$\begin{array}{c}\hfill {\overline{\tau }}_h(z_0,z_1,\dots ,z_d)=(-\overline{z_0},-\overline{z_1},\overline{z_2},\dots ,\overline{z_d}).\end{array}$$

Note that, in $\mathfrak{g}$, we have ${\tau }_h(h)=h$ and ${\tau }_h(h_d)=-h_d$, so that $h\in {\mathfrak{q}}_{\mathfrak{p}}$ and $h_d\in {\mathfrak{h}}_{\mathfrak{p}}$.

In ${\mathbb{C}}^{1+d}$, we consider the domain

$$\begin{array}{c}\hfill \mathrm{\Xi }:=\{z=x+iy\in {\mathbb{C}}^{1+d}:y_0>0,y_0^2>y_1^2+\cdots +y_d^2\}.\end{array}$$

On $\mathrm{\Xi }$ the antiholomorphic involution ${\overline{\tau }}_h$ has the fixed point set

$$\begin{array}{cc}\hfill {\mathrm{\Xi }}^{{\overline{\tau }}_h}& =\mathrm{\Xi }\cap (i{\mathbb{R}}^2\oplus {\mathbb{R}}^{d-1})\hfill \\ \hfill & =\{(i{x}_0,i{x}_1,x_2,\dots ,x_d):x_0>|x_1|,-x_0^2+x_1^2-x_2^2-\dots -x_d^2=-1\}\hfill \\ \hfill & =\{(i{x}_0,i{x}_1,x_2,\dots ,x_d):x_0>|x_1|,\underset{>0}{\underbrace{x_0^2-x_1^2}}+x_2^2+\cdots +x_d^2=1\}.\hfill \end{array}$$

It follows in particular that

$$\begin{array}{c}\hfill x_0^2-x_1^2\in (0,1].\end{array}$$

The analytic extension of the modular flow ${({\alpha }_t)}_{t\in \mathbb{R}}$ acts on $\mathrm{\Xi }$ by

$$\begin{array}{c}\hfill {\alpha }_{\mathit{it}}(z_0,\dots ,z_d)=(cost·z_0+isint·z_1,isint·z_0+cost·z_1,z_2,\dots ,z_d).\end{array}$$

Starting with a ${\overline{\tau }}_h$-fixed element $z=(i{x}_0,i{x}_1,x_2,\dots ,x_d)$ in $\mathrm{\Xi }$, this leads to

$$\begin{array}{c}\hfill {\alpha }_{\mathit{it}}(i{x}_0,i{x}_1,x_2,\dots ,x_d)=(cost·i{x}_0-sint·x_1,-sint·x_0+cost·i{x}_1,x_2,\dots ,x_d)\end{array}$$

with imaginary part

$$\begin{array}{c}\hfill (x_{0}cost,x_{1}cost,0,\dots ,0),\end{array}$$

so that we obtain for $|t|<\pi /2$ that

$$\begin{array}{c}\hfill |x_{0}cost|=x_{0}cost>|x_1|cost,\end{array}$$

which implies that

$$\begin{array}{c}\hfill {\alpha }_{\mathit{it}}(z)\in \mathrm{\Xi }\text{for}z\in {\mathrm{\Xi }}^{{\overline{\tau }}_h}\text{and}|t|<\pi /2.\end{array}$$ D.1

Example D.2

For the special case $d=2$, we have ${\mathfrak{sl}}_2(\mathbb{R})\cong {\mathbb{R}}^{1,2}$ and the Euler element

$$\begin{array}{c}\hfill h^0=\frac{1}{2}\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\in {\mathfrak{sl}}_2(\mathbb{R})\cong {\mathbb{R}}^{1,2}\end{array}$$

corresponds to the base point ${\mathbf{e}}_2$ (see [52]), so that

$$\begin{array}{c}\hfill {\mathfrak{sl}}_2(\mathbb{R})\supseteq {\mathcal{O}}_h\cong {\text{dS}}^2\subseteq {\mathbb{R}}^{1,2}.\end{array}$$

Accordingly,

$$\begin{array}{cc}\hfill C=& \text{cone}(e^0,f^0),C^c=\text{cone}(e^0,-f^0),\text{and}{x}_0:=\frac{1}{2}(e^0-f^0)\hfill \\ \hfill =& \frac{1}{2}\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\in C^c.\hfill \end{array}$$

For $g_t:=exp(t{x}_0)$ we then have

$$\begin{array}{c}\hfill \text{Ad}(g_{\pi /2})h^0=-h^1,\text{Ad}(g_{\pi /2})h^1=h^0\text{and}\text{Ad}(g_{\pi })h^0=-h^0.\end{array}$$

We also note that, for $0<t<\pi$, the Lie algebra element $\text{Ad}(g_t)h^0$ corresponds to ${\text{Exp}}_{{\mathbf{e}}_2}(t{\mathbf{e}}_1)\in W_M^{+}(h^0)$. Note that

$$\begin{array}{c}\hfill g_{\pi }\in K^{{\tau }_h^G}=K^G.\end{array}$$

Author Contributions

VM, KHN, GO wrote the manuscript on equal parts.

Funding

Open Access funding enabled and organized by Projekt DEAL.

Declaration

Conflicts of interest

The authors declare no competing interests.