Abstract
Cooling of electronic components is one of the most important concerns of manufacturers. Using heatsinks with different models is one of the recommended methods for cooling. To compare 12 types of heatsinks, including 3 types of fin-pin heatsinks with rectangular pins, 3 types of fin-pin heatsinks with circular pins, 3 types of fin-pin heatsinks with conical pins, and 3 types of simple fin heatsinks in 5, 7, and 9 fin types regarding forced displacement heat transfer, an experiment was conducted. A special setup designed and built for these types of heatsinks was used to conduct the test. The setup had dimensions of 100 cm × 12 cm x 3 cm with an opening of 120 cm × 120 cm for placing a fan to create airflow with variable speeds and a place for placing the heatsink at the end of the wind tunnel under variable temperatures. The test results showed that the maximum error in the two experimental tests was 6 %. Also, the results showed that in all 4 types of heatsinks, 7-fin pin types had 4 to 20% lower thermal resistance and 20 to 100% higher convection heat transfer coefficient compared to the 5- and 9-fin pin types respectively. When comparing the heatsinks with the same number of fins, it was observed that the 7 and 9-fin types of heatsinks with conical fins have lower thermal resistance and higher convection heat transfer coefficient than other types of heatsinks with the same number of fins, The conical fins having more than 81 % convection heat transfer coefficient compared to the plate fin heatsink. It was also observed that in the 5-pin fin heatsink design, the plate-fin heat sink had the lowest amount of heat resistance due to its higher surface area with the flowing air current.
Keywords: Thermal resistance, Thermal boundary layer, Displacement heat transfer coefficient
Nomenclature
- A
Surface Areas [m2]
- C
Constant in turbulent model
- H
Height [m]
- L
Distance from base in x-direction [m]
- N
Fin number [−]
- p
Pressure [pa]
- E
Pumping power [W]
- Q
Heating power [W]
- R
Resistance []
- Re
Reynolds number [−]
- T
Temperature [K]
- x, y, z
Cartesian coordinates
- X, Y, Z
Dimensionless cartesian coordinates
- U, V, W
Dimensionless velocity
Greek symbols
Constant in turbulent model
Fin spacing [mm]
Differential
Viscosity []
Density []
Dimensionless temperature
Subscripts
- i, j
Repeated-subscript indices
- in
Inlet
- t
Turbulent flow
- out
Outlet
- th
Thermal
- p
Flow passage
- s
Solid
- w
Wall
- f
Fluid
1. Introduction
Heat transfer is one of the most important concerns for manufacturing across all fields such as electronic devices and factories. One method of improving heat transfer rates is using heat sinks, which come in all shapes and sizes and dissipate heat through active and passive convection heat transfer. In passive heat sinks, heat is transferred via free convection; in active heat sinks, this is done by forced convection with a fan or a water current. Due to the nature of forced convection, it has higher heat transfer when compared to passive heat transfer. But because it uses fluid currents to cool it requires an external force to achieve it.
Al-Nabas [1], a significant number of experimental/numerical work has been done according to the problems raised by him, who raised the first problem of displacement between two parallel planes. In 1963, Stanner and McManus [2], who calculated the average heat transfer efficiency not only in the horizontal mode but also in the 45° and vertical modes, showed the first work on rectangular horizontal fins, they showed that the application Misalignment of fins on a surface can reduce the overall heat transfer compared to when a base is used alone. In 1965, Welling and Wooldridge [3] conducted their laboratory studies on fixed-length angled rectangular heatsinks that were located on a vertical surface and were able to calculate the optimal height of the fins to create maximum heat transfer rate.
Salami Tijani and Benti Jafari [4] investigated forced displacement heat transfer numerically and experimentally on heatsinks with pinholes in 2017. They found that the perforated pin heatsink temperature distribution is higher than the other models. They also found that Perforated pins also reduced pressure drop which reduced the required energy to pump. Also, the Nusselt number for the pinhole heatsink is higher than other numerical models.
In 2019, Moradi Kazroni et al. [5] investigated the heatsink of the computer processor under slowly forced displacement using the structural stability method. They found that the number of fins as well as fin height significantly affected heat transfer rates. In 2017, Karvinen and Lindstedt [6] worked analytically on the case that produces heat or has a constant maximum temperature. The results of their research helped to determine the minimum mass of the blades. Nilpong et al., in 2021 [7] observed heatsinks' thermal performance under the effects of different pin configurations.
In 2021, Sin Chen et al. [8] investigated a thermoelectric generator and its performance with an installed heatsink. In this experiment, they compared the characteristics and output power of a thermoelectric generator by investigating the device with and without a heatsink. They concluded that although installing more square pin blades increased the pressure drop, the net power output was also increased. In 2021, Al-Saeed et al. [9] experimentally investigated the effects of twist angle on the thermo-hydraulic performance of hexagonal and square pins in forced displacement. They found that by increasing the twist angles, the Nusselt number and the heat transfer coefficient were also increased. They also discovered that using a hexagonal cross-section creates a larger Nusselt number compared to using the square cross-section, as well as a reduction in thermal resistance with the increase of the Reynolds number.
In 2018, Yun et al. [10] numerically and experimentally studied heatsink performances based on distance optimization. The optimal distance was discovered to be far from the upper flow of heat loss, which increased the efficiency by 30 % compared to other modes. In 2016, Chingulpitak et al. [11] investigated the effects of the heatsink with a cross-section on flow characteristics. The experimental results showed that the cross-sectional distance of one and a half millimeters creates the lowest thermal resistance. In 2021, Mitt and Thiel [12] studied fin arrangement effects on the heatsink's thermal and characteristic performance. The experimental investigation of forced convection heat transfer was carried out on parallel W-shaped grooved surfaces. They discovered that the W-shaped grooved surface has a higher convection heat transfer coefficient compared to the parallel grooved surface because the W-shaped fin creates a larger cross-sectional area for heat transfer. The W-shaped fin angles also blocked air from spreading in that area. Creates that causes the air to spread in that area and thus reduces the heat.
Ebrahim et al. [13] experimentally and numerically studied the increase of heatsink heat transfer by using new hole-making techniques. In this research, Ann Head addressed the effect of circular holes by changing the holes' number and sizes, changing air flow speed, and also changing input powers to find its effects on the heatsink fins' thermal and hydraulic performance. It was discovered perforated fins' thermal performance is higher when compared to the non-perforated fins and it reduced fin temperatures by 8.5C. In addition, the results showed that convection heat transfer was improved with the increase in hole size and numbers. When comparing hydraulic performance, perforated vanes showed better results when compared with solid vanes due to the lower pumping power required. Prasad and Gupta [14] investigated the removal of a semicircular piece from the top of a rectangular fin and its effects on the heatsink performance. The results showed that the removal process was effective as it increased the efficiency of the heatsink fins.
Shadlaghani et al. [15] investigated the triangular fin thermal performance with/without longitudinal holes and numerically optimized its performance by changing the shapes and the dimensions of the fins while keeping it at constant volume. The results showed that the heat transfer rate in the triangular fins has a direct correlation with the ratio of height to thickness. It also showed that holes of square and circular shape increased the thermal performance compared to the triangular holes. Niranjan et al. [16] studied the thermal and hydraulic performance of a heatskin with square micro-pin vanes under forced convection heat transfer. They considered the square micro-pin to be the most suitable fin geometry under forced convection. In this study,25 heatsinks were tested. The results showed that lower thermal resistance is related to the high pressure drop and the heat transfer coefficient increased with the increase in fin height while it decreased with the increase of fin distance. Somin et al. [17] investigated the increase of forced convection heat transfer with a fin-plate heatsink with a fractal insert. In this experiment, they concluded that the existence of the fractal network in the forced convection heat transfer in the plate heat sink significantly improved the thermal performance. Chen et al. [18] numerically studied the effects of fin spacing and airflow velocity on a plate fin heatsink under mixed heat transfer to investigate the flow characteristics and thermal performance of the device. Kwalramani et al. [19] investigated and researched the smooth single-phase friction coefficient along with the Nusselt number for an in-line micro pin fin heatsink by analyzing the thermodynamic characteristic of the heatsink when constant heat flux is transferred from the bottom of the heatsink. They discovered that the heat transfer coefficient changes repeatedly on each oval fin after the fifth row fins from the entrance of the micro heatsink. Bassim et al. [20] researched the increase of heat transfer in plate-fin heat sinks with fillets using Computational Fluid Dynamics (CFD) analysis. This research develops a new thermal design for plate-fin heatsinks with a fillet profile so that the material removed from the base is attached to the plate fins in the form of half-round pins to produce fillets. The evaluation of the device and its thermal performance was done using CFD commercial codes. In this study, semi-circular pins are arranged in different positions and are under two different types of flow which include parallel and impingement flow. The results of this study showed that the vertical arrangement of the semi-circular pins under the impingement flow had better thermal performance than the other configurations. Javad et al. [21] conducted a numerical investigation on cooling LEDs using circular heatsinks. In this study, the heatsink was cooled using a two-phase turbulence nanofluid flow under different positions. The results of this study indicated that nanofluid flow velocity is directly correlated to the thermal performance of the heatsink. Fares et al. [22] investigated and evaluated the thermohydraulic characteristics and performance of a 3D printed circuit heatsink using a Shear stress turbulence model with water and critical CO2 as coolants. The results show that the performance of the 3D-printed heatsink is significantly superior to the classic design which can be used in future designing of heatsinks. Haque et al. [23] studied and investigated the thermal heat transfer of several types of heatsink designs. These designs included rectangular, elliptical, and airfoil-shaped pins. This study shows that pin-fin with elliptical-shaped geometry is an important factor in increasing the thermal and hydro-thermal performance.
Increasing the surface area of a heatskin may improve heat transfer rate and thermal performance but it may also have a negative effect on electromagnetic compatibility (EMC) [24]. Adding more surface area blocks the dimensions of the heatsink comparable with the operating frequency wavelength, thereby making the heatsink behave similarly to that of an antenna. in cases where circuit elements are placed around the heatsink, the base part of the heatsink behaves like a patch antenna and the vertical pins and fins on the heatsink will act like a monopole antenna, thereby causing electromagnetic interference (EMI) [25]. Basyigit et all [26] studied the effects of fin types of the heatsinks on radiated emission on the printed circuit board at the S–C band. They simulated and compared the effects of operating frequency on heatsinks with different designs such as heatsinks with parabole-plate fin, square-pin fin, and circular-pin fin with different orientations and positioning. They have concluded different heatsinks perform differently under certain frequencies. In this study for example it is better to use fin-pin type heatsinks for frequencies of 2–3.4 GHz, and 4.7–5.6 GHz to reduce radiation emissions (RE) and have less EMI. Jin et al. [27] studied a novel heatsink with a mushroom-type electromagnetic band gap (EGB). This EGB structure is attached to the bottom of the heatsink device to suppress high EMI radiation of packages with certain specific frequency ranges. The results of this study show that by attacking the mushroom-type EGB, it offers remarkable suppression of EMI radiation at high frequencies from 9.2 to 15.8 GHz.Genc et al. [28] investigated several heatsinks with horizontal and vertical orientations to reduce the EMI caused by heatsinks on the electronic components. It was discovered that horizontal orientation is recommended for 10 % of the whole frequency region of operation while vertical orientation is preferred for 24 % regardless of the heatsink type.
Despite numerous types of research in the field of heatsinks, there seem to be many gaps regarding their best construction in terms of higher heat transfer coefficient and lower thermal resistance. It is not even possible to recommend a specific building for all conditions and it is necessary to test the proposed buildings in different conditions. This research was also carried out to evaluate a variety of heatsinks with a new design in specific environmental conditions. The goal is to achieve the optimal distance of the fins for the formation of a complete boundary layer and better heat transfer at a lower cost, as well as to achieve the best possible design based on the geometric shape of the pins. In this experiment, new designs of pins with different geometric shapes and the optimal distance between them based on experiments and calculations were used. A design including 4 models with different pins has been compared, which has not been done before in this scope. Also, the laboratory setup has been designed and optimized based on the built heat sink.
2. Experimental setup
To investigate the heat transfer of the joint displacement, a device was needed that, while having the ability to accurately measure various thermal and electrical parameters, would provide the necessary and suitable conditions for the laboratory. For this purpose, a device was made. The schematics of this device can be seen in Figure and the picture of the device can be seen in Fig. 2.
Fig. 2.
Picture of the setup.
This test was performed on 12 heatsink models under forced convection heat transfer using the setup device. The heatsinks in this experiment include a simple fin model, a pin fin with conical pins, a pin fin with circular pins, and a pin fin with cubic pins with the number 5, 7, and 9 fins/pin row for each of the heatsinks. The heatsinks were placed in a special place inside the setup according to Fig. 1. Under the heatsinks, a heat source was added which was responsible for the heatsink temperature adjustment. At the beginning of the setup, a variable-speed fan was added. The fan speed can be adjusted by a digital dimmer. Also, an anemometer was placed at the end of the tunnel to determine the average wind speed. A differential pressure gauge was placed before and after the heatsink to calculate the pressure drop. Experiments were performed for heatsinks at average speeds of 1, 1.5, 2, 2.5, 3, and 3.5 m/s. The experiment was carried out at a constant temperature of 60, 70, 80, and 90° Celsius. The temperature of the heatsink in its different parts was measured by a 12-channel thermometer. These experiments were repeated twice and the error coefficient was also calculated.
Fig. 1.
Schematic of Heatsink testing device.
3. Heat sink design
The heatsink designs can be seen in Fig. 3 and the information regarding the heatsink geometric design can be seen in Table 1 and Table 2. Fig. 3 shows all the heatsink designs used, including plate fin heat sinks (PFHS), Pin plate fin heatsink with square (PPFHSS), circle (PPFHS Circle), and cone (PPFHS Cone) with pin fin rows of 5,7, and 9. Table 1 includes the type of heatsink, Fin spacing, number of pins, and distance between fin columns while Table 2 shows common heatsink dimensions shared between all the heatsink types.
Fig. 3.
All models of heatsink used in the experimental setup with different pin fin row (A) 5-PFHS (B) 7-PFHS (C) 9-PFHS (D)5-PPFHSS (E) 7-PPFHSS (F) 9-PPFHSS (G) 5-PPFHS Cricle (H) 7-PPFHS Cricle (I) 9-PPFHS Cricle (J) 5-PPFHS Cone (K) -PPFHS Cone (L) 9-PPFHS Cone.
Table 1.
Information regarding each type of heatsink used in the experimental setup.
| Type of heatsink | Fin Spacing S (mm) |
Fin-Pin Row (n) | Number of pins | Distance between pin columns s (mm) |
|---|---|---|---|---|
| PFHS | 12.5 | 5 | N/A | N/A |
| PFHS | 7.68 | 7 | N/A | N/A |
| PFHS | 5.25 | 9 | N/A | N/A |
| PPFHSS | 12.5 | 5 | 13 | 4.5 |
| PPFHSS | 7.68 | 7 | 13 | 4.5 |
| PPFHSS | 5.25 | 9 | 13 | 4.5 |
| PPFHS Circle | 12.5 | 5 | 13 | 4.5 |
| PPFHS Circle | 7.68 | 7 | 13 | 4.5 |
| PPFHS Circle | 5.25 | 9 | 13 | 4.5 |
| PPFHS Cone | 12.5 | 5 | 13 | 4.5 |
| PPFHS Cone | 7.68 | 7 | 13 | 4.5 |
| PPFHS Cone | 5.25 | 9 | 13 | 4.5 |
Table 2.
Common geometrical information regarding heatsinks.
| Basepin Thickness d (mm) | Fin/Pin Height H (mm) |
Base Heatsink Length L (mm) |
Base Heatsink width W (mm) |
Base Fin Thickness D (mm) |
|---|---|---|---|---|
| 2 | 24 | 80 | 60 | 2 |
Dimensionless equations of continuity, momentum, and energy equations are as follows [29]:
| (1) |
Momentum equations in x, y, and z directions are as follows [29]:
| (2) |
| (3) |
| (4) |
The energy equation is as follows:
| (5) |
The dimensionless parameters are obtained as follows [29]:
Heat sink resistance is obtained from the following formula [30]:
| (6) |
ΔT is the temperature difference between the base of the heatsink and the surrounding air, and Q is the thermal power applied to the base of the heatsink. This equation is used to calculate the thermal performance of heatsinks.
The Reynolds number is calculated as follows [30]:
| (7) |
The Nusselt number inside the tube is obtained from the following equation:
| (8) |
Continuity equation, momentum for turbulent flow is as follows [30]:
| (9) |
| (10) |
To calculate the measurement uncertainty, it is necessary to first identify the sources of uncertainty and then calculate the amount of uncertainty related to each of the sources. Then by combining all the uncertainties, the total uncertainty is obtained. There are two general methods to evaluate and calculate the uncertainty of each parameter:
Type A evaluation: Usually, the uncertainty is calculated according to the repetition of measurements and with the help of statistical analysis. In fact, during repeated measurement, when faced with a set of data, and in this case, the average of the data and the standard deviation was used to determine the uncertainty of the measurement [30]:
| (11) |
Type B evaluation: This uncertainty can be obtained based on calibration certificates and information from manufacturers of measuring instruments, etc. It needed measurement tools to calculate the uncertainty:
| (12) |
To calculate the overall uncertainty of each variable, it is necessary to combine the uncertainties of type A and B according to the formula of the root of the sum of squares of each of them.
| (13) |
The results of the experimental uncertainty can be seen in Table 3.
Table 3.
Uncertainty of different models of heatsinks temperatures.
| Type of Heatsink | Velocity (m/s) | Instrumental Uncertainty | Uncertainty of Replication | Total Uncertainty |
|---|---|---|---|---|
| 9-PPFHS Cone | 3.5 | 0.0289 | 0.493 | 0.4938 |
| 9-PPFHS Circle | 3.5 | 0.0289 | 0.594 | 0.5947 |
| 9-PPFHSS | 3.5 | 0.0289 | 0.287 | 0.2884 |
| 9-PFHS | 3.5 | 0.0289 | 0.652 | 0.6526 |
The experiment was performed twice to confirm the accuracy of it. The results shown here are within acceptable parameters. All other heatsinks were tested as well and the results were within this range.
4. Results and discussion
The Convection heat transfer coefficient in terms of the pin row distance for the plate-fin heat sink is shown in Fig. 4 for the temperature of 80C. As can be seen in this figure, the heat transfer coefficient increased with the increase of the distance between the rows of fins. As the distance increased and the number of vanes decreased, the displacement heat transfer coefficient decreased. The change in the temperature difference did not affect the behavioral process and only at a fixed distance, the increase in the temperature difference caused an increase in the displacement heat transfer coefficient.
Fig. 4.
The trend of changes in forced convection heat transfer coefficient according to the distance between the rows of fin arrangement at 80 °C for the plate fin heatsink.
To investigate the effect of the distance between the rows of vanes on the thermal resistance, the trend of changes in the ratio of the thermal resistance of the arrangement of the vanes, according to the distance between the vanes, at the temperature of 70° Celsius is shown in Fig. 5 As can be seen, by increasing the distance between the blades, first the thermal resistance decreases with the increase of the distance up to 7.68 mm and then it increases. It seems that the distance of 7.68 mm is the appropriate distance between the rows of fins in this type of simple heatsink, having 30.97 % more convection heat transfer coefficient than when the pin-fin distance is 5.25 mm and more than 30.26 % than when the distance is 12.5 mm. By comparing the heat resistance, the heatsinks with the 7.68 mm fin pin spacing have 4 % less heat resistance than the heatsinks with the 5.25 mm fin spacing and 16.2 % less than the 12.5 mm fin-pin space heatsinks. By analyzing this trend, it is shown that in the 5-fin plate heatsink, the distance between the fins is large, as well as having fewer fins compared to the other models. Due to the large distance between the fins, a suitable boundary layer is not formed between fin space, and also due to less surface area in comparison to the other two heat sinks, it has a lower convection heat transfer coefficient. However, in the 7-fin model, the distance is very close to the optimal distance, and the boundary layer is completely formed and overlapped, and the cross-section is also suitable. But in the 9-fin model, because the distance between the fins has decreased, the boundary layers between the fin space interfere with each other, and although the number of fins is more than in the previous models, due to the interference of the boundary layer, the convection heat transfer coefficient is decreased.
Fig. 5.
The trend of changes in thermal resistance about the distance of the vanes for a temperature of 70° Celsius for plate-fin heatsink.
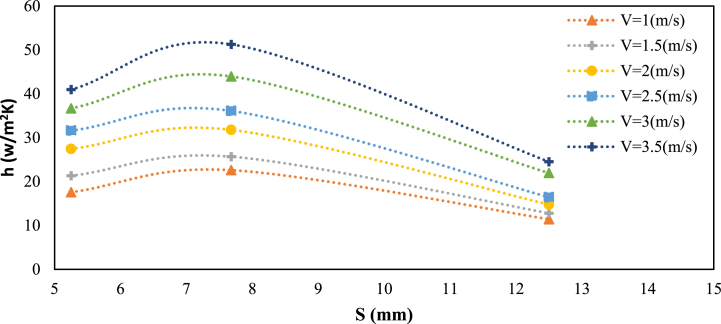
In Fig. 6, the heat transfer coefficient of the displacement according to the distance between the rows of pins at 90C for the square pin fin heatsink is shown in Fig. 6. It can be seen that the heat transfer coefficient increased by increasing the distance between the rows of fins. However, the displacement heat transfer coefficient decreased with a further increase in the distance and a decrease in the number of rows. The change in the temperature difference did not affect the behavioral process and only at a fixed distance, the increase in the temperature difference caused an increase in the displacement heat transfer coefficient.
Fig. 6.
The trend of changes in the forced displacement heat transfer coefficient in terms of the distance between the rows of fin arrangement in fin-pin heatsinks at a temperature of 90° Celsius for square-pin fin heatsinks of different models.
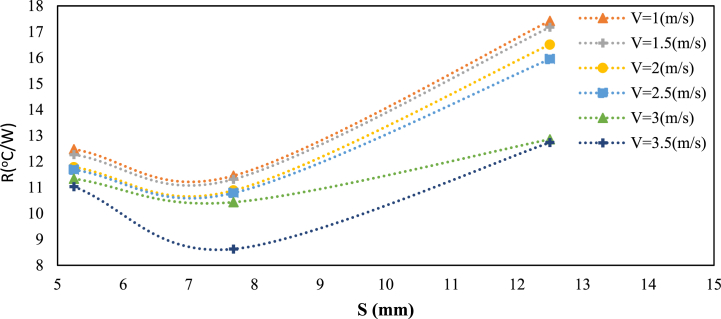
In Fig. 7, the trend of changes in the thermal resistance of the pin arrangement is shown about the distance between the vanes at the temperature of 60° Celsius for the different models of square pin heatsink. It can be seen that by increasing the distance between the vanes, first, the thermal resistance decreases with the increase of the distance up to 7.68 mm and then it increases. It seems that the distance of 7.68 mm is the appropriate distance between the rows of fins in this type of simple heatsink. No consistent trend was seen in all the distances compared to the resistance. This can be caused by possible errors during measurements. Comparing the results, the 7.68 mm fin space heatsinks have 28.19 and 29.10% more convection heat transfer than the 5.25 mm and 12.5 mm fin space heatsinks respectively. The reason can be attributed to the optimal fin-pin spacing. This fin spacing produces the optimal boundary layer which is the reason for the higther convection heat transfer coefficient. Comparing the heat resistance, it is shown that the 7-pin fin heat sink design has 6.53 and 11.58% less heat resistance than the 5.25 and 12.5 mm heatsinks respectively. Here it can be seen that the surface area has more of an effect here.
Fig. 7.
The trend of changes in thermal resistance about the distance between blades for a temperature of 60° Celsius for square pin fin heatsink.
In examining the heat transfer coefficient of forced displacement according to the distance between the blade rows. These types of heatsinks behaved similarly to the behavior of other fin-pin heatsinks so that by increasing the distance between the rows of fins up to 7.68 mm, the displacement heat transfer coefficient increased and then decreased. As can be seen in Fig. 8, the temperature change does not affect the behavior, and at any given distance, the increase in temperature difference caused an increase in the displacement heat transfer coefficient.
Fig. 8.
The trend of changes in the forced displacement heat transfer coefficient according to the distance between the rows of fin arrangement in fin-pin heatsinks at a temperature of 60° Celsius for colonial pin fin heatsink.
In Fig. 9, the trend of changes in the thermal resistance of the vanes arrangement is shown about the distance between the vanes at temperatures of 60, degrees Celsius. It can be seen that by increasing the distance between the vanes, first, the thermal resistance decreases with the increase of the distance up to 7.68 mm and then it increases. It seems that the distance of 7.68 mm is the appropriate distance between the rows of fins in this type of simple heatsink. The 7.68 mm fin spacing heatsink has 20.4% and 107% more convection heat transfer coefficient than the 5.25 mm and the 12.5 mm fin spacing heatsinks. It also has 9.96 and 21.17% less heat resistance respectively.
Fig. 9.
The trend of changes in thermal resistance about the distance between blades for a temperature of 60° Celsius (conical pin fin heatsink).
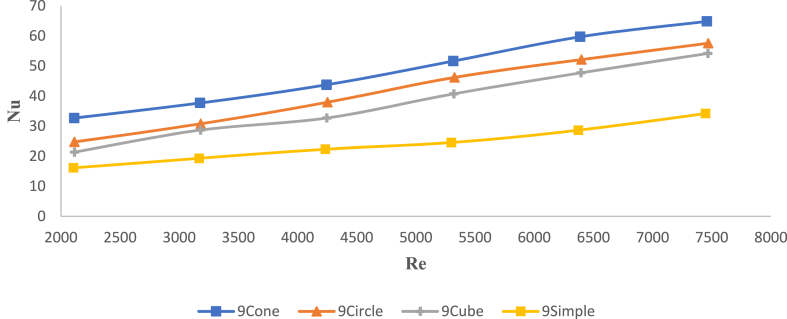
Fig. 10 shows the changes in the Nusselt number compared to the Reynolds number for four 9-blade heatsink models at four temperatures of 60, 70, 80, and 90° Celsius. The results showed that the Nusselt numbers of square fin-pini and circular fin-pini heatsinks are 47–50 % higher than the simple heatsink model. In addition, the conical fin-pin heatsink had a higher Nusselt number compared to other fin-pin heatsink models. Compared to the simple heatsink, the Nusselt number of the conical fin-pin heatsink was 81.4 % higher. This is due to having a better path for airflow in the fin-cone heatsink. While the simple heatsink has the largest cross-sectional area for heat transfer, the less path between the fins of the simple heatsink prevents better convective heat transfer. When fins are replaced with pins, the fan-driven air has a larger path to pass through the fins of the heatsink. This phenomenon led to higher Nusselt numbers and higher heat transfer coefficients in fin-pin heatsinks compared to the simple heatsink model. In the fin-pin heatsink model, the cone-shaped fin-pin heatsink geometry creates a better path for airflow through the fins of the heatsink. While the number of fins of this heatsink is the same as the number of square and circular fins, the figures show that these models have a lower Nusselt number than the conical fin-pin heatsink. The reason for the difference is the geometry of circular and square pins. The circular base is similar to the conical pin in terms of having the same base with the same cross-sectional area and the same diameter of 2 mm, but the difference in the geometry of these two bases shows that the convection heat increases with the addition of fins. Having less cross-sectional area blocking airflow through the fins of the heatsink allows the flowing air to make better contact with the heatsink as well as creating a more optimal boundry layer for convenction heat transfer, resulting in a better Nusselt number. Airflow contact is also affected by pin geometry. When comparing the fin-circular fin heatsink and the fin-pin square heatsink, it is clear that the fin-fin square heatsink has a lower Nusselt number than the fin-fin heatsink, despite having a larger cross-sectional area. This is also a result of the square pin geometry, which causes the airflow to stagnate as it reaches the front end of the heatsink, resulting in less contact between the air and the heatsink cross-section, both for the pins and fins and a less optimal boundry layer compared to the cone pin-fin heatsink.
Fig. 10.
Comparison of the changes in the ratio of Nusselt number to Reynolds number for 4 types of 9-blade heatsinks at 70° Celsius.
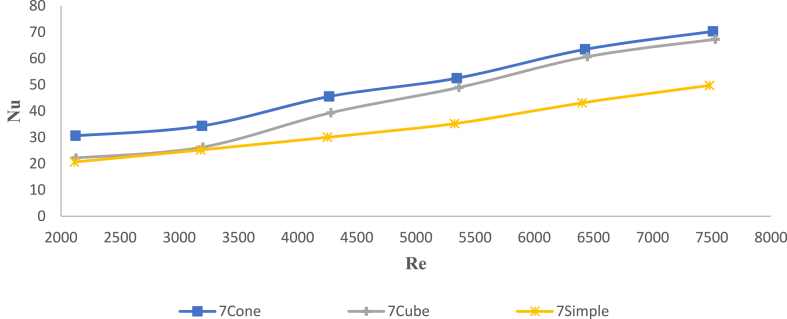
Fig. 11 shows the Nusselt number for the 7-pin heatsinks. In the heatsinks with 7 simple fins and fin-pini, it was observed that the increase of Nusselt number for the two heatsink models of square and conical fin-pini is close to each other and they have a larger Nusselt number than the simple type. This process is similar to 9-pin heatsinks. The reason for this was the proper geometry of the pins as well as the proper number of blades. The Nusselt number of 7-pin heatsinks was the largest compared to 9-pin and 5-pin heatsinks.
Fig. 11.
Comparison of the changes in the ratio of Nusselt number to Reynolds number for 3 types of 7-blade heatsinks at a temperature of 70° Celsius.
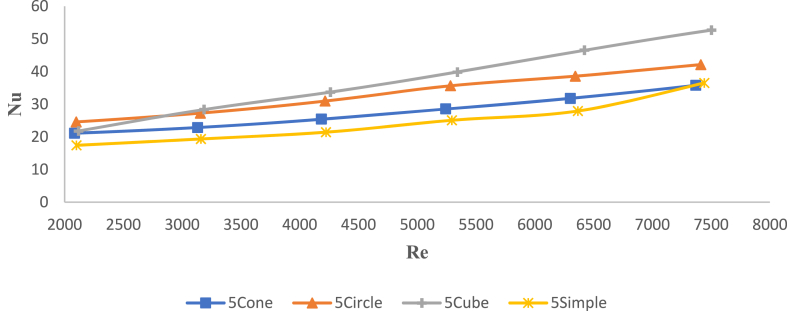
In the case of four types of simple 5-blade heatsinks and fin-pin shown in Fig. 12, it was observed that with the increase of Reynolds number, the amount of Nusselt number of the square fin-pini heatsink increased more than other heatsinks. The reason for this is due to the presence of a larger cross-sectional area than other heatsinks. This process is for four temperatures 60, 70, and 80. 90 °C was true. In the lower Reynolds number, it was observed that the square fin-pini heatsink and the circular fin-pini heatsink overlap in terms of the Nusselt number. But at higher Reynolds numbers, this difference increased. This is due to the effect of pin geometry at higher speeds.
Fig. 12.
Comparing the changes in the ratio of Nusselt number to Reynolds number for 4 types of 5-blade heatsinks at 70° Celsius.
The thermal resistance comparison between these models of 9-pin heatsinks is shown in Fig. 13. It can be interpreted in this way that the lowest thermal resistance at 60 °C is related to the square fin-pin heatsink model and simple heatsink. At higher temperatures, conical, circular, and square fin-pin heatsinks had similar performance and their thermal resistance was lower than the simple heatsink type. This was due to the proper geometry of fin-pin heatsinks. In general, thermal resistance decreased with increasing temperature. The contact area of the square fin-pin heatsink is more than other types of fin-pin. Although the simple heatsink has a larger cross-sectional area than the square fin-pin heatsink; the simple heatsink passes less airflow. In a square fin-pin heatsink, placing pins instead of fins allows for more contact surface for heat exchange and transfer, in addition to allowing more air to pass through.
Fig. 13.
Comparison of changes in the ratio of thermal resistance to Reynolds number for 4 types of 9-blade heatsinks at 80° Celsius.
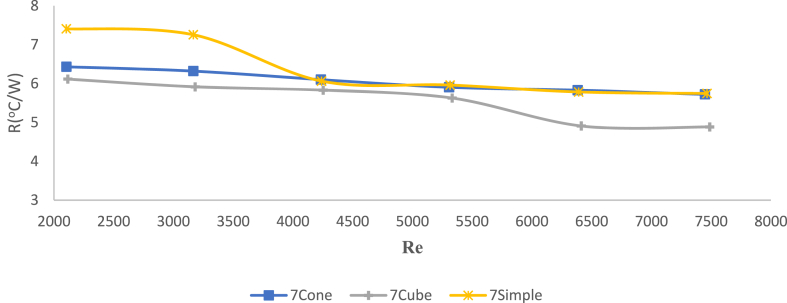
The ratio of thermal resistance to Reynolds number for 7-pin heatsinks is shown in Fig. 14. It was observed that at 60 °C, the thermal resistance of the conical and square fin-pin heatsinks had lower thermal resistance than the simple model. At higher temperatures, this difference decreased so that in some Reynolds numbers, an overlap between the thermal resistances of the heatsinks was observed. The result was similar to the results of the 9-pin heatsinks, so the square-pin heatsinks had lower thermal resistance than other heatsinks. This was due to the formation of a complete thermal boundary layer between the 7-pin square fin heatsink and better heat transfer.
Fig. 14.
Comparison of changes in the ratio of thermal resistance to Reynolds number for 3 types of 7-blade heatsinks at 80° Celsius.
The ratio of thermal resistance to Reynolds number for 5-pin heatsinks is shown in Fig. 15. It was observed that at all temperatures, the simple heatsink has a lower thermal resistance than the fin-pin heatsinks. This is due to the influence of the cross-sectional area instead of the formation of the boundary layer in heatsinks with less number of fins and greater distance between fins.
Fig. 15.
Comparison of changes in the ratio of thermal resistance to Reynolds number for 4 types of 5-blade heatsinks at 80° Celsius.
5. Conclusions
In this experiment, various new designs of heatsinks with different fin and pin arrangements including different fin-pin spacing with different geometries were tested under a special setup designed and built for these types of heatsinks. These heat sink designs consisted of different fin pin geometry including plate fins and heatsinks with square, circle, and cone pins with different fin spacing parameters. These heatsink were tested under different airflow speeds and compared in terms of thermal resistance, Nusselt number, and the effect of fin spacing. It is concluded that:
-
•
Heat sink designs with 7-pin fin rows had the highest amount of convection heat transfer coefficient compared to the other models of heatsink due to having optimal fin spacing compared to the other two models of the heatsink
-
•
Heatsink design with 7 fins was also shown to have lower heat resistance compared to the other two models even with the 9 fin pin row having more surface area compared to the other heatsinks. This shows the importance of optimization of fin spacing.
-
•
When comparing heatsinks with different pin geometry and with the same amount of pin fin rows, it is shown that for the 5-pin fin row heat sink the rectangular pin fin heat sink has the highest Nusselt number compared to the other models of the heatsink. This is the result of having a better surface area compared to the other models
-
•
While comparing the 7-pin fin row heatsinks and the 9-pin fin row heatsinks separately, it is concluded that the cone fin pin heat sink had the highest amount of Nusselt number compared to the other models due to having better geometry for the development of the boundary layer compared to the other models.
-
•
Comparing the heat resistance of the heatsink, it was concluded that for the 5-pin fin row heatsinks, the plate fin heatsink has the lowest heat resistance because of its higher surface area compared to the other models and with the boundary layer not being as efficient in this design, this was the logical conclusion
-
•
While comparing the other fin pin models, for the 7-pin fin heat sink the square pin heatsink had the lowest heat resistance on average while in the 9-fin pin model it was between the cone and the square pin model that had the lowest amount of heat resistance
Authors’ contributions
Soheil Sadarbadi Haghighi, Hamid Reza Goshayeshi, and Iman Zahmatkesh contributed to the study's conception and design. Soheil Sadrabadi Haghighi performed material preparation, data collection, and analysis. Soheil Sadrabadi Haghighi wrote the first draft of the manuscript. Hamid Reza Goshayeshi and Iman Zahmatkesh commented on the first versions of the manuscript. All authors read and approved the final manuscript.
Funding
No funding has been received for this project.
Data availability
All data generated or analyzed during this study are included in this published article. More data will be made availablie on request.
Ethics approval
The research did not involve human participants and/or animals.
Consent to participate
All authors have agreed to participate in this research.
Consent for publication
The article was written by the named authors, who are all aware of its content and have given their permission for it to be published.
CRediT authorship contribution statement
Soheil Sadrabadi Haghighi: Writing – review & editing, Writing – original draft, Software, Methodology, Investigation, Funding acquisition, Formal analysis, Conceptualization. Hamid Reza Goshayeshi: Writing – review & editing, Writing – original draft, Project administration, Methodology, Conceptualization. Iman Zahmatkesh: Supervision, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We want to thank Saman Sadrabadi Haghighi for helping with this project.
References
- 1.Elenbaas W. The dissipation of heat by free convection the inner surface of vertical tubes of different shapes of cross-section. Physica. 1942;9(8):865–874. doi: 10.1016/S0031-8914(42)80062-2. [DOI] [Google Scholar]
- 2.Starner K., McManus H., Jr. 1963. An Experimental Investigation of Free-Convection Heat Transfer from Rectangular-Fin Arrays. [DOI] [Google Scholar]
- 3.Welling J.R., Wooldridge C. 1965. Free Convection Heat Transfer Coefficients from Rectangular Vertical Fins. [DOI] [Google Scholar]
- 4.Tijani A.S., Jaffri N.B. Thermal analysis of perforated pin-fins heat sink under forced convection condition. Procedia Manuf. 2018;24:290–298. doi: 10.1016/j.promfg.2018.06.025. [DOI] [Google Scholar]
- 5.Moradikazerouni A., Afrand M., Alsarraf J., Wongwises S., Asadi A., Nguyen T.K. Investigation of a computer CPU heat sink under laminar forced convection using a structural stability method. Int. J. Heat Mass Tran. 2019;134:1218–1226. doi: 10.1016/j.ijheatmasstransfer.2019.02.029. [DOI] [Google Scholar]
- 6.Lindstedt M., Karvinen R. Conjugated heat transfer from a uniformly heated plate and a plate fin with uniform base heat flux. Int. J. Heat Mass Tran. 2017;107:89–95. doi: 10.1016/j.ijheatmasstransfer.2016.10.079. [DOI] [Google Scholar]
- 7.Nilpueng K., Mesgarpour M., Asirvatham L.G., Dalkılıç A.S., Ahn H.S., Mahian O., et al. Effect of pin fin configuration on the thermal performance of plate pin fin heat sinks. Case Stud. Therm. Eng. 2021;27 doi: 10.1016/j.csite.2021.101269. [DOI] [Google Scholar]
- 8.Chen W.-H., Wang C.-M., Saw L.H., Hoang A.T., Bandala A.A. Performance evaluation and improvement of thermoelectric generators (TEG): fin installation and compromise optimization. Energy Convers. Manag. 2021;250 doi: 10.1016/j.enconman.2021.114858. [DOI] [Google Scholar]
- 9.El-Said E.M., Abdelaziz G.B., Sharshir S.W., Elsheikh A.H., Elsaid A.M. Experimental investigation of the twist angle effects on the thermo-hydraulic performance of a square and hexagonal pin fin array in forced convection. Int. Commun. Heat Mass Tran. 2021;126 doi: 10.1016/j.icheatmasstransfer.2021.105374. [DOI] [Google Scholar]
- 10.Yoon Y., Park S.-J., Kim D.R., Lee K.-S. Thermal performance improvement based on the partial heating position of a heat sink. Int. J. Heat Mass Tran. 2018;124:752–760. doi: 10.1016/j.ijheatmasstransfer.2018.03.080. [DOI] [Google Scholar]
- 11.Chingulpitak S., Chimres N., Nilpueng K., Wongwises S. Experimental and numerical investigations of heat transfer and flow characteristics of cross-cut heat sinks. Int. J. Heat Mass Tran. 2016;102:142–153. doi: 10.1016/j.ijheatmasstransfer.2016.05.098. [DOI] [Google Scholar]
- 12.Mate D.M., Tale V.T. Effects of pin fin arrangement and its heat transfer characteristics on performance of heat sink. Mater. Today: Proc. 2021;43:2377–2382. doi: 10.1016/j.matpr.2021.01.940. [DOI] [Google Scholar]
- 13.Ibrahim T.K., Al-Sammarraie A.T., Al-Taha W.H., Salimpour M.R., Al-Jethelah M., Abdalla A.N., et al. Experimental and numerical investigation of heat transfer augmentation in heat sinks using perforation technique. Appl. Therm. Eng. 2019;160 doi: 10.1016/j.applthermaleng.2019.113974. [DOI] [Google Scholar]
- 14.Prasad B., Gupta A. Note on the performance of an optimal straight rectangular fin with a semicircular cut at the tip. Heat Tran. Eng. 1998;19(1):53–58. doi: 10.1080/01457639808939914. [DOI] [Google Scholar]
- 15.Shadlaghani A., Tavakoli M., Farzaneh M., Salimpour M. Optimization of triangular fins with/without longitudinal perforate for thermal performance enhancement. J. Mech. Sci. Technol. 2016;30(4):1903–1910. doi: 10.1007/s12206-016-0349-5. [DOI] [Google Scholar]
- 16.Singh N.R., Onkar S., Ramkumar J. Thermo-hydraulic performance of square micro pin fins under forced convection. Journal homepage. 2021;39(1):170–178. doi: 10.18280/ijht.390118. http://iietaorg/journals/ijht [DOI] [Google Scholar]
- 17.Hoi S.M., Teh A.L., Ooi E.H., Chew I.M.L., Foo J.J. Plate-fin heat sink forced convective heat transfer augmentation with a fractal insert. Int. J. Therm. Sci. 2019;142:392–406. doi: 10.1016/j.ijthermalsci.2019.04.035. [DOI] [Google Scholar]
- 18.Chen H.-T., Tseng H.-C., Jhu S.-W., Chang J.-R. Numerical and experimental study of mixed convection heat transfer and fluid flow characteristics of plate-fin heat sinks. Int. J. Heat Mass Tran. 2017;111:1050–1062. doi: 10.1016/j.ijheatmasstransfer.2017.04.065. [DOI] [Google Scholar]
- 19.Kewalramani G.V., Hedau G., Saha S.K., Agrawal A. Study of laminar single phase frictional factor and Nusselt number in In-line micro pin-fin heat sink for electronic cooling applications. Int. J. Heat Mass Tran. 2019;138:796–808. doi: 10.1016/j.ijheatmasstransfer.2019.04.118. [DOI] [Google Scholar]
- 20.Freegah B., Hussain A.A., Falih A.H., Towsyfyan H. CFD analysis of heat transfer enhancement in plate-fin heat sinks with fillet profile: investigation of new designs. Therm. Sci. Eng. Prog. 2020;17 doi: 10.1016/j.tsep.2019.100458\. [DOI] [Google Scholar]
- 21.Mustafa J., Abdullah M.M., Ahmad M.Z., Husain S., Sharifpur M. Numerical study of two-phase turbulence nanofluid flow in a circular heatsink for cooling LEDs by changing their location and dimensions. Eng. Anal. Bound. Elem. 2023;149:248–260. doi: 10.1016/j.enganabound.2023.01.029. [DOI] [Google Scholar]
- 22.Alawwa F., Saeed M., Homsi R., Zhu H., Berrouk A.S., Khalil M., Xie G., Al Wahedi Y. Thermohydraulic performance comparison of 3D printed circuit heatsinks with conventional integral fin heatsinks. Appl. Therm. Eng. 2023;226 doi: 10.1016/j.applthermaleng.2023.120356. [DOI] [Google Scholar]
- 23.Haque M.R., Redu R.R., Rafi M.A., Haque M.M., Rahman M.Z. Numerical investigation of heat transfer performance for rectangular, elliptical, and airfoil-shaped pin fin heatsinks through the novel combination of perforation and bulge inserts. Int. Commun. Heat Mass Tran. 2022;138 doi: 10.1016/j.icheatmasstransfer.2022.106352. [DOI] [Google Scholar]
- 24.Park H.H., Jung J.H., Jang T.S., Han S.T., Song S.H., Park J.J., Park H.B. Prediction of radiated EMI from PCB excited by switching noise of IC. Microw. Opt. Technol. Lett. 2009;51(10):2262–2266. doi: 10.1002/mop.24603. [DOI] [Google Scholar]
- 25.Ahn C.H., Oh J. Resistive grounding technique of heat sink for reducing radiation noise. Journal of Electrical Engineering & Technology. 2014;9(5):1724–1728. [Google Scholar]
- 26.Basyigit I.B., Genc A., Dogan H., Helhel S. The effect of fin types of the heatsinks on radiated emission on the printed circuit board at S‐C band. Microw. Opt. Technol. Lett. 2020 Oct;62(10):3099–3106. doi: 10.1002/mop.32420. [DOI] [Google Scholar]
- 27.Jin H., Zhang L., Yang X.L., Cheng P., Li E.P., Zhang Y.J. 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility. EMC/APEMC); 2018. A novel heatsink with mushroom-type EBG structure for EMI radiation suppression; pp. 772–775. IEEE. [DOI] [Google Scholar]
- 28.Genc A., Dogan H., Basyigit I.B., Helhel S. Heatsink preselection chart to minimize radiated emission in broadband on the PCB. IEEE Trans. Electromagn C. 2020;63(2):419–426. doi: 10.1109/TEMC.2020.3019958. [DOI] [Google Scholar]
- 29.Yuan W., Zhao J., Tso C.P., Wu T., Liu W., Ming T. Numerical simulation of the thermal hydraulic performance of a plate pin fin heat sink. Appl. Therm. Eng. 2012;48:81–88. [Google Scholar]
- 30.Bergman T.L., Lavine A.S., Incropera F.P., DeWitt D.P. John Wiley & Sons; 2011. Introduction to Heat Transfer. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during this study are included in this published article. More data will be made availablie on request.