Transforming representations of movement from body- to world-centric space

Abstract

When an animal moves through the world, its brain receives a stream of information about the body’s translational velocity from motor commands and sensory feedback signals. These incoming signals are referenced to the body, but ultimately, they must be transformed into world-centric coordinates for navigation^1,2. Here we show that this computation occurs in the fan-shaped body in the Drosophila brain. We identify two cell types, PFNd and PFNv^3–5, that conjunctively encode translational velocity and heading as a fly walks. In these cells, velocity signals are acquired from locomotor brain regions⁶ and are multiplied with heading signals from the compass system. PFNd neurons prefer forward-ipsilateral movement, whereas PFNv neurons prefer backward-contralateral movement, and perturbing PFNd neurons disrupts idiothetic path integration in walking flies⁷. Downstream, PFNd and PFNv neurons converge onto hΔB neurons, with a connectivity pattern that pools together heading and translation direction combinations corresponding to the same movement in world-centric space. This network motif effectively performs a rotation of the brain’s representation of body-centric translational velocity according to the current heading direction. Consistent with our predictions, we observe that hΔB neurons form a representation of velocity in world-centric coordinates. By integrating this representation over time, it should be possible for the brain to form a working memory of the path traveled through the environment^8–10.

Insects can perform remarkable feats of navigation. For example, a desert ant can track its walking path using “dead reckoning” (path integration)^9,11, and the same is true of Drosophila melanogaster^7,8,12. For accurate navigation, the brain needs to track the body’s velocity in all three degrees of freedom: rotation, forward translation, and lateral translation (Fig. 1a; Extended Data Fig. 1). Velocity information comes from sense organs – optic flow on the retina^13,14 and mechanical input on limb proprioceptors^15,16 – and likely also from copies of motor commands. Thus, velocity information arrives in body-centric coordinates. The brain must transform translational velocity signals into a world-centric coordinate frame by combining its estimate of body-centric translation direction ($\phi$) with its estimate of world-centric heading direction (θ), to predict the animal’s world-centric travel direction ($\phi$+θ; Fig. 1a).

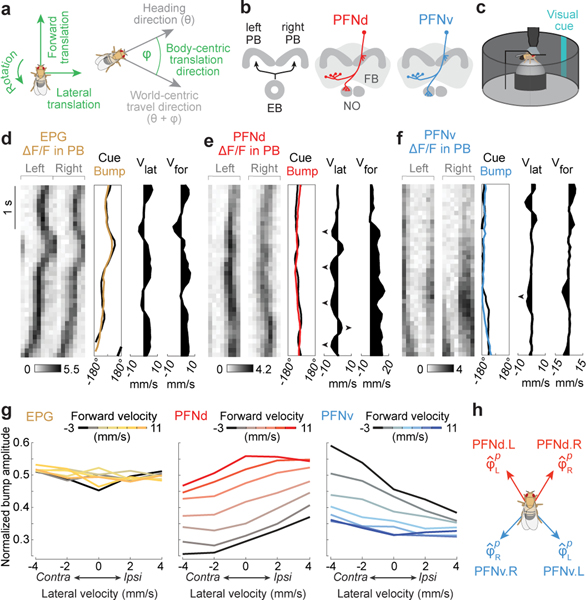
Figure 1. PFN neurons that encode heading and translational velocity.

a. Body-centric variables are green, world-centric are gray.

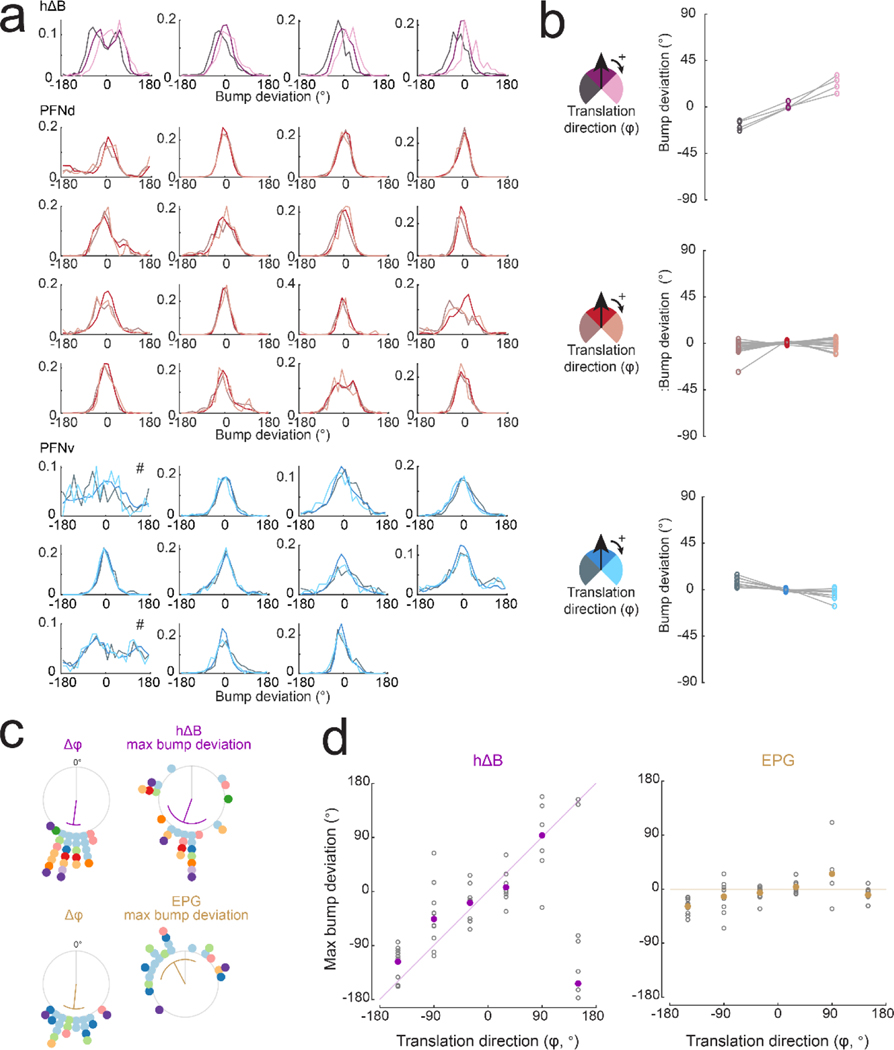
b. The right and left PB receive a heading map from the EB. PFNd and PFNv neurons receive input in the PB and NO, and they send output to the FB. There are 40 PFNd and 20 PFNv neurons, tiling the PB and FB²⁴.

c. Two-photon calcium imaging as a fly walks on a spherical treadmill with a visual heading cue in closed loop.

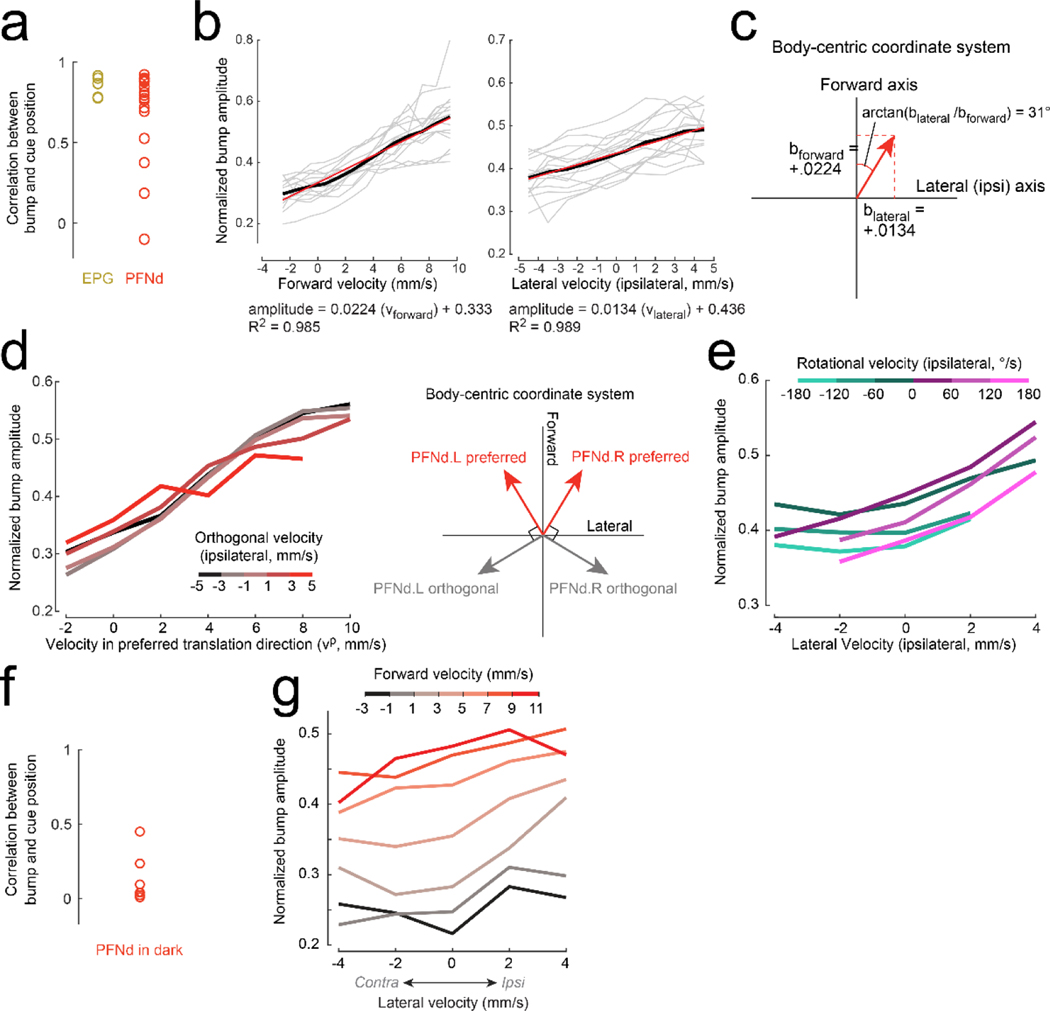
d. EPG bump amplitude is relatively constant. First column (from left to right): ΔF/F in the PB. Second column: bump position, shifted to overlap with cue position, correcting for the arbitrary offset between the bump and the cue¹⁷. Third column: lateral velocity. Fourth column: forward velocity.

e. PFNd bump amplitude increases when forward velocity is high. When lateral velocity is leftward (◄), activity is higher on the left, and vice versa.

f. PFNv bump amplitude increases during backward walking. When lateral velocity is leftward, activity is higher on the right.

g. Normalized bump amplitude versus lateral velocity in the ipsilateral direction (right for the right hemisphere and left for the left hemisphere), binned and color-coded by forward velocity. Data are combined across hemispheres and averaged across flies (n = 5 flies for EPG, 16 PFNd, 11 PFNv). Forward and lateral velocity have a significant effect for PFNd and PFNv (2-way ANCOVA, P<10⁻¹⁰ for each factor in both cell types) but no significant effect for EPG (P=0.8 and 0.08).

h. Preferred body-centric translational direction (${\phi }^{\text{p}}$) of each cell type, fit to data in (g); ${\phi }^{\text{p}}$ is ±31° for PFNd, ±137° for PFNv.

The central complex is the primary locus of spatial computations in arthropods. Here, world-centric heading direction (θ) is computed in the ellipsoid body and sent to the protocerebral bridge (PB)^17–19 while body-centric translation direction ($\phi$) is relayed to the nodulus (NO)²⁰. We therefore hypothesized that θ and $\phi$ are combined in a specific cell class (PFN) that receives input from both the PB and the NO^3,4,21 (Fig. 1b).

Neurons encoding heading and velocity

We used specific genetic driver lines⁴ to express a fast calcium indicator (jGCaMP7f)²² in two types of PFN neurons, PFNd and PFNv^3–5 (Fig. 1b). We imaged the dendrites of these neurons in the PB as the fly walked on a spherical treadmill, surrounded by a 360° virtual reality environment²³ with a heading cue in closed loop with the fly’s rotational velocity (Fig. 1c). For comparison, we also imaged the axon terminals of EPG neurons in the PB. EPG neurons are a core element of the ring attractor that computes the fly’s heading direction^17–19, and their axons in the PB synapse onto PFN dendrites⁵.

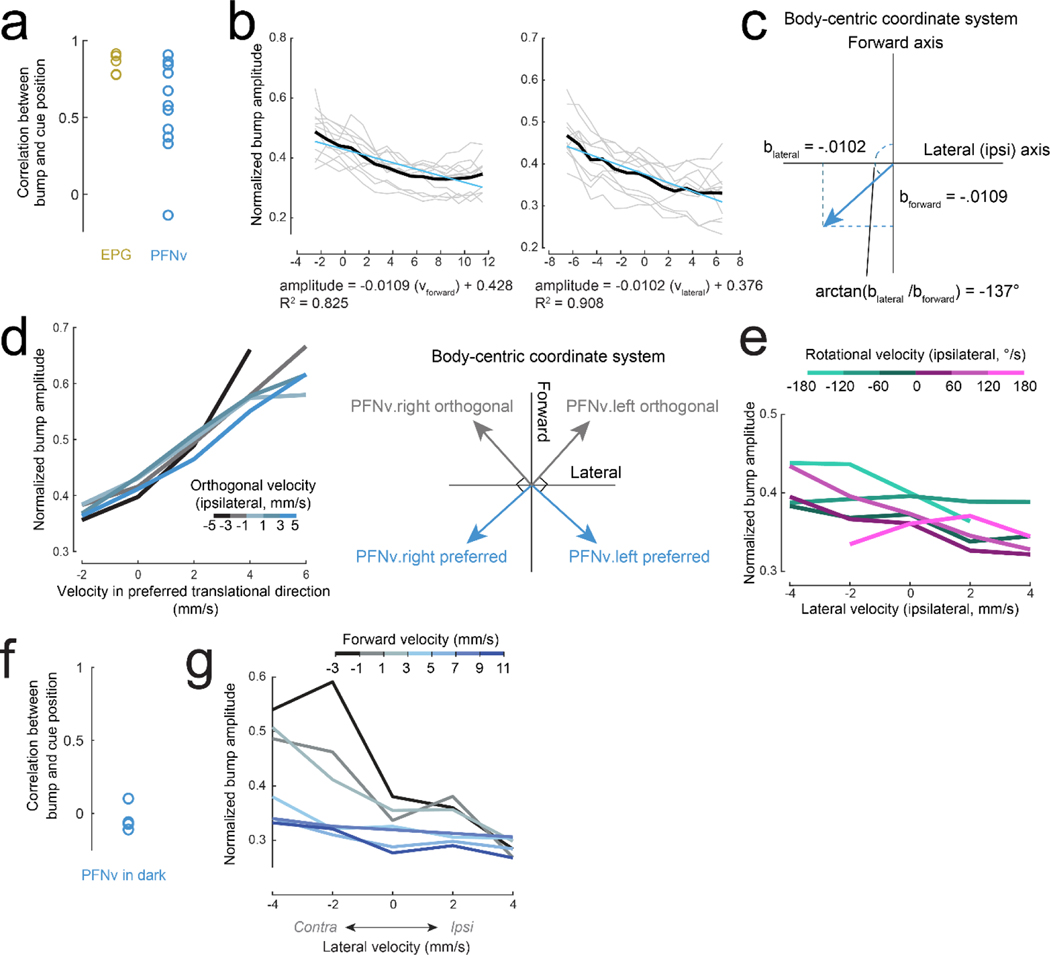
We found that in each brain hemisphere, PFNd and PFNv neurons form topographic maps of heading, which they likely inherit from EPG neurons (Fig. 1d-f, Extended Data Fig. 2, 3). Moreover, PFNd and PFNv neurons also form a Cartesian representation of translational velocity. PFNd neurons in the right and left PB prefer forward-right and forward-left translation, respectively (Fig. 1g-h). Meanwhile, PFNv neurons in the right and left PB prefer backward-left and backward-right translation (Fig. 1g-h). Thus, each neuron has a preferred translation direction (${\phi }^{\text{p}}$) and a preferred heading direction (θ^p), with preferences that collectively tile the space of all possible combinations of ${\phi }^{\text{p}}$ and θ^p. As expected, we confirmed that EPG neurons are relatively insensitive to translational velocity during walking bouts (Fig. 1g).

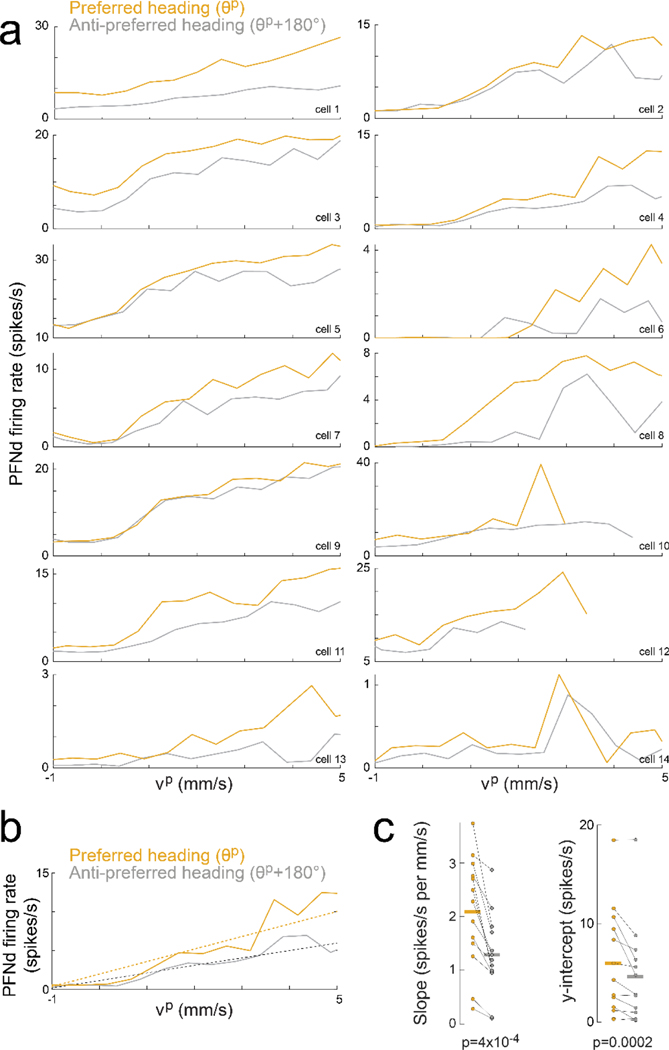
In whole-cell recordings from PFNd neurons, we found that changes in PFNd firing rate are nearly synchronous with velocity changes in the preferred translation direction (v^p), with a tendency for the neuron to lead the behavior (Fig. 2a). This result suggests that PFNd neurons are receiving copies of descending motor commands from locomotor brain regions⁶, as these signals should not lag locomotion as sensory feedback does. Moreover, the relationship between v^p and firing rate is fairly linear, with a steeper slope at the cell’s preferred heading (Fig. 2b), implying a multiplicative relationship between velocity signals and heading signals (Extended Data Fig. 4).

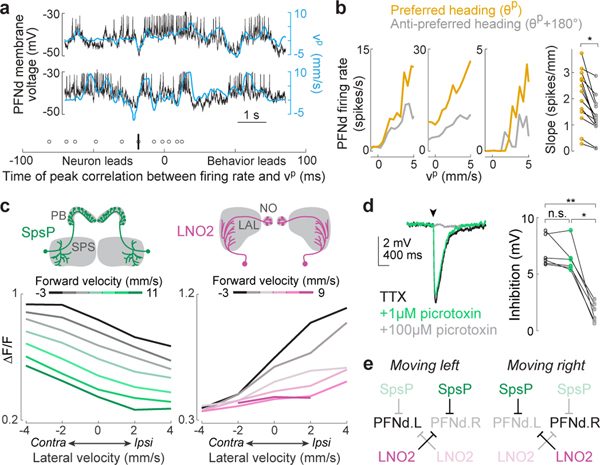
Figure 2. Velocity tuning in PFNd neurons from graded release of inhibition.

a. Top: example PFNd voltage (black) with velocity in the cell’s preferred translation direction (blue, $V^p=\text{V}\cdot {\widehat{\phi }}^p$, where v is translational velocity and $\widehat{\phi }$^p is the unit vector in the direction ${\phi }^{\text{p}}$, Fig. 1h). Bottom: time of peak cross–correlation between firing rate and v^p; median is −18 ms (vertical bar), n=11 cells in 9 flies.

b. Left: firing rate versus v^p for three example neurons. When heading is close to θ^p for this cell (gold), the slope is steeper than when heading is opposite to θ^p (gray). Right: slope of a linear fit is significantly higher near the preferred heading (n=14 cells in 11 flies, * P= 2×10⁻⁴, 2-sided paired t-test).

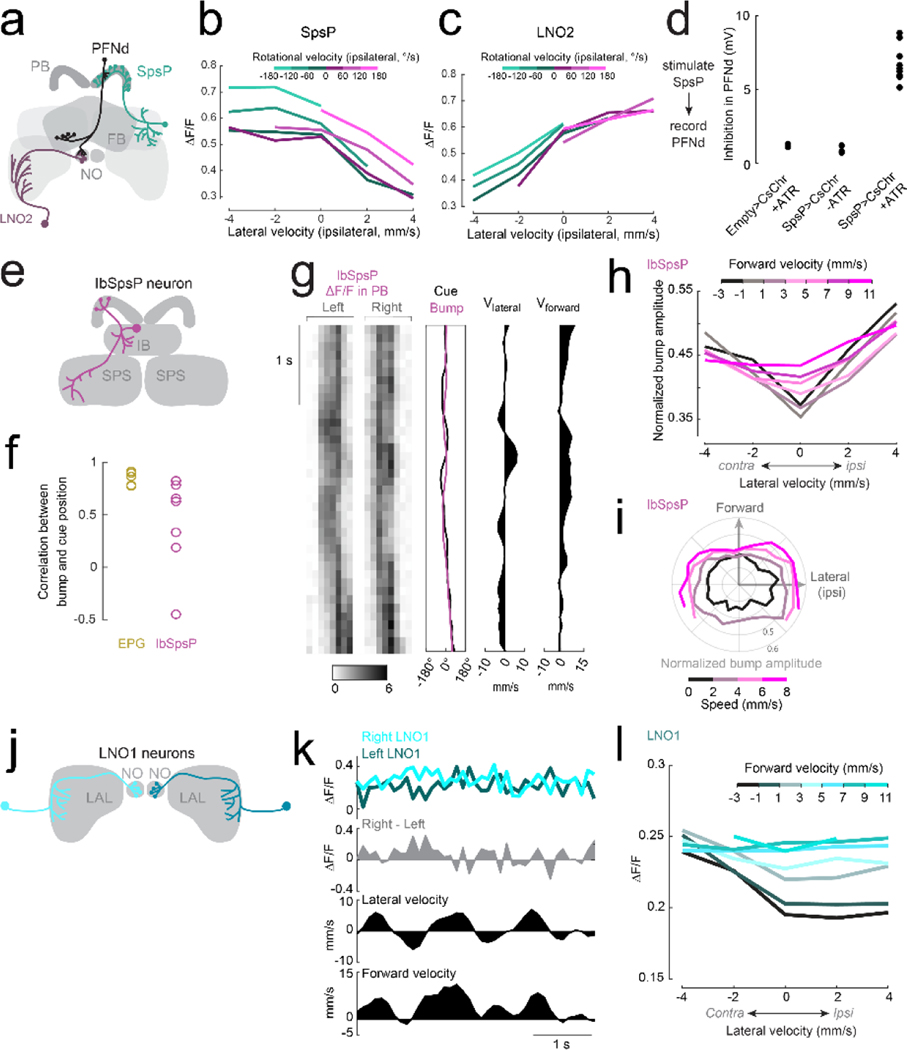
c. ΔF/F versus lateral velocity in the ipsilateral direction (n=8 flies for SpsP, n=4 flies for LNO2). Both forward and lateral velocity have a significant effect (2-way ANCOVA, P<10⁻¹⁰ for each factor in both cell types).

d. Left: whole-cell voltage response of a PFNd neuron to SpsP optogenetic stimulation (arrowhead), recorded in TTX (to isolate monosynaptic input), TTX+1 μM picrotoxin (to block GABA_A receptors⁴²), and TTX+100 μM picrotoxin (to block GluCl receptors²⁷). Each trace is an average of >50 trials. Right: stimulus-evoked inhibition (n=6 cells in 6 flies, ** P= 2.67×10⁻⁴, * P=7.02×10⁻⁴, 2-sided paired t-tests with Bonferroni-corrected α = 0.0167).

e. Schematic: LNO2 and SpsP disinhibit PFNd on the left during a leftward movement, and vice versa (Extended Data Fig. 7a).

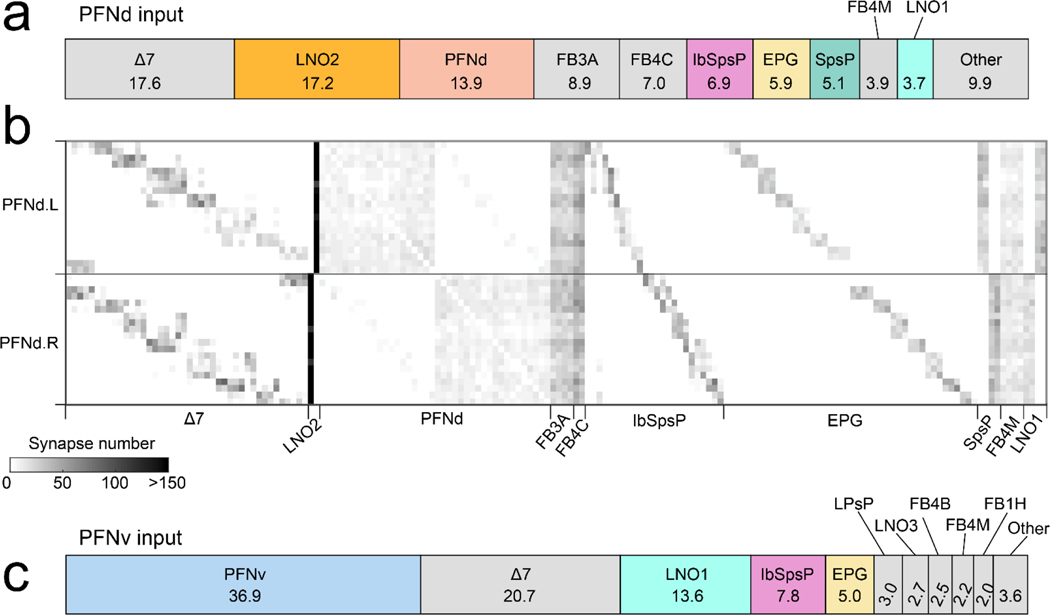
Several cell types provide major unilateral input to PFNd, based on the partial (‘hemibrain’) connectome²⁴ (Extended Data Fig. 5). We found strong direction-selective translational velocity signals in two of these cell types, SpsP^3,4 and LNO2⁵ (Fig. 2c). Both project from locomotor brain regions (the superior posterior slope or SPS, and the lateral accessory lobe or LAL)⁶. Notably, both are anti-correlated with forward velocity (Fig. 2c), which is opposite to the preference of PFNd neurons. To determine whether SpsP and LNO2 neurons might be inhibitory, we reconstructed examples of these neurons in the full adult fly brain electron microscopy dataset²⁵ and used machine learning²⁶ to infer that both cells are glutamatergic, and thus likely inhibitory²⁷. Indeed we confirmed that optogenetic activation of SpsP neurons produces PFNd neuron hyperpolarization, with the pharmacological signature of glutamate-gated chloride channels²⁷ (Fig. 2d). We also confirmed that a split-Gal4 hemidriver reporting vesicular glutamate transporter expression²⁸ drives expression in LNO2 neurons (Extended Data Fig. 6). Importantly, SpsP and LNO2 neurons are sensitive to lateral as well as forward velocity (Fig. 2c), with a lateral direction selectivity consistent with PFNd tuning. Specifically, when the fly moves laterally to the right, SpsP and LNO2 neurons will inhibit PFNd neurons in the left PB while disinhibiting PFNd neurons in the right PB (Fig. 2e, Extended Data Fig. 7).

Meanwhile, the hemibrain connectome reveals different locomotor-related neurons that project to PFNv (Extended Data Fig. 5). Moreover, we observed that the major locomotor-related input to PFNv (LNO1) has a tuning profile opposite to that of LNO2 and SpsP neurons (Extended Data Fig. 7). These results suggest that distinct locomotor inputs are the source of opposite ${\phi }^{\text{p}}$ tuning in PFNd and PFNv neurons.

PFNd neurons in path integration

Next, we asked whether perturbing PFN neurons disrupts path integration. We focused on PFNd neurons because they should be more active than PFNv neurons during forward walking. To perturb these cells, we overexpressed the potassium channel Kir2.1 (PFNd-split-Gal4×UAS-Kir2.1). As a control, we replaced the PFNd-split-Gal4 driver construct⁴ with an “empty” split-Gal4²⁹. We placed individual flies in a ring-shaped channel that constrains their path²⁹ (Fig. 3a). For 5 minutes at the start of each trial, we optogenetically activated fructose receptor neurons (Gr43a-LexA) whenever the fly entered a designated activation zone. After 5 minutes, we stopped delivering optogenetic stimuli, causing the fly to leave the activation zone (Fig. 3b).

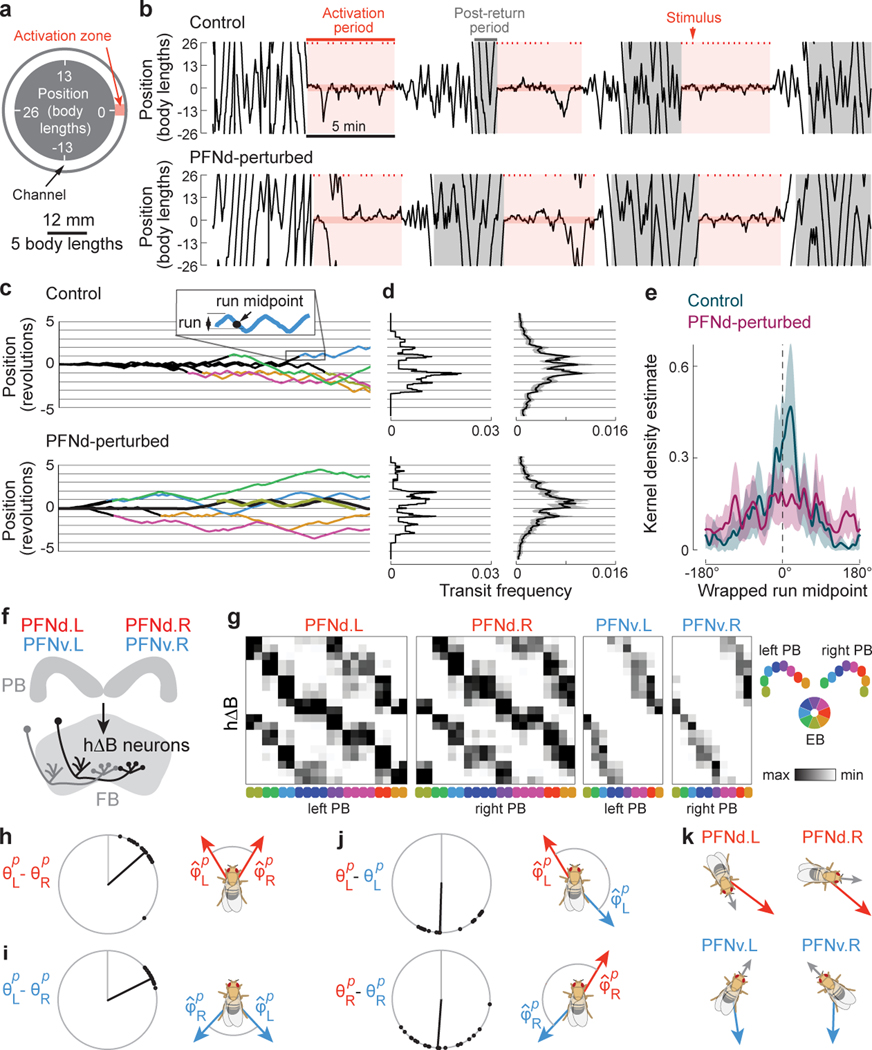
Figure 3. Behavior and connections downstream from PFN neurons.

a. Experimental setup.

b. Example trajectories (1D wrapped paths). Ticks are fictive fructose stimuli. After the 5-min activation period, the stimulus disappears, and the fly strays from the activation zone. The post-return period starts when the fly walks 1 revolution from the activation zone.

c. Trajectories from one control and one PFNd-perturbed fly, shown from the end of the activation period, and colored during the post-return period. A run is defined as a segment between consecutive reversals.

d. Left: mean distribution of transits for post-return trajectories in (c). Right: mean transit distributions for 27 control flies (162 trials) and 25 PFN-perturbed flies (150 trials), ± 95% CI.

e. Normalized kernel density estimate of the wrapped run midpoint in the post-return period (mean ± 95% CI).

f. Schematic: each hΔB neuron receives PFNd and PFNv input from both hemispheres.

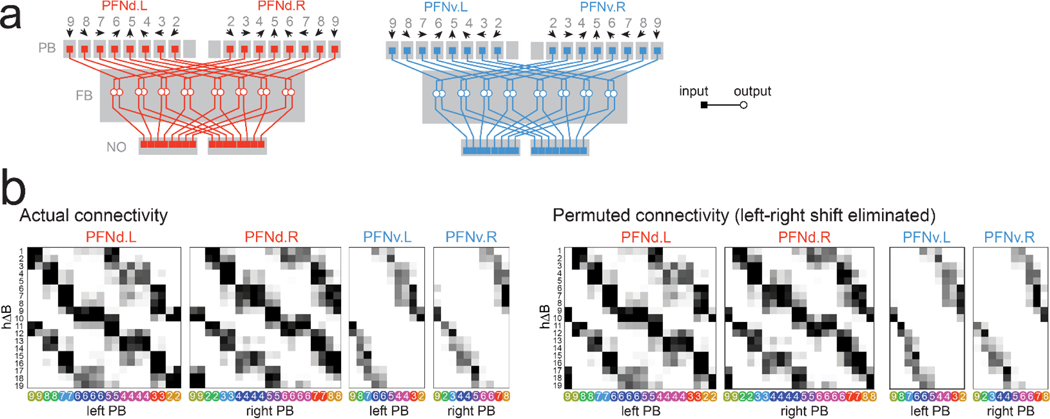
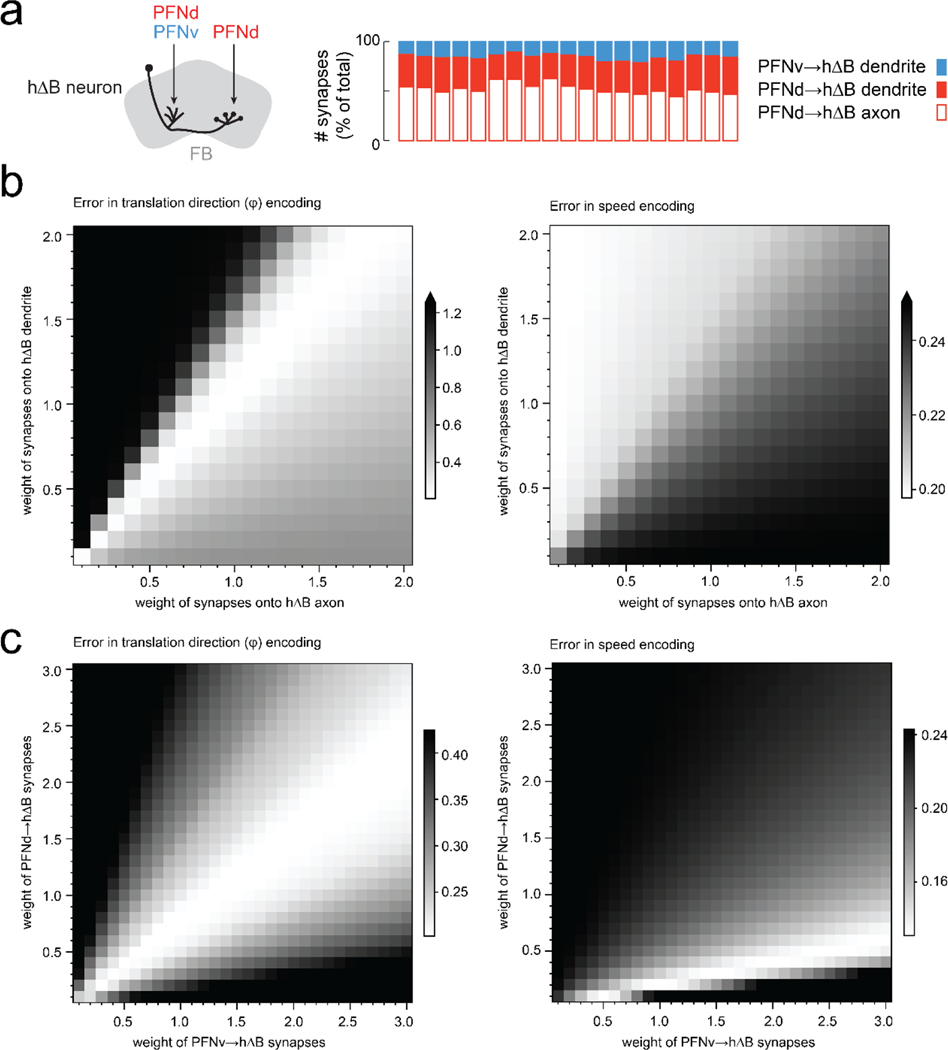
g. Synapses per connection (hemibrain dataset²⁴). Rows are hΔB neurons (19 in total). Columns are PFNd/v neurons (40 and 20 in total) sorted and color-coded by θ^p. Because PFNd neurons target hΔB axons and dendrites, there are two “hotspots” per column; because PFNv neurons target only dendrites, there is one hotspot per column (Extended Data Fig. 9a).

h. Left: difference in θ^p between PFNd.R and PFNd.L inputs to the same hΔB neuron. Each dot is a hΔB neuron (n=19 cells), black line is the circular median, gray line is 0°. Right: shift in ${\phi }^{\text{p}}$ in PFNd.R and PFNd.L.

i. Same for PFNv.

j. PFNd and PFNv inputs from the same hemisphere have opposite values of θ^p and ${\phi }^{\text{p}}$.

k. Summary of PFN inputs to an example hΔB neuron (top row in g). Each input has a different ${\phi }^{\text{p}}$ (red/blue) and θ^p (gray). Red arrows point in the same direction, as do blue arrows, although red and blue are not quite aligned.

We found that control flies often reinstate local search behavior upon returning to the location of the former activation zone (Fig. 3b). Local search behavior consists of back-and-forth runs centered across the site where fictive fructose had been previously delivered (Fig. 3c-e). The fly’s ability to remember this site likely requires idiothetic path integration, because the experiment is performed in darkness, and control experiments have shown that a fly does not rely on chemical or other cues to track its position in this apparatus²⁹.

We found that PFNd-perturbed flies also perform local searches, sometimes in the correct location. Frequently, however, they search in the wrong location (Fig. 3c-e). These results imply that path integration becomes less accurate when PFNd neurons are perturbed. This raises the question of what computations occur downstream from these neurons.

Connectivity downstream from PFN neurons

PFNd and PFNv neurons project to the fan-shaped body (FB), where they converge onto hΔB neurons (Fig. 3f, Extended Data Fig. 8). If we visualize the pattern of PFN→hΔB connections as a weight matrix, we see that right and left PFNd neurons with the same preferred heading have outputs that are shifted relative to each other (Fig. 3g). Thus, from the perspective of an hΔB neuron, PFNd inputs from the left and right hemispheres have different preferred headings. Indeed, this difference (${\theta }_L^p-{\theta }_R^p$) is roughly equal and opposite to the difference in preferred translation directions (${\phi }_L^p-{\phi }_R^p$) for these PFNd inputs (Fig. 3h). The same is true for PFNv (Fig. 3i). Moreover, from the perspective of an hΔB neuron, PFNd and PFNv inputs from the same hemisphere (Fig. 3j) have opposite preferred headings (${\theta }_L^p-{\theta }_R^p$ ≈180°) as well as opposite preferred translation directions (${\phi }_L^p-{\phi }_R^p$ ≈180°).

More generally, PFN neurons that connect to the same hΔB neuron have differences in θ^p that are equal and opposite to their differences in ${\phi }^{\text{p}}$. In other words, these inputs have the same sum ${\phi }^{\text{p}}+{\theta }^p$, which specifies a particular world-centric movement direction. Thus, hΔB neurons should encode world-centered travel direction (Fig. 3k).

World-centric travel in hΔB neurons

To evaluate this idea explicitly, we implemented a computational model comprising 40 PFNd, 20 PFNv, and 19 hΔB neurons, identical to the cell numbers in the hemibrain connectome²⁴. For simplicity, we directly modeled the activity of PFN neurons as a function of heading and body-centric translational velocity using our physiology data. In the model, the nonnegative component of v^p (the fly’s translational velocity in the cell’s preferred direction ${\phi }^{\text{p}}$) is used to scale the θ signal of each PFN neuron (Fig. 4a). This follows what we see in PFN membrane voltage data, where v^p signals and θ signals interact multiplicatively (Fig. 2b). PFN→hΔB connections are taken from the connectome, with weights proportional to the number of synapses per connection (Fig. 3g). Finally, each hΔB neuron in the model simply sums its PFN inputs.

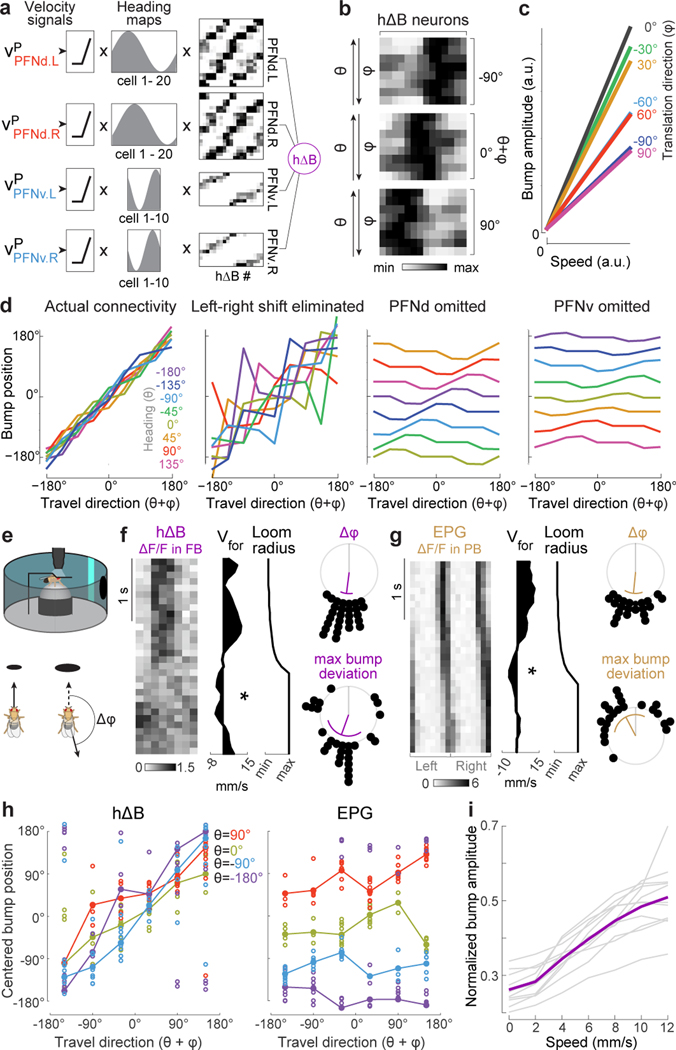
Figure 4. From heading and body-centric velocity to world-centric velocity.

a. Model: rectified v^p scales the heading map in each PFN population. These values are multiplied by PFN→hΔB weights and summed before adding noise.

b. Model: hΔB population activity. The fly’s path is a straight line at a fixed speed. Each row is normalized to its maximum. Across rows, θ is rotated through 360°, while $\phi$ is counter-rotated, so θ+φ is constant within a block.

c. Model: hΔB bump amplitude versus translation speed.

d. Model: hΔB bump position versus world-centric travel direction with actual connectivity, with permuted connectivity that removes the left-right phase shift (Extended Data Fig. 8b), and with PFNv or PFNd omitted.

e. A looming stimulus in front of the fly induces a change in $\phi$.

f. Left: when an example fly walks backward in response to loom (✻), the hΔB bump jumps. Right: 28 backward-walking events in 10 flies; purple line is the circular mean, purple arc is the circular SD, gray line is 0°. Top shows change in $\phi$; bottom shows maximum difference between cue position and bump position, relative to where the bump would be if the fly were walking forward.

g. The EPG bump does not jump during backward-walking events (n=22 events in 6 flies).

h. Centered bump position versus travel direction, in epochs ≥300 ms when $\phi$ was consistent (10 flies each for hΔB and EPG). Epochs are binned by θ and averaged within a fly (○) and across flies (●). Here “centering” means correcting for the arbitrary compass offset in each fly. For hΔB, circular-linear fits to the data are close to the line of unity (slope≈1, intercept≈0°), whereas for EPG, fits are close to y=θ (see Methods for statistical tests).

i. Normalized hΔB bump amplitude versus translation speed. Each gray line is a fly; purple is mean across flies (n=11 flies).

This model predicts a localized bump of activity in the hΔB population (Fig. 4b). The bump’s amplitude scales with translation speed, although the slope of this relationship is steepest when heading and travel are aligned (Fig. 4c). Meanwhile, the position of the bump tracks world-centric travel direction ($\phi +\theta$), irrespective of heading (Fig. 4b,d). This travel direction encoding is disrupted if we permute the connectivity matrix to remove the left-right shift in the pattern of PFN→hΔB connections (Fig. 4d, Extended Data Fig. 8). It is even more disrupted if we remove PFNv or PFNd neurons from the model (Fig. 4d). Although PFNv neurons contribute fewer synapses than PFNd neurons do (Fig. 3g, Extended Data Fig. 9), they are essential because their velocity tuning opposes that of PFNd neurons. Note that our model treats all PFN→hΔB synapses equally, regardless of whether they terminate on a dendrite or an axon; treating these synapses differently actually degrades the model’s travel direction encoding (Extended Data Fig. 9).

We then imaged the hΔB population to test the predictions of this model. We observed a localized calcium “bump”, suggesting that although each hΔB neuron straddles half the FB, calcium fluctuations are mainly restricted to its dendrites or (more probably) its axon terminals. As expected, the position of the bump tracks the fly’s heading θ when the fly is walking forward (φ=0°), often deviating slightly when the fly steps laterally (φ≠0°, Extended Data Fig. 10a-c), consistent with the prediction that the bump is sensitive to both θ and $\phi$; however, these deviations are small during normal walking because lateral movements are small and transient^30,31.

To induce larger changes in $\phi$, we presented a looming dark object in the fly’s path (Fig. 4e). When a fly walked backward in response to the looming object, we typically observed the hΔB bump jump halfway across the FB (Fig. 4f). Across all instances of backward walking, the average maximum bump deviation was about 180°, similar to the change in $\phi$ (Fig. 4f, Extended Data Fig. 10d). As expected, the EPG bump does not jump when the fly walks backward (Fig. 4g, Extended Data Fig. 10d).

We then identified all the prolonged epochs (≥ 300 ms) of stable translation direction $\phi$. This allowed us to capture moments of lateral translation in addition to backward walking. In each epoch, we measured θ and $\phi$, and we also measured the maximum deviation of the bump’s position from the heading cue; when we then corrected for the arbitrary compass offset in every fly, we found that, on average, the hΔB bump position tracks the fly’s travel direction ($\phi +\theta$), regardless of the fly’s heading θ. In contrast, the EPG bump only tracks θ, with no systematic effect of $\phi$ (Fig. 4h, Extended Data Fig. 10e).

Finally, the amplitude of the hΔB bump scales with the fly’s translational speed (Fig. 4i). The slope of this relationship is steepest when heading and travel are aligned (Extended Data Fig. 10f). These findings match the predictions of our model.

Discussion

Path integration requires the brain to integrate estimates of both direction and distance (or speed). A classic model proposed by Wittmann and Schwegler³² proposed that the output of the compass heading direction system in the insect brain³³ is multiplicatively scaled by forward speed and then integrated over time to produce a vectorial representation of displacement. A limitation of this model is that it assumes that translational velocity is always forward, with no lateral component.

A recent model proposed by Webb and colleagues²⁰ overcomes this limitation with a Cartesian system for translational velocity, consisting of one neuron tuned to forward-right velocity, and another neuron tuned to forward-left velocity. Each velocity neuron projects to a population of “integrator” neurons, proposed to be PFN neurons (also known as CPU4). In each integrator population, this velocity signal is added to a heading map, and the result is summed over time. This model does not contain an explicit representation of world-centric travel velocity; instead, it stores path components separately along two orthogonal axes of translation.

Here we show that PFN neurons indeed combine heading and translational velocity signals. Remarkably, we find four populations of PFN neurons that collectively tile the entire 360° of velocity space in a full Cartesian coordinate system. We have no evidence that these neurons integrate velocity over time; instead, they appear to simply record ongoing velocity and heading. Collectively, they represent all possible combinations of translation direction preferences and heading preferences.

Next, PFN neurons converging onto the same hΔB neuron share a common preferred world-centric direction (heading + translation direction). As a result of this wiring pattern, hΔB neurons form a topographic map of the body’s velocity in world-centric coordinates. Thus, for example, the same hΔB neurons will prefer northward travel whether or not the fly is facing north. It is tempting to imagine that an analogous wiring pattern occurs in the vertebrate brain, in the arrangement of inputs to world-centric velocity-vector cells³⁴. More generally, there are many vectorial codes in mammalian navigation systems^1,2, including some in body-centric coordinates^34,35, and others in world-centric coordinates^34,36–38. It has been proposed that the outputs of body-centric vector cells are combined to produce world-centric vector cells in the mammalian brain^39,40. Our results show that this does in fact occur – and indeed how it occurs – in an insect brain. A parallel study reports related results and conclusions⁴¹.

We conjecture that path integration occurs downstream from the representation of world-centric translational velocity in hΔB neurons. We show that the amplitude of hΔB activity scales with translational speed during walking, which aligns with behavioral evidence that walking^13,14 and flying⁴² insects are sensitive to groundspeed cues during path integration. Although it is possible to navigate using purely idiothetic (self-motion) cues, it would be nonetheless ideal to do this in an inferred world-centric reference frame, so as to be ready to incorporate external spatial position cues as they become available. Accordingly, our data argue that idiothetic path integration is impaired when PFNd neurons are perturbed.

Ultimately, the brain’s path integral must be compared to the animal’s spatial goal, and then transposed back into a body-centric reference frame for steering control³¹. By identifying wiring patterns in the connectome⁵, exploring these patterns in computational models, and testing these models through physiology experiments, it should be possible to understand these computations at an algorithmic and biophysical level.

Online Methods

Flies:

Unless otherwise specified, flies were raised on cornmeal-molasses food (Archon Scientific) in an incubator on a 12-hour:12-hour light:dark cycle at 25°C at 50–70% relative humidity. Flies for the experiments in Fig. 2d and Extended Data Fig. 7d were cultured on Nutri-Fly GF German Food (Genessee Scientific) with 0.1% Tegosept (p-hydroxy-benzoic acid, Genessee Scientific), 80 mM propionic acid (Sigma-Aldrich), and 0.6 mM all trans-retinal (ATR; Sigma-Aldrich). Vials containing ATR food were shielded from light with aluminum foil to prevent photoconversion of ATR. The no-ATR control flies for Extended Data Fig. 7d were kept on cornmeal-molasses food. Flies for the experiments in Figs. 3a-e were reared on standard cornmeal fly food in darkness at 22°C containing 0.2 mM all trans-Retinal (ATR; Sigma-Aldrich) and transferred 0–2 days post-eclosion onto standard cornmeal fly food with 0.4 mM ATR and additional dry yeast. Experimenters were not blinded to fly genotype. For optogenetic activation experiments (Fig. 2f, Extended Data Fig. 7d) and for behavioral experiments (Fig. 3a-e) flies were grouped for analysis based on genotype. Flies were never arbitrarily assigned to treatment groups, and therefore there were no experiments where randomization could have been performed. Sample sizes were chosen based on conventions in our field for standard sample sizes; these sample sizes are conventionally determined on the basis of the expected magnitude of animal-to-animal variability, given published results and pilot data.

All experiments used flies with at least one wild-type copy of the white gene. Genotypes of fly stocks used in each figure are as follows:

Fig. 1

EPG calcium imaging:

w/+; +; P{GMR60D05-GAL4}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

PFNd calcium imaging:

w/+; P{R16D01-p65.AD}attP40/+; P{R15E01-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

PFNv calcium imaging:

w/+; P{R22G07-p65.AD}attP40/+; P{VT063307-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

Fig. 2

PFNd whole-cell recording:

w/+; P{R16D01-p65.AD}attP40/P{20XUAS-IVS-mCD8::GFP}attP40; P{R15E01-Gal4.DBD}attP2/+

SpsP calcium imaging:

w/+; P{VT019012-p65.AD}attP40/+; P{R72C10-Gal4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7f}VK00005

LNO2 calcium imaging:

+; Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2]/+; P{VT008681-Gal4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7f}VK00005

SpsP optogenetic activation with PFNd whole-cell recording:

w/+; P{GMR16D01-lexA}attP40/ P{VT019012-p65.AD}attP40; P{13xLexAop2-IVS-pmyr::GFP}VK00005, P{20xUAS-CsChrimson-mCherry-trafficked}su(Hw)attP1/ P{R72C10-Gal4.DBD}attP2

Fig. 3:

Behavior (control):

w/+; Gr43a-LexA/P{p65.AD.Uw}attP40; PBac{13XLexAop2-IVS-Syn21-Chrimson-tdT-3.1-p10}VK00005, P{10xUAS-IVS-hKCNJ2.EGFP}attP2/P{GAL4.DBD.Uw}attP2

Behavior (PFNd perturbed):

w/+; Gr43a-LexA/P{R16D01-p65.AD}attP40; PBac{13XLexAop2-IVS-Syn21-Chrimson-tdT-3.1-p10}VK00005, P{10xUAS-IVS-hKCNJ2.EGFP}attP2/P{R15E01-Gal4.DBD}attP2

Fig. 4:

hΔB calcium imaging:

+; P{R72B05-p65.AD}attP40/+; P{VT055827-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

EPG calcium imaging:

w/+; +; P{GMR60D05-GAL4}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

Extended Data Fig. 2:

PFNd calcium imaging:

w/+; P{R16D01-p65.AD}attP40/+; P{R15E01-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

Extended Data Fig. 3:

PFNv calcium imaging:

w/+; P{R22G07-p65.AD}attP40/+; P{VT063307-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

Extended Data Fig. 4:

PFNd whole-cell recording:

w/+; P{R16D01-p65.AD}attP40/ P{20XUAS-IVS-mCD8::GFP}attP40; P{R15E01-Gal4.DBD}attP2/+

Extended Data Fig. 6:

LNO2 GFP expression pattern:

+; Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2]/P{20XUAS-IVS-mCD8::GFP}attP40; P{VT008681-Gal4.DBD}attP2/+

LNO2 MultiColor Flip Out (MCFO):

+/ w[1118], P{R57C10-FLPL}su(Hw)attP8; Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2]/+; P{VT008681-Gal4.DBD}attP2/PBac{10xUAS(FRT.stop)myr::smGdP-HA}VK00005, P{10xUAS(FRT.stop)myr::smGdP-V5-THS-10xUAS(FRT.stop)myr::smGdP-FLAG}su(Hw)attP1

hΔB MultiColor Flip Out (MCFO):

+/w[1118] P{y[+t7.7] w[+mC]=R57C10-FLPG5}su(Hw)attP8; P{R72B05-p65.AD}attP40/+; P{VT055827-Gal4.DBD}attP2/PBac{10xUAS(FRT.stop)myr::smGdP-HA}VK00005, P{y[+t7.7] P{10xUAS(FRT.stop)myr::smGdP-V5-THS-10xUAS(FRT.stop)myr::smGdP-FLAG}su(Hw)attP1

Extended Data Fig. 7:

SpsP optogenetic activation with PFNd whole-cell recording:

w/+; P{GMR16D01-lexA}attP40/ P{VT019012-p65.AD}attP40; P{13xLexAop2-IVS-pmyr::GFP}VK00005, P{20xUAS-CsChrimson-mCherry-trafficked}su(Hw)attP1/ P{R72C10-Gal4.DBD}attP2

Empty split-Gal4 optogenetic activation control with PFNd whole-cell recording:

w/+; P{GMR16D01-lexA}attP40/ P{p65.AD.Uw}attP40; P{13xLexAop2-IVS-pmyr::GFP}VK00005, P{20xUAS-CsChrimson-mCherry-trafficked}su(Hw)attP1/ P{GAL4.DBD.Uw}attP2

IbSpsP calcium imaging:

w/+; P{R47G08-p65.AD}attP40/+; P{VT012791-Gal4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7f}VK00005

SpsP calcium imaging:

w/+; P{VT019012-p65.AD}attP40/+; P{R72C10-Gal4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7f}VK00005

LNO2 calcium imaging:

+; Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2]/+; P{VT008681-Gal4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7f}VK00005

LNO1 calcium imaging:

+; P{VT020742-p65.AD}attP40/+; P{VT017270-GAL4.DBD}attP2/ PBac{20XUAS-IVS-jGCaMP7s}VK00005

Extended Data Fig. 10:

hΔB calcium imaging:

+; P{R72B05-p65.AD}attP40/+; P{VT055827-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

EPG calcium imaging:

w/+; +; P{GMR60D05-GAL4}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

PFNd calcium imaging:

w/+; P{R16D01-p65.AD}attP40/+; P{R15E01-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

PFNv calcium imaging:

w/+; P{R22G07-p65.AD}attP40/+; P{VT063307-Gal4.DBD}attP2/PBac{20XUAS-IVS-jGCaMP7f}VK00005

Origins of transgenic stocks:

The following stocks were obtained from the Bloomington Drosophila Stock Center (BDSC) and published as follows: P{GMR60D05-GAL4}attP2 (BDSC 39247)⁴⁴, P{GMR16D01-lexA}attP40 (BDSC 52503)⁴⁴ P{R72B05-p65.AD}attP40 (BDSC 70939)⁴⁴, P{VT055827-Gal4.DBD}attP2 (BDSC 71851)⁴⁵, P{VT008681-Gal4.DBD}attP2 (BDSC 73701)⁴⁵, Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2] (BDSC 82986)²⁸, PBac{20XUAS-IVS-jGCaMP7f}VK00005 (BDSC 79031)²², and P{p65.AD.Uw}attP40; P{GAL4.DBD.Uw}attP2 (BDSC 79603)²⁹. MCFO experiments used w[1118], P{R57C10-FLPL}su(Hw)attP8; +; PBac{10xUAS(FRT.stop)myr::smGdP-HA}VK00005, P{10xUAS(FRT.stop)myr::smGdP-V5-THS-10xUAS(FRT.stop)myr::smGdP-FLAG}su(Hw)attP1 (BDSC 64087) and w[1118], P{R57C10-FLPG5}su(Hw)attP8; +; PBac{10xUAS(FRT.stop)myr::smGdP-HA}VK00005, P{10xUAS(FRT.stop)myr::smGdP-V5-THS-10xUAS(FRT.stop)myr::smGdP-FLAG}su(Hw)attP1 (BDSC 64088)⁴⁶.

The split-Gal4 line targeting PFNd neurons was ss00078 (P{R16D01-p65.AD}attP40; P{R15E01-Gal4.DBD}attP2). The split-Gal4 line targeting SpsP neurons was ss52267 (P{VT019012-p65.AD}attP40; P{R72C10-Gal4.DBD}attP2). The split-Gal4 line targeting IbSpsP neurons was ss04778 (P{R47G08-p65.AD}attP40; P{VT012791-Gal4.DBD}attP2). The split-Gal4 line targeting PFNv neurons was ss52628 (P{R22G07-p65.AD}attP40;P{VT063307-Gal4.DBD}attP2). The split-Gal4 line targeting LNO1 neurons was ss47398 (P{VT020742-p65.AD}attP40; P{VT017270-GAL4.DBD}attP2). These lines were obtained from the Janelia Research Campus FlyBank and have been described previously⁴.

P{20XUAS-IVS-mCD8::GFP}attP40 was a gift from Barret Pfeiffer and Gerald Rubin and was described previously⁴⁴. The recombinant chromosome P{13xLexAop2-IVS-pmyr::GFP}VK00005, P{20xUAS-CsChrimson-mCherry-trafficked}su(Hw)attP1 was a gift from Vivek Jayaraman. Gr43a-LexA was a gift from Hubert Amrein and was described previously⁴⁷. 13XLexAop2-IVS-Syn21- Chrimson::tdT-3.1-p10-F8 (VK00005) was a gift from Barret Pfeiffer and David Anderson and was described previously^44,48,49. P{10xUAS-IVS-hKCNJ2.EGFP}attP2 was a gift from Gwyneth Card (via Barret Pfeiffer and Gerry Rubin) and was described previously⁵⁰.

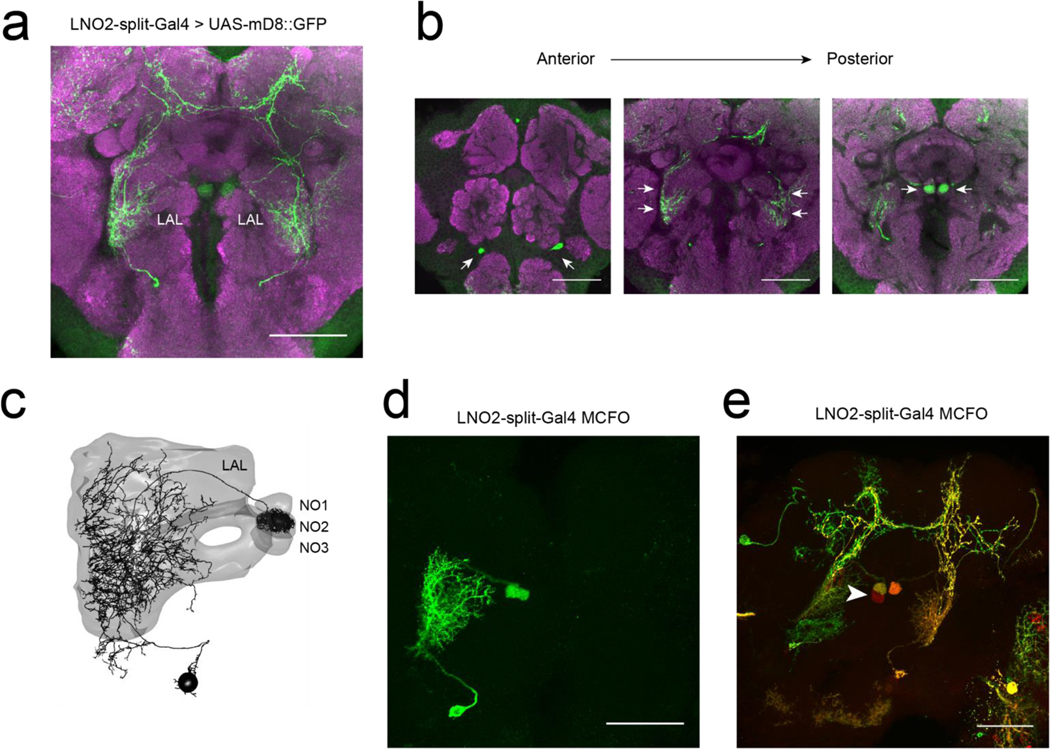
We constructed a split-Gal4 line to target LNO2 neurons that incorporates the Vglut^AD transgene²⁸. This split-Gal4 line is +;Mi{Trojan-p65AD.2}Vglut[MI04979-Tp65AD.2]; P{VT008681-Gal4.DBD}attP2. We validated the expression of this line using immunohistochemical anti-GFP staining, and also using Multi-Color-Flip-Out (MCFO) to visualize single-cell morphologies. On occasion, this split line labels a cell type innervating nodulus subunit 3 (NO3); MCFO results suggest that this is a separate cell type from LNO2 and does not innervate NO2 (Extended Data Fig. 6).

We constructed a split-Gal4 line to target hΔB neurons. This split-Gal4 line is +; P{R72B05-p65.AD}attP40; P{VT055827-Gal4.DBD}attP2. We validated the expression of this line using Multi-Color-Flip-Out (MCFO) to visualize single-cell morphologies (Extended Data Fig. 6).

Fly preparation and dissection

For calcium imaging experiments, we used female flies 20–50 hours post-eclosion and food-deprived (providing only a tissue (KimTech, Kimberly-Clark) with water) for at least 5 hours prior to the experiment. No circadian restriction was imposed for the time of experiments. For optogenetic activation experiments in Fig. 2d and Extended Data Fig. 7d, we used female flies 1–5 days post-eclosion. Flies were kept on Nutri-Fly GF German Food with 0.6 mM ATR. For all other electrophysiology experiments, we used female flies 24–48 hours old; 5/7 flies included in our dataset were food-deprived for 12–24 hours. No circadian restriction was imposed for the time of experiments. For behavior experiments, we used 3–5 days old female flies; flies were wet-starved prior to experiments for 24–42 hours in a vial supplied with a tissue containing 1 mL of distilled water with 800 μM ATR and subsequently dry-starved for up to 90 minutes—including an acclimation period in the experimental arena.

Prior to dissection, flies were briefly cold anesthetized. For calcium imaging experiments and electrophysiology experiments during walking behavior, we secured the fly in an inverted pyramidal platform CNC-machined from black Delrin (Autotiv, Protolabs) with the head pitched forward so that the posterior surface of the head was more accessible to the microscope objective. For electrophysiology experiments with optogenetic activation, we used a photochemically-etched, flat stainless-steel shim stock platform (Etchit), and the head was oriented normally (dorsal-side up). The wings were removed, and the fly head and thorax were secured to the holder using UV-curable glue (Loctite AA 3972) and cured with ultraviolet light (LED-200, Electro-Lite Co). To remove large brain movements, the proboscis was glued using UV-curable glue. The extracellular saline composition was: 103 mM NaCl, 3 mM KCl, 5 mM TES, 8 mM trehalose, 10 mM glucose, 26 mM NaHCO₃, 1 mM NaH₂PO₄, 1.5 mM CaCl₂, and 4 mM MgCl₂ (osmolarity 270–275 mOsm). The saline was bubbled with 95% O₂ and 5% CO₂ to reach a final pH of ~7.3. A window was opened in the head cuticle, and trachea and fat were removed to expose the brain. To further reduce brain movement, muscle 16 was inactivated by gently tugging or clipping the esophagus posteriorly, or by clipping the muscle anteriorly. For electrophysiology experiments, the perineural sheath was removed with fine forceps over the brain region of interest. For all electrophysiology experiments, saline was continuously superfused over the brain; for calcium imaging, saline was superfused prior to experiments.

Two-photon calcium imaging

We used a galvo-galvo-resonant two-photon microscope (Thorlabs Bergamo II, Vidrio RMR Scanner) with a fast piezoelectric objective scanner (Physik Instrumente P725) and a 20×/1.0 NA objective (XLUMPLFLN20XW, Olympus) for volumetric imaging. We used a Chameleon Vision-S Ti-Sapphire femtosecond laser tuned to 940 nm for two-photon GCaMP excitation. Emission was collected on GaAsP PMT detectors (Hamamatsu) through a 525-nm bandpass filter (Thorlabs). We used ScanImage 2018 software⁵¹ (Vidrio Technologies) to control the microscope, and imaging data were collected in ScanImage using National Instruments PXIe-6341 hardware.

The imaging region for all experiments was 256×128 pixels, with 12 slices in the z-axis for each volume (3–5 μm per slice) resulting in a ~10 Hz volumetric scanning rate. For EPG, PFNd, PFNv, SpsP, and IbSpsP imaging experiments, we imaged the PB. For LNO2 and LNO1 imaging experiments, we imaged the NO. For hΔB imaging experiments, we imaged the FB.

Patch-clamp recordings

Thick-wall filamented borosilicate glass (OD 1.5, ID 0.86 mm, Sutter) pipettes with a resistance range of 9–12 MΩ were pulled using a P-97 Sutter puller. Pipettes were filled with an internal solution⁵¹ consisting of 140 mM KOH, 140 mM aspartic acid, 1 mM KCl, 10 mM HEPES, 1 mM EGTA, 4 mM MgATP, 0.5 mM Na₃GTP, and 13 mM biocytin hydrazide, filtered twice through a 0.22-μm PVDF filter. To visualize the cells for recording, we used a FLIR camera (Chameleon3 CM-U3–13Y3C) mounted on an upright compound microscope (Olympus BX51WI) with a 40× water immersion objective (LUMPlanFLN 40XW, Olympus). We used a 100W Hg arc lamp (Olympus, U-LH100HG) and an eGFP long-pass filter to detect GFP fluorescence. For optogenetics experiments, the brain was illuminated from below using bright field transmitted light through the microscope condenser to identify cell bodies for recording, which was then turned off prior to optogenetic stimulus delivery. For walking experiments, the fly was illuminated from below using a fiber optic coupled LED (M740F2, Thorlabs) coupled to a ferrule-terminated patch cable (200-μM core, 0.22 n.a., Thorlabs) attached to a fiber optic cannula (200-μM core, 0.22 n.a., Thorlabs). The cannula was glued to the ventral side of the holder and positioned approximately 135° from the front of the fly so as to be unobtrusive to the fly’s visual field. Throughout the experiment, saline bubbled with 95% O₂ and 5% CO₂ was superfused over the fly using a gravity pump at a rate of 2 mL/min. Whole cell recordings were performed using an Axopatch 200B amplifier with a CV-203BU headstage (Molecular Devices). Data were low-pass filtered at 5 kHz and acquired on a NiDAQ PCIe-6363 card (National Instruments) at 20 kHz. The liquid junction potential was corrected by subtracting 13 mV from recorded voltages⁵².

Spherical treadmill and locomotion measurement

For calcium imaging experiments, flies were positioned on a 9-mm ball made from foam (FR-4615, General Plastics). The ball was painted with a black pattern using model paint (Vallejo Black Model Color Paint). The spherical treadmill consisted of this ball floating on air in a concave hemispherical depression on a plenum 3-D printed from clear acrylic (Autotiv). Medical-grade breathing air was flowed through a hole at the bottom of the depression. The ball was illuminated with a round-board 36 infrared LED lamp (SODIAL). Ball movement was tracked using a video camera (CM3-U3–13Y3M-CS, FLIR) fitted with a macro zoom lens (Tamron 23FM08L 8-mm 1:1.4 lens). The camera faced the ball from the right side of the fly at a 90° angle. We removed one panel of the visual panorama to accommodate the camera view of the ball. The camera frame rate was 50 Hz. Machine vision software (FicTrac v2.0) was used to track the position of the ball⁵³. We modified FicTrac to output computed ball position parameters in real time through the Redis publish/subscribe messaging paradigm. We wrote custom Python software to read in FicTrac outputs from Redis and to produce analog voltage signals through a Phidget analog output device (Phidget Analog 4-Output 1002_0B). The forward axis ball displacement, yaw axis ball displacement, gain-modified forward ball displacement (not used for experiments in this study), and gain-modified yaw ball displacement were output through the Phidget analog device. For closed-loop experiments, the gain-modified yaw ball displacement voltage signal was used to update the azimuthal position of the visual cues displayed by the visual panorama. All voltage analog signals were digitized and acquired using NiDAQ PCI-6341 (National Instruments) at 4 kHz. The pitch, roll, and yaw positions of the ball were recorded by the custom Python software and saved to a HDF5 file for each experiment, along with their timestamps. These were used to infer the fly’s fictive forward, lateral, and rotational movements, respectively. Positive lateral and rotational velocity values denote rightward steering movements.

For electrophysiology experiments, the following parameters were altered. The ball was illuminated using a 780 nm mounted LED source (M780L3, Thorlabs). The ball’s movement was tracked using a GS3-U3–41C6NIR video camera (FLIR) fitted with an InfiniStix 94-mm 0.5× macro zoom lens. One panel 180° behind the fly was removed to accommodate the camera view of the ball and the light source. FicTrac v2.1 was used to track the position of the ball in real time⁵³. We recorded the forward, side, and yaw displacement of the ball via a NiDAQ PCIe-6363 card at 20 kHz. Via built-in serial communication support, we used a custom Python script to output FicTrac parameters to a Phidget analog output device (Phidget Analog 4-Output 1002_0B).

We do not think that optic flow cues from the surface of the spherical treadmill were responsible for PFN velocity responses in our experiments, because these responses were unchanged when we removed visible light from the setup (Extended Data Fig. 2g-h and Extended Data Fig. 3g-h).

Visual panorama and visual stimuli

To display visual stimuli, we used a circular panorama built from modular square (8×8 pixel) LED panels²³. The circular arena was 12 panels in circumference and 2 panels tall. For calcium imaging experiments, we removed one panel 90° to the right of the fly; the bottom panel at that azimuth remained to display stimuli. For electrophysiology experiments, we removed one panel 180° behind the fly. In all experiments, the modular panels contained blue LEDs with peak blue (470 nm) emission; blue LEDs were chosen to reduce overlap with the GCaMP emission spectrum. For calcium imaging experiments, four layers of filters were added in front of the LED arena (Rosco, R381) to further reduce overlap in spectra. A final diffuser layer was placed in front of the filters (SXF-0600, Snow White Light Diffuser, Decorative Films). For electrophysiology experiments, only the diffuser layer was used.

The visual stimulus displayed was a bright 2-pixel-wide vertical bar. The bar’s height was the full 2-panel height of the area (except for 75–105° to the right of the fly, when the bar was 1 full panel in height). For calcium imaging experiments in closed loop without loom stimulus, the bar intensity was set at a luminance value of 4 (maximum value 15). The azimuth position of the bar was controlled during closed-loop experiments via the voltage signal from the Phidget device, which was used to convert FicTrac outputs to an analog voltage signal. For calcium imaging experiments, a 0.8× yaw gain was used; this meant that for a given yaw displacement of the ball, the visual cue displacement was 0.8× the ball’s yaw displacement. For electrophysiology experiments, a 1× yaw gain was used.

For loom stimulus experiments, the heading-landmark stimulus displayed was a bright 2-pixel-wide vertical bar on a background of lower intensity. The brightness of the bar was set to the maximum value 15, and the background was set to 3. The loom stimulus was a dark circular disc expanding from 5° to 90° in horizontal diameter (or cut off by the vertical extent of the panel arena), with a r/v of 130 ms, and was constructed with the help of published code⁵⁴. The loom stimulus was presented at the center of the visual arena in front of the fly. The loom stimulus (~3 s in length) was preceded by a 12 second presentation of the dark disc at minimum diameter. The panel arena was tilted ~10° from horizontal level and positioned such that the loom stimulus appeared ~30° below the fly, which had its head pitched forward and downward for calcium imaging of the PB and FB.

Experimental trial structure during calcium imaging

For calcium imaging experiments without loom stimulus, prior to data collection, all flies walked for 5 minutes in darkness and then at least 10 minutes in closed loop with the visual cue. For calcium imaging experiments, data were collected in two 300-s trials in closed loop with a bright bar; there was a 5 second interval of darkness between trials. On some experiments, we collected one 300-s trial in darkness following closed loop bar trials. For electrophysiology experiments, flies were given at least 10 minutes of walking in closed loop with the visual cue prior to data collection. Each electrophysiology experiment consisted of 3 continuous 200 second closed loop trials with a 1 second inter-trial interval in darkness.

For calcium imaging experiments with loom stimulus presentation, flies walked for at least 20 minutes in closed loop with the heading landmark stimulus (bright bar) without any loom stimulus. Flies were then given 300 second or 320 second trials with a loom stimulus every 60 seconds. Because loom stimulus presentations frequently elicited stopping motion or behaviors other than backward walking, trials were run until the fly stopped walking.

Optogenetic stimuli and pharmacology

Optogenetic stimuli were delivered using a Hg lamp and an ET-Cy5 long-pass filter (590–650nm, Chroma), with a power of ~10 mW/mm². A shutter (Uniblitz Electronic) was used to control the light pulse duration. Light pulses (10 ms) were delivered at 4-s inter-pulse intervals, in three sessions of 150 pulses each. In the first session, the extracellular saline contained 1 μM TTX (554412, EMD Biosciences). In the second session, 1μM picrotoxin (CAS 124–87-8, Sigma Aldrich) was added. In the third session, picrotoxin was increased to 100 μM. In no-ATR control experiments, the light pulse was 50 ms long.

Behavioral arena experiments with walking flies

All experiments were conducted in a 40 mm-diameter, 4 mm-wide annular arena (Fig. 3a). An infrared (IR) backlight and IR-transmitting lid enable behavioral tracking while otherwise maintaining complete darkness for the fly aside from the brief optogenetic pulses. An overhead camera (FLIR Blackfly) and a Python-based machine vision system tracked the fly position in real-time. The arena and setup are identical to the one used in a prior study⁶. Briefly, for each experiment, a single fly was aspirated into the behavioral chamber and allowed to acclimate for up to 90 minutes. After acclimation, experiments consisted of a specified time-course of a single baseline period followed by multiple 5 minute activation periods (APs) and 5 minute post activation-periods (post-APs). During APs, 628 nm LEDs (CP41B-RHS, Cree, Inc.) beneath the food zone were turned on for 1 second whenever the centroid of the fly occupied its virtual perimeter (=2.6 body lengths). Each 1 second pulse was followed by a 15 second refractory period during which the LED remained off, regardless of the fly’s position. During the baseline period and post-APs, food zones were not operational such that flies could not receive optogenetic activation. Each AP and subsequent post-AP was treated as a single trial. Each fly was exposed to 6 trials.

Immunohistochemistry

General immunochemistry procedures:

Brains were dissected from female flies 2–3 days post-eclosion in Drosophila external saline (see above) and fixed in 4% paraformaldehyde (PFA, Electron Microscopy Sciences) in phosphate-buffered saline (PBS, Thermo Fisher Scientific) for 15 min. Brains were then washed with PBS before adding a blocking solution containing 5% normal goat serum (NGS, Sigma-Aldrich) in PBST (PBS with 0.44% Triton-X, Sigma-Aldrich) for 20 minutes. Brains were then incubated in primary antibody with blocking solution for 24 hrs at room temperature, washed in PBST, and then incubated in secondary antibody with blocking solution for 24 hrs at room temperature. After a final wash in PBST, brains were mounted using Vectashield (Vector Laboratories) for imaging. For MCFO protocols, a tertiary incubation step for 24 hours at room temperature and wash with PBST was performed prior to mounting. Mounted brains were imaged on a Leica SPE confocal microscope using a 40× oil-immersion objective with 1.3 n.a. Image stacks comprised 100–250 z-slices at a depth of 1 μm per slice. Image resolution was 1024×1024 pixels.

Visualizing Gal4 expression patterns:

The primary antibody solution contained chicken anti-GFP (1:1000, Abcam) and mouse anti-Bruchpilot (1:30, Developmental Studies Hybridoma Bank, nc82). The secondary antibody solution contained Alexa Fluor 488 goat anti-chicken (1:250, Invitrogen) and Alexa Fluor 633 goat anti-mouse (1:250, Invitrogen).

MCFO:

The primary antibody solution contained mouse anti-Bruchpilot (1:30, Developmental Studies Hybridoma Bank, nc82), rat anti-FLAG (1:200, Novus Biologicals), and rabbit anti-HA (1:300, Cell Signal Technologies). The secondary antibody solution contained Alexa Fluor 488 goat anti-rabbit (1:250, Invitrogen), ATTO 647 goat anti-rat (1:400, Rockland), and Alexa Fluor 405 goat anti-mouse (1:500, Invitrogen). Tertiary antibody solution contained DyLight 550 mouse anti-V5 (1:500, AbD Serotec).

Data analysis for imaging and electrophysiology experiments

Calcium imaging data analysis was performed on MATLAB 2018a and 2018b; electrophysiology data analysis was performed on MATLAB 2019b. For calcium imaging data analysis for closed loop walking behavior without loom stimulus, no flies were excluded from the dataset. For calcium imaging data analysis for loom experiments, we excluded flies where fluorescence was too dim or when the bump position offsets from heading cue position during forward walking bouts were highly unstable (1/11 flies in EPG dataset, and 6/17 flies in the hΔB dataset). We identified large backward walking epochs in 5/10 remaining flies in the EPG dataset and 10/11 flies in the hΔB dataset. Analyses for calcium imaging datasets were parallelized on a high-performance computing cluster (O2 High Performance Compute Cluster, HMS Research Computing Group). For electrophysiology analysis, we excluded experiments if the fly did not sample the full 360-degree heading range, if there was large electrical noise, or if the fly’s total speed was not above a minimum threshold of 0.5 mm/s for over 20% the total experimental period. This occurred in 14/28 cells recorded; we included 14 cells across 11 flies in our dataset.

Calcium imaging alignment and processing:

Rigid motion correction in the x, y, and z axes was performed for each trial using the NoRMCorre algorithm⁵⁵. Each region of interest (ROI) was defined in a single z-plane. For each ROI, a ΔF/F metric was calculated, with the baseline fluorescence (F) defined as the mean of the bottom 5% of fluorescence values within the given trial (300 s in length). For PB imaging, 16 ROIs were defined, one for each of the 16 glomeruli occupied by PFNd dendrites, PFNv dendrites, EPG axons, or IbSpsP axons; these ROIs were drawn based on visible anatomical boundaries. For PB imaging of SpsP axons, an ROI was defined for the entire left or right PB. For FB imaging, eight ROIs were defined manually over hΔB neurites to correspond to eight columns spanning the horizontal axis of the FB. ROIs were defined to be of roughly equal width and collectively cover the lateral span of the FB without overlap between ROIs. For NO imaging, an ROI was defined for the left and right NO subunit 2, which were anatomically separable.

Processing locomotion data in calcium imaging experiments:

The displacement of the spherical treadmill was computed by FicTrac in the yaw and forward directions, output from the Phidget device as a voltage signal, and collected by the NI data acquisition device (DAQ). The FicTrac-computed displacements along the yaw, forward, and lateral axes were also saved directly to an HDF5 file. To get the forward and yaw velocity, the voltage signal from the DAQ was first downsampled (using MATLAB downsample function) to the FicTrac output rate (50 Hz), converted to radians, and unwrapped. A second-order Butterworth low-pass filter was applied to the displacement, and velocity was calculated using the MATLAB gradient function. To get the lateral velocity, the FicTrac outputs saved to the HDF5 file needed to be aligned to the DAQ-collected inputs. To do this, the integrated forward displacement was first linearly interpolated to the time points of the DAQ signal (after downsampling to 50 Hz). The interpolated integrated forward displacement was then low-pass filtered using a second-order Butterworth function, and velocity was calculated using the MATLAB gradient function. The forward velocity computed from the HDF5 file was then aligned to the forward velocity computed using voltage signals from the DAQ using the MATLAB finddelay function. The delay calculated between the HDF5 forward velocity signal and the DAQ-input forward velocity signal was found to be consistent across channels, and the aligned HDF5 forward velocity and DAQ-input forward velocity traces were nearly identical. Moreover, applying the interpolation, smoothing, velocity calculation, and delay adjustment procedure to the HDF5 unwrapped heading signal resulted in a yaw velocity trace nearly identical to the one computed using the DAQ-input voltage signal. Thus, we applied the same procedure to the HDF5 integrated lateral displacement to obtain the lateral velocity. Finally, velocity calculated along all three axes were resampled to the volumetric imaging rate.

For all analyses, we removed the first 3s of every trial to account for the delay in visual stimulus display. For all analyses except Fig. 4f-h and Extended Data Fig. 10d-e, we also removed time periods around starting/stopping transitions to account for jGCaMP7 rise and decay kinetics. Specifically, for each trial, a walking transition ‘cutoff’ for the total speed of the fly (forward speed + lateral speed + yaw speed) was computed by fitting the speed distribution to a bimodal normal mixture model using maximum likelihood estimation and finding the speed at which contribution of the two normal distributions to the mixture PDF was equal. For cases when the mixture model fit was relatively poor and generated a speed cutoff less than 0.1 rad/s, we used a cutoff value of 0.1 rad/s; when the speed cutoff estimate was greater than 0.5 rad/s, we used a cutoff value of 0.5 rad/s. This speed threshold and an additional requirement that walking and stopping epochs be at least 0.5 s in length were used to determine walking transition time points. For PFN, EPG, IbSpsP, and LNO1 imaging, we removed 2∙τ_rise after stop→walk transitions and 2∙τ_decay after walk→stop transitions. For SpsP and LNO2 imaging, this correspondence was flipped. Based on published data²³, we used τ_rise=75 ms and τ_decay=520 ms for jGCaMP7f experiments and τ_rise=70 ms and τ_decay=1.69 s for jGCaMP7s experiments. The 200 ms prior to every transition was also removed in our analyses.

In Figs. 1d-f, 4f-g, Extended Data Figs. 7b,g,k, and Extended Data Fig. 10a, velocity traces were lightly smoothed using a 300-ms moving average filter for display only.

Processing locomotion data in electrophysiology experiments:

The displacement of the spherical treadmill was computed by FicTrac in the yaw, forward, and lateral directions, output from the Phidget device as a voltage signal, and collected by the NI data acquisition device (DAQ). The voltage signal from the DAQ was first converted into radians and unwrapped. The displacement was then downsampled to half the FicTrac camera frame rate and smoothed using the MATLAB smoothdata loess function. Velocity was calculated using the MATLAB gradient function and interpolated up to 1 kHz using the MATLAB resample function.

Ensemble representation of heading direction:

To determine the position of the heading bump in the PB (in PFNd, EPG, IbSpsP, and PFNv neurons), we took the spatial Fourier transform of the ΔF/F across the 16 PB glomeruli at every time point¹⁹. In order to ensure a period of 8 glomeruli in the spatial Fourier transform, we re-arranged the PB glomeruli for each cell type, following published maps³. Specifically, for EPG neurons (in which our driver line does not contain neurites in glomeruli L9 and R9), the PB glomeruli were arranged in the following order: L8-L7-L6-L5-L4-L3-L2-L1-R2-R3-R4-R5-R6-R7-R8-R1. For PFNd, PFNv, and IbSpsP neurons (which do not contain neurites in glomeruli L1 and R1), the arrangement was: L9-L8-L7-L6-L5-L4-L3-L2-R9-R2-R3-R4-R5-R6-R7-R8. We defined the bump position as the phase of the Fourier component at a period of eight glomeruli; we used the sign convention in which positive phase change corresponds to rightward movement of the bump in the protocerebral bridge when viewed posteriorly.

To determine the neural heading coding in the FB, we defined each FB column as representing 1/8 of the full 360° space. Using the centers of each bin of heading space and the ΔF/F for the given column as weights, we calculated the population vector average across the eight FB ROI columns for each time point. We defined a positive phase change to be a rightward movement of the bump in the FB when viewed from the posterior side of the head.

Normalized bump amplitude:

For each half of the PB, we defined the bump amplitude as the maximum ΔF/F – minimum ΔF/F across the eight glomeruli. Then, for each fly, we performed min-max normalization of the bump amplitudes, using the mean of the bottom 5% of bump amplitudes as the minimum and the top 5% of bump amplitudes as the maximum. We performed this rescaling of bump amplitudes for each side of the protocerebral bridge separately. This rescaling, which we call the normalized bump amplitude, enabled us to compare between the right and left halves of the protocerebral bridge and average data across flies.

For the FB, we defined the bump amplitude as the maximum ΔF/F – minimum ΔF/F across the eight columns. Then, for each fly, we performed min-max normalization of the bump amplitudes to calculate the normalized bump amplitude, using the mean of the bottom 5% of bump amplitudes as the minimum and the top 5% of bump amplitudes as the maximum.

Computing population activity in the PB as a function of translational velocity:

For the family of curve plots of population activity versus forward and lateral velocity, we binned each time point based on the forward and lateral velocity of the fly. Lateral velocity was defined in the ipsilateral direction (right was positive in analyzing the right PB, while left was positive in analyzing the left PB).

For rose plots, we binned each time point based on the translation angle and translation speed of the fly, where translational angle was calculated as the vector angle and the translation speed as the vector magnitude of the vector sum of forward and lateral velocity. A vector angle of zero was defined as aligned with the heading of the fly (i.e. lateral velocity was zero), and positive angles were defined to be to the ipsilateral direction of the population (e.g. for PFNd.right neurons, positive angle was to the right; for PFNd.left, a positive angle was to the left).

We then pooled data across the left and right PB. We required that each 2D velocity bin contain at least 10 datapoints (or approximately 1s of data) for a given fly to qualify for inclusion in the group analysis. We excluded timepoints where the sum of the yaw, forward, and lateral speeds were less than 0.5 rad/s. We then calculated the mean normalized bump amplitude within each bin for every fly. We then took the mean across flies. If fewer than four flies in the dataset had enough observations for a given bin, we excluded the bin entirely from our dataset; otherwise, we took the mean across the flies that had enough observations to be included in the dataset. For these analyses, we used a time lag that produced the maximally steep relationship between activity and velocity. For EPG and PFNd neurons, this time lag was 0.2 s. For PFNv neurons, this time lag was 0.3 s. For IbSpsP neurons, this lag was 0.1 s. For Extended Data Fig. 2f and 3f, we performed the same analyses but with binning based on lateral and rotational velocity (in the ipsilateral direction). For Extended Data Fig. 2e and 3e, used the vector sum of forward and lateral velocity and computed the fly’s velocity in preferred translation direction (v^p = v·$\widehat{\phi }$^p, see below) or orthogonal to preferred translation direction. We then binned based on velocity in preferred direction or orthogonal direction.

For each family of curves, we ran a 2-way additive (no-interaction) ANCOVA (using the MATLAB anovan function). For EPG, there was no significant effect of forward velocity (P = 0.8, F(1, 165)=0.06) or lateral velocity (P = 0.08, F(1, 165) = 3) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA. For PFNd, there was a significant effect of forward velocity (P < 10⁻¹⁰, F(1, 538) = 844) and lateral velocity (P < 10⁻¹⁰, F(1, 538) = 191) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA. For PFNd with fly walking in darkness, there was a significant effect of forward velocity (P < 10⁻¹⁰, F(1, 227) = 220) and lateral velocity (P < 10⁻⁵, F(1, 227) = 24) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA. For PFNd, there was a significant effect of lateral velocity (P < 10⁻¹⁰, F(1, 377) = 76) but not rotational velocity (P = 0.59, F(1, 377) = 0.30) on normalized bump amplitude in a 2-way lateral × rotational velocity ANCOVA. For PFNd, there was a significant effect of preferred direction velocity (P < 10⁻¹⁰, F(1, 508) = 891) but not orthogonal to preferred direction velocity (P = 0.97, F(1, 508) = 0.001) on normalized bump amplitude in a 2-way preferred × orthogonal velocity ANCOVA. For PFNv, there was a significant effect of forward velocity (P < 10⁻¹⁰, F(1, 382) = 207) and lateral velocity (P < 10⁻¹⁰, F(1, 382) = 91) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA. For PFNv with fly walking in darkness, there was a significant effect of forward velocity (P < 10⁻⁷, F(1, 127) = 34) and lateral velocity (P < 10⁻⁷, F(1, 127) = 33) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA. For PFNv, there was a significant effect of lateral velocity (P < 10⁻¹⁰, F(1, 271) = 22) and rotational velocity (P < 0.005, F(1, 271) = 9) on normalized bump amplitude in a 2-way lateral × rotational velocity ANCOVA. For PFNv, there was a significant effect of preferred direction velocity (P < 10⁻¹⁰, F(1, 233) = 265) but not orthogonal to preferred direction velocity (P = 0.30, F(1, 233) = 1) on normalized bump amplitude in a 2-way preferred × orthogonal velocity ANCOVA. For IbSpsP, there was a significant effect of lateral velocity (P < .01, F(1, 266) = 7.6) but not forward velocity (P = 0.21, F(1, 266) = 0.21) on normalized bump amplitude in a 2-way forward × lateral velocity ANCOVA.

Correlation between bump position and heading:

We calculated the circular-circular correlation coefficient between the visual cue position and the position of the heading bump for each fly. We limited the correlation calculation to periods when the bump amplitude (defined as the maximum ΔF/F – minimum ΔF/F across the glomeruli for each half of PB) was > 0.8. For each cell type, we used the time lags as above.

Computing preferred translation direction:

We first calculated the mean normalized PB bump amplitude over binned forward or lateral velocities for each fly (combining the data from the left and right PB by representing lateral velocity in the ipsilateral direction). We then took the mean across flies. For both PFNd and PFNv neurons, these relationships were linear (Extended Data Figs. 2b, 3b). We computed the slope of the linear regression between normalized bump amplitude and forward velocity, as well as the slope of the linear regression between normalized bump amplitude and ipsilateral side velocity (Extended Data Figs. 2b, 3b). To calculate the preferred translation direction, we took the arctangent of the ratio between the slope of the normalized bump amplitude versus lateral velocity and the slope of the normalized bump amplitude versus forward velocity (Extended Data Figs. 2c, 3c). We assumed that the preferred directions of the left and right PB were mirror-symmetric.

PFNd electrophysiology analysis during walking behavior:

Voltage traces were downsampled to 1000 Hz using the MATLAB resample function. To remove spikes, voltage traces were then median filtered using the medfilt1 MATLAB function. To calculate firing rate, the median filtered trace was subtracted from the downsampled trace to isolate spike times. Timepoints of spikes were identified using the MATLAB findpeaks function on the baselined trace with the minimum peak height specified for every experiment. To estimate firing rate, identified spikes were smoothed using a 2.5 ms Gaussian kernel.

In each PFNd whole-cell recording, the preferred heading direction of the recorded neuron was estimated by visually inspecting heatmaps of membrane voltage and firing rate as a function of heading and forward velocity, in which heading was binned in 10° segments from −180° to 180°. Based on our calcium imaging data, we infer that all PFNd neurons prefer translation directions ${\phi }^{\text{p}}$ of −31° or + 31° (for PFNd neurons in the left and right PB, respectively). Therefore, we generated heatmaps of the membrane potential and firing rate binned by forward velocity and lateral velocity for each cell to determine which of these two directions was a better fit to the data; we then computed the fly’s velocity in this preferred direction ($V^p=\mathbf{v}\cdot {\widehat{\phi }}^p$, where ${\widehat{\phi }}^p$. is the unit vector in the direction ${\phi }^{\text{p}}$).

Next, we used the MATLAB xcorr function to determine the cross correlation between PFNd firing rate and v^p. A peak in the cross correlation at negative time values indicates that changes in firing rate precede changes in v^p. The cross correlation was calculated over continuous segments of at least 1 s during which the fly’s translational speed was >0.5 mm/s, over a range of lag values from −500 ms to +500 ms; cross-correlation functions were then averaged across segments within a fly. Three cells were excluded from this analysis because the cross correlation did not show a clear peak.

Finally, to summarize the relationship between firing rate and v^p for each neuron, we binned firing rate by v^p and also by heading. The preferred heading bin was 120° wide and centered on the cell’s preferred heading of the cell (θ^p). The anti-preferred heading bin was equally wide and centered on (θ^p-180°). The slope of the linear relationship between firing rate and v^p was determined by using the MATLAB polyfit function of degree 1 over v^p from −2 to 6 mm/s.

Computing SpsP, LNO2, and LNO1 activity as a function of translational velocity:

We combined data for the left and right hemisphere and binned each time point based on forward and lateral velocity (in the ipsilateral direction). For each fly, we required that a given 2D velocity bin contain at least 10 datapoints (or approximately 1s of data) for inclusion. We excluded timepoints where the sum of the yaw, forward, and lateral speeds were less than 0.5 rad/s. We then calculated the mean ΔF/F within each velocity bin. To produce the family of curves in Figs. 2c and Extended Data Fig. 7l, we took the mean across flies for each velocity bin. A velocity bin was only included in the figure if every fly in the dataset had the minimum required number of datapoints for that bin. For these analyses, we used a time lag that produced the maximally steep relationship between activity and velocity. For SpsP the lag was 0.1 s; for LNO2, the lag was 0.1 s; for LNO1, the lag was 0.2 s. For Extended Data Fig. 7c, we performed the same analyses but with binning based on lateral and rotational velocity (in the ipsilateral direction).

For each family of curves, we ran a 2-way additive (no-interaction) ANCOVA (using the MATLAB anovan function). For SpsP, there was a significant effect of forward velocity (p < 10⁻¹⁰, F(1, 277) = 128) and lateral velocity (p < 10⁻¹⁰, F(1, 277) = 65) on ΔF/F in a 2-way forward × lateral velocity ANCOVA. For SpsP, there was a significant effect of lateral velocity (p < 10⁻¹⁰, F(1, 189) = 53) but not rotational velocity (p = 0.59, F(1, 189) = 0.29) on ΔF/F in a 2-way lateral × rotational velocity ANCOVA. For LNO2, there was a significant effect of forward velocity (p < 10⁻¹⁰, F(1, 113) = 66) and lateral velocity (p < 10⁻¹⁰, F(1, 113) = 123) on ΔF/F in a 2-way forward × lateral velocity ANCOVA. For LNO2, there was a significant effect of lateral velocity (p < 10⁻¹⁰, F(1, 77) = 63) but not rotational velocity (p = 0.14, F(1, 77) = 2.2) on ΔF/F in a 2-way lateral × rotational velocity ANCOVA. For LNO1, there was a significant effect of forward velocity (p < 10⁻¹⁰, F(1, 261) = 22) and lateral velocity (p < 0.01, F(1, 261) = 7.0) on ΔF/F in a 2-way forward × lateral velocity ANCOVA.

Optogenetic stimulation during patch-clamp recording:

In Fig. 2d, the response to the optogenetic stimulus in each pharmacological condition was averaged over 50–90 trials where the response was stable. The pre-stimulus baseline was defined as the mean voltage in the window 2-s prior to the stimulus. The stimulus response was taken as the maximum voltage deviation from baseline within 200 ms after stimulus onset. We found that differences in inhibition are significant comparing TTX condition to TTX + 100 μM picrotoxin (P<0.001, paired-sample t-test with Bonferroni-corrected α = 0.0167, Bonferroni-corrected CI = [−7.4, −3.3] mV), and comparing to TTX + 1 μM picrotoxin condition to TTX + 100 μM picrotoxin condition (P<0.001, paired-sample t-test with Bonferroni-corrected α = 0.0167, Bonferroni-corrected CI = [−7.0, −2.5] mV). Differences in inhibition are not significant comparing TTX condition with TTX + 1 μM picrotoxin condition (P=.19, paired-sample t-test with Bonferroni-corrected α = 0.0167, Bonferroni-corrected CI = [−2.0, 0.81] mV). Statistical testing used all 6 experiments where each pharmacological treatment was tested.

Computing hΔB population activity as a function of translational speed:

We binned each timepoint by the translational speed of the fly, defined as the magnitude of the vector sum of the forward and lateral velocity. We then calculated the mean normalized FB bump amplitude within each speed bin for every fly. We also calculated the mean across flies. We required that all flies contain at least 10 datapoints within a given speed bin for inclusion. We excluded timepoints where the sum of the yaw, forward, and lateral speeds were less than 0.5 rad/s. For hΔB neurons, we used a lag of 0.2 s. For this analysis, we used the dataset of n=11 flies collected from the looming stimulus experiment.

Computing hΔB population activity as a function of translational velocity angle:

We binned each time point based on the translation angle and translation speed of the fly, where translational angle was calculated as the vector angle and the translation speed as the vector magnitude defined by the vector sum of forward and lateral velocity. A vector angle of zero was defined as aligned with the heading of the fly (i.e., lateral velocity was zero), and positive angles were defined to be to the right of the fly. We then calculated the mean normalized FB bump amplitude within each bin for every fly, requiring that each 2D velocity bin contain at least 10 datapoints (or approximately 1s of data) for a given fly to qualify for inclusion in the group analysis. We excluded timepoints where the sum of the yaw, forward, and lateral speeds were less than 0.5 rad/s. We calculated the mean normalized bump amplitude within each velocity bin for every fly. We then took the mean across flies. If fewer than four flies in the dataset had enough observations for a given angle/magnitude bin, we excluded the bin entirely from our dataset; otherwise, we took the mean across the flies that had enough observations to be included in the dataset. We used the same time lags as above. For this analysis, we used the dataset of n=11 flies collected from the looming stimulus experiment.

Computing bump deviation as a function of translational angle (Extended Data Fig. 10b,c):

For PFNd and PFNv neurons, we defined the bump position as the phase of the spatial Fourier transform at a period of eight glomeruli (see above). For hΔB neurons, we defined the bump position as the population vector average across the eight columns (see above). In heading-only representations, the bump position should move to the right the same amount as the cue moves to the right, which occurs when the fly is rotating to the left. Thus, we computed an offset value defined as (cue position – bump position). We then mean centered the offset across the experiment to compute the bump deviation. Mean centering was performed because the heading representation in the EB and PB is arbitrary relative to the cue position¹⁷. Positive deviation values indicate that the bump position is further to the left than the cue position, and negative deviation values indicate that the bump position is further to the right than the cue position. We also computed the translation angle as the arctangent of the lateral velocity and the forward velocity; positive angles denote rightward translation. For all cell types, we used a lag value of 0.2 s. We restricted our analysis to timepoints when the bump amplitude (max-min ΔF/F) was greater than 0.5. For each fly, we displayed a histogram of offset values binned by translation angle. We omitted the 180° translation angle bin representing backwards walking because that bin was sparsely sampled. For each translation angle bin, we found the circular mean for each histogram. For this analysis, we used the hΔB dataset of n=4 flies collected under closed loop walking with a bright bar.

Identifying backward walking epochs during loom stimulus presentations:

We searched for backward walking epochs from the time of loom stimulus to 10 s following loom stimulus. Backward walking epochs were required to have >400 ms when smoothed forward velocity (300 ms moving average filter) was < −0.5 mm/s and had a ‘peak’ unsmoothed forward velocity < −5 mm/s. If a loom stimulus resulted in more than one backward epoch, the epoch with greatest peak backward velocity was used.

Relating bump position to travel direction:

Here we outline our analysis pipeline, reserving details for the next section. Our model predicts that hΔB bump position encodes travel direction ($\phi +\theta$):

$$\text{−bump position}=\phi +\theta +{\text{offset}}_{\phi =0}$$ Equation 1

where $\phi$ is body-centric translation direction, and θ is heading (recalling that θ = –cue position in a closed-loop experiment). The last term, offset_{φ = 0}, is a constant, which is needed because the bump position in the compass system has an arbitrary offset to the position of the visual heading cue¹⁷. We can ignore this offset in our computational model (Fig. 4a-d), but we need to take this offset into account when we analyze our imaging data. We measure this constant separately in each experiment by extracting epochs when the fly is walking straight forward (φ=0), and then comparing the cue position to the bump position (offset_{φ = 0} ≡ cue position – bump position). The minus sign on the left side of Equation 1 is needed because the bump position should move left across the PB and FB (decreasing bump position values) when the fly translates to the right ($\phi$ increasing) or makes a clockwise/right turn (θ increasing)^18,19.

In principle, according to Equation 1, the corrected bump position (offset_{φ = 0} – bump position) should always equal the fly’s travel direction ($\phi +\theta$). However, in practice, this is not the case, because $\phi$ tends to fluctuate rapidly in a walking fly (on a timescale of ~200 ms³¹), and it is difficult for calcium imaging to capture changes in bump position on this timescale. Our solution was to restrict our analysis (in Fig. 4h, Extended Data Fig. 10e) to those epochs where $\phi$ was stable. In each epoch, we measure the bump’s new offset (offset_φ ≡ cue position – bump position). We then subtract the offset measured during forward walking (offset_{φ = 0}) to obtain a new quantity (offset_φ – offset_{φ = 0}) which we call “bump deviation”. From these definitions, and from Equation 1, it follows that

$$\phi ={\text{offset}}_{\phi }-{\text{offset}}_{\phi =0}\equiv \text{bump deviation}$$ Equation 2

Equation 2 tells us that, if our hypothesis is correct, bump deviation encodes the change in the cue-bump offset due to non-forward-translation. In other words, it represents the tendency of the hΔB bump to deviate from the compass system when the fly walks laterally or backwards. Indeed, we find that measured bump deviation does change with $\phi$, but these changes are small if we consider all timepoints indiscriminately (Extended Data Fig. 10a-c). When we instead identify every epoch of at least 300 ms where $\phi$ is stable, and we then calculate the maximum bump deviation during each of those epochs, we find that the average maximum bump deviation is close to $\phi$ (Extended Data Fig. 10e). Thus, the prediction expressed by Equation 2 is supported by our data, provided that we focus on epochs where $\phi$ is not fluctuating rapidly. (As a control, we confirmed that the average maximum EPG bump deviation is always close to zero regardless of $\phi$; Extended Data Fig. 10e.)

Notice that we have transformed our bump data into body-centric coordinates, in order to focus on epochs where body-centric translation direction ($\phi$) is stable. As a final step, we need to re-transform our bump data back into world-centric coordinates. World-centric travel direction ($\phi +\theta$) should equal the (maximum) bump deviation corrected for heading, which we call the “centered bump position”:

$$\phi +\theta =\text{bump deviation}+\theta =\text{bump deviation}-\text{cue position}\equiv \text{centered bump position}$$ Equation 3

In essence, the centered bump position is the displacement of the bump away from the heading cue, relative to where the bump would be if the fly were walking forward, minus the cue position. As expected, we found that the average centered bump position is close to $\phi +\theta$, for all values of $\phi$ and θ (Fig. 4h).

In summary, Equation 2 allows us to condition our data based on the stability of $\phi$, and Equation 3 then brings our data back into world-centric coordinates. Below we provide details on each step in this analysis pipeline.

Computing max bump deviation and translation angle during backward walking epochs:

For each backward walking epoch, we defined a 10-s pre-loom period prior to the loom stimulus. During the pre-loom period, we identified moments when the fly’s translation angle (the arctangent of lateral velocity and forward velocity) was within 45° of straight-forward walking. We used these timepoints to compute the circular mean of the (cue position – bump position), or the offset_{φ = 0} during the pre-loom period. We calculated the translation angle during these timepoints as the arctangent of the mean lateral velocity and mean forward velocity.

We also calculated the translation angle during the backward epoch. We then calculated the change in translation angle as the circular difference between the backward walking translation angle and the pre-loom forward-walking translation angle. For the timepoints in the backward epoch, we identified maximum deviation of the (cue position – bump position) value from the offset of forward walking during the pre-loom period. This value is the maximum bump deviation.

For this analysis, we excluded trials when the standard deviation of the offset values during the forward walking pre-loom period was > 45°. We also excluded timepoints when the sum of the yaw, forward, and lateral speeds was less than 29°/s (0.5 rad/s) or when the bump amplitude was less than 0.5, and we required every trial have at least 1 s during the pre-loom period and at least 300 ms during the backward epoch of unexcluded data. We did not exclude timepoints around stop-start transitions. For all cell types, we used a lag value of 0.2 s.

Identifying epochs of stable translation direction:

For every experiment, we computed a 300-ms moving circular standard deviation of the fly’s smoothened translation angle, calculated as the arctangent of the lateral and forward velocity that were each smoothened using a 300-ms moving average filter. We then identified all epochs when the moving circular standard deviation was less than 22.5° (π/8 rad) for at least 300-ms.

Computing max bump deviation during stable translation angle epochs:

For every experiment, we first identified all timepoints when the translation angle (the arctangent of the lateral and forward velocity) was within 45° of straight-forward walking. We used these timepoints to compute the circular mean of the (cue position – bump position), or the offset_φ=0.

For each epoch of stable translation direction, we identified maximum deviation of the (cue position – bump position) value from offset_φ=0. This value is the max bump deviation. For Fig. 4h, we also calculated the “centered bump position”, which is defined as the max bump deviation + θ = max bump deviation – cue position.

We computed the translation angle $\phi$ as the arctangent of the mean lateral and mean forward velocity during the stable translation epoch. We also computed the heading angle θ as the circular mean of −cue position. We computed the travel angle ($\phi +\theta$).

We only included an experiment if the circular standard deviation of the offsets for forward walking was within 45°. We excluded timepoints when the sum of the yaw, forward, and lateral speeds was less than 29°/s (0.5 rad/s) or when the bump amplitude was less than 0.5. For all cell types, we used a lag value of 0.2 s.

For each fly, we binned epochs by translation angle (60° bins) and calculated the circular mean of the max bump deviations for each bin (Extended Data Fig. 10e). We also binned epochs by travel angle $\phi +\theta$ (60° bins) and heading angle θ (90° bins) (Fig. 4h). We only show bins that have at least 2 epochs for a given fly. For this analysis, we used all hΔB datasets and EPG datasets. This resulted in a dataset of n=10 flies for hΔB cells and n=10 flies for EPG cells.

To evaluate our results in Fig. 4h, we performed circular-linear fits⁵⁶ to the data. For hΔB neurons, circular-linear fits to the data are close to the line of unity (slope≈1, intercept≈0°), whereas for EPG neurons, fits are close to the line y=θ. Specifically, the fitted parameters were as follows. For hΔB, θ = 0°: (slope = 0.6, intercept = 0°), circular-linear correlation r = 0.49; θ = 90°: (slope = 0.6, intercept = 40°), r = 0.77; θ = 180°: (slope = 1.1, intercept = 17°), r = 0.57; θ = 270° (slope = 1.0, intercept = 0°), r = 0.64. For EPG, circular-linear fits produced the following (slope, intercept) values: θ = 0°: (slope = 0.1, intercept = −23°), circular-linear correlation r = 0.16; θ = 90°: (slope = 0.3, intercept = 74.5°), r = 0.61; θ = 180°: (slope = −0.1, intercept = −172°), r = −0.42; θ = 270°: (slope = 0.0, intercept = 257°), r = 0.15.

Behavioral arena analysis

We defined the time in the post-AP period after the fly completed a full revolution in either direction for the first time as the post-return period. In the annular arena, flies can either walk clockwise, walk counterclockwise, pause, or change direction in a quick reversal. We defined a run as the path between two consecutive reversals. To derive an estimate of the flies’ spatial memory within the arena, we developed a method by which we measured the midpoint of each run and then convolved each midpoint location with a von Mises distribution (κ = 200), thereby generating a kernel density estimate (KDE) of where in the arena the fly was focusing its search. Flies with fewer than 8 runs in their six trials are excluded from the analysis. We counted transits for post-return trajectories using bins of 2 body lengths; a transit was counted when a fly entered a bin from one side and exited from the other side.

Connectomics analysis

For Fig. 3g, using the partial connectome of the adult female fly brain (hemibrain v1.1)²⁴, we first obtained the neuron IDs for all hΔB neurons in the dataset (19 in total), and we performed a neuprint⁵⁶ Common Input search to obtain all the inputs to all hΔB neurons. We then discarded all neurons not identified as PFNd or PFNv to obtain a connectivity matrix, which tabulated the number of synapses connecting all PFNd/PFNv neurons to all hΔB neurons.

For Extended Data Fig. 5, we performed a neuprint Common Input search to obtain all the inputs to PFNd and PFNv neurons. We grouped input synapses by cell type and discarded synapses where the input cell type was undefined or where the cell type made three or fewer synapses across all PFNd/PFNv neurons. We then plotted the distribution of input synapses across cell type using the Total Weight values. In addition, for PFNd neurons, we created a connectivity matrix between PFNd neurons and all input neurons belonging to the top ten input cell types. We discarded any input weight values of three or fewer.

For Fig. 3h-j, we assigned each PFNd and PFNv neuron a preferred heading, based on its cognate PB glomerulus. For example, neurons in L5 or R5 were assigned a preferred heading of 0°, while neurons in L7 and R3 were assigned a preferred heading of +90°. We assumed that all PFN neurons are cosine tuned to heading. For each hΔB neuron, we summed these cosine heading tuning curves for each input group (PFNd.right, PFNd.left, PFNv.right, PFNv.left) using weights from the connectivity matrix (proportional to the number of synapses in the connection). This generated the heading tuning for each input group onto an individual hΔB neuron (Fig. 3h). For each hΔB neuron, we located the maximum of each tuning curve to obtain the preferred heading tuning (θ^p) for that input group; this is equivalent to taking the circular weighted mean of all θ^p values over all PFN neurons within that group.

For Extended Data Fig. 9a, we assigned each hΔB axon to one of 12 vertical FB columns. We then assigned each PFNd and PFNv neuron to one of 8 vertical FB columns. Using the column designations, we determined the relative lateral location of each neuron along the FB. Using the connectivity matrix, we evaluated every synaptic connection between an hΔB neuron and a PFNd or PFNv neuron by calculating the relative distance between the hΔB axon and the PFNd or PFNv axon. If the distance between the PFN axon and the hΔB axon was <20% of FB’s horizontal extent, we categorized the synapses between the pair as axo-axonic. If the distance between PFN axon and hΔB axon was 30–70% of the FB’s horizontal extent, we categorized the synapses as axo-dendritic. Only two synapses from this analysis were indeterminate, and we manually classified them as axodendritic.

For Extended Data Fig. 6c and 6f, we used neuprintr and natverse software⁵⁷ to display the LNO2 skeleton and hΔB skeletons from the hemibrain dataset.

To obtain neurotransmitter predictions for SpsP and LNO2 neurons, we manually reconstructed examples of these neurons in the full adult fly brain dataset (FAFB)²⁵, as well as several hundred presynaptic sites in each reconstructed neuron. Based on these data, we obtained machine vision predictions of the neurotransmitters associated with each synapse. In SpsP neurons, a prediction for glutamate was >7× more common than a prediction for acetylcholine, which was the second-most common outcome (n=572 synapses in 2 neurons). In LNO2, a prediction of glutamate was 2× more common than a prediction for GABA, which was the second-most-common outcome (n=279 synapses in 1 neuron).

Computational model

The model was built based on experimentally estimated number, connectivity, and activity of three populations of neurons: PFNd, PFNv, and hΔB. The model comprised 40 PFNd neurons, 20 PFNv neurons, and 19 hΔB neurons whose activity is given by the following equations:

$$PFN{v}_i\left(t\right)=f\left(m(v^{fly},v_i^p)\mathrm{*}{n}_i^{PFNv}\left({\theta }^{fly}\right)\right)$$

$$PFN{d}_i\left(t\right)=f\left(m(v^{fly},v_i^p)\mathrm{*}{n}_i^{PFNd}\left({\theta }^{fly}\right)\right)$$

$$h\Delta B_i\left(t\right)=\sum W_{ij}^{h\Delta B,PFNd}\mathrm{*}PFN{d}_j\left(t\right)+\sum W_{ij}^{h\Delta B,PFNv}\mathrm{*}PFN{v}_j\left(t\right)+ϵ\left(t\right)$$

where $v^{fly}$ is the current body-centric velocity vector and $v_i^p$ is the preferred direction of the population. $f$ denotes a monotonic non-linearity. For simplicity, we take $f$ to be a threshold-linear function. The form of $m$ was chosen to approximate measured activity and for simplicity kept the same across both PFN populations (but with differing preferred velocity direction). It is given by:

$$m(v^{fly},v_i^p)=1+5\mathrm{*}ReLU(v^{fly}\cdot v_i^p)$$

where $\cdot$ corresponds to a dot product and ReLU is a function that equals $x$ if $x\ge 0$ and $0$ otherwise. The dependence of PFN activity on current heading approximates the inheritance of heading tuning through the protocerebral bridge and is given by:

$$n_i^{PFNv}=\sum D_{ij}^{PFNv,PB}\mathrm{*}r({\theta }^{fly},{\theta }_j^p)$$

$$n_i^{PFNd}=\sum D_{ij}^{PFNd,PB}\mathrm{*}r({\theta }^{fly},{\theta }_j^p)$$

$$r({\theta }^{fly},{\theta }_j^p)=\frac{1}{2}(1+cos({\theta }^{fly}-{\theta }^p\left)\right)$$

where $r$ corresponds to a simplified description of heading tuning in the protocerebral bridge, with ${\theta }^{fly}$ the fly’s current heading. The matrices $D$ are based on anatomical data and map PFN neurons to the protocerebral bridge. The structure of connections from the PFNd and PFNv populations to hΔB in the model were taken directly from the hemibrain connectome²⁴, based on the assumption that functional connection weights scale with the number of synapses per connection, as has been demonstrated previously⁵⁷; these weights were then scaled uniformly by a single, positive scalar value to generate the connectivity matrices $W.ϵ$ denotes Gaussian output noise. Simulations were performed in Python.

For the parameter search of relative PFNd and PFNv weighting (Extended Data Fig. 9c), two additional parameters $k^{PFNv}$ and $k^{PFNd}$ were added to the calculations of the activity of PFN neurons as follows:

$$PFN{v}_i\left(t\right)=f\left(k^{PFNv}m(v^{fly},v_i^p)\mathrm{*}{n}_i^{PFNv}\left({\theta }^{fly}\right)\right)$$

$$PFN{d}_i\left(t\right)=f\left(k^{PFNd}m(v^{fly},v_i^p)\mathrm{*}{n}_i^{PFNd}\left({\theta }^{fly}\right)\right)$$

These parameters were varied from 0.1 to 3, and the model was run at each time step using values of $v^{fly}\left(t\right)$ and ${\theta }^{fly}\left(t\right)$ from an experimental fly walking trajectory. The relative error in translational direction as encoded by hΔB population vector average was calculated by:

$${\delta }_{direction}=\frac{\left|\left|{\varphi }^{actual}\left(t\right)-{\varphi }^{encoded}\left(t\right)\right|\right|}{\left|\left|{\varphi }^{actual}\left(t\right)\right|\right|}$$

The relative error in speed as encoded by hΔB peak height was calculated by:

$${\delta }_{speed}=\frac{\left|\left|s^{actual}\left(t\right)-s^{encoded}\left(t\right)\right|\right|}{\left|\left|s^{actual}\left(t\right)\right|\right|}$$

For the parameter search of axo-dendritic and axo-axonic weighting (Extended Data Fig. 9b), the connectivity matrices W that describe the connections between the PFNd and PFNv populations to hΔB in the model were broken into two parts based on whether the connections to hΔB were axo-dendritic or axo-axonic. Two additional parameters k^axo and k^dend were added to the equation for the activity of hΔB neurons as follows:

$$\begin{gathered} h\Delta B_i\left(t\right)=\sum {k^{dend}W}_{ij}^{h\Delta B,PFNd,dend}\mathrm{*}PFN{d}_j\left(t\right)+\sum {k^{axo}W}_{ij}^{h\Delta B,PFNd,axon}\mathrm{*}PFN{d}_j\left(t\right) \\ +\sum {k^{dend}W}_{ij}^{h\Delta B,PFNv,dend}\mathrm{*}PFN{v}_j\left(t\right)+ϵ\left(t\right) \end{gathered}$$

Since there are no axo-axonic connections from PFNv to hΔB, that term is omitted from the above equation. The connectivity matrices W were scaled such that the PFNd to PFNv ratio was unchanged relative to the base model when $k^{dend}=k^{axo}=1$. These parameters were varied from 0.1 to 2, and the relative errors were calculated as described above.

Extended Data

Extended Data Figure 1: Walking statistics on a spherical treadmill.

a. Distribution of forward × lateral, forward × rotational, and lateral × rotational velocities. Shown along each axis is the marginal distribution (gray lines on top right of each heatmap denote scale for the marginal distribution). Data are pooled across n=27 flies. We used the velocities recorded at the camera sampling rate (50 Hz) prior to down-sampling to volumetric calcium imaging rate.

b. An example walking bout (30 seconds). Shown are the fly’s forward, lateral, and rotational velocity as well as its heading (based on the position of the visual cue shown in closed loop; note that we used a visual closed loop gain of 0.8×, meaning that the landmark is displaced by an azimuthal angle equal to 0.8× the ball’s yaw displacement).

c. Fictive trajectory of the fly in 2D space based on the walking parameters in the example bout shown in b. The dotted line shows the calculated trajectory using only the forward velocity and the heading of the fly, ignoring the lateral velocity. The solid line shows the calculated trajectory using the forward velocity, lateral velocity, and heading of the fly. Note that the dotted line underestimates the curvature of the fly’s path.

Extended Data Figure 2: PFNd tuning properties.

a. Circular correlation between bump and cue position for PFNd (n=16 flies) and EPG neurons (n=5 flies). Note that PFNd bump position is not as correlated with heading as EPG activity is. This is because PFNd neurons conjunctively encode velocity and heading, whereas EPG neurons encode only heading. For example, when the fly walks forward right, the PFNd bump on the left diminishes in amplitude, and vice versa. When the left and right bumps have different amplitudes, this diminishes the accuracy of our estimate of the bump position. Moreover, when the fly steps backward, both PFNd bumps diminish in amplitude, which again makes it difficult to accurately estimate bump position.

b. Normalized PFNd PB bump amplitude versus forward velocity (left), and lateral velocity (right). Gray lines are individual flies and the black line is the mean across flies (n=16 flies). Data from the right and left PB are combined, and lateral velocity is computed in the ipsilateral direction (so that, for PFNd.L neurons, leftward lateral velocity is positive and rightward lateral velocity is negative). The red line shows the linear fit to the mean line, with the fitted equation below each plot.

c. Computation of preferred translational direction angle using the linear regression slopes for forward and lateral velocity. We used the ratio of the slopes of the linear fits to lateral and forward velocity to calculate the angle of preferred translational direction.

d. PFNd data from Fig. 1g, re-plotted in polar coordinates. Here, normalized bump amplitude is displayed as a function of body-centric translation direction and binned by speed.

e. Normalized PFNd bump amplitude versus velocity in the preferred translational direction (v^p). Data from the right and left PB are combined and binned by the fly’s velocity orthogonal to the preferred translational direction (see schematic at right). Shown is the mean across flies (n=16 flies). Note that a positive value in the orthogonal axis is in the ipsilateral direction. Whereas there is a significant effect of velocity in the preferred direction (2-way ANCOVA, P<10⁻¹⁰), there is no significant effect of velocity in the orthogonal direction (p=0.97).

f. Normalized PFNd bump amplitude versus lateral velocity in the ipsilateral direction. Data from the right and left PB are combined, binned by ipsilateral rotational velocity, and averaged across flies (n=16 flies). Whereas there is a significant effect of lateral velocity (2-way ANCOVA, P<10⁻¹⁰), there is no significant effect of rotational velocity (p=0.59). This analysis shows that there is little or no systematic relationship between PFNd activity and rotational velocity once we account for the effect of lateral velocity. Note that, because rotational and lateral velocity are correlated, rotational velocity bins are asymmetrically populated.

g. Circular correlation between bump and cue position for PFNd neurons when the fly walks in darkness (n=7 flies).

h. Normalized bump amplitude versus lateral velocity in the ipsilateral direction, binned and color-coded by forward velocity, for PFNd neurons when the fly walks in darkness (n=7 flies). Lateral velocity is measured in the ipsilateral direction, and data from the right and left PB are combined and then averaged across flies. Both forward and lateral velocity have a significant effect (2-way ANCOVA, P<10⁻¹⁰ and P<10⁻⁵).

Extended Data Figure 3: PFNv tuning properties.

a. Circular correlation between bump and cue position for EPG (n=5 flies, reproduced from Extended Data Fig. 2a) and PFNv neurons (n=11 flies). Note that PFNv bump position is not as correlated with heading as EPG activity is. This is because PFNv neurons conjunctively encode velocity and heading, whereas EPG neurons encode only heading. In particular, PFNv bump amplitude is generally quite low when the fly is walking forward.

b. Normalized PFNv PB bump amplitude versus forward velocity (left), and lateral velocity (right). Gray lines correspond to individual flies and the black line corresponds to the mean across flies (n=11 flies). Data for the right and left PB are combined, and lateral velocity is computed in the ipsilateral direction. The blue line shows the linear fit to the mean line, with the fitted equation below each plot.

c. Computation of preferred translational direction angle using the linear regression slopes for forward and lateral velocity. We used the ratio of the slopes of the linear fits to lateral and forward velocity to calculate the angle of preferred translational direction.

d. PFNv data from Fig. 1g, re-plotted in polar coordinates. Here, normalized bump amplitude is displayed as a function of body-centric translation direction and binned by speed.

e. Normalized PFNv bump amplitude versus velocity along the angle of preferred translational direction (v^p). Data are combined between the right and left PB and binned by the velocity along the angle of translational movement orthogonal to the preferred direction (see schematic at right). Shown is the mean across flies (n=11 flies). The orthogonal directions for the right and left PFNv population are shown (right); note that a positive value in the orthogonal axis remains in the contralateral direction for the given right/left population. Whereas there is a significant effect of velocity in the preferred direction (2-way ANCOVA, P<10⁻¹⁰), there is no significant effect of velocity in the orthogonal direction (p=0.30).

f. Normalized PFNv bump amplitude versus lateral velocity in the ipsilateral direction. Data for the right and left PB are combined, binned by the ipsilateral rotational velocity, and averaged across flies (n=11 flies). For this cell type, both lateral and rotational velocity have significant effects (2-way ANCOVA, P<10⁻¹⁰ and P<0.005). Note that, because rotational and lateral velocity is correlated, rotational velocity bins are asymmetrically populated.

g. Circular correlation between bump and cue position for PFNv neurons when the fly walks in darkness (n=4 flies).

h. Normalized bump amplitude versus lateral velocity in the ipsilateral direction, binned and color-coded by forward velocity, for PFNv neurons when the fly walks in darkness (n=4 flies). Lateral velocity is measured in the ipsilateral direction, and data from the right and left PB are combined and then averaged across flies. Both forward and lateral velocity have a significant effect (2-way ANCOVA, p<10⁻⁷ for each factor).

Extended Data Figure 4: Interaction between heading and velocity tuning in PFNd neurons.

a. Firing rate versus v^p for all PFNd recordings. Data are divided into bins based on the proximity of the fly’s heading to the neuron’s preferred heading. Three of these cells are shown in Fig. 2b.

b. Linear fits for one example cell.

c. Fitted slope values (reproduced from Fig. 2b) and y-intercept values for all cells (n=14 cells in 9 flies). Horizontal lines indicate mean values. For both parameters, there is a statistically significant effect of heading (2-way paired t-tests, Bonferroni-corrected p values). However, the effect of heading on the slope is relatively large and consistent, as compared to the effect on the y-intercept, which is smaller and less consistent. This implies that the effect of heading (θ) on the cell’s firing rate (f) is largely multiplicative, i.e., it controls the slope of the relationship between f and v^p, as in

f ∝ (cos(θ – θ^p) + a) v^p + b

where θ^p, a, and b are constants. In our computational model (Fig. 4a-d), we use this same relationship, with θ^p=0, a=1, b=0.

Extended Data Figure 5: Connectomics analysis of inputs to PFNd and PFNv neurons.

a. Distribution of input synapses onto PFNd neurons from the hemibrain connectome²⁴, grouped by cell type. Shown are the top ten cell type inputs onto PFNd neurons; all other identified cell types are grouped into “Other.” Collectively, the distribution shown comprises 94.2% of all input synapses onto PFNd neurons. Numbers indicate the percentage of synapses contributed by each input cell type. Note that Δ7 neurons and FB3A/4C/4M neurons are major inputs to PFNd neurons, but we did not screen these neurons as part of our search for the origin of body-centric velocity signals in PFNd neurons, for the following reasons:

Δ7 neurons: Δ7 population activity is known to encode the fly’s heading direction, reflecting the strong input to Δ7 neurons from EPG neurons. It has been proposed that the function of Δ7 neurons is to reshape the heading bump into a cosine-shaped activity profile^5,34. Thus, much of the “compass input” that we refer to in our study as originating from EPG neurons is probably due to the combined action of EPG neurons (which constitute the primary computational map of the compass system) and Δ7 neurons (which reshape and reinforce the compass system output).

FB3A/4C/4M neurons: These neurons are FB tangential cells, meaning their axons run across the entire horizontal extent of the FB, perpendicular to PFNd dendrites⁵. Like other FB tangential cells, these neurons receive input from outside the central complex and they synapse onto a variety of cell types in the FB. There is evidence that FB tangential cells encode information about context, behavioral state, and internal physiological needs, including the need for sleep⁵.

b. Input connectivity matrix for PFNd neurons, shown for the top ten input cell types. Connections comprising 3 or fewer synapses are not shown. Note that the cell types that provide major unilateral input to PFNd neurons are LNO2, IbSpsP, EPG, SpsP, and LNO1.

c. Same as (a) but for PFNv neurons. Collectively, the distribution shown comprises 93.1% of all input synapses onto PFNv neurons.

Extended Data Figure 6: LNO2 and hΔB split-Gal4 line characterization.

a. GFP expression driven by the LNO2 split-Gal4 line: +; Mi{Trojan-p65AD.2}VGlut[MI04979-Tp65AD.2]; P{VT008681-Gal4.DBD}attP2. Shown is a coronal projection of a confocal stack through the anterior half of the brain. GFP staining is shown in green, and neuropil staining (nc82) is shown in magenta. The scale bar is 50 μm. Note that, in addition to targeting LNO2 neurons in the LAL, there are some cells labeled in the superior brain which are not LNO2 cells. The observation that this VGlut-split-Gal4 construct drives expression in LNO2 neurons is evidence in support of the conclusion that LNO2 neurons are glutamatergic.

b. Same as (a) but for individual optical slices. Shown are the location of the LNO2 cell bodies (left, arrows), neurites in the LAL (middle, arrows), and neurites in NO2 (right, arrows). Scale bars are 50 μm.

c. Skeleton of LNO2 neuron from the hemibrain dataset. Overlaid are the anatomical boundaries of the LAL and the NO (divided into subunits NO1, NO2, and NO3). The black sphere denotes the position of the cell body. There is one LNO2 neuron per hemisphere.

d. MCFO labeling of a single LNO2 neuron from the LNO2-split Gal4 line. Scale bar is 50 μm.

e. On occasion, the LNO2 split-Gal4 line shows expression in NO3. Shown is an MCFO sample from the LNO2-split Gal4 line that labels this additional neuron in NO3 (arrow). Given that two channels (green and red) label the LNO2 on the ipsilateral side, whereas only one channel (red) shows the NO3-innervating neuron, this neuron appears to be a distinct neuron from LNO2. Scale bar is 50 μm.

f. Skeletons of two hΔB neurons from the hembrain dataset. Overlaid are the anatomical boundaries of the FB. Spheres denote soma positions.

g. MCFO labeling of two hΔB neurons from the hΔB split Gal4 line +; P{R72B05-p65.AD}attP40; P{VT055827-Gal4.DBD}attP2. Scale bar is 20 μm.

Extended Data Figure 7: SpsP, LNO2, IbSpsP, and LNO1 physiology.

a. Schematic of SpsP and LNO2 input onto a single PFNd neuron. PFNd neurons have dendrites in the PB on the side ipsilateral to their soma, and dendrites in the NO on the side contralateral to their soma. As a result, PFNd neurons receive input from ipsilateral SpsP neurons and the contralateral LNO2 neuron. Thus, although SpsP and LNO2 neurons have opposite velocity preferences (Fig. 2c), they have congruent effects on PFNd neurons.

b. SpsP and LNO2 activity as a fly walks in closed loop with a visual cue.

c. SpsP and LNO2 ΔF/F versus lateral velocity in the ipsilateral direction. Data for the right and left PB are combined, binned by the ipsilateral rotational velocity, and averaged across flies (n=8 flies for SPS, 4 flies for LNO2). Because rotational and lateral velocity are correlated, rotational velocity bins are asymmetrically populated. There is a significant effect of lateral velocity (2-way ANCOVA, P<10⁻¹⁰ for both SpsP and LNO2) but not rotational velocity (p=0.59 for SpsP, p=0.14 for LNO2). Note however that SpsP activity increases when rotational speed is high, for both ipsi- and contralateral rotations.

d. Control experiments for SpsP optogenetic activation. There is little effect of light in PFNd recordings from flies where an empty split-Gal4 line is combined with UAS-CsChrimson (n=3) or in flies with UAS-CsChrimson expressed under SpsP split-Gal4 control (ss52267) but reared in the absence of all-trans-retinal (ATR; n=3). We consistently see strong inhibition in flies that express UAS-CsChrimson under SpsP split-Gal4 control (ss52267) and that are raised on culture media containing ATR (n=9, reproduced from Fig. 2d). PFNd recordings were performed in TTX to isolate monosynaptic responses (see Methods).

e. Each IbSpsP neuron receives input from the inferior bridge (IB) and SPS, and projects to a few adjacent PB glomeruli.

f. Circular correlation between visual cue position and IbSpsP bump position (n=8 flies). Shown for comparison is the circular correlation for EPG neurons (n=5 flies), reproduced from Extended Data Fig. 2a.

g. IbSpsP population activity in the PB as a fly walks in closed loop with a visual cue.

h. Normalized IbSpsP bump amplitude versus forward velocity. Data are binned by lateral velocity in the ipsilateral direction, combined for the right and left PB, and averaged across flies (n=8 flies). There is a significant effect of lateral velocity (P<0.01) but not forward velocity (p=0.65, 2-way ANCOVA).

i. Normalized IbSpsP bump amplitude in the PB, versus body-centric translational direction. Data are binned by speed. Lateral velocity is expressed in the direction ipsilateral to the imaged PB, allowing us to combine data from the right and left PB before averaging across flies (n=8 flies).

j. Each LNO1 neuron receives input from the LAL and synapses onto PFNv and PFNd dendrites in the NO.

k. LNO1 activity as a fly walks in closed loop with a visual cue. We used jGCaMP7s in these experiments (rather than jGCaMP7f) because LNO1 fluorescence was dim with jGCaMP7f.

l. LNO1 activity versus forward velocity. Data for the left and right NO are combined, binned by lateral velocity in the ipsilateral direction, and averaged across flies (n=8 flies). LNO1 activity decreases slightly with ipsilateral backward movement. There is a significant effect of both forward velocity (P<10⁻¹⁰) and lateral velocity (P<0.01, 2-way ANCOVAs).

Extended Data Figure 8: PFN→hΔB connectivity.

a. Schematized projections of the PFNd and PFNv populations, from the hemibrain connectome. Gray numbers denote PB glomeruli³. Note that the mapping from PB glomeruli to FB horizontal locations is the same for PFNd (red) and PFNv (blue). For each cell type, each half of the PB contains a complete heading map (black arrows) which is projected onto the full horizontal axis of the FB.

b. Top: PFN→hΔB connection matrix from the hemibrain connectome, reproduced from Fig. 3g. Note that, for a given hΔB neuron, PFN projections from the left and right PB are horizontally shifted, corresponding to the morphologies in (a). Bottom: Permuted PFN→hΔB connection matrix. Here, the shifts between left and right PFN matrices are eliminated. We used this permuted connection matrix in Fig. 4d (“left-right shift eliminated”).

Extended Data Figure 9: Model performance as a function of relative synaptic weight.

a. hΔB dendrites receive PFNd and PFNv inputs at their dendrites. By contrast, hΔB axon terminals receive PFNd inputs but no PFNv input. In the bar plot at right, each bar represents one hΔB neuron in the hemibrain connectome (n = 19 neurons). The computational model in Fig. 4a-d assigns an equal weight to all synapses, meaning that all connections are simply weighted by the number of synapses they contain, regardless of whether they are axo-dendritic or axo-axonic connections.

b. To determine if the model might perform better if we treated these connections differently, we systematically varied the weight of PFN synapses onto hΔB dendrites versus axons, and we used the population vector average of hΔB activity to decode the fly’s simulated movement. Grayscale heatmap shows the error in translational direction encoding (left) and speed encoding (right), with lower values indicating more accurate encoding. Note that we obtain the best translation direction encoding if we apply equal weight to axo-dendritic or axo-axonic connections (as we do in Fig. 4a-d). Speed encoding improves if we minimize the weight at the synapses onto hΔB axons; this is because this reduces the contribution of PFNd inputs (relative to PFNv), and so it tends to reduce the disproportionate gain when the fly is walking in the preferred direction ${\phi }^{\text{p}}$ of the PFNd population (Fig. 4c). We do not know whether axo-dendritic and axo-axonic connections are actually weighted equally in the real network, but the fact that we observe good encoding of $\phi$ in the hΔB population (Fig. 4h) suggests that these connections carry similar weight, at least as measured with jGCaMP7f.

c. We also systematically varied the weight of PFNd and PFNv synapses. We obtain the best translation direction encoding if we apply equal weight to PFNd and PFNv connections (as we do in Fig. 4a-d). Speed encoding improves if we reduce PFNd weights, again because this reduces the disproportionate gain when the fly is walking in the preferred direction ${\phi }^{\text{p}}$ of the PFNd population (Fig. 4c).

Extended Data Figure 10: hΔB bump deviations.

a. hΔB ΔF/F in each FB column as a fly walks in closed loop with a visual cue. When the fly steps laterally (◄), the bump deviates from the cue.

b. Histograms showing the difference between cue position and bump position, mean-centered in each experiment, and binned by translation direction; n=4 flies for hΔB, 16 flies for PFNd, and 11 flies for PFNv, # = relatively poor correlation between cue and bump; these experiments are omitted from panel c. At more lateral translation angles, the hΔB bump deviates away from where it would be when the fly is walking forward.

c. Mean difference between cue position and bump position. Each set of connected symbols is one experiment. For hΔB neurons (n=4 flies), we found the shift was significant when comparing left translation-heading deviations to centered translation-heading deviations (P=0.0013, 2-sided paired-sample t-test with Bonferroni-corrected α = 0.0167, CI = [−0.460, −0.191] radians) and when comparing right translation-heading deviations to centered translation-heading deviations (P=0.0115, α = 0.0167, CI = [−0.698, −0.0473] radians). For PFNd neurons (n=16 flies), the shift is not significant when comparing left translation-heading deviations to centered translation-heading deviations (P=0.0215, 2-sided paired-sample t-test with Bonferroni-corrected α = 0.0167, CI = [−0.180, 0.0044] radians) or when comparing right translation-heading deviations to centered translation-heading deviations (P=0.4790, α = 0.0167, CI = [−0.0467, 0.0812] radians). For PFNv neurons (n=9 flies; 2 flies were excluded from our analysis), this shift is significant when comparing left translation-heading deviations to centered translation-heading deviations (P=0.0011, 2-sided paired-sample t-test with Bonferroni-corrected α = 0.0167, CI = [0.0544, 0.222] radians) but not significant when comparing right translation-heading deviations to centered translation-heading deviations (P=0.0313, α = 0.0167, CI = [−0.0135, 0.1848] radians); note that the shift is opposite to hΔB neurons.

d. Same as Fig. 4f-g but color-coded by fly (n=28 epochs in 10 flies for hΔB, n=22 epochs in 6 flies for EPG).

e. Maximum bump deviation versus $\phi$, measured in all epochs ≥300ms when the $\phi$ was consistent over the epoch. Within each fly, epochs are binned by $\phi$ and then averaged (○) before averaging across flies (●). For hΔB neurons, the data are close to the identity line (purple); while for EPG neurons, the data are close to the zero line (gold). n=10 flies for hΔB, n=10 flies for EPG.

f. Normalized hΔB bump amplitude versus $\phi$, binned by speed (n=11 flies).

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.