Abstract
The genotype by environment interaction significantly influences plant yield, making it imperative to understand its nature for the creation of breeding programs to enhance crop production. However, this is not the only obstacle in the yield improvement process. Breeders also face the significant challenge of unfavorable and negative correlations among key traits. In this study, the stability of root yield and white sugar yield, and the association between the key traits of root yield, sugar content, nitrogen, sodium, and potassium were examined in 20 sugar beet genotypes. The study was conducted using a randomized complete block design with four replications over two consecutive years across five locations. The combined analysis of variance results revealed significant main effects of year, location, and genotype on both root yield and white sugar yield. Notably, two-way and three-way interactions between these main effects on root yield and white sugar yield resulted in a significant difference. The additive main effect and multiplicative interaction analysis revealed that the first five interaction principal components significantly impacted both the root yield and white sugar yield. The linear mixed model results for root yield and white sugar yield indicated that the genotype effect and the genotype by environment interaction were significant. The weighted average absolute scores of the best linear unbiased predictions biplot demonstrated that genotypes 20, 4, 7, 2, 16, 3, 6, 1, 14, and 15 were superior in terms of root yield. For white sugar yield, genotypes 4, 16, 3, 7, 5, 1, 10, 20, 2, and 6 stood out. These genotypes were not only stable but also had a yield value higher than the total average. All key traits, which include sugar content, sodium, potassium, and alpha amino nitrogen, demonstrated a negative correlation with root yield. Based on the genotype by yield*trait analysis results, genotypes 20, 19, and 16 demonstrated optimal performance when considering the combination of root yield with sugar content, sodium, alpha amino nitrogen, and potassium. The multi-trait stability study, genotype 13 ranked first, and genotypes 10, 8, and 9 were identified as the most ideal stable genotypes across all traits. According to the multi-trait stability index, genotype 13 emerged as the top-ranking genotype. Additionally, genotypes 10, 8, and 9 were recognized as the most stable genotypes.
Subject terms: Plant breeding, Plant sciences
Introduction
Sugar beet, due to its diverse applications and nutritional benefits, holds significant importance1–4. It is packed with a high concentration of sucrose5, making it a substantial source of sugar. This makes it the world second most cultivated crop for white sugar production, after sugarcane6. With the growing population7 and consequent increase in societal needs, plant breeders are striving to enhance the yield and quality of sugar beet8–11. However, the crop yield is determined by the genotype, environment, and genotype by environment interaction (GEI); Given its polygenic nature, the sugar beet yield is heavily influenced by environmental factors. As a result, significant fluctuations in its yield can lead to instability in production9; Therefore, maintaining the yield stability of genotypes has become a critical aspect of the breeding process12. The GEI plays a crucial role in determining the yield stability of genotypes across different environments8,13,14. This phenomenon shows that the environment in which a trait is expressed can affect how a given genotype (gene arrangement) affects that trait15,16. In layman's words, this phenomenon explains how the expression of genetic features can change based on certain environmental conditions9, resulting in various phenotypic outcomes for a genotype with the same gene organization in various environments. This complexity presents a significant challenge to breeding for yield increase. To address this, breeders can identify genotypes that consistently perform well in various environmental conditions by extensively testing the genotypes in locations with a range of environmental conditions13. This approach aids in the selection of genotypes with broad adaptability and stability11,17, ultimately leading to stability in yield increase.
Sophisticated statistical methods have been developed to study and expose patterns of GEI comprehensively. The model known as additive main effects and multiplicative interaction (AMMI) is a significant statistical method that combines the analysis of variance with principal component analysis18. The model plays a crucial role in examining the impact of GEI and visualizing its patterns. This model aids in identifying stable genotypes across varying environments19. However, the AMMI model has its limitations20,21. It assumes that the effects of genotypes and environments are additive, which may not always be true22. This assumption can lead to skewed estimates of genotype and environment effects. Furthermore, this model is designed to explore linear associations between genotype and environment, but non-linear associations may exist23. The best linear unbiased predictions (BLUP) model addresses some of the AMMI model limitations, particularly regarding non-additivity and the analysis of the linear mixed model (LMM) structure. The BLUP model provides estimations of the yield average of high-performing genotypes. To leverage the strengths of both the AMMI and BLUP models, an index called the stability index of the weighted average absolute scores of BLUPs (WAASB) was introduced20. This index is used to select superior genotypes. The combination of the AMMI model's power and the BLUP model's prediction accuracy enhances the efficiency of both models in studying GEI20. However, when introducing a new cultivar, both the yield stability and the yield value are considered; As such, the WAASBY index was introduced based on the WAASB and yield value. This index as a measure of phenotypic stability and product yield allows for the selection of genotypes with high yield potential while reducing GEI. These selected genotypes can then be included in the cultivar introduction program.
The GEI is not the only hurdle in the breeding process aimed at enhancing yield24. Another significant obstacle breeders encounter is the unfavorable and negative correlation among crucial traits25–27. In sugar beet, the white sugar yield (WSY) is determined by a combination of quantitative and qualitative traits such as root yield (RY), sugar content (SC), alpha amino nitrogen (N), sodium (Na+) and potassium (K+)28–30. The correlation among these traits ranges from negative to positive31,32, adding complexity to sugar beet breeding programs10. Negative correlation among traits can cause a dilemma; when one trait is selected for improvement, it may unintentionally lead to a decrease in another trait33. Therefore, breeders must find a way to improve multiple traits while managing the negative correlations among them. Breeders can mitigate these negative effects by employing techniques like tandem selection, independent culling, and index selection approaches, thereby improving multiple traits at once24,34,35. However, these techniques have their own challenges and can potentially lead to biased results24,36. The responsibility of assigning weights to each trait in the index selection and determining the cutoff points for each trait in independent culling lies with the breeder. Consequently, the assigned weights and cutoff points can vary from one researcher to another and over time24. The Genotype by yield*trait (GYT) biplot graphic method has been proposed as a solution to these problems. This method assumes that yield is the most essential trait, and other key traits are only significant when they correlate with high yield and the superiority of a genotype should be evaluated based on its ability to combine high yield with other traits24. In essence, yield is the sole trait that can determine a genotype efficiency, and other traits are only valuable when they correlate with suitable yield levels. Thus, when selecting superior cultivars, the combination of yield with traits is more important than assessing cultivars based on each trait. An ideal genotype is one that achieves the optimal level of each trait, balancing the negative effect of trait correlations and demonstrating suitable yield across different environments36.
In a recent study by Olivoto et al.37, they introduced a new index called the multi-trait stability index (MTSI). This index is highly efficient in selecting stable genotypes in multi-environment experiments based on multiple traits8,11,38,39. It considers the correlation structure among traits and provides a unique selection process that is easy to interpret37. As a result, breeders who aim to simultaneously select for multiple traits can find it useful. The main objective of the study was to identify superior genotypes from a pool of promising sugar beet genotypes. In this regard, the study examined the influence of GEI on the yield stability of sugar beet genotypes. It also analyzed the correlation among critical traits that affect yield and finally, the superior sugar beet genotypes were selected.
Materials and methods
Plant materials
For this study, a total of 20 sugar beet genotypes were utilized, comprising 16 recently developed hybrids and four control cultivars (Table 1). The hybrids were developed at the Sugar Beet Seed Institute (SBSI), Karaj, Alborz, Iran, with the specific aim of introducing the resistance gene for rhizomania disease into genotypes that exhibited favorable quantitative and qualitative traits. From this set of hybrids, the 16 superior hybrids, as determined by their quantitative and qualitative traits, were chosen for further evaluations. Prior to the evaluations, the hybrids resistance against rhizomania disease was verified through both field and molecular assessments.
Table 1.
List of examined sugar beet genotypes and control cultivars.
| Genotype code | Genotype | Genotype code | Genotype |
|---|---|---|---|
| 1 | SBSI 124 | 11 | SBSI 134 |
| 2 | SBSI 125 | 12 | SBSI 135 |
| 3 | SBSI 126 | 13 | SBSI 136 |
| 4 | SBSI 127 | 14 | SBSI 137 |
| 5 | SBSI 128 | 15 | SBSI 138 |
| 6 | SBSI 129 | 16 | SBSI 068 |
| 7 | SBSI 130 | 17 | Shokoufa (check) |
| 8 | SBSI 131 | 18 | Arta (check) |
| 9 | SBSI 132 | 19 | Azare (check) |
| 10 | SBSI 133 | 20 | Rosire (check) |
Research sites and experimental design
Phenotypic assessments of experimental genotypes were conducted over two consecutive crop years (2020 and 2021) at five agricultural research stations located in Hamadan, Karaj, Mashhad, Miandoab, and Shiraz. These selected sites differed in terms of altitude, latitude and longitude (Table 2), atmospheric temperature and precipitation (Tables 3), and Physical and chemical characteristics of soil (Table 4). The experiments at each research station were carried out using a randomized complete block design with four replications. Each genotype was planted in a separate plot measuring 30 m2, consisting of six cultivation rows with a length of 10 m and a distance of 50 cm interrow. The experiments were conducted from April 10th to April 20th in both years. Throughout the growing season, weed control, irrigation, fertilizer application, and other field management activities were performed based on the recommendations of experts. Additionally, regular monitoring and prevention of pests and diseases specific to sugar beet were conducted at each research station. From October 20th to October 30th in both 2 years, the roots of four rows in the middle of the cultivation area were harvested, counted, and weighed, with one meter excluded from the beginning and end of the rows.
Table 2.
Characteristics of environmental conditions at experimental research stations.
| Environment code | Year | Location of the research station | Altitude (m) | Latitude | Longitude |
|---|---|---|---|---|---|
| E1 | 2020 | Karaj, Alborz, Iran | 1312 | 35°55′N | 50°54′E |
| E2 | 2021 | ||||
| E3 | 2020 | Mashhad, Khorasan Razavi, Iran | 1316 | 36°30′N | 59°37′E |
| E4 | 2021 | ||||
| E5 | 2020 | Miandoab, West Azarbaijan, Iran | 1296 | 36°58′N | 46°05′E |
| E6 | 2021 | ||||
| E7 | 2020 | Shiraz, Fars, Iran | 1484 | 29°32′N | 52°36′E |
| E8 | 2021 | ||||
| E9 | 2020 | Hamedan, Iran | 1818 | 34°47′N | 48°30′E |
| E10 | 2021 |
Table 3.
Weather characteristics at the experimental research stations.
| Location of the research station | Parameter | April | May | June | July | August | September | October |
|---|---|---|---|---|---|---|---|---|
| Karaj, Alborz, Iran | Temperature (°C) | 9.40–19.40 | 15.00–25.55 | 19.42–31.74 | 21.70–33.92 | 21.10–33.34 | 16.73–28.90 | 10.50–21.11 |
| Rainfall (mm) | 20.30 | 10.11 | 2.50 | 2.52 | 2.51 | 15.22 | 30.53 | |
| Mashhad, Khorasan Razavi, Iran | Temperature (°C) | 9.40–21.61 | 14.44–27.23 | 18.94–32.85 | 21.13–34.47 | 18.90–33.33 | 13.90–28.96 | 8.32–22.22 |
| Rainfall (mm) | 15.21 | 7.60 | 2.53 | 0.00 | 0.00 | 2.51 | 2.52 | |
| Miandoab, West Azarbaijan, Iran | Temperature (°C) | 6.75–18.90 | 11.18–25.00 | 16.12–31.31 | 20.00–34.41 | 19.48–34.46 | 14.40–29.40 | 8.93–21.70 |
| Rainfall (mm) | 27.91 | 20.32 | 7.61 | 2.50 | 2.50 | 5.00 | 17.81 | |
| Shiraz, Fars, Iran | Temperature (°C) | 10.00–23.92 | 15.60–30.53 | 30.53–35.50 | 21.74–37.21 | 20.50–36.10 | 16.10–32.81 | 10.50–26.73 |
| Rainfall (mm) | 15.22 | 5.00 | 2.52 | 2.52 | 2.51 | 0.00 | 5.00 | |
| Hamedan, Iran | Temperature (°C) | 5.55–17.20 | 10.50–23.33 | 15.00–30.01 | 18.92–33.83 | 17.80–32.81 | 12.81–28.34 | 7.80–21.11 |
| Rainfall (mm) | 27.93 | 12.71 | 5.00 | 2.54 | 5.00 | 10.62 | 22.81 |
Table 4.
Physical and chemical characteristics of soil at the experimental research stations.
| Location of the research station | Year | pH | EC (ds.m-1) | O.C. (%) | P (ppm) | K (ppm) | Clay (%) | Silt (%) | Sand (%) | Texture |
|---|---|---|---|---|---|---|---|---|---|---|
| Karaj, Alborz, Iran | 2020 | 7.21 | 0.53 | 0.74 | 8.24 | 596.00 | 37.30 | 41.40 | 21.30 | Clay-loam |
| 2021 | 7.30 | 0.77 | 1.01 | 1.97 | 398.00 | 37.30 | 41.40 | 21.30 | Clay-loam | |
| Mashhad, Khorasan Razavi, Iran | 2020 | 7.90 | 1.55 | 0.70 | 12.00 | 261.00 | 21.00 | 57.00 | 20.00 | Silty-clay-loam |
| 2021 | 7.65 | 1.67 | 0.75 | 12.10 | 296.00 | 16.00 | 36.00 | 48.00 | Silty-loam | |
| Miandoab, West Azarbaijan, Iran | 2020 | 7.30 | 0.83 | 49.00 | 13.00 | 402.00 | 65.00 | 58.00 | 25.00 | Silty-loam |
| 2021 | 7.10 | 0.78 | 56.00 | 17.00 | 521.00 | 61.10 | 55.40 | 23.70 | Silty-clay-loam | |
| Shiraz, Fars, Iran | 2020 | 8.00 | 0.93 | 0.74 | 1.02 | 490.00 | 36.00 | 43.20 | 20.80 | Clay-loam |
| 2021 | 7.80 | 2.01 | 0.76 | 4.40 | 264.00 | 36.00 | 43.20 | 20.80 | Clay-loam | |
| Hamedan, Iran | 2020 | 7.93 | 6.14 | 0.45 | 47.60 | 499.00 | 15.50 | 27.50 | 53.00 | Silty-loam |
| 2021 | 7.90 | 6.00 | 0.42 | 47.65 | 498.00 | 15.50 | 27.50 | 53.00 | Silty-loam |
Data collection
After the field evaluations, the experimental genotypes were transferred to the quality control laboratory of the SBSI for the evaluation of their quality traits. The roots were washed and a pulp sample was prepared using an automatic machine. The sample was then stored in a freezer at − 18 °C. In due time, 26 g of the frozen samples were taken and mixed with 177 ml of lead (II) hydroxide acetate for three minutes in a mixer. The resulting solution was then passed through a sieve to obtain a clear liquid. This liquid was used in the Betalyser device (an automatic system for the analysis of sugar beet quality) to measure the SC, N, Na+, and K+ elements29. To calculate the WSY for each genotype, the molasses sugar and the white sugar content were estimated using Eqs. (1) and (2)30. These values, along with the RY of each experimental genotype, were then used in Eq. (3) to obtain the WSY28. However, all international, national and institutional guidelines have been taken into account in various stages of experiments.
| 1 |
| 2 |
| 3 |
where MS is molasses sugar (%), K+ is potassium (meq.100 g−1), Na+ is sodium (meq.100 g−1), alpha-amino-N is nitrogen (meq.100 g−1), WSC is white sugar content (%), SC is sugar content (%), WSY is white sugar yield (t ha−1) and RY is root yield (t ha−1).
Statistical analysis
Before undertaking any form of analysis, first was applied the Grubbs test40 to the data, operating under the assumption of normality. As well, the Bartlett test41 was employed to check the homogeneity of the variance of experimental errors across various years and locations. After verifying the uniformity of the variance of these errors, the combined analysis of variance was carried out. This analysis was performed on a random year effect, while the location and genotype effects were assumed to be fixed. The analysis was applied to the RY and WSY using Eq. (4)42.
| 4 |
where is the response measured on the experimental unit (plot), is the overall mean, is the effect of the year, is the effect of the location, is the interaction effect of the level of Y with the level of L, is the effect of the block within the location, is the effect of the treatment, is the interaction effect of the level of Y with the level of T, is the interaction effect of the level of L with the level of T, is the interaction effect of the level of Y with the level of L and the level of T, and is experimental error.
To integrate the features of AMMI and BLUP models, the initial step involved computing the scores of these models for each genotype that was tested. These scores were then combined using the WAASB index, as per Eq. (5), resulting in a unified score that included elements from both the AMMI and BLUP modelst>.
| 5 |
where (Eq. 5) is the weighted average of absolute scores of the genotype or environment; is the absolute score of the genotype or environment in the interaction principal component (IPC); and is the magnitude of the variance explained by the IPC. Given that the attainment of high-performance, stable genotypes is a primary objective, the individual contributions of GEI were examined using a BLUP matrix. Following this analysis, the WAASBY index, which measures both yield average and stability, was calculated for each genotype as per Eq. (6)37.
| 6 |
where is the superiority index with different weights between yield and stability for the genotype; and are the weights for yield and stability, respectively; and are the rescaled values of the genotype for yield and WAASB, respectively. The correlation analysis of key traits was performed using the Pearson method. The first step in examining the GYT involved standardizing the original data. This was done following Eq. (7), as suggested by Yan and Frégeau-Reid24.
| 7 |
where is the standardized value of genotype i for trait or yield-trait combination j in the standardized table, is the original value of genotype i for trait or yield-trait combination j, is the mean across genotypes for trait or yield-trait combination j, and is the standard deviation for yield-trait combination j. The biplot representing the GYT was constructed using the first and second principal components (PCs) derived from the singular value decomposition of the standardized data. In this model, the singular value decomposition breaks down the GYT data into genotype eigenvalues, yield-trait combination eigenvalues, and singular values. This process is based on Eq. (8) as proposed by Yan and Frégeau-Reid24.
| 8 |
where and are the eigenvalues for PC1 and PC2, respectively, for genotype i; and are the eigenvalues for PC1 and PC2, respectively for trait j, and is the residual from fitting the PC1 and PC2 for genotype i on trait j; and are the singular values for PC1 and PC2, respectively. α is the singular value partitioning factor. The GYT biplot is created by plotting against for genotypes, and against for yield-trait combinations. This analysis focuses on four main patterns: (1) Exploring the associations between different yield-trait combinations, (2) Identifying the best genotype for each yield-trait combination, (3) Ranking genotypes based on a superiority index and evaluating their strengths and weaknesses, and (4) Ranking genotypes based on an ideal hypothetical genotype.
To identify the most superior sugar beet genotypes, a comprehensive evaluation of key traits such as RY, SC, N, Na+, and K+ is necessary. In order to assess the stability of these traits simultaneously, the MTSI index was calculated using Eq. (9)37.
| 9 |
where is the multi-trait stability index of the genotype i, is the score of the genotype i in the factor j, and is the score of the ideal genotype in the factor j. The scores were calculated using factor analysis for genotypes and traits. Finally, stable genotypes were selected based on positive selection differentials for traits intended to increase and negative selection differentials for traits intended to decrease.
Results and discussion
Combined analysis of variance
The non-significance of the G statistic in the Grubbs test was determined based on the normality of the experimental data for RY and WSY. The non-significant chi-square values obtained from Bartlett test for RY and WSY further confirmed the uniformity of experimental error variance across 10 environments (five regions in two years). After confirming these hypotheses, a combined analysis of variance was conducted to describe the main effects and quantify the interactions between different sources of variations. The mean of square of the main effects of year and genotype at the 1% probability level, and location at the 5% probability level, showed significant differences for both RY and WSY. The interaction effects of year-location, genotype-year, and genotype-year-location at the 1% probability level, as well as genotype-location at the 5% probability level, resulted in a significant difference in RY. These interaction effects, except for the year-genotype interaction, had a similar impact on WSY as they did on RY (Table 5). The significant variations observed in experimental years, locations, and genotypes can be attributed to changes in environmental conditions and the genetic makeup of plants, which vary from one environment to another. This leads to variations in RY and WSY among different experimental genotypes in different environments. These findings confirm the inevitability of various interactions in agricultural research26,43. The GEI primarily indicates that genotypes respond differently to various locations, emphasizing the need to evaluate genotypes in diverse environments. Based on the obtained results from the experiment conducted by Sadeghzadeh Hemayati et al.9 the environment and its interaction with the genetic structure of different genotypes played a significant role in the phenotypic expression of WSY in sugar beet genotypes. This resulted in different responses in terms of WSY based on the conditions of different environments. Similarly, the study conducted by Saremirad and Taleghani13 indicated that GEI outweighs the quantitative and qualitative characteristics of sugar yield in sugar beet hybrids. Therefore, this interaction should be considered when breeding new hybrids, as it allows for decisions regarding breeding for general or specific adaptation, depending on the yield stability in different environmental conditions. In order to better understand and reveal the GEI, multivariate statistical methods can be more useful. These methods can provide insights into the complex relationships between genotypes and environments, allowing for a more comprehensive understanding of the factors influencing crop yield and the development of cultivars with stability and adaptability to target environments.
Table 5.
Combined analysis of variance of root and white sugar yields in experimental sugar beet genotypes.
| Source of variation | df | Root yield | White sugar yield | ||
|---|---|---|---|---|---|
| Sum of square | Mean of square | Sum of square | Mean of square | ||
| Year | 1 | 17,160.54 | 17,160.54** | 184.86 | 184.86** |
| Location | 4 | 130,304.80 | 32,576.20* | 3129.38 | 782.34* |
| Year × locality | 4 | 15,725.22 | 3931.30** | 324.82 | 81.20** |
| Error 1 | 30 | 3256.01 | 108.53 | 190.16 | 6.34 |
| Genotype | 19 | 5760.54 | 303.19** | 270.29 | 14.23** |
| Year × genotype | 19 | 2037.18 | 107.22** | 35.70 | 1.88 ns |
| Locality × genotype | 76 | 12,582.24 | 165.56* | 286.76 | 3.77* |
| Year × locality × genotype | 76 | 7932.13 | 104.37** | 180.21 | 2.37** |
| Error 2 | 570 | 28,409.00 | 49.84 | 905.95 | 1.59 |
**: 1% probability level of significance; *: 5% probability level of significance; ns: non-significant.
Integration of AMMI and BLUP models
To enhance the reliability of analysis results in multi-environment experiments and gain a more precise understanding of GEI, was conducted an analysis of RY and WSY data using a combination of AMMI and BLUP models. The RY and WSY of the experimental genotypes were significantly influenced by the effects of environment, genotype, and GEI, according to the results of the analysis of variance based on the AMMI model. These factors accounted for 66.41%, 2.41%, and 9.18% of the variations in RY and 60.54%, 4.50%, and 8.36% of the variations in WSY, respectively (Table 6). Thus, the phenotypic expression of RY and WSY is determined by the genotype's genetic makeup, the field's environmental factors, and how these factors interact. Due to the polygenic nature of these qualities, environmental factors, genomic regions with linked genes, and quantitative trait loci all continuously affect them44. The genes that affect yield and its components are highly sensitive to environmental conditions and exhibit an interaction between quantitative trait loci and the environment. This interaction can either facilitate or limit the response to selection45. Therefore, it is crucial for breeding programs to consider and manage these effects properly46.
Table 6.
An AMMI-based analysis of variance, likelihood ratio test, and estimation of genetic variance components for root and white sugar yields in experimental sugar beet genotypes.
| Source of variation | df | Root yield | White sugar yield | ||||
|---|---|---|---|---|---|---|---|
| Mean of square | Pro. | Acc. | Mean of square | Pro. | Acc. | ||
| Environment | 9 | 18,132.28** | 66.41 | 66.41 | 404.34** | 60.54 | 60.54 |
| Replication (environment) | 30 | 108.53 | – | – | 6.34 | – | – |
| Genotype | 19 | 303.19** | 2.34 | 70.08 | 14.23** | 4.50 | 68.20 |
| Genotype × environment | 171 | 131.88** | 9.18 | 79.26 | 2.94** | 8.36 | 76.57 |
| PC1 | 27 | 241.30** | 28.90 | 28.90 | 5.18** | 27.80 | 27.80 |
| PC2 | 25 | 192.93** | 21.40 | 50.30 | 4.51** | 22.40 | 50.30 |
| PC3 | 23 | 183.30** | 18.70 | 69.00 | 3.48** | 15.90 | 66.20 |
| PC4 | 21 | 121.26** | 11.30 | 80.30 | 2.55* | 10.70 | 76.90 |
| PC5 | 19 | 109.65** | 9.20 | 89.50 | 2.76* | 10.40 | 87.30 |
| PC6 | 17 | 59.30ns | 4.50 | 94.00 | 1.76ns | 5.90 | 93.30 |
| PC7 | 15 | 40.90ns | 2.70 | 96.70 | 1.11ns | 3.30 | 96.60 |
| PC8 | 13 | 43.51ns | 2.50 | 99.20 | 0.84ns | 2.20 | 98.80 |
| PC9 | 11 | 16.34ns | 0.80 | 100.00 | 0.56ns | 1.20 | 100.00 |
| Residuals | 570 | 49.84 | – | – | 1.59 | – | – |
| Total | 970 | 253.32 | – | – | 6.20 | – | – |
| Likelihood ratio test | |||||||
| Environment | 49.84** | 66.78 | 66.78 | 1.59** | 71.95 | 71.95 | |
| Genotype | 4.30** | 5.74 | 72.52 | 0.28** | 12.77 | 84.72 | |
| Genotype × environment | 20.51** | 27.48 | 100 | 0.34** | 15.28 | 100 | |
| Genetic variance component | |||||||
| 74.63 | 2.21 | ||||||
| 0.56 | 0.79 | ||||||
| genotype × environment | 0.27 | 0.15 | |||||
| Accuracy | 0.75 | 0.89 | |||||
**: 1% probability level of significance; *: 5% probability level of significance; ns: non-significant; Pro: proportion variance; Acc: accumulated variance.
The analysis of the multiplicative interaction on RY was performed using principal components analysis. The first five IPCs were found to have significant differences at the 1% probability level and collectively accounted for 89.50% of the GEI sum of square. The contribution of each IPC was as follows 28.90%, 21.40%, 18.70%, 11.30%, and 9.20%, respectively. A similar analysis was conducted WSY, and the first, second, and third IPCs were found to be significantly different at the 1% probability level, while the fourth and fifth IPCs were significantly different at the 5% probability level. These IPCs explained 87.30% of the GEI variations, with contributions of 27.80%, 22.40%, 15.90%, 10.70%, and 10.40%, respectively. Other studies have also investigated the GEI using different models. Omrani et al.47 found that the first four IPCs explained 83% of the GEI variations. Fathi et al.48 estimated the contribution of the first and second IPCs to be 49.10% and 22.50%, respectively, accounting for 71.60% of the GEI variations. Mostafavi and Saremirad49 reported that the first IPC explained about 63% of the data variation. Rajabi et al.8 found that the first six IPCs of the GEI had a significant effect and explained 98.80% of the total variations. Sadeghzadeh Hemayati et al.9 identified seven significant IPCs that explained 95.50% of the variations related to the GEI. Based on the results of these studies and the present study, it is clear that the first two IPCs of the GEI alone may not fully explain the variation. Therefore, it is recommended to combine the AMMI model power with the BLUP model prediction accuracy for a more comprehensive interpretation.
The likelihood ratio test (LRT) confirmed the results of the AMMI analysis. The results indicated that the effects of genotype, environment, and GEI were significant at the 1% probability level for both RY and WSY. The significant effect of GEI suggests that the experimental genotypes respond to changes in environmental conditions. In other words, the strengths and weaknesses of each experimental genotype are determined by the environmental conditions. In such situations, using BLUP analysis to estimate genetic variance components can provide more reliable and accurate results37. Consequently, the REML/BLUP method was used to estimate the values of genetic variance components for both studied traits (Table 6). The environmental variance accounted for the highest proportion of phenotypic variance in RY (66.78%) and WSY (71.95%). The GEI variance ranked second, explaining 27.48% of the phenotypic variation in RY and 15.28% in WSY. The genotypic variance ranked third, explaining 5.74% of the phenotypic variation in RY and 12.77% in WSY. The genotypic variance had the lowest share of phenotypic variance in both studied traits. This suggests that environmental factors have a greater impact on the expression and variation of these traits compared to genetic factors. In other words, the influence of genes in creating diversity among genotypes is low. Therefore, it can be concluded that the genotypes are strongly influenced by environmental conditions in terms of RY and WSY. Consequently, the efficiency of selection decreases, and the identification and selection of desirable genotypes become less accurate50. The low variance of the GEI compared to the environmental variance indicates that the genetic variation has a limited effect on the phenotypic expression of RY and WSY in different sugar beet genotypes. This leads to low yields fluctuating from one environment to another. When the GEI variance is low compared to the environmental variance, it suggests that genetic factors have a limited influence on the phenotypic expression of desired traits51. This finding is important for breeders in terms of trait selection. The study by Taleghani et al.17 on sugar beet winter cultivation confirmed that the environment has the greatest effect on WSY, explaining 71.50% of the data variations. The genotype accounted for 9.80% of the justified variance, while the GEI accounted for 7.20% of the data variations. In the study by Basafa and Taherian52, the variance justified by GEI was 7.84%. Mostafavi and Saremirad49 reported that the environment, genotype, and GEI justified variances of 17.69%, 32.79%, and 17.90% of the total sum of squares, respectively. Their study also found that genotype had the greatest variation in yield, indicating a high diversity of genotypes.
Heritability plays a crucial role in breeding program, helping plant breeders select plants with desirable traits and develop effective breeding strategies37,53. Breeders can choose which traits to target for improvement and what breeding techniques to employ by studying the heritability of traits54,55. The degree of agreement between a trait's genotypic and phenotypic values is measured statistically as heritability. It measures the proportion of genetic influences that are responsible for the observed variation in a trait within a population. An estimate of the trait's heritability, with a possible range of 0 to 1, is made. Low heritability is defined as a heredity value less than 0.2, medium heritability is defined as a heritability value between 0.2 and 0.5, and high heritability is defined as a heritability value larger than 0.5. In the case of RY and WSY, the results obtained showed moderate to high heritability. This means that the phenotype of these traits is a good indicator of the underlying genotype and selection based on phenotype is likely to be effective. The genotypic correlation between environments was found to be low. A low correlation suggests difficulties in selecting superior stable genotypes across different environments. In the context of RY and WSY, the low correlation indicates that the genetic effects of these traits were not consistent across different environments. Therefore, accurate information and details are needed to select superior genotypes in such cases38. Selection accuracy is another important metric in breeding programs. It measures the correlation between observed and predicted values37. In the case of the mentioned traits, RY and WSY, the selection accuracy was high, with values of 0.75 and 0.89, respectively (Table 6). These high selection accuracy values indicate the reliability of the model in identifying superior genotypes for these traits.
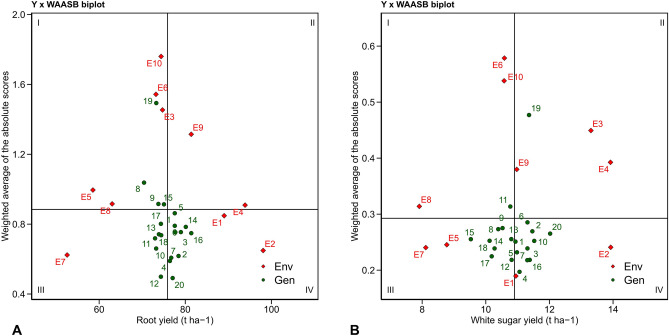
Although most genotypes variation can be explained by the first two IPCs obtained from the AMMI model, it is possible that some genotypes may require more IPCs. Therefore, the WAASB index can be used as a quantitative measure of stability that considers these variations. Figure 1 depicts a biplot where performance traits, such as RY and WSY, are represented on the horizontal axis, while WAASB index values are shown on the vertical axis. In this biplot, the vertical line in the middle represents the total yield average in the experimental environments. Genotypes and environments to the right of this line have a yield value higher than the total average, whereas those to the left have a lower yield value. The horizontal axis in the middle of the biplot represents the average area of the WAASB index. The intersection of this axis with the vertical axis (yield average) divides the biplot into four quadrants. Based on their stability in various environments, genotypes may be categorized into the biplot's several quadrants. In particular, the first quadrants of the RY biplot (genotypes 19, 8, 9, and 15, and environments E10, E6, E3, and E5) and the WSY biplot (genotype 11 and environments E6, E10, and E8) had genotypes and environments with high WAASB values and yields that were below the total average. This reveals both their very variable and unstable character and their yield value, which is below average. In other words, these genotypes and environments played a significant role in GEI, and they are not recommended for cultivation. On the other hand, the environments E9 and E4 in the second quadrant of the RY biplot and genotype 19 and environments E3, E4, and E9 in the same quadrant of the WSY biplot had high WAASB values and yields higher than the total average. These genotypes have good recognition ability and, when the environmental conditions are favorable, can achieve very high yield values. Therefore, they can be recommended for cultivation in areas with ideal conditions for sugar beet growth and development. In the RY biplot, genotypes 12, 10, 11, 18, 13, and 17, as well as environment E7, were placed in the third quadrant. In the WSY biplot, genotypes 12, 17, 18, 14, 15, 13, 8, and 9, along with environments E5 and E7, were also placed in the third quadrant. These genotypes and environments exhibited a lower WAASB index, indicating their stability and lack of influence from environmental conditions. Additionally, these genotypes showed low yield values. Essentially, the mentioned genotypes had low yield and high stability in this quadrant. On the other hand, the environments in this quadrant had low efficiency and a lower separation capability due to having the lowest WAASB values among all the environments. In contrast, genotypes 20, 4, 7, 2, 16, 3, 6, 1, 14, and 15, along with environments E2 and E1, were located in the fourth quadrant of the RY biplot. Similarly, genotypes 4, 16, 3, 7, 5, 1, 10, 20, 2, and 6, along with environments E1 and E2, were located in the fourth quadrant of the WSY biplot. These genotypes and environments had low WAASB index values and higher yield values compared to the total average. Genotypes in this biplot quadrant are considered stable and optimal in terms of yield because they have minimal influence on environmental conditions while achieving proper yields. The environments placed in the fourth quadrant had high production capacity and low WAASB values among the 10 experimental environments. The WAASB index is used to identify genotypes with optimal and stable yield in various plants, including wheat56, soybeans57, lentils58, rice59, corn 60, and sugar beet9,11. Unlike the AMMI model, which considers only the first IPC, the WAASB index expresses stability based on all scores of the IPCs. Therefore, WAASB considers the total GEI variance in identifying stable genotypes. In situations where the number of significant IPCs is high and the IPC1 cannot explain most of the GEI, it is suggested to use the WAASB index. This index fully applies the variance of GEI in identifying stable genotypes. The BLUP-based mixed model, which incorporates the WAASB index, has been shown to perform more accurately than the fixed-effects AMMI model in identifying stable genotypes60–63. The WAASB index has been successfully used, and provides useful results in identifying genotypes with optimal and stable yield.
Figure 1.
Biplot analysis of root yield (A) and white sugar yield (B) of sugar beet genotypes, evaluated by weighted average absolute scores of the best linear unbiased predictions (WAASB).
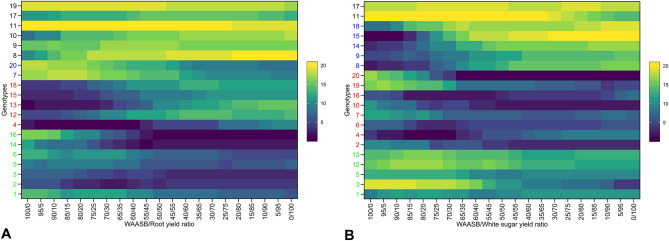
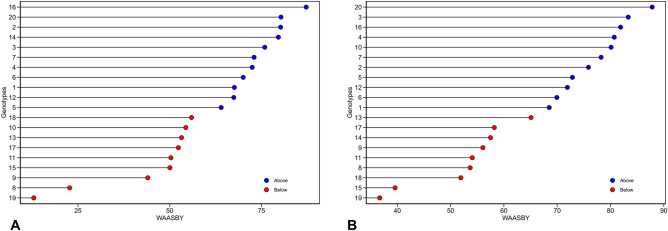
To evaluate yield and stability with greater precision, experimental genotypes were ranked based on their WAASBY index scores, as depicted in Fig. 2. These scores, which take into account various ratios of WAASB index to yield, were illustrated in a heatmap for RY (Fig. 2A) and WSY (Fig. 2B). The ranking of genotypes via the WAASBY index can fluctuate depending on the ratio of the WAASB index to yield. The first component (on the left side of the diagonal line) of the WAASB index to yield ratio (WAASB/RY or WSY) pertains to environmental stability, while the second component (on the right side of the diagonal line) relates to yield (RY or WSY). Thus, in the genotype ranking, a 0/100 ratio corresponds to stability, while the same ratio is also assigned to yield. Indeed, moving one unit from left to right in this plot decreases the environmental stability component by five percent and increases the yield component, such that at the end, genotypes are ranked solely based on yield (0/100). Based on the WAASBY index scores, the experimental genotypes were categorized into four groups. The first group (green) includes genotypes 1, 2, 3, 5, 6, 14, and 16 for RY, and genotypes 1, 3, 5, 12, and 13 for WSY. These genotypes were identified as stable with optimal yield. The second group (red), with poor yield values and instability, includes genotypes 4, 12, 13, 15, and 18 for RY, and genotypes 2, 4, 6, 7, 10, 16, 19, and 20 for WSY. The third group (blue), which includes genotypes 7 and 20 for RY and genotypes 8, 9, 14, 15, and 18 for WSY, demonstrated high yield values but instability. The fourth group (black) contains genotypes 8, 9, 10, 11, 17, and 19 for RY, and genotypes 11 and 17 for WSY, which showed poor yield values but were stable otherwise. In multi-environment experiments, the WAASBY index has proven to be a valuable selection index for both stability and yield, as it allows breeders to select genotypes with varying ratios of stability and yield based on their breeding program objectives. Figure 3 is particularly useful for selecting genotypes with an equal ratio. This figure allows for the simultaneous ranking and selection of experimental genotypes based on a 50:50 ratio for the WAASB index and RY (Fig. 3A) and WSY (Fig. 3B). Blue circles indicate a WAASBY index above the total average, while red circles indicate a WAASBY index below the total average. In summary, for RY, 11 genotypes, including genotypes 16, 20, 2, 14, 3, 7, 4, 6, 1, 12, and 5, had a higher than WAASBY index. Specifically, genotype 16 and thereafter genotypes 20, 2, and 14 had relatively higher WAASBY index values compared to other genotypes. For WSY, the results were largely similar to RY, with only the ranking of genotypes differing. On this trait, 11 genotypes, including genotypes 20, 3, 16, 4, 10, 7, 2, 5, 12, 6, and 1, had a higher than WAASBY index. In this case, genotype 20, followed by genotypes 3, 16, 4, and 10 had relatively higher WAASBY index values compared to other genotypes. According to these results, genotypes 16, 20, 2, and 14 for RY values and yield stability, and genotypes 20, 3, 16, 4, and 10 for WSY values and yield stability were identified as suitable genotypes. Sugar beet, a critical sugar plant that provides about 30% (approximately 42 million tons) of the world sugar needs (FAO, 2018), is of considerable importance, especially in light of climate change concerns and the need to transition from fossil fuel consumption to renewable fuels. Developing genotypes with high and stable performance under varying environmental conditions is a significant solution8,9,11. In light of this, the WAASBY index, a quantitative stability measure, is used to balance yield average and stability. This index allows for the selection of genotypes that have both high yield and yield stability11,64,65.
Figure 2.
Ranking of sugar beet genotypes based on varying importance of stability and root yield (A)/white sugar yield (B).
Figure 3.
Calculation of WAASBY in sugar beet genotypes, considering equal weights of 50 for root yield (A)/white sugar yield (B), and WAASB.
Exploring the correlation and graphical analysis of genotype by yield*trait (GYT)
The Pearson correlation coefficient was utilized to determine the degree of association between various traits. The values of this coefficient range from − 1 to 1. A correlation coefficient of 1 indicates a complete direct association between two traits, meaning that if one trait increases or decreases, the other will also increase or decrease proportionally. As the coefficient approaches zero, the direct association weakens, resulting in no linear association between the two traits. Conversely, as the coefficient approaches − 1, the inverse association between the two traits intensifies, leading to a complete inverse association when the correlation coefficient is − 1. This implies that if one trait increases, the other decreases and vice versa. The results of Pearson's correlation of various studied traits of experimental sugar beet genotypes are depicted in Fig. 4. The highest positive correlation between N and K+ was observed at a rate of 0.71. This high degree of correlation between the two traits suggests that an increase in the amount of N also results in an increase in the amount of K+. The traits of Na with N (r = 0.49), SC with K+ (r = 0.45), and Na+ with K+ (r = 0.41) exhibited a weak positive correlation. RY exhibited a negative correlation with all traits, including the SC, Na+, K+, and N. However, the highest negative correlation between RY and K+ (r = − 0.65) was observed, indicating that K+ decreases with an increase in RY. There was a weak negative correlation between RY with SC (r = − 0.44), RY with N (r = − 0.37), and RY with Na+ (r = − 0.19). A similar relationship between RY and SC has been reported previously66,67. The correlation of SC with Na was estimated to be negative but non-significant. The associations between the key traits of sugar beet can pose complications in the process of improving these traits. Therefore, breeders must strike a balance while managing the associations imposed by negative correlations between key traits. In this context, the GYT graphical method proves to be comprehensive and efficient24.
Figure 4.
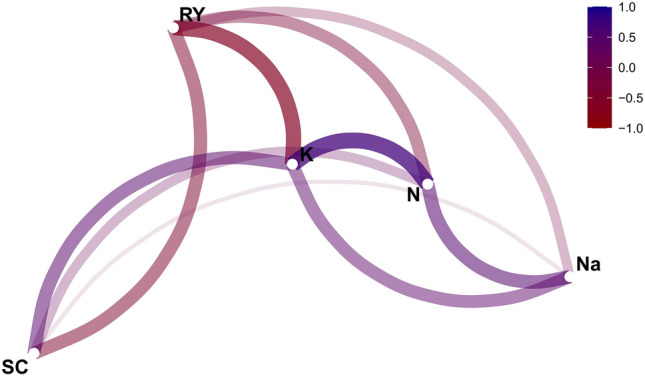
Pearson correlation analysis among key traits of sugar beet genotypes.
To comprehend the impact of genetic factors on crop productivity, was employed a method known as GYT graphical analysis. The results revealed that the first and second PCs accounted for 50.53% and 34.96% of the total variance in RY data, respectively, summing up to 85.49%. Given that these two PCs explain over 70% of the data variance, this affirms the high validity of the biplots obtained from this study in elucidating the variations in GYT68. However, if the sum of the first two PCs does not account for the majority of the data variation, it indicates the data complex nature69. Nevertheless, this does not invalidate the biplot27. Research by Shojaei et al.70 demonstrated that about 50% of the variation in GYT is explained by the first two PCs. In an experiment conducted by Faheem et al.36, they estimated that the sum of the first two PCs was close to 85%, with the PC1 accounting for approximately 74% and the PC2 for around 11% of the total data variations.
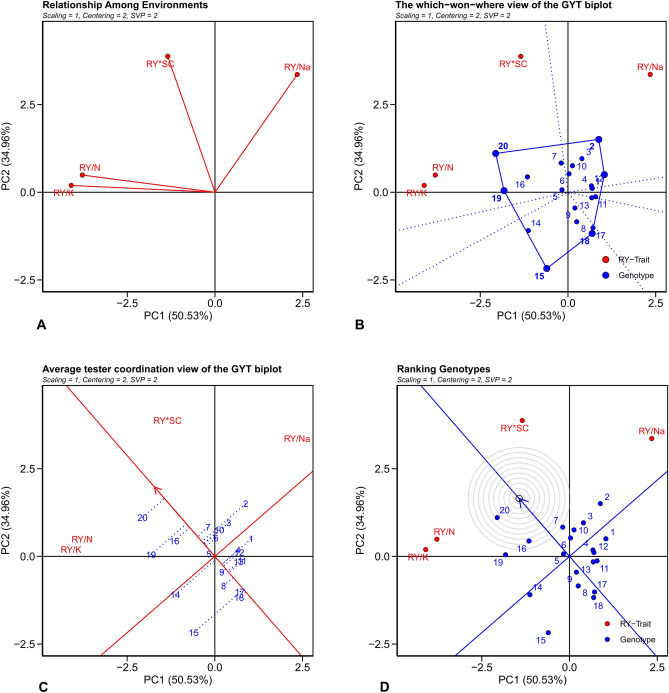
The quality and yield of sugar from sugar beet roots are influenced by impurities such as N, Na+, and K+. The N content, which is a combination of soluble amino acids and amide groups, plays a significant role in sugar extraction efficiency71. Although high N levels can impede sugar extraction, it is a vital factor in the storage life and quality of sugar beet. Hence, managing N levels, which can be affected by temperature, storage duration, and beet genetic diversity, is critical72. Na+ and K+ in sugar beet roots are considered molasses substances. They increase the solubility of sucrose, reducing its crystallization, which in turn decreases the quality of sugar beet and the efficiency of sugar extraction73–76. A high concentration of these elements can limit their use in certain applications due to their impact on the quality of molasses. Therefore, it is essential to design corrective programs that increase RY while also reducing the concentration of impurities. Studying the correlation between yield-trait combinations can identify the association among traits, aiding future experiments in creating new genotypes. In this context, the acute angle between the majority of vectors in a graph indicates a positive correlation among yield-trait combinations, mainly due to yield being a PC in these combinations24. This high correlation suggests a strong relationship among the rank of genotypes based on these combinations. The biplot (Fig. 5A) reveals a high positive correlation between RY/N and RY/K+. This indicates that reducing the content of one of these traits will likely result in a reduction in the other. There is also a weak positive correlation among these compounds and the combination of RY*SC. However, they show a negative correlation with RY/Na+. There is a moderate positive correlation between RY*SC and RY/Na+. The positive correlation between RY*SC and other compounds suggests that it is possible to increase the SC by reducing the N, Na+, and K+ in a genotype. However, the negative correlation among RY/N, RY/K+, and RY/Na+ complicates the breeding process to reduce all three impurities, necessitating detailed planning (Fig. 5A).
Figure 5.
Different views of the genotype by root yield*trait biplot for yield-trait associations (A), highlighting genotypes with outstanding profiles (B), ranking genotypes based on their overall superiority and their strengths and weaknesses (C) and ranking genotypes based on the ideal genotype (D).
In Fig. 5B, a polygon is visible, formed by connecting genotypes 2, 12, 18, 15, 19, and 20, which are furthest from the coordinate origin. Perpendicular lines extending from the coordinate origin to the polygon sides helped determine the grouping of GYT combinations. When yield-trait combinations are positioned with genotypes at their apex, it suggests these genotypes yield well in terms of those combinations. In other words, these are the best genotypes with respect to yield-traits. genotypes 2 and 12 excel in the RY/Na+. For the combinations of RY*SC, RY/N, and RY/K+, genotypes 20, 19, and 16 respectively, are the best genotypes (Fig. 5B). Genotypes located in sections devoid of combinations are not desirable for any combination and are considered weaker genotypes. The polygonal biplot also helped group yield-trait combinations into two groups. The RY/Na+ was placed in one group, while RY*SC, RY/N, and RY/K+ were grouped together (Fig. 5B).
The genotypes ranking, based on the yield-trait combination, was determined using the average tester coordinate biplot (Fig. 5C) and the superiority index (Table 7). The axis on the biplot, represented by an arrow originating from the coordinate’s origin, illustrates the mean of all yield-trait combinations. The axis perpendicular to this average axis signifies the measurement of the genotypes balance in terms of compounds. From this information, genotype 20 was identified as the best, followed by genotypes 19 and 16, due to their high yield average. On the other hand, genotypes 15, 18, and 17 exhibited the lowest yield average. These biplot results were corroborated by the superiority index. Various studies have been conducted24,36,70, including the present one, which concludes that the average tester coordinate biplot is a useful method in the GYT biplot analysis. This method provides valuable information about genotypes. The identification of the ideal genotype is based on the concepts of balance and high yield. Accordingly, the most desirable genotype is one that has the highest yield and maximum balance. Genotypes that are closest to this ideal are deemed superior, while those farthest are considered the undesirable. According to the biplot, genotypes 20, 16, 7, and 19 were identified as the best genotypes due to their minimal distance from the ideal genotype. Conversely, genotypes 15, 18, and 17 were identified as unfavorable genotypes because they were the furthest from the ideal genotype (Fig. 5D).
Table 7.
Standardized data of genotype by root yield*trait and superiority index for sugar beet genotypes.
| Genotype | Root yield × sugar content | Root yield/ | Root yield/ | Root yield/alpha amino N | Mean superiority index |
|---|---|---|---|---|---|
| 1 | 0.31 | 0.85 | − 1.21 | − 0.93 | − 0.24 |
| 2 | 1.27 | 1.69 | − 0.84 | − 0.74 | 0.35 |
| 3 | 1.10 | 0.74 | − 0.41 | − 0.50 | 0.23 |
| 4 | 0.44 | 0.04 | − 0.82 | − 0.95 | − 0.32 |
| 5 | 0.44 | − 0.37 | − 0.01 | 0.06 | 0.03 |
| 6 | 0.76 | 0.20 | − 0.06 | − 0.16 | 0.18 |
| 7 | 0.48 | 0.99 | 0.23 | 0.70 | 0.60 |
| 8 | − 1.59 | 0.13 | − 0.23 | 0.26 | − 0.36 |
| 9 | − 0.88 | 0.09 | − 0.52 | 0.43 | − 0.22 |
| 10 | 0.31 | 1.20 | 0.94 | − 0.72 | 0.43 |
| 11 | − 0.59 | 0.54 | − 0.97 | − 0.42 | − 0.36 |
| 12 | − 0.35 | 0.73 | − 0.73 | − 0.41 | − 0.19 |
| 13 | − 0.39 | 0.28 | − 0.64 | − 0.72 | − 0.37 |
| 14 | − 0.08 | − 2.18 | 1.33 | 0.13 | − 0.20 |
| 15 | − 1.89 | − 2.20 | 0.89 | − 0.11 | − 0.82 |
| 16 | 1.17 | − 0.62 | 1.64 | 0.38 | 0.64 |
| 17 | − 1.21 | − 0.48 | − 1.01 | − 0.60 | − 0.82 |
| 18 | − 1.26 | − 0.71 | − 0.89 | − 0.80 | − 0.92 |
| 19 | 0.32 | − 0.75 | 1.22 | 2.77 | 0.89 |
| 20 | 1.66 | − 0.17 | 2.07 | 2.34 | 1.48 |
| Mean | 0.00 | 0.00 | 0.00 | 0.00 | – |
| Standard deviation | 1.00 | 1.00 | 1.00 | 1.00 | – |
Multi-trait stability index (MTSI)
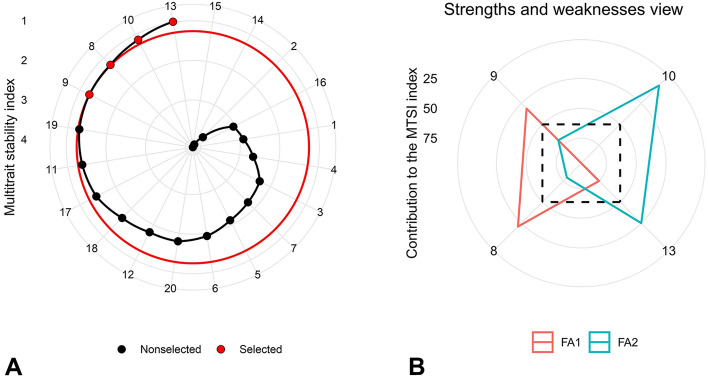
Factor analysis was performed using principal component analysis, and the interpretation of the results was carried out after Varimax rotation. Table 8 presents the results of the factor analysis, where factors with eigenvalues greater than one were selected. The variance of each factor was expressed as a percentage, indicating its importance in interpreting the overall variations in the data. In this analysis, two independent factors accounted for a total of 78.24% of the data variations. The first factor explained 41.76% of the total variance and had an eigenvalue of 2.09. It had large positive coefficients for RY and negative coefficients for K+ and N. The second factor, with eigenvalues of 1.82, accounted for 36.48% of the variations and included large negative factor coefficients for SC and Na+. The MTSI index of the studied genotypes was calculated based on the factor scores of the two mentioned factors. The MTSI index is used to assess the stability of genotypes, with lower values indicating closer proximity to the stable ideal genotype. Conversely, higher values suggest a greater distance from the ideal stable genotype and should not be selected. Figure 6A shows the ranking of the experimental genotypes based on the MTSI index, with the genotype having the highest value in the center and the genotype with the lowest value placed in the outermost circle. Applying a selection pressure of 20%, genotype 13 ranked first, and genotypes 10, 8, and 9 were identified as the most ideal stable genotypes across all traits. Comparing the trait values in the selected genotypes based on the MTSI index with the trait values in all experimental genotypes revealed that the mean value of SC increased in the selected genotypes, while the mean values of RY, K+, N, and Na+ decreased. Increasing SC aligns with the goals of the sugar beet improvement programs, but reducing RY is not one of the objectives. The goals for Na+, K+, and N are to decrease their values, and the selected genotypes showed a significant reduction in these traits. The selected genotypes resulted in selection differential and favorable selection gain in all traits except RY. Except for RY, the other traits exhibited high heritability in the selected genotypes. Figure 6B provides a visual representation of the strengths and weaknesses of the selected genotypes based on the contribution of each factor in the MTSI index. The lower the share justified by a factor (close to the outer edge), the closer the attributes within that factor are to the stable ideal state. Genotypes 8 and 9, which had the lowest value in the first factor, were close to the ideal genotype for the RY, K+, and N. Genotypes 10 and 13 had the lowest share of the second factor, indicating their proximity to the ideal genotype in terms of SC and Na+. The MTSI index has been successfully used in previous studies to evaluate yield and other agronomical traits in various genotypes. Sharifi, Abbasian and Mohaddesi39 applied the MTSI index to evaluate rice genotypes and identify superior genotypes in terms of yield, yield stability, and other agronomical traits. Similarly, Rajabi et al.8 used the MTSI index to identify stable sugar beet genotypes under conditions infected with rhizomania disease. Taleghani et al.11 also employed the MTSI index to identify ideal genotypes in terms of RY, WSY, SC, and extraction coefficient of sugar. The findings of these study align with the results obtained, which demonstrate the effectiveness of the MTSI index in identifying superior genotypes.
Table 8.
Prediction of selection differential for studied traits based on the multi-trait stability index (MTSI).
| Variable | FA1 | FA2 | Communality | Uniqueness’s | Goal | h2 | SD (%) | SG (%) |
|---|---|---|---|---|---|---|---|---|
| Root yield | 0.79 | 0.12 | 0.64 | 0.36 | Increase | 0.57 | − 4.03 | − 2.28 |
| − 0.83 | − 0.10 | 0.70 | 0.30 | Decrease | 0.92 | − 3.57 | − 3.29 | |
| alpha amino N | − 0.83 | 0.39 | 0.84 | 0.16 | Decrease | 0.91 | − 3.16 | − 2.87 |
| Sugar content | − 0.01 | − 0.94 | 0.89 | 0.11 | Increase | 0.91 | 1.46 | 1.33 |
| − 0.02 | − 0.92 | 0.84 | 0.16 | Decrease | 0.95 | − 14.54 | − 13.76 | |
| Mean | – | – | 0.78 | 0.22 | – | – | – | – |
| Total decrease | – | – | – | – | – | – | − 25.30 | − 22.19 |
| Total increase | – | – | – | – | – | – | 1.46 | 1.33 |
| Eigenvalues | 2.09 | 1.82 | – | – | – | – | – | – |
| Variance (%) | 41.76 | 36.48 | – | – | – | – | – | – |
| Cum. variance (%) | 41.76 | 78.24 | – | – | – | – | – | – |
FA: Factor, h2: Heritability, SD: Selection differential, SG: Selection gain.
Figure 6.
Ranking of genotypes in ascending order based on the multitrait stability index (A), and evaluation of selected genotypes in terms of their strengths and weaknesses represented as the ratio of each factor in the calculated mult-itrait stability index (B).
Conclusion
According to the results, the AMMI model demonstrated significant additive and multiplicative effects at the 1% probability level. However, the LMM indicated that the genotype and GEI had significant effects at the same probability level. Consequently, relying solely on the AMMI model for analyzing the structure of the LMM would not be successful. In such situations, utilizing BLUP analysis can yield better and more reliable results due to its high efficiency in estimating the average performance of genotypes in mixed models. By integrating the power of the AMMI method and the prediction accuracy of the BLUP method, it becomes possible to examine genotypic stability and GEI in the form of the WAASB index, while overcoming the limitations of the AMMI model. This comprehensive approach provides a complete picture of the GEI in sugar beet. In the selection and introduction of superior cultivars, it is necessary to consider both stability and yield value. In addition to reducing GEI, genotypes with high yield potential can be selected. Therefore, the WAASBY index can provide useful results. The results demonstrate that the environment and its interaction with the genetic structure of different genotypes significantly influence the phenotypic expression of RY and WSY. This leads to different responses in terms of RY and WSY among genotypes based on varying environmental conditions. In terms of RY values and stability, genotypes 16, 20, 2, and 14 were recognized as stable genotypes with high yield. Similarly, genotypes 20, 3, 16, 4, and 10 exhibited high WSY values and stability. Consequently, these genotypes can be recommended as new genetic sources for sugar beet breeding programs. In such programs, cultivars with high RY, high SC, and low impurities are preferred over other cultivars. The correlation analysis results revealed that all key traits, including SC, Na+, K+, and N, demonstrated a negative correlation with RY. Genotypes 20, 19, and 16 were identified as the best performers when considering the combination of RY with other key traits. Furthermore, the MTSI identified genotypes 13, 10, 8, and 9 as the most stable genotypes. These genotypes emerged as the top-ranking genotypes, suggesting them as a potential candidate for further breeding programs. In total, this study provides valuable insights into the complex interactions between genotype, environment, and key traits in sugar beet genotypes. This knowledge can guide the development of effective breeding programs aimed at enhancing crop production.
Acknowledgements
The authors express their gratitude to the technicians at the Sugar Beet Seed Institute (SBSI), Karaj, Iran, for their assistance in conducting the experiments.
Author contributions
M.H., S.B.M and D.T. methodology, A.S.R. software, A.S.R. and M.H. validation, A.S.R. investigation, M.H. and S.B.M. data curation, A.S.R. writing—original draft preparation, A.S.R. and M.H writing—review and editing, D.T. and A.S.R. visualization, M.H. project administration. All authors have read and agreed to the published version of the manuscript.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Akyüz A, Ersus S. Optimization of enzyme assisted extraction of protein from the sugar beet (Beta vulgaris L.) leaves for alternative plant protein concentrate production. Food Chem. 2021;335:127673. doi: 10.1016/j.foodchem.2020.127673. [DOI] [PubMed] [Google Scholar]
- 2.Lammens T, Franssen M, Scott E, Sanders J. Availability of protein-derived amino acids as feedstock for the production of bio-based chemicals. Biomass Bioenergy. 2012;44:168–181. doi: 10.1016/j.biombioe.2012.04.021. [DOI] [Google Scholar]
- 3.Tenorio AT, Schreuders F, Zisopoulos F, Boom R, Van der Goot A. Processing concepts for the use of green leaves as raw materials for the food industry. J. Clean. Prod. 2017;164:736–748. doi: 10.1016/j.jclepro.2017.06.248. [DOI] [Google Scholar]
- 4.Tomaszewska J, et al. Products of sugar beet processing as raw materials for chemicals and biodegradable polymers. RSC Adv. 2018;8:3161–3177. doi: 10.1039/C7RA12782K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dohm JC, et al. The genome of the recently domesticated crop plant sugar beet (Beta vulgaris) Nature. 2014;505:546–549. doi: 10.1038/nature12817. [DOI] [PubMed] [Google Scholar]
- 6.Monteiro F, et al. Genetic and genomic tools to asssist sugar beet improvement: The value of the crop wild relatives. Front. Plant Sci. 2018;9:74–85. doi: 10.3389/fpls.2018.00074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.United Nations. World population prospects 2019: Highlights. (Department of Economic and Social Affairs, Population Division). Retrieved from Retrieved from (2019).
- 8.Rajabi A, Ahmadi M, Bazrafshan M, Hassani M, Saremirad A. Evaluation of resistance and determination of stability of different sugar beet (Beta vulgaris L.) genotypes in rhizomania-infected conditions. Food Sci. Nutr. 2022;11:1403–1414. doi: 10.1002/fsn3.3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sadeghzadeh Hemayati S, et al. Evaluation of white sugar yield stability of some commercially released sugar beet cultivars in Iran from 2011–2020. Seed Plant J. 2022;38:339–364. doi: 10.22092/spj.2023.362024.1305. [DOI] [Google Scholar]
- 10.Taleghani D, Rajabi A, Sadeghzadeh Hemayati S, Saremirad A. Improvement and selection for drought-tolerant sugar beet (Beta vulgaris L.) pollinator lines. Results Eng. 2022;13:100367. doi: 10.1016/j.rineng.2022.100367. [DOI] [Google Scholar]
- 11.Taleghani D, Rajabi A, Saremirad A, Fasahat P. Stability analysis and selection of sugar beet (Beta vulgaris L.) genotypes using AMMI, BLUP, GGE biplot and MTSI. Sci. Rep. 2023;13:10019. doi: 10.1038/s41598-023-37217-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rani R, et al. Analysis of genotype × environment interactions for agronomic traits of soybean (Glycine max [L.] Merr.) using association mapping. Front. Genet. 2023;13:1090994. doi: 10.3389/fgene.2022.1090994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Saremirad A, Taleghani D. Utilization of univariate parametric and non-parametric methods in the stability analysis of sugar yield in sugar beet (Beta vulgaris L.) hybrids. J. Crop Breed. 2022;14:49–63. doi: 10.52547/jcb.14.43.49. [DOI] [Google Scholar]
- 14.Taleghani D, Saremirad A. Investigation of genotype-environment interaction effect on sugar yield and determination of stability of sugar beet (Beta vulgaris L.) hybrids. J. Crop Breed. 2022;14:103–118. doi: 10.52547/jcb.14.44.103. [DOI] [Google Scholar]
- 15.Kang M. Breeding: genotype by environment interaction. In: Goodman RM, editor. Encyclopedia of Plant and Crop Science. Marcel Dekker; 2004. [Google Scholar]
- 16.Kang MS. Using genotype-by-environment interaction for crop cultivar development. Adv. Agron. 1997;62:199–252. doi: 10.1016/S0065-2113(08)60569-6. [DOI] [Google Scholar]
- 17.Taleghani D, Saremirad A, Hosseinpour M, Ahmadi M, Hamidi H, Nemati R. Genotype × environment interaction effect on white sugar yield of winter-sown short-season sugar beet (Beta vulgaris L.) cultivars. Seed Plant J. 2022;38:53–69. doi: 10.22092/spj.2022.360021.1275. [DOI] [Google Scholar]
- 18.Gauch H. Statistical Analysis of Regional Yield Trials: AMMI Analysis of Factorial Designs. Elsevier Science Publishers; 1992. [Google Scholar]
- 19.Senguttuvel P, et al. Evaluation of genotype by environment interaction and adaptability in lowland irrigated rice hybrids for grain yield under high temperature. Sci. Rep. 2021;11:15825. doi: 10.1038/s41598-021-95264-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Olivoto T, Lúcio ADC, da Silva JAG, Marchioro VS, de Souza VQ, Jost E. Mean performance and stability in multi-environment trials I: Combining features of AMMI and BLUP techniques. Agron. J. 2019;111:2949–2960. doi: 10.2134/agronj2019.03.0220. [DOI] [Google Scholar]
- 21.Rodrigues PC, Monteiro A, Lourenço VM. A robust AMMI model for the analysis of genotype-by-environment data. Bioinformatics. 2016;32:58–66. doi: 10.1093/bioinformatics/btv533. [DOI] [PubMed] [Google Scholar]
- 22.Malosetti M, Ribaut J-M, van Eeuwijk FA. The statistical analysis of multi-environment data: Modeling genotype-by-environment interaction and its genetic basis. Front. Physiol. 2013;4:44. doi: 10.3389/fphys.2013.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mohammadi R, Armion M, Zadhasan E, Ahmadi MM, Amri A. The use of AMMI model for interpreting genotype × environment interaction in durum wheat. Exp. Agric. 2018;54:670–683. doi: 10.1017/S0014479717000308. [DOI] [Google Scholar]
- 24.Yan W, Frégeau-Reid J. Genotype by yield∗ trait (GYT) biplot: A novel approach for genotype selection based on multiple traits. Sci. Rep. 2018;8:1–10. doi: 10.1038/s41598-018-26688-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yan W. Crop Variety Trials: Data Management and Analysis. Wiley; 2014. [Google Scholar]
- 26.Yan W, Kang MS. GGE Biplot Analysis: A Graphical Tool for Breeders, Geneticists, and Agronomists. CRC Press; 2002. [Google Scholar]
- 27.Yan W, et al. Development and evaluation of a core subset of the USDA rice germplasm collection. Crop Sci. 2007;47:869–876. doi: 10.2135/cropsci2006.07.0444. [DOI] [Google Scholar]
- 28.Cook D, Scott R. The Sugar Beet Crop: Science into Practice. Champan and Hall Press; 1993. [Google Scholar]
- 29.Kunz M, Martin D, Puke H. Precision of beet analyses in Germany explained for polarization. Zuckerindustrie. 2002;127:13–21. [Google Scholar]
- 30.Reinfeld, E., Emmerich, G., Baumgarten, C., Winner & Beiss, U. Zur Voraussage des Melassez zuckersaus Ruben analysen Zucker. (Chapman & Hall, World Crop Series, 1974).
- 31.Rašovský M, Pačuta V, Ducsay L, Lenická D. Quantity and quality changes in sugar beet (Beta vulgaris Provar. Altissima Doel) induced by different sources of biostimulants. Plants. 2022 doi: 10.3390/plants11172222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tsialtas JT, Maslaris N. Sugar beet root shape and its relation with yield and quality. Sugar Tech. 2010;12:47–52. doi: 10.1007/s12355-010-0009-5. [DOI] [Google Scholar]
- 33.Neyhart JL, Lorenz AJ, Smith KP. Multi-trait improvement by predicting genetic correlations in breeding crosses. G3. 2019;9:3153–3165. doi: 10.1534/g3.119.400406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Boureima S, Abdoua Y. Genotype by yield* trait combination biplot approach to evaluate sesame genotypes on multiple traits basis. Turk. J. Field Crops. 2019;24:237–244. doi: 10.17557/tjfc.655165. [DOI] [Google Scholar]
- 35.Xu N, Fok M, Li J, Yang X, Yan W. Optimization of cotton variety registration criteria aided with a genotype-by-trait biplot analysis. Sci. Rep. 2017;7:17237. doi: 10.1038/s41598-017-17631-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Faheem M, Arain SM, Sial MA, Laghari KA, Qayyum A. Genotype by yield*trait (GYT) biplot analysis: A novel approach for evaluating advance lines of durum wheat. Cereal Res. Commun. 2023;51:447–456. doi: 10.1007/s42976-022-00298-7. [DOI] [Google Scholar]
- 37.Olivoto T, Lúcio AD, da Silva JA, Sari BG, Diel MI. Mean performance and stability in multi-environment trials II: Selection based on multiple traits. Agron. J. 2019;111:2961–2969. doi: 10.2134/agronj2019.03.0221. [DOI] [Google Scholar]
- 38.Koundinya A, Ajeesh B, Hegde V, Sheela M, Mohan C, Asha K. Genetic parameters, stability and selection of cassava genotypes between rainy and water stress conditions using AMMI, WAAS, BLUP and MTSI. Sci. Hortic. 2021;281:109949. doi: 10.1016/j.scienta.2021.109949. [DOI] [Google Scholar]
- 39.Sharifi P, Abbasian A, Mohaddesi A. Evaluation the mean performance and stability of rice genotypes by combining features of AMMI and BLUP techniques and selection based on multiple traits. Plant Genet. Res. 2021;7:163–180. doi: 10.52547/pgr.7.2.13. [DOI] [Google Scholar]
- 40.Grubbs FE. Procedures for detecting outlying observations in samples. Technometrics. 1969;11:1–21. doi: 10.1080/00401706.1969.10490657. [DOI] [Google Scholar]
- 41.Bartlett MS. Properties of sufficiency and statistical tests. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937;160:268–282. [Google Scholar]
- 42.Moore KJ, Dixon PM. Analysis of combined experiments revisited. Agron. J. 2015;107:763–771. doi: 10.2134/agronj13.0485. [DOI] [Google Scholar]
- 43.Sabaghnia N, Dehghani H, Alizadeh B, Mohghaddam M. Genetic analysis of oil yield, seed yield, and yield components in rapeseed using additive main effects and multiplicative interaction biplots. Agron. J. 2010;102:1361–1368. doi: 10.2134/agronj2010.0084. [DOI] [Google Scholar]
- 44.Said AA, MacQueen AH, Shawky H, Reynolds M, Juenger TE, El-Soda M. Genome-wide association mapping of genotype-environment interactions affecting yield-related traits of spring wheat grown in three watering regimes. Environ. Exp. Bot. 2022;194:104740. doi: 10.1016/j.envexpbot.2021.104740. [DOI] [Google Scholar]
- 45.Falconer DS. The problem of environment and selection. Am. Nat. 1952;86:293–298. doi: 10.1086/281736. [DOI] [Google Scholar]
- 46.El-Soda M, Sarhan MS. From gene mapping to gene editing, a guide from the Arabidopsis research. Annu. Plant Rev. Online. 2021;4:1–32. [Google Scholar]
- 47.Omrani S, Omrani A, Afshari M, Saremirad A, Bardehji S, Foroozesh P. Application of additive main effects and multiplicative interaction and biplot graphical analysis multivariate methods to study of genotype-environment interaction on safflower genotypes grain yield. J. Crop Breed. 2019;11:153–163. doi: 10.29252/jcb.11.31.153. [DOI] [Google Scholar]
- 48.Fathi M, Ranjbar G, Zangi M, Tabar S, Zarini HN. Analysis of stability and adaptation of cotton genotypes using GGE biplot method. Trakia J. Sci. 2018;16:51. doi: 10.15547/tjs.2018.01.009. [DOI] [Google Scholar]
- 49.Mostafavi K, Saremirad A. Genotype–environment interaction study in corn genotypes using additive main effects and multiplicative interaction method and GGE-biplot method. J. Crop Prod. 2021;14:1–12. doi: 10.22069/ejcp.2022.17527.2293. [DOI] [Google Scholar]
- 50.Saremirad A, Bihamta MR, Malihipour A, Mostafavi K, Alipour H. Genome-wide association study in diverse Iranian wheat germplasms detected several putative genomic regions associated with stem rust resistance. Food Sci. Nutr. 2021;9:1357–1374. doi: 10.1002/fsn3.2082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Saltz JB, Bell AM, Flint J, Gomulkiewicz R, Hughes KA, Keagy J. Why does the magnitude of genotype-by-environment interaction vary? Ecol. Evol. 2018;8:6342–6353. doi: 10.1002/ece3.4128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Basafa M, Taherian M. Analysis of stability and adaptability of forage yield among silage corn hybrids. J. Crop Breed. 2016;8:185–191. [Google Scholar]
- 53.Benakanahalli NK, et al. A framework for identification of stable genotypes Basedon MTSI and MGDII indexes: An example in guar (Cymopsis tetragonoloba L.) Agronomy. 2021;11:1221. doi: 10.3390/agronomy11061221. [DOI] [Google Scholar]
- 54.Majhi PK. Advances in Genetics and Plant Breeding. AkiNik Publications; 2019. Heritability and its genetic worth for plant breeding; pp. 69–75. [Google Scholar]
- 55.Schmidt U, Thöni H, Kaupenjohann M. Using a boundary line approach to analyze N2O flux data from agricultural soils. Nutr. Cycl. Agroecosyst. 2000;57:119–129. doi: 10.1023/A:1009854220769. [DOI] [Google Scholar]
- 56.Verma A, Singh G. Stability index based on weighted average of absolute scores of AMMI and yield of wheat genotypes evaluated under restricted irrigated conditions for peninsular zone. Int. J. Agric. Environ. Biotechnol. 2020;13:371–381. [Google Scholar]
- 57.Abdelghany AM, et al. Exploring the phenotypic stability of soybean seed compositions using multi-trait stability index approach. Agronomy. 2021;11:2200. doi: 10.3390/agronomy11112200. [DOI] [Google Scholar]
- 58.Sellami MH, Pulvento C, Lavini A. Selection of suitable genotypes of lentil (Lens culinaris Medik.) under rainfed conditions in south Italy using multi-trait stability index (MTSI) Agronomy. 2021;11:1807. doi: 10.3390/agronomy11091807. [DOI] [Google Scholar]
- 59.Sharifi P, Erfani A, Abbasian A, Mohaddesi A. Stability of some of rice genotypes based on WAASB and MTSI indices. Iran. J. Genet. Plant Breed. 2020;9:1–11. [Google Scholar]
- 60.Yue H, et al. Genotype by environment interaction analysis for grain yield and yield components of summer maize hybrids across the huanghuaihai region in China. Agriculture. 2022;12:602. doi: 10.3390/agriculture12050602. [DOI] [Google Scholar]
- 61.Hilmarsson HS, Rio S, Sánchez JIY. Genotype by environment interaction analysis of agronomic spring barley traits in Iceland using AMMI, factorial regression model and linear mixed model. Agronomy. 2021;11:499. doi: 10.3390/agronomy11030499. [DOI] [Google Scholar]
- 62.Piepho H, Möhring J, Melchinger A, Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 2008;161:209–228. doi: 10.1007/s10681-007-9449-8. [DOI] [Google Scholar]
- 63.Piepho H-P. Best linear unbiased prediction (BLUP) for regional yield trials: A comparison to additive main effects and multiplicative interaction (AMMI) analysis. Theor. Appl. Genet. 1994;89:647–654. doi: 10.1007/BF00222462. [DOI] [PubMed] [Google Scholar]
- 64.Lee SY, et al. Multi-environment trials and stability analysis for yield-related traits of commercial rice cultivars. Agriculture. 2023;13:256. doi: 10.3390/agriculture13020256. [DOI] [Google Scholar]
- 65.Nataraj V, et al. WAASB-based stability analysis and simultaneous selection for grain yield and early maturity in soybean. Agron. J. 2021;113:3089–3099. doi: 10.1002/agj2.20750. [DOI] [Google Scholar]
- 66.Nasri R, Kashani A, Paknejad F, Sadeghi SM, Ghorbani S. Correlation and path analysis of qualitative and quantitative yield in sugar beet in transplant and direct cultivation method in saline lands. Agron. Plant Breed. 2012;8:213–226. [Google Scholar]
- 67.Saremirad A, Hamdi F, Taleghani D. Evaluation of genetic diversity in sugar beet (Beta vulgaris L.) hybrids in terms of yield, qualitative and germination traits. Appl. Field Crops Res. 2023;35:87–67. doi: 10.22092/aj.2023.357194.1580. [DOI] [Google Scholar]
- 68.Cruz C, Regazzi A, Carneiro P. Modelos biométricos aplicados ao melhoramento. UFV; 2012. [Google Scholar]
- 69.Yan W, Tinker NA. An integrated biplot analysis system for displaying, interpreting, and exploring genotype× environment interaction. Crop Sci. 2005;45:1004–1016. doi: 10.2135/cropsci2004.0076. [DOI] [Google Scholar]
- 70.Shojaei SH, et al. Comparison of genotype × trait and genotype× yield-trait biplots in sunflower cultivars. Int. J. Agric. Environ. Food Sci. 2023;7:136–147. [Google Scholar]
- 71.Martínez-Arias R, Müller BU, Schechert A. Near-infrared determination of total soluble nitrogen and betaine in sugar beet. Sugar Tech. 2017;19:526–531. doi: 10.1007/s12355-016-0496-0. [DOI] [Google Scholar]
- 72.Gippert A-L, et al. Unraveling metabolic patterns and molecular mechanisms underlying storability in sugar beet. BMC Plant Biol. 2022;22:430. doi: 10.1186/s12870-022-03784-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Aljabri M, Alharbi S, Al-Qthanin RN, Ismaeil FM, Chen J, Abou-Elwafa SF. Recycling of beet sugar byproducts and wastes enhances sugar beet productivity and salt redistribution in saline soils. Environ. Sci. Pollut. Res. 2021;28:45745–45755. doi: 10.1007/s11356-021-13860-3. [DOI] [PubMed] [Google Scholar]
- 74.Makhlouf BSI, Khalil SRAE, Saudy HS. Efficacy of humic acids and chitosan for enhancing yield and sugar quality of sugar beet under moderate and severe drought. J. Soil Sci. Plant Nutr. 2022;22:1676–1691. doi: 10.1007/s42729-022-00762-7. [DOI] [Google Scholar]
- 75.Muir BM. Sugar Beet Cultivation, Management and Processing. Springer; 2022. pp. 837–862. [Google Scholar]
- 76.Xie X, Zhu Q, Xu Y, Ma X, Ding F, Li G. Potassium determines sugar beets’ yield and sugar content under drip irrigation condition. Sustainability. 2022;14:12520. doi: 10.3390/su141912520. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.