Fitness Landscapes for Effects of Shape on Chemotaxis and Other Behaviors of Bacteria

Abstract

Data on the shapes of 218 genera of free-floating or free-swimming bacteria reveal groupings around spherical shapes and around rod-like shapes of axial ratio about 3. Motile genera are less likely to be spherical and have larger axial ratios than nonmotile genera. The effects of shape on seven possible components of biological fitness were determined, and actual fitness landscapes in phenotype space are presented. Ellipsoidal shapes were used as models, since their hydrodynamic drag coefficients can be rigorously calculated in the world of low Reynolds number, where bacteria live. Comparing various shapes of the same volume, and assuming that departures from spherical have a cost that varies with the minimum radius of curvature, led to the following conclusions. Spherical shapes have the largest random dispersal by Brownian motion. Increased surface area occurs in oblate ellipsoids (disk-like), which rarely occur. Elongation into prolate ellipsoids (rod-like) reduces sinking speed, and this may explain why some nonmotile genera are rod-like. Elongation also favors swimming efficiency (to a limited extent) and the ability to detect stimulus gradients by any of three mechanisms. By far the largest effect (several hundred-fold) is on temporal detection of stimulus gradients, and this explains why rod-like shapes and this mechanism of chemotaxis are common.

The first bacteria to be observed were classified by their shapes (23), and in the three centuries since, shape has continued to be used for classification (e.g., coccus or bacillus). However, only modest efforts have been devoted to the mechanistic question of how the shapes of single-cell organisms are determined (3, 9), and the functional question of why bacteria have particular shapes has been even more neglected. The latter question is addressed here.

It seems reasonable to assume that early organisms were spherical as a result of surface tension (9), but the advent of cell walls opened up the option of different shapes. I consider an organism that is initially spherical and ask how its shape might evolve, if certain properties were important components of its fitness.

Shape can potentially affect many of the processes necessary for cell survival, growth, and reproduction. Some of these, like the transport of metabolites or chromosome segregation, are internal to the cell; the impact of shape on such processes depends on the details of the mechanisms and will not be considered here. Rather, my focus is on fundamental interactions between the organism and its environment that are independent of specific mechanisms employed by the organism.

Although the concept of the fitness landscape has been much discussed since its introduction by Wright (25) in 1932, examples of fitness landscapes in nature have been hard to come by. However, for small microbes that live free of any but hydrodynamic constraint on movement, it is possible to rigorously calculate portions of actual fitness landscapes in phenotype coordinates and gain insight into why bacteria have certain shapes and not others. In particular, I asked why rod-like shapes are common but disk-like shapes are not found.

MATERIALS AND METHODS

Data.

I checked each genus of bacteria described in all four volumes of Bergey’s Manual of Systematic Bacteriology (10). The prime objective was to obtain data for an unbiased sample of actual microbes, and objective criteria were established for the selection of data. Only one set of size range and motility status was recorded for each genus in the hope of reducing the overrepresentation of human pathogens that would have occurred if each described species contributed a data set.

Only genera that appeared to consist of unattached, free-swimming, or free-floating types were included; genera described as having mycelial growth forms, gliding motility, or magnetic particles or engaging in intracellular parasitism were excluded. In most cases, a numerical range for both width and length was given, and these four numbers were entered into a database. The motility status for each genus was also recorded in a parameter distinguishing between (i) nearly all strains (or cells) motile, (ii) nearly all strains (or cells) nonmotile, and (iii) mixed (some strains [or cells] motile and others not).

If a numerical size range and motility status were not described for the genus, the type species for the genus was examined; if its description was deficient, the first species description in the genus that contained the required information was used. When a genus was described in more than one location, only the first description was used.

All descriptions indicated that the cells were either spherical (diameter = length) or elongated along one dimension into a cylindrical or rod shape (diameter < length). Consequently, I characterized all of the different shapes by their axial ratio, α (=length/diameter). (The axial ratio appears to be characteristic of a given strain; when bacteria grow under different conditions, cell volume increases with growth rate, but the axial ratio remains constant (3 [p.217–218]). Where a range of diameters (D) or length (L) was given, the geometric mean, which equals the arithmetic mean on a log scale, was used. Thus, log α = [log(L_min) + log(L_max) − log(D_min) − log(D_max)]/2.

Calculations.

The shapes considered were all ellipsoids, defined by semiaxes a, b, and c. Included among them is the special case of the sphere, where a = b = c = r, the radius of the sphere. In comparisons of different shapes, the volume was kept constant. Since the volume of an ellipsoid is 4πabc/3 and a sphere is 4πr³/3, the two volumes are equal if r = (abc)^1/3.

In general, the surface area of ellipsoids can be calculated only by evaluation of elliptic integrals. This was done by using Mathematica to evaluate equation 3 in reference 15.

The hydrodynamic resistance of rigid ellipsoids can be worked out exactly in the limit of low Reynolds number (references in reference 5), which easily applies to bacteria (1 [p. 76, 6, 18), and I assume that the organisms of interest can be approximated by such ellipsoids. Unfortunately, the general formulas involve the values of definite integrals that have no solution in common functions except in special cases. General solutions are as follows:

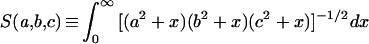1

(16 [equation 3]), and for convenience, the following variations:

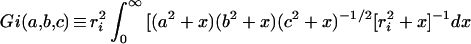2

where x is a dummy variable, i refers to any of the three axes, r_a = a, r_b = b, and r_c = c. A useful relation is G_a + G_b + G_c = S (16 [equation 4]). It is also useful to define

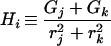3

where i, j, and k refer to any permutation of axes a, b, and c.

Motility is most effective when an organism swims along one of its axes of symmetry, which I call axis a. (If the organism is not motile, it doesn’t matter how axes are assigned.) I am primarily interested in two types of motion of the organism: translation parallel to the a axis, and rotation of this axis about any perpendicular axis (some combination of axes b and c.)

For translation parallel to axis i, the frictional drag coefficient is f_i(a, b, c) = 16πη/(S + G_i), which is equivalent to the formulas of Lamb (12 [p. 605, equation 15]) and Perrin (16 [equation 5]). A sphere has a translational frictional coefficient of f_S(r) = 6πηr (16 [equation 11]). Taking the ratio, with r = (abc)^1/3

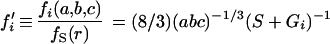4

At low Reynolds numbers, speed (v) is equal to the force (F) applied to a particle divided by the appropriate frictional drag coefficient, v = F/f. Since power (P) is work per unit time and work is force times distance, P = Fv. Combining these relations,

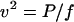5

and speed is inversely proportional to the square root of the frictional drag coefficient.

For diffusion in any one direction or rotation about any one axis, the diffusion coefficient is D_i = kT/f_i, where k is Boltzmann’s constant (1.38 × 10⁻¹⁶ erg K⁻¹) and T is absolute temperature (20°C = 293 K). For diffusion averaged over all directions, the effective frictional coefficient is the harmonic mean of the coefficients for each of the three orthogonal axes (17 [equation 96), and D = (kT/3) (f_a⁻¹ + f_b⁻¹ + f_c⁻¹). Taking the ratio of the diffusion coefficient of an ellipsoid (D) to that of an equal-volume sphere (D_s),

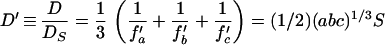6

Brownian motion also causes rotation of particles, and the rotation of any rigid shape can be described in terms of a time constant (τ) during which time the average of the squares of the angles rotated increases to one radian (1 [p. 82]) and the average of the cosines of the angles of orientation decays from 1 to e⁻¹ (20 [p. 437]). For rotation about a single axis or rotation of a sphere, τ = f_R / 2kT, where f_R is the frictional drag coefficient for rotation (20 [equation 25-12]). For a sphere, f_RS = 8πηr³, and the rotational time constant is τ_S = 4πηr³/kT (16 [equation 94]).

For ellipsoids, there are generally distinct frictional constants for rotation about each of the three axes (f_Ra, f_Rb, and f_Rc), and their values are f_Ri = 16 πη/3 H_i (16 [equation 6]). For rotation about more than one axis, the effective frictional coefficient is the harmonic mean of the coefficients for each axis involved. Thus, for rotation of one axis (i) about any perpendicular axis, the time constant for rotation of the axis is τ_i = (kT)⁻¹ (f_Rj⁻¹ + f_Rk⁻¹)⁻¹ (16 [equations 90 and 91). Using the general formulas (16 [equation 6]) and dividing by the time constant for rotation of an equal-volume sphere,

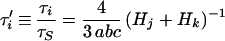7

where the subscripts i, j, and k refer to any permutation of axes a, b, and c.

Plots.

To plot parameter values for all possible ellipsoids without favoring a particular axis, I take advantage of the trigonometric identity sin(θ) + sin(θ + 2π/3) + sin(θ + 4π/3) = 0 and choose the semiaxes from

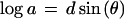8

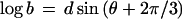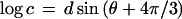where d is the degree of distortion from sphericity (0 to 1) and θ varies the proportion of the three axes. The identity ensures that abc = 1 and the volume of all the ellipsoids is 4π/3, for any value of d or θ.

The results are presented in polar plots, where the plot radius represents the minimum radius of curvature of the ellipsoid. The minimum radius of curvature (R) for an ellipsoid is the minimum of r_i²/r_j when r_i and r_j take on all six combinations of a, b, and c (13 [p. 78]). R′ is the minimum radius of curvature relative to the radius of the equal-volume sphere (R′ = R/r). In the plots presented, the horizontal and vertical positions are defined by x = − log(R′) sin(θ) and y = − log(R′) cos(θ), respectively. The maximum radius in the plots corresponds to a minimum radius of curvature of 1% of the equal-volume sphere (R′ = 0.01), which occurs in prolate ellipsoids of revolution with semiaxes (10, 10^−1/2, 10^−1/2) and in oblate ellipsoids of revolution with semiaxes (10^−4/5, 10^2/5, 10^2/5).

The equations were evaluated with Mathematica 2.0, the contours were plotted with DeltaGraph Professional 2.0, and the plots were finished with Adobe Illustrator 5.5 and 6, all on Apple Macintosh computers.

RESULTS

Observed shapes.

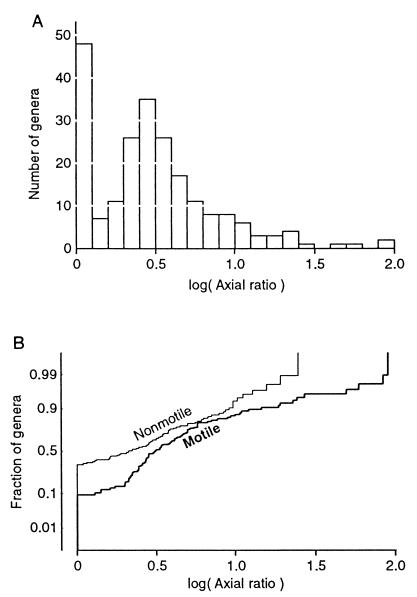
The selection of data on bacterial shapes and motility produced usable data for 218 genera, of which 97 were characterized as motile, 94 were characterized as nonmotile, and 27 were characterized as a mixture of motile and nonmotile types. All descriptions indicated that the cells were either spherical or elongated along one dimension into a cylindrical or rod-like shape. Figure 1A shows that there are two clusters of axial ratios. Twenty-one percent of the genera are described as spherical (log α = 0), and another peak occurs near an axial ratio of 3 (log α = 0.48).

FIG. 1.

Distribution of axial ratios. (A) Distribution of axial ratios for 218 genera of unconstrained bacteria. The median axial ratio is 2.82. (B) Cumulative distributions for the 97 motile and 94 nonmotile genera. On the cumulative probability scale (19 [p. 118]), a normal distribution falls on a straight line.

Since some of the possible adaptations apply only to motile bacteria, the data were separated according to motility. Nonparametric statistical testing indicated that the probability that the motile and nonmotile groups are drawn from the same distribution is only 0.0012 by the Mann-Whitney U test and 0.0001 by the Kolmogorov-Smirnov test. Cumulative distributions for log α of motile and nonmotile genera are presented separately in Fig. 1B. A larger fraction of the nonmotile genera are spherical (34% versus 10%). The nonmotile genera that are not spherical have nearly a normal distribution of log α, but among the motile genera, low axial ratios are less common and large axial ratios are more common than expected for a normal distribution. Clearly, motile genera tend to be more elongated than nonmotile genera. Why?

The ellipsoidal model.

To assess the effects of changes in shape systematically, I model the organisms as rigid ellipsoids in which all three axes are free to change size independently of one another. This model has the advantages that it does not bias the study toward certain shapes and rigorous formulas are available for ellipsoids but not for some properties of other shapes. Although bacteria rarely have ellipsoidal shapes, the model can approximate most simple shapes and be used to rigorously explore the effects of shape on an organism. Similarly, chemists use the ellipsoidal model to study the shapes of molecules (20, 22), although molecules are even less like ellipsoids than are bacteria.

In general, ellipsoids are characterized by three perpendicular semiaxes (a, b, and c), which are analogous to radii of a sphere. Prolate ellipsoids of revolution (e.g., a > b = c) are representative of cylindrical shapes; oblate ellipsoids of revolution (e.g., a < b = c) represent disk-like shapes. An ellipsoid with all three axes equal (a = b = c) is a sphere.

To separate the effects of shape from those of size, different ellipsoids with the same volume are compared, and the properties of the ellipsoids are presented relative to the equal-volume sphere. Consequently, all of the properties equal unity for the spherical shape, and it is immediately evident how the property differs from that of the spherical shape.

The results are presented in polar plots, where the proportion of the three ellipsoid axes varies with direction from the center of the plot (azimuth) through all possible combinations, and the plot radius is a measure of the degree of distortion from sphericity. For this measure, I chose the minimum radius of curvature of the ellipsoid, which is thought to provide a good indication of the difficulty an organism faces in producing the shape. The range of axial ratios (1 to 32) included in the plots includes all but 4 (motile) genera of the 218 in Fig. 1.

Surface area.

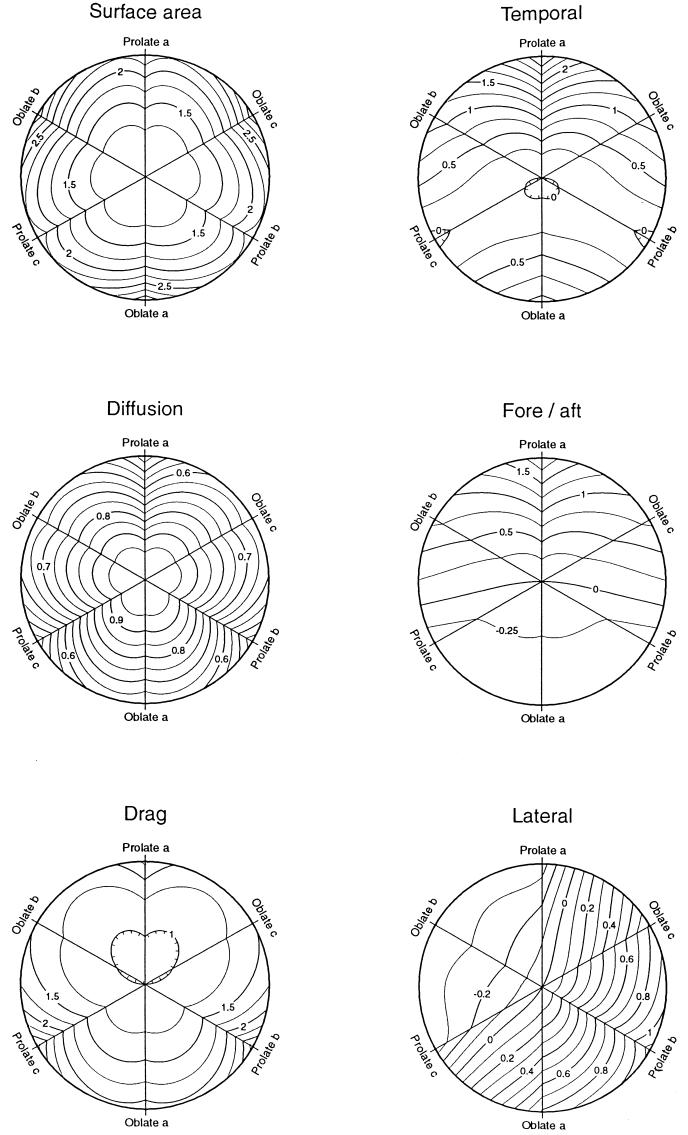
Organisms must take up nutrients and dispose of waste products across their surface, and bacteria might find it advantageous to change shape so as to increase surface area. Figure 2 (Surface area) shows a contour plot of how surface area changes with shape for equal-volume ellipsoids. The sphere has the minimum surface area, as is well known. In addition, the figure reveals that oblate (disk-shaped) ellipsoids have a larger surface for a given minimum radius of curvature. Thus, an organism experiencing enhanced fitness from increased surface area is expected to evolve by spreading in two axes forming a disk-like shape, other things being equal. Within the limit of radius of curvature equal to 1% of the equal-volume sphere, the optimal shape has semiaxes (0.158, 2.51, 2.51) and an axial ratio of 0.063, and the surface is increased to 3.198 times that of the equal-volume sphere. Prolate ellipsoids have a maximal surface area 2.48 times that of the sphere.

FIG. 2.

Contour plots of possible fitness components for equal-volume ellipsoids of all shapes. The values of the contours are relative to an equal-volume sphere. The sphere (a = b = c) is at the center, and the distance from the center is proportional to the negative log of the minimum radius of curvature occurring in each ellipsoid compared to the radius of the equal-volume sphere. At the outer edge of the plots, ellipsoids have a minimum radius of curvature of 1% that of the sphere. The three axes of the plots encompass the shapes in which two axes of the ellipsoid are identical (ellipsoids of revolution). At one end of each axis, prolate ellipsoids, with semiaxes equal to some permutation of (10, 10^−1/2, 10^−1/2), resemble rods, with axial ratios of 32; at the opposite end, oblate ellipsoids with semiaxes (10^−4/5, 10^2/5, 10^2/5) resemble disks with axial ratios of 0.063. (Left) in Surface area, the contour values are the surface area of equal-volume ellipsoids; in Diffusion, the contours are the diffusion coefficients of equal-volume ellipsoids (equation 6); in Drag, the contour values are the frictional drag coefficient (f_a′) for translation along axis a (equation 4). For the latter, the values within the innermost contour are less than 1, indicating that these shapes have a lower drag than an equal-volume sphere. (Right) Contour values are measures of the sensitivity a free-swimming organism can have in detecting the direction of a stimulus gradient by one of three mechanisms. In all three plots, the contour value is the log of a parameter proportional to the signal-to-noise ratio and sensitive to the shape of the organism. In Temporal, the parameter is (τ_a′^3/2 f_a′^−1/2), which is proportional to the maximum signal-to-noise ratio for organisms employing temporal mechanisms and swimming in the direction of axis a. In Fore/aft, the parameter is (a τ_a′^1/2), which is proportional to the maximum signal-to-noise ratio for organisms employing fore-and-aft comparisons. In Lateral, the parameter is (bτ′^1/2), which is proportional to the signal-to-noise ratio for organisms employing lateral comparisons, and τ′ is the smaller of τ_a′ or τ_b′.

Hydrodynamic constraints.

The resistance to movement of a rigid particle in a fluid is summarized by the frictional drag coefficient, f. This coefficient generally varies for movement along different axes or rotation about different axes, and coefficients for different types of motion are distinguished by subscripts to f. At low Reynolds numbers, which easily applies to bacteria (6), speed varies in proportion to the square root of f (equation 5).

Approximate formulas for the frictional drag coefficients are commonly available for prolate ellipsoids of revolution with the major axis more than five times the two equal minor axes (1 [p. 57, 84], 20 [p. 436], 22 [p. 95]). However, exact equations for any ellipsoidal shape are available (16) and used here, although they require evaluation of definite integrals. The ratio of the frictional coefficient for any shape to that of the equal-volume sphere has been called the coefficient of form resistance (11).

Random dispersal.

All organisms face the problem of dispersing progeny away from one another to avoid competition and to new environments to avoid extinction when the local environment changes. Bacteria are small enough that Brownian motion may play an important role in dispersal. The rate of dispersal is then measured by a diffusion coefficient, and I asked whether an organism can increase its diffusion coefficient by changing its shape.

From knowledge of the frictional drag coefficients for the three orthogonal axes, it is possible to rigorously calculate the diffusion coefficient for any ellipsoidal particle (equation 6). The value of the diffusion coefficient relative to that of the equal-volume sphere is plotted in Fig. 2 (Diffusion).

All values are less than 1, except for the central point representing a sphere. Thus, a spherical shape has the largest diffusion coefficient for any given volume. If an organism were originally spherical because of surface tension, selection for more rapid dispersal would not lead to changes in its shape.

Reduction of sinking.

Most organisms are denser than water, and those that do not attach to a substrate face the potential problem that they will sink away from resources such as oxygen or sunlight. Shape influences the rate of sinking, and some bacteria may adopt shapes that minimize sinking rate.

The theory for sinking rate has been well documented and exploited to estimate the size and shape of macromolecules by measuring sedimentation rates in centrifuges (1 [p. 59], 20 [p. 365] 22 [p. 116]). Assuming that the volume and total mass of an organism are constant and that the organism is randomly oriented, its sedimentation velocity is proportional to its diffusion coefficient (1 [p. 59], 20 [p. 380]). Thus, sedimentation rate is maximum for a spherical shape and can be reduced by changing to any other equal-volume shape. Examination of Fig. 2 (Diffusion) indicates that the minimum sinking rate with minimum distortion of shape is obtained by elongating along one axis into a prolate ellipsoid or toward a rod-like shape. Within the curvature limit, the sinking rate would be reduced to 0.415 that of the sphere. The smallest value for oblate ellipsoids is 0.601.

Swimming efficiency.

Many bacteria expend precious energy on swimming, and shape influences the efficiency of locomotion. Bacteria may adopt a shape that allows faster swimming with less energy, because of streamlining. If we assume that a particular organism requires a certain volume and devotes a certain amount of power to locomotion, we can obtain specific predictions about the speeds it can obtain if it adopts different shapes. In particular, what shape minimizes the frictional drag coefficient and thus maximizes the efficiency obtained?

Figure 2 (Drag) demonstrates that an organism benefiting from increased swimming efficiency should evolve from the spherical shape at the center to the minimum drag shape above the center. Although it is often stated that the sphere is the shape with minimum drag (24 [p. 247]) (e.g., see reference 22 [p. 95]), in fact the minimum drag occurs for a prolate ellipsoid of revolution with semiaxes in the ratio (1.562, 0.800, 0.800). This ellipsoid has an axial ratio of 1.952, and its drag is 0.9555 that of an equal-volume sphere. For more elongated shapes, the frictional coefficient increases because the increase in surface area increases drag more than the reduction in cross-sectional area reduces it (24 [p. 247]).

Thus, if swimming efficiency were commonly the major component of fitness, we would expect motile bacteria to have shapes similar to prolate ellipsoids of axial ratio approximately 2 and swim parallel to their long axis. In fact, most bacteria are like this except that 69% have axial ratios greater than 1.952 and the median axial ratio is 2.83. Efficiency of swimming provides no explanation for why such long rods might evolve.

Following stimuli.

Swimming is most useful when it is directed in a favorable direction, and most motile bacteria are probably capable of moving up or down chemical gradients. To determine the direction of a gradient, its concentration must be determined at two points separated by some distance, δ, and for the small distances of interest here, the difference in concentration is proportional to δ (6). Detection will also be influenced by the noise in measuring the two intensities, and the effect of noise is generally reduced in proportion to the square root of the time (t) over which the measurement is integrated (6). However, for free-swimming organisms, this time is limited by the rate at which orientation is lost as a result of rotational diffusion caused by Brownian motion (2, 6), which is influenced by shape. These general considerations lead to the expectation that the signal-to-noise ratio (S/N) is influenced as S/N ∝ Gδt^1/2, where G is the stimulus gradient (6). Since S/N ≃ 1 at the limit of detection, the shallowest detectable gradient is proportional to 1/(δt^1/2), and δt^1/2 is a measure of the relative sensitivity for gradient detection.

There are several ways in which an organism can separate the two positions at which intensity is determined. With temporal (sequential) comparisons the organism moves between the two positions, and δ ≤ vt, where v is the speed of swimming and t is the time between measurements. This is the only mechanism currently known to be employed by free-swimming bacteria (14). As an estimate of the maximum time useful to the organism, I use the relaxation time (τ) for decay of an initial orientation (equation 7). Since at any particular specific power consumption, v is inversely proportional to the square root of the frictional drag coefficient (equation 5), for movement along axis a, S/N ∝ δ τ_a^1/2 = v τ_a^3/2 ∝ τ_a^3/2 f_a^−1/2, where f_a is the frictional drag coefficient for translation along axis a (equation 4) and τ_a is the relaxation time for loss of orientation of the axis (equation 7).

This relationship is plotted in Fig. 2 (Temporal), which indicates that spherical organisms could improve gradient detection by elongating along the axis parallel to the direction of swimming. Within the curvature limit, gradient detection is improved by a factor of 10^2.81 = 647 over the equal-volume sphere.

An alternative mechanism for gradient direction is to employ spatial (simultaneous) comparisons (7 [p. 415]), in which receptors on different parts of the organism are compared. In this case, δ represents the distance between these body parts. If the comparison is fore-and-aft, δ ≤ 2a, and at best S/N ∝ a τ_a^1/2. (I ignore the complication that swimming may cause a difference in stimulation between the front and back [2] because the organism could compensate for this effect.) This relationship is plotted in Fig. 2 (Fore/aft), which demonstrates that the greatest gain with minimal departure from a spherical shape is again obtained by elongating along the axis parallel to the direction of locomotion, toward rod-like shapes. The same shape is optimal, but performance is superior to a sphere by the smaller factor of 10^1.98 = 96.

The other mechanism for spatial comparison is with receptors lateral to the direction of swimming. Taking the b axis in the direction between receptors, δ ≤ 2b. To detect the gradient, axis b must maintain its orientation for a sufficiently long period. The organism can then turn in the appropriate direction. However, the orientation of this axis might be maintained while more rapid rotations occurred around the axis. These latter rotations would not interfere with detecting the gradient, but once the organism had turned to the gradient, such rotations would randomly point the organism up, down, and across the gradient. Thus, this mechanism requires that rotations around all three axes be minimized, in contrast to previous mechanisms where symmetry made rotation around one axis inconsequential. For calculation, I use the smaller of the time constants for rotation around the a or b axis.

Consequently, S/N ∝ b τ^1/2, where τ is the smaller of τ_a and τ_b. This relationship is plotted in Fig. 2 (Lateral). A spherical organism maximizing this component of fitness with minimal change in shape should evolve along a path toward a prolate ellipsoid of revolution around axis b. Within the curvature limit, the optimal shape has semiaxes (0.32, 10, 0.32), swims perpendicular to its long axis, and is superior to the sphere by the still smaller factor of 10^1.06 = 11.5. The relatively small improvement explains why this behavior is not observed.

DISCUSSION

The results for all of the different types of adaptation are summarized in Table 1. We see that evolution toward increased surface area should lead to disk-like shapes, and the fact that these are rarely observed suggests that increasing surface area is not a major component of fitness for bacteria.

TABLE 1.

Optimal shapes for different adaptations

Adaptation	Optimal shape	Dimensionsa (a, b, c)	Improvement factor
Increased surface area	Oblate ellipsoid of small axial ratio	0.158, 2.51, 2.51	3.20
Increased diffusion	Sphere	1, 1, 1	1.00
Reduced sinking	Prolate ellipsoid of large axial ratio	10, 0.316, 0.316	2.41
Low translational drag	Prolate ellipsoid of axial ratio about 2	1.56, 0.80, 0.80	1.05
Gradient detection by temporal mechanism	Prolate ellipsoid of large axial ratio	10, 0.316, 0.316	647
Gradient detection by fore-and-aft mechanism	Prolate ellipsoid of large axial ratio	10, 0.316, 0.316	96
Gradient detection by lateral mechanism	Prolate ellipsoid of large axial ratio	0.316, 10, 0.316	12

^aFor volume of 4π/3 and limited to a minimum radius of curvature of 1% of the radius of the equal-volume sphere. Locomotion occurs along axis a, and lateral detection occurs across axis b. For surface area and sinking, the three axes are equivalent to one another. 

Adaptation to increase rates of dispersal via Brownian motion does not explain nonspherical organisms because the spherical shape has the largest diffusion coefficient, but some bacteria may have retained spherical shapes for this reason.

Reduction of sinking rate occurs with elongation, and this could be the reason that some nonmotile bacteria are elongated. For random orientations, the minimum sinking rate is 0.415 that of the equal-volume sphere (Fig. 2, Diffusion). If horizontally oriented, the sinking rate would be 0.349 (=1/2.869 from Fig. 2, Drag). If vertically oriented, the value is 0.548 (=1/1.826).

Reduction of translational drag for increased swimming efficiency can occur by elongation in the direction of swimming, but the effect is small, and an optimum is reached at an axial ratio of only 1.95, while most motile bacteria have axial ratios greater than 2.8. It might be noted here that a recent report (4) suggesting much larger effects of axial ratio on frictional drag, with an optimum at larger ratios, is based on approximate formulas that are accurate only for slender shapes (21) and are thus inappropriate for this application.

In contrast to these relatively small effects, shape has a large impact on a bacterium’s ability to detect stimulus gradients, no matter which sensory mechanism is employed. This results primarily from decreases in rotational diffusion that allow the organism to measure stimulus intensities over longer time periods. The effect is largest for temporal mechanisms with the potential to increase the signal-to-noise ratio several hundred-fold (Table 1). A recent analysis suggests that contrary to common notions, spatial gradient detection mechanisms are not inherently less sensitive than temporal mechanisms for spherical free-swimming organisms (8). However, the finding here that temporal mechanisms can be enhanced more effectively by changes in shape provides a clear explanation for why rod-like shapes and temporal detection mechanisms are commonly observed.