Abstract
Rhenium-186 (186Re) labeled nanoliposome (RNL) therapy for recurrent glioblastoma patients has shown promise to improve outcomes by locally delivering radiation to affected areas. To optimize the delivery of RNL, we have developed a framework to predict patient-specific response to RNL using image-guided mathematical models.
Methods:
We calibrated a family of reaction-diffusion type models with multi-modality imaging data from ten patients (NCR01906385) to predict the spatio-temporal dynamics of each patient’s tumor. The data consisted of longitudinal magnetic resonance imaging (MRI) and single photon emission computed tomography (SPECT) to estimate tumor burden and local RNL activity, respectively. The optimal model from the family was selected and used to predict future growth. A simplified version of the model was used in a leave-one-out analysis to predict the development of an individual patient’s tumor, based on cohort parameters.
Results:
Across the cohort, predictions using patient-specific parameters with the selected model were able to achieve Spearman correlation coefficients (SCC) of 0.98 and 0.93 for tumor volume and total cell number, respectively, when compared to the measured data. Predictions utilizing the leave-one-out method achieved SCCs of 0.89 and 0.88 for volume and total cell number across the population, respectively.
Conclusion:
We have shown that patient-specific calibrations of a biology-based mathematical model can be used to make early predictions of response to RNL therapy. Furthermore, the leave-one-out framework indicates that radiation doses determined by SPECT can be used to assign model parameters to make predictions directly following the conclusion of RNL treatment.
Statement of Significance:
This manuscript explores the application of computational models to predict response to radionuclide therapy in glioblastoma. There are few, to our knowledge, examples of mathematical models used in clinical radionuclide therapy. We have tested a family of models to determine the applicability of different radiation coupling terms for response to the localized radiation delivery. We show that with patient-specific parameter estimation, we can make accurate predictions of future glioblastoma response to the treatment. As a comparison, we have shown that population trends in response can be used to forecast growth from the moment the treatment has been delivered.
In addition to the high simulation and prediction accuracy our modeling methods have achieved, the evaluation of a family of models has given insight into the response dynamics of radionuclide therapy. These dynamics, while different than we had initially hypothesized, should encourage future imaging studies involving high dosage radiation treatments, with specific emphasis on the local immune and vascular response.
Keywords: Computational model, Patient calibration, Theranostic, SPECT, Mathematical model
1. Introduction
Glioblastoma multiforme (GBM) is the deadliest primary brain cancer [1], with a median survival of only 15 months [2]. The standard-of-care treatment for recurrent GBM typically consists of gross resection of the primary tumor, followed by external beam radiotherapy and/or concurrent chemotherapy to target residual disease [3]. Given the limited success of this approach in achieving tumor control, alternative methods of treatment have been desperately sought. This study focuses on mathematically modeling the response of GBM to an intracranial injection of rhenium-186 (186Re) labeled nanoliposomes (RNL) [4]. During decay, 186Re emits beta particles and a gamma ray, the former providing the radiation dose while the latter can be captured by single photon emission computed tomography (SPECT) to image it’s in vivo distribution. Intracranially injected RNL has the potential to deliver radiation doses (e.g., > 140 Gy) [4,5] well above those that can be achieved by external beam methods (approximately 60 Gy) [2,3]. Providing accurate predictions of response to RNL treatment would enable patient-specific delivery protocols [6] potentially yielding improved outcomes.
There is now a mature literature on mathematical models describing the growth and response of GBM to treatment with radiotherapy, chemotherapy, and surgery [7-11]. The most common modeling framework for these studies is the reaction-diffusion model, which simplifies GBM behavior to infiltration (via a diffusion term) and proliferation (via a reaction term). While this approach has been widely applied to modeling external beam radiation, [12-14], there is only minimal applications to radionuclide therapy in the preclinical setting [15], and no examples in the clinical setting. The present study serves as an initial application of predicting the spatio-temporal response of GBM to high dose, continuous radiation treatments in patients.
We utilize longitudinal magnetic resonance images (MRI) to estimate the total tumor burden and cellularity, and SPECT to estimate the RNL spatiotemporal distribution, which allows for personalizing the parameters within the mathematical models. We investigated two different methods to accomplish this goal. First, we calibrate a family of models to the patient-specific imaging data, select the highest performing model, and use it to predict each patient’s response to therapy. Second, we utilize a training cohort to build distributions of model parameters as a function of mean absorbed dose due to RNL delivery. Utilizing the predetermined distributions, predictions were made for the testing patient using a leave-one-out cross validation (LOOCV) approach. These two methods show how mathematical modeling can be used to predict the growth and response of GBM to locoregional cancer therapy via interstitial infusion of radionuclides.
2. Methods
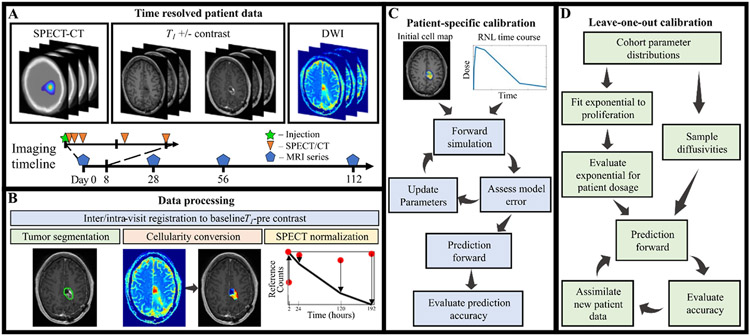
Fig. 1 provides an overview of the entire process, and the reader is encouraged to refer to it as they proceed through the following sections.
Fig. 1.
Schematic of the experimental-computational framework. Panel A displays the imaging datatypes used in this study. The timeline in the bottom of panel A visualizes the imaging acquisitions, with SPECT-CT occurring during the first week and MRI after treatment with RNL. Panel B highlights the image processing techniques used in this study. The patient-specific calibration flowchart is in panel C, which starts with the processed cell maps and RNL time course, loops through the calibration sequence, and outputs a prediction to be assessed. The leave-one-out method in panel D begins with parameters from the calibrated cohort to make an initial prediction for the patient, new data is then added to improve subsequent predictions.
2.1. Clinical protocol
Ten adult patients from the Phase I/II clinical trial of RNL (NCT01906385), presenting with Grade III/IV recurrent GBM after initial tumor resection were included in the study. These patients were recruited during phase I of the study, each receiving an increasing concentration of RNL according to their place in the dose escalation arm. Patients were excluded from the retrospective study only if the minimum MRI data were not available (five patients removed, full details of exclusion can be found in Appendix table A.1). A minimum of a baseline, plus two follow-up imaging sessions were required to make predictions with both frameworks described below (Fig. 1C and D). While a complete description of the trial can be found at [16], here we summarize only the salient details relevant to our study.
Patients included in the clinical trial undergo a pre-treatment screening and imaging session (see Imaging data below), prior to the insertion of an intra-cranial catheter(s) at the site of infusion. After the prescribed activity has been selected, RNL is delivered through the catheter(s) with a syringe pump. Simultaneously, combination SPECT/x-ray computed tomography (CT) scans are acquired to assess local delivery and radiation exposure. Following treatment and removal of the catheter, patients return for follow-up MR imaging sessions to monitor tumor response. Table 1 summarizes key details of the patient protocol, while Table A.2 of Appendix A provides additional patient information (e.g., infusion details, prior treatment status, and tumor volumes).
Table 1.
Key details from the patient imaging and treatment protocol.
| Patient | RNL delivered [MBq (mCi)] |
Average accumulated dose [Gy] |
MRI scan times [Days after treatment] |
SPECT/CT scan times [Hours after infusion starts] |
|---|---|---|---|---|
| 1 | 37.0 (1.0) | 26.5 | 0, 28, 56, 112 | 1, 2, 26, 120, 194 |
| 2 | 37.0 (1.0) | 4.6 | 0, 28, 56 | 1, 2, 26, 120, 194 |
| 3 | 55.5 (1.5) | 40.4 | 0, 28, 56, 112 | 2, 4, 28, 124, 196 |
| 4 | 148 (4.0) | 49.7 | 0, 28, 56 | 4, 9, 33, 153, 205 |
| 5 | 148 (4.0) | 19.8 | 0, 28, 56, 112 | 4, 9, 33, 129, 205 |
| 6 | 296 (8.0) | 22.1 | 0, 28, 56, 112 | 4, 9, 33, 129, 201 |
| 7 | 296 (8.0) | 160.5 | 0, 28, 56, 112 | 4, 9, 33, 129 |
| 8 | 495.8 (13.4) | 155.3 | 0, 28, 56 | 2, 9, 33, 129, 201 |
| 9 | 495.8 (13.4) | 166.3 | 0, 56, 112 | 1, 6, 30, 126, 198 |
| 10 | 495.8 (13.4) | 79.4 | 0, 56, 112 | 1, 3, 6, 30, 126, 198 |
2.2. Imaging data
SPECT images were collected with a GE Healthcare (Milwaukee, WI) Infinia SPECT/ CT scanner. During the first imaging visit, a 186Re source with known radioactivity was placed in the imaging field of view to allow for quantifying all SPECT data to radioactivity in megabecquerels (MBq). SPECT/CT images are collected halfway through the delivery of RNL, at the end of infusion (2 - 9 h), and 24, 120/144, and 192/196 h post infusion.
Patients also undergo pre- and post-treatment MRI on a Phillips Acheiva 3T (Best, Netherlands) scanner or a Siemens Skyra 3T (Malvern, PA) using an 8-channel coil. The protocol includes pre- and post-intravenous contrast injection (Gadovist; Bayer, Whippany, NJ) T1-weighted images, and diffusion weighted images. Apparent diffusion coefficient (ADC) maps are computed on the scanner from the diffusion weighted MRI data. Additionally, T2-weighted, T2-fluid attenuated inversion recovery, and diffusion tensor images were obtained, but not utilized, in this study. The imaging timeline for each patient is presented in Table 1 and acquisition details are available in Table 2.
Table 2.
Imaging resolutions.
| Modality | In-plane resolution (mm) |
Slice resolution (mm) |
FOV (Voxels) |
|---|---|---|---|
| T1 | 1.0 | 1.0 | 256 × 256 × 165 |
| T1+Contrast | 1.0 | 1.0 | 256 × 256 × 165 |
| ADC | 1.0 | 5.0 | 256 × 256 × 30 |
| SPECT | 4.42 | 4.42 | 128 × 128 × 128 |
| CT | 1.10 | 6.10 | 512 × 512 × 90 |
2.3. Image processing
All image processing was performed in MATLAB 2021a (MathWorks, Natick, MA) using the Image Processing Toolbox. MATLAB’s rigid registration functions are used to align all images to the pre-treatment, T1-weighted scan. Prior to registration, the field-of-view of the SPECT/CT images must be manually cropped to closely match that of the MRI data. Following cropping, all SPECT/CT images are registered in CT space to align with the 24-hour CT scan. The 24-hour CT scan is then registered to the pre-treatment, T1-weighted image. The resulting transformation is then applied to all other SPECT/CT images. Magnetic resonance (MR) scans from all visits are registered individually to the pre-treatment, T1-weighted image. MATLAB’s “imregtform” and “imwarp” functions can register structural components and interpolate imaging resolutions in the same step with high accuracy.
The MR images are processed to determine the total volume and cellularity at each imaging visit as follows. Contrast enhanced images and CT scans are used to determine the tumor and skull regions-of-interest, respectively. To determine the total tumor boundary, first the pre-contrast, T1-weighted images are subtracted from the T1-weighted, post contrast images to estimate the enhancing boundary. A threshold is applied to remove noise from background regions. The 3D regions of interest (ROI) are then manually generated by traveling slice-by-slice and outlining the T1 hyperintensity with MATLAB’s “roipoly”. This is repeated for each MRI timepoint to have the tumor segmented over time. Similarly, a segmentation defining the brain boundary is determined from intensity thresholds on the baseline CT scan. The skull is then removed from the domain by manually correcting the generated segmentation on a slice-by-slice basis. This segmentation defines the computational domain for the mathematical model. We return to the limitations of this segmentation approach in the Discussion section.
Next, voxel-wise cellularity estimates are based on assuming a linear relationship between with total cells in a voxel and the measured ADC, determined by Eq. (1):
| (1) |
where is the ADC of water at 37 °C (2.5 × 10−3 mm2/s), is the ADC at position of imaging time point , is the minimum ADC found within tumor ROIs for a specific patient, and is the voxel-specific carrying capacity. For details on this method, see refs. [17-19]. The local cell number map is then set to zero outside of the determined tumor region-of-interest for each time point.
The SPECT data are first normalized across imaging time points using a field-of-view based method [20] to quantify the radioactivity in MBq. To accomplish this, a phantom with known activity is placed in the field-of-view at the beginning of the SPECT acquisition. The remaining activity in the phantom at subsequent scans is estimated based on the half-life of 186Re and applied to determine a correction factor for SPECT images using Eq. (2):
| (2) |
where is the activity initially placed in the phantom, is the phantom intensity in counts, and the half-life of RNL is 90 h [21]. SPECT images at time t are multiplied by the correction factors, , to transform the images into maps of activity.
Spatially resolved dose rates are estimated by determining the spread of ionizing radiation from each voxel to its nearest neighbors with a dose-point kernel method [22]. Each processed SPECT image is used individually to determine the dose rate at the respective time point, using Eq. (3):
| (3) |
where is the local activity at position , the mass contained in a voxel, represents the absorbed fraction of energy in voxel per disintegration in voxel , and is the set of neighboring voxels with significant energy deposition. A discrete dose-kernel for 186Re defines the energy deposition fraction, . [23]. The dose-rates at each SPECT time point are linearly interpolated between scans to determine the spatio-temporally resolved, dose-rate.
2.4. Mathematical model
The standard reaction-diffusion equation [7] is used with variations to model the spatiotemporal response of each patient’s tumor to RNL:
| (4) |
where cell motion and proliferation are described by a diffusivity, , and rate , respectively. Table 3 lists how different terms are incorporated into Eq. (4) to build the model family; each resulting model is then calibrated to the measured data (see Table 4 for parameter descriptions). Models 0 and 1 consist of the base model (i.e., Eq. (4)) where cell death is incorporated via a global (i.e., one value per tumor) or local (i.e., one value per voxel) net proliferation rate, respectively. In these two models, is allowed to take on negative values, allowing for treatment to be modeled implicitly; in all subsequent radiation coupled models where treatment effects are explicitly defined, this proliferation rate is nonnegative.
Table 3.
Mathematical model family.
| Model | Equation | Description | Proliferation bounds |
|---|---|---|---|
| M0 | Global net proliferation | ||
| M1 | Local net proliferation | ||
| M2 | Proliferation reduction – local RNL | ||
| M3 | Proliferation reduction – global RNL | ||
| M4 | Proliferation reduction – accumulated RNL | ||
| M5 | Proliferation reduction – control | ||
| M6 | Cell death – local RNL | ||
| M7 | Cell death – global RNL | ||
| M8 | Cell death – accumulated RNL | ||
| M9 | Cell death – control |
Table 4.
Model parameter descriptions.
| Parameter | Description | Units | Assigned by |
|---|---|---|---|
| Cell count | Cells | DW-MRI | |
| Cell diffusivity | mm2 day−1 | Calibration | |
| Cell proliferation | day−1 | Calibration | |
| Radiation effect rate, dose-rate | Gy−1 | Calibration | |
| Radiation effect rate, accumulated dose | Gy−1 day−1 | Calibration | |
| Recovery rate | day−1 | Fixed (see A.1) | |
| Voxel carrying capacity | Cells | Image resolution | |
| Dose rate | Gy day−1 | SPECT | |
| Coupling constant | Gy day−1 | Calculated |
Models 2–5 (Table 3) incorporate radiation damage to reduce the effective proliferation rate [24,25]. This is assumed to account for fatal DNA damage manifesting over time as cell divisions are completed, resulting in fewer proliferating cells [26]. The sigmoid scaling of the radiation term follows a classic assumption in radiation response, that response levels off at higher cell densities as proliferation slows down [27]. Models 6–9 (Table 3) include cell death directly due to ionizing radiation [15,25]. These models assume that apoptosis occurs based on a calibrated radiation sensitivity and activity concentration. For both mechanisms of response, the RNL distribution is coupled with one of four terms (described below) to find the optimal link between measured response and activity distribution.
Models 2 and 6 directly use the spatio-temporal distribution of absorbed-dose rate determined from the SPECT data. In this formulation, cell death is due to the current activity provided by RNL in each voxel, giving individual voxels high flexibility in their response to therapy throughout time. In contrast, Models 3 and 7 utilize a global RNL coupling, which models radiation response based on the mean absorbed-dose rate at the current time step. This method assumes that the spatially resolved distribution of RNL does not provide enough information to inform local response, so the radiation must be averaged across the tumor. Models 4 and 8 assume that the radiation effects linger past the expiration of ionizing particles due to residual DNA damage taking several cell cycles to manifest itself and cause cell death. Here the accumulated dose each voxel is exposed to determines the magnitude of the initial effect. The impact on proliferation (Model 4) and cell death (Model 8) recovers to baseline over time. Finally, Models 5 and 9 do not explicitly incorporate RNL information into the coupling term, leaving behind a single calibrated parameter to capture the radiation effects.
2.5. Numerical implementation
The MRI gridding serves as the basis for discretizing the images into a grid for finite difference method (FDM) simulations in 3-dimensions; that is, each voxel in the MR image becomes a single point on the FDM grid. Images are interpolated resulting in a grid spacing of 2 × 2 × 2 mm3, or halfway between the ADC and SPECT resolutions. For each member of the model family determined by Eq. (4), the model is run forward with a time step of 2 days, chosen to ensure numerical stability of the simulation with the chosen grid size and range of potential diffusivities [28]. The RNL spatiotemporal distribution is interpolated to match the grid and time spacing of the simulation, using MATLAB’s “interpn” function.
To reduce the computational burden of the simulations, the domain is reduced to surround the maximum extent of tumor with additional padding to prevent cell build up around the boundaries. This is performed by first finding the voxels where the tumor exists at any measured time point, then extending the domain past the tumor edges in each direction by 10 mm, or until the brain segmentation is reached. These steps allow for up to an 80 % reduction in domain size compared to utilizing the whole brain and can be seen in Fig. 2, showing the simulation does not reach the edge of this reduced domain. Neumann conditions are specified at all boundaries, skull, or domain, to allow for zero-flux, preventing movement of cells out of these regions.
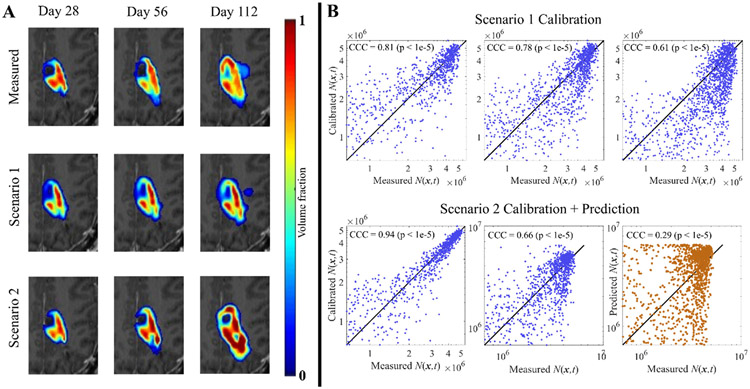
Fig. 2. Visualization of the patient-specific M1 calibration for patient 7.
Panel A shows measured cell counts in the central slice from the four imaging time points for one patient, with red corresponding to a voxel filled with cells. Panel B displays the local cellularity results from the two calibration scenarios, Scenario 1 on the top row and Scenario 2 on the bottom. All correlation plots in the top row correspond to calibrated time points (blue), and all display a strong correlation with the measured data. In the bottom row, only the first two time points are from calibrated images (blue) and the last is a prediction (orange), displaying a large drop in CCC.
2.6. Patient-specific calibration and prediction
Early response predictions are determined by a patient-specific calibration [15,29]. We utilize a Levenberg–Marquardt scheme [30] to update the model parameters until the change in the sum-squared errors between successful updates has converged (change in SSE < 1e-6) or a maximum number of iterations is reached (see reference [31] for full details on Levenberg–Marquardt implementation). Two calibration scenarios are evaluated. Scenario 1 focuses on model fit, using all available imaging time points for each respective patient to calibrate the model parameters. Scenario 2 focuses on prediction, leaving the last imaging time out of the data set to be calibrated. Parameters from Scenario 2 calibrations are then used to predict the local tumor burden at the final imaging time point.
The Akaike Information Criterion (AIC) [32] is used to select the optimal model from the family based on the results from the Scenario 1 calibrations. The raw AIC value is calculated using Eq. (5):
| (5) |
where is the number of voxels in the domain and is the number of calibrated parameters. The SSE and are calculated by including only non-zero voxels. The raw AIC value is then converted into an AIC weighting with Eqs. (6) and (7):
| (6) |
| (7) |
where is the current patient, and is the number of patients included in the study. Eq. (6) is used to determine the change in raw AIC obtained from each model, , relative to the minimum value. Eq. (7) then uses this difference to determine the probability that each model fits the data.
Outputs from the Scenario 1 (i.e., full time course calibration) and Scenario 2 (i.e., final visit left out of calibration and used for prediction) calibrations are then analyzed at the local level using the concordance correlation coefficient (CCC) [33], and at the global level using the Sorenson-Dice coefficient [34], for all patients and models individually. The CCC quantifies the degree of movement away from the line of unity when comparing the measured and simulated cellularity maps. The Dice is used to ensure that a low percent error between measured and simulated volumes, also represents a high degree of overlap between the measured and simulated tumors. We also tabulate the absolute percent error between the measured and calibrated/predicted volumes and total cell numbers to further assess global accuracy. At the cohort level we will also use the concordance Spearman correlation coefficient (SCC) to assess the strength of association between the measured and simulated values for volume and cell number. For Scenario 1 calibrations where all patient data is used, all simulations are compared together, whereas for Scenario 2, calibrated and predicted time points are separated for analysis.
2.7. Leave-one-out validation
The simplest model (M0; see Table 3) is used to validate a population based forecast for individual patients, due to its reduced parameter burden. The Scenario 1 calibration results from M0 are separated based on each patient’s mean accumulated dose to the tumor. A testing patient is selected, and their parameter values are subsequently removed from the parameter distributions, leaving a training dataset of nine patients (i.e., one has been “left out”). An initial guess for the diffusivity of the test patient is obtained by fitting the calibrated values of from the training dataset to a truncated normal distribution (Shapiro-Wilk test; ), with mean and standard deviation from the population, and sampling. An initial guess for is obtained by fitting an exponential function to the training dataset and is sampled based on the confidence of the fit. For the diffusivity and proliferation, we sample from the fit normal distribution or exponential function, respectively, 100 times for each parameter, yielding a range of parameter values to make predictions.
The simulation is run forward until the patient’s first imaging time point is reached with each sampled diffusivity/proliferation combination, resulting in a mean and 95 % confidence interval for the prediction. Imaging data from the current time point is then used to update parameters from the initial sampling and serves as the starting point for the next forward evaluation. This assimilation starts with a Levenberg–Marquardt calibration, to all currently acquired MRI data, providing patient-specific values of and . Parameter estimates for proliferation and diffusivity are weighted equally between the original one hundred samples and the new calibrated values using Eqs. (8) and (9), respectively:
| (8) |
| (9) |
where is the current scan number (e.g., 1 at baseline), and and are the outputs from the calibration (with and being the initial sampled parameters). This results in one hundred new samples for and to be used in a prediction, starting from the most recent measured tumor burden. The sequence is repeated for each imaging time point available. Each patient serves as the testing patient once with this method. Absolute percent error is evaluated at all time points for tumor volume and total cell number. Cohort predictions for volume and total cell number are analyzed with the SCC.
3. Results
3.1. Model selection
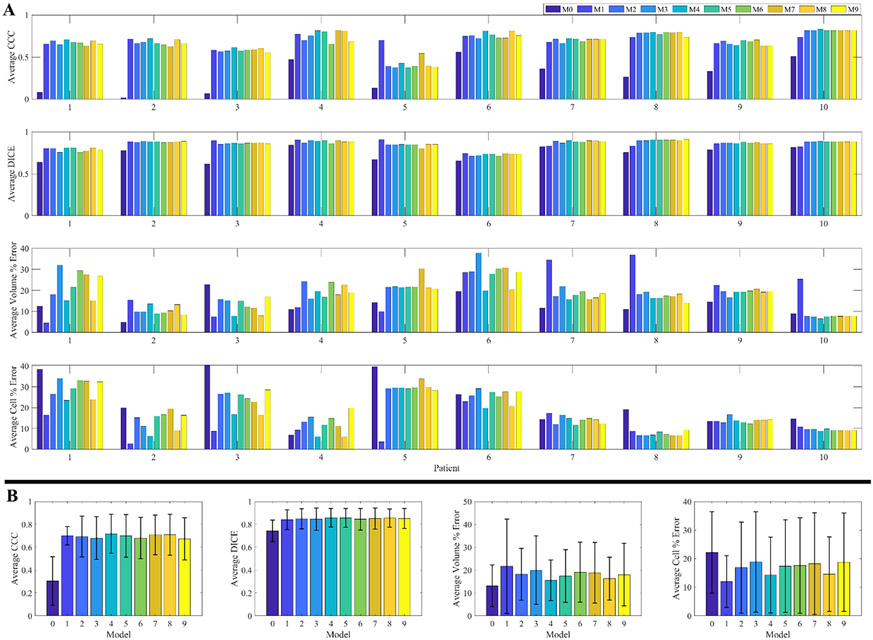
Table 5 present the results of the model selection analysis. M1 was the highest performing model, as seen by having a higher average AIC weight (0.6) than all the other models. The middle rankings (M2 to M9) display a large standard deviation in the average ranking. Despite the substantial reduction in parameters from M1 to M0 (due to accounting for a single global proliferation value, rather than a field of proliferation values in other models), the high sum of squared errors results in M0 being the worst performing model across most patients (Rank = 9.5 ± 0.9). As M1 was identified as the optimal model from AIC, it is used to generate the results in Sections 3.2 and 3.3 (See Fig. A.1 in Appendix A for results from all models).
Table 5.
Model selection rankings.
| Model | M0 | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 |
|---|---|---|---|---|---|---|---|---|---|---|
| AIC Weight | 0 | 0.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.1 |
| Rank | 9.5 ± 0.9 | 1.5 ± 1.2 | 5.7 ± 2.1 | 4.7 ± 1.9 | 6.1 ± 2.4 | 7.6 ± 2.8 | 6.3 ± 1.9 | 4.3 ± 1.3 | 4.7 ± 2.7 | 4.6 ± 2.2 |
3.2. Visualization of the model calibration
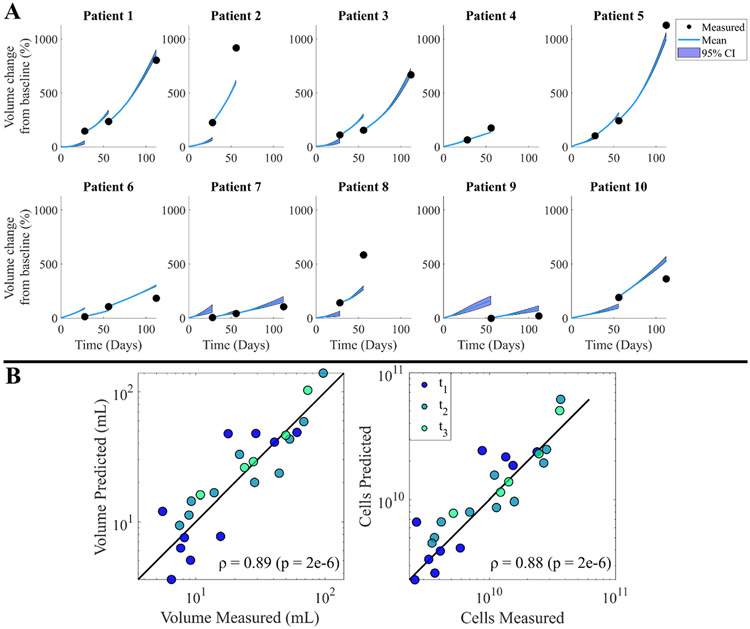
Fig. 2 shows results from the M1 calibration for patient 7. In panel A we focus only on the central slice to visualize the differences between the cellularity estimates of simulations and measured data. The middle row shows the results from the Scenario 1 (calibrated to full data set) calibration and the bottom presents the Scenario 2 (last follow-up used for prediction) calibration results. In panel B, cellularity measurements for individual voxels are plotted against the simulated counterpart from the same time point to assess the local correlations. For Scenario 1, the calibrations across all time points show a high overlap (Dice = 0.82 ± 0.02) with a strong local correlation (CCC = 0.73 ± 0.09). The Scenario 2 calibrations display a slight improvement (but not significant, p = 0.20 for Dice, p = 0.80 for CCC) in the Dice and CCC values for calibrated time points, 0.91 ± 0.02 and 0.80 ± 0.14, respectively. Lastly, the predicted time point in the Scenario 2 calibration displays a sharp drop in CCC (0.29), and a slight decrease in Dice (0.75). In the following section, we present the results across the entire cohort of patients.
3.3. Cohort calibration results
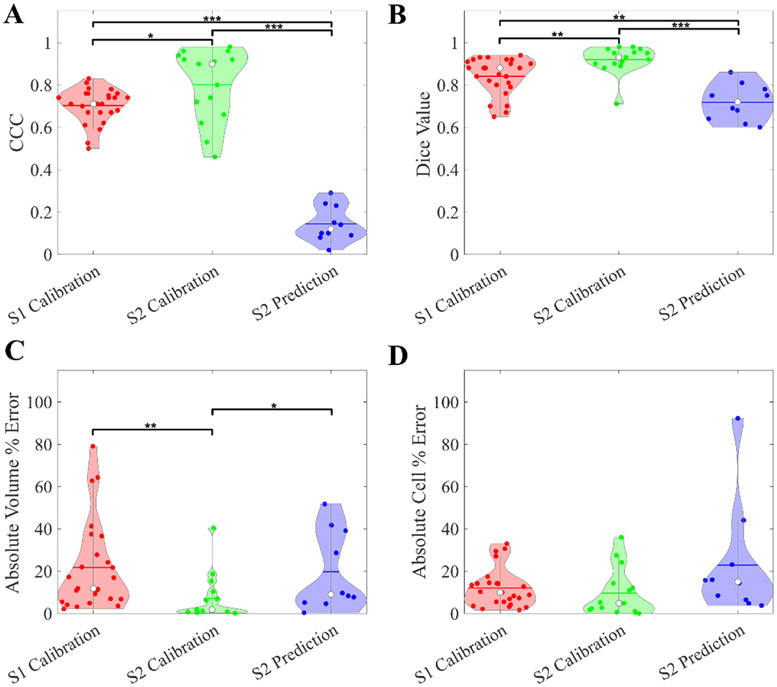
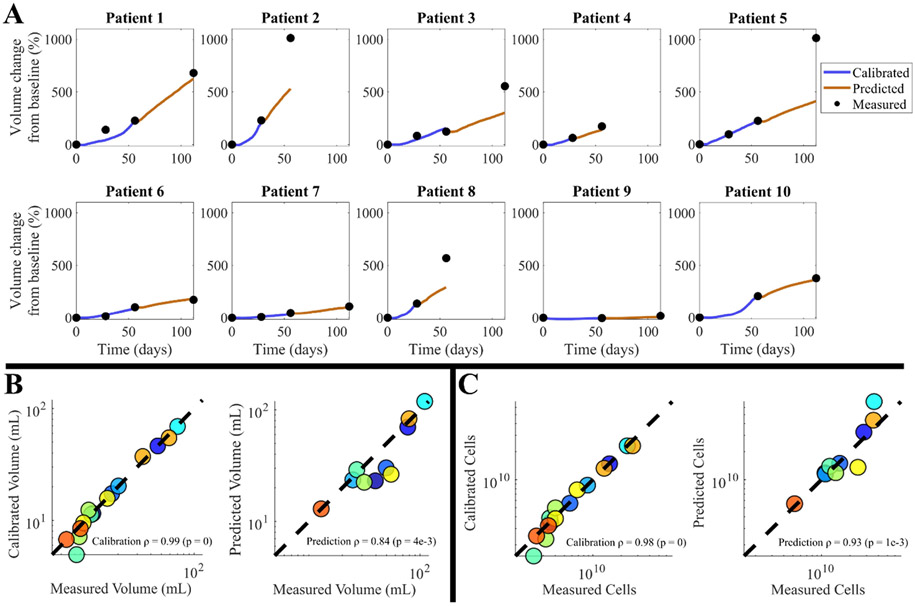
Results of global and local metrics can be found in Fig. 3. Median CCC values for calibrations from Scenarios 1 and 2 are 0.71 (range = [0.50, 0.83]) and 0.90 (range = [0.46, 0.98]), respectively; these values drop considerably when moving to the predictions from Scenario 2 where CCC = 0.12 (range = [0.02, 0.29]). Similarly, the median Dice scores for Scenarios 1 and 2 calibrations are 0.88 (range = [0.65, 0.94]) and 0.92 (range = [0.71, 0.98]), respectively, dropping to 0.72 (range = [0.60, 0.86]) for the Scenario 2 prediction. The median absolute volume error increases from 1.84 % (range = [0.12, 40.41]) to 8.97 % (range = [0.37, 51.69]), and total cell number error increases from 4.81 % (range = [0.04, 35.97]) to 14.98 % (range = [3.75, 92.96]) for Scenario 2 calibrations and predictions, respectively. The volume time courses of individual patients can be found in Fig. 4A. Here the low calibration error is visible, with an increase when predicting that depends on how the volume changes with respect to the previous follow-up. For the Scenario 1 calibrations, volumes and cell counts exhibit high correlation between measurements and calibrations (SCC = 0.98, p-values < 7e-7). For the Scenario 2 calibrations (Fig. 4B and C), global metrics display a SCC = 0.99 (p-value ~ 0) and SCC = 0.98 (p-value ~ 0) between measured and calibrated volumes and cell counts, respectively. These correlations drop slightly for the predictions, with a SCC of 0.84 (p-value = 4.0e-3) for volumes and 0.93 (p = 1.0e-3) for total cell numbers.
Fig. 3. Patient-specific M1 calibration results.
Cohort statistics from the M1 calibration are presented from both calibration scenarios. In Panel A, we see consistent CCC values across all patients from the calibrated time points, with a significant drop when we move to the Scenario 2 prediction. Panel B shows the Dice metric, which have a similar trend to the CCCs, with a less significant drop in the prediction accuracy. Panels C and D show high global accuracy across both scenarios and simulation types. Significance is calculated with the paired Mann–Whitney test and marked where applicable (* p < 0.05, ** p < 0.01, *** p < 0.001).
Fig. 4. Patient-specific time course and correlation for M1.
Panel A shows the time course of percent volume change from the Scenario 2 calibrations. Here we see first the calibrated trajectory (dark blue line) aligns closely to the measured data; however, the prediction accuracy (orange) is dependent on whether the tumor experiences consistent growth to the final time point. The absolute volume error of the predictions for these 10 patients ranges from 0.37 % to 51.69 % (median = 8.97 %). Panels B and C display the volume and cell count Spearman correlation from the Scenario 2 calibrations, respectively. Calibration SCC values are remarkably high for both metrics, and prediction SCC values suggest high correlation. Marker colors correspond to individual patients and are consistent across charts.
3.4. Leave-one-out distributions and sampling
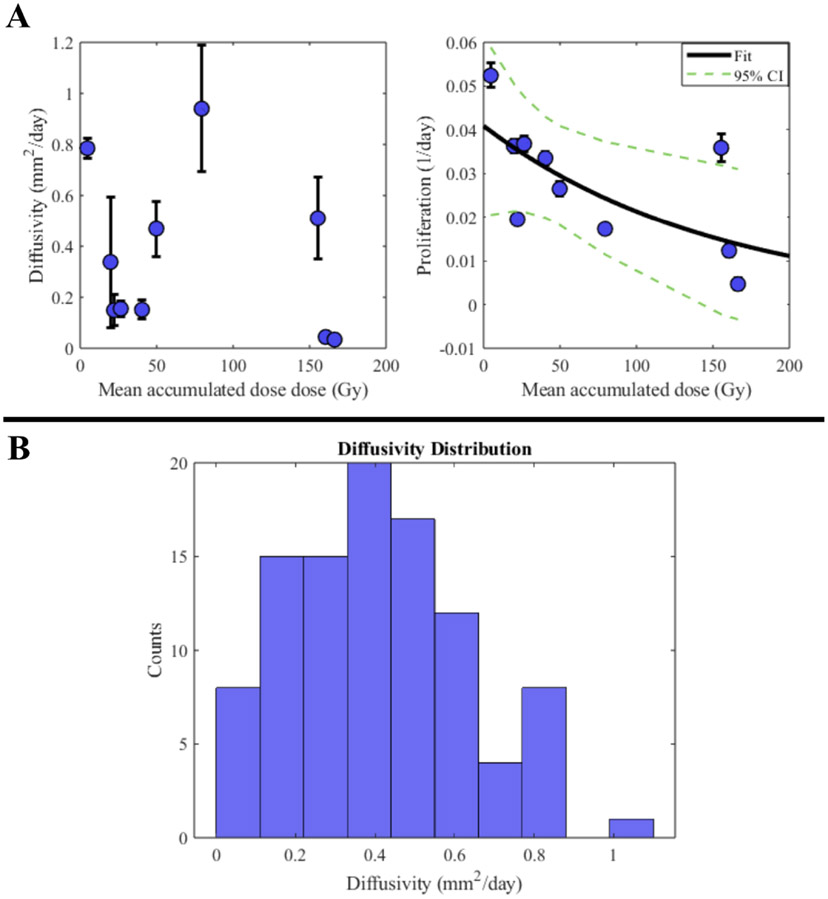
Fig. 5 shows the results for parameter distributions used in the leave-one-out study. Panel A of Fig. 5 shows the diffusivity and proliferation values calibrated from M0 versus the dose absorbed for each patient. The diffusivity shows no correlation, PCC = −0.25 (p = 0.49), whereas the proliferation shows a significant negative correlation, with a PCC of −0.64 (p = 0.049). Panel B of Fig. 5 shows an example histogram from the sampled diffusivities, with a normal distribution centered around the cohort mean. The median absolute error for the initial proliferation estimate is 45.16 % (range = [2.56, 695.51]) and the mean is 120.63 %, which is driven upwards by the outlier patients 7 (error = −209.74 %) and 9 (error = −695.51 %), as seen in Table 6.
Fig. 5. Leave-one-out parameter distribution and sampling.
Panel A shows the population parameter values for diffusivity (left) and proliferation rate (right) plotted versus calculated dose for all patient M0 calibrations. Proliferation rates have a visible correlation with dose (shown with exponential fit over the cohort), whereas diffusivities do not. Thus, the exponential fit to the proliferation rates from the training patients allows us to assign a growth rate to the test patient based on the accumulated dose, whereas the diffusivity is sampled one hundred times from a truncated normal distribution for each testing patient (an example distribution is shown in panel B). The confidence intervals from the fit of the exponential function (panel A right) allow for sampling to yield a distribution of 100 potential proliferation rates.
Table 6.
Leave-one-out proliferation results.
| Patient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Proliferation Rate | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Calibrated (day−1) | 3.7e-2 | 5.2e-2 | 3.3e-2 | 2.6e-2 | 3.6e-2 | 1.9e-2 | 1.2e-2 | 3.6e-2 | 4.7e-3 | 1.7e-2 |
| Mean initial estimate (day−1) | 3.3e-2 | 3.6e-2 | 3.2e-2 | 3.1e-2 | 3..4e-2 | 3.9e-2 | 3.8e-2 | 1.5e-2 | 3.7e-2 | 3.1e-2 |
| Parameter Error (%) | 9.43 | 31.36 | 2.56 | −15.08 | 7.37 | −98.78 | −209.74 | 58.96 | −695.51 | −77.58 |
3.5. Leave-one-out results
Fig. 6A displays the predicted paths for each patient’s volume time course using the leave-one-out method and M0, with the 95 % confidence intervals tightly following the mean prediction. The absolute volume error reduces with each additional calibration step; in particular, the median error at time points 1, 2, and 3 are 44.68 % (range = [4.03, 206.38]), 30.57 % (range = [15.84, 67.72]), and 9.82 % (range = [5.63, 55.89]), respectively. Fig. 6B shows the cohort comparison plots for volume and cell numbers, with a SCC between measured and predicted tumors of 0.89 (p = 2e-6) for volumes and 0.88 for cell counts (p = 2e-6).
Fig. 6. Leave-one-out prediction results.
Each plot in panel A corresponds to a forecast for the respective patient using M0, with the blue lines charting the predicted path and the black dots representing the measured data for the time point. Light blue shading represents the 95 % confidence interval of the charted path indicating slight deviations from the mean. Panel B displays the final volume (left) and cell number (right) for each acquisition time point compared to the measured result from imaging data for all patients, where consistent error is visible across all patients and time points.
4. Discussion
In this work we have presented results from two different prediction methods for GBM response to RNL therapy, both a patient-specific and population based prediction; we first focus on the patient specific calibration. Model selection with the patient-specific calibrations showed that a local proliferation model with no additional treatment effects (M1) was the highest scoring in most patients. This is not a surprising finding as combining treatment effects into a net proliferation term allows for the highest flexibility of predicted cell changes. Forecasting responses with patient-specific parameters provided high global accuracy of tumor volume and cell number, and a strong degree of overlap between predictions and measured tumors but was unsuccessful at predicting local cellularity changes. This suggests that the total tumor burden is predictable with a patient-specific model and would allow for an early assessment of response.
The downside of using this model is that the radionuclide distribution is not explicitly included in predictions, but rather assumed by the calibrated proliferation rates. However, this does not imply that the radiation coupled models were unsuccessful, M8 and M9 were the highest performing in three and one patients, respectively, but they were unable to consistently model the changes in cell number across the cohort. Despite the benefits of patient specific calibrations, the heterogeneity of response proved to be too great across the cohort to be captured with the available data and a single, radiation coupled mathematical model. (We return to the desire for more comprehensive imaging data below.)
In contrast to the patient-specific calibration, the LOOCV utilizes population trends to assign parameters based off the measured radio-nuclide distributions. The predictions with this method performed similarly to the patient-specific calibrations at the cohort level. Initial global error was higher, but improved over time as additional, patient-specific data became available and was assimilated into the prediction. This method provides the benefit of being able to predict immediately following the conclusion of RNL imaging with SPECT/CT or, potentially, before treatment begins if a planned or simulated RNL distribution is provided. The computational burden for the leave-one-out method is also significantly lower, requiring less than 1 h for the cohort, versus 10+ hours for a single patient-specific calibration with local parameters.
Unfortunately, we are currently limited to employing M0 for the LOOCV due to the small number of parameters included in this model. While calibrating proliferation on a local basis (i.e., at the voxel level) has shown great accuracy when predicting the growth of GBM (see ref. [14], as well as in the present effort), there is currently not an established method to assign locally distributed parameters a priori. Additionally, ten patients is a small sample size to statistically validate the found parameter distributions. This leads to large errors in the few outlier patients (e.g., Patients 7 and 9 in Table 7) for parameter assignment. These two example patients had the least tumor growth between scans (Table A.1) and were poorly represented by the rest of the population. A larger cohort would prove invaluable for validating the LOOCV method.
All mathematical modeling studies are built on imaging data containing uncertainty from a variety of sources, including errors during data acquisition, image segmentation, and model calibration. Uncertainty in cellularity estimates has been previously studied in relation to a patient specific calibration [35] and was found to have a limited effect on parameter estimation. The authors showed that parameters could be calibrated to noisy data with high correlation to true parameters (PCC > 0.80). In addition to uncertainty in estimating the cellularity, spatial dose-rate calculations also can be inaccurate due to the limited spatial resolution of SPECT, and difficulty quantifying energy deposition in vivo [36]. Despite the assumed imaging uncertainties, we were able to confirm that for the models we evaluated, all calibrated parameters were identifiable (Fig. A.2). This translated to consistent error between simulations and measured data in vivo with both prediction frameworks, regardless of an individual patient’s presentation and response trajectory.
Tumor segmentation potentially plays a key role in simulation results near the periphery of the tumor where boundaries can be inaccurate due to manual drawing of the region of interest. A multi-institutional study showed high agreement in bulk tumor boundaries with a median Dice of 0.85 [37], suggesting that our predicted metrics for total tumor volume and cell number should have minimal dependence on our manual tumor segmentation, however it should be noted that the segmentations were not performed by a trained radiologist. As the treatment under consideration is a radionuclide therapy providing elevated dosages compared to the well-studied external beam therapy, we want to focus the discussion of segmentation inaccuracies on the assumptions employed in defining tumor boundaries, rather than the exact segmentation methodology used. For this study, tumor segmentations are based on identifying the brain regions that display post-contrast enhancement, which has the possibility to contain pseudo-progression unrelated to the tumor burden we are modeling [38]. Imaging techniques such as delayed contrast enhanced [39] MRI or dynamic susceptibility contrast MRI [40] could be used to further refine these boundaries. To add to this, studies have shown that high dosages can cause permanent damage to vascular networks [41,42], potentially resulting in lasting enhancement on MRI despite a lack of tumor. The in vivo response to high dosage therapy must be further explored to fully validate this type of mathematical model.
While providing evidence that the reaction-diffusion based model fits the growth of GBM treated with RNL, we were unable to verify that including an RNL spatiotemporal distribution in the modeling efforts would significantly improve the predictive accuracy of the models for all patients. The leave-one-out method did provide a correlation in the mean accumulated dose and resulting proliferation but lacks the connection to cell death seen when modeling global exposure with external beam radiation therapy [13,24,25]. We have identified potential reasons for these observations. First, the RNL exposure could act in a manner which cannot be explicitly defined by an additional term in the mathematical model. Second, the model itself only accounts for proliferating tumor cells, whereas areas receiving exceedingly high radiation dose may be comprised of immune and vascular cells [43], and additional tumor cell phenotypes, all invading the site and affecting the ADC estimates of tumor cell number. Without accounting for the uncertainty described in the previous discussion sections, further exploration of potential mechanisms of action or numerical methods would be needed to address these points of concern. There are other mechanisms found in the GBM literature used to define radiation response that we could look to evaluate in our modeling framework, including carrying capacity reductions [44,45] or hypoxia induced radiation resistance [9,46,47]; however, the in vivo imaging data available is currently a major limitation in exploring these further. We also chose to focus on spatially resolved models due to the highly heterogenous nature of rGBM growth and response [48,49]. Future work could approach this from a global perspective to focus on defining the mechanisms that best predict changes in cellularity across a whole tumor, rather than at individual voxels [50,51].
This study represents a novel direction for modeling the effects of radionuclide treatment, however there are numerous opportunities for further investigation which could improve the applications to RNL therapy. In particular, we described eight different mechanism-based models coupled to the radionuclide distribution, a fraction of what is possible depending on the data types available. Future work should expand on these models, performing additional sensitivity analysis to quantify the assumptions made by each. Additionally, the sample size for the retrospective study was limited to just ten patients for both prediction methods, resulting in large variability between patients in terms of average dose absorbed, tumor location, baseline tumor size, and observed growth rates. Increasing the number of patients could alter trends found with the prediction methods, so further validation on a larger cohort is necessary before application in a clinical setting. These suggestions for future work only focus on the advancements in predictive modeling required to clinically validate personalized radionuclide therapy, but additional work in optimizing the convection enhanced delivery of RNL [6,52,53] is needed, both in silico and in vivo, before this goal can be realized.
5. Conclusion
We have proposed a family of mathematical models for predicting the in vivo response of glioblastoma multiform to convection enhanced delivery of Rhenium labeled nanoliposomes. A biology-based, reaction-diffusion model with a net proliferation term proved to be the most accurate for both calibrations and predictions. This model can make an early, accurate prediction of tumor response when using early time point, patient-specific data to calibrate the model on a patient-specific basis. Additionally, we have shown that model parameters obtained from calibrating a simplified version of the model to a training set of patients allows for accurate predictions of tumor development from baseline on a patient-specific basis.
Acknowledgments
We thank the National Cancer Institute for funding through R01 CA235800, T32 EB007507, and U01 CA174706. We thank the Cancer Research and Prevention Institute of Texas for funding through RR160005 and RP220225. T.E.Y. is a CPRIT Scholar of Cancer Research.
Funding
We the National Cancer Institute for funding through R01 CA235800, T32 EB007507, and U01 CA174706. We thank the Cancer-Research and Prevention Institute of Texas for funding through RR160005 and RP220225.
Appendix
Table A.1.
Full patient imaging details with exclusion criteria.
| Original Patient # (study #) |
T1 scan times [Day] |
T1 + Contrast scan times [Day] |
ADC scan times [Day] |
SPECT/CT scan times [Hours after infusion] |
Exclusion reason |
|---|---|---|---|---|---|
| 1 | 56, 112 | 56, 112 | 0, 56, 112 | 1, 2, 26, 120, 194 | No baseline MRI to initialize model |
| 2 (1) | 0, 28, 56, 112 | 0, 28, 56, 112 | 0, 28, 56, 112 | 1, 2, 26, 120, 194 | N/A |
| 3 (2) | 0, 28, 56 | 0, 28, 56 | 0, 28, 56 | 1, 2, 26, 120, 194 | N/A |
| 4 | 0, 28, 112 | 0, 28, 112 | 0, 28, 112 | 2, 4 | No post infusion SPECT/CT to track RNL |
| 5 (3) | 0, 28, 56, 112 | 0, 28, 56, 112 | 0, 28, 56, 112 | 2, 4, 28, 124, 196 | N/A |
| 7 | 0 | 0 | 0 | 2, 4, 28, 124, 196 | No follow up MRI available |
| 8 (4) | 0, 28, 56 | 0, 28, 56 | 0, 28, 56 | 4, 9, 33, 153, 205 | N/A |
| 10 (5) | 0, 28, 56, 112 | 0, 28, 56, 112 | 0, 28, 56, 112 | 4, 9, 33, 129, 205 | N/A |
| 11 | 0, 28 | 0, 28 | 0, 28 | 4, 9, 33, 129, 205 | Only one follow up image available, cannot predict response |
| 12 | 0, 28, 56, 112 | 0, 28, 56, 112 | 28, 56, 112 | 4, 9, 33, 129, 201 | Baseline ADC unavailable to initialize cell density |
| 13 (6) | 0, 28, 56, 112 | 0, 28, 56, 112 | 0, 28, 56, 112 | 4, 9, 33, 129, 201 | N/A |
| 14 (7) | 0, 28, 56, 112 | 0, 28, 56, 112 | 0, 28, 56, 112 | 4, 9, 33, 129 | N/A |
| 16 (8) | 0, 28, 56 | 0, 28, 56 | 0, 28, 56 | 2, 9, 33, 129, 201 | N/A |
| 17 (9) | 0, 56, 112 | 0, 56, 112 | 0, 56, 112 | 1, 6, 30, 126, 198 | N/A |
| 18 (10) | 0, 56, 112 | 0, 56, 112 | 0, 56, 112 | 1, 3, 6, 30, 126, 198 | N/A |
Table A.2.
Extended patient details.
| Patient | Infused volume (mL) | Infusion time (min) | Number of catheters | # Of prior treatment(s) | Baseline tumor volume (cm3) | Final tumor volume (cm3) |
|---|---|---|---|---|---|---|
| 1 | 0.66 | 132 | 1 | 1 | 5.24 | 25.83 |
| 2 | 0.66 | 132 | 1 | 2 | 3.24 | 43.32 |
| 3 | 1.32 | 264 | 1 | 1 | 4.47 | 29.19 |
| 4 | 2.64 | 528 | 1 | 2 | 29.04 | 72.94 |
| 5 | 2.64 | 528 | 1 | 2 | 4.37 | 52.73 |
| 6 | 5.28 | 528 | 2 | 2 | 28.22 | 78.26 |
| 7 | 5.28 | 528 | 2 | 1 | 6.21 | 12.18 |
| 8 | 5.28 | 528 | 2 | 3 | 6.97 | 49.99 |
| 9 | 5.28 | 352 | 3 | 2 | 26.77 | 23.54 |
| 10 | 5.28 | 352 | 3 | 2 | 22.30 | 113.99 |
Fig. A.1. Full patient-specific calibration results.
Panel A provides results from all Scenario 1 calibrations. For CCC and Dice accuracy, M0 consistently has the worst performance for all patients, other models all perform similarly in these two metrics. The global metrics, volume, and cell % error, have more variation across each patient, with no clear and consistent best performing model. These trends are confirmed when looking at the averages across patients in Panel B, where the high variation leads to insignificant differences between all groups, except for the CCC with M0 being the worst performer.
Table A.3.
In-silico study for parameter identifiability.
| Model | M0 | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| % Error | 0.21 ± 3.6e-4 | 0.32 ± 0.73 | 0.37 ± 3.1e-3 | 0.37 ± 2.7e-2 | 3.01 ± 18.25 | 0.38 ± 0.24 | 1.61 ± 6.65 | 0.23 ± 3.2e-5 | −0.58 ± 1.91 | 0.94 ± 3.36 | |
| −0.023 ± 5.2e-5 | −1.95 ± 11.87 | −0.29 ± 0.02 | −0.49 ± 0.36 | 6.53 ± 15.54 | −1.32 ± 3.41 | −4.68 ± 15.61 | −0.19 ± 4.9e-4 | −1.28 ± 7.05 | −5.01 ± 28.7 | ||
| – | – | −0.042 ± 4.1e-3 | −0.082 ± 5.6e-2 | −6.63 ± 24.84 | −0.26 ± 0.63 | −1.81 ± 6.59 | −0.044 ± 1.4e-4 | −24.61 ± 36.41 | −0.77 ± 4.30 | ||
| – | – | – | – | 1e5 ± 3e5 | – | – | – | 3e4 ± 5e4 | – |
A.1. In-silico study
The models presented in this study have a large number of calibrated parameters due to the spatially varying proliferation rate. In order to determine the feasibility of each model we have performed an additional calibration study with in-silico data. These tumors were generated from a single in-vivo tumor, with the patient’s measured distribution used as an input. For each model, the required parameters were sampled 50 times followed by forward simulations to day 112. The true data was finalized by applying gaussian white noise (MATLAB’s "awgn") to each time point. Model calibrations were performed to the longitudinal scans of the virtual tumors for each sampled parameter set. A model was determined identifiable if all parameters had less than 10 % error across the calibrated samples.
In Table A.3 the results are presented for each model. All models have consistent parameter error except for M4 and M8, which contain an additional calibrated parameter () for the decay of the radiation effects over time. With a fixed value of , the data generation for these two models was repeated, which provided in an improved ability to identify the remaining parameters through calibration. In M4, that was seen with reductions in average percent error for , and , now equaling 0.50 %, 0.39 %, and 0.0027 %, respectively. A similar trend was seen with M8 where the average percent error is now, d = −0.86 %, kp = 0.071 % and kd = 0.095 %. The fixing of is represented in Table 3 and was used for all applicable calibrations in the study (M4 and M8 Scenario 1 calibrations). The actual value for this parameter was determined by evaluating a range across all patients for M4 and M8 individually. For both models, the value that provided the highest AIC weighting across all patients was chosen to calculate the results in Table 5.
Footnotes
Financial interests
Chase Christenson, Chengyue Wu, David Hormuth, Shiliang Huang, and Thomas Yankeelov have no conflicts of interests in this work. Andrew Brenner and Ande Bao have received stock and royalties from NanoTX Therapeutics. Andrew Brenner and Ande Bao have consulting agreements with Plus Therapeutics. Andrew Brenner has received research support from Plus Therapeutics.
Ethics approval
This study was performed with ethical considerations for the approvals granted by NCT01906385
Consent to participate
Informed consent was obtained by all patient analyzed in this study
CRediT authorship contribution statement
Chase Christenson: Conceptualization, Formal analysis, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. Chengyue Wu: Conceptualization, Methodology, Software, Supervision, Writing – review & editing. David A. Hormuth: Conceptualization, Methodology, Supervision, Writing – review & editing. Shiliang Huang: Conceptualization, Methodology, Writing – review & editing. Ande Bao: Conceptualization, Formal analysis, Methodology, Writing – review & editing. Andrew Brenner: Conceptualization, Project administration, Data curation, Investigation, Resources, Writing – review & editing. Thomas E. Yankeelov: Conceptualization, Project administration, Funding acquisition, Methodology, Resources, Supervision, Writing – review & editing.
Declaration of Competing Interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Andrew Brenner reports a relationship with NanoTX Therapeutics that includes: equity or stocks. Andrew Brenner reports a relationship with Plus Therapeutics that includes: consulting or advisory and non-financial support. Ande Bao reports a relationship with NanoTX Therapeutics that includes: equity or stocks. Ande Bao reports a relationship with Plus Therapeutics that includes: consulting or advisory.
Data availability
The data that has been used is confidential.
References
- [1].Wen PY, Weller M, Lee EQ, et al. , Glioblastoma in adults: a Society for Neuro-Oncology (SNO) and European Society of Neuro-Oncology (EANO) consensus review on current management and future directions, Neuro Oncol. 22 (8) (2020) 1073–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Fernandes C, Cost A, Osório L, et al. , Current standards of care in glioblastoma therapy, in: Vleeschouwer SD (Ed.), Glioblastoma, 2017, pp. 197–241. Brisbane, AU. [PubMed] [Google Scholar]
- [3].Stupp R, Mason WP, van den Bent MJ, et al. , Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma, N. Engl. J. Med 352 (2005) 987–996. [DOI] [PubMed] [Google Scholar]
- [4].Phillips WT, Goins B, Bao A, et al. , Rhenium-186 liposomes as convection-enhanced nanoparticle brachytherapy for treatment of glioblastoma, Neuro Oncol. 14 (4) (2012) 416–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Floyd J, Phillips W, Goins B, Bao A, Brenner A, ATNT-03 First in human study of rhenium nanoliposomes for intratumoral therapy of glioma [abstract], Neuro Oncol. (2015) 17. [Google Scholar]
- [6].Woodall RT, Hormuth DA II, Wu C, et al. , Patient specific, imaging-informed modeling of rhenium-186 nanoliposome delivery via convection-enhanced delivery in glioblastoma multiforme, Biomed. Phys. Eng. Express 7 (4) (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Swanson KR, Alvord EC, Murray JD, A quantitative model for differential motility of gliomas in grey and white matter, Cell Prolif. 33 (2000) 317–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Alfonso JCL, Talkenberger K, Seifert M, et al. , The biology and mathematical modelling of glioma invasion: a review, J. R Soc. Interface 14 (136) (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Saut O, Lagaert JB, Colin T, Fathallah-Shaykh HM, A multilayer grow-or-go model for GBM: effects of invasive cells and anti-angiogenesis on growth, Bull. Math. Biol 76 (9) (2014) 2306–2333. [DOI] [PubMed] [Google Scholar]
- [10].Subramanian S, Gholami A, Biros G, Simulation of glioblastoma growth using a 3D multispecies tumor model with mass effect, J. Math. Biol 79 (3) (2019) 941–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hormuth DA II, Farhat M, Christenson C, et al. , Opportunities for improving brain cancer treatment outcomes through imaging-based mathematical modeling of the delivery of radiotherapy and immunotherapy, Adv. Drug Deliv. Rev 187 (2022), 114367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].McMahon SJ, The linear quadratic model: usage, interpretation and challenges, Phys. Med. Biol 64 (2019) 01TR01. [DOI] [PubMed] [Google Scholar]
- [13].Rockne R, Alvord EC, Rockhill JK, Swanson KR, A mathematical model for brain tumor response to radiation therapy, J. Math. Biol 58 (4–5) (2009) 561–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hormuth II, Al DA, Feghali KA, Elliott AM, Yankeelov TE, Chung C, Image-based personalization of computational models for predicting response of high-grade glioma to chemoradiation, Sci. Rep 11 (1) (2021) 8520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Annede P, Cosset JM, Van Limbergen E, et al. , Radiobiology: foundation and new insights in modeling brachytherapy effects, Semin. Radiat. Oncol 30 (1) (2020) 4–15. [DOI] [PubMed] [Google Scholar]
- [16].Hedrick MDM, A Dual Phase 1/2 Study to Determine the Maximum Tolerated Dose, Safety, and Efficacy of 186rhenium Nanoliposomes (186rnl) in Recurrent Glioma. Identifier NCT01906385, 2015. https://www.clinicaltrials.gov/ct2/show/NCT01906385. [Google Scholar]
- [17].Atuegwu NC, Gore JC, Yankeelov TE, The integration of quantitative multi-modality imaging data into mathematical models of tumors, Phys. Med. Biol 55 (9) (2010) 2429–2449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Anderson AW, Xie J, Pizzonia J, Bronen RA, Spencer DD, Gore JC, Effects of cell volume fraction changes on apparent diffusion in human cells, Magn. Reson. Imaging 18 (6) (2000) 689–695. [DOI] [PubMed] [Google Scholar]
- [19].Atuegwu NC, Colvin DC, Loveless ME, et al. , Incorporation of diffusion-weighted magnetic resonance imaging data into a simple mathematical model of tumor growth, Phys Med Biol 57 (1) (2012) 225–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mezzenga E, D’Errico V, D’Arienzo M, et al. , Quantitative accuracy of 177Lu SPECT imaging for molecular radiotherapy, PLoS ONE 12 (8) (2017), e0182888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].PubChem compound summary for CID 161105, Rhenium-186, Nat. Center Biotechnol. Infor 6 (2022). https://pubchem.ncbi.nlm.nih.gov/compound/Rhenium-186. Updated Sept. 3, 2022. Accessed Sept. [Google Scholar]
- [22].Ramonaheng K, van Staden JA, du Raan H, Accuracy of two dosimetry software programs for (177)Lu radiopharmaceutical therapy using voxel-based patient-specific phantoms, Heliyon 8 (7) (2022) e09830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Reiner D, Blaickner M, Rattay F, Discrete beta dose kernel matrices for nuclides applied in targeted radionuclide therapy (TRT) calculated with MCNP5, Med. Phys 36 (11) (2009) 4890–4896. [DOI] [PubMed] [Google Scholar]
- [24].Rockne R, Rockhill JK, Mrugala M, et al. , Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach, Phys. Med. Biol 55 (12) (2010) 3271–3285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Liu J, Hormuth II, Yang J DA, Yankeelov TE, A multi-compartment model of glioma response to fractionated radiation therapy parameterized via time-resolved microscopy data, Front. Oncol 12 (2022), 811415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wouters BG, Cell death after irradiation: how, when, and why cells die. Basic Clinical Radiobiology, 5th ed., CRC Press, 2018. [Google Scholar]
- [27].Joiner MC, Quantifying cell kill and cell survival, Basic Clin. Radiobiol (2018). [Google Scholar]
- [28].Li N, Steiner J, Tang S, Convergence and stability analysis of an explicit finite difference method for 2-dimensional reaction-diffusion equations, The ANZIAM J. 36.2 (1994) 234–241. [Google Scholar]
- [29].Hormuth DA II, Jarrett AM, Yankeelov TE, Forecasting tumor and vasculature response dynamics to radiation therapy via image based mathematical modeling, Radiat Oncol 15 (1) (2020) 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Levenberg K, A method for the solution of certain non-linear problems in least squares, Q. Appl. Math (2) (1944) 164–168. [Google Scholar]
- [31].Hormuth DA II, Eldridge SL, Weis JA, et al. , Mechanically coupled reaction-diffusion model to predict Glioma growth: methodological details, Methods Mol. Biol 1711 (2018) 225–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Akaike H, Information theory and an extension of the maximum likelihood principle, in: Breakthroughs in Statistics, 1, Springer, 1973, pp. 610–624. [Google Scholar]
- [33].Lin LI, A concordance correlation coefficient to evaluate reproducibility, Biometrics 45 (1) (1989) 255–268. [PubMed] [Google Scholar]
- [34].Dice LR, Measures of the amount of ecologic association between species, Ecology 26 (3) (1945) 297–302. [Google Scholar]
- [35].Hormuth DA II, Weis JA, Barnes SL, et al. , Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data, Phys. Biol 12 (4) (2015), 046006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Tran-Gia J, Salas-Ramirez M, Lassmann M, What you see is not what you get: on the accuracy of voxel-based dosimetry in molecular radiotherapy, J. Nucl. Med 61 (8) (2020) 1178–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Pati S, Verma R, Akbari H, et al. , Reproducibility analysis of multi-institutional paired expert annotations and radiomic features of the ivy glioblastoma atlas project (Ivy GAP) dataset, Med. Phys 47 (12) (2020) 6039–6052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Hygino da Cruz LC Jr, Rodriguez I, Domingues RC, et al. , Pseudoprogression and pseudoresponse: imaging challenges in the assessment of posttreatment glioma, AJNR Am. J. Neuroradiol 32 (11) (2011) 1978–1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Zach L, Guez D, Last D, et al. , Delayed contrast extravasation MRI: a new paradigm in neuro-oncology, Neuro Oncol 17 (3) (2015) 457–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Elshafeey N, Kotrotsou A, Hassan A, et al. , Multicenter study demonstrates radiomic features derived from magnetic resonance perfusion images identify pseudoprogression in glioblastoma, Nat Commun 10 (1) (2019) 3170–3179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Arnold KM, Flynn NJ, Raben A, et al. , The impact of radiation on the tumor microenvironment: effect of dose and fractionation schedules, Cancer Growth Metastasis (2018) 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Rahmathulla G, Marko NF, Weil RJ, Cerebral radiation necrosis: a review of the pathology, diagnosis and management considerations, J. Clin. Neurosci 20 (2013) 485–502. [DOI] [PubMed] [Google Scholar]
- [43].Lorimore S, Coates P, Scobie G, et al. , Inflammatory-type responses after exposure to ionizing radiation in vivo: a mechanism for radiation-induced bystander effects? Oncogene (20) (2001) 7085–7095. [DOI] [PubMed] [Google Scholar]
- [44].Zahid MU, Mohsin N, Mohamed ASR, et al. , Forecasting individual patient response to radiation therapy in head and neck cancer with a dynamic carrying capacity model, Int. J Radiat. Onco. Biol. Phys 1113 (2021) 693–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Hormuth DA II, Weis JA, Barnes SL, et al. , A mechanically coupled reaction–diffusion model that incorporates intra-tumoural heterogeneity to predict in vivo glioma growth, J. R Soc. Interface 14 (128) (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Rockne RC, Trister AD, Jacobs J, et al. , A patient-specific computational model of hypoxia-modulated radiation resistance in glioblastoma using 18F-FMISO-PET, J. R Soc. Interface 12 (103) (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Yan H, Romero-Lopez M, Benitez LI, et al. , 3D mathematical modeling of glioblastoma suggests that transdifferentiated vascular endothelial cells mediate resistance to current standard-of-care therapy, Cancer Res. 77 (15) (2017) 4171–4184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Ali MY, Oliva CR, Noman ASM, et al. , Radioresistance in glioblastoma and the development of radiosensitizers, Cancers (Basel) 12 (9) (2020) 2511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Parker NR, Khong P, Parkinson JF, et al. , Molecular heterogeneity in glioblastoma: potential clinical implications, Front. Oncol 5 (2015) 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Ribba B, Kaloshi G, Peyre M, et al. , A tumor growth model for low-grade glioma treated with chemotherapy or radiotherapy, Cancer Chemother.: Basic Clin. Appl., Hahnemann Symp., 15th 18 (18) (2012) 5071–5080. [DOI] [PubMed] [Google Scholar]
- [51].Ollier E, Mazzocco P, Ricard D, et al. , Analysis of temozolomide resistance in low-grade gliomas using a mechanistic mathematical model, Fundamentals Clinic. Pharmacol 31 (3) (2017) 347–358. [DOI] [PubMed] [Google Scholar]
- [52].Chengyue Wu, Hormuth DA, Christenson C, et al. , RADT-14. Towards image-guided modeling of patient-specific Rhenium-186 nanoliposome distribution via convection-enhanced delivery for glioblastoma multiforme [Abstract], Neuro-oncol. (Charlottesville, Va.) 23 (Supplement_6) (2021) vi44.–vi44. [Google Scholar]
- [53].Antoine LH, Koomullil RP, Wick TM, A Nakhmani, Optimization of catheter placement for convection-enhanced delivery to brain tumors, F1000Res 10 (2021) 18. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.