The effect of temporal data aggregation to assess the impact of changing temperatures in Europe: an epidemiological modelling study

Summary

Background

Daily time-series regression models are commonly used to estimate the lagged nonlinear relation between temperature and mortality. A major impediment to this type of analysis is the restricted access to daily health records. The use of weekly and monthly data represents a possible solution unexplored to date.

Methods

We temporally aggregated daily temperatures and mortality records from 147 contiguous regions in 16 European countries, representing their entire population of over 400 million people. We estimated temperature-lag-mortality relationships by using standard time-series quasi-Poisson regression models applied to daily data, and compared the results with those obtained with different degrees of temporal aggregation.

Findings

We observed progressively larger differences in the epidemiological estimates with the degree of temporal data aggregation. The daily data model estimated an annual cold and heat-related mortality of 290,104 (213,745–359,636) and 39,434 (30,782–47,084) deaths, respectively, and the weekly model underestimated these numbers by 8.56% and 21.56%. Importantly, differences were systematically smaller during extreme cold and heat periods, such as the summer of 2003, with an underestimation of only 4.62% in the weekly data model. We applied this framework to infer that the heat-related mortality burden during the year 2022 in Europe may have exceeded the 70,000 deaths.

Interpretation

The present work represents a first reference study validating the use of weekly time series as an approximation to the short-term effects of cold and heat on human mortality. This approach can be adopted to complement access-restricted data networks, and facilitate data access for research, translation and policy-making.

Funding

The study was supported by the ERC Consolidator Grant EARLY-ADAPT (https://www.early-adapt.eu/), and the ERC Proof-of-Concept Grants HHS-EWS and FORECAST-AIR.

Research in context.

Evidence before this study

We searched PubMed from study conception to May 1st 2023 for articles published in English using the search words “temperature”, “mortality”, “dlnm” AND “aggregation”. We only found an interesting theoretical study introducing a general methodology dealing with aggregated health time-series, which is an approach that better represents the spread of the health response to an exposure, and reduces the noise in the health data. The proposed methodology is illustrated by modelling the influence of temperature on cardiovascular mortality in Canada. The study is however different from the present work in the sense that it analyses moving averages of health data, thus not reducing the number of data points in the health time-series, as we would expect when using weekly or monthly health data.

Added value of this study

A major impediment to large-scale epidemiological studies analysing the short-term health effects of ambient temperatures is the restricted access to daily health records in many countries, regions and cities. A possible solution to circumvent this problem would be the use of weekly or monthly time-series of health outcomes, which are more readily available in open access due to the lower level of temporal disaggregation. We here temporally aggregate a daily temperature and mortality database from 147 contiguous regions in 16 European countries, and analyse and contrast the estimates obtained from daily, weekly, 2-weekly and monthly data models. We estimated temperature-lag-mortality relationships by using standard time-series quasi-Poisson regression models applied to daily data, and compared the results with those obtained with different degrees of temporal data aggregation. To our knowledge, this is the first study to analyse the effect of temporal data aggregation in time-series epidemiological studies of temperature and mortality.

Implications of all the available evidence

We generally found that the degree of aggregation of the monthly data is temporally too coarse to be used for the purpose of estimating the short-term health effects of ambient temperatures on human mortality. Instead, aggregated weekly time-series of temperature and mortality data have been shown to represent an approximation of the estimates obtained in the daily data model. Therefore, the present work represents a first reference study validating the use of weekly time series as an approximation to the delayed nonlinear relation between daily temperatures and mortality records. As such, this approach can be adopted to complement existing, large-scale, access-restricted, data networks, and to facilitate data access for research, translation and policy-making by using complementary sources of data not explored to date.

Introduction

Exposure to ambient temperatures represents a major threat to vulnerable populations by substantially contributing to increased morbidity and mortality.¹ According to the best available global estimates for urban populations,² 9.43% (95% confidence interval [CI] 7.58–11.07) of all-cause mortality is related to non-optimal temperatures, with 8.52% (6.19–10.47) for cold and 0.91% (0.56–1.36) for heat. In Europe, the whole population estimates (i.e. both urban and rural) indicate that temperatures are related to 7.17% (5.81–8.50) of all deaths, with 6.51% (5.14–7.80) for cold and 0.65% (0.40–0.89) for heat.^3,4 Distributed lag nonlinear models^5,6 are commonly used to quantify the short-term health effects of ambient temperatures, which generally include controls for seasonal and long-term trends, and a cross-basis modelling the delayed nonlinear relation between exposure and response.1, 2, 3, 4^,7, 8, 9, 10, 11, 12 For mortality, available studies have consistently shown that the effects of cold are distributed along a wide range of lags, of up to a month, while the effects of heat are more immediate and do not usually last for more than a week.

As a result of the distributed nature of the approach modelling these short-term lagged effects, studies generally rely on regression models applied to daily time-series of the environmental exposure and the health response. A major impediment to this type of large-scale analysis is the restricted access to daily health records in many countries, regions and cities, which limits the homogeneity, comparability, spatiotemporal coverage and population disaggregation of the results. Projects and initiatives, such as PHEWE,^13,14 NMMAPS,¹⁵ EUROHEAT,¹⁶ CIRCE,¹⁷ PHASE,¹⁸ MCC^2,9 and EARLY-ADAPT,¹ have been designed to compile and jointly analyse daily health databases covering large continental or global domains. Nonetheless, confidentiality requirements, legal constraints, time needed to obtain the data and the bureaucratic obstacles of data transfer agreements continue to be major limiting factors for research. These limitations are particularly consequential when counts of health outcomes need to be temporally disaggregated at the daily resolution, for example in the estimation of the distributed lagged effects of cold and heat.

A possible solution to circumvent this kind of problems would be the use of weekly or monthly time-series of health outcomes, which are more readily available in open access due to the lower level of temporal disaggregation. For example, an open access weekly mortality database from Eurostat has been recently used to develop data-driven indicators tracking progress on health and climate change,¹¹ or to quantify the heat-related mortality burden of the record-breaking temperatures registered during the summer of 2022 in Europe.¹ Nonetheless, it remains to be determined if, when and to which extent it is possible to use temporally aggregated data to generate accurate temperature-related mortality estimates. Therefore, the aim of the present work is to temporally aggregate a daily temperature and mortality database from 147 contiguous regions in 16 European countries, and to analyse and contrast the estimates obtained from daily, weekly, 2-weekly and 4-weekly data models. To address this aim, we estimated temperature-lag-mortality relationships by using standard time-series quasi-Poisson regression models applied to daily time-series, and compared the results with those obtained with different degrees of temporal data aggregation.

Methods

Data sources

We used the spatiotemporally homogeneous mortality database originally used in Robine et al.¹⁹ Further details are provided in subsequent studies using the same or similar data.20, 21, 22, 23 The dataset included 27,444,314 daily all-cause mortality counts for the period 1998–2004 in 147 contiguous regions from 16 European countries, representing their whole population (i.e. rural and urban) of over 400 million people. These countries are Austria (9 regions), Belgium (11), Croatia (2), Czech Republic (8), Denmark (1), France (22), Germany (16), Italy (21), Luxembourg (1), the Netherlands (1), Poland (16), Portugal (5), Slovenia (1), Spain (16), Switzerland (7) and the United Kingdom (10 regions in England and Wales only). There were no missing values in the dataset. We transformed the daily gridded (0.1° × 0.1°) 2-m temperature data from E-OBS²⁴ into daily regional averages.

Temporal data aggregation

We restricted the analysis to the period spanning from Monday 5th January 1998 to Sunday 26th December 2004, because it includes N = 2548 days and N/7 = 364 weekly, N/14 = 182 2-weekly and N/28 = 91 4-weekly Monday-to-Sunday non-overlapping periods. We temporally averaged (aggregated) the daily regional temperature (mortality) data into these weekly, 2-weekly and 4-weekly time periods, and performed separate epidemiological models for each temporal data aggregation.

Statistical analysis

The statistical analyses were performed in two steps, following the methodology of Ballester et al.¹ In the first stage, we used quasi-Poisson regression models, which allow for overdispersed counts of deaths, to calculate the location-specific temperature-lag-mortality relation in each European region6, 7, 8:

Daily: log(E(mort)) = intercept + ns(time, 8 df per year) + crossbasis(temp; 0–28 days) + dow.

Weekly: log(E(mort)) = intercept + ns(time, 8 df per year) + crossbasis(temp; 0,1,2,3,4 weeks).

2-Weekly: log(E(mort)) = intercept + ns(time, 8 df per year) + crossbasis(temp; 0,1,2 2-weeks).

4-Weekly: log(E(mort)) = intercept + ns(time, 8 df per year) + crossbasis(temp; 0,1 4-weeks).

The models included (i) an intercept, (ii) a natural cubic spline (ns) of time with 8 degrees of freedom (df) per year to control for seasonal and long-term trends, and (iii) a cross-basis function to estimate the exposure-lag-response association between temperatures (temp) and mortality counts (mort). The daily data model also included a categorical variable to control for the day of the week (dow). The exposure-response function of the cross-basis was modelled with a natural cubic spline with three internal knots at the 10th, 75th and 90th percentiles of the corresponding location-specific daily, weekly, 2-weekly and 4-weekly temperature distribution. The lag-response function of the cross-basis in the daily data model included three internal knots placed at equally spaced intervals on the log scale, with a maximum lag of 28 days to account for the long-delayed effects of cold temperatures and short-term harvesting. Regarding the other data models, the lag-response function was modelled with integer lag values of 0, 1, 2, 3 and 4 weeks for the weekly data model; 0, 1 and 2 2-weeks for the 2-weekly data model, and 0 and 1 4-weeks for the 4-weekly data model. Model parameters were tested in sensitivity analyses, showing reasonably small differences in the estimates, especially in the daily and weekly data models (Table S1).

In the second stage, we used multivariate, multilevel meta-regression analyses²⁵ to separately pool the location-specific coefficients obtained in the first step for each data model. The meta-regression included country random effects and the location-specific temperature average and interquartile range as meta-predictors.²⁶ Separately for each data model, we derived the best linear unbiased predictions of the temperature–mortality relationship in each region from the meta-regression²⁷ to obtain the location-specific minimum mortality temperature (MMT), and to transform the regional temperature and mortality time series into temperature-related mortality numbers (i.e. attributable number, AN) and fractions (i.e. attributable fraction, AF), following the methodology described in Gasparrini and Leone.²⁸ Heat- (cold-) related mortality was calculated for the days, weeks, 2-weeks and 4-weeks with average temperatures above (below) the location-specific MMT in the corresponding data model.²⁹ Regional temperature-related mortality was aggregated to obtain the national and European burdens.^3,4 Similarly, we computed 1000 Monte Carlo simulations of the regional temperature-related mortality, and separately aggregated them in each simulation to calculate the 95% empirical CI at the national and continental levels.^7,8,26

Role of the funding source

The funders of the study had no role in study design, data collection, data analysis, data interpretation, or writing of the report.

Results

Fig. 1 compares the exposure-lag-response association in the four temporally aggregated data models, i.e. daily, weekly, 2-weekly and 4-weekly. The cumulative exposure-response association in the daily data model depicts the asymmetric V-shaped relation described in several previous studies,^1,3,7, 8, 9 with relative risk (RR) values monotonically increasing for temperatures above and below the MMT (Fig. 1a). The association in the weekly and 2-weekly data models is similar to the daily model, but the 4-weekly model shows a more symmetric association with small RR values in the central part of the temperature distribution. At the temperature extremes, the lag-response association in the weekly data model is similar to the one from the daily model, but with RR values sampled at lags every seven days (Fig. 1b and c). On the one hand, for cold temperatures, the effect of same-week temperatures is negligible, with significant RR values starting at lag one week. On the other hand, for hot temperatures, the RR values monotonically decrease with the lag, and their effect is only evident at weeks zero and, to a much lesser extent, one.

Fig. 1.

Exposure-lag-response association. Results pooled over the ensemble of European regions are shown for the cumulative exposure-response association (a), and the lag-response associations at the 1st (b) and 99th (c) temperature percentiles. The shading in panels (a–c) represents the 95% confidence interval, and the solid circles in panel (a) the minimum mortality temperature and the 1st and 99th temperature percentiles. Regional values are shown for the minimum mortality temperature (°C) (d) and the relative risk (unitless) at the 1st (e) and 99th (f) temperature percentiles. The solid and dashed lines in panels (d–f) correspond to the identity and the best linear fitting, respectively, with Pearson correlations [r] and mean differences [d] in the top left corner. Results are shown for the daily (black in a-c, x-axis in d-f), weekly (red), 2-weekly (blue) and 4-weekly (grey) data models.

As a general principle, when compared with the daily data model, differences in the regional values of the MMT and the RR monotonically increase as the degree of temporal data aggregation increases (see the Pearson correlations [r] and mean differences [d] in Fig. 1d–f, and maps in Figure S1). The relation between the regional values of the MMT in the daily, weekly and 2-weekly data models is modest, with Pearson correlations in the range between 0.50 and 0.60, and mean differences smaller than 0.20 °C in magnitude (Fig. 1d). We found no spatial relation between the MMT of the daily and 4-weekly data models, possibly due to the small RR values in the central part of the temperature distribution in the 4-weekly data model (Fig. 1a). At the extremes, the relation between the regional RR values in the daily and weekly data models is strong and linear (r = 0.88 for cold and r = 0.82 for heat), which progressively decreases in the other models with generally increasing negative mean differences (Fig. 1e and f).

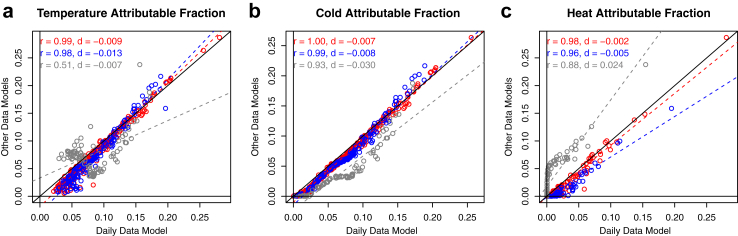
We used these associations, together with the time-series of temporally aggregated temperature and mortality, to estimate the AN (Table 1, Table S1) and AF (Tables S2 and S3 and Fig. 2, Fig. 3, Fig. 4, Fig. 5, Figures S2–S4) at each temporal resolution. Fig. 2 shows the AF for each weekly (red), 2-weekly (blue) and 4-weekly (grey) time period as estimated by the four temporally aggregated data models. The daily values in the daily data model were aggregated to each weekly, 2-weekly and 4-weekly time period for a direct comparison with the other models. The Pearson correlations [r] and mean differences [d] are shown in each panel of Fig. 2, and we used the 1000 Monte Carlo simulations (see Methods) to estimate their uncertainty in Figure S3 as density plots of the simulated correlations and differences. Although the relations between the daily, weekly and 2-weekly data models are generally strong and linear, we also find systematic differences in the associations. For cold temperatures, the weekly and 2-weekly data models systematically underestimate the lowest AF values, which are the most frequent ones, while they marginally overestimate the highest ones (Fig. 2b). For hot temperatures, we observe a general underestimation of all the AF values in the weekly and 2-weekly models, although differences are generally smaller for the highest values (Fig. 2c). Finally, regarding the 4-weekly data model, the systematic underestimation (overestimation) of the cold (heat) AF is directly related to the underestimation of the MMT in many regions (Fig. 1d), given that this value is used to define the range of temperatures corresponding to cold and heat days.

Table 1.

Attributable Number (deaths) by temperature range, month, season and year in the daily, weekly, 2-weekly and 4-weekly data models.

Groups of days	Data model
	Daily	Weekly	2-Weekly	4-Weekly
All Temperatures	329,538 (250,681, 399,741)	296,215 (204,224, 386,523)	280,268 (225,333, 335,723)	296,321 (229,950, 329,004)
Total Cold	290,104 (213,745, 359,636)	265,284 (178,260, 353,938)	258,903 (199,524, 320,232)	172,342 (17,683, 300,248)
Moderate Cold	261,267 (189,315, 326,545)	237,324 (154,039, 321,803)	231,848 (175,271, 288,025)	145,785 (3008, 266,541)
Extreme Cold	28,836 (21,172, 35,828)	27,960 (21,407, 34,246)	27,055 (21,367, 32,186)	26,557 (14,572, 36,509)
Total Heat	39,434 (30,782, 47,084)	30,931 (15,260, 46,379)	21,365 (12,737, 29,361)	123,979 (17,722, 214,544)
Moderate Heat	17,281 (12,874, 21,327)	13,224 (5886, 20,577)	9125 (4697, 13,436)	102,166 (3712, 187,872)
Extreme Heat	22,150 (16,844, 26,305)	17,707 (8740, 26,252)	12,242 (7921, 16,326)	21,813 (14,076, 28,585)
January	49,773 (33,582, 63,992)	50,125 (36,335, 64,210)	47,462 (36,249, 58,272)	38,802 (13,551, 59,847)
February	39,481 (26,133, 50,937)	37,440 (26,369, 48,633)	37,570 (28,262, 46,216)	28,118 (5233, 46,859)
March	31,295 (20,928, 40,778)	28,098 (17,951, 38,437)	29,153 (21,391, 37,096)	14,921 (−4001, 30,215)
April	24,463 (17,347, 30,681)	22,577 (12,679, 32,518)	21,371 (14,484, 28,171)	11,444 (−2281, 23,142)
May	17,852 (13,269, 21,669)	14,955 (7514, 22,361)	14,660 (7901, 21,325)	22,283 (13,384, 29,828)
June	16,173 (13,303, 18,509)	10,719 (6757, 14,344)	8765 (6288, 11,294)	25,571 (8813, 39,552)
July	17,568 (14,414, 20,335)	13,572 (7640, 19,133)	7900 (6027, 9684)	39,340 (14,108, 60,471)
August	21,833 (17,886, 25,099)	17,910 (10,062, 25,575)	13,889 (9540, 17,952)	29,324 (5286, 49,167)
September	14,647 (11,060, 17,711)	11,124 (5539, 16,859)	11,440 (6164, 16,658)	21,851 (11,439, 30,322)
October	23,585 (17,580, 28,610)	20,611 (10,812, 30,553)	19,897 (11,910, 27,545)	16,162 (5877, 24,673)
November	30,547 (20,320, 39,740)	28,620 (18,594, 38,996)	30,171 (22,573, 37,821)	18,810 (328, 33,885)
December	42,321 (28,544, 54,406)	40,464 (29,122, 51,922)	37,991 (28,741, 46,781)	29,696 (8372, 47,083)
December–February	131,575 (88,572, 169,225)	128,030 (92,075, 164,818)	123,023 (93,033, 151,218)	96,616 (26,859, 153,493)
March–May	73,610 (53,109, 91,294)	65,630 (39,333, 92,532)	65,184 (46,789, 83,766)	48,648 (16,504, 73,638)
June–August	55,574 (45,697, 63,766)	42,200 (25,083, 58,075)	30,554 (23,807, 37,322)	94,235 (28,741, 149,197)
September–November	68,778 (52,173, 83,342)	60,355 (35,479, 85,125)	61,507 (43,726, 79,512)	56,822 (32,423, 75,751)
Year 1998	341,186 (258,644, 414,558)	309,978 (211,406, 406,098)	297,251 (236,558, 359,185)	306,520 (224,873, 351,338)
Year 1999	338,200 (254,975, 412,500)	299,511 (206,637, 388,498)	284,988 (225,322, 345,150)	300,417 (225,938, 333,189)
Year 2000	306,131 (230,102, 373,922)	264,794 (175,751, 352,266)	253,641 (196,717, 310,249)	257,110 (198,110, 286,403)
Year 2001	340,368 (260,272, 412,154)	307,293 (213,290, 398,759)	287,607 (229,856, 346,447)	303,447 (237,477, 332,281)
Year 2002	310,188 (232,172, 378,567)	274,925 (181,135, 368,014)	258,484 (201,663, 315,092)	273,780 (204,875, 312,480)
Year 2003	396,123 (305,675, 474,498)	367,341 (262,035, 471,108)	347,261 (295,702, 398,094)	380,299 (304,600, 418,444)
Year 2004	274,568 (210,794, 330,303)	249,663 (170,367, 328,695)	232,642 (183,806, 281,031)	252,675 (203,114, 277,464)

Fig. 2.

Weekly, 2-weekly and 4-weekly values of the attributable fraction. The weekly (red), 2-weekly (blue) and 4-weekly (grey) values of the Attributable Fraction aggregated over the ensemble of European regions are shown for all temperatures (a), cold (b) and heat (c) in the daily (x-axis), weekly (red), 2-weekly (blue) and 4-weekly (grey) data models. The solid and dashed lines correspond to the identity and the best linear fitting, respectively, with Pearson correlations [r] and mean differences [d] in the top left corner.

Fig. 3.

Seasonality of the attributable fraction. The mean annual cycle of the Attributable Fraction aggregated over the ensemble of European regions is shown for all temperatures (a), cold (b) and heat (c) in the daily (black), weekly (red), 2-weekly (blue) and 4-weekly (grey) data models. The shading represents the 95% confidence interval. The horizontal lines correspond to the average of the monthly values. Note: in panel (a), the horizontal red and grey lines cover each other.

Fig. 4.

Annual values of the attributable fraction. The annual values of the Attributable Fraction aggregated over the ensemble of European regions are shown for all temperatures (a), cold (b) and heat (c) in the daily (black), weekly (red), 2-weekly (blue) and 4-weekly (grey) data models. The shading represents the 95% confidence interval. The straight lines correspond to the linear trend.

Fig. 5.

Difference of the annual attributable fraction between data models. The horizontal axis shows the annual values of the Attributable Fraction aggregated over the ensemble of European regions for all temperatures (a, d), cold (b, e) and heat (c, f) in the daily data model. The vertical axis depicts the absolute difference (model minus daily) and the relative difference (model minus daily, divided by daily; in %) between the weekly (red) or 2-weekly (blue) data models and the daily model. Lines correspond to the best linear (a, b, d, e) or exponential (c, f) fittings, with Pearson correlations [r] between y-axis values of observations (circles) and fitted predictions (curves) included in the panels.

Accumulated over time, these systematic differences generally explain some of the differences in the seasonality (Fig. 3) and year-to-year variability (Fig. 4) of the attributable mortality. For cold temperatures, the seasonality of the AF is generally well reproduced by the weekly and 2-weekly data models in the winter months, somewhat underestimated in spring and autumn, and largely underestimated in summer (Fig. 3b). For hot temperatures, the AF is generally underestimated from May to September (Fig. 3c). When both components are combined, the weekly and 2-weekly data models correctly reproduce the winter mortality, slightly underestimate the spring and autumn temperature-related deaths, and underestimate the summer mortality (Fig. 3a). In absolute numbers, the daily, weekly and 2-weekly data models estimate an average AN equal to 131,575 (95% CI 88,572–169,225), 128,030 (92,075–164,818) and 123,023 (93,033–151,218) temperature-related deaths in winter (December–February), respectively, and 55,574 (45,697–63,766), 42,200 (25,083–58,075) and 30,554 (23,807–37,322) in summer (June–August, Table 1). Regarding the 4-weekly data model, we found generally much larger differences for the total, cold- and heat-related mortality in all the months and seasons.

Fig. 4 analyses the year-to-year time-series of the attributable mortality, showing that the weekly and 2-weekly data models systematically underestimate the total, cold and heat AF in all the years. To a first-order approximation, this difference is found to be relatively constant throughout the years, and therefore the linear trends are preserved to a very large degree (compare the straight lines in Fig. 4). In absolute numbers, the daily, weekly and 2-weekly data models estimate an AN equal to 329,538 (95% CI 250,681–399,741), 296,215 (204,224–386,523) and 280,268 (225,333–335,723) deaths on average over the whole period (Table 1). In relative terms, the weekly and 2-weekly data models underestimate the total attributable mortality by −10.11% and −14.95%, respectively, the cold attributable mortality by −8.56% and −10.76%, and the heat attributable mortality by −21.56% and −45.82% (Table S3). Again, we found much larger differences in annual cold- and heat-related mortality in the 4-weekly data model.

Fig. 5 performs a more in-depth analysis of the annual values of the total, cold- and heat AF in the daily data model, by exploring their relationship with the absolute differences (i.e. other data models minus daily model) and the relative differences (i.e. other minus daily, divided by daily) found in the weekly and 2-weekly models. Figure S4 additionally shows the differences as a function of the annual values in the weekly data model. In all cases, the relation between the annual AF in the daily data model and differences with the other models is stronger for the relative differences (Fig. 5d–f, Figure S4d–f) than for the absolute ones (Fig. 5a–c, Figure S4a–c), showing that the relative underestimation of the temporally aggregated models monotonically decreases with the increase in the magnitude of the annual AF. This general finding holds for all temperatures, cold and heat, and both for the weekly and 2-weekly data models (compare the Pearson correlations [r] in panels a–c and d–f). Interestingly, these relationships are found to be linear for all temperatures and cold, while they are clearly non-linear for heat. We found that the weekly data model underestimated the heat-related mortality by only −4.62% in 2003, which was the year with the highest estimated mortality (Table S3, see also the rightmost red circles in Fig. 5c, f and Figure S4c and f). Importantly, the strong non-linear association found for heat indicates that the underestimation of the heat-related mortality in the weekly data model would still be relatively small for less extreme summers (i.e. an underestimation of 10% for a heat AF equal to 0.0144 in the daily data model, or 0.0126 in the weekly model, see dashed red lines in Fig. 5f and Figure S4f).

Discussion

To our knowledge, this is the first study to analyse the effect of temporal data aggregation in time-series epidemiological studies of temperature and mortality. We analysed differences in the temperature-related mortality estimates by temporally averaging (aggregating) the daily temperature (mortality) time-series into weekly, 2-weekly and 4-weekly data values. We separately estimated temperature-lag-mortality relationships by using state-of-the-art time-series quasi-Poisson regression models adapted to each of the data aggregations. Results revealed a progressive increase in differences with the degree of temporal data aggregation, with generally increasing underestimations of the MMT, the RR and the attributable mortality. Regardless of the magnitude of the differences, we generally found a good qualitative agreement between the daily, weekly and 2-weekly data models, with comparable results in terms of exposure-lag-response association and the weekly, monthly, seasonal and annual variability of the total, cold- and heat-related mortality. This was however not the case of the 4-weekly data model, due to the rather symmetric exposure-response association, with small RR values in the central part of the temperature distribution.

This study revealed important differences between the cold and heat effects. Although differences with the daily data model generally increased with the degree of temporal data aggregation, we found larger differences for cold in absolute numbers, but for heat in relative terms. On the one hand, the larger absolute differences for cold are simply explained by the fact that the effects of cold temperatures (AF = 0.0751, 95% CI 0.0554–0.0931) are nearly one order of magnitude higher than those of heat (AF = 0.0102, 0.0080–0.0122; Table S2). On the other hand, the larger relative differences for heat are likely related to the distribution of RR values across the lags, given that the temporal data aggregation is expected to underestimate the day-to-day variability of the time-series, and possibly, their lagged short-term associations.¹ This is particularly important for heat, as its health effects are immediate and do not last for more than a week. Instead, the effects of cold are distributed over a longer time period, lagged by up to a month, with a smoother lag-response association. Moreover, temporally aggregated periods with average temperature near the MMT, which may simultaneously include days colder and warmer than the MMT, are expected to be misclassified as either cold-only or heat-only aggregated periods. This is shown by the systematic underestimation of the lowest AF values by the weekly and 2-weekly data models (see circles in Fig. 2 with AF > 0 in the daily data model and AF = 0 in the weekly and/or 2-weekly models). These misclassified aggregated periods, which are generally expected to increase with the degree of temporal data aggregation, represent an important fraction of the total, cold and heat attributable mortality. Given the asymmetric V-shaped relation between temperature and mortality, with the MMT displaced towards warm percentiles (Fig. 1a), the relative contribution of these misclassified aggregated periods is expected to be higher in the case of heat-related mortality.

We analysed the sensitivity of the weekly, monthly, seasonal and annual variability of the attributable mortality to the degree of temporal aggregation of the data. Although the weekly and 2-weekly data models systematically underestimated the lowest AF values, a similar systematic underestimation was not found for the highest AF values (Fig. 2). This asymmetry suggests that the magnitude of differences is smaller during extreme cold and heat conditions, likely explaining why the underestimation of the heat-related mortality was the smallest during the record-breaking hot summer of 2003,¹⁹ i.e. an underestimation of 4.62% in the weekly data model (Table S3). Recently, Ballester et al.¹ used a large weekly temperature and mortality database for 35 European countries to estimate a heat-related mortality burden of 62,862 (95% CI 37,935–88,780) deaths during the year of 2022. Authors compared their estimates based on weekly data models with those of a previous study using daily temperature and mortality data in Spain only,³⁰ and found that the summer heat-related mortality in the country was underestimated by 6.06% (i.e. 11,324 vs. 12,054). This underestimation is aligned with the analysis shown in Fig. 5c, f and Figure S4c and f, given that the weekly data model used in Ballester et al.¹ estimated a heat AF of 0.03014 (0.02066–0.04031) during the year 2022 in Spain, which would correspond to an underestimation of 4.08% (3.96–5.05). Conversely, if we use the associations in Fig. 5c, f and Figure S4c and f, we can speculatively infer the heat-related mortality burden for 2022 that would have been estimated by the daily data model. Ballester et al.¹ estimated a heat AF of 0.01252 (0.00767–0.01760) during the year of 2022 in the 35 European countries, which would correspond to an underestimation of 10.28% (6.10–21.12). Taking the point estimate, i.e. −10.28%, we would infer a heat-related mortality burden of 70,066 (42,283–98,955) deaths during the year of 2022 in the daily data model.

Although temporally aggregated data models underestimate the annual values of the attributable mortality, absolute differences with the daily data model are found to be relatively constant throughout the years (Fig. 5a–c, Figure S4a–c), and therefore, the linear trends of the annual mortality are generally preserved (compare the straight lines in Fig. 4). The cancellation of the absolute differences in the linear trends can for example be used to develop fit-for-purpose indicators to track the health impacts of climate change in a larger domain of countries, regions and cities where daily mortality records are currently not available as open access data. This property was for example used in the Lancet Countdown Europe to track the trend in heat-related mortality from open access weekly temperature and mortality records.¹¹

We tested three types of alternative models, those corresponding to weekly, 2-weekly and 4-weekly aggregations of data. In practical terms, our interest was in the results of the aggregation models that correspond to data that is more easily accessible from the national agencies for statistics and public repositories. In most cases, this usually corresponds to weekly and monthly aggregated data, which in our framework corresponds to the weekly and 4-weekly data models. We purposely designed the aggregations as multiples of seven days to describe the progressive increase in the differences of the temperature-related mortality estimates, but also to analyse these two types of data aggregations. We generally found that the degree of aggregation of the monthly data is temporally too coarse to be used for the purpose of estimating the short-term health effects of cold and heat on human mortality. Instead, aggregated weekly time-series of temperature and mortality data have been shown to represent an approximation of the estimates obtained in the daily data model.

We finally acknowledge several related scientific questions that have not been addressed in the present work, and that will be considered in future studies. Firstly, we used data from a large ensemble of regions in order to analyse spatial differences in the relationship between the four data models (Fig. 1d–f, Figures S1 and S2). Despite the similarities in temperature-lag-mortality associations across worldwide locations,² our results cannot be immediately generalised to other continents without comparing the data models calibrated with data representing other climate regimes and socioeconomic and demographic settings. Moreover, regions here analysed are relatively large, with an average population of 2.7 million inhabitants, and therefore results cannot be immediately generalised to smaller regions or cities with lower mortality counts, or stratified by sex and age groups. Secondly, we did not consider the short-term effects of ambient temperatures on other health outcomes, such as hospital admissions or occupational accidents.³¹ In these cases, the lag-response association is sometimes simpler and/or distributed along a shorter range of lags, and therefore the aggregation models are expected to behave differently. Finally, we did not analyse the short-term health effects of other environmental exposures, such as air pollution, which will be assessed in a separate study. In many cases (e.g.,³²), models analysing the short-term health effects of air pollution include terms controlling for temperature and other climate variables, and therefore, they are necessarily more complex than those here analysed.

In all these cases, temporal data aggregation is yet an unexplored option that, if properly justified with sensitivity analyses, has the potential to circumvent current data access restrictions. The present work represents a first reference study towards this aim. This approach has the potential to complement existing, large-scale, access-restricted, data networks, and to facilitate data access for research, translation and policy-making by using complementary sources of data not explored to date.

Contributors

JB conceived the study idea and did the statistical analyses. JMR and FRH collected, pre-processed and validated the mortality data. JB wrote the first draft of the manuscript, and all authors contributed to subsequent versions, as well as to the interpretation of data and results. All authors reviewed and approved the final version of the manuscript.

Data sharing statement

The temperature data can be freely downloaded from E-OBS (https://www.ecad.eu/download/ensembles/download.php). The mortality data, which cannot be shared to third parties, can be obtained from the respective National agencies for statistics under request.

Declaration of interests

We declare no competing interests.

Appendix A. Supplementary data

The following are the supplementary data related to this article: