Abstract
Purpose:
High dose-rate conditions, coupled with problems related to small field dosimetry, make dose characterization for FLASH-RT challenging. Most conventional dosimeters show significant dependence on dose rate at ultra-high dose rate conditions or fail to provide sufficiently fast temporal data for pulse to pulse dosimetry. Here fast 2D imaging of radioluminescence from a water and quinine phantom was tested for dosimetry of individual 4 μs linac pulses.
Methods:
A modified clinical linac delivered an electron FLASH beam of >50 Gy/s to clinical isocenter. This modification removed the X-ray target and flattening filter, leading to a beam that was symmetric and gaussian, as verified with GafChromic EBT-XD film. Lateral projected 2D dose distributions for each linac pulse were imaged in a quinine-doped water tank using a gated intensified camera, and an inverse Abel transform reconstruction provided 3D images for on-axis depth dose values. A total of 20 pulses were delivered with a 10 MeV, 1.5 cm circular beam and beam with jaws wide open (40 × 40 cm2), and a 3D dose distribution was recovered for each pulse. Beam output was analyzed on a pulse by pulse basis.
Results:
The Rp, Dmax and the R50 measured with film and optical methods agreed to within 1 mm for the 1.5 cm circular beam and the beam with jaws wide open. Cross beam profiles for both beams agreed with film data with > 95 % passing rate (2%/2mm gamma criteria). The optical central axis depth dose agreed with film data, except for near the surface. A temporal pulse analysis revealed a ramp-up period where the dose per pulse increased for the first few pulses and then stabilized.
Conclusions:
Optical imaging of radioluminescence was presented as a valuable tool for establishing a baseline for the recently initiated electron FLASH beam at our institution.
Keywords: Scintillation, Optical Dosimetry, Cherenkov, 3D Dosimetry, FLASH, Single Pulse
1. Introduction:
A novel form of radiation therapy termed FLASH is emerging where the dose is delivered at mean dose rates upwards of 40 Gy/s. This approach has been found to protect normal tissue while maintaining similar tumor control, as compared to conventional radiotherapy dose rates.1-3 This novel modality has garnered considerable interest and was recently used to treat the first human patient4. Unfortunately, high average and instantaneous dose rates and high doses per pulse make dosimetry for FLASH exceptionally challenging.5-12 Most conventional dosimeters either show significant dependence on dose rate at high dose rate conditions or fail to provide any temporal information. Generally, detectors can be divided into three main categories based on the underlying physical mechanism governing the detector’s response to radiation: 1) charge, 2) chemical, and 3) luminescence. Most charge based dosimeters such as ionization chambers, diodes and diamond detectors show significant dependence on dose per pulse and dose rate and are therefore not suitable for FLASH.10,11,13-17 Chemical based dosimeters, such as radiochromic film and alanine offer excellent dose rate independence and dynamic range.9,18,19 However, these detectors tend to be passive and provide no real-time information about dose delivery. The ability to analyze beam output on a per pulse basis is of great importance in FLASH, where a 1 Gy dose from each pulse can lead to large potential variations in delivered dose based upon the number of pulses or the variation per pulse. In FLASH, a single treatment fraction could be as few as two to ten pulses, making dosimetry on a per pulse basis essential.
Due to the widespread interest in FLASH, multiple groups have now modified commercially available linacs to deliver FLASH beams.20-22 FLASH dose rates upwards of 300 Gy/s can be achieved at iso-center by retracting the target and flattening filter in the treatment head, resulting in an intense scattering-foil-free electron beam. Importantly, all dose feedback mechanisms to the linac need to be turned off, which makes single-pulse temporal analysis of the beam absolutely necessary.
In order to perform accurate dosimetry for pre-clinical FLASH experiments, a baseline dataset similar to the commissioning data acquired for a conventional clinical linac is needed. This dataset requires accurate measurement of depth dose curves and cross beam profiles at different depths. These measurements were performed primarily with radiochromic film at our institution. Although radiochromic film provide excellent dose rate independence, one major drawback is that only discrete data points can be obtained for depth dose measurements when the film is placed perpendicular to the beam axis. Additionally, film provides no real-time information of beam stability on per-pulse basis. Diodes and ionization chambers cannot provide full beam characterization on per-pulse basis and are therefore not suitable for FLASH characterization either.
Optical imaging of radioluminescence has been shown to successfully image small beams and complex stereotactic radiosurgery plans.23 Additionally, the technique was also used successfully to image high dose rate scanned proton pencil beams and was shown to be independent of any dose rate dependencies up to dose rates of ~ 20 Gy/s.24 In both cases, however, only 2D projected dose distributions were measured and important central axis information was lost. To measure these central axis quantities, a 3D dose reconstruction algorithm would be needed. One option would adopt an approach which combines the lateral optical image with a beam’s eye view image.25-28 Another option could be to acquire multiple view of the beam and perform filtered back projection.29,30 In this study, we make use of a single optical camera to extract important central axis quantities from projected 2D images. By utilizing the axial symmetry of the primary beam, and by using circular copper cutout as a main electron beam collimator, the beam fluence incident on the water tank is also assumed to be radially symmetric. In theory, a single projection of a radially symmetric object is all that is required to obtain the original distribution. The recovery of the original radial distribution from its projection is performed via a process known as Abel inversion.31 The Inverse Abel transform has been regularly used in a wide range of techniques such as color-ratio pyrometry,32 imaging 2D distributions of charged particles33 and plasma spectroscopy.34 Due to the radial symmetry of the FLASH electron beam, Abel inversion can be used to extract the 3D dose distributions from individual projected 2D optical images of each beam pulse.
2. Materials and Methods:
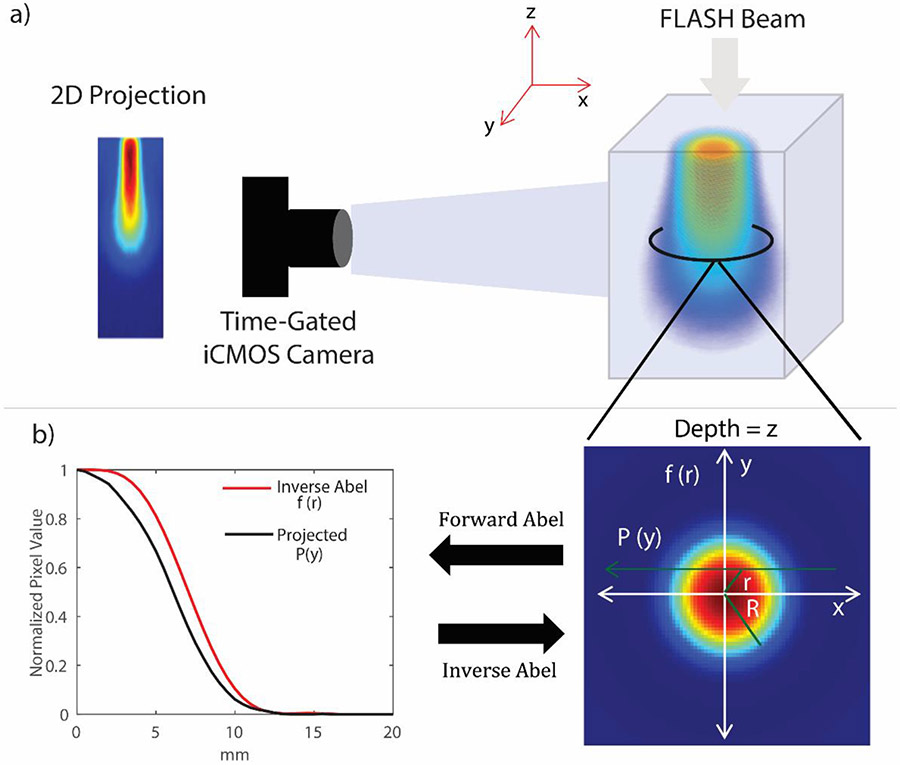
A schematic of the experimental setup is shown in Figure 1a. A commercial intensified CMOS camera (DoseOptics, Lebanon, NH, USA) was used to capture radioluminescence emitted from a 40 × 40 × 40 cm3 water tank. The camera was equipped with a 50 mm lens (Canon, Tokyo, Japan), with an aperture of F/22. Additionally, the camera was time-gated to the linear accelerator pulses. The time-gating allowed us to image individual linac pulses in real-time. Two field sizes were used for this study; 1) a beam with jaws wide open (i.e jaws set to 40 × 40 cm2) and 2) a small 1.5 cm ⌀ circular beam. Twenty pulses were delivered with both beams at a repetition rate of 60 Hz (corresponding to 100 MU/min for Varian manufactured linacs). At iso-center (100 cm SSD), the dose per pulse was measured to be around 1 Gy for the broad beam, which translates into a mean dose rate of ~ 60-70 Gy/s. The camera exposure time was set such that each individual frame corresponded to a single linac pulse.
Figure 1.
a) Schematic of the experimental setup showing the 1.5 cm beam imaged with the time-gated intensified camera. b) Circular symmetry of the beam at a specific depth z. An inverse Abel transform can be employed to reconstruct the 2D cross-section of the beam at each depth for a 3D volume.
The water tank was doped with 1 g/L quinine sulfate (Sigma Aldrich, St. Louis, MO) solution, which was pre-dissolved in 0.05 M sulfuric acid. Optical photons emitted from the quinine doped water solution can be produced through three different physical mechanisms: 1) excitation of quinine via energy transfer through the bulk medium; 2) direct Cherenkov generation in water; and 3) Cherenkov excited quinine emission.35 Unfortunately, Cherenkov radiation has an inherent energy dependence; it has been shown that Cherenkov emission does not perfectly correlate to dose deposition.36,37 Therefore, it is imperative that the Cherenkov signal is suppressed. For this purpose, the lens was fitted with a 50 nm bandpass filter, centered around 450 nm, which is the also peak emission wavelength of the quinine solution used in this study.
The technique used for Abel inversion in this study was based on the method proposed by Pretzler et al.38 For completeness, the technique and forward and inverse Abel transform pair are described again. For a radially symmetric 3D object, the 2D projection of the object is linked to its cross section by the forward and inverse Abel transform pair (equation 1 and 2, respectively):
| (1) |
| (2) |
where is the line integral of the underlying radial distribution . In the context of this study, the two integrals can be understood by envisioning each row of the optical image as the line of sight integral along the beam axis and applying inverse Abel transform for each row would then yield the central axis radial dose distribution ( in this case) at each depth. The line of sight approximation is valid in this study because of the small aperture size ~ F/22 of the lens. The process is also visually depicted in Figure 1 b). Unfortunately, direct Abel inversion is difficult because of the pole at y = r and the derivative in equation 2 which can amplify noise. In the method proposed by Pretzler et al, the underlying radial dose distribution at each depth can be expressed as a linear sum of cosines with some unknown amplitudes, :
| (3) |
| (4) |
Substituting equation 3 into equation 1 for yields a line of sight integral in terms of the cosine distribution with some unknown coefficients :
| (5) |
The problem becomes one of minimizing the least squares difference between the measured and the unknown . A set of coefficients of which minimize the difference, are then substituted back into equation 3 which yields , the underlying central axis dose distribution at each depth. Accurate reconstruction using this technique is highly dependent on the upper frequency limit set by . A high upper frequency limit would result in amplification of noise and oscillatory behavior in the reconstructed profiles. For this study, we found that resulted in profiles that did not exhibit oscillatory behavior and worked universally for both beam sizes used.
Prior to reconstruction, multiple image processing steps had to be performed, which are described below.
Filtering: Acquired images were filtered with a 5 × 5 pixel spatial median filter.
Flatfield Correction: Each image in the 20 pulse image stack was background and flatfield corrected to account for vignetting effects and stray light in the linac bunker.
Centering and Rotational Alignment: Despite carefully aligning the camera to the iso-center, it is expected that there might be some lateral shift and rotation with respect to the actual center. These issues were accounted for by determining the line of symmetry (LOS) of each acquisition and the angle the LOS subtends with the horizontal (i.e., center row of the image sensor). Any angular offset was then corrected via MATLAB’s built-in imrotate function using bilinear interpolation.
Symmetrization: To remove asymmetry in the projected images due to experimental noise, the images were divided into two halves along the LOS and averaged together to yield one half of the projection. Abel inversion was carried out on this halve and later mirrored and interpolated on a circle to yield the dose distribution along the optical axis.
The reconstructed cumulative optical data was compared to data acquired with a radiochromic film (EBT-XD, Ashland, Wilmington, DE, USA). Radiochromic film was chosen as the reference dosimeter in this study because it is known to exhibit excellent dose rate independence.39 Depth dose data was acquired with multiple calibrated film pieces stacked perpendicular to the beam axis at different depths. All measurements with film were repeated three times. In addition to cumulative analysis, beam variation on a per pulse basis was also analyzed using the optical data.
3. Results:
3.1. Cumulative Analysis
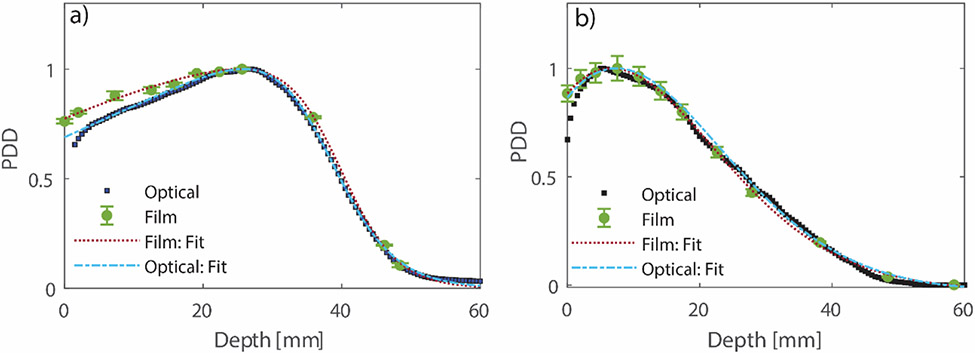
The two beams were reconstructed at a voxel size of 0.5 mm3. For the small field, leakage through the electron applicator was detected in the 2D projected images. This leakage signal was subtracted off from the original image by delivering a beam with the same parameters through the same applicator with a copper beam block of same thickness as beam cutout. The role of leakage and its effect on the radial symmetry of the small beam are discussed in detail later in the discussion section. Comparison of the central axis depth dose distribution measured with film and the optical data is shown in Figure 2. It can be seen that in both cases, beyond the buildup region, the optical depth dose curve closely follows the data measured with film at discrete depths. A comparison of typical electron beam characteristics between the two techniques is shown in Table 1. Dmax is the depth at which maximum dose occurs, R50 is the point at which 50% of Dmax occurs, and Rp (Practical Range) is the point at which the tangent plotted through the inflection point of the electron depth dose curve intersects the extrapolated bremsstrahlung tail. The uncertainty reported for film data represents standard deviation from three repeated measurements, whereas the uncertainty in the optical data is the standard deviation obtained across the 20 pulses for one acquisition. It can be seen that the values reported by the two techniques are within 1 mm of each other. For accurate characterization of Rp and R50, the depth dose data had to be fitted with a functional form which can accurately describe an electron depth dose distribution. Fortunately, the depth dose can be represented using a 2nd order polynomial multiplied by a Fermi-Dirac function as proposed by Meigooni and Das.40 The fits are depicted in Figure 2.
Figure 2.
Comparison of central axis percentage depth dose (PDD) between optical and film for the beam with a) jaws wide open and the b) 1.5 cm diameter beam. The error bars on the film data represent standard deviation from three different measurements. The measured data were fitted to an analytical function describing electron PDD curves as proposed by Meigooni and Das.40 R2 for all fits were >0.99.
Table 1:
Comparison of Depth Dose Characteristics between Optical and Film Data
| Dmax(mm) | R50(mm) | Rp(mm) | ||||
|---|---|---|---|---|---|---|
| Optical | Film | Optical | Film | Optical | Film | |
| Jaws Open | 25.0 ± 0.3 | 26.0 ± 0.3 | 39.0 ± 0.3 | 40.0 ± 0.3 | 48.0 ± 0.2 | 48.0 ± 0.2 |
| 1.5 cm | 8.0 ± 0.5 | 8.0 ± 0.2 | 26.0 ± 0.9 | 26.0 ± 0.1 | 41.0 ± 0.8 | 40.0 ± 0.1 |
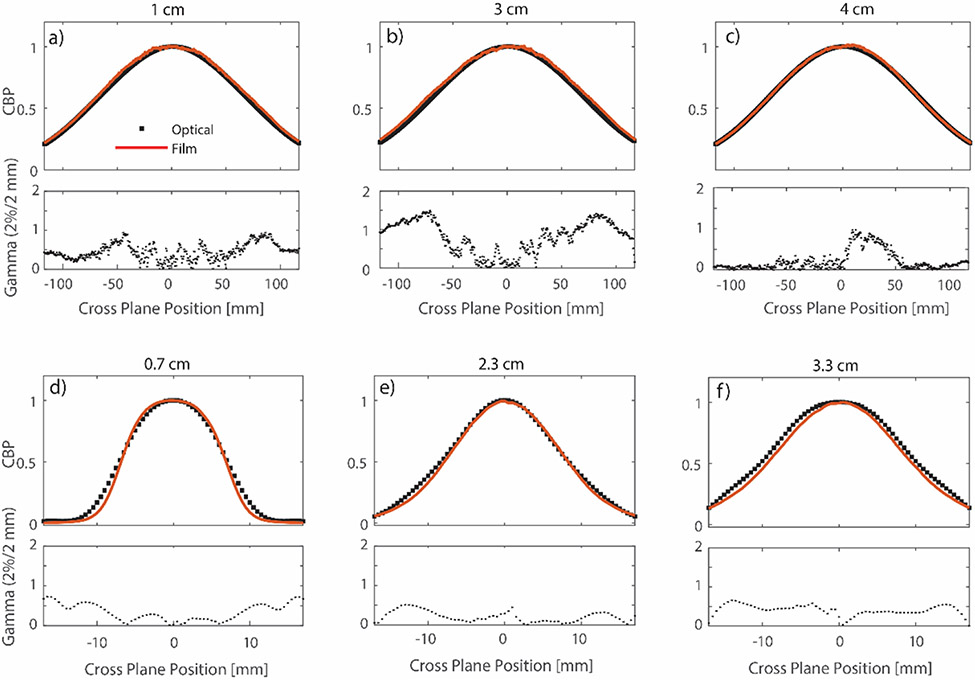
Comparison of central axis cross beam profiles (CBP) at different depths for the broad and small beam is shown in Figure 3. For the broad beam, the optical profiles were compared to film at depths of 1, 3 and 4 cm. For the small beam, comparisons were performed at 0.7 cm, 2.3 cm, and 3.3 cm. CBP at all depths were normalized to an average of ± 5 pixel values around the central axis point at that depth. In all but one case, optical cross beam profiles exhibited a 100 % (2%/2 mm) gamma index passing rate (Low et al 41). The largest discrepancy is seen at a depth of 3 cm for the broad beam. Good agreement between cross beam profiles at different depths shows that the Abel inversion is accurate at multiple depths. It is important to note here that the broad beam (jaws set to 40 × 40 cm2) had a full width half maximum (FWHM) of ~ 16 cm at Dmax. For the broad beam, it is the focal size of the electron beam exiting the bending magnet which dictates the field size, since the beam moves unimpeded through the treatment head.
Figure 3).
Comparison of optical and film based central axis cross beam profiles at different depths for the jaws wide open (a,b, and c) and the 1.5 cm diameter field (d,e, and f). At each depth, the optical data is compared to film using the gamma criteria of 2%/2mm. In most cases the optical passing rate was found to be 100%, except for the profile at depth 2 cm where significant disagreement was seen in the penumbra region. At each depth, profiles are normalized to an average of ± 5 pixels around the central axis point.
3.2. Per Pulse Analysis
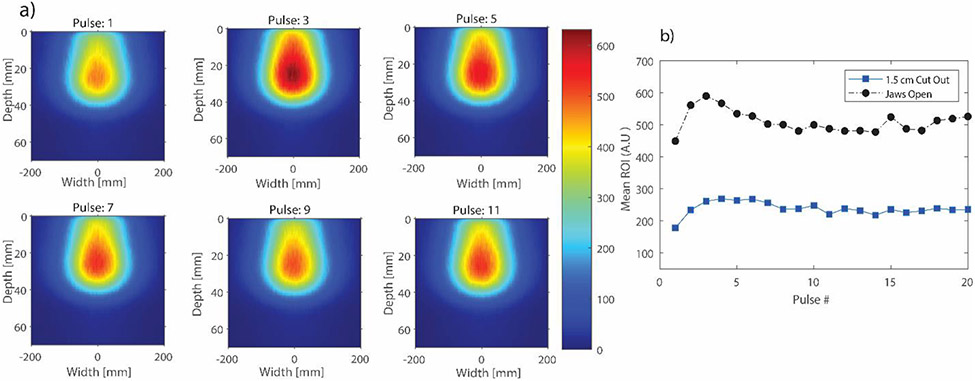
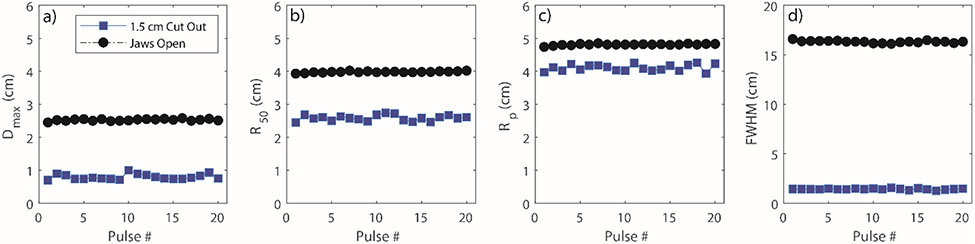
As previously stated, the ability to analyze individual linac pulses is important in FLASH-RT. In particular, the beam intensity was assessed on a pulse by pulse basis. Beam intensity analysis was performed directly on the 2D projected images since any variation in the 2D images will also be reflected in the reconstructed 3D dose distribution. An ROI was drawn near the point of maximum dose for both the small and broad beam. The results are presented in Figure 4. It can be clearly seen that there is intensity variation between adjacent linac pulses. More importantly, there is a brief ramp-up period after which the beam output stabilizes. In addition to intensity variation, it was also important to quantify spatial variation of the beam as a function of time. The results for this particular study, are presented in Figure 5. The figure shows the variation of typical electron beam characteristics on a pulse by pulse basis. To note, the depth dose profiles in this case were parametrized in terms of the Fermi-Dirac distribution used earlier for film depth dose curves.40 The parametrized fit was then evaluated at a grid size of 0.1 mm/pixel. Curve fitting was performed in this case to account for low signal to noise ratio when performing analysis on individual frames for the small beam. However, for the broad beam, even individual frames yielded a good signal to noise ratio that no curve fitting was required; to keep the analysis consistent, the broad beam depth dose was also fitted. It can be seen that the Dmax, RP and FWHM at Dmax, remain relatively consistent for the 20 pulses.
Figure 4.
a) 2D projected images of individual linac pulses for the jaws wide open beam. Only 6 pulses are shown here. b) Beam intensity variation for the broad and small beam. The mean pixel value was obtained from a region of interest (ROI) near the point of maximum dose for each beam.
Figure 5.
a-d) Variation in Dmax, R50, Rp and FWHM at Dmax, respectively for the small and broad beam over the course of 20 pulses.
4. Discussion:
Optical imaging of radioluminescence was presented as a valuable tool for establishing a base line for the recently initiated electron FLASH beam at our institution. Dosimetry for ultra-high dose rate fields is complicated by a number of factors that were highlighted in the introduction section. In addition, it was imperative that the beam be monitored on an individual pulse basis because most feedback mechanisms used in a conventional linac were turned off when the machine was converted to FLASH. In this study, data was acquired at a theoretical spatial resolution of ~ 1 mm3 for each individual linac pulse. Beams in this study were delivered at a repetition rate of 60 Hz (100 MU/min), which resulted in a dose rate of 50-70 Gy/s. This is above the lowest dose rate (30 Gy/s) reported in literature required to elicit the FLASH effect.42 However, this camera can be used to image at 360 Hz (> 300 Gy/s), by choosing a smaller ROI if the purpose is to only monitor beam output, and faster cameras can be implemented in the future with significantly higher frame rate. Current commercial detectors used for obtaining central axis dosimetric quantities tend to be point detectors which have to be scanned in a water tank to obtain dosimetric quantities of interest. This solution is not viable because most commercial point based dosimeters tend to be charge based devices which suffer from ion-recombination issues at high dose rates and doses per pulse. Essentially, a detector with excellent spatial resolution and dose rate linearity is required. Plastic scintillator detectors fulfill these requirements. However, most commercially available scintillator detectors tend to be point based, which again limits their usability for FLASH-RT. Another potential dosimeter of interest would be Gel-based dosimeter43 which can provide true 3D-dose distribution. However, gel dosimeters are passive detectors and will not provide any temporal information. Additionally, certain gel dosimeters tend to exhibit dose rate dependence44, making them a non-ideal option for FLASH.
It is important to address the radial symmetry of the beam since accurate dose reconstruction relies on this underlying assumption. In this study, the FLASH beam was obtained by retracting the target from the beam’s path. In doing so, the shape of the electron beam is dictated by the narrow electron beam obtained after the bending magnets. Varian manufactured linacs use a 270° achromatic bending magnet system which results in a very narrow circular beam spot. In the absence of the target and the scattering foil, which is typically used to provide a uniform dose distribution over a large area, the beam fluence incident on the water phantom was gaussian. The radial symmetry of the beam was confirmed with GafChromic film on multiple occasions. Additionally, a vertically mounted camera was used to image a scintillating sheet placed on top of the water phantom, providing a view similar to the beam’s eye view. Excellent radial symmetry was confirmed with this arrangement as well. In future iterations, the vertically mounted camera will acquire images concurrently with a camera at the foot of the couch acquiring the depth dose distribution. Any major asymmetry can then be easily identified.
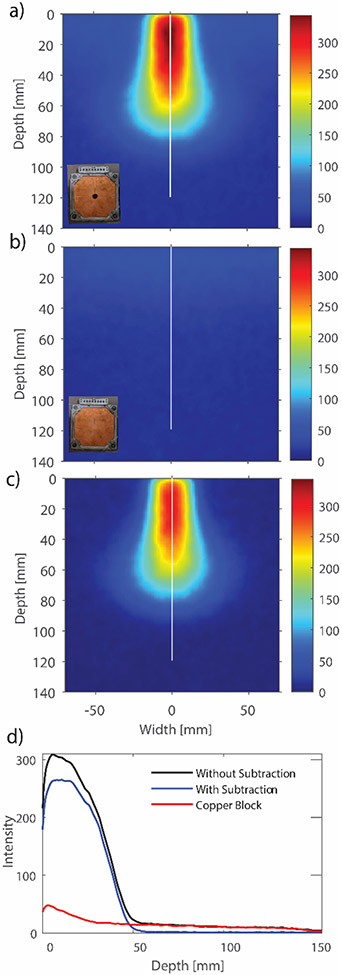
For pre-clinical FLASH studies, the use of smaller field sizes is of more interest than broad beams. For most mice studies performed at our institution, a circular 1.5 cm cut was used to conform the FLASH beam to a small size. Dosimetric data for this beam was also quantified using the optical technique. The issue of leakage through the electron applicator was briefly discussed earlier and is now discussed in detail. While imaging the small beam, stray leakage was detected in the 2D projected images (Figure 6a). This leakage, which may be insignificant while measuring central axis quantities using point detectors, shows up clearly in the projected optical images because optical signal is integrated along the whole width of tank. This leakage signal, which is superimposed on the circular beam distorts the radial symmetry of the beam which can lead to erroneous reconstruction using the Abel Inversion technique. To account for this, beam leakage through a similar electron beam block was imaged with the same camera settings. It should be noted that measuring the leakage signal in such a way will result in slight overestimation of the signal. However, for the purpose of this study we found this method sufficient since the primary beam is magnitudes of order more intense when compared to the leakage signal. The resulting 2D optical image is presented in Figure 6b). The leakage signal projected and summed along camera’s optical axis can be clearly seen. Figure 6d) shows a line profile through the central axis for 6a) and 6c). The leakage was subtracted off from the original image, and Abel inversion was performed on this subtracted image.
Figure 6.
a) Optical Image with the 1.5 cm cut-out. A leakage signal can be seen around the beam. b) To correct for this leakage, a ‘cut-out’ with no aperture was also imaged. c) Image obtained after subtracting the figures in a) and b). d) A line profile through the central axis for the 6 a) and 6 c).
The under estimation of dose in the buildup region might be attributed to the energy dependence of Cherenkov emission. This effect is more pronounced for the large field as compared to the small field, where the energy spectrum is more uniform due to a decrease in phantom scatter. Therefore, it is important to remove the Cherenkov signal. To this end, a bandpass filter was employed. However, because Cherenkov radiation is broadband and spans across the entire visible spectrum, it is expected that Cherenkov radiation and Cherenkov-excited fluorescence is not fully removed. For a more robust Cherenkov removal method, spectral filtering technique similar to the one proposed by Fontbonne et al.45 would have to be implemented. Nonetheless, we found that the 50 nm bandpass filter was sufficient for relative beam profiling of the FLASH beam.
5. Conclusion:
Optical imaging was presented as a 2D imaging tool with potential for 3D in symmetric beams for single pulse quality assurance in FLASH-RT. The technique can be used to characterize the practical range, central axis profiles, and temporal stability of the beam. For absolute dose calibration, a robust Cherenkov removal technique will be required.
Acknowledgements
This work was supported by the Norris Cotton Cancer Center seed funding through core grant P30 CA023108 and through seed funding from the Thayer School of Engineering, as well as support from grant R01 EB024498.
Footnotes
Conflict of Interest
Dr. Pogue reports personal fees from DoseOptics LLC, outside the submitted work.
Dr. Bruza reports non-financial support from DoseOptics LLC, during the conduct of the study; personal fees and non-financial support from DoseOptics LLC, outside the submitted work; In addition, Dr. Bruza has a patent 62/967,302 pending, a patent 62/873,155 pending, a patent PCT/US19/14242 pending, and a patent PCT/US19/19135 pending.
8. References:
- 1.Favaudon V, Caplier L, Monceau V, et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med. 2014;6(245):245ra93. doi: 10.1126/scitranslmed.3008973 [DOI] [PubMed] [Google Scholar]
- 2.Fouillade C, Curras-Alonso S, Giuranno L, et al. FLASH Irradiation Spares Lung Progenitor Cells and Limits the Incidence of Radio-induced Senescence. Clin Cancer Res. 2020;26(6):1497–1506. doi: 10.1158/1078-0432.CCR-19-1440 [DOI] [PubMed] [Google Scholar]
- 3.Levy K, Natarajan S, Wang J, et al. FLASH irradiation enhances the therapeutic index of abdominal radiotherapy in mice. bioRxiv. Published online December 12, 2019:2019.12.12.873414. doi: 10.1101/2019.12.12.873414 [DOI] [Google Scholar]
- 4.Bourhis J, Sozzi WJ, Jorge PG, et al. Treatment of a first patient with FLASH-radiotherapy. Radiother Oncol. 2019;139:18–22. doi: 10.1016/j.radonc.2019.06.019 [DOI] [PubMed] [Google Scholar]
- 5.Ashraf MR, Rahman M, Zhang R, et al. Dosimetry for FLASH Radiotherapy: A Review of Tools and the Role of Radioluminescence and Cherenkov Emission. Front Phys. 2020;8. doi: 10.3389/fphy.2020.00328 [DOI] [Google Scholar]
- 6.Favaudon V, Lentz J-M, Heinrich S, et al. Time-resolved dosimetry of pulsed electron beams in very high dose-rate, FLASH irradiation for radiotherapy preclinical studies. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip. 2019;944:162537. doi: 10.1016/j.nima.2019.162537 [DOI] [Google Scholar]
- 7.Bourhis J, Montay-Gruel P, Gonçalves Jorge P, et al. Clinical translation of FLASH radiotherapy: Why and how? Radiother Oncol J Eur Soc Ther Radiol Oncol. 2019;139:11–17. doi: 10.1016/j.radonc.2019.04.008 [DOI] [PubMed] [Google Scholar]
- 8.Esplen NM, Mendonca MS, Bazalova-Carter M. Physics and biology of ultrahigh dose-rate (FLASH) radiotherapy: a topical review. Phys Med Biol. Published online 2020. doi: 10.1088/1361-6560/abaa28 [DOI] [PubMed] [Google Scholar]
- 9.Jorge PG, Jaccard M, Petersson K, et al. Dosimetric and preparation procedures for irradiating biological models with pulsed electron beam at ultra-high dose-rate. Radiother Oncol. 2019;139:34–39. doi: 10.1016/j.radonc.2019.05.004 [DOI] [PubMed] [Google Scholar]
- 10.Jaccard M, Petersson K, Buchillier T, et al. High dose-per-pulse electron beam dosimetry: Usability and dose-rate independence of EBT3 Gafchromic films. Med Phys. 2017;44(2):725–735. doi: 10.1002/mp.12066 [DOI] [PubMed] [Google Scholar]
- 11.Petersson K, Jaccard M, Germond J-F, et al. High dose-per-pulse electron beam dosimetry - A model to correct for the ion recombination in the Advanced Markus ionization chamber. Med Phys. 2017;44(3):1157–1167. doi: 10.1002/mp.12111 [DOI] [PubMed] [Google Scholar]
- 12.Diffenderfer ES, Verginadis II, Kim MM, et al. Design, Implementation, and in Vivo Validation of a Novel Proton FLASH Radiation Therapy System. Int J Radiat Oncol. 2020;106(2):440–448. doi: 10.1016/j.ijrobp.2019.10.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jursinic PA. Dependence of diode sensitivity on the pulse rate of delivered radiation. Med Phys. 2013;40(2):021720. doi: 10.1118/1.4788763 [DOI] [PubMed] [Google Scholar]
- 14.Ade N, Nam TL, Derry TE, Mhlanga SH. The dose rate dependence of synthetic diamond detectors in the relative dosimetry of high-energy electron therapy beams. Radiat Phys Chem. 2014;98:155–162. doi: 10.1016/j.radphyschem.2014.02.003 [DOI] [Google Scholar]
- 15.McManus M, Romano F, Lee ND, et al. The challenge of ionisation chamber dosimetry in ultra-short pulsed high dose-rate Very High Energy Electron beams. Sci Rep. 2020;10(1):9089. doi: 10.1038/s41598-020-65819-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kranzer R, Poppinga D, Weidner J, et al. Ion collection efficiency of ionization chambers in ultra-high dose-per-pulse electron beams. Med Phys. n/a(n/a). doi: 10.1002/mp.14620 [DOI] [PubMed] [Google Scholar]
- 17.Konradsson E, Ceberg C, Lempart M, et al. Correction for Ion Recombination in a Built-in Monitor Chamber of a Clinical Linear Accelerator at Ultra-High Dose Rates. Radiat Res. 2020;194(6):580–586. doi: 10.1667/RADE-19-00012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vozenin M-C, De Fornel P, Petersson K, et al. The Advantage of FLASH Radiotherapy Confirmed in Mini-pig and Cat-cancer Patients. Clin Cancer Res Off J Am Assoc Cancer Res. 2019;25(1):35–42. doi: 10.1158/1078-0432.CCR-17-3375 [DOI] [PubMed] [Google Scholar]
- 19.Patriarca A, Fouillade C, Auger M, et al. Experimental Set-up for FLASH Proton Irradiation of Small Animals Using a Clinical System. Int J Radiat Oncol. 2018;102(3):619–626. doi: 10.1016/j.ijrobp.2018.06.403 [DOI] [PubMed] [Google Scholar]
- 20.Schüler E, Trovati S, King G, et al. Experimental Platform for Ultra-high Dose Rate FLASH Irradiation of Small Animals Using a Clinical Linear Accelerator. Int J Radiat Oncol Biol Phys. 2017;97(1):195–203. doi: 10.1016/j.ijrobp.2016.09.018 [DOI] [PubMed] [Google Scholar]
- 21.Lempart M, Blad B, Adrian G, et al. Modifying a clinical linear accelerator for delivery of ultra-high dose rate irradiation. Radiother Oncol. 2019;139:40–45. doi: 10.1016/j.radonc.2019.01.031 [DOI] [PubMed] [Google Scholar]
- 22.Rahman M, Ashraf MR, Zhang R, et al. Electron FLASH Delivery at Treatment Room Isocenter for Efficient Reversible Conversion of a Clinical LINAC. Int J Radiat Oncol Biol Phys. 2021;0(0). doi: 10.1016/j.ijrobp.2021.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ashraf MR, Bruza P, Pogue BW, et al. Optical imaging provides rapid verification of static small beams, radiosurgery, and VMAT plans with millimeter resolution. Med Phys. 2019;46(11):5227–5237. doi: 10.1002/mp.13797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rahman M, Bruza P, Langen KM, et al. Characterization of a new scintillation imaging system for proton pencil beam dose rate measurements. Phys Med Biol. Published online 2020. doi: 10.1088/1361-6560/ab9452 [DOI] [PubMed] [Google Scholar]
- 25.Bruza P, Andreozzi JM, Gladstone DJ, Jarvis LA, Rottmann J, Pogue BW. Online Combination of EPID Cherenkov Imaging for 3-D Dosimetry in a Liquid Phantom. IEEE Trans Med Imaging. 2017;36(10):2099–2103. doi: 10.1109/TMI.2017.2717800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goulet M, Rilling M, Gingras L, Beddar S, Beaulieu L, Archambault L. Novel, full 3D scintillation dosimetry using a static plenoptic camera. Med Phys. 2014;41(8). doi: 10.1118/1.4884036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Darne CD, Alsanea F, Robertson DG, Hojo Y, Sahoo N, Beddar S. 3D Scintillator Detector System for Proton Scanning Beam Therapy. Int J Radiat Oncol • Biol • Phys. 2019;105(1):S89–S90. doi: 10.1016/j.ijrobp.2019.06.563 [DOI] [Google Scholar]
- 28.Beddar S. 3D dosimetry for proton therapy. J Phys Conf Ser. 2019;1305:012038. doi: 10.1088/1742-6596/1305/1/012038 [DOI] [Google Scholar]
- 29.Glaser AK, Voigt WHA, Davis SC, Zhang R, Gladstone DJ, Pogue BW. Three-dimensional Čerenkov tomography of energy deposition from ionizing radiation beams. Opt Lett. 2013;38(5):634. doi: 10.1364/OL.38.000634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rilling M, Allain G, Thibault S, Archambault L. Tomographic-based 3D scintillation dosimetry using a three-view plenoptic imaging system. Med Phys. 2020;47(8):3636–3646. doi: 10.1002/mp.14213 [DOI] [PubMed] [Google Scholar]
- 31.Bracewell R. Fourier Analysis and Imaging. Springer Science & Business Media; 2004. [Google Scholar]
- 32.Dreyer JAH, Slavchov RI, Rees EJ, et al. Improved methodology for performing the inverse Abel transform of flame images for color ratio pyrometry. Appl Opt. 2019;58(10):2662. doi: 10.1364/AO.58.002662 [DOI] [PubMed] [Google Scholar]
- 33.Garcia GA, Nahon L, Powis I. Two-dimensional charged particle image inversion using a polar basis function expansion. Rev Sci Instrum. 2004;75(11):4989–4996. doi: 10.1063/1.1807578 [DOI] [Google Scholar]
- 34.Glasser J, Chapelle J, Boettner JC. Abel inversion applied to plasma spectroscopy: a new interactive method. Appl Opt. 1978;17(23):3750–3754. doi: 10.1364/AO.17.003750 [DOI] [PubMed] [Google Scholar]
- 35.Jean E, Delage M-È, Beaulieu L. Investigation of the quinine sulfate dihydrate spectral properties and its effects on Cherenkov dosimetry. Phys Med Biol. 2019;64(15):155019. doi: 10.1088/1361-6560/ab2827 [DOI] [PubMed] [Google Scholar]
- 36.Glaser AK, Zhang R, Gladstone DJ, Pogue BW. Optical dosimetry of radiotherapy beams using Cherenkov radiation: the relationship between light emission and dose. Phys Med Biol. 2014;59(14):3789–3811. doi: 10.1088/0031-9155/59/14/3789 [DOI] [PubMed] [Google Scholar]
- 37.Helo Y, Rosenberg I, D’Souza D, et al. Imaging Cerenkov emission as a quality assurance tool in electron radiotherapy. Phys Med Biol. 2014;59(8):1963–1978. doi: 10.1088/0031-9155/59/8/1963 [DOI] [PubMed] [Google Scholar]
- 38.Pretzier G. A New Method for Numerical Abel-Inversion. Z Für Naturforschung A. 1991;46(7):639–641. doi: 10.1515/zna-1991-0715 [DOI] [Google Scholar]
- 39.Karsch L, Beyreuther E, Burris-Mog T, et al. Dose rate dependence for different dosimeters and detectors: TLD, OSL, EBT films, and diamond detectors. Med Phys. 2012;39(5):2447–2455. doi: 10.1118/1.3700400 [DOI] [PubMed] [Google Scholar]
- 40.Meigooni AS, Das IJ. Parametrization of depth dose for electron beams. Phys Med Biol. 1987;32(6):761–768. doi: 10.1088/0031-9155/32/6/008 [DOI] [PubMed] [Google Scholar]
- 41.Low DA, Harms WB, Mutic S, Purdy JA. A technique for the quantitative evaluation of dose distributions. Med Phys. 1998;25(5):656–661. doi: 10.1118/1.598248 [DOI] [PubMed] [Google Scholar]
- 42.Montay-Gruel P, Petersson K, Jaccard M, et al. Irradiation in a flash: Unique sparing of memory in mice after whole brain irradiation with dose rates above 100 Gy/s. Radiother Oncol. 2017;124(3):365–369. doi: 10.1016/j.radonc.2017.05.003 [DOI] [PubMed] [Google Scholar]
- 43.Guo P, Adamovics J, Oldham M. A practical three-dimensional dosimetry system for radiation therapy. Med Phys. 2006;33(10):3962–3972. doi: 10.1118/1.2349686 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pappas EP, Zoros E, Zourari K, et al. PO-0774: Investigation of dose-rate dependence at an extensive range for PRESAGE radiochromic dosimeter. Radiother Oncol. 2017;123:S410. doi: 10.1016/S0167-8140(17)31211-2 [DOI] [Google Scholar]
- 45.Fontbonne JM, Iltis G, Ban G, et al. Scintillating fiber dosimeter for radiation therapy accelerator. IEEE Trans Nucl Sci. 2002;49(5):2223–2227. doi: 10.1109/TNS.2002.803680 [DOI] [Google Scholar]