Abstract
Background
The inference of homology between proteins is a key problem in molecular biology The current best approaches only identify ~50% of homologies (with a false positive rate set at 1/1000).
Results
We present Homology Induction (HI), a new approach to inferring homology. HI uses machine learning to bootstrap from standard sequence similarity search methods. First a standard method is run, then HI learns rules which are true for sequences of high similarity to the target (assumed homologues) and not true for general sequences, these rules are then used to discriminate sequences in the twilight zone. To learn the rules HI describes the sequences in a novel way based on a bioinformatic knowledge base, and the machine learning method of inductive logic programming. To evaluate HI we used the PDB40D benchmark which lists sequences of known homology but low sequence similarity. We compared the HI methodoly with PSI-BLAST alone and found HI performed significantly better. In addition, Receiver Operating Characteristic (ROC) curve analysis showed that these improvements were robust for all reasonable error costs. The predictive homology rules learnt by HI by can be interpreted biologically to provide insight into conserved features of homologous protein families.
Conclusions
HI is a new technique for the detection of remote protein homolgy – a central bioinformatic problem. HI with PSI-BLAST is shown to outperform PSI-BLAST for all error costs. It is expect that similar improvements would be obtained using HI with any sequence similarity method.
Background
The development of computer programs to identify homologous relationships between proteins is a key problem in computational molecular biology. Homology relationships between proteins allows the probabilistic inference of knowledge about their structure and function. Such inferences are the basis of most of our knowledge of the sequenced genomes. Homology between proteins is typically inferred using computer programs to identify similarities between their sequences. Here we introduce a new and general approach for improving sequence similarity searches called Homology Induction (HI). Please note we have published a precursor to this paper addressing the machine learning aspects of the HI methodology in a conference proceedigs [1]. HI is based on using machine learning, specifically Inductive Logic Programming (ILP), to improve results from conventional sequence similarity searches. The basic HI methodology is as follows:
1. Run your favorite sequence similarity search method on the target.
2. Divide the results of the search into "clear hits" (sequences with very high probability of being homologous to the target) and the "twilight zone" (sequences where the sequence statistics are ambiguous about homology).
3. Collect a set of random sequences that have very low probability of being homologous to the target.
4. Use machine learning to form classification rules which are true about the probable homologous sequences (positive examples) and not true for the probable non-homologous sequences (negative examples).
5. Use the classification rules to discriminate the examples in the "twilight zone" between the homologous and non-homologous classes.
HI is based on two premises:
• The prediction of homology is a statistical discrimination task, and therefore discrimination algorithms are the most suited to the task (conventional sequence similarity methods do not explicitly use discrimination methods).
• All available relevant information should be used to make decisions over homology [2] (conventional sequence similarity search methods only use a small set of local sequence based properties).
The most similar work to HI is that of Jaakola et al. [3] who employed a Fisher kernel method as a discriminative method on top of a HMM for detecting remote homologues. Also related to HI are the program BLAST PRINTS [4]. A similar approach was taken by MacCallum et al. [5] and Chang et al. [6] who use literature annotations and text-similarity measures to modify PSI-BLAST. HI is distinguished from these approaches by its ability to use all available background knowledge, its more general learning ability, and by its more comprehensive experimental validation.
Sequence similarity searches
Sequence similarity searches (SSSs) are probably the single most commonly used class of bioinformatic programs. Many different approaches exist to the problem of predicting whether two protein sequences resemble each other enough to imply homology, [7-17]. There are two main parts to the problem in designing a good SSS program: developing an accurate statistical model of sequence similarity (or more correctly sequence divergence), and making the program efficient enough to search the very large sequence databases which are characteristic of current bioinformatic knowledge.
The most commonly used sequence similarity search methods are probably those of the BLAST family [18]. BLAST is based on an extension of the statistics of ungapped local alignments for high-scoring segment pairs (HSP) [19], and is highly efficient at searching as it uses heuristics to reduce the search space. We chose to use PSI-BLAST as our standard SSS [19]. PSI-BLAST is a state-of-the-art SSS incorporating sophisticated statistics and a highly efficient search method. The PSI-BLAST algorithm is also iterative, a feature characteristic of the most sensitive methods. PSI-BLAST performs an initial SSS through a database according to the gapped BLAST algorithm [19], using a standard weight matrix [20]. After this initial iteration, the program constructs a profile [10,15,16] from closely related proteins, using a so-called inclusion E-value. This procedure iterates until, either the profile converges, i.e. no new closely related proteins can be found, or the number of iterations has reached a certain threshold. The result of such a PSI-BLAST search is a list of possible homologues, sorted by their E-value. The lower the E-value, the higher the probability that the match does not randomly occur in the database, which implies that the matches are homologous.
Assessing the success of sequence similarity searches in detecting homology
To test whether HI can improve on standard SSSs in detecting homology we require a method of determining whether sequences are truly homologous to each other or not, i.e. we need a "gold standard". Most approaches to developing a "gold-standard" have been based on analysis of protein three-dimensional structure. The justification for this is that protein structure is better conserved than sequence, and so if two sequences have a closely related conformation, they are almost certainly homologous. Early applications of this idea used extensively studied hand-curated protein families or small example sets to measure the effectiveness of the SSS tested [7,12,16,19,21]. A more systematic approach was proposed by Park et al. [22]. This approach is based on using a subset of the Structural Classification of Protein (SCOP) database [23]. We adopt the Park approach.
Using this benchmark Park et al. [22] showed that the intermediate-sequence search method (ISS) outperforms FASTA. This work was later extended to compare single and multiple database pass SSS methods [24]. These results show that PSI-BLAST is among the best SSS methods, but it still misses ~50% of all homologies when using a rate of false positives of 1/1000.
ROC curves
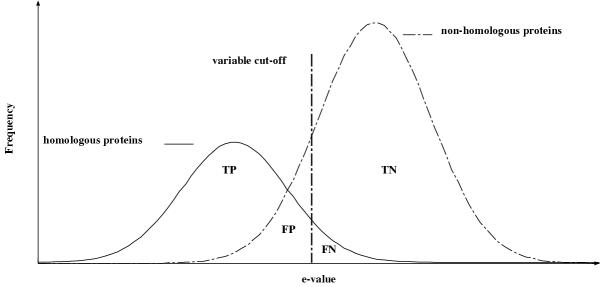
Ideally a SSS should identify all the homologous sequences to the target in the database and no other sequences (i.e. be complete and consistent). However in practice the SSS results may overlap with homologous sequences missed and/or non-homologous sequences identified as homologous. The problem is illustrated in Figure 1 where the two separate distributions overlap: the first distribution closer to the y-axis and with lower E-values represents the true homologous proteins; while the second distribution represents the non-homologous proteins. The dilemma is that for a high SSS cut-off value non-homologous sequences will be considered to be homologous; while for a low cut-off value homologous sequences will be considered not to be homologous.
Figure 1.
A graphical representation of two different distributions of a homology search. The first distribution represents homologous sequences found by the search; while the second distribution represents the non-homologous hits produced by the search. Depending on the cut-off value used, a part of the distribution is called true positives (TP) as they were predicted by the search to be homologous and are homologous; while a small part of the real homologous proteins is predicted to be non-homologous proteins. This part of the distribution is called false negatives (FN). The second distribution is split as well into two parts: the first part being the so-called false positives (FP), non-homologous proteins being predicted to be homologous. The second part of this distribution are non-homologous proteins predicted to be non-homologous. This part is called true negatives (TN). The cut-off value is indicated by a vertical line. It is clear that for any cut-off value, false positives will be included in a prediction.
Two separate types of error are possible when inferring homology: errors of commission, and errors of omission. In an error of commission a homology relationship is inferred when no such relationship truly exists: in an error of omission, a true homologous relationship is missed. The costs associated with these two types of error are not in general equal, and these costs will vary from application to application. For example, with conservative cut-offs the implicit assumption is that it costs more to miss-identify a sequence as homologous when it is not, than to miss a homologous sequence. It is therefore clear that using a fixed cut-off value together with a simple error rate is a crude measure for comparison of homology searches. A better measure is to use Receiver Operating Characteristic (ROC) curves. ROC curves were first developed for signal detection [25-28]. The main value of ROC curves in comparing homology detection approaches is that: if one prediction method produces a curve to the left of another method, then the method to the left is superior regardless of the particular costs associated with errors of commission and omission (assuming linearity of costs) [26,27,29]. ROC curves are produced by plotting the true positive rate (or sensitivity) against the false positive rate (1-specificity) for all possible cut-off values of a criterion value. Sensitivity is the probability that a sequence is predicted to be homologous when the protein is actually homologous. Specificity is the probability that a sequence is predicted to be non-homologous when the protein is actually non-homologous. Both measures are expressed as percentages. A ROC curve is produced by ordering the predictions by some sort of criterion value (typically some kind of confidence in a prediction), and then plotting the measures against each other. The true positive rate is plotted along the y-axis, while the false positive rate is plotted against the x-axis. As both measures are expressed as percentages, the range of both values is between 0 and 100%. This produces a square space ranging from 0 to 1 along the two axes, or unit-square. This space is called the ROC space. An ideal ROC curve, resulting from a perfect discrimination between homologous and non-homologous proteins, would be a line along the left-hand border of the ROC space, as it would not produce any false positives. In most applications this rarely occurs, instead, the ROC curve for a good prediction should always be to the left of the diagonal between the two axes. The closer the curve follows the left-hand border and the top border of the ROC curve, the more accurate are the predictions made. In general a ROC curve indicates the trade-off between sensitivity and specificity, as an increase in sensitivity is accompanied by an decrease of specificity. The ROC curve can be seen to summarise all possible sets of confusion matrices that result when the cut-off value of the criterion value is continuously varied from the smallest to the largest possible value.
To compare two different prediction methods, both ROC curves are plotted in the same ROC space. The curve running closer to the left and top border is considered to originate from the better prediction. A good measurement to compare ROC curves analysis is that of the area under the ROC curve (AUROC) [28,29]. The AUROC gives an overall measure of accuracy of a prediction. The best possible prediction would have an area of 1, while the worst would be 0.5, running along the diagonal. This can be used to make an overall comparison of two predictions. However, it is possible when comparing predictions using ROC curve analysis, that for certain trade-offs one prediction is better than the other one. Or, when comparing more than one prediction, that switching between multiple predictions will give the best trade-offs.
Information describing sequences
Sequence similarity searches are used for many bioinformatic purposes. Perhaps the two most important are: to predict the function of a newly sequenced gene based on homology to a protein of known function, and to predict the conformation of a protein based on homology to a protein of known conformation. The information available on the sequence will tend to be different under these two conditions. In the case of a newly sequenced gene, all that is likely to be known about the protein is its sequence. However, in cases where a structure is sought much more information may be known about the protein. We tested HI under both information poor and information rich circumstances.
Algorithm
The HI approach is based on the following steps:
1. Collection of possible homologous sequences using PSI-BLAST.
2. Accumulation of information on these homologous sequences;
3. The use of machine learning (ILP) to infer rules which are true for the sequences which are clearly homologous (training-set positive examples), and not true for sequences which are not homologous.
4. Application of these rules to a set of more remote homologues (the "twilight zone").
5. Comparison of the HI predictions with PSI-BLAST
Collecting possible homologous sequences
Our methodology for comparing SSS methods is based on the PDB40D database method first described by Park et al.[22], and subsequently used by Brenner et al.[30]. The PDB40D database is a subset of the Structural Classification of Protein (SCOP) database [23], consisting of all SCOP entries with 40 percent or less sequence similarity. We used version 37 with 1434 sequence entries; 4011 pairs are considered to be homologues. It was not possible to directly compare our results with those of Park et al.[22], or Brenner et al.[30] as the SCOP databases they used are not available from SCOP nor the authors of the papers.
We concatenated the PDB40D database with a large non-redundant database of primary sequence structures (specifically: Nr-Prot database 16.11.1998) from the National Center of Biotechnology Information. This concatenation was necessary to achieve the best possible starting results from the SSS. The Nr-Prot database is assembled daily by collecting protein sequences from multiple sources world-wide, and clustering together all sequences with 100 per cent sequence similarity.
We used PSI-BAST as our SSS method. It is state-of-the-art, very commonly used, and allows qualitative comparison with the results of Park et al.[24] and Brenner et al. [30]. However HI is not specific to PSI-BLAST and could be applied with other methods, e.g. FASTA [12], hidden Markov Models [13,14,21].
For each of the 1434 entries in the PDB40D database a PSI-BLAST run was performed to collect a set of possible homologous proteins. We used 10 as the E-value to report hits, 0.0005 as inclusion value for building up the profile, and allowed up twenty PSI-BLAST iterations – following Park et al.[24]. The rest of the PSI-BLAST parameters were left in their default values. As the PSI-BLAST profiles sometimes vary extremely from previous iterations, we allowed the good hits to be kept as results; hits occurring in a previous iteration as close homologous proteins, and not occurring in the final result, were assumed to be good hits. The cut-off value taken for these proteins was the E-value of 0.0001 [24]. The individual results of each run were parsed to extract all sequence hits having a SWISS-PROT entry, and split into a set of positive homologous proteins to learn from, and a set of uncertain proteins to test. A third set of random SWISS-PROT entries was generated for each test protein. The list with E-values of ≤ 0.0005 were considered positive examples. The list with E-values of (> 0.0005 and ≤ 10) were considered to be uncertain examples. Machine learning methods work most efficiently with positive and negative examples, as the negative examples stop the over generalisation of prediction rules [31]. To form these negative examples we randomly selected for each case 1000 SWISS-PROT entries that did not occur in either the positive or uncertain examples.
Data Accumulation and Data Preparation
For each example in the three different example sets information was collected from a database. This included all the translated SWISS-PROT annotation, as well as the frequency of singlets and pairs of residues and the proteins predicted secondary structure. This information was selected for relevance to the detection of homology. For each target sequence we collected:
1. Its amino acid distribution for singlets and pairs of residues, as used by the PROPSEARCH algorithm [32].
2. Directly from SWISS-PROT: the description, keywords, organism's classification, molecular weight, and database references (PROSITE, HSSP, EMBL, PIR – excluding SCOP classifications) from each sequence found by the SSS to be homologous to the target.
3. The predicted secondary structure – we used the DSC method [33] on single sequences (as a multiple sequence method would require a homology search).
4. The predicted cleavage sites from the SignalIP [34].
5. The total hydrophobic moment assuming secondary structure [33,35].
6. The length and starting point of local PSI-BLAST alignments.
A complete list of the predicates generated and their descriptions is in Additional File.
This information was taken from our local bioinformatics databases. These databases are formed with datalog [36]. The advantage of using datalog is that it allows easy incorporation of deduction and induction. The flexibility of such datalog bioinformatic databases is shown by essentially the same databases being used to predict the function of proteins [37-39].
Assembling all the information for each target into one large table would in principle be possible, but highly complex and inefficient. However, the assembly of such a table is required as the staring point for statistical, neural networks, or standard machine learning. This limitation of standard learning techniques is known as the "multi-table problem", i.e. learning from multi-relational data stored in multiple tables [40,41].
Machine Learning
The most natural solution to the multi-table problem is to use inductive logic programming (ILP) [42]. ILP is the form of machine learning that is based on first-order logic and is particularly suitable for problems where the data is structured, there is a large amount of background knowledge, and where the formation of comprehensible rules is desirable. We used the ILP system Aleph [43] version 2.75 which is based on inverse entailment. Aleph (and the related program Progol) have been successfully applied to a variety of problems in computational biology, such as learning rules to obtain Structure-Activity Relationships (SARs) [44], and protein topology prediction [45].
Aleph searches for rules (logic programs) which are true for positive examples and not true for the negative examples. In HI the positive examples are the sequences known to be homologous by use of the SSS, and the negative examples are 1000 random sequences that are not homologous. As the problem of remote homology detection is a real world application, one cannot omit the possibility of errors in the data. To accommodate this possibility, Aleph was set to accept learning rules with up to 15% noise. Furthermore, to avoid overfitting of the rules, a minimum of ten positive examples is required to allow to proceed to the induction step.
Aleph is in general versatile, bringing together the power of first order logic and the possibility of using background knowledge. However, it is not very suitable for use directly on numerical values, as Aleph searches the lattice for each single value for one attribute; the search using numerical values can be inefficient, depending on the number of distinctively different values. Possible solutions are to introduce operators, such as < and ≥ or to use discretisation. We choose to discretise all numerical values into 10 levels.
Application of the rules
After the rules were learnt they were applied to the uncertain examples. If the rule was true for an uncertain example, this was considered evidence, along with the weak sequence similarity towards identifying the example as homologous. We therefore used the rules to identify proteins which have uncertain evidence for homology based only on sequence, but have sufficient evidence based on sequence and the other information from our annotated deductive database. Following the induction step, initial results collected from PSI-BLAST are re-arranged according to the rules found by Aleph. This is done by modifying the original E-value reported by PSI-BLAST. The results covered by the rules found, are assigned with an lower E-value, while proteins not covered persist with the same value as before. This is done by multiplying the original E-value, received by PSI-BLAST, with a constant evidence factor (EF; with EF < 1). This approach is based on the assumption that if protein covered by a rule then this gives further evidence of homology. Hence, it should be moved further up the list of close homologous sequences found by PSI-BLAST. We call the resulting value EHI-value.
Comparing the HI predictions with PSI-BLAST
Following the methodology of Park et al. [24] we used the sub set of SCOP, the PDB40D database as our gold-standard:
• Every PDB40D entry found, sharing the same family or superfamily with the query entry was considered to be a true positive.
• Every entry found, sharing the same fold was considered to be of type uncertain.
• Every other entry was considered as a false positive.
We applied this testing procedure to the HI algorithm. However, there are certain technical bioinformatic technical limitations with testing using the PDB40D database. The database consists of PDB entries, while HI uses the SWISS-PROT annotation data to induce homologous relations. Therefore a database look-up table has to be constructed dealing with a mapping between SWISS-PROT accession numbers and PDB accession numbers. This could generally be done relatively easily, by parsing the SWISS-PROT database reference annotation to get an explicit pointer to the PDB database; or by parsing the PDB annotation for references to SWISS-PROT. However, this was not always possible: some PDB entries do not occur in SWISS-PROT; while some references in SWISS-PROT point towards a wrong PDB entry; and vice versa, the PDB annotation points to the wrong SWISS-PROT accession number. In the case of the PDB40D database used here, there were 10 unresolved relations between the PDB40D database and SWISS-PROT (given in the form [PDB accession, SCOP classification]: [1alla, 1.1.1.2.3], [1tnm, 2.1.1.4.5], [1wiu, 2.1.1.4.6], [1smva, 2.8.1.2.3], [2tpra1, 3.4.1.4.3], [2tpra2, 3.4.1.4.3], [1nzya, 3.8.1.1.1], [1leha1, 3.19.1.7.3], [1leha2, 3.54.1.1.3], [1idm, 3.57.1.1.1]).
Another source of uncertainty originates from the design of the PDB40D database and the use of a homology search method based on SWISS-PROT annotation. Assume a SWISS-PROT protein s1 with the PDB domain d1 and another protein s2 with domains d1' and d2, with d1 being in the same SCOP family as d1' (having a sequence similarity of over 40 per cent), and d1 and d2 being in the PDB40D database but not homologous. A PSI-BLAST search for d1 in the SWISS-PROT database should result in s1 and s2 being detected as homologous sequences based on the homology of d1 and d1'. However, as d1' is not in the PDB40D database the hit would be counted as a false positive as d1 and d2 are not homologous; while it genuinely has a homologous domain. In our analysis these cases were labeled uncertain and not counted as false or true positives.
Results
To illustrate that the HI approach is universal and can work equally well with data generated from sequence alone, two different settings were used:
• The first setting made use of all the available information – HIall.
• The second setting used information that can directly be computed from sequence, called HIseq.
The information used for the HIall setting, was taken from a datalog database containing annotated facts from SWISS-PROT [46] like keywords or descriptions, as well as information purely based on the amino acid sequences alone. The HIseq setting used all entries from the datalog database not originating from SWISS-PROT, except mol_weight and seq_length, as they can be calculated from the primary structure. This left 19 possible predicates to be used in learning (see Additional File of data types available).
For the HIall setting, HI induced rules for 1,015 PDB40D examples. The original PSI-BLAST results were used for the sequences where no rules could be induced. In total HIall produced 1851 rules for the 1,015 PDB40D entries. The most commonly used predicate of the single predicate rules was db_ref, utilized by 651 rules. These rules consisted mainly of references to PROSITE (639) [47] and some to the HSSP database [48]. This was expected as both databases cluster homologous families of proteins together.
For the HIseq setting HI induced rules for 949 PDB40D entries, and the original PSI-BLAST output was taken in cases where no rules could be learnt. The distribution of the number of the rules in the HIseq rule sets is quite different from HIall (Table 2). This reflects the lower expressive power of the information used in HIseq compared to HIall.
Table 2.
The distribution of number of rules learnt for different targets using HIall and HIseq. HIall can generally describe patterns using fewer rules. This is expected as it uses more background types of biological knowledge. Note the strange bimodal distribution for HIseq rules. The reason for this is unknown.
| Rule number | HIall | HIseq |
|---|---|---|
| 0 | 423 | 485 |
| 1 | 425 | 371 |
| 2 | 701 | 228 |
| 3 | 133 | 137 |
| 4 | 38 | 81 |
| 5 | 37 | 49 |
| 6 | 37 | 38 |
| 7 | 14 | 31 |
| 8 | 11 | 119 |
| 9 | 2 | 4 |
| 10 | 1 | 0 |
The distributions of the size and complexity of the rules found by HIall and HIseq are in Table 3 and Table 4.
Table 3.
The distribution of the size of the rules learnt, i.e. the number of predicates used in each rule in a rule set. The most common predicate used in the HIall setting with only one predicate was references to databases, followed by SWISS-PROT description arguments and keywords. The larger the number of predicates used in this setting, the more dominant becomes the use of predicates based on pure amino acid distributions and predicted secondary structure. In the HIseq setting a similar shift of use from predicates involving amino acid distributions towards predicted secondary structure predicates was observed. Rules with more than eight predicated are solely based on secondary structure.
| Number of predicates used in each rule | HIall | HIseq |
|---|---|---|
| 1 | 1030 | 169 |
| 2 | 369 | 940 |
| 3 | 314 | 810 |
| 4 | 121 | 340 |
| 5 | 14 | 86 |
| 6 | 1 | 18 |
| 7 | 1 | 6 |
| 8 | 1 | 1 |
| 9 | 0 | 1 |
Table 4.
The precision and recall for PSI-BLAST, HIall and HIseq.
| Method | Precision | Recall |
|---|---|---|
| PSI-BLAST | 0.34 | 0.717 |
| HIall | 0.32 | 0.787 |
| HIseq | 0.30 | 0.789 |
ROC analysis
The first method we investigated to compare PSI-BLAST and HI with PSI-BLAST was based on the concepts of precision and recall from information retrieval [49]. This comparison is more elementary than that of ROC curves. Precision is defined as follows: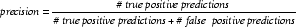
Recall is defined as follows:
Table 4 shows the precision and recall for PSI-BLAST, HIall and HIseq using a cut-off E-value of 10. The recall of both HI methods exceed the recall of PSI-BLAST alone. However, the precision decreases slightly with HIall and HIseq compared with PSI-BLAST, i.e. at the cut-off value HI identifies less homologous sequences than PSI-BLAST, but makes more right identifications, as expected. It is therefore unclear if the large gain in recall is worth the loss in precision. The answer to this question is determined by the relative cost of the errors of commission and omission.
The most common measure for comparing two prediction methods is to use accuracy. Accuracy is defined as follows: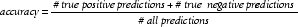
In the PDB40D database there are 8022 true homology relationships, and 2,046,900 false ones. This makes the measure of accuracy inappropriate, as the number of negative relationships compared to the number of positive relations is very large. The accuracy for PSI-BLAST is 99.68991%, for HIall it is 99.70072%, and for HIseq it is 99.69449%. Although both HI with PSI-BLAST accuracies are higher than PSI-BLAST alone, it is not clear at first sight if it is significantly higher. To test significance we performed a two-sample χ2 test to compare the actual frequency of a prediction with the estimated frequency of the prediction. The contingency table and the expected values for the test set in the "twilight zone" are shown in Table 5. χ2 is calculated as follows: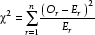
Table 5.
The contingency tables for χ2 comparing PSI-BLAST with HIall and HIseq in the twilight zone. The numbers in brackets are the expected values.
| PSI-BLAST | HIall | ||
|---|---|---|---|
| True Positives | 460 (512.68) | 312 (259.32) | 772 |
| False Positives | 574 (521.32) | 211 (263.68) | 785 |
| 1034 | 523 | 1557 | |
| PSI-BLAST | HIseq | ||
| True Positives | 460 (490.21) | 208 (177.79) | 668 |
| False Positives | 574 (543.79) | 167 (197.21) | 741 |
| 1034 | 375 | 1409 | |
Where Or is the observed value and Er is the expected value. For HIall theχ2 value is 45.35 and for HIseq is 47.85. Comparing these values with the critical χ2 values from a significance table, indicate that both methods are independent from each other. The critical value of χ2 for 1 degree of freedom and 99.995% confidence is 7.879, which indicates that HIseq and HIall are both significantly better than PSI-BLAST alone.
This test is based on one cut-off value (i.e. one set of costs). To test all linear costs we performed a ROC analysis. In this ROC analysis both HI set-ups (HIall and HIseq) were compared with PSI-BLAST (Figure 2). As described in the methods section, the HI results for the twilight examples are re-ordered according to their E-values. This is done by multiplying the original E-value, received by PSI-BLAST, with a constant evidence factor. To optimise this factor, the area under the ROC curve (AUROC) [28,29] was calculated systematically for different possible factors settings in order to choose the factor setting which minimizes the area. A variety of different factors was used, starting with 9 × 10-1, ending with 1 × 10-100. The initial step for changing a factor is 0.1, resulting in the AUROCs calculated for the factors 0.9, 0.8, 0.7, ..., 0.1. Then the factors were changed an order of magnitude to 0.09, 0.08, 0.07, ..., 0.01.
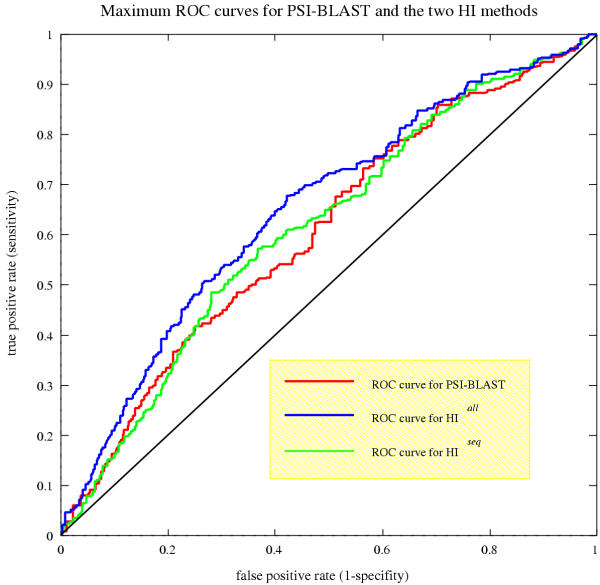
Figure 2.
The three ROC curves produced by PSI-BLAST, HIall, and HIseq for predictions in the twilight zone. While the ROC curve for PSI-BLAST results from applying ROC analysis directly to the results produced, the ROC curves for both HI methods are maximized using an optimal value for re-sorting. The ROC curve for HIall dominates over the other two curves at all times; while the curves for PSI-BLAST and HIseq oscillate around each other. HIseq dominates the PSI-BLAST curve between ~0.38 and ~0.5.
To find the optimal re-sorting factor f for both HI approaches, a k-fold cross-validation (with k = 5, 10, and 25) was performed on the set of uncertain examples in the twilight zone. The set of uncertain examples was therefore randomly split into k subsets. For each of the subsets Si, with I = 1,....,k the factor fi was calculated maximising the AUROC for the whole set of uncertain examples without Si. This factor fi was then applied to the subset Si and the AUROC calculated. The averages of these factors and the average AUROC for each of the k-fold cross-validations can be seen in table 6. This cross-validation was necessary as no independent test set was available.
Table 6.
The results of the k-fold cross-validation with the different areas inder ROC curve and the optimal parameters. The varations in the optimal factors are due to some factors fi being an order of magnitude higher than the rest of the factors.
| k | AUROC Hiall | factor f Hiall | AUROC Hiseq | factor f Hiseq |
|---|---|---|---|---|
| 5 | 0.6525 ± 0.059 | 9.6 × 10-5 ± 6.07 × 10-5 | 0.6135 ± 0.0589 | 6.0 × 10-2 ± 2.82 × 10-2 |
| 10 | 0.6728 ± 0.1085 | 7.8 × 10-5 ± 4.47 × 10-5 | 0.6391 ± 0.1022 | 7.5 × 10-2 ± 2.12 × 10-2 |
| 25 | 0.7342 ± 0.1234 | 6.6 × 10-5 ± 2.8 × 10-5 | 0.6951 ± 0.1029 | 7.56 × 10-2 ± 1.73 × 10-2 |
Figure 3 shows the different results from this analysis for the whole set of examples in the twilight zone. This is for illustration purposes only, as the optimal re-sorting factor was calculated using a k-fold cross validation. For HIall the AUROC peaked at 2 × 10-5 while for HIseq it peaked at 8 × 10-2. The AUROC value using the optimal factor from the 10-fold cross-validation for the whole set of uncertain examples the maximum AUROC value for HIall is 0.652892, and the maximum for HIseq is 0.613196. As expected the AUROC for HIall is greater than for HIseq as more information is used. The AUROC for PSI-BLAST is 0.608506, both HIall and HIseq have greater AUROCs indicating that they are better than PSI-BLAST alone at predicting homology. The ROC curve for PSI-BLAST along with the optimal ROC curves for HIall and HIseq are shown in Figure 2. The dominating curve is that of HIall, being to the left of the other two curves. The ROC curve of HIseq does not entirely dominate the PSI-BLAST ROC curve, and for large sections of the false positive axis, the two curves have a similar true positive rate. However for the false positive rate interval of 0.38 to 0.5 the ROC curve produced by HIseq does clearly dominate that of PSI-BLAST.
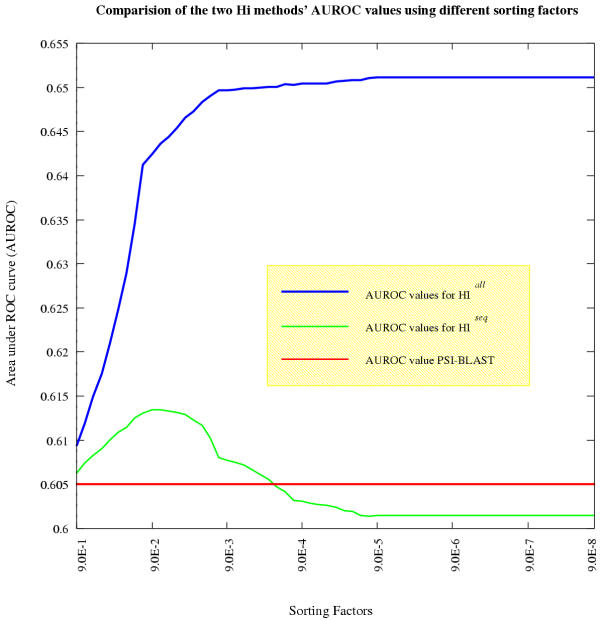
Figure 3.
This figure shows the calculated areas under ROC curve for both HI methods (HIall and HIseq) for a range of re-sorting factors. The AUROC values for HIall increases steadily and reaches its maximum value at 6 × 10-5 with a value of 0.651; while the AUROC values for HIseq first increases and then decreases again with a peak at 8 × 10-2 with an AUROC value of 0.613. Comparing both methods with PSI-BLAST shows that HIseq has a smaller improvement over PSI-BLAST which has an AUROC value of 0.607. HIall increases the AUROC value by approximately 7.4 per cent.
Analysis of typical HI rules
To illustrate the biological utility of the HI rules we have selected three examples for in-depth analysis: C-Phycocyanin (1CPC), Malonyl-Co-enzyme A Acyl Carrier Protein Transacylase (1MLA), Pepsin (1MPP), and Cyclodextrin Glycosyltransferase (1CDG) see Table 7.
Table 7.
Three selected examples of rules generated by HIall and HIseq. Where # rules is the total number of rules found, # pc is the number of positive examples covered in the training data, # pnc is the number of positive examples not covered in the training data, % CovP is the percentage coverage of the positive examples in the training data, % CovN is the percentage coverage of negative examples in the training data, # uc is the number of uncertain examples covered, and # unc the number of uncertain examples not covered.
| HIall | |||||||
|---|---|---|---|---|---|---|---|
| HIall | |||||||
| 1CPC | 2 | 120 | 0 | 100.00 | 1.00 | 1 | 2 |
| 1MPP | 1 | 91 | 1 | 98.91 | 0.00 | 2 | 13 |
| 1MLA | 1 | 17 | 5 | 77.27 | 0.00 | 4 | 13 |
| HIseq | |||||||
| PDB | # rules | # pc | # pnc | % CovP | % CovN | # uc | # unc |
| 1CPC | 2 | 89 | 31 | 74.17 | 1.20 | 1 | 2 |
| 1MPP | 3 | 62 | 30 | 67.39 | 1.20 | 3 | 12 |
| 1MLA | 1 | 16 | 6 | 72.73 | 0.20 | 5 | 12 |
Table 8 shows the rules learnt for C-Phycocyanin both in their original Prolog form and in English translation. Phycocyanins are light harvesting proteins. Applying PSI-BLAST to the data produced three proteins in the twilight zone: allophycocyanin alpha-b chain (Anabena), erythroid transcription factor (gata-1 Mus musculus), and oryzain gamma chain precursor (Oryza sativa). All the rules in the HIall and HIseq rule-sets correctly identified the allophycocyanin as homologous to 1CPC – there is convincing experimental evidence for this homology [50]. No rule in any rule-set identified the other two twilight sequences as homologous, and this would appear to be correct (no structures exist to be certain). Further evidence for the power of the HI rules is that the HI analysis was done on version 37.0 of SWISS-PROT, and each of the 13 positive examples not covered by this rule have had the keyword "phycobilisome" added to their annotation since version 38.0 of SWISS-PROT. It is particularly intriguing that the most characteristic feature of the amino-acid type rules is low histidine and trypotophan content, and that both amino-acids have nitro-cyclic aromatic rings. Phycocyanins have covalently linked bilin prosthetic groups which consist of linked nitro-cyclic aromatic rings. We hypothesise that evolution has selected for low histidine and trypotophan content in phycocyanins to reduce electron transport interference. The requirement for a high number of leucine-arginine pairs is also structurally significant as these arginines from salt-bridges with the prosthetic groups [51]. The structural rule s2 is also consistent with the known structure of phycocyanins which are well known to have an all α-helix globin like fold.
Table 8.
The HI rules learnt to identify 1CPC (C-Phycocyanin) are illustrated first in their original Prolog form and in English translation. Two sets of rules are shown those using HIall, and those learnt from HIseq. All numbers were discretised into 10 levels for ease of symbolic induction (1 low – 10 high).
| PDB 1CPC C-Phycocyanin | |
| HIall | |
| Prolog | |
| homologous(A) :- | |
| desc(A,chain), | |
| amino_acid_ratio_rule(A,h,1). | |
| homologous(A) :- | |
| keyword(A,phycobilisome). | |
| English | |
| A protein is homologous if | |
| a1 | it has the word 'chain' in its SWISS-PROT description line and |
| it has a level 1 histidine content in the residue chain and | |
| a2 | or it has the word 'phycobilisome' as a SWISS-PROT keyword. |
| HIseq | |
| Prolog | |
| homologous(A) :- | |
| amino_acid_ratio_rule(A,w,1), | |
| amino_acid_ratio_rule(A,h,1), | |
| amino_acid_pair_ratio_rule(A,l,r,10). | |
| homologous(A):- | |
| mol_wt_rule(A,3), | |
| sec_struc_distribution_rule(A,a,10). | |
| English | |
| A protein is homologous if | |
| s1 | it has a level 1 tryptophan content and |
| it has a level 1 histidine content and | |
| it has a level 10 leucine-arginine pair content. | |
| s2 | or |
| it has a level 3 molecular weight and | |
| it has a level 10 predicted α-helix content. | |
The rules for Malonyl-Co-enzyme A Acyl Carrier Protein Transacylase are shown in Table 9. The catalytic activity of the enzyme is: malonyl-coa + [acyl-carrier protein] = coa + malonyl-[acyl-carrier protein]. The HIall rule covers 4 out of a possible 17 test proteins in the twilight zone. All four are alpha subunits of fatty acid synthase (SWISS-PROT: FAS2_CANAL, FAS2_PENPA, FAS2_SCHPO, and FAS2_YEAST). Only one fatty acid synthase is not covered by this rule (SWISS-PROT: FAS_CAPHI); despite having the SWISS-PROT annotation of "synthase", it has only a sequence length of 35 residues – not long enough for the second part of the rule, and suspiciously small. The other proteins in the twilight zone are SWISS-PROT: ANP4_PSEAM, BRAB_PSEAE, CA16_MOUSE, CAPP_MYCLE, COBS_MYCTU, CYAA_STIAU, DCUP_MYCLE, HUR_STRAU, PUM_DROME, SRF1_BACSU, THL_BACSU, and XYLB_STRRU. The HIseq rule covers five test proteins in the twilight zone. The same fatty acid synthase subunits as HIall and a surfactin synthetase subunit 1 (SWISS-PROT: SRF1_BACSU). It would seem at least possible that SRF1_BACSU is related to the target 1MLA as their functions are somewhat related. Both rule-sets rely highly on predicted secondary structure. It is surprising how well the rules do considering how notoriously difficult it is to predict secondary structure. The rules concentrate on the C-terminal end of the predicted structure, but vary on the type of secondary structure they focus on. According to SCOP the catalytic domain of the enzyme has: "3 layers,α/β/α; core: parallelβ-sheet of 4 strands, order 2134".
Table 9.
The HI rules learnt to identify IMLA are shown in English translation. The secondary structure elements along the sequence are ordered into ten equal groups (deciles). The 1st decile are the 10% of elements near the N-teminal and the 10th decile at the C-terminal.
| PDB 1MLA Malonyl-Co-enzyme A Acyl Carrier Protein Transacylase | |
| HIall | |
| A protein is homologous if | |
| a1 | it has the word 'synthase' in its description line and |
| it is in the 10th decile of predicted secondary structures a coil of length level 4. | |
| HIseq | |
| A protein is homologous if | |
| s1 | it has in the 10th decile of predicted α-helices a helix of length level 3 and |
| it has in the 10th decile of predicted β-strands a strand of length level 1. | |
The rules for pepsin are shown in Table 10. Pepsin is an acid protease formed from the zymogen pepsinogen. The HIall rule uses the PROSITE pattern "PS00141" with the additional condition of the sequence coming from a eukaryotic species. The PROSITE pattern PS00141 is that for aspertate proteases, as expected. However, this pattern is designed for "Eukaryotic and viral aspartyl proteases active site(s)". Note that the HI rule is specific for eukaryotes. This is structurally significant as SCOP draws a distinction in the super-family "Acid Proteases" between the "Pepsin-like" family where all the structures crystallised so far have been eukaryotic (SCOP: duplication: consists of two similar barrel domains N-terminal: barrel, partly opened; n* = 6, S* = 10), and the "Retroviral protease family" (dimer of identical mono-domain chains, each containing (6,10) barrel). This distinction was automatically formed by HI. In the twilight zone the HIall rule correctly covers two proteins: SWISS-PROT: PEPC_PIG a pepsinogen [52] and SWISS-PROT: CHYM_FELCA a chymosin [53]. There were no other clear pepsinogens in the twilight zone. The HIseq rule-set is interesting in the selectivity of the three separate rules. For s1 nearly a third of the positives covered by the first rule are direct pepsin hits (with EC number 3.4.23.1), while the main group in the positives covered by s3 are acid/aspartic protease precursors. The second part of the rule does not seem to have any tendency towards any particular pepsin group. The emphasis in s1 on SER-SER and GLY-SER residue pairs is intriguing and may have something to do with low pH stability. The HIseq rule-set is not very effective in the twilight zone covering three example SAS2_YEAST (a SAS2 protein), YJ83_MYCTU (a hypothetical pe-pgrs family protein) and PDR5_YEAST (a possible ABC transport protein).
Table 10.
The HI rules learnt to identify 1MPP are shown in English translation.
| PDB 1MPP Pepsin (Renin). | |
| HIall | |
| A protein is homologous if | |
| a1 | it has the classification 'eukaryota' and |
| it has the PROSITE pattern 'PS00141'. | |
| HIseq | |
| A protein is homologous if | |
| s1 | it has it has a level 10 serine-serine pair content and |
| it has it has a level 10 glycine-serine pair content and | |
| it has in the 8th decile of predicted β-strands a strand of length level 9 | |
| or | |
| s2 | it has a molecular weight of level 7 and |
| it has in the 9th decile of predicted coils a coil of length level 1 | |
| or | |
| s3 | it has it has a level 2 histidine content and |
| it has in the 7th decile of predicted secondary structures a β-strand of lengthlevel 5 and | |
| it has in the 7th decile of predicted secondary structures a coil of lengthlevel 5 and | |
| it has in the 4th decile of predicted secondary structures a β-strand of length level 6. | |
Web server
To make the HI method generally available we have developed a web/email server http://www.aber.ac.uk/~phiwww/hi_V2/. To the best of our knowledge this is the first bioinformatics server providing an ILP service. The server is a simple HTML form, supplying the desired information to a CGI-Perl script. The user has the opportunity to select the parameters of the initial PSI-BLAST search, like inclusion E-value, maximum E-value to be reported, number of PSI-BLAST iterations, and if a low complexity sequence filter should be used. The user is also offered the possibility to select a different E-value to divide between positive examples and examples in the twilight zone. In the induction step, it is possible to select which descriptors to use in the induction, as well as ILP specific options, like the minimum number of positive examples required and the percentage of noise allowed.
Discussion
Many improvements are possible to HI. The existing sequence description is simply the percentage composition of singlets and pairs of residues. Although this is surprisingly effective it can clearly be improved. Avenues for improvement are to use wavelets [54] to describe the sequences, and the Santa Cruz approach [3]. Other sources of bioinformatic data and more biological background knowledge could be used, for example: comment lines from SWISS-PROT could be included (although this would require a more refined computational linguistic analysis); database links to Medline abstracts could be exploited, etc. In addition much of the data in the logical database is still propositional in form, and this does not allow us to fully exploit the power of ILP. More background knowledge could also be used to allow ILP to use: ≥ and ≤, numerical neighbourhoods, hierarchies of keywords, phylogenic trees, etc. The learning step in HI could be improved by using resampling approaches such as cross-validation [31] to get better estimates of the accuracy of rules. Data mining algorithms such as Warmr [55] could be used to pre-process the data to find frequent patterns which would make learning easier and more successful. Warmr can naturally include relational information such as sequence and could be use to find frequent sub-sequences that characterise sequences [55,56]. Multiple theories could be learnt and combined, e.g. using boosting and bagging [57,58]. Also different algorithms could be used and their predictions combined together [59]. We expect that these improvements would greatly improve the sensitivity of homology detection over the level achieved by HI.
HI provides a new approach to homology prediction. One of the most interesting results of Park et al.[24] was how relatively uncorrelated the errors were for the three different homology prediction methods examined. This means that better results could be obtained by combining prediction methods when inferring homology. Combining prediction methods with different biases is a standard method of improving prediction method accuracies [60].
The inference of homology based on sequence similarity is generally based on a threshold approach: homology is inferred if a sequence similarity search detects a match over a threshold probability; if the match is below this threshold, no matter by how little, no homology is inferred. This is a mistake. In decision theory this approach is equivalent to assigning a particular loss function to errors of commission and omission. Generally we wish to make the decision which minimises the expected loss, and this is achieved if:
The use of ROC curves allows us to show that one prediction method dominates others over all standard loss functions [29]. In this paper we have shown that HI with PSI-BLAST dominates PSI-BLAST alone. We recommend that in future work on homology prediction that ROC curves are adopted as the standard analysis method.
Conclusions
Within molecular biology there is an urgent need for new approaches to inferring protein homology. The results of Park et al.[24] show that ~50% of homologous relationships are currently identified by the best methods using standard cut-offs. HI is a first step in the application of machine learning to aid in the inference of homology by exploiting bioinformatic data other than that of local sequence. We have shown that HI is more sensitive than the state-of-the-art sequence method PSI-BLAST, and that HI performs better for all reasonable error costs. Comparison over different error costs is essential in comparison of homology prediction methods. Although our result only shows that HI is an improvement over PSI-BLAST, the basic approach of HI is applicable to all sequence based homology search methods.
Supplementary Material
Describes the title organims species declaration in one string
Contributor Information
Andreas Karwath, Email: adk@aber.ac.uk.
Ross D King, Email: rdk@aber.ac.uk.
Acknowledgments
Andreas Karwath and Ross D. King were supported by the EPSRC grant GR/L62849. We would like to thank Mohammed Ouali, Luc Dehaspe, and Steffen Schulze-Kremer for helpful discussions.
References
- Karwath A, King RD. In: Proceedings of the Eleventh International Conference on Inductive Logic Programming (ILP'01). Lecture Notes in A.I. 2157. C Rouveirol, M Sebag, editor. Sringer-Verlag, Heidelberg; 2001. An Automated ILP Server in the Field of Bioinformatics. pp. 91–103. [Google Scholar]
- Jaynes ET. Probability Theory: The Logic of Science. 1994. http://omega.albany.edu:8008/JaynesBook.html
- Jaakola T, Diekhans M, Haussler D. Using Fisher kernel method to detect remote protein homologies. ISMB'99; Proc. Int. Conf. on Intelligent Systems for Molecular Biology Cambridge, AAAI/MIT Press. 1999. pp. 149–158. [PubMed]
- Wright W, Scordis P, Attwood TK. BLAST PRINTS – alternative perspectives on sequence similarities. Bioinformatics. 1999;15:532–524. doi: 10.1093/bioinformatics/15.6.523. [DOI] [PubMed] [Google Scholar]
- MacCallum RM, Kelley LA, Sternberg MJE. Structure Assignment With Text Description – Enhanced detection of remote homologues with automated SWISS-PROT annotation comparison. Bioinformatics. 2000;16:125–129. doi: 10.1093/bioinformatics/16.2.125. [DOI] [PubMed] [Google Scholar]
- Chang JT, Raychaudhuri S, Altman RB. Including Biological Literature Improves Homology Search. Pacific Symposium on Biocomputing 6. 2001. pp. 374–383. [DOI] [PMC free article] [PubMed]
- Needleman SB, Wunsch CD. A general method applicable to the research for similarities in the amino acid sequences of two proteins. J. Mol. Biol., 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- Smith TF, Waterman MS. Identication of common molecular subsequences. J. Mol. Biol. 1981;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- Taylor WR. Identification of Protein Sequence Homology by Consensus Template Alignment. J. Mol. Biol. 1986;188:233–258. doi: 10.1016/0022-2836(86)90308-6. [DOI] [PubMed] [Google Scholar]
- Gribskov M, McLachlan AD, Eisenberg D. Profile Analysis: Detection of distantly related Proteins. Proc. Natl. Acad. Sci. USA. 1987;84:4355–4358. doi: 10.1073/pnas.84.13.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor WR. Dynamic Sequence Databank Searching with Templates and Multiple Alignments. J. Mol. Biol. 1998;280:375–406. doi: 10.1006/jmbi.1998.1853. [DOI] [PubMed] [Google Scholar]
- Pearson WR, Lipman DJ. Improved tools for biological sequence comparison. Proc. Natl. Acad. Sci. USA. 1988;85:2444–2448. doi: 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldi P, Chauvin Y, Hunkapiller T, McClure MA. Hidden Markov models of biological primary sequence information. Proc. Natl. Acad. Sci. USA. 1994;91:1059–1063. doi: 10.1073/pnas.91.3.1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogh A, Brown M, Mian IS, Sjölander K, Haussler D. Hidden Markov Models in Computational Biology. J. Mol. Biol. 1994;235:1501–1531. doi: 10.1006/jmbi.1994.1104. [DOI] [PubMed] [Google Scholar]
- Tatusov RL, Altschul SF, Koonin EV. Detection of conserved segments in proteins: Iterative scanning od sequence databases with alignment blocks. Proc. Natl. Acad. Sci. USA. 1994;91:12091–12095. doi: 10.1073/pnas.91.25.12091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gribskov M, Veretnik S. Identification of sequence pattern with profile analysis. Methods Enzymol. 1996;266:198–212. doi: 10.1016/S0076-6879(96)66015-7. [DOI] [PubMed] [Google Scholar]
- Hughey R, Krogh A. Hidden Markov Models for sequence analysis: extension and analysis of the basic method. CABIOS. 1996;12:95–107. doi: 10.1093/bioinformatics/12.2.95. [DOI] [PubMed] [Google Scholar]
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic Local Alignment Search Tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1006/jmbi.1990.9999. [DOI] [PubMed] [Google Scholar]
- Altschul SF, Madden TL, Schäffer A, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucl. Acid Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S, Henikoff JG. Amino acid substitution matrices. Adv. Protein Chem., 2000;54:73–97. doi: 10.1016/S0065-3233(00)54003-0. [DOI] [PubMed] [Google Scholar]
- Eddy S. Multiple alignment using hidden Markov models. Proc. Int. Conf. on Intelligent Systems for Molecular Biology Cambridge, AAAI/MIT Press. 1995. pp. 114–120. [PubMed]
- Park J, Teichmann SA, Hubbard T, Chotia C. Intermediate Sequences Increase the Detection of Homology Between Sequences. J. Mol. Biol. 1997;273:349–354. doi: 10.1006/jmbi.1997.1288. [DOI] [PubMed] [Google Scholar]
- Murzin AG, Brenner SE, Hubbard T, Chothia. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- Park J, Karplus K, Barrett C, Hughey R, Haussler D, Hubbard T, Chothia. Sequence Comparisons Using Multiple Sequences Detect Three Times as Many Remote Homologues as Pairwise Methods. J. Mol. Biol. 1998;284:1201–1210. doi: 10.1006/jmbi.1998.2221. [DOI] [PubMed] [Google Scholar]
- Van Trees HL. Detection, estimation, and modulation theory. New York, Wiley. 1971.
- Egan JP. Signal Detection Theory and ROC Analysis. New York, Academic Press. 1975.
- Swets J. Measuring the accuracy of diagnostic systems. Science, 1988;240:1285–1293. doi: 10.1126/science.3287615. [DOI] [PubMed] [Google Scholar]
- Bradley AP. The use of area under ROC curve in the evaluation of learning algorithms. Pattern Recognition. 1995;30:1145–1159. doi: 10.1016/S0031-3203(96)00142-2. [DOI] [Google Scholar]
- Provost F, Fawcett T. In: Proceedings of KDD-97. Heckerman D, Mannila H, Pregibon D, editor. AAAI Press, Menlo Park; 1997. Analysis and Visualization of Classifier Performance: Comparison under Imprecise Class and Cost Distributions. pp. 43–48. [Google Scholar]
- Brenner SE, Chothia C, Hubbard TJP. Assessing sequence comparison methods with reliable structurally identified distant evolutionary relationships. Proc. Natl. Acad. Sci. USA. 1998;95:6073–6078. doi: 10.1073/pnas.95.11.6073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell TM. Machine Learning. McGraw-Hill. 1997.
- Hobohm U, Sander C. A sequence property approach to searching protein database. J. Mol. Biol. 1995;251:390–399. doi: 10.1006/jmbi.1995.0442. [DOI] [PubMed] [Google Scholar]
- King RD, Sternberg MJE. Identification and application of concepts important for accurate and reliable protein secondary structure prediction. Protein Sci. 1996;5:2298–2310. doi: 10.1002/pro.5560051116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen H, Engelbrecht J, Brunack S, von Heijne G. Identification of prokaryotic and eukariotic signal peptides and prediction of their cleavage sites. Protein Engineering. 1997;10:1–6. doi: 10.1093/protein/10.1.1. [DOI] [PubMed] [Google Scholar]
- Eisenberg D. Three-dimensional Structure of Membrane and Surface Proteins. Ann. Rev. Biochem. 1984;53:595–623. doi: 10.1146/annurev.bi.53.070184.003115. [DOI] [PubMed] [Google Scholar]
- Ullman JD. Principles of database and knowledge-base systems, Vol 1. Rockville, MD, Computer Science Press, 1988.
- King RD, Karwath A, Clare A, Dehaspe L. In: The Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-2000) Ramakrishnan R, Stolfo S, Bayardo R, Parsa I, editor. New York, The Association for Computing Machinery.; 2000. Genome scale prediction of protein functional class from sequence using data mining. pp. 384–389. [Google Scholar]
- King RD, Karwath A, Clare A, Dehaspe L. Accurate prediction of protein functional class in the M. tuberculosis and E. coli genomes using data mining. Yeast (Comparative and Functional Genomics. 2000;17:283–293. doi: 10.1002/1097-0061(200012)17:4<283::AID-YEA52>3.0.CO;2-F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King RD, Karwath A, Clare A, Dehaspe L. The Utility of Different Representations of Protein Sequence for Predicting Functional Class. Bioinformatics, 2001;17:445–454. doi: 10.1093/bioinformatics/17.5.445. [DOI] [PubMed] [Google Scholar]
- Lavrac N, Dzeroski S. Inductive Logic Programming: Techniques and Applications. Ellis Horwood. 1994.
- Dzeroski S. In: Advances in Knowledge Discovery and Data Mining. UM Fayyad, G Piatetsky-Sharpiro, P Smyth, R Uthurusamy, editor. AAAI/MIT Press; 1996. Inductive Logic Programming and Knowledge Discovery. pp. 117–152. [Google Scholar]
- Muggleton S. Inductive logic programming. Proceedings of the First Conference on Algorithmic Learning Theory, Tokyo, Ohmsha. 1990.
- Muggleton S. Inverse Entailment and Progol. New Generation Computing Journal. 1995;13:245–286. [Google Scholar]
- King RD, Srinivasan A. The discovery of indicator variables for QSAR using inductive logic programming. Journal of Computer-Aided Molecular Design. 1997;11:571–580. doi: 10.1023/A:1007967728701. [DOI] [PubMed] [Google Scholar]
- Turcotte M, Muggleton S, Sternberg MJE. In: Proc. 8th International Conference on Inductive Logic Programming (ILP-98) CD Page, editor. Berlin, Spinger-Verlag; 1998. Application of Inductive Logic Programming to Discover Rules Governing the Three-Dimensional Topology of Protein Structure. pp. 53–64. [Google Scholar]
- Bairoch A, Apweiler R. The SWISS-PROT protein sequence database and its supplement TrEMBL in 2000. Nucl. Acid Res., 2000;28:45–48. doi: 10.1093/nar/28.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmann K, Bucher P, Falquet L, Bairoch A. The PROSITE database, its status in 1999. Nucleic Acids Res, 1999;27:215–219. doi: 10.1093/nar/27.1.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sander C, Schneider R. Database of homology derived protein structures and the structural meaning of sequence alignment. Proteins. 1991;9:56–68. doi: 10.1002/prot.340090107. [DOI] [PubMed] [Google Scholar]
- Raghavan V, Bollmann P, Jung GS. A critical investigation of recall and presicion as measuers of retrievel system performance. ACM Transactions of Information Systems. 1989;7:205–229. doi: 10.1145/65943.65945. [DOI] [Google Scholar]
- Ducret A, Sidler W, Wehrli E, Frank G, Zuber H. Isolation, characterization and electron microscopy analysis of a hemidiscoidal phycobilisome type from the cyanobacterium Anabaena sp. PCC 7120. Eur. J. Biochem., 1996;236:1010–24. doi: 10.1111/j.1432-1033.1996.01010.x. [DOI] [PubMed] [Google Scholar]
- Schirmer T, Bode W, Huber R. Refined three-dimensional structures of two cyanobacterial c-phycocyanins at 2.1 and 2.5 Å resolution. J. Mol. Biol. 1987;196:677–695. doi: 10.1016/0022-2836(87)90040-4. [DOI] [PubMed] [Google Scholar]
- Foltmann B, Drohse HB, Nielsen PK, James MNG. Separation of porcine pepsinogen A and progastricsin. Sequencing of the first 73 amino acid residues in progastricsin. Biochim. Biophys. Acta. 1992;1121:75–82. doi: 10.1016/0167-4838(92)90339-F. [DOI] [PubMed] [Google Scholar]
- Jensen T, Axelsen NH, Foltmann B. Isolation and partial characterization of prochymosin and chymosin from cat. Biochim. Biophys. 1982;705:249–256. doi: 10.1016/0167-4838(82)90185-6. [DOI] [PubMed] [Google Scholar]
- Mallat SG. A theory for multiresolution signal decomposition and wavelet representation. IEEE Trans. On Pattern Analysis and Machine Intelligence. 1989;11:674–693. doi: 10.1109/34.192463. [DOI] [Google Scholar]
- Dehaspe L, Toivonen H, King RD. In: The Fourth International Conference on Knowledge Discovery and Data Mining. Agrawal R, Stolorez P, Piatetsky G, editor. AAAI Press, Menlo Park; 1998. Finding frequent substructures in chemical compounds. pp. 30–36. [Google Scholar]
- Muggleton S, King RD, Sternberg MJE. Protein secondary structure prediction using logic. Protein Engineering. 1992;5:647–657. doi: 10.1093/protein/5.7.647. [DOI] [PubMed] [Google Scholar]
- Freud Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences. 1997;55:119–139. doi: 10.1006/jcss.1997.1504. [DOI] [Google Scholar]
- Breiman L. Bagging Predictors. Machine Learning. 1996;26:123–140. doi: 10.1023/A:1018054314350. [DOI] [Google Scholar]
- Tecuci G. Building Intelligent Agents: An Apprenticeship Multistrategy Learning Theory, Methodology, Tool and Case Studies. Academic Press. 1998.
- Dieterich TG. Machine learning research: Four current directions. AI Magazine. 1997;18:97–136. [Google Scholar]
- Karwath A, King RD. In: Proceedings of the Eleventh International Conference on Inductive Logic Programming (ILP'01). Lecture Notes in A.I. 2157. C Rouveirol, M Sebag, editor. Sringer-Verlag, Heidelberg; 2001. An Automated ILP Server in the Field of Bioinformatics. pp. 91–103. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Describes the title organims species declaration in one string