Abstract
Dynamic gravity field measurement based on the cold atom absolute gravity measurement system has important applications in geological exploration, gravity field mapping and other fields. The inertial stabilized platform is the key component of the dynamic cold atom absolute gravity measurement system, which can isolate the interference of carrier angle motion and keep the atomic gravimeter probe in the horizontal attitude during the measurement process. In this paper, according to the dynamic measurement requirements of atomic gravimeter, a high-precision two-axis inertial stabilized platform system is designed. The relationship between attitude angle and gravity measurement error is analyzed, and the stability of the system is enhanced by lead-lag method. Then the static vertical vibration power spectrum of the platform is measured to consider its influence on dynamic gravity measurement. Finally, a dynamic gravity test experiment was conducted in the Yellow Sea to verify the attitude control accuracy of the platform, and the attitude data of the platform under different heading were evaluated. The attitude standard deviation of the platform was better than 4 × 10−5 rad, and the absolute gravity standard deviation of the linear round-trip measurement reached 1.49 mGal. The experimental data show that the inertial stabilized platform can meet the dynamic measurement requirements of the cold atom gravimeter.
Keywords: Inertially stabilized platform, High precision horizontal attitude, Cold atomic gravimeter, Absolute gravity measurement
1. Introduction
At present, high precision ground gravity observation information, which can obtained from the gravimeter, is the basic data for studying the characteristics of the earth's internal structure, density and stress distribution [1,2]. The instruments used for gravity measurement are divided into two categories, relative gravimeters and absolute gravimeters [3]. The working principle and application of the two are different. The absolute gravimeter can directly measure the value of the acceleration of gravity where it is, which is the reference information of gravity, and then the relative gravimeter can be measured around, it can not directly measure the acceleration of gravity, it can only measure the difference between two points. However, the relative gravimeter often needs to be calibrated at the reference point because of the problems such as instrument drift, spring response and calibration factor change [4,5].
Absolute gravimeters have been developed in the last thirty years, it is mainly divided into two categories, optical absolute gravimeter [6] and cold atom absolute gravimeter [7]. The optical absolute gravimeter uses laser to measure the falling distance of the slider in the vacuum channel and then calculates the gravitational acceleration. The rapid development of atomic interferometer has been driven by laser-cooled atomic technology and matter-wave interference methods [8,9]. Nowadays, the measurement accuracy of cold atomic gravimeter(CAG) is the same as the optical absolute gravimeters [10]. Compared with the these, the volume of cold atom is very small, and the miniaturized vacuum measuring device is easy to achieve, while the mechanical transmission device of optical gravimeter is complex, which is not conducive to the development of dynamic absolute gravity measurement. The miniaturized and movable CAG has been taken out of the laboratory [[11], [12], [13]] and gradually applied in geophysics, space exploration, resource exploration and marine physical field mapping due to the integration of embedded control technology into the atomic gravimeter [[14], [15], [16]].
Since the acceleration of gravity itself is vertical downward, for both the absolute gravimeter and the relative gravimeter, it is necessary to maintain a horizontal attitude when measuring gravity, which can reduce the measurement error [[17], [18], [19]]. The researchers have carried out the relative gravity measurement combined the inertially stabilized platform and the relative gravimeter [[20], [21], [22]], such as the CHZ-II relative gravimeter combined with a strapdown stabilized platform to form a dynamic measurement system, the control accuracy of the platform is greater than 1.45 × 10−4 rad, but the device was unable to complete the long-distance and long-term gravity measurement tasks. Based on the advantages of absolute gravity measurement, dynamic absolute gravity measurement experiments on ship, vehicle and airborne have been carried out. The team of Bidel.Y has conduct several dynamic comparative experiments between the CAG and the relative gravimeter on shipborne and airborne from 2016 to 2022 [[23], [24], [25]]. In these experiments, the CAG has been fixed in a two-axis Inertially Stabilized Platform(ISP) in order to ensure that the axis of Raman optical coincides with the gravitational acceleration perpendicular, the result show a good agreement for the cold atom gravimeter with standard deviation and means on difference below or equal to 2 mGal, the attitude control accuracy of the platform is 0.1 × 10−3 rad. The team of Che also carried out a test using a CAG and a ISP on Qiandao Lake in 2022, the control accuracy of the roll is 0.08 × 10−3 rad, and the pitch is 0.03 × 10−3 rad [26].
Our team carried out a vehicle-mounted fixed-point absolute gravity experiment on the roadside of Xianlin Reservoir in Hangzhou, we used a three-axis leveling platform to control the tilt angle which is unsuitable for dynamic measurement [27]. Therefore, we have developed a set of ISP in order to further develop the dynamic experiment of CAG. Then, our team has formed a dynamic absolute gravity measurement system combining an ISP and a CAG, and gradually carried out moving experiments [28], mooring experiments [29], lake and ocean comparison experiments [30].
Inertially stabilized platform [[31], [32], [33]] are widely used in image tracking [34,35], attitude control [36,37] and so on. The main function of the ISP is to restrain the interference torque and isolate the carrier movement to ensure that the frame is always in the geographical horizontal plane. The structure of the platform is composed of the frame, motor, sensor and controller, and the system is divided into the correction loop and the stabilization loop. The correction loop can calculate the angle and angle velocity of the platform based on information from the accelerometer and gyro; the stabilization loop is used to restrain the interference torque and keep the platform attitude stable.
The CAG is larger and heavier than relative gravimeters. The vacuum probe for cold atom interferometry used in this paper is a cylinder with a diameter of 520 mm and a weight of 60 kg. To ensure the rigidity of the platform, the thickness of the platform frame and the rotational inertia must be excessive. Based on the practical needs of dynamic absolute gravimetry, this paper designs a highly precision ISP, analyzes how much the control accuracy of the platform that can meet the measurement requirements, introduces the frame structure and control system structure of the platform, assesses the impact of the platform on the sensitivity of the CAG, and analyzing the attitude data of the ISP from dynamic absolute gravimetry field experiments on the Yellow Sea.
2. Principle and structure
2.1. The principle of ISP
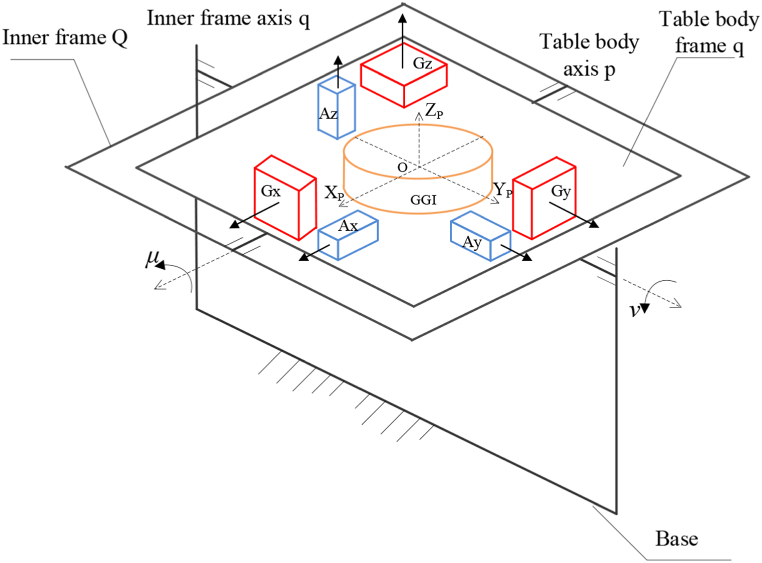
The two-axis stabilized platform actually causes the platform coordinate system (p coordinate system) to track the horizontal attitude angle of the geographic coordinate system (n coordinate system), so there is only the azimuth angle H between the p coordinate system and the n coordinate system, maintaining the geographic horizontal attitude, as shown in Fig. 1.
Fig. 1.
Schematic diagram of two-axis platform's principle.
Take the frame axis q as an example, when the carrier has an angular velocity v around the frame axis q direction, the corresponding Gy gyroscope is sensitive to the angular velocity information and sends the angular velocity increment to the stabilization control loop, which generates a torque signal of equal magnitude and opposite direction to the angular velocity to control the rotation of the torque motor of the axis, so as to keep the axis stable and isolate the influence of disturbance.
2.2. The attitude index of ISP
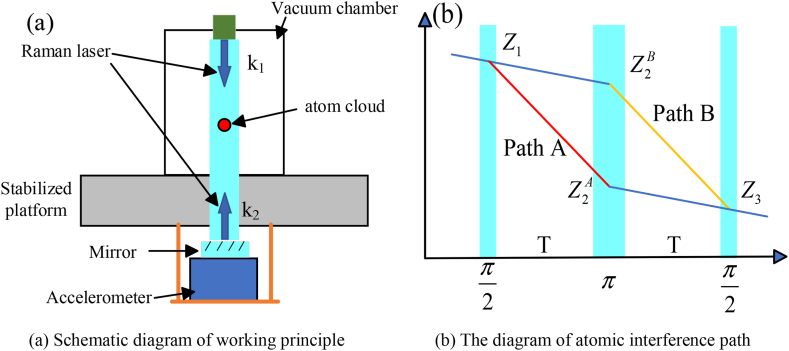
The CAG developed by our team is based on a Mach-Zehnder atomic interferometer [15]. The basic principle is that the cold atom cloud falls freely in the vacuum probe, and it splits, deflects and combines by three pulses of reversed Raman light, and finally realizes the interference of atomic matter waves, as shown in Fig. 2(a)(b).
Fig. 2.
The schematic diagram of absolute gravity measurement system.
The atom cloud after split by the Raman lights goes through two paths A and B respectively, and the total phase of the atomic interference is related to the trajectory of the two paths and the phase sum of the two beams of Raman light, the expression is shown in Formula (1),
| (1) |
z1, zA 2, zB 2, z3 is the position of the atom in the light field, Φ is the phase of light. The main gravity error of the measurement comes from changing of the total phase during the interference process, furthermore, the main reason of changing of the total phase is the vibration or rotation of the mirror which cause a change in phase of the reflected Raman light. From Fig. 2(a), the mirror is fixed on the accelerometer and also on the ISP frame, then the attitude change of the platform leads to the vibration and rotation of the mirror, so a change in the total phase is caused finally. Under the static conditions, the simple formula for calculating the tilt of an axis and gravity error is shown in Formula (2) [19],
| (2) |
in the formula: Δg is the measurement error, g is the acceleration of gravity and θ is the tilt angle. The way to decrease measurement error is to reduce the value of the attitude tilt, for example, if we want to keep it within 1 mGal, we can calculate the corresponding θ to be 1.4 × 10−3 rad. However, in the process of a dynamic measurement, due to the horizontal acceleration of the carrier and the tilt of the platform, there is relative motion between the cold atom cloud and the Raman light. So, at the same value of tilt, the gravity error which is show in Formula (3) [24] must be greater than the calculation result of Formula (2),
| (3) |
in the formula: ax, ay is the horizontal acceleration. If assumed that the horizontal acceleration is 0.01 m/s2, we also want to keep it within 1 mGal, then the value of θx and θy should be less than 0.5 × 10−3 rad. By the way, the process of atomic interference does not require the azimuth of the carrier, and the gravitational error caused by the rotation of the Earth can be calculated by the Coriolis effect.
In summary, in dynamic measurement environment for CAG, the carrier is subjected to random external disturbance torque and horizontal acceleration, according to the working principle of the atomic gravimeter, we need a two-axis ISP to isolate the disturbance and keep the tilt value small, so that higher accuracy can be obtained.
2.3. The structure of ISP
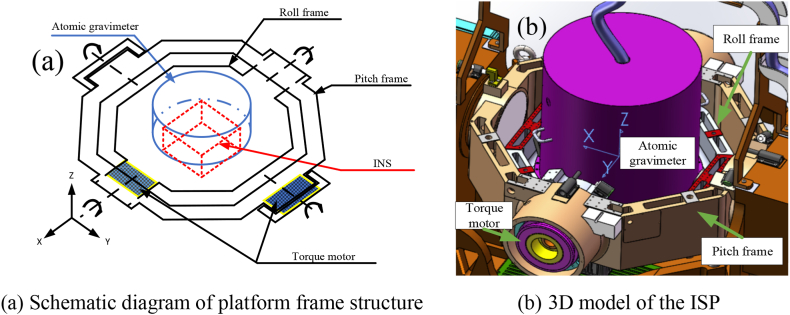
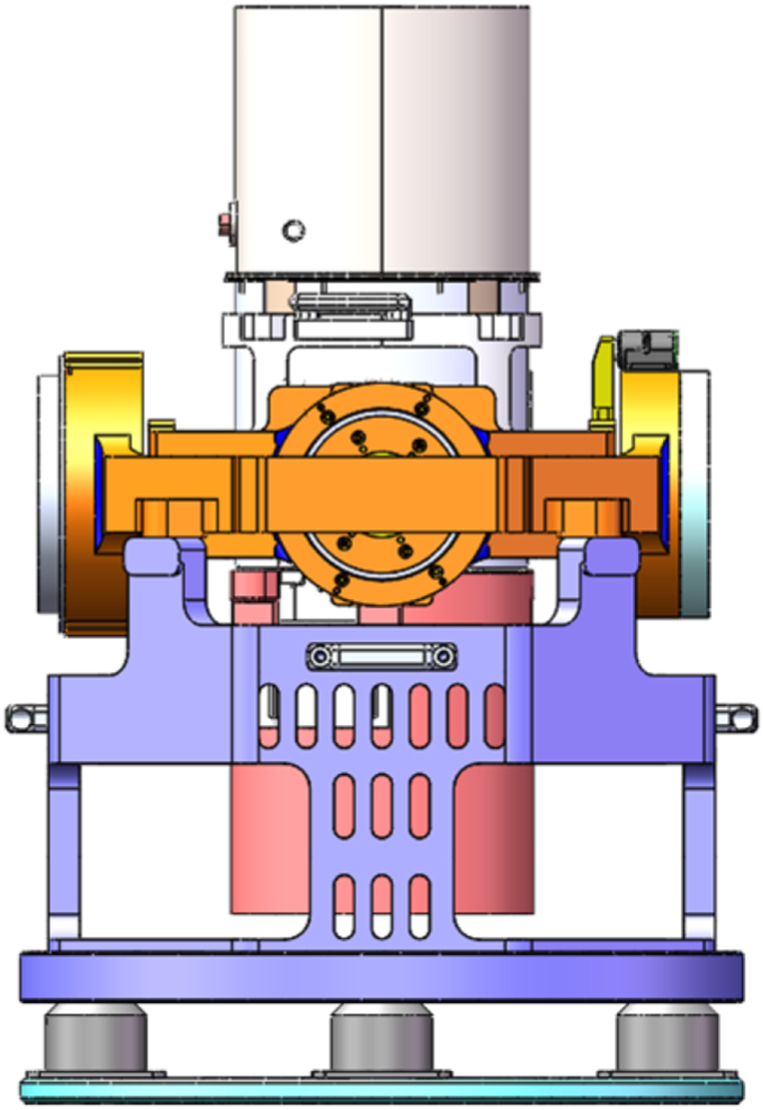
The structure of the platform is shown in Fig. 3(a)(b). As can be seen from Fig. 3(a), the ISP consists of an inertial navigation system (INS), a frame (roll and pitch) and motors. The two axis are vertically mounted and fixed at both ends, the cross section of the two frames is hollow hexagonal structure, with the characteristics of large moment of inertia and strong stiffness, and the material is cast aluminum alloy. The 3D model effect is shown in Fig. 3(b), so that the structure of the platform can be intuitively understood. The atomic gravimeter is fixed on the roll frame, the outside of the roll frame is the pitch frame, and the DC motor marked in the figure is fixed on the roll frame, however the pitch frame motor is not marked in Fig. 3(b) due to line of sight obstruction.
Fig. 3.
Structure diagram of inertially stabilized platform.
The cylinder is the vacuum probe of the cold atom gravimeter, which is installed in the center of the platform table.The INS is mounted below the vacuum probe and is used to calculate the relevant information of the platform frame in inertial space, including the local geo-level and the carrier of the acceleration, angle, and angular velocity. The measurement accuracy of INS determines the attitude control effect. The high precision F120HC interferometric fiber optic gyro is selected as the angular velocity sensor of INS, constant drift is , which produces a horizontal attitude error of 2.5 × 10−5 rad in undamped state. The quartz flexible accelerometer was selected as the accelerometer sensor of INS, zero bias is ≤ 0.02 mg, it also produces a horizontal attitude error of 2.0 × 10−5 rad in undamped state. In combination with GPS antenna and receiver, INS estimates and compensates the measurement error through Kalman filter to improve the navigation accuracy.
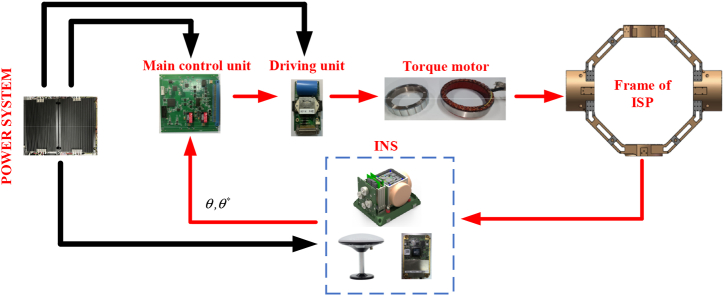
The control system of the ISP is mainly composed of power supply system, main control unit, drive unit, torque motor, frame and INS, as shown in Fig. 4. The main components of the main control unit include microcontroller chip STM32F429 of ST Company. The main control unit outputs analog signals to the drive unit, and the drive unit uses PWM amplifier to generate DC linear voltage to control the torque motor rotation. The DC torque motor in the frame can control the rotation of frame at a very low speed, and the motor is in a blocked state, so the locked-torque of motor is greater than the moment of inertia of the frame. The models of two motors are 180LYX50 and 250LYX45, the corresponding peak locked-rotor moment is 25 N m and 65 N m. The motor shape is hollow structure, easy to thread and install.
Fig. 4.
The schematic of platform attitude control system.
3. Control parameter design and simulation
3.1. Parameter design
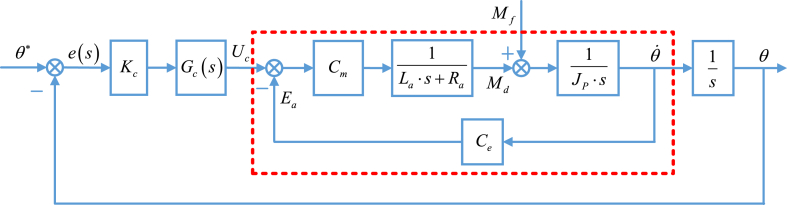
In order to realize the high precision attitude angle, the relevant parameters in the controller are designed and simulated. The block diagram of the torque motor control principle is shown in Fig. 5. In the figure, the equivalent control model of the DC motor is in the dotted box, Cm is the torque coefficient of the torque motor, Ce is the back-electromotive force coefficient of the torque motor, Ea is the back-electromotive force of armature, La is the armature inductance of armature, Ra is the armature resistance of armature, Jp is the total moment of inertia of the frame and the probe of gravimeter, Md is the output torque of the torque motor, Mf is the disturbance torque on the frame, θ is the attitude angle of the frame, ω is the angular velocity of the frame. Kc is the open-loop gain, Uc is voltage output of the controller, Gc(s) is the controller transfer function, θ∗ is the local geographic horizontal attitude angle from INS.
Fig. 5.
The equivalent control diagram of DC torque motor.
Firstly, we simplify the motor model. Assuming the external interference is 0, the transfer function between the output of the motor and the control voltage is Formula (4),
| (4) |
where, Tm is electrical time constant,Te is mechanical time constant. Then, assuming the control voltage is 0, the transfer function between the output of the motor and the interference torque is Formula (5),
| (5) |
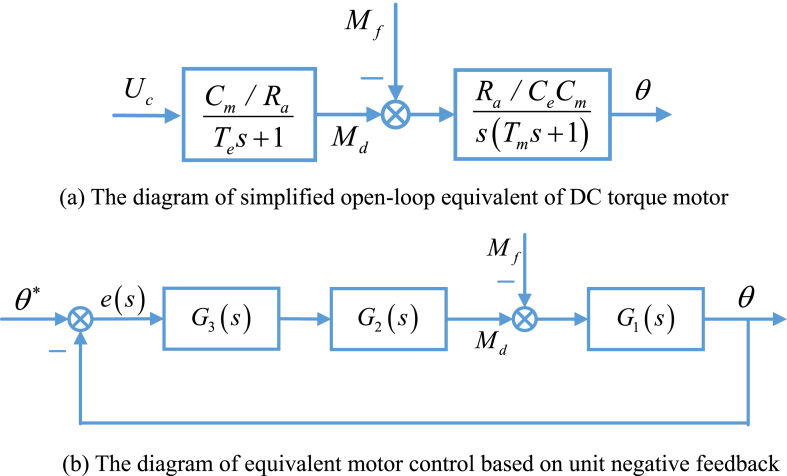
The simplified motor model is open-loop structure, which is shown as in Fig. 6(a). The control system is organized into a unit negative-feedback structure, which is shown as in Fig. 6(b), which combines the open-loop gain and the corrector transfer function.
Fig. 6.
The equivalent control diagram of DC torque motor.
The three transfer functions in the forward channel are shown in (6), (7), (8),
| (6) |
| (7) |
| (8) |
From Fig. 6(b), the input of the control system is the set angle and interference torque of the platform, the output is the actual angle of the platform. In order to effectively suppress the influence of interference torque and improve the accuracy of the following the set angle, we deduce closed-loop transfer functions of angle following and interference suppression respectively which is shown in (9), (10),
| (9) |
| (10) |
According to the final-value theorem in the principle of automatic control, the stiffness coefficient is defined as ks which is Formula (11),
| (11) |
Taking the roll frame as an example for analysis, according to the measurement requirements of the cold atomic gravimeter, the maximum disturbance torque is set at 3.92 N⋅m, and the angle variation range is at 4.85 × 10−5 rad, the value of ks is 8.1 × 104 N m rad−1, in addition, the Cm is 7.64 N m A−1 and Ra is 22.67Ω. Then the open-loop gain Kc is calculated to be 2.4503 × 105.
If the open-loop gain is used directly into the control system, the close-loop system is unstable. So we use traditional lead-lag correctors which is shown as Formula (12) to make the system stable.
| (12) |
3.2. Control system simulation
The simulation is used to verify that the parameters of the corrector can meet the stability requirements of the system, such as the open-loop bode diagram, the steady-state error of angle following, and the dynamic response of disturbance torque.
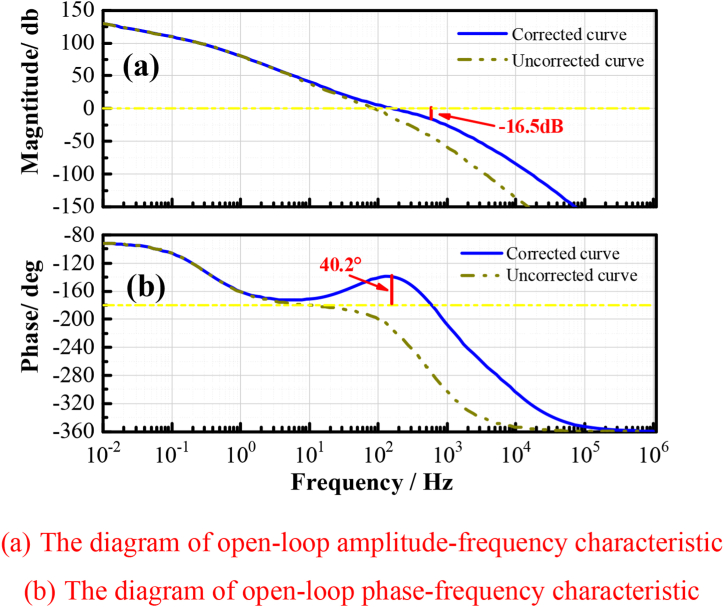
Taking the roll frame as an example. The calibrator parameters were chosen as a1 = 0.0015, a2 = 0, b1 = 0.00009, b2 = 0, La = 43.8 mH, Ce = 7.64V.(rad/s)−1 and JP = 7.5 kg m2. The amplitude-frequency and phase-frequency characteristics curves of the open-loop transfer function before and after correction is shown in Fig. 7(a)(b), the solid blue line is the curve after correction, and the dashed brown line is the curve before correction.
Fig. 7.
Comparison chart of open-loop frequency response curve of rolling frame system between before and after correction.
It can be seen that the system is unstable before correction, after correction the system has a phase angle margin of 40.2° in Fig. 7(b) and an amplitude margin of 16.5 dB in Figure(a), which meets the stability requirements.
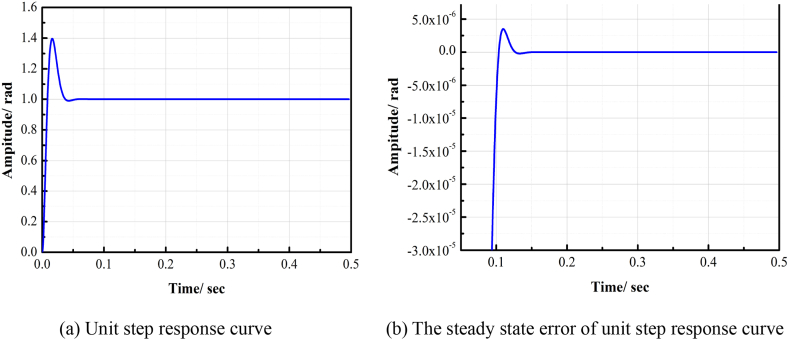
Then we analyze the steady-state error of the system. The motor parameters, calibration parameters, open-loop gain are brought into the close-loop transfer function such as Formula (9), the input is a unit step response, the response curve is shown in Fig. 8(a). It can be seen that the response curve has an overshoot of 40 % and a regulation time of 50 ms, the steady-state error curve is shown in Fig. 8(b).
Fig. 8.
The result of steady-state error simulation on unit step response.
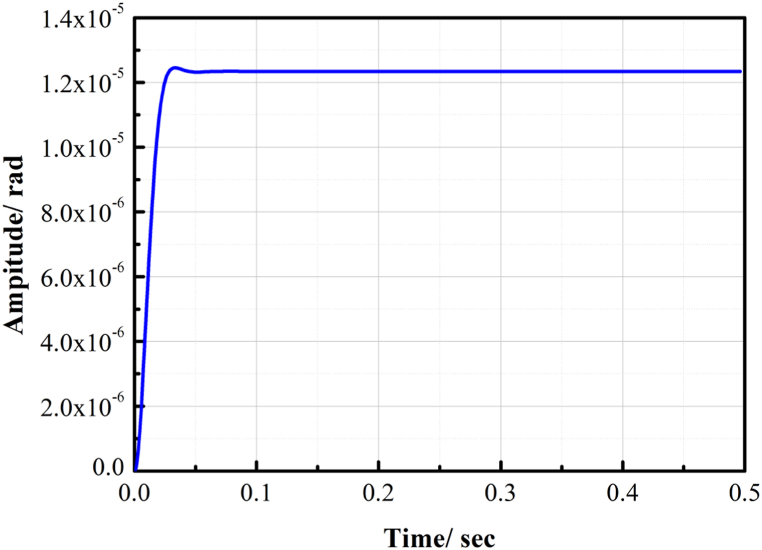
Finally, we analyze the dynamic response of interference torque, the parameters are also brought into the close-loop transfer function such as Formula (10). The input is a step signal of 3.92 N m, the response curve is shown in Fig. 9, with a regulation time of 30 ms and an attitude change amplitude of 1.23 × 10−5 rad.
Fig. 9.
Response curve of restraining disturbance torque of corrected system of rolling frame.
The simulation results show that the amount of overshoot is sacrificed to speed up the adjustment time, and the overshoot of the angle following is large. The stabilization loop is able to accurately follow the local geographical level solved by the correction loop, the curve of interference moment suppression is smooth, and the stabilization loop can effectively suppress the interference moment and keep the attitude stable to meet the measurement requirements of the atomic gravimeter.
4. Experiment
To investigate the working performance of the inertially stabilized platform, a set of dynamic absolute gravity measurement system was composed by the cold atomic gravimeter and the inertially stabilized platform, and the static vertical vibration performance of the platform was evaluated, and absolute gravity measurement experiments were carried out under ship mooring and under navigation in the Yellow Sea.
4.1. Vertical vibration test
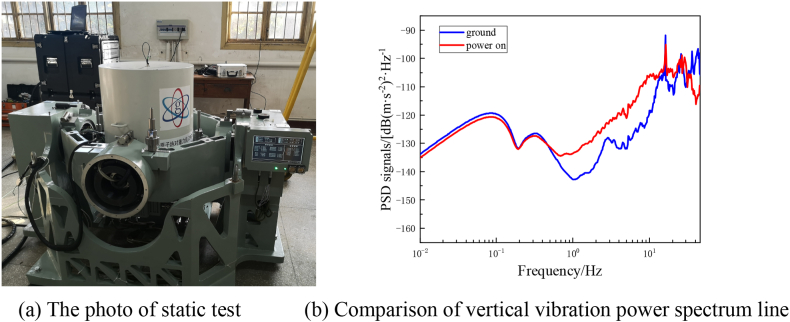
When the platform is in operation, the stabilization loop generates a small angular acceleration during the adjustment process, the projection of which in the vertical direction is equivalent to a vertical vibration. Consequently, the effect of operating the inertially stabilized platform on vertical vibration is first assessed, as shown in Fig. 10(a). In the experiment, the vacuum probe was rigidly connected to the inertial stabilization platform and then rested on the laboratory floor with shock absorbers during the night (when there was little human activity).The test instrument uses a seismometer (Güralp 3ESPC) as a vibration sensor with an effective bandwidth of 0.017–100Hz, a sensitivity of approximately 2000 Vm−1s−1 and a noise floor below NLNM (New Low Noise Model) [38]. Fig. 9(b) shows the test results.
Fig. 10.
Comparison experiment of vertical vibration test of platform.
The blue curve in Fig. 10(b) shows the vibration power spectrum at ground level, which mainly reflects the environmental vibration information at the measurement site, and the red power spectrum is the power spectrum when the platform is operating, which includes the vertical vibration information when the motor is operating. From the figure it can be seen that the vibration noise generated by the operation of the platform is mainly concentrated in the range 0.5Hz–20Hz. The sensitivity of atomic gravimetry is mainly limited by vibrational noise [39], which impacts the measurement sensitivity of atomic interferometry by affecting the stability of the Raman light phase. The transfer function of vibration noise can be expressed as Formula (13) [40]:
| (13) |
where ω is the angular frequency of the vibration and T is the Raman pulse interval.
Taking T = 55 ms,we can calculate the effect of environmental vibration on the gravimeter as 71.162 μGal/Hz1/2 and the effect of vibration on the gravimeter as 101.8327 μGal/Hz1/2 during regular operation of the platform.
4.2. Shipboard experiment
Our group conducted absolute gravity measurement experiments at Zhoushan under ship mooring conditions [29], and the results showed that the platform was able to meet the requirements for static absolute gravity measurements on board. Subsequently, absolute gravity measurement experiments were carried out in the Yellow Sea for long-distance ocean voyages, as shown in Fig. 11.
Fig. 11.
The photo of hoisting dynamic absolute gravimetry system.
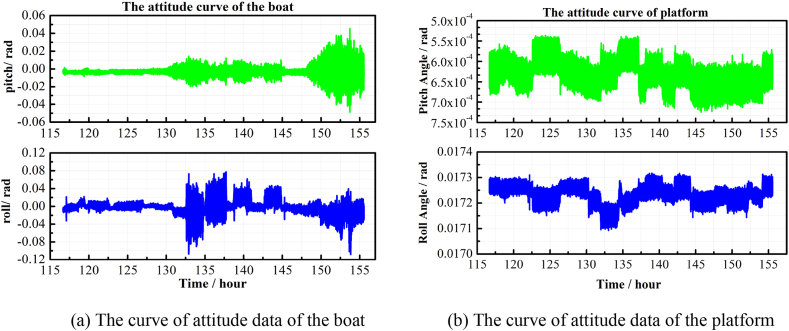
We selected one of the navigation data of 36 h to compare the attitude of the hull with that of the ISP, and the comparison curves are shown in Fig. 12(a)(b). Fig. 12(a) shows the pitch and roll attitude data of the hull, and the maximum peak-to-peak value of the attitude angle of the hull reaches 0.2 rad.
Fig. 12.
Comparison of attitude data from boat and platform.
The stability accuracy curve of the ISP is shown in Fig. 12(b) and the statistical results of mean and standard deviation are shown in Table 1. The standard deviation of both the pitch and roll is less than 4 × 10−5 rad, which meets the requirements of dynamic absolute gravity measurement for the angle of attitude. The reason for the non-zero mean value is the artificially set angle value to compensate for the installation error of the Raman light mirror.
Table 1.
Statistical results of platform attitude data during navigation.
| Platform attitude data | Roll angle/rad | Pitch angle/rad |
|---|---|---|
| Average | 0.017 | 6.32 × 10−4 |
| Standard deviation | 3.84 × 10−5 | 3.32 × 10−5 |
The platform attitude curve in Fig. 12(b) shows a step caused by a solution error in the INS during the course change. The standard deviation of the platform attitude when the research vessel is travelling in a straight line meets the measurement requirements of the Cold Atomic Gravimeter.
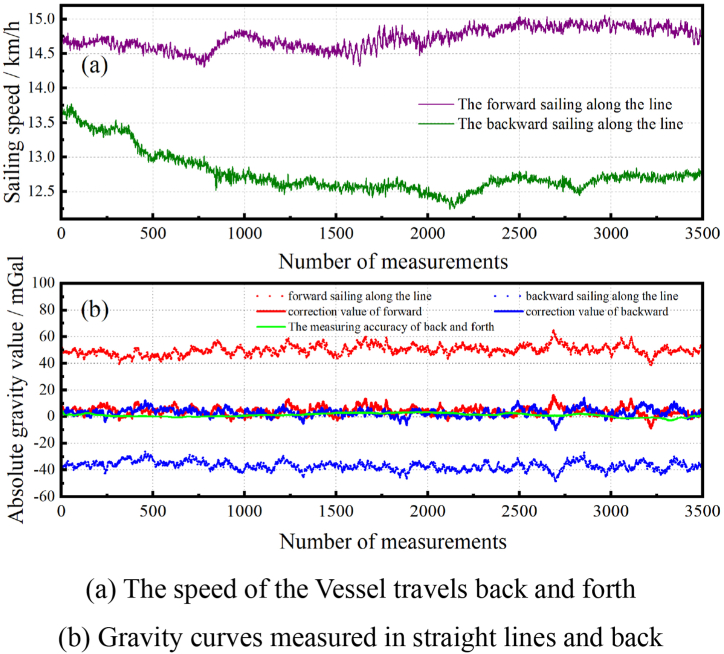
Then we select the absolute gravity measurement data obtained in one section of the straight round-trip route, subtract the absolute gravity value from the reference value 9.7934 m/s2, as shown in red dots and blue dots point in Fig. 13(b), where the speed of ship on round-trip sailing is shown in Fig. 13(a), and the curve of the two sets of absolute gravity data after the corrected Coriolis effect is shown in red line and blue line in Fig. 13(b). After filtering, the gravity value curve measured on this line is shown in green line in Fig. 13(b), and its standard deviation is 1.4 mGal. The results show that ISP provides a high-precision horizontal attitude for dynamic absolute gravity measurement.
Fig. 13.
The result of a straight round-trip measurement of gravity.
However, the current atomic gravimeter and inertially stabilized platform are too bulky and massive, making the process of transfer and assembly difficult. In the future, work will focus on developing a portable cold atomic gravimeter and a miniaturized inertially stabilized platform, reducing the size of the gravity probe, and combining the inertial navigation assembly with the gravity probe for attitude control, as shown in Figure (14).
Fig. 14.
Portable cold atomic absolute gravity measurement system.
5. Conclusion
Based on the measurement principle of cold atomic absolute gravimeter, this paper designs a high precision two-axis inertially stabilized platform for cold atomic absolute gravimeter and evaluates the stage vertical vibration noise. The effect of the vibration noise caused by the regular operation of the platform on the gravimetric measurement is 101.8327 μGal/Hz1/2. Subsequently, a Yellow Sea navigation cruise test was conducted and the cruise attitude data showed that the platform had an attitude standard deviation of ≤4 × 10−5 rad, and The standard deviation of the absolute gravity value of the linear round-trip measurement is 1.4 mGal, and the result achieves the expected goal of the dynamic measurement. The ISP is able to provide reliable attitude accuracy for dynamic absolute gravity measurements when the heading was held constant.
Data availability statement
The data that support the findings of this study are available from the corresponding author, Peng, upon reasonable request.
CRediT authorship contribution statement
Pei-jun Chen: Writing – review & editing, Writing – original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Min-rui Jiang: Writing – review & editing, Writing – original draft, Software, Resources, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Xiao-feng Lv: Writing – review & editing, Writing – original draft, Methodology. Hang Zhou: Methodology, Investigation. Di Yang: Investigation. Ying Zhou: Writing – review & editing, Resources, Project administration, Methodology. Zifan Jin: Investigation. Shu-ping Peng: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Shu-ping Peng reports financial support was provided by National Natural Science Foundation of China.
Footnotes
Funded by the National Natural Science Foundation of China (Grant No. 51905482).
References
- 1.Sofyan Y., Daud Y., Nishijima J., Fujimitsu Y., Kamah Y., Yani A., Fukuda Y., Taniguchi M. The first repeated absolute gravity measurement for geothermal monitoring in the Kamojang Geothermal Field, Indonesia. Geothermics. 2015;53:114–124. [Google Scholar]
- 2.Fukuda Y., Okuno J.i., Doi K., Lee C.-K. Gravity observations at Jang Bogo Station, Antarctica, and scale factor calibrations of different relative gravimeters. Polar Science. 2021;29 [Google Scholar]
- 3.Niebauer T. In: Treatise on Geophysics. second ed. Schubert G., editor. Elsevier; Oxford: 2015. Gravimetric methods -absolute and relative gravity meter: instruments concepts and implementation; pp. 37–57. [Google Scholar]
- 4.Yu H., Guo J., Li J., Mu D., Kong Q. Zero drift and solid Earth tide extracted from relative gravimetric data with principal component analysis. Geodesy and Geodynamics. 2015;6(2):143–150. [Google Scholar]
- 5.Fores B., Champollion C., Moigne N.L., Chery J. Impact of ambient temperature on spring-based relative gravimeter measurements. J. Geodesy. 2017;91(3):269–277. [Google Scholar]
- 6.Křen P., Pálinkáš V., Vaľko M., Mašika P. Improved measurement model for FG5/X gravimeters. Measurement. 2021;171 [Google Scholar]
- 7.Snadden M.J., McGuirk J.M., Bouyer P., Haritos K.G., Kasevich M.A. Measurement of the Earth's gravity gradient with an atom interferometer-based gravity gradiometer. Phys. Rev. Lett. 1998;81(5):971–974. [Google Scholar]
- 8.Keith D.W., Ekstrom C.R., Turchette Q.A., Pritchard D.E. An interferometer for atoms. Phys. Rev. Lett. 1991;66(21):2693–2696. doi: 10.1103/PhysRevLett.66.2693. [DOI] [PubMed] [Google Scholar]
- 9.Schwarz J.P., Robertson D.S., Niebauer T.M., Faller J.E. A free-fall determination of the Newtonian constant of gravity. Science. 1998;282(5397):2230–2234. doi: 10.1126/science.282.5397.2230. [DOI] [PubMed] [Google Scholar]
- 10.Merlet S., Bodart Q., Malossi N., Landragin A., Santos F.P.D., Gitlein O., Timmen L. Comparison between two mobile absolute gravimeters: optical versus atomic interferometers. Metrologia. 2010;47(4):L9. [Google Scholar]
- 11.Bongs K., Holynski M., Vovrosh J., Bouyer P., Condon G., Rasel E., Schubert C., Schleich W.P., Roura A. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nature Reviews Physics. 2019;1(12):731–739. [Google Scholar]
- 12.Fang B., Dutta I., Gillot P., Savoie D., Lautier J., Cheng B., Alzar C., Geiger R., Merlet S., Pereira dos Santos F., Landragin A. Metrology with atom interferometry: inertial sensors from laboratory to field applications. J. Phys. Conf. 2016:723. [Google Scholar]
- 13.Panda C.D., Tao M., Ceja M., Reynoso A., Müller H. Atomic gravimeter robust to environmental effects. Appl. Phys. Lett. 2023;123(6) [Google Scholar]
- 14.Malek B.S., Pagel Z., Wu X., Müller H. Embedded control system for mobile atom interferometers. Rev. Sci. Instrum. 2019;90(7) doi: 10.1063/1.5083981. [DOI] [PubMed] [Google Scholar]
- 15.Peters A., Chung K.Y., Chu S. High-precision gravity measurements using atom interferometry. Metrologia. 2001;38(1):25. [Google Scholar]
- 16.Menoret V., Vermeulen P., Le Moigne N., Bonvalot S., Bouyer P., Landragin A., Desruelle B. Gravity measurements below 10-9 g with a transportable absolute quantum gravimeter. Sci. Rep. 2018;8(1) doi: 10.1038/s41598-018-30608-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reudink R., Klees R., Francis O., Kusche J., Schlesinger R., Shabanloui A., Sneeuw N., Timmen L. High tilt susceptibility of the Scintrex CG-5 relative gravimeters. J. Geodesy. 2014;88(6):617–622. [Google Scholar]
- 18.Pyrchla K., Pająk M., Gołyga J., Pyrchla J. A model of the response of the MGS-6 gravity sensor to tilting. Measurement. 2022;188 [Google Scholar]
- 19.Wu B., Cheng B., Fu Z.-J., Zhu D., Zhou Y., Weng K.-X., Wang X.-L., Lin Q. Measurement of absolute gravity based on cold atom gravimeter at large tilt angle. Acta Phys. Sin. 2018;67(19) 190302-190302. [Google Scholar]
- 20.Glennie C., Schwarz K.P., Bruton A.M., Forsberg R., Olesen A.V., Keller K. A comparison of stable platform and strapdown airborne gravity. J. Geodesy. 2000;74:383–389. [Google Scholar]
- 21.Cai S.K., Tie J.B., Zhang K.D., Cao J.L., Wu M.P. Marine gravimetry using the strapdown gravimeter SGA-WZ. MARINE GEOPHYSICAL RESEARCH. 2017;38(4):325–340. [Google Scholar]
- 22.Wu P., Liu L., Wang L., Wang Y., Zhong M., Zhou Z., Zou Z. A gyro-stabilized platform leveling loop for marine gravimeter. Rev. Sci. Instrum. 2017;88 doi: 10.1063/1.4984824. [DOI] [PubMed] [Google Scholar]
- 23.Bidel Y., Zahzam N., Blanchard C., Bonnin A., Cadoret M., Bresson A., Rouxel D., Lequentrec-Lalancette M.F. Absolute marine gravimetry with matter-wave interferometry. Nat. Commun. 2018;9(1):627. doi: 10.1038/s41467-018-03040-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bidel Y., Zahzam N., Bresson A., Blanchard C., Cadoret M., Olesen A., Forsberg R. Absolute airborne gravimetry with a cold atom sensor. J. Geodesy. 2020:94. [Google Scholar]
- 25.Bidel Y., Zahzam N., Bresson A., Blanchard C., Bonnin A., Bernard J., Cadoret M., Jensen T.E., Forsberg R., Salaun C., Lucas S., Lequentrec-Lalancette M.F., Rouxel D., Gabalda G., Seoane L., Vu D.T., Bruinsma S., Bonvalot S. Airborne absolute gravimetry with a quantum sensor, comparison with classical technologies. J. Geophys. Res. Solid Earth. 2023;128(4) [Google Scholar]
- 26.Che H., Li A., Fang J., Ge G.-G., Gao W., Zhang Y., Liu C., Xu J.-N., Chang L.-B., Huang C.-F., Gong W.-B., Li D.-Y., Chen X., Qin F.-J. Ship-borne dynamic absolute gravity measurement based on cold atom gravimeter. Acta Phys. Sin. 2022;71(11) [Google Scholar]
- 27.Wu B., Zhou Y., Cheng B., Zhu D., Wang K.-N., Zhu X.-X., Chen P.-J., Weng K.-X., Yang Q.-H., Lin J.-H., Zhang K.-J., Wang H.-L., Lin Q. Static measurement of absolute gravity in truck based on atomic gravimeter. Acta Phys. Sin. 2020;69(6) [Google Scholar]
- 28.Cheng B., Chen P.-J., Zhou Y., Wang K.-N., Zhu D., Chu L., Weng K.-X., Wang H.-L., Peng S.-P., Wang X.-L., Wu B., Lin Q. Experiment on dynamic absolute gravity measurement based on cold atom gravimeter. Acta Phys. Sin. 2022;71(2) [Google Scholar]
- 29.Cheng B., Zhou Y., Chen P.-J., Zhang K.-J., Zhu D., Wang K.-N., Weng K.-X., Wang H.-L., Peng S.-P., Wang X.-L., Wu B., Lin Q. Absolute gravity measurement based on atomic gravimeter under mooring state of a ship. Acta Phys. Sin. 2021;70(4) [Google Scholar]
- 30.Zhou Y., Zhang C., Chen P.J., Cheng B., Zhu D., Wang K.A., Wang X.L., Wu B., Qiao Z.K., Lin Q., Li R. A testing method for shipborne atomic gravimeter based on the modulated Coriolis effect. SENSORS. 2023;23(2) doi: 10.3390/s23020881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.M M.K. Inertially stabilized platforms for optical imaging systems. IEEE Control Syst. Mag. 2008;28(1):47–64. [Google Scholar]
- 32.H J.M. Inertially stabilized platform technology Concepts and principles. IEEE Control Syst. Mag. 2008;28(1):26–46. [Google Scholar]
- 33.W H.G., Williams T.C. Strategic inertial navigation systems - high-accuracy inertially stabilized platforms for hostile environments. IEEE Control Syst. Mag. 2008;28(1):65–85. [Google Scholar]
- 34.Huynh T., Tran M.-T., Lee D.-H., Chakir S., Kim Y.-B. A study on vision-based backstepping control for a target tracking system. Actuators. 2021;10(5) [Google Scholar]
- 35.Guo J., Yuan C., Zhang X., Chen F. Vision-based target detection and tracking for a miniature pan-tilt inertially stabilized platform. Electronics. 2021;10(18) [Google Scholar]
- 36.Zhou X., Zhao B., Liu W., Yue H., Yu R., Zhao Y. A compound scheme on parameters identification and adaptive compensation of nonlinear friction disturbance for the aerial inertially stabilized platform. ISA Trans. 2017;67:293–305. doi: 10.1016/j.isatra.2017.01.003. [DOI] [PubMed] [Google Scholar]
- 37.Dong F., Lei X., Chou W. A dynamic model and control method for a two-Axis inertially stabilized platform. IEEE Trans. Ind. Electron. 2017;64(1):432–439. [Google Scholar]
- 38.Peterson J. u.s.geological survey open file report; 1993. Observations and Modeling of Seismic Background Noise. [Google Scholar]
- 39.Le Gouët J., Mehlstäubler T.E., Kim J., Merlet S., Clairon A., Landragin A., Pereira Dos Santos F. Limits to the sensitivity of a low noise compact atomic gravimeter. Appl. Phys. B. 2008;92(2):133–144. [Google Scholar]
- 40.Tino G.M., Rosi G., Sorrentino F., Cacciapuoti L., Prevedelli M. 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium. EFTF/IFC; 2013. Precision measurement of the gravitational constant with atom interferometry; pp. 593–598. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, Peng, upon reasonable request.