ABSTRACT
Background
Analyses of collective cell migration and orientation phenomena are needed to assess the behavior of multicellular clusters. While some tools to the authors’ knowledge none is capable to analyze collective migration, cellular orientation and proliferation in phase contrast images simultaneously.
Methods
We provide a tool based to analyze phase contrast images of dense cell layers. PIV is used to calculatevelocity fields, while the structure tensor provides cellular orientation. An artificial neural network is used to identify cell division events, allowing to correlate migratory and organizational phenomena with cell density.
Conclusion
The presented tool allows the simultaneous analysis of collective cell behavior from phase contrast images in terms of migration, (self-)organization and proliferation.
KEYWORDS: Cell migration, collective migration, image analysis, orientation, proliferation
Background
Self-organization and migration are important aspects for understanding fundamental processes such as embryogenesis, wound healing or tumor migration and metastasis [1]. Due to its more complex nature, including cell–cell interactions, cell-density and cell-alignment dependencies, collective cell behavior is less well understood than single-cell behavior. One reinforcing factor for the knowledge gap is the more complex data analysis needed to evaluate collective migration or cellular organization phenomena. As manual approaches are often insufficient for analyzing collective behavior, a multitude of additional approaches have been applied. Notably, these include methods to calculate local velocity fields, cellular organization and cell density.
For calculation of (local) migration speeds inside of dense cell layers mainly three approaches were used: 1) Determination from all single cells inside the layer, 2) determination via cross-correlation (particle image velocimetry, PIV) and 3) via optical flows. While all methods provide very good results, they are limited in their applicability. For example, the determination of individual cells needs a very good and reliable segmentation to minimize errors [2–4]. Consequently, this approach is only feasible if the contrast of cell-cell-junctions is high or if nuclei or cell membranes are fluorescently labeled to facilitate segmentation [2–4]. Usage of traditional optical flow algorithms is challenged by large displacements and tends to focus the movement on high gradient structures, while low-contrast regions are underrepresented [5]. Consequently, for reliable usage fluorescence labeling of e.g. cell membranes is necessary [6]. Another noteworthy point is the phototoxicity in fluorescently labeled cells. It may limit the observation time or temporal resolution due to photobleaching or even alter the measurement results by changes in cytoskeleton. PIV, on the other hand, has a broad general applicability to phase contrast images [7–16] but suffers from comparably high computation times [17] and smooths out high local velocities with spatial dimensions significantly lower than the template size used for pattern matching [18]. Furthermore, the spatial resolution of velocity fields is limited to the usage of (overlapping) templates. Due to its broad applicability and label-free usage, PIV was chosen here.
For the analysis of (local) cell orientation mainly two types of methods are used: segmentation-based [19–22] and gradient-based methods [23,24]. Segmentation-based approaches provide very good results if segmentation works well but have the same limitations, as discussed before. In contrast, gradient-based methods are prone to noise and thus need additional pre-processing [23]. Due to broader applicability, here a structure tensor-based approach combined with an additional de-noising step using the BM3D filter was used [23,25].
As cell migration often depends on (local) cell density [8,16,26,27] it is necessary to assess this parameter in parallel. Previous studies mostly relied on segmentation of labeled nuclei [4,28], cell membranes [6,29] or whole cells in phase contrast images [30], suffering from the same issues discussed above. Some more advanced algorithms relying on machine learning, pattern recognition and topological features also exist [31,32]. Notably, the segmentation and identification of single cells in phase contrast images become increasingly more complicated with rising cell density [10]. Nonetheless, for the presented work a cell-division detection algorithm based on pattern matching and an artificial neural network was developed to identify dividing cells in phase contrast images.
Taken together, here we present a tool-box allowing for the parallel determination of cell velocities, orientation and cell density changes in phase contrast images, allowing a broad applicability.
Materials and methods
Cell culture and experiments
U138 cells were purchased from the American Type Culture Collection (Manassas, VA, USA). The primary glioblastoma line #4 was isolated from a human brain tumor biopsy, as described previously [33]. The study was conducted in accordance with the Declaration of Helsinki and was approved by the local ethics committee of the University Halle-Wittenberg (project reference number: 2015–144). All patients provided signed written informed consent.
All cells were cultured in 89% (v/v) DMEM (Invitrogen, Carlsbad, CA, USA 41,965–062), supplemented with 10% (v/v) FBS (Gibco 10,500–064) and 1% (v/v) penicillin/streptomycin (Gibco 15,140–122).
For the analysis of collective migration 400,000 cells were seeded into 12-well plates and 24 h afterward transferred to an inverted microscope (DMi 8, Leica, Wetzlar, Germany) with temperature (37°C) and CO2 (5% (v/v)) control. Images were taken every 3 min for up to 60 h. All experiments were performed three times and five fields of view imaged per experiment and cell line.
Image analysis
The source code and software described here are available on GitHub, using the following link: https://github.com/Herodot1/CollectiveCellMigration. The provided toolbox was written using MatLab 2021a and a documentation for usage and detailed dependencies is provided with the link above. The provided framework uses the following external code or code snippets: PIVlab toolbox for calculating the local velocity fields [34], the BM3D filter for de-noising [25], the circular statistics toolbox [35], an external function for the display of error bars as shaded areas [36], the calculation of the structure tensor as implemented by Zhang et al. [23], and an external peak finding function [37]. The generation of velocity fields, orientation fields and cell division detection is parallelized, and computation times on an i7 single core for one image of resolution 1280 × 960 pixels are summarized in Table 1.
Table 1.
Computation times on a single i7 core for an image of size 1280 × 960 pixels.
| Step | Computation time [s] |
|---|---|
| De-noising (BM3D) | 6.9 |
| PIV (4x pass with 128x128, 64x64, 32x32, 32x32 window width) | 1.1 |
| Cell Division Detection | 1.2 |
| Orientation Analysis | 0.3 |
| Sum | 9.5 |
An outline of the image analysis pipeline is depicted in Figure 1. Prior to the image analysis images can be optionally de-noised using the BM3D filter, to remove small intracellular noise (Figure 2), improving the results of the PIV, orientation and cell division analysis. Albeit clearly visible, the effect of de-noising is relatively small (<3%, Fig S1A-E), except for the orientation analysis (up to 6%, Fig S1F) in a representative field of view.
Figure 1.
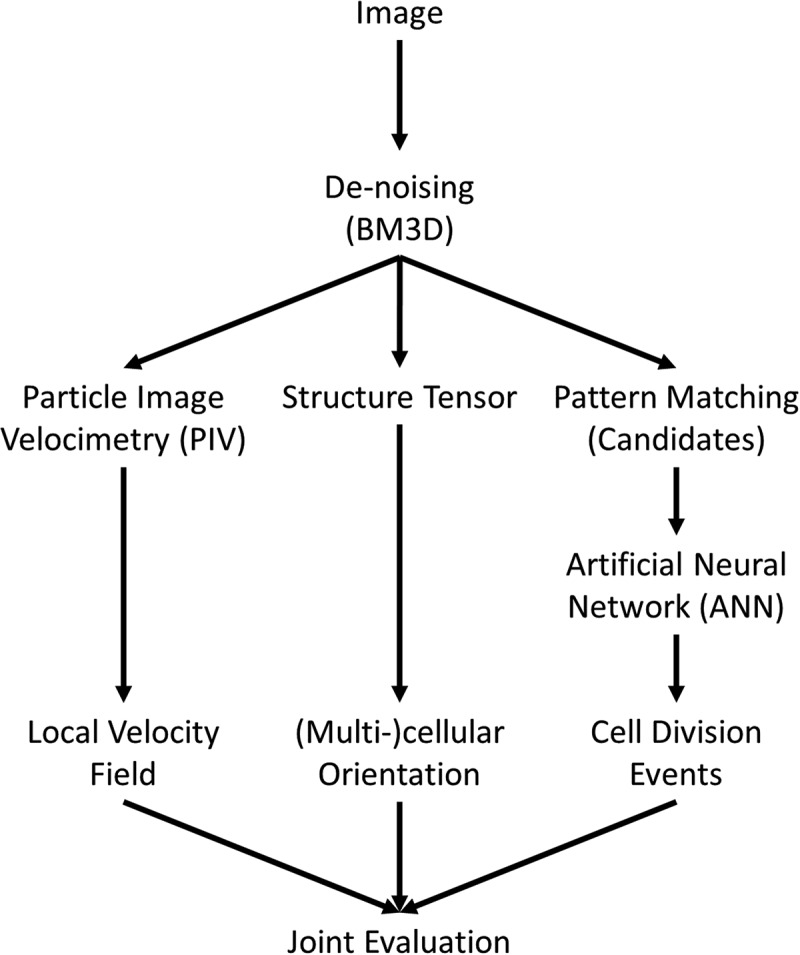
Scheme of image analysis. At first an optional de-noising of the image is performed. Afterwards local velocity fields are calculated using particle image velocimetry, a cross-correlation based pattern matching approach. Using the eigenvectors of the structure tensor an orientation map of the cell layer is generated and lastly cell divisions are identified using a combination of pattern matching and artificial neural networks. The data of local velocity, orientation, cell division events and cell density can be used for a joint analysis of all parameters and their interdependencies.
Figure 2.
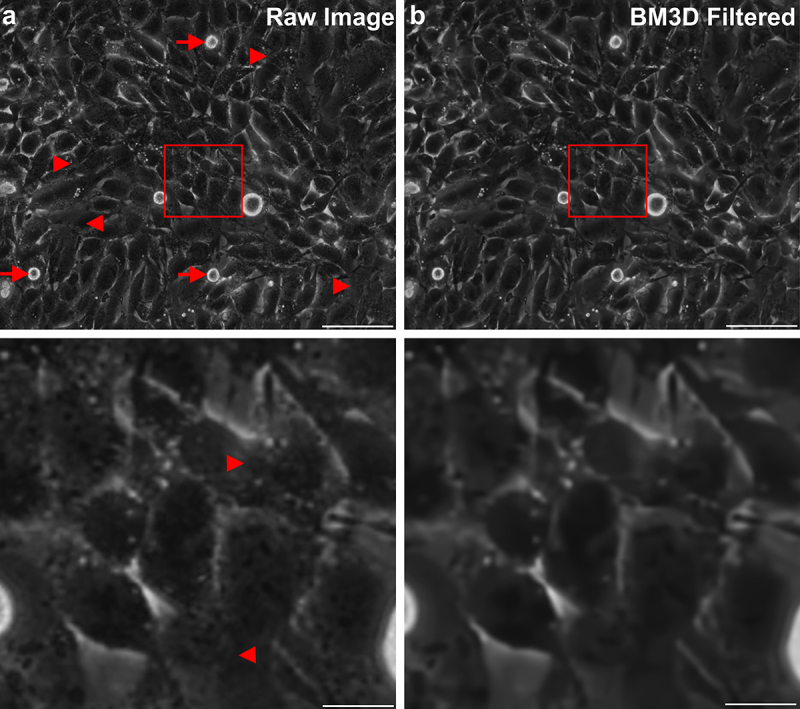
Effects of de-noising. a) typical unfiltered image of a dense layer of U138 glioblastoma cells. Arrows point to cell division events and arrowheads to regions of unclear cell-cell boundaries. The bottom image corresponds to an enlarged version of the marked region of the full size image. b) De-noised version of the image shown in a) and the respective magnification. Please denote the reduction of small intracellular structures and conservation of edges. Scale bars depict 100 µm (top row) or 20 µm (bottom row).
Analysis of local velocities
Particle image velocimetry (PIV) is used for calculating local velocities. The technique relies on cross-correlation based pattern matching in subsequent images. The implementation here is based on PIVlab and thus supports the same types of features for configuring the PIV calculation [34]. Of note, an optional PIV-based drift correction was implemented.
For subsequent analysis of the velocity fields, a calculation of the average instantaneous speed is implemented (Figure 3a, b). Furthermore, calculation of the self-overlap function Q(Δt) and 4-point susceptibility χ(Δt) were performed (Figure 3c, d) [14,38,39]. The self-overlap function is defined as follows:
Figure 3.
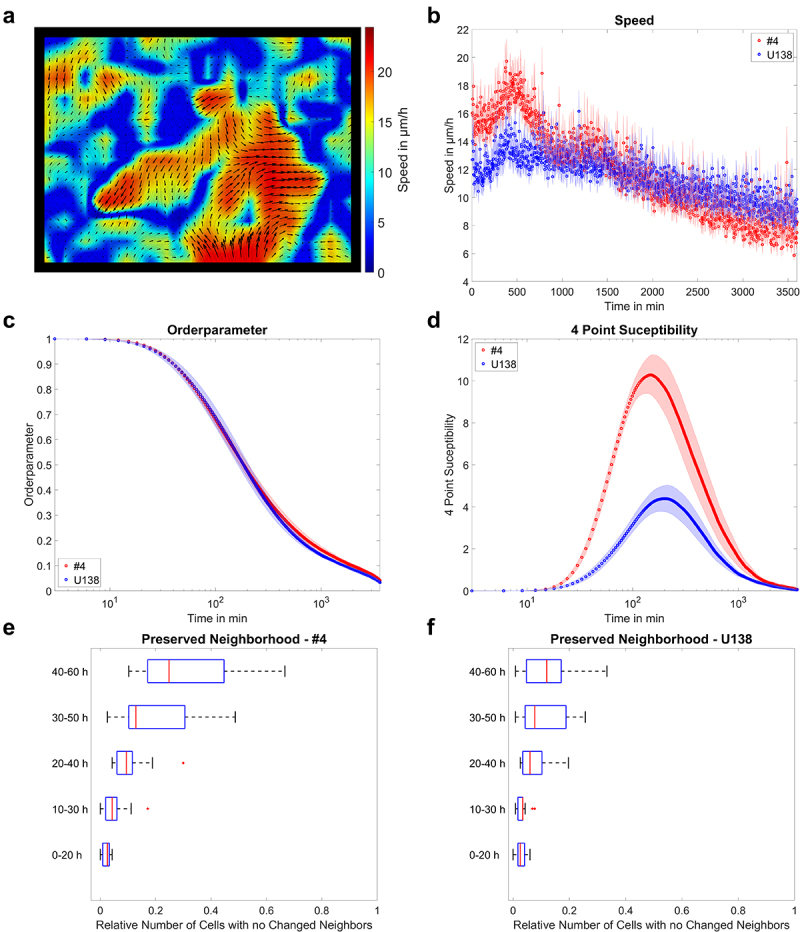
Example of migration analysis. a) velocity field of U138 cells, showing streaming motion. b) mean instantaneous layer speed for two glioblastoma cell lines as a function of time. c, d) mean order parameter and 4-point susceptibility as a function of time. Peak positions of the 4-point susceptibility correspond to the average life time of collectively moving groups of cells. Error bars and shaded areas depict the standard error of the mean. e, f) quantification of changes in monolayer reorganization for different time windows after start of the measurement for both glioblastoma cell lines. Box plots show the median (red line), 25 and 75%ile (box), non-outlier range (whiskers) and outliers (red dots). Line plots: mean ± SEM for n = 3 and a total of 15 fields of view.
Here, N defines the number of virtual particles and Δr the distance to the initial position of each cell and d the average cell diameter. Here, d = 80px (≈38.4 µm) was used, corresponding approximately to the cell diameter of both cell types. Q quantifies the proportion of virtual particles that moved away at least 20% of a cell size from the initial position. For the quantification of cooperativity, the 4-point susceptibility χ(Δt) was calculated:
The peak height of χ(Δt) is proportional to the number of cells moving collectively, and the peak position corresponds to the average lifetime of collectively moving cell packs [38,39] and both parameters are given as additional output in the toolbox.
In addition, neighborhood changes, based on Euclidean distance, can be calculated [7,15]. Therefore, virtual particles are placed on a mesh grid across the image and tracked over time. If a virtual particle had different neighbors at the end of the measurement the neighborhood was considered to be different (Figure 3e, f). High numbers of neighborhood exchanges correspond to strong reorganization of the monolayer.
Also, the mean squared displacement (MSD) and its scaling coefficient α(Δt), based on the following equation can be calculated:
With the generalized diffusion coefficient K. The scaling coefficient reveals information of the type of motion observed inside the monolayer, with sub-diffusive behavior for α < 1, diffusive behavior for α = 1 and super-diffuse behavior for α > 1.
Identification and tracking of cell division events
Before generation of candidates for cell division, the image contrast was enhanced using contrast limited adaptive histogram equalization (CLAHE), to adjust for changes in illumination relative to the used template. For the identification of cell division events 18 typical mitosis events per cell type were manually cropped out and used as template for pattern matching. Pattern matching was done using cross correlation of the input image and each of the individual templates. As individual cross-correlation maps were considerably noisy (Figure 4), the product of all individual cross-correlation maps was calculated and normalized to [0,1], leading to an improvement of the signal-to-noise ratio (Figure 4). Afterward, peaks were identified and used as candidates for an artificial neural network (ANN) using the GoogLeNet architecture [40], differentiating between true division events and false positive signals. The network was trained with annotated data of 22,851 candidates, consisting of 7783 cell divisions and 15,068 false positives. Notably, the ANN was trained on images of the glioblastoma cell line LN229 and #4 but not on images of U138.
Figure 4.
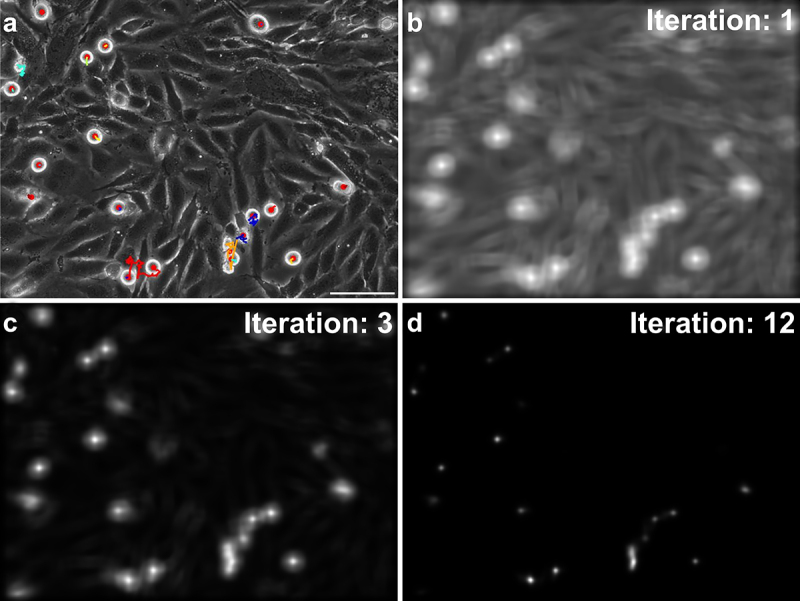
Identification of cell division events. a) image of an U138 cell monolayer, with marked division events (red dots) and associated tracks (colored lines). b) cross correlation map used for the identification of candidates for cell divisions fed into the neural network, when using only one template for matching. c, d) evolution of the cross correlation map when using 3 or 12 templates for matching. Denote the improved signal-to-noise ratio and sharper localization of potential divisions. The scale bar depicts 100 µm.
Application of the ANN yielded the final positions of individual cell divisions in each image. As a single division event may be present in multiple images, a track matching algorithm was employed to match detections to tracks. For detection to track assignment, the Munkres global nearest neighbor algorithm was used. The cost of assignment for a detection d to a track t was determined as the product of its Euclidean distance Δx(d,t) to the last detection assigned to track t and the number of images the respective track was invisible n:
If the assignment cost for a detection to all existing tracks was too high, a new track was created. If a track was unassigned for too long (here: n > 25 images) no detection was assigned to the respective track. Using this approach allowed to reliably identify cell division events and track them in space and time.
The spatial and temporal information of cell divisions allowed to characterize changes in cell density during the measurement and its impact on other measurement parameters, such as the local velocity field or cellular organization (Figures 5, 6).
Figure 5.
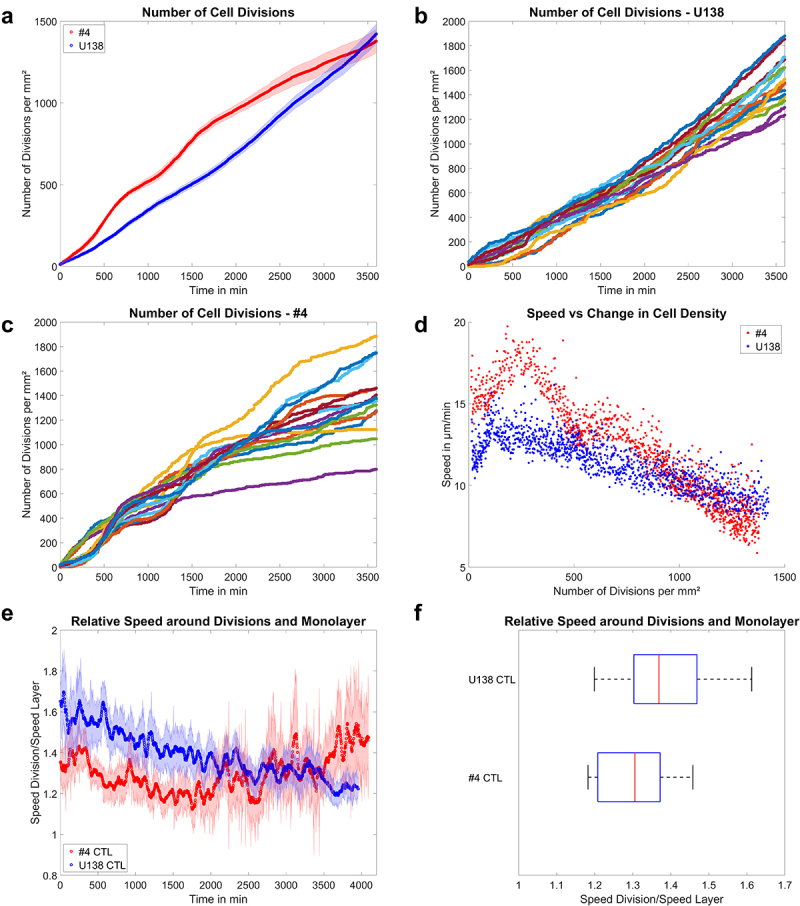
Applications of the cell division detection a) mean number of cell divisions tracked over 60 h for U138 and GBM #4. Shaded areas depict the standard error of the mean. b, c) division events observed in individual fields of view for U138 and GBM #4. d) plot of the mean instantaneous layer speed as a function of the mean change in cell density for both GBM lines. e) mean ratio of the instantaneous speed of the monolayer around divisions to the rest of the layer as a function of time. Shaded areas depict the standard error of the mean. f) time averaged ratio of the speed of the monolayer around divisions to the rest of the layer. Box plots show the median (red line), 25 and 75%ile (box), non-outlier range (whiskers) and outliers (red dots). Line plots: mean ± SEM for n = 3 and a total of 15 fields of view.
Figure 6.
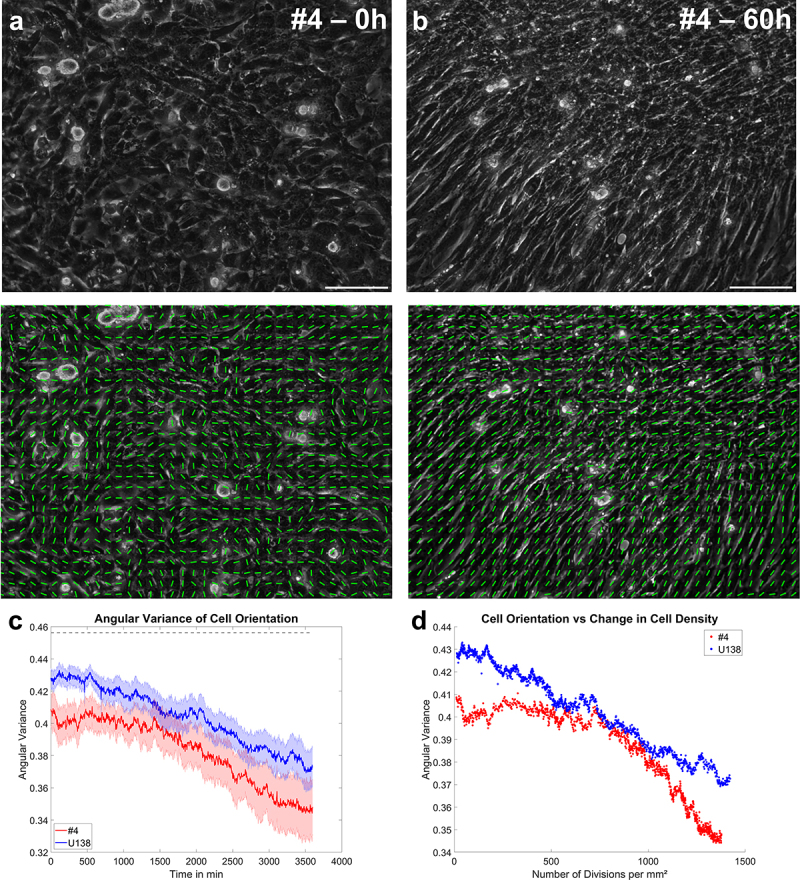
Application of the orientation analysis. a, b) typical images of GBM #4 at the beginning and end of a measurement, together with the overlaid local cellular orientation. The scale bar depicts 100 µm. c) mean angular variation of the cell orientation as a function of time. The dotted line shows the expected value for a random distribution of angles from 0 to π/2. Error bars and shaded areas depict the standard error of the mean. d) scatter plot of the mean angular variation of cell orientation as a function the mean change in cell density. Line plots: mean ± SEM for n = 3 and a total of 15 fields of view.
Analysis of local cellular orientation
For the analysis of local orientation, the orientation of the largest eigenvector of the structure tensor J of the image I was used. The structure tensor J was defined as [23]
with the Gaussian window function w. As the given system does not necessarily have a defined favored direction, the angular variance for each eigenvector in an image with direction θ was calculated. It is defined as:
The angular variance is bound to values of zero (no variance) to (maximal variance). A combination of the calculation of angular variance and change in cell density is also implemented.
Results
To illustrate the capabilities of the presented approach, measurements of two different glioblastoma cell lines over the time course of 60 h were performed. For the experiments, the well-established cell line U138 and a primary GBM line called #4 were used. Inside the monolayer GBM cells are expected to be motile, showing significant amounts of layer reorganization and proliferation throughout the whole duration of experiments.
Different glioblastoma cells show distinct migratory patterns
Analysis of the velocity fields of U138 and #4 cells revealed regions of high and low velocities, with some high-velocity regions showing anti-parallel movement (Figure 3a). Analysis of the instantaneous speed revealed that the monolayer of both cell lines had mean velocities of ≈ 12 or 16 µm/h initially, decreasing to ≈ 10 or 8 µm/h over time (Figure 3b). Next, the order parameter was evaluated to analyze if cells were stationary inside the layer (Figure 3c). Both cell lines showed significant layer-movements on a timescale of ≈150 min. Based on the order parameter the 4-point-susceptibility was calculated (Figure 4d) to assess characteristic reorganization times (peak position) and estimate the number of cells moving collectively (proportional to peak height). Both cell lines showed similar characteristic times of 153 or 204 min, respectively, thus showing marked reorganization during the measurement time. Notably, calculating the number of cells moving as a collective pack revealed U138 moved in groups of 11 cells, while #4 cells moved in packs of 28 cells, showing more coordination. Lastly, it was analyzed how well the neighborhood of individual cells was preserved over time. Thereby, #4 cells tended to undergo less reorganization (Figure 3e), while the same phenomenon was less pronounced in U138 (Figure 3f).
Glioblastoma cell lines show different proliferative behavior
Next, the presented approach for detection of cell divisions was tested and applied. Testing was performed on an independent candidate set obtained from LN229 and #4 cells, containing 928 events, of which 227 were divisions. The training and testing of the used model gave a validation accuracy of 92.2%, with most of the errors occurring due to false negatives. The given accuracy likely underestimated the capabilities of detecting divisions in the given setup, because division events were present for multiple successive images and thus were more likely to be detected. The idea was supported by manual inspection of the resulting detections in U138 cells showing a high recall of division events, with only very low numbers of false positive detections, albeit U138 cells were not part of the training data (Vid S1). Consequently, the change in cell density over time was analyzed for both cell lines, either averaged over all experiments and fields of view (Figure 5a) or individually for each field of view (Figure 5b, c). In line with visual inspection of the images, #4 cells showed initially faster proliferation than U138 cells, but eventually proliferation in #4 declined (Figure 5a). Interestingly, there was a linear increase in cell density for U138 cells and no apparent slowdown in proliferation, implying a time dependent, decreasing doubling time (Figure 5a, b). Evaluating individual fields of view for U138 cells yielded only little variation throughout individual experiments (Figure 5b), hinting toward a well-reproducible experimental system and analysis scheme. In contrast, #4 cells showed proliferative phases, followed by a very low occurrence of proliferative events and eventually ceased to proliferate (Figure 5c). Such behavior might indicate synchronization of cells inside the layer and some form of contact inhibition of proliferation. Using the information on the change of cell density, a cell density dependent instantaneous speed was obtained (Figure 5d). Two regimes of the speed as function of cell density were observed for both cell types. The first was characterized by increasing speed with increasing cell densities and after reaching the peak speed a continuous decrease with cell density that was more pronounced in the #4 cells was found. As the literature implies cell division events to be an inducer of (local) fluidization inside a monolayer [27,29], we tested whether the local velocities around cell division events were distinct from the rest of the monolayer (Figure 5e, f). For both cell lines, the average speed immediately around division events was significantly higher than in the rest of the monolayer (Figure 5e, f). Please denote the slight decrease in the ratio for U138 cells over time and the increase in GBM #4 (Figure 5e). Currently, we partially attribute the decrease to the detection of cell extrusions in U138 that arise for very high cell densities. For #4 cells it appears plausible that the ratio increases from 1500 min onwards mostly as a result of the overall decrease in the monolayer speed.
Glioblastoma cell lines can show signs of self-organization
Lastly, changes in the morphology of the monolayer formed by the two cell lines were analyzed over time (Figure 6a, b). For both cell types, a transition from a largely unorganized monolayer to the formation of parallel strands for very high cell densities was observed. Quantification of cell orientation supported this observation (Figure 6c), demonstrating the self-alignment of both cell lines over time, with #4 cells showing stronger alignment. Plotting the change in cell density over the cellular orientation variance, a steady decrease in cell orientation variance (increase in alignment) was observed for U138 cells, while a similar decrease was found for #4 cells only after a significant increase in cell density. Thus, it is tempting to speculate that a critical cell density for U138 cells was achieved from the beginning of the experiment, while it was not initially reached for #4 cells. Yet, other explanations such as the time-dependent formation of aligned extra-cellular matrix components or others cannot be excluded. Nonetheless, the results show the capability of the presented methods to analyze questions of cell-density dependent self-organization.
Discussion
The present study was performed to introduce an easy-to-use method for the analysis of collective behavior that is capable to simultaneously assess migration, organization and proliferation of cells in phase contrast images without additional (fluorescent) labeling.
The presented version uses a very well but optional de-noising step via BM3D [25] combined with state of the art PIV in the form of PIVlab [34], automated orientation analysis and an ANN designed to identify proliferation events. The presented results demonstrate the capability of the system to not only analyze migration but also identify correlations between changes in migratory properties, cell density and cellular organization. It should be denoted that the accuracy for cell division detection is similar to other presented label-free methods [31,32,41,42]. To the authors knowledge, there is no single framework combining all of the analysis parameters as presented here in one tool.
Even though the presented framework shows good results, some limitations have to be taken into account. One issue is the de-noising strategy taking a significant amount of calculation time (≈50%). While BM3D is highly effective, it is still an intense and ongoing matter of research on how to significantly reduce the computation time [43,44]. While the de-noising step is optional and has only comparable little effect on the velocity calculations, it still reduces image and thus PIV noise through elimination of small intracellular structures. Usage of classical filters like Gaussian, Wiener or median filters would blur edges and other intracellular structures, affecting calculation of orientation, divisions and velocity. Nonetheless, the provided toolbox does not only provide the optional BM3D filter but also the methods provided by PIVlab [34] Wiener and Gaussian filter. Still, as the BM3D filter provides only comparably little benefit while taking up ≈ 50% of computation time, it is recommended to be turned off when analyzing large amounts of data.
As the generation of candidate divisions use cross correlation it is – albeit the usage of CLAHE – prone to unequal or changing illumination, compared to the templates. An alternative to this approach might be the usage of contrast independent features for candidate selection [45–47]. Furthermore, the cell division detection was trained on data of only two cell lines (LN229, #4) and validated on a third one (U138). Thus, it is likely that the detection accuracy will be lower for cells that appear morphologically distinct. Consequently, a broader set of training data will be needed to circumvent this issue. Another issue with the cell division detection is the occurrence of cell-extrusions being especially evident for very high cell densities. Currently, due to the nearly identical appearance of extrusions and mitotic cells, the proposed algorithm identifies these extrusions as division events. As extrusion events normally persist significantly longer than divisions they are filtered out this way, albeit this approach is limited in efficiency. Despite the extension of the ANN by introducing a third object class (extrusion), potential further strategies could take advantage of the significantly increased velocities around cell divisions that should not be present for cell extrusions. It may also be feasible to check if cell extrusions are associated with nematic defects as reported before [48], so they can be excluded or used for additional analysis. Yet, these approaches still have to be tested.
Conclusion
Here, we presented a versatile toolbox to analyze the collective behavior of a dense cell monolayer to study migration, self-organization and proliferation in phase contrast images. Due to the low demands to the input images, it is expected that the presented approach can have a wide variety of applications.
Supplementary Material
Funding Statement
Tim Hohmann was supported by the Open Access Fund of the Martin-Luther University Halle-Wittenberg.
Disclosure statement
No potential conflict of interest was reported by the authors.
Data availability statement
All relevant data is contained in the manuscript.
Supplementary material
Supplemental data for this article can be accessed online at https://doi.org/10.1080/19336918.2023.2276615
References
- [1].Zegers MM, Friedl P.. Rho GTPases in collective cell migration. Small GTPases. 2014;5(3):e983869. doi: 10.4161/sgtp.28997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Marel AK, Zorn M, Klingner C, et al. Flow and diffusion in channel-guided cell migration. Biophys J. 2014;107(5):1054–1064. doi: 10.1016/j.bpj.2014.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].McMahon A, Supatto W, Fraser SE, et al. Dynamic analyses of Drosophila. Science. 2008;80(322):1546–1550. doi: 10.1126/science.1167094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gamboa Castro M, Leggett SE, Wong IY.. Clustering and jamming in epithelial–mesenchymal co-cultures. Soft Matter. 2016;12(40):8327–8337. doi: 10.1039/C6SM01287F [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Shah STH, Xuezhi X. Traditional and modern strategies for optical flow: an investigation. SN Appl Sci. 2021;3(3):1–14. doi: 10.1007/s42452-021-04227-x [DOI] [Google Scholar]
- [6].Mitchel JA, Das A, O’Sullivan MJ, et al. In primary airway epithelial cells, the unjamming transition is distinct from the epithelial-to-mesenchymal transition. Nat Commun. 2020;11(1):1–14. doi: 10.1038/s41467-020-18841-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Hohmann T, Hohmann U, Dahlmann M, et al. MACC1-induced collective migration is promoted by proliferation rather than single cell biomechanics. Cancers (Basel). 2022;14(12):2857. doi: 10.3390/cancers14122857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Angelini TE, Hannezo E, Trepat X, et al. Glass-like dynamics of collective cell migration. Proc Natl Acad Sci U S A. 2011;108(12):4714–4719. doi: 10.1073/pnas.1010059108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bazellières E, Conte V, Elosegui-Artola A, et al. Control of cell–cell forces and collective cell dynamics by the intercellular adhesome. Nat Cell Biol. 2015;17(4):409–420. doi: 10.1038/ncb3135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Garcia S, Hannezo E, Elgeti J, et al. Physics of active jamming during collective cellular motion in a monolayer. Proc Natl Acad Sci U S A. 2015;112(50):15314–15319. doi: 10.1073/pnas.1510973112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Park JA, Kim JH, Bi D, et al. Unjamming and cell shape in the asthmatic airway epithelium. Nat Mater. 2015;14(10):1040–1048. doi: 10.1038/nmat4357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Nnetu KD, Knorr M, Käs J, et al. The impact of jamming on boundaries of collectively moving weak-interacting cells. New J Phys. 2012;14(11):115012. doi: 10.1088/1367-2630/14/11/115012 [DOI] [Google Scholar]
- [13].Nnetu KD, Knorr M, Pawlizak S, et al. Slow and anomalous dynamics of an MCF-10A epithelial cell monolayer. Soft Matter. 2013;9(39):9335–9341. doi: 10.1039/c3sm50806d [DOI] [Google Scholar]
- [14].Hohmann U, Walsleben C, Ghadban C, et al. Interaction of glia cells with glioblastoma and melanoma cells under the influence of phytocannabinoids. Cells. 2022;11(1):147. doi: 10.3390/cells11010147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hohmann U, Cardinal von Widdern J, Ghadban C, et al. Jamming transitions in astrocytes and glioblastoma are induced by cell density and tension. Cells. 2023;12(1):1–23. doi: 10.3390/cells12010029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Saraswathibhatla A, Notbohm J. Tractions and stress fibers control cell shape and rearrangements in collective cell migration. Phys Rev X. 2020;10(1):11016. doi: 10.1103/PhysRevX.10.011016 [DOI] [Google Scholar]
- [17].Champagnat F, Plyer A, Le Besnerais G, et al. Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp Fluids. 2011;50(4):1169–1182. doi: 10.1007/s00348-011-1054-x [DOI] [Google Scholar]
- [18].Beresh SJ The influence of velocity gradients on PIV measurements of turbulence statistics: a preliminary study. 26th AIAA Aerodyn. Meas. Technol. Gr. Test. Conf. 1–12. 2008. doi: 10.2514/6.2008-3710. [DOI] [Google Scholar]
- [19].Xu F, Beyazoglu T, Hefner E, et al. Automated and adaptable quantification of cellular alignment from microscopic images for tissue engineering applications. Tissue Eng - Part C Methods. 2011;17(6):641–649. doi: 10.1089/ten.tec.2011.0038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Kim J, Ishikawa K, Sunaga J, et al. Uniaxially fixed mechanical boundary condition elicits cellular alignment in collagen matrix with induction of osteogenesis. Sci Rep. 2021;11(1):1–9. doi: 10.1038/s41598-021-88505-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Raymond MJ, Ray P, Kaur G, et al. Cellular and nuclear alignment analysis for determining epithelial cell chirality. Ann Biomed Eng. 2016;44(5):1475–1486. doi: 10.1007/s10439-015-1431-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Martella D, Pattelli L, Matassini C, et al. Liquid Crystal-Induced Myoblast Alignment. Adv Healthc Mater. 2019;8(3):1–10. doi: 10.1002/adhm.201801489 [DOI] [PubMed] [Google Scholar]
- [23].Zhang W, Fehrenbach J, Desmaison A, et al. Structure tensor based analysis of cells and nuclei organization in tissues. IEEE Trans Med Imaging. 2016;35(1):294–306. doi: 10.1109/TMI.2015.2470093 [DOI] [PubMed] [Google Scholar]
- [24].Karlon WJ, Hsu P-P, Li S, et al. Measurement of orientation and distribution of cellular alignment and cytoskeletal organization. Ann Biomed Eng. 1999;27(6):712–720. doi: 10.1114/1.226 [DOI] [PubMed] [Google Scholar]
- [25].Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans Image Process. 2007;16(8):2080–2095. doi: 10.1109/TIP.2007.901238 [DOI] [PubMed] [Google Scholar]
- [26].Ilina O, Gritsenko PG, Syga S, et al. Cell–cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion. Nat Cell Biol. 2020;22(9):1103–1115. doi: 10.1038/s41556-020-0552-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ranft J, Basan M, Elgeti J, et al. Fluidization of tissues by cell division and apoptosis. Proc Natl Acad Sci U S A. 2010;107(49):20863–20868. doi: 10.1073/pnas.1011086107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Gauquelin E, Tlili S, Gay C, et al. Influence of proliferation on the motions of epithelial monolayers invading adherent strips. Soft Matter. 2019;15(13):2798–2810. doi: 10.1039/C9SM00105K [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Devany J, Sussman DM, Yamamoto T, et al. Cell cycle–dependent active stress drives epithelia remodeling. Proc Natl Acad Sci U S A. 2021;118(10). doi: 10.1073/pnas.1917853118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Puliafito A, Hufnagel L, Neveu P, et al. Collective and single cell behavior in epithelial contact inhibition. Proc Natl Acad Sci U S A. 2012;109(3):739–744. doi: 10.1073/pnas.1007809109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Huh S, Eom S, Ker DFE, et al. Mitosis detection of hematopoietic stem cell populations in time-lapse phase-contrast microscopy images. Proc - Int Symp Biomed Imaging. 2012;30:390–393. [Google Scholar]
- [32].Thirusittampalam K, Hossain MJ, Ghita O, et al. A novel framework for cellular tracking and mitosis detection in dense phase contrast microscopy images. IEEE J Biomed Heal INFORMATICS. 2013;17(3):642–653. doi: 10.1109/TITB.2012.2228663 [DOI] [PubMed] [Google Scholar]
- [33].Kolbe MR, Hohmann T, Hohmann U, et al. Thc reduces ki67-immunoreactive cells derived from human primary glioblastoma in a gpr55-dependent manner. Cancers (Basel). 2021;13(5):1–21. doi: 10.3390/cancers13051064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Thielicke W, Sonntag R. Particle image velocimetry for MATLAB: accuracy and enhanced algorithms in PIVlab. J Open Res Softw. 2021;9(1):12–14. doi: 10.5334/jors.334 [DOI] [Google Scholar]
- [35].Berens P. CircStat: A MATLAB Toolbox for Circular Statistics. J Stat Softw. 2009;31(10):1–21. doi: 10.18637/jss.v031.i10 [DOI] [Google Scholar]
- [36].Campbell R. raacampbell/shadedErrorBar. 2004. https://github.com/raacampbell/shadedErrorBar
- [37].Natan A Fast 2D peak finder. 2022. https://www.mathworks.com/matlabcentral/fileexchange/37388-fast-2d-peak-finder
- [38].Tambe DT, Corey Hardin C, Angelini TE, et al. Collective cell guidance by cooperative intercellular forces. Nat Mater. 2011;10(6):469–475. doi: 10.1038/nmat3025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Abate AR, Durian DJ. Topological persistence and dynamical heterogeneities near jamming. Phys Rev E - Stat Nonlinear Soft Matter Phys. 2007;76(2):1–9. doi: 10.1103/PhysRevE.76.021306 [DOI] [PubMed] [Google Scholar]
- [40].Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. 07-12-June, 1–9 (2015). Boston, MA, USA. [Google Scholar]
- [41].Su YT, Lu Y, Liu J, et al. Spatio-temporal mitosis detection in time-lapse phase-contrast microscopy image sequences: a benchmark. IEEE Trans Med Imaging. 2021;40(5):1319–1328. doi: 10.1109/TMI.2021.3052854 [DOI] [PubMed] [Google Scholar]
- [42].Grah JS, Harrington JA, Koh SB, et al. Mathematical imaging methods for mitosis analysis in live-cell phase contrast microscopy. Methods. 2017;115:91–99. doi: 10.1016/j.ymeth.2017.02.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Sarjanoja S, Boutellier J, Hannuksela J. BM3D image denoising using heterogeneous computing platforms. Conf. Des. Archit. Signal Image Process. Krakow, Poland: DASIP; 2015 Dec, 2015. [Google Scholar]
- [44].Sanders T, Larkin S. New Computational Techniques for a Faster Variation of BM3D Image Denoising. 2021;1–10. [Google Scholar]
- [45].Obara B, Fricker M, Gavaghan D, et al. Contrast-independent curvilinear structure detection in biomedical images. IEEE Trans Image Process. 2012;21(5):2572–2581. doi: 10.1109/TIP.2012.2185938 [DOI] [PubMed] [Google Scholar]
- [46].Chen D, Odobez JM, Thiran JP. A localization/verification scheme for finding text in images and video frames based on contrast independent features and machine learning methods. Signal Process Image Commun. 2004;19(3):205–217. doi: 10.1016/S0923-5965(03)00075-4 [DOI] [Google Scholar]
- [47].Sazak C, Obara B. CONTRAST-INDEPENDENT CURVILINEAR STRUCTURE ENHANCEMENT IN 3D BIOMEDICAL IMAGES. Sazak, C., Obara, B. (2017). Contrast-independent curvilinear Struct. Enhanc. 3D Biomed. images. 2017 IEEE 14th Int. Symp. Biomed. Imaging (ISBI 2017). 2017. 10.1109/isbi.2017.7950723. [DOI] [Google Scholar]
- [48].Saw TB, Doostmohammadi A, Nier V, et al. Topological defects in epithelia govern cell death and extrusion. Nature. 2017;544(7649):212–216. doi: 10.1038/nature21718 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant data is contained in the manuscript.


