Abstract
Equipment-free pumping is a challenging problem and an active area of research in microfluidics, with applications for both laboratory and limited-resource settings. This paper describes the pumping lid method, a strategy to achieve equipment-free pumping by controlled generation of pressure. Pressure was generated using portable, lightweight, and disposable parts that can be integrated with existing microfluidic devices to simplify workflow and eliminate the need for pumping equipment. The development of this method was enabled by multi-material 3D printing, which allows fast prototyping, including composite parts that combine materials with different mechanical properties (e.g. both rigid and elastic materials in the same part). The first type of pumping lids we describe was used to produce predictable positive or negative pressures via controlled compression or expansion of gases. A model was developed to describe the pressures and flow rates generated with this approach and it was validated experimentally. Pressures were pre-programmed by the geometry of the parts and could be tuned further even while the experiment was in progress. Using multiple lids or a composite lid with different inlets enabled several solutions to be pumped independently in a single device. The second type of pumping lids, which relied on vapor-liquid equilibrium to generate pressure, was designed, modeled, and experimentally characterized. The pumping lid method was validated by controlling flow in different types of microfluidic applications, including the production of droplets, control of laminar flow profiles, and loading of SlipChip devices. We believe that applying the pumping lid methodology to existing microfluidic devices will enhance their use as portable diagnostic tools in limited resource settings as well as accelerate adoption of microfluidics in laboratories.
Introduction
This paper describes an equipment-free method for generating positive and negative pressures in a microfluidic device using a pumping lid. Most of the microfluidic devices developed in the past two decades rely on external equipment for operation, including the use of pumps, gas cylinders or other external controllers1–5 for precise pumping and loading. Achieving the same degree of flow control without expensive or bulky equipment is necessary for making microfluidic devices more accessible. Currently, equipment-free pumping is both a challenging problem and an active area of research, with several proposed approaches.6–15 For applications in which the total sample volume is less than the internal volume of the device, the sample’s surface energy is known and stable flow rate isn’t required, capillary-based pumping (wicking) can be used.6–10 This has been done by flowing samples through microchannels9,10 or using fibrous materials, such as paper.6–8 For cases when the device can be pre-loaded with a solution, and the solution’s surface energy is known, the flow of the solution can be driven by the difference in capillary pressure between droplets of different sizes of this solution placed at the inlet and outlet of the device. For this method the pressure difference can be restored constantly by the addition of solution to the smaller droplet.11,12 When only small sample volumes are used (a few microliters or less) and the application does not require flow rates greater than a few nanoliters per second, pre-degassed microfluidic devices can be used to generate flow.13,14 Finally, when the density and volume of the sample are known, and the device can be stabilized in a precisely horizontal position, gravity can generate predictable pressure drops and drive the flow in a microfluidic device. In this approach, the difference in height of fluid in separate reservoirs generates the desired pressure drop.15 These methods have wide-ranging applications, but none can provide precise and predictable control of pumping in the absence of external equipment, independent of the sample’s volume, surface energy and density, while still achieving a wide range of flow rates.
Here we describe the theory, characterize the method, and validate the design of a range of equipment-free pumping lids for controlled-pressure generation in microfluidic applications. This pressure generation approach is based on controlled gas expansion or compression, so it does not depend on the nature of the liquid being pumped, the geometry of the channels, or the device’s orientation. It can also be coupled with evaporation of a volatile liquid to generate pressure. Development and characterization of this method was enabled by multi-material 3D printing which allows fast prototyping of composite parts that have sections with different mechanical properties. In addition, the pumping lid approach has the following beneficial features that have not been combined previously in a single method:
The same setup can pump liquids of different density and/or surface energy with no difference in the resulting flow rate.
The pressure source is integrated with the device, so the method does not require the use of external connectors or tubing.
A simple model can be used to predict the pressure/flow rate generated by a specific lid/cup combination.
Pumping lids are interchangeable, so the same microfluidic device can be used with different lids to generate different flow rates. Pressures can be tuned by choosing the pumping lid with the appropriate dimensions and/or by modifying the lid’s geometry.
The user can alter the pressure by simply changing the position of the pumping lid, without interrupting the experiment.
Flow rates can be tuned precisely, with values ranging from a few nanoliters to more than a microliter per second, and remain consistent for long periods (hours in some cases).
The sample volume pumped can be larger than the internal volume of the device, making the method appropriate for handling samples that range from a few microliters to milliliters.
Both positive and negative pressures can be produced in predictable way and used to generate and control flow.
While pumping is in progress, the lid keeps the sample isolated from the external environment, preventing contamination and evaporation.
The combined weight of all parts is less than 50 g, making it portable.
The device can be made of low-cost, disposable/recyclable polymeric materials, making it adaptable to resource-limited settings.
Results and discussion
Principle of pumping lid operation
The pumping lid method described in this paper is based on controlled compression or expansion of gas (Figure 1). To generate positive pressure, the user places the sample at the device inlet and then places the pumping lid on the cup integrated into the microfluidic device (Figure 1A). When the user pushes the lid down to its final position, the air in the lid’s cavity is isolated and compressed, creating positive-gauge pressure. The lid’s position is held by friction, but to increase robustness, guiding and locking structures can be integrated into the design (Figure 1A–1B). Conversely, to create negative pressure, a pumping lid is pre-placed on the cup (Figure 1B) and the user pulls up on the pumping lid, expanding the air in the cavity. The degree of expansion is controlled by guiding structures.
Figure 1.

Principle of pumping lid operation. (A) Schematic of the method to generate positive pressure. A device is equipped with a cup (black) and locks (green). A sample (red) is placed in the cup before pumping. The pumping lid (grey) contains a cavity as shown in the side view. Part of the pumping lid is composed of a soft, deformable material (blue). Placing the lid on the cup compresses the air in the cavity and generates the pressure used to pump the sample in the device. The locks hold the lid in place to maintain the pressure over time. (B) Schematic of the method to generate negative pressure. The pumping lid (grey) is placed on the inner cup (black, visible only in the side view) before the experiment, and is equipped with guiding pins (red). These pins slide on a guiding structure (black) to guide the movement of the lid. When the user pulls the lid, the air in the cavity expands, creating a negative gauge pressure that pumps the sample into the device. (C) Pressures obtained from 40 experimental cup-lid combinations (N=3) plotted against the pressure values obtained from the model (Eq. 2 and Eq. 6). The colors denote lids of different cavity volumes. The dashed black line indicates the linear fit of the data and its parameters are reported in the graph.
Theoretical model for prediction of the pressure generated with the pumping lid
First, we analyze the initial pressure generated by the pumping lid and cup, prior to pumping. We use the Boyle law for isothermal gas compression: ; assumptions of ideal gas behavior are appropriate in this case because the pressures are low (~ 1 atm) and the temperatures are sufficiently high (~ 300K).
Positive pressures
The positive pumping pressure depends on four main parameters: the volume of the cavity in the pumping lid (), the volume of the cup walls (), the volume of the empty space inside the cup () and the volume of sample loaded in the cup (). When the lid is placed on the cup and first creates the seal, the volume of air enclosed is defined as , and the initial pressure is ~1 atm (Figure S1, Option 1). After the user pushes down the lid, the air is compressed and the final volume is given by . Applying Boyle’s law, the pressure at this point is calculated as follows:
| (Eq. 1) |
A more generalized formula can be used for the case when the lid is already pre-placed on the cup, at a distance from the final position (Figure S1, Option 2). The pressure is generated when the user pushes the lid to the final position. In this case, the pressure depends on the four volumes described above ( and ) and on the ratio , between and the total height of the cup (), defined as . The initial volume in this case is given by and the initial pressure is again, the atmospheric pressure, ~ 1 atm. After the lid has been pushed down by a distance , the final volume is given by . The pressure at this point is calculated by using the same relation, , and is defined as:
| (Eq. 2) |
defines the initial sample volume.
Second, we analyzed changes in pressure due to pumping. The pressure as a function of time is expressed as:
| (Eq. 3) |
defines the volume of sample present in the cup at time . When the sample volume is substantially smaller than the difference between the cavity and pumping cup volumes, , the change in the only time-dependent term, , becomes negligible and the pressure can be considered constant, and Eq. 3 becomes identical to Eq. 2. This assumption was verified in all the experiments described in this paper, unless otherwise stated. Eq. 3 can be used to guide the design of pumping lids and cups, to predict the variation in pressure due to pumping and tune it if needed.
When the sample volume is large enough to affect the pressure, the following set of equations can be used to describe the change in pressure. Given the hydraulic resistance () of the device, the time-resolved drop in positive pressure can be calculated as the sample is pumped out of the cup:
| (Eq. 4) |
Eq. 4 is only valid for and while pumping is in progress. We assumed that the values of remained constant in our experiments, because we pre-filled the channels with the solution being pumped. If the channel is not pre-filled, the initial variation of during filling would need to be accounted for. To calculate the time required to pump the whole sample volume, the following equation is used:
| (Eq. 5) |
Negative pressures
For generation of negative gauge pressures, the pumping lid is pre-placed onto the cup, and the user pulls it by a distance . Assuming the cup is empty prior to pumping, the initial volume is given by . The initial pressure is the atmospheric pressure, ~1 atm. If the channel is not pre-filled with solution prior to pumping, the channel volume needs to be accounted for in . After the lid has been pulled by a length , the final volume of air is given by . Using previously defined parameters and the relation , the pressure at this point is defined as:
| (Eq. 6) |
Similarly to the case of the positive pressure, once pumping commences, the time dependence of is given by the expression:
| (Eq. 7) |
represents the volume of sample pumped into the cup at a given time . When the sample volume is much smaller than , the only time dependent term in Eq. 7, , becomes negligible and the pressure can be considered constant. Whenever this assumption cannot be made, one can calculate the time-resolved drop in pressure as the sample is pumped into the cup, given the hydraulic resistance () of the device:
| (Eq. 8) |
Eq. 8 is only valid for and while pumping is in progress. To calculate the time required to pump a given sample volume one should use the following equation:
| (Eq. 9) |
represents the total sample volume to be pumped into the cup.
Generation of predictable positive and negative pressures
We experimentally tested (Figure 1C) predictions of the model for generating both positive (Figure 1A) and negative (Figure 1B) gauge pressures. We report (Figure 1C) the pressures obtained from 40 combinations of cups and pumping lids, plotted against the pressure value predicted by Eq. 2 and Eq. 6. Cups were 3D-printed directly on a rigid support and not connected to a device. We used a 5 psi differential pressure sensor (PXCPC-005DV, Omega Engineering), which was connected to a power supply (Portrans FS-02512–1M, 12V, 2.1 Amp power supply, Jameco Electronics) and to a data acquisition board (OMB-DAQ-2408, Omega Engineering). A custom program was written in LabVIEW (National Instruments) to convert the signal collected by the sensor to gauge pressure. The sampling frequency was 2 Hz. Each condition varied in at least one model parameter (). The pumping lids used for these experiments included a nozzle that could be connected to the positive side of the pressure sensor using a short piece of Tygon tubing (1 cm long). Lid volumes were calculated using CAD software, accounting for the extra volume introduced by the nozzle, tubing, and the sensor. The other side of the sensor was exposed to the external environment, so all data collected were in terms of gauge pressure. The results were a close match to the predicted outcome, with an R2 value of 0.9995 and a slope of 0.96. The pressures produced in this experiment spanned more than an order of magnitude (Table S1). Furthermore, the model predicts that even higher pressure could be obtained by decreasing the volume of the empty parts () and/or by increasing the other volumes ( and ).
Design guidelines for the pumping lid and cup
We found three guidelines to be helpful in designing pumping lids and cups: (1) the model can be used to either predict the pressure generated by a particular lid/cup combination, or to determine the lid and cup dimensions needed to achieve a particular pressure. All parameters can be tuned and the resulting pressure for each combination can be predicted using the equations described in the previous section. (2) To ensure effective sealing between the pumping lid and the cup, at least one of the two parts (lid or cup) should contain a deformable (soft) portion. The design requires a small overlap between the parts, so the soft portion is forced to deform when the lid is placed on the cup, thus creating a hermetic seal. Typical overlaps were in the order of 100 μm to 200 μm, which corresponds to ~ 1–2% of the cup diameter. We used multi-material 3D printing provided by Objet 260 system (Stratasys, Eden Prairie, MN, USA), which can produce parts composed of two different materials, and mixtures of these two materials. (3) Compression deforms the soft portion of the lid, and the material tends to be squeezed laterally. We observed that if this deformed material goes between the pumping lid and the base of the cup, the lid cannot be pushed to its final position and the obtained pressure will be lower than the one predicted by the model. This effect can be minimized by ensuring that the thickness of the soft layer is significantly larger than the overlap between the lid and cup, typically in the order of 1–1.5 mm. Another solution is to use soft layers with a tapered profile (Figure 1A).
Controlled pressure variation during an experiment
Next, we wished to test whether it would be possible to switch the pressure applied by the pumping lid without interrupting the flow or exposing the sample to the environment (to minimize contamination or evaporation). This capability is desired when several flow rates need to be tested in one continuous experiment. Pressure is changed by compressing or expanding air in the cavity. Therefore, here we investigated whether the level of compression or expansion, and therefore the pressure, can be controlled precisely by using the guiding structures (Figure 2). For example, for both positive- and negative-gauge pressures, we designed lids that can be placed in three positions, labeled (i) (ii) and (iii). Each position provides a defined, specific pressure, and the user can switch between the positions by rotating the lid on its axis (Figures 2D, 2H). The lids for these experiments were 3D-printed with a nozzle for the pressure sensor and pressure data was collected with the same setup as described in previous sections. For both positive- and negative-pressure devices, the starting position, (i), corresponds to zero gauge pressure (Figure 2). This adjustable design thus enables customized, “pre-programmed” pressure control during an experiment (e.g. to initiate or stop flow, and to change the flow rate) and allows the fully assembled device to be stored without applying pressure before use. While the devices demonstrated here are able to produce three specific pressures, more lid positions can be designed to enable finer tuning.
Figure 2.

Strategies for producing multiple pressure values in a single device using a cup and pumping lid. (A-D) Positive pressures produced by turning a pumping lid (grey) using a cup (blue) fit with a guiding structure (black) (A). Turning the lid within the guiding structure yields three potential lid positions, which are shown in side (B) and top (C) views, each of which produces a different pressure. In Position (i) the lid is not in contact with the cup, so no pressure is produced. In Position (ii) the lid is lowered and positive pressure is produced. In Position (iii) the lid is lowered further, and the pressure increases. The horizontal dashed lines show the level of the lid in the three positions. Panel D shows an experimental pressure profile obtained by turning the lid between the three positions. (E-H) Negative pressures produced by turning a pumping lid (grey), using an cup (blue) fit with a guiding structure (black) (E). Turning the guiding structure yields three potential lid positions, which are shown in side (F) and top (G) views, each of which produce a different pressure. The pumping lid and the cup have via-holes that align only in Position (i), so there is no gauge pressure in this configuration. In Position (ii) the lid is raised and negative pressure is produced. In Position (iii) the lid is raised further, and the pressure decreases. The horizontal dashed lines show the level of the lid in the three positions. Panel H shows an experimental pressure profile obtained by turning the lid between the three positions.
Generation of flow using the pumping lid approach
Next, we tested the prediction that for a given channel geometry, the pumping lid method would provide consistent flow rate that depends on viscosity, but not on surface energy or density of the fluid being pumped. We used Eq. 1 to predict the pressure applied by the pumping lid, and Eq. 10 to predict hydraulic resistance that depends on the viscosity and the dimensions of the channel16.
| (Eq. 10) |
defines the channel length, the channel height, and the width of the channel. The volumetric flow rate can thus be predicted with Eq. 11:
| (Eq. 11) |
To test these predictions, we first characterized pumping of water through a microfluidic device using seven pumping lids, each providing a different pressure (Figure 3A). The device consisted of glass-bonded PDMS layer17, pumping cup, PTFE tubing, and the pumping lid (Figure S3). A 30.8 cm long, 58 μm high, 110 μm wide serpentine was molded into the PDMS layer, and was pre-filled with each solution prior to pumping experiment, as described in SI. The slope of the fitting curve is the inverse of the hydraulic resistance () for the experimental setup, as suggested by Eq. 11.
Figure 3.

Experimentally and quantitatively testing the model describing pumping with a pumping lid as a function of hydraulic resistance of the channel and properties of the fluid. (A) Flow rate of water in a microfluidic device using different pumping lids to generate different pressures. The dotted red line indicates the predicted flow rate based on the device geometry, while the dotted blue line shows the linear fit of the data and its parameters are reported on the graph (N=3; error bars smaller than the size of the marker). (B) A plot of experimental flow rates, multiplied by the viscosity, for different aqueous solutions. Flow rates were inversely proportional to viscosity and independent of the surface energy or density of the solutions. Schematics of the setup used for these experiments are provided in the supplementary material. (Figure S3).
The experimental value for obtained from the fit is 2.59*1014 Pa s/m3, which matched the theoretical value calculated for the microfluidic channel geometry: 2.58*1014 Pa s/m3 16 . Thus, it was possible to predict the flow rate for a given pumping lid used with a given microfluidic device, and the design was robust enough to give reproducible results. The flow rates in this experiment were 1 – 5 μL/min, and this range was chosen to minimize the experimental errors when measuring flowing time. Higher flow rates could be produced by increasing the pressure generated by the pumping lid (as described in the previous sections), or by using a device with lower hydraulic resistance. For example, a device with a channel 150 μm tall x 150 μm wide x 20 mm long will have a hydraulic resistance almost 200 times less than the devices used for these experiments, so the flow rate generated with the same pumping lids would approach 1 mL/min.
Generation of flow rate independent of density and surface energy
To verify that the flow rate in the pumping lid method is independent of solution density and surface energy, we pumped nine aqueous solutions of different properties (Table S2) using seven different lids to measure the flow rate at different inlet pressures. Solutions of viscosity similar to water, but with different surface energies (30 – 72 mN/m) and different densities (1 – 1.9 g/mL), had flow rates comparable to those obtained for water. We experimentally measured viscosities of all nine solutions to confirm this result. Note that the viscosity-adjusted flow rate values () were similar for all liquids (Figure 3B), which is explained in the next section.
Generation of flow for solutions of different viscosities
We then tested whether the pumping lid is appropriate to produce flow in solutions with viscosities higher than that of water. In our experiments, solutions had viscosities between 1 mPa*s and 4 mPa*s (Figure 3B). The flow rates for high viscosity solutions were lower than those obtained for pure water, because the value of the hydraulic resistance described above is directly proportional to the viscosity of the liquid pumped (Eq. 10)16. Eq. 11 can be re-written as:
| (Eq. 12) |
Eq. 12 predicts that if the same lid-cup combination is used on the same device, the product of the flow rate and the viscosity of the solution will be constant16. Our experimental results (Figure 3B) corroborated this prediction, since the values for all the solutions analyzed were comparable to those obtained for water (Figure 3B). This means that the pressure generated by a pumping lid depended solely on the lid-cup dimensions, and not on the nature of the solution to be pumped.
Use of multiple lids on the same device to achieve complex flow control over long timescales
Next, we tested the idea that using separate cups and lids at different inlets makes it possible to simultaneously pump more than one solution and to independently control the pressure imposed at each inlet (Figure 4A). First, we used multiple lids to produce nanoliter droplets (Figure 4B)18–20. Immiscible fluids can be difficult to handle under pressure-driven flow because the applied pressure should be higher than capillary pressure but not so high to generate an excessive capillary number that would cause droplet deformation21. Also, when multiple inlets are controlled with different pressures, liquid could potentially flow from one cup to another. To avoid this, we designed devices with geometries that included a serpentine channel between the inlets and the junction used to produce the droplets. This serpentine channel had a fluidic resistance higher than that of the outlet channel, and ensured that liquids were not transferred from one cup to the other during experiments. This approach was used to generate nanoliter droplets (plugs) of water in fluorinated oil, using flow focusing and T-junction geometries (Figure 4B), with volumes that ranged from 0.5 to 2.5 nL.
Figure 4.

Use of the pumping lid approach to control pumping of each of several fluids with different properties in a microfluidic device. (A) Schematic of the pumping approach using multiple solutions in the same device. Each sample was pumped in the device with a different pumping lid, each lid producing a different pressure. (B) Left: Experimental photographs illustrating production of nanoliter plugs (red) in fluorinated oil (transparent), using a microfluidic device with flow focusing geometry. Right: Production of multicomponent aqueous droplets in fluorinated oil using a T-junction. The solutions (red, transparent and green) were pumped independently and used to produce nanoliter plugs. (C) Experimental photographs illustrating that the parallel laminar flow profile of three separate streams of aqueous solution (red, transparent and light blue) was stable even after 165 min (2.75 h). A total volume of 0.9 mL (300 μL of each solution) was pumped in this experiment.
Parallel laminar flow profiles can also be produced (Figure 4C). We achieved stable flow patterns for more than 2.5 h, with a total pumped amount of 0.9 mL. The predicted decrease of flow rate in this system over a 2.5 h period was 45% of the original value (Eq. 4), which was consistent with our experimental observations (Figure 4C). Increased diffusion between the dyes was observed, due to the longer residence time in the channel. Because we used lids of the same size and loaded samples of the same volume and viscosity, over time we observed a decrease in the absolute value of the flow rates, but not a decrease in their ratios. We emphasize that if the volumes of the lids, cups, sample volumes and/or viscosities are different, the flow rates will drop at different rates (Eq. 4).
Use of composite lids to produce different flow patterns in the same device
A “composite lid,” a pumping lid with multiple cavities, was designed to simultaneously seal multiple cups (Figure 5). The cavities in the composite lid can be isolated or connected to one another. For example, if inlets require identical pressures, their corresponding cavities can be linked (Figure 5C).
Figure 5.

Production of different flow profiles in the same device using composite pumping lids. (A) Schematics of the setup used for the experiments. The microfluidic device has three cups, each dedicated to a different aqueous solution (from left to right: green, transparent, and red). A composite lid controls the pressure at each of the three inlets, thus controlling the flow rate of each solution. (B) Micrograph of the junction at which the three inlet branches combine into a single channel and the streams from the three inlets produce parallel laminar flow. (C) Different composite lids can be used to produce different flow profiles. The top row shows the cross-section of five different lids, cut along the red dashed line in panel A. The middle row shows the experimental flow profiles obtained with these five lids in the same microfluidic device. The sketches (bottom row) show the expected flow profiles based on the pressures produced by the lids and the device geometry. For the channel used in these experiments the width (1.5 mm) was more than 35 times bigger than the channel height (40 μm), so the effect of parabolic flow near the lateral walls was negligible16
To test these devices quantitatively, we measured the width of each solution stream in the three-stream aqueous laminar flow, (the Reynolds number was always less than 1 in our experiments). The gauge pressures at the three inlets are defined as and , while the pressure at the device outlet is zero. Fluidic resistances for the three inlet branches (before the junction) are defined as , while the resistance of the main channel (formed by the junction of the three inlet branches) is defined as . In the experiments described in this paper, the fluidic resistance of the inlet branches was intentionally set larger than the outlet resistance , to increase the range of pressures that could be applied to the three inlets without generating back-flow in the branch with the lowest pressure. Under these conditions, theory predicts that is proportional to and can be approximated by Eq. 11. Ignoring the effects of three-dimensional diffusion22, 23 and ignoring the effect of the parabolic flow profile for these wide channels, we predicted the flow profiles as described in the supplementary material, and found them to be in good agreement with experiments.
These lids were used to produce parallel laminar flow profiles in a microfluidic device (Figure 5B). Each composite lid had a different geometry (Figure 5C) and generated a different set of pressures at the three device inlets. These pressures were used to predict the flow profile in the microfluidic device, as described in the supplementary material, and experimental results matched the flow profiles predicted by the flow rate model (Figure 5C). Based on the geometries of the device and the composite pumping lid, flow profiles can be controlled and predicted.
Use of pumping lids to load SlipChip devices by positive and negative pressures
Next, we showed that the pumping lid could be used to reliably and easily load SlipChip devices24 using either positive or negative pressures. This is a good test because loading SlipChip devices requires control of the inlet pressure within a defined range,25 and SlipChips are intended to be used in limited resource settings (LRS) by untrained users.26–29 First, we tested the pumping lid on a SlipChip designed for a digital nucleic acid detection assay26 (Figure 6A), pumping a total of 5 μL of solution with 0.03 atm pressure (Eq. 1). We asked a 6-year-old volunteer to use the pumping lid to operate the device. We found that pumping proceeded to completion despite the variation of pressure applied to the pumping lid by the volunteer.30, 31 We expect the simplicity of the pumping lid to be valuable in both LRS and laboratory settings, e.g. for digital single-molecule measurements.31
Figure 6.

Use of the pumping lid for loading of SlipChip devices. (A) Photographs of a 6-year-old volunteer with minimal training using the pumping lid to load a SlipChip device. The sample is placed in the cup at the device inlet (A1), the pumping lid is placed on the cup, and when the lid is pushed, positive pressure is generated and sample pumping starts (A2). Once the sample loading is complete, slipping two plates generates discrete compartments (A3). A video of this experiment is provided.30 (B) SlipChip sample loading by negative pressure. (B1) Schematic outline of the steps. The lid is pre-placed on the cup, and the sample is placed at a separate inlet in the device. Pulling the lid creates negative gauge pressure and initiates loading. Dead-end filling ensures that the loading stops once the device is completely filled. (B2) Photograph of a multivolume SlipChip device for digital nucleic acid quantification loaded with negative pressure pumping lid method.
In another experiment, we tested loading of a different SlipChip device by negative pressure. To further illustrate the applicability of the pumping lid method to complex tests, we used a SlipChip designed for multivolume digital nucleic acid amplification,32, 33 which presents challenges in filling due to variation of capillary pressure among wells of different sizes. Previously this type of device was filled by positive pressure and dead end filling.25 We modified the device for negative-pressure filling by adding a sealing ring filled with high-vacuum grease (sealing structure) around the active area containing the amplification wells (Figure 6B). We also added an outlet for oil to the device, over which the negative-pressure pumping lid was placed. The device was assembled such that the lubricating oil (5 cSt silicone oil) was filling the wells. For loading, sample (50 μL of 0.5 M FeSCN aqueous solution) was placed onto the inlet, and the pumping lid was pulled up to create negative pressure of 0.1 atm, remove excess oil and draw the sample into all of the wells of the device (Figure 6B). This experiment demonstrated that bubble-free filling can be accomplished using the pumping lid, and that complex devices (a combination of immiscible fluids and wells with different capillary pressures) can be handled.
Vapor-liquid equilibrium (VLE) method for pressure generation
We then explored how vapor pressure of a volatile liquid can aid the pumping process by isolating its effect from compression, and investigated the potential to harness the vapor pressure for pumping a non-volatile sample. Our hypotheses were that (i) by taking advantage of vapor-liquid equilibrium (VLE), one would be able to pump large volumes of liquid over extended periods of time at a relatively constant pressure, without the need to compress a large volume of a gas inside the device; (ii) a single lid design could be used to generate different pressures by using liquids of different vapor pressure; (iii) a single combination of a lid design and a volatile liquid could be used to generate different pressures by tuning the temperature. In this approach, a volatile liquid is stored in a sealed compartment inside a pre-assembled vapor pressure pump, comprised of a lid and cup (Figure 7A). The design of this lid and cup differ from those described previously, as turning this lid connects or disconnects the compartments in the cup, rather than compressing or expanding the gas enclosed in the cavity, as in a SlipChip device24. In addition, the cup is divided to contain the volatile liquid and one or more separate sample compartments. When the user turns the lid, the volatile liquid evaporates into the cavity (Figure 7B). The cavity in the pumping lid is isolated from the atmosphere, so evaporation of the volatile liquid increases the pressure in the cavity. Once the volatile liquid reaches equilibrium with its vapor, the pressure will be higher than the atmospheric pressure, and its value can be calculated using the thermodynamic VLE model. The user can initiate pumping by opening a valve or removing a plug. During pumping, evaporation of additional liquid provides additional pressure, although there is a drop in pressure, since the volume previously occupied by sample is now available to the gas phase, effectively causing expansion. Similarly to the pressure change observed in the pumping lid method, this pressure drop can often be neglected, if the sample volume being pumped is much smaller than the pump gas compartment volume. Once the entire sample has been pumped through the device, the vapor in the lid connects to the atmosphere and the gauge pressure drops to zero. This method of vapor pressure pumping can be used independently or in conjunction with compression.
Figure 7.
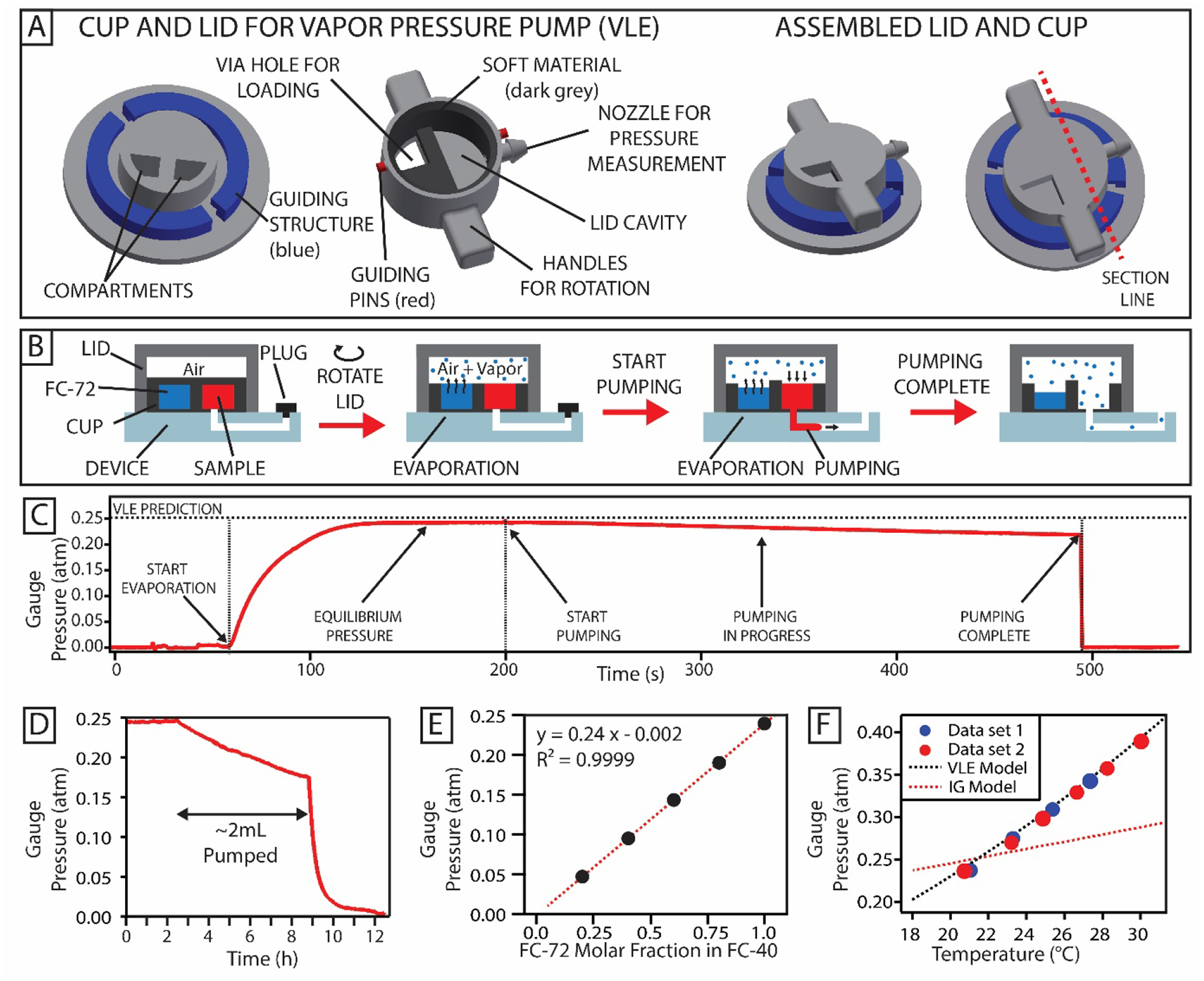
Generation of pressure using vapor liquid equilibrium (VLE). (A) Schematics of the parts used for VLE pressure generation. (B) Schematics of the method used to generate pressure. The figures show the cross section of the lid and cup assembly along the red line shown in panel A. Prior to the experiment, a volatile liquid (FC-72, blue) and the sample (red) are placed in isolated compartments of the cup. At this stage, the pressure in the lid cavity is equilibrated with the atmosphere. When the lid is rotated, the volatile liquid is exposed to the air in the cavity and starts to evaporate to reach its equilibrium pressure. When the plug is removed from the device outlet, the sample starts flowing. After the entire sample has been pumped, the cavity is in contact with the external atmosphere and the pressure returns to zero. (C) An experimental pressure profile obtained by performing the steps described in panel B, for pumping 20 μL of water. (D) Pressure profile obtained when pumping a 2 mL sample volume through a microfluidic device. (E) Equilibrium pressures obtained by using mixtures of liquids (FC-72 and FC-40) at different molar fractions (N=3; error bars smaller than the size of the marker). The dashed line indicates the linear fit of the data and its parameters are reported in the graph. (F) Equilibrium pressure obtained using FC-72 at different temperatures. The dashed line shows the values predicted by the VLE model (Eq. 16). Each point represents the average over at least 62 and up to 87811 pressure measurements after the system has equilibrated.
Model for VLE pressure generation using perfluorohexane (FC-72)
To find the predicted pressure at VLE, the fugacities of perfluorohexane in both liquid (right hand side in Eq. 13) and gas (left hand side in Eq. 13) phases are set equal. The general expression for VLE is:
| (Eq. 13) |
Where: = fugacity coefficient of FC-72 in gas phase at T, P
= equilibrium mole fraction of FC-72 in the gas phase at T, P
P = equilibrium system pressure
= FC-72 activity coefficient in liquid phase
= equilibrium mole fraction of FC-72 in the liquid phase at T, P
= fugacity coefficient for pure FC-72 at T,
= FC-72 saturation pressure at T, oftained from Antoine equation
= FC-72 liquid molar volume
R = ideal gas constant
T = system temperature
To simplify the calculation, we made the following assumptions:
Liquid phase is pure FC-72 (ignoring air dissolving in FC-72), = 1
Liquid phase behaves ideally, = 1
- Gas phase also behaves ideally, = 1 and = 1, and that Dalton’s law applies:
- , where
T is constant
After simplification, the equation becomes:
| (Eq. 14a) |
Or, equivalently:
| (Eq. 14b) |
Because the Poynting factor (exponential term in Eq.14a) is close to unity, the equilibrium system pressure P is almost equal to the initial pressure plus FC-72 saturation pressure. This equation was analysed numerically to calculate the predicted total pressure in the system (equal to ). If vapor pressure pumping is used in combination with the pumping lid approach, the final pressure should be used in place of .
The values of were obtained with the Antoine equation:
| (Eq. 15)34 |
Model for temperature dependence of VLE pressure
Vapor pressure of the volatile liquid, and therefore the performance of this pumping approach, is affected by temperature. To make accurate predictions of the pressure generated by this vapor pressure pump, the ideal gas law was substituted for (the initial pressure), which allowed us to take into account both the change in vapor pressure and gas expansion as the temperature is changed:
| (Eq. 16) |
Eq. 16 was used to calculate the predicted value of P at different temperatures. The total volume available for gas in the device () was calculated in CAD software. The initial number of moles of air in the gas compartment () remains constant, and is dictated by the temperature at which the compartment was initially sealed from atmosphere (21.5° C). The device was designed specifically to avoid any compression during the turning of the lid, to isolate the effects of VLE on pressure. For VLE pumping, we neglected the vapor pressure of the aqueous sample, because the vapor pressure of water is much lower than that of perfluorohexane (0.025 atm vs. 0.248 atm) at 21.5° C.
Pressure and flow generation using the VLE method
The experimental behavior of pressure agreed with the theoretical predictions (Figure 7C). The equilibrium pressure obtained experimentally approached the pressure predicted by the simplified VLE model (Eq. 14), and the system was used to pump 20 μL of water through a microfluidic device in ~ 280 s (4.7 min). The VLE method could be used for pumping volumes in the milliliter range, for example 2 mL of water was pumped in more than 7 h, showing less than 30% reduction in the input pressure using a lid with a 30 mL gas compartment (Figure 7D). This reduction was caused by the fact that the volume previously occupied by sample became available to the gas phase to expand. As expected, larger lids took longer to equilibrate because more liquid needed to evaporate. However, the pressure remained stable when pumping was not in progress (Figure 7D), so equilibration can be done prior to the pumping experiment. Alternatively, if the pressure does not need to be controlled precisely, the pumping can be started as soon as evaporation is initiated.
Tuning of VLE pressure by changing composition of the volatile liquid or temperature
To test our second hypothesis, we investigated generating pumping pressures by liquids with different vapor pressures. The equilibrium gauge pressure reached by the VLE system is related (but not necessarily equal) to the vapor pressure of the volatile liquid, according to Eq. 13. For a mixture of liquids, vapor pressure depends on the molar fraction of each component, amongst other factors. We measured the equilibrium pressures for different mixtures of FC-40 (vapor pressure 0.003 atm at 21.5° C) and FC-72 (vapor pressure 0.248 atm at 21.5° C). Equilibrium VLE pressure scaled linearly with the FC-72 molar fraction (R2 = 0.9999) and approached ~ 0.003 atm for pure FC-40 (Figure 7E), as expected.
To test our third hypothesis, we investigated pressure generated by this vapor pressure pump at different temperatures using FC-72 as the volatile liquid. Because vapor pressure is a function of temperature (Eq. 15 and Eq. 16), the equilibrium pressure of FC-72/air system increased with temperature, yielding values consistent with those predicted by the VLE model (Figure 7F). Note that the change in pressure with temperature far exceeded the one predicted for heating of an ideal gas in a closed volume. This presents an opportunity to incorporate simple microfabricated heaters35, 36 to precisely control the pressures provided by this pump, and emphasizes the importance of temperature control for the operation of the vapor pressure pump. As mentioned earlier, VLE pumping can potentially be used in combination with the pumping lid gas compression or expansion. When generating positive pressure, the compression can be used to increase the range of pressures that can be achieved with the VLE approach. In the case of gas expansion, the use of VLE sets a lower limit to the pressure that can be obtained to the vapor pressure of the volatile liquid. The long-term stability of volatile liquids in the acrylic-based resins used for 3D-printing was not characterized, but preliminary experiments with the same liquids pre-packed in blister packs showed that it is possible to obtain similar pressures.
Conclusions
Here we described a way of generating positive and negative pressures with an equipment-free pumping lid and demonstrated its utility to induce flow in microfluidic devices. We used multi-material 3D printing to produce the parts, allowing fast prototyping without reducing their quality. This fabrication process is attractive because it allows rapid design iterations, and can also be scaled up to mass production using overmolding techniques. Here, pumping cups were attached to the device post-fabrication, but they can be included as part of the device during manufacturing. The first method described in this work relies on controlled compression or expansion of gas. While compression of gas has been demonstrated previously for pumping in microfluidic applications,37 this work extends the previous approach. It demonstrates new capabilities, including (i) enabling the generation of both positive and negative pressures, (ii) the capability to adjust pressure in a programmed way while pumping is in progress; (iii) the use of multiple lids or a composite lid to control pressure at different inlets within the same device; and (iv) in addition to device loading applications, here we show more complex fluid manipulations, such as stable long-term laminar flow of multiple solutions and nanoliter droplet formation in two-phase flows. Furthermore, this work will enable others to use this approach more easily because (i) the method has been modeled and the model was quantitatively validated by experimentally measuring the pressures generated by the pumping lids; and (ii) the model was used to provide guidelines for the design of cups and pumping lids. We also demonstrated a complementary second method for generating pressure via evaporation of a volatile liquid in the pumping lid. The equilibrium pressure generated with this approach (before pumping starts) depends on the nature of the volatile liquid and on its temperature, but is not dependent on the geometry of the lid used for the experiment.
The approaches described in this work address many of the fluid-handling challenges that are faced when working with microfluidic devices1–15 including those involving laminar flow,22,38 droplets,21,39–41 and cell culture experiments.42–44 The simplicity of this pumping method overall and the use of the guiding structures make it robust to differences in pushing/pulling force; the user simply places a sample at the inlet and then pushes/pulls the pumping lid to generate the flow. Even when the user is applying excessive force (see video30), the method still operates as programmed; this makes it suitable for even the most minimally trained users. The pumping lid approach is thus appropriate for a variety of applications in different settings. Experiments taking place in a research lab can benefit from this compact and equipment-free approach, reducing the need for external connectors and simplifying the workflow, especially when experiments are conducted in the controlled environments of a cell culture incubator42–44 or an anaerobic chamber.45 Additionally, contamination from the external environment and evaporation are minimized because the sample is contained in the pumping cup during the entire experiment. The pumping lid also allows flow rates to be tuned in real time while the experiment is in progress. The isolation and containment of samples is a characteristic that is highly desirable for cell culturing,42 particularly when dealing with biohazardous samples and “organs-on-chip” technologies.43,44 Such experiments are usually performed in controlled conditions (temperature, gas composition, etc.) and often require long pumping times.15 With this approach, the entire pumping lid setup can be placed inside an incubator, without the need for external controllers. The use of VLE pumping is particularly suitable for temperature-controlled environments. Due to its portability and programmability, the pumping lid can also benefit applications in resource-limited settings, specifically for portable diagnostic devices.6, 7, 24, 26, 28, 46, 47
Supplementary Material
Acknowledgements
This work was funded in part by DARPA Cooperative Agreement HR0011-11-2-0006 and National Institutes of Health NRSA training grant 5T32GM07616NSF (to D.A.S.). This material is also based upon work supported by a National Science Foundation Graduate Research Fellowship under Grant No. DGE-1144469 (to D.V.Z.). This paper does not necessarily reflect the position or policy of the U.S. government or these agencies, and no official endorsement should be inferred. We wish to thank Mikhail Karymov for preliminary experiments, Roberta Poceviciute for help with the theoretical analysis, and Natasha Shelby for contributions to writing and editing this manuscript. We also wish to thank the 6-year-old volunteer for performing the demonstrations shown in Figure 6. Disclosure: R.F.I. and L.L. have a financial interest in SlipChip Corp.
References
- 1.Herr AE, Molho JI, Santiago JG, Mungal MG, Kenny TW and Garguilo MG, Analytical Chemistry, 2000, 72, 1053–1057. [DOI] [PubMed] [Google Scholar]
- 2.Choi K, Ng AHC, Fobel R and Wheeler AR, Annual Review of Analytical Chemistry, 2012, 5, 413–440. [DOI] [PubMed] [Google Scholar]
- 3.Darhuber AA, Valentino JP, Davis JM, Troian SM and Wagner S, Applied Physics Letters, 2003, 82, 657–659. [Google Scholar]
- 4.Tang S-Y, Khoshmanesh K, Sivan V, Petersen P, O’Mullane AP, Abbott D, Mitchell A and Kalantar-zadeh K, Proceedings of the National Academy of Sciences, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Futterer C, Minc N, Bormuth V, Codarbox JH, Laval P, Rossier J and Viovy JL, Lab Chip, 2004, 4, 351–356. [DOI] [PubMed] [Google Scholar]
- 6.Martinez AW, Phillips ST, Whitesides GM and Carrilho E, Analytical Chemistry, 2009, 82, 3–10. [DOI] [PubMed] [Google Scholar]
- 7.Martinez AW, Phillips ST, Butte MJ and Whitesides GM, Angewandte Chemie International Edition, 2007, 46, 1318–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Osborn JL, Lutz B, Fu E, Kauffman P, Stevens DY and Yager P, Lab Chip, 2010, 10, 2659–2665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Safavieh R and Juncker D, Lab Chip, 2013, 13, 4180–4189. [DOI] [PubMed] [Google Scholar]
- 10.Zimmermann M, Schmid H, Hunziker P and Delamarche E, Lab Chip, 2007, 7, 119–125. [DOI] [PubMed] [Google Scholar]
- 11.Resto PJ, Berthier E, Beebe DJ and Williams JC, Lab Chip, 2012, 12, 2221–2228. [DOI] [PubMed] [Google Scholar]
- 12.Walker GM and Beebe DJ, Lab Chip, 2002, 2, 131–134. [DOI] [PubMed] [Google Scholar]
- 13.Dimov IK, Basabe-Desmonts L, Garcia-Cordero JL, Ross BM, Ricco AJ and Lee LP, Lab Chip, 2011, 11, 845–850. [DOI] [PubMed] [Google Scholar]
- 14.Liang DY, Tentori AM, Dimov IK and Lee LP, Biomicrofluidics, 2011, 5, −. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hsu Y-H, Moya ML, Hughes CCW, George SC and Lee AP, Lab Chip, 2013, 13, 2990–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bruus H, Theoretical microfluidics, Oxford University Press, 2008. [Google Scholar]
- 17.Duffy DC, McDonald JC, Schueller OJA and Whitesides GM, Analytical Chemistry, 1998, 70, 4974–4984. [DOI] [PubMed] [Google Scholar]
- 18.Anna SL, Bontoux N and Stone HA, Applied Physics Letters, 2003, 82, 364–366. [Google Scholar]
- 19.Song H, Tice JD and Ismagilov RF, Angewandte Chemie International Edition, 2003, 42, 768–772. [DOI] [PubMed] [Google Scholar]
- 20.Thorsen T, Roberts RW, Arnold FH and Quake SR, Physical Review Letters, 2001, 86, 4163–4166. [DOI] [PubMed] [Google Scholar]
- 21.Baroud CN, Gallaire F and Dangla R, Lab Chip, 2010, 10, 2032–2045. [DOI] [PubMed] [Google Scholar]
- 22.Kenis PJA, Ismagilov RF and Whitesides GM, Science, 1999, 285, 83–85. [DOI] [PubMed] [Google Scholar]
- 23.Ismagilov RF, Stroock AD, Kenis PJA, Whitesides G and Stone HA, Applied Physics Letters, 2000, 76, 2376–2378. [Google Scholar]
- 24.Du W, Li L, Nichols KP and Ismagilov RF, Lab Chip, 2009, 8, 2286–2292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li L, Karymov MA, Nichols KP and Ismagilov RF, Langmuir, 2010, 26, 12465–12471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shen F, Davydova EK, Du W, Kreutz JE, Piepenburg O and Ismagilov RF, Analytical Chemistry, 2011, 83, 3533–3540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shen F, Du W, Kreutz JE, Fok A and Ismagilov RF, Lab Chip, 2010, 10, 2666–2672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sun B, Shen F, McCalla SE, Kreutz JE, Karymov MA and Ismagilov RF, Analytical Chemistry, 2013, 85, 1540–1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sun B, Rodriguez-Manzano J, Selck DA, Khorosheva E, Karymov MA and Ismagilov RF, Angewandte Chemie International Edition, 2014, 53, 8088–8092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. http://ismagilovlab.caltech.edu/multimedia/slip_chip_movies.shtml.
- 31.Witters D, Sun B, Begolo S, Rodriguez-Manzano J, Robles W and Ismagilov RF, Lab Chip, 2014. [DOI] [PubMed] [Google Scholar]
- 32.Shen F, Sun B, Kreutz JE, Davydova EK, Du W, Reddy PL, Joseph LJ and Ismagilov RF, Journal of the American Chemical Society, 2011, 133, 17705–17712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kreutz JE, Munson T, Huynh T, Shen F, Du W and Ismagilov RF, Analytical Chemistry, 2011, 83, 8158–8168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Reid RC, Prausnitz JM and Sherwood TK, The properties of gases and liquids, McGraw-Hill, 1977. [Google Scholar]
- 35.Takagi H, Maeda R, Ozaki K, Parameswaran M and Mehta M, Phase transformation type micro pump, 1994. [Google Scholar]
- 36.Zhizhong Y and Andrea P, Journal of Micromechanics and Microengineering, 2005, 15, 643. [Google Scholar]
- 37.Begolo S, Shen F and Ismagilov RF, Lab Chip, 2013, 13, 4331–4342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kane RS, Takayama S, Ostuni E, Ingber DE and Whitesides GM, Biomaterials, 1999, 20, 2363–2376. [DOI] [PubMed] [Google Scholar]
- 39.Song H, Chen DL and Ismagilov RF, Angewandte Chemie-International Edition, 2006, 45, 7336–7356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Teh S-Y, Lin R, Hung L-H and Lee AP, Lab Chip, 2008, 8, 198–220. [DOI] [PubMed] [Google Scholar]
- 41.Theberge AB, Courtois F, Schaerli Y, Fischlechner M, Abell C, Hollfelder F and Huck WTS, Angewandte Chemie International Edition, 2010, 49, 5846–5868. [DOI] [PubMed] [Google Scholar]
- 42.Sackmann EK, Fulton AL and Beebe DJ, Nature, 2014, 507, 181–189. [DOI] [PubMed] [Google Scholar]
- 43.Huh D, Hamilton GA and Ingber DE, Trends in Cell Biology, 2011, 21, 745–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Huh D, Torisawa Y.-s., Hamilton GA, Kim HJ and Ingber DE, Lab Chip, 2012, 12, 2156–2164. [DOI] [PubMed] [Google Scholar]
- 45.Ma L, Kim J, Hatzenpichler R, Karymov MA, Hubert N, Hanan IM, Chang EB and Ismagilov RF, Proceedings of the National Academy of Sciences, 2014, 111, 9768–9773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yager P, Edwards T, Fu E, Helton K, Nelson K, Tam MR and Weigl BH, Nature, 2006, 442, 412–418. [DOI] [PubMed] [Google Scholar]
- 47.Yager P, Domingo GJ and Gerdes J, Annual Review of Biomedical Engineering, 2008, 10, 107–144. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


