Reshaping the Cortical Connectivity Gradient by Long-Term Cognitive Training During Development

Abstract

The organization of the brain follows a topological hierarchy that changes dynamically during development. However, it remains unknown whether and how cognitive training administered over multiple years during development can modify this hierarchical topology. By measuring the brain and behavior of school children who had carried out abacus-based mental calculation (AMC) training for five years (starting from 7 years to 12 years old) in pre-training and post-training, we revealed the reshaping effect of long-term AMC intervention during development on the brain hierarchical topology. We observed the development-induced emergence of the default network, AMC training-promoted shifting, and regional changes in cortical gradients. Moreover, the training-induced gradient changes were located in visual and somatomotor areas in association with the visuospatial/motor-imagery strategy. We found that gradient-based features can predict the math ability within groups. Our findings provide novel insights into the dynamic nature of network recruitment impacted by long-term cognitive training during development.

Supplementary Information

The online version contains supplementary material available at 10.1007/s12264-023-01108-8.

Introduction

One of the major organizing principles in the brain is hierarchy [1–3], which supports highly-efficient information integration across the cortex, as reflected by gene expression [4–6], cytoarchitecture [5, 7], functional connectivity [8, 9], and task processing [10, 11]. Recently, the connectivity gradient derived from resting-state functional magnetic resonance imaging (rs-fMRI) data was proposed to construct functional hierarchy coordinates using diffusion maps [12], a nonlinear manifold learning approach; such gradients could manifest the functional systems of the brain in a continuous way, in which the principal gradient in adults anchors primary sensory areas at one end and transmodal areas at the other end [2, 8]. Notably, this connectivity gradient across the cortex can be modified by multiple factors, such as development [13], aging [14], and cognitive disorders [9, 15–18]. Moreover, an alteration in gradient has been found to be associated with gains or deficits in cognitive performance [9, 14, 18]. Since several studies have shown the functional network recruitment induced by training [19–22], whether and how might cognitive training affect the brain connectivity gradient? This question remains to be investigated.

Cognitive training facilitated by neural plasticity, is a kind of target-oriented learning for skill acquisition and expertise [23–31], which has proven to have a great impact on specific cognitive performance, brain structure, and function. Through cognitive training, large-scale functional neural circuitry is recruited and integrated to promote the acquisition of unique skills [19, 20, 32, 33]. Here, abacus-based mental calculation (AMC) training, a unique form of cognitive training, is a good window with which to explore the cognitive training effect on the hierarchical topology of the brain. This training, featuring visuospatial strategies to imagine and manipulate virtual beads [23, 34], promotes cognitive performance in visuospatial working memory [35–38], executive function [39, 40], and numerical processing efficiency [41, 42]; and the corresponding brain changes in the frontoparietal and occipital regions that support these behavioral improvements have been confirmed in studies of brain anatomy [43, 44], activation [37, 45], and functional topology [21, 22, 40, 46]. Especially, AMC training enhances local efficiency in the visual network [22, 46] and promotes segregation in the visual, somatomotor, and default-mode networks [21]. Given the evidence that AMC training reshapes the functional architecture of primary and default-mode regions, exploration of the training-induced gradient changes has great potential.

During childhood, cognitive training can be administered over many years for the acquisition of specific skills. However, the effect of long-term cognitive training during development on the brain connectivity gradient remains to be explored. Development plays a critical role in promoting the dynamic reorganization of brain function [47–50], which is supported by the ground truth of gradual maturation of brain structure [51–53] during early life. Notably, gradient studies have captured the switch in connectivity gradient ranks from neonatal/childhood to adolescence [13, 54, 55]. More specifically, this switch involves the rank exchange of explained variance between primary–transmodal and sensorimotor–visual gradients, where the former gradient represents the information integration along the hierarchical organization from primary sensory to transmodal regions, and the latter reveals the segregated pattern with information inputs received from different primary sensory areas [2]. This emergence of a primary–transmodal gradient as the principal gradient might result from the different maturation peaks of functional systems [13], and be associated with the conceptual shift from concrete recognition to abstract logical thinking [56, 57], as well as closely related to the dynamic balance of local segregation and global integration [47–49] in brain organization. Researchers have also depicted the longitudinal gradient changes including expansion of global topography and focal tuning in primary and default-mode regions [55], which is mediated by the dynamic nature of network recruitment during development.

To date, studies on this topic have characterized the connectivity gradient at the group population level [8, 9, 13, 54]; however, it is essential to examine and interpret the connectivity gradient at the level of individual brains. The inter-subject differences in thought or behavior may result from individual differences in brain anatomy and function. It draws research attention to the individuals [58–60], as traditional group research has highlighted the average characteristics of cohorts but ignores the variability among individuals. Brain functional networks are highly stable within a single individual [61, 62] but vary widely across individuals [61, 63, 64]. Thus, it would be of benefit to depict connectivity gradients at the individual level.

Drawing on the above investigation, we propose the following hypotheses: (1) Long-term AMC training may affect the typical developmental gradient changes including the rank switch and regional changes in gradients; (2) The training can induce regional gradient changes in primary and default-mode regions due to its visuospatial dependence; and (3) These gradient changes may be associated with the training-related improvement in cognitive ability. To test these hypotheses, we applied a longitudinal (pre-test vs post-test) and cross-sectional (training vs controls) dataset with a 5-year AMC training intervention. More specifically, we first characterized typical and training-intervened developmental gradient changes between childhood and adolescence using the longitudinal dataset. Next, we investigated changes in the training-induced regional gradient using the cross-sectional dataset for a large sample size. Finally, we assessed the association between the observed gradient changes and gains in math ability across participants using prediction models.

Materials and Methods

Participants

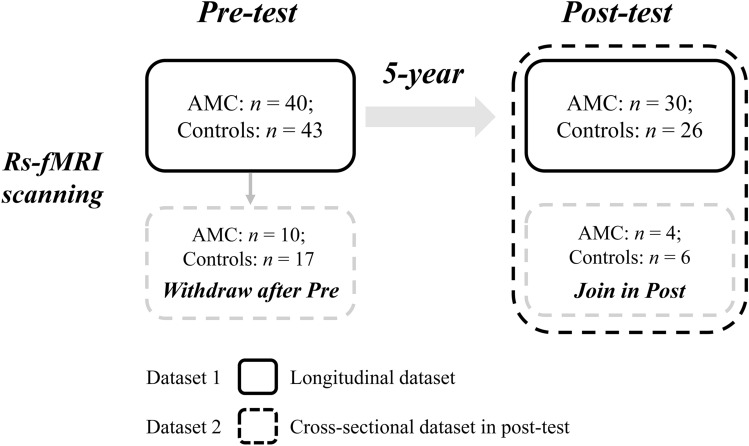
All participants were from a longitudinal AMC study conducted in Qiqihar, China, which aimed to investigate the potential change in brain and behavior with 5-year continuous training. They were taught by the same elementary school curriculum and were randomly assigned into two groups (AMC and control) at the baseline of recruitment. The current study included a total of 93 children (AMC, n = 44; controls, n = 49), who attended the pre-test fMRI and post-test (5 years after the pre-test). In the pre-test stage, 83 participants in the first grade of primary school participated in fMRI scanning; of them, 27 children dropped out of the test after completing the pre-test (Fig. 1). After 5 years, 66 participants (AMC, n = 34; controls, n = 32) attended the post-test fMRI scanning to form the cross-sectional dataset, including 10 participants who lacked fMRI scanning in the pre-test stage. The longitudinal dataset comprised the data of 56 children who underwent two scans in both the pre- and post-test stages, and the AMC (n = 30) and control (n = 26) groups in this dataset also did not differ significantly in terms of age (t_[54] = −1.984, P = 0.052) and gender (χ² = 0.107, P = 0.743; for details, see Table S1). Sixteen children (9 in the pre-test and 7 in the post-test) in the longitudinal dataset were excluded because of excessive head motion (3 mm and 3° in max head motion; Fig. S1) or poor imaging quality. Participants in the post-test cross-sectional dataset between groups did not show significant differences in terms of age (t_[64] = −1.428, P = 0.158) and gender (χ² = 0.001, P = 0.976). Intelligence in the groups was also matched in both pre-test (t_[77] = 0.651, P = 0.517) and post-test (t_[63] = 1.079, P = 0.284; Fig. S2) stages, which was measured by the combined Raven test [65].

Fig. 1.

Schematic of the longitudinal and cross-sectional dataset composition.

Accordingly, 40 children (AMC, n = 24) in the longitudinal dataset and 59 (AMC, n = 31) in the cross-sectional dataset were included for further analyses. All participants had normal hearing and normal or corrected-to-normal vision, no known neurological or psychiatric disorders, and no special educational assistance requirements. This study protocol was approved by the Research Ethics Review Board of Zhejiang University in China. Informed consent was signed by the parents (or other guardians) of the participants. Though it was unavoidable that many subjects withdrew during the long-term training schedule, this dataset provided a precious opportunity to explore the development of the brain and behavior of primary school children under the interplay of cognitive training and development.

Training Procedure

The AMC children had received five years of training when in the post-test stage, with 2 h of training per week. At the beginning of training, children were taught the basic principles of physical abacus operations: addition, subtraction, multiplication, and division. After mastering the basic principles, they learned to solve arithmetic problems by operating virtual beads in their mind. In the early stage, finger movements were allowed and encouraged to assist mental calculation. Further, children were asked to do mental calculations without finger movements as quickly and accurately as they could. Throughout the long-term course training, children mastered advanced AMC skills to solve more difficult arithmetic problems by increasing the difficulty level of practice. Meanwhile, children in the control group did not receive any physical or mental instructions in the abacus but received traditional school education. Further details about this long-term training procedure can also be found in our previous studies [21, 22, 38].

Math Ability

The math ability of participants in the post-test was measured using the Chinese version of the Heidelberger Rechentest [66], which is a paper-pencil test with good test-retest reliability. The raw score of each participant was converted into a T-score based on the Chinese-adapted city norm [67] for further analysis. Math ability was not tested in the pre-test stage because the participants had not yet received much education in mathematics. The random assignment of these participants to the AMC and control groups should have eliminated the risk of a pre-test group difference in this variable.

Data Acquisition and Preprocessing

MRI scans were acquired using a 1.5-T MR scanner (Achieva, Philips, Amsterdam, Netherlands) with an eight-channel head coil in the First Hospital of Qiqihar. Resting-state functional images were collected using a single-shot echo planer imaging (EPI) sequence as follows: repetition time (TR) = 2000 ms, echo time (TE) = 50 ms, flip angle (FA) = 90°, field of view (FOV) = 230 mm × 230 mm, matrix size = 64 × 64, slice thickness/gap = 5 mm/0.8 mm, and acquisition = 22 slices interleaved. The duration of resting-state data collection was 6 min (180 volumes). High-resolution T1-weighted structural images were acquired using a three-dimensional fast echo sequence as follows: TR = 25 ms, TE = 4.6 ms, FA = 15°, FOV = 256 mm × 256 mm, matrix size = 256 × 256, voxel size = 1 mm³, and acquisition = 150 slices in the sagittal plane.

Rs-fMRI data were preprocessed using DPABI (http://rfmri.org/dpabi) and SPM12 (http://www.fil.ion.ucl.ac.uk/spm) in MATLAB (version 2019b, MathWorks, Natick, USA). The first five images were discarded to eliminate the effects of potentially unstable initial MR signals. The remaining functional images were corrected for differences in slice acquisition timing differences and realigned to account for head motion. All images were aligned to the corresponding T1-weighted images and normalized to the Chinese pediatric template [68] with a resampling voxel size of 4 mm × 4 mm × 4 mm. Some nuisance variables were removed in multiple linear regression analysis, including 24 Friston body-motion parameters and average white matter, cerebrospinal fluid, and global signals. The images were smoothed using a 6-mm full-width half maximum (FWHM) Gaussian kernel and then de-trended. Finally, a band-pass (0.01–0.1 Hz) filter was applied to reduce the effects of physiological noise. The scans with excessive head motion (3 mm and 3° in max head motion) were excluded, so that the influence of head motion was minimized (see details in Fig. S1).

Connectivity Gradient Analysis

Connectivity gradient analysis was applied to reveal low-dimensional functional architecture from high-dimensional connectivity data. The following procedures were conducted for each participant to determine their gradient components: (1) The time series for 22,969 voxels were extracted within a 4-mm mask defined by the automated anatomical labeling template [69], including the subcortical areas. (2) Then the functional connectivity (FC) matrix was constructed by calculating the Pearson correlation between voxels, and the Fisher-Z value was further obtained with a hyperbolic tangent function. (3) The top 10% of weighted connections per row in the FC matrix were retained as in previous studies [8, 9], while other elements were set to 0 for sparsity. (4) The symmetric affinity matrix A was obtained using the normalized cosine distance between each pair of connectivity profiles (every two rows in the FC matrix). (5) Gradient components were calculated by diffusion maps [12] using the BrainSpace toolbox [70]. Details of this algorithm can also be checked in the following description or supplementary materials of a previous study [8].

Diffusion maps are a one-parameter (α) family of graph Laplacians that integrate local information into a global description. It is a non-linear dimensionality reduction technique to seek nonlinear mapping based on the diffusion operator P_α defined as P_α = D_α⁻¹W_α, where W_α = D^−1/αAD^−1/α is calculated by normalizing the affinity matrix A and D_α is the degree matrix derived from W_α [70]. The diffusion parameter α in this study was set to 0.5, which retains the global relations between data points in the embedding space as suggested by previous studies [8, 9]. With an appropriately normalized random walk process, the parameter α controls the influence of sampling point density on the manifold (α = 0, maximal influence; α = 1, no influence) to reflect the geometry of the set in low-dimensional embedding. Next, the eigenvalues and eigenvectors of the diffusion operator P_α were computed to build the new low-dimensional representation. This mapping technique translates the connectivity relationship into distance and represents the global connectivity architecture as a distribution of cortical points in embedding space. The cortical points in this space are close when their connectivity profiles are highly similar, and far apart with lower similarity of connectivity profiles. Regarding the high explained variance (>50%) of dominant gradients, the current study only focused on the first two gradient components for further analyses: the primary–transmodal gradient and sensorimotor–visual gradient.

Gradient Alignment

A common functional coordinate space enabling comparison across individuals is essential for understanding individual differences. Several orthonormal alignment approaches [70–72] allow the alignment from an individual gradient to the group-level gradient component template to improve comparability and correspondence. For example, for a source Φ_S and a target Φ_T, Procrustes analysis can seek an orthogonal linear transformation Q_S,T = VU^T via singular value decomposition (SVD; UΣV^T = Φ_T^T⊙Φ_S, the symbol ⊙ is the Hadamard product) to align the source to the target through multiple iterations. To investigate the developmental rank switch in the longitudinal dataset, we aligned the gradient components of each individual across stages and groups by Procrustes rotation to the corresponding template, which was generated from each stage and each group separately. When exploring the regional gradient changes in the longitudinal or cross-sectional dataset, we also performed Procrustes alignment to align each individual’s components in the post-test to the group-level gradient template [71], which was from an average connectivity matrix with both the AMC and control groups in the post-test. Gradient alignment is critical for detecting the regional changes of cortical points in common gradient space.

Gradient Rotation Estimation

Rotation angle (RA) can be derived from the two-dimensional (2D) gradient transformation matrix, which is calculated as the indicator to measure the rotational shifting between two gradient representations with the first two components using Procrustes rotation. For a source Φ_S and a target Φ_T, Procrustes analysis can seek an orthogonal linear transformation Q_S,T = VU^T via SVD to align the source to the target [70, 71, 73]. Given any pair of 2D gradient embedding representations, we can get the RA between source and target from the 2D transformation matrix Q_S,T, which is equal to the 2D rotation matrix. This allows us to estimate gradient shifting more precisely with quantitative RA.

Ability Prediction

We built prediction models to associate our gradient features with math ability by testing cross-sectional (post-test) datasets. In this model, input data were the aligned gradient scores and math ability scores. We applied leave-one-out cross validation (LOOCV) to assess the prediction model, which divided the input data into a training set and a testing set. A feature selection procedure was carried out based on the voxel-wise brain-behavior partial correlation between gradient score and math ability, in which the covariates (age, sex, and head motion) were controlled. The mean gradient scores of these clusters (P < 0.05, cluster size > 50) were used as brain features, thus the number of brain features was the number of clusters. Next, a linear predictive model was built between the gradient features and math ability scores using the training set. The math ability score for the left-out test participant was predicted with the input of gradient features in the testing set into the predictive model. With LOOCV, we obtained the predicted math ability score for each participant, and the correlation coefficient between predicted scores and actual scores was accessed as the measurement of performance for this model. Finally, we tested the significance and validity of the predictive model with permutation testing (1000 random shuffling).

Results

Improvement of Math Ability in the Training Group

After 5 years of training, the AMC group (mean ± SD = 72.0 ± 7.9) showed significantly better math ability than the control group (mean ± SD = 56.5 ± 8.5) (t_[58] = 7.183, P < 0.0001; Fig. S2A) in the post-test stage.

Rank Switch of Developmental Gradient Across Individuals

Focusing on development, we combined both the AMC and control groups in the longitudinal dataset (see Materials) and constructed stage-averaged gradient templates of the pre-test (7 years old) and post-test (12 years old). The gradient components were not only discriminated by the explained variance rank: the component with the largest variance was the principal gradient (G1), and that with the second highest variance was the secondary gradient (G2); but also by spatial distribution: the primary–transmodal gradient placed the primary sensory areas at one end and the transmodal areas at the other end, while the sensorimotor–visual gradient separated the sensorimotor and visual areas. We found that the ranks of these first two gradients switched between the 7- and 12-year-old stages (Fig. 2). In the 7-year-old stage, G1 corresponded to the sensorimotor–visual gradient, while G2 corresponded to the primary–transmodal gradient [13, 54]. In contrast, the 12-year-old stage exhibited adult-like gradient ranks [8, 9, 54], where G1 and G2 corresponded to the primary–transmodal and sensorimotor–visual gradients, respectively (Fig. 2A). Such exchange of explained variance rank between primary–transmodal and sensorimotor–visual gradients from the 7- to the 12-year-old stage signified a rank switch in gradient across development.

Fig. 2.

Developmental rank switching in the first two leading gradients across individuals. A Developmental rank switches across individuals revealed by greater similarity in the gradient pairs of 7-year G2 (7y-G2) and 12-year G1 (12y-G1), and of 7-year G1 (7y-G1) and 12-year G2 (12y-G2) than that in other pairs. The similarity in the spatial distribution between gradient pairs was measured using Pearson’s correlations. The topological maps on the left and bottom of the matrix represent the gradient spatial distribution of the stage-averaged templates, with 7y-G1 and 12y-G2 corresponding to the sensorimotor–visual gradient as well as 7y-G2 and 12y-G1 to the primary–transmodal gradients. B The rank of the primary–transmodal gradient switched from 7y-G2 to 12y-G1, with an increase in explained variance for each participant. The explained variance for each individual across the stages is indicated by solid lines.

The longitudinal nature of the current data allowed the tracking of each participant’s gradient shift across development. Consistent with our findings with the stage-averaged template, we also found the gradient rank switch in individual participants (Fig. 2). Specifically, we evaluated the similarity of the gradient pattern (i.e., the spatial distribution of G1/G2) between the pre- and post-test scans for each participant and identified the rank switch across individuals (Fig. 2A). The similarity in spatial distributions of 7y-G1 and 12y-G2 (both sensorimotor–visual gradients) was higher than that of 7y-G1 and 12y-G1. A similar result was obtained when comparing the similarity in spatial distributions of 7y-G2 and 12y-G1 (both primary–transmodal gradients) with that of 7y-G2 and 12y-G2. We also tracked the explained variances of the first two gradients across developmental stages at the individual level. As shown in Fig. 2B, all of the participants exhibited an increased variance of the primary–transmodal component (from 7y-G2 to 12y-G1) from childhood to adolescence. We also found that most participants had > 50% variance explained by the first two components in this longitudinal dataset. Specifically, the proportion of such participants was 63% in the pre-test and 85% in the post-test (see Fig. S3). Interestingly, the paired t-test in the summed variance of the first two components demonstrated a significant difference between training stages (t_[39] = −2.94, P < 0.01), indicating the increase of variance of the first two components across development.

Training-Induced Modulation in Developmental Gradients

Next, we characterized the longitudinal training-induced changes in developmental gradients with the longitudinal dataset, including global rank switch and regional tuning. To further quantify the gradient rank switch, we calculated the RA (see Methods) between each pair of 2D gradient patterns across groups and stages. Notably, AMC training affected the developmental gradient switch with significant differences of between-group RAs across the pre- and post-tests (Fig. 3A), which resulted in a 46.0° between-group RA in the post-test compared with the 1.5° between-group RA in the pre-test. This revealed the modulation of typical developmental gradients by long-term training. Specifically, in the control group with typically developing individuals, the gradient rank switch between the pre- and post-test stages yielded a developmental clock-wise RA of 96.2°. This shifting of gradient patterns in the control group from pre- to post-test (Fig. 3A, lower) indicated the emergence of a primary–transmodal gradient (sensorimotor and visual systems situated at one end with similarly low locations and default-mode network (DMN) at the other end in G1) as the dominant component during brain maturation, and the controls in the post-test (Fig. 3A, lower-right) presented a gradient pattern similar to that of adults [13]. While in the AMC group, long-term training showed further modification of the developmental RA, which had an increased value to 143.7°, consistent with the individual level (p < 0.001, Fig. 3B). This further rotation of RA in AMC showed that in addition to the development of the primary–transmodal gradient where the DMN came to be located at the upper end of the first principal component (G1) as in the control group, there was a change of the relative location in G1 for the sensorimotor system to shift between DMN and visual (Fig. 3A, upper-right), as compared to similar low-end locations of both sensorimotor and visual systems in G1 in the controls (Fig. 3A, lower-right). These findings are consistent with the fact that AMC is a cognitive training intervention with visuospatial strategy dependence, and are also in line with previous neuroimaging studies of long-term training that has been shown to promote segregation of functional networks [21, 22, 46], while typical development is mainly focused on brain integration for abstract thinking [47–49, 56, 57]. Thus, RA derived from 2D gradient shapes provides a quantitative measure of gradient shifting and the difference of developmental RAs between groups indicates the long-term training effect on the modified balance of different gradient components in AMC relative to that in controls across development.

Fig. 3.

Modulation of the developmental gradient rank switching by long-term AMC training. A RAs of 2D gradient patterns across groups and stages. The 2D gradient space is spanned by G1 and G2 at each stage. The sign of RA is positive along with the clockwise direction from the control group to the AMC group or from pre- to post-test. The scatter plots present the cortical points of the first two gradients at the voxel level, parcellated using the Schaefer atlas into seven networks [91]. Please note that here, the symbols of the first two gradient axes in the pre-test are reversed in both groups for better visualization and understanding, which might result in different developmental RAs compared to the originals (Fig. S4). However, this finding remained robust, in that there is a significant between-group RA difference across pre- and post-test regardless of whether the symbol of the gradient axis in the pre-test is reversed or not. Abbreviations: VN, visual network; SMN, somatosensory/motor network; DAN, dorsal attention network; VAN, ventral attention network; LIB, limbic network; FP, frontoparietal network; DMN, default mode network. B Significant group difference in the developmental RAs in individuals (independent sample t-test, t_[38] = 23.442, ***p < 0.001).

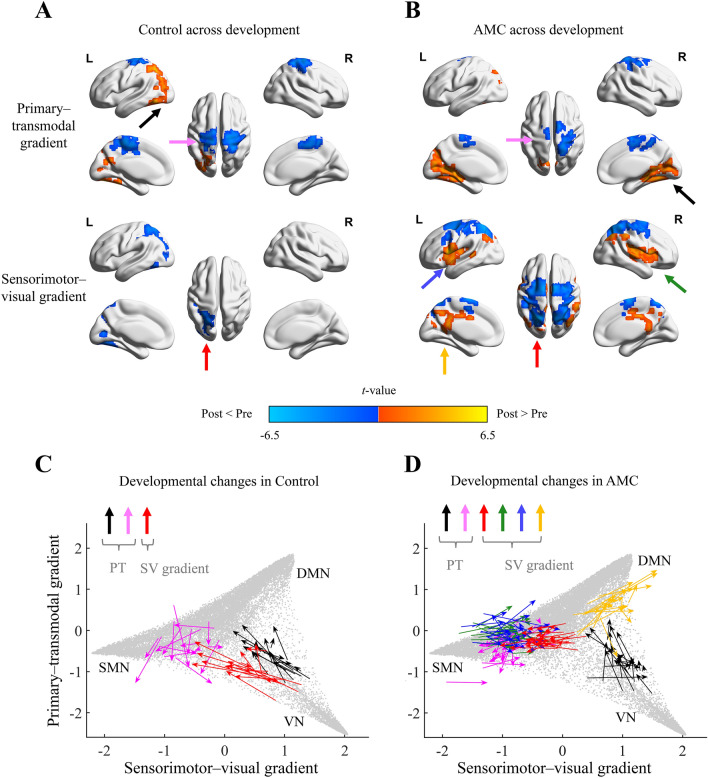
Besides the developmental rank switch, we also investigated regional changes in developmental gradients after aligning each individual’s components at each stage to the post-test gradient template (see “Methods”). In the control group with typical development, regional changes in gradients (P_corrected < 0.05) were mainly located in the somatomotor, parietal, and occipital regions (Fig. 4A, see details in Table S3). As for the AMC group, we found longitudinal changes (P_corrected < 0.05) in the sensorimotor, parietal, and hippocampal regions (Fig. 4B), suggesting an interplay of development and training. We next compared the aligned gradient scores at the post-test stage between groups and identified significant regional changes (P_corrected < 0.05) in the visual and somatomotor areas (Fig. S5A), demonstrating the unique impact of training. Significant interaction effects of the stage (pre-test, post-test) and group (AMC, control) of regional gradient values in these areas were obtained through repeated-measures analysis of variance (ANOVA, P < 0.05, Fig. S5B–D). No significant group difference at the pre-test stage was found after multiple comparison corrections.

Fig. 4.

Longitudinal regional gradient changes modulated by training. A In the control group, the between-stage comparison across pre- and post-test reveals significant regional changes of the primary–transmodal gradient in the somatomotor, parietal, and occipital areas. Decrease and increase of the gradient scores are denoted by cold and warm colors, respectively. B In the AMC group, significant between-stage changes occur in the hippocampal and somatomotor areas along the primary–transmodal gradient, as well as in the sensorimotor, parietal, and cingulate cortical areas along the sensorimotor–visual gradient. C, D Regional gradient changes, denoted by colored arrows in 2D gradient common space, represent the individual shifts from pre- to post-test in the control group (C) and the AMC group (D). The gray dots in the background were generated from the post-test average gradient template. And these colored arrows presented the developmental gradient changes of clusters in individual level within groups. Note that the gradient components for each individual in each stage have been aligned to the post-test average gradient template prior to the between-group or between-stage gradient comparison.

Regional Changes in Gradient Induced by Training

We next applied the cross-sectional (post-test) dataset to localize the regions with significant training-induced changes in the primary–transmodal and sensorimotor–visual gradients, after the alignment from each individual gradient to the post-test template (see Methods). A significant decrease of primary–transmodal gradient score was found in the visual-related areas and decreased sensorimotor–visual gradient score in the somatomotor area (Fig. 5A, P_corrected < 0.05; Table 1); this between-group difference was consistent with that obtained using the longitudinal dataset (Fig. S5A). Both the visual and somatomotor cortical points shifted along the corresponding gradient axes to a more prominent position (i.e., toward the tip) in the hierarchical organization of functional systems as shown in Fig. 5B. These regional changes in gradients were also characterized at the individual level (Fig. 5C).

Fig. 5.

Brain regions with significant training-induced changes in gradients. A The top and bottom panels show decreased scores in the AMC relative to the control group in the primary–transmodal and sensorimotor–visual gradients, respectively. These decreases are denoted by the blue areas. The details, such as the coordinates of the peak points or the voxel size of the labeled clusters C1, C2, and C3, can be checked in Table 1. B Scatter plot for the trajectory of the shifted clusters (C1, C2, and C3) from the control group to the AMC group (denoted by yellow arrows) in the 2D gradient coordinate system. The background dots were generated from the post-test AMC group. C Individual gradient shifts from the control group (black open circles) to the AMC group (black filled circles) were characterized by calculating the mean gradients of these three clusters (C1, C2, and C3). The yellow arrow in each figure represents the group-level gradient shift from the control to the AMC group in the post-test.

Table 1.

Details of significantly changed regions in gradients.

Cluster label	Anatomical regions	MNI coordinates	Cluster size (voxels)
C1	Left SOG/MOG/IOG/MTG/FG	(− 38, − 76, 16)	465
C2	Right SOG/MOG/IOG/MTG/ITG/FG/CAL/CUN	(26, − 78, 32)	423
C3	Left SFG/MFG/PreCG/PostCG/SPG/PCUN/PCL, L/R SMA	(− 10, 6, 68)	375

As shown in Fig. 5A, cluster C1 corresponds to the left visual area of the primary–transmodal gradient, C2 to the right visual area of the primary–transmodal gradient, and C3 to the somatomotor area of the sensorimotor–visual gradient. Abbreviations: FG, fusiform gyrus; IOG, inferior occipital gyrus; ITG, inferior temporal gyrus; MFG, middle frontal gyrus; MOG, middle occipital gyrus; MTG, middle temporal gyrus; PCL, paracentral lobule; PCUN, precuneus; PostCG, postcentral gyrus; PreCG, precentral gyrus; SFG, superior frontal gyrus; SMA, supplement motor area; SOG, superior occipital gyrus; SPG, superior parietal gyrus.

Seed-based functional connectivity analysis revealed that the bilateral visual-related areas in AMC showed increased connections with each other and decreased connections with the medial default-mode network areas, including the precuneus and posterior cingulate gyrus. In addition, the somatomotor area exhibited increased connections with the postcentral gyrus (PostCG), supramarginal gyrus (SMG), superior temporal gyrus, and inferior parietal lobule (Fig. S6). This evidence indicated enhanced segregation of the visual, somatomotor, and default-mode networks, which resulted in regional gradient changes with long-term training. These results remained stable when the covariates (age, sex, and head motion) were controlled (Fig. S7), except that the right visual area showed a marginally significant group difference in the primary–transmodal gradient. The reliability of the results was also confirmed when scrubbing fMRI volumes with framewise displacement >0.3 mm (Figs S8, 9).

Relation to Math Ability

We finally associated gradient scores with math ability in the post-test (see “Methods”). The top related features were identified in the sensorimotor–visual gradient when the covariates (age, sex, and head motion) were controlled. Specifically, it included the middle frontal gyrus (MFG), parietal lobe, and calcarine sulcus of the AMC group (Fig. 6A), as well as the somatomotor, medial prefrontal cortex (mPFC), and anterior cingulate cortex (ACC) of the control group (Fig. 6C). Using the mean gradient scores of the above clusters as features, these prediction models showed good performance in the AMC (r = 0.476, P_permute < 0.01, Fig. 6B) and control groups (r = 0.603, P_permute <0.005, Fig. 6B). These results demonstrated that gradient features can predict math ability well, and the long-term training reshapes the gradient-based features underlying math ability relative to the control group.

Fig. 6.

Prediction of math ability with the sensorimotor–visual gradient scores. A The most related features are located in the MFG, parietal lobule, and calcarine sulcus in the AMC. Clusters with a positive correlation between gradient scores and math scores are denoted in red, and negative correlation in blue. B The predictive model shows good performance in the AMC group (r = 0.476, P_permute < 0.01). C, D In the control group, these gradient features in the somatomotor, mPFC, and ACC areas predict math scores well (r = 0.603, P_permute < 0.005).

Discussion

Using a randomized controlled study design with longitudinal and cross-sectional assessments, we revealed the reshaping effect of long-term AMC training on the developmental brain functional hierarchy. Briefly, we found that (1) development, as the main power, drove the developmental gradient changes including both the rank switch and regional changes in connectivity gradients across individuals; (2) long-term AMC training, a cognitive training intervention with visuospatial strategy dependence, modified the developmental rank switch and reorganized the connectivity gradient regionally; and (3) the predictive models performed well in predicting the math ability, indicating different gradient-based features across groups. These results shed light on the impact of cognitive training on the developmental functional architecture and also have implications for extracurricular education.

Training Modulates the Developmental Gradients During Adolescence

Neural development is a key driver of gradient reconfiguration in developing children. At the group level, our longitudinal results (Fig. 2) confirmed previous direct [13, 55] and indirect findings [8, 54] in typically developing children, namely the rank switch between the primary–transmodal and sensorimotor–visual gradients from childhood to adolescence. We further focused on the gradient rank switch in individuals (Fig. 2A). The robust rank switches across individuals in both the AMC and control groups were in line with the growth trajectory of the human brain, which is characterized by later structural maturation in the association cortex relative to the unimodal areas [51–53], and by the shift in functional systems from a local anatomical emphasis to a more distributed architecture [47–49]. Connectivity gradients capture multiple brain functional architectures, while the rank switch involves the primary–transmodal and sensorimotor–visual gradients that have the leading dominance in these modes. And the first two gradients played a more important role in brain function development (Fig. S3). The primary–transmodal gradient leads the integrated mode for information processing, while the sensorimotor–visual gradient exhibits a relatively segregated pattern [2, 8]. The emergence of the more integrated primary–transmodal gradient from childhood to adolescence coincides with the conceptual shift from concrete recognition to abstract logical thinking [56, 57]. The global transition in gradient rank results from the dynamic nature of network recruitment during adolescence, and results in a new balance in brain integration and segregation.

Furthermore, with development, long-term training exerted an additional impact on longitudinal gradient changes. To be precise, we found a developmental RA close to 90° in typically developing controls, while a larger developmental RA was found in the AMC group (Fig. 3), which resulted in a significant difference between group RAs across the pre- and post-tests. These training-induced additional developmental RAs implied different demands of development and training on brain global integration and local segregation, where development promoted the emergence of the more integrated pattern (primary–transmodal gradient) for information integration but the training required more weight on the segregated pattern (sensorimotor–visual gradient) for high-efficient localized sensory processing. These findings are consistent with evidence that cognitive training promotes the segregation of sensory systems [19, 21, 22, 33] for high processing efficiency. The changes in global developmental RA (Fig. 3) and regional gradient (Fig. 4) were pushed by development and further modified by long-term AMC training. Long-term training administered over the years modified the typical developmental gradient changes to form a new trade-off between integration and segregation, towards high-level skill acquisition.

The Important Role of Visuospatial Strategy in AMC Training

We applied an independent sample t-test in the cross-sectional dataset to assess the regional gradient changes in the post-test (Fig. 5). Decreased gradient scores were found in visual and somatomotor areas, which play important roles in visuospatial/visuomotor processing [21, 22, 74, 75], revealing more involvement of visuospatial/motor processing in abacus trainees [23, 75–77]. Specifically, the altered gradient scores of visual clusters showed that the cortical points of these two clusters became closer to the primary visual (V1) area, which is the reference point in the visual network, as well as the somatomotor cluster closer to the primary sensorimotor (M1/S1) area, which is the reference point in the sensorimotor network [2, 8], indicating the higher similarity of connectivity profiles between these areas and the reference points in networks after training. These regional gradient shifts from a more central point to tips in the sensory system imply a training-induced trend to more local segregation for more efficient information processing, as reflected by the localized network recruitment in sensory systems with training [19–22, 46]. Notably, the more segregated sensory systems were also evidenced by increased functional connections within visual areas, decreased connections between visual and medial DMN areas, and enhanced connections between somatomotor and PostCG areas (Fig. S6). This corresponds well to the enhanced local efficiency of the visual area [22, 46] and stronger segregation of visual and somatomotor networks [21] after long-term AMC training, which promoted higher efficiency in sensory information processing. These functional changes were also supported by the strengthened sensory structure with training, including enhanced white matter in the occipitotemporal and premotor projections [43] and decreased gray matter volume in the fusiform gyrus [44] with training.

Therefore, our gradient-based analysis extended the previous findings using graph theory or module analyses [21, 22, 46] to identify training-induced brain functional changes along the macroscale functional hierarchy. This demonstrated that long-term AMC training is powerful enough to change the brain's functional architecture in facilitating skill acquisition on the basis of visuospatial strategy dependence. Collectively, regional gradient changes in visual and somatomotor areas revealed the integral enhancement of information processing efficiency in these sensory systems. The more segregation in sensory systems, resulting from high dependence on visuospatial strategy in AMC training, is of great benefit for the autonomy of skill.

Discrepancy of Gradient-based Features Between Groups

The discrepancy of gradient-based features in the prediction model between groups implied a distinct neural mechanism of AMC training underlying math ability (Fig. 6). In the AMC group, the most related features mainly involved the MFG, calcarine sulcus, and parietal regions (Fig. 6A), which are vital in motor-imagery processing [78, 79] and visuospatial working memory [45, 74]. The critical role of the motor-imagery network in AMC was also revealed by the enhanced connections with PostCG/SMG areas in seed-based connectivity analysis (Fig. S6C). In the control group, a significant association of sensorimotor–visual gradient scores and math ability was found in the somatomotor, mPFC, and ACC areas (Fig. 6B). Among these areas, the somatomotor area is involved in executive control and visuomotor functions [80–82]. The mPFC, as the transmodal hub, plays an important role in the retrieval of long-term memory and decision-making [83]. The involvement of the ACC in attention allocation in mental arithmetic tasks has also been reported [74, 84–87]. These features in the control group demonstrated the greater dependence of normal mental arithmetic on higher cognitive attention and control. Notably, this somatomotor cluster was a subset of the somatomotor cluster C3 (Fig. 5A), which showed a significantly decreased gradient score of AMC relative to controls. Collectively, this systematic shift of gradient-based features between groups indicates that AMC training has a unique shaping effect on the math ability functional system. Such training reshapes the macroscale connectivity profiles to enable the formation and consolidation of more efficient processing modes in mental calculation, and ultimately may mediate the brain-behavior relationship at the system level.

Reshaping Brain Functional Architecture by Cognitive Training

The brain is a multiscale system in which the functional architecture comprises multiple hierarchical connectome modes [8, 88, 89] to support diverse and flexible tasks through dynamic processes [89]. The efficient neural plasticity during development enables long-term cognitive training as an effective intervention to further reconfigure brain function along the functional hierarchy. Here, we suggest that, with skill acquisition, the training reshapes functional circuits with enhanced local efficiency for the sake of more efficient sensory information processing. Further, training promotes a new trade-off between brain integration and segregation to achieve the autonomy of task processing, in which controls rely on the integration of the association cortex to complete math tasks while AMC-trained individuals focus on the efficient localized processing of sensory systems. Overall, long-term cognitive training based on a specific strategy has a unique reshaping effect on the developmental functional architecture and promotes behavioral performance by placing different demands on local segregation and global integration [19, 20, 89].

Limitations and Extensions

Several limitations should be noted when interpreting this work. First, although the study had a longitudinal design, we mainly focused on the post-test stage because of the limited number of overlapped sample points. A longitudinal design with denser sampling points is necessary for a more systematic exploration of the dynamic process of the training-induced changes in the developmental gradient. Second, searching for the appropriate intrinsic coordinate system remains a challenge in connectivity gradient studies. It would be beneficial to establish an intrinsic coordinate [2] for a precise description of gradient changes. Third, the small sample size must be noted as a limitation of this study. A larger sample size is important to improve reliability and reproducibility in future studies. We already identified changes in gradient scores in specific regions. However, gradient rank switching and regional shifting induced by training are macroscopic changes that may impact other cognitive abilities. Therefore, it will be interesting to study the transfer effect of cognitive training with macroscopic gradient changes. Mapping the training-induced gradient changes has important implications for characterizing the development of children’s cognitive function [90]. Besides, the connectivity gradient exhibits stable architecture in large cohorts but also presents individual differences. It offers high potential to explore the “fingerprint” of macroscale connectivity gradients in individuals.

Conclusion

Our findings revealed the changes in developmental gradients induced by long-term AMC training. By demonstrating the emergence of default networks in adolescents, we found that long-term training modulated the shifting and regional changes in gradients across development. Furthermore, the training-induced regional gradient changes in visual and somatomotor areas revealed the reorganization of functional architecture in sensory systems towards high local efficiency with more segregation. The sensorimotor–visual gradient scores predicted math ability well, indicating a systematic shift of gradient-based features underlying math ability. These findings offer novel insights into the cognitive training-induced reconfiguration of functional architecture and have implications for extracurricular education.

Supplementary Information

Below is the link to the electronic supplementary material.

Data and Code Availability

The gradient analysis codes are adapted from the open-access toolbox BrainSpace developed by Vos de Wael [70], which is available at https://github.com/MICA-MNI/BrainSpace. The datasets that support the findings of this study are only available on reasonable request to chenfy@zju.edu.cn.

Conflict of interest

The authors declare that there are no conflicts of interest.