Antifragility as a complex system’s response to perturbations, volatility, and time

Abstract

Antifragility characterizes the benefit of a dynamical system derived from the variability in environmental perturbations. Antifragility carries a precise definition that quantifies a system’s output response to input variability. Systems may respond poorly to perturbations (fragile) or benefit from perturbations (antifragile). In this manuscript, we review a range of applications of antifragility theory in technical systems (e.g., traffic control, robotics) and natural systems (e.g., cancer therapy, antibiotics). While there is a broad overlap in methods used to quantify and apply antifragility across disciplines, there is a need for precisely defining the scales at which antifragility operates. Thus, we provide a brief general introduction to the properties of antifragility in applied systems and review relevant literature for both natural and technical systems’ antifragility. We frame this review within three scales common to technical systems: intrinsic (input-output nonlinearity), inherited (extrinsic environmental signals), and interventional (feedback control), with associated counterparts in biological systems: ecological (homogeneous systems), evolutionary (heterogeneous systems), and interventional (control). We use the common noun in designing systems that exhibit antifragile behavior across scales and guide the reader along the spectrum of fragility–adaptiveness–resilience–robustness–antifragility, the principles behind it, and its practical implications.

1. Introduction

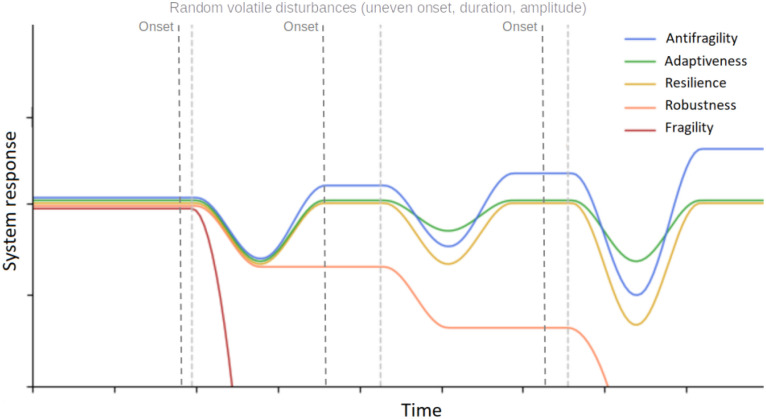
Antifragile is a term coined to describe the opposite of fragile, as defined in a recent book that generated significant interest in both the public and scientific domain¹. Although the term has a wide range of applications, it contains a precise and mathematical definition. Systems or organisms can be defined as antifragile if they derive benefit from systemic variability, volatility, randomness, or disorder². To get an intuition, we provided samples of a system’s reference behaviors in Fig. 1, where three small and large disruptions (i.e., in amplitude) occur at random times and inject, through their unexpected onset and duration, volatility, randomness, or disorder in a system’s dynamics.

Figure 1.

Figure adapted from Axenie et Saveriano³ - Perspective on a dynamical system’s behaviors spectrum: Fragile–Adaptive–Resilient–Robust–Antifragile responses. Example disturbances have random onset, duration (i.e., volatility), and amplitude. Each type of system response captures the predominant traits of the spectrum members.

In mathematical terms, antifragility is a nonlinear convex response to a well-defined payoff function that a system exhibits in the face of volatility. This response enhances the system’s ability to not only withstand perturbations (robust) but even benefit from them (antifragile). Although the antifragility framework emerged in the context of financial risk analysis, due to its universal mathematical formalism and principles, it has recently drawn attention and has been applied within different concepts across domains: in biology⁴, in socio-economics⁵, in urban planning⁶, and risk analysis⁷. Applied antifragility theory extends Nassim Taleb’s antifragility principle to the rank of system design methodology across disciplines¹.

1.1. Defining terms across technical and natural systems

Herein, we draw from the body of literature on technical systems (e.g., road traffic and robotics control systems) and biological systems (e.g., cancer therapy, antibiotics, and agricultural pest management) to define the scales of antifragility theory and unify definitions from natural and technical systems. The perspective manuscript is organized into three major sections that describe the scales of the applied antifragility spectrum in technical systems: 1) intrinsic, 2) inherited, and 3) induced antifragility. Each scale of antifragility in technical systems has its analogue in natural (biological) systems: ecological, evolutionary, and interventional antifragility. We provide definitions for each proposed antifragility scale and review existing literature to provide examples of successful practical instantiations to a broad audience.

As we go up in the spectrum from the bottom (i.e., intrinsic or ecological antifragility), the response properties of the dynamical system and its capacity to gain from stressors and anticipate random and volatile events increase. Intrinsic/ecological antifragility describes the system’s internal dynamics without external interactions and intervention. Inherited/evolutionary antifragility describes the system’s dynamics under external signals that modulate the system’s internal dynamics. Finally, induced/interventional antifragility introduces the closed-loop (behaviour) dimension of antifragility, where the system is connected to control or driving signals. Across these scales, the recently formed Applied Antifragility Group¹ has proposed three Paths forward for characterizing, designing, and building systems that behave antifragile in the face of uncertainty, volatility, and randomness:

• Path 1 to reach intrinsic/ecological antifragility: Mathematical identification of second-order effects in the system response characterizing antifragile behaviour;

• Path 2 to reach inherited/evolutionary antifragility: Mapping the dynamics of the system to physical principles of criticality and evolution to describe reaching an antifragile state;

• Path 3 to reach induced/interventional antifragility: Nonlinear control synthesis or learning of optimal driving signals to push dynamical systems to antifragile regions in their response spectrum;

It is important to note that, technical systems are typically built as homogeneous systems, i.e., all components share the same properties (i.e., spatial, temporal, structural, and functional). However, most natural systems are heterogeneous, where a few components are closer, faster, stronger, or more relevant than others. Even if we analyze across scales, the common denominator is time. Each scale or property of the system evolves, be it slower or faster. When defining antifragility, time plays an important role. The study of natural systems within the antifragility concept needs special treatment as we typically use limited models for complex, nonlinear natural phenomena and processes where the design principles are rooted in evolution, as described in the work on resilience, reactivity, and variability of Arnoldi et al.⁸, the control theoretic perspective of Marom et al.⁹, and the geometric robustness of Ay et al.¹⁰. The study of technical systems differs because we better understand their design principles. Therefore, before discussing whether a system is antifragile or not, we need to define the environment in which the system operates and the objectives of the system. Finally, it should be noted that given the environment and the objectives, there may be multiple payoff functions that can be considered for quantification of the system’s performance, as shown in the systematic work of Kraskova et al.¹¹. Depending on the indicators or metrics we adopt, the conclusions regarding the system’s fragility can differ. Consequently, in the following section, we will discuss the differences between intrinsic, inherited, and induced antifragility, given certain specifications and intuitive examples in both technical and natural systems.

2. Intrinsic and ecological antifragility

Intrinsic/ecological antifragility (or fragility) quantifies the benefit (or harm) of input distribution unevenness, volatility, or perturbations attributed to the nonlinearity of the system’s payoff function.

2.1. Technical systems: intrinsic (anti)-fragility

When considering intrinsic antifragility, the fundamental aspect is dynamics’ time-scale separation describing the input-output coupling. An example is shown in figure 3 which illustrates the fragile operation of the transport systems, where exponentially increasing delays (output) occur with the increasing flow (input)¹². Management strategies, such as those suggested in¹³, aim to push the operation of the system towards the critical density. Such strategies consider the effect of variation in input (traffic flow) on the outcome (delays), which are modulated by the shape of the input-output function (exponential), as illustrated in schematic figure 1 schematic).

Figure 3.

Source: Wardrop¹² - Delay at a major intersection of two groups of streets in Central London.

In another example, given the interactions between multiple control loops (e.g., the internal DC motor control loop and outer robot position control loop³, the oscillators models of traffic flow inputs¹⁴, and the coupled traffic dynamics^15,16), the definition and quantification of antifragility emerge in the context of input-output mappings of time scales separation performed to handle uncertainty and high-frequency phenomena. However, please note that such systems employ intrinsic antifragility to achieve their prescribed objectives by design, given the specifications and constraints imposed by the physics of the operational space of the system, as described amply in the work on driver models of Kesting et al.^17–19 and traffic dynamics, as in the work of Du et al.²⁰, Daganzo et al.²¹, and Messner et al.²².

When unpredictable fluctuations start developing in a dynamical system that is on the verge of losing its stability, it is commonly referred to as criticality. Intrinsic antifragility can be cast around a system’s criticality. The ability to absorb and respond to stresses, due to the appearance of scale-free temporal fluctuations, slowing dynamics, and multistability, are the fundamental indicators of criticality. Here, antifragility can be viewed as the motion of a system from an existing steady state to a better one in the aftermath of a change in conditions. This transfer among steady states may be continuous (second-order phase transition) or discontinuous (first-order phase transition), as formalized in the work of Schaffer et al.²³.

2.2. Natural systems: ecological (anti)-fragility

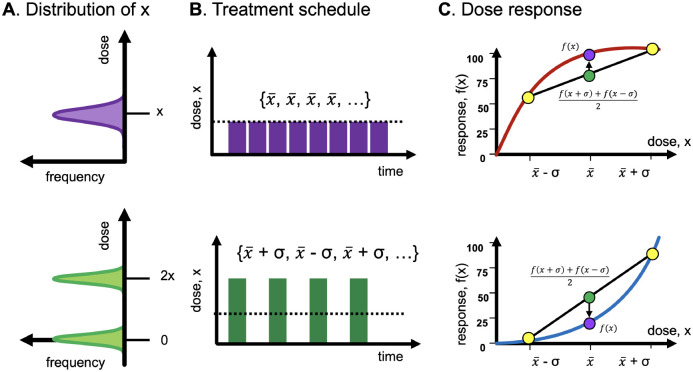
In biological systems, changes in environmental conditions can decrease the survival and fecundity of individuals based on a species’ Darwinian fitness. The rate of change in environmental perturbations may reduce fitness in response to stochastic fluctuations and seasonal variation, as formalized in the work of Taleb²⁴. The payoff function associated with the system response to environmental variation may be concave (fragile), convex (antifragile), or linear (neutral), as suggested in the work of Danchin et al.²⁵ and Taleb¹. An example is shown in figure 4, where there exists a dose distribution mean and variance (panel A) associated with each anti-cancer treatment protocol (panel B), where the outcome depends on the concave (top) or convex (bottom) dose-response function (panel C). Concave functions (red) should employ low-variance protocols, while concave functions (blue) should employ high-variance intermittent protocols. Ecological antifragility is the natural systems correlate to intrinsic antifragility and may defined as the system benefit derived from input volatility²⁶. Defining ecological fragility or antifragility is useful for the control of a biological population. For example, mathematical models describing the response to anti-cancer drugs measure the ecological effect of volatile versus continuous treatment schedules, as shown in the work of West et al.²⁷ or the pharmacokinetics study of Pierik et al.²⁸.

Figure 4.

Figure reproduced from Taleb, 2023²⁶ - Example treatment-scheduling protocols. (A) Example dose distribution with low (top) or high variance (bottom). (B) Associated protocols. (C) Low variance protocols are optimal to maximize response for concavity; high variance protocols for convexity.

In this context one can also build a rigorous description of all aspects of ecosystem antifragility and its applications, as detailed in the work of Equihua et al.²⁹. Antifragility requires optimal computational and inference capabilities that most interestingly occur within another fundamental concept of complex systems: criticality. As highlighted by Hidalgo³⁰, empirical investigations have suggested that living systems operate in the proximity of critical thresholds, existing at the delicate boundary between order and randomness demonstrated across various domains including electrical heart activity and brain function, among others^31–34. Precise measurement of the payoff function for predicting antifragility plays a key role. López-Corona and coworkers³⁵ applied these ideas discussed above to the scale of planetary ecosystem antifragility by integrating well-established principles from non-equilibrium thermodynamics and adopting a system dynamics approach using Fisher’s information on Earth’s entropy production^36,37.

3. Inherited & evolutionary antifragility

Inherited/evolutionary antifragility (or fragility) quantifies the benefit (or harm) of input distribution unevenness, volatility, or perturbations attributed to the system’s response to external signals.

3.1. Technical systems: inherited (anti)-fragility

Antifragility is correlated with increased system heterogeneity at the inherited scale, as shown in the work of Lopez-Otrasenda et al.³⁸ and Makridis et al.³⁹. This aspect comes into play when considering the system’s capacity to build extra capacity in anticipation of perturbations. More precisely, to achieve inherited antifragility, a system designer builds upon the time-scale separation of a redundant overcompensation component, as shown in robotics³, traffic control¹⁴, and medical⁴⁰ instantiations of applied antifragility.

Similarly, machine learning systems developed in the work of Sun et al.¹⁵ maintain time scale separation through the formulation of the learning task. More precisely, the system determines the best action at which the system yields the maximum possible discounted future reward. Isolating only the contribution of the time scale separation and the redundant overcompensation term, the machine learning inherited antifragility controller gained in the skewness (i.e., convexity) of the disruption magnitude over surging demand. In such systems, antifragility is quantified as the geometric properties of the anticipating control actions and the shape of the response in the face of high-magnitude external perturbations.

Finally, criticality also plays a role in inherited antifragility by allowing a system to leave the current steady state, for a different one. The trigger for state switching may come from a change in the parameters of the system, noise being externally enforced, or from an increase in the rates of the system from neighbouring entities in a competition of cooperation with the system, as shown in the works of Angeli et al.⁴¹ and Hizanidis et al.⁴².

3.2. Natural systems: evolutionary (anti)-fragility

Evolution, defined here as the change in heritable traits within a population over time, is also influenced by environmental perturbations⁴³. In the previous section, ecological antifragility considered individual species in isolation to quantify the response to perturbation. Evolutionary antifragility quantifies how a population of interacting species is affected by perturbations. For example, in cancer, competition between heterogeneous populations of cell types modulates antifragility⁴⁴. In natural biological systems, we investigate complexity (which implies maximum computational capabilities) and how systems reach criticality^45–47. Adaptive mechanisms of living systems do more than merely react to the environment’s variability through random mutations followed by selection; they must have built-in characteristics that enable them to discover alternatives to cope with adversity, variability, and uncertainty²⁹.

Using theoretical arguments, it has been proposed that systems under eco-evolution tend to be at criticality, implying maximum complexity and computational and inferential capabilities; and then they are also at maximum antifragility^29,48,49. Stability plays a central role for function, in both natural and technical dynamical systems. Paradoxically, the only way a dynamical system can remain stable is if it is excitable and able to change its behavior in reaction to outside stimuli. It is flexible, thus it is stable; in fact, the organism’s true stability depends on its modest instability, as beautifully described by Cannon⁵⁰.

Inherited antifragility in natural systems is a consequence of the self-organized configuration of a natural system that arises from the interactions among all components through evolutionary processes (e.g., genetic inheritance, microbiome inheritance, and social inheritance), constrained by external conditions. Antifragile natural systems derive benefits under uncertainty, stressors, and perturbations in both ecological and evolutionary scales. Evolution by natural selection itself can be thought of as an antifragile process, whereby a population is maintained amidst environmental perturbations through genetic variation. For example, although individuals within a population may die, the population evolves toward a more antifragile state, increasingly higher fitness to address fluctuating environmental conditions^25,51.

4. Induced & interventional antifragility

Induced/interventional antifragility (or fragility) quantifies the benefit (or harm) of input distribution unevenness, volatility, or perturbations attributed to the system’s response to closed-loop controllers.

4.1. Technical systems: induced (anti)-fragility

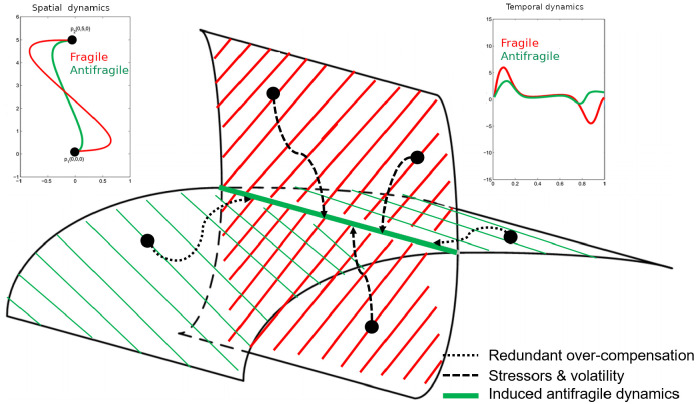
The control theoretic approach to induced antifragility focuses on the combination of time-scale separation and redundant overcompensation with variable structure control. Put simply, the system is now pushed to the antifragile region of its operational domain through a judicious choice of an external control or regulation signal, as shown by Axenie and Saveriano³. This can be accomplished by properly synthesizing a control law, which develops a redundant over-compensation capacity to handle uncertainty regarding the sensor and actuator failures by pushing the closed-loop system dynamics to prescribed dynamics. This is captured in Figure 5, where the fragile–antifragile behavior is depicted across spatiotemporal dynamics of a robot in uncertain environments.

Figure 5.

Figure reproduced from Axenie et Saveriano³ - Spatial and temporal dynamics of fragile and antifragile behaviours of a robot in uncertain environments. Closed-loop dynamics in the presence of stressors and volatility.

Antifragility was quantified in this case through the quality of the dynamics tracking and the speed of reaching the desired region of the desired dynamics manifold in the presence of uncertainty and volatility through adaptive control⁵², robust control⁵³, and resilient control⁵⁴ strategies. In a large-scale traffic control instantiation by Axenie et al.¹⁴, the antifragile controller demonstrated statistically significant gains given increasing traffic disruptions amplitude over time. The systematic evaluation demonstrates that the control law selection based on the second-order effects of the signal re-computation may capture the volatile dynamics of the closed-loop system.

Considering machine learning approaches to induced antifragility, the work of Sun et al.¹⁵ designed a traffic reinforcement learning agent that learns to be conservative when regulating the controlled region. Here, we have again a clear quantification of the system’s antifragility based on a dynamics response curve to external uncertainty (i.e., amplitude of traffic disruptions) and volatility (i.e., onset and offset of traffic disruptions) overcoming the baseline approach (i.e., static police-made traffic light control), a state-of-the-art model predictive control⁵⁵, and other reinforcement learning approaches⁵⁶.

Finally, when considering criticality, the control of multi-stability deals with the transition of the system to a more desired steady state and also preventing it from moving to an inferior one, as shown in the work of Pisarchik et al.⁵⁷. From the control point of view, it is beneficial to predict the tipping points well before they occur so that remedial actions can be adopted, as demonstrated in the work of Grziwotz et al.⁵⁸.

4.2. Natural systems: interventional (anti)-fragility

Eradication of a heterogeneous population may be exceedingly difficult due to the evolution of resistance to interventional treatments. For example, the continuous administration of anti-cancer drugs^59,60 or antibiotics⁶¹ selects for resistant sub-populations rendering subsequent treatments ineffective. Recent work to apply principles learned from agricultural methods known as “Integrative Pest Management” (IPM) has shown some success in the management of cancer^62,63. For example, adaptive cancer therapy uses a simple rule-of-thumb protocol to adapt treatment administration and treatment break time intervals based on tumor response⁶⁴. Importantly, this adaptive protocol in an increase in dose variance (prolonged periods of high dose followed by prolonged periods of zero dose)⁶⁵. This is part of a broader effort to design treatment protocols using evolutionary principles that increase the treatment-induced volatility that tumor cells undergo during the course of treatment to maximize tumor regression⁶⁶. Mathematical models of tumor-immune-drug interactions can drive chemotherapy optimization regimens to maximize the efficacy/toxicity ratio, as shown by West et al.⁶⁷ and Axenie et al.⁴⁰.

In another interventional example, in ecological processes of terrestrial ecosystems, the complexity of interactions, and costs involved, among other technical complications, but also, maybe more importantly, due to ethical concerns because of path dependence, computational irreducibility, and unseen consequences, there are very few interventions that aim to restore ecosystem antifragility, as shown in the work of Ripple et al.⁶⁸, Beschta et al.⁶⁹, and Wright et al.⁷⁰.

Furthermore, a series of recent papers^71,72 have shown that dietary patterns might influence network communication along the brain-gut axis, especially at the age that both systems go through maturation processes. From an ecological perspective, an adequate level of connectivity dissipates the effect of perturbations in the distribution of species and enhances ecosystem stability. A loss in connectivity leads to a loss in gut microbiota ecosystem antifragility. The basic rationale is that a system’s response to perturbation requires an efficient flow of information. For maximum antifragility, this flow must be optimal, implying maximum connectivity, as shown in the papers of Isaac et al.⁷² and Equihua et al.²⁹.

5. Discussion

In this perspective, we have reviewed efforts to apply antifragility theory to both technical/physical systems as well as natural/biological systems. We provide a conceptual framework to unify the language across both systems and define the relevant scales of fragility, summarized below.

Trademarks of intrinsic & ecological antifragility:

Intrinsic and ecological antifragile systems benefit from harm derived from internal dynamics distribution unevenness, based on the convexity of the response function of the system without external input and solely based on the internal components’ heterogeneity and resilience. Features such as stability describe the most simple system response with minimal antifragile characteristics. Within this scale, precise characterization of the payoff function describing the relationship between system inputs and outputs is of critical importance.

Trademarks of inherited & evolutionary antifragility:

Homogeneity and heterogeneity play a crucial role in the design and synthesis of inherited and evolutionary antifragile systems. From criticality and multi-level interactions of multiple time scales to quantifying criticality margins, such a design scheme leverages local interactions of the system to make it benefit from perturbations. In other words, inherited and evolutionary antifragile systems benefit from harm derived from input distribution unevenness, based on the emergent system dynamics and its interactions with the operating environment (i.e. disturbances, noise, modulated perturbations).

Trademarks of induced & interventional antifragility:

Inducing a desired behaviour within interventional antifragility requires an innovative, control-theoretic, design and synthesis approach. Here, nonlinear dynamics across both space and time can promote the system’s capacity to absorb internal and external disruptions. Induced and interventional antifragile systems benefit from harm derived from input distribution unevenness based on emergent system dynamics in closed-loop with a controller driving the system towards prescribed dynamics in the presence of modulated or non-stationary disturbances, noise, and volatility.

It is also important to note that we need not constrain ourselves to search only for systems that are antifragile. First, a system may be fragile on the intrinsic or inherited scales yet still be amenable to interventions that are antifragile through clever design of feedback controllers. Second, fragility (or antifragility) is a measurable quantity: the response of a system to volatility. Some systems (e.g., tumors) may respond in a fragile manner to given perturbations (e.g., chemotherapy) and thus it is critical to characterize the system along the fragile-antifragile spectrum. Finally, though we consider a discrete layering of antifragility types, we are aware that this structure can be applied systematically across scales. In other words, even the simplest systems can be subject to all three types of antifragility.

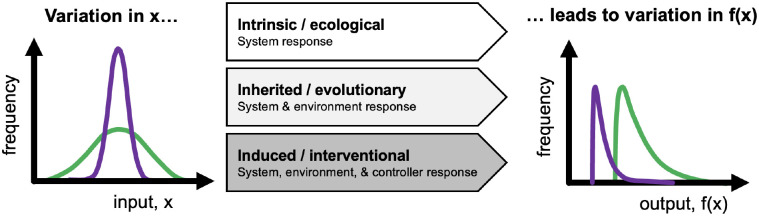
Figure 2.

Antifragility-associated terms, defined for technical and natural (biological) systems.