Room-temperature quantum coherence of entangled multiexcitons in a metal-organic framework

Abstract

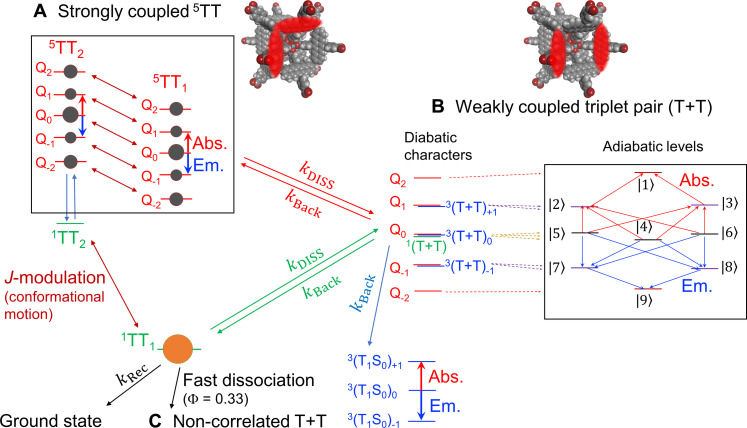
Singlet fission can generate an exchange-coupled quintet triplet pair state ⁵TT, which could lead to the realization of quantum computing and quantum sensing using entangled multiple qubits even at room temperature. However, the observation of the quantum coherence of ⁵TT has been limited to cryogenic temperatures, and the fundamental question is what kind of material design will enable its room-temperature quantum coherence. Here, we show that the quantum coherence of singlet fission–derived ⁵TT in a chromophore-integrated metal-organic framework can be over hundred nanoseconds at room temperature. The suppressed motion of the chromophores in ordered domains within the metal-organic framework leads to the enough fluctuation of the exchange interaction necessary for ⁵TT generation but, at the same time, does not cause severe ⁵TT decoherence. Furthermore, the phase and amplitude of quantum beating depend on the molecular motion, opening the way to room-temperature molecular quantum computing based on multiple quantum gate control.

Room-temperature quantum coherence of entangled multiexcitons is realized by suppressed chromophore motion.

INTRODUCTION

We are currently experiencing a second quantum revolution. Quantum information science (QIS) uses the principles of quantum mechanics for various applications such as quantum computing (1, 2), quantum communication (3, 4), and quantum sensing (5–7). The most basic information unit in QIS is a quantum bit (qubit). Among various types of qubit, those using molecular materials generally have the following advantages: the ability to precisely create a specific qubit structure, the ability to control qubit properties by changing the chemical structure, and the scalability to integrate many qubits (8–10). While most qubits require cryogenic temperatures, some molecular qubits can be initialized by photoexcitation (11, 12), making them particularly promising for quantum computing at room temperature and quantum sensing of living systems.

Among the photogenerated molecular qubits, singlet fission (SF) has the unique feature of being able to generate high-spin quintet state, which is useful for advanced logic gate operations and entanglement-enhanced sensing (13–26). SF is a process in which two triplet excitons (T₁) are generated from one photoexcited singlet (S₁) and has been studied mainly in the energy field to improve the efficiency of solar cells (27–29). On the other hand, many studies on the mechanism of SF have revealed that the triplet pair with singlet multiplicity ¹TT, in which two T₁ are strongly coupled by an exchange interaction (J), arises from S₁, and the following spin evolution of the triplet pair leads to the formation of a four-spin entangled quintet multiexciton ⁵TT (13–26). SF-derived ⁵TT can play an important role in the future development of molecular quantum computing using multiple qubits such as CNOT gate operation. ⁵TT can not only be generated by light but also be detected by light through the inverse process of SF, triplet-triplet annihilation, and thus has the potential to be addressed in a single spin level (15).

To maximize the potential of these SF-derived ⁵TT as qubits, it is crucial to generate quantum spin coherence in the quintet sublevels by microwave manipulation at room temperature. However, only a few cases of ⁵TT quantum coherence have been observed so far, and these cases are limited to cryogenic temperatures of 75 K or lower (13–19). This poses a major challenge for the development of SF-derived ⁵TT qubits. Most of the reported examples are based on molecular crystals of tetracene derivatives, where the two triplet excitons move apart, weakening the exchange interaction J and causing mixing between ¹TT and ⁵TT, and then the triplets come close to each other again, producing a strongly exchange-coupled ⁵TT. In this mechanism, delicate control of molecular packing is required to make the interaction between chromophores strong enough to cause SF but weak enough to suppress the triplet diffusion (15). In particular, at room temperature, the triplet diffusion is so pronounced that the ⁵TT pairs quickly dissociate to form noncorrelated T + T states, and no coherence can be observed (13).

Another mechanism for SF-based ⁵TT generation is the modulation of exchange interactions between chromophores by molecular motion, causing the conversion of ¹TT to ⁵TT (19–22). Such a conformational change has been observed in intramolecular SF systems consisting of discrete molecules of covalently linked acene units dispersed in a low-temperature glass matrix and may also occur in acene dimers doped in molecular crystals (18–20). However, while molecular motion is necessary for the generation of ⁵TT, decoherence may be induced by fluctuations in the zero-field splitting interaction (19). That is, it remains unclear what kind of molecular motion can simultaneously achieve efficient ⁵TT generation and noise-suppressed qubits.

Here, we report the first room-temperature observation of the quantum coherence of SF-derived ⁵TT by the suppressed molecular motion in a metal-organic framework (MOF). MOFs are nanoporous crystalline materials composed of metal ions and organic ligands (30–37). By integrating chromophores into the ligand, the distance and angle between chromophores can be precisely regulated in MOFs (31–33). Unlike dense molecular crystals, MOFs have nanoscale voids in the crystals, which allow the chromophores to move, and this movement can be controlled by the topology of the network and the local molecular density around the chromophores. As a proof of concept, we prepare a UiO-type (37) pentacene-based MOF (Pn-MOF), which is synthesized by combining diamagnetic Zr ions with a dicarboxylate ligand containing pentacene (38–40), the most representative chromophore exhibiting exothermic SF. Note that this Pn-MOF is the first example of an MOF exhibiting SF to the best of our knowledge. The noninterpenetrated UiO-type structure can prevent π-stacking between pentacene planes, which gives the pentacene units enough motion to make the conversion from ¹TT to ⁵TT (Fig. 1). The dense integration in the Pn-MOF makes the pentacene motion sufficiently suppressive that the quantum coherence of ⁵TT generated by microwave irradiation was observed for over hundred nanoseconds even at room temperature. Furthermore, the phase and amplitude of quantum beating can be dependent on the molecular motion. The decay of the echo signal from the quintet observed by pulsed electron paramagnetic resonance (EPR) was considerably longer than the decay of the quintet-derived signal in continuous-wave time-resolved EPR (CW-TREPR) measurements, suggesting that two components with different degree of order exist and the highly crystalline domains present as minor components in the disordered MOF structure exhibit the long quantum coherence. These results reveal how molecular motions should be designed to achieve quantum coherence of multilevel distinct quantum systems, referred to as qudits, even at room temperature. This provides a fundamental guideline for the future development of molecular-based QIS.

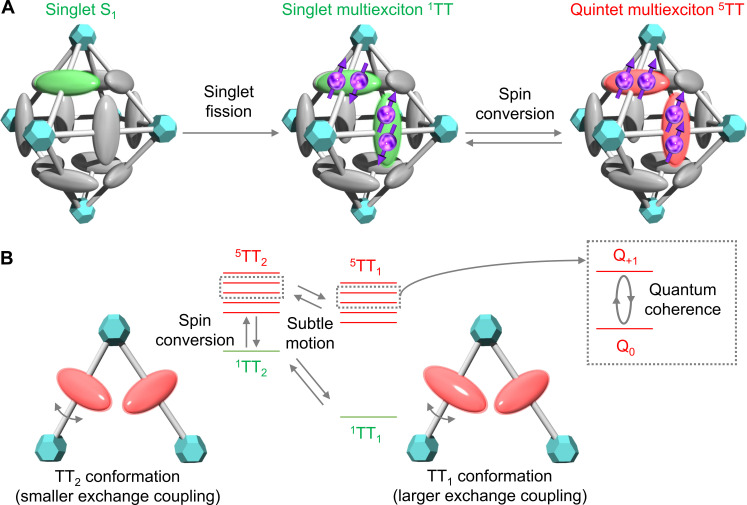
Fig. 1. Quintet multiexciton generation and its quantum coherence in an MOF.

(A) SF followed by spin evolution via modulation of exchange interactions results in the formation of quintet multiexciton ⁵TT in an MOF. (B) Suppressed chromophore motion in an MOF enables not only the spin conversion from ¹TT to ⁵TT but also the quantum coherence of ⁵TT over hundred nanoseconds even at room temperature.

RESULTS

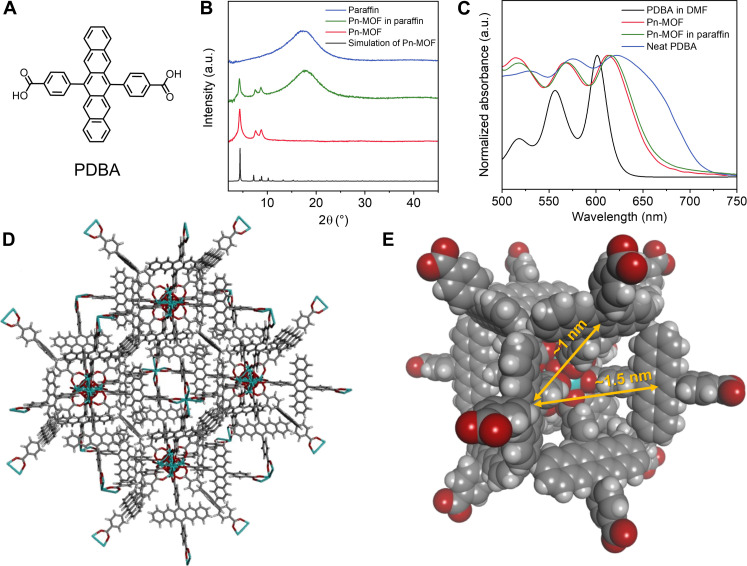
As a dicarboxylate ligand containing a pentacene moiety, we used 4,4′-(pentacene-6,13-diyl)dibenzoic acid (PDBA; Fig. 2A), which we had previously developed for other purposes (36, 41). The energy levels of excited states of PDBA were estimated from time-dependent density functional theory calculations. B3LYP/6-31G (d,p) and ωB97X/6-31G (d,p) were used from the ground-state optimization and excited-state calculations, respectively. It was confirmed that PDBA has the similar S₁ (2.34 eV) and T₁ (0.93 eV) energy levels compared with those of pentacene (S₁, 2.45 eV; T₁, 0.89 eV) (42), and exothermic SF is expected to occur for PDBA as well. We have previously confirmed that aggregates of PDBA in water exhibit SF (41). Pn-MOF with pentacene integrated in a UiO-type structure was synthesized by a hydrothermal method using ZrCl₄ and PDBA in the presence of acetic acid as the modulator in deaerated N,N′-dimethylformamide (DMF) at 403 K. The coordination of the carboxylic acid of PDBA to the Zr-based cluster was confirmed by the shift to lower wave number of the peak originating from carbonyl stretching from 1685 to 1595 cm⁻¹ (asymmetric) and 1540 cm⁻¹ (symmetric) (fig. S1) (43). The structure of Pn-MOF was confirmed by powder x-ray diffraction (PXRD) measurements. The peak positions of the experimental PXRD pattern of Pn-MOF matches well with those of the simulated pattern (Fig. 2B). The simulated structure with UiO-68–type topology using PDBA as a ligand is shown in Fig. 2D. The center-to-center distance between the nearest pentacene moieties is 1 nm, and the dihedral angle is 120°. The distance between the nearest carbons of the nearest pentacene pair is 0.35 nm, which is close enough for SF to occur. The distance between the second nearest pentacene sites is 1.5 nm, and the dihedral angle is 90°. The relatively broad PXRD peaks of Pn-MOF suggest that the structure is partially disordered (44). Scanning electron microscopy images of Pn-MOF showed a rounded morphology with a grain size of ~50 to 100 nm (fig. S2), suggesting not high crystallinity of Pn-MOF, consistent with the PXRD results. In Pn-MOF, pentacene moieties do not form π-stacking with each other, which is expected to suppress immediate deactivation of triplet dimer by triplet-triplet annihilation and to fluctuate the exchange interaction by changing the dihedral angle between pentacene units. These moderate interpentacene interactions were also confirmed by ultraviolet (UV)–visible (vis) absorption measurements (Fig. 2C). The 0-0 absorption peak of the π-π* transition of the pentacene moiety was located at 602 nm in DMF solution of PDBA, while the absorption peak of Pn-MOF showed a slight broadening and red-shift to 612 nm, indicating the presence of excitonic interactions between the pentacene moieties. On the other hand, in the neat PDBA solid, the absorption peak was located at a longer wavelength of 622 nm with more broadening. This indicates that the interaction is properly modulated in Pn-MOF by preventing π-stacking between pentacene moieties.

Fig. 2. Characterizations of Pn-MOF.

(A) Chemical structure of PDBA. (B) Simulated PXRD pattern of Pn-MOF (black line) and experimental PXRD patterns of Pn-MOF (red line), Pn-MOF in paraffin (green line), and paraffin (blue line). a.u., arbitrary units. (C) UV-vis absorption spectra of 1 mM PDBA in DMF (black line), Pn-MOF (red line), neat PDBA solid (blue line), and Pn-MOF in paraffin (green line). (D) Simulated structure of Pn-MOF with UiO-68–type topology. (E) The nearest and second nearest pentacene moieties in Pn-MOF.

From thermogravimetric analysis, it was found that Pn-MOF has high thermal stability up to about 573 K and also adsorbs water from the air into its nanopores (fig. S3). The existence of nanopores in Pn-MOF was also confirmed by nitrogen gas adsorption measurements at 77 K after activation of Pn-MOF at 373 K under vacuum (fig. S4). The adsorption isotherm of Pn-MOF showed a steep rise in the low-pressure region, which is typical for microporous materials and classified as International Union of Pure and Applied Chemistry (IUPAC) type I. Gradual rise was also observed in the high-pressure region, implying the broad distribution of the pore sizes and the existence of defects. Once the nanoporous structure of Pn-MOF was confirmed, Pn-MOF was soaked in paraffin. Paraffin is nonvolatile, useful for dispersing MOF solids, and is sometimes used for time-resolved transient EPR measurements as an inert matrix. The PXRD pattern of activated Pn-MOF soaked in paraffin retained the original peaks, indicating that the UiO-68–type topology was preserved (Fig. 2B). The UV-vis absorption peak shift of Pn-MOF was very small (612 to 615 nm) before and after the paraffin soaking (Fig. 2C). Therefore, it is likely that paraffin in the MOF nanopores does not have any strong interactions with chromophores and interchromophore interactions were not affected by the introduction of guest paraffin molecules.

SF in Pn-MOF

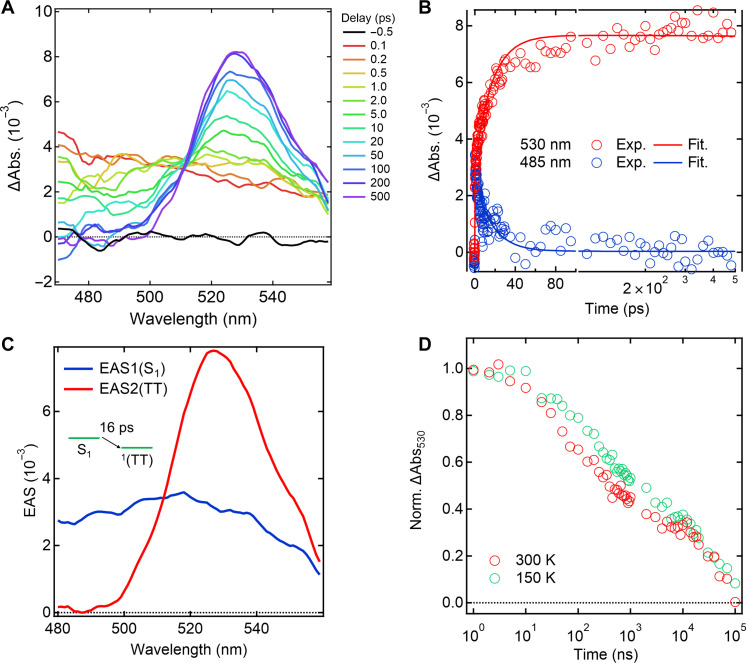
To investigate the SF dynamics in Pn-MOF in paraffin, we carried out pump-probe–type transient absorption spectroscopy (TAS) in the 460- to 550-nm range (Fig. 3), commonly used for tracking SF dynamics in pentacene-based systems. Upon excitation by an ultrashort pump pulse at 600 nm, we observed a broad transient absorption spectrum around 450 to 500 nm, typically attributed to the feature of S₁-S_n absorption of pentacene chromophore. The spectrum subsequently transformed to a different shape with a peak at 530 nm within a hundred picoseconds (Fig. 3, A and B). Since the signal at 530 nm is indicative of T₁-T_n absorption of pentacene chromophore (39, 45), we confirmed the ultrafast generation of the triplet pair state through SF. We can assign the second component as the triplet pair state with singlet multiplicity, ¹TT, because the spin multiplicity is conserved in the ultrafast timescale. We performed global analysis assuming a sequential model with two components to analyze time constants and spectral features (Fig. 3, B and C). The first and second components of the evolution-associated spectra (EAS) can reasonably be assigned from their shapes to the spectra from S₁ and ¹TT, respectively. The S₁ state was converted to the ¹TT state with a time constant of 16.8 ± 0.1 ps, followed by negligible decay (>1 ns) in the current time window. The timescale of transition was slower than the typical timescale of SF in pentacene crystal (~100 fs) but still much quicker than the timescale of the typical intersystem crossing of pentacene in solution (>1 ns). The ¹TT generation process likely outcompetes other photophysical processes such as intersystem crossing in a single chromophore. This is consistent with successful fine tuning of moderate intermolecular interaction required for efficient ⁵TT generation.

Fig. 3. TAS measurements of Pn-MOF.

(A) Experimentally observed spectral evolution of the femtosecond TAS (excitation wavelength, 600 nm) of Pn-MOF in paraffin. (B) Temporal change of transient absorption at selected wavelengths and fitting curves from global analysis. (C) EAS obtained from global analysis based on the sequential model based on two components. EAS1 and EAS2 indicate the first and second components of EAS, respectively. (D) Temperature dependence of the transient absorption at 530 nm of Pn-MOF.

We then investigated the kinetics of the triplet pair state via nanosecond TAS in the Pn-MOF (Fig. 3D, red), which is crucial for QIS. Although the spectral shape was almost constant over time (fig. S5), multicomponent decay profile was observed. This complex kinetics suggests that alternating spin multiplicity via interaction fluctuation affects the deactivation of the triplet pair state. To confirm the origin of the multiple decays, we performed low-temperature (150 K) measurements (Fig. 3D, green), which clearly revealed slowed-down dynamics in the nanosecond timescale without altering the spectral shape (fig. S5), providing compelling evidence of the role of conformational fluctuation in the electron-spin coupled dynamics.

Quintet multiexciton formation in Pn-MOF

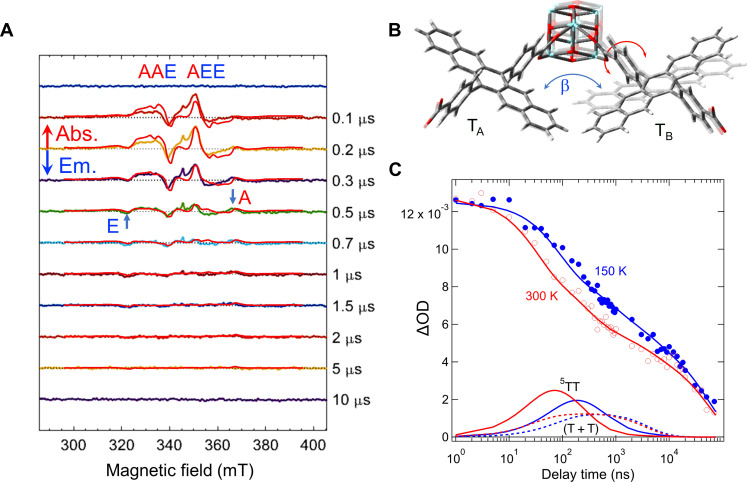
To quantitatively explore the spin dynamics in Pn-MOF, we performed CW-TREPR measurements of Pn-MOF in paraffin at room temperature. Spin polarization signals with typical A/A/E/A/E/E pattern of quintet (A and E represent microwave absorption and emission, respectively) and E/A pattern of triplet were observed on inner and outer side of the spectra, respectively (Fig. 4A).

Fig. 4. Transient EPR spectra of Pn-MOF.

(A) TREPR spectra for different delay times of Pn-MOF in paraffin at room temperature. Spectrum simulations by the rotation model analysis in Fig. 5 are shown by the red lines. (B) Conformations of the quintet TT₁ and TT₂. The blue arrow represents dihedral angle (β) of the aromatic plane in T_B relative to T_A in the T_AT_B pair. (C) Decay profiles of the absorbance changes in nanosecond TAS (ΔOD) by the multiexcitons at temperatures of 300 K (red circles) and 150 K (blue circles), together with simulated profiles by the rotation model analysis (red and blue lines). Contributions of ⁵TT and SCTP (T + T) are shown by the solid and dashed lines, respectively, at 300 K (red line) and 150 K (blue line).

As mentioned above with the femtosecond TAS data, the EPR-silent ¹TT state should be initially populated by SF. The spin conversion from ¹TT to ⁵TT has been explained by the modulation of spin-spin exchange coupling J, where 6J = E(¹TT) − E(⁵TT), with a conformational change in the covalently linked chromophore dimers. In this case, the chromophores remain strongly coupled to each other although the conformation of the dimer changes. In contrast, in dense organic crystals, triplet hopping forms weakly coupled triplet pairs, and mixing occurs between ¹TT and ⁵TT, which are close to each other in energy level. The triplets then reencounter to produce a strongly coupled ⁵TT. The MOF in this work is a unique system that combines the characteristics of both dimers and crystals because it not only has a structure in which many chromophores are accumulated but also has nanopores inside the crystal, which allows the chromophores to rotate and change their interactions. Therefore, it is appropriate to analyze the system using a model that assumes both J-modulation in the strongly coupled TT pair and spin mixing in the weakly coupled TT pair (Fig. 5).

Fig. 5. Model of the density matrix formalism analysis.

Different multiexcitons, (A) strongly coupled triplet pair ⁵TT (⁵TT₁ and ⁵TT₂), (B) weakly coupled SCTP (T + T), and (C) noncorrelated two triplets T + T, are included with considering molecular rotation, exciton migration, and reencounter processes.

The ⁵TT formation by the modulation of J through the chromophore rotations within the strongly coupled triplet pair in the 1-nm separated nearest pair shown in Fig. 2E (Fig. 5A) competes with the initial exciton migration to form the separated multiexcitons (Fig. 5, B and C). Depending on local exciton mobility by crystallinity or disorder, the weakly coupled triplet pair (Fig. 5B) and the noncorrelated two triplets T + T (Fig. 5C) can separately be generated by the exciton migration. The quick triplet exciton dissociation at the crystalline domain would preferentially produce well-separated noncorrelated T + T and does not contribute to the electron spin polarization. In contrast, the weakly coupled triplet pair states are anticipated to be generated at the disorder region of the MOF to form the spin-correlated triplet pair (SCTP) (T + T) causing the nine adiabatic states (|1>, |2>, ⋯and |9>) by quantum superpositions of the nine of singlet, triplet, and quintet diabatic characters, as shown in Fig. 5B. These SCTP contributions are observed at the peak positions of the outermost magnetic fields (321 and 365 mT) exhibiting the E/A spin polarization pattern in Fig. 4A by the spin-spin exchange coupling of J = 1 mT in the 1.5-nm separated exciton pair (Fig. 2E).

From Fig. 5, we computed time development of the singlet, triplet, and quintet diabatic characters for the three different exciton-pair conformations [TT₁, TT₂, and weakly coupled (T + T)] together with the different J values to reproduce the time-dependent EPR data using the density matrix formalism analysis (table S3).

These diabatic spin characters in Fig. 5 are described by the density matrix formalism of the equation of motions as follows:

$$\begin{array}{c}{\dot{\mathbf{\rho }}}_{{\text{TT}}_1}=-i[{\widehat{\mathbf{H}}}_{{\text{TT}}_1},{\mathbf{\rho }}_{{\text{TT}}_1}]-(k_{12}+k_{\text{DISS}}){\mathbf{\rho }}_{{\text{TT}}_1}\\ +k_{\text{Back}}{\mathbf{\rho }}_{\mathrm{T}+\mathrm{T}}+k_{21}{\mathbf{\rho }}_{{\text{TT}}_2}+{\widehat{\mathbf{K}}}_{\text{Rec}}{\mathbf{\rho }}_{{\text{TT}}_1}\end{array}$$ (1)

$${\dot{\mathbf{\rho }}}_{{\text{TT}}_2}=-i[{\widehat{\mathbf{H}}}_{{\text{TT}}_2},{\mathbf{\rho }}_{{\text{TT}}_2}]-k_{21}{\mathbf{\rho }}_{{\text{TT}}_2}+k_{12}{\mathbf{\rho }}_{{\text{TT}}_1}$$ (2)

$${\dot{\mathbf{\rho }}}_{\mathrm{T}+\mathrm{T}}=-i[{\widehat{\mathbf{H}}}_{\mathrm{T}+\mathrm{T}},{\mathbf{\rho }}_{\mathrm{T}+\mathrm{T}}]+k_{\text{DISS}}{\mathbf{\rho }}_{{\text{TT}}_1}-k_{\text{Back}}{\mathbf{\rho }}_{\mathrm{T}+\mathrm{T}}-{\widehat{\mathbf{K}}}_{\mathrm{T}}{\mathbf{\rho }}_{\mathrm{T}+\mathrm{T}}$$ (3)

where ρ represents the density matrix for TT₁, TT₂, and T + T states and is numerically solved with the spin Hamiltonian $\widehat{\mathbf{H}}$ composed of the Zeeman interaction ( ${\widehat{\mathbf{H}}}_{\text{TTz}}$ ), the zero-field splitting interactions ( ${\widehat{\mathbf{H}}}_{\text{TTzfs}}$ ) in the individual two triplets, the spin-spin dipolar coupling ( ${\widehat{\mathbf{H}}}_{\text{TTss}}$ ) between the triplets, and the exchange interaction ( ${\widehat{\mathbf{H}}}_{\text{TTex}}$ ), as reported previously. Because ${\widehat{\mathbf{H}}}_{\text{TTzfs}}$ and ${\widehat{\mathbf{H}}}_{\text{TTss}}$ are anisotropic and dependent on the TT conformations, the J values are also altered by the molecular motions, resulting in the anisotropic electron spin polarization in Fig. 4A caused by the conformation dynamics. This exchange process by k₁₂ and k₂₁ in Eqs. 1 and 2 is thus regarded as the noise to fluctuate the J corresponding to the Debye exponential model (26).

The EPR spectra were simulated as shown by the red lines in Fig. 4A. The electron spin polarization pattern (A/A/E/A/E/E) in the quintet is sensitive to the mutual orientations of the excitons in the TT and are generated by fluctuation of the exchange coupling. For the simulation of the EPR spectra, we started with the dihedral angle (β = 130°) between the aromatic planes in TT₁ as shown in Fig. 4B. We then carefully examined effects of the molecular conformation angles of T_B (eq. S14) in the T_A-T_B pairs on the electron spin polarization of the quintet state. The dihedral angles (β) of the TT₁ or TT₂ states largely alter the spin polarization pattern (fig. S6). To examine whether the uniqueness of the motion is extracted from the spectrum, we also consider the angle distributions in the TT₂ conformations with fixing the TT₁ conformation (β = 130°) by averaging the five transverse magnetizations with weighting 1:4:6:4:1 amplitude for β = 130°, 140°, 150°, 160°, and 170° in the TT₂, as shown by the blue line in fig. S7A. In addition, averaging by the angle distribution is performed in the TT₁ conformation, as shown in fig. S7B. Because the 130° to 150° spectrum (solid red lines in fig. S7) well agrees with the averaged spectra (dashed blue lines in fig. S7), it is concluded that the computation obtained by the 130° to 150° angle change may include the inhomogeneous distribution in the conformations with a large variation of ±20°. Within this inhomogeneity, the average angle β = 150° is extracted for the T_B moiety in the TT₂ state as imposed in Fig. 4B, denoting that the conformation changes by molecular rotations (red arrows in Fig. 4B) are coupled to the modulation of the exchange interaction in table S3. The stronger J (=−1.4 × 10⁵ MHz) in the TT₁ than that (J = −1.9 × 10⁴ MHz) in the TT₂ is consistent with the dimer model average geometry of TT₁ and TT₂ causing contact edge-to-edge separations (0.29 and 0.30 nm, respectively) between carbon atoms in the Pn moieties in Fig. 4B based on the simulated structure (Fig. 2E). This supports the molecular rotation along with the Pn-ligating direction for the J-modulation. We would like to emphasize that we do not want to have a quantitative discussion regarding the dihedral angle because of the heterogeneity in the MOF structure but rather to qualitatively understand the importance of the suppressed motion with average angles.

Longer-lived multiexciton EPR signals are also obtained at 150 K (fig. S8). Experimental and simulated EPR spectra showed better agreement at 150 K than at 300 K. This may be due to the activation of several different low-frequency modes of conformational change at higher temperatures, making a perfect fit at 300 K difficult by considering only a single mode of conformational change. We performed the computation of the quintet EPR spectra with setting β = 125° and θ = 40° in TT₁ with varying the TT₂ conformation (fig. S9 and table S4). The center-field absorptive spectrum is obtained when we consider the motion between β = 125° in TT₁ and β = 110° in TT₂, as shown by the red line in fig. S9A. We also computed the time development of the transverse magnetization using the above conformation motion (fig. S10B) and added to the data in Fig. 4A to obtain the data (red lines) shown in fig. S10C. The better fit with the experimental results strongly supports that the highly heterogeneous conformation motions dominate the multiexciton dynamics. The time development of spin polarization coincides with the nanosecond TAS data, demonstrating that the ⁵TT should be formed by the large and disorder conformational motions depicted in Fig. 4B. The reliability of the present numerical model analysis was confirmed by reproducing the EPR patterns of previous rigid tetracene dimers (fig. S11) (14). The EPR pattern of Pn-MOF could not be reproduced well without taking motility into account, confirming that the pentacene moieties in the Pn-MOF have rotational dynamics.

As a result, the time evolution of the EPR spectra was successfully reproduced by the model of Fig. 5 in which the hopping dissociation (k_DISS) and reencounter (k_Back) to form the quintet ⁵TT, triplet ³(T₁S₀), and singlet ¹TT via triplet-triplet annihilation of ³(T + T)₀ are considered together with the J-modulation between TT₁ and TT₂ to generate the anisotropy in the quintet sublevel populations (Fig. 4A, red lines). This analysis was also applied to understand the time development of the transient absorption signals in paraffin for t ≥ 1 ns in the absence of the magnetic field. Notably, the profiles (solid lines in Fig. 4C) of the sum of the triplet excitons [⁵TT₁ + ⁵TT₂ + ³T₁S₀ + ¹TT₁ + ¹TT₂ + SCTP (T + T) + noncorrelated T + T] are consistent with the deactivation kinetics of the spin-polarized exciton pairs with ⁵TT and (T + T) in Fig. 4A. Quick nanosecond decays in Fig. 4C are originating from the singlet deactivation process (k_Rec = 5.6 × 10⁷ s⁻¹ at room temperature) of ¹TT that is in equilibrium with ⁵TT and (T + T). The longer-lived transient absorption profile at 150 K than at 300 K is due to slower singlet deactivation (k_Rec = 2.0 × 10⁷ s⁻¹). It is possible to reproduce the nanosecond TAS decay profile even in a scenario that does not include the J-modulation, where first (T + T) is generated by triplet diffusion and then ⁵TT is generated by reencounter (fig. S12). However, in this scenario, the ⁵TT should still be hardly generated at 100 ns after photoexcitation, which contradicts the actual result that the EPR spectrum at 100 ns showed a strong ⁵TT-derived signal (Fig. 4A). This confirms that J-modulation plays a major role in the generation of ⁵TT.

Room-temperature coherence control of quintet state

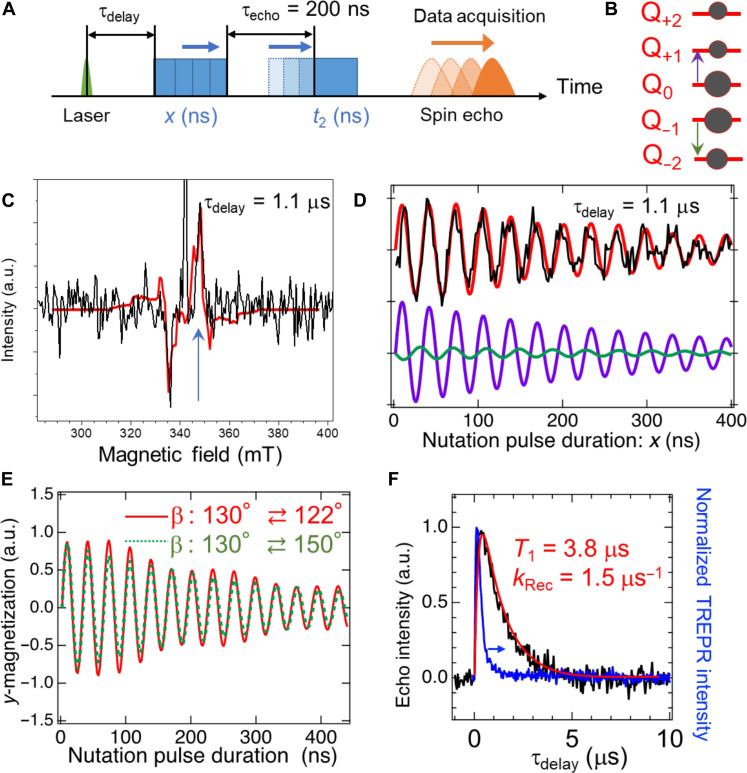
To directly control the four spin qubits of the quintet multiexciton at room temperature, we applied a transient nutation microwave pulse sequence using an X-band pulsed EPR spectroscopy (Fig. 6, A and B). Although the quintet states are minor at the later delay time exceeding 1 μs in Fig. 4, A and C because of the quick deactivation in the strongly coupled TT pair to the ground state, the echo-detected EPR spectrum of the quintet is observed even at τ_delay = 1.1 μs (Fig. 6C). This suggests that some of the strongly coupled TT states survive, while other dominant TT states undergo quick deactivation and dissociation by hot exciton characters with relatively large angular molecular rotation shown in Fig. 4B. These hot multiexcitons should also be subject to substantial transverse spin relaxation and not contribute to the echo signal. At the field strength of B₀ = 348.1 mT (blue arrow in Fig. 6C), we obtained the microwave-induced spin coherence of the quintet as shown in Fig. 6D. This profile is successively explained by the superpositions of the nutation frequencies (ω_mS) contributed by the quintet quantum gates of Δm_S = ±1 in Fig. 6B (Fig. 5A) described by the following equation

$${\mathrm{\omega }}_{m_S}=\frac{g{\mathrm{\mu }}_{\mathrm{B}}{B}_1}{\mathrm{\hslash }}\sqrt{S(S+1)-m_S(m_S\pm 1)}$$ (4)

where m_S (= 0, ±1, and ±2) represent the quintet sublevel quantum numbers causing the transitions of Δm_S = ±1 with S = 2 in Fig. 5A (detailed analysis method is described in table S5). A decoherence time constant of T_2D = 150 ns is used. This is consistent with the transverse relaxation time of T₂ = 122 ns in fig. S16D. B₁ is the microwave field strength in Eq. 1 and is set to be B₁ = 0.45 mT. The nutation frequency varies with the quantum gate: ω_mS = $\sqrt{6}$ gμ_BB₁/ℏ for the gates (Q_0,±1) between Q₀ and Q_±1 and ω_mS = 2gμ_BB₁/ℏ for the gates (Q_±2,±1) between Q_±2 and Q_±1. Therefore, anisotropic quintet sublevel distribution by the S-Q_mS interconversion in Fig. 5A highly influences the frequencies and amplitudes of the quantum beats induced by the coherent microwave pulses at a field strength of B₀. The quantum beat profile is well reproduced by the dynamic model of the quintet populations considering subtle conformational motion between the dihedral angles of β = 130° and 122° in the T_AT_B exciton pair for TT₁ and TT₂, respectively, which causes the fluctuation in the through-space separations between 0.29 and 0.32 nm (fig. S10A). In the simulated profile (red lines in Fig. 6, D and E), a minor lower-frequency component (green line in Fig. 6D) is included by the gates between Q_±2 and Q_±1, denoting that the two different nutation frequencies of 25 and 31 MHz are involved with opposite polarizations (Fig. 6B) in the experimental profile.

Fig. 6. Transient nutation of the quintet state at room temperature.

(A) Pulse sequence of the transient nutation measurement. (B) Two main quantum gates detected by the pulsed microwave at B₀ = 348.1 mT in the quintet sublevels. (C) Echo-detected EPR spectrum at τ_delay = 1.1 μs. The durations of the first and second pulses are x = 8 ns and t₂ = 16 ns, respectively. Fitting result using eq. S15 and table S5 is shown as a red line. (D) Transient nutation profiles as a function of x in (A) at τ_delay = 1.1 μs using t₂ = 16 ns. The simulated profile is shown by a red line considering the anisotropic sublevel populations. At the bottom, decomposition of the computed nutation data by the gates Q_0,±1 and Q_±2,±1 are shown by purple and green lines, respectively. (E) Simulated profiles by the different rotation models. The red solid line corresponding to the red line in (D) is computed by the conformation motion between the dihedral angles of β = 130° and 122° of the T_B molecule in the T_AT_B pair for TT₁ and TT₂, respectively. Green dashed line is obtained with considering the large dihedral angle change between β = 130° and 150° in Fig. 4B. (F) Dependence of τ_delay on the echo intensity (black line) employing x = 8 ns, t₂ = 16 ns, and τ_echo = 200 ns with B₁ = 0.45 mT together with delay time dependence of the CW-TREPR intensity at 351 mT in Fig. 4A (blue line). Fitting result using eq. S1 and table S5 is shown as a red line.

The ⁵TT-derived signal observed in CW-TREPR was reproduced by a large dihedral motion between β = 130° and 150°, but such a large conformational change would cause a large fluctuation of the zero-field splitting interaction, leading to a severe quantum decoherence (fig. S17). The pulse EPR nutation profile could not be reproduced by dihedral motion between β = 130° and 150° (green dashed line in Fig. 6E) but could be reproduced by the subtle conformational motion between the dihedral angles of β = 130° and 122°. This suggests that large and small conformational motions coexist as major and minor components, respectively, in the Pn-MOF. Since the Pn-MOF in this study was not very crystalline, we assume that majority of the MOF structure (source of CW-TREPR signal) was disordered, resulting in large conformational changes, while the conformational change was suppressed in some minor domains with high crystallinity (source of pulse EPR echo signal). There are probably many disorders near the surface of the rounded nanoparticles (fig. S2), and the chromophores in this disordered region should cause the larger dihedral motion and the quicker dephasing in the quintet coherence and thus do not contribute to the spin echo signal. It is anticipated, however, that the ordered 22 cm⁻¹ collective motions occur at the ordered domains most probably in the center core region of the MOF nanocrystals with preventions of the conformation motions. These minor TT pairs are possibly responsible for the weak echo signals.

To corroborate this mode of motion, we additionally carried out terahertz spectroscopy of Pn-MOF (fig. S18). Although the frequency of the large conformational change (14 cm⁻¹) was outside the measurement range, sharp Lorentzian lines were observed at around 25 cm⁻¹ near the simulated frequency of the small conformational change (22 cm⁻¹). Similar low-frequency motion modes have been observed in other MOFs in systems with restricted ligand mobility (46), supporting the idea that suppressive collective molecular motion is occurring in the Pn-MOF. The sharp terahertz signals in fig. S18 indicate that the ordered collective modes (>22 cm⁻¹) originate from the motion of the entire framework via the metal-ligand coordination bonds. Although the detailed assignment of the collective mode is out of the scope of the current work, these phonon modes might couple with the local molecular rotations of the chromophores. For the singlet-quintet conversion in the strongly coupled TT with the negative exchange coupling, it is essential that the frequency of the J-modulation is closer to the frequency relevant to the quintet-singlet energy gap based on the Redfield theory, as reported previously (20, 26). In addition, the quintet-singlet energy gap is required to be thermally accessible to get the quintet populations. In the present analysis, quintet-triplet energy gap is set to be ~1 THz corresponding to the −6J value (30 cm⁻¹) that is close to the reported values (47, 48). In this case, the higher frequency vibrations (>50 cm⁻¹) in the terahertz spectrum should not contribute to minor quintet production because these frequencies are much higher than −6J. The broad and congested spectral component around 20 to 30 cm⁻¹ should be responsible for the disordered motions causing the major echo-silent quintet EPR. Therefore, it is reasonable to hypothesize that the low-frequency Debye peak should contribute to the echo-silent quintet due to the disordered, nonstate-specific vibronic coupling, while the ordered motion characterized by the Lorentzian peak at 25 cm⁻¹ should contribute to the minor long-lasting echo due to the ordered molecular motions with the suppressive conformation dynamics. While it is not the main topic and beyond the scope of the current work, we will test this hypothesis using MOFs with different crystallinity and structures.

Specifically, the limited dihedral angle fluctuation in β is revealed to result in superposition of the transverse magnetization by the gates of Q_0,1 (purple in Fig. 6, B and D) and Q_−2,−1 (green in Fig. 6, B and D) at B₀ = 348.1 mT from fig. S19A, while the magnetization by the Q_±2,±1 gates is minor for the larger angle-fluctuation case in fig. S19B. The hindered rotation thus leads to detections of the high- and low-frequency nutation components determined by ω₀ = $\sqrt{6}$ gμ_BB₁/ℏ and ω₋₂ = 2gμ_BB₁/ℏ. This is also consistent with the echo-detected EPR spectrum (red line in Fig. 6C) obtained using this rotation model. These results imply that the quantum beating behavior can be altered by the degree of the structural fluctuation.

DISCUSSION

For quintet multiple excitons generated by photo-induced SF, it has been unclear what kind of molecular motion is required to achieve both (i) effective quintet generation and (ii) noise suppressed qubits. Conformational motion is necessary for the spin conversion from ¹TT to ⁵TT. However, if the change in orientation angle of the chromophore relative to the magnetic field is too large, then not only does exciton hopping cause dissociation and recombination between excitons but also ⁵TT quantum decoherence occurs, making it impossible to use as a qubit. On the other hand, low-mobility triplet pairs with small orientation angle changes prevent exciton hopping and recombination. In addition, the suppression of transverse relaxation due to fluctuations in the zero-field splitting interaction makes it possible to slow down decoherence and function as qubits even at room temperature.

To explicitly understand this trap characteristic for manipulation of the microwave-induced spin coherences, we plotted the echo intensity at 348.1 mT as a function of the delay time (τ_delay) (Fig. 6F). The decay time (1.2 μs) of the echo signal of the quintet is much longer than the decay time (0.2 μs) of the quintet signals (blue line in Fig. 6F) detected by the CW-TREPR and TAS methods and is well fitted by the rotation model calculations (red lines in Fig. 6, C and F) using k_Rec = 1.5 × 10⁶ s⁻¹ at room temperature (table S5), demonstrating that the minor quintet species in some ordered domain are only responsible for the quantum coherence. This room-temperature ⁵TT quantum coherence based on moderate suppression of chromophore motion in MOFs is in contrast to previous ⁵TT generation based on exciton diffusion in dense molecular crystals, which is not immune to triplet separation and decoherence at room temperature. The usefulness of ⁵TT as qubits has been demonstrated at cryogenic temperatures, but appropriate suppression of molecular motion in MOFs leads to room-temperature drive of ⁵TT qubits.

Previous studies treated that the quintet generations for the different sublevels are based on the Fermi’s golden rule (and by Redfield theory) by which the spin conversion is caused as the perturbation between the ¹TT and ⁵TT under the J-fluctuations (14, 49). This treatment is valid for the large positive J-coupling by which the ⁵TT energy is notably lower and longer-lived with respect to the ¹TT in the covalently linked chromophore dimer systems. In the present sample, however, we conclude that the J-coupling is negative and that its magnitude is smaller than the thermal energy. In this case, Fermi’s golden rule treatment is no longer valid because the ¹TT is stable and thus interacting with the ⁵TT during the measurements. This is well consistent with the quick quintet deactivation in nanosecond timescales (Fig. 4C). This negative J is reasonably caused by the direct through-space orbital overlap between the pentacene chromophores in Pn-MOF structure (Fig. 4B).

We incorporated the effect of the spin lattice relaxation within the quintet sublevels to reproduce the delay time dependence of the echo (red line in Fig. 6F) in eq. S17. The T₁ value of 3.8 μs is longer than the deactivation time of the quintet polarization (blue line) in the TREPR measurement. This T₁ (and T₂ = 150 ns) is another strong evidence for the ordered molecular motions dominating the very minor quintet component in the pulsed EPR detection. Furthermore, k_Rec = 1.5 μs⁻¹ determined by the echo trace is much smaller than k_Rec = 56 μs⁻¹ obtained by the TREPR analysis. This slow recombination process well supports the suppressive conformation dynamics for restriction of the too much orbital overlap to lengthen the quintet lifetime in Fig. 6F.

The high sensitivity of the pulsed EPR spectroscopy enables one to selectively observe the minor species when the phase memory time is long enough, while the nanosecond T₂ species originated from the major species are completely filtered out. It is also noted that the pulsed EPR spectroscopy filters out the short T₂ components because it is required to place a waiting delay time of at least 200 ns between the second microwave pulse and the first pulse (Fig. 6A) due to an unavoidable deadtime problem originating from the defense pulse introduced during the strong microwave irradiations, meaning that T₂ of ~20 ns is out of the detection. The notable mismatches between the CW-TREPR measurement (Fig. 4) and the pulsed EPR data (Fig. 6) at room temperature suggest the presence of more than one component in the MOF. The one is a high-crystalline ordered component that gives a spin echo signal, and the other is a less-crystalline disordered component that does not give a spin echo signal and whose EPR signal mostly disappears within one microsecond.

We revealed that the chromophore motion alters the phase and amplitude of the frequency component of its quantum beating. The control of multiple quantum gates is also extremely important for future developments in molecular quantum computing with multiple qubits, such as verification of CNOT gates.

It is notable that not only the generation of quantum coherence by microwave irradiation has been demonstrated at room temperature by simulating chromophore motion in an MOF but also the details of molecular motion (change in molecular orientation) that enable the realization of room-temperature qubits have been found. In the present system, the low-mobility part that can generate ⁵TT coherence is only a part of the MOF. It will be possible to generate ⁵TT qubits more efficiently in the future by searching for guest molecules that can induce more such suppressed motions and by developing suitable MOF structures. Precise control of the assembly structure and motion of the chromophores in MOFs is expected to lead to the development of innovative materials useful for the molecular-based QIS.

MATERIALS AND METHODS

All reagents were used as received unless otherwise noted. Dry tetrahydrofuran (THF) was prepared by treating with Molecular Sieves 4A 1/8, Wako. Liquid paraffin, n-butyl lithium in hexane, and zirconium tetrachloride (ZrCl₄) were purchased from Sigma-Aldrich. p-toluene sulfonic acid, tin(II) chloride dihydrate (SnCl₂·2H₂O), sodium chlorite (NaClO₂), sodium dihydrogen phosphate (NaH₂PO₄), and acetic acid were purchased from FUJIFILM Wako Pure Chemical. 4-Bromobenzaldehyde, ethylene glycol, 6,13-pentacenedione, and 2-methyl-2-butene were purchased from TCI.

General characterization

¹H nuclear magnetic resonance (NMR) (400 MHz) spectra were recorded on a JEOL JNM-ECZ400 spectrometer using tetramethylsilane (TMS) as the internal standard. Elemental analysis was carried out using a Yanaco CHN Corder MT-5 at the Elemental Analysis Center, Kyushu University. PXRD patterns were measured on a Bruker D2 Phaser (Cu-Kα, 30 kV, 10 mA). For making the simulated structure and corresponding simulated PXRD pattern, Materials Studio software was used (Accelrys, Material Studio Release Notes, Release 4.2, Accelrys Software, San Diego, 2006). The geometry and unit cell were optimized by Materials Studio Forcite tool (50). Scanning electron microscopy image was collected by a Hitachi SU8000 with an accelerating voltage of 2.3 kV. Thermogravimetric analysis was conducted on a Rigaku Thermo Plus EVO2 under N₂. N₂ adsorption isotherm measurements were carried out on a Bel BELSORP-max. UV-vis absorption spectra were obtained on a JASCO V-670 spectrophotometer. Fourier transform infrared spectra were recorded on a SHIMADZU IRTracer-100 with a Smiths DuraSamplIR II ATR device.

Sample preparation

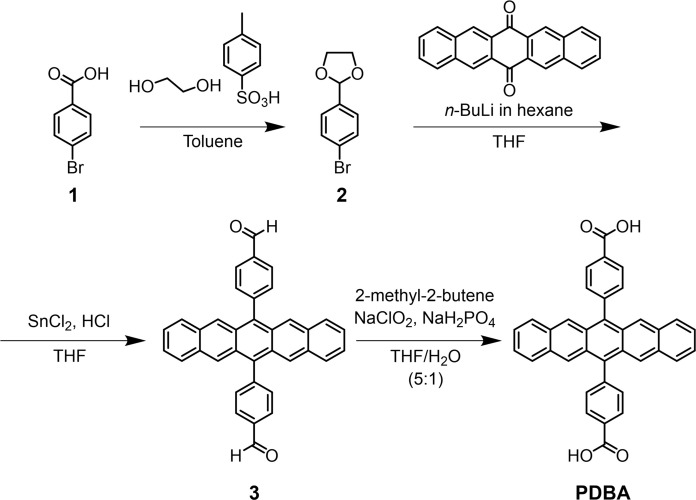
PDBA was prepared (Fig. 7) according to our previously reported method (36).

Fig. 7. Synthetic route of PDBA.

Synthesis of 2-(4-bromophenyl)-1,3-dioxolane (2)

Sixty milliliters of a toluene solution of 4-bromobenzaldehyde (5.0 g, 27 mmol), ethylene glycol (4.3 g, 54 mmol), and p-toluene sulfonic acid (0.17 g, 0.90 mmol) was refluxed with a Dean-Stark trap for 8 hours. The solution was neutralized with 50 ml of K₂CO₃ aqueous solution and then extracted with ethyl acetate (3 × 50 ml). The organic layer was dehydrated by Na₂SO₄, filtrated, and dried under reduced pressure. The orange crude oil was purified using silica gel column chromatography (chloroform/hexane = 1:1), giving a compound 2 as yellow oil. Yield: 5.24 g (85%). ¹H NMR (400 MHz, DMSO-d₆, TMS): δ = 7.57 to 7.64 (d, 2H), 7.35 to 7.45 (d, 2H), 5.73 (s, 1H), and 3.90 to 4.08 (m, 4H).

Synthesis of 4,4′-(pentacene-6,13-diyl)dibenzaldehyde (3)

n-butyl lithium in hexane (2.5 M, 6.0 ml, 15 mmol) was dropped to a solution of 2 (3 g, 13.1 mmol) in dry THF (120 ml) at −78°C under N₂ atmosphere. A 20-ml THF solution of 6,13-pentacenedione (1.24 g, 4.0 mmol) was added after stirring for 1 hour at −78°C. The reaction was warmed to room temperature and stirred for 24 hours. A saturated aqueous NH₄Cl (150 ml) was added to quench the reaction. The mixture was filtered and dried under vacuum. The dark-red oil-like crude was dissolved in 30 ml of THF and added SnCl₂·2H₂O (4.2 g, 22 mmol) and 9 ml of concentrated HCl. To avoid the light exposure, the reaction mixture was covered by an aluminum foil and stirred at room temperature for 24 hours. The resulting solution was added 150 ml of H₂O and extracted with chloroform (3 × 100 ml). The organic layer was dehydrated by Na₂SO₄, filtrated, and dried under vacuum. Silica gel column chromatography (chloroform/hexane = 1:1) gave 3 as a dark purple powder. Yield: 1.61 g (82%). ¹H NMR (400 MHz, DMSO-d₆, TMS): δ = 10.32 (s, 2H), 8.32 (t, 4H), 8.25(s, 4H), 7.90 to 7.95 (d, 4H), 7.84 to 7.88 (m, 4H), and 7.31 to 7.35 (m, 4H).

Synthesis of PDBA

3 (1.61 g, 3.31 mmol) and 2-methyl-2-butene (35 ml, 331 mmol) were dissolved in THF (200 ml) at 0°C under Ar atmosphere. NaClO₂ (1.2 g, 13.2 mmol) and NaH₂PO₄ (2.50 g, 20.9 mmol) in H₂O (40 ml) were added to the suspension and stirred for 3 hours. The reaction was slowly warmed to room temperature and stirred for 24 hours under dark. After removing THF under reduced pressure, the residue was diluted with water and washed with chloroform and methanol, giving compound PDBA as a dark purple powder. Yield: 1.05 g (65%). ¹H NMR (400 MHz, DMSO-d₆, TMS): δ = 8.32 to 8.37 (d, 4H), 8.25 (s, 4H), 7.85 to 7.88 (q, 4H), and 7.78 to 7.82 (d, 4H). Mass spectrometry (matrix-assisted laser desorption/ionization–time-of-flight mass spectrometry): mass/charge ratio [M+] calculated C₃₆H₂₂O₄, 518.57; found 518.33. Elemental analysis for C₃₆H₂₂O₄·2H₂O: calculated (%) H 4.73, C 77.97, and N 0.00; found (%) H 4.92, C 77.90, and N 0.13.

Synthesis of Pn-MOF

ZrCl₄ (9 mg, 0.0385 mmol) and acetic acid (220 μl, 3.85 mmol) in 2.26 ml of DMF were ultrasonically dissolved in a 6-ml screw vial. After stirring for 6 hours at room temperature, PDBA (20 mg, 0.0385 mmol) was added, and the mixture was ultrasonicated again. The obtained purple solution was degassed two times by freeze-pump-thaw in a 10-ml ampule and flame-sealed under vacuum. The degassed sample was wrapped with aluminum foil to minimize light exposure and kept in an oven at 403 K for 48 hours. The mixture was cooled to room temperature over 72 hours, filtered, and soaked in methanol for 12 hours. After removing the solvent by filtration and drying for 5 hours at 323 K, dark green powder was obtained.

TAS measurement

The femtosecond TAS and nanosecond TAS experiments were performed using home-built pump-probe setups. A Ti:sapphire regenerative amplifier (Spectra-Physics, Spitfire Ace) was used as the light source, (pulse duration, 120 fs; repetition rate, 1 kHz; pulse energy, 4 mJ per pulse; central wavelength, 800 nm), seeded by a Ti:sapphire femtosecond mode-locked oscillator (Spectra-Physics, Tsunami) with a pulse duration of 120 fs, a repetition rate of 80 MHz, and a pulse energy of 10 nJ per pulse. For femtosecond TAS, one of the outputs from the amplifier was directed toward an optical parametric amplifier (Light Conversion, TOPAS), where the output wavelength was tuned to 600 nm for use as the pump pulse. The other output was focused on a sapphire crystal (3 mm in thickness), generating white light in the 450- to 750-nm range for use as the probe pulse. For nanosecond TAS, output pulses from an optical parametric oscillator (Light Conversion, NT242; central wavelength, 600 nm; pulse duration, 3 ns) using the third harmonic generation (THG) of a Nd:YAG laser as the excitation pulse were used as a pump pulse. The magic angle (~54.7°) was adopted between the pump and probe polarizations. The probe pulse that passed through the sample was dispersed by a polychromator (JASCO, CT-10; 300 grooves/500 nm) and detected by a multichannel detection system with a complementary metal-oxide semiconductor sensor (UNISOKU, USP-PSMM-NP). The Pn-MOF sample was enclosed between quartz glass plates under an inert gas atmosphere. The TAS measurements were conducted in a semitransparent position on the Pn-MOF sample.

CW-TREPR and pulsed EPR measurements

TREPR measurements were carried out at room temperature using an X-band (9.682 GHz in the CW-TREPR and 9.589 GHz in the pulsed EPR) CW/fourier transform (FT) EPR spectrometer (ELEXSYS II E580) with a dielectric resonator using a quadrature detection. Samples were photoexcited by the second harmonics (532 nm) of a Nd:YAG laser (Continuum, Minilite II; full width at half maximum of ∼5 ns). A laser depolarizer (SIGMA KOKI, DEQ 1 N) was placed between the laser exit and the microwave cavity. Repetition rate and pulse energy were 10 Hz, and 1 mJ per pulse, respectively. The CW-TREPR spectra were obtained using a transient mode in the Bruker Elexsys spectrometer with a microwave power of 4.7 mW. The TREPR signals were directly amplified by a video amplifier using a control program (Xepr) for a digitizer of SpecJet-II. The TREPR data were smoothed for denoising using a binomial-weighted moving average to time course with a window of 300 ns for the spectra and the two-dimensional plot. The spin echo measurements in Fig. 6 were performed by using PatternJet-II controlled by the Xepr program. Pulse sequence of the Hahn echo detection (laser-τ_delay-π/2-τ_echo-π-τ_echo-echo) was used in the pulse-EPR measurements. The power of microwave pulse was set to maximize the intensity of the spin echo signal of oxidized pentacene species (fig. S16) observed in the absence of the laser irradiations following the CW-TREPR measurement. In this, the pulse durations were x = 16 ns and t₂ = 32 ns, respectively. The echo-detected field sweep measurements of the triplet pairs were performed by using τ_delay = 1.1 μs, τ_echo = 200 ns, x = 8 ns, and t₂ = 16 ns, and the magnetic field was varied. Transient nutation measurements were performed by varying x from 0 to 400 ns.

Pn-MOF was put into 2-mm capillaries, with or without paraffin. The capillaries were degassed at room temperature with an oil pump and sealed with a flame.

From Fig. 5, we computed time development of the singlet, triplet, and quintet characters for the different exciton-pair conformations together with the J values using coupled stochastic Liouville equations, as reported previously (20, 51). In the details of the applied parameters for the multiexciton conformations, the kinetics are listed in tables S3 and S4 to compute the CW-TREPR data and the pulsed EPR data, respectively. The singlet, triplet, and quintet diagonal terms in density matrix elements were used to obtain delay time dependences of the excitons (Fig. 4C) of ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{TT}1}$ , ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{TT}2}$ , ${\mathrm{\rho }}_{m_S{m}_S}^{\mathrm{TT}1}$ , ${\mathrm{\rho }}_{m_S{m}_S}^{\mathrm{TT}2}$ , ${\mathrm{\rho }}_{\mathit{mm}}^{\mathrm{T}1\mathrm{S}0}$ , ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{T}+\mathrm{T}}$ , ${\mathrm{\rho }}_{\mathit{mm}}^{\mathrm{T}+\mathrm{T}}$ , and ${\mathrm{\rho }}_{m_S{m}_S}^{\mathrm{T}+\mathrm{T}}$ where m (= +1, 0, −1) represents the quantum number of the triplet sublevels. From Fig. 5, the following relations were used: ⁵TT₁ = ${\sum }_{m_S}{\mathrm{\rho }}_{m_S{m}_S}^{\text{TT}1}$ , ⁵TT₂ = ${\sum }_{m_S}{\mathrm{\rho }}_{m_S{m}_S}^{\text{TT}2}$ , ³T₁S₀ = ${\sum }_m{\mathrm{\rho }}_{\mathit{mm}}^{\mathrm{T}1\mathrm{S}0}$ , ¹TT₁ = ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{TT}1}$ , ¹TT₂ = ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{TT}2}$ , and SCTP = ${\mathrm{\rho }}_{\mathit{SS}}^{\mathrm{T}+\mathrm{T}}+{\sum }_m{\mathrm{\rho }}_{\mathit{mm}}^{\mathrm{T}+\mathrm{T}}+{\sum }_{m_S}{\mathrm{\rho }}_{m_S{m}_S}^{\mathrm{T}+\mathrm{T}}$ (20, 51).

Terahertz-TDS spectroscopy

Terahertz spectra of MOF were measured by terahertz–time domain spectroscopy (TDS) spectrometer (Advantest TAS7400) in a transmission setup. The frequency resolution of the spectra obtained by the system was 7.6 GHz. The number of accumulations was 1024 at room temperature. MOF in paraffin was measured with polyethylene cell, and solid MOF samples were measured without polyethylene cell.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S19

Tables S1 to S5

References