AI-aided geometric design of anti-infection catheters

Abstract

Bacteria can swim upstream in a narrow tube and pose a clinical threat of urinary tract infection to patients implanted with catheters. Coatings and structured surfaces have been proposed to repel bacteria, but no such approach thoroughly addresses the contamination problem in catheters. Here, on the basis of the physical mechanism of upstream swimming, we propose a novel geometric design, optimized by an artificial intelligence model. Using Escherichia coli, we demonstrate the anti-infection mechanism in microfluidic experiments and evaluate the effectiveness of the design in three-dimensionally printed prototype catheters under clinical flow rates. Our catheter design shows that one to two orders of magnitude improved suppression of bacterial contamination at the upstream end, potentially prolonging the in-dwelling time for catheter use and reducing the overall risk of catheter-associated urinary tract infection.

A geometric design provides a simple solution for catheter-associated urinary tract infections.

INTRODUCTION

Catheter-associated urinary tract infections (CAUTIs) (1–5) are among the most common infections in hospitalized patients, costing about 30 million U.S. dollars annually (6). From a materials/device perspective, previous methods to prevent such infections included catheter impregnation with antimicrobial silver nanoparticles (7) or the use of antibiotic lock solutions, anti-adhesion, or antimicrobial materials (8, 9). However, none of these methods surpasses the effect of stricter nursing procedures, and current clinical practice to prevent CAUTI focuses on reducing catheter in-dwelling time to prevent CAUTI. The design of catheters that reduce bacteria motility in the presence of fluids would offer a substantial improvement to the state-of-the-art management of CAUTI.

Such design requires us to understand the locomotion patterns of microbes in the presence of fluid flow under confinement. A typical microbial trajectory alternates between periods of running (propelling themselves in a straight line) and tumbling (randomly changing direction) to explore the environment (10–13). Hydrodynamic interactions and quorum sensing lead to more complicated dynamics, such as enhanced attraction to the surface (14, 15), and collective swarming motion (16–19). In shear flows, microscopic run-and-tumble (RTP) motion can lead to macroscopic upstream swimming (20–27). Normally, passive particles are convected downstream in addition to diffusive spreading (28). However, the self-propulsion of microbes results in qualitatively different macroscopic transport: The body of a bacterium crossing the tract is rotated by fluid vorticity, which leads them to swim against the flow direction. Both biological micro-swimmers and synthetic active particles exhibit upstream motility. For biological micro-swimmers such as Escherichia coli and mammalian sperm, the fore-aft body asymmetry and the resulting hydrodynamic interactions with the wall are often used to explain their upstream swimming behavior (20, 21, 25, 29–31). On the other hand, for point-like active particles with negligible size, upstream swimming is still present (24, 27). Consider a point-like active particle when it is approaching a wall: Its forefront must point to the wall. Near the wall, the vorticity of the Poiseuille flow (at its maximum) acts to always reorient the particle toward the upstream direction (also see Materials and Methods) (27), and then they swim upstream along the wall (Fig. 1, A and B). Many other factors such as body shape asymmetry, flagellar chirality, and hydrodynamic interactions between the bacteria and the boundary also influence the upstream swimming behaviors. Recent experiments (32) have demonstrated super-contamination of E. coli in a microfluidic channel, highlighting the importance of their power-law runtime distribution, which dramatically enhances the tendency of bacteria to swim upstream, and the bacteria can swim persistently against the flow.

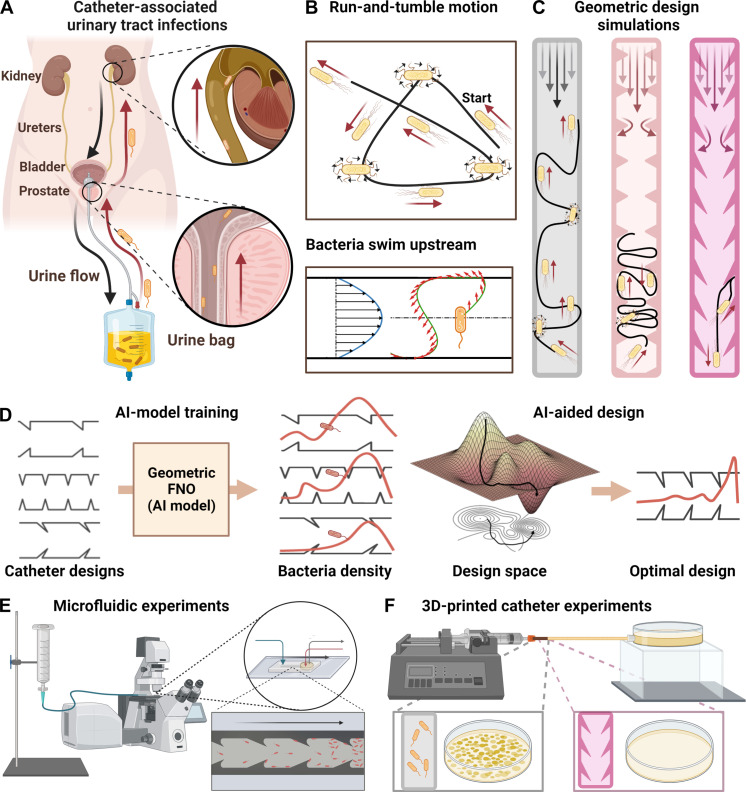
Fig. 1. Schematic of proposed CAUTI mechanism and anti-infection design process.

(A) Proposed mechanism for CAUTI. The urine flows from within the patient’s bladder outward through a catheter, while bacteria swim upstream into the patient’s body. (B) The run-and-tumble motion of bacteria and upstream swimming mechanism. (C) Simulations to explore catheter shapes suppressing upstream swimming. (D) AI-assisted optimization using the geo-FNO framework. (E) Microfluidic experiments to test the design in 2D channels. (F) 3D experiment with designed real-size catheters.

Mainstream strategies to prevent bacterial contamination include the following: (i) physical barriers, such as filters or membranes (33–38); (ii) antimicrobial agents, such as antibiotics (36, 37); (iii) surface modifications of medical equipment to reduce bacterial adhesion and biofilm formation (38–44); (iv) control of physical/chemical environment, such as high/low temperatures, low oxygen levels, or disinfectants to suppress bacterial growth and survival (45–48); (v) strict sterilization procedures, such as gloving and gowning (49–51); and (vi) regularly monitoring patient conditions to detect and treat bacterial contamination early on (52–54). Although various surface modifications or coatings have been proposed to reduce bacterial adhesion, none has been shown to prevent upstream swimming or catheter contamination effectively (38–40). Other passive antibacterial methods, such as membranes or filtration, may be difficult to apply directly to patients with indwelling catheters.

Geometric control of microbial distribution is safer than antibiotics or other chemical methods regarding antibiotic resistance (55–58). Specific shapes have been used in other contexts to confine and trap undesirable bacteria (59). Asymmetric shapes can also bias the partitioning of motile bacteria (60, 61) due to the “dry” geometric rectification effect, and extruded boundary shapes can locally enhance the vorticity of Poiseuille flow proportional to the extrusion curvature.

We sought to engineer catheters that prevent bacteria from swimming upstream and minimize contamination. To optimize the geometry of the catheters, we constrained the design space to placing triangular obstacles on the interior catheter’s wall. Capturing the simplest physical mechanism of upstream swimming that emerges for self-propelling spheres (27), we performed fluid and particle dynamics simulations to find geometric design principles (Fig. 1C). We modeled the bacteria distribution by coupling the hydrodynamics and geometric rectification effects as a stochastic partial differential equation (SPDE). We then used the simulation data to train an artificial intelligence (AI) model based on geometry focused Fourier neural operators (Geo-FNO) (62, 63) to learn the solutions of the SPDE and use the trained model to optimize the catheter geometry (Fig. 1D). On the basis of the optimized design, we fabricated quasi–two-dimensional (2D) microfluidic devices (Fig. 1E) and 3D print prototype catheters (Fig. 1F) to evaluate the effectiveness of our concept. Our experimental results show that up to two orders of magnitude improved suppression of bacterial super-contamination compared to standard catheters, suggesting a pathway for the management of CAUTI.

RESULTS

Investigating the microscopic mechanism

We adopt a simple model (27) for bacteria dynamics in the presence of shear flow. Bacteria are approximated as spheres with negligible sizes, and their orientation q follows from the equation $d\mathit{q}/\mathit{dt}=\left[1/2\mathbf{\omega }+\sqrt{2/{\mathrm{\tau }}_R}\mathbf{\eta }\left(\mathit{t}\right)\right]\times \mathit{q}$ , where ω is the local flow vorticity. More detailed hydrodynamic effects can be incorporated (64) into ω. η is Gaussian noise with ⟨η(t)⟩ = 0 and ⟨η(0)η(t)⟩ = δ(t)I. τ_R is the average runtime (see Materials and Methods for more details). We first numerically studied the role of conventional surface modifications, such as antimicrobial nanoparticle coatings (36, 42), engineered roughness, or hydrophobicity (65, 66), in the suppression of bacteria’s upstream swimming. These modified surfaces can prevent bacteria from getting too close to the wall. To model their presence, we assumed that they cause the bacteria to detach from the surfaces and dwell at a distance of at least 3 μm away from the surface, which is above the typical body length of E. coli (1 to 2 μm). Surface modifications may also influence hydrodynamic interactions between the bacteria and the wall, but they are neglected in our simple general model based on point-like spheres. We find that the upstream swimming behavior is not much affected by surface repulsion at all flow rates tested in our simulations. Comparing the simulated trajectories of a persistent bacterium inside a smooth channel (Fig. 2D) and a surface-modified channel (Fig. 2E), the upstream swimming behaviors are similar. We quantify the effectiveness for the suppression of bacterial upstream swimming by two population statistics: (i) the averaged upstream swimming distance $⟨x_{\text{up}}⟩=-{\int }_0^{-\infty }\mathrm{\rho }(x)x\mathrm{d}x$ , where ρ(x) is the bacteria distribution function; (ii) the distance that the top 1% upstream swimmers arrive at x_1%. The simulated surface modification only slightly reduces ⟨x_up⟩ at intermediate flow rates but barely changes x_1% (blue and pink lines in Fig. 2F). The poor effectiveness of surface modifications is consistent with current experimental observations (39, 40).

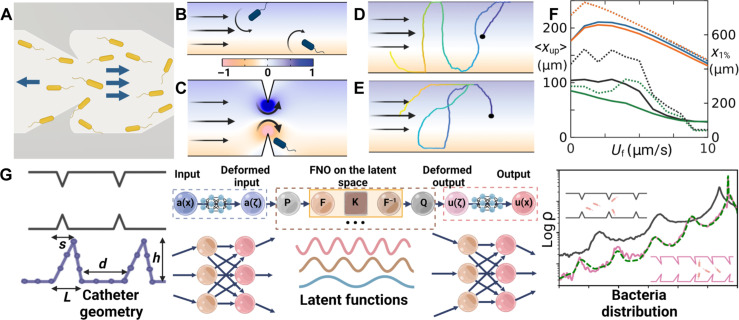
Fig. 2. Physical mechanism of obstacle suppressing upstream swimming and geometric optimization.

(A) Geometric rectification effect without flow. (B to E) Color background shows the relative magnitude of flow vorticity (darker is larger; blue, counterclockwise; yellow, clockwise). (B) Poiseuille flow in a smooth channel. The vorticity rotates the head of the bacteria downstream. (C) Flow in a channel with symmetric obstacles. Flow speed and vorticity are enhanced near the top of the obstacle, leading to stronger torque redirecting the bacteria downstream. (D) and (E) Simulated trajectories of a persistent bacterium in 2D channels of width 50 μm under different conditions: (D) a smooth channel, (E) a surface-modified channel that repels bacteria. (F) Population statistics of upstream swimming. Solid lines (left y axis) show the average upstream distance. Dashed lines (right y axis) show the upstream distance of the top 1% swimmers in the population. Blue lines for smooth channels, orange for surface-modified channels, black for symmetric obstacles, and green for asymmetric obstacles. (G) The AI model and the result. The Geo-FNO model is designed to learn the relationship between catheter geometry and bacteria distribution. It accomplishes this through a series of neural operator layers. The Geo-FNO first maps the irregular channel geometry to a unit segment [0,1], then applies Fourier-based kernels in the latent space, and, finally, transforms the predicted bacteria distribution in the latent space back to the physical space. The right panel shows the random initial condition (black) and the optimized design (pink). The bacteria distribution corresponding to the optimized design predicted by Geo-FNO (pink) is verified by the fluid and particle dynamics simulation (green dashed line).

We then explored the role of catheters’ surface geometry by adding physical obstacles. We find that symmetric and asymmetric obstacles significantly suppress upstream swimming (black and green lines in Fig. 2F). We identify two synergistic effects: First, the slope of the obstacles redirects the bacteria’s swimming direction when they take off from the top of the obstacle, interrupting the continuous climbing along the wall’s surface. Asymmetric shapes bias bacteria motion downstream (Fig. 2A), as shown by simulated trajectories at 0 flow rate (Supplementary Materials and fig. S1) and the difference in the upstream swimming statistics (black and green lines of Fig. 2F) at low flow rates. Second, at a finite flow rate, the flow field differs from the Poiseuille flow in a smooth channel (Fig. 2B). In the Poiseuille flow, the vorticity turns the bacteria downstream. Near the top of the obstacle, the flow speed and vorticity are greatly enhanced (Fig. 2C and fig. S2), boosting the turning mechanism. Combining these two effects, we expect upstream swimming to be significantly reduced in channels with optimized obstacle geometry.

The parameter space for design optimization is characterized by four parameters: obstacle base length L, height h, tip position s, and inter-obstacle distance d; we denote the channel width by W (Fig. 2G). To optimize this space, we placed two constraints. First, if neighboring obstacles get too close, the vortices at their tips start to overlap. Both the magnitude of the maximum effective vorticity (right at the obstacle tips; see the mathematical definition of the effective vorticity in the Supplementary Materials) and the effective sizes of the vortices are reduced because of the overlap. Besides, larger boundary layer and stagnation zones develop (fig. S2, A and B). Hence, we constrain the inter-obstacle distance d > 0.5 W (fig. S2G). Second, with other parameters fixed, the effective vorticity at the obstacle tips increases as h increases (fig. S2, C to H), which is desirable to promote the vortex-redirecting effect. However, the tube obviously gets clogged when h = W/2. This trend of stronger clogging as h increases is reflected in the continuous increase of pressure drop that is needed to maintain the same effective flow speed (fig. S2I). To avoid clogging, we constrain the height h < 0.3 W.

AI-aided optimization of geometric conditions

Recently, AI-based models such as neural operators have been used to learn surrogates for forward simulation or observational models in fluid dynamics and other domains. Since these models are differentiable, they can be directly used for inverse design, i.e., we can use gradients to optimize in the design space directly. This makes generating previously unstudied designs much more streamlined. We used an AI model to optimize the channel shape, characterized by the four parameters and the two constraints described above (Fig. 2G). This method first maps the irregular channel geometry to a function in the latent space (a unit segment [0,1]), then applies the FNO model in the latent space, and finally transforms the bacteria distribution back to the physical space (Fig. 2G). We then used this trained surrogate model for inverse design optimization to determine the optimal channel shape. To evaluate the effectiveness of each design, we measure the averaged ⟨x_up⟩ at T = 500 s for three flow speeds (5, 10, and 15 μm/s). Our AI-aided shape design, based on geometry-aware Fourier neural operator, outperforms given shapes in training data by about 20% in terms of weighted bacteria distribution. The whole design optimization process is fast: It took 30 min each to generate a training instance for a total of 1000 instances in parallel (on 50 GPUs for 10 hours), 20 min on 1 GPU to train the model, and 15 s on 1 GPU for our trained AI model to generate the optimal design. The optimization procedure leads to the optimal structure of d = 62.26 μm, h = 30.0 μm, s = −19.56 μm, and L = 12.27 μm for channel width W = 100 μm. According to the mechanism presented above, this structure provides strong geometric rectification and vortex-redirecting effects to suppress upstream swimming.

Microfluidic experiments

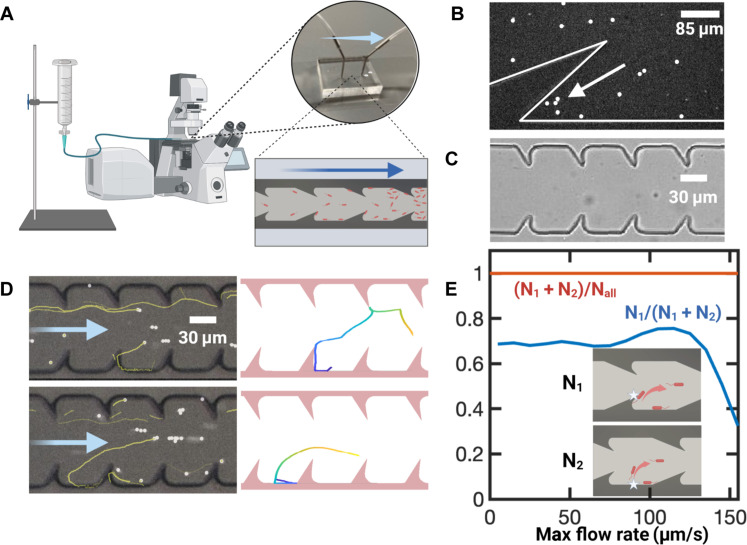
To evaluate the effectiveness of the optimized structure, we fabricated quasi-2D microfluidic channels of width W = 100 μm (wall-to-wall distance) and vertical depth 20 μm to observe bacterial movement under a microscope (Fig. 3A). We selected the subset of upstream swimming bacteria and categorized them according to where they detach from the walls. A trajectory is denoted as “type 1” if it detaches from the top of the obstacle (Fig. 3D, top) and “type 2” if it detaches from the smooth part of the wall (Fig. 3D, bottom). Type 1 trajectories experience both geometric rectification and enhanced hydrodynamic rotational disruption effects. Type 2 trajectories do not experience geometric rectification effect, and only mild vortex-redirecting effect, as the vorticity enhancement is strongest at the obstacle tips. Between 70 and 80% of upstream swimming trajectories belong to type 1 for flow speed U₀ < 100 μm/s (Fig. 3E). We also noticed that all the upstream swimming trajectories observed from these experiments are redirected downstream (Fig. 3E, red line). Bacteria accumulation was observed near a sharp corner (Fig. 3B), possibly due to the stagnation zone (Fig. 2C and fig. S1, white color near the corner). To prevent bacteria accumulation at the corners, we rounded the geometry with an arc of radius r = h/2 (Fig. 3C).

Fig. 3. Microfluidic experiments.

(A) Schematic of the microfluidic experiments. One end of the microfluidic channel is connected to a syringe filled with imaging solution, while the other end is connected to a reservoir of E. coli. The long arrow denotes the flow direction. (B) Bacteria accumulation at the sharp corner due to flow stagnation. (C) Bright-field image of the microfluidic channel. (D) Typical events of bacteria (white dots) falling off the channel walls, with their trajectories of the past 5 s shown in yellow lines. The top image shows a type 1 trajectory, where the bacteria fall off from the obstacle tip. The bottom image shows a typical type 2 trajectory, where the bacteria fall off from the smooth part of the wall. Left column, experimental; right column, simulation. (E) Statistics of fall-off events.

Macro-scale catheter experiments

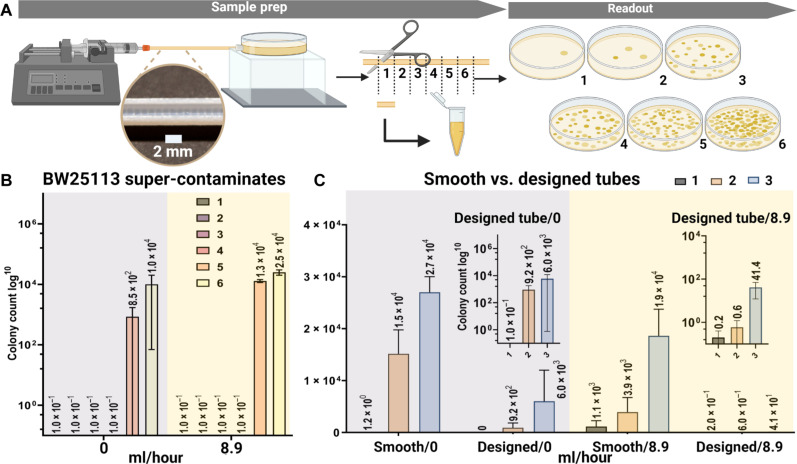
The mechanisms and design principles demonstrated above are readily scaled up to catheters. In 3D tubes, bacteria can traverse the tube through any cutting line of the cross section (fig. S2J). Bacteria moving near the boundary (trajectory 1 of fig. S2J) can still swim upstream due to the same mechanism shown above (Fig. 2, A, B, and F to I, and fig. S1), where only the dimensionless shear rate near the wall matters (27). The run length of super-contaminating bacteria can exceed 1 mm (32), comparable to the rescaled obstacle size, and the rectification effect is expected to persist at these scales (61). An order of magnitude estimate indicates that the Reynolds number inside urinary catheters is O (1) so that our results obtained from Stokes flow still works reasonably well after rescaled, and the rescaled round-off of the corners will still eliminate flow stagnation zones. We note that although the numerical results of 3D simulations may differ from those of the 2D results presented above, the qualitative trend stays the same. The 2D optimal structure then provides sufficient guidance to 3D experiments since the optimization process relies on relative trends rather than absolute values. We 3D printed prototype catheters to test design effectiveness at medically relevant spatial and temporal scales. For these, we enlarged the obstacle’s size to scale for a catheter with a 1.6-mm inner diameter and revolve their geometry around the center line. The obstacles become extruded rings, 0.4-μm tall with 1-mm spacing. The typical human urine rate is estimated to be 25 to 60 ml/hour (67–69) for adults, and lower for children. Since upstream contamination is stronger at lower flow rates, we test between 0 and 10 ml/hour. One end of the tube is connected to a syringe controlled by a mechanical pump, and the other is connected to an E. coli reservoir (Fig. 4A). After 1 hour, the tube is cut into 2-cm-long segments, discarding the two end segments, and the liquid inside is transferred to culturing plates. We quantified the distribution of bacteria in each segment by counting colonies after culturing the plates for 24 hours at room temperature (Supplementary Materials and fig. S5). We observed upstream contamination in smooth tubes (16 cm long) at various flow rates (0, 2.0, and 8.9 ml/hour Fig. 4B and fig. S4). With a bacteria velocity of 20 μm/s, the most persistent ones reach about 7 cm upstream in 1 hour. As a result, most bacteria concentrate in the two segments near the reservoir. We then tested the difference between smooth and designed tubes (8 cm long). The designed tubes show one to two orders of magnitude fewer bacteria contamination compared to the smooth tubes at the same positions (Fig. 4C). At 0 ml/hour, the suppression is about 10 times due to the geometric rectification effect (Fig. 2A). At 8.9 ml/hour, we observed more than 100-fold suppression due to the combined effects of geometric rectification and vortex redirecting (Fig. 2B).

Fig. 4. Experiments on 3D-printed catheter prototypes.

(A) Experimental setup. The downstream end of the tube was connected to a reservoir of E. coli, and the upstream end was connected to a syringe full of culture solution controlled by a syringe pump. After 1 hour, the tube was cut into equally long segments, and the liquid inside was extracted to culture for 24 hours. The number of E. coli colonies was counted under a microscope to reflect the number of bacteria in each segment. (B) Super-contamination of E. coli in smooth tubes. (C) Comparison of designed versus smooth tubes. Insets show the same data plotted on log-scale.

DISCUSSION

In this work, we introduce an effective geometrical design of the interior surfaces of medical catheters for suppressing bacterial upstream swimming and super-contamination. Our design approach is based on impeding the physical mechanism for bacterial upstream swimming, considering the general model of spherical particle rheotaxis with power-law dynamics. Infectious microbes vary in shape, flagella features, and hydrodynamic interactions. The simple model adopted here neglects details of the bacterial locomotion, such as their flagella chirality (29) and hydrodynamic interaction with the boundary (20), for both simplicity and generality of the design. The simulation results are used to guide the design of the experiments, rather than providing accurate predictions of the experimental outcomes specifically with E. coli. More sophisticated models considering the details regarding certain microbial species can be used in future studies. We find a lower bound on the separation between obstacles to maximize the effective vorticity near the tip of obstacles due to the interaction of overlapping vortices (fig. S2 and the Supplementary Materials). The constraint on obstacle heights is a trade-off between enhancing effective vorticity and avoiding clogging of the tube (fig. S2). While we chose to use this AI framework for the optimization of the catheter’s geometry, other methods, such as genetic algorithm with numerical solvers (70) or gradient descent with adjoint methods (71), could also have been deployed. We note that the geometrical design cannot completely eliminate bacterial upstream swimming, especially at near-zero flow rates. However, it drastically reduces the amount of super-contamination and may significantly prolong the indwelling time of catheters. Using our designed catheters is not expected to require changes to the regular clinical protocols or retraining of medical personnel. Moreover, our solution does not introduce chemicals into the catheters, and thus is safe and does not require additional maintenance. Our geometrical design approach is expected to be compatible with other procedural measures, antibacterial surface modification, and environmental control methods.

MATERIALS AND METHODS

Fluid and particle dynamics simulations

We simulated the Stokes flow inside a channel with no-slip boundary conditions using the COMSOL software (72). The resulting velocity and vorticity fields are then coupled into the particle dynamics simulations, while the feedback of particle motion on the fluid dynamics is neglected in the limit of dilute suspensions and small particle sizes. The particle dynamics is described by the active Brownian particle (ABP) model with Gaussian statistics and the RTP model with power-law (Levy) statistics. The simulations were performed with our in-house GPU Julia code with a simulation timestep of 10⁻⁴ s. In the ABP model, individual particle dynamics is integrated according to the over-damped Langevin equation

$$\begin{array}{c}0=-\mathrm{\zeta }(\mathit{U}-\mathit{u})+\mathrm{\zeta }{U}_0\mathit{q}\left(t\right)+\sqrt{\mathbf{2}{\mathit{D}}_{\mathit{T}}\mathbf{\xi }\left(\mathit{t}\right)}\\ d\mathit{q}/\mathit{dt}=\left[1/2\mathbf{\omega }+B\mathit{q}\times (\mathbf{E}\cdot \mathit{q})+\sqrt{2/{\mathrm{\tau }}_R\mathbf{\eta }\left(\mathit{t}\right)}\right]\times \mathit{q}\end{array}$$

where ζ is the viscous drag coefficient, U is the particle’s velocity, q is the particle’s orientation vector, u is the local flow velocity, ω is the local flow vorticity vector, and E is the local strain-rate tensor of the flow. B is a geometric coefficient (73, 74), which is equal to 1 for infinitely thin rods and 0 for spheres. We present the results here for B = 0 since its value does not significantly affect the upstream swimming statistics (27). ξ(t) is Gaussian random noise satisfying ⟨ξ(t)⟩ = 0 and ⟨ξ(0)ξ(t)⟩ = δ(t)I. As bacteria are micrometer-sized particles, their Brownian motion is relatively weak, and we set the translational diffusivity D_T = 0.1 μm²/s in the simulations. Varying this value does not affect the results much as long as it remains small. η is Gaussian noise with ⟨η(t)⟩ = 0 and ⟨η(0)η(t)⟩ = δ(t)I, and τ_R is the average runtime. In the RTP model, individual particles will be displaced with η(t) = 0 (the “run” phase) for 0 < t < τ_R. Then, q is changed instantaneously to a random new direction (the “tumble”) $\mathit{q}\prime$ and the process is repeated with a new runtime ${\mathrm{\tau }}_R^{\prime }$ . For Levy swimmers, the runtime is sampled from Pareto distribution $\mathrm{\varphi }(\mathrm{\tau })=(\mathrm{\alpha }{\mathrm{\tau }}_0^{\mathrm{\alpha }})/{(\mathrm{\tau }+{\mathrm{\tau }}_0)}^{\mathrm{\alpha }+1}$ , where the parameter 1 < α < 2 controls the power-law index (75). Bacteria shape was simplified as spheres with negligible size. For the mechanism demonstration in Fig. 2J, we simulate 1,000,000 particles with a persistent runtime τ_R = 2 s for 200 s in a 2D channel 50 μm wide. A periodic boundary condition for both the flow field and the particle dynamics is always imposed along the direction of the channel. As a result, the channel is effectively infinitely long, and the obstacles are also repeated every 100 μm. The particles are released at x = 0 in the computational domain, initially uniformly distributed across the channel and randomly oriented. For the designed channels, sliding (for the particle dynamics) and no-slip (for the fluid dynamics) boundary conditions are imposed at the geometric boundary of the walls, except for the surface coating case where the no-slip boundary is at the wall, and the sliding boundary condition for the particles are set at 3 μm away from the wall.

Geo-FNO model and machine learning setup

The catheter design problem is an SPDE constrained optimization problem, where the objective function $⟨x_{\text{up}}⟩=-{\int }_0^{-\infty }\mathrm{\rho }(x)\mathit{xdx}\approx -\frac{1}{N}{\sum }_{i=1}^N{x}_i$ depends on the SPDE solution of the fluid and particle dynamics problem. Here, ρ(x) is the empirical bacteria distribution function at T = 500 s, approximated by N bacteria. Traditional optimization approaches require repeatedly evaluating such expensive computational models, and an adjoint solver is required when gradient-based optimization is applied. To overcome these computational challenges, we trained a Geo-FNO G as a surrogate model for the forward fluid and particle dynamics simulation that maps the channel geometry to the bacteria population function G : c → ρ. In contrast, prior work using AI approaches for various design problems only chose a few parameters that are input to traditional solvers of SPDE (76, 77). The full model consists of five Fourier neural layers with Gaussian error linear unit (GeLU) activation layers and has a fast quasi-linear time complexity. We performed fluid and particle dynamics simulations using both the ABP and Levy RTP models for three maximum flow speeds (5, 10, and 15 μm/s) to generate training and testing data for the Geo-FNO. For the training data, we generated 1000 simulations in parallel on 50 GPUs for 10 hours, with the design in each simulation randomly selected from the following parameter space: Obstacles with height 20 μm < h < 30 μm are periodically placed on the channel walls with inter-obstacle distance 60 μm < d < 250 μm, the base length satisfies 15 μm < L < d/4, and the tip position satisfies −d/4 < s < d/4. The constraints on these parameters were chosen to satisfy fabrication limits and physical conditions for the vortex generation mechanism (Fig. 2, B and C; see more discussions in Supplementary Text and fig.S2). The dataset is stored to be reused for future tasks. We used the relative empirical mean square error as the loss function. The model training took 20 min with the Adam optimizer on 1 GPU. It gets around 4% relative error on the 100 testing data points.

Fast inverse design with gradient-based optimization

The benefit of our AI approach is the speedup compared to traditional solvers, and differentiability allows the use of fast gradient-based methods for geometry design optimization. Each evaluation takes only 0.005 s on GPUs in contrast to 10 min by using GPU-based fluid and particle dynamics simulations, and, therefore, it is affordable to do thousands of evaluations in the optimization procedure. Moreover, we use automatic differentiation tools of deep learning packages to efficiently compute gradients with respect to design variables enabling the use of gradient-based design optimization methods. During optimization, we start from initial design parameters (d = 100 μm, h = 25 μm, s = 10 μm, L = 20 μm) and update them using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to minimize the objective function ⟨x_up⟩ post-processed from the bacteria population predicted by Geo-FNO. When the optimization gets trapped in a local minimizer, the optimization restarts from an initial condition obtained by perturbing the recorded global minimizer with a random Gaussian noise sampled from N(0, I). The proposed randomized BFGS algorithm guarantees that the recorded global minimizer monotonically decreases. The optimization loss trajectory is depicted in fig.S1, which is reduced from L = 6.68 × 10⁵ to L = 2.18 × 10⁵. The AI-based optimization took approximately 1500 iterations to reach the optimal design. The entire process, from data generation (which took 30 min each on 1000 instances in parallel on 50 GPUs for 10 hours) to training (20 min on 1 GPU), design optimization (15 s on 1 GPU), and final verification (10 min on 1 GPU), took less than 1 day. Within imposed parameter constraints, ⟨x_up⟩ is neither convex nor monotonic with respect to these design variables but is generally smaller with larger h, smaller d, and larger s (fig. S3). The final optimized design is d = 62.26 μm, h = 30.0 μm, s = −19.56 μm, and L = 15.27 μm.

Bacterial strains, culture conditions, materials, and chemicals

We used wild-type BW25113 E. coli with kanamycin resistance for the 3D catheter long-term experiment and BW25113 E. coli expressing mScarlet red fluorescent protein with kanamycin resistance for the microfluidic experiments. A single colony of the bacterium of interest was picked from a freshly streaked plate and suspended in LB medium to create a bacterial inoculum. The starting culture was cultured overnight at 37°C in LB medium to achieve a final concentration of approximately OD₆₀₀ (optical density at 600 nm) = 0.4. For the microfluidic experiments, 300 μl of the starting culture is transferred to a new flask with 100 ml of LB median and cultured at 16°C until OD₆₀₀ reaches 0.1 to 0.2. Bacteria are washed twice by centrifugation (2300g for 15 min), and the cells were suspended in a motility imaging medium composed of 10 mM potassium phosphate (pH 7.0), 0.1 mM K-EDTA, 34 mM K-acetate, 20 mM sodium lactate, and 0.005% polyvinylpyrrolidone (32).The use of this medium allows for the preservation of bacterial motility while inhibiting cellular division. The final concentration of the bacteria in the reservoir has OD₆₀₀ at 0.02. For the 3D catheter long-term experiments, 3 ml of the starter culture is transferred to a new flask with 500 ml of LB median and cultured at 16°C until OD₆₀₀ reaches 0.4. The bacteria are directly used and injected into the bacteria reservoir. Kanamycin was added to all the culture median and LB plates. The mobility of the bacteria was checked under the fluorescence microscope 10 min before the experiment (observed under Differential Interference Contrast (DIC) optics for BW25113 and red channel epifluorsence fluorescent protein for the BW25113 mScarlet strain).

Microfluidic experiments

To demonstrate the mechanism of our design and test the effectiveness of the optimized structure, we fabricated quasi-2D microfluidic channels to observe bacteria motion under a microscope. These microfluidic devices were fabricated using photolithography and polydimethylsiloxane soft lithography. As shown in the schematic of Fig. 3A, one end of the microfluidic channel connects to a syringe filled with imaging solution, and the other end connects to a reservoir of E. coli. The flow rate is controlled by tuning the height of the syringe with respect to the outlet downstream. Fluorescent beads were injected into the imaging solution as passive tracers to monitor the flow rate in real time. The high-speed video was achieved using an Olympus BX51WI microscope with two Photometrics Prime95B cameras connected using a W-View Gemini-2 Optical Splitter from Hamamatsu. An Olympus 20× dry objective lens was used. Time-lapse images were acquired at 12.4 frames/s with 488-nm laser intensity set at 20%. The microscope’s focal plane was fixed near the middle of the channel in the depth z direction to avoid recording bacteria crawling on the top and bottom sides of the channel. Experiments were performed on three different days with independent batches of E. coli cultures, with five 15-min recordings each day. ImageJ software (Fiji) was used for video post-processing (78, 79) to extract the trajectories of the bacteria. The trajectories are filtered by their linearity of forward progression to eliminate the fast-moving downstream ones and visually highlight the upstream swimming ones. We estimate the time interval for the upstream swimming to be 10 s before the fall-off. The maximum flow speed is defined as the highest flow speed along the channel’s centerline. The instantaneous maximum flow rate is estimated by averaging the fastest velocities of bacteria and fluorescent beads along the centerline during the upstream fall-off interval. Several video recordings are provided in the Supplementary Materials.

3D catheter long-time experiments

Prototype catheter tubes (both geometric designs and smooth tubes) were printed using a Connex-Triplex 3D printer. The inside of the tubes with the designed obstacles are similar to the quasi-2D structures but enlarged and revolved about the center line of the channel so that the obstacles are extruded rings on the inner walls. Considering the 3D printing accuracy available and the scale of typical catheters, these prototypes are 1.6 cm in inner diameter. For the designed tubes, the spacing between the extruded rings is 1 mm. For ease of clearing the supporting material from 3D printing, each tube is printed as two halves with a tenon shape along the long side and assembled into a complete tube after removing the supporting material. As shown in Fig. 4A, the top end of the tube is connected to a syringe controlled by a mechanical pump that keeps a constant flow rate. The bottom end of the tube is connected to an 80-mm-diameter petri dish as a reservoir for E. coli. After 1 hour, the tube is cut into 2-cm-long segments, and the liquid contained inside each segment is transferred to a culturing plate, discarding the most upstream and downstream segments. After culturing the plates for 24 hours at room temperature, the number of bacteria colonies in each plate is counted to reflect the amount of contamination in the corresponding part of the tube. We selected four circular, equally distant regions of 8-mm diameter in plate to count the number of colonies in these four areas (fig. S5). The total number of colonies in the plate is estimated by multiplying the total number in the four circles by the area ratio 25, of the entire plate versus the four areas. We denote the total number in the plate to be 30,000 when too many colonies are on the plate, and they become too crowded/overlapping to count precisely.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S5

Legends for movies S1 to S3

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S3