Abstract
We review recent progress in the electronic structure study of intrinsic magnetic topological insulators (MnBi2Te4) · (Bi2Te3)n ( ) family. Specifically, we focus on the ubiquitously (nearly) gapless behavior of the topological Dirac surface state observed by photoemission spectroscopy, even though a large Dirac gap is expected because of surface ferromagnetic order. The dichotomy between experiment and theory concerning this gap behavior is perhaps the most critical and puzzling question in this frontier. We discuss various proposals accounting for the lack of magnetic effect on the topological Dirac surface state, which are mainly categorized into two pictures, magnetic reconfiguration and topological surface state redistribution. Band engineering towards opening a magnetic gap of topological surface states provides great opportunities to realize quantized topological transport and axion electrodynamics at higher temperatures.
) family. Specifically, we focus on the ubiquitously (nearly) gapless behavior of the topological Dirac surface state observed by photoemission spectroscopy, even though a large Dirac gap is expected because of surface ferromagnetic order. The dichotomy between experiment and theory concerning this gap behavior is perhaps the most critical and puzzling question in this frontier. We discuss various proposals accounting for the lack of magnetic effect on the topological Dirac surface state, which are mainly categorized into two pictures, magnetic reconfiguration and topological surface state redistribution. Band engineering towards opening a magnetic gap of topological surface states provides great opportunities to realize quantized topological transport and axion electrodynamics at higher temperatures.
Keywords: intrinsic magnetic topological insulator, topological surface states, magnetic gap, magnetic reconfiguration, topological surface state redistribution, van der Waals spacing expansion
This work reviews recent progress in the electronic structure study of intrinsic magnetic topological insulators Mn-Bi-Te family, discusses the puzzling behavior of the topological surface state subject to bulk magnetic order, and potential route to realize the magnetic gap towards high temperature topological quantized transport.
INTRODUCTION
Magnetism has been used and studied over millennia. Yet, this branch of physics keeps flourishing in recent years with emerging states of magnetic matters such as quantum spin liquid [1,2] and two-dimensional (2D) magnets [3,4]. By comparison, the first two decades of the new millennium embraced the triumph of topological states of matter, which has revolutionized our knowledge of crystalline materials by introducing topological invariants to categorize their electronic structure [5,6]. In 2007, the realization of the quantum spin Hall effect (QSHE) based on a 2D HgTe/CdTe quantum well [7,8] opened a new era of exploring topological phases and materials in condensed matter. Electronically, this QSH state is insulating with a bulk gap separating the conduction and valence bands but has a pair of one-dimensional (1D) conducting edge states. These 1D topological edge states are protected by time-reversal symmetry, wherein elastic backscattering by nonmagnetic impurities are forbidden, holding the potential for dissipationless spintronics. The QSHE state can be classified by a type of topological invariant called the  invariant [9] and is now recognized as the first example of a 2D time-reversal invariant topological insulator (TI) with
invariant [9] and is now recognized as the first example of a 2D time-reversal invariant topological insulator (TI) with 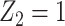 .
. 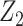 classification can be generalized to three-dimensional (3D) to describe ‘weak’ and ‘strong’ TIs [10]. A 3D strong TI has a ubiquitous, gapless topological surface state (TSS) with helical spin texture due to spin-momentum locking. In 2008, 3D TI was first realized based on Bi-Sb alloys [11] with multiple TSSs crossing the Fermi level five times. Up to now, there have been hundreds of materials predicted as 3D strong TI [12–14] and dozens of them have been experimentally verified, usually through direct observation of their Dirac cones at the surface by angle-resolved photoemission spectroscopy (ARPES) [15–17]. Among them, the most representative one is Bi2Se3 and its family of materials [18–21] found in 2009. The Bi2Se3 family is now considered the ‘hydrogen atom’ of topological materials due to its simple and elegant electronic structure. It is a semiconductor with a bulk gap of
classification can be generalized to three-dimensional (3D) to describe ‘weak’ and ‘strong’ TIs [10]. A 3D strong TI has a ubiquitous, gapless topological surface state (TSS) with helical spin texture due to spin-momentum locking. In 2008, 3D TI was first realized based on Bi-Sb alloys [11] with multiple TSSs crossing the Fermi level five times. Up to now, there have been hundreds of materials predicted as 3D strong TI [12–14] and dozens of them have been experimentally verified, usually through direct observation of their Dirac cones at the surface by angle-resolved photoemission spectroscopy (ARPES) [15–17]. Among them, the most representative one is Bi2Se3 and its family of materials [18–21] found in 2009. The Bi2Se3 family is now considered the ‘hydrogen atom’ of topological materials due to its simple and elegant electronic structure. It is a semiconductor with a bulk gap of 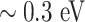 , among the few with sizable bulk gap to manifest surface state transport. It has only one TSS Dirac cone at the center of the Brillouin zone, with the Dirac point located close to the middle of bulk gap. It consists of -Se-Bi-Se-Bi-Se- quintuple layers (QLs) stacking along c axis bounded by van der Waals (vdW) interaction, easy for device fabrication and epitaxial growth. Importantly, the TSS is confirmed to be robust in ambient environments because of the topological protection [22]. These excellent properties distinguish the Bi2Se3 family from others for the exploration of novel topological effects. Particularly, the quantum anomalous Hall effect (QAHE), a time-reversal-symmetry-breaking version of QSHE, was predicted in 2010 [23] and then realized in 2013 [24] based on magnetically doped films of this family (Fig. 1).
, among the few with sizable bulk gap to manifest surface state transport. It has only one TSS Dirac cone at the center of the Brillouin zone, with the Dirac point located close to the middle of bulk gap. It consists of -Se-Bi-Se-Bi-Se- quintuple layers (QLs) stacking along c axis bounded by van der Waals (vdW) interaction, easy for device fabrication and epitaxial growth. Importantly, the TSS is confirmed to be robust in ambient environments because of the topological protection [22]. These excellent properties distinguish the Bi2Se3 family from others for the exploration of novel topological effects. Particularly, the quantum anomalous Hall effect (QAHE), a time-reversal-symmetry-breaking version of QSHE, was predicted in 2010 [23] and then realized in 2013 [24] based on magnetically doped films of this family (Fig. 1).
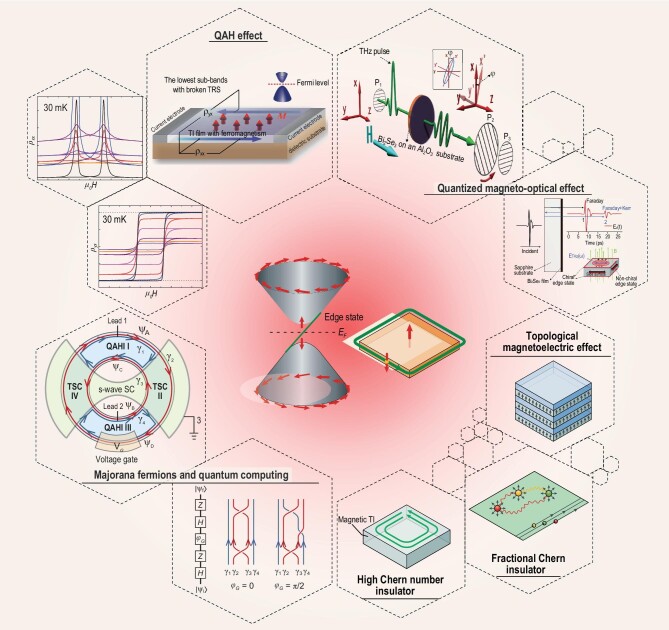
Figure 1.
Emergent topological phenomena arising from an intrinsic magnetic TI. The interplay of magnetism and band topology offers a great chance to explore the QAHE previously realized on magnetically doped TI films (adapted from [24]) but now potentially at much higher temperatures, the chiral Majorana fermion at the interface of QAHE state and s-wave superconductor which forms the basis of topological quantum computing (from [35]), quantized magneto-optical effect (from [36]), topological magnetoelectric effect, fractional Chern insulator, high Chern number insulator and so on (from [37]).
Our story of topological states of matter has reached a point where this rising star meets a classic field of physics, magnetism. However, this is not their first rendezvous. Back in 1980, the quantum Hall effect (QHE) was observed from a 2D electron gas system subjected to a strong magnetic field [25]. This phenomenon was later explained theoretically as a topological property of the occupied bands in the Brillouin zone [26]. In the current context, we can call the QHE the first topological insulator ever found, classified by a time-reversal-symmetry-breaking topological invariant called Chern number C (originally the well-known Thouless–Kohmoto–Nightingale–Nijs invariant [26]). The applied magnetic field in QHE can be replaced by the intrinsic magnetization of the material, leading to QAHE. In this regard, QHE and QAHE states are both Chern insulators. In 2D Chern insulators, 1D gapless edge states emerge at the boundary between the Chern insulator and ordinary insulator (vacuum) because of the distinct band topology. Like the 1D helical edge states of QSHE, the 1D chiral edge state in QAHE can propagate along one direction with forbidden backscattering, suitable for developing low-power-consumption electronics without the need for an applied magnetic field.
The prediction and realization of QAHE [23,24] represent a breakthrough in fundamental physics, yet much effort is needed toward its practical application. On the one hand, Hall bar devices based on magnetically doped films require sophisticated epitaxial growth and microfabrication procedures that only a few labs in the world can accomplish [24,27–34]. On the other hand, atomic doping brings disorder to the crystal and inhomogeneity to the electronic structure, resulting in a much reduced effective exchange gap of the TSS, where the realization temperature was as low as 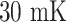 at first [24] and the current record is
at first [24] and the current record is 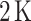 [30] after 10 years’ effort. In this context, intrinsic magnetic TI, which combines magnetic order and band topology in the same material without the need of doping, is highly desired.
[30] after 10 years’ effort. In this context, intrinsic magnetic TI, which combines magnetic order and band topology in the same material without the need of doping, is highly desired.
In a magnetic TI, while the time-reversal symmetry 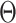 is broken by the magnetic order, its combination with certain magnetic lattice symmetry such as rotation
is broken by the magnetic order, its combination with certain magnetic lattice symmetry such as rotation 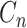 and fractional translation
and fractional translation 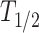 can retain an equivalent time-reversal symmetry and the system can still be classified by the topological
can retain an equivalent time-reversal symmetry and the system can still be classified by the topological 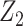 invariant. This was first discussed in the theoretical proposal of antiferromagnetic TI in 2010 [38]. In an antiferromagnetic TI, both
invariant. This was first discussed in the theoretical proposal of antiferromagnetic TI in 2010 [38]. In an antiferromagnetic TI, both 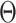 and
and 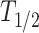 are broken but the combination
are broken but the combination 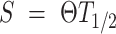 is preserved, leading to a topologically nontrivial phase which shares the topological
is preserved, leading to a topologically nontrivial phase which shares the topological  invariant and quantized magnetoelectric effect in a 3D strong TI. The difference is that, while 3D TIs have symmetry-protected gapless TSS at all surfaces, 3D antiferromagnetic TIs have intrinsically gapped TSS at certain surfaces with broken S symmetry. The gapped TSSs in 3D antiferromagnetic TIs carry a half-quantized Hall conductivity (
invariant and quantized magnetoelectric effect in a 3D strong TI. The difference is that, while 3D TIs have symmetry-protected gapless TSS at all surfaces, 3D antiferromagnetic TIs have intrinsically gapped TSS at certain surfaces with broken S symmetry. The gapped TSSs in 3D antiferromagnetic TIs carry a half-quantized Hall conductivity (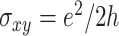 ), which may aid experimental confirmation of quantized magnetoelectric coupling (Fig. 1). Although with fascinating properties, the material realization of an intrinsic antiferromagnetic TI was not initiated until 2017. First-principles calculation proposed that by inserting an MnTe bilayer into the first quintuple layer of Bi2Te3, a septuple layer of MnBi2Te4 is constructed and the TSS opens a sizable magnetic gap, promising a robust QAH state [39,40]. The material was first experimentally realized with thin films via molecular beam epitaxy [41]. Theoretical works on single crystalline MnBi2Te4 were reported in 2019 and revealed its fertile topological states of matter [42–45]. Since the successful preparation of single crystal MnBi2Te4, the surge of intrinsic magnetic TI based on MnBi2Te4 and its family of materials has begun.
), which may aid experimental confirmation of quantized magnetoelectric coupling (Fig. 1). Although with fascinating properties, the material realization of an intrinsic antiferromagnetic TI was not initiated until 2017. First-principles calculation proposed that by inserting an MnTe bilayer into the first quintuple layer of Bi2Te3, a septuple layer of MnBi2Te4 is constructed and the TSS opens a sizable magnetic gap, promising a robust QAH state [39,40]. The material was first experimentally realized with thin films via molecular beam epitaxy [41]. Theoretical works on single crystalline MnBi2Te4 were reported in 2019 and revealed its fertile topological states of matter [42–45]. Since the successful preparation of single crystal MnBi2Te4, the surge of intrinsic magnetic TI based on MnBi2Te4 and its family of materials has begun.
Now we know more details concerning the structural, magnetic, and topological aspects of MnBi2Te4 antiferromagnetic TI. Its  lattice consists of layered -Te-Bi-Te-Mn-Te-Bi-Te- units (SL) stacking along the c axis and the layers are bounded by vdW force [46,47]. In the ground state below
lattice consists of layered -Te-Bi-Te-Mn-Te-Bi-Te- units (SL) stacking along the c axis and the layers are bounded by vdW force [46,47]. In the ground state below 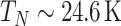 , Mn ions (
, Mn ions (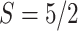 of
of 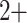 valence) with a large magnetic moment of
valence) with a large magnetic moment of 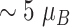 form a ferromagnetic layer with moments pointing out-of-plane. These ferromagnetic layers couple each other in an antiferromagnetic way along the c-axis [48,49] (A-type AFM). The bulk gap is around
form a ferromagnetic layer with moments pointing out-of-plane. These ferromagnetic layers couple each other in an antiferromagnetic way along the c-axis [48,49] (A-type AFM). The bulk gap is around 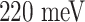 from calculation [45] but only
from calculation [45] but only 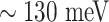 as directly observed by ARPES [50–52]. At the natural cleavage plane (0001), the TSS gap of
as directly observed by ARPES [50–52]. At the natural cleavage plane (0001), the TSS gap of 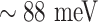 at the Dirac point is expected due to S breaking [42–45]. This sizable TSS gap is the key ingredient enabling the observation of exotic phenomena such as quantized magnetoelectric coupling [38,53,54], axion electrodynamics [55–57], QAHE [24,27–34,58], and chiral Majorana fermions [59–62] at much higher temperatures. In fact, quantum transport experiments have revealed the existence of a 2D Chern insulator with QAHE observed at
at the Dirac point is expected due to S breaking [42–45]. This sizable TSS gap is the key ingredient enabling the observation of exotic phenomena such as quantized magnetoelectric coupling [38,53,54], axion electrodynamics [55–57], QAHE [24,27–34,58], and chiral Majorana fermions [59–62] at much higher temperatures. In fact, quantum transport experiments have revealed the existence of a 2D Chern insulator with QAHE observed at 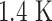 based on 5 SLs [63], and the characteristics of an axion insulator state based on 6 SLs [64], both at zero magnetic field. Under a perpendicular magnetic field (
based on 5 SLs [63], and the characteristics of an axion insulator state based on 6 SLs [64], both at zero magnetic field. Under a perpendicular magnetic field (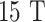 ), characteristics of high-Chern-number quantum Hall effect without Landau levels contributed by dissipationless chiral edge states are observed, indicating a well-defined Chern insulator state with
), characteristics of high-Chern-number quantum Hall effect without Landau levels contributed by dissipationless chiral edge states are observed, indicating a well-defined Chern insulator state with 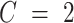 (9, 10 SLs) [65]. Its intralayer ferromagnetic and interlayer antiferromagnetic configuration exhibits the layer Hall effect in which electrons from the top and bottom layers deflect in opposite directions due to the layer-locked Berry curvature, resulting in the characteristic of the axion insulator state (6 SLs) [66]. In addition to these experimental observations, it is further shown by theory that manipulating its magnetic and structural configuration can give rise to many new topological states. For example, the flat Chern band in twisted bilayer MnBi2Te4 may boost the fractional Chern insulator and
(9, 10 SLs) [65]. Its intralayer ferromagnetic and interlayer antiferromagnetic configuration exhibits the layer Hall effect in which electrons from the top and bottom layers deflect in opposite directions due to the layer-locked Berry curvature, resulting in the characteristic of the axion insulator state (6 SLs) [66]. In addition to these experimental observations, it is further shown by theory that manipulating its magnetic and structural configuration can give rise to many new topological states. For example, the flat Chern band in twisted bilayer MnBi2Te4 may boost the fractional Chern insulator and 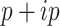 topological superconductor [67]; changing the stacking order between MnBi2Te4 SL and Bi2Te3 QL may lead to novel states such as QSHE insulator with and without time-reversal symmetry [68]; magnetic ground states other than A-type AFM may lead to different phases such as Weyl semimetal [69,70] and higher-order topological Möbius insulator [71]. These predictions (Fig. 1) certainly deserve further experimental efforts.
topological superconductor [67]; changing the stacking order between MnBi2Te4 SL and Bi2Te3 QL may lead to novel states such as QSHE insulator with and without time-reversal symmetry [68]; magnetic ground states other than A-type AFM may lead to different phases such as Weyl semimetal [69,70] and higher-order topological Möbius insulator [71]. These predictions (Fig. 1) certainly deserve further experimental efforts.
There have been several reviews/perspectives on this intrinsic magnetic TI family [72–76], with distinct emphases on theoretical, computational, and transport studies, respectively. In this review, we focus on the electronic structure of (MnBi2Te4) · (Bi2Te3)n (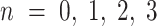 ) family, which has long been a subject of much debate. We will first review the ARPES observation of ubiquitously (nearly) gapless behavior of TSS Dirac cone from MnBi2Te4 and MnBi2Te4 SL termination, as well as the band hybridization features from Bi2Te3 QL terminations. While the significantly reduced TSS gap size of MnBi2Te4 termination deviates from that obtained by first-principles calculations, it is not against the relatively low temperature for the observation of QAHE, suggesting that the effective magnetic moments for the TSS may be diminished. There is also experimental evidence suggesting the robust A-type AFM order at the topmost SL layers from magnetic force microscopy (MFM), polar reflective magnetic circular dichroism (RMCD) and X-ray magnetic circular/linear dichroism (XMCD/XMLD) measurements. Furthermore, the magnetic splitting of certain bulk quasi-2D bands seems to validate the effect of magnetic order on the low-energy band structure. Bearing these established experimental results in mind, we then discuss the validity of possible scenarios proposed to account for the (nearly) gapless TSS from MnBi2Te4 termination, such as surface magnetic reconstruction, TSS redistribution, defect and self-doping effects, etc. Future band engineering towards opening a magnetic gap at the TSS Dirac point via approaches such as magnetic manipulation, element substitution, chemical potential and material optimization is proposed, which would provide great opportunities to the realization of QAHE and topological magnetoelectric effect at higher temperatures.
) family, which has long been a subject of much debate. We will first review the ARPES observation of ubiquitously (nearly) gapless behavior of TSS Dirac cone from MnBi2Te4 and MnBi2Te4 SL termination, as well as the band hybridization features from Bi2Te3 QL terminations. While the significantly reduced TSS gap size of MnBi2Te4 termination deviates from that obtained by first-principles calculations, it is not against the relatively low temperature for the observation of QAHE, suggesting that the effective magnetic moments for the TSS may be diminished. There is also experimental evidence suggesting the robust A-type AFM order at the topmost SL layers from magnetic force microscopy (MFM), polar reflective magnetic circular dichroism (RMCD) and X-ray magnetic circular/linear dichroism (XMCD/XMLD) measurements. Furthermore, the magnetic splitting of certain bulk quasi-2D bands seems to validate the effect of magnetic order on the low-energy band structure. Bearing these established experimental results in mind, we then discuss the validity of possible scenarios proposed to account for the (nearly) gapless TSS from MnBi2Te4 termination, such as surface magnetic reconstruction, TSS redistribution, defect and self-doping effects, etc. Future band engineering towards opening a magnetic gap at the TSS Dirac point via approaches such as magnetic manipulation, element substitution, chemical potential and material optimization is proposed, which would provide great opportunities to the realization of QAHE and topological magnetoelectric effect at higher temperatures.
UBIQUITOUSLY GAPLESS TSSs
Due to the S breaking at the natural cleavage plane (0001), below 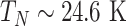 antiferromagnetic TI MnBi2Te4 is expected to show a magnetic gap
antiferromagnetic TI MnBi2Te4 is expected to show a magnetic gap 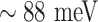 at the Dirac point of TSS [42–45]. Earlier ARPES investigations on the single crystals reported gapped TSS behavior with a Dirac gap ranging from
at the Dirac point of TSS [42–45]. Earlier ARPES investigations on the single crystals reported gapped TSS behavior with a Dirac gap ranging from 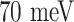 to
to 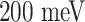 [45,77,78], in line with the theoretical prediction. However, the photon-energy dependent gap size indicates its bulk nature rather than a surface origin. Indeed, our systematic photon-energy-dependent ARPES measurements show that the bulk gap separating the bulk valence and conduction bands varies from 130 meV to 200 meV from bulk Brillouin zone
[45,77,78], in line with the theoretical prediction. However, the photon-energy dependent gap size indicates its bulk nature rather than a surface origin. Indeed, our systematic photon-energy-dependent ARPES measurements show that the bulk gap separating the bulk valence and conduction bands varies from 130 meV to 200 meV from bulk Brillouin zone 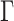 to Z [50]. Astonishingly, the TSS Dirac cone remains gapless below or above
to Z [50]. Astonishingly, the TSS Dirac cone remains gapless below or above 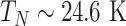 , as first reported by our group (data shown in Fig. 2a) and others [50–52]. Such observations of (nearly) gapless TSS Dirac cone on MnBi2Te4 (0001) surface below and above the antiferromagnetic order temperature have been further repeated [79–84]. To date, there have been extensive efforts to explain the origin of this gapless behavior, which will be reviewed in the following sections.
, as first reported by our group (data shown in Fig. 2a) and others [50–52]. Such observations of (nearly) gapless TSS Dirac cone on MnBi2Te4 (0001) surface below and above the antiferromagnetic order temperature have been further repeated [79–84]. To date, there have been extensive efforts to explain the origin of this gapless behavior, which will be reviewed in the following sections.
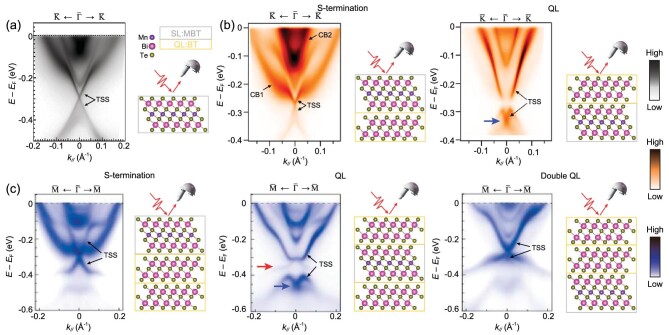
Figure 2.
Gapless TSSs from all the terminations of (MnBi2Te4) · (Bi2Te3)n (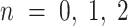 ). (a) Gapless TSS from the (0001) surface of MnBi2Te4, measured at
). (a) Gapless TSS from the (0001) surface of MnBi2Te4, measured at 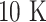 using photon energy
using photon energy 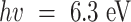 [50]. (b) Gapless TSSs from the SL (left) and QL (right) terminations of MnBi4Te7, measured at
[50]. (b) Gapless TSSs from the SL (left) and QL (right) terminations of MnBi4Te7, measured at 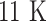 using photon energy
using photon energy 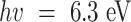 [85]. (c) Gapless TSSs from the SL (left), QL (middle) and double QL (right) terminations of MnBi6Te10, measured at
[85]. (c) Gapless TSSs from the SL (left), QL (middle) and double QL (right) terminations of MnBi6Te10, measured at 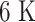 using photon energy
using photon energy 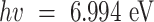 [79]. Red arrow emphasizes the in-gap states inside the hybridization gap between TSS and bulk valence band while blue arrow indicates the TSS Dirac point.
[79]. Red arrow emphasizes the in-gap states inside the hybridization gap between TSS and bulk valence band while blue arrow indicates the TSS Dirac point.
This striking violation against the theoretical picture has inspired intensive ARPES measurements extended to the antiferromagnetic heterostructure members of this family, i.e. MnBi4Te7 consisting of alternating SL and QL sequence and MnBi6Te10 consisting of alternating SL and two QLs sequence [47,86]. The enlarged distance between SLs in MnBi4Te7 and MnBi6Te10 reduces the antiferromagnetic exchange interaction. Consequently, MnBi4Te7 has an antiferromagnetic ground state with 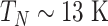 , while MnBi6Te10 is antiferromagnetic below
, while MnBi6Te10 is antiferromagnetic below 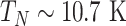 . [87–90]. Due to the vdW interaction between SLs and QLs, MnBi4Te7 has two natural cleavage planes (SL and QL terminations) while MnBi6Te10 has three (SL, QL, and double QL terminations). Since the intralayer ferromagnetic order comes from Mn residing in the central layer of SL, one would expect magnetic gap opening from SL termination and gapless TSS from QL and double QL terminations. However, similar to the case of MnBi2Te4 (0001) surface, all the SL terminations from MnBi4Te7 [52,79,85,91] and MnBi6Te10 [79,89,90,92] show (nearly) gapless TSS Dirac cone as presented in Fig. 2b and c. These results suggest that the (nearly) gapless behavior of the TSS Dirac cone is ubiquitous for all the SL terminations of (MnBi2Te4) · (Bi2Te3)n (
. [87–90]. Due to the vdW interaction between SLs and QLs, MnBi4Te7 has two natural cleavage planes (SL and QL terminations) while MnBi6Te10 has three (SL, QL, and double QL terminations). Since the intralayer ferromagnetic order comes from Mn residing in the central layer of SL, one would expect magnetic gap opening from SL termination and gapless TSS from QL and double QL terminations. However, similar to the case of MnBi2Te4 (0001) surface, all the SL terminations from MnBi4Te7 [52,79,85,91] and MnBi6Te10 [79,89,90,92] show (nearly) gapless TSS Dirac cone as presented in Fig. 2b and c. These results suggest that the (nearly) gapless behavior of the TSS Dirac cone is ubiquitous for all the SL terminations of (MnBi2Te4) · (Bi2Te3)n ( ).
).
It is also interesting to look at the TSS behavior from QL and double QL terminations. Both QL terminations from MnBi4Te7 (Fig. 2b, right) and MnBi6Te10 (Fig. 2c, middle) present similar features for the TSS. First of all, the TSS Dirac point is buried inside the bulk valence band region as indicated by blue arrows. Second, an apparent gap is opened at the upper TSS Dirac cone due to its hybridization with one neighboring bulk valence band. Third, below this hybridization gap, the residual TSS and bulk valance band compose a Rashba-split band (RSB) feature, with the new RSB Dirac point coming from the original TSS Dirac point. Last and more importantly, there appears a new band inside the hybridization gap, with its top touching the upper part of the gapped TSS, forming a new gapless Dirac cone. This in-gap state extends from the new Dirac point down to the valence band region, resulting in the generally gapless surface and bulk spectra. The appearance of this new in-gap Dirac cone is intriguing. Based on the above band features, a TSS-RSB hybridization picture has been proposed to explain the complicated band features from both SL and QL terminations [90]. Combining circular dichroism ARPES and first-principles calculations, the existence of RSB and its hybridization with TSS have been firmly established by works from several groups [77,83,85,90,93]. The TSS-RSB hybridization can be simulated in a tight-binding simulation. By tuning the hybridization strength, the QL ARPES spectra can be reproduced. According to the simulation, the new in-gap Dirac cone indeed comes from the original bulk RSB (see Fig. 4b–d in ref. [90]). This hybridization picture can also reproduce well the ARPES spectra on the SL termination and potentially explain the puzzling gapless behavior of the TSS Dirac point, which will be discussed in detail in the following section. For the double QL termination of MnBi6Te10, similar band hybridization features are observed (Fig. 2c, right), but the hybridization gap is too narrow for the investigation of the in-gap state.
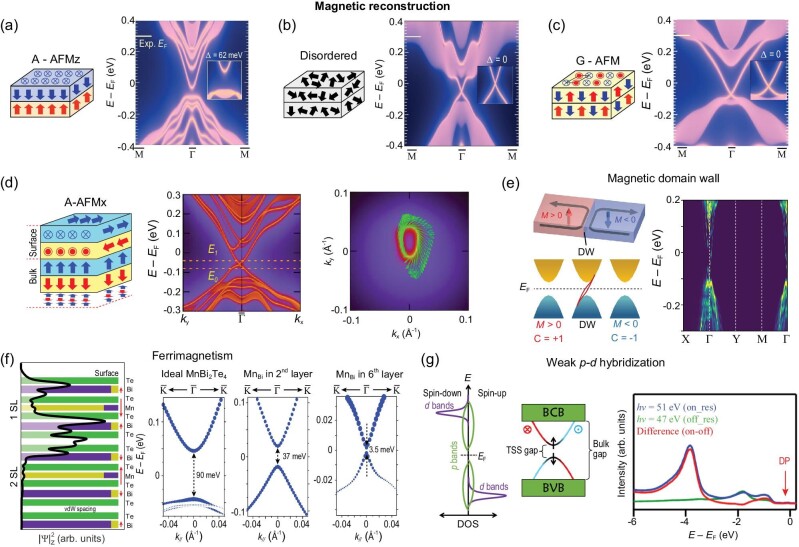
Figure 4.
Various magnetic reconfigurations accounting for the (nearly) gapless behavior of MnBi2Te4 TSSs. (a–c) Prototypical magnetic reconstructions leading to different gap behavior of TSS, including A-type AFM with out-of-plane ferromagnetic moments (A-AFMz) (a), disordered magnetic moments (b), G-type AFM (c) (adapted from [50]) and A-type AFM with the magnetic moments along the x-axis (A-AFMx) (d) from [113]. (e) Magnetical domain wall edge states (left, from [28]) resemble the gapless TSS, which is further discussed in a first-principles-based tight-binding model (right, from [115]). (f) Native point defects 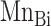 can introduce ferrimagnetism and reduce the TSS gap, from [103]. (g) The hybridization between the Mn
can introduce ferrimagnetism and reduce the TSS gap, from [103]. (g) The hybridization between the Mn 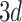 and Te
and Te 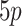 states, as schematically shown in the left two panels (from [73]) is too weak according to the resonant photoemission spectra (right, from [52]) to induce TSS magnetic gap.
states, as schematically shown in the left two panels (from [73]) is too weak according to the resonant photoemission spectra (right, from [52]) to induce TSS magnetic gap.
KEY PROPERTIES RELATED TO THE TSS GAP
Since its first observation, attempts had been made to explain the gapless behavior at the Dirac point of the SL termination with S breaking under antiferromagnetic order [50–52]. Before going to the bewildering variety of proposals, we would like to mention the key properties established by various experimental probes, which are closely related to the gapless/gapped behavior of TSS at the SL.
The first one comes from the experimental realization of QAHE in a 5 SLs MnBi2Te4 device [63], as shown in Fig. 3a, strongly suggesting the existence of a 2D Chern insulator state with gapped TSS. By fitting the Arrhenius plot of longitudinal resistance 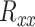 as a function of
as a function of 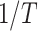 , the energy gap of the thermally activated charge transport can be obtained as
, the energy gap of the thermally activated charge transport can be obtained as 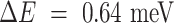 at zero-field [63]. This energy scale characterizes the minimum energy required to excite an electron from the surface valence band to the surface conduction band, two orders of magnitude smaller than the predicted exchange gap [45]. On the other hand, the gapless behavior of the TSS observed by ARPES may just represent the resolving power of the instrument, and the TSS gap could still exist but be smaller than the energy resolution (typically
at zero-field [63]. This energy scale characterizes the minimum energy required to excite an electron from the surface valence band to the surface conduction band, two orders of magnitude smaller than the predicted exchange gap [45]. On the other hand, the gapless behavior of the TSS observed by ARPES may just represent the resolving power of the instrument, and the TSS gap could still exist but be smaller than the energy resolution (typically 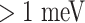 ). The TSS gap size from ARPES measurements varies from being diminished [50,51], to
). The TSS gap size from ARPES measurements varies from being diminished [50,51], to 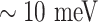 [52] or even larger, with strong sample and spatial dependence [94,95]. The above observations suggest that the gapless behavior of the TSS Dirac point at SL termination at the antiferromagnetic phase is unlikely to be symmetry enforced. It is worth noting that, according to the theoretical definition of antiferromagnetic TI, the TSS is protected in a weaker sense than the 3D strong TI, indicating that it is generally not stable to disorder [38].
[52] or even larger, with strong sample and spatial dependence [94,95]. The above observations suggest that the gapless behavior of the TSS Dirac point at SL termination at the antiferromagnetic phase is unlikely to be symmetry enforced. It is worth noting that, according to the theoretical definition of antiferromagnetic TI, the TSS is protected in a weaker sense than the 3D strong TI, indicating that it is generally not stable to disorder [38].
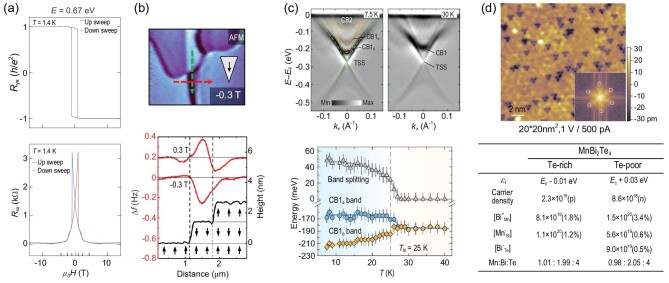
Figure 3.
Key physical properties related to the gap behavior of TSS in Mn-Bi-Te family. (a) Realization of QAHE reveals an extremely small TSS gap (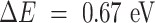 ), from [63]. (b) Robust uniaxial A-type AFM order to the surface layers and antiferromagnetic domains observed using MFM, from [96]. (c) Bulk conduction band splitting related to the antiferromagnetic order as observed directly in ARPES spectra, from [51]. (d) Top panel shows two types of surface point defects (bright dots and dark triangles, probably corresponding to BiTe/MnTe and MnBi, respectively) found in atomically resolved topographic image, from [49]; Bottom panel lists the calculated Fermi level (
), from [63]. (b) Robust uniaxial A-type AFM order to the surface layers and antiferromagnetic domains observed using MFM, from [96]. (c) Bulk conduction band splitting related to the antiferromagnetic order as observed directly in ARPES spectra, from [51]. (d) Top panel shows two types of surface point defects (bright dots and dark triangles, probably corresponding to BiTe/MnTe and MnBi, respectively) found in atomically resolved topographic image, from [49]; Bottom panel lists the calculated Fermi level ( ), free carrier density (and the type of the carrier), as well as densities of the most important intrinsic defects (and concentrations in atomic %) at both Te-rich and Te-poor limits in MnBi2Te4, from [97].
), free carrier density (and the type of the carrier), as well as densities of the most important intrinsic defects (and concentrations in atomic %) at both Te-rich and Te-poor limits in MnBi2Te4, from [97].
The second key property is the robust A-type AFM order at the surface SL layers as evidenced by measurements using MFM [96] and other techniques. Fig. 3b shows the MFM image taken after field cooling at 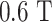 , with the tip polarized by a magnetic field of
, with the tip polarized by a magnetic field of 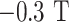 perpendicular to the sample surface. Clear contrast in the image illustrates several domains, where the magnetic signal changes its sign when crossing the domain walls. If the magnetic moment on the tip is reversed by a magnetic field of
perpendicular to the sample surface. Clear contrast in the image illustrates several domains, where the magnetic signal changes its sign when crossing the domain walls. If the magnetic moment on the tip is reversed by a magnetic field of 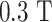 , all the domains and domain walls change their contrast. Further analysis of the screening effect from fractional QL impurity phases supports the persistence of uniaxial A-type spin order at the top SL layers. One may wonder if the robustness of A-AFM at the top SL layers is also sample dependent. It is thus important to note that other techniques, such as polar reflective magnetic circular dichroism (RMCD) [98] and X-ray magnetic circular/linear dichroism (XMCD/XMLD) [45,48,94,99–101] spectroscopies, also give strong evidence for the existence of net out-of-plane magnetic moments at the sample surfaces.
, all the domains and domain walls change their contrast. Further analysis of the screening effect from fractional QL impurity phases supports the persistence of uniaxial A-type spin order at the top SL layers. One may wonder if the robustness of A-AFM at the top SL layers is also sample dependent. It is thus important to note that other techniques, such as polar reflective magnetic circular dichroism (RMCD) [98] and X-ray magnetic circular/linear dichroism (XMCD/XMLD) [45,48,94,99–101] spectroscopies, also give strong evidence for the existence of net out-of-plane magnetic moments at the sample surfaces.
Even though the robust A-type AFM order is confirmed, what about its influence on the low-energy electronic structure? The (nearly) gapless behavior and its weak temperature dependence across the magnetic transition suggest a negligible effect of the magnetic order on the TSS. However, there are other bands close to the Fermi level which are surprisingly affected by the magnetic order. As exemplified in Fig. 3c by the bulk conduction bands labeled as CB1a and CB1b, at high temperatures they merge into one band CB1, while their splitting starts when the temperature decreased to 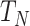 and reaches
and reaches 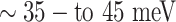 below
below 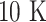 [51,52,102]. It is further reported that CB2 also shows a Rashba-like feature and band splitting below
[51,52,102]. It is further reported that CB2 also shows a Rashba-like feature and band splitting below 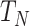 [80]. These results demonstrated the third key property of MnBi2Te4, i.e. the coupling between antiferromagnetic order and the low-energy bands.
[80]. These results demonstrated the third key property of MnBi2Te4, i.e. the coupling between antiferromagnetic order and the low-energy bands.
The fourth one comes from a material point of view concerning the disorders typically present in transition metal chalcogenides. In MnBi2Te4 family, various types of disorders, such as 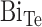 antisites (i.e. Bi atoms at the Te sites) located in the surface layer,
antisites (i.e. Bi atoms at the Te sites) located in the surface layer, 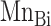 substitutions (Mn-Bi intermixing) in the second and central atomic layer, and Mn vacancies (
substitutions (Mn-Bi intermixing) in the second and central atomic layer, and Mn vacancies (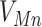 ) are observed by combining many experimental tools such as scanning transmission electron microscopy (STEM), scanning tunneling microscopy (STM), single-crystal X-ray diffraction (XRD), energy dispersive X-ray (EDX) analysis in scanning electron microscope (SEM) [48,49,78,103–112] and even density functional theory (DFT) calculations [97]. We will show in the next section that certain types of disorders may strongly affect the magnetic response of the TSS.
) are observed by combining many experimental tools such as scanning transmission electron microscopy (STEM), scanning tunneling microscopy (STM), single-crystal X-ray diffraction (XRD), energy dispersive X-ray (EDX) analysis in scanning electron microscope (SEM) [48,49,78,103–112] and even density functional theory (DFT) calculations [97]. We will show in the next section that certain types of disorders may strongly affect the magnetic response of the TSS.
MAGNETIC RECONFIGURATION TO EXPLAIN THE (NEARLY) GAPLESS TSSs
The (nearly) gapless behavior of TSS and its weak temperature dependence across the antiferromagnetic order lead to natural speculation of magnetic surface reconstruction. Deviations from the A-AFMz type (Fig. 4a), such as disordered magnetic structure (Fig. 4b), G-AFM with intralayer and interlayer antiferromagnetic (Fig. 4c) and AFMx with ferromagnetic in-plane moments (Fig. 4d), are considered in calculations [50,69,71,113]. As shown in Fig. 4b–d, all three deviations can lead to gapless TSS. Since it remains a technical challenge to determine the magnetic structure for the topmost SL, it would be insightful to examine the specific features from ARPES spectra and check their correspondence to the various magnetic structures. As shown in the right panel of Fig. 4d, for A-AFMx, the net magnetic moments break the in-plane rotation symmetry and lead to a TSS constant energy contour with only mirror symmetry. Further consideration of spin texture will result in mirror symmetry breaking [113]. For G-AFM, the double-sized unit cell in the antiferromagnetic phase may lead to in-plane band folding feature compared to the paramagnetic phase. For the disordered case, the lack of any oriented moment would retain the sixfold rotation symmetry of the constant energy contour of the TSS, while for the A-AFMz, the net out-of-plane moments in the top SL layer coupled to the TSS will break the sixfold rotation symmetry and leave only a threefold rotation symmetry. Further ARPES studies with ultrahigh energy, momentum resolution, and spin resolution from three directional components (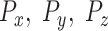 ) are highly encouraged to distinguish the above features.
) are highly encouraged to distinguish the above features.
Another type of magnetic reconfiguration is the formation of domains and domain walls illustrated in Fig. 4e (left panel [28]). The existence of magnetic domain walls in MnBi2Te4 surface has been observed experimentally [96,114]. In the presence of such opposing magnetic domains, first-principles calculations and tight-binding model analysis proposed that gapless chiral boundary modes can exist [37] (Fig. 4d, right panel [115]). Note that this edge mode is strictly gapless, while the TSS gap size in MnBi2Te4 shows sample and spatial dependence [94,95]. As the typical magnetic domain size is ∼10 μm, the contribution of chiral edge states at domain walls could be too tiny to explain the gapless topological surface states [96].
One more sophisticated ferrimagnetic structure has been experimentally observed [107,108] and employed to account for the much-reduced TSS gap [103]. As shown in Fig. 4f, the Mn-Bi intermixing could introduce 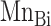 defects in the 2nd and 6th atomic layers counting from the surface, with its moments antiparallel to that of the central Mn layer. Due to the predominant localization of TSS density of states to the Te-Bi-Te layer, the moments of
defects in the 2nd and 6th atomic layers counting from the surface, with its moments antiparallel to that of the central Mn layer. Due to the predominant localization of TSS density of states to the Te-Bi-Te layer, the moments of 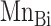 defects counteract that from the central Mn layer, leading to a reduction of the TSS gap. The inhomogeneity of
defects counteract that from the central Mn layer, leading to a reduction of the TSS gap. The inhomogeneity of 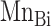 defects could explain the sample and spatial dependence of TSS gap size, suggesting that improving the crystalline quality with suppressed Mn-Bi intermixing is a crucial task for studies in the near future [103]. However, to better correlate the
defects could explain the sample and spatial dependence of TSS gap size, suggesting that improving the crystalline quality with suppressed Mn-Bi intermixing is a crucial task for studies in the near future [103]. However, to better correlate the 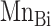 defect density to the TSS gap size, one needs to perform in situ ARPES and STM measurements for the same region of the sample surface, which is hardly feasible considering that these two techniques have ‘field of view’ with orders of magnitude difference.
defect density to the TSS gap size, one needs to perform in situ ARPES and STM measurements for the same region of the sample surface, which is hardly feasible considering that these two techniques have ‘field of view’ with orders of magnitude difference.
It is also reasonable to check the effective coupling between Mn d orbitals contributing magnetism and Bi/Te p orbitals related to the TSS. According to a resonant photoemission study [52], the Mn  states are mainly located
states are mainly located 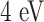 below the Fermi level (Fig. 4g), negligible in the energy range where nontrivial topology arises, leading to the speculation of weak
below the Fermi level (Fig. 4g), negligible in the energy range where nontrivial topology arises, leading to the speculation of weak 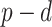 hybridization. This speculation is against first-principles calculations which predict sizable TSS gaps [116] and contradicts the observation of magnetism-induced conduction band splitting as discussed in ‘key properties related to the TSS gap’ (above). It is noted that a recent ultrafast magnetic dynamic study reveals large
hybridization. This speculation is against first-principles calculations which predict sizable TSS gaps [116] and contradicts the observation of magnetism-induced conduction band splitting as discussed in ‘key properties related to the TSS gap’ (above). It is noted that a recent ultrafast magnetic dynamic study reveals large 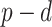 exchange coupling (
exchange coupling (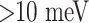 ) [117]. Based on the above analyses, there remain plenty of challenging experimental investigations, microscopically or spectroscopically, to determine the magnetic structure of the topmost SL accounting for the (nearly) gapless TSS.
) [117]. Based on the above analyses, there remain plenty of challenging experimental investigations, microscopically or spectroscopically, to determine the magnetic structure of the topmost SL accounting for the (nearly) gapless TSS.
TSS REDISTRIBUTION TO EXPLAIN ITS (NEARLY) GAPLESS BEHAVIOR
In this section we introduce the TSS redistribution picture where the TSS distribution can be extended from the topmost SL to the layers beneath, leading to a (nearly) gapless TSS as it feels a compromised effective magnetic moment. The compensation of the effective magnetic moments relies on the fact that the topmost SL and the second SL have antiparallel and comparable moments, meaning that this TSS redistribution picture is only applicable to MnBi2Te4 but not the heterostructure members containing nonmagnetic QLs. However, the potential origins of a redistributed TSS, such as band hybridization, vdW spacing expansion, or charge/defect effect, may generally exist in all the members of this family. In the following, we briefly introduce these mechanisms.
Based on the observation of hybridization between the TSS and a pair of RSBs, A TSS-RSB hybridization picture has been proposed [90] to explain the origin of sophisticated band structure for both QL and SL terminations in this material family (see details in ‘ubiquitouly gapless TSSs’ above). Specifically for SL as shown in Fig. 5a, tight-binding model simulation reveals that the TSS Dirac cone has a bulk origin. This inspires a TSS redistribution picture to account for the lack of magnetic effect on TSS in MnBi2Te4. As schematically illustrated in Fig. 5b, in an ideal case, the TSS predominantly locates on the topmost SL. In the A-AFM configuration, the effective magnetic moments for the TSS are approximately equal to the net ferromagnetic moments from one SL, which is large enough to open a sizable TSS Dirac gap as expected. In the actual case, the TSS distribution extends to the second SL. The interlayer antiferromagnetic order results in zero net magnetization for the top two SLs and consequently compensated effective magnetic moments for the TSS. In an extreme situation where the top two SLs equally share 50% of TSS localization, gapless TSS appears regardless of the robust surface A-AFM order and its coupling to the band structure. Based on this TSS redistribution picture, a sizeable TSS magnetic gap can be expected if the magnetic compensation effect is eliminated, e.g. in a ferromagnetic ground state. This expected case will be discussed in the next section.
Figure 5.
TSS redistribution picture explaining the (nearly) gapless behavior of MnBi2Te4 TSSs. (a) ARPES spectra and tight-binding model simulation show the hybridization between TSS and Rashba-split bands, from [90]. (b) Schematic showing the redistribution of TSS density of states and gapped/gapless Dirac cone corresponding to an ideal antiferromagnetic phase (left), an actual antiferromagnetic phase (middle) and an expected ferromagnetic phase (right). (c) Distribution of bulk magnetization (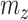 ) and surface state envelope function
) and surface state envelope function 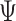 according to effective model analysis, from [118]. (d) Surface excess charge induced redistribution of TSS top/bottom cone localization, from [95]. (e) TSS redistribution due to the vdW spacing expansion, from [94]. (f) Three-Dirac-fermion approach to the gapless TSS under vdW spacing expansion, from [119]. (g) Co-antisites (exchanging Mn and Bi atoms in the surface layer) can strongly suppress the magnetic gap down to several
according to effective model analysis, from [118]. (d) Surface excess charge induced redistribution of TSS top/bottom cone localization, from [95]. (e) TSS redistribution due to the vdW spacing expansion, from [94]. (f) Three-Dirac-fermion approach to the gapless TSS under vdW spacing expansion, from [119]. (g) Co-antisites (exchanging Mn and Bi atoms in the surface layer) can strongly suppress the magnetic gap down to several 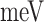 in the antiferromagnetic phase, from [120].
in the antiferromagnetic phase, from [120].
Such a TSS redistribution picture has been supported by numerous model analyses and distinct calculations-based approaches. Starting from a 3D Hamiltonian for bulk MnBi2Te4 and taking into account the spatial profile of the bulk magnetization, an effective model for the TSS has been derived [118]. This model suggests that the diminished surface gap may be caused by a much smaller and more localized intralayer ferromagnetic order and the fact that the surface states are mainly embedded in the first two SLs from the terminating surface (Fig. 5c). To be specific, by using the envelope function the penetration depth of TSS is calculated as ∼16.2 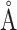 , larger than the thickness of one SL (∼13.7
, larger than the thickness of one SL (∼13.7 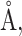 ). This is in agreement with the results obtained by ab initio calculations, which present the spatial charge distribution of the TSS Dirac state between the first and second SL expanded by 15.3% at equilibrium structure and for vdW spacing (Fig. 5e from ref. [94]). With increasing vdW spacing, the TSS is found to shift its dominant occupation from the top SL to the second SL, resulting in reduced effective moments. The TSS Dirac gap is found to decrease and vanish at 15.3% expansion. As the vdW spacing modulation is likely to occur in both magnetic and nonmagnetic vdW TIs, a general three-Dirac-fermion approach can be developed [119] to describe the TSS behavior. As shown in Fig. 5f, the three-Dirac-fermion refers to three TSS Dirac cones located at the top surface of the topmost SL/QL (
). This is in agreement with the results obtained by ab initio calculations, which present the spatial charge distribution of the TSS Dirac state between the first and second SL expanded by 15.3% at equilibrium structure and for vdW spacing (Fig. 5e from ref. [94]). With increasing vdW spacing, the TSS is found to shift its dominant occupation from the top SL to the second SL, resulting in reduced effective moments. The TSS Dirac gap is found to decrease and vanish at 15.3% expansion. As the vdW spacing modulation is likely to occur in both magnetic and nonmagnetic vdW TIs, a general three-Dirac-fermion approach can be developed [119] to describe the TSS behavior. As shown in Fig. 5f, the three-Dirac-fermion refers to three TSS Dirac cones located at the top surface of the topmost SL/QL (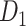 ), the bottom surface of the topmost SL/QL (
), the bottom surface of the topmost SL/QL (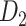 ) and the top surface of the second SL/QL (
) and the top surface of the second SL/QL (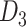 ), respectively. Their coupling is tuned by coupling energies
), respectively. Their coupling is tuned by coupling energies 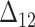 and
and 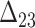 , with the latter being dependent on the topmost interlayer vdW spacing d. Remarkably, unexpected gapless TSS Dirac cones are found to arise due to d expansion, when the total Chern number of the system changes by 1 in this expansion process. It should be emphasized that, in this three-Dirac-fermion approach, the gapless point is topologically protected and comes from the competition between the Zeeman coupling and the Dirac fermion coupling. Such vdW spacing expansion may be introduced by the mechanical cleavage process [22,121] before ARPES and STM measurements, yet the direct evidence is still missing from atomic layer resolved probes such as STEM.
, with the latter being dependent on the topmost interlayer vdW spacing d. Remarkably, unexpected gapless TSS Dirac cones are found to arise due to d expansion, when the total Chern number of the system changes by 1 in this expansion process. It should be emphasized that, in this three-Dirac-fermion approach, the gapless point is topologically protected and comes from the competition between the Zeeman coupling and the Dirac fermion coupling. Such vdW spacing expansion may be introduced by the mechanical cleavage process [22,121] before ARPES and STM measurements, yet the direct evidence is still missing from atomic layer resolved probes such as STEM.
Excess surface charge is found to affect the distribution of TSS in a top/bottom cone-dependent manner [95]. Obviously, the smallest gap values should be achieved when the top and bottom TSS cones are mostly and independently located in two adjacent SLs, as they experience an exchange field of the opposite sign (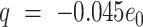 in Fig. 5d). Furthermore, from an ab initio calculation, cation co-antisites
in Fig. 5d). Furthermore, from an ab initio calculation, cation co-antisites 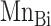 and
and 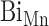 (extra Bi replacing Mn) can push the TSS charge toward the second SL. Therefore, the influence on the magnetic gap from the top SL is reduced while the second SL influence is simultaneously enhanced (Fig. 5g) [120], resulting in compensated effective magnetic moments and reduced TSS magnetic gap. It is noted that the existence of excess charge and Mn-Bi intermixing defects are well established in this material family.
(extra Bi replacing Mn) can push the TSS charge toward the second SL. Therefore, the influence on the magnetic gap from the top SL is reduced while the second SL influence is simultaneously enhanced (Fig. 5g) [120], resulting in compensated effective magnetic moments and reduced TSS magnetic gap. It is noted that the existence of excess charge and Mn-Bi intermixing defects are well established in this material family.
PERSPECTIVES TO OPEN THE TSS MAGNETIC GAP
In the context of the TSS redistribution picture, gapless TSS comes from compensated magnetic moments as a nature of the A-AFM order. Assuming a ferromagnetic background, no compensation exists no matter how the TSS redistributes. This offers a great chance to realize a sizeable TSS gap through magnetic engineering based on MnBi2Te4. In fact, a large amount of Sb substitution in the Bi sites can indeed transform the MnBi2Te4 ground state from antiferromagnetic to ferromagnetic or ferrimagnetic order [104,107,123–125]. The TSS band structure study by ARPES, however, is difficult due to the heavy hole doping induced by Sb substitution. It is worth noting that with a small amount of Sb doping, we have observed a TSS gap opening in MnBi2Te4 samples which stay at the antiferromagnetic phase. Surprisingly this TSS gap size is proportional to the doping level and carrier density, allowing a continuous tunability of gap size [126]. However, this TSS gap is independent of the antiferromagnetic-paramagnetic transition, with the origin of the gap remaining to be investigated.
Another way to realize the ferromagnetic ground state is through heterostructure engineering. As mentioned in ‘ubiquitouly gapless TSSs’, in (MnBi2Te4) · (Bi2Te3)n (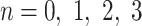 ) family the interlayer antiferromagnetic coupling between the ferromagnetic SLs can be reduced by QL spacing. In fact, with 3 QLs spacing (
) family the interlayer antiferromagnetic coupling between the ferromagnetic SLs can be reduced by QL spacing. In fact, with 3 QLs spacing (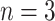 ), MnBi8Te13 develops a long-range ferromagnetic order below
), MnBi8Te13 develops a long-range ferromagnetic order below 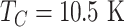 [127]. This provides a valuable chance to realize the magnetic gap in TSS from SL termination. High-quality MnBi8Te13 single crystals are grown and characterized through structural, magnetic, transport, and electronic structure studies [122]. Its crystal structure shown in Fig. 6a was obtained from single-crystal XRD and powder XRD refinement. The temperature-dependent anisotropic magnetic susceptibility (Fig. 6b) shows Curie-Weiss (CW) behavior above
[127]. This provides a valuable chance to realize the magnetic gap in TSS from SL termination. High-quality MnBi8Te13 single crystals are grown and characterized through structural, magnetic, transport, and electronic structure studies [122]. Its crystal structure shown in Fig. 6a was obtained from single-crystal XRD and powder XRD refinement. The temperature-dependent anisotropic magnetic susceptibility (Fig. 6b) shows Curie-Weiss (CW) behavior above 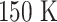 (inset) with the characteristic temperature
(inset) with the characteristic temperature 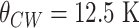 and
and 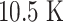 for
for 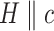 and
and 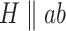 , respectively. The larger bifurcation between zero-field cooling (ZFC) and field cooling (FC) magnetization and magnetic hysteresis loop (Fig. 6c) indicate an easy axis along the c-axis and an Ising-type exchange interaction between adjacent Mn layers. These properties suggest a ferromagnetic order with an out-of-plane magnetic moment configuration in MnBi8Te13.
, respectively. The larger bifurcation between zero-field cooling (ZFC) and field cooling (FC) magnetization and magnetic hysteresis loop (Fig. 6c) indicate an easy axis along the c-axis and an Ising-type exchange interaction between adjacent Mn layers. These properties suggest a ferromagnetic order with an out-of-plane magnetic moment configuration in MnBi8Te13.
Figure 6.
Realization of TSS magnetic gap from the S-termination of ferromagnetic MnBi8Te13, from [122]. (a) Schematic crystal structure with one unit of -SL-QL-QL-QL- sequences. (b) magnetic susceptibility shows the ferromagnetic order with Curie temperature  . (c) Field-dependent magnetization hysteresis at
. (c) Field-dependent magnetization hysteresis at 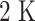 . (d) TSS gap size vs temperature shows its ferromagnetic origin. The gap size is extracted from the TSS of S-termination as shown in (e). (e–h) Termination-dependent band structure measured at
. (d) TSS gap size vs temperature shows its ferromagnetic origin. The gap size is extracted from the TSS of S-termination as shown in (e). (e–h) Termination-dependent band structure measured at 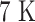 in ferromagnetic state. The TSS Dirac gap is indicated by a black arrow in (e).
in ferromagnetic state. The TSS Dirac gap is indicated by a black arrow in (e).
The heterostructure lattice of MnBi8Te13 naturally yields four types of terminations by cleaving the single crystal perpendicular to the c axis, namely, SL, QL, double QL, and triple QL terminations. A spatial-resolved ARPES with a laser beam spot ∼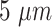 was employed to resolve the intrinsic surface band structure from these four distinct terminations and the results are shown here in Fig. 6e–h. We start with those three nonmagnetic QL terminations and find very similar TSS-RSB hybridization features as we discovered from QL and double QL terminations of MnBi6Te10 (Fig. 2c [90]), while the triple QL termination shows a TSS Dirac cone resembling that of Bi2Te3. Emphasis was put on the SL termination and a clear gap can be found at the TSS Dirac point as indicated by the black arrow in Fig. 6e. The gap size is extracted by fitting the energy distribution curves (EDCs) using multiple Lorentzian peaks. The fitting yields a TSS Dirac gap
was employed to resolve the intrinsic surface band structure from these four distinct terminations and the results are shown here in Fig. 6e–h. We start with those three nonmagnetic QL terminations and find very similar TSS-RSB hybridization features as we discovered from QL and double QL terminations of MnBi6Te10 (Fig. 2c [90]), while the triple QL termination shows a TSS Dirac cone resembling that of Bi2Te3. Emphasis was put on the SL termination and a clear gap can be found at the TSS Dirac point as indicated by the black arrow in Fig. 6e. The gap size is extracted by fitting the energy distribution curves (EDCs) using multiple Lorentzian peaks. The fitting yields a TSS Dirac gap 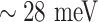 at
at 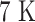 . Furthermore, this gap exhibits a monotonical decrease with increasing temperature (Fig. 6d) and finally closes at
. Furthermore, this gap exhibits a monotonical decrease with increasing temperature (Fig. 6d) and finally closes at 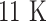 , right above
, right above 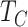 , establishing a ferromagnetic-induced Dirac-point gap in the SL termination. Although TSS gaps have been observed in other members of this materials family and doped TIs, their magnetic origin remains controversial with, particularly, the lack of clear temperature dependence [50,51,79,90,128]. Consequently, this observation—that a TSS Dirac cone gap decreases monotonically with increasing temperature and closes right at
, establishing a ferromagnetic-induced Dirac-point gap in the SL termination. Although TSS gaps have been observed in other members of this materials family and doped TIs, their magnetic origin remains controversial with, particularly, the lack of clear temperature dependence [50,51,79,90,128]. Consequently, this observation—that a TSS Dirac cone gap decreases monotonically with increasing temperature and closes right at 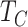 , forming a gapless Dirac cone—represents direct evidence of TSSs gapped by the magnetic order among all known magnetic topological materials. It is still more desirable to realize the magnetic gap of TSSs in MnBi2Te4 rather than its heterostructure cousins as the latter contains uncontrollable terminations with different magnetism from the exfoliation process. The realization of the TSS magnetic gap in ferromagnetic MnBi8Te13 seems to be consistent with the TSS redistribution picture.
, forming a gapless Dirac cone—represents direct evidence of TSSs gapped by the magnetic order among all known magnetic topological materials. It is still more desirable to realize the magnetic gap of TSSs in MnBi2Te4 rather than its heterostructure cousins as the latter contains uncontrollable terminations with different magnetism from the exfoliation process. The realization of the TSS magnetic gap in ferromagnetic MnBi8Te13 seems to be consistent with the TSS redistribution picture.
We have discussed several possible microscopic mechanisms of TSS in two aspects, i.e. magnetic configuration (such as disordered magnetic structure and A-AFMx with ferromagnetic in-plane moments) and TSS redistribution (such as TSS-RSB hybridization, vdW spacing expansion, excess surface charge, and cation co-antistites effect). It should be noted that, to reach any of these situations, an energy barrier needs to be overcome due to its deviation from the bulk ground states. Hence, a natural question arises: why would these situations occur? Is it an occasional case for Mn-Bi-Te family or does there exist some general fundamental mechanism? From the perspective of energy competition, a more general self-doping scenario in real samples had been proposed as the essential force that may lead to such situations based on Koopmans’ theorem [129]. For the gapped TSS, the energy level of the conduction band minimum is higher than that for the case of the gapless Dirac point. According to Koopmans’ theorem, an electronic self-doping would naturally save energy for the gapless TSS. Once such energy gain overwhelms the energy barrier of the redistribution of the TSS or magnetization, the gapless behavior of TSS emerges. In this sense, the self-doping may be the underlying origin of the nearly gapless TSS, while the TSS redistribution or magnetic reconfiguration serves as the intermediate. In this view, the emergence of the magnetic gap of MnBi8Te13 could also be understood. Instead of staying at the surface SL that contributes to the TSS, most of the self-doped electrons enter the bulk QL bands, thus suppressing the gapless transition of TSS [129]. Therefore, to open the TSS magnetic gap it is favorable to recover its charge neutrality via doping or material optimizing.
Despite the remaining puzzles of the microscopic mechanism of the TSS, there are currently experimental advances that may be informative. Related to the vdW gap mechanism, point contact tunneling spectroscopy on MnBi2Te4 reveals the signature of the TSS gap, which indicates that a moderate pressure on the surface may deduce the vdW gap expansion to restore the effective magnetic moments for a gapped TSS [130]. Related to the excess surface charge and antisite effect, improving the crystalline quality is a direct way to eliminate such effects. Recent efforts in growing MnBi2Te4 single crystals using chemical-vapor-transport (CVT) methods [131,132] have reported samples marked with higher Mn occupancy on the Mn site, slightly higher 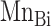 antisites, smaller carrier concentration, and a Fermi level closer to the Dirac point, yielding highest mobility of
antisites, smaller carrier concentration, and a Fermi level closer to the Dirac point, yielding highest mobility of 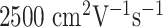 in MnBi2Te4 devices [131]. ARPES measurement with ultrahigh energy and momentum resolution, as in the previous studies [50–52,122,126], is called for the exploration of spectroscopic signature of coupling between the ferromagnetic order and TSS, such as magnetic gap opening and sixfold rotation symmetry breaking [119,133]. Quantum transport measurement is highly expected for thin layer devices based on CVT single crystals in pursuit of quantized conductivity at higher temperature.
in MnBi2Te4 devices [131]. ARPES measurement with ultrahigh energy and momentum resolution, as in the previous studies [50–52,122,126], is called for the exploration of spectroscopic signature of coupling between the ferromagnetic order and TSS, such as magnetic gap opening and sixfold rotation symmetry breaking [119,133]. Quantum transport measurement is highly expected for thin layer devices based on CVT single crystals in pursuit of quantized conductivity at higher temperature.
Contributor Information
Yuan Wang, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Xiao-Ming Ma, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Zhanyang Hao, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Yongqing Cai, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Hongtao Rong, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Fayuan Zhang, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Weizhao Chen, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Chengcheng Zhang, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Junhao Lin, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Yue Zhao, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Chang Liu, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Qihang Liu, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
Chaoyu Chen, Shenzhen Institute for Quantum Science and Engineering (SIQSE) and Department of Physics, Southern University of Science and Technology (SUSTech), Shenzhen 518055, China.
FUNDING
This work is supported by the National Key R&D Program of China (2022YFA1403700 and 2020YFA0308900), the National Natural Science Foundation of China (NSFC) (12074163, 12074161 and 11504159), the Guangdong Basic and Applied Basic Research Foundation (2022B1515020046, 2022B1515130005 and 2021B1515130007), the Guangdong Innovative and Entrepreneurial Research Team Program (2019ZT08C044), the Shenzhen Science and Technology Program (KQTD20190929173815000). C.C. acknowledges the assistance of SUSTech Core Research Facilities.
Conflict of interest statement. None declared.
REFERENCES
- 1. Savary L, Balents L. Quantum spin liquids: a review. Rep Prog Phys 2017; 80: 016502. 10.1088/0034-4885/80/1/016502 [DOI] [PubMed] [Google Scholar]
- 2. Zhou Y, Kanoda K, Ng T-K. Quantum spin liquid states. Rev Mod Phys 2017; 89: 025003. 10.1103/RevModPhys.89.025003 [DOI] [Google Scholar]
- 3. Gong C, Li L, Li Zet al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017; 546: 265–9. 10.1038/nature22060 [DOI] [PubMed] [Google Scholar]
- 4. Huang B, Clark G, Navarro-Moratalla Eet al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017; 546: 270–3. 10.1038/nature22391 [DOI] [PubMed] [Google Scholar]
- 5. Hasan MZ, Kane CL. Colloquium: topological insulators. Rev Mod Phys 2010; 82: 3045–67. 10.1103/RevModPhys.82.3045 [DOI] [Google Scholar]
- 6. Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev Mod Phys 2011; 83: 1057–110. 10.1103/RevModPhys.83.1057 [DOI] [Google Scholar]
- 7. Bernevig BA, Hughes TL, Zhang SC. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006; 314: 1757–61. 10.1126/science.1133734 [DOI] [PubMed] [Google Scholar]
- 8. König M, Wiedmann S, Brüne Cet al. Quantum spin hall insulator state in HgTe quantum wells. Science 2007; 318: 766–70. 10.1126/science.1148047 [DOI] [PubMed] [Google Scholar]
- 9. Kane CL, Mele EJ. Z2 topological order and the quantum spin Hall effect. Phys Rev Lett 2005; 95: 146802. 10.1103/PhysRevLett.95.146802 [DOI] [PubMed] [Google Scholar]
- 10. Fu L, Kane CL, Mele EJ. Topological insulators in three dimensions. Phys Rev Lett 2007; 98: 106803. 10.1103/PhysRevLett.98.106803 [DOI] [PubMed] [Google Scholar]
- 11. Hsieh D, Qian D, Wray Let al. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008; 452: 970–4. 10.1038/nature06843 [DOI] [PubMed] [Google Scholar]
- 12. Tang F, Po HC, Vishwanath Aet al. Comprehensive search for topological materials using symmetry indicators. Nature 2019; 566: 486–9. 10.1038/s41586-019-0937-5 [DOI] [PubMed] [Google Scholar]
- 13. Vergniory MG, Elcoro L, Felser Cet al. A complete catalogue of high-quality topological materials. Nature 2019; 566: 480–5. 10.1038/s41586-019-0954-4 [DOI] [PubMed] [Google Scholar]
- 14. Zhang T, Jiang Y, Song Zet al. Catalogue of topological electronic materials. Nature 2019; 566: 475–9. 10.1038/s41586-019-0944-6 [DOI] [PubMed] [Google Scholar]
- 15. Liu C, Liu XR. Angle resolved photoemission spectroscopy studies on three dimensional strong topological insulators and magnetic topological insulators. Acta Phys Sin 2019; 68: 227901. [Google Scholar]
- 16. Ando Y. Topological insulator materials. J Phys Soc Jpn 2013; 82: 102001. 10.7566/JPSJ.82.102001 [DOI] [Google Scholar]
- 17. Sobota JA, He Y, Shen Z-X. Angle-resolved photoemission studies of quantum materials. Rev Mod Phys 2021; 93: 025006. 10.1103/RevModPhys.93.025006 [DOI] [Google Scholar]
- 18. Chen YL, Analytis JG, Chu JHet al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 2009; 325: 178–81. 10.1126/science.1173034 [DOI] [PubMed] [Google Scholar]
- 19. Hsieh D, Xia Y, Qian Det al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 2009; 460: 1101–5. 10.1038/nature08234 [DOI] [PubMed] [Google Scholar]
- 20. Xia Y, Qian D, Hsieh Det al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys 2009; 5: 398–402. 10.1038/nphys1274 [DOI] [Google Scholar]
- 21. Zhang HJ, Liu CX, Qi XLet al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys 2009; 5: 438–42. 10.1038/nphys1270 [DOI] [Google Scholar]
- 22. Chen C, He S, Weng Het al. Robustness of topological order and formation of quantum well states in topological insulators exposed to ambient environment. Proc Natl Acad Sci USA 2012; 109: 3694–8. 10.1073/pnas.1115555109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Yu R, Zhang W, Zhang H-Jet al. Quantized anomalous Hall effect in magnetic topological insulators. Science 2010; 329: 61–4. 10.1126/science.1187485 [DOI] [PubMed] [Google Scholar]
- 24. Chang C-Z, Zhang J, Feng Xet al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 2013; 340: 167–70. 10.1126/science.1234414 [DOI] [PubMed] [Google Scholar]
- 25. Vonklitzing K, Dorda G, Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys Rev Lett 1980; 45: 494–7. 10.1103/PhysRevLett.45.494 [DOI] [Google Scholar]
- 26. Thouless DJ, Kohmoto M, Nightingale MPet al. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett 1982; 49: 405–8. 10.1103/PhysRevLett.49.405 [DOI] [Google Scholar]
- 27. Mogi M, Okamura Y, Kawamura Met al. Experimental signature of the parity anomaly in a semi-magnetic topological insulator. Nat Phys 2022; 18: 390–4. 10.1038/s41567-021-01490-y [DOI] [Google Scholar]
- 28. Yasuda K, Mogi M, Yoshimi Ret al. Quantized chiral edge conduction on domain walls of a magnetic topological insulator. Science 2017; 358: 1311–4. 10.1126/science.aan5991 [DOI] [PubMed] [Google Scholar]
- 29. Mogi M, Kawamura M, Tsukazaki Aet al. Tailoring tricolor structure of magnetic topological insulator for robust axion insulator. Sci Adv 2017; 3: eaao1669. 10.1126/sciadv.aao1669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Mogi M, Yoshimi R, Tsukazaki Aet al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl Phys Lett 2015; 107: 182401. 10.1063/1.4935075 [DOI] [Google Scholar]
- 31. Chang CZ, Zhao W, Kim DYet al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nature Mater 2015; 14: 473–7. 10.1038/nmat4204 [DOI] [PubMed] [Google Scholar]
- 32. Bestwick AJ, Fox EJ, Kou Xet al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys Rev Lett 2015; 114: 187201. 10.1103/PhysRevLett.114.187201 [DOI] [PubMed] [Google Scholar]
- 33. Kou X, Guo ST, Fan Yet al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys Rev Lett 2014; 113: 137201. 10.1103/PhysRevLett.113.137201 [DOI] [PubMed] [Google Scholar]
- 34. Checkelsky JG, Yoshimi R, Tsukazaki Aet al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat Phys 2014; 10: 731–6. 10.1038/nphys3053 [DOI] [Google Scholar]
- 35. Lian B, Sun XQ, Vaezi Aet al. Topological quantum computation based on chiral Majorana fermions. Proc Natl Acad Sci USA 2018; 115: 10938–42. 10.1073/pnas.1810003115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wu L, Salehi M, Koirala Net al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 2016; 354: 1124–7. 10.1126/science.aaf5541 [DOI] [PubMed] [Google Scholar]
- 37. Tokura Y, Yasuda K, Tsukazaki A. Magnetic topological insulators. Nat Rev Phys 2019; 1: 126–43. 10.1038/s42254-018-0011-5 [DOI] [Google Scholar]
- 38. Mong RSK, Essin AM, Moore JE. Antiferromagnetic topological insulators. Phys Rev B 2010; 81: 245209. 10.1103/PhysRevB.81.245209 [DOI] [Google Scholar]
- 39. Otrokov MM, Menshchikova TV, Vergniory MGet al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects. 2D Mater 2017; 4: 025082. 10.1088/2053-1583/aa6bec [DOI] [Google Scholar]
- 40. Otrokov MM, Menshchikova TV, Rusinov IPet al. Magnetic extension as an efficient method for realizing the quantum anomalous Hall state in topological insulators. JETP Lett 2017; 105: 297–302. 10.1134/S0021364017050113 [DOI] [Google Scholar]
- 41. Gong Y, Guo J, Li Jet al. Experimental realization of an intrinsic magnetic topological insulator. Chin Phys Lett 2019; 36: 076801. 10.1088/0256-307X/36/7/076801 [DOI] [Google Scholar]
- 42. Zhang D, Shi M, Zhu Tet al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys Rev Lett 2019; 122: 206401. 10.1103/PhysRevLett.122.206401 [DOI] [PubMed] [Google Scholar]
- 43. Otrokov MM, Rusinov IP, Blanco-Rey Met al. Unique thickness-dependent properties of the van der Waals interlayer antiferromagnet MnBi2Te4 films. Phys Rev Lett 2019; 122: 107202. 10.1103/PhysRevLett.122.107202 [DOI] [PubMed] [Google Scholar]
- 44. Li J, Li Y, Du Set al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci Adv 2019;5: eaaw5685. 10.1126/sciadv.aaw5685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Otrokov MM, Klimovskikh II, Bentmann Het al. Prediction and observation of an antiferromagnetic topological insulator. Nature 2019; 576: 416–22. 10.1038/s41586-019-1840-9 [DOI] [PubMed] [Google Scholar]
- 46. Lee DS, Kim T-H, Park C-Het al. Crystal structure, properties and nanostructuring of a new layered chalcogenide semiconductor, Bi2MnTe4. CrystEngComm 2013; 15: 5532–8. 10.1039/c3ce40643a [DOI] [Google Scholar]
- 47. Aliev ZS, Amiraslanov IR, Nasonova DIet al. Novel ternary layered manganese bismuth tellurides of the MnTe-Bi2Te3 system: synthesis and crystal structure. J Alloys Compd 2019; 789: 443–50. 10.1016/j.jallcom.2019.03.030 [DOI] [Google Scholar]
- 48. Zeugner A, Nietschke F, Wolter AUBet al. Chemical aspects of the candidate antiferromagnetic topological insulator MnBi2Te4. Chem Mater 2019; 31: 2795–806. 10.1021/acs.chemmater.8b05017 [DOI] [Google Scholar]
- 49. Yan JQ, Zhang Q, Heitmann Tet al. Crystal growth and magnetic structure of MnBi2Te4. Phys Rev Mater 2019; 3: 064202. 10.1103/PhysRevMaterials.3.064202 [DOI] [Google Scholar]
- 50. Hao Y-J, Liu P, Feng Yet al. Gapless surface Dirac cone in antiferromagnetic topological insulator MnBi2Te4. Phys Rev X 2019; 9: 041038. 10.1103/PhysRevX.9.041038 [DOI] [Google Scholar]
- 51. Chen YJ, Xu LX, Li JHet al. Topological electronic structure and its temperature evolution in antiferromagnetic topological insulator MnBi2Te4. Phys Rev X 2019; 9: 041040. 10.1103/PhysRevX.9.041040 [DOI] [Google Scholar]
- 52. Li H, Gao S-Y, Duan S-Fet al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys Rev X 2019; 9: 041039. 10.1103/PhysRevX.9.041039 [DOI] [Google Scholar]
- 53. Qi X-L, Hughes TL, Zhang S-C. Topological field theory of time-reversal invariant insulators. Phys Rev B 2008; 78: 195424. 10.1103/PhysRevB.78.195424 [DOI] [Google Scholar]
- 54. Essin AM, Moore JE, Vanderbilt D.. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys Rev Lett 2009; 102: 146805. 10.1103/PhysRevLett.102.146805 [DOI] [PubMed] [Google Scholar]
- 55. Li R, Wang J, Qi X-Let al. Dynamical axion field in topological magnetic insulators. Nat Phys 2010; 6: 284–8. 10.1038/nphys1534 [DOI] [Google Scholar]
- 56. Wang J, Lian B, Zhang S-C. Dynamical axion field in a magnetic topological insulator superlattice. Phys Rev B 2016; 93: 045115. 10.1103/PhysRevB.93.045115 [DOI] [Google Scholar]
- 57. Sekine A, Nomura K. Axion electrodynamics in topological materials. J Appl Phys 2021; 129: 141101. 10.1063/5.0038804 [DOI] [Google Scholar]
- 58. Fu H, Liu C-X, Yan B. Exchange bias and quantum anomalous Hall effect in the MnBi2Te4/CrI3 heterostructure. Sci Adv 2020; 6: eaaz0948. 10.1126/sciadv.aaz0948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Wang Z, Rodriguez JO, Jiao Let al. Evidence for dispersing 1D Majorana channels in an iron-based superconductor. Science 2020; 367: 104–8. 10.1126/science.aaw8419 [DOI] [PubMed] [Google Scholar]
- 60. Palacio-Morales A, Mascot E, Cocklin Set al. Atomic-scale interface engineering of Majorana edge modes in a 2D magnet-superconductor hybrid system. Sci Adv 2019; 5: eaav6600. 10.1126/sciadv.aav6600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Yasuda K, Mogi M, Yoshimi Ret al. Quantized chiral edge conduction on domain walls of a magnetic topological insulator. Science 2017; 358: 1311–4. 10.1126/science.aan5991 [DOI] [PubMed] [Google Scholar]
- 62. He QL, Pan L, Stern ALet al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 2017; 357: 294–9. 10.1126/science.aag2792 [DOI] [PubMed] [Google Scholar]
- 63. Deng Y, Yu Y, Shi MZet al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020; 367: 895–900. 10.1126/science.aax8156 [DOI] [PubMed] [Google Scholar]
- 64. Liu C, Wang Y, Li Het al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat Mater 2020; 19: 522–7. 10.1038/s41563-019-0573-3 [DOI] [PubMed] [Google Scholar]
- 65. Ge J, Liu Y, Li Jet al. High-Chern-number and high-temperature quantum Hall effect without Landau levels. Natl Sci Rev 2020; 7: 1280–7. 10.1093/nsr/nwaa089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Gao A, Liu YF, Hu Cet al. Layer Hall effect in a 2D topological axion antiferromagnet. Nature 2021; 595: 521–5. 10.1038/s41586-021-03679-w [DOI] [PubMed] [Google Scholar]
- 67. Lian B, Liu Z, Zhang Yet al. Flat Chern band from twisted bilayer MnBi2Te4. Phys Rev Lett 2020; 124: 126402. 10.1103/PhysRevLett.124.126402 [DOI] [PubMed] [Google Scholar]
- 68. Sun H, Xia B, Chen Zet al. Rational design principles of the quantum anomalous Hall effect in superlatticelike magnetic topological insulators. Phys Rev Lett 2019; 123: 096401. 10.1103/PhysRevLett.123.096401 [DOI] [PubMed] [Google Scholar]
- 69. Li J, Wang C, Zhang Zet al. Magnetically controllable topological quantum phase transitions in the antiferromagnetic topological insulator MnBi2Te4. Phys Rev B 2019; 100: 121103. 10.1103/PhysRevB.100.121103 [DOI] [Google Scholar]
- 70. Chowdhury S, Garrity KF, Tavazza F. Prediction of Weyl semimetal and antiferromagnetic topological insulator phases in Bi2MnSe4. npj Comput Mater 2019; 5: 33. 10.1038/s41524-019-0168-1 [DOI] [Google Scholar]
- 71. Zhang RX, Wu F, Das Sarma S. Mobius Insulator and Higher-Order Topology in MnBi2nTe3n+1. Phys Rev Lett 2020; 124: 136407. 10.1103/PhysRevLett.124.136407 [DOI] [PubMed] [Google Scholar]
- 72. Zhan GH, Wang HQ, Zhang HJ. Antiferromagnetic topological insulators and axion insulators–MnBi2Te4 family magnetic systems. Phys 2020; 49: 817–27. [Google Scholar]
- 73. He K. MnBi2Te4-family intrinsic magnetic topological materials. npj Quantum Mater 2020; 5: 90. 10.1038/s41535-020-00291-5 [DOI] [Google Scholar]
- 74. Li Y, Xu Y. First-principles discovery of novel quantum physics and materials: from theory to experiment. Comput Mater Sci 2021; 190: 110262. 10.1016/j.commatsci.2020.110262 [DOI] [Google Scholar]
- 75. Wang P, Ge J, Li Jet al. Intrinsic magnetic topological insulators. Innovation 2021; 2: 100098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Zhao Y, Liu Q. Routes to realize the axion-insulator phase in MnBi2Te4(Bi2Te3)n family. Appl Phys Lett 2021; 119: 060502. 10.1063/5.0059447 [DOI] [Google Scholar]
- 77. Vidal RC, Bentmann H, Peixoto TRFet al. Surface states and Rashba-type spin polarization in antiferromagnetic MnBi2Te4 (0001). Phys Rev B 2019; 100: 121104. 10.1103/PhysRevB.100.121104 [DOI] [Google Scholar]
- 78. Lee SH, Zhu Y, Wang Yet al. Spin scattering and noncollinear spin structure-induced intrinsic anomalous Hall effect in antiferromagnetic topological insulator MnBi2Te4. Phys Rev Res 2019; 1: 012011. 10.1103/PhysRevResearch.1.012011 [DOI] [Google Scholar]
- 79. Hu Y, Xu L, Shi Met al. Universal gapless Dirac cone and tunable topological states in (MnBi2Te4)m(Bi2Te3)n heterostructures. Phys Rev B 2020; 101: 161113(R). 10.1103/PhysRevB.101.161113 [DOI] [Google Scholar]
- 80. Nevola D, Li HX, Yan JQet al. Coexistence of surface ferromagnetism and a gapless topological state in MnBi2Te4. Phys Rev Lett 2020; 125: 117205. 10.1103/PhysRevLett.125.117205 [DOI] [PubMed] [Google Scholar]
- 81. Swatek P, Wu Y, Wang L-Let al. Gapless Dirac surface states in the antiferromagnetic topological insulator MnBi2Te4. Phys Rev B 2020; 101: 161109. 10.1103/PhysRevB.101.161109 [DOI] [Google Scholar]
- 82. Fukasawa T, Kusaka S, Sumida Ket al. Absence of ferromagnetism in MnBi2Te4/Bi2Te3 down to 6 K. Phys Rev B 2021; 103: 205405. 10.1103/PhysRevB.103.205405 [DOI] [Google Scholar]
- 83. Yan C, Fernandez-Mulligan S, Mei Ret al. Origins of electronic bands in the antiferromagnetic topological insulator MnBi2Te4. Phys Rev B 2021; 104: L041102. 10.1103/PhysRevB.104.L041102 [DOI] [Google Scholar]
- 84. Xu R, Bai Y, Zhou Jet al. Evolution of the electronic structure of ultrathin MnBi2Te4 films. Nano Lett 2022; 22: 6320–7. 10.1021/acs.nanolett.2c02034 [DOI] [PubMed] [Google Scholar]
- 85. Vidal RC, Bentmann H, Facio JIet al. Orbital complexity in intrinsic magnetic topological insulators MnBi4Te7 and MnBi6Te10. Phys Rev Lett 2021; 126: 176403. 10.1103/PhysRevLett.126.176403 [DOI] [PubMed] [Google Scholar]
- 86. Wu J, Liu F, Liu Cet al. Toward 2D magnets in the (MnBi2 Te4)(Bi2 Te3)n bulk crystal. Adv Mater 2020; 32: e2001815. 10.1002/adma.202001815 [DOI] [PubMed] [Google Scholar]
- 87. Yan JQ, Liu YH, Parker DSet al. A-type antiferromagnetic order in MnBi4Te7 and MnBi6Te10 single crystals. Phys Rev Mater 2020; 4: 054202. 10.1103/PhysRevMaterials.4.054202 [DOI] [Google Scholar]
- 88. Ding L, Hu C, Ye Fet al. Crystal and magnetic structures of magnetic topological insulators MnBi2Te4 and MnBi4Te7. Phys Rev B 2020; 101: 020412. 10.1103/PhysRevB.101.020412 [DOI] [Google Scholar]
- 89. Tian S, Gao S, Nie Set al. Magnetic topological insulator MnBi6Te10 with a zero-field ferromagnetic state and gapped Dirac surface states. Phys Rev B 2020; 102: 035144. 10.1103/PhysRevB.102.035144 [DOI] [Google Scholar]
- 90. Ma X-M, Chen Z, Schwier EFet al. Hybridization-induced gapped and gapless states on the surface of magnetic topological insulators. Phys Rev B 2020; 102: 245136. 10.1103/PhysRevB.102.245136 [DOI] [Google Scholar]
- 91. Wu X, Li J, Ma X-Met al. Distinct topological surface states on the two terminations of MnBi4Te7. Phys Rev X 2020; 10: 031013. 10.1103/PhysRevX.10.031013 [DOI] [Google Scholar]
- 92. Jo NH, Wang L-L, Slager R-Jet al. Intrinsic axion insulating behavior in antiferromagnetic MnBi6Te10. Phys Rev B 2020; 102: 045130. 10.1103/PhysRevB.102.045130 [DOI] [Google Scholar]
- 93. Liang A, Chen C, Zheng Het al. Approaching a minimal topological electronic structure in antiferromagnetic topological insulator MnBi2Te4 via surface modification. Nano Lett 2022; 22: 4307–14. 10.1021/acs.nanolett.1c04930 [DOI] [PubMed] [Google Scholar]
- 94. Shikin AM, Estyunin DA, Klimovskikh IIet al. Nature of the Dirac gap modulation and surface magnetic interaction in axion antiferromagnetic topological insulator MnBi2Te4. Sci Rep 2020; 10: 13226. 10.1038/s41598-020-70089-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Shikin AM, Estyunin DA, Zaitsev NLet al. Sample-dependent Dirac-point gap in MnBi2Te4 and its response to applied surface charge: a combined photoemission and ab initio study. Phys Rev B 2021; 104: 115168. 10.1103/PhysRevB.104.115168 [DOI] [Google Scholar]
- 96. Sass PM, Kim J, Vanderbilt Det al. Robust A-type order and spin-flop transition on the surface of the antiferromagnetic topological insulator MnBi2Te4. Phys Rev Lett 2020; 125: 037201. 10.1103/PhysRevLett.125.037201 [DOI] [PubMed] [Google Scholar]
- 97. Du MH, Yan J, Cooper VRet al. Tuning Fermi levels in intrinsic antiferromagnetic topological insulators MnBi2Te4 and MnBi4Te7 by defect engineering and chemical doping. Adv Funct Mater 2021; 31: 2006516. 10.1002/adfm.202006516 [DOI] [Google Scholar]
- 98. Yang S, Xu X, Zhu Yet al. Odd-even layer-number effect and layer-dependent magnetic phase diagrams in MnBi2Te4. Phys Rev X 2021; 11: 011003. 10.1103/PhysRevX.11.011003 [DOI] [Google Scholar]
- 99. Kagerer P, Fornari CI, Buchberger Set al. Molecular beam epitaxy of antiferromagnetic (MnBi2Te4)(Bi2Te3) thin films on BaF2 (111). J Appl Phys 2020; 128: 135303. 10.1063/5.0025933 [DOI] [Google Scholar]
- 100. Hirahara T, Otrokov MM, Sasaki TTet al. Fabrication of a novel magnetic topological heterostructure and temperature evolution of its massive Dirac cone. Nat Commun 2020; 11: 4821. 10.1038/s41467-020-18645-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Vidal RC, Zeugner A, Facio JIet al. Topological electronic structure and intrinsic magnetization in MnBi4Te7: a Bi2Te3 derivative with a periodic Mn sublattice. Phys Rev X 2019; 9: 041065. 10.1103/PhysRevX.9.041065 [DOI] [Google Scholar]
- 102. Estyunin DA, Klimovskikh II, Shikin AMet al. Signatures of temperature driven antiferromagnetic transition in the electronic structure of topological insulator MnBi2Te4. APL Mater 2020; 8: 021105. 10.1063/1.5142846 [DOI] [Google Scholar]
- 103. Garnica M, Otrokov MM, Aguilar PCet al. Native point defects and their implications for the Dirac point gap at MnBi2Te4(0001). npj Quantum Mater 2022; 7: 7. 10.1038/s41535-021-00414-6 [DOI] [Google Scholar]
- 104. Wimmer S, Sánchez-Barriga J, Küppers Pet al. Mn-rich MnSb2 Te4: a topological insulator with magnetic gap closing at high Curie temperatures of 45–50 K. Adv Mater 2021; 33: e2102935. 10.1002/adma.202102935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105. Sitnicka J, Park K, Skupiński Pet al. Systemic consequences of disorder in magnetically self-organized topological MnBi2Te4/(Bi2Te3)n superlattices. 2D Mater 2022; 9: 015026. 10.1088/2053-1583/ac3cc6 [DOI] [Google Scholar]
- 106. Shikin AM, Estyunin DA, Zaitsev NLet al. Sample-dependent Dirac-point gap in MnBi2Te4 and its response to applied surface charge: a combined photoemission and ab initio study. Phys Rev B 2021; 104: 115168. 10.1103/PhysRevB.104.115168 [DOI] [Google Scholar]
- 107. Liu Y, Wang L-L, Zheng Qet al. Site mixing for engineering magnetic topological insulators. Phys Rev X 2021; 11: 021033. 10.1103/PhysRevX.11.021033 [DOI] [Google Scholar]
- 108. Lai Y, Ke L, Yan Jet al. Defect-driven ferrimagnetism and hidden magnetization in MnBi2Te4. Phys Rev B 2021; 103: 184429. 10.1103/PhysRevB.103.184429 [DOI] [Google Scholar]
- 109. Hu C, Lien S-W, Feng Eet al. Tuning magnetism and band topology through antisite defects in Sb-doped MnBi4Te7. Phys Rev B 2021; 104: 054422. 10.1103/PhysRevB.104.054422 [DOI] [Google Scholar]
- 110. Yuan Y, Wang X, Li Het al. Electronic states and magnetic response of MnBi2Te4 by scanning tunneling microscopy and spectroscopy. Nano Lett 2020; 20: 3271–7. 10.1021/acs.nanolett.0c00031 [DOI] [PubMed] [Google Scholar]
- 111. Liang Z, Luo A, Shi Met al. Mapping Dirac fermions in the intrinsic antiferromagnetic topological insulators (MnBi2Te4)(Bi2Te3)n (n = 0,1). Phys Rev B 2020; 102: 161115. 10.1103/PhysRevB.102.161115 [DOI] [Google Scholar]
- 112. Huang Z, Du M-H, Yan Jet al. Native defects in antiferromagnetic topological insulator MnBi2Te4. Phys Rev Mater 2020; 4: 121202. 10.1103/PhysRevMaterials.4.121202 [DOI] [Google Scholar]
- 113. Yang Z, Zhang H. Evolution of surface states of antiferromagnetic topological insulator MnBi2Te4 with tuning the surface magnetization. New J Phys 2022; 24: 073034. 10.1088/1367-2630/ac7e64 [DOI] [Google Scholar]
- 114. Sass PM, Ge W, Yan Jet al. Magnetic imaging of domain walls in the antiferromagnetic topological insulator MnBi2Te4. Nano Lett 2020; 20: 2609–14. 10.1021/acs.nanolett.0c00114 [DOI] [PubMed] [Google Scholar]
- 115. Garrity KF, Chowdhury S, Tavazza FM. Topological surface states of MnBi2Te4 at finite temperatures and at domain walls. Phys Rev Mater 2021; 5: 024207. 10.1103/PhysRevMaterials.5.024207 [DOI] [Google Scholar]
- 116. Xu ZM, Duan WH, Xu Y. Controllable chirality and band gap of quantum anomalous Hall insulators. Nano Lett 2023; 23: 305–11. [DOI] [PubMed] [Google Scholar]
- 117. Padmanabhan H, Stoica VA, Kim PKet al. Large exchange coupling between localized spins and topological bands in MnBi2Te4. Adv Mater 2022; 34: e2202841. 10.1002/adma.202202841 [DOI] [PubMed] [Google Scholar]
- 118. Sun H-P, Wang CM, Zhang S-Bet al. Analytical solution for the surface states of the antiferromagnetic topological insulator MnBi2Te4. Phys Rev B 2020; 102: 241406(R). 10.1103/PhysRevB.102.241406 [DOI] [Google Scholar]
- 119. Wang D, Wang H, Xing D. Three-Dirac-fermion approach to unexpected gapless surface states of van der Waals magnetic topological insulators. Sci China Phys Mech Astron 2023; 66: 297211. [Google Scholar]
- 120. Tan H, Yan B. Distinct magnetic gaps between antiferromagnetic and ferromagnetic orders driven by surface defects in the topological magnet MnBi2Te4. Phys Rev Lett 2023; 130: 126702. [DOI] [PubMed] [Google Scholar]
- 121. Menshchikova TV, Eremeev SV, Chulkov EV. On the origin of two-dimensional electron gas states at the surface of topological insulators. JETP Lett 2011; 94: 106–11. 10.1134/S0021364011140104 [DOI] [Google Scholar]
- 122. Lu R, Sun H, Kumar Set al. Half-magnetic topological insulator with magnetization-induced Dirac gap at a selected surface. Phys Rev X 2021; 11: 011039. [Google Scholar]
- 123. Chen Y, Chuang Y-W, Lee SHet al. Ferromagnetism in van der Waals compound MnSb1.8Bi0.2Te4. Phys Rev Mater 2020; 4: 064411. [Google Scholar]
- 124. Yan JQ, Okamoto S, McGuire MAet al. Evolution of structural, magnetic, and transport properties in MnBi2−xSbxTe4. Phys Rev B 2019; 100: 104409. 10.1103/PhysRevB.100.104409 [DOI] [Google Scholar]
- 125. Murakami T, Nambu Y, Koretsune Tet al. Realization of interlayer ferromagnetic interaction in MnSb2Te4 toward the magnetic Weyl semimetal state. Phys Rev B 2019; 100: 195103. 10.1103/PhysRevB.100.195103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Ma X-M, Zhao Y, Zhang Ket al. Realization of a tunable surface Dirac gap in Sb-doped MnBi2Te4. Phys Rev B 2021; 103: L121112. 10.1103/PhysRevB.103.L121112 [DOI] [Google Scholar]
- 127. Hu C, Ding L, Gordon KNet al. Realization of an intrinsic ferromagnetic topological state in MnBi8Te13. Sci Adv 2020; 6: eaba4275. 10.1126/sciadv.aba4275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Xu L, Mao Y, Wang Het al. Persistent surface states with diminishing gap in MnBi2Te4/Bi2Te3 superlattice antiferromagnetic topological insulator. Sci Bull 2020; 65: 2086–93. 10.1016/j.scib.2020.07.032 [DOI] [PubMed] [Google Scholar]
- 129. Chen W, Zhao Y, Yao Qet al. Koopmans’ theorem as the mechanism of nearly gapless surface states in self-doped magnetic topological insulators. Phys Rev B 2021; 103: L201102. 10.1103/PhysRevB.103.L201102 [DOI] [Google Scholar]
- 130. Ji H-R, Liu Y-Z, Wang Het al. Detection of magnetic gap in topological surface states of MnBi2Te4. Chin Phys Lett 2021; 38: 107404. 10.1088/0256-307X/38/10/107404 [DOI] [Google Scholar]
- 131. Hu C, Gao A, Berggren BSet al. Growth, characterization, and Chern insulator state in MnBi2Te4 via the chemical vapor transport method. Phys Rev Mater 2021; 5: 124206. 10.1103/PhysRevMaterials.5.124206 [DOI] [Google Scholar]
- 132. Yan JQ, Huang Z, Wu Wet al. Vapor transport growth of MnBi2Te4 and related compounds. J Alloys Compd 2022; 906: 164327. 10.1016/j.jallcom.2022.164327 [DOI] [Google Scholar]
- 133. Tan H, Kaplan D, Yan B. Momentum-inversion symmetry breaking on the Fermi surface of magnetic topological insulators. Phys Rev Mater 2022; 6: 104204. [Google Scholar]