A deep learning solution to recommend laboratory reduction strategies in ICU

Abstract

Objective:

To build a machine-learning model that predicts laboratory test results and provides a promising lab test reduction strategy, using spatial-temporal correlations.

Materials and Methods:

We developed a global prediction model to treat laboratory testing as a series of decisions by considering contextual information over time and across modalities. We validated our method using a critical care database (MIMIC III), which includes 4,570,709 observations of 12 standard laboratory tests, among 38,773 critical care patients. Our deep-learning model made real-time laboratory reduction recommendations and predicted the properties of lab tests, including values, normal/abnormal (whether labs were within the normal range) and transition (normal to abnormal or abnormal to normal from the latest lab test). We reported area under the receiver operating characteristic curve (AUC) for predicting normal/abnormal, evaluated accuracy and absolute bias on prediction vs. observation against lab test reduction proportion. We compared our model against baseline models and analyzed the impact of variations on the recommended reduction strategy.

Results:

Our best model offered a 20.26% reduction in the number of laboratory tests. By applying the recommended reduction policy on the hold-out dataset (7,755 patients), our model predicted normality/abnormality of laboratory tests with a 98.27% accuracy (AUC, 0.9885; sensitivity, 97.84%; specificity, 98.80%; PPV, 99.01%; NPV, 97.39%) on 20.26% reduced lab tests, and recommended 98.10% of transitions to be checked. Our model performed better than the greedy models, and the recommended reduction strategy was robust.

Discussion

Strong spatial and temporal correlations between laboratory tests can be used to optimize policies for reducing laboratory tests throughout the hospital course. Our method allows for iterative predictions and provides a superior solution for the dynamic decision-making laboratory reduction problem.

Conclusion

This work demonstrates a machine-learning model that assists physicians in determining which laboratory tests may be omitted.

INTRODUCTION

Low-value laboratory tests have been recognized as one contributor to waste in the healthcare system [1, 2]. In the Choosing Wisely campaign, four different professional medical associations have identified unnecessary tests as a problem and have issued general guidelines to reduce the number of laboratory tests [3–6]. Unnecessary tests lead to increased costs [7–9], risk of hospital-acquired anemia, and its concomitant morbidities [10–15].

Although unnecessary testing is common, identifying and reducing unnecessary tests is challenging. Numerous papers have discussed ways to reduce the number of laboratory tests ordered [16], including displaying costs at order entry [17, 18], restructuring electronic laboratory utilization systems [19], introducing financial incentive programs [20], creating awareness through training and education [21–23], and developing evidence-based guidelines [24]. Several papers conducted a quality improvement project to verify the impact of intervention based on guidelines such as education and order information on reducing unnecessary laboratory testing [25, 26]. Most successful interventions are multifaceted and include a combination of education, audit, feedback, and administrative changes [27]. Another approach is to develop data-driven algorithms to help clinicians recognize when certain laboratory tests are not needed.

There are a few machine learning articles that describe novel methods to reduce laboratory tests by leveraging electronic laboratory data. Aikens et al. [28] used predictive models to infer the likelihood that a future laboratory test would “change” or “stay the same” compared to the previous measurement. Their near-future prediction of stable laboratory tests (troponin I, thyroid-stimulating hormone, platelet count, etc.) reported an Area Under the receiver operating Characteristic curve (AUC) of approximately 0.75 for predicting whether a lab test will “change” or “stay the same”. Cismondi et al. [29] used an artificial intelligence tool, fuzzy modeling, to predict whether the lab test contributed an “information gain” which was introduced to represent the necessity of the lab test based on a defined threshold for normal ranges for each lab. They considered 11 variables, including 10 variables from vital signs and transfusion information and the immediate previous lab value or the first lab value of the morning, as the input for their model. The accuracy of prediction was greater than 80% for all lab tests. Both studies recommended reducing lab tests because the values were expected to “stay the same”, or there was no “information gain”. However, it is possible that these labs may be of interest to clinicians in a certain context. Another study by Xu et al. [30] outlined a set of six machine learning models (regularized logistic regression, regress and round, naive Bayes, neural network multilayer perceptrons, decision tree, random forest, AdaBoost, and XGBoost) to predict the normality of near-future laboratory tests using data from 191,506 patients treated at three academic medical centers. Their best model had an AUC of 0.90~0.96 for 12 stand-alone laboratory tests (e.g., sodium, lactate dehydrogenase, hemoglobin, etc.), but the study did not recommend a strategy to reduce lab tests. These studies show that it is possible to predict near-future laboratory tests with relatively high accuracy.

However, making predictions based on observation is not equivalent to providing a useful strategy to reduce resource utilization. The former is a one-time reduction, while the latter is an iterative process that accounts for the fact that later decisions can be affected by earlier decisions. Creating a useful policy for lab reduction requires the capacity to consider incomplete information dynamically due to lab reduction. Recently, Yu et al. proposed the first deep-learning model that is able to provide a lab test reduction strategy and to predict the lab test value dynamically [31]. The study introduced a self-feeding structure and devised a loss function that pushes the predicted value in convergence with the actual laboratory value while considering the incomplete information. The model achieved 95% accuracy of prediction for abnormality of tests that were recommended to be omitted, using a reduction strategy with a 15% reduction proportion. In this study, to obtain more accurate predictions on reduced lab tests, we developed a deep-learning, multi-task model, and used the self-feeding model as the baseline model. We also introduced a corruption strategy (inspired by the successful BERT [32] model that masks words for inference in the training step) to simulate the incomplete input data due to the lab test reduction during the training of the model. We also devised a new loss function to account for the trade-off between prediction accuracy and omitted lab tests. Finally, we analyzed the impact of variation on the recommended lab test reduction strategy to verify its robustness.

METHODS

We developed a deep-learning, multi-task model that learns and recommends a laboratory reduction policy while considering the long-term loss of data due to omitted labs. In our model, we simultaneously predict four targets for future laboratory tests: (1) the necessity (in terms of probability) of conducting certain laboratory tests, (2) lab values, (3) abnormalities (i.e., normal or abnormal, as defined as within or out of normal range, respectively), and (4) transitions (from normal/abnormal to abnormal/normal). We aim to reduce laboratory tests while maintaining high accuracy of prediction on the reduced lab tests throughout the intensive care course, rather than simply the near-future test result. Note that we used the normal range of healthy males and females to determine normal lab ranges for our tests, which is very conservative for an ICU setting (see Appendix eTable 5).

The key insight of our proposed model is to link the necessity of conducting certain laboratory tests with the prediction accuracy for the entire hospital course. That is, if a laboratory test can be predicted using prior observations and other laboratory tests, its presence or absence will not change future decisions, and therefore, can be omitted. In other words, highly predictable results can be omitted without affecting subsequent predictions. It is important to note that our model differs from all previous models because our model was trained to compensate for the information loss due to reduction in terms of making full use of correlations at the same time step in addition to the temporal transitions in the laboratory test sequences.

The proposed model is composed of two double-layered Long Short-Term Memory Networks (LSTM) [33], one for laboratory tests and another one for vital sign data, followed by four modules that predict the four targets described above. Each module consists of two fully-connected layers. We introduced a corruption strategy into our training phase by randomly masking the observations with a probability of 5% and letting the model learn the spatial-temporal context by inferring these missing values.

The test phase applies the reduction strategy that is generated by the trained model. The predicted necessity for conducting each laboratory test was translated into a decision recommendation: “checking the lab” vs. “reducing, or omitting, the lab” based on a given threshold. This process is different from the training process because we actually omitted lab data based on the recommended reduction strategy and treated the omitted laboratory tests as missing values for subsequent predictions in the test model.

Dataset and inclusion criteria

The Medical Information Mart for Intensive Care III (MIMIC III) [34] dataset contained 53,423 distinct hospital admissions for adult patients admitted to intensive care units (ICU) at Beth Israel Deaconess Medical Center. We focused on 12 common laboratory tests, which can be grouped into panels or ordered individually:

• Electrolytes: Na (sodium), K (potassium), Cl (chloride) and HCO3 (serum bicarbonate), Ca (total calcium), Mg (magnesium) and PO4 (phosphate)

• Renal function: BUN (Blood Urea Nitrogen), Cr (creatinine)

• Complete Blood Count (CBC): Hgb (hemoglobin), Plt (platelet count), WBC (white blood count cell)

The laboratory results for each patient were treated as a collection of consecutive sequences. Because the vast majority of patients had less than 30 blood draws in their sequences, we capped the length of the sequences at 30. In order to learn transition and have a basic understanding of laboratory values for each patient, we required a dense observation of laboratory tests at the first blood draw to start our prediction model. The majority of the samples had a dense observation for their first time. For sequences that had an inadequate density of labs in the initial timestamp, we truncated the initial sequences until an adequate density of observations in a timestamp was reached. We excluded patients with only one blood draw. Then we had a dataset, including the laboratory results of 38,773 patients with an ‘EMERGENCE’ admission state. We split the dataset randomly into a training set (80%) and a hold-out set (20%). The laboratory results for each patient in MIMIC III might contain missing values because a few lab tests might not be ordered. We encoded the missing values as zeros. eTable 1 shows the data descriptions of the training set, and the hold-out set including mean, the standard deviation of lab test values, percentage of lab tests with a missing value.

Input features of the model

Our method is data-driven. Although we primarily used laboratory tests to make predictions, we also considered individual patients’ characteristics, including vital signs, time differences from the last record, and demographics (race, gender). Vital signs were monitored more frequently than laboratory tests, and they were measured at different times. To provide consistent inputs for our model, we averaged vital signs data by hours if multiple readings were available in the same hour, and capped the length of the vitals sequence at 200.

Model outputs and evaluation metrics

Because omitting more laboratory tests can lead to more errors, there is a trade-off between prediction accuracy and reduction. Focusing on the four estimation targets (introduced at the beginning of the method section), we trained a model for four different tasks. The first task was to estimate the likelihood of reducing (low yield) laboratory tests, while the remaining tasks were to make predictions for three different clinically-relevant metrics: abnormality, transition, test value. With a decision threshold for the likelihood of reduction, the model will recommend whether each laboratory test should be omitted or conducted in the next timestamp (lab test reduction strategy) and execute predictions. So, each threshold corresponded to a lab reduction strategy, with a particular reduction proportion and a prediction performance. We evaluated the reduction proportion for a lab reduction strategy by calculating the proportion of lab tests to be reduced in the dataset, excluding the initial lab tests (the lab tests at the first timestamp). Since the values of the lab tests, which were checked, would be observed, we focused on the prediction of properties of the lab tests, which were recommended to be reduced. Table 1 describes the evaluation metrics for three predictions.

Table 1:

Evaluation metrics table. The area under the ROC Curve (AUC), accuracy (Acc), sensitivity (Sens), specificity (Spec), positive predictive value (PPV), and negative predictive value (NPV).

Prediction	Lab tests for evaluation	Evaluation Metrics
Abnormality	Lab tests with non-missing values recommended to be reduced	AUC, Acc, Sens, Spec, PPV, NPV
Transition	Lab tests with non-missing values in two consecutive timestamps	Proportion of transitions that were recommended to be checked among all transitions (% of transition checked), Acc. on the reduced lab tests
Value	Lab tests with non-missing values recommended to be reduced	Absolute difference from the real value, i.e., absolute bias

We computed the evaluation metrics and plotted curves that represented different trade-offs based on a sequence of thresholds of necessity from 0.02 to 1, with 0.02 interval (threshold list) to state the relationship between reduction and prediction. We used the proportion of lab tests that were recommended to be checked by the model (Check proportion) to represent the reduction for trade-off curves. Note that from a trained model, one can apply different thresholds on the predicted necessity of conducting the lab tests, which leads to different laboratory reduction strategies.

Model development

We built a deep-learning model and designed a novel loss function. We developed five model variants for each of the combinations of input features: (1) laboratory tests; (2) laboratory tests and time differences between two adjacent visits; (3) laboratory tests and vitals; (4) laboratory tests, time differences and demographics; (5) laboratory tests, vitals, time differences, and demographics.

Our model consisted of three modules: a corruption module, an LSTM module, and an output module for four tasks. For the corruption module, the values of laboratory testing were randomly masked as 0 with a probability of 5%, which was a corruption probability (conducting a random mask operation followed Bernoulli distribution). The corrupted formula for lab testing value ${\mathit{v}}_{\mathit{i}}=\left(v_i{}^1,v_i{}^2,\cdots ,{v_i}^K\right)$ was as follows, where $K$ was the number of lab tests and = 12 in this paper.

Corruption module:

${\mathit{v}}_{\mathit{i}}^{\prime }={\mathit{v}}_{\mathit{i}}\odot {\mathit{r}}_{\mathit{i}}$ where ${\mathit{r}}_{\mathit{i}}=\left(r_i^1,r_i^2,\dots ,r_i^K\right),r_i^k~Bernoulli(1-crpt)$ for $k=\mathrm{1,2},\dots ,K$, and $crpt$ is a corruption probability

As shown in Figure 1, the corrupted lab test values concatenated with time differences were fed into a two-layer LSTM neural network where the output of the first layer concatenated with the input of the first layer was fed into the second layer, and the vital sign values followed the similar pipeline. Then, two outputs from the corrupted laboratory test data and vital sign data were aligned by their timestamps and concatenated with the embedding vectors of the race and gender of the patient, followed by four multilayer perceptrons (MLP) with one hidden layer and ‘ReLU’ activation function. Three of these MLPs were followed by a sigmoid function to output predicted scores for the necessity of checking, abnormality, and transition, ranging between 0 and 1. The fourth MLP outputted the predicted lab value. For models with fewer input features, the relative architecture would be reduced. Unlike the training phase, the testing phase of our model implemented a real-time prediction applying a lab reduction strategy (See Figure 2).

Figure 1:

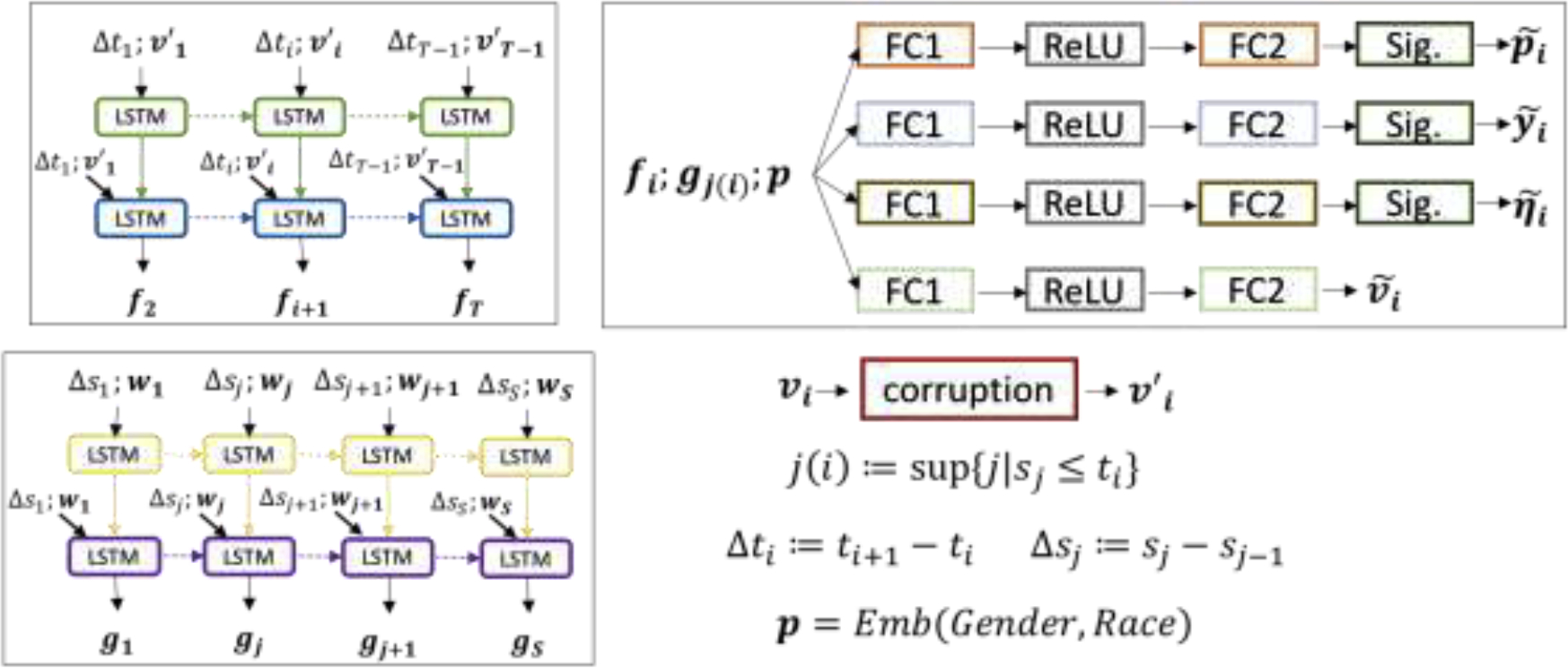
Deep learning pipeline (training phase): the pipeline of the proposed model with all input features, including lab testing value, vital value, time differences, and demographic data. The input features are lab testing value ${\mathit{v}}_{\mathit{i}}=\left(v_i{}^1,v_i{}^2,\cdots ,{v_i}^K\right)$, vital sign value ${\mathit{w}}_{\mathit{i}}=\left(w_i{}^1,w_i{}^2,\cdots ,{w_i}^J\right)$, time differences of lab testings and vital value $\mathrm{\Delta }{t}_i$, $\mathrm{\Delta }{s}_j$, demographic data including gender and race, where $K$, $J$ are the number of lab tests, vital readings, and $t_i$, $s_j$ are the timestamps of lab testing order ${\mathit{v}}_{\mathit{i}}$ and the vital testings ${\mathit{w}}_{\mathit{j}}$, respectively. $T,$ $S$ denotes the fixed length of lab testing orders and vital records, respectively. The output of the first LSTM layer concatenated with the input of the first layer will be fed into the second LSTM layer. There are four FC1 and FC2, which are fully-connected layers without sharing parameters. The terms “ReLU” and “Sig.” refer to the ReLU and Sigmoid activation functions. The corruption module here is to corrupt each lab testing value ${v_i}^k$ into missing with probability 5% randomly. “Emb” means embedding layers for gender and race, which outputs the concatenated embedding of gender and race. The sizes of embeddings for gender and race are 4, respectively. The sizes of the hidden layer in LSTM cell for lab testing value and vital value are 60, 40, respectively. The sizes of the first and second fully-connected layers are 128 and 12 (which is the number of lab tests we worked on.) Four final outputs ${\tilde{\mathit{p}}}_{\mathit{i}}=\left({{\tilde{p}}_i}^1,{{\tilde{p}}_i}^2,\cdots ,{{\tilde{p}}_i}^K\right)$, ${\tilde{\mathit{y}}}_{\mathit{i}}=\left({{\tilde{y}}_i}^1,{{\tilde{y}}_i}^2,\cdots ,{{\tilde{y}}_i}^K\right)$, ${\tilde{\mathit{\eta }}}_{\mathit{i}}=\left({{\tilde{\eta }}_i}^1,{{\tilde{\eta }}_i}^2,\cdots ,{{\tilde{\eta }}_i}^K\right)$ and ${\tilde{\mathit{v}}}_{\mathit{i}}=\left({{\tilde{v}}_i}^1,{{\tilde{v}}_i}^2,\cdots ,{{\tilde{v}}_i}^K\right)$ are predicted scores of being checked, abnormality, transition and predicted values for all lab tests at timestamp $t_i$.

Figure 2:

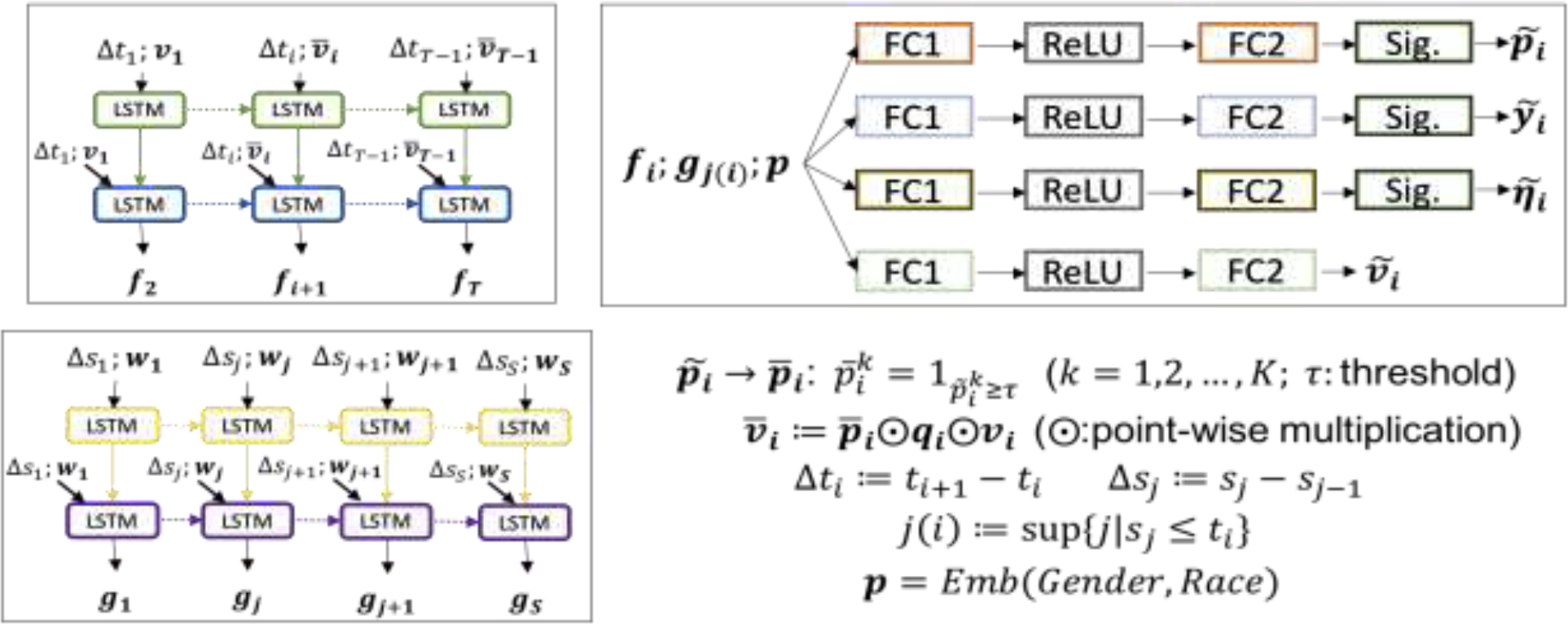
Model testing pipeline: the pipeline of applying on-time our trained model in the testing session. In contrast to the retrospective training pipeline, the testing pipeline implements a real-time prediction by using a reduction policy. Given a threshold $\tau$, the predicted necessity of checking lab tests at the next timestamp is translated into checking (1) or reducing (0). Then, the values of lab tests to be cut would be missing in the future prediction. ${\stackrel{-}{\mathit{p}}}_{\mathit{i}}=\left({{\bar{p}}_i}^1,{{\bar{p}}_i}^2,\cdots ,{{\bar{p}}_i}^K\right)$ is a reduction strategy, i.e., checking vs. reducing, on the lab tests at $i$-th time step. ${\stackrel{-}{\mathit{v}}}_{\mathit{i}}=\left({\bar{v}}_i,{{\bar{v}}_i}^2,\cdots ,{{\bar{v}}_i}^K\right)$ is the observed value at $i$-th time step after reduction.

We devised a loss function to implement the idea that the laboratory tests with less predictable properties had a greater need to be checked due to their unpredictability. The loss function of one sample was defined as follows where Table 2 is a nomenclature table:

$$\begin{gathered} loss=-\sum _{i>1,k}\left(q_i^{k}log\left(1-{\tilde{p}}_i^k\right)\right)/\sum _{i>1,k}{q}_i^k \\ +\sum _{i>1,k}{q}_i^{k}log{\tilde{p}}_i^k\left(y_i^{k}log{\tilde{\mathrm{y}}}_i^k+\left(1-y_i^k\right)log\left(1-{\tilde{y}}_i^k\right)\right)/\sum _{i>1,k}{q}_i^k \\ +\sum _{i>1,k}{l}_i^{k}log{\tilde{p}}_i{}^k\left({\eta }_i^{k}log{\tilde{\eta }}_i^k+\left(1-{\eta }_i^k\right)log\left(1-{\tilde{\eta }}_i^k\right)\right)/\sum _{i>1,k}{l}_i^k \\ +\sum _{i>1,k}{q}_i^{k}log{\tilde{p}}_i^k{(\frac{{\tilde{v}}_i^k-v_i^k}{b_k-a_k})}^2\left(1-1_{v_i{}^k,{\tilde{v}}_i{}^k\in \left[a_k,b_k\right]}\right)/\sum _{i>1,k}{q}_i^k \end{gathered}$$

Table 2:

Nomenclature table - notations for the symbols in our loss functions

Symbols	Descriptions
${v_i}^k$	Value of the k-the lab testing at the i-the time step, where $k=\mathrm{1,2},\dots ,12$
$a_k,b_k$	The lower, the upper bounds of the normal range of the k-th lab testing
${q_i}^k$	Indicating whether ${v_i}^k$ is observed (1) or missing (0)
${l_i}^k$	Indicating whether the state of a transition is observed (1) or missing (0) from (i − 1)-th to i-th time step for the k-th lab testing
${y_i}^k$	Indicating whether the k-th lab testing at i-th time step is abnormal (1) or normal (0)
${{\eta }_i}^k$	Indicating whether there is a transition (1) or not (0) from (i − 1)-th to i-th time step for the k-th lab testing
${{\tilde{p}}_i}^k$	Predicted necessity (probability) of checking the k-th lab testing at the i-th time step
${{\tilde{v}}_i}^k$	The predicted value of the k-th lab testing at the i-th time step
${{\tilde{y}}_i}^k$	The predicted probability of the k-th lab testing at the i-th time step is abnormal
${{\tilde{\eta }}_i}^k$	The predicted probability of there is a transition from (i − 1)-th to i-th time step for the k-th lab testing

Three baseline models

We developed two greedy baseline models, which only considered the loss of near-future laboratory tests without considering global loss. These models predicted transitions using a moving window of inputs. The guiding principle of these baseline models was that a lab test with no transition imparted less information than the lab test with the transition. So, we made a lab test reduction criterion for two baseline models: a lab test with no transition might be omitted. However, because the models did not learn the full trajectory of laboratory tests, they were unable to handle missing values directly. The ad-hoc strategy here was to impute the missing values. Baseline model 1 (Baseline 1) used the predicted value, and baseline model 2 (Baseline 2) used the latest observed laboratory values to replace the missing values. As shown in Figure 3, the MLP module consisted of 4 fully-connected layers with the ReLU activation function. Baseline 1 used two MLP modules to predict the value and score of being a transition of lab tests at the next timestamp, while Baseline 2 used one MLP module to predict the score of transition. During the testing session, they all derived reduction policies by using a threshold on the probability of transition. We compared the performance of the baseline models against our model with only laboratory test data as input on the prediction of transitions.

Figure 3:

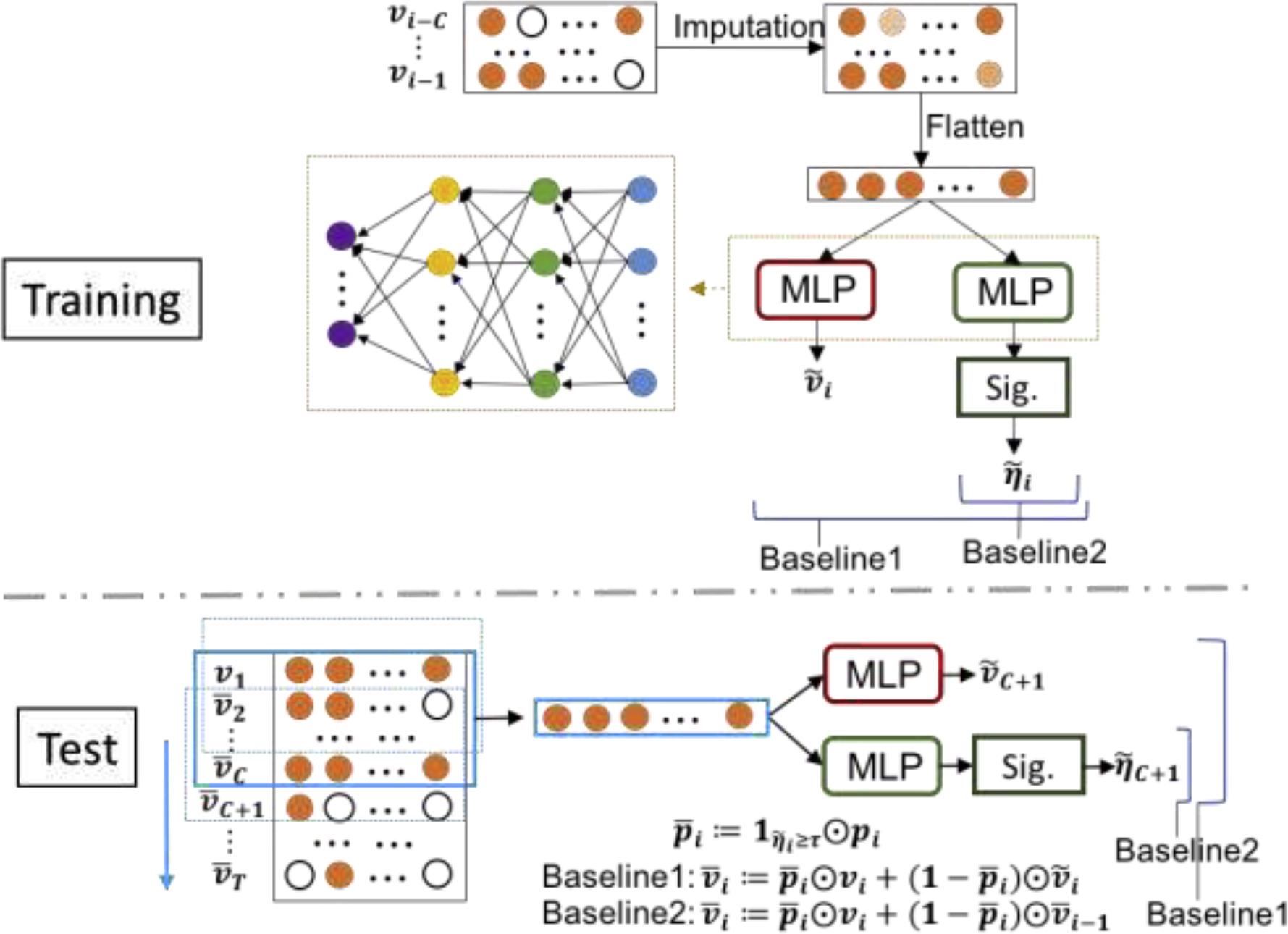
Pipeline of two greedy baseline models for training and testing sessions. ${\mathit{v}}_{\mathit{i}}=\left({v_i}^1,{v_i}^2,\cdots ,{v_i}^K\right)$. Two final outputs ${\tilde{\mathit{\eta }}}_{\mathit{i}}=\left({{\tilde{\eta }}_i}^1,{{\tilde{\eta }}_i}^2,\cdots ,{{\tilde{\eta }}_i}^K\right)$ and ${\tilde{\mathit{v}}}_{\mathit{i}}=\left({{\tilde{v}}_i}^1,{{\tilde{v}}_i}^2,\cdots ,{{\tilde{v}}_i}^K\right)$ are the predicted scores of being transition and the predicted values for all lab tests at the $i$-th time step. The term $C$ refers to the window size, and “Sig.” refers to the sigmoid activation function. The missing input data were imputed using the value of lab tests at the previous time step. During the test session. ${\stackrel{-}{\mathit{p}}}_{\mathit{i}}=\left({{\bar{p}}_i}^1,{{\bar{p}}_i}^2,\cdots ,{{\bar{p}}_i}^K\right)$ is the reduction strategy derived from the predicted score for transition and a given threshold $\tau$, i.e. checking vs reducing, for the lab tests at the $i$-th time step. Note that ${\stackrel{\mathit{‾}}{\mathit{v}}}_{\mathit{i}}=\left({{\bar{v}}_i}^1,{{\bar{v}}_i}^2,\cdots ,{{\bar{v}}_i}^K\right)$ is the real-time values considering reduction policy.

Our third baseline model was Yu’s model with a self-feeding structure (Self-feeding model) [31]. The model determined abnormality by comparing predicted values against the normal range for the lab tests. Since we conducted experiments on the MIMIC III for the same 12 lab tests, we compared the result of our best model with its best result for the evaluation of abnormality on the lab tests that were recommended to be omitted.

Experiments

We trained our models using different combinations of input data. We also trained a model without the corruption strategy in order to assess the value of adding a corruption strategy. An Adam optimizer with a 0.0001 learning rate was used for the training and optimization. Note that using a small value for the initial learning rate ensures that we do not miss the minimum in the beginning phase of gradient descent. We use the Adam algorithm (a built-in function of PyTorch, which automatically updates the learning rate) to optimize. Each model was trained for 2,000 epochs to ensure the converge of the algorithm, and the batch size was 128.

Variations on the recommended lab reduction strategy

In order to show the advantages of our reduction policy, two additional experiments were conducted:

Completely-random Reduction Policy:

We omitted laboratory tests randomly with a probability equal to a pre-determined proportion of lab test reduction, then applied our trained prediction model.

Partially Perturbed recommended Reduction Policy:

To evaluate the robustness of our recommended reduction policy, we conducted a partially perturbed recommended reduction experiment. Given a threshold to determine the necessity of checking laboratory tests, our model recommended a reduction policy. We perturbed the reduction policy in two ways: (1) flip each recommended omit/check decision (to check/omit) with a probability of 10%, and (2) flip each recommended omit (to check) with a probability of 10%. We applied our trained prediction model using these two perturbed policies to predict the normality/abnormality of lab tests. We compared their prediction accuracy against that from the unaltered reduction policy.

RESULTS

Performance comparison against different feature combinations and hyperparameters

First, we compared five variants of our model with different input feature combinations to determine which features contribute the most to the model’s accuracy. The corruption module contributed significantly, followed by time differences and demographics (Figure 4: a–d). The contribution of vital signs was marginal. The best performing model was the corrupted laboratory model with time difference and demographics, which correctly predicted 98.27% of normal/abnormal results, 98.48% of transition/non-transition among the laboratory tests recommended to be omitted where the reduction proportion was 20.26%. The model recommended 98.10% of transitions to be checked. The high proportion of transition recommended to be checked for our proposed model was consistent with the fact that the lab test as a transition was always less predictable than a non-transition. We computed the evaluation metrics of predicting abnormality and transition for 12 laboratory tests by the given threshold list for necessity (excerpt in Table 3, complete table in eTable2). The prediction performance on the training set and the hold-out set were consistent (see eFigure 2). Therefore the user could choose a threshold based on the result on the training set for a particular reduction proportion and prediction accuracy. We also analyzed the impact of two hyperparameters: learning rate (LR) and corruption probability (crpt) based on the best performing model (Lab + T + D). Figure 4e showed 5%, 15%, and 25% corruption probability had a similar performance, and the 0.0001 learning rate provided a better model optimization that the 0.005 learning rate. The performances of two models with 0% corruption probability (Lab, Lab + T + D) were worse compared to the version with the corruption strategy, as shown in Figure 4a and 4e. The corruption strategy, which provided a random situation with missing lab test values combining the devised loss function, forced the model to learn the optimal lab test reduction strategy under different amounts of information. The input of less information increased the uncertainty of future prediction resulting in less lab test reduction. The corruption strategy reduces the amount of information in the training process, forcing it to learn these missing values from the context, therefore, increase the robustness of the prediction performance.

Figure 4:

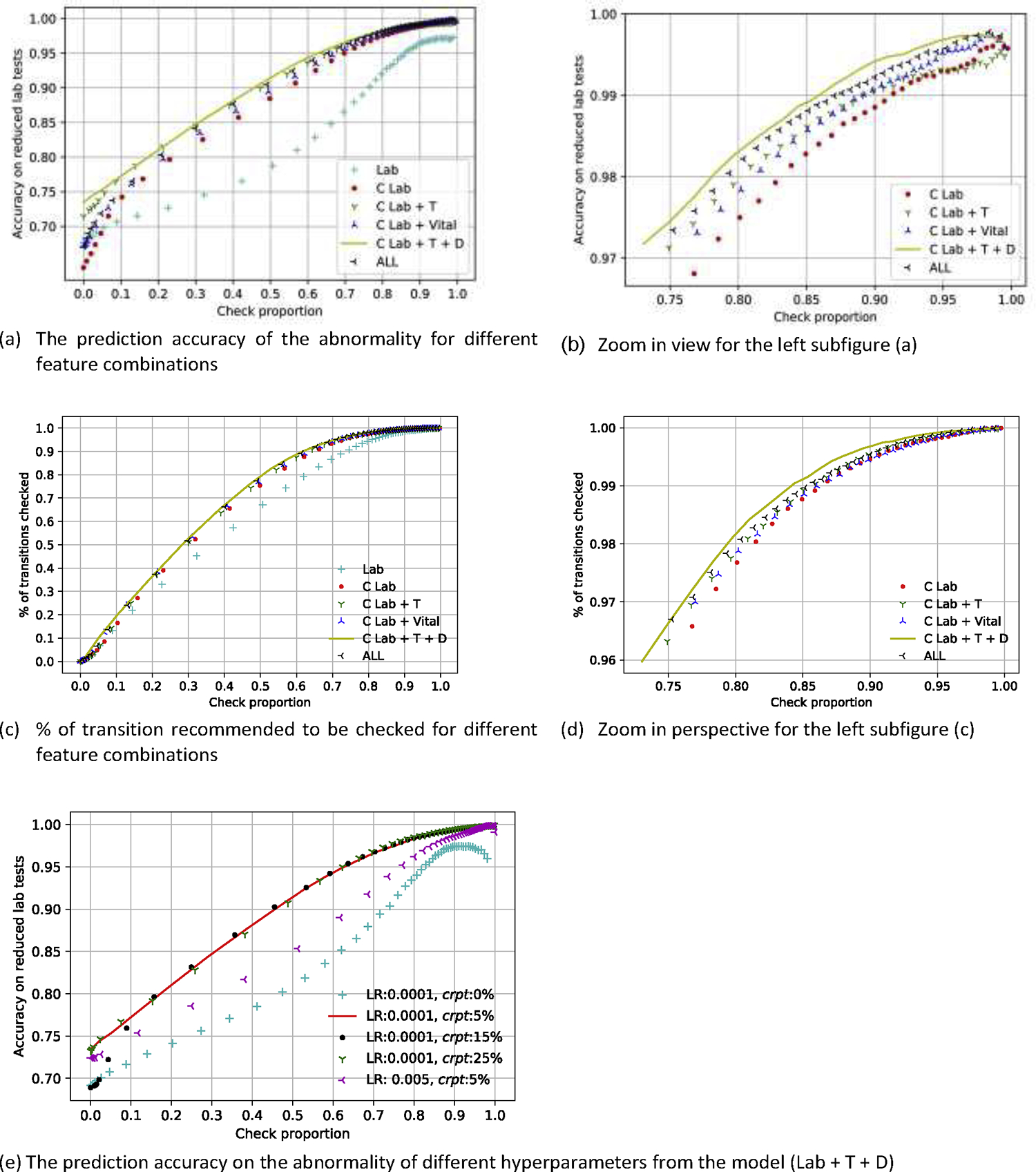
Accuracy of predicting abnormality on reduced lab tests and proportion of transition recommended to be checked vs. the proportion of checked laboratory tests for different feature combinations and hyperparameters of our proposed model. There are six different models in comparison. Lab: raw laboratory, C Lab: corrupted laboratory, C Lab + T: corrupted laboratory plus time, C Lab + Vital: corrupted laboratory plus vital data, C Lab + T + D: corrupted laboratory plus time and demographics, All: corrupted laboratory plus time, vital and demographics, LR: learning rate, crpt: corruption probability.

Table 3:

Evaluation metrics for 12 laboratory tests of predicting of abnormality of the reduced laboratory tests for 5%, 10%, 15%, 20%, 25%, 30% and 50% reduction proportions from the best model. eTable 2 is the complete version of the evaluation metrics table for all given thresholds. Abbreviations: prop., proportion; AUC, area under the receiver operating characteristic curve; Acc., accuracy; Prev., prevalence; NPV, negative predictive value; PPV, positive predictive value; Sens, sensitivity; Spec, specificity.

Reduction policy				Performance on transition		Performance of predicting abnormality on reduced lab tests
Threshold for reduction	Reduced Vol	Reduce Prop. (%)	Check Prop. (%)	% of transition checked	Acc. on reduced lab tests (%)	AUC	Acc. (%)	Prev. (%)	NPV (%)	PPV (%)	Sens (%)	Spec (%)
0.20	43351	5.26	94.74	99.91	99.71	0.9953	99.67	81.85	99.25	99.77	99.83	98.96
0.36	86441	10.50	89.50	99.65	99.45	0.9952	99.38	69.28	98.88	99.60	99.50	99.10
0.46	120750	14.66	85.34	99.15	99.61	0.9928	98.94	62.24	98.26	99.35	98.94	98.94
0.56	166867	20.26	79.74	98.10	98.48	0.9885	98.27	55.12	97.39	99.01	97.84	98.80
0.62	206092	25.03	74.97	96.63	97.82	0.9830	97.45	50.93	96.40	98.50	96.46	98.48
0.66	239628	29.10	70.90	95.22	97.35	0.9779	96.79	48.02	95.64	98.12	95.14	98.31
0.76	387821	47.10	52.90	82.58	94.11	0.9447	92.36	41.68	90.82	94.88	86.33	96.67

Performance comparison against baseline models

Our proposed model (C Lab) outperformed both greedy baseline models when more than 40% of the laboratory tests were checked (Figure 5), and our best result from the proposed model (C Lab+T+D) was better than the Self-feeding model in predicting abnormality of the reduced lab tests (Figure 6). Of note, the Self-feeding model derives the abnormality of a lab test indirectly by using the predicted lab test values, and it was difficult to determine accurately the abnormality of the lab tests whose values were at the extremes of the normal range because little bias of their predicted value might lead to an incorrect prediction of abnormality. Our proposed model treated the prediction on the abnormality as a classification task (normal or abnormal), which was one reason why our work was much better than the self-feeding model on the prediction on the abnormality.

Figure 5:

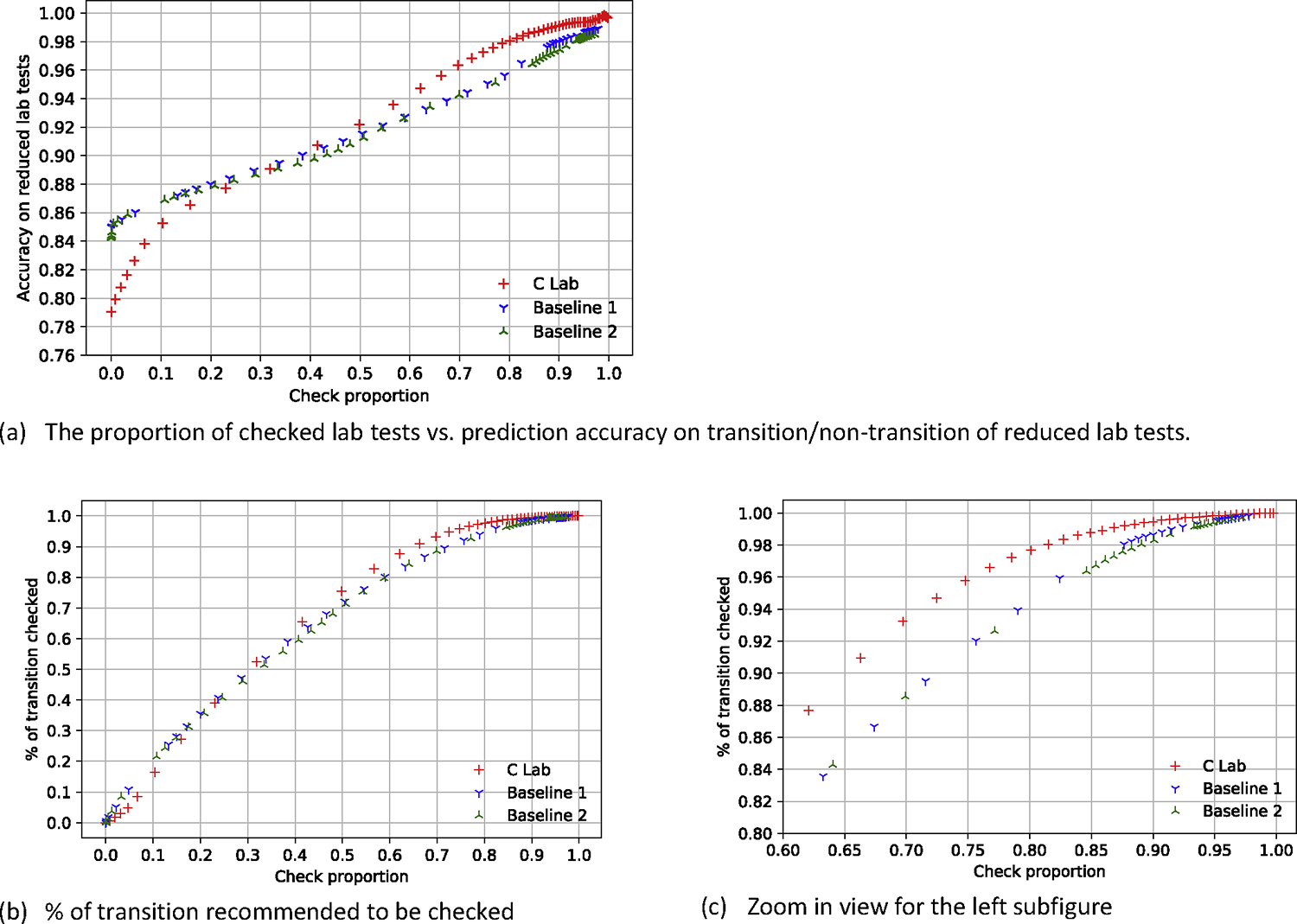
Model performance with different proportions of lab tests that were checked against two greedy baseline models. C lab stands for the corruption strategy using only laboratory test data.

Figure 6:

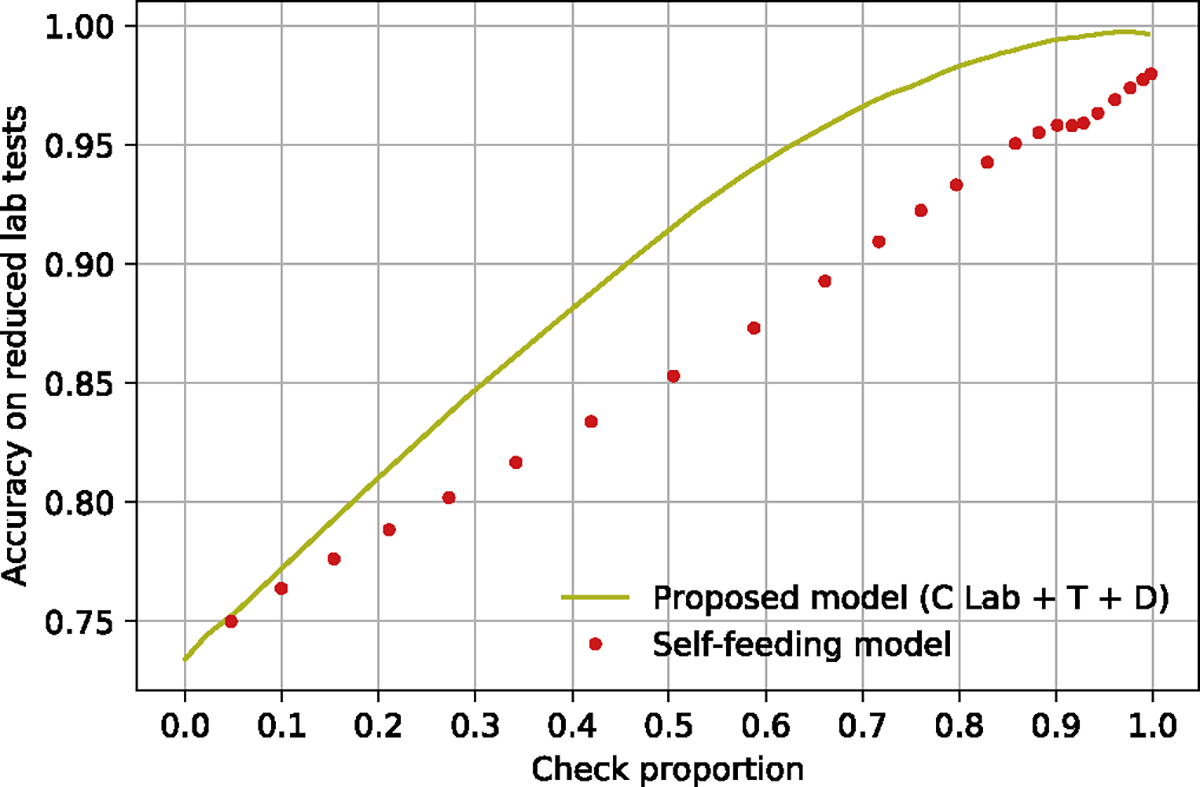
Result comparison between our proposed model with the baseline model (Self-feeding model) on the accuracy of abnormality on the reduced lab tests. C Lab + T + D: corrupted laboratory plus time and demographics.

Recommended reduction strategies vs. completely-random policy vs. partially perturbed policies

We compared the efficacy of the recommended policy against two alternative approaches: (1) completely-random laboratory reduction, (2) partially perturbed reduction policies. As illustrated in Figure 7, our model significantly outperforms the random strategy. Figure 7(b) shows that even randomly adding more than 10% of laboratory tests back does not improve performance, but randomly omitting a few of the laboratory tests that were recommended to be checked eroded the prediction performance (see the curve of Intervention 1). These experiments showed that the lab test reduction strategy from our method was near-optimal.

Figure 7:

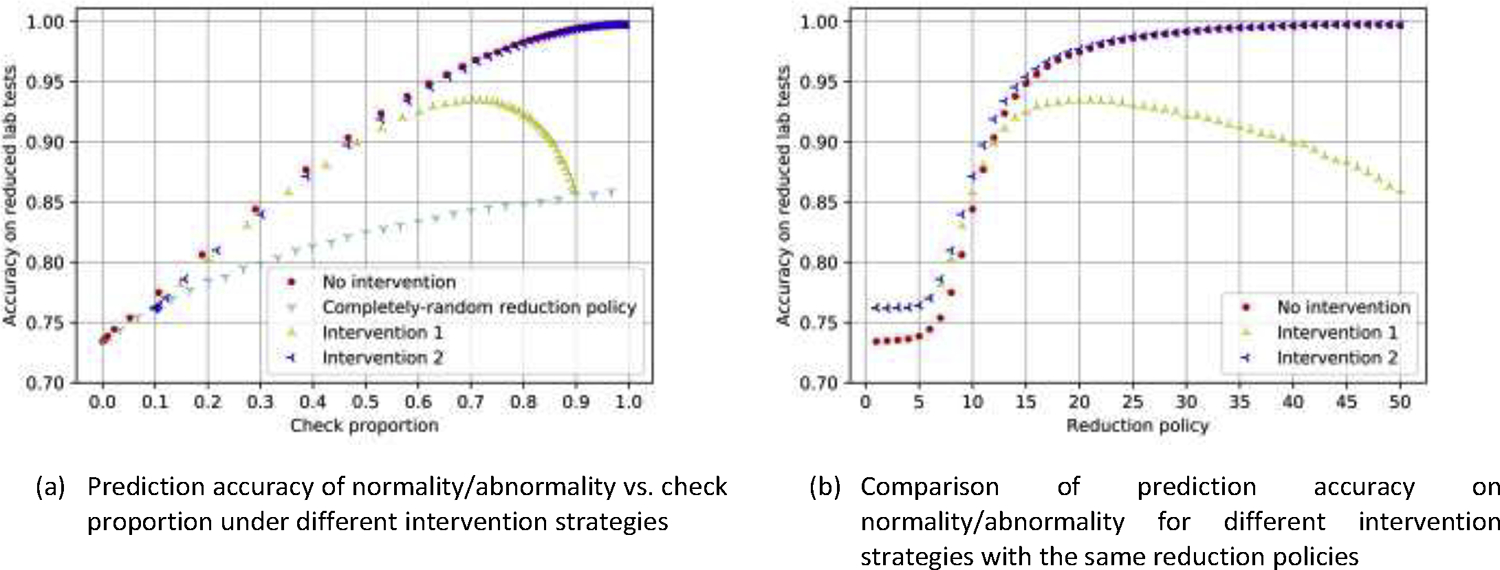
Prediction accuracy on reduced laboratory tests (abnormality) using different strategies. No intervention stands for the original reduction policy from our model; Intervention 1: randomly reverses the action of each lab test from checked to omitted, or omitted to check, with a probability of 10%; Intervention 2: randomly reverses each lab test that was recommended to be reduced by our model and checks it instead, with a probability of 10%. The reduction policy on the right subfigure corresponds to the 50 reduction models, which are induced by different cutoff thresholds.

Other experiments and detailed results

We compared model performance on the training set and the hold-out set (supplement eFigure 1–2). The dataset descriptions, detailed results of experiments in this section, and the normal ranges are also in the supplement (eFigure 3–5, eTable 1–5.).

DISCUSSION

We described a deep learning model to solve the lab test reduction problem based on the idea that a laboratory test that could be accurately predicted might be omitted. The key insights (inspired by the clinical observations that some lab values remain stable for certain patients) contributed to model design. We introduced a novel corruption strategy that significantly improved model performance and devised a new loss function to guarantee the idea. Our study provided a lab test reduction strategy and predictions of the lab tests whose values were unknown because of reduction, and our model could successfully omit 20% of lab tests while maintaining 98% accuracy of abnormality predictions of the omitted tests. We leveraged laboratory test values and multiple additional data features, including demographics, vital signs, and time differences between laboratory tests, the model performances for different feature combinations showed little difference (accuracy difference < 0.7%). By analyzing the impact of hyperparameters of the model, we demonstrated the learning rate affected the convergence of the model, and the corruption probability for the corruption strategy could be chosen in a wide range (0.05~0.25). Our model performed better than all three baseline models. For our model, the accuracy of the prediction improves as the proportion of measured labs grow, but this trend is no longer stable when the proportion of measured tests is large, exceeding >97%. This is due to the smaller denominator (i.e., the number of the omitted tests), in which case, each mistake has a larger effect on the error rate, even as the likelihood of error decreases (eTable 3). Our main message is that drawing too much blood is also accompanied with increased risks of anemia, morbidity, etc. The model we produce here is to provide a tool for clinicians to consider the necessity of an extra blood draw when patients are seemingly stable (from previous observations).

In this study, we used an extremely conservative normal range (eTable 5) for the patients in ICU. Our normal range is based on healthy people rather than critically ill patients in the ICU. For the latter, critically abnormal ranges (suggested by ICU practitioners) are far more deranged and critical care specialists tolerated a wider range before a lab was deemed “critically abnormal”. The ranges that we use remained within a very safe normal range. In this case, even if the algorithm makes a mistake and reduces a lab test, it is unlikely that the omission will lead to devastating results, and there will be subsequent laboratory checks following the omitted lab. Also, we are not suggesting that our model should be used as an automatic decision-maker, but rather, a reference for the clinicians to use to make their own decisions. For different clinical scenarios, relevant cutoff threshold might be different from the normal range. Determining a universal threshold is difficult because the threshold will differ case by case. Since we chose conservative ranges for normal/abnormality, labs that we omit are not expected to have any effect on clinical care, unless for some reason, a clinician is trying to keep a lab to a tighter parameter than the accepted normal range. Clinicians will make the final decision to conduct the blood draw, and our model will dynamically adjust itself to provide conditioned estimates based on what has been observed/decided, which is a feature that previous models do not have.

Our trained method provided prediction on the reduced lab tests, based on the values of the observed lab tests, to compensate for the information loss for the users by providing the predicted values, abnormality, and transition. Experiments demonstrated using a completely-random reduction strategy resulted in poor accuracy of prediction. We also analyzed the impact of the variation of the lab test reduction strategy on the prediction of our model, and found checking the lab tests recommended to be omitted back would not hurt the performance of the model, in other words, it did not decrease the performance of the prediction on the future lab tests. On the contrary, omitting the lab tests recommended to be checked would decrease the accuracy of prediction. These results show that the lab test reduction strategy by our model is close to optimal, and suggest that the users have to follow the recommendation of reducing lab tests, but is free to check labs that were recommended to be omitted, when applying a lab test reduction strategy for high accuracy of prediction.

The three laboratory tests that were most commonly omitted were hemoglobin, platelet count, and magnesium. Hemoglobin and platelet counts are commonly obtained as part of the complete blood count, with hematocrit and WBC completing the panel. Therefore the recommended omission may or may not be applicable. Of note, magnesium is often ordered independently and maybe a good candidate for elimination. Again, our model was derived from an adult inpatient intensive care unit population, and the recommended strategies described above may or may not apply to another patient population. However, this general strategy may be replicated at another institution or patient population, and the model may be fine-tuned to the local data.

Our work has several limitations. First, we used data from a single-institution. Therefore, it is possible that the performance may decrease when the model is used on a different dataset. The model has not been customized to accommodate clinical needs by weighting type I and type II error differently, and we did not consider the importance of the weight of prediction tasks or lab tests. Also, there are known clinical associations between vital signs and laboratory tests – such as heart rate and hemoglobin – that were not explicitly modeled. However, these connections may have been established implicitly during the training phase. Adding these logical relationships may further improve performance. As mentioned above, considering the use of laboratory panels rather than individual tests is necessary for more practical analysis, and omitting a panel of labs may have a different impact on subsequent reduction recommendations and accuracy. Furthermore, we plan to include additional clinical information from the electronic health record, such as radiology results and transfusion information. It was not our intent for the algorithm to not eliminate all labs except for the clinically actionable ones. Indeed, the algorithm will have clinicians check labs that they will not do anything about. For example, a clinician using the algorithm may follow a decreasing hemoglobin trend, without intervening, until the hemoglobin reaches another threshold to be determined by the clinician. In this instance, the algorithm adds information by predicting the rate of decrease or indicating a steady state before the lab is drawn.

Our work shows a medical informatics effort to conduct a proof of concept for unnecessary lab test reduction before we translate it to real clinical settings. We applied our algorithms to the MIMIC III database, which allows other researchers to obtain and reproduce the study. We are planning to employ our algorithm in other clinical settings, with the plan to adjust the algorithm according to the particular scenario.

CONCLUSION

We demonstrated a novel machine-learning lab test reduction recommendation model that helps physicians choose whether or not to conduct each laboratory test and provide them the predicted properties (values, normal/abnormal) of the lab tests recommended to be omitted with high accuracy. And the operation of checking the lab tests recommended to be reduced back by our model would not hurt the model performance, and the physicians did not need to follow the recommendation for reducing. The model can assist throughout the hospital course by utilizing spatial-temporal correlations. Our model achieves 20.26% of reduction with a tiny prediction error of abnormality (<2% on the reduced labs) and recommended 98.10% of transitions to be checked.

Summary table.

What was already know on the topic

What this study added to our knowledge

1, A large volume of unnecessary laboratory tests for inpatients lead to increased costs, risk of iatrogenic anemia, and its concomitant morbidities. 2, Almost of prior studies predicted one-time future lab test values without account for long-term prediction results in a suboptimal reduction strategy

1. Different lab tests have different autocorrelations, and therefore, different error rates when predicted using previously observed lab tests. A dynamic long-term prediction model would account for the variabilities of autocorrelations of different lab tests to recommend near-optimal reduction strategies. 2. Lab reduction recommendation is not one-time decision support but a simulated policy that should accommodate changes in an online manner. Our model can adjust to expert’s decisions (i.e., reject certain lab test reduction recommendations) and suggest alternative lab test reduction strategies. 3. Our study provides a lab test reduction strategy and predictions of the lab tests whose values are unknown because of reduction, and our model could successfully omit 20% of lab tests while maintaining 98% accuracy of abnormality predictions of the omitted tests.

Highlights.

• Achieving >98% accuracy on the abnormality prediction on a nearly 20% recommended reduction of lab tests

• A joint consideration of the optimal reduction strategy with long-term prediction (rather than short-term prediction and greedy reduction strategy)

• Online adjustable model to accommodate expert decisions and change recommendations in a dynamic manner

• Lab reductions resulted in approximately $8 million (~$1,035/patient) in cost savings