Abstract
Due to their geometry and thermal physiology, hands are most vulnerable to cold weather injuries and loss of dexterity. Gloves are the most common for hand protection during exposure to extreme thermal and hazardous environments. Although glove microclimate properties such as area factor, air gap thickness, and contact area play a significant role in thermal protection, identifying local (at individual hand segments) glove microclimate properties is still a research gap. For the first time, the glove-microclimate properties for 16 hand segments at high spatial resolution were analyzed by employing state-of-the-art hand-held 3D scanner and post-processing techniques for different glove types. Our results clearly indicate that the glove area factor for distal phalanges is significantly higher (by 49.8 %) than that for other hand segments, which increases the heat transfer from distal phalanges. In contrast, average air gap thickness was relatively uniform across all hand segments. The glove type had a pronounced effect on glove microclimate properties, e.g., bulky and heavy cold weather protective gloves had a larger average air gap thickness and glove area factor. Regression models are also developed to estimate the glove microclimate properties from simple measurement (i.e., ease allowance). Overall, this study provides essential information for the design and development of protective gloves that can help improve safety, comfort, and dexterity. Methods and mathematical models developed in this study also contribute to facilitating extremity (e.g., hand) focused thermoregulation modeling, hazard simulation, injury prediction, ergonomic design, optimum performance (dexterity and tactility) along with thermal protection.
Keywords: Human hand, Area factor, Air gap thickness, Thermal insulation, Glove, 3D scanning
Graphical abstract

Highlights
-
•
Significant variation in area factor for the local hand segments was found.
-
•
Glove type and fit affects area factor, air gap thickness, and contact area.
-
•
Regression model for the predicting area factor and air gap thickness.
-
•
3D scanning method for the analysis of glove microclimate properties was developed.
1. Introduction
Millions of occupational workers suffer from hand injuries and illnesses that lead to significant healthcare burdens and lost productivity [[1], [2], [3], [4]]. Apart from ergonomic factors such as exposure to mechanical hazards and repetitive work tasks, environmental factors such as exposure to cold and wet conditions represent major contributors to hand injuries and illnesses [[5], [6], [7]]. Exposure to cold environments may cause cold injuries such as frostnip and frostbite [8] along with local peripheral cooling which adversely affects the physiological, biomechanical, and neurological functions of hands and fingers [8,9]. Reduced hand functionality may cause accidents and further hand injuries and illnesses [1,10]. However, many occupational workers simply cannot avoid working in cold and wet conditions, such as miners, construction workers, or poultry and warehouse workers having to work in indoor cold storage rooms. Protecting these workers from adverse environmental conditions is pivotal for maintaining their health and safety while allowing them to carry out their tasks. Furthermore, hands are anatomically and physiologically unique and play a critical role in human thermoregulation by acting as an excellent radiator, insulator, and evaporator of heat [11]. As per the cortical sensory representation, hands are very sensitive to thermal aspects and account for about 50 % of the body's overall sensitivity [12]. Although all extremities of the human body are vulnerable to cold exposure, hands are especially prone to cold weather injuries because of their unique anatomical characteristics and thermal physiology. Furthermore, cold exposure can lead to reduced blood flow, skin temperature, and increased viscosity of the synovial fluid, which all negatively affect the hand's dexterity, tactile sensitivity (touch perception), grip strength, and haptic feedback [8,9]. Maintaining hand dexterity is extremely important, as it is essential for most occupations such as industrial workers, military personnel, first responders, and astronauts. Gloves are the most common type of protection used to shield hands from extreme thermal and hazardous environments.
Generally, gloves' thermal protective performance is assessed through an evaluation of their overall thermal insulation, determined by the material and the air layer characteristics of the glove. This assessment typically involves the utilization of sweating hand thermal manikins and mathematical models like hand thermoregulation models [10,[12], [13], [14], [15], [16]]. The total thermal insulation of gloves can be divided into two components: (i) intrinsic thermal insulation and (ii) thermal insulation related to the boundary air layer. The boundary air layer thermal insulation is often measured using a bare (without clothing/glove) sweating hand thermal manikin, which cannot accurately represent the effect of the larger surface area of the glove (compared to bare hand) on heat transfer. This needs to be accounted for by a glove (clothing) area factor that is required as a correction both in experimental setups and in mathematical models [17]. The glove area factor is an important parameter in all commonly used and accepted thermal comfort models and standards [18,19]. Furthermore, the gloves' total thermal insulation is notably influenced by the low thermal conductivity of air and the moisture diffusion of water vapor in the surrounding air, which collectively impact thermal and evaporative resistance. Furthermore, the direct contact between skin and clothing has a significant effect on heat and mass transfer because the thermal conductivity of air and diffusion of water vapor in the air gap is a function of the thickness of the air layer [20]. The direct skin-to-fabric contact enhances conductive heat transfer and facilitates moisture wicking, directing sweat from the skin to the clothing surface. This process significantly influences both mass transfer and evaporation. As a result, the average air gap thickness and the extent of the contact area between the skin and fabric are pivotal factors in determining clothing thermal insulation. With the advancements in computing technology, mathematical models are increasingly employed for predicting and analyzing the thermal insulation of clothing and gloves [[21], [22], [23], [24], [25], [26], [27], [28], [29]]. These models offer intricate insights into diverse heat and mass transfer processes, providing essential information for the design, development, and enhancement of personal protective equipment (PPE) [[24], [25], [26]]. These mathematical models calculate the heat and mass transfer from human skin to the environment through PPE and require a range of input parameters such as temperature, relative humidity, wind speed, fabric properties (thermal and evaporative resistances), and clothing microclimate properties such as clothing area factor, air gap thickness, and contact area (between skin and fabric) [25]. Due to their significant impact on total thermal insulation and glove performance, glove microclimate properties are among the most important input parameters for mathematical models and are essential for analyzing experimental results. However, clothing/glove microclimate properties are often unknown, which represents a major obstacle to the development of mathematical models.
Various methods have been employed to characterize clothing microclimates, such as 3D scanning [15,[29], [30], [31], [32], [33], [34]], photographic techniques [35,36], and tracer gas dilution [[37], [38], [39]]. Havenith et al. [37] stated that for the analysis of microclimate volumes, the tracer gas method was cumbersome, laborious, and prone to errors compared to alternative methods such as 3D scanning or photography. The photographic technique, on the other hand, is often perceived as cumbersome and involves intricate laboratory procedures and obtained data lacks fine spatial resolution (local body segments). In contrast, due to its precision and reproducibility, the 3D scanning method has been extensively adopted in numerous studies for the quantitative evaluation of clothing microclimates [15,[29], [30], [31], [32], [33], [34]]. This approach enables an in-depth exploration of the impact of air gap thickness/microclimate volume and clothing area factor on clothing thermal insulation and thermal protective performance with high spatial resolution, facilitating more precise predictions related to human thermal comfort and burn injuries [15,22,[40], [41], [42]]. Furthermore, researchers have also delved into investigating various factors influencing clothing microclimates, including body posture, the presence of moisture, and gender (anatomy) [43]. Recently, the 3D scanning method has been employed to analyze the clothing microclimate of specific garment types (body segments) such as hip protective garments, hats, and seasonal clothing for infants [36,44,45]. However, the microclimate properties of clothing for human extremities such as hands and feet are still unknown. While ISO 9920:2007 (E) [17] provides a useful database regarding clothing area factors for various clothing ensembles, no data is available for gloves and individual hand segments. Existing empirical relations can be used to estimate the area factors for clothing ensembles based on thermal insulation measurements using thermal manikins [46,47], however, details of individual hand segments are not available. Although several studies analyzed the thermal and evaporative resistance of gloves [10,[12], [13], [14]], there are no existing empirical relations to link glove thermal insulation to glove microclimate properties. This knowledge poses a significant hindrance to both theoretical/experimental investigations into the dissipation of heat from hands to the environment when using protective gloves. Heat transfer from the hand varies considerably depending on the hand segment (e.g., distal phalanges, palm) [48] which makes it necessary to resolve the individual hand segments when conducting an analysis of clothing/glove microclimate properties. Although the 3D scanning method is highly accurate and reliable, it is also very time-consuming and expensive which makes it desirable to also create a database and regression model for estimating glove microclimate properties. In summary, it is important to determine the clothing microclimate properties of the hand-glove system due to its major contribution to overall thermoregulation and to ensure health, safety, and dexterity. However, the lack of even the most basic clothing microclimate data hinders the development of extremity-focused clothing (gloves, socks, and shoes) and thermoregulation models (hand and feet) as well as the design and development of personal protective equipment.
The aim of the study was to analyze glove microclimate properties such as glove (clothing) area factor, air gap thickness, and magnitude of contact area at a high spatial resolution (16 hand segments: palm, dorsal, distal, and proximal of all 5 fingers and middle phalanges of index, middle, ring, and little fingers) using a 3D scanning method. The proposed study will produce an important database of 3D scanned gloves, including a total of 22 firefighter glove types, 12 cold-weather protective gloves, 17 vibration-reducing (VR) gloves, and 14 light-duty work gloves of various sizes/fit level (S to XXXL), materials, weights, and designs. This database will form the basis for further statistical analyses to develop empirical regression models to estimate the glove area factor, air gap thickness, and magnitude of contact area to evaluate glove performance and optimize glove design for superior protection and dexterity. Knowledge of these glove microclimate properties and the resulting database is essential to evaluate glove performance with regard to thermal comfort and protection, maintaining dexterity and tactility, and preventing cold/burn injury at individual hand segments such as distal phalanges. Furthermore, the resulting glove microclimate data will facilitate the development/modification of standards for measuring and assessing glove properties such as fit and ergonomics. Our results may also lead to improved extremity-specific thermoregulation and clothing models as both require microclimate properties as one of their key inputs.
2. Methods
2.1. Hand manikin and gloves
For the measurement of glove thermal insulation and 3D scanning, a hand manikin (Thermetrics, Seattle, WA, USA) that represents the 50-percentile western male hand size with an open hand posture (human hand at rest) (Fig. 1a) [49] was scanned using the handheld 3D scanner (HandySCAN BLACK Elite, developed by Creaform, Levis, Canada). The hand manikin with open hand posture had sufficient space between fingers with an articulated thumb to allow easy donning and doffing of gloves (Fig. 1b).
Fig. 1.
Measurement location of circumference of (a) hand manikin and (b) hand manikin with glove.
For the glove microclimate analysis, gloves with a wide range of sizes (ease allowances (EA)/fit level), thicknesses, weights, fabric layers (single/multiple), and structures (Fig. 2) were analyzed. This included different types of commercially available gloves typically worn by various occupational groups such as firefighter gloves (n = 22), cold weather gloves (n = 12), vibration-reducing gloves (n = 17), and light-duty work gloves (n = 14). The material properties, thickness, and design vary depending on the glove type. For example, firefighter and cold weather gloves are bulky and thick for added thermal protection which makes them less dexterous, while light-duty work gloves are thin and provide the hand with more dexterity. The size and glove fit level were quantified as the ease allowance, defined as the difference between glove circumference and hand circumference measured at the base of the little finger's proximal phalanx. The circumference of the hand manikin is 174.1 mm. The resulting EA for each glove is reported in Fig. 2. The thickness and weight of the gloves were measured by thickness tester (Checkline, MTG-D-W, Electromatic Equipment Co., New York, NY, USA) and electronic scale in accordance with the ASTM D 1777-96 and ASTM D3776-96 standards, respectively [50,51]. The different sizes of gloves were analyzed on single-sized hand which will allow us to analyze the effect of EA on glove microclimate properties. The smaller EA results in tight-fitting gloves compared to larger EA, but EA itself does not imply which fit is a “good fit” or the ease of donning and doffing [52,53].
Fig. 2.
Details of the gloves used for the microclimate analysis (EA = ease allowance).
The thermal insulation of gloves was measured using hand thermal manikin, which consisted of the eight zones (four fingers, thumb, dorsal, palm, and wrist). The hand thermal manikin also consisted of a guard zone adjacent to the wrist to eliminate/minimize heat leakage and improve the accuracy of measurements. Each zone has evenly distributed heating elements (for homogeneous temperature distribution) and temperature sensors; which control the temperature/heat flux of each zone independently. The thermal insulation of each glove (Fig. 2) was measured according to ASTM F1291 standard [49]. The skin temperature of the hand thermal manikin was set at 35 °C, ambient temperature was at 23 °C, relative humidity was 50 %, and wind speed was at 0.4 m/s. The heat flux from each zone was measured and the thermal insulation of gloves were measured as expressed in Eqs. (1), (2), (3).
| (1) |
| (2) |
| (3) |
Where, is total thermal resistance of the glove , is surface(skin) temperature of thermal manikin , is air temperature , is heat flux from hand thermal manikin (when it is covered with glove) , is air thermal resistance of nude (without glove) hand thermal manikin , is heat flux from nude hand thermal manikin , is intrinsic thermal resistance of glove , is glove area factor ().
2.2. 3D scanning and post-processing
The handheld 3D scanner was used to digitize the surface geometry of the hand manikin and gloves. The handheld 3D scanner projects quadrilateral blue laser lines onto an object and measures the surface geometry using two cameras. Stickers are placed on the surface of the hand manikin and glove that serve as reference points that allow calculation of the relative position between the handheld scanner and hand manikin. For object sizes ranging from 50 mm to 4 m, the surface is represented by a mesh with a grid size of 0.1 mm, which ensures high spatial resolution of the 3D scanned object. Several studies have shown that this method yields an accurate, reliable, and repeatable digital representation of 3D objects [30,31]. The glove dressing protocol consists of a gentle downward pull of the glove at the wrist to ensure that the glove is properly dressed on the hand manikin. To determine the reproducibility and resolution of the present 3D scanning approach, a glove from each category was scanned three times. As the distribution of air gaps was variable between scans and depended on the draping of gloves on the hand manikin, variation of air gaps between scans was measured to determine the reproducibility. The reproducibility of the 3D scanning method was very good with an average deviation of 0.3 mm (less than 2.5 %), which is in line with the previous 3D scanning approaches [31,43,54].
As a first step, we scanned the bare manikin hand which serves as the reference object; then, the hand manikin fitted with a glove was scanned which acts as a test object (Fig. 3). The 3D scans were saved as stereolithography images (.STL file format) for post-processing using a Geomagic Wrap 2021 (3D Systems, USA). Post-processing included a series of operations such as removing redundant texture, filling voids (portions of the manikin/glove surface that were not captured during the 3D scanning), and defining the hand segments. Then, the 3D scans of the reference object (scan of bare thermal manikin) and test object (scan of the gloves) were aligned and superimposed. To generate the subdivision of the hand into 16 hand segments for a more realistic representation of the hand and its skeletal anatomy and geometry (Fig. 3). The division of the digitized hand and glove geometry was performed by cutting the scan through planes and splines.
Fig. 3.
3D scanning and post-processing to analyze the glove microclimate.
The quantitative analysis of the glove microclimate was performed as follows.
-
●
The surface area of the gloved and bare manikin hand was calculated using the inbuilt function of the post-processing software. Then, the glove area factor () was calculated as the ratio of the gloved and bare hand surface areas as expressed in Eq. (4) [55]:
| (4) |
where, is glove area factor (−), is the outer surface area of the glove (), and is the surface area of the bare hand ()
-
●
The 3D scan of the gloved hand manikin (test object) captures the glove surface, displaced away from the surface of the bare hand manikin (reference object). This displacement is due to an entrapped air layer and the thickness of the glove itself. Therefore, the air layer thickness can be obtained by subtracting the thickness of the glove material and the resolution of the 3D scanner from the total displacement. The average distance (air layer thickness) between the surface of each segment of bare hand manikin to the inner surface of the glove was determined. The percentage of the glove inner surface area that is in contact with the manikin surface is quantified as expressed in Eq. (5) [29]:
| (5) |
where, is the inner surface area of the glove that is in contact with the skin () and is the total surface area of bare hand segment ()
2.3. Statistical analysis
The glove microclimate properties, namely glove area factor, air gap thickness, and contact area were analyzed for each hand segment and glove type. A linear regression analysis was performed to develop the predictive model of the glove microclimate properties. The strength and direction of linear regression was quantified using the Pearson correlation. In linear regression, glove area factor, average air gap thickness, and contact area were considered the dependent variables and ease allowance was the independent variable. Data was analyzed using one-way analysis of variance (ANOVA) in MS Excel 2016. The accuracy of the regression model was quantified based on the root mean square error as expressed in Eqs. (6), (7):
| (6) |
| (7) |
where, and are the measured values, and are the estimated value, is the predicted value, and n is the number of observations.
3. Results and discussion
The glove microclimate properties (glove area factor, average air-gap thickness, and contact area) were quantified and analyzed for 16 hand segments and 67 different (for various occupational glove types and sizes) gloves using an advanced 3D scanning method. This is the first time the glove microclimate properties for the hand segments were evaluated quantitatively along with regression models to estimate glove microclimate properties for any glove type and glove fit. The variation of glove microclimate properties over various hand segments were analyzed and its effect on thermal protective performance of gloves was discussed. To achieve high spatial resolution, the hand was divided into 16 segments that represent the details of skeletal anatomy and geometry: distal phalanges of four fingers and thumb, middle phalanges of four fingers, proximal phalanges of four fingers and thumb, palm, and dorsal. Based on the database of measured glove microclimate properties, an empirical regression model was developed that can estimate the glove microclimate properties based on easy-to-measure independent parameters (ease allowance).
3.1. Glove microclimate for different hand segments
The variation of glove area factor, average air gap thickness, and contact area for different types of gloves and hand segments were analyzed and the results are presented separately for each glove type (firefighter, cold weather, vibration-reducing, and light duty work glove) (Fig. 4, Fig. 5, Fig. 6).
Fig. 4.
Glove area factor for different hand segments (error bars represent the standard deviation of data in any given group of gloves).
Fig. 5.
(a) Average air gap thickness over different hand segments (error bars represent the standard deviation of data in any given group of gloves) and (b) relation between average air gap thickness and intrinsic thermal insulation; (R2 = coefficient of determination, r = Pearson correlation, p = statistical significance. Statistical significant correlation is shown at p < 0.05).
Fig. 6.
Magnitude of contact area over different hand segments (error bars represent the standard deviation of data in any given group of gloves).
3.1.1. Glove area factor
As presented in Fig. 4, the glove area factor varies significantly between hand segments. On average, distal phalanges have a 49.8 % larger glove area factor compared to the other hand segments, although this value varies for different fingers. The distal phalanx of the little finger has the largest glove area factor (67.4 %) followed by the thumb (50.8 %), index (49.1 %), middle (41.4 %), and ring (40.0 %) finger compared to the average value of the hand. This indicates that the distal phalanx of the little finger will experience the highest heat transfer amongst the entire hand and potentially be more vulnerable to cold weather injury and loss of dexterity (if air gap thickness and material are evenly distributed across all hand segments).
As different glove types have different designs this also affects the glove area factor (Fig. 4). The gloves were grouped into four segments namely Firefighter gloves, Cold weather gloves, Vibration-reducing gloves, and Light duty work gloves. Each group consisted of several gloves (Fig. 2) varying in size, design, and material. Cold weather gloves have the highest glove area factor, mostly due to their bulkiness and thickness, followed by firefighter, vibration-reducing, and lastly light duty working gloves. The average glove area factors of distal phalanges were 2.14 (SD ± 0.40) (firefighter gloves), 2.46 (SD ± 0.49) (cold weather gloves), 1.80 (SD ± 0.25) (vibration-reducing gloves), and 1.26 (SD ± 0.18) (light duty work gloves), which is respectively 57.9 %, 73.11 %, 44.9 %, and 15.0 % higher than for the entire hand. ISO 9920:2007 [17] provides a useful database regarding clothing area factors for various clothing ensembles, however, no specific data is available for gloves and individual hand segments. The observed values of gloved area factor for the distal phalanges are considerably higher than the clothing area factors reported for the whole body and different clothing ensembles in ISO 9920:2007 [17].
Heat transfer between the hand's skin surface and the environment is affected by the thermal insulation of the air gap between skin and glove, of the material/glove layer, and of the boundary air layer. The thermal insulation of a glove can thus be divided into two components. First, the thermal insulation from the skin surface to the outer glove surface which includes the air gap and material/glove layer is known as intrinsic/basic thermal insulation [17]. Second, the thermal insulation provided by the air layer around the glove surface is known as boundary air layer insulation. Both components (Intrinsic and boundary air layer) of thermal insulation cannot simply be added to obtain the total thermal insulation due to the difference in surface areas of the hand skin and glove. The larger surface area of the gloved hand compared to the bare hand increases the heat transfer from the glove's surface to the environment, thus, reducing the thermal insulative effect. The higher heat transfer from distal phalanges compared to other hand segments indicates that it is more vulnerable to cold weather injuries. The existing assumption that the average glove area factor is evenly distributed over the entire hand can lead to misleading results and potentially put the individual wearer at risk.
3.1.2. Average air gap thickness and contact area
The variation in average air gap thickness between hand segments for any given glove was minimal (on average below ±2.5 %). Similarly, the variation in contact area distribution over hand segments was minimal between different hand segments (on average below ±4 %) except for the palm, where average contact area was lower due to the complex anatomical shape of the palm caused by the thenar and hypothenar muscles of the hand, especially for vibration reducing and light duty work gloves (Fig. 6).
As shown in Fig. 5a and b, the average air gap thickness and contact area varies considerably based on glove type. Cold-weather protective gloves have the largest air gap followed by firefighter, vibration-reducing, and light-duty work gloves. As the contact area is inversely related to the air gap thickness, the light-duty work gloves had the largest contact area followed by vibration-reducing, firefighter, and cold weather protective gloves (Fig. 6). As vibration-reducing gloves are focused on attenuating vibrations mostly in the palm region with damping material [56], the average air gap thickness and contact area in the palm were 55.4 % higher, and 41.7 % lower than the average value of the rest of the hand segments, respectively.
Several studies have analyzed the effect of air gap thickness (garment fit) and contact area on clothing thermal insulation [25,57]. The average air gap thickness has a significant impact on the intrinsic glove thermal insulation as the thermal conductivity of air is low. As shown in Fig. 5b, the intrinsic glove thermal insulation increases with increasing air layer thickness until natural convection occurs [25]. Higher values of coefficient of determination (R2: above 0.86) and Pearson correlation (r: 0.93) indicates the better fit of model, stronger linear relationship between average air gap thickness and glove thermal insulation. A low p-value (p < 0.05) indicates statistical significance i.e., intrinsic thermal insulation of glove is significantly associated with the average air gap thickness. Similarly, direct contact between the hand skin surface and glove surface eliminates the air gap between skin and glove (or results in lower average air gap thickness) resulting in high conductive heat transfer that depends on the glove material properties. As reported by Mert et al. [58], the thermal insulation of clothing decreases sharply if the contact area between skin and fabric exceeds 42 %, which also affects mass transfer and evaporative cooling [57]. For most firefighter and cold weather protective gloves the average contact area was below 42 %. However, light-duty work gloves and vibration-reducing gloves had contact areas above 42 % for all hand segments, irrespective of glove size, which indicates lower thermal insulation by air gap r due to predominant conductive heat transfer. Both these glove types focus on maintaining high levels of dexterity and tactile sensitivity (touch perception) to facilitate a good glove fit that allows the safe and efficient handling of objects. Since both dexterity and tactile sensitivity are negatively affected by a low contact area/large air gap thickness, light-duty work gloves do not possess adequate thermal insulation [59]. In contrast, cold weather gloves are designed to provide maximum thermal protection while dexterity/tactility are of secondary importance, which is why these gloves have a larger average air gap thickness/lower contact area.
The 3D scanned data of glove microclimate properties with high spatial resolution of the hand segment are useful for analyzing the intrinsic and boundary air layer thermal insulation characteristics. The most advanced, commonly used sweating hand thermal manikin (Thermetrics) has 7 hand segments (five fingers, palm, and dorsal) along with segments for the forearm and guard zone (to minimize heat loss and improve the accuracy of thermal manikin). However, this type of manikin cannot provide any information regarding the individual finger segments (distal, middle, and proximal phalanges) which makes it difficult to analyze the heat dissipation from these segments. The findings from the present study indicate that the intrinsic thermal insulation is evenly distributed over the entire finger as variations in air gap thickness and contact area are negligible (0.7 mm and 9.4 %). However, to calculate the total thermal insulation for individual hand segments the variation in glove area factor must be taken into account as it varies significantly (more than 26.2 %) between different phalanges of the same finger, with particularly high values at the distal phalanges. As a result, the computed intrinsic thermal insulation (Fig. 5b) shows a linear correlation with the average air gap thickness. Thus, the data from this study will help with the interpretation of experimental results and the development of mathematical models.
One of the main advantages of the 3D scanning approach is that it can provide high-resolution quantitative information of the air gap thickness and contact area for different glove types (Fig. 7a to 6d). The visualizations will allow researchers to identify the locations (based on air gap thickness/contact area) where natural convection, conduction, and moisture wicking can occur, thus facilitating improved glove designs and accurate placement of sensors for smart gloves. The major advantage of 3D scanning over other methods (tracer gas, vacuum suit, and photographic method) is that it is easy to use and delivers high spatial resolution data with good accuracy. Though the 3D scanning method is easy to deploy and straightforward to use, it is expensive and time-consuming, therefore, a regression model that can estimate the glove microclimate properties based on easy-to-measure input parameters is highly desirable.
Fig. 7.
Visualizations of air gap thickness for different glove types: (a) light-duty work glove, (b) vibration-reducing glove, (c) firefighter glove, and (d) cold weather glove.
3.2. Regression model for predicting glove microclimate properties
Empirical equations provide a simple and efficient method for estimating clothing microclimate properties based on input parameters like weight or ease allowance (size) that are easy to measure. Several researchers have emphasized that ease allowance affects clothing microclimate properties and thermal insulation [42,60,61]. However, the details of glove microclimate properties were not available till date, due to this there are no empirical equations that can estimate the glove microclimate properties. Therefore, based on 3D scanning data and regression analysis we have developed empirical equations that can accurately predict the glove microclimate properties from the glove's ease allowance. As the weight of gloves varies depending on fabric material and its density, the ease allowance of gloves were selected as input variables to estimate the glove microclimate properties.
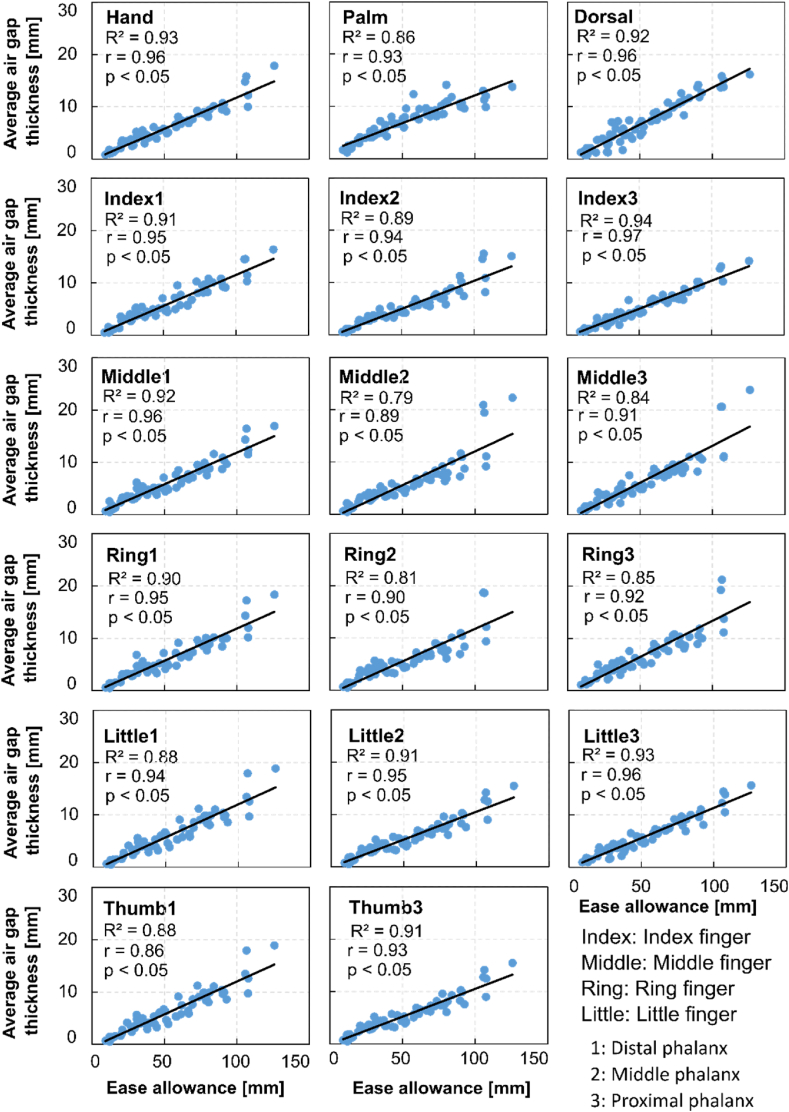
Fig. 8, Fig. 9 represents the glove area factor and air gap thickness of 16 different hand segments as a function of ease allowance of gloves (measured at the base of the little finger's proximal phalanx, shown in Fig. 1b). Linear correlation was observed between glove area factor and ease allowance for the most hand segments (except middle and proximal phalanx of ring and middle fingers) with Pearson correlation (r) above 0.75, which indicates the glove area factor linearly increased with ease allowance. For middle and proximal phalanx of ring and middle fingers, the correlation was inversely correlated with Pearson correlation (r) ranging between −0.19 and −0.47. The glove area factor of the middle phalanges and proximal phalanges of the middle and ring fingers do not show any significant change with increasing ease allowance (Fig. 8). Average air gap thickness also linearly increased with increasing ease allowance with strong linear Pearson correlation (r > 0.86) for all hand segments (Fig. 9). A low p-value (p < 0.05) indicates statistical significance i.e., glove area factor and average air gap thickness are significantly associated with the ease allowance of glove. The glove microclimate properties can thus be calculated using a simple linear polynomial.
| (8) |
where Y is the dependent variable (glove area factor, average/air gap thickness), X is the independent variable (ease allowance: as measured at the base of the little finger's proximal phalanx), a is the slope (see Table 1), and b the intercept (see Table 1).
Fig. 8.
The glove area factor as a function of ease allowance for various hand segments; (R2 = coefficient of determination, r = Pearson correlation, p = statistical significance. Statistical significant correlation is shown at p < 0.05).
Fig. 9.
The average air gap thickness (glove microclimate) as a function of ease allowance for various hand segments; (R2 = coefficient of determination, r = Pearson correlation, p = statistical significance. Statistical significant correlation is shown at p < 0.05).
Table 1.
Coefficients from the linear regression analysis, RMSE, Pearson coefficient (r), and R2 for glove area factor and average air gap thickness.
| Hand segments | Glove area factor [−] |
Average air gap thickness [mm] |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope |
Intercept |
RMSE |
r |
R2 |
Slope |
Intercept |
RMSE |
r |
R2 |
||
| (a) | (b) | [−] | [−] | [−] | (a) | (b) | [mm] | [−] | [−] | ||
| Hand | 0.0048 | 1.0430 | 0.04 | 0.93 | 0.86 | 0.1193 | −0.1589 | 0.67 | 0.96 | 0.93 | |
| Palm | 0.0015 | 1.0062 | 0.03 | 0.75 | 0.56 | 0.1060 | 1.4948 | 0.91 | 0.93 | 0.86 | |
| Dorsal | 0.0037 | 1.0093 | 0.04 | 0.89 | 0.79 | 0.1406 | −0.4274 | 0.94 | 0.96 | 0.92 | |
| Index | Distal Phalanx | 0.0172 | 1.0320 | 0.17 | 0.93 | 0.86 | 0.1185 | −0.3119 | 0.89 | 0.95 | 0.91 |
| Middle Phalanx | 0.0041 | 1.0898 | 0.07 | 0.82 | 0.67 | 0.1077 | −0.4490 | 0.77 | 0.94 | 0.89 | |
| Proximal Phalanx | 0.0041 | 0.9922 | 0.04 | 0.90 | 0.82 | 0.1075 | −0.3312 | 0.60 | 0.97 | 0.94 | |
| Middle | Distal Phalanx | 0.0122 | 1.1888 | 0.17 | 0.86 | 0.73 | 0.1213 | −0.2336 | 0.83 | 0.96 | 0.92 |
| Middle Phalanx | −0.0016 | 1.2186 | 0.08 | −0.43 | 0.18 | 0.1291 | −0.8779 | 1.24 | 0.89 | 0.79 | |
| Proximal Phalanx | −0.0014 | 1.0559 | 0.06 | −0.47 | 0.23 | 0.1417 | −0.9995 | 1.19 | 0.91 | 0.84 | |
| Ring | Distal Phalanx | 0.0126 | 1.1483 | 0.16 | 0.88 | 0.78 | 0.1231 | −0.4153 | 0.86 | 0.95 | 0.90 |
| Middle Phalanx | −0.0007 | 1.2099 | 0.08 | −0.20 | 0.04 | 0.1242 | −0.6738 | 1.20 | 0.90 | 0.81 | |
| Proximal Phalanx | −0.0006 | 1.0565 | 0.07 | −0.19 | 0.03 | 0.1385 | −0.4914 | 1.18 | 0.92 | 0.85 | |
| Little | Distal Phalanx | 0.0236 | 0.9397 | 0.22 | 0.92 | 0.84 | 0.1256 | −0.5489 | 0.98 | 0.94 | 0.88 |
| Middle Phalanx | 0.0054 | 1.1642 | 0.09 | 0.81 | 0.66 | 0.1060 | −0.0927 | 0.78 | 0.95 | 0.91 | |
| Proximal Phalanx | 0.0060 | 0.9948 | 0.05 | 0.93 | 0.86 | 0.1150 | −0.1909 | 0.71 | 0.96 | 0.93 | |
| Thumb | Distal Phalanx | 0.0168 | 1.0731 | 0.21 | 0.89 | 0.79 | 0.1256 | −0.5489 | 1.36 | 0.86 | 0.88 |
| Proximal Phalanx | 0.0074 | 1.2181 | 0.10 | 0.88 | 0.77 | 0.1060 | −0.0927 | 0.87 | 0.93 | 0.91 | |
The summary of linear regression analysis is provided in Table 1 for individual hand segments. The Root Mean Squared Error (RMSE) was calculated as a measure of the accuracy of the regression model in predicting values compared to the actual measured values using 3D scanning. The RMSE for the predicted glove area factor ranges from 0.03 (at palm) to 0.21 (thumb tip), which indicates a much better accuracy of the present model compared to existing models for predicting clothing area factor [62]. The maximum RMSE of predicted average air gap thickness for hand segments is 1.36 mm at the thumb distal phalanx (with an average RMSE of 0.94 mm and SD of 0.2 mm), which indicates notably higher accuracy compared to existing models for clothing ensembles [42].
Traditionally, the focus of glove design was on material development, novel fabrics, and membranes are developed to maintain thermal balance and protect against extreme environments and injuries [10,63], while elements of glove microclimate properties (which is related to glove fit) such as area factor, microclimate volume/air gap thickness, contact area between skin and gloves were often neglected. The findings of the presented study will help to improve the glove design to provide better thermal protection while maintaining the highest possible dexterity/tactility. Results highlighted the larger variation of glove area factor across the hand segments and glove types. It also emphasizes the underlying need to consider the high spatial resolution of the hand segment especially at distal phalanges in predicting and preventing cold weather injuries to the hand. The anatomic shape, thermal physiology of the human body, and higher heat transfer at distal phalanges due to higher glove area factor which make distal phalanges most vulnerable to cold weather injuries. Thus, the glove microclimate properties affect ergonomics, dexterity, gripping force, thermal protection, and thermal comfort. Therefore, the outcomes of the present study will help in understanding the various components of glove thermal insulation and necessary inputs for the advanced modeling of heat dissipation through extremities (hands) and hand-specific thermoregulation models. Furthermore, the study will also provide essential data to optimize the glove sizes, thermal properties of the fabric, and identify the ideal locations for sensor placement in smart gloves.
4. Conclusion
This study provided the first quantitative analysis of glove microclimate properties, namely glove area factor, average air gap thickness, and contact area. The importance of glove microclimate properties on thermal protective performance and dexterity was discussed. The high spatial resolution of the hand segments (16 segments) were considered and a regression-based model was proposed to estimate the glove microclimate properties based on easy-to-measure input (ease allowance). The results revealed considerable variations in glove area factor, average air gap thickness, and contact area between different hand segments and glove types. The study highlighted that the glove area factor for distal phalanges was higher compared to other hand segments. Average air gap thickness and contact area were evenly distributed across most hand segments. From among the different glove types analyzed (firefighter, cold weather, vibration-reducing, and light duty work gloves), cold weather protective gloves had the highest glove area factor and average air gap thickness followed by firefighter, vibration-reducing, and light duty work gloves. On the contrary, the contact area was largest for the light-duty work gloves followed by the vibration-reducing, firefighters, and cold weather protective gloves. Moreover, the regression models developed in this study provide a valuable tool to estimate glove microclimate properties based on easy-to-measure parameters like ease allowance. This study provides essential information for the design and development of protective gloves to improve their safety, comfort, and dexterity while facilitating the development of mathematical models to investigate extremity (hand) focused thermoregulation model, hazard simulation (e.g., skin burn injury), clothing models, ergonomics, apparel design, wearable devices, heating/cooling gloves, optimum performance (dexterity and tactility) along with thermal protection.
Data availability statement
The data underlying this study will be made available upon request. Researchers interested in accessing the dataset may contact corresponding author Prof. Guowen Song at gwsong@iastate.edu to obtain the necessary information.
CRediT authorship contribution statement
Ankit Joshi: Writing - original draft, Software, Methodology, Conceptualization. Rui Li: Writing - review & editing, Software, Resources, Methodology, Data curation. Yulin Wu: Visualization, Software. Mengying Zhang: Writing - review & editing, Software, Data curation. Guowen Song: Writing - review & editing, Supervision, Funding acquisition, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
Acknowledgements
The work was supported by the Fire Prevention and Safety (FP&S) Research and Development (R&D) Grants from the U.S. Department of Homeland Security (DHS), Federal Emergency Management Agency (FEMA), project number EMW-2018-FP-00649. The authors gratefully acknowledge Ava Depping, Saloni Purandare, and Matthew Greiner from Iowa State University for their valuable time as lab assistant for the work on Geomagic Wrap 2021 (3D Systems, USA) software.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e23596.
Appendix A. Supplementary data
The following is/are the supplementary data to this article.
References
- 1.Heberger J.R., et al. The necessity for improved hand and finger protection in mining. Mining, Metallurgy & Exploration. 2022;39(2):507–520. doi: 10.1007/s42461-022-00557-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.BLS U.S. 2020. Number of Nonfatal Occupational Injuries and Illnesses Involving Days Away from Work by Industry and Selected Parts of Body Affected by Injury or Illness, Private Industry.https://www.bls.gov/iif/soii-data.htm 2019. Available from: [Google Scholar]
- 3.Johns A.M. Time off work after hand injury. Injury. 1981;12(5):417–424. doi: 10.1016/0020-1383(81)90015-2. [DOI] [PubMed] [Google Scholar]
- 4.Wong J.Y.P. Time off work in hand injury patients. J. Hand Surg. 2008;33(5):718–725. doi: 10.1016/j.jhsa.2008.01.015. [DOI] [PubMed] [Google Scholar]
- 5.OSHA . U.S. Department of Labor; 2013. Prevention of Musculoskeletal Injuries in Poultry Processing. [Google Scholar]
- 6.Parsons K. CRC press; Boca Raton: 2014. Human Thermal Environments: the Effects of Hot, Moderate, and Cold Environments on Human Health, Comfort, and Performance. [DOI] [Google Scholar]
- 7.National Research C., Institute D. Musculoskeletal Disorders and the Workplace: Low Back and Upper Extremities. 2001. National Academies Press (US) Copyright; Washington (DC): 2001. Of medicine panel on musculoskeletal, and W. The. by the National Academy of Sciences. All rights reserved. [PubMed] [Google Scholar]
- 8.Holewijn M., Heus R. Effects of temperature on electromyogram and muscle function. Eur. J. Appl. Physiol. Occup. Physiol. 1992;65(6):541–545. doi: 10.1007/BF00602362. [DOI] [PubMed] [Google Scholar]
- 9.Hunter J., Kerr E.H., Whillans M.G. The relation between joint stiffness upon exposure to cold and the characteristics of synovial fluid. Can. J. Med. Sci. 1952;30(5):367–377. doi: 10.1139/cjms52-047. [DOI] [PubMed] [Google Scholar]
- 10.Santee W.R., Potter A.W., Friedl K.E. Talk to the hand: us army biophysical testing. Mil. Med. 2017;182(7):e1702–e1705. doi: 10.7205/MILMED-D-16-00156. [DOI] [PubMed] [Google Scholar]
- 11.Taylor N.A.S., et al. Hands and feet: physiological insulators, radiators and evaporators. Eur. J. Appl. Physiol. 2014;114(10):2037–2060. doi: 10.1007/s00421-014-2940-8. [DOI] [PubMed] [Google Scholar]
- 12.Sari H., et al. Glove thermal insulation: local heat transfer measures and relevance. Eur. J. Appl. Physiol. 2004;92(6):702–705. doi: 10.1007/s00421-004-1136-z. [DOI] [PubMed] [Google Scholar]
- 13.Chen F., Nilsson H., Holmer I. Evaluation of hand and finger heat loss with a heated hand model. J. Physiol. Anthropol. 1999;18(4):135–140. doi: 10.2114/jpa.18.135. [DOI] [PubMed] [Google Scholar]
- 14.Hummel A., et al. Development of instrumented manikin hands for characterizing the thermal protective performance of gloves in flash fire exposures. Fire Technol. 2011;47(3):615–629. doi: 10.1007/s10694-010-0190-9. [DOI] [Google Scholar]
- 15.Song G. Clothing air gap layers and thermal protective performance in single layer garment. J. Ind. Textil. 2007;36(3):193–205. doi: 10.1177/1528083707069506. [DOI] [Google Scholar]
- 16.Zhang M., et al. A 3d multi-segment thermoregulation model of the hand with realistic anatomy: development, validation, and parametric analysis. Build. Environ. 2021;201 doi: 10.1016/j.buildenv.2021.107964. [DOI] [Google Scholar]
- 17.ISO . International Organization for Standardization; Geneva, Switzerland: 2007. 9920, Ergonomics of the Thermal Environment—Estimation of Thermal Insulation and Water Vapour Resistance of a Clothing Ensemble. [Google Scholar]
- 18.ISO . International Organization for Standardization; Geneva, Switzerland: 2005. 2005 Ergonomics of the Thermal Environment — Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the Pmv and Ppd Indices and Local Thermal Comfort Criteria. [Google Scholar]
- 19.ASHRAE, American society of heating . vol. 1. 2009. (Refrigerating and Air-Conditioning Engineers). [Google Scholar]
- 20.Umeno T., Hokoi S., Takada S. Prediction of skin and clothing temperatures under thermal transient considering moisture accumulation in clothing/discussion. Build. Eng. 2001;107:71. [Google Scholar]
- 21.Lotens W.A., Havenith G. Calculation of clothing insulation and vapour resistance. Ergonomics. 1991;34(2):233–254. doi: 10.1080/00140139108967309. [DOI] [Google Scholar]
- 22.Kim Il Y., et al. Investigation of air gaps entrapped in protective clothing systems. Fire Mater. 2002;26(3):121–126. doi: 10.1002/fam.790. [DOI] [Google Scholar]
- 23.Wang F., et al. Real evaporative cooling efficiency of one-layer tight-fitting sportswear in a hot environment. Scand. J. Med. Sci. Sports. 2014;24(3):e129–e139. doi: 10.1111/sms.12117. [DOI] [PubMed] [Google Scholar]
- 24.Joshi A., et al. A three-dimensional thermoregulatory model for predicting human thermophysiological responses in various thermal environments. Build. Environ. 2022;207 doi: 10.1016/j.buildenv.2021.108506. [DOI] [Google Scholar]
- 25.Joshi A. Université de Haute Alsace - Mulhouse; 2019. Comprehensive model for heat and mass transfer in human skin-clothing-environment system modélisation des transferts de chaleur et de masse au porter dans le cas du système peau humaine-vêtement.https://theses.hal.science/tel-03606520 [Google Scholar]
- 26.Joshi A., et al. Effect of movement on convection and ventilation in a skin-clothing-environment system. Int. J. Therm. Sci. 2021;166 doi: 10.1016/j.ijthermalsci.2021.106965. [DOI] [Google Scholar]
- 27.Yang J., et al. Integrating a human thermoregulatory model with a clothing model to predict core and skin temperatures. Appl. Ergon. 2017;61:168–177. doi: 10.1016/j.apergo.2017.01.014. [DOI] [PubMed] [Google Scholar]
- 28.Yang J., et al. A new approach to predict heat stress and skin burn of firefighter under low-level thermal radiation. Int. J. Therm. Sci. 2019;145 doi: 10.1016/j.ijthermalsci.2019.106021. [DOI] [Google Scholar]
- 29.Psikuta A., et al. Quantitative evaluation of air gap thickness and contact area between body and garment. Textil. Res. J. 2012;82(14):1405–1413. doi: 10.1177/0040517512436823. [DOI] [Google Scholar]
- 30.Daanen H.A.M., Ter Haar F.B. 3d whole body scanners revisited. Displays. 2013;34(4):270–275. doi: 10.1016/j.displa.2013.08.011. [DOI] [Google Scholar]
- 31.Psikuta A., et al. Validation of a novel 3d scanning method for determination of the air gap in clothing. Measurement. 2015;67:61–70. doi: 10.1016/j.measurement.2015.02.024. [DOI] [Google Scholar]
- 32.Frackiewicz-Kaczmarek J., et al. Air gap thickness and contact area in undershirts with various moisture contents: influence of garment fit, fabric structure and fiber composition. Textil. Res. J. 2015;85(20):2196–2207. doi: 10.1177/0040517514551458. [DOI] [Google Scholar]
- 33.Mert E., et al. The effect of body postures on the distribution of air gap thickness and contact area. Int. J. Biometeorol. 2017;61(2):363–375. doi: 10.1007/s00484-016-1217-9. [DOI] [PubMed] [Google Scholar]
- 34.Wang S., Wang X., Wang Y. Effects of clothing ease and body postures on the air gap and clothing coverage. Int. J. Cloth. Sci. Technol. 2019;31(4):578–594. doi: 10.1108/IJCST-12-2018-0158. [DOI] [Google Scholar]
- 35.Kakitsuba N. Investigation into clothing area factors for tight and loose fitting clothing in three different body positions. 人間-生活環境系学会英文誌. 2004;7(2):75–81. doi: 10.1618/jhes.7.75. [DOI] [Google Scholar]
- 36.Kurazumi Y., et al. Clothing area factor for typical seasonal clothing of infant. Health. 2021;13(4):15. doi: 10.4236/health.2021.134031. [DOI] [Google Scholar]
- 37.Havenith G., et al. Comparison of two tracer gas dilution methods for the determination of clothing ventilation and of vapour resistance. Ergonomics. 2010;53(4):548–558. doi: 10.1080/00140130903528152. [DOI] [PubMed] [Google Scholar]
- 38.Crockford G.W., Crowder M., Prestidge S.P. A trace gas technique for measuring clothing microclimate air exchange rates. Br. J. Ind. Med. 1972;29(4):378–386. doi: 10.1136/oem.29.4.378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Birnbaum R.R., Crockford G.W. Measurement of the clothing ventilation index. Appl. Ergon. 1978;9(4):194–200. doi: 10.1016/0003-6870(78)90079-0. [DOI] [PubMed] [Google Scholar]
- 40.Mert E., et al. Contribution of garment fit and style to thermal comfort at the lower body. Int. J. Biometeorol. 2016;60(12):1995–2004. doi: 10.1007/s00484-016-1258-0. [DOI] [PubMed] [Google Scholar]
- 41.Fojtlín M., et al. Local clothing properties for thermo-physiological modelling: comparison of methods and body positions. Build. Environ. 2019;155:376–388. doi: 10.1016/j.buildenv.2019.03.026. [DOI] [Google Scholar]
- 42.Psikuta A., et al. Local air gap thickness and contact area models for realistic simulation of human thermo-physiological response. Int. J. Biometeorol. 2018;62(7):1121–1134. doi: 10.1007/s00484-018-1515-5. [DOI] [PubMed] [Google Scholar]
- 43.Mah T., Guowen S. Investigation of the contribution of garment design to thermal protection. Part 1: characterizing air gaps using three-dimensional body scanning for women's protective clothing. Textil. Res. J. 2010;80(13):1317–1329. doi: 10.1177/0040517509358795. [DOI] [Google Scholar]
- 44.Wardiningsih W., Nawaz N., Troynikov O. Performance relevant to the thermophysiological wear comfort of hip protective garments, part i: clothing area factor of hip protective garments in clothing ensembles. J. Text. Inst. 2019;110(6):924–931. doi: 10.1080/00405000.2018.1541435. [DOI] [Google Scholar]
- 45.Ashdown S.P., Slocum A.C., Lee Y.-A. The third dimension for apparel designers: visual assessment of hat designs for sun protection using 3-d body scanning. Cloth. Text. Res. J. 2005;23(3):151–164. doi: 10.1177/0887302x0502300302. [DOI] [Google Scholar]
- 46.McCullough E.A., Jones B.W., Huck J. A comprehensive data base for estimating clothing insulation. Ashrae Trans. 1985;91(2):29–47. [Google Scholar]
- 47.McCullough E., Jones B. Institute for Environmental Research Technical Report; 1983. Measuring and Estimating the Clothing Area Factor. 83-02. [Google Scholar]
- 48.Zhang M., et al. Numerical study of the convective heat transfer coefficient of the hand and the effect of wind. Build. Environ. 2021;188 doi: 10.1016/j.buildenv.2020.107482. [DOI] [Google Scholar]
- 49.ASTM . ASTM International; West Conshohocken, PA: 2022. F1291-22 Standard Test Method for Measuring the Thermal Insulation of Clothing Using a Heated Manikin. [DOI] [Google Scholar]
- 50.ASTM . American Society for Testing and Materials; West Conshohocken: 1996. D1777 − 96 Standard Test Method for Thickness of Textile Materials. [DOI] [Google Scholar]
- 51.ASTM . ASTM International; West Conshohocken, PA: 2020. D3776/d3776m − 09a Standard Test Methods for Mass Per Unit Area (Weight) of Fabric. [DOI] [Google Scholar]
- 52.Preece D., Lewis R., Carré M. Efficiency of donning and doffing medical examination gloves. Int. J. Ergon. 2020;10(1):1–17. [Google Scholar]
- 53.Yu A., et al. Case study on the effects of fit and material of sports gloves on hand performance. Appl. Ergon. 2019;75:17–26. doi: 10.1016/j.apergo.2018.09.007. [DOI] [PubMed] [Google Scholar]
- 54.Gao C., Kuklane K., Holmér I. 11th International Conference on Environmental Ergonomics. Lund University; 2005. Using 3d whole body scanning to determine clothing area factor. [Google Scholar]
- 55.ISO . International Organization for Standardization; Geneva, Switzerland: 2007. Iso 9920:2007 Ergonomics of Thermal Environment-Estimation of the Thermal Insulation and Evaporative Resistance of a Clothing Ensemble. [Google Scholar]
- 56.Yao Y., Rakheja S., Marcotte P. A methodology for integrated performance analyses of vibration reducing gloves. Int. J. Ind. Ergon. 2021;85 doi: 10.1016/j.ergon.2021.103174. [DOI] [Google Scholar]
- 57.Joshi A., et al. Modelling of heat and mass transfer in clothing considering evaporation, condensation, and wet conduction with case study. Build. Environ. 2023;228 doi: 10.1016/j.buildenv.2022.109786. [DOI] [Google Scholar]
- 58.Mert E., et al. Effect of heterogenous and homogenous air gaps on dry heat loss through the garment. Int. J. Biometeorol. 2015;59(11):1701–1710. doi: 10.1007/s00484-015-0978-x. [DOI] [PubMed] [Google Scholar]
- 59.Iwata H., Sugano S. 2009 IEEE/SICE International Symposium on System Integration (SII) 2009. Design of anthropomorphic dexterous hand with passive joints and sensitive soft skins. [DOI] [Google Scholar]
- 60.Watanabe S. Influence of air temperature and wind velocity and clothing fit on clothing insulation. Trans. AIJ. 1999:391–392. [Google Scholar]
- 61.Kakitsuba N., Suzuki K. The effect of clothing fit on clothing area factor. Journal of Architecture and Planning (transactions of Aij) 1997;62:37–41. [Google Scholar]
- 62.Rioux T., Li P., Xu X. 12th International Manikin and Modelling Meeting. St. Gallen; Switzerland: 2018. Clothing area factor measurements and estimations for cold‐weather clothing. [DOI] [Google Scholar]
- 63.Xu S.S., Pollard J., Zhao W. Modeling and analyzing for thermal protection of firefighters' glove by phase change material. J Environ Occup Sci. 2022;12(2):118–127. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this study will be made available upon request. Researchers interested in accessing the dataset may contact corresponding author Prof. Guowen Song at gwsong@iastate.edu to obtain the necessary information.