Elucidating Dynamics of Adenylate Kinase from Enzyme Opening to Ligand Release

Abstract

This study explores ligand-driven conformational changes in adenylate kinase (AK), which is known for its open-to-close conformational transitions upon ligand binding and release. By utilizing string free energy simulations, we determine the free energy profiles for both enzyme opening and ligand release and compare them with profiles from the apoenzyme. Results reveal a three-step ligand release process, which initiates with the opening of the adenosine triphosphate-binding subdomain (ATP lid), followed by ligand release and concomitant opening of the adenosine monophosphate-binding subdomain (AMP lid). The ligands then transition to nonspecific positions before complete dissociation. In these processes, the first step is energetically driven by ATP lid opening, whereas the second step is driven by ATP release. In contrast, the AMP lid opening and its ligand release make minor contributions to the total free energy for enzyme opening. Regarding the ligand binding mechanism, our results suggest that AMP lid closure occurs via an induced-fit mechanism triggered by AMP binding, whereas ATP lid closure follows conformational selection. This difference in the closure mechanisms provides an explanation with implications for the debate on ligand-driven conformational changes of AK. Additionally, we determine an X-ray structure of an AK variant that exhibits significant rearrangements in the stacking of catalytic arginines, explaining its reduced catalytic activity. In the context of apoenzyme opening, the sequence of events is different. Here, the AMP lid opens first while the ATP lid remains closed, and the free energy associated with ATP lid opening varies with orientation, aligning with the reported AK opening and closing rate heterogeneity. Finally, this study, in conjunction with our previous research, provides a comprehensive view of the intricate interplay between various structural elements, ligands, and catalytic residues that collectively contribute to the robust catalytic power of the enzyme.

Introduction

Enzymes catalyze various biological processes by undergoing large-scale conformational changes, yet the mechanisms behind these changes remain a topic of debate.¹⁻⁸ One particularly active area of research is ligand binding, where two models, namely, conformational selection and induced-fit,⁹ are at the center of debate.¹⁰⁻¹⁷ Conformational selection, also known as population-shift,¹⁸ assumes that enzymes exist in a pre-equilibrium between different conformational states, with selective binding of ligands to one state while enzymes spontaneously transition between them. In contrast, the induced-fit model requires ligand binding to trigger the conformational change. Despite this apparent difference, distinguishing between these models in real enzymes has been challenging^10,19−21 because ligands may initially establish nonspecific contacts with the enzyme, followed by a transition resembling an induced-fit to the bound state. Meanwhile, the apo-state enzyme may dynamically explore both conformations, as often observed through nuclear magnetic resonance (NMR)²²⁻²⁴ and single-molecule spectroscopy.^15,25,26 In such cases, a comprehensive understanding of the mechanism, the energetics of the enzyme’s conformational change, and the influence of ligand binding on it can help resolve the difference between the two models.

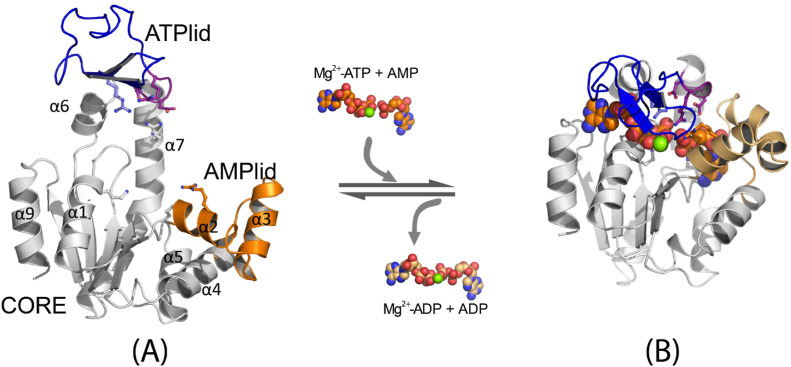
Adenylate kinase (AK) is a well-studied enzyme that offers a unique opportunity for investigating the mechanisms of ligand-induced conformational change.²⁷⁻²⁹ This enzyme plays a vital role in maintaining cellular energy homeostasis by catalyzing a reversible phosphoryl transfer between adenosine tri- and monophosphates (ATP and AMP).³⁰⁻³² Numerous X-ray and NMR studies have established that AK undergoes a conformational transition between the open and closed conformations, characterized by the orientations of the ATP-binding and AMP-binding lids relative to the static CORE subdomain (Figure 1).^4,22,33−36 For this conformational change, this enzyme has been extensively studied experimentally^25,27,37,38 and computationally^28,39−41 to probe the interplay between ligand binding and the conformational change of the enzyme. These studies, at the same time, have provided evidence that supports both the induced-fit and conformational selection models. For instance, X-ray crystallographic structures of the enzyme with substrate-like ligands, such as guanosine triphosphate (GTP), forming nonspecific contacts in the open conformation,⁴² demonstrate the structure of the enzyme in the initial stages of ligand binding, supporting an induced-fit model for substrate binding. This result aligns with the NMR studies exploring the enzyme surface involved in the initial ATP interaction with mutations at various ligand binding sites.³⁸ Additionally, kinetic studies that utilized a truncated nucleoside and a phosphite dianion, together mimicking the AMP substrate, showed that ligand binding drives conformational change in catalysis and contributes to the stabilization of the reaction transition state.⁴³ On the other hand, NMR and single-molecule Förster resonance energy transfer (sm-FRET) studies have reported access to both the open and closed conformations of the enzyme even in the absence of substrates (i.e., apo-state), suggesting that conformational selection is also at play.^22,25

Figure 1.

Ligand-induced conformational change of Escherichia coli AK: (A) open conformation (PDB ID: 4AKE(34)) and (B) closed conformation (PDB ID: 4APU(36)). The ligands (Mg²⁺-ATP, AMP, Mg²⁺-ADP, and ADP) are shown in the space-fill model. The ATP lid is shown in blue cartoon, the catalytic loop⁴⁷ in purple cartoon, the AMP lid in orange cartoon, and the rest of the protein in gray cartoon, respectively.

This enzyme has also been extensively studied as a model system for investigating the role of close-to-open conformational motion in catalytic turnover.^22,36,44,45 Initially, NMR studies proposed that the rate-determining step in overall catalysis is the enzyme’s opening after the catalytic reaction.^22,44 This was based on the observation that the measured time scales of the ATP/AMP-binding lid motion (286 ± 85 s^–1) matched the catalytic turnover rate of the enzyme (263 ± 30 s^–1).²² This model is challenged by recent experiments and simulations.^{36,40,43,45−47} For example, Aviram et al. used the sm-FRET technique and reported substantially faster opening rates (∼45 μs)⁴⁶ compared to those measured by NMR²² and another sm-FRET study.²⁵ They also noted different rates of opening between the apo- and holo-state enzymes, with the opening in the holo-state being faster. More recent sm-FRET studies further confirmed this result with the suggestion of multiple conformational transitions before establishing the correct binding poses of reaction substrates.⁴⁸ Similarly, Zheng and Cui, utilizing molecular dynamics (MD) simulations and Markov state modeling (MSM), reported opening rates of an apo-state AK that were orders of magnitude faster than the catalytic turnover rate.⁴⁰ Our own studies have corroborated these results by showing that the time scales of AK opening differ between the reactant and product states; between the two states, the opening in the product state is faster.³⁶ Moreover, the free energy barrier determined for the chemical step closely matched the overall catalytic turnover barrier,³⁶ thereby challenging the prevailing view that the rate-limiting step of the enzyme involves its opening coupled with the release of reaction products. Our more recent study further supports this result, where we show a linear correlation between the barriers calculated for the phosphoryl transfer reaction step [using the hybrid quantum mechanical/molecular mechanical (QM/MM) simulations] and the barriers estimated based on the experimentally determined k_cat values for various AK catalytic mutants.⁴⁷ Intriguingly, several of these mutants even exhibited significantly enhanced opening, suggesting that the residues involved in facilitating the phosphoryl transfer reaction also contribute to the slow opening of the enzyme, collectively acting as the bottleneck of the entire catalytic process. These results suggest complexities underlying the enzyme’s mechanism in ligand binding and catalytic turnover, thus requiring further investigation.

In this work, we employed the string method in collective variables (SMCV)^49,50 to investigate the mechanisms of AK’s conformational change and ligand release. This method has been successfully used by our group to study this enzyme^36,47 and other enzymes,⁵¹⁻⁵⁴ providing valuable insights into their mechanisms. By comparing the free energy profiles determined for the enzyme in various states, including the reactant and product states, as well as the apo- and holo-states, we showed the involvement of both the induced-fit and conformational selection mechanisms in AK. Specifically, the binding of ATP’s phosphoryl groups and AMP ligand occurs through an induced-fit mechanism for the closure of the AMP lid. Subsequently, the ATP lid undergoes a conformational selection closing with the base and ribose groups of ATP binding to their respective binding pockets. This mechanistic understanding is consistent with our recent studies of AK^36,47 and helps interpret different experiments^22,25,38,46 and simulations.^28,29,40,55 In the following section, we provide a detailed description of the setup of our MD and SMCV simulations and the procedure for AK variant production and X-ray crystallography. We then present and discuss the results obtained from these simulations and compare the results to the X-ray structure determined for an AK variant with reduced catalytic activity. Finally, we highlight our findings and the significance of this study in advancing our understanding of AK’s conformational dynamics and underlying mechanisms.

Materials and Methods

MD System Preparation and Equilibration

The reactant and product state systems were prepared using the atomic coordinates of the wild-type (WT) Escherichia coli AK structure (PDB ID: 1AKE(34)) in the closed conformation, where the reactant state (RS) system was prepared with ATP and AMP and the product state (PS) system with two molecules of adenosine diphosphate (ADP) as their respective ligands. In both systems, the coordinates of the ligands (ATP, ADP, and AMP) and Mg²⁺ ions were prepared following the procedure described in ref (36). In particular, the coordinates of the Mg²⁺ ion, the coordinating waters, and phosphoryl oxygen atoms of the X-ray structure of Bacillus stearothermophilus AK (AK_bs; PDB: 1ZIO) were used to model the initial reactant and product state geometries, respectively, followed by local energy minimizations to relax the rest of the ligand geometries. To determine the protonation state of each histidine residue, the hydrogen bond interactions within their local environment were considered. For other charged residues, their protonation states were assigned based on the residue’s pK_a value in water. In addition, we protonated ATP in RS and one of the two ADPs in PS. Thus, the charges of fully deprotonated AMP and singly protonated ADP are −2, and the charges of fully deprotonated ADP and singly protonated ATP are −3. As described in our previous studies, the removal of these protons led to significant distortions in the orientations of these molecules within the active site of AK during MD simulation.³⁶ All crystal waters were included. Each system was then solvated with a 72 Å cubic box of TIP3P waters⁵⁶ and neutralized at 150 mM NaCl, followed by the removal of waters within 2.5 Å from the protein/ligand heavy atoms. The resultant systems were sized 36,200 atoms.

For the apo-state enzyme, the system was prepared based on the atomic coordinates prepared by Zheng and Cui.⁴⁰ In particular, three MSM trajectories with different closing time scales (i.e., 12.2, 58.3, and 357.7 μs) were selected, each representing the pathways with fast, middle, and slow closing rates. For each MSM pathway, a total of 40 coordinate sets were selected to represent the (initial) opening/closing pathway, followed by the solvation with an 80 Å cubic box of TIP3P waters and neutralization at 150 mM NaCl. After the removal of water molecules that overlapped with the protein, the system was sized of 48,193 atoms, where the total number of TIP3P waters was adjusted to make them the same between the different coordinate sets. Here, we used a larger water box for the apo-state enzyme compared to that for the holo-state enzyme. This was done to fully solvate the enzyme in the open state, with an extended ATP lid loop conformation observed in the MSM pathway.

The systems prepared were first energy-minimized, followed by heating to 298.15 K for 24 ps. They were then equilibrated for 176 ps at a constant volume. During the MD simulations, the proteins and ions were represented by the CHARMM36 force fields^57,58 with the CMAP correction^59,60 for protein backbone dihedrals; for the water molecules, the TIP3P model was used. All energy minimizations and equilibration MD simulations were performed using the CAHRMM program.⁶¹ The MD simulation was carried out using the leapfrog Verlet and the 2 fs time integration, and SHAKE⁶² was applied to constrain all bonds involving hydrogen atoms. Electrostatic interactions were evaluated using the particle mesh Ewald method^63,64 and van der Waals interactions with force switching between 10 and 12 Å.

SMCV Simulation

To generate the initial pathway for the SMCV simulation,⁵⁰ 2.0 μs MD simulations were performed for the product state system at 298.15 K and 1 bar using the CHARMM⁶¹/OpenMM⁶⁵ program (CHARMM version c45a2 and OpenMM version 7.3). The temperature and pressure of the simulated systems were controlled using the Langevin thermostat⁶⁶ and the Monte Carlo barostat,^67,68 respectively. During the MD simulations, the enzyme opened around 1 μs, while its ligands (i.e., 2 ADP) remained interacting with the enzyme. To complete the ligand release and to generate the paths for ligand release, the ligands were then gradually pulled away from the enzyme in a manner similar to the steered MD with distance restraints for their centers of mass from their respective binding pockets, over 600 ps of MD simulations. This was followed by 500 ps of equilibration at the different release positions. The trajectory thus obtained was used as the initial pathway for the SMCV simulation in PS, which was represented with 64 SM images. For the reactant state, the same length of MD simulations did not open the enzyme as we discussed in our recent study.³⁶ Thus, the trajectory obtained in PS was adopted with modification of the ligands to ATP and AMP, followed by 1 ns MD simulations before starting the SMCV simulation.

Starting from the initial pathways generated for each system, the SMCV path optimization was performed for 20 ns for RS and 28 ns for PS (for each SM image) in an iterative manner (Scheme S1).^50,53 Namely, in each iteration, the system was first simulated for 4 ps, during which each SM image was harmonically restrained with a force constant of 100.0 kcal/mol-Ų to each CV. The path (i.e., CV positions along the path) was then evolved with the free energy gradients evaluated during the MD simulation, followed by reparameterization of the CV positions to have an equal distance between neighboring images. As CVs, three center of mass (COM) distances, i.e., the CORE-ATP lid, the CORE-AMP lid, and the ATP lid-AMP lid distances, were defined to describe the opening of the enzyme and two COM distances, i.e., the ATP/ADP-ATP lid and the AMP/ADP-AMP lid distances, to describe the release of bound ligands (Figure S1). Once the path optimization was completed, we performed additional 60 ns MD simulations for RS and 100 ns MD simulations for PS for each SM image without updating the CV positions to determine the potential of mean force (PMF) along the path (Figure 2A). The thermodynamic integration was used to compute the free energy (i.e., PMF) as a function of α, i.e.,

1

where α represents the normalized path between α = 0.0 (closed state) and 1.0 (fully open state with ligands released from the enzyme), ΔF is the free energy value at each α relative to the free energy at α = 0.0, and dF/dα is the free energy gradient computed as a time average of the force acting on the path. Collectively, a total of 5.12 μs SMCV simulations were performed for the RS system, in which 1.28 μs was for path optimization and 3.84 μs for PMF calculation, and a total of 8.19 μs SMCV simulations for the PS system with 1.79 μs for path optimization and 6.4 μs for PMF calculation, respectively. All SMCV simulations were performed using the CHARMM DOMDEC-GPU module⁶⁹ with the implementation of the string method module.^50,53

Figure 2.

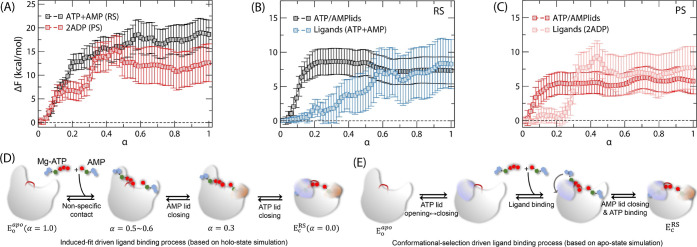
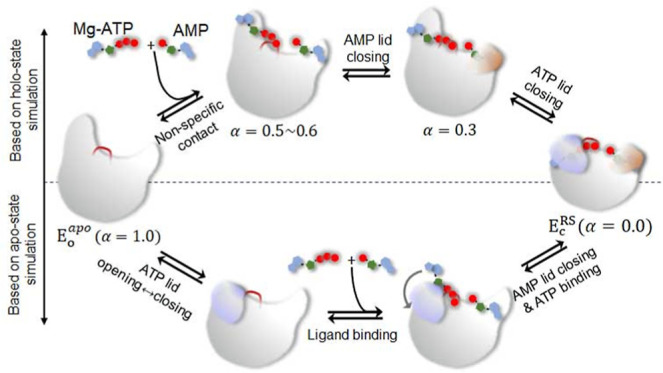
(A) SMCV free energy (FE) profiles of AK opening and ligand release determined for the reactant (ATP + AMP; black) and product states (2ADP; red). The reaction coordinate α represents the normalized reaction coordinate describing both the ATP/AMP lid motions and ligand release between the closed (α = 0.0) and open (α = 1.0) conformations. Decomposition of the FE contributions of ATP and AMP lid opening and ligand release (B) for the reactant state and (C) for the product state shown in (A). Proposed models of ligand binding were based on (D) holo-state simulation and (E) apo-state simulation.

For the apo-state system, the entire opening/closing path was represented with 40 SM images and three COM distances as CVs—the CORE-ATP lid, CORE-AMP lid, and ATPlid-AMP lid distances. The SMCV simulations then followed the procedure described above for the holo-system simulations. Thus, a total of 1.76 μs SMCV MD simulations—0.56 μs (14 ns for each SM image) for path optimization and 1.2 μs (30 ns for each SM image) for PMF calculation—were performed for each opening/closing pathway.

Alchemical Transformation Simulation of the Catalytic Reaction

The alchemical free energy simulation method⁷⁰ was utilized to simulate the phosphoryl transfer reaction and the enzyme’s response, achieving a time scale longer than typically feasible with hybrid QM/MM simulation methods.³⁶ This was accomplished by alchemically mutating the reactant species (ATP + AMP) into the product species (i.e., 2 ADPs). In this approach, the two end states were represented using their respective topologies and parameters with a single set of coordinates for both the reactant and product species, i.e., the dual topology and single coordinate approach.^71,72 The simulation was performed by mixing the Hamiltonians representing the two end states using a coupling parameter λ, as in eq 2

2

where H_λ, H_RS, and H_PS refer to the Hamiltonians of the hybrid system, the reactant state and the product states, respectively. Hence, the system is fully described by H_RS at λ = 0.0 (the reactant state) and H_PS at λ = 1.0 (the product state). At intermediate λ values, the system exhibits behaviors between RS and PS. For example, at λ = 0.5, the system mimics the reaction’s transition state.

Starting from the reactant state, the system was progressively mutated to the product state through 17 discrete λ steps (i.e., λ = 0.0, 0.01, 0.02, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.98, 0.99, and 1.0). At each λ value, the system was simulated for 1 ns using the same nonbonded interaction options employed in the SMCV simulations. Then, the λ value was updated to the next λ value. Upon reaching a λ value of 1.0 (product state), the transformation simulation was reversed toward the reactant state (λ = 0.0). This bidirectional sweeping simulation was repeated five times, totaling 10 ns MD simulations at each λ value. Throughout the simulations, coordinate snapshots were saved at 2 ps intervals for subsequent analysis. All alchemical transformation simulations were carried out using the CHARMM DOMDEC-GPU module⁶⁹ within the CHARMM program (version c47a2), which was modified to support the dual topology and single coordinate approach.

AK Mutant Protein Production and Purification

The D158A AK variant was prepared as outlined in ref (47). In short, the enzyme was produced in E. coli cells (BL21DE3) by making use of a self-inducing plasmid (pEAK91) carrying the D158A replacement, where the site-directed mutagenesis was carried out by applying the QuikChange approach (Stratagene) with primers from GenScript (Leiden, The Netherlands). Purification of the AK variant was accomplished by employing affinity chromatography on a blue Sepharose column, followed by size exclusion chromatography.

X-ray Crystallography

Crystallization setups contained 2 μL of the purified D158A AK protein at 16.4 mg/mL, mixed with the nonhydrolyzable inhibitor P¹,P⁵-di(adenosine-5′) pentaphosphate (Ap5A) at a concentration of 5 mM and 2 μL of precipitant buffer containing 32% PEG 8K, 0.2 M AmSO4, and 0.1 M cacodylate at pH 6.5. Crystals grew at 293 K within 5 days to a size of 0.4 × 0.4 × 0.1 mm³ and were vitrified at 100 K in a nitrogen gas stream (Oxford CryoSystems Ltd., UK). X-ray diffraction data were collected from cryo-cooled D158A AK cocrystals with Ap5A at a wavelength of λ = 0.87293 Å onto a Pilatus 6 M detector (Dectris) at beamline ID23–2 of the European Synchrotron Radiation Facility, ESRF, in Grenoble, France. Crystals diffracted to a d-spacing of 1.76 Å. The diffraction intensities were indexed, integrated with XDS,⁷³ and prepared for scaling with Pointless.⁷⁴ The intensities were scaled and merged using Aimless⁷⁵ and converted to structure factors with cTruncate.⁷⁶ About 5.1% of the data was marked for the R_free calculation.

Phases were obtained by molecular replacement (MR) using the E. coli apo-AK structure (PDB ID: 4AKE(34)) as the search model in Phaser from the Phenix program package (version 1.19.2-4158). The CCP4 program suite⁷⁶ was used for data analysis and manipulation. Iterative rounds of manual model building with Coot (version 0.8.9.2-EL)⁷⁷ and structure refinement against data extending to 1.76 Å with phenix.refine^78,79 of the Phenix program package were carried out until the R_free and R_factor values converged. The data processing and refinement statistics are listed in Table S1. The atomic coordinates and structure factors for D158A AK in complex with Ap5A have been deposited with the Worldwide Protein Data Bank (wwPDB) under code 8Q2B.

Results

Free Energy Profiles of Holo-Enzyme Opening and Ligand Release

In our recent studies,^36,47 we discovered that AK has a higher tendency for opening in the product state (PS), where it is bound to two molecules of ADP. Consistent with this tendency, the product state exhibited a notably diminished free energy barrier for opening in comparison to the reactant state (ATP + AMP; RS). Furthermore, we established a mechanistic linkage between the catalytic phosphoryl transfer and the enzyme’s opening dynamics, proposed based on the finding that both processes are modulated by the active site residues and take place on a similar time scale. These findings have motivated us to explore the mechanism of ligand release from the enzyme’s active site, for a comprehensive understanding of the enzyme’s complete catalytic cycle.

To accomplish this, we conducted the SMCV free energy simulations of enzyme opening while concurrently releasing bound ligands (i.e., substrates and products) from the enzyme. The resultant free energy profiles are presented in Figure 2A, where α represents the normalized reaction coordinate describing both the ATP/AMP lid motions and ligand release. Figure 3 provides snapshots of the bound ligands and their interactions at different α values for the RS; analogous snapshots for the PS are presented in Figure S2. The free energy profiles exhibit distinctive patterns during various stages of the opening process and also between the reactant and product states. Specifically, we observe that the free energy profile between α = 0.0 and 0.3 is predominantly influenced by the opening of the enzyme, while for α > 0.3, it is dominated by the release of ligands (i.e., ATP + AMP in RS and ADP + ADP in PS). In addition, during the opening step (α < 0.3), the free energy barrier for opening in PS is notably lower, with a value of 7.1 ± 1.7 kcal/mol, compared to 13.8 ± 2.4 in RS. This difference can be linked to an earlier transition state for opening in PS (α = 0.16) compared to that in RS (α = 0.29). These findings are consistent with our previously reported free energies of enzyme opening, which were determined in the presence of ligands but without incorporating their motions into the CVs. Following the opening, the bound ligands undergo release with an increase in free energy to 18.6 ± 3.0 kcal/mol in RS and 12.6 ± 4.0 kcal/mol in PS, respectively. Notably, the contributions of the ligands to this increase in free energy are similar between RS (8.3 ± 3.6 kcal/mol; Figure 2B) and PS (7.7 ± 3.1 kcal/mol; Figure 2C), suggesting that the protein’s contributions dominate the overall difference in the free energy profiles between the two states.

Figure 3.

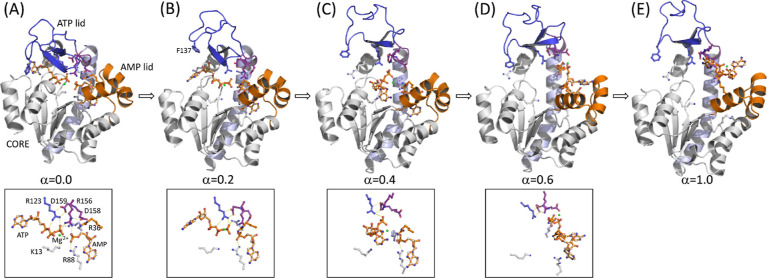
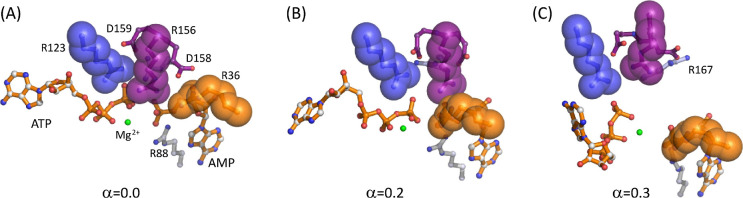
Representative snapshots of the enzyme and substrates (RS) along the SMCV pathway determined in Figure 2A: (A) α = 0.0, (B) α = 0.2, (C) α = 0.4, (D) α = 0.6, and (E) α = 1.0. For (A–D), the close-up view of the substrates (ATP, AMP, and Mg²⁺) with residues that interact with them is shown in the bottom panel. For the PS system, analogous snapshots are shown in Figure S2. In the figure, the ATP lid is shown in blue cartoon, the AMP lid in gold cartoon, the CORE subdomain in white cartoon, the α7 helix in light blue cartoon, and the catalytic loop composed of residues 156–159 in purple cartoon, respectively. In each figure, key enzyme residues and substrates (ATP, AMP, and Mg²⁺) are shown in the ball-and-stick model. In the bottom panel, key interactions are indicated with a dashed line.

Detailed Sequence of Events

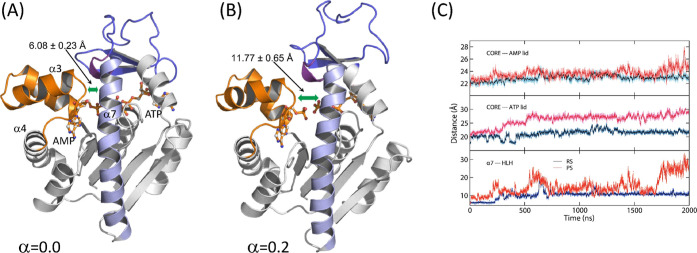
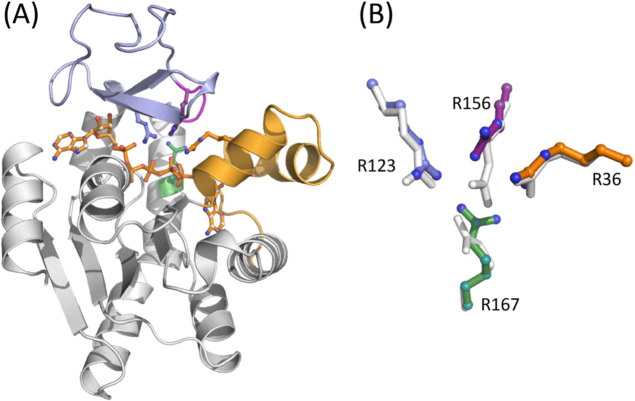
Between α = 0.0 and 0.3, several rearrangements take place around the ATP lid. The first is the loss of contact between helix α7 and the loop connecting helices α3 and 4 (HLH) of the AMP lid (Figure 4). This contact contributes to the stability of the closed conformation via anchoring the ATP lid to the AMP lid. Thus, the loss of this contact releases the α7 helix to allow its slight displacement toward the α6 helix, which was also observed in our previous study,³⁶ and subsequently, Arg 156 (R156) lifts upward (Figure 5). R156 is, particularly, a key residue in the catalytic loop of the enzyme (shown in a purple cartoon in Figure 3), which is located right above the site of phosphoryl transfer and connected to helix α7. Moreover, this residue forms stacking interactions with Arg 123 and 36 (R123 and R36) in the closed conformation (Figure 5), together coordinating the catalytic reaction. Any mutation thereof has shown substantially reduced catalytic activity.^44,47,80 The lifting of R156, therefore, breaks the stacking interaction with R123 and R36, as well as the interaction with bound ligands. Interestingly, the R156 lifting occurs at different α values between the reactant and product states: α ≈ 0.12 in PS and α = 0.18–0.28 in RS. Despite this difference, this event seems to occur immediately prior to the transition state of opening in both states, suggesting that the lifting and breakage of the R123-R156-R36 stack are the first critical events for the opening of the enzyme. It therefore makes sense to observe the facilitated opening of the enzyme via any mutation that breaks or removes the stacking interactions.⁴⁷ On the other side of the enzyme, the adenine base of ATP (and that of ADP in the product state) is released from the binding pocket formed by the ATP recognition loop, Arg 119 (R119), and Phe 137 (F137), where R119 stacks with the adenine base in the closed conformation (Figure S4).^81,82 These changes allow the upward movement of the ATP lid and free the AMP lid. After this, the two lids seemed to move independently of each other.

Figure 4.

Snapshots of the enzyme and substrates (RS) complex at two different states: (A) α = 0.0 and (B) α = 0.2 of the SMCV simulation. These snapshots illustrate the loss of contact between helix α7 and the loop connecting helices α3 and 4 of the AMP lid. The distances shown are the helix α7 – α3-loop-α4 (HLH) distance at (A) α = 0.0 and (B) α = 0.2, respectively. The color scheme is the same as that in Figure 3. (C) Time course of distances over time from the MD simulations in RS and PS: CORE – AMP lid (top panel), CORE – ATP lid (middle panel), and helix α7 – α3-loop-α4 (HLH) distances (bottom panel). The distances in RS are colored blue, and those in PS are shown in red.

Figure 5.

R123-R156-R36 stack at three different states for the RS system: (A) α = 0.0, (B) α = 0.2, and (C) α = 0.3. The three arginine residues are shown on the van der Waals surface (R36 in gold, R123 in blue, and R156 in purple). The substrates (ATP and AMP) are shown in gold, the Mg²⁺ ion in green, D158 and 159 in purple, and R88 in gray. At α = 0.2, R156 shifts away from R36, and at α = 0.3, the stacking interaction is completely broken with R156 lifted upward, away from the substrates.

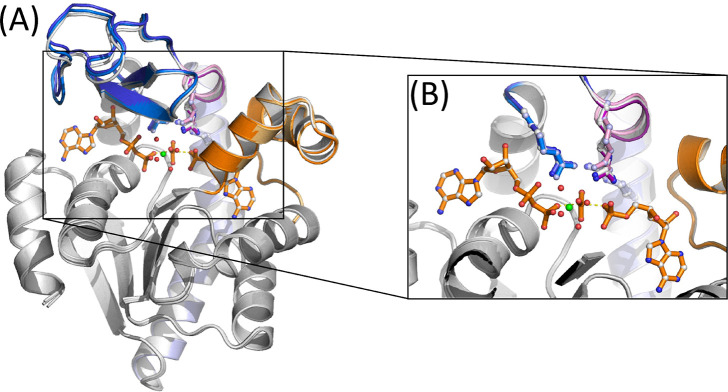
In our recent study, we observed that a replacement of Asp158 with alanine (D158A) stimulated opening of the enzyme.⁴⁷ This can be linked to the fact that D158 is engaged in a bidentate hydrogen bonding interaction with the side chain of R156 in the closed state.³³ Since this interaction is absent in the open state,³⁴ it likely plays a role in the stabilization of the closed conformation and thus in the opening dynamics of the enzyme through perturbing the R156 interaction in the closed state. In this study, we determined the crystallographic structure of the D158A AK variant in complex with Ap5A to search for an explanation of the increased opening rate and to probe whether this feature is linked to the R123-R156-R36 stacking interaction. The overall structure of the variant, elucidated at a resolution of 1.76 Å, is virtually identical to that of the wild-type enzyme (Figure 6A). The structure also reveals significant but localized rearrangements in the orientation of the catalytic side chains (Figure 6B), suggesting that the loss of the hydrogen bonding interaction between D158 and R156 is propagated to both the stacking interaction with R123 and R36 and also the orientation of R167. Ultimately, these changes lead to a loss of direct hydrogen bonds from R156 and R167 to the bound inhibitor. Our MD simulations of the D158A mutant also confirmed similar rearrangements.⁴⁷ These results collectively support the idea that the interaction between D158 and R156 is necessary to maintain an optimal geometry of the active site residues and that loss of this interaction is a key step in the opening reaction that eventually leads to the release of bound ligands (e.g., substrates and products). The “lift” of R156 linked to substrate release may, therefore, be a cooperative event that depends on both the loss of contacts between the ATP lid and the AMP lid and also the loss of contacts with the substrate.

Figure 6.

(A) Crystallographic structure of the D158A mutant in complex with Ap5A. The ATPlid and AMP lid are colored in blue and orange, and the catalytic arginine side chains are indicated and colored as in Figure 3. (B) Zoom in on the stacking interaction of the catalytic side chains R123 (blue), R156 (purple), and R36 (orange) in the D158A variant. The position of R167 (green) is also indicated, and the side chain orientations of the catalytic arginines are perturbed following the shift/lift of R156. The orientation of the corresponding side chains in the closed wild-type enzyme is shown in gray.

At around α ≈ 0.3, the ATP lid is almost fully open, while the AMP lid remains closed (Figure S6). This difference in the opening between the two lids is consistent with our previous MD simulations,³⁶ where a slight loosening of the AMP lid was observed before the full opening of the ATP lid. Dulko-Smith et al. also reported a similar sequence of events.⁴⁷ During the ATP lid opening, the adenine base and ribose group of ATP/ADP (in the ATP-binding pocket) unbind from the binding pocket, while its phosphoryl groups remain bound via interactions with the enzyme’s P-loop and lysine 13 (K13) (Figure 3B). At α = 0.3, R123 and R156 have lost their direct contacts with the phosphoryl groups of bound ligands, and at α ≈ 0.45, the ligand in the ATP-binding pocket is completely released from its binding site, including its phosphoryl groups from the P-loop. The unbound ATP/ADP (of the ATP-binding site) then regains its direct contacts with R123 and R156, while the ATP lid remains open in both the RS (Figure 3D) and PS (Figure S2D). In RS, ATP also interacts with R167 of the α7 helix. Even at this point, however, the ligand in the AMP-binding pocket remains bound, including its deeply bound base, where another catalytic residue, Arg 88 (R88), interacts with the α-phosphoryl group of the ligand. The release of AMP/ADP from the AMP-binding pocket is observed at a much later α value (α > 0.6) in both the reactant and product states, where the AMP lid swings open.

Free Energy Contributions of Ligands and Enzyme’s Lids

In Figure 2A, the free energy continues to rise between α = 0.3 and 0.5, where the ATP lid remains open and the AMP lid remains closed. Therefore, this change in free energy is mainly due to the release of ligands, particularly, the phosphoryl groups of ATP/ADP and the base of AMP/ADP. In contrast, the free energy increase before α = 0.2 is primarily contributed by the opening of the ATP lid, including the changes of interactions around R156. To gain further insights into the energetic contributions of lid opening vs ligand release, we decomposed the SMCV free energy profiles into the contributions of the protein and the bound ligands, as shown in Figure 2B for RS and 2C for PS, respectively. [See the Supporting Information for free energy decomposition.] Further decomposition of the free energy contributions between the two lids reveals that the increase of free energy between α = 0.0–0.2 is indeed dominated by the ATP-lid opening. Then, the free energy profile of the two lids’ opening remains relatively flat between α = 0.2–0.5 (Figure 2B,C), during which the AMP lid opens. In contrast, the contribution of ligands to the free energy is relatively small until α = 0.2, after which it increases until α reaches 0.6 in RS and 0.5 in PS. The free energy then remains relatively unchanged until α = 1.0.

Between RS and PS, a steep increase of the ligands’ contribution is notable for PS between α = 0.2 and 0.5 (Figure 2C), while in RS, it increases gradually between α = 0.2 and 0.6 (Figure 2B). This increase in both systems suggests a significant contribution from the release of the ATP/ADP’s phosphoryl groups from the P-loop and a relatively small contribution of AMP/ADP. Conversely, unbinding of ATP/ADP’s base and ribose (between α = 0.0–0.2) and the AMP lid opening (α = 0.3–0.5) has relatively small contributions to the overall free energy profile of enzyme opening and ligand release.

The distinctive contributions of ligand release and enzyme opening described above suggest a three-step process for enzyme opening and ligand release, as depicted in Figure 2D. In the first step, the ATP lid opens with the release of ligand in the ATP-binding pocket, while its phosphoryl groups and the ligand in the AMP-binding site remain bound. This step is primarily driven by the free energy of enzyme opening, where a critical event is the loss of contact between the two lids. Subsequently, the AMP lid opens with a relatively minor energetic contribution to the enzyme’s opening, and the two ligands (i.e., ATP and AMP in the reactant state and 2 ADPs in the product state) are released from their respective binding pockets. Notably, the release of the ligand in the AMP-binding pocket (i.e., AMP in RS and ADP in PS) requires a substantial opening of the AMP lid to allow for the release of the bound base (Figure S3). Once released, the ligands make nonspecific contacts with the enzyme until they are fully released, representing the third step in this process. Our findings are in line with the results reported by Matsunaga et al., who performed the on-the-fly SM simulations of AK opening in the presence of Ap5A and in the apo-state.³⁹ While their simulations yielded a similar free energy barrier for opening compared to what we observed in the product state simulation, their study had limitations in elucidating the specific details of ligand release, particularly the release of ATP’s phosphoryl groups. This limitation was due to the use of the Ap5A inhibitor and the absence of the Mg²⁺ cofactor. In contrast, our study considers both ligands and the Mg²⁺ ion as independent entities, revealing realistic details of the ligand release process.

Regarding the thermodynamics of ligand release, our simulations provide an accurate prediction for the free energy of 2 ADP (i.e., product) release, which is estimated as the difference in free energy between α = 0.0 and 1.0 (i.e., the sum of the free energies of enzyme opening and ligand release). Specifically, we obtained 12.6 ± 4.0 kcal/mol as the calculated value, which is close to the value estimated based on the experimental K_d value of 9 μM for ADP³⁶ (corresponding to 13.9 kcal/mol for 2 ADPs, assuming that the two ADP molecules bind with the same K_d value). In contrast, our calculations overestimated the free energy for ATP + AMP (i.e., substrates) release by 7.7 kcal/mol: 18.6 ± 3.0 kcal/mol from SMCV simulations compared to the experimental K_d values of 53 μM for ATP and 210 μM for AMP,⁸³ corresponding to a free energy of 10.9 kcal/mol. We speculate that the large errors in the computed free energies, ranging from 2.8 to 3.4 kcal/mol between α = 0.5 and 1.0 (Figure 2A), underlie the overestimation of the substrates’ release. In particular, significant errors occur in both enzyme opening and ligand release (Figure 2B,C), which likely result from the large fluctuations of the ligands after forming nonspecific contacts with the protein. In the present case, however, directly computing the free energy of ligand release using methods such as free energy perturbation⁷⁰ may not be straightforward due to the conformational changes in the protein and changes of coordination around the Mg²⁺ cofactor during ligand release. Nevertheless, our simulations show that ATP requires more energy to be released compared to AMP, which is consistent with its smaller K_d value.⁸³ Likewise, the release of ADP from the ATP-binding pocket requires more free energy than the release of ATP, which is also consistent with the smaller K_d value for ADP.³⁶

Rearrangement of Enzymes during the Catalytic Phosphoryl Transfer Reaction

In our recent study³⁶ and in Figure 4A,B, we discussed the importance of the interaction between helix α7 and the loop positioned between helices α3 and 4 (HLH) to enzyme opening. To further characterize the loss of this contact in relation to the motions of the ATP and AMP lids, we performed MD simulations in both the reactant and product states. These simulations were extended to 2 μs as a continuation of our previous MD simulations.³⁶ The results of these simulations are presented in Figure 4C, where the time course of the α7–HLH distance is compared with the changes in the CORE–ATP lid and CORE–AMP lid distances for both RS and PS. The comparison clearly shows the early occurrence of the loss of this contact in both RS and PS, and between the two states, it occurs significantly earlier in PS compared to RS. This disparity in the contact between the two reaction states may underlie the pronounced fluctuations observed in the ATP and AMP lids in PS, as opposed to RS (Figure 4C).

To provide deeper insights into the differences between enzyme opening in RS and PS, we employed the alchemical simulation method⁷⁰ to model the transition between the two reaction states (see the Materials and Methods section). Specifically, the simulation was performed by gradually mutating the ligands from reactants (ATP and AMP) to products (2 ADPs). We note that while a similar simulation could be carried out using QM/MM potentials,^36,47 the utilization of MM potentials enables access to significantly longer time scales to observe rearrangements in the enzyme following the phosphoryl transfer reaction. In Figure 7, we superimpose the averaged structures of the enzymes in RS vs PS. In this figure, the ligand coordinates shown are taken at λ = 0.5, where both RS and PS topologies contributed equally, as a mimic of the catalytic reaction transition state (TS). While the RS and PS structures show high levels of similarity, the catalytic loop of the enzyme, represented by the purple and light pink cartoons for RS and PS, respectively, exhibits a notable difference in its relative orientation. In particular, the catalytic loop shifts slightly upward in PS (light pink) compared to that in RS (purple), which seems to be a result of the upward movement of R156 in PS and that of the TS-mimic state being positioned between the two states. We suggest that this upshift of R156 is required to allow the transfer of the γ-phosphoryl group from ATP to AMP, thereby inducing the upward shift of the catalytic loop. Furthermore, as shown in Figure S5, the ATP lid moves downward following the phosphoryl transfer reaction, with the CORE–ATP lid distance being shortest around λ = 0.6, which can be a consequence of the sidewise/titling movement of the ATP lid associated with the upward shifting of the catalytic core.⁴⁷ This observation supports the pivotal role played by the active site/catalytic residues in modulating both the catalytic reaction and the opening dynamics of the ATP lid.^36,47

Figure 7.

Superposition of the AdK structure obtained from the alchemical transformation simulation between RS and PS: (A) overall structure and (B) zoom-in view of the active site showing the relative orientation of the R123, 156, and 167 residues and the catalytic loop between RS (λ = 0.0) and PS (λ = 1.0). In the figure, the CORE subdomain is shown in gray cartoons, blue and light blue cartoons for the ATP lid (blue for RS and light blue for PS), and orange and light orange cartoons for the AMP lid (orange for RS and light orange for PS). The catalytic loop shown in purple is for RS and light pink is for PS. In addition, the gray cartoon is shown for the TS-mimic state, i.e., the λ = 0.5 state.

Opening ↔ Closing of Apoenzyme and Its Free Energy Profile

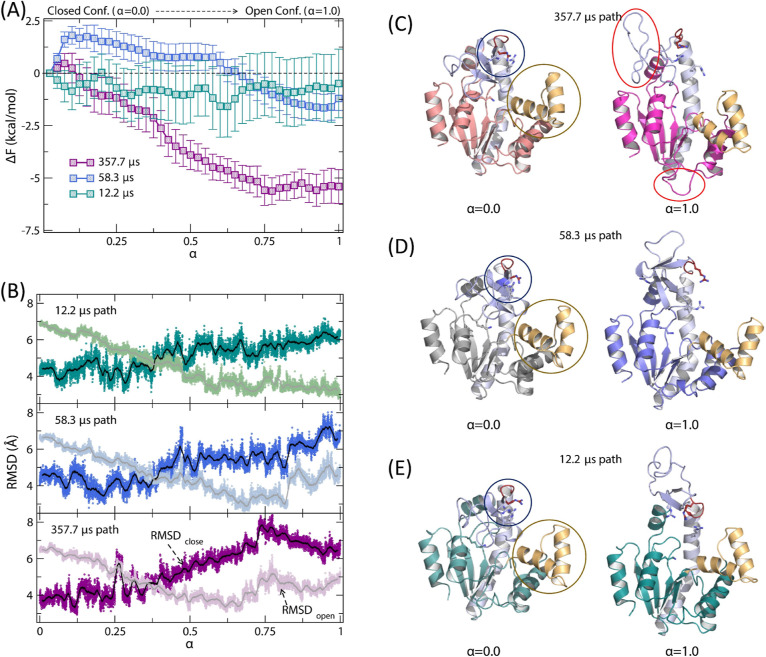
A recent study of AK opening and closing by Zheng and Cui revealed multiple pathways for the close-to-open and open-to-close transitions of an apo-state enzyme, with conformational transition times ranging between 1.8 and 77.2 μs and between 12.2 and 357.7 μs, respectively.⁴⁰ This study also found that the AMP lid remained open, even in the closed state. To better understand the pathways with different time scales, we carried out the SMCV free energy simulations starting from three selected open-to-close conformational transition pathways of Zheng and Cui⁴⁰ with different closing times (12.2, 58.3, and 357.7 μs, respectively). The resulting free energy profiles are presented in Figure 8A, with the profile shown in cyan for the 12.2 μs pathway, blue for the 58.3 μs pathway, and purple for the 357.7 μs pathway, respectively. In the figure, the free energy profiles are plotted in the direction of opening (i.e., α = 0.0 → 1.0) for comparison with the free energy profiles of the holo-enzyme opening (Figure 2A). Notably, the free energy profiles show different free energies of opening (i.e., in the direction of close to open), ranging from −0.7 ± 1.7 to −5.6 ± 0.6 kcal/mol, and very small opening barriers (<1.8 ± 0.4 kcal/mol). For closing, the free energy barriers range from 1.6 ± 1.7 to 6.1 ± 0.8 kcal/mol, with their orders following their opening time scales.

Figure 8.

(A) SMCV FE profiles of apo-state AK opening between the closed (α = 0.0) and open conformation (α = 1.0): green for the 12.2 μs closing path, blue for the 58.3 μs closing path, and purple for the 357.7 μs closing path. (B) Changes of root-mean-squared displacement (rmsd) values relative to the open and closed conformations of AK along the opening path. Representative snapshots at α = 0.0 (left) and 1.0 (right): (C) for the 357.7 μs closing path, (D) for the 58.3 μs closing path, and (E) for the 12.2 μs closing path. For the α = 0.0 state, the circled regions highlight the different orientations of R123, 156, and 167 (blue circle) and the AMP lid orientation (gold). In (C), the red circled regions for α = 1.0 show the partially unfolded regions; the top circle shows the unfolding of the INSERT region of the ATP lid.

Inspection of the apo-state SMCV pathways reveals several notable differences in the details of the ATP lid opening and motion (Figure 8B–E). First, the slowest opening path (i.e., the path with a 357.7 μs opening time) displays the most distorted ATP lid, with its INSERT segment partially unfolded, in the open conformation (Figure 8C). In contrast, the other two paths exhibit a similar open ATP lid conformation. In the closed conformational state (i.e., at α = 0), the AMP lid shows a similar open conformation across all three paths, although the slowest-opening path has a slightly more closed AMP lid. Consequently, the two lids have adopted different open and closed conformations between the three pathways. Among the observed differences, variations in the orientation and conformation of the INSERT segment in the open conformation (Figure 8C–E) are particularly noteworthy. This suggests that the ATP lid, particularly the INSERT segment, may undergo cracking or local unfolding in the open state.^84,85 In this case, the lid needs to refold before closure or adopts different closing pathways, both of which may contribute to the slower opening/closing rates reported by Zheng and Cui.⁴⁰ Likewise, similar variations in opening and closing rates may be expected in NMR²² and sm-FRET experiments,^25,46 but their direct observation may be difficult due to the spatiotemporal resolution of the measurements utilized. Therefore, although the local unfolding may not be directly relevant to the enzyme’s opening/closing mechanism, it could impact the time scale of the enzyme’s closing as its refolding must take place during or before the closing of the ATP lid.

Together, our simulations in the apo-state are in agreement with the findings of Zheng and Cui,⁴⁰ indicating that the opening of the AMP lid takes place before the opening of the ATP lid, as the dominant pathway of opening in the apo-state. However, this result contrasts with the sequence of events in the holo-state, where the ATP lid opens first, followed by the opening of the AMP lid, and the respective ligands are released during or after the opening of each lid. This discrepancy suggests that the closure of the AMP lid is energetically unfavorable in the apo-state, requiring the binding of AMP in the binding pocket to achieve the lid’s closure. As a result, the opening and closing processes of the two lids follow different sequences of events between the apo and holo-state enzymes (Figure 2D–E).

Discussion

The present study can help distinguish between the two mechanisms of ligand binding, i.e., conformational selection and induced-fit. This distinction is achieved by comparing the free energy profiles associated with enzyme closure in both the apo- and holo-states and analyzing the free energy contributions of both the protein and ligands to the free energy profile of enzyme opening in the holo-state, which were determined as a function of a reaction coordinate α between the closed (α = 0.0) and open-state enzymes (α = 1.0). Our results indicate that the induced-fit mechanism primarily governs the early stages of ligand binding. This is evident from the formation of nonspecific contacts at α = 0.4 (Figures 3C and S2C), during which the ATP lid remains in the open conformation and in later states where both lids are open but the ligands have not been fully released (Figures 3D and S2D). Furthermore, at α ≈ 0.3, ATP interacts with the P-loop, while AMP remains bound in its binding pocket until the AMP lid initiates its opening (Figure S6). Thus, during the initial stages of ligand binding, the two ligands first establish nonspecific contacts with the enzyme. Subsequently, ATP binds to the P-loop, and AMP binds directly to the AMP binding pocket, inducing the closure of the AMP lid. At this stage, most of the free energy associated with enzyme closure and ligand binding is contributed by the ligands. The mode of ligand binding then shifts to conformational selection, with the ATP lid fluctuating between the open and closed conformations until the base and ribose of ATP finally find their respective binding pockets. This transition in the mechanism is summarized in Figure 2D and compared with the ligand binding model based on the apo-state simulations (Figure 2E). Furthermore, our simulations do not find any causal relationship between ATP base binding and ATP lid closure, suggesting that the two events occur independently of each other. In summary, our results suggest that AMP binding and ATP binding to the P-loop occur via the induced-fit mechanism for AMP lid closure, whereas ATP base binding and ATP lid closure follow the conformational selection mechanism.

Significantly, a similar hybrid mode of ligand binding has been proposed by previous simulations by Matsunaga et al.,³⁹ and these results are supported by experiments by Ådén et al., who have extensively studied the surface of ligand binding using ATP as a probe molecule.³⁸ In addition, our results have implications for understanding the allosteric communication between AMP binding and ATP lid closure rates, which is recently proposed by Scheerer et al.⁴⁸ In particular, they observed increased rates of ATP lid closure in the presence of AMP, while AMP did not interfere with the binding of ATP to its cognate binding pocket. In a related study, Lu et al. proposed that repeated conformational transitions are required for proper substrate binding.²⁹ These studies are consistent with our results and emphasize the role of AMP binding in facilitating the closure of the AMP lid. This closure, in turn, contributes to the stabilization of the closed ATP lid through interactions with bound ligands (e.g., ATP + AMP in RS and 2 ADPs in PS). In contrast, if AMP is incorrectly bound, the closed conformation of the AMP lid is not stable enough, as observed in the apo-state simulations, and thus the lid opens rapidly. While these studies corroborate our SMCV simulation results, it is worth noting that alternative pathways are also possible for the opening and closing of AK in the holo-state. For example, ligand binding may first induce the closing of the ATP lid, followed by the closing of the AMP lid. This closing sequence has been observed predominantly in the apo-state enzyme, in both all-atom⁸⁶⁻⁸⁸ and coarse-grained simulations,^41,89 as well as in several holo-state studies, e.g., with ATP-Mg²⁺ and AMP or with Ap5A inhibitors.^90,91 However, in contrast to these observations, our SMCV simulation suggests a different sequence for the holo-state enzyme closing/opening. Specifically, we propose that in the holo-state, the enzyme closes first with induced-fit AMP lid closure, followed by conformational-selection ATP lid closure, with their timing of closure depending on the binding of their cognate ligands, e.g., ATP-Mg²⁺ for ATP lid and AMP for AMP lid in the reactant state. This proposal is based on the fact that the SMCV pathways determined for the holo-state systems originate from the unbiased opening path of AK with bound ligands. Therefore, these pathways are expected to represent the most likely opening path of the enzyme, and it is less likely that alternative pathways are major contributors and thus may not significantly affect the overall rates of enzyme opening and closing for the holo-state enzyme. Furthermore, as proposed in this study, the opening of the ATP lid (in the enzyme opening event) is triggered by the dynamic motion of the ATP’s base and ribose. Thus, if they remain tightly bound to their respective binding pockets, then the opening of the ATP lid may be delayed accordingly. In this case, it may be possible to observe the opening dynamics of the AMP lid first. In both cases, nevertheless, any perturbation of the interaction network with bound ligands in the active site may be critical to initiate the opening of either the ATP or AMP lids or both, as observed in our recent AK mutant study.⁴⁷

Furthermore, our simulations provide valuable insights that can aid in the interpretation of the experimental data. First, our results suggest that the X-ray structures of AK with nonspecific ligands may represent enzyme–ligand complexes formed through nonspecific contacts (Figure S7).⁴² This finding is consistent with the contacts observed in the enzymes characterized using NMR and enzyme variants that hinder enzyme closing.^38,92 Second, our simulations reveal distinct sequences of events in the closing dynamics of the two lids between the apo- and holo-states. This implies that previous measurements of closing dynamics using NMR²² and sm-FRET,²⁵ which were fitted to a two-state model with a single rate, as discussed by Orädd et al.,⁹³ may not fully capture the details of the opening/closing processes of the two lids. For example, the rates of opening/closing measured by NMR may reflect residence times in the open versus closed conformations rather than their actual time scales of conformational changes. Moreover, these residence times may differ between the ATP lid and the AMP lid, and this difference can be further influenced by the presence of Ap5A inhibitors or natural substrates, as compared with the apo-state enzyme. In line with this concept, previous sm-FRET studies conducted by Hanson et al.²⁵ and Aviram et al.⁴⁶ used probes positioned between the ATP lid and CORE domains or closer to the AMP lid, respectively, suggesting that they may have captured different lid dynamics. In contrast, both our apo-state simulations and those of Zheng and Cui observed relatively rapid opening ↔ closing dynamics of the ATP lid while the AMP lid remained open.⁴⁰ Regarding the wide range of opening/closing time scales observed by Zheng and Cui,⁴⁰ our simulations propose that the slower rates of opening/closing may be linked to a partial unfolding of the ATP lid in the open-state conformation. This unfolding hinders the intrinsic opening and closing motions of the two lids and thus complicates the interpretation of the NMR and sm-FRET data. Furthermore, both these experiments and simulations, which primarily focused on the dynamics of the two lids, did not investigate the mechanism of ligand release and its associated time scale, although its understanding would be more relevant in determining the steps contributing to the catalytic turnover rate.

Finally, we note the distinct behavior of AK between the apo- and holo-states, which stems from the unique architecture of its active site. The active site of AK consists of six positively charged catalytic residues (5 arginines and 1 lysine) that, together with the Mg²⁺ cofactor, stabilize the negative charges of the substrates, e.g., ATP and AMP, in the closed state.^47,94,95 Consequently, substantial electrostatic repulsion is expected in the apoenzyme during the closing process. This is in line with the closed conformation observed in the apo-state simulations, where the ATP lid adopts a more collapsed orientation in the ATP-base binding site, while the binding pocket of ATP’s phosphoryl groups (e.g., P-loop) remains open to the solvent. In this conformation, residues R123, 156, and 167 are exposed to the solvent (Figure 8C–E), while still retaining their respective interactions with D158 and 159. Therefore, although ATP may be able to bind in the P-loop in this conformation, transitioning directly to the closed state could be challenging due to the collapsed ATP-base binding pocket, and the opening of the ATP lid becomes necessary before ATP base binding can occur. In contrast, in the presence of ligands, these catalytic residues actively engage with the bound ligands during the closing process. This difference in behavior leads to different mechanisms of enzyme closing and their detailed sequences of events between the apo- and holo-enzymes. In the holo-state, ligand-induced closing occurs with the binding of ATP and AMP to their respective binding pockets. However, in the apoenzyme, the closing process involves overcoming substantial electrostatic repulsion, resulting in distorted closed conformations. This unique difference between the apo- and holo-state enzymes suggests the critical role of ligand binding in modulating the conformational dynamics of AK and the need for a cautious interpretation of experimental data.

Data Availability Statement

Initial PDB coordinates of all systems were obtained from the RCSB Protein Data Bank (https://www.rcsb.org/). The CHARMM (https://www.charmm.org/) and OpenMM programs (https://openmm.org/) are available from their respective home pages. The CHARMM parameters, topologies, example inputs, and system files are available in the Supporting Information. Data (MD trajectories) obtained in this work can be obtained from the authors of the manuscript upon request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.3c01618.

• Details of crystallographic data, definition of CVs for the string method simulations, snapshots in the product state, stacking interactions at the ATP-base binding pocket, representative snapshot of the reactant state system opening at α = 0.3, and X-ray crystallographic structures of nonspecific contacts (PDF)

• MD input files and topology/parameter files (ZIP)

• SMCV input files for the holo-system and topology/parameter files (ZIP)

• SMCV input files for the apo-system and topology/parameter files (ZIP)

This research was financially supported by the National Institute of General Medical Sciences of the National Institute of Health (R01GM132481 to K.N.) and the Swedish Research Council (2021-04513 to M.W.W.).

The authors declare no competing financial interest.