Clots reveal anomalous elastic behavior of fiber networks

Abstract

The adaptive mechanical properties of soft and fibrous biological materials are relevant to their functionality. The emergence of the macroscopic response of these materials to external stress and intrinsic cell traction from local deformations of their structural components is not well understood. Here, we investigate the nonlinear elastic behavior of blood clots by combining microscopy, rheology, and an elastic network model that incorporates the stretching, bending, and buckling of constituent fibrin fibers. By inhibiting fibrin cross-linking in blood clots, we observe an anomalous softening regime in the macroscopic shear response as well as a reduction in platelet-induced clot contractility. Our model explains these observations from two independent macroscopic measurements in a unified manner, through a single mechanical parameter, the bending stiffness of individual fibers. Supported by experimental evidence, our mechanics-based model provides a framework for predicting and comprehending the nonlinear elastic behavior of blood clots and other active biopolymer networks in general.

Softer fibrin fibers lead to an anomalous shear softening and weakened contractility in cross-link–inhibited clots.

INTRODUCTION

Many fibrous biomaterials including actin, collagen, and fibrin occur as networks endowed with unique, nonlinear mechanical properties (1). The structural and mechanical properties of the materials are key to their biological function such as maintaining structural integrity and tissue architecture and facilitating cell-cell communication (2), which typically requires an adaptive mechanical response. Fiber networks should be soft enough to remodel but also stiff enough to resist damage. Notably, the branched network of fibrin fibers is the fundamental building block of blood clots and of fibrin gels used in biomedical applications such as tissue scaffolds and surgical adhesives (3). Fibrin networks provide optimal strength, stiffness, and stability appropriate for these physiological processes (4). A fibrin network results from the thrombin-catalyzed polymerization of fibrinogen monomers into protofibrils, which are cross-linked by the transglutaminase enzyme FXIII-A to form the complex hierarchical structure of fibrin fibers (1). In blood clots, the network is strengthened by forces generated by the active contraction of platelets bound to fibrin that prestress the network (5); it is also modified to a lesser, nonetheless important, extent by the passive inclusions of red blood cells (RBCs) (6).

The micromechanical properties of fibrin (7) and the response of fibrin and clot networks to different types of loading have been extensively investigated (8–11). Experiments have shown that cross-linking increases the extensibility and elasticity of single fibrin fibers (12, 13) and also increases clot compaction, confers mechanical stability, and enhances chemical stability by protecting against fibrinolysis (14–16). Several biomechanical models of fibrin and clot networks of varying scope and scale have been developed [recently reviewed in (17)]. These include macroscopic continuum models for large deformation, viscoelastic response, and rupture of clots (18–21); mesoscopic models of the network that explicitly account for the mechanics of individual fibers (22–24); and microscale, molecular models of the unfolding of single fibrin fibers (25). However, it remains underexplored how the nonlinear mechanical behavior of clots emerges from the interplay between fibrin cross-linking, platelet contractility, and network topology. Thus, it is important to investigate how local deformations mediate the transmission of contractile forces generated by the platelets through the cross-linked fibrin network and the ensuing macroscale mechanical response of the clot (26–29).

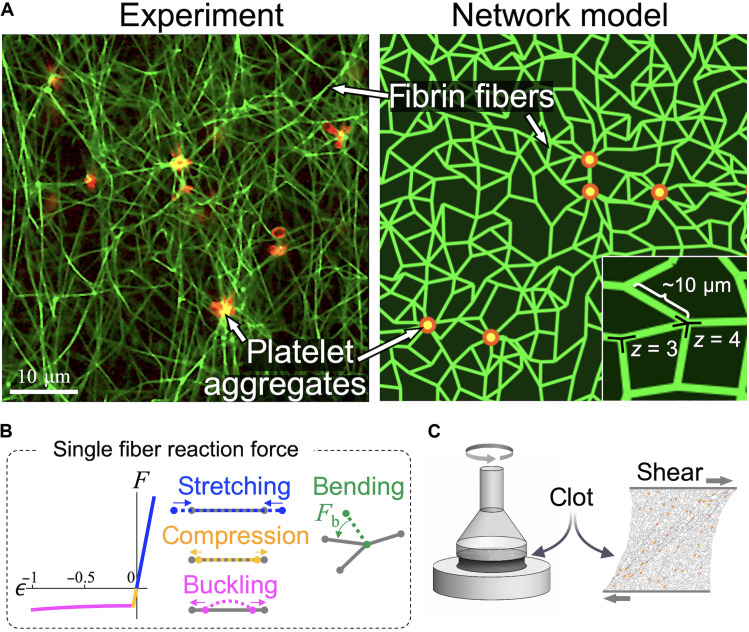
We hypothesize that molecular cross-linking alters the mechanics of individual fibers, particularly its stiffness to bending or buckling, and this change in stiffness affects clot mechanics. To test this hypothesis, we combine experimental measurements with detailed numerical simulations to investigate the emergence of complex mechanical responses including platelet-mediated contraction, and nonlinear elastic behavior of sheared blood clots composed of uncross-linked or cross-linked fibrin fibers. Our experiments reveal a heretofore unreported, anomalous regime of shear softening in clots, characterized by an unexpected dip in the shear modulus with increasing shear stress, when fibrin cross-linking is inhibited. This softening occurs in a physiologically relevant regime of shear, similar to stresses induced by blood flow (30). We also find that unlike elastic solids under compression, softer, uncross-linked clot networks under internal platelet-generated stresses contract less than their stiffer, cross-linked counterparts. Motivated by these observations, we develop a minimal elastic network model to quantitatively study clot mechanics and examine the network response to internal contraction and external shear. To describe the typical structure of a fibrin network (green) with embedded platelet aggregates (red) shown in the experimental image in Fig. 1A, we create a two-dimensional (2D) elastic network model comprising fibers represented by bonds in an irregular triangular network. The mechanical response of a 2D planar network is similar to and captures the stiffening behavior of a 3D network (31). Disorder in the network is introduced by removing bonds randomly with a probability 1 − p to reach an average coordination number ⟨z⟩. It is expected that 3 ≤ ⟨z⟩ ≤ 4 for fiber networks, with these values corresponding to branching and crossing fibers, respectively.

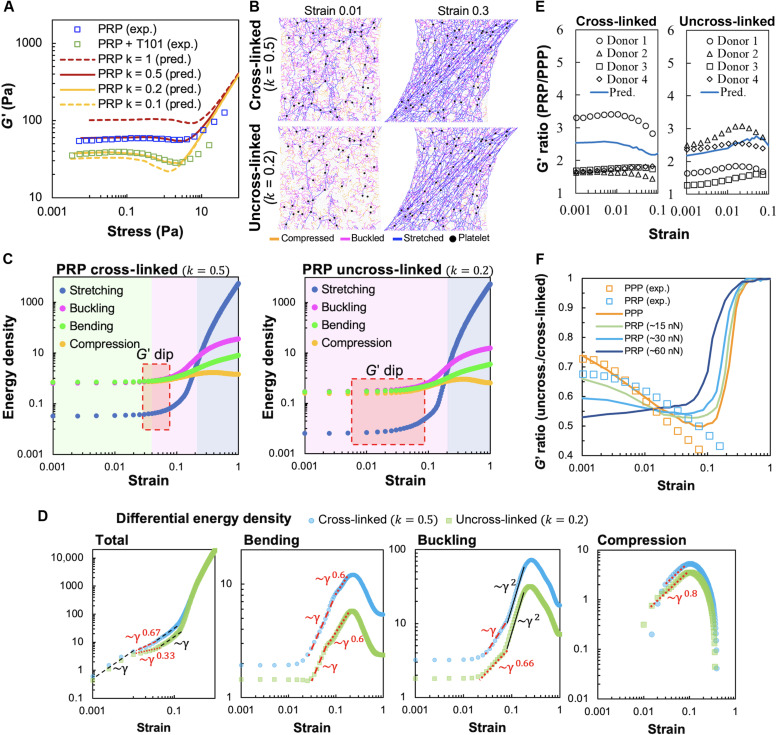
Fig. 1. Active network model of plasma clots.

(A) Microscopic image of PRP clot and a clot approximation by a 2D elastic network model of similar connectivity and length scale (scale bar, 10 μm). Fibrin fibers (green) forming the network are modeled by randomly oriented bonds connected at nodes representing branch points. Platelets (red) are modeled as point sources of contractile forces. The network topology is determined by the number of bonds connected at each node (the average coordination number ⟨z⟩) and by the spacing between the nodes (here, the average value is chosen to be 10 μm, similar to the average fibrin length observed in microscope images). (B) The reaction force F of each fiber to an applied axial strain ϵ exhibits three distinct regimes: stiff linear stretching, compression, and soft buckling when axial compression exceeds a small critical value. In addition, a transverse load acting on a fiber is resisted by bending forces (F_b) at each node when the angle between any two neighboring bonds deviates from its reference value. (C) Shear strain was applied to plasma clots in rheometry experiments, and in model elastic network simulations, to test their elastic response to deformation.

The elastic response of a fiber network to external shear depends on both individual fiber mechanics as well as the network architecture (32). Although the network is sheared at a macroscopic scale, individual fibers may stretch, compress, bend, and buckle under imposed forces, where the typical constitutive relation for a fiber is depicted in Fig. 1B. The network stability is governed by the rigidity percolation threshold, which for a network of central force springs (equal and opposite forces along the spring on a connected pair of nodes) in 2D is predicted from constraint counting originally due to Maxwell (33) to be ⟨z⟩ = 4. Below this isostatic point for central force springs, a fiber network can be stabilized by the bending rigidity of fibers (34, 35). Since the characteristic bending energy of slender fibers is much lower than stretching energy (36), networks in the under-coordinated regime (⟨z⟩ < 4) respond to external shear through floppy, bending-dominated deformation modes. These floppy modes comprising collections of rotating bonds result in unusual elastic response not captured by a continuum elastic theory (37). At higher shear, bonds align in the shear direction, and such floppy modes are no longer available. As a result, the network exhibits a stiffening transition from a bending to a stretching-dominated regime (38). Such a bending-to-stretching stiffening transition has been shown to occur in collagen (31, 39) and is expected to be a key contributor to the nonlinear shear stiffening of biopolymer networks in general.

We numerically compute the mechanical equilibrium states of the model elastic networks under external shear, as detailed in Materials and Methods. The model results are then compared with experiments that subject clots to shear in a rheometer (Fig. 1C) to infer mechanical properties of the fibrin network. Consistent with experimental observations and conventional understanding of biopolymer networks (22), our model predicts an abrupt clot stiffening associated with transition to stretching dominated regime when strain increases. However, it also predicts an unexpected softening dip in the shear modulus when the bending stiffness of individual fibers is reduced. In analogy with prior works that show unusual elastic behavior in networks (34, 40), we describe this softening as “anomalous.” We reveal a signature of this anomalous behavior by analyzing the various regimes of network deformation. Specifically, the increase in differential elastic energy with shear strain exhibits an additional power law regime with an exponent that predicts softening of the shear modulus. To better understand this anomalous behavior and the different observed regimes in the macroscopic mechanical response of the clot, we quantitatively analyze the competition between elastic energy contributions from different fiber deformation modes.

Our model also reveals that the mechanical force transmission through the network is strongly influenced by cross-linking. Specifically, inhibition of cross-linking is expected to result in a network that is floppy, which unevenly distributes and transmits lower force to the network boundaries, resulting in a reduction contraction. Thus, our model relates the effect of cross-linking to two independent macroscopic measurements: stiffness under shear and contractile normal force at zero shear. We provide insights into how cross-linking affects platelet-induced prestress and the stress distribution in the fibrin network. Understanding and characterizing the atypical stress-strain relationships in elastic fiber networks not only are limited to predicting mechanical behavior of clots but also have practical implications in the design and engineering of synthetic materials with tailored mechanical properties (41).

RESULTS

Cross-linking alters the shear response of fibrin networks by enhancing bending stiffness

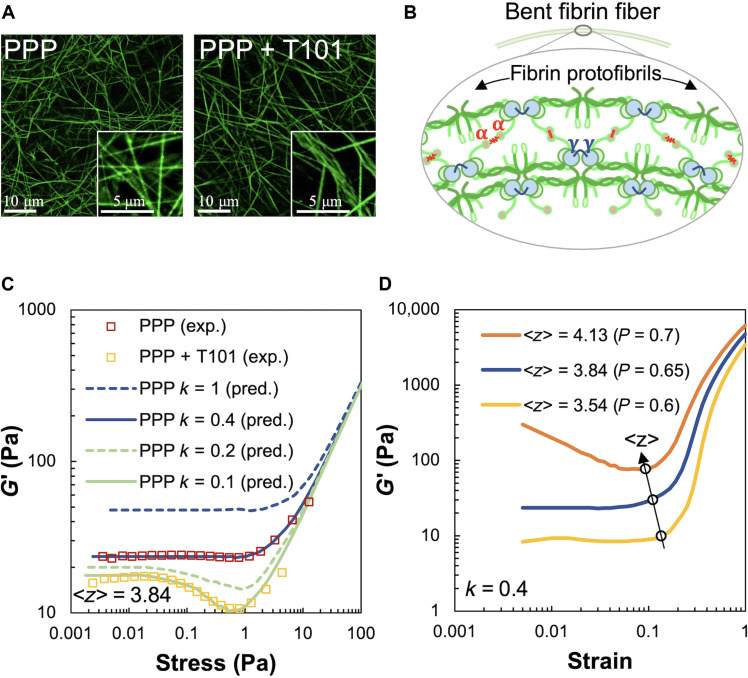
To examine the mechanical properties of fibrin networks derived from blood clots, we performed rheological experiments on plasma devoid of RBCs. We thus avoid the possible complicating modifications that RBCs make to the structure and mechanics of clots, such as enhanced viscosity (6) and compressive stiffening (42). To further isolate the contribution of platelets, we first prepared platelet-poor plasma (PPP) clots. The “clot stabilizing factor” FXIII-A cross-links (or ligates) protofibrils within fibrin fibers by introducing covalent linkages between the α chains and γ chains of fibrin monomers. The γ-γ cross-links are formed between adjacent fibrinogen monomers within a protofibril, while the α-α cross-links ligate across two protofibril strands. To understand the importance of protofibril cross-linking to clot structure and mechanics, we also inhibited the cross-linker FXIII-A by treatment with the small-molecule inhibitor T101 (15). The resulting structural differences between PPP clots with and without cross-linking are shown in Fig. 2A. The inhibition of the cross-linker FXIII-A by T101 degenerates inter-protofibril lateral α-α interactions and also weakens intra-protofibril end-to-end γ-γ interactions in a dose-dependent manner (43). The inhibition of these cross-links does not affect the formation of protofibrils but reduces the rates of their lateral aggregation and branching. On purely mechanical grounds, we expect that reduced lateral links between protofibrils will result in easier bending of the composite fibers they constitute (44), as illustrated in Fig. 2B. Consistent with this expectation, more bent and buckled fiber shapes, including kinks, are observed in Fig. 2A (right) when cross-linking is inhibited by T101 treatment. Sharp bends along with wavy and crimped structures of uncross-linked fibrin are clearly visible in the inset of Fig. 2A (right), to be contrasted with the relatively straight fibers in the untreated case shown in the inset of Fig. 2A (left).

Fig. 2. Effect of fibrin cross-linking on shear stiffness regimes of passive PPP clots.

(A) Microscopy images of cross-linked (PPP) and uncross-linked (PPP + T101) clots. Inset on the right shows loosely cross-linked and crimped protofibrils due to inhibition of FXIII-A by T101 treatment. Scale bars, 10 μm (5 μm for insets). (B) Schematic of bent fibrin fiber showing protofibril structure. Fibrin oligomers assemble into protofibrils, which, in turn, are cross-linked by γ-γ, α-α, and α-γ interactions by FXIII-A. The cross-links are expected to enhance bending stiffness of fibers. (C) Shear modulus (G′) of cross-linked (PPP) and uncross-linked (PPP + T101) clots show a highly nonlinear dependence on applied stress in both experiments (squares, four donors) and simulations (lines). The factor k and ⟨z⟩ in the simulated curves represent the reduced bending modulus from a reference value and average coordination number of network nodes, respectively. Simulations were performed at varying values of the parameters k and ⟨z⟩ to match the experimental data. The model results, at a reduced bending modulus (k = 0.1, solid green line), capture the effect of cross-linker inhibition by T101 treatment on the measured shear modulus (experiments, yellow squares). Both experimental data and model prediction in this case exhibit a noticeable softening dip at ~0.2 Pa. (D) Increasing the average coordination number ⟨z⟩, realized in simulations through less removal of random bonds (p denotes probability of bonds being present), leads to higher shear moduli due to greater number of bond springs and concomitantly reduces the critical strain at which the network abruptly transitions to a stiffer regime. Thus, the position of the transition point in strain can be used to determine the ⟨z⟩ appropriate for the experimental data.

Plasma clots were then prepared between the plates of a rheometer for a subsequent shear assay (see Materials and Methods). Clot gelation was monitored at low oscillatory strain (<1%) at low frequency of oscillation (1 Hz) in a linear viscoelastic regime. The elastic storage modulus (G′) increased over the loss modulus (G″) during gelation and reached a saturation value of about ~50 Pa after 45 min (fig. S1). Because of abundant exogenous thrombin, the lag phase typical of clot initiation was not observable, but the rapid lag phase due to fibrin polymerization was followed by a saturation, indicating the formation of a stable clot structure. T101 treatment reduced the initial clot stiffness (at time t = 0) but had no impact on the fibrin polymerization rate as indicated by constancy in the slope of the lag phase. Overall, PPP clots treated with T101 demonstrated up to threefold lowering in stiffness in the steady state compared to untreated clots.

Following the initial period of gelation, we recorded the storage modulus G′ of PPP clots as a function of the applied amplitude of shear stress (data shown as red squares in Fig. 2C). The loss modulus G″ remained low, indicating that the mechanical response is primarily elastic. At low shear stress (<1 Pa), the clot stiffness stayed constant, but with increasing shear (up to 10 Pa), there was a considerable ~3-fold increase in stiffness. In our experiments, we observed that at stresses higher than 70 Pa, G′ decreased rapidly, indicating irreversible plastic deformations. The T101-treated, uncross-linked PPP clots (data shown as yellow squares) also showed a near-constant shear modulus at low shear stress (<0.1 Pa) and stiffening at high stress (~10 Pa). However, at intermediate stresses between 0.1 and 1 Pa, unlike the cross-linked clots, the uncross-linked clots showed a noticeable decrease in shear modulus by ~10 Pa. For comparison, we also examined the response of fibrin gels formed from fibrinogen (3 mg/ml) by the addition of thrombin (1 U/ml) and 20 mM CaCl₂ and from uncross-linked fibrin gels formed in the presence of 100 μM T101. As shown in fig. S2, the response of cross-linked fibrin gels to shear stresses was similar to that of cross-linked PPP clots: strain-independent linear regime at low applied stress and strain stiffening at high applied stress. The uncross-linked fibrin gels showed a response similar to uncross-linked PPP clots: strain-independent, strain-softening, and strain-stiffening behavior at low, intermediate, and high stress, respectively. The reproducibility of this mechanical behavior between plasma clots and fibrin gels suggests that this is a characteristic elastic response of the fibrin network, independent of other blood proteins.

To explain the highly nonlinear strain-dependent softening and stiffening in cross-linked and uncross-linked clots, we simulate the response of our model elastic network to shear stress (see Materials and Methods). To find the mechanical equilibrium condition under applied load, we implement overdamped dynamics to find the minimum of the total elastic energy. This expression for energy (Eq. 1) is given by contributions from bond stretching/compression, bending, and buckling as

$$\begin{array}{c}{E}_{\mathit{tot}}=\frac{\mathrm{\mu }}{2}{\displaystyle \sum _{<\mathit{ij}>}}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{ij}}-{\mathrm{ϵ}}_{\mathit{cr}}){\mathrm{ϵ}}_{\mathit{ij}}^2+\hfill \\ \frac{K}{l_0^2}{\displaystyle \sum _{<\mathit{ijk}>}}2{\text{sin}}^2\frac{{\mathrm{\delta }\mathrm{\theta }}_{\mathit{ijk}}}{2}+\frac{K}{l_0^2}{\displaystyle \sum _{<\mathit{ij}>}}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{cr}}-{\mathrm{ϵ}}_{\mathit{ij}})2{\mathrm{\varphi }}^2({\mathrm{ϵ}}_{\mathit{ij}})\hfill \end{array}$$ (1)

where the first term represents the total stretching and compression energy per unit volume calculated over all bonds, i and j are nearest neighbor nodes connected by bonds, ϵ_ij is the corresponding axial strain (negative for compression), μ is the stretching stiffness, and Θ is the Heaviside step function that picks out bonds that are not compressed below the critical buckling strain, ϵ_cr < 0. The second term is the total bending energy calculated over sets of three connected consecutive nodes, where δθ is the angle change between neighboring bonds of rest length l₀, and κ is the bending modulus. The third term corresponds to the total buckling energy calculated over all buckled bonds (i.e., which carry compressive strain above an estimated Euler buckling threshold ϵ_cr), where ϕ is the deflection angle of a bond in a buckled shape. Although we do not explicitly model the post-buckled shape of a bond, its deflection angle in the lowest buckling mode can be related to the shortening of its reference end-to-end distance from l₀ to a different length l. For practical purposes, we approximate the resulting nonlinear relation between the deflection angle ϕ and l/l₀ in our computation (45). The expressions of the corresponding forces and the simulation details are given in Materials and Methods.

There are two important reduced dimensionless parameters in the network model: one corresponding to the fiber mechanical properties, namely, the ratio between bending and stretching stiffnesses, κ/(μl₀²), where l₀ is a characteristic fiber length scale given by the distance between branch points, and the connectivity between the fibers in the network, represented by an average coordination number ⟨z⟩. The bending to stretching stiffness ratio κ/(μl₀²) depends on the ratio of fiber diameter to length, which do not appear explicitly in the model, and is therefore expected to be small for slender fibers. Connectivity in fibrin networks is due to the branching of a single fiber into two (or rarely three) fibers or due to the mutual crossing of two individual fibers leading to entanglement and possible cohesion (46). The resulting coordination number (the number of fibers at a branchpoint) is set between three and four (47), leading to a dilute, under-coordinated network that has connectivity below the isostatic point (⟨z⟩ = 4 in 2D) for a network of central force springs. The structure of a fibrin fiber is complex (10) and includes multiple hierarchical levels. To build a minimal model and avoid the structural complexity of fibrin, we treat a fibrin fiber as a single mechanical structure and estimate the typical bending to stretching ratio κ/(μl₀²) for a uniform elastic rod (κ ~ Ed⁴, μ ~ Ed²) using typical, measured values for Young’s modulus (E), fiber length (l), and diameter (d) (7). We then allow the bending modulus to be scaled by a free “softening” parameter, 0 < k < 1, that captures the difference in the bending modulus of fibrin, a cross-linked bundle of protofibrils, from the estimated value for a uniform elastic rod. Prior experimental work, which measures the elastic modulus for individual uncross-linked fibers under bending deformation, suggests that this factor k is further reduced when the cross-linking FXIII-A is inhibited (7).

The bending stiffness scaling factor k and coordination number ⟨z⟩ were tuned in simulations to match the experimental shear modulus for PPP clots (Fig. 2C). While the shear modulus at small external shear is expected to be dominated by softer, bending modes and thus scales with k (48), we show that the critical strain for the onset of shear stiffening is relatively insensitive to k instead of depending on ⟨z⟩. This lets us match the flat low shear region, as well as the stiffening transition point, in the experimental G′ versus stress curve for PPP clots, by varying k and ⟨z⟩, respectively. The fitted value of the bending stiffness factor k = 0.4 is smaller than the idealized limit of a uniform elastic rod corresponding to k = 1, as expected for a cross-linked bundle of protofilaments (44). The coordination number of 3.85 that is found to describe the data well lies between 3 and 4, as expected for fibrous networks. Consistent with our hypothesis that the bending stiffness is reduced for uncross-linked fibrin, the model captures the response of uncross-linked PPP clots, for k = 0.1. This lowered bending stiffness also led to a softening dip in the shear modulus at intermediate strains, similar to that observed in the experimental data. We explored further the effects of varying network connectivity by simulating the shear response of over- and under-coordinated networks. As shown in Fig. 2D, increasing the average coordination number ⟨z⟩ leads to stiffer networks while slightly shifting the critical strain associated with the onset of network stiffening to smaller values. This is consistent with the lack of floppy, purely bending modes as the network connectivity increases beyond the isostatic point (⟨z⟩ > 4). Last, we checked that the observed strain-softening and stiffening occur for different realizations of the network with the same average coordination number. We find only a small variation in the shear modulus versus strain curves for different (n = 6) randomly generated network configurations (fig. S5, A to C).

Shear softening arises from interplay of bending- and buckling-dominated modes

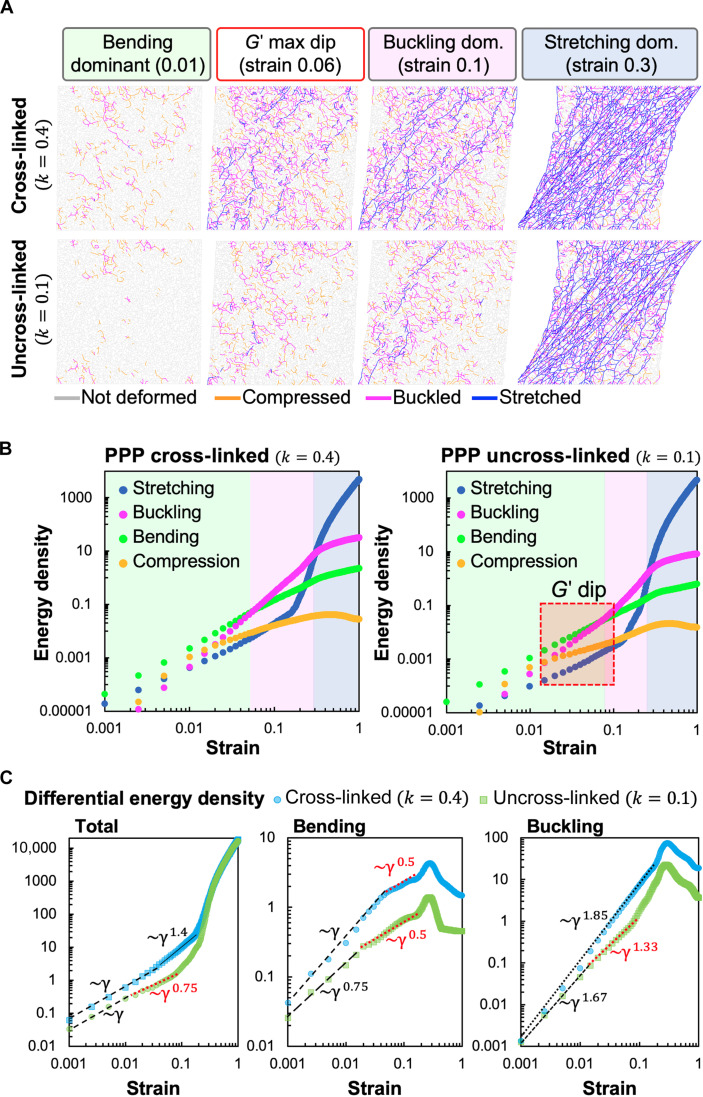
Since it is experimentally challenging to discern the mechanical state of individual fibers under a given applied shear strain, we use simulations to identify the contributions of different fiber deformation modes to the total elastic energy of the network. These are shown in Fig. 3 for the bending stiffness factors obtained in Fig. 2C, which corresponds to cross-linked and uncross-linked fibrin, respectively. We found that both networks comprising fibers with stiffer (k = 0.4) and softer (k = 0.1) bending moduli exhibit three regimes dominated by fiber bending, buckling, and stretching, respectively. Typical simulated, mechanically equilibrated network configurations at representative strain values corresponding to these regimes are shown in Fig. 3A. The different colors represent the type of strain in the corresponding bond, i.e., whether it is stretched (blue), compressed (yellow), or buckled (magenta). Gray (unstrained) bonds can participate in bending modes by changing their mutual angles (not visualized).

Fig. 3. Contribution of different deformation modes to shear response of model elastic networks.

(A) Simulation snapshots of deformations of cross-linked and uncross-linked networks at various applied shear strains. Individual bonds in the network are colored according to whether they are stretched, compressed, or buckled. The relative occurrence of the different deformation modes depends on both applied strain and fiber cross-linking (corresponds to the value of the bending and buckling stiffness parameter k). The simulation box has dimensions of 70 × 70 bonds and corresponds to an area of 0.5 mm². (B) Calculated elastic energy densities corresponding to stretching, compression, bending, and buckling modes in model simulations for cross-linked (left) and uncross-linked (right) cases. The model predicts that both cross-linked (PPP) and uncross-linked (PPP + T101) clots exhibit three distinct deformation regimes shown by the colored regions, dominated by fiber bending, buckling, and stretching, respectively. The red box indicates the regime of strains where the softening dip in the shear modulus is seen in Fig. 2C and occurs here near the bending-to-buckling transition. This transition occurs at a higher strain for the uncross-linked/lower k network (right), resulting in a broader bending-dominated (green) region. (C) Differential total (left), bending (middle), and buckling (right) energy densities clearly show reduced power law regimes versus applied strain. Unlike cross-linked networks, all energy densities in the uncross-linked (k = 0.1) case demonstrate an additional shallower regime with a lower slope in the region of the softening dip. At larger strains, they exhibit steeper slopes associated with stiffening. This is consistent with the delayed bending-to-buckling transition seen in (B) and also fewer buckled bonds in (A).

At very low applied strains (less than 5%), deformations in an under-coordinated network are dominated by bending modes because slender fibers are easier to bend or buckle and incur less elastic energy cost than when stretched or compressed [κ/(μl₀²) ≪ 1]. As a result, only a few bonds are seen to be stretched at 1% strain at k = 0.4, and the network avoids buckling and compression in bonds at k = 0.1. The constant shear modulus in this low-strain regime scales with the fiber bending modulus (34). At higher applied strains (greater than 10%), individual bonds align along the principal tension direction, resulting in many stretched bonds tilted approximately 45° along the shearing direction. In this regime, the network becomes much stiffer since the stretching energy of individual bonds is high and a different scaling law of shear modulus with strain results. This is consistent with the well-known rigidity transition from the bending to the stretching-dominated regime under external strain that removes the available bending degrees of freedom (49). At very high applied strains, the shear modulus reaches the upper limit of stiffness set by aligned and stretching Hookean springs, and the curves corresponding to different bending moduli converge in the simulations (Fig. 2, C and D). This limit is not attained in our experiments as the clots start to undergo irreversible plastic deformations at large applied strain (50).

For both cross-linked and uncross-linked networks, there exists an intermediate regime between the low shear, bending-dominated and high shear, stretching-dominated regimes (magenta region in Fig. 3B). In this intermediate regime, the greatest contribution to elastic energy comes from buckled bonds under large compression. In the simulation snapshots in Fig. 3A, this strong influence from buckling is manifested as a relatively high fraction of buckled bonds at intermediate strains (5 to 10%), with the fiber compression oriented approximately transverse to the principal stretching direction. At such low-to-intermediate strain values, the compression of these bonds exceeds the buckling threshold, while the stretching is still relatively small. As seen in Fig. 3B, this intermediate buckling-dominated regime occurs in both the k = 0.4 and k = 0.1 networks. However, the transition from bending-to-buckling–dominated regimes occurs at slightly higher strains for the k = 0.1, compared to the k = 0.4 network. This delayed bending-to-buckling transition allows for the intermediate, shear softening region (indicated by red box in Fig. 3B, right) corresponding to the dip in the G′ curves, seen only for k = 0.1.

To better understand the origin of this shear softening (seen only in uncross-linked networks at lower k) and to identify how the different energy contributions scale with increasing shear strain, we plot the differential energy densities ε against strain for different k values in Fig. 3C. We identify appropriate power law scalings (dε/dγ ~ γ^α) in each regime. The slope of the total differential energy density also relates to the shear modulus, G′ ~ d²ε/dγ² ~ γ^α−1. The total differential energy densities for both values of k follow a linear regime (α = 1) at small strains where G′ is constant but exhibit different slopes at the intermediate strains, where we observe a softening regime corresponding to the shallow slope (α < 1) at lower k. This difference in the slopes of total energy densities is a combined effect of energy contributions from all four deformation modes. Both bending and buckling differential energy densities at k = 0.1 show a transition from a steeper to a shallower slope power law regime, with the transition strain being larger for higher values of k. This shift in transition strain indicates that the bending and buckling energies grow slower with strain, and then the stretching mode takes over. However, for k = 0.1, a shallow-slope regime not only is wider in the differential bending energy but also occurs in the differential buckling energy. This correlates with the later onset of the buckling-dominated regime for k = 0.1 seen in Fig. 3B, when compared to cases with higher values of k. Stretching and compression energy densities are not included in the plot because they are lower than bending and buckling at the intermediate strains and do not contribute substantially either to the slope of differential total energy density or to the softening dip. Together, these suggest that the softening dip in shear modulus is a result of buckling of initially compressed bonds as the strain increases from very low values. Reducing exclusively bending stiffness of fibrin fibers does not lead to appearance of softening dip (fig. S5D), showing that the ability of fibers to buckle is essential for this feature. For k = 0.1, this dip is fully expressed since the number of stretched bonds is still very small at this strain regime, while the effect is lost at higher k when a substantially larger number of bonds gets stretched. Thus, by inhibiting fibrin cross-linking, our experiments offer a direct confirmation of this intermediate shear softening effect, which was previously noted only in simulated elastic networks with buckling (51–53).

Fiber cross-linking promotes efficient force transmission in platelet-contracted networks

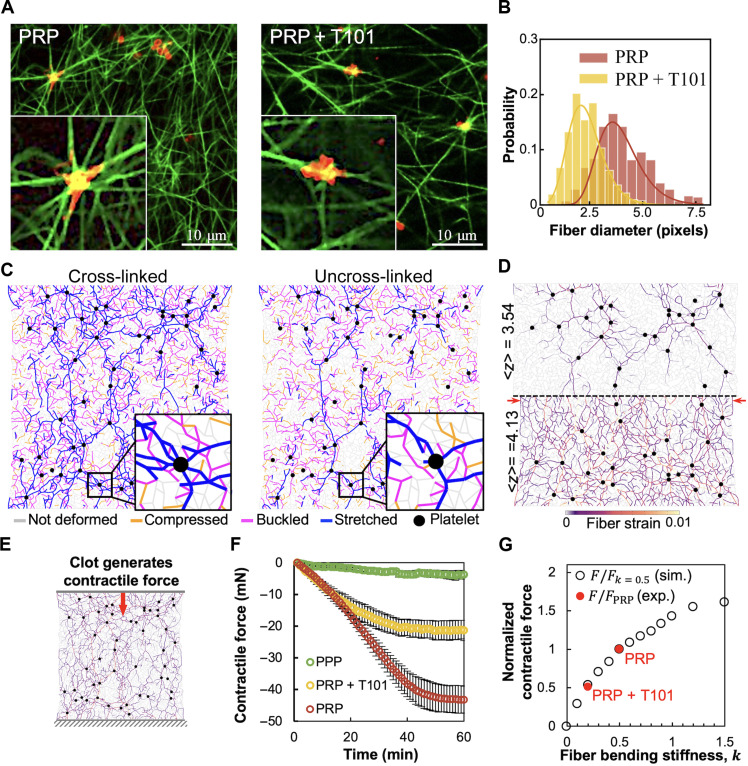
Having examined the behavior of passive fibrin networks, we next sought to examine the differences in the interaction of platelets with cross-linked and uncross-linked fibrin networks. The differences in platelet morphology and fiber distribution around the platelets are highlighted in Fig. 4A. As shown in the inset for the platelet-rich plasma (PRP) clot, the fibers are more uniformly oriented around the platelet cluster, which then extend filopodia along these fibers, resulting in a more isotropic configuration. In contrast, the T101-treated (i.e., uncross-linked) PRP clot exhibits irregular distribution of fibers around the platelet aggregate, lacks filopodia, and has more anisotropic morphology. In addition, our analysis of the relative fiber diameter around platelets (Fig. 4B) indicates that T101-treated clots tend to have thinner fibers than cross-linked PRP clots, which suggests that uncross-linked clots may have weaker platelet-fibrin interaction. It is also known that platelets place vicinal fibrin fibers under tension, shortly after initiation of the clot (54), which facilitates platelet aggregation. The strength of platelet contractility reaches a steady state as the clot is stabilized (55). Thus, while the local mechanical deformations of the fibrin network cannot be quantified as yet, the organization of fibers and filopodia is expected to be correlated with local strains.

Fig. 4. Fibrin cross-linking is critical to platelet-fibrin interactions and to the formation of force chains.

(A) Fluorescence microscopy images of PRP clots with cross-linked fibrin (left) and with T101 inhibition of cross-linking (right). Insets clearly show that fibrin (green) distribution is more uniform around platelets (red) in the cross-linked clots, with the platelets also showing a more isotropic morphology with pronounced filopodia in these cases. Scale bar, 10 μm. (B) Quantification of apparent fiber diameter around platelet clusters (four donors; 70 fibers per sample). T101 treatment of PRP clots leads to thinner fibers around platelets. (C) Model network simulations show the heterogeneous distribution of forces around actively contractile nodes representing platelets (black). The stretched fibers (blue) form force chains that propagate from one platelet to another and are sparser and more localized in the uncross-linked network (right). (D) Force chains are denser and longer-ranged in over-coordinated (⟨z⟩ > 4) than under-coordinated networks (⟨z⟩ < 4). For lower bending stiffness (k) or lower ⟨z⟩, there are many floppy bending modes that reduce fiber stretching. This reduces force propagation to the network boundary, predicting an anomalous effect of less macroscopic contraction in softer networks (retraction difference indicated by red arrows). (E) Activated platelets generate contractile forces that result in macroscopic contraction of the fibrin network. This can be measured as the normal force on the network boundaries, corresponding to the top and bottom plates of the rheometer to which the clot is attached. (F) Time evolution of the contractile force measured experimentally on the upper plate (three donors). (G) Dependence of normalized contractile force on k obtained from simulations (black circles) and normalized contractile force measured in experiment (red dots, negative values indicate inward or contractile force). The k values corresponding to PRP and PRP + T101 were inferred from rheometry.

To connect the fiber width distribution and platelet morphology to local deformations, we simulated the response of our elastic network to active contraction by introducing contractile platelets into the passive fibrin network. The platelet aggregates are modeled as isotropic force dipoles that continuously generate contractile force. This is realized in the model by changing the reference lengths of all bonds attached to the “platelet” nodes to a shorter value, which depends on the effective contractile force generated by platelets (see Materials and Methods for details). Uncross-linked and cross-linked active networks were modeled by modifying the bending-to-stretching stiffness ratio, represented by the stiffness factor, k. Our previous experimental estimate of about 140 platelet aggregates/mm² in a cross section of contracted clots (5) was used to seed the network with ~70 active nodes in the simulation box size that corresponds to an area of 0.5 mm². The contractile forces exerted by the platelet aggregates were obtained from published estimates from micropost measurements as ~30 nN (56). The contractile prestress exerted by the platelets on the fibers manifests as an increase in the stiffness of PRP clots compared to PPP clots. The gelation kinetics showed that the presence of platelets increased the stiffness of clots even at the onset of gelation (fig. S1). In fully formed clots, platelets increased the shear modulus of the plasma clots by threefold, while a twofold increase due to platelets was also seen in uncross-linked clots.

The simulation results showed that the platelet contraction does not increase the strain uniformly in all bonds but only in some, which together form an interconnected subnetwork of stretched bonds highlighted in blue (Fig. 4C). Similar to experiment, we observed a denser subnetwork of fibers in clots with higher bending rigidity, i.e., corresponding to cross-linked fiber networks. In case of uncross-linked fibers with lower bending rigidity, the high-strain subnetwork is sparse and appears as a few long and connected chains. This difference is again because more bonds can easily rotate to relax their tension at lower values of k. The subnetworks of stretched fibers or “force chains” originate from and extend to distant platelet aggregates, and thus serve as conduits for the transmission of forces exerted by the platelets. Consequently, the cross-linked PRP clots, which are made of fibrin fibers with higher bending rigidity and denser force chains, are expected to contract more than the uncross-linked clots (28).

For the same underlying reason as networks with stiffer bending (high k), networks with higher coordination number also exhibit denser force chains (Fig. 4D). The availability of low-energy bending modes in under-coordinated networks (lower ⟨z⟩) causes the stress generated by platelet aggregates to be localized only along a few force chains. In denser networks at larger average coordination number ⟨z⟩,stresses propagate more uniformly throughout the network (more fibers under strain), and as a result, the range of force transmission and bulk network contraction is expected to be larger. The difference in the range of stress propagation is qualitatively seen at the midline of the network depicted by the dashed black line in Fig. 4D (for better comparison, only mirror halves of networks are shown). A greater number of force chains reach the midline for the higher ⟨z⟩ case. We chose ⟨z⟩ = 4.13 in the simulation for representational purposes to show this marked contrast, although we do not expect fibrin networks to exhibit an average coordination number greater than 4. Although it is difficult to directly quantify from experimental images how the coordination number of fibrin networks in clots changes upon T101 treatment, it is plausible that cross-linker inhibition may reduce the number of branch points along with the bending stiffness at these branch points. Thus, our model allows us to make predictions that cross-linker inhibition will lead to fewer force chains, less efficient transmission of forces in the network, and less overall retraction of the clot. This behavior can be detrimental to the strength and stability of fibrin networks and can lead to clot failure.

To elucidate the fiber redistribution around platelets revealed by the experimental micrographs (insets in Fig. 4A), we focus on the force chains around active nodes shown for the simulated networks as insets in Fig. 4C. The fibers directed radially outward from the active nodes transmit the highest tensile strain (blue), while those along the orthogonal direction tend to be compressed and then buckled (purple). The stretched fibers are more numerous for the higher k-network, as expected, due to larger bending and buckling resistive forces from other fibers. In contrast, simulations show fewer force chains for the network with lower k, which propagate along fewer directions. To relate this observation to experiments, we quantified in Fig. 4B the apparent diameter of fibers around the platelet aggregate using images such as in Fig. 4A. These fibers close to platelets were found to be thicker in the cross-linked case, with mean and SD values of 3.62 ± 1.13 pixels for PRP and 2.12 ± 0.734 pixels for PRP clots treated with T101 (n = 4 donors with about 70 fibers per donor; P < 0.001, two-tailed t test). Diameters are compared in pixels to quantify relative dimensions, given that fluorescence microscopy at this magnification does not provide deterministic submicrometer resolution. Our model predictions for the force distribution around platelets (Fig. 4C) suggest a plausible explanation for this observation. The more numerous force chains that develop between two nearby platelet aggregates in the stiffer cross-linked networks can lead to the alignment and bundling of fibers between them, which may then be further stabilized by FXIII-A–mediated lateral cross-linking. Contractile cells (fibroblasts) in fibrin gels have been shown to form such densified and aligned bands of fibers around them, through which they mechanically interact (26). For uncross-linked fiber networks, our model suggests that there are fewer force chains between platelet aggregates, which will therefore lead to weaker bundling of the fibers and lower effective fiber diameter, as observed. This hypothesis is further supported by the observation that the diameter of the fibers far from the platelets is comparable between cross-linked and uncross-linked clots, demonstrating that platelet activity was responsible for fiber bundling (57, 58). Our model (Fig. 4C) also predicts a higher proportion of bent and buckled fibers (increasing by ~40%) for the cross-linked network compared to the uncross-linked case. To corroborate this observation experimentally, we applied curvature analysis (59) to confocal microscope images of PRP clots with and without T101 (fig. S6), which confirmed that there is more curvature present in the cross-linked (i.e., no T101) case. Although individual fibers with lower rigidity k would buckle more readily, in the uncross-linked networks, there are just a few such fibers, mostly localized around the force chains.

An important implication of our model is that cross-linking reinforces force chains. We thus expect that the transmission of forces generated by contracting platelets will be impaired if cross-linking is inhibited. To test this hypothesis, we measured the boundary normal forces at the surface of the clot from the resistance required to maintain at a stationary position, the otherwise mobile top plate of the rheometer (Fig. 4E). As shown in Fig. 4F, the normal force (negative sign implies contractile force) generated by cross-linked PRP clots steadily increases during ~35 min of gelation, after which it slows down and saturates to ~45 mN. In contrast, the normal force generated by the uncross-linked clots saturates at lower values ~20 mN after increasing steadily at a lower rate. The force generated in PPP clots is much lower (<4 mN), thus confirming our hypothesis. In addition, we estimate on the basis of platelet density that the measured normal force translates to sub-nanonewton platelet forces. This value is consistent with previous bulk contractility measurements but lower than what has been reported in single platelet studies, presumably due to the more complex environment and interactions between platelet aggregates and fibrin network in a clot than in a single platelet spreading on a fibrin matrix (29).

Since we already established in Fig. 2 that T101 treatment reduces fiber stiffness under bending and buckling, we computationally mapped the dependence of macroscopic contractile force at network boundary on the fiber bending stiffness factor k. This factor is treated as an unknown free parameter that is independently obtained from fitting the model data to shear rheometry for the two relevant cases of control (k = 0.5) and T101-treated PRP clots (k = 0.2), which is explored in detail in the next section and plotted in Fig. 5A. Both experimental (red) and simulation (black) data points were then normalized by the nominal force of PRP clots and plotted against the corresponding fiber bending stiffness parameter k in Fig. 4G. In close agreement with the experiment, our model predicts a twofold reduction in clot contraction force for T101-treated clots. We note that this prediction does not involve any fitting since the two experimental k values corresponding to PRP and T101-treated PRP were inferred from rheometry. Thus, our model successfully connects two independent macroscopic mechanical measurements (shear modulus and contractile normal force without shear) and shows that both datasets can be explained as an effect of cross-linking on fiber stiffness. Together, the findings depicted in Fig. 4 highlight the strong impact of the inhibition of cross-linking on the active deformation of the fibrin network around platelets, notably leading to a weakened macroscopic clot contraction.

Fig. 5. Shear stiffness of active networks representing PRP clots.

(A) Shear modulus (G′) versus stress for PRP clots (squares, four donors), with and without T101, and for simulated networks (lines) at <z> = 3.84, ~30 nN initial platelet contractile force, and different values of the fiber bending stiffness parameter, k. Uncross-linked PRP clots demonstrate a pronounced softening dip, unlike PPP. (B) Simulation snapshots of networks with individual bonds colored by strain. The number of stretched bonds is high due to platelet-generated prestress and increases further with applied shear strain. (C) Elastic energy density, corresponding to the different deformation modes versus applied strain in simulations. The colored regions indicate the deformation mode that is the largest contributor to the total energy. The red box indicates the region of observed softening dip in G′ in (A). (D) Softening dip in G′ is associated with shallower slopes (γ^α, α ≤ 1) in the differential energy densities dε/dγ. Differential compression energy density is negative at small strains (<0.01). (E) Ratio of shear moduli of PRP to PPP clots at different applied shear strains, shown for four donors (data points) and corresponding simulations (line), for both cross-linked (left) and uncross-linked (right) cases. Platelets stiffen the network by different amounts depending on applied shear. Unlike cross-linked networks, the stiffening factor increases with strain (up to 6%) in uncross-linked networks. (F) Ratio of G′ of uncross-linked to cross-linked networks in simulations (lines) and experiments. Simulation curves correspond to different values of platelet contractility (initial force values in legend).

Active stiffening is dependent on magnitude of shear stress and extent of cross-linking

Next, we examined the mechanical response of cross-linked and uncross-linked PRP clots to shear stress (Fig. 5A). PRP clots were prepared between the plates of a rheometer, allowed to gel, and then subjected to shear. To simulate this process, we first allowed the model networks to contract under active forces, as described in the previous section, but now with nodes on the network boundary held fixed. Subsequently, these clots were subjected to shear strain as described previously for PPP clots but now with randomly placed “active nodes” representing platelet aggregates that actively pull on the fiber network. The PRP network simulation results capture the experimental results with the same coordination number as the passive networks (⟨z⟩ = 3.84) but with a modest increase in the bending stiffness parameter, k. This may indicate that fibers become stiffer to bend in the presence of platelets, possibly through platelet-induced cross-linking. The comparable estimates of model parameters in the passive and active networks from the low and moderate shear regimes suggest that platelets at this density primarily modify the mechanical prestress in the network and not its connectivity ⟨z⟩ or fiber structure. Overall, the response of PRP clots is similar to PPP clots and shows a stiffening transition at large strains. However, unlike PPP clots, platelets not only stiffen the network but also cause a softening dip of different magnitudes in both cross-linked and uncross-linked networks (Fig. 5A). The softening regime in PRP clots occurs at about the same strains as in PPP clots and is also more pronounced in the uncross-linked networks. The modulus of PRP clots treated with 50 μM blebbistatin and 100 μM eptifibatide was identical to those of PPP clots, indicating that the mere presence of platelets does not contribute to the stiffness of the clots but is due to platelet contraction and platelet-fibrin interactions.

To gain qualitative insight into the different regimes of the shear modulus versus shear stress curves in Fig. 5A, we show representative snapshots of the simulated active networks at low and high strains in Fig. 5B. Individual network bonds are colored to show their deformation state, i.e., whether it is stretched (blue), compressed (yellow), or buckled, i.e., compressed beyond the critical strain (magenta). Unlike similar snapshots for networks without active platelet contractility shown previously in Fig. 3A, these networks have considerable stretched and buckled bonds even at the very low strain value of 1% due to the prestress induced by platelets. The number of stretched bonds increases rapidly with applied stress because the prestress pulls out floppy bending modes. The corresponding bending-to-stretching stiffening transition happens at lower applied strains in the case of larger platelet density, in both uncross-linked (fig. S4A) and cross-linked networks (fig. S4B), as a result of this. The force chains propagating from the platelets intensify with applied strain (Fig. 5B), but they remain more localized to the paths connecting platelets in uncross-linked networks. The effects of both cross-linking and platelet prestress are eliminated in the stretching dominated regime at larger strains, e.g., at 30%. Similarly to Fig. 3B for networks without platelets, we now consider in Fig. 5C the contributions to elastic energy density of the different deformation modes. We observe two distinct differences between active networks with platelets and passive networks without platelets (Fig. 3C). First, the platelet-induced prestress creates an initial plateau of energy for all deformation modes at low applied strain. In this initial regime, the effect of the platelet prestress dominates that of the applied stress. Second, unlike passive networks, which have predominantly bending modes at low strains, the platelets induce compression and buckling with energies comparable to that of bending (Fig. 5C). The absence of a purely bending-dominated regime is due to platelets, which are more effective at pulling out floppy modes in uncross-linked networks that have smaller bending forces.

The effect of platelet-induced prestress on softening becomes more evident in the plots of differential energy densities (Fig. 5D). At small strains, both bending and buckling differential energies have very shallow slopes, in contrast with the corresponding energies for the passive networks (PPP cases) shown in Fig. 3C. This is because the additional deformation introduced by the applied shear strain is compensated by the unbending/unbuckling of previously bent/buckled bonds visible in Fig. 4C. In contrast to PPP clots that are stress-free at zero shear, platelets generate a number of compressed bonds that are about to buckle. Therefore, as shear strain is applied, these “compressed” bonds turn into “buckled,” giving an initially negative differential energy density for the compression mode. The subsequent transition from a compressed to buckled state causes an increased slope of the differential buckling energy density and a decreased slope of the differential compression energy at intermediate strains of γ > 0.1 (Fig. 5D). Since all the differential energy contributions in both cross-linked and uncross-linked PRP clots follow linear (~γ) or sublinear (~γ^α, α < 1) power laws at intermediate strains, that is until the stretching begins to dominate, the differential total energy density also demonstrates shallower power law regimes. This reduced power law behavior of the total differential energy density (α = 0.33, 0.67 < 1) leads to the anomalous softening in G′ at intermediate strains seen for both cross-linked and uncross-linked PRP clots. The effect of platelets disappears at large strains in the stretching-dominated regime when external shear forces are much larger than intrinsic platelet forces. The much steeper slope in the total differential energy in this regime is predominantly a result of the same steep slope in the differential stretching energy.

While it is expected that platelets will stiffen the fibrin network by introducing prestress, we next examine the magnitude of this stiffening. The stiffening effect of platelets on clots is seen in terms of the ratio of the shear modulus G′ for PRP to PPP, shown separately for uncross-linked and cross-linked networks (Fig. 5E). Both the measurements for individual donors (discrete markers) and the model calculations (solid line) show at least a twofold increase in shear modulus produced by platelets. The stiffening is shear dependent for both cross-linked and uncross-linked networks. In cross-linked networks, the stiffening due to platelets is most appreciable at low strains and decreases weakly with strain. On the other hand, this stiffening in uncross-linked networks exhibits a noticeable maximum at intermediate shear. This is consistent with the model prediction that platelets stiffen most at strains where the maximum softening dip in G′ occurs for PPP (~6%). By pulling on the surrounding fibers, platelets stiffen the network through a reduction in the number of floppy, low-energy bending modes. In the high-strain regime, however, the applied external force becomes much larger than the force generated by platelets. Thus, at high strain, PPP and PRP clots should have the same value (i.e., G′ ratio trending toward 1). To summarize, the results in Fig. 5E indicate that platelet-fibrin interactions depend on both the amount of applied stress and the fiber bending stiffness associated with fibrin cross-linking. The larger stiffening effect of platelet-generated prestress in uncross-linked networks suggests that prestress may serve as a compensating mechanism for restoring clot stiffness in the absence of cross-linking. The platelets are most effective and provide sufficient clot stiffening at small and moderate strains (up to 10% strain), which may be physiologically relevant at early stages of clot formation.

To examine the effect of prestress due to platelets on networks with and without cross-linking, we plot the ratio of shear moduli of uncross-linked to cross-linked clots predicted from simulations at different values of platelet contractility (Fig. 5F). The corresponding shear moduli for simulated networks at higher and lower bending stiffness are shown in fig. S4 (D and E). Unlike PRP clots, the PPP data (orange squares) show closer agreement with simulations (orange line) at low-to-intermediate strain (<10%). This suggests that platelets induce strain-dependent changes to network mechanics, which are not fully captured by our simple model, which does not strictly control platelet contractility. In the simulation curves in Fig. 5F, all ratios start less than 1 in the bending-dominated low-strain regime and approach 1 at much higher strain values where stretching dominates and the differences in k are not relevant. In the intermediate regime, the shear moduli ratio is sensitive to the contractile forces generated by platelets. For platelets with weaker contractile forces [half the estimated initial value, ~15 nN (56)], the pronounced dip in the G′ versus strain curves for uncross-linked networks leads to an initial decrease and subsequent increase in this ratio. However, stronger platelet contraction (double the estimated initial value, ~60 nN) shows greater softening for the uncross-linked networks before external shear is applied. In addition, platelets with higher contractility express a softening dip in the G′-versus-strain curves for both cross-linked (k = 0.5) and uncross-linked (k = 0.2) networks (see fig. S4, D and E). This behavior is different from networks with lower platelet contractility, which show a pronounced softening dip only at lower k values. The stronger platelets soften the network more when cross-linking is inhibited at small strains than at intermediate strains. Together, the simulation curves in Fig. 5F show that the manner in which platelet contractility influences modulus (specifically the G′ ratio for uncross-linked versus cross-linked fibers) is dependent on the magnitude of strain. This may arise because of the adaptive dependence of platelet contractile force on network stiffness (60) or enhanced fibrin stability under stress (61), through which platelets possibly exert lower initial force, e.g., 15 nN, at low strains (below 1%), and exert higher force at intermediate strains (1 to 10%). Such mechano-adaptation is typical in contractile cells that exert greater traction force when the extracellular environment is stiffer. In addition, we note that the simulation curves predict a crossover in the ratio of shear moduli where these values become identical for networks at different contractility (~2%). This crossover change in slope—seen in both simulation and experimentation—suggests that there is a strong interaction effect between platelet force and magnitude of strain.

DISCUSSION

In this work, we combined modeling and experiments to characterize the macroscopic mechanical responses of cross-linked and uncross-linked plasma clots to shear strain in the presence and absence of active prestress induced by platelets. To understand the micromechanical origins of these responses, we resolved the contribution of individual fiber deformations to the overall mechanical behavior using a minimal elastic network model parameterized from experiments. Our results show that the network response at various shear strains is dominated by different deformation modes of individual fibers and depends on fiber cross-linking, network connectivity, and platelet contraction–induced network prestress. We show with our model that the experimentally observed shear softening transition occurs because of the propensity of uncross-linked fibers to buckle and bend rather than to stretch or compress. Our model also maps the macroscopic shear response to an independent mechanical measurement: that of the platelet-induced contractile normal forces at the network boundary, successfully predicting the factor by which the contractile force is reduced in the uncross-linked network. Our model can thus capture the effect of a biochemical perturbation–induced change in fiber structure through a single coarse-grained parameter (k) corresponding to fiber buckling and bending, thereby linking molecular-scale structure to a macroscopic mechanical property (47).

While the rheology of fibrin gels is well characterized (62), we focus on understanding the physical mechanisms governing the effects of fiber cross-linking and platelet-induced contraction on clot mechanics. Fibrin gels stiffen under increasing shear, although the extent and nature of stiffening vary depending on the polymerization conditions. Consistent with previous reports, we show that fibrin gels and PPP clots transition from linear response characterized by a constant shear modulus to shear dependence at ~10% strain or at a stress of ~1 Pa (63, 64). This strain-stiffening phenomenon is well established in other biopolymer networks such as actin and collagen (19) and in fibrous networks in general (65). Biopolymer networks typically comprise semiflexible polymers that show nonlinear force-extension curves with stiffening under tension, which pulls out thermal fluctuation modes, and softening under compression. Semiflexible polymer networks are expected to stiffen according to a specific power law with shear stress, G′ ~ σ^3/2 (66), as has been demonstrated in the case of cross-linked actin gels (67). Strain stiffening may also arise as a collective effect in athermal fiber networks due to the purely geometric effect of strain-induced fiber alignment (68), as well as the strain-induced transition from a bending-dominated to stretching-dominated response in under-coordinated networks (49). To investigate the nonlinear strain-response regimes of plasma clots, we developed and compared experiments with a general, athermal model of fibrin networks wherein the network mechanics is governed by the bending, buckling, and stretching modes of the constituent fibrin fibers (38). Alternative theoretical approaches to the elasticity of fiber networks, including continuum models with nonlinear constitutive relations (69) and mean field models, exist in the literature (70). One such successful approach is the effective medium theory that captures the elastic response of a disordered network by constructing a uniform network with modified stiffness constants. While this approach can capture rigidity percolation in bending-dominated networks (71, 72), to our knowledge, this has not been extended to describe strain-controlled stiffening (or softening) and active contractility. Therefore, we rely on numeric simulations of a discrete network model to describe these experimentally relevant effects. At higher strains where clot rupture occurs, the irreversible dissociation of bonds between fibrin monomers might become more important, but we ignore this effect in our model since we aim to capture experiments at low to intermediate shear where network response remains reversible and elastic (73).

The agreement between model predictions and experimental measurements of shear modulus at different applied strains demonstrates that the bending and buckling modes of fibers are important for describing the shear response of fibrin networks. Individual fibrin fibers buckle as much as one-third their unstrained length under compression, and they stretch nearly two times their original length under tension (11, 13). Under compression, clots may expel fluid leading to poroelastic effects that are not considered in the present model (74). We focus here on the elastic response of the clots and not plastic or possible viscoelastic effects that are undeniably important for understanding the full regime of clot dynamic behavior. Elastic energy calculations show that the mechanics of the network is governed by bending, buckling, and stretching with the dominant mode strongly dependent on applied strain. The rate of increase of energy contribution with strain is different for the various deformation modes, characterized by different power laws that depend on the bending/buckling stiffness parameter, k. With increase in applied strain, two distinct transitions in predominant modes of deformation occur, namely, bending-to-buckling and buckling-to-stretching. The latter is manifested as an abrupt increase in G′ independent of cross-linking, and this transition is well documented as the strain-stiffening response of biopolymer networks (22). Although softening of fiber networks has been reported in simulations (51, 52), in this work, we provide the first experimental validation of this effect in cross-linking–inhibited plasma clots. We also show that this arises from the bending-to-buckling transition, which occurs at low strains, and is an anomalous elastic effect associated with a different, additional power law regime. This effect may be a broader phenomenon: Recent rheological measurements of clots from rats (75) reported a decrease in shear modulus with increasing shear deformation, although the mechanistic or mechanical basis of such softening response was not investigated. Here, by comparing the mechanics of uncross-linked and cross-linked PPP networks, we show that the anomalous softening-stiffening behavior of uncross-linked fibers is due to a transition from bending to buckling-dominated response, which softens a fraction of the fibers originally under compression.

We explored heterogeneous force transmission in the elastic network subjected to externally applied shear or due to internal platelet contraction. Our simulations show that the fibers transverse to the direction of external load are under compressive stresses and they eventually buckle, while fibers longitudinal to the direction of external load are under tension and get stretched. This orientational anisotropy gives rise to spatial heterogeneity in microscale stress distributions that govern their overall behavior including nonlinear stiffness and tendency to rupture (76, 77). The local heterogeneity in strain distribution also manifests as disordered patterns of force transmission through tensile force chains (26, 27, 78). Force chains are believed to be the conduits for long-range force transmission between contractile cells in a fibrous matrix (79, 80). Previous models have shown that fiber buckling leads to pronounced force chains and enhanced range of force propagation, relative to linear elastic media (81, 82). We find here that easier buckling and bending reduces the extent of force propagation in the network (see Fig. 4) because bonds can bend/buckle more to reduce strain. This points to the role of bending in “screening out” network strain, which has also been recently shown for isolated force dipoles in bending-dominated fiber networks (83). We thus find that the decrease in bending stiffness of fibers results in fewer force chains that extend through the network. Likewise, we observed more numerous and longer force chains connecting platelets in higher bending stiffness networks corresponding to cross-linked fibrin. We relate this to the experimental observation of thicker aligned bundles of fibers around platelets in a cross-linked fibrin network and a more isotropic and well-spread platelet shape.

Last, our analysis shows that a lack of sufficient number of force chains results in an inability to transmit the contractile forces generated by platelets in uncross-linked PRP clots. This provides an explanation of the experimental observation that T101-treated PRP clots generated less contraction. Our model quantitatively predicts a twofold reduction in net contractile force. Thus, we demonstrate another anomalous aspect of elastic behavior in contracting networks: Stiffer fibers result in greater network contraction under internal active stresses, which is counterintuitive for a solid under external compression. Further, our model successfully connects two independent macroscopic mechanical measurements (shear stress and contractile normal force), showing that the reduction of shear modulus as well as contractile force upon can be explained in a unified manner in terms of a single parameter: the reduced bending/buckling stiffness of individual fibers. This provides additional evidence that cross-linking primarily affects fiber bending modulus—in support of the central hypothesis of our work—and also suggests that the normal force reduction is not merely due to platelets exerting smaller contraction in the T101-treated clot. In terms of clot biology, our work suggests that the reduced mechanical strength of clots upon FXIII-A inhibition results not only from softer fibers per se but also from the inability of the softer fibers to effectively transmit the platelet forces to a compacted clot (84).

We have investigated the response of the fibrin networks to shear stresses, which are well within physiological and pathophysiological ranges: The wall shear stresses in blood vessels range widely between 0.1 Pa (in veins) and 10 Pa (in stenosed arteries and arterioles) (30); indirect estimates of stresses at various regions of blood clots are reported to vary widely between 0.1 and >100 Pa (85, 86), and the shear stresses experienced by thrombi may increase by several fold during stenosis (87) or due to local variations in clot porosity (88). Therefore, the increasing stiffness beyond 2 Pa may serve to mitigate spontaneous mechanical damage to the clots in regions of high shear stress. Strain stiffening of fibrin networks is a remarkable phenomenon that may have evolved to maintain the integrity of blood clots and fibrin sealants under large deformation such as when exposed to shear stresses due to blood flow. The implications of our findings at stresses lower than 2 Pa might be particularly important at earlier stages of clot formation. Stresses below 2 Pa arise not only in slower blood flows but also in the remodeling of fibrin networks during cell contraction (89). At these low shear stresses, we noticed qualitatively different behaviors of cross-linked and uncross-linked PPP clots (Fig. 2), and the maximum shear stiffening effect of platelets on uncross-linked, but not on cross-linked, PRP clots (Fig. 5). Of consideration is the timing of FXIII-A–mediated cross-linking in the formation of mature, fully contracted clots since weakly compacted and uncross-linked bundles of protofibrils are simultaneously remodeled by FXIII-A and by platelets (90, 91). The pronounced shear softening observed in our experiments for uncross-linked networks, attributed to the easier buckling of the fibers as confirmed by simulations, suggests a higher susceptibility of uncross-linked networks to undergo local rearrangement in response to platelet-generated forces. Hence, the time evolution of mechanical properties of clots is influenced not only by the direct modification of fiber thickness and branching but also by the heterogeneous distribution of stresses throughout the network.

Overall, we have described a general elastic network model that incorporates platelet activity and can accurately capture the shear response of PPP and PRP clots, as well as the contraction of PRP clots. The model accounts for different fiber deformation modes (stretching, compression, bending, and buckling), the extent of fibrin cross-linking, and the contractility of platelets. We have also described a potentially overlooked softening regime in fibrin networks at intermediate shear before the well-known onset of strain stiffening. The softening is shown to arise because of reduction in bending stiffness of uncross-linked fibers and a delayed bending-to-buckling transition. This softer regime may arise in early stages of clot formation, allowing for greater restructuring by platelets. We also show that, unlike usual elastic solids under external compression, fiber networks under internal active stresses contract less when softer. Last, we show that cross-linking also modulates the distribution of prestress imposed on the network by platelet contraction and changes the deformation modes of the network to applied shear. Our work provides biophysical insights into how mechanical cues from the fibrin network, external stress, and platelet contraction work together to modulate macroscopic clot stiffness, and provokes the possibility of adaptive mechanical regulation in the clotting process.

MATERIALS AND METHODS

Experimental methods

Isolation of PRP and PPP

Blood was obtained by phlebotomy after informed consent from healthy volunteers between 20 and 30 years of age who did not have any chronic conditions or medications known to alter platelet function (approved by San José State University IRB protocol F16134). The blood was drawn in vacutainer tubes containing 3.2% buffered sodium citrate (BD Biosciences, San Jose, CA, USA). The blood was centrifuged at 250 RCF (relative centrifugal force) and 7 rad/s² acceleration for 20 min (5810 R, Eppendorf, Hamburg, Germany). The PRP supernatant was separated from the RBC sediment. To obtain PPP, 10 μM prostaglandin I₂ (PGI₂) (Sigma-Aldrich) was added to PRP and was further centrifuged at 600 RCF and 9 rad/s² acceleration with brakes for 15 min. The supernatant PPP was separated from the platelet pellet. The platelet densities in PRP and PPP were 342,333 ± 19,140 per microliter versus 3133 ± 525 per microliter (mean ± SD, three donors), respectively. For rheometry experiments, the PRP and PPP were used within 4 and 6 hours of isolation, respectively, and the PPP experiments were performed at least after 3 hours of centrifugation.

Shear rheometry and contractility of PRP and PPP clots

Shear experiments were executed on 600 μl of PRP or PPP mixed with thrombin (1 U/ml; catalog no. HT1002a, Enzyme Research Laboratories, South Bend, IN, USA) and 20 mM CaCl₂ (Millipore Sigma, St. Louis, MO, USA) subjected to shear strain at 22°C in between two plates of a rheometer separated by 1-mm gap in two stages (MCR 302, Anton Paar, Graz, Austria) (92). First, a small amplitude oscillatory test at low strain (0.5%) and 1 Hz was applied for 45 min. In 45 min, the gelation was nearly complete as the G′ increased only modestly and slowly until 90 min (57, 58). Second, after clot gelation, shear strain was progressively increased from 0.001 to 250% at a constant frequency of 1 Hz. The shear stress and shear modulus were recorded. To prevent evaporation, a thin immiscible oil layer (Vapor-Lock liquid vapor barrier, QIAGEN, Valencia, CA, USA) was applied along the rim of the clot, and the setup was covered with a humidifying chamber. For experiments involving inhibition of factor XIII (FXIII-A)–mediated cross-linking, 100 μM T101 (Zedira GmbH, Darmstadt, Germany) was added to PRP or PPP before performing the experiments.

To measure contractile forces generated by the platelets, 600 μl of PRP or PPP or PRP with 100 μM T101 mixed with thrombin (1 U/ml) and 20 mM CaCl₂ was placed between the bottom and top plates of the rheometer. The gap between the two plates was set as 1 mm. The resistive normal force on the top plate to maintain the constant gap between the plates, against the contractile pull exerted by the clot, was measured for 60 min.

Clot microstructure

To prepare PRP clots for visualization, 100 μl of PRP was incubated with AF647-conjugated CD42b rabbit anti-human antibody (1 μg/ml; catalog no. 303923, BioLegend, San Diego, CA, USA) to label the platelets, and 1% AF488-conjugated fibrinogen (catalog no. F13191, BioLegend, San Diego, CA, USA) to label fibrinogen for 10 min on a rocker with gentle rocking frequency of approximately 2 Hz (Vari-mix Platform Rocker, Thermo Fisher Scientific, Waltham, MA, USA). After incubation, clots were prepared by adding 20 mM CaCl₂ and thrombin (0.2 U/ml). Immediately, 50 μl of the mixture was added on ethanol-cleaned 1-mm microscope slides (Thermo Fisher Scientific, Waltham, MA, USA). PPP clots were prepared in a similar fashion but without the platelet antibody. The clots were formed at 22°C for 45 min. The clots were sandwiched between coverslip and slide and imaged by confocal microscopy with an Apochromat 63× oil objective with a vertical stack interval of 1 μm (Zeiss LSM 700) for quantitative analyses. The images were analyzed using Imaris v9.5 (Oxford Instruments, MA) and National Institutes of Health ImageJ (93).

Computational model

Network model setup

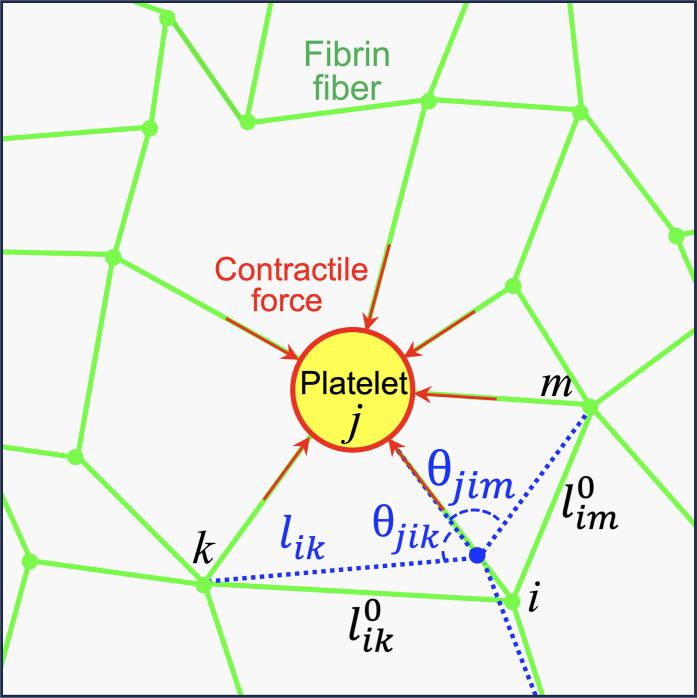
The initial network was generated with Delaunay triangulation in a 2D square domain using the software tool Gmsh (94). The triangulated network had an average spacing l₀ = ⟨l_ij⟩ between neighboring nodes i and j and consisted of about 5000 nodes arranged in a box of size 70 × 70 node spacings. The initial network configuration without platelets is assumed to be stress free. Each bond in the network is then at its rest length, l_ij, and each junction at its rest angle, θ_ijk, initially (Fig. 6). The average node spacing was set to correspond to the approximate average branch length, 10 μm, typically seen in experimental images. Image analysis based on fluorescence microscopy showed no difference between fiber lengths for clots with and without the T101 cross-linking inhibitor (fig. S3). The coordination number was varied by randomly removing a fraction of bonds in the initially fully coordinated network. To prevent dangling bonds, the coordination number at each connecting node was not allowed to be smaller than 3. The probability of a bond being present, p, determines the average network coordination number ⟨z⟩. To increase the network irregularity, the position of each node x_i was additionally perturbed by a small random displacement, δx_i = 0.1 η l₀, where η is a uniformly distributed random number from the interval [−1, 1]. The active nodes representing platelets were randomly placed throughout the mesh to reach a typical platelet seeding density. To prevent large local deformations in the network caused by locally biased density or a lack of connected fibers at the boundary, active nodes were not allowed to be at the boundary and two platelets were not allowed to share the same bond.

Fig. 6. Geometry of the elastic network model.

The model comprises uniform spring-like bonds connected at nodes of different coordination. Some nodes are “active” and represent aggregates of platelets generating contractile forces on connected fibers. Under the action of active nodes and applied strain, the initial rest configuration (green bonds) deforms to a new stressed configuration (representative blue bonds) by displacing connected nodes. This deformation is associated with changing fiber’s end-to-end lengths (stretching/compression/buckling) and changing the angles between bonds (bending). Both these deformation modes result in an elastic restoring force on the concerned node. The calculated forces lead to the overdamped dynamics of the node toward the mechanical equilibrium state where all forces are balanced.

Network model dynamics

The dynamics of the simulated network mimics the inertia-free and viscous-dominated clot dynamics. Thus, the position of each node in the network was updated following equations for noise-free and overdamped dynamics designed to find the mechanical equilibrium state

$${\mathrm{\gamma }}_f\frac{d{\overrightarrow{x}}_i}{d_t}={\overrightarrow{F}}_i^{\mathit{\text{stretching}}}+{\overrightarrow{F}}_i^{\mathit{\text{bending}}}+{\overrightarrow{F}}_i^{\mathit{\text{buckling}}}$$ (2)

where γ_f is the drag coefficient arising from friction due to the surrounding viscous medium, and the total force acting on the i^th node includes contributions from bond stretching (or compressing), bond bending, i.e., changing their relative orientation at junctions, and bond buckling forces, given by

$${\overrightarrow{F}}_i^{\mathit{\text{stretching}}}=\mathrm{\mu }{\displaystyle \sum _{<j>}}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{ij}}-{\mathrm{ϵ}}_{\mathit{cr}}){\mathrm{ϵ}}_{\mathit{ij}}{\widehat{l}}_{\mathit{ij}}$$ (3a)

$${\overrightarrow{F}}_i^{\mathit{\text{bending}}}=\frac{{\mathrm{\kappa }}_b}{l_0^2}\sum _{<\mathit{jk}>}\text{sin}\frac{\mathrm{\delta }{\mathrm{\theta }}_{\mathit{jik}}}{2}{\widehat{n}}_i$$ (3b)

$${\overrightarrow{F}}_i^{\mathit{\text{buckling}}}=-\frac{{\mathrm{\kappa }}_f}{l_0^2}\sum _{<j>}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{cr}}-{\mathrm{ϵ}}_{\mathit{ij}})f\left({\mathrm{ϵ}}_{\mathit{ij}}\right){\widehat{l}}_{\mathit{ij}}$$ (3c)

Here, μ is the stretching modulus of individual bonds and κ_b is the bending modulus at junctions between two bonds, which penalizes change in the bond angle and can include contributions both from the entanglement between neighboring fibers and from the bending of individual fibers. ${\widehat{l}}_{\mathit{ij}}$ represents the unit bond vector connecting the i^th to the j^th node, and the strain in this bond is given by ϵ_ij = (l_ij/l_ij – 1), where l_ij is the actual bond length and l_ij is the target rest length. The direction of the bending force is along ${\widehat{n}}_i=({\widehat{l}}_{\mathit{ij}}+{\widehat{l}}_{\mathit{ik}})/\mid {\widehat{l}}_{\mathit{ij}}+{\widehat{l}}_{\mathit{ik}}\mid$. The buckling force arises when the critical compressive strain is exceeded, i.e., ϵ < ϵ _cr, and opposes the compression. It scales with the bending modulus of an individual fiber, κ_f, and is a nonlinear function of compressive strain, f(ϵ_ij) (45). The Heaviside function Θ takes the value Θ = 1 when its argument is positive, and Θ = 0 in the other cases, and therefore determines whether the fiber is stretched, compressed, or buckled. In our model, we do not calculate the bent shape of the fibers but instead model the effect of buckling as a force that resists compression, with an effective modulus that is much smaller than the stretching modulus, μ. Further, while the bending stiffness of individual fibers κ_f can be different in principle from the bending stiffness κ_b at a branch point between two fibers, we assume them to be equal κ_b = κ_f = κ because they both have contributions from the same underlying molecular cross-linking. This “equal constant” approximation reduces the number of free parameters in the model. In fig. S4F, we consider the effects of having different values of buckling and bending stiffness.

By choosing the length scale as l₀, force scale as μ, and timescale as γl₀/μ, the dynamical equation (obtained by combining Eq. 1 with Eqs. 3a to 3c) can be rewritten in nondimensional form as

$$\begin{array}{c}\frac{d{\widehat{x}}_i^{*}}{{\mathit{dt}}^{*}}=\sum _{<j>}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{ij}}-{\mathrm{ϵ}}_{\mathit{cr}}){\mathrm{ϵ}}_{\mathit{ij}}{\widehat{l}}_{\mathit{ij}}+\hfill \\ \frac{\mathrm{\kappa }}{\mathrm{\mu }{l}_0^2}\sum _{<\mathit{jk}>}\text{sin}\frac{\mathrm{\delta }{\mathrm{\theta }}_{\mathit{jik}}}{2}{\widehat{n}}_i-\frac{\mathrm{\kappa }}{\mathrm{\mu }{l}_0^2}\mathrm{\Theta }({\mathrm{ϵ}}_{\mathit{cr}}-{\mathrm{ϵ}}_{\mathit{ij}})f\left({\mathrm{ϵ}}_{\mathit{ij}}\right){\widehat{l}}_{\mathit{ij}}\hfill \end{array}$$ (4)

where starred quantities indicate dimensionless variables. The important nondimensional parameter that emerges is the ratio of bending to stretching stiffness, κ^* = κ/μl₀².

For Euler-Bernoulli beams, the stretching and bending moduli are given by μ = EA and κ = EI, where E is Young’s modulus and A and I are the cross-sectional area and the second moment of inertia, respectively (36). For a beam of circular cross section, A = πr², I = πr⁴/4, and the expected bending to stretching ratio is then κ/(μl₀²) = r²/(2 l₀²). A fibrin fiber is estimated to be l₀ ≅ 10 μm long and 2r ≅ 280 nm thick (7, 76). Since fibrin is a bundle of protofibrils with bending modulus expected to be smaller than that of a uniform cylinder, we set the nondimensionalized ratio of bending to stretching stiffness parameter in the simulations to be κ^* = k·[r²/(2l₀²)], where r²/(2l₀²) is on the order of 10⁻⁶. Here, k is a factor less than unity, which accounts for the difference of fiber bending stiffness from the ideal limit of a uniform cylinder. The critical buckling strain is set to that of a uniform cylinder, ϵ_cr = −π²r²/l₀². The Young’s modulus of individual fibers was chosen to E = 1.4 MPa to match experimental shear modulus measurements. This comparatively low modulus is consistent with and lies within the wide range of measured stiffness of single fibrin fibers (7, 13, 95, 96). Using E = 1.4 MPa, we estimate the critical buckling load, P_cr = Eπ³r⁴/l₀² ≅ 0.17 nN, which is about two orders of magnitude smaller than the contractile force of an activated platelet (~30 nN) (56). This suggests that there is considerable platelet-induced fiber buckling in a typical PRP.

The network contraction due to platelets is modeled by prescribing shorter reference length for all bonds attached to a platelet. Assuming that an activated platelet can generate maximum contraction force F_p^max, which corresponds to maximum generated strain ϵ_p^max = F_p^max/μ, the corresponding reference bond length is given by l_ij / (1 + ϵ_p^max). Thus, given values of platelet force correspond to the initial situation without any network deformation and externally applied shear strain. The forces in bonds attached to platelets are reduced via the initial relaxation at zero applied strain and increase when shear strain is applied.

We perform the relaxation dynamics, and integrate Eq. 3 in time, until a mechanical equilibrium state is reached, implying that the change in net force becomes negligibly small (typically less than 10⁻⁶%). Shear is applied on the network by displacing the upper and bottom boundary nodes by a fixed amount while letting the other nodes move freely to balance forces in response to the applied strain. When the network reaches mechanical equilibrium, the applied strain is increased and the network relaxes to a new mechanical equilibrium. The increment of applied strain is chosen to be small (0.0005) to avoid large deformations near the boundary. Similar to the experiment, the upper and bottom boundaries were always clamped.

Supplementary Materials

This PDF file includes:

Figs. S1 to S6

References