HPTAD: A computational method to identify topologically associating domains from HiChIP and PLAC-seq datasets

Abstract

High-throughput chromatin conformation capture technologies, such as Hi-C and Micro-C, have enabled genome-wide view of chromatin spatial organization. Most recently, Hi-C-derived enrichment-based technologies, including HiChIP and PLAC-seq, offer attractive alternatives due to their high signal-to-noise ratio and low cost. While a series of computational tools have been developed for Hi-C data, methods tailored for HiChIP and PLAC-seq data are still under development. Here we present HPTAD, a computational method to identify topologically associating domains (TADs) from HiChIP and PLAC-seq data. We performed comprehensive benchmark analysis to demonstrate its superior performance over existing TAD callers designed for Hi-C data. HPTAD is freely available at https://github.com/yunliUNC/HPTAD.

1. Introduction

How chromatin folds in three-dimensional (3D) space plays a critical role in genome function. High-throughput chromatin conformation capture technologies [1], such as Hi-C [2] and Micro-C [3], provide powerful tools to study genome-wide chromatin folding, and have revealed a series of structural features, including megabase (Mb) and 100 kilobase (Kb) resolution A/B compartments [2], 40 Kb resolution topologically associating domains (TADs) [4], [5], and Kb-resolution chromatin loops [6]. Among these structural features, TADs are characterized as ∼1 Mb contiguous regions of the genome where within-TAD interactions are more frequent than between-TAD interactions, thus posited to serve as the basic unit of genome structure. Extensive studies have been performed to investigate the functional implications of TADs [7], [8], [9], in particular, disruption of TAD boundaries has been associated with cellular dysfunction [10] and complex human diseases [11], [12] including developmental diseases [13], [14] and psychiatric diseases [15], [16].

Given the functional importance of TADs, many computational methods have been proposed for the accurate and robust detection of TADs from Hi-C data. Most TAD callers use metrics derived directly from the Hi-C contact frequency matrix to detect TAD boundaries [4], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], while others rely on statistical [27], [28], [29], [30], [31], clustering-based [32], [33], [34], network-based [35], [36], [37], and machine learning-based [38] methods. Results obtained from these methods have been shown to vary greatly in terms of number, size, and biological relevance [39], even when controlling for factors such as technical variation, read depth, etc.

While deeply sequenced Hi-C datasets remain the preferred input data for TAD detection, cost limitations can make the acquisition of deep Hi-C data infeasible. Recent advances in chromatin conformation capture technologies have provided alternatives that can achieve Kb resolution with reduced cost relative to Hi-C. Two such methods, HiChIP [40] and PLAC-seq [41] (herein referred to as HP for brevity) achieve this by combining chromatin immunoprecipitation (ChIP) with in situ Hi-C to capture interactions bound by specific proteins or histone modifications. HP data is primarily used for the detection of enhancer-promoter interactions at high resolution (5 Kb or 10 Kb). Considering the similarity between HP data and Hi-C data, we explore the use of HP data to identify TADs in this work. Specifically, we developed HPTAD, a TAD caller tailored for HP data. We benchmarked the performance of HPTAD against several publicly available TAD callers designed for Hi-C data, using H3K4me3 PLAC-seq data generated from both mouse embryonic stem cells (mESCs) [42] and H3K27ac HiChIP data generated from human lymphoblastoid cells GM12878 [43], and demonstrated its superior performance. We also applied HPTAD to H3K4me3 PLAC-seq data generated from four human brain fetal cell types [44], and for the first time, identified TADs in the developing human cortex. Notably, HPTAD is not intended to compete with other TAD callers using Hi-C data, but rather to call TADs from HP data when Hi-C data is not available.

2. Materials and methods

2.1. The HPTAD algorithm

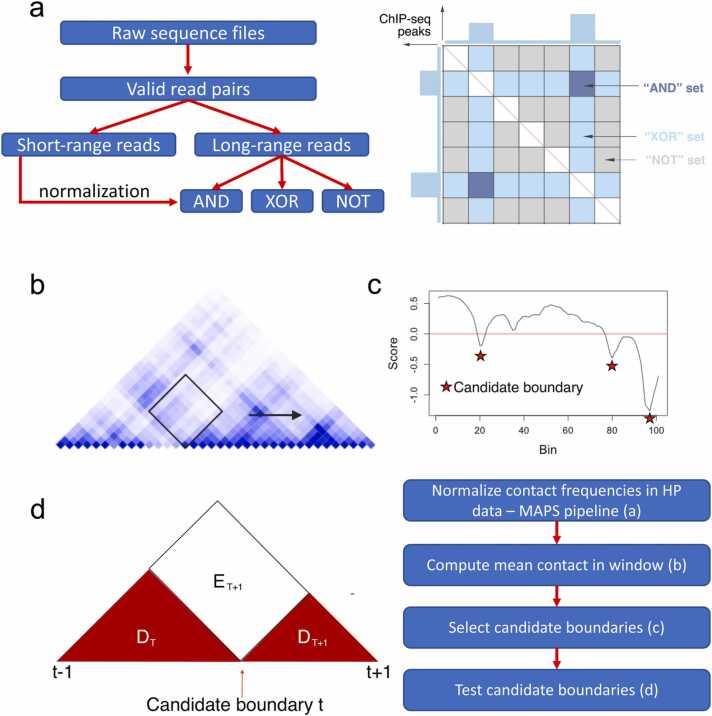
HPTAD starts from the processed HP data, following our previous work [42]. Briefly, we start from intra-chromosomal reads, and split them into two groups: short-range reads (≤1 Kb) and long-range reads (>1 Kb), which are used to measure ChIP efficiency and quantify long-range chromatin interactions, respectively. We further group long-range reads into AND, XOR and NOT sets, depending on whether both of the two ends, only one end, and none of the two reads overlap with the ChIP-seq peaks for the protein of interest.

The HPTAD algorithm consists of the following four steps (Fig. 1). First, we model the non-negative intra-chromosomal contacts as a zero-truncated Poisson distribution with mean $p_{\mathit{ij}}$. We consider the following covariates: effective fragment length (FL), GC content (GC), mappability score (MS), ChIP enrichment level (IP), and 1D genomic distance (D), as described in our previous study [42]. The values used in the regression model are specified as $\log (x_i\cdot x_j)$, where $x_i$ and $x_j$ are the corresponding covariates for bin $i$ and bin $j$, respectively. $D_{\mathit{ij}}$ is the 1D genomic distance between bin $i$ and bin $j$. Unless otherwise stated, the bin size is 40 Kb. We fit zero-truncated Poisson regression models for the AND, XOR, and NOT sets separately:

$$\log \left(p_{\mathit{ij}}\right)={\beta }_0+{\beta }_1\cdot F{L}_{\mathit{ij}}+{\beta }_2\cdot G{C}_{\mathit{ij}}+{\beta }_3\cdot M{S}_{\mathit{ij}}+{\beta }_4\cdot I{P}_{\mathit{ij}}+{\beta }_5\cdot D_{\mathit{ij}}.$$

Fig. 1.

Cartoon illustration of HPTAD pipeline. (a) An outline of the general HP data processing pipeline with a graphical depiction of the “AND”, “XOR”, and “NOT” interaction sets. These represent bin pairs with both, one, or neither end overlapping with ChIP-seq peaks respectively. (b) We calculate the mean normalized contact frequency in a square region, sliding the window along the diagonal. (c) We determine candidate boundaries from scores derived from these values and then formally test these candidates. Diagram (d) is provided to illustrate the regions defined in MethodsSection 2.1. The red areas are separate TAD regions assuming candidates t - 1, t, and t + 1 are actual boundaries, however all three illustrated triangular regions $\left(D_T,D_{T+1},E_{T+1}\right)$ are a single TAD if candidate t isn’t a boundary. A flowchart is provided to illustrate the order of pipeline steps.

We then define the normalized HP contact frequency as the ratio between observed count and expected count.

Secondly, let $X_{\mathit{ij}}$ represent the normalized HP contact frequency between bin $i$ and bin $j$. For each bin $k$, we calculate the arithmetic mean of all $X_{\mathit{ij}}$ within a specified window of $w$ bin units (tuning description in Supplemental Text S1) such that the following is satisfied:

$$\{\left(i,j\right):k-w<i\le k,k<j\le k+w\}$$

(see Fig. 1a). Let $X_k$ represent this value, we then calculated the score $S_k$ as

$$S_k={\log }_2\left(\frac{X_k}{\stackrel{\circledR }{X}}\right)$$

where $\stackrel{\circledR }{X}$ is the average value of $X_k$ across all bins.

Thirdly, the resulting vector of $S_k$ values is smoothed using the “ksmooth” R function, using a box kernel with bandwidth = 3. From this smoothed vector of scores, we select candidate TAD boundaries as the set of points satisfying the following two criteria: (1) the score is identified as a local minimum, and (2) the value is below zero (red stars in Fig. 1b). The rationale for the first criterion follows the original Crane et al., 2015 paper [22] and the second requirement ensures the local minima are below the average score.

Lastly, from the set of candidate boundaries, we choose the final TAD boundaries by first assuming that $X_{\mathit{ij}}\sim N({\mu }_{\mathit{ij}},{\sigma }^2)$. We define $k_t$ as the locus (bin) corresponding to the candidate TAD boundary $t$, and define domain ($D_T$) as the TAD region bounded by candidate boundaries $t-1$ and $t$. Therefore,

$$D_T=\{\left(i,j\right):k_{t-1}\le i<j<k_t\}.$$

We assume that intra-TAD interactions share a common mean, that is

$${\mu }_{\mathit{ij}}={\mu }_T\text{if}\left(i,j\right)\in D_T.$$

Further, we define an exterior region between two TADs ($E_T$) as

$$E_T=\{\left(i,j\right):k_{t-1}\le i<j<k_{t+1}\}-D_T-D_{T+1}.$$

as illustrated in Fig. 1c. Now we assume

$${\mu }_{\mathit{ij}}={\mu }_{E_T}\text{if}\left(i,j\right)\in E_T,$$

and we expect ${\mu }_T={\mu }_{T+1}={\mu }_{E_T}$ if $t$ is not a TAD boundary. We formally test this null hypothesis against the alternative using a likelihood ratio test (Supplemental Text S2).

2.2. Modified Jaccard index

We use a modified Jaccard index for comparing sets of TAD boundaries. The intersecting set contains boundaries that are within one bin unit, upstream or downstream. Recognizing that such an offset could introduce double counting of a boundary within one bin unit of two others, we do not allow any boundary being counted more than once.

Let $A$ and $B$ be two sets of TAD boundaries, and $r$ represent the resolution of the analyses in base pairs. The intersecting set $I$ consists of elements $b\in B$ such that there exists at least one element $a\in A$ where $a-r\le b\le a+r$. We sequentially test elements $b$. If one $a\in A$ satisfies $a-r\le b\le a+r$, it is removed from $A$ to prevent double counting and $b$ is added to intersecting set $I$. If more than one $a\in A$ satisfies $-r\le b\le a+r$, the lowest value is removed from $A$. The modified Jaccard index $J$ is then defined as:

$$J=\frac{\left|I\right|}{\left|A\right|+\left|B\right|-\left|I\right|},$$

where | • | represents the cardinality of the corresponding set.

2.3. Measure of concordance

The measure of concordance (MoC) is a widely-used metric to compare clustering assignments, and it has been used to compare TAD regions [39]. Specifically, let $A$ and $B$ represent two sets of TAD regions with cardinality $N_A$ and $N_B$ respectively, with each region being defined as a range of contiguous bin intervals. Let ${\mathit{AB}}_{\mathit{ij}}$ be the set of bins in both TAD regions, and let | • | indicate the size of the corresponding TAD region in bins. We then define the MoC between $A$ and $B$ as:

$$\mathit{MoC}\left(A,B\right)=\frac{1}{\sqrt{N_A{N}_B}-1}\left(\sum _{i=1}^{N_A}\sum _{j=1}^{N_B}\frac{{\left|{\mathit{AB}}_{\mathit{ij}}\right|}^2}{\left|A_i\right|\left|B_j\right|}-1\right).$$

This metric is a formal measure with range [0,1]: values closer to 1 indicate better agreement between TAD regions, with 1 achieved if and only if $A$ and $B$ are identical.

3. Results

3.1. Performance assessment against the “ground truth”

One key challenge to benchmark the performance of TAD callers is the lack of an objective ground truth. Consequently, significant variability exists among results obtained from numerous published TAD callers [39]. Despite this, some boundaries have been reported to be reproducible not only across samples, but are also preserved across different cell types [45]. In this work, we used TAD boundaries identified from deeply sequenced Hi-C data (Supplemental Text S3) as the working truth to benchmark the relative performances of TAD callers.

We compare the performance of HPTAD to four publicly available TAD callers (OnTAD [26], Grinch [46], TopDom [25], and the insulation score [IS] [23]; Supplemental Text S4). Our inclusion of TopDom and IS as comparators was motivated by Zufferey et. al. [39], which identified those methods as top performers with sparse data. Grinch and OnTAD are newer methods that were not evaluated in Zufferey et. al. [39], however both were benchmarked against TopDom and performed favorably. Grinch was also benchmarked against IS and compared favorably and was designed to be well-suited to sparse datasets (see more details in Section 4). An issue when comparing TAD callers is that methods differ in how they report TAD regions. OnTAD and TopDom define continuous regions as TADs, Grinch reports TADs separated by one bin width and the IS method outputs boundary bins. To ensure consistent comparisons, we define TAD boundaries as bins. We also exclude undefined regions in methods where they are specified (TopDom) rather than folding them into a neighboring TAD or splitting between two neighbors. Consequently, we utilize a modified Jaccard index to compare TAD boundaries (Section 2.2). The key modification to the standard Jaccard index is that we consider boundaries that overlap within one bin upstream and downstream to be matched. The interpretability of this modified Jaccard index is unchanged from the standard index.

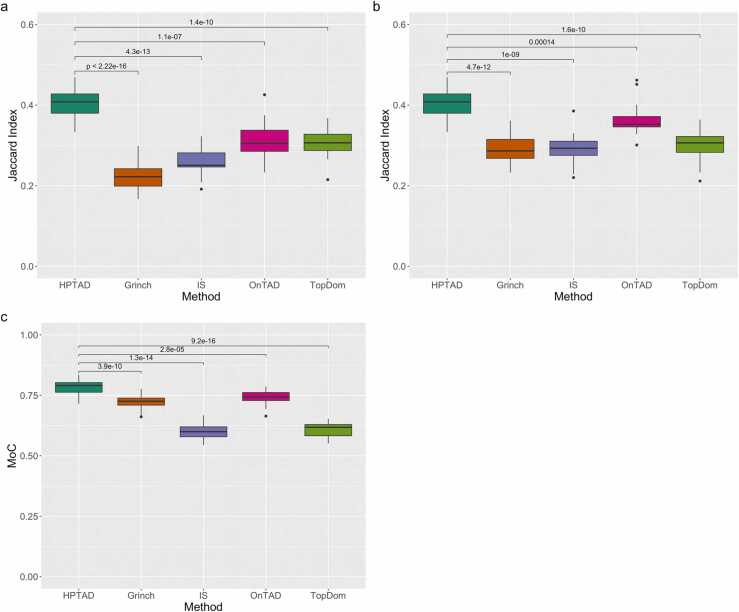
We applied each method to H3K4me3 PLAC-seq data generated from mouse embryonic stem cells (mESC) [42], and used TADs identified from mESC Hi-C data [4] as the ground truth. For the four Hi-C-based TAD callers, we initially used raw counts for the AND, XOR, and NOT sets as input. Considering the biases introduced by the chromatin immunoprecipitation step in HiChIP and PLAC-seq experiments, it is not surprising that HPTAD outperforms the other methods (Fig. 2a, paired t-test p-value ≤ 1.1 ×10⁻⁷) since HPTAD input is normalized to account for these biases. We repeated the experiment, normalizing the counts for effective fragment length, GC content, mappability, and ChIP enrichment level (Fig. 2b). As expected, the mean Jaccard indices for the Hi-C specific methods increased, with the exception of TopDom, which was unchanged. For Grinch, the mean Jaccard index improved from 0.225 to 0.291, for IS it improved from 0.257 to 0.294, and for OnTAD it improved from 0.312 to 0.364. The mean Jaccard index for HPTAD was 0.404. All comparisons by paired t-test were again significant (p-value ≤ 1.4 ×10⁻⁴. In terms of MoC (Fig. 2c), HPTAD also outperformed the other four methods. The mean MoC over all 20 mouse chromosomes was 0.784 for HPTAD compared to 0.723, 0.601, 0.741, and 0.609 for Grinch, IS, OnTAD, and TopDom, respectively (p-value ≤ 2.8 ×10⁻⁵).

Fig. 2.

Performance in mESC H3K4me3 PLAC-seq data. (a) Boxplots displaying modified Jaccard index results for HPTAD and four TAD callers developed for Hi-C data, using raw contact counts as input. (b) Boxplots displaying modified Jaccard index results and (c) Measure of Concordance for HPTAD and four TAD callers developed for Hi-C data, using normalized counts as input. Displayed results are for all 20 mouse chromosomes. The numbers above pairs of boxes represent the p-value from a paired t-test comparing two methods.

We next repeated the previous experiment applying each method to H3K27ac HiChIP data generated from human lymphoblastoid cell line GM12878 [43], and used TADs identified from GM12878 Hi-C data [47] as the ground truth. We observed consistent relative performances of different TAD callers (Fig. S1). Again, HPTAD outperformed the other methods with respect to both Jaccard index and MoC. We observed that for all methods, both the Jaccard indices and MoC are lower for the GM12878 results relative to the mESC experiment. This is likely attributable to the lower depth of the GM12878 experiment with respect to the mESC experiment (∼644 million vs. 1.1 billion raw reads) [48].

3.2. Reproducibility of TAD calling results

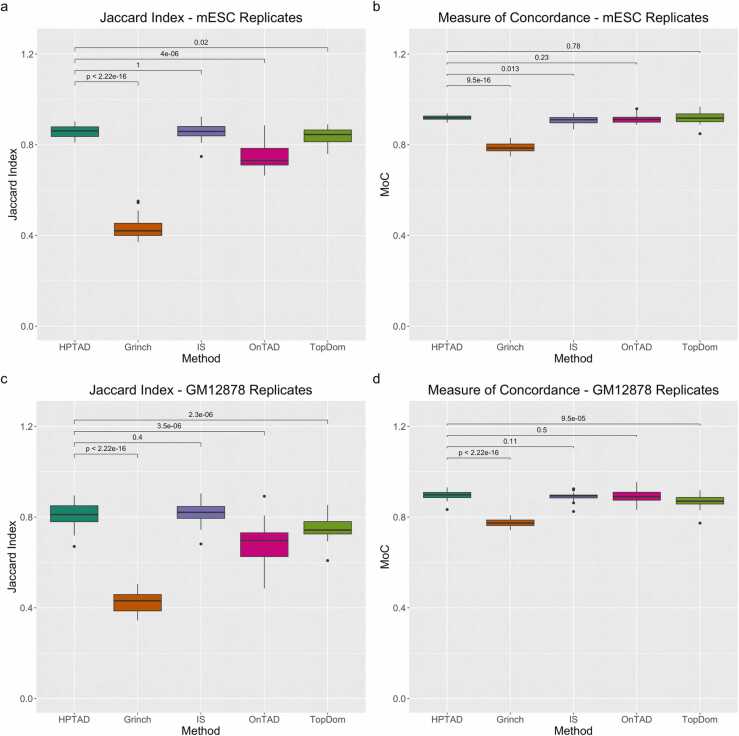
A reasonable TAD caller should be able to generate reproducible results across biological replicates of the same cell type. To benchmark the reproducibility of different methods, we compared results from the five TAD callers using two biological replicates from mESC H3K4me3 PLAC-seq data [4] and GM12878 H3K27ac HiChIP data [43]. We observed strong agreement between biological replicates for all methods except for Grinch (Fig. 3). The mean Jaccard indices for the other four methods ranged from 0.756 (OnTAD) to 0.857 (HPTAD) and the MoC values ranged from 0.909 (IS) to 0.923 (HPTAD) for the mESC replicates (Figs. 3a, 3c). Similarly, for the GM12878 replicates the mean Jaccard indices for the same methods ranged from 0.684 (OnTAD) to 0.817 (IS) and the MoC values ranged from 0.870 (TopDom) to 0.895 (HPTAD) (Figs. 3b, 3d). Taken together, our results show that HPTAD achieves high reproducibility of TAD calling results between biological replicates.

Fig. 3.

Consistency between biological replicates. (a) mESC Jaccard index and (b) Measure of Concordance, (c) GM12878 Jaccard index and (d) Measure of Concordance. All boxplots display results for HPTAD and four TAD callers developed for Hi-C data, using normalized contact counts as input. Displayed results are for all 20 mouse or 23 human chromosomes.

3.3. CTCF enrichment

Previous studies have showed that the transcription factor CTCF is enriched at TAD boundaries [4]. Since different TAD callers vary in the number and identity of TADs, we evaluated the magnitude of CTCF enrichment at TAD boundaries identified by each method. Specifically, we first examined the number of CTCF peaks as a function of distance from TAD boundaries within a window of± 500 Kb. Reassuringly, for all five methods, we observed CTCF enrichment at TAD boundary, and a rapid decrease in average peak density with increasing distance from a boundary (Fig. 4a).

Fig. 4.

CTCF enrichment for mESC data. Number of CTCF peaks as a function of distance from HPTAD boundaries (a), and average number of peaks per TAD boundary (b). Boxplots displaying results for HPTAD and four TAD callers developed for Hi-C data, using normalized contact counts as input. Displayed results are for all 20 mouse chromosomes.

We then compared CTCF enrichment between methods using two metrics (Supplemental Text S5): (1) the mean number of CTCF peaks per TAD boundary, and (2) the fold change enrichment based on the number of boundaries that overlap CTCF peaks (percentage boundaries containing CTCF peaks / percentage bins containing CTCF peaks). The rationale of the second metric is to mitigate the possibility that a method is capturing a few dense CTCF peak regions but many non-overlapping regions. This does not appear to be the case, however, considering the relative performances of the methods are identical under both metrics (Fig. 4b and Fig. S2). OnTAD exhibits the highest average peak density per TAD boundary and fold enrichment (1.59 and 2.16 respectively), followed by TopDom (1.43, 1.93), HPTAD (1.32, 1.90), Grinch (1.23, 1.76), and IS (1.00, 1.49). Similar relative results were observed repeating the experiment with GM12878 H3K27ac HiChIP data (Fig. S3). Sources of CTCF peak data are provided in Table S1.

3.4. Number of TADs called

To better understand the differences among different methods, we analyzed the number of TAD regions in the H3K4me3 PLAC-seq data from mESC (Fig. S4). Not surprisingly, TopDOM and IS, the methods that call the largest numbers of TADs, are among the worst performers with respect to both the Jaccard index and MoC (Fig. 2 and Fig. S1).

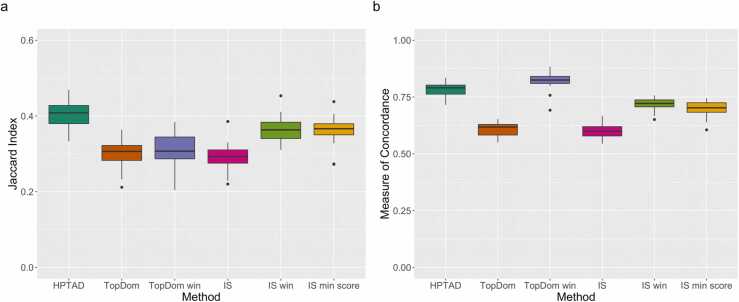
Both the TopDom and IS utilize method-specific tuning parameters. While we conducted our primary analyses using default options (see section S4), we modified parameters to intentionally reduce the number of TADs called to more closely match the “ground truth” numbers (Fig. S5). We then compared the Jaccard indices and MoCs obtained using the results with fewer called TADs.

TopDom has one user-defined parameter, “window.size”, which defines the number of bins to extend for locus evaluation. Larger window sizes lead to fewer called TADs so we extended this to the maximum recommended value of 20. This reduced the mean number of TADs called per chromosome from 319 to 181, which is still greater than the mean number of “ground truth” TADs (158). For the IS method, we modified two parameters independently, window size and minimum score, a threshold used to determine whether the change in insulation score between loci is sufficient to indicate a TAD boundary (default is 0). Both parameters are inversely related to the number of called TADs, that is, increasing their values results in fewer TADs. By increasing the window size, we reduced the mean number of TADs called from 246 to 164, and by increasing the minimum score, we similarly reduced the number of called TADs to 166. As expected, we observed improvements in both the Jaccard index and MoC in all three cases, however the performance still lagged behind HPTAD except for the MoC for TopDom (Fig. 5). For TopDom, the mean Jaccard index increased only modestly from 0.303 to 0.307, while for IS the mean Jaccard index increased more substantially from 0.294 to 0.364 (window size adjustment) and 0.360 (minimum score adjustment). All of these are below 0.404, the mean Jaccard index for HPTAD. The mean MoC for TopDom increased from 0.609 to 0.822 (now exceeding 0.786 for HPTAD), and for IS increased from 0.601 to 0.719 (window size adjustment) and 0.697 (minimum score adjustment).

Fig. 5.

Intentional reduction in number of TADs called in mESC H3K4me3 PLAC-seq data. (a) Jaccard index and (b) Measure of Concordance for HPTAD, TopDom (default, same as in Fig. 2), and IS (default, same as in Fig. 2), TopDom win (TopDom with adjusted window size), IS win (IS with adjusted window size) and IS min score (IS with adjusted minimum score). Displayed results are for all 20 mouse chromosomes.

As one illustrative example, we evaluated the TAD at the Sox2 locus using both mESC Hi-C data [49] and mESC H3K4me3 PLAC-seq data [42] (Fig. S6). We found that HPTAD-identified TAD from PLAC-seq data achieved the best match with TAD identified from Hi-C data. OnTAD performed the second best, with a slight shift at the TAD boundary regions. The other three methods, TopDom, Grinch and IS, all divided one TAD into a few sub-TADs. Taken together, this example showcased the satisfactory performance of HPTAD on PLAC-seq data.

3.5. Application to H3K4me3 PLAC-seq data generated from four human fetal brain cell types

Our group has recently performed H3K4me3 PLAC-seq experiments on four human fetal brain cell types, including radial glia (RG), intermediate progenitor cells (IPCs), excitatory neurons (eNs) and interneurons (iNs) [44]. We applied HPTAD to H3K4me3 PLAC-seq data generated from these four cell types at 5 Kb bin resolution, and identified 4285, 4046, 4501 and 4537 TADs with size 200 Kb ∼ 1 Mb in RG, IPCs, eNs and iNs, respectively (Table S2). We first evaluated the cell-type-specificity of TADs. Specifically, we defined a TAD boundary as cell-type-specific, if it is at least 100 Kb away from TAD boundaries identified from other cell types. Consistent with previous findings [4], the majority (86.6% ∼ 88.4%) of TAD boundaries are shared across cell types (Fig. 6a). Next, we integrated TADs with 35,552, 26,138, 29,104 and 22,598 enhancer-promoter (E-P) interactions identified from RG, IPCs, eNs and iNs [44], and found that most (74.1% ∼ 81.6%) E-P interactions are within TADs (Fig. 6b), and such proportion is consistent across all four cell types. We further performed an integrative analysis of TAD boundary regions and ATAC-seq peaks generated from the original study [44]. For all four cell types, the cell-type-specific TAD boundary regions contain significantly fewer ATAC-seq peaks than that in the cell-type-shared TAD boundary regions (Fig. 6c). The Chi-square test P-value is 1.68e-8, 3.90e-4, 7.63e-4 and 3.11e-14 for RG, IPCs, eNs and iNs, respectively. Taken together, our results are consistent with the literature which show that TADs provide a constitutive structural basis for fine tuning of gene regulation, and we hypothesize that the cell-type-specific TAD boundary regions may enrich for cell-type-specific inactive heterochromatin regions.

Fig. 6.

TADs identified from four fetal brain cell types. (a) The proportion of cell-type-shared TAD boundaries in each of four cell types. (b) The proportion of intra-TAD enhancer-promoter interactions in each of four cell types. (c) The proportion of TAD boundary regions containing ATAC-seq peaks, for both cell-type-specific TAD boundary regions (represented by black bars) and cell-type-shared TAD boundary regions (represented by grey bars).

4. Conclusions

Compared to genome-wide Hi-C assay, lower-cost and more targeted methods such as HiChIP and PLAC-seq provide attractive alternatives. Here we present HPTAD, a novel method for TAD identification in HP data. We benchmarked the performance of HPTAD to four publicly available TAD calling methods designed for Hi-C data and demonstrate the superior performance of HPTAD in HP data. In addition, we demonstrate that HPTAD can achieve high reproducibility between biological replicates. We further manipulated the number of TADs called by two methods assuming oracular knowledge of the true number of TADs. Even with such matching HPTAD still outperforms these methods.

HPTAD is most similar in principle to the insulation score (IS) method, which scans the diagonal of a Hi-C contact matrix and computes the insulation score, which is the sum of interactions spanning that locus with a pre-specified neighborhood. TAD boundaries are then identified as local minima of the insulation score. In contrast, TopDom measures average upstream and downstream contacts from a specific bin, called bin scores, and identifies TAD boundaries as inflection points determined by a piecewise linear function. Similar to IS, OnTAD calculates average contact frequencies within specific windows of each locus by scanning along the diagonal, repeating the process for varying window sizes. Hierarchical TADs are called from the union of potential boundaries at different window sizes using a dynamic programming algorithm. Grinch utilizes a fundamentally different methodology: non-negative matrix factorization of the Hi-C contact matrix is followed by a local smoothing procedure and TADs are identified by the application of k-medoids clustering. All of these TAD callers designed for Hi-C data require the N by N Hi-C contact matrix as input (where N is the number of bin pairs), whereas HPTAD requires a list of bin pairs after adjusting for ChIP enrichment bias as input.

The protein immunoprecipitation step of HP technologies biases the distribution of reads towards regions containing the corresponding histone marker (H3K27ac, H3K4me3, etc.), and even with the inclusion of the “NOT” set of interactions in addition to the “AND” and “XOR” sets, HP data is still more sparse than the typical Hi-C data. Tailoring HPTAD to the unique format of HP data is the primary reason for the improved performance, but the aforementioned sparsity also introduces the possibility of regions of the genome for which insufficient reads are collected to determine TADs, a significant shortcoming of our method.

In terms of computational efficiency, we processed the mESC data in 1 h and 12 min using a single core on a 2.50 GHz Intel processor with 9 GB of RAM. This represents the time to sequentially run all 20 chromosomes.

In sum, we developed HPTAD, a TAD caller tailored for HP data. Compared to existing TAD callers designed for Hi-C data, HPTAD can achieve higher or at least comparable accuracy and demonstrates high reproducibility between biological replicates. HPTAD has potential to become a useful tool for analyzing datasets generated from cost-efficient PLAC-seq and HiChIP experiments.

Funding

This study was funded by the NIH grants R35HG011922 (to M.H.) and U01DA052713 (to Y.L.). This work was funded in part by a training grant from the National Heart, Lung, and Blood Institute T32HL129982 (to J.R.).

CRediT authorship contribution statement

Jonathan Rosen: Software, Formal analysis, Writing – original draft, Writing – review & editing. Lindsay Lee: Formal analysis, Writing – original draft, Writing – review & editing. Armen Abnousi: Software. Jiawen Chen: Formal analysis. Jia Wen: Formal analysis. Ming Hu: Supervision, Methodology, Funding acquisition, Writing – original draft, Writing – review & editing. Yun Li: Supervision, Methodology, Funding acquisition, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.