Three dimensional study for entropy optimization in nanofluid flow through a compliant curved duct: A drug delivery and therapy application

Abstract

This research explores the three-dimensional characteristics of nanofluid dynamics within curved ducts, in contrast to earlier studies that mainly focus on two-dimensional flow. By using this ground-breaking method, we can capture a more accurate depiction of fluid behavior that complies with the intricate duct design. In this study, we investigate the three dimensional flow and entropic analysis of peristaltic nanofluid flows in a flexible curved duct, comparing the effects of silver and copper nanoparticles. To obtain accurate results, we assume physical constraints such as long wavelength and low Reynolds number and used a perturbation technique through NDSolve commands for finding exact solutions of the obtained differential equations. A comprehensive error analysis is provided through residual error table and figures to estimate a suitable range of the physical factors. Our findings indicate that the velocity of the nanofluid is directly proportional to the elasticity of the walls, while the mass per unit volume inversely affects velocity. We show that reducing the aspect ratio of the duct rectangular section can decrease entropy generation by raising magnitudes of damping force exerted by to the flexible walls of the enclosure. Additionally, using a larger height of the channel than the breadth can reduce stream boluses. The practical implications of this study extend beyond turbines and endoscopy to biomedical processes such as drug delivery and microfluidic systems.

1. Introduction

Peristalsis is a vital mechanism that involves the movement of materials in various biological processes in the human body. Because of its widespread benefits, many scientists are now exploring peristaltic flows. The article by Vaidya et al. [1] examines blood flow analysis through a non-uniform inclined channel by treating blood as a non-Newtonian Phan-Thien-Tanner (PTT) liquid. The authors found that peristaltic flows at low Reynolds numbers and large wave number have approached significant attention in recent years. In another work, Nadeem et al. [2] established an exact solution data against the governing system of peristaltic flows, thermal, and mass exchange using a sinusoidal channel. The contributors presented axially symmetric and parabolic velocity, concentration, and temperature profiles. These studies demonstrate the importance of understanding peristaltic flows in various biological processes and their applications. Furthermore, they highlight the requirement for accurate quantitative models and methods of solution to examine the complex behavior of fluids in peristaltic motion. The article by Hasona et al. [3] investigates the effects of thermal radiation and electrical conductivity on the peristaltic flow of a Carreau Nanofluid. Thermal radiation is found to be a decreasing function of fluid temperature, according to the scientists. Peristaltic flow is a sort of fluid motion that physicists, mathematicians, and engineers frequently study, particularly in the context of peristaltic pumps. There is a substantial amount of work on the characteristics of such liquids in peristaltic pumping, as illustrated by Refs. [[4], [5], [6]]. Noreen et al. [7] examine the influence of a magnetic field on peristaltic flow in a Casson fluid model in another study. A lubrication scheme is executed to examine the flow characteristics. The scientists analyzed that when the Hartmann number M increases towards the channel walls, so does the velocity field, whereas it decreases in the channel center. Overall, these investigations show the complex behaviour of fluids in peristaltic motion and illustrate the need of taking into account elements like heat radiation, electrical conductivity, and magnetic fields when researching such systems.

The flow of fluids across curved geometries occurs often in several domains, including microfluidics, industrial ducts, and medical equipment. Essentially, peristaltic flows—which include manipulating walls to contract and expand and promote the transit of items like blood, urine, food, and sperm—are what drive the majority of material movement through the body. This is essential to many biological activities. Researchers have conducted multiple studies to examine the effects of various viscosities and geometries on peristaltic flows. A curved conduit with changing viscosity model and electro-osmotic effects were used by Salahuddin et al. [8] to work on the peristaltic movement of carbon nanotubes. They found that increasing the viscosity parameter decreased flow velocity and temperature while altering the temperature profile for carbon nanotubes (CNTs) by increasing the heat absorption value. Additional studies have looked at peristaltic movement calculations in curved shapes using mathematical models. While McCash et al. [9] looked at the mathematical model of peristaltic flow in an elliptic duct with ciliary walls, Barton and Raynor [10] provided a theoretical analysis of wavy movement in tubes. The distribution of velocity and temperature profiles showed axial symmetry in both cases, the authors found. Studies in Refs. [[11], [12], [13]] have described peristaltic transports in curved enclosures for a variety of fluid models. The effect of curvature-dependent channel walls on laminar viscous material flow peristalsis through a curved geometry was investigated by Saba et al. [14]. The researchers found that when modeling flows in curved channels, the curvature parameter should be taken into account because it has a significant impact on the mechanical and thermal characteristics of the flow. These works highlight the significance of investigating the effects of curvature and changing viscosity on peristaltic flows in curved geometries as well as the requirement for accurate mathematical models and solution methodologies to comprehend these challenging systems.

Small, fewer than 100 nm-diameter-diameter particles are known as nanoparticles. Nanoparticles like carbon nanotubes (CNTs) have the potential to revolutionize medical imaging, treatments, diagnostics, and other biological processes because of their small size and physical interaction with biological components. However, the low thermal conductivity of fluids typically limits the industrial applications of heat transfer analysis. To solve this problem, the amount of nanoparticles in the fluid might be increased. An experimental study by Choi and Eastman [15] shown how adding nanoparticles to a fluid can enhance its thermal conductivity, viscosity, thermal diffusivity, and heat transfer rate [ [16,17]]. Using ion-slip and Hall effects, Qureshi et al. [18] calculated the dispersion of nanoparticles in magnetohydrodynamic (MHD) liquid. According to Akram et al. [19], the addition of nanoparticles to base liquids alters the thermal properties and viscosity of the resulting nanoliquids. Viscosity is a significant industrial economic variable. Some more interesting works on the topic can be cited in [[20], [21], [22], [23], [24]].

The majority of flows in the medical industry and in the human body are by their very nature three-dimensional. Due to the relevance of three-dimensional peristaltic flows to both the mechanics of roller pumps and blood flow within arteries, research has concentrated on these flows. Nadeem et al. [25], explored the effect of intricate conduits on pumping flow was investigated by resolving the resulting coupled and nonlinear equations numerically and by series solutions. In order to account for low Reynolds number and long wavelength restrictions, Ellahi et al. [26] carried out a theoretical examination of the impact of magnetohydrodynamics on the peristaltic flow of Jeffrey fluid in a rectangular duct. The mathematical model for the peristaltic flow of Jeffrey fluid containing nanoparticles in a three dimensional conduit was examined in the wave frame in another work by Nadeem et al. [27]. The peristaltic flow of a pair stress fluid in a non-uniform rectangular duct with compliant walls was also studied by Ellahi et al. [28] in their final study.

Entropy, which counts the different ways a thermodynamic system can be built, is a commonly used thermodynamics term that is frequently used to indicate the degree of disorder or the advancement of thermodynamic equilibrium. Understanding and raising the effectiveness of energy conversion technology, such as heat exchangers and combustion engines, are applications of entropy generation in fluid flow. Entropy generation analysis can help with the design and optimization of microfluidic devices and drug delivery systems in the medical profession. Overall, improving energy efficiency and creating efficient technologies in a variety of disciplines depend on research into entropy formation in fluid movement. Researchers have investigated the creation and prediction of entropy in a variety of flow conditions in non-Newtonian fluids. While Ellahi et al. [29] researched the peristaltic flow of nanofluid with entropy formation in a porous media; Abu-Hijleh et al. [30] investigated the numerical prediction of entropy generation from natural convection in a horizontal cylinder. Hayat et al. [31] looked into the impact of entropy generation on the peristaltic flow of nanoparticles in a rotating frame, whereas Reddy et al. [32] researched entropy production for the peristaltic flow of gold-blood nanofluid under electrokinetic force in a microchannel. In order to study entropy formation in peristaltic flow utilizing single and multi-wall carbon nanotubes, Ijaz Khan et al. [33] utilized numerical simulations. Numerous biomedical and industrial industries use peristaltic flows in curved conduits. For instance, they are employed in artificial organs, bioreactors, microfluidics, and drug delivery systems. Peristaltic pumps are used in medicine delivery to accurately control the flow rate of pharmaceuticals. They are employed in microfluidics to mix and move fluids. Peristaltic flows are employed in bioreactors to produce an environment that is conducive to the growth of microorganisms. Peristaltic flows are utilized in artificial organs to replicate the body's normal blood flow. There are a few more recent researches on the subject that may be found in Refs. [[34], [35], [36]].

The explanation above makes it clear that little research has been done on the peristaltic process of nanofluid in curved duct sections. But a study of this kind would be very helpful for both biomedical and commercial uses. Understanding peristaltic flows in curved ducts is essential since most flow patterns are curved in shape. Additionally, because it may improve the thermal conductivity of ordinary fluids, the usage of nanofluids is becoming more and more significant in the medical industry. In this inquiry, peristaltic nanofluid flows in a curved duct with rectangular sides and flexible walls are studied in three dimensions to address these problems. To examine how different types of nanoparticles affect wavy flows, copper and silver nanoparticles are taken into consideration. The physical structure is mathematically represented under specific constraints in order to analyze the issue statistically, and then linear transformations are used to add a non-dimensional collection of new factors. By doing this, a complex system of equations is reduced to a manageable, concise set. The series solution technique is then used to solve the issue. The results are thoroughly described in the concluding section, and essential amounts are visually displayed with respect to specific criteria. This study is anticipated to shed important light on the peristaltic flows of nanofluids in curved ducts and has the potential to significantly affect biomedical and industrial applications.

2. Mathematical modeling

In this work, we take into account the flow of a viscous nanofluid in a curved rectangular duct (CRD) that has a 2h height and 2d width. Water is mixed with silver (Ag) and copper (Cu) nanoparticles, and a peristaltic wave travels along the axial direction at a constant speed of c. As a function of angle and time t, the conduit's geometry is set up so that orthogonal line (y-axis) assumes the peristaltic walls, L stands for the reference distance from the center line. The cylindrical coordinate system is more practical because the flow geometry is curved. The lower walls' temperature is given a magnitude of $T_1$, whereas the lower portion has a temperature of $T_0$ (see Fig. 1).

Fig. 1.

Geometrical picture of the CRD.

We consider the curved duct model for the nanofluid as [ [8,12,17,24,[37], [38], [39]]].

$$r\frac{\partial u}{\partial r}+\frac{\partial w}{\partial \theta }+r\frac{\partial v}{\partial y}+u=0..$$ (1)

$${\rho }_{nf}\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+\frac{w}{r}\frac{\partial u}{\partial \theta }+v\frac{\partial u}{\partial y}-\frac{{\mathrm{w}}^2}{r}\right)=-\frac{\partial p}{\partial r}+{\mu }_{nf}\left(\begin{array}{c}\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}u}{\partial {\theta }^2}+\\ \frac{{\partial }^{2}u}{\partial y^2}-\frac{u}{r^2}-\frac{2}{r^2}\frac{\partial w}{\partial \theta }\end{array}\right)..$$ (2)

$${\rho }_{nf}\left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+\frac{w}{r}\frac{\partial w}{\partial \theta }+v\frac{\partial w}{\partial y}-\frac{uw}{r}\right)=-\frac{1}{r}\frac{\partial p}{\partial \theta }+{\mu }_{nf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}w}{\partial {\theta }^2}+\frac{{\partial }^{2}w}{\partial y^2}-\frac{w}{r^2\theta }+\frac{2}{r^2}\frac{\partial u}{\partial \theta }\right)\text{.}$$ (3)

$${\rho }_{nf}\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial r}+\frac{w}{r}\frac{\partial v}{\partial \theta }+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+{\mu }_{nf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}v}{\partial {\theta }^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)..$$ (4)

$${\left(\mathrm{\rho }{c}_p\right)}_{nf}\left(\frac{\partial \bar{T}}{\partial t}+u\frac{\partial \bar{T}}{\partial r}+\frac{w}{r}\frac{\partial \bar{T}}{\partial \vartheta }+v\frac{\partial \bar{T}}{\partial y}\right)=k_{nf}\left(\frac{{\partial }^2\bar{T}}{\partial r^2}+\frac{1}{r^2}\frac{{\partial }^2\bar{T}}{\partial {\vartheta }^2}+\frac{{\partial }^2\bar{T}}{\partial y^2}+\frac{1}{r}\frac{\partial \bar{T}}{\partial r}\right)+{\mu }_{nf}\left(2{\left(\frac{\partial u}{\partial r}\right)}^2+{\left(\frac{\partial w}{\partial r}+\frac{1}{r}\frac{\partial u}{\partial \vartheta }-\frac{w}{r}\right)}^2+{\left(\frac{\partial v}{\partial r}+\frac{\partial u}{\partial y}\right)}^2+2{\left(\frac{1}{r}\frac{\partial w}{\partial \vartheta }+\frac{u}{r}\right)}^2{\left(\frac{\partial w}{\partial y}+\frac{1}{r}\frac{\partial v}{\partial \vartheta }\right)}^2+{2\left(\frac{\partial v}{\partial y}\right)}^2\right)\text{.}$$ (5)

A representation of the peristaltic walls is [ [38,39]]

$$\tilde{a}\left(\theta ,t\right)=h+bcos\frac{2\pi }{\lambda }\left(L\theta -ct\right)\text{.}$$ (6)

The nomenclature table contains the parameters that are mentioned in the problem. The following transformations are performed to eliminate problem dimensions that complicate the system:

$$\bar{t}=\frac{c}{\lambda }t,\bar{u}=\frac{1}{c\xi }u,\bar{v}=\frac{1}{c\xi }v,\bar{w}=\frac{1}{c}w,r=L+d\bar{x},y=h\bar{y},z=\lambda \bar{z},\bar{p}=\frac{d^2}{c\lambda \mu }p,\vartheta =\frac{\bar{T}-T_0}{T_1-T_0},\alpha =\frac{h}{d},\delta =\frac{d}{L},Re=\frac{\rho dc}{\mu },\xi =\frac{h}{\lambda },\phi =\frac{b}{h}\text{.}$$ (7)

By incorporating the aforementioned modifications into equations (1), (2), (3), (4), (5), (6), we obtain

$$\alpha \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{1}{1+\delta \bar{x}}\frac{\partial \bar{w}}{\partial \bar{z}}+\frac{\partial \bar{v}}{\partial \bar{y}}+\frac{\alpha \delta }{1+\delta \bar{x}}\bar{u}=0\text{.}$$ (8)

$$\frac{{\rho }_{nf}}{{\rho }_f}Re\xi \left({\xi }^2\frac{\partial \bar{u}}{\partial \bar{t}}+{\xi }^2\alpha \bar{u}\frac{\partial \bar{u}}{\partial \bar{x}}+{\xi }^2\bar{v}\frac{\partial \bar{u}}{\partial \bar{y}}+{\xi }^2\frac{\bar{w}}{1+\delta \bar{x}}\frac{\partial \bar{u}}{\partial \bar{z}}-\frac{\alpha \delta }{1+\delta \bar{x}}{\bar{w}}^2\right)=\frac{{\mu }_{nf}}{{\mu }_f}\frac{{\xi }^2}{\alpha }\left({\alpha }^2\frac{{\partial }^2\bar{u}}{\partial {\bar{x}}^2}+\frac{{\alpha }^2\delta }{1+\delta \bar{x}}\frac{\partial \bar{u}}{\partial \bar{x}}+\frac{{\xi }^2}{{\left(1+\delta x\right)}^2}\frac{{\partial }^2\bar{u}}{\partial {\bar{y}}^2}-{\left(\frac{\alpha \delta }{1+\delta \bar{x}}\right)}^2\bar{u}-2\alpha {\left(\frac{{\delta }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1+\delta x}\right)}^2\frac{\partial \bar{w}}{\partial \bar{z}}\right)-{\alpha }^2\frac{\partial \bar{p}}{\partial \bar{x}}\text{.}$$ (9)

$$\frac{{\rho }_{nf}}{{\rho }_f}Re\xi \left(\alpha \frac{\partial \bar{w}}{\partial \bar{t}}+{\alpha }^2\bar{u}\frac{\partial \bar{w}}{\partial \bar{x}}+\alpha \bar{v}\frac{\partial \bar{w}}{\partial \bar{y}}+\frac{\alpha \bar{w}}{1+\delta \bar{x}}\frac{\partial \bar{w}}{\partial \bar{z}}+\frac{{\alpha }^2\delta }{1+\delta \bar{x}}\bar{u}\bar{w}\right)=\frac{{\mu }_{nf}}{{\mu }_f}\left({\alpha }^2\frac{{\partial }^2\bar{w}}{\partial {\bar{x}}^2}+\frac{{\alpha }^2\delta }{1+\delta \bar{x}}\frac{\partial \bar{w}}{\partial \bar{x}}+\frac{{\xi }^2}{{\left(1+\delta x\right)}^2}\frac{{\partial }^2\bar{w}}{\partial {\bar{z}}^2}+\frac{{\partial }^2\bar{w}}{\partial {\bar{y}}^2}-{\left(\frac{\alpha \delta }{1+\delta \bar{x}}\right)}^2\bar{w}+2\alpha {\xi }^2{\left(\frac{{\delta }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1+\delta x}\right)}^2\frac{\partial \bar{u}}{\partial \bar{z}}\right)-\frac{{\alpha }^2}{1+\delta \bar{x}}\frac{\partial \bar{p}}{\partial \bar{z}}\text{.}$$ (10)

$$\frac{{\rho }_{nf}}{{\rho }_f}Re{\xi }^3\left(\frac{1}{\alpha }\frac{\partial \bar{v}}{\partial \bar{t}}+\bar{u}\frac{\partial \bar{v}}{\partial \bar{x}}+\frac{1}{\alpha }\bar{v}\frac{\partial \bar{v}}{\partial \bar{y}}+\frac{\bar{w}}{\alpha (1+\delta \bar{x}}\frac{\partial \bar{v}}{\partial \bar{z}}\right)=\frac{{\mu }_{nf}}{{\mu }_f}{\xi }^2\left(\frac{{\partial }^2\bar{v}}{\partial {\bar{x}}^2}+\frac{\delta }{1+\delta \bar{x}}\frac{\partial \bar{v}}{\partial \bar{x}}+\frac{{\xi }^2}{{\alpha }^2{\left(1+\delta \bar{x}\right)}^2}\frac{{\partial }^2\bar{v}}{\partial {\bar{z}}^2}+\frac{1}{{\alpha }^2}\frac{{\partial }^2\bar{v}}{\partial {\bar{y}}^2}\right)-\frac{\partial \bar{p}}{\partial \bar{y}}\text{.}$$ (11)

$$Re\alpha \xi \mathrm{Pr}\left(\frac{\partial \vartheta }{\partial t}+\alpha \bar{u}\frac{\partial \vartheta }{\partial \bar{x}}+\frac{\bar{w}}{1+\delta \bar{x}}\frac{\partial \vartheta }{\partial \bar{z}}+\bar{v}\frac{\partial \vartheta }{\partial \bar{y}}\right)=\frac{k_{nf}}{k_f}\left({\alpha }^2\frac{{\partial }^2\vartheta }{\partial {\bar{x}}^2}+\frac{{\xi }^2}{{\left(1+\delta \bar{x}\right)}^2}\frac{{\partial }^2\vartheta }{\partial {\bar{z}}^2}+\frac{{\partial }^2\vartheta }{\partial {\bar{y}}^2}+\frac{{\alpha }^2\delta }{1+\delta \bar{x}}\frac{\partial \vartheta }{\partial \bar{x}}\right)+\frac{{\mu }_{nf}}{{\mu }_f}Br\left(2{\xi }^2{\alpha }^2{\left(\frac{\partial \bar{u}}{\partial \bar{x}}\right)}^2+{\left(\alpha \frac{\partial \bar{w}}{\partial \bar{x}}+\frac{{\xi }^2}{1+\delta \bar{x}}\frac{\partial \bar{u}}{\partial \bar{z}}-\frac{\alpha \delta \bar{w}}{1+\delta \bar{x}}\right)}^2+{\left(\xi \alpha \frac{\partial \bar{v}}{\partial \bar{x}}+\xi \frac{\partial \bar{u}}{\partial \bar{y}}\right)}^2+2{\left(\frac{\xi }{1+\delta \bar{x}}\frac{\partial \bar{w}}{\partial \bar{z}}+\alpha \xi \delta \frac{\bar{u}}{1+\delta \bar{x}}\right)}^2+{\left(\frac{\partial \bar{w}}{\partial \bar{y}}+\frac{{\xi }^2}{1+\delta \bar{x}}\frac{\partial \bar{v}}{\partial \bar{z}}\right)}^2+{\xi }^2{\left(\frac{\partial \bar{v}}{\partial \bar{y}}\right)}^2\right)\text{.}$$ (12)

The parameters generated above that are dimensionless are defined as

$$\mathit{Pr}=\frac{{\mu }_f{\left(c_p\right)}_f}{k_f},Ec=\frac{c^2}{{\left(c_p\right)}_f\left(T_1-T_0\right)},Br=\mathit{Pr}Ec\text{.}$$

The wave-like border given in equation (6) takes on a dimensionless form

$$a\left(z,t\right)=1+\phi \mathit{cos}2\pi \left(z-t\right)\text{.}$$ (13)

Adjusting the lubrication approximation, i.e., ($\xi =0)\text{,}$ equations (8), (9), (10), (11), (12) provide (the bar symbols excluded)

$$\frac{\partial p}{\partial x}=0\text{.}$$ (14)

$$\frac{{\mu }_{nf}}{{\mu }_f}\left({\alpha }^2\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\alpha }^2\delta }{1+\delta x}\frac{\partial w}{\partial x}+\frac{{\partial }^{2}w}{\partial y^2}-{\left(\frac{\alpha \delta }{1+\delta x}\right)}^{2}w\right)-\frac{{\alpha }^2}{1+\delta x}\frac{\partial p}{\partial z}=0\text{.}$$ (15)

$$\frac{\partial p}{\partial y}=0\text{.}$$ (16)

$$\frac{k_{nf}}{k_f}\left({\alpha }^2\frac{{\partial }^2\vartheta }{\partial {\bar{x}}^2}+\frac{{\partial }^2\vartheta }{\partial {\bar{y}}^2}+\frac{{\alpha }^2\delta }{1+\delta \bar{x}}\frac{\partial \vartheta }{\partial \bar{x}}\right)+\frac{{\mu }_{nf}}{{\mu }_f}Br\left[{\left(\alpha \frac{\partial \bar{w}}{\partial \bar{x}}-\frac{\alpha \delta \bar{w}}{1+\delta \bar{x}}\right)}^2+{\left(\frac{\partial w}{\partial y}\right)}^2\right]=0\text{,}$$ (17)

Here is a description of the thermophysical characteristics of nanofluid [28,40,41]

$${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-{\phi }_s\right)}^{2.5}},k_{nf}=k_f\left(\frac{k_s+2k_f-2{\phi }_s\left(k_f-k_s\right)}{k_s+2k_f+2{\phi }_s\left(k_f-k_s\right)}\right),{\alpha }_{nf}=\frac{k_{nf}}{{\left(\rho c_p\right)}_{nf}},{\rho }_{nf}=\left(1-{\phi }_s\right){\rho }_f+{\phi }_s{\rho }_s,\rho {\left(c_p\right)}_{nf}=\left(1-{\phi }_s\right)\rho {\left(c_p\right)}_f+{\phi }_s{\left(\rho c_p\right)}_s$$ (18)

The boundary conditions are chosen by employing no-slip conditions, which maintain velocity at the walls with the static walls as [[37], [38], [39]].

$$w\left(x,\pm a\right)=0\text{and }w\left(\pm d,y\right)=0\text{.}$$ (19)

$$\vartheta \left(-a\right)=1\text{,}\vartheta \left(a\right)=0\text{.}$$ (20)

The peristaltic walls are now thought to constitute a complaint, and their basic equation is

$$\left(-\tau \frac{{\partial }^3}{\partial z^3}+\sigma \frac{{\partial }^3}{\partial z\partial t^2}+\epsilon \frac{{\partial }^2}{\partial z\partial t}\right)\tilde{a}=\frac{\partial p}{\partial z},atz=\pm \tilde{a}\text{.}$$ (21)

Compliant walls are viewed in dimensionless form as [ [12,13,28,37]]

$$\left(E_1\frac{{\partial }^3}{\partial z^3}+E_2\frac{{\partial }^3}{\partial z\partial t^2}+E_3\frac{{\partial }^2}{\partial z\partial t}\right)a=\frac{\partial p}{\partial z},atz=\pm a\text{,}$$ (22)

where $a$ is given in equation (13) and

$$E_1=-\tau \frac{h{d}^2}{c\mu {\lambda }^3},E_2=\sigma \frac{h{d}^{2}c}{\mu {\lambda }^3},E_3=\epsilon \frac{h{d}^{2}c}{\mu {\lambda }^2}\text{.}$$

Table 1 lists the physical characteristics of base fluid and nanoparticles:

Table 1.

Thermo-physical factors of nanofluid [40, 41].

	$\mathit{k}\left(\mathit{W}/\mathit{m}\mathit{k}\right)$	$\mathit{\rho }\left(\mathit{k}\mathit{g}/{\mathit{m}}^{\mathbf{3}}\right)$	${\mathit{c}}_{\mathit{p}}\left(\mathit{J}/\mathit{k}\mathit{g}\mathit{k}\right)$	$\mathit{\rho }{\mathit{c}}_{\mathit{p}}\left(\mathit{j}/{\mathit{m}}^{\mathbf{3}}\mathit{k}\right)$
Silver (Ag)	429	10,490	235	2465150
Copper (Cu)	401	8933	385	3439205
Water ($H_{2}O)$	0.613	997.1	4179	4166880.9

3. Method of solution

Equations (14), (15), (16), (17), (18), (19), (20), (21), (22), which were systems of equations and boundary conditions, are mixed partial differential equations having variable coefficients. The boundary conditions also depend on the boundary expression $a\left(\theta ,t\right)$, hence a perfect or numerical solution to this problem is not achievable. The issue can, however, be resolved quantitatively. We have a highly effective analytic series solution approach called the homotopy perturbation method [42], which is based on topology and perturbation theory. The kind of complex PDEs that are being described here might have solutions thanks to this technique. Following, in the proper order, is the deformation equation for the momentum equation (15) and the energy equation (17):

$$\left(1-p^{*}\right)\left[\mathcal{L}\left(\overbrace{w}\right)-\mathcal{L}\left(w_0\right)\right]+p^{*}\left[\begin{array}{c}\mathcal{L}\left(\overbrace{w}\right)+{\alpha }^2{\mathcal{L}}_{xx}\left(\overbrace{w}\right)+\frac{\delta {\alpha }^2}{1+\delta x}{\mathcal{L}}_x\left(\overbrace{w}\right)\\ -\frac{{\mu }_f}{{\mu }_{nf}}\frac{{\alpha }^2}{1+\delta x}\frac{\partial p}{\partial z}\end{array}\right]=0\text{,}$$ (23)

$$\left(1-p^{*}\right)\left[{\mathcal{L}}_{yy}\left(\overbrace{\vartheta }\right)-{\mathcal{L}}_{yy}\left({\vartheta }_0\right)\right]+p^{*}[\frac{k_{nf}}{k_f}\left({\mathcal{L}}_{yy}\left(\overbrace{\vartheta }\right)+{\alpha }^2{\mathcal{L}}_{xx}\left(\overbrace{\vartheta }\right)+\frac{\delta {\alpha }^2}{1+\delta x}{\mathcal{L}}_x\left(\overbrace{\vartheta }\right)\right)+\frac{{\mu }_{nf}}{{\mu }_f}Br{\left(\alpha {\mathcal{L}}_x\left(\overbrace{w}\right)-\frac{\alpha \delta }{1+\delta x}\overbrace{w}\right)}^2+{\left({\mathcal{L}}_y\overbrace{w}\right)}^2]=0\text{.}$$ (24)

The x-operator ${\mathcal{L}}_{xx}$ and the y-operator ${\mathcal{L}}_{yy}$ (shown below) are two alternative types of linear differential operators that can be used in the aforementioned equations; however we chose the y-part of derivative to be a linear operator for the heat equation (17). For momentum equation (15), on the other hand, the following defined linear operator L is used to provide the most accurate results.

$${\mathcal{L}}_{xx}=\frac{{\partial }^2}{\partial x^2},{\mathcal{L}}_{yy}=\frac{{\partial }^2}{\partial y^2},\mathcal{L}={\mathcal{L}}_{yy}-{\left(\frac{\alpha \delta }{1+\delta x}\right)}^2\text{,}$$ (25)

Below is an initial approximation for the velocity function $w$ and temperature function given in equation (26)

$$w_0=e^{-\frac{y\alpha \delta }{1+\delta x}}\left(e^{\frac{a\alpha \delta }{1+\delta x}}-e^{\frac{y\alpha \delta }{1+\delta x}}-e^{\frac{2a\alpha \delta }{1+\delta x}+\frac{y\alpha \delta }{1+\delta x}}+e^{\frac{a\alpha \delta }{1+\delta x}+\frac{2y\alpha \delta }{1+\delta x}}\right)\frac{\partial p}{\partial z}\times \left(1+\delta \mathrm{x}\right){\mu }_f)/\left(\left(1+e^{\frac{2a\alpha \delta }{1+\delta x}}\right){\delta }^2{\mu }_{nf}\right),{\vartheta }_0=\frac{a-a^3-y+a{y}^2}{2a}..$$ (26)

Taking the embedding parameter $p^{*}$ into consideration, consider the following perturbation equation

$$<\overbrace{w},\overbrace{\vartheta }>=<{\tilde{w}}_0+p^{*}{\tilde{w}}_1+p^{*2}{\tilde{w}}_2+\dots ,{\tilde{\vartheta }}_0+p^{*}{\tilde{\vartheta }}_1+p^{*2}{\tilde{\vartheta }}_2+\dots >$$ (27)

The zeroth order systems are then obtained by applying the aforementioned series to the respective deformation equations (23), (24) a with operator defined in equation (25) and equating the coefficients of exponents of $p^{*}$.

$$\mathcal{L}\left({\tilde{w}}_0\right)-\mathcal{L}\left(w_0\right)=0\text{,}$$ (28)

with boundary limits

$${\mathrm{w}}_0(\mathrm{x},\pm a)=0\text{and}{\mathrm{w}}_0\left(\pm 1,\mathrm{y}\right)=0\text{.}$$ (29)

$${\mathcal{L}}_{yy}\left({\tilde{\vartheta }}_0\right)-{\mathcal{L}}_{yy}\left({\vartheta }_0\right)=0\text{,}$$ (30)

whose surface equations are

$${\tilde{\vartheta }}_0\left(-a\right)=1\text{,}{\tilde{\vartheta }}_0\left(a\right)=0\text{.}$$ (31)

The first order sets of equations are structured as

$$\mathcal{L}\left({\tilde{w}}_1\right)+{\alpha }^2{\mathcal{L}}_{xx}\left({\tilde{w}}_0\right)+\frac{\delta {\alpha }^2}{1+\delta x}{\mathcal{L}}_x\left({\tilde{w}}_0\right)-\frac{{\mu }_f}{{\mu }_{nf}}\frac{{\alpha }^2}{1+\delta x}\frac{\partial p}{\partial z}=0\text{,}$$ (32)

The boundary relations are given as

$${\tilde{w}}_1\left(x,\pm a\right)=0\text{and}{\tilde{w}}_1\left(\pm 1,y\right)=0\text{.}$$ (33)

and

$${\mathcal{L}}_{yy}\left({\tilde{\vartheta }}_1\right)+\frac{k_{nf}}{k_f}\left({\mathcal{L}}_{yy}\left({\tilde{\vartheta }}_0\right)+{\alpha }^2{\mathcal{L}}_{xx}\left({\tilde{\vartheta }}_0\right)+\frac{\delta {\alpha }^2}{1+\delta x}{\mathcal{L}}_x\left({\tilde{\vartheta }}_0\right)\right)+\frac{{\mu }_{nf}}{{\mu }_f}Br\left({\left(\alpha {\mathcal{L}}_x\left({\tilde{w}}_0\right)-\frac{\alpha \delta }{1+\delta x}{\tilde{w}}_0\right)}^2+{\left({\mathcal{L}}_y{\tilde{w}}_0\right)}^2\right)=0\text{,}$$ (34)

along with the limitations

$${\vartheta }_1\left(-a\right)=0\text{,}{\vartheta }_1\left(a\right)=0\text{.}$$ (35)

After handling Eqs. (28), (32) by incorporating equations (29), (33), we receive

$$w_0=e^{\frac{y\alpha \delta }{1+\delta x}}C\left[1\right]+e^{-\frac{y\alpha \delta }{1+\delta x}}C\left[2\right]-A^{\prime }\left(1+\delta x\right){\mu }_f/\left({\delta }^2{\mu }_{nf}\right)\text{,}$$ (36)

$$w_1=1/\left(6{\delta }^2{\left(1+\delta x\right)}^3{\mu }_{nf}\right)e^{-\frac{y\alpha \delta }{1+\delta x}}\left(-6e^{\frac{y\alpha \delta }{1+\delta x}}{A}^{\prime }{\left(1+\delta x\right)}^4{\mu }_f+{\delta }^2\left(y^3{\alpha }^3{\delta }^{3}C\left[2\right]+e^{\frac{2y\alpha \delta }{1+\delta x}}(-y^3{\alpha }^3{\delta }^{3}C\left[1\right]+6{\left(1+\delta x\right)}^{3}C\left[3\right]\right)+6{\left(1+\delta x\right)}^{3}C\left[4\right]){\mu }_{nf}\right)$$ (37)

By solving Eqs. (30), (31), (34), (34), (35), we collect

$${\vartheta }_0=y^2/2+C\left[5\right]+yC\left[6\right]\text{,}$$ (38)

$${\vartheta }_1=C\left[7\right]+yC\left[8\right]-\frac{1}{12{\left(1+\delta x\right)}^4{k}_f{\mu }_f}(6y^2{\left(1+\delta x\right)}^4{k}_{nf}{\mu }_f+3/2e^{\frac{2a\alpha \delta }{1+\delta x}}{\left(1+\delta x\right)}^2(3+\delta (6x+3x^2\delta +2y^2{\alpha }^2\delta \left)\right)\eta {C\left[1\right]}^2{k}_f{\mu }_{nf}-2y^4{\alpha }^4{\delta }^4\eta C\left[1\right]C\left[2\right]k_f{\mu }_{nf}+\frac{3}{2e^{-\frac{2y\alpha \delta }{1+\delta x}}}{\left(1+\delta x\right)}^2(3+\delta (6x+3x^2\delta +2y^2{\alpha }^2\delta \left)\right)\eta C{\left[2\right]}^2{k}_f{\mu }_{nf}),$$ (39)

where the constants appearing in equations (36), (37), (38), (39) are given as

$$A^{\prime }=-E_1\phi \mathit{cos}\left[t-z\right]-E_2\phi \mathit{cos}\left[t-z\right]+E_3\phi \mathit{cos}\left[t-z\right].C\left[1\right]=\left(e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }(1+\delta x\right){\mu }_f)/\left(\left(1+e^{\frac{2a\alpha \delta }{1+\delta x}}\right){\delta }^2{\mu }_{nf}\right),C\left[2\right]=\frac{e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }\left(1+\delta x\right){\mu }_f}{\left(1+e^{\frac{2a\alpha \delta }{1+\delta x}}\right){\delta }^2{\mu }_{nf}}\text{,}$$

$$C\left[3\right]=-\left(\frac{1}{-e^{-\frac{2a\alpha \delta }{1+\delta x}}+e^{\frac{2a\alpha \delta }{1+\delta x}}}\right)e^{\frac{a\alpha \delta }{1+\delta x}}\left(\begin{array}{c}-\left(\begin{array}{c}\frac{a^3{e}^{\frac{a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{3}C\left[1\right]}{6{\left(1+\delta x\right)}^3}+\frac{a^3{e}^{-\frac{a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{3}C\left[2\right]}{6{\left(1+\delta x\right)}^3}\\ -\frac{A^{\prime }\left(1+\delta x\right){\mu }_f}{{\delta }^2{\mu }_{nf}}\end{array}\right)-e^{-\frac{a\alpha \delta }{1+\delta x}}\\ \left(\begin{array}{c}\frac{a^3{e}^{-\frac{a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{3}C\left[1\right]}{6{\left(1+\delta x\right)}^3}-\\ \frac{a^3{e}^{\frac{a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{3}C\left[2\right]}{6{\left(1+\delta x\right)}^3}-\frac{A^{\prime }\left(1+\delta x\right){\mu }_f}{{\delta }^2{\mu }_{nf}}\end{array}\right)\end{array}\right)\text{,}$$

$$C\left[4\right]=-\frac{\left(\begin{array}{c}6e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime {\mu }_f}-6e^{\frac{3a\alpha \delta }{1+\delta x}}{A}^{\prime }{\mu }_f+24e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }x\delta {\mu }_f-24e^{\frac{3a\alpha \delta }{1+\delta x}}{A}^{\prime }x\delta {\mu }_f+\\ 36e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^2{\delta }^2{\mu }_f-36e^{\frac{3a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^2{\delta }^2{\mu }_f+24e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^3{\delta }^3{\mu }_f-\\ 24e^{\frac{3a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^3{\delta }^3{\mu }_f+6e^{\frac{a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^4{\delta }^4{\mu }_f-6e^{\frac{3a\alpha \delta }{1+\delta x}}{A}^{\prime }{x}^4{\delta }^4{\mu }_f+\\ 2a^3{e}^{\frac{2a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{5}C\left[1\right]{\mu }_{nf}-a^3{\alpha }^3{\delta }^{5}C\left[2\right]{\mu }_{nf}-a^3{e}^{\frac{4a\alpha \delta }{1+\delta x}}{\alpha }^3{\delta }^{5}C\left[2\right]{\mu }_{nf}\end{array}\right)}{6\left(-1+e^{\frac{4a\alpha \delta }{1+\delta x}}\right){\delta }^2{\left(1+\delta x\right)}^3{\mu }_{nf}}\text{,}$$

$$C\left[5\right]=1/2\left(1-a^2\right),C\left[6\right]=-\left(\frac{1}{2a}\right)\text{,}$$

$C\left[7\right]=-1/\left(2a\right)(-1/\left(12{\left(1+\delta x\right)}^4{k}_f{\mu }_f\right)a(6a^2{\left(1+\delta x\right)}^4{k}_{nf}{\mu }_f+3/2e^{\frac{2a\alpha \delta }{1+\delta x}}{\left(1+\delta x\right)}^2(3+\delta \left(6x+3x^2\delta +2a^2{\alpha }^2\delta \right))\eta {C\left[1\right]}^2{k}_f{\mu }_{nf}-2a^4{\alpha }^4{\delta }^4\eta C\left[1\right]C\left[2\right]k_f{\mu }_{nf}+3/2e^{-\frac{2a\alpha \delta }{1+\delta x}}{\left(1+\delta x\right)}^2(3+\delta (6x+3x^2\delta +a^2{\alpha }^2\delta \left)\right)\eta {C\left[2\right]}^2{k}_f{\mu }_{nf})-1/(12{\left(1+\delta x\right)}^4{k}_f{\mu }_f)$

$C\left[8\right]=-1/\left(16a{\left(1+\delta x\right)}^2{\mu }_f\right)e^{-\frac{2a\alpha \delta }{1+\delta x}}(3\eta {C\left[1\right]}^2{\mu }_{nf}-3e^{\frac{4a\alpha \delta }{1+\delta x}}\eta {C\left[1\right]}^2{\mu }_{nf}$$+6x\delta \eta {C\left[1\right]}^2{\mu }_{nf}-6e^{\frac{4a\alpha \delta }{1+\delta x}}x\delta \eta {C\left[1\right]}^2{\mu }_{nf}+3x^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}-$$3e^{\frac{4a\alpha \delta }{1+\delta x}}{x}^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}+2a^2{\alpha }^2\delta \eta {C\left[1\right]}^2{\mu }_{nf}-2a^2{e}^{\frac{4a\alpha \delta }{1+\delta x}}{\alpha }^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}$$-3\eta {C\left[2\right]}^2{\mu }_{nf}+3e^{\frac{4a\alpha \delta }{1+\delta x}}\eta {C\left[2\right]}^2{\mu }_{nf}-6x\delta \eta {C\left[2\right]}^2{\mu }_{nf}+6e^{\frac{4a\alpha \delta }{1+\delta x}}x\delta \eta {C\left[2\right]}^2{\mu }_{nf}-3x^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}+3e^{\frac{4a\alpha \delta }{1+\delta x}}{x}^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}-2a^2{\alpha }^2\delta \eta {C\left[2\right]}^2{\mu }_{nf}+2a^2{e}^{\frac{4a\alpha \delta }{1+\delta x}}{\alpha }^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}\text{.}$.

Final form of the solutions can be found by using the limitation of $p^{*}\to 1$ in.

$C\left[8\right]=-1/\left(16a{\left(1+\delta x\right)}^2{\mu }_f\right)e^{-\frac{2a\alpha \delta }{1+\delta x}}(3\eta {C\left[1\right]}^2{\mu }_{nf}-3e^{\frac{4a\alpha \delta }{1+\delta x}}\eta {C\left[1\right]}^2{\mu }_{nf}$$+6x\delta \eta {C\left[1\right]}^2{\mu }_{nf}-6e^{\frac{4a\alpha \delta }{1+\delta x}}x\delta \eta {C\left[1\right]}^2{\mu }_{nf}+3x^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}-$$3e^{\frac{4a\alpha \delta }{1+\delta x}}{x}^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}+2a^2{\alpha }^2\delta \eta {C\left[1\right]}^2{\mu }_{nf}-2a^2{e}^{\frac{4a\alpha \delta }{1+\delta x}}{\alpha }^2{\delta }^2\eta {C\left[1\right]}^2{\mu }_{nf}$$-3\eta {C\left[2\right]}^2{\mu }_{nf}+3e^{\frac{4a\alpha \delta }{1+\delta x}}\eta {C\left[2\right]}^2{\mu }_{nf}-6x\delta \eta {C\left[2\right]}^2{\mu }_{nf}+6e^{\frac{4a\alpha \delta }{1+\delta x}}x\delta \eta {C\left[2\right]}^2{\mu }_{nf}-3x^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}+3e^{\frac{4a\alpha \delta }{1+\delta x}}{x}^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}-2a^2{\alpha }^2\delta \eta {C\left[2\right]}^2{\mu }_{nf}+2a^2{e}^{\frac{4a\alpha \delta }{1+\delta x}}{\alpha }^2{\delta }^2\eta {C\left[2\right]}^2{\mu }_{nf}\text{.}$.

Final form of the solutions can be found by using the limitation of $p^{*}\to 1$ in equation (27).

4. Entropy analysis

The standard shape of entropy equation is [29–33]

$$S_{gen}=k_{nf}{\left(\frac{\nabla T}{T_0}\right)}^2+\frac{{\mu }_{nf}}{T_0}\frac{1}{2}trace{A_1}^2\text{,}$$ (40)

In component form, equation (40) can be expressed as

$$S_{gen}=\frac{k_{nf}}{{T_0}^2}\left[{\left(\frac{\partial T}{\partial r}\right)}^2+{\left(\frac{1}{r}\frac{\partial T}{\partial \theta }\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2\right]+\frac{{\mu }_{nf}}{T_0}\left[2{\left(\frac{\partial u}{\partial r}\right)}^2+{\left(\frac{\partial w}{\partial r}+\frac{1}{r}\frac{\partial u}{\partial \theta }-\frac{w}{r}\right)}^2+{\left(\frac{1}{r}\frac{\partial v}{\partial \theta }-\frac{\partial w}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial r}-\frac{\partial u}{\partial y}\right)}^2+2{\left(\frac{1}{r}\frac{\partial w}{\partial \theta }+\frac{u}{r}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2\right]$$ (41)

Using formulas displayed in Eq. (7) in aforementioned equation (41), we have

$$N_s=\frac{k_{nf}}{k_f}\left[{\alpha }^2{\left(\frac{\partial \vartheta }{\partial \bar{x}}\right)}^2+{\xi }^2{\left(\frac{1}{1+\delta \bar{x}}\frac{\partial \vartheta }{\partial \bar{z}}\right)}^2+{\left(\frac{\partial \vartheta }{\partial \bar{y}}\right)}^2\right]+\frac{Br}{\mathrm{\Omega }}\left[2{\xi }^2{\alpha }^2{\left(\frac{\partial \bar{u}}{\partial \bar{x}}\right)}^2+{\left(\alpha \frac{\partial \bar{w}}{\partial \bar{x}}+\frac{{\xi }^2}{1+\delta \bar{x}}\frac{\partial \bar{u}}{\partial \bar{z}}-\alpha \delta \frac{\bar{w}}{1+\delta \bar{x}}\right)}^2+{\left(\frac{{\xi }^2}{1+\delta \bar{x}}\frac{\partial \bar{v}}{\partial \bar{z}}+\frac{\partial \bar{w}}{\partial \bar{y}}\right)}^2+{\left(\xi \alpha \frac{\partial \bar{v}}{\partial \bar{x}}+\xi \frac{\partial \bar{u}}{\partial \bar{y}}\right)}^2+2{\left(\frac{\xi }{1+\delta \bar{x}}\frac{\partial \bar{w}}{\partial \bar{z}}+\alpha \xi \delta \frac{\bar{u}}{1+\delta \bar{x}}\right)}^2+2{\xi }^2{\left(\frac{\partial \bar{v}}{\partial \bar{y}}\right)}^2\right]$$ (42)

Injecting physical constraint of small wave number in equation (42)$\text{,}$ we have

$$N_s=\frac{k_{nf}}{k_f}\left[{\alpha }^2{\left(\frac{\partial \vartheta }{\partial \bar{x}}\right)}^2+{\left(\frac{\partial \vartheta }{\partial \bar{y}}\right)}^2\right]+\frac{Br}{\mathrm{\Omega }}\left[{\left(\alpha \frac{\partial \bar{w}}{\partial \bar{x}}-\alpha \delta \frac{\bar{w}}{1+\delta \bar{x}}\right)}^2+{\left(\frac{\partial \bar{w}}{\partial \bar{y}}\right)}^2\right]\text{,}$$ (43)

where $N_S$ in equation (43) is entropy generation number and some new found expressions are stated below

$$N_s=\frac{S_{gen}}{S_G},S_G=\frac{k_f{\left(T_1-T_0\right)}^2}{{T_0}^2{h}^2},\mathrm{\Omega }=\frac{\left(T_1-T_0\right)}{T_0}\text{.}$$

Bejan number Be is the ratio of heat entropy and the whole system entropy and is given below in equation (44)

$$Be=\frac{\frac{k_{nf}}{k_f}\left[{\alpha }^2{\left(\frac{\partial \vartheta }{\partial \bar{x}}\right)}^2+{\left(\frac{\partial \vartheta }{\partial \bar{y}}\right)}^2\right]}{\frac{k_{nf}}{k_f}\left[{\alpha }^2{\left(\frac{\partial \vartheta }{\partial \bar{x}}\right)}^2+{\left(\frac{\partial \vartheta }{\partial \bar{y}}\right)}^2\right]+\frac{Br}{\mathrm{\Omega }}\left[{\left(\alpha \frac{\partial \bar{w}}{\partial \bar{x}}-\alpha \delta \frac{\bar{w}}{1+\delta \bar{x}}\right)}^2+{\left(\frac{\partial \bar{w}}{\partial \bar{y}}\right)}^2\right]}\text{.}$$ (44)

5. Results and discussion

In this section, we've made a number of graphs that illustrate how different physical characteristics like temperature, velocity, entropy production, Bejan number, and stream function affect different profiles. We can learn about the behavior of the system under examination by studying these graphical elements. We have supplied Fig. 2(a-d)–10 in order to investigate the study's findings. By developing residual error changing charts, Fig. 2 suggests the parametric value ranges of certain relevant problem components. Fig. 3, Fig. 4 depict velocity fluctuations with respect to coordinate y, allowing us to observe the impacts of the curvature aspect ratio, amplitude ratio, elastic tension $E_1$, and mass per unit volume $E_2$. Temperature profiles for various values of the parameter $\delta$ and $E_1$ are shown in Fig. 5, Fig. 6. Furthermore, we used Fig. 7, Fig. 8 to show the entropy generation curves, which show the system's irreversible losses. Fig. 9, Fig. 10 examine the Bejan number, which is a measure of the system's heat transmission efficiency. Finally, Fig. 11, Fig. 12 show the streamlines, which provide a visual representation of the system's flow patterns. We may acquire a full understanding of the system's behavior under various conditions by evaluating all of these graphs together.

Fig. 2.

Residual error curves (a) for $\phi$ (b) for $\delta$ (c) for $E_1$ (d) for $E_2$.

Fig. 3.

Axial velocity variation with respect to aspect ratio $\delta$ and $\phi$, (a) two dimensional (b) three dimensional.

Fig. 4.

Axial velocity variation with respect to the elastic tension $E_1$, (a) two dimensional (b) three dimensional.

Fig. 5.

Heat transfer for the aspect ratio $\delta$ (a,b) for silver particles.

Fig. 6.

Heat transfer for $E_1$ (a,b) for silver particles.

Fig. 7.

Entropy generation for mass per unit area $E_2$.

Fig. 8.

Entropy generation for damping force $E_3$.

Fig. 9.

Bejan number for the curvature $\alpha$.

Fig. 10.

Bejan number for the elastic tension $E_1$.

Fig. 11.

(a,b,c): Flow pattern for $E_1$.

Fig. 12.

(a,b,c): Flow pattern for $\delta$.

5.1. Residual error

In this part, we draw a Table 2 and sketch graphs for various graphs showing the accuracy of the results collected through the solution section. From the table and graphs we can also imagine about possible ranges of the parameters on which the solution remains convergent. In this regard, Fig. 2 is placed with part (a) showing curves of residual error for the aspect ratio factor $\phi$ (b) for the curvature ratio $\delta$ (c) for the elastic tension $E_1$ and (d) for the mass per unit volume constant $E_2$. It can be demonstrated from these figures that if we fix an upper error bound as $E\le 1.4\times {10}^{-7}$, the possible parametric intervals satisfying the prescribed error bound suggest that the approximate suitable range are $0\le \phi \le 1,0.1\le \delta \le 3.1,1\le E_1\le 2,0\le E_2\le 1\text{.}$.

Table 2.

Method's convergence and valid parametric range.

Fixed parameters	Parametric range				Residual error $\left|\mathit{R}\mathit{E}\right|\le \mathbf{1.4}\times {\mathbf{10}}^{-\mathbf{7}}$
${\mu }_f=3.55\text{,}$ $\alpha =0.1\text{,}$$z=0.3\text{,}$ $t=0.6\text{,}$ $\phi =0.8\text{,}$ $E_3=1.1\text{,}$$x=0.2\text{,}$ $y=0.5$	$\phi$	$\delta$	$E_1$	$E_2$
	0.0	$0.1$	0.12	0.1	$1.4512\times {10}^{-9}$
	0.2				$8.30717\times {10}^{-10}$
	0.4				$4.04675\times {10}^{-10}$
	0.6				$1.46851\times {10}^{-10}$
	0.8				$2.59599\times {10}^{-11}$
	1.0				0.0000000
	0.1	0.1	0.12	0.1	$9.91356\times {10}^{-10}$
		0.9			$1.05491\times {10}^{-7}$
		1.7			$1.44462\times {10}^{-7}$
		2.5			$1.45316\times {10}^{-7}$
		3.3			$1.36395\times {10}^{-7}$
		4.1			$1.25685\times {10}^{-7}$
		4.9			$1.15439\times {10}^{-7}$
	0.1	0.12	1	0.1	$7.33872\times {10}^{-9}$
			1.2		$8.60743\times {10}^{-9}$
			1.4		$9.87613\times {10}^{-9}$
			1.6		$1.11448\times {10}^{-8}$
			1.8		$1.24135\times {10}^{-8}$
			2		$1.36822\times {10}^{-8}$
	0.1	0.12	1	0	$6.70437\times {10}^{-9}$
				0.2	$7.97307\times {10}^{-9}$
				0.4	$9.24178\times {10}^{-9}$
				0.6	$1.05105\times {10}^{-8}$
				0.8	$1.17792\times {10}^{-8}$
				1.0	$1.30479\times {10}^{-8}$

5.2. Flow velocity

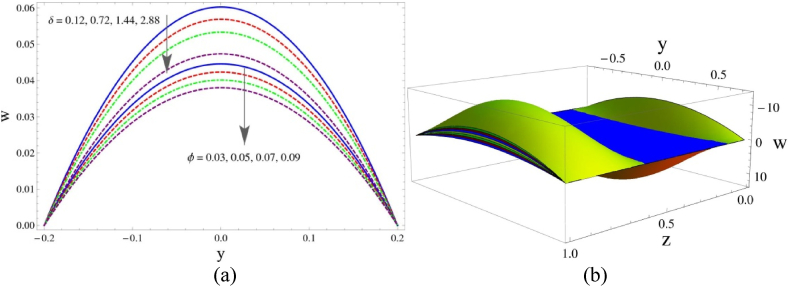
Fig. 3(a and b) illustrates that the velocity decreases as the curvature aspect ratio $\delta$ and amplitude ratio $\phi$ increase. A curved duct's aspect ratio is the ratio of its radius of curvature to its hydraulic diameter. The diameter of a circular pipe with the same cross-sectional area as the duct is described as the hydraulic diameter. A curved duct's aspect ratio can have a substantial impact on the axial velocity of the fluid flowing through it. A smaller aspect ratio (i.e., a tighter curvature) can lead to higher axial velocity, whereas a wider aspect ratio (i.e., a more gradual curvature) can lead to lower axial velocity. Because of the way fluid travels via a curved conduit, this effect happens. This centrifugal force causes the fluid velocity to increase perpendicular to the direction of flow, causing the axial velocity to decrease. As a result of this centrifugal force, the fluid velocity, perpendicular to the flow direction is rising while falling in the axial direction. Conversely, when the aspect ratio is larger, the centrifugal force is weaker, and the decrease in axial velocity is less pronounced. In practical applications, the effect of aspect ratio on axial velocity can have important implications for the design and performance of duct systems. For example, in fluid transport systems, a more gradual curvature (i.e., larger aspect ratio) may be necessary to prevent excessive turbulence and pressure losses. Fig. 3 also shows that the velocity varies inversely with the bigger the influence of the amplitude ratio $\phi$. This underlines the physical fact that a larger amplitude of the peristaltic wave than the duct height results in a slower fluid flow. This is explained by the fact that a larger peristaltic wave transmits more energy to the fluid particles in the vertical direction to the flow side, resulting in a decrease in their velocity. This figure also contains a three dimensional graph of the velocity which reflects that in the axial direction of $z$-axis, the velocity curves are showing sinusoidal wave nature which represents that in a small interval $0<z<0.33$ and $0.66<z<1$, the velocity remains negative and in the interval $0.33<z<0.66$, it is positive. It implies that in peristaltic motions, the fluid particles are pushed forward after a uniform interval by stretching the remaining particles backward by boundary contraction. This is accomplished by the extension and compression of the flexible surface walls.

In Fig. 4(a), higher elastic tension ($E_1$) causes the fluid particles to push forward, resulting in a similar behavior to that shown in the aspect ratio graph. The compliant walls in peristaltic flow refer to the walls of the conduit that are elastic or flexible. These walls can adjust in response to the regular contracting waves moving along the conduit, which might influence the flow behavior of the fluid flowing in the container. The elastic stretch of the walls, or their opposing ability to distortion, is a significant component in this situation. The elastic tension of compliant walls may have a substantial effect on the velocity of peristaltic flow. More specifically, a greater elastic tension has the potential to increase flow velocity whereas a lower elastic tension has the potential to decrease flow velocity. This effect is brought about by the elastic tension of the walls, which affects the pressure gradient that propels fluid flow. Greater pressure gradient and resistance to deformation are produced by more elastic walls, which boost flow velocity. In contrast, less elastic barriers bend more readily and produce a smaller pressure gradient, which lowers flow velocity. The form and propagation of the peristaltic waves themselves can also be impacted by the elasticized strain of the boundaries. More elastic barriers allow the waves to be propelled more efficiently while maintaining their amplitude and shape. Lower flow velocity may come from the walls' reduced elasticity, which may soften the waves and lessen their amplitude. When constructing peristaltic devices, it is important to consider how elastic tension influences the velocity of peristaltic flow in real-world applications. For example, the peristaltic pump, a piece of medical equipment used to administer drugs, have walls with elastic tension that may change the drug's dose and flow rate to the patient. The system's effectiveness and performance may be impacted by the elastic tension in industrial applications like fluid mixing and transport. This figure also demonstrates how the velocity function is directly inversely proportional to the effect of the compliant walls' mass per unit factor $E_2$. This demonstrates that the fluid speed increases as the mass per unit of the compliant walls increases. This can be explained by the fluid particles' increased velocity due to the flexible barriers' encouragement of faster transit. On the other hand Fig. 4(b) is a three dimensional view of the same function under similar variations of the parameter. It is obvious to note from this part that velocity curves are showing up and down behavior along the axial coordinate z which is due to the peristaltic type of nanolfuid motion, however similar curves are found along the domain of x coordinate.

5.3. Heat transfer

The temperature profile's behavior in relation to the curvature aspect ratio parameter $\delta$ is depicted in Fig. 5(a–d). According to the graph, a greater fluid flow temperature is caused by a bigger curvature aspect ratio. It can be explained as when the values of aspect ratio is increased the isothermal bolus expands which means that the heat is transferred at higher rate as compares to the previous graph. This suggests that a rectangular curved duct is preferable to a square-shaped arrangement for heat transfer. This happens as a result of a higher surface area-to-volume ratio, which expands the region where heat transmission can take place. Furthermore, a greater aspect ratio might result in more complicated flow patterns inside the duct, which can boost turbulence and convectional heat transfer. Additionally, a reduced aspect ratio may result in the duct's flow patterns being simpler, which can lessen turbulence and restrict the convection of heat. In applications like heat exchangers, where heat transfer efficiency is crucial, the impact of aspect ratio on heat transfer in curved ducts is especially pertinent. It is possible to obtain the desired heat transfer rate in these applications by optimizing the aspect ratio of the curved duct while reducing pressure drop and other performance variables. Additionally, it has been found that copper nanoparticles transfer heat more quickly than silver particles. The middle of the flow region has greater heat transmission than the boundaries, according to the altitude of the curves from the left to right boundaries. According to the graph, copper particles transfer heat more quickly than silver nanoparticles. The effects of the factor $E_1$ on the thermal profile are shown in Fig. 6(a–d). It is clear that the isothermal contours are expanded by large impact of the parameter which means that rate of thermal exchange is accelerated by the compliant walls' elasticity. It is crucial to remember that as greater values for the elastic tension parameter are provided, the temperature differences between copper (Cu) and silver (Ag) particles grow, accordingly. The system's compliant walls have elasticity, which means they can bend or stretch in response to applied forces. The flexibility of these walls is critical in permitting the previously indicated faster rate of thermal exchange. It indicates that the dynamic responsiveness of the walls to external pressures improves thermal transfer efficiency inside the system.

5.4. Entropy generation

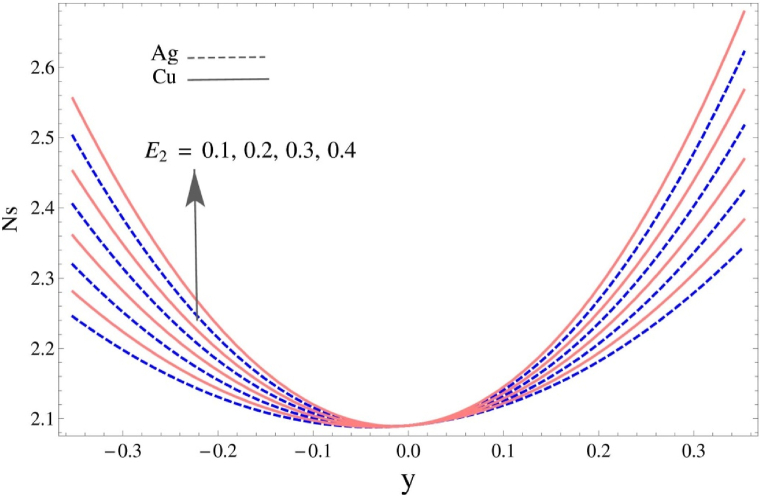
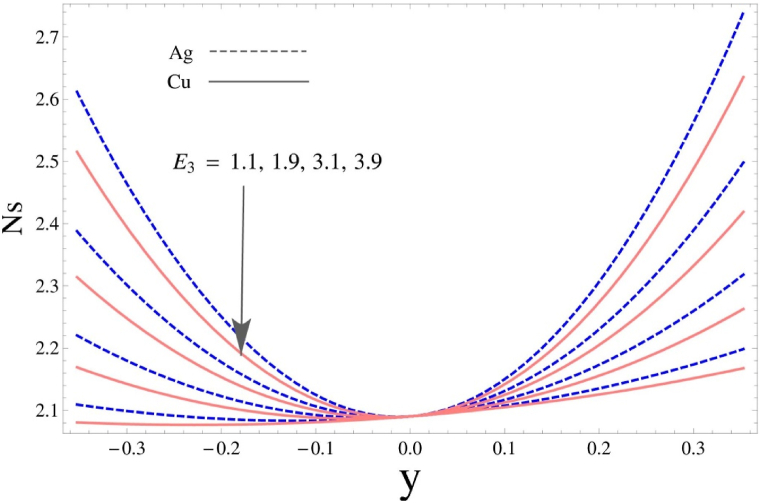
The entropy generation function, which is a crucial component to understanding the heat loss during the flow, is seen in Fig. 7, Fig. 8. The mass per unit area $E_2$ of compliant walls in a peristaltic flow system can have a considerable effect on entropy creation, which is a measure of the degree of irreversibility in a thermodynamic process. The deformation and movement of the walls are influenced by the mass per unit area of the walls, which in turn impacts the flow patterns and heat transmission in the system and alters entropy generation. A higher mass per unit area of the compliant walls can lead to an increase in entropy generation as observed in Fig. 7. This occurs because a higher mass per unit area results in stiffer walls that are more resistant to deformation, which increases the pressure drop and flow resistance in the system. This increase in flow resistance leads to more viscous dissipation, which is a source of entropy generation. Additionally, the higher mass per unit area can reduce the deformability of the walls, leading to less efficient pumping action and further increase in entropy generation. It is also worth noting that the least entropy may be obtained at the conduit's central line, although it grows significantly towards the lower and higher surfaces for both parametric variation and the independent coordinate y. Furthermore, the entropy generation rate of copper (Cu) particles is found to be greater than that of silver (Ag) particles. Fig. 8 suggests the opposite scene for viscous damping force on the profile of entropy generation. It can be found that entropy generation becomes smaller for large viscous damping force $E_3$ and it goes to zero at the central point of the domain $y=0$, however for copper particles it remains lower than the silver particles. This indicates that larger damping force levels tend to diminish or enhance entropy within the system.

5.5. Bejan number curves

Fig. 9 shows the Bejan number plotted against the curvature aspect ratio. It illustrates how the Bejan number fluctuates in the corners but stays constant in the middle. This indicates that while the total entropy is greater than the thermal entropy along the walls, the entropy produced by thermal exchange in the flow is more than the total entropy at the center flow position, $y\in \left[-0.2,0.2\right]$. Moreover, more energy is lost in the center than on the other sides due to the high heat transfer rate. Additionally, the graph demonstrates that while the mid-region exhibits the opposite tendency, Cu particles produce more uniform entropy than Ag particles along the side walls. Notably, the entropy ratio is unaffected by the variation in aspect ratio at the center point ($y=0$). The inverse effect of the walls' elastic tension ($E_1$) on the entropy ratio is shown in Fig. 10, which implies that the thermal entropy is lower than the overall entropy. The graph demonstrates that the Bejan number of Cu particles is lower than that of Ag particles. It is also noteworthy that while the curves show variance on the corner sides, the Bejan number's behavior is unaffected in the middle.

5.6. Streamlines

The flow pattern and bolus phenomena for various conduit elastic tension values are shown in Fig. 11. From left to right, the graph is divided into four quadrants. It is evident in the first quadrant that as $E_1$ rises, so does the bolus size. The bolus size, however, grows in the second quadrant. The remaining two parts of the graph show comparable tendencies. Compliant walls are essential in peristaltic flow because they produce the wave-like motion that forces fluid through a duct. The creation and spread of the boluses, the fluid regions that are propelled forward by the peristaltic wave, can be impacted by elastic tension in the compliant walls. The compliant walls stiffen and lose some of their flexibility when they are under tension. As the peristaltic wave travels down the tube, this may have an impact on the size and shape of the boluses that form. Because the walls are more rigid, they can withstand deformation and movement, resulting in narrower, longer boluses that advance more slowly. This may lead to lower mixing and transit efficiency, as well as slower flow rates. On the other hand, the compliant walls are more malleable and easier to follow the flow of the fluid when they are not under tension. This can result in boluses that are pushed forward more quickly and are wider and shorter. This may lead to higher flow rates, better mixing, and more effective conveyance. We can infer from Fig. 12's discussion of the trapping bolus mechanism for the curvature ratio that, while the bolus size does not change in the first and third quadrants, it does fluctuate randomly in the second and third quadrants when the curvature ratio varies.

5.7. Comparison with existing literature

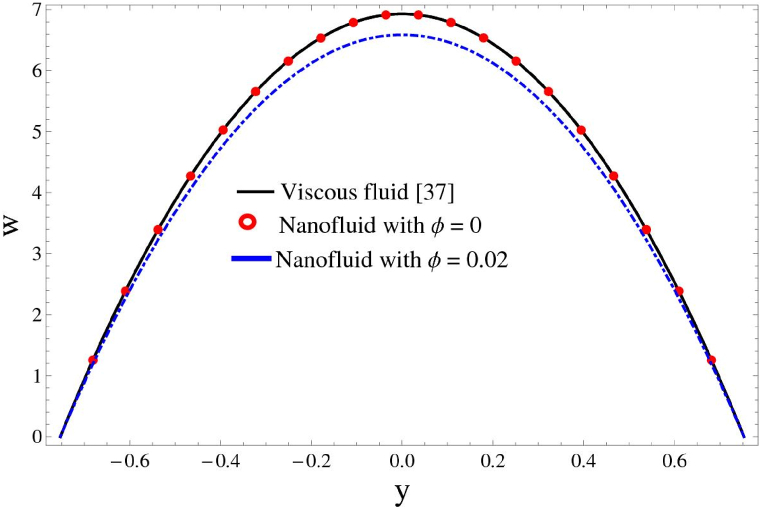
Fig. 13 is drawn to examine the comparison of current work with the existing literature done by Alfwzan, Wafa F. et al. [37]. This graph not only depicts the current work matching with previous study through limiting a specific parameter $\phi =0$ (neglecting the nanofluid effects) but also equate the current nanofluid analysis with viscous fluid case. We can judge from this graph that current work is overlapping the previous readings made by Alfwzan, Wafa F. et al. [37] if we neglect the nanoparticles volume fraction $\phi$ which shows that the current data is accurate. Moreover, if we do not neglect the said factor, we can see that the velocity goes down for nanofluid as compared to the simple base fluid.

Fig. 13.

Comparison of current work with Alfwzan, Wafa F. et al. [37].

6. Conclusions

In this study, the authors have focused on gathering data for three-dimensional, wavy nanofluid flow involving two distinct particle types (Ag and Cu) and on analyzing the formation of entropy that occurs during the heat transfer. Assuming a curved duct configuration, the governing equations for this have been found and simplified using a three-dimensional cylindrical system followed by the relevant curvilinear transformations. There are some physical limitations in place, such as long wavelength and low Reynolds number. The homotopy perturbation approach has been used to solve the obtained systems of partial differential equations up to second order. Through the practice of including amounts in cases of several important flow parameters, the findings have been given and illustrated graphically. Following are some major findings from the graphical approach:

• •It is determined that the aspect ratio of the duct section and the surface elasticity created by the compliant walls are directly connected to the flow speed.
• •Curvature aspect ratio and amplitude ratio cause the velocity field to decrease, yet quicker flow is produced by the mass of the compliant walls and the elasticity of the walls.
• •It is also known that Ag particles emit less heat than Cu particles when all other factors are held constant. It is found that the density of the walls generates a lot more entropy than the damping force. Furthermore, it is shown that copper (Cu) particles produce less entropy than silver particles Ag.
• •It is concluded that the speed of flow is directly correlated with the aspect ratio of the duct section and the surface elasticity produced by the compliant walls.
• •The velocity field is decreasing with curvature aspect ratio and amplitude ratio, but the elasticity of the walls and the mass of the compliant walls produce faster flow.
• •It is also acknowledged that, when all other parameters are held constant, Cu particles produce more heat than Ag particles. It is obtained that the walls density produces much entropy than what damping force creates. It is further noted that silver particles Ag generate more entropy than copper Cu.
• •Theoretically, for characteristics like curvature aspect ratio, heat exchange generates less entropy than total energy loss; however the elasticity of the walls generates a lot of entropy.
• •The growing variation in the border elasticity causes stream boluses to enlarge in size, but their number is found to be unaffected.
• •From three dimensional views, it is interesting to examine that the velocity profile follows the wavy path along the axial direction which reflects the effects of curvature on the flow attributes.
• •Accuracy of the results has been established from the residual graphs.

7. Future directions

• •Following the conclusions presented above, the following are some potential future lines of inquiry:
• •Analyzing the effects of various nanoparticle types on the three-dimensional, wavy flows of nanofluids and the entropy they generate during heat transfer.
• •Analyzing how different duct forms and geometries affect the flow characteristics and entropy generation in nanofluids.
• •Examining the effects of extra variables on the flow and entropy production of nanofluids, such as base fluid viscosity, particle volume fraction, and thermal conductivity of the nanoparticles.
• •Developing new analytical or numerical methods to solve the governing equations of entropy generation and nanofluid flows more precisely and effectively.
• •Performing experiments to verify the theoretical conclusions and look into the applicability of the events that are being observed.

Data availability statement

No data was used for the research described in the article.

Additional information

No additional information is available for this paper.

CRediT authorship contribution statement

F.M. Allehiany: Validation. Arshad Riaz: Methodology, Supervision. Sadia Shoukat: Investigation, Writing – original draft. Ghaliah Alhamzi: Writing – review & editing. Emad E. Mahmoud: Formal analysis, Resources, Software.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Nomenclature

Symbol Definition

u, w, v

Cylindrical coordinate

b

Wave amplitude

t

Time

a

Wave height function

L

Length of rectangular duct

p

Pressure

h

Height of rectangular duct

d

Distance

T

Temperature

k

Thermal conductivity

$c_p$

Heat capacity

Pr

Prandtl number

Re

Reynolds number

Br

Brinkman number

$E_1$

Flexure rigidity

$E_2$

Mass per unit area

$E_3$

Viscous damping force

Be

Bejan number

Greek symbol

$\alpha$

Cross sectional aspect ratio

$\vartheta$

Dimensionless temperature

$\lambda$

Wavelength

$\mu$

Viscosity

$\eta$

Dynamic viscosity

$\phi$

Amplitude ratio

$\delta$

Curvature aspect ratio

$\xi$

Wave number

$\rho$

Density

Subscripts

F

Fluid

nf

Nano fluid