LEARNING MRI CONTRAST-AGNOSTIC REGISTRATION

Abstract

We introduce a strategy for learning image registration without acquired imaging data, producing powerful networks agnostic to magnetic resonance imaging (MRI) contrast. While classical methods accurately estimate the spatial correspondence between images, they solve an optimization problem for every new image pair. Learning methods are fast at test time but limited to images with contrasts and geometric content similar to those seen during training. We propose to remove this dependency using a generative strategy that exposes networks to a wide range of images synthesized from segmentations during training, forcing them to generalize across contrasts. We show that networks trained within this framework generalize to a broad array of unseen MRI contrasts and surpass classical state-of-the-art brain registration accuracy by up to 12.4 Dice points for a variety of tested contrast combinations. Critically, training on arbitrary shapes synthesized from noise distributions results in competitive performance, removing the dependency on acquired data of any kind. Additionally, since anatomical label maps are often available for the anatomy of interest, we show that synthesizing images from these dramatically boosts performance, while still avoiding the need for real intensity images during training.

1. INTRODUCTION

Image registration estimates spatial correspondences between images and is a fundamental component of many neuroimaging pipelines [1-3]. This work focuses on networks agnostic to magnetic resonance imaging (MRI) contrast that excel both at same-contrast registration (e.g. between two T1-weighted scans, T1w), as well as across contrasts (e.g. T1w to T2-weighted, T2w). Both are important in neuroimaging, where different contrasts are commonly acquired, such as T1w for visualizing anatomy or T2w contrast for detecting abnormal fluids [4]. These scans yield images of different appearance for the same anatomy. For morphometric analyses [1-3], images often need to be registered to an existing atlas, which is typically of a different contrast [5]. Classical methods estimate a deformation field by optimizing an objective that balances image similarity with field regularity [6-10]. While these methods provide strong theory and good results, the optimization needs to be repeated for each image pair, and the objective and optimization have to be adapted to the image type. In contrast, learning methods learn a function that maps an image pair to a deformation field from datasets [11-16]. These methods are fast and have the potential to improve accuracy and robustness to local minima. Unfortunately, learning approaches do not generalize well to new image types unobserved at training. For example, a model trained on T1w-T1w pairs will not accurately register proton-density weighted (PDw) to T1w scans.

Contribution

We propose SynthMorph: a general strategy for learning contrast agnostic registration that can handle unseen MRI contrasts at test time. SynthMorph enables registration within and across contrasts, without the need for real imaging data at training. We first introduce a generative model for label maps of random geometric shape. Second, we generate images of arbitrary contrast conditioned on these maps. Third, the strategy enables us to use a contrast-agnostic loss that measures label overlap. This leads to two network variants with unprecedented generalizability, that register any contrast combination tested without retraining: sm-shapes trains without acquired data of any kind and matches state-of-the-art registration of neuroanatomical MRI, sm-brains trains on images synthesized from brain segmentations only and substantially outperforms all other methods tested. We emphasize that neither variant requires real intensity images.

2. METHOD

Background

Let $m$ and $f$ be a moving and a fixed 3D image, respectively. We build on unsupervised learning frameworks for non-linear registration: a U-Net-style [17] CNN $h_{\theta }$ with parameters $\theta$ implementing the VoxelMorph architecture [11,18] outputs the deformation ${\varphi }_{\theta }=h_{\theta }(m,f)$ for image pair {$m$, $f$}. At each training iteration, $h_{\theta }$ is given images {$m$, $f$}, and network parameters are updated to minimize a loss $ℒ(\theta ;m,f,{\varphi }_{\theta })$ that contains a dissimilarity term ${ℒ}_{dis}(m\circ {\varphi }_{\theta },f)$ and a regularization term ${ℒ}_{reg}(\varphi ):ℒ(\theta ;m,f,{\varphi }_{\theta })={ℒ}_{dis}(m\circ {\varphi }_{\theta },f)+\lambda {ℒ}_{reg}({\varphi }_{\theta })$, where ${\varphi }_{\theta }=h_{\theta }(m,f)$ is the network output, and $\lambda$ is a constant.

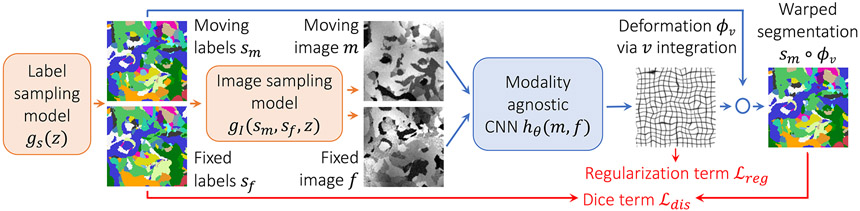
Proposed method overview

We eliminate the need for acquired training data by synthesizing arbitrary shapes and contrasts from scratch (Figure 1). We generate two paired 3D label maps {$s_m$, $s_f$} using a function $g_s(z)=\{s_m,s_f\}$ described below given random seed $z$. However, if anatomical labels are available, generating images from these can further improve accuracy, and we can use these instead of synthesizing segmentations. We then define another function $g_i(s_m,s_f,z)=\{m,f\}$ described below that synthesizes two intensity volumes {$m$, $f$} from {$s_m$, $s_f$} and $z$. Crucially, synthesizing images from label maps enables us to obviate the dependency of the loss on image contrast and instead use a similarity function that measures label overlap using (soft) Dice [19]:

$${ℒ}_{dis}^{\prime }(\varphi ,s_m,s_f)=-\frac{2}{J}\sum _{j=1}^J\frac{\mid (s_m^j\circ \varphi )\odot s_f^j)\mid }{\mid (s_m^j\circ \varphi )\oplus s_f^j)\mid },$$ (1)

where $s^j$ is the one-hot encoded label $j\in \{1,2,\dots ,J\}$ of label map $s$, and $\odot$ and $\oplus$ denote voxel-wise multiplication and addition, respectively. We parameterize the deformation $\varphi$ with a stationary velocity field (SVF) $v$, which we integrate within the network to obtain a diffeomorphism [6,18,20]. We regularize $\varphi$ using ${ℒ}_{reg}(\varphi )=\frac{1}{2}{\Vert \nabla \mathbf{u}\Vert }^2$, where $\mathbf{u}$ is the displacement of deformation field $\varphi =Id+\mathbf{u}$.

Fig. 1.

Strategy for learning contrast-agnostic deformable registration. At every mini batch, we synthesize a pair of 3D label maps {$s_m$, $s_f$} and then the corresponding 3D images {$m$, $f$} with random contrast. The images are used to train a U-Net-style network, and the label maps are incorporated into a loss that is independent of image contrast.

Label maps

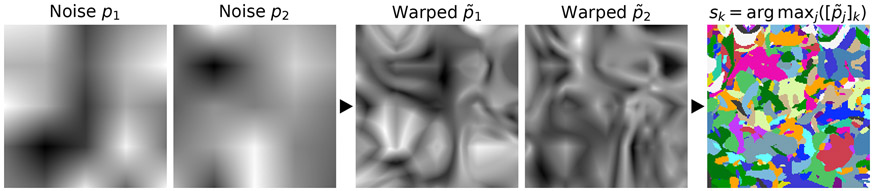
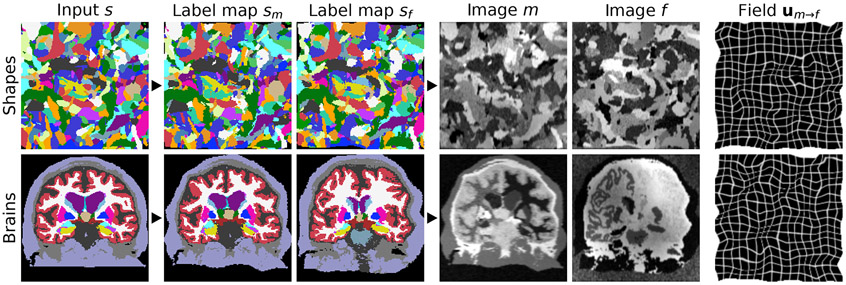
To generate random input label maps with $J$ labels, we first draw $J$ smooth noise images $p_j(j\in \{1,2,\dots ,J\})$ by sampling voxels from a normal distribution at lower resolution $r_p$ and upsampling (Figure 2). Second, we warp each image $p_j$ with a random deformation field ${\varphi }_j$ (see below) to obtain images ${\tilde{p}}_j=p_j\circ {\varphi }_j$. Third, we create an input label map $s$ by assigning, for each voxel $k$ of $s$, the label $j$ with the highest intensity among the images ${\tilde{p}}_j$, i.e. $s_k={\text{arg max}}_j({[{\tilde{p}}_j]}_k)$. Given label map $s$, we generate two new label maps by deforming $s$ with a random smooth deformation ${\varphi }_m$ (see below) to produce the moving map $s_m=s\circ {\varphi }_m$ and similarly the fixed map $s_f$. Alternatively, if segmentations are available for the anatomy of interest, such as the brain, we deform two label maps from separate subjects, selected at random, and only synthesize the images. We emphasize that no acquired images (e.g. a T1w MRI) are used during training (Figure 3).

Fig. 2.

Generation of input label maps. A set of smooth 3D noise images $p_j(j\in \{1,2,\dots ,J\})$ is sampled from a standard distribution, then warped by random deformation fields ${\varphi }_j$. The label map $s$ is synthesized from the warped images ${\tilde{p}}_j=p_j\circ {\varphi }_j$: for each voxel $k$ of $s$, we determine in which ${\tilde{p}}_j$ that voxel has the highest intensity and assign the corresponding label $j$, i.e. $s_k={\text{arg max}}_j({[{\tilde{p}}_j]}_k)$. The example uses $J=26$.

Fig. 3.

Data synthesis. Top: from random shapes. Bottom: if available, the synthesis can be initialized with anatomical labels. We generate a pair of label maps {$s_m$, $s_f$} and from them images {$m$, $f$} with arbitrary contrast. The registration network then predicts the displacement ${\mathbf{u}}_{m\to f}$. If anatomical labels are used, we generate {$s_m$, $s_f$} from separate subjects.

Synthetic images

From the label maps {$s_m$, $s_f$}, we synthesize gray-scale images {$m$, $f$} [21-23], building on our recent work on segmentation [24]. Given a label map $s$, we draw the intensities of all image voxels for label $j$ from the normal distribution $𝒩({\mu }_j,{\sigma }_j^2)$. We sample the mean ${\mu }_j$ and standard deviation (SD) ${\sigma }_j$ from continuous distributions $𝒰(a_{\mu },b_{\mu })$ and $𝒰(a_{\sigma },b_{\sigma })$, respectively, where $a_{\mu }$, $b_{\mu }$, $a_{\sigma }$, and $b_{\sigma }$ are hyperparameters. We convolve the image with a Gaussian kernel $K({\sigma }_{i=1,2,3})$ where ${\sigma }_{i=1,2,3}\sim 𝒰(0,b_K)$. We further corrupt the image with an intensity bias field $B$ [25,26], whose voxels we draw from a normal distribution $𝒩(0,{\sigma }_B^2)$ at lower resolution $r_B$, with ${\sigma }_B\sim 𝒰(0,b_B)$. We upsample $B$ and take the exponential of each voxel to yield positive values before applying $B$ via voxel-wise multiplication. We obtain the images {$m$, $f$} after min-max normalization and voxel-wise contrast exponentiation using parameter $\gamma \sim 𝒩(0,{\sigma }_{\gamma }^2):m={\tilde{m}}^{\text{exp}(\gamma )}$, where $\tilde{m}$ is the normalized moving image (similarly for the fixed image).

Random transforms

We obtain the transforms ${\varphi }_j(j=1,2,\dots ,J)$ for noise image $p_j$ by integrating random SVFs $v_j$ [6,18,20,27]. We draw each voxel of $v_j$ as an independent sample of a normal distribution $𝒩(0,{\sigma }_j^2)$ at reduced resolution $r_p$, where ${\sigma }_j\sim 𝒰(0,b_p)$, and each SVF is integrated and upsampled to full size. We obtain the transforms ${\varphi }_m$ and ${\varphi }_f$ similarly, based on hyperparameters $r_v$ and $b_v$.

3. EXPERIMENTS

We evaluate network variants trained with the proposed strategy and compare to several baselines. SynthMorph achieves unprecedented generalizability among neural networks, matching or exceeding the accuracy of all classical and learning baselines tested.

Data

We test cross-subject registration of 3D brain-MRI scans compiled from the HCP-A [28, 29] and OASIS [30] datasets, which include T1w and T2w acquisitions at 1.5T and 3T with ${\sim (1\text{mm})}^3$ resolution. We also use BIRN [31] PDw scans from 8 subjects. For training sm-brains, we obtain 40 distinct-subject segmentations from the Buckner40 dataset [32], a subset of the fMRIDC structural data [33]. We derive brain and non-brain labels using SAMSEG [3], except for the PDw data, which include manual brain label maps. As we focus on deformable registration, we map all images to a common affine space [1,34] at 1 mm isotropic resolution.

Setup

For each contrast, we test the networks on 30 image pairs, except for PDw, of which we have only 8. We test registration within and across datasets, with and without skull-stripping, using held-out datasets of the same size. To measure registration accuracy, we propagate the moving labels using the predicted warps and compute the Dice metric $D$ across the largest $J=26$ brain labels.

Baselines

We test classical registration with ANTs (SyN) [7] using recommended parameters [35] since these methods are already optimized for brain MRI, with the NCC metric within and MI across contrasts. We test NiftyReg [8] with NMI and diffeomorphic transforms as in our approach. We also run deedsBCV [10], where we reduce the grid spacing, search radius and quantization step to improve accuracy in our experiments. As a learning baseline, we train VoxelMorph (vm), using an NCC-based loss and the same architecture as SynthMorph, on 100 skull-stripped T1w images from HCP-A that do not overlap with the validation set. Similarly, we train a model with an NMI-based loss on combinations of 100 T1w and 100 T2w images.

SynthMorph variants

For contrast and shape agnostic training, we generate {$s_m,s_f$} from one of 100 random-shape segmentations $s$ at each iteration (sm-shapes). Each $s$ contains $J=26$ labels, all included in the loss ${ℒ}_{dis}$. We train another network on the Buckner40 anatomical labels instead of shapes (sm-brains) and optimize the $J=26$ largest brain labels in ${ℒ}_{dis}$ We emphasize that no acquired intensity images are used.

Analyses

We conduct extensive hyperparameter analyses (not shown due to space limitations) using skull-stripped HCP-A T1w pairs that do not overlap with the test set and select the values shown in Table 1. Accuracy is mildly sensitive to regularization, and we choose $\lambda =1$. Using higher numbers of convolutional features per layer boosts accuracy; we choose a network width of $n=256$.

Table 1.

Hyperparameters. Spatial measures are given in voxels. Our data are 160×160×192 volumes. For fields sampled at a lower resolution $r$, we obtain the volume size by multiplying each dimension by $r$ and rounding up (e.g. 4×4×5 for $r=1:40$).

Hyperparameter	$\lambda$	$r_p$	$b_p$	$a_{\mu }$	$b_{\mu }$	$a_{\sigma }$	$b_{\sigma }$	$r_B$	$b_B$	$b_K$	${\sigma }_{\gamma }$	$r_v$	$b_v$
Value	1	1:32	100	25	225	5	25	1:40	0.3	1	0.25	1:16	3

Results

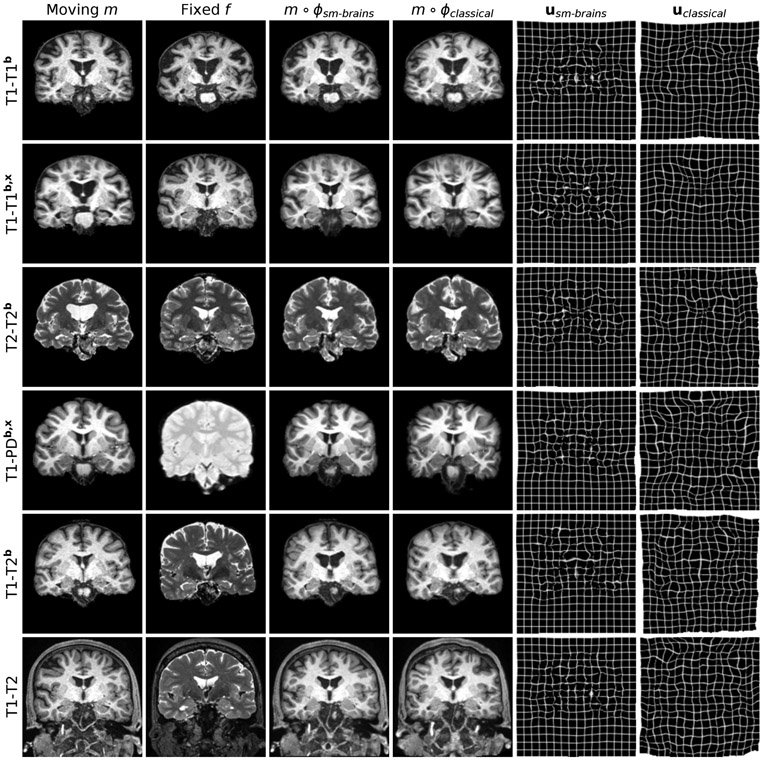
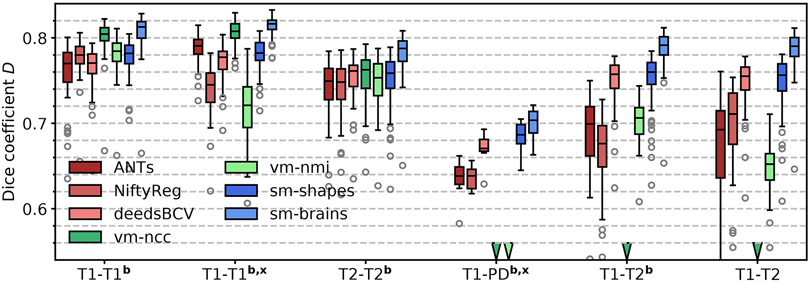
We show typical examples in Figure 4. Figure 5 compares Dice scores across structures. Exploiting the information in a set of brain labels, sm-brains achieves the highest accuracy throughout, even though no real images are used for training: for T1w-T2w/PDw pairs, sm-brains leads by at least 3 Dice points. The shape and contrast-agnostic network sm-shapes matches the best classical methods at same-contrast and exceeds all methods except sm-brains at cross-contrast registration, despite never having seen real MR images nor brain anatomy. The learning baselines perform well but break down for unseen contrast pairs, while SynthMorph remains robust. The learning methods take less than 1 second per 3D registration on an Nvidia Tesla V100 GPU, whereas NiftyReg, ANTs and deedsBCV take ~0.5 h, ~1.2 h and ~3 min on a 3.3-GHz Intel Xeon CPU, respectively (single-threaded).

Fig. 4.

Typical results for sm-brains and classical methods. Each row shows a pair from the datasets indicated on the left, where the letters b and x mark skull-stripping and registration across datasets (e.g. OASIS-HCP), respectively. We show the best-performing classical baseline: NiftyReg on the 1^st, ANTs on the 2^nd, and deedsBCV on all other rows.

Fig. 5.

Registration accuracy: overlap of brain structures for 30 subject pairs (8 for PD). The letters b and x indicate skull-stripping and registration across datasets (e.g. OASIS-HCP).

4. CONCLUSION

We introduce a general framework for learning registration that does not require any real imaging data during training. Instead, we synthesize random label maps and images with widely varying shape and contrast from noise distributions. This strategy produces powerful contrast-agnostic networks that surpass classical accuracy at all contrasts tested, while being substantially faster. Learning methods like VoxelMorph yield results similar to SynthMorph for contrasts observed at training but break down for unseen (new) image types. In contrast, networks trained in the SynthMorph framework remain robust, obviating the need for retraining given a new sequence. In the case where (few) brain segmentations are available, training on images synthesized from these produces networks that substantially outperform the state of the art.

5. COMPLIANCE WITH ETHICAL STANDARDS

This retrospective research study uses human subject data. Analysis of locally acquired HCP-A data was last approved on 2020-12-22 by IRBs at Washington University in St. Louis (201603117) and Mass General Brigham (2016p001689). No ethical approval was required for retrospective analysis of open access data from OASIS, BIRN and fMRIDC.