Abstract
A central question in the debate over privatized Medicare is whether increased government payments to private Medicare Advantage (MA) plans generate lower premiums for consumers or higher profits for producers. Using difference-in-differences variation brought about by a sharp legislative change, we find that MA insurers pass through 45 percent of increased payments in lower premiums and an additional 9 percent in more generous benefits. We show that advantageous selection into MA cannot explain this incomplete pass-through. Instead, our evidence suggests that market power is important, with premium pass-through rates of 13 percent in the least competitive markets and 74 percent in the most competitive.
Keywords: G22, H51, I11, I13, I18
Medicare is the second largest social insurance program in the United States and the primary source of health insurance for the elderly. In 2012, Medicare spent $572.5 billion on health care, a 4.8 percent increase over the previous year.1 Given the large scale of the program and rapid growth in spending, reforming Medicare is a perpetual policy issue.
One commonly discussed proposal is adjusting subsidies to private Medicare Advantage plans.2 Proponents of larger subsidies argue that increased payments will result in lower premiums or more generous benefits for Medicare beneficiaries. Opponents argue that such a move would lead to larger profits for insurance companies and health care providers. Naturally, the lines of argument are reversed when a reduction in payments is proposed. At its core, these debates are about economic incidence: does increasing government subsidies to private Medicare Advantage plans benefit patients or producers?
In most regions of the country, Medicare beneficiaries can choose to be covered by public fee-for-service Traditional Medicare (TM) or to obtain subsidized coverage through their choice of a private Medicare Advantage (MA) insurance plan. MA plans are differentiated from Traditional Medicare in having restricted provider networks, alternative cost-sharing arrangements, and additional benefits, such as vision and dental coverage. MA plans have historically been offered by health maintenance organizations (HMOs). Plans receive a capitation payment from Medicare for each enrolled beneficiary and often charge beneficiaries a supplemental premium.
We examine the incidence of subsidies to private Medicare Advantage plans by studying a sharp change in capitation payments brought about by the 2000 Benefits Improvement and Protection Act (BIPA). MA capitation payments vary at the county level. Prior to BIPA, payments were largely determined by historical TM expenditures in the county. BIPA reformed these payments by instituting a system of rural and urban payment floors that raised payments in 72 percent of counties. We show that MA capitation payments in the counties where these floors were binding were on parallel trends before the payment reform but increased by an average of about $600 per beneficiary per year or 12 percent when BIPA was implemented, providing us with a source of difference-in-differences variation.
Using this difference-in-differences variation, we find that MA plans passed through approximately one-half of their capitation payment increases. For each $1 in higher payments, consumer premiums were reduced by $0.45 at three years following the reform. Using rich data on product characteristics, we find an additional $0.09 of pass-through in the actuarial value of plan benefits.3 A 95 percent confidence interval allows us to rule out a combined pass-through rate outside of 37 percent to 71 percent. Difference-in-differences plots that flexibly allow the effect of the 2001 payment shocks to vary by year show no impacts in the pre-reform years, providing evidence in support of the parallel trends identifying assumption.
We confirm the robustness of our findings by estimating difference-in-differences specifications that isolate subsets of the identifying variation, which is a function of both urban/rural status and pre-BIPA Medicare expenditure. We obtain similar estimates when we isolate variation in the size of payment increases between urban and rural counties with the same pre-BIPA Medicare expenditure, reducing concerns that differential medical cost growth rates across high- and low-spending areas are biasing our results. We obtain similar estimates when we use complementary variation in the size of payment increases within the sets of urban and rural counties, reducing concerns about bias from separate urban and rural time trends.
The second part of the paper investigates why consumers receive only one-half of the marginal surplus from this increase in payments.4 Drawing on prior work by Einav, Finkelstein, and Cullen (2010) and Mahoney and Weyl (2017), we build a model that illustrates that the observed incomplete pass-through could potentially be explained by two factors: the degree of advantageous selection in the market and the market power of private MA insurance plans. If there is substantial advantageous selection into MA, then private plans will not pass through the increased payments in reduced premiums because lower premiums will attract enrollees who are differentially more costly on the margin. If firms have market power, then they may not face competitive pressure to pass through increased payments into lower premiums or more generous benefits.
We use the same difference-in-differences variation to estimate the degree of selection into MA. The BIPA-induced variation in payments creates variation in premiums and thereby generates quasi-exogenous variation in MA enrollment. We use this variation in insurance coverage, combined with administrative data on the near-universe of TM beneficiaries, to estimate the slope of the industry cost curve. Our estimates indicate there is limited advantageous selection into MA on the margin we study. Within our theoretical framework, the estimates imply that advantageous selection would reduce pass-through under the benchmark of perfect competition to 85 percent. Alternatively put, of the combined $0.46 in payments that is not passed through to beneficiaries, selection can account for $0.15 or about one-third of the shortfall.
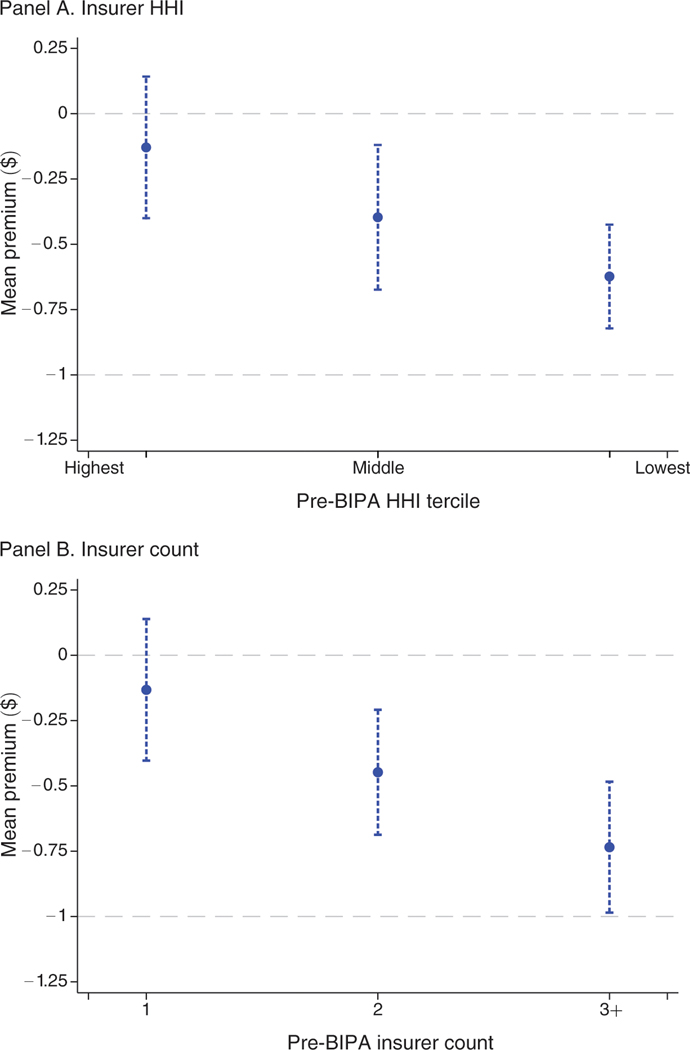
We then provide evidence that suggests insurer market power is an important determinant of incomplete pass-through. Using our difference-in-differences variation, we estimate premium pass-through rates of 74 percent in the most competitive markets compared to 13 percent in the markets with the least competition. This heterogeneity is statistically significant and is robust to measuring market concentration by the pre-reform number of insurers in each market and the pre-reform insurance market Herfindahl-Hirschman Index (HHI).
Our research contributes to a rich literature in public finance that examines the pass-through of government taxes and subsidies in health insurance. This includes work on health insurance mandates (Hackmann, Kolstad, and Kowalski 2015), physician and hospital payments (Dafny 2005; Clemens and Gottlieb 2017), Medicaid premium subsidies (Dague 2014), and payments to Medicare Part D plans (Carey 2014). In addition, our research complements a prior literature that uses discrete choice models to examine the relationship between market power and welfare in Medicare Advantage (Town and Liu 2003; Dunn 2010; Lustig 2010; Curto et al. 2015).5 Our finding of an average premium pass-through of 45 percent, with rates approaching 74 percent in the most competitive counties, suggests that private markets can efficiently provide Medicare benefits but that not all markets may be competitive enough to achieve this objective.
Our paper also contributes to a literature on selection in Medicare, with Brown et al. (2014) arguing that selection generates overpayments to MA plans and Newhouse et al. (2012) responding that selection has been mitigated by improved risk adjustment and other reforms. Prior studies have investigated selection by examining the cost of individuals who choose to switch from TM to MA or vice versa. Like these papers, we use data on TM costs to estimate selection into MA. Unlike these papers, our approach allows us to estimate selection using plausibly exogenous payment variation (Einav, Finkelstein, and Cullen 2010).6 Our finding of little advantageous selection suggests that policies that aim to reduce selection, while perhaps worthwhile from a cost-benefit standpoint, would have limited scope to increase pass-through to consumers.
Our estimates of pass-through are directly relevant for the $156 billion in MA payment reductions scheduled to take effect under the Affordable Care Act. Counter to claims made by some commentators, our results predict that the incidence of such payment reductions would fall only partially on Medicare beneficiaries, with a significant fraction of these cuts borne by the supply side of the market.7,8
More generally, we view our results as emphasizing the importance of market power in health insurance markets. The delivery of publicly funded health care in the United States has become increasingly privatized over the past 25 years, with Medicare, Medicaid, and the Affordable Care Act exchanges adopting managed competition to varying degrees. Although evaluating the merits of specific policy proposals is outside the scope of our analysis, our estimates indicate that efforts to make insurance markets more competitive may be key to increasing consumer surplus in such settings.
The remainder of the paper proceeds as follows. Section I provides background information on MA payments and describes our data. Section II presents our empirical strategy. Section III reports estimates of pass-through. In Section IV we present the model that allows us to investigate the determinants of pass-through. Section V empirically evaluates the role of selection in explaining incomplete pass-through. In Section VI we examine the relationship between pass-through and market concentration. Section VII concludes.
I. Background and Data
A. Medicare Advantage Payments
Private Medicare Advantage (MA) insurance plans are given monthly capitated payments for each enrolled Medicare beneficiary, equal to a base payment multiplied by the enrollee’s risk score. Insurers can supplement these payments by charging premiums directly to enrollees. Base payments to MA plans are determined at the county level and are somewhat complex, reflecting the accumulation of legislation over the life of the program. Payments were originally intended to reflect the costs an individual would incur in Traditional Medicare (TM). Prior to 2001, base payments were largely determined by historical average monthly costs for the TM program in the enrollee’s county of residence.9
Our source of identifying variation arises from the 2000 Benefits Improvement and Protection Act (BIPA). The historical context for BIPA was a contraction in the MA program in the late 1990s following the 1997 Balanced Budget Act (BBA). The BBA was designed to reduce variation in base payments across counties with different levels of Medicare spending. The legislation put in place a payment floor that increased base payments in counties with the lowest TM costs and mechanisms to limit the growth of payments in counties with high TM costs. As a result of this reform, enrollment growth in the MA program slowed, and between 1999 and 2000 the number of MA enrollees shrunk for the first time since the program’s inception in 1985. Under pressure from insurers to reverse the payment cuts, Congress passed BIPA in December 2000 (Achman and Gold 2002).10
BIPA implemented two floors for county base payments in March 2001. These floors varied with whether the county was rural or urban and were scheduled to update over time.11 Counties already receiving base payments in excess of the floors received a uniform 1 percent increase in their base payment rates in March 2001. Let denote counties and denote years. Base payments are given by
| (1) |
where is the base payment absent the BIPA floors and is the relevant BIPA payment floor, which depends on the county’s urban status, In our main analysis, we use premium data from July of each year. Because BIPA modified payments beginning in March 2001, and plans received special permission to adjust premiums and benefits packages in February 2001 (Committee on Ways and Means 2004), we assign 2001 as the first post-reform year for all of our variables. We discuss the regulations that affected the precise timing of plan responses in more detail in online Appendix A.2.
The final capitation payment received by MA insurers is determined by multiplying the county base payment rate by an individual risk adjustment factor to account for the relative costliness of MA versus TM enrollees. Prior to 2000, this adjustment was done using demographic information: age, sex, Medicaid status, working status, institutionalization status, and disability status. From 2000 to 2003, the risk adjustment formula additionally placed a small weight on inpatient diagnoses. Overall, the risk adjustment done prior to 2004 explained no more than 1.5 percent of the variation in medical spending (Brown et al. 2014).12 Extensive risk adjustment of MA capitation payments was introduced in 2004 (see Brown et al. 2014; McWilliams, Hsu, and Newhouse 2012), after our study period.
The Centers for Medicare and Medicaid Services (CMS) constructs the risk adjustment factors to equal 1.0 on average across the TM population. Because the risk adjustment factor averages 0.94 in our estimation sample, in the analysis that follows we multiply all county base payments by 0.94 to more accurately track average payments to plans.13 To be consistent, we normalize the risk scores to have a mean of 1.0 in our sample when, in Section V, we separately and explicitly estimate selection between MA and TM.
B. Data
We focus on the seven-year time period from 1997 to 2003, which provides us with 4 years of data from before the passage of BIPA and three years of data after the bill was signed into law. We end our sample in 2003 to avoid confounding factors introduced by the 2004 implementation of the Medicare Modernization Act of 2003 (MMA), which reformed the capitation payment system extensively.14
Most of our analysis relies on publicly available administrative data on the MA program. We combine data from several sources: MA rate books, which list the administered payment rates for each county in each year; the annual census of MA insurer contracts offered by county; county-level MA enrollment summaries; and plan premium data.15 For 2000 to 2003, we are able to obtain information on the benefits (e.g., copayments, drug coverage) offered by each plan.16 We supplement the data on plan characteristics with data on subjective consumer evaluations of all MA plans from the Consumer Assessment of Health Plans Survey (CAHPS) and clinical quality of care measures from Healthcare Effectiveness Data and Information Set (HEDIS). These data are available from 1999 to 2003.
To investigate the importance of selection, we use administrative data on costs and demographics for the near-universe of Medicare beneficiaries. We use the CMS Beneficiary Summary File from 1999 to 2003, which includes information on spending for the universe of Traditional Medicare beneficiaries. Additionally, we use the CMS Denominator File from 1999 to 2003, which provides demographic information for all Medicare beneficiaries.17
We conduct our analysis on a county-year panel dataset. We weight county-level observations by the number of Medicare beneficiaries in each county so that our findings reflect the experience of the average Medicare beneficiary. To construct county-level outcomes from plan-level data, we weight plan level attributes by the plan’s enrollment share in that county. We inflation-adjust all monetary variables to year 2000 using the CPI-U.
Table 1 displays summary statistics for the pooled 1997 to 2003 sample. Panel A shows values for the full panel of 3,143 counties. Panel B shows summary statistics for plan characteristics, which require us to restrict the sample to county-years that have at least one MA plan. In 2000, the year just prior to the enactment of BIPA, MA plans were available in 680 out of 3,143 counties. These 680 counties collectively contain 67 percent of all Medicare beneficiaries (19.4 million individuals). In the pooled 1997 to 2003 panel, MA plans were available in 4,262 out of 22,001 county-years. These county-years collectively contain 64 percent of beneficiary-years.18
Table 1—
Summary Statistics
| Mean | SD | Min | Max | |
|---|---|---|---|---|
|
| ||||
| Panel A. All counties, 1997 to 2003 | ||||
| Base payment ($ per month) | 490.58 | 83.96 | 222.99 | 777.91 |
| At least one plan (%) | 64.4 | 47.9 | 0 | 100 |
| Number of plans | 1.46 | 1.33 | 0 | 6 |
| MA enrollment (%) | 19.0 | 18.3 | 0 | 67.6 |
| TM costs ($ per month) | 486.53 | 103.94 | 136.87 | 940.08 |
| Panel B. County × years with at least one plan, 1997 to 2003 | ||||
| County-level premium ($ per month) | ||||
| Mean | 22.77 | 27.94 | 0 | 156.29 |
| Min | 15.47 | 26.35 | 0 | 156.29 |
| Median | 21.83 | 29.67 | 0 | 156.29 |
| Max | 31.73 | 33.23 | 0 | 194.47 |
| County-level benefits | ||||
| Physician copay ($ per visit) | 8.02 | 5.31 | 0 | 21.62 |
| Specialist copay ($ per visit) | 15.62 | 7.10 | 0 | 95.72 |
| Drug coverage (%) | 68.7 | 42.5 | 0 | 100 |
| Dental coverage (%) | 28.0 | 37.3 | 0 | 100 |
| Vision coverage (%) | 68.1 | 41.3 | 0 | 100 |
| Hearing aid coverage (%) | 38.2 | 43.2 | 0 | 100 |
| Number of plans | 2.26 | 0.97 | 1 | 6 |
| HHI | 6,030 | 2,460 | 1,920 | 10,000 |
| MA enrollment (%) | 28.6 | 16.2 | 0.8 | 67.6 |
| TM costs ($ per month) | 521.56 | 106.60 | 254.96 | 940.08 |
Notes: Table shows county-level summary statistics for the pooled 1997 to 2003 sample. Panel A shows values for the full set of county × years () that includes 100 percent of the Medicare population over this period. Panel B restricts the sample to county × years with at least one MA plan, which includes 4,262 county-years and 64 percent of all Medicare beneficiary-years. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. All monetary values are inflation adjusted to 2000 using the CPI-U. County-level benefits are available for only 2000 to 2003.
Panel A shows that base payments average $491 per month for all counties but range from $223 to $778 per month across the sample. MA plans enroll 19 percent Medicare beneficiaries on average, although counties with the highest MA penetration rates have enrollment rates close to 70 percent. In the average county, TM beneficiaries cost $487 per month.
Panel B restricts the sample to counties with at least one plan. Premiums average $23 per month and vary substantially. The minimum premium within a county averages $15 per month and the maximum averages $32. Copayments for physician and specialists visits average $8 and $16, respectively. Approximately 70 percent of plans offer drug and vision coverage, 28 percent of plans offer dental coverage, and 38 percent cover hearing products. Beneficiaries in the restricted sample can choose among 2.3 plans on average, and enrollment is higher with an MA penetration rate of 29 percent. Average TM costs, at $522 per month, are somewhat higher as well.
II. Research Design
In this section we present the research design we use to examine the effects of the Benefits Improvement and Protection Act (BIPA). We start by showing descriptive evidence of the change in payments and then present our econometric model.
A. Identifying Variation
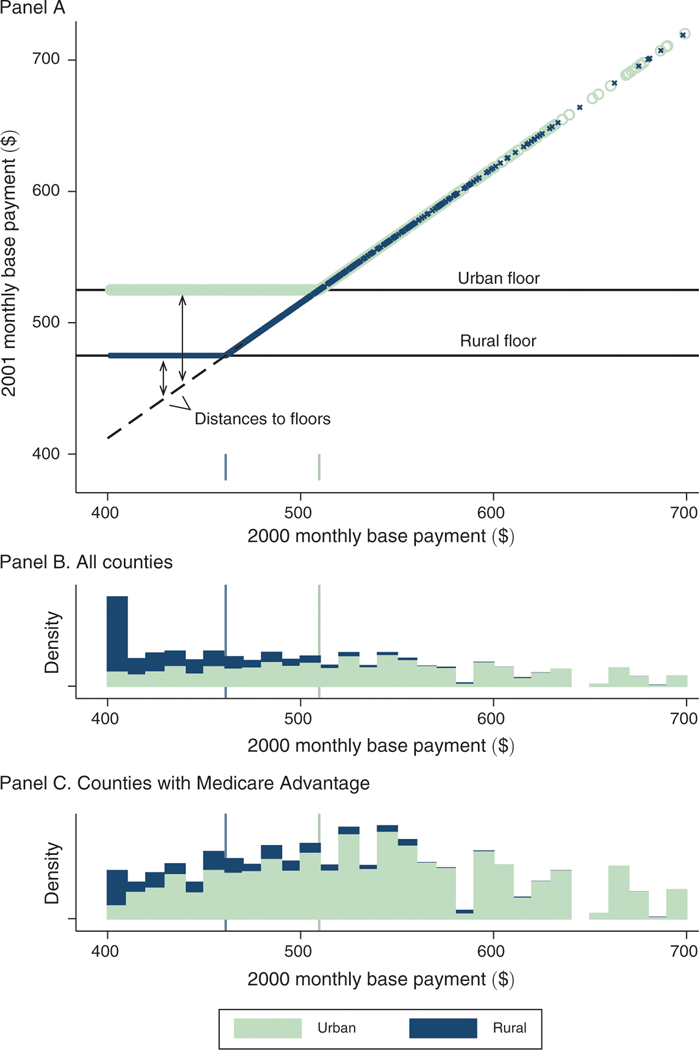
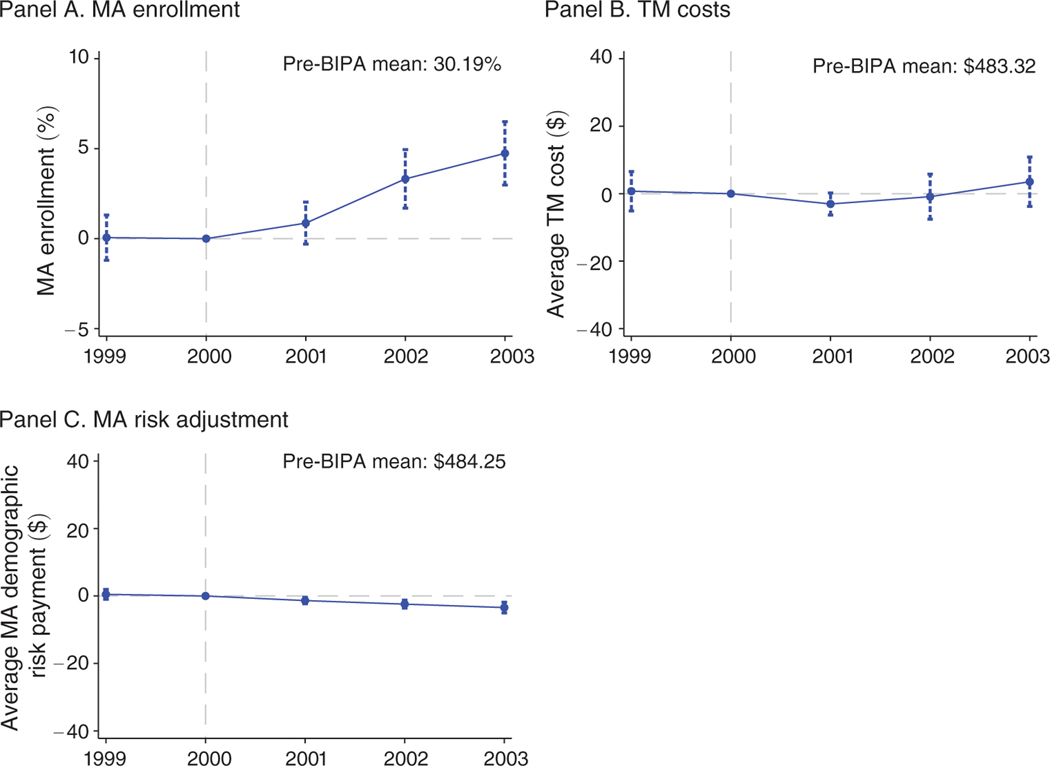
Panel A of Figure 1 plots payments for each county in the year before (-axis) and after (-axis) the BIPA payment floors came into effect. Panels B and C plot histograms of the 2000 base payments, weighted by the county’s Medicare population, for all counties (panel B) and for counties with an MA plan in at least one year of the 1997–2003 study period (panel C). The figure shows that BIPA led to a sharp increase in payments for a large share of counties, with urban counties having their base payment rates raised to a minimum of $525 per month and rural counties having their base payment rates raised to a minimum of $475 per month.19
Figure 1. Payment Floors: Pre- and Post-BIPA Monthly Base Payments.
Notes: Figure illustrates the identifying variation arising from BIPA. Panel A shows county base payments before (-axis) and after (-axis) the implementation of the BIPA urban and rural payment floors in 2001. Urban counties are represented in light green and rural counties in blue. The dashed line in panel A indicates the uniform 3 percent increase that was applied to all counties between 2000 and 2001 and traces the counterfactual payment rule in absence of the floors. The distance to the floor defines our identifying payment variation and is a function of both the pre-BIPA base payment and a county’s urban rural classification. Panels B and C plot histograms of the base payments in 2000, stacking rural and urban counties and weighting by county Medicare population, for all counties (panel B) and for counties with an MA plan in at least one year of the 1997–2003 study period (panel C). All values are denominated in dollars per beneficiary per month. Base payments in this figure are not adjusted for inflation and are not normalized for the sample average demographic risk adjustment factor. The sample in the top two panels is 3,143 counties that include 100 percent of the Medicare population in 2000. The sample in the bottom is 880 counties that include 73 percent of the Medicare population in 2000.
Figure 1 also illustrates the two key sources of variation that we use in our analysis. The first source of variation arises from the fact that counties with the same base payments prior to BIPA received different payment increases depending on their urban or rural status, with urban counties receiving increases of $50 per month more than rural counties with the same pre-BIPA base payment level. The second source of variation arises from the fact that counties with the same urban or rural status received different payment increases depending on their pre-BIPA base payment level. For example, among urban counties affected by the floor, those with lower pre-BIPA base payments received relatively larger payment increases than those with higher pre-BIPA base payments.
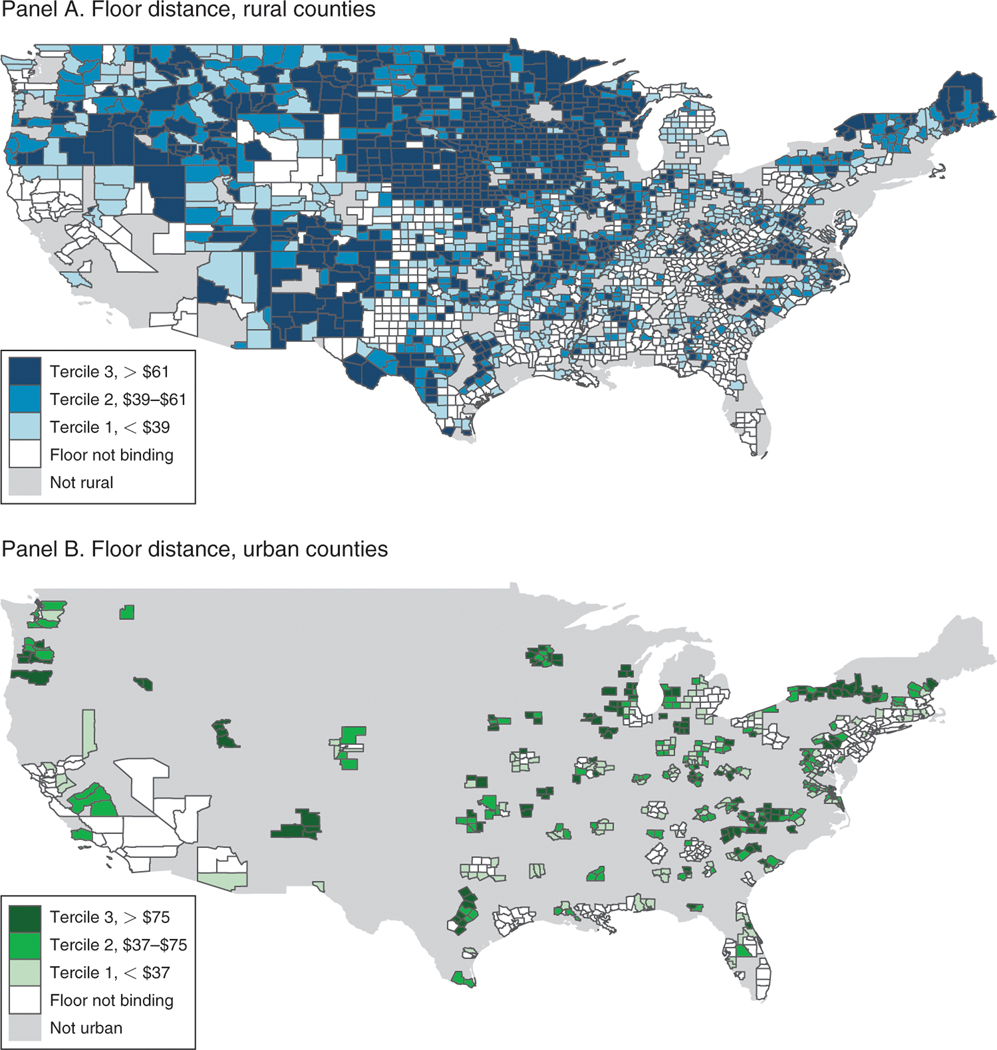
Figure 2 presents maps of this variation separately for rural counties (panel A) and urban counties (panel B). The shading corresponds to the magnitude of the treatment: the difference between the applicable payment floor and the base rate that would have applied absent the BIPA reform. This is the “distance-to-floor” variable that we define more precisely below. Darker shading indicates a larger distance-to-floor, and counties for which the floors were not binding are shaded white. These maps show that the implementation of the BIPA payment floors, which were binding for 72 percent of counties, provides us with a large and geographically diverse source of identifying variation.20,21
Figure 2. Effect of BIPA on County Base Payments.
Notes: Map shows the geography of the identifying variation across urban and rural counties. Counties are binned according to their tercile of distance-to-floor, separately for rural counties (panel A) and urban counties (panel B). Legends indicate the bin ranges, and counties for which the floors were not binding are shaded white. The distance-to-floor variable, which describes the payment shock between 2000 and 2001, is defined precisely in equation (2) and is graphically illustrated in the panel A of Figure 1. Base payments in this figure are not adjusted for inflation and are not normalized for the sample average demographic risk adjustment factor. Alaska and Hawaii are excluded from these maps but included in all of the other analysis. Inclusive of AK and HI, the sample is 3,143 counties that include 100 percent of the Medicare population in 2000.
Table 2 provides some basic statistics on the increase in payments. On average, the payment floors led to a 14.1 percent payment increase in affected rural counties and a 16.1 percent increase in affected urban counties. There was substantial variation. For example, the bottom quartile of urban floor counties received a payment increase below 8.8 percent, and the top quartile received an increase above 22.7 percent.
Table 2—
Effect of BIPA on County Base Payments
| Percentiles | |||||
|---|---|---|---|---|---|
|
|
|||||
| Mean | SD | 25th | 50th | 75th | |
|
| |||||
| Non-floor county () | |||||
| base payment ($ per month) | 14.39 | 1.58 | 13.17 | 14.03 | 15.10 |
| Change in base payment (%) | 3.0 | 0.0 | 3.0 | 3.0 | 3.0 |
| Rural floor county () | |||||
| base payment ($ per month) | 52.94 | 17.16 | 39.67 | 62.59 | 67.18 |
| Change in base payment (%) | 14.1 | 4.9 | 10.0 | 16.8 | 18.3 |
| Urban floor county () | |||||
| base payment ($ per month) | 64.67 | 29.56 | 38.90 | 62.33 | 89.05 |
| Change in base payment (%) | 16.1 | 8.4 | 8.8 | 14.9 | 22.7 |
Notes: Table shows the effect of BIPA on base payments for non-floor counties and counties that were affected by the rural and urban floors. The base payment rows show the difference between the 2001 base payment and the 2000 base payment in dollars per beneficiary per month. The change in base payment rows show this difference as a percentage of the 2000 base payment. The sample is the full set of counties in 2000 () that includes 100 percent of the Medicare population. Base payments in this table are not adjusted for inflation but are normalized for the sample average demographic risk adjustment factor. See text for additional information on data construction.
B. Econometric Model
We examine the effects of this payment change using a difference-in-differences research design that compares outcomes across counties that were differentially exposed to the BIPA payment floors. Let denote counties and denote years. We measure exposure to BIPA with a distance-to-floor variable, , which isolates the increase in payments solely due to the payment floors:
| (2) |
where is the monthly payment in the absence of the floor and is the relevant urban or rural payment floor. We define the instrument in all of the years in our sample so we can test for spurious responses prior to BIPA and any phased adjustment after the law came into effect.
Post-BIPA, we observe the actual county base payment but not the payment in the absence of the floor. During the post-period, non-floor counties received a 2 percent update each year. Therefore, to calculate counterfactual payments for floor counties in the post-BIPA period, , we simply update the pre-BIPA payments that we observe by 2 percent each year:22
| (3) |
where is the county base payment that we observe in the pre-BIPA period. Similarly, floors are observed in the post-BIPA period only. The law specified that floors be increased by 2 percent each year.23 We define counterfactual floors, , in the pre-BIPA period by deflating the 2001 floor by 2 percent per year:
| (4) |
where is the base payment floor that we observe during the post-BIPA period.
Our baseline econometric model is a difference-in-differences specification that allows the coefficient on the distance-to-floor variable, , to flexibly vary by year. Letting be an outcome in county in year , our baseline regression specification takes the form
| (5) |
where and are county and year fixed effects, is a flexible set of controls discussed in more detail below, and is the error term. The are the coefficients of interest, and we use the summation notation to make explicit that separate coefficients are estimated for each calendar year. We normalize so that these estimates can be interpreted as the change in the outcomes relative to year 2000 when BIPA was passed. We consider to be our preferred estimate because the three-year horizon allows us to capture medium-run effects of the change in payments.
The identifying assumption for this difference-in-differences research design is the parallel trends assumption: in the absence of BIPA, outcomes for counties that were differentially affected by the payment floors would have evolved in parallel. We take two approaches to assess the validity of this assumption. Our first approach is to plot the coefficients over time. This approach allows us to visually determine whether there is evidence of spurious preexisting trends and to observe any anticipatory or delayed response to the BIPA payment increases.
Our second approach is to estimate specifications that isolate the two key subsets of our identifying variation, each addressing a different class of potential confounders. Pre-BIPA base payments are not randomly assigned and reflect historical FFS costs, raising the possibility that time trends in relevant characteristics like population health, market structure, and health care spending could be correlated with the distance-to-floor variable. We address this potential concern by estimating an alternative specification which isolates variation in distance-to-floor due to urban or rural status while controlling for differential trends in the outcome variable by pre-BIPA base payments. Specifically, we include as controls quartiles of the base payment in year 2000 interacted with year indicators.24 With this approach, the estimates are largely identified by differences in the payment increases between urban and rural counties with the same pre-BIPA base payments.
To isolate the complementary variation, we estimate a separate specification that includes as controls the urban status of the county interacted with year indicators. This approach controls for differential time trends across urban and rural counties, and the estimates are identified by differences in the size of the payment increase within the sets of urban and rural counties.25
A recent paper by Duggan, Starc, and Vabson (2016), conducted in parallel to our study, uses cross-sectional variation in capitation payments between urban and rural counties to estimate pass-through in MA. Using data from the post-BIPA time period, the authors estimate a premium pass-through rate of zero, although their standard errors do not allow them to reject a relatively wide range of parameters (including our baseline estimate of 45 percent pass-through below). In contrast, our difference-in-differences strategy allows us to control for county fixed effects and to estimate specifications that control for differential time trends across counties. Given the importance of place-specific determinants of medical spending (Finkelstein, Gentzkow, and Williams 2014), we see the ability to control for county fixed effects and differential time trends as a major advantage of our strategy.
As discussed in Section I, Congress instituted several earlier payment reforms that affected payments during the pre-period. The most important of these was the payment floor established by the 1997 Balanced Budget Act (BBA) and an additional update to payments for some counties in 2000. To address any correlation between the effects of these payment reforms and BIPA, we explicitly control for these two events in all our regression specifications. We control for the BBA floor by constructing a distance-to-floor measure that is analogous to our BIPA distance-to-floor variable and interacting this variable with year fixed effects for 1998 onward. We control for the 2000 payment increases by constructing a variable defined as the difference between the 2 percent update and the actual update in 2000 and interacting this variable with year fixed effects for 2000 onward. See online Appendix A.1 for more details on these payment changes.
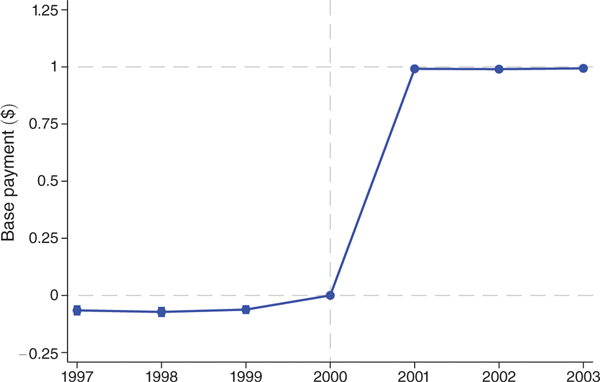
Figure 3 shows the first-stage effect of our constructed change in payments variable on actual monthly payment rates. It plots the coefficients on distance-to-floor × year interactions from the baseline difference-in-differences specifications (equation (5)) with base payments as the dependent variable. Table 3 presents parameter estimates from the corresponding regressions. Column 1 shows estimates from the baseline specification with county and year fixed effects. Column 2 adds controls for the base payment level in the year 2000 interacted with year indicators to isolate variation due to the difference between the urban and rural floor. Column 3 includes as controls an urban indicator interacted with year indicators to isolate variation due to differences in base payments conditional on urban or rural status. Standard errors in all specifications are clustered by county, with the (barely visible) capped vertical bars in the plot showing 95 percent confidence intervals.
Figure 3. First-Stage Effect on Base Payments: Impact of $1 Increase in Distance-to-Floor.
Notes: Figure shows coefficients on distance-to-the-floor × year interactions from difference-in-differences regressions with the monthly base payments as the dependent variable. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Controls include year and county fixed effects as well as flexible controls for the 1998 payment floor introduction and the blended payment increase in 2000. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. Year 2000, which is the year prior to BIPA implementation, is the omitted category and denoted with a vertical dashed line. Horizontal dashed lines are plotted at the reference values of 0 and 1.
Table 3—
First-Stage Effect on Base Payments: Impact of $1 Increase in Distance-to-Floor
| Base payment ($) | |||
|---|---|---|---|
|
|
|||
| (1) | (2) | (3) | |
|
| |||
| 0.992 | 0.992 | 0.992 | |
| (0.003) | (0.004) | (0.003) | |
| 0.990 | 0.999 | 0.987 | |
| (0.005) | (0.005) | (0.005) | |
| 0.994 | 1.002 | 0.990 | |
| (0.004) | (0.005) | (0.005) | |
| Main effects | |||
| County FE | X | X | X |
| Year FE | X | X | X |
| Additional controls | |||
| Pre-BIPA payment × year fixed effects | X | ||
| Urban × year fixed effects | X | ||
| Pre-BIPA mean of dependent variable | 510.84 | 510.84 | 510.84 |
| 0.9998 | 0.9999 | 0.9999 | |
Notes: Table shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions with monthly base payments as the dependent variable. Although the estimation includes distance-to-floor interactions for all the years in our sample, we display coefficients for the post-reform years (2001–2003) above for brevity. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Year 2000, which is the year prior to BIPA implementation, is the omitted category. Additional controls in column 2 include quartiles of year 2000 county base payments interacted with year indicators and in column 3 include an indicator for urban status interacted with year indicators. Flexible controls for the 1998 payment floor introduction and 2000 blended payment increase are included in all specifications. All monetary values are inflation adjusted to 2000 using the CPI-U. Robust standard errors clustered at the county level are reported in parentheses.
Both the figure and table show that $1 increase in our distance-to-floor variable translates one-for-one into a change in payments to plans. This first stage is very precisely estimated, with all specifications yielding a coefficient of 0.987 to 1.002 for each post-BIPA year and with standard errors no larger than 0.005. Because the first stage is one and precisely estimated, in the remainder of the paper, we interpret reduced-form effects of distance-to-floor on outcomes, such as premiums and benefits, as resulting from a one-for-one change in monthly base payments.
III. Main Results
In this section, we examine the pass-through of the increase in payments. We start by presenting the effects on premiums. We then examine the pass-through into plan benefits, such as copayments and drug coverage. Finally, we examine impacts on plan availability.
A. Pass-Through into Premiums
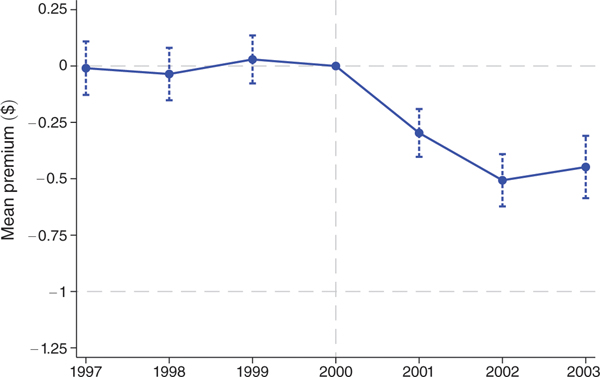
Figure 4 examines the effect on premiums by plotting the coefficients on distance-to-floor × year interactions from the baseline difference-in-differences specifications (equation (5)) with county-level mean premiums as the dependent variable.26 The dashed horizontal line at zero in Figure 4 indicates no pass-through and the dashed horizontal line at 1 indicates full pass-through, which occurs when a $1 increase in payments translates one-for-one into a $1 decline in premiums. Table 4 presents parameter estimates from the corresponding regression, which includes year and county fixed effects. Table 4 also reports parameter estimates from additional specifications that isolate different subsets of the identifying variation described in Section II. Standard errors in all specifications are clustered by county, with the capped vertical bars in the plot showing 95 percent confidence intervals.
Figure 4. Premium Pass-Through: Impact of $1 Increase in Monthly Payments.
Notes: Figure shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. The dependent variable is the mean monthly premiums weighted by enrollment in the plan. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The county-level measures are constructed using plan-level data weighted by plan enrollment. The sample is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Controls are identical to those in Figure 3. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. Horizontal dashed lines are plotted at the reference values of 0 and −1, where −1 corresponds to 100 percent pass-through.
Table 4—
Premium Pass-Through: Impact of $1 Increase in Monthly Payments
| Base payment ($) | |||
|---|---|---|---|
|
|
|||
| (1) | (2) | (3) | |
|
| |||
| −0.297 | −0.180 | −0.308 | |
| (0.054) | (0.093) | (0.055) | |
| −0.507 | −0.369 | −0.519 | |
| (0.059) | (0.122) | (0.059) | |
| −0.448 | −0.321 | −0.451 | |
| (0.071) | (0.126) | (0.072) | |
| Main effects | |||
| County fixed effects | X | X | X |
| Year fixed effects | X | X | X |
| Additional controls | |||
| Pre-BIPA payment × Year fixed effects | X | ||
| Urban × Year fixed effects | X | ||
| Pre-BIPA mean of dependent variable | 12.58 | 12.58 | 12.58 |
| 0.71 | 0.71 | 0.71 | |
Notes: Table shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions. Although the estimation includes distance-to-floor interactions for all the years in our sample, we display coefficients for the post-reform years (2001–2003) above for brevity. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The county-level measures are constructed using plan-level data weighted by plan enrollment. The sample is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Year 2000, which is the year prior to BIPA implementation, is the omitted category. Controls are identical to those in Table 3. All monetary values are inflation adjusted to 2000 using the CPI-U. Robust standard errors clustered at the county level are reported in parentheses.
The plot shows no evidence of a trend in the period prior to the Benefits Improvement and Protection Act (BIPA), providing support for our parallel trends identifying assumption. In the first year following implementation, mean premiums decline by $0.30 for each $1 increase in payments and level off at a decline of approximately $0.45 in the third year after the reform. The size of effects in the third year are stable across specifications in Table 4, ranging from $0.32 to $0.45: not statistically different from each other, and in all cases statistically different from zero (no pass-through) and from one (full pass-through). Difference-in-differences plots corresponding to the alternative specifications in columns 2 and 3 of Table 4 are displayed in online Appendix Figures A4 and A5. Similar to the baseline result in Figure 4, these plots show no evidence of a differential trend in premiums prior to the reform. Our preferred estimate of mean pass-through is $0.45, which is the 2003 estimate from the baseline specification shown in column 1.
Online Appendix Figure A6 illustrates the effect of this change in monthly payments on the median premium (panel A), minimum premium (panel B), and maximum premium (panel C). Since the typical county has between two and three plans, these statistics provide an exhaustive characterization of the distribution of premiums in the typical county. The effects on these other statistics are similar to the effect on the mean, with the plots showing no evidence of a pre-BIPA effect and a sharp decline following implementation of the payment floors. The point estimates for these other statistics, shown in online Appendix Table A1, are similar in magnitude to the mean effect, with the 2003 estimates ranging from $0.37 to $0.49 for the baseline specification. Like the effect on the mean, the results are robust to specifications that isolate different subsets of the identifying variation.
One factor that could affect our interpretation of the premiums and benefits pass-through estimates is the fact that plans could not set negative premiums during our time period.27 In principle, a plan that was constrained from further reducing premiums would have an incentive to pass-through higher payments in the form of more generous benefits. Relative to an unconstrained setting, this would bias downward our estimate of premium pass-though and bias upward our estimate of pass-through into benefits, but might not impact on our combined pass-through estimate. In online Appendix Section A.3, we examine this potential issue by estimating Tobit specifications that account for insurers’ inability to set negative premiums. The magnitude of the Tobit estimates are very similar to, and statistically indistinguishable from, our baseline non-Tobit estimates, confirming that our baseline results are not driven by this feature of the market.
To summarize the premium pass-through results, we find that mean premiums decline by $0.45 for every $1 of increased monthly payments at 3 years following the reform. This result is robust to alternative specifications that isolate different subsets of our identifying variation, to other statistics describing the premium distribution (median, minimum, and maximum), and to Tobit specifications that explicitly account for the fact that plans could not give rebates (charge a negative premium) during our sample period. Online Appendix A.2 presents additional analysis that illustrates that the decline in premiums occurs precisely in the first month that these changes were permitted by the regulator.28
B. Pass-Through into Benefits
In addition to lowering premiums, plans may have responded to the increased payments by raising the generosity of their coverage.29 In the standard model of insurance demand, such a change in plan generosity would operate through an income effect. Consumers facing lower premiums would be richer and thus might demand more or less generous insurance coverage.30
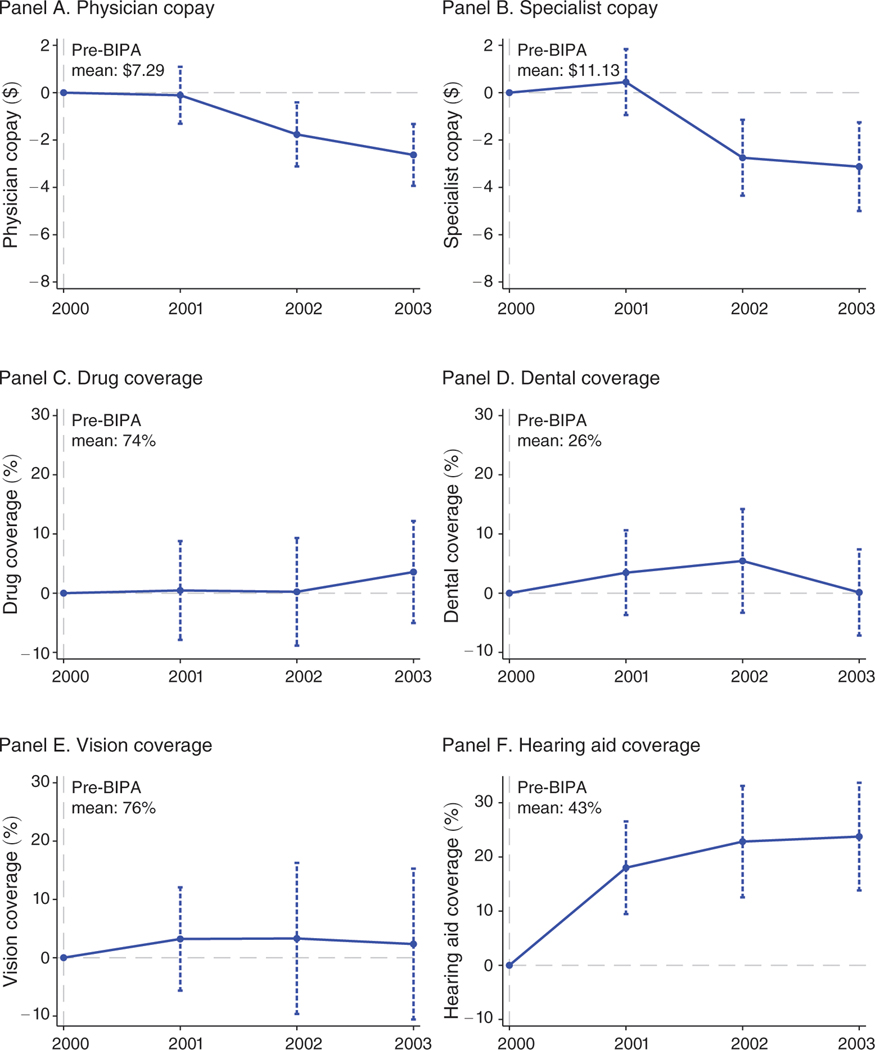
We investigate pass-through into benefits using data on the main MA plan characteristics marketed to Medicare beneficiaries at the time of enrollment. Specifically, we examine the effect of BIPA on the mean county-level copayments for physician and specialist visits and the percentage of plans providing coverage for prescription drugs, dental, vision, and hearing aids. Figure 5 plots the coefficients on distance-to-floor × year interactions from difference-in-differences specifications (equation (5)) with measures of plan benefits as the dependent variable. To aid interpretation, we scale the coefficient on the distance-to-floor variable by $50, which is approximately 10 percent of the $511 mean pre-BIPA base payment. We have information on plan benefits for 2000 to 2003 and therefore only have one year of pre-BIPA data. These data are sufficient to identify the effect of BIPA but do not allow us to perform falsification tests for preexisting trends, warranting more caution in interpreting the results. Table 5 displays parameter estimates from the corresponding difference-in-differences regressions where the coefficient is similarly scaled by $50. The table shows coefficients from the baseline regression specification, with online Appendix Table A2 showing the specifications that isolate different subsets of the identifying variation. Standard errors in all specifications are clustered by county and the capped vertical bars in the plots show 95 percent confidence intervals.
Figure 5. Benefits Generosity: Impact of $50 Increase in Monthly Payments.
Notes: Figure shows scaled coefficients on distance-to-floor × year interactions from difference-in-differences regressions. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. The dependent variables are physician copays in dollars (panel A), specialist copays in dollars (panel B), and indicators for coverage of outpatient prescription drugs (panel C), dental (panel D), corrective lenses (panel E), and hearing aids (panel F). The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 2000 to 2003. This sample includes 2,250 of 12,572 possible county-years and 62 percent of all Medicare beneficiaries. Controls are identical to those in Figure 3. In panels A and B, the vertical axes measure the effect on copays in dollars of a $50 difference in monthly payments. In panels C through F, the vertical axes measure the effect on the probability that a plan offers each benefit, again for a $50 difference in monthly payments. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. Year 2000, which is the year prior to BIPA implementation, is the omitted category. The horizontal dashed line is plotted at 0.
Table 5—
Benefits Generosity: Impact of Increase in Monthly Payments
| Physician copay ($) | Specialist copay ($) | Drug coverage (%) | Dental coverage (%) | Vision coverage (%) | Hearing aid coverage (%) | Actuarial value ($) | |
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|
| |||||||
| * | −0.110 | 0.448 | 0.457 | 3.459 | 3.212 | 18.010 | 0.019 |
| (0.613) | (0.710) | (4.258) | (3.653) | (4.514) | (4.357) | (0.047) | |
| * | −1.765 | −2.749 | 0.230 | 5.445 | 3.301 | 22.838 | 0.056 |
| (0.691) | (0.818) | (4.641) | (4.470) | (6.605) | (5.245) | (0.050) | |
| * | −2.630 | −3.128 | 3.574 | 0.124 | 2.343 | 23.760 | 0.087 |
| (0.667) | (0.956) | (4.398) | (3.717) | (6.598) | (5.071) | (0.045) | |
| Main effects | |||||||
| County fixed effects | X | X | X | X | X | X | X |
| Year fixed effects | X | X | X | X | X | X | X |
| Pre-BIPA mean of dependent variable | 7.29 | 11.13 | 73.62 | 25.77 | 75.68 | 42.58 | n/a |
| 0.67 | 0.70 | 0.83 | 0.67 | 0.74 | 0.83 | 0.82 | |
Notes: Table shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions. Although the estimation includes distance-to-floor interactions for all the years in our sample, we display coefficients for the post-reform years (2001–2003) above for brevity. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. In columns 1 to 6, the dependent variables are measures of benefit generosity, and the coefficient on distance-to-floor is scaled by $50. In column 7, the dependent variable is the monthly actuarial value of benefits, and the coefficient on distance-to-floor is not rescaled. See text for details on the construction of the monthly actuarial value of benefits. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 2000 to 2003. This sample includes 2,250 of 12,572 possible county-years and 62 percent of all Medicare beneficiaries. Year 2000, which is the year prior to BIPA implementation, is the omitted category. Controls are identical to those in Table 3. All monetary values are inflation adjusted to 2000 using the CPI-U. Robust standard errors clustered at the county level are reported in parentheses.
Impact of $50 increase in columns 1 to 6. Effect of $1 increase in column 7.
Panels A and B of Figure 5 show that the increase in payments had a sharp effect on mean personal physician and specialist copayments. By 2003, the $50 increase in monthly payments reduced physician copayments by $2.63 on a pre-BIPA base of $7.29 and reduced specialist copayments by $3.13 on a pre-BIPA base of $11.13. The effects are highly statistically significant but modest in economic magnitude. The average Medicare beneficiary had 8 combined physician and specialist visits per year or two-thirds of a visit per month, implying that the $50 increase in monthly payments reduced copayment spending by approximately $2 per month.31
Panels C to F of Figure 5 show the effects on the percentage of plans offering drug, dental, vision, and hearing aid coverage. As before, the effects are scaled to a $50 increase in monthly payments. The plots show that the increased payments have no effect on drug, dental, and vision coverage but a relatively large effect on the percentage of plans offering hearing aids.32 By 2003, the parameter estimate for the effect on hearing aids, shown in column 6 of Table 5, indicates that the $50 increase in payments raised the share of plans offering hearing aids by 23.8 percentage points on a base of 42.6 percent. Online Appendix Table A2 shows that the benefits effects are stable across our alternative specifications.
To quantify the actuarial value of the change in benefit generosity, we combine these estimates with data on utilization and payments from the 2000 Medical Expenditure Panel Survey (MEPS), restricting the sample to individuals who are 65 or older. For dental, vision, hearing aids, and drug coverage, we calculate the actuarial value of these benefits as the monthly costs paid by the insurance provider.33 For copayments, we calculate the actuarial value of the insurer’s share of costs by taking the negative of the copayment amount multiplied by the monthly number of visits.34
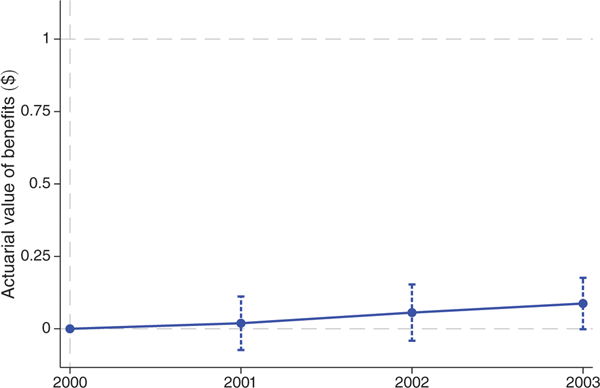
Figure 6 plots effects of a $1 increase in payments on this measure of the actuarial value of benefits. The vertical axis offers the same pass-through interpretation as in the premium figures, where a coefficient of 1 indicates that a $1 increase in plan subsidies increases the actuarial value of plan benefits by a dollar. Pass-through is small. The point estimate for 2003, shown in column 7 of the table, indicates a pass-through rate of $0.09 on the dollar and is marginally statistically significant with a -value of 0.05.35 Specifications that isolate alternative subsets of the identifying variation, shown in online Appendix Table A2, confirm the robustness of this finding.
Figure 6. Actuarial Value of Benefits: Impact of $1 Increase in Monthly Payments.
Note: Figure shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of a $1 increase in monthly payments. The dependent variable is the actuarial value of benefits, which is constructed based on observed plan benefits in our main analysis dataset and utilization and cost data from the 2000 Medical Expenditure Panel Survey. See text for full details. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 2000 to 2003. This sample includes 2,250 of 12,572 possible county-years and 62 percent of all Medicare beneficiaries. Controls are identical to those in Figure 3. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. Horizontal dashed lines are plotted at 0 and 1.
One potential concern with all pass-through papers is that firms may change product characteristics that the researcher does not observe. We think this is a relatively minor concern in our setting for two reasons. First, we see all of the product characteristics (e.g., premiums, copayment, vision coverage) that the consumer sees when purchasing the plan. These are the characteristics that plans should be most likely to change as they are the most salient plan features and thus the most likely to affect enrollment. Second, for every Medicare Advantage plan, we also have data on the subjective plan evaluations of enrolled consumers. These survey data allow us to investigate unobservable (to the econometrician) changes in plan quality that might not be picked up by our analysis of product characteristics. In online Appendix A.7, we show that our identifying variation has a precisely estimated zero effect on these evaluations and other measures of plan quality, including measures of clinical care quality and beneficiary-reported quality of care. This finding is consistent with other research which shows limited pass-through into plan characteristics that are not easily observed (e.g., Stockley et al. 2015; Agarwal et al. 2014, 2015).
Taken together, the premiums and benefits results for 2003 yield a combined pass-through estimate of $0.54 on the dollar. A 95 percent confidence interval allows us to rule out a combined pass-through effect outside the range of $0.37 to $0.71.36
C. Plan Availability
If there are fixed costs of entry, then the increase in payments might have had an effect on plan availability. Figure 7 plots the coefficients on distance-to-floor × year interactions from difference-in-differences specifications (equation (5)) with different measures of plan availability as the dependent variable.37 Table 6 shows the corresponding regression estimates, including alternative specifications that isolate different subsets of the identifying variation.
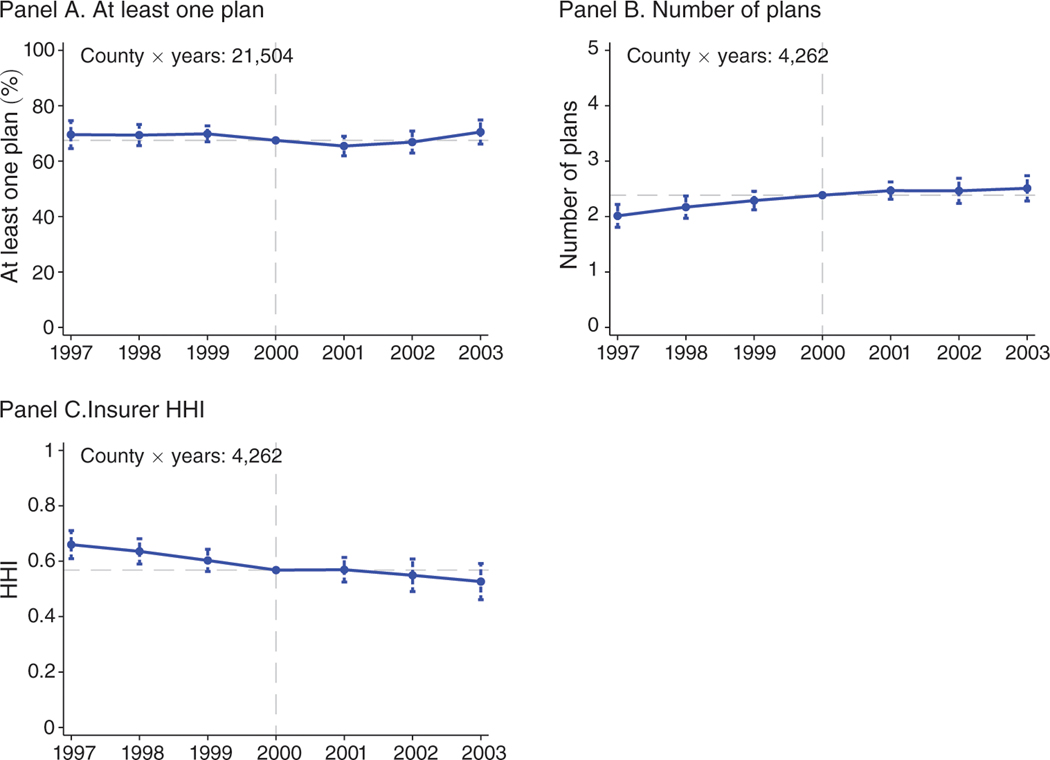
Figure 7. Plan Availability: Impact of $50 Increase in Monthly Payments.
Notes: Figure shows scaled coefficients on distance-to-floor × year interactions from difference-in-differences regressions. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. Coefficients are scaled to reflect the impact of a $50 increase in monthly payments. The dependent variable in panel A is an indicator for at least one plan. The dependent variable in panel B is the number of plans conditional on at least one plan. The dependent variable in panel C is a Herfindahl-Hirschman Index (HHI) with a scale of 0 to 1. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample in panel A is the balanced panel of county-years with non-missing information on base rates and Medicare beneficiaries during 1997 to 2003. This sample includes 21,504 of 22,001 county-years and more than 99.9 percent of all Medicare beneficiaries. The sample in panels B and C is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Controls are identical to those in Figure 3. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. The horizontal dashed lines are plotted at the sample means, which are added to the coefficients.
Table 6—
Plan Availability: Impact of $50 Increase in Monthly Payments
| At least one plan (%) | Number of plans | HHI | |||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|
| |||||||||
| −2.04 | −3.35 | −2.32 | 0.082 | −0.104 | 0.103 | 0.001 | 0.038 | −0.002 | |
| (1.79) | (2.46) | (1.78) | (0.079) | (0.142) | (0.082) | (0.023) | (0.036) | (0.023) | |
| −0.62 | −6.57 | −0.24 | 0.079 | −0.114 | 0.092 | −0.019 | 0.015 | −0.024 | |
| (2.02) | (3.13) | (2.04) | (0.116) | (0.191) | (0.119) | (0.030) | (0.046) | (0.031) | |
| 3.01 | −2.60 | 3.39 | 0.124 | −0.011 | 0.139 | −0.041 | −0.011 | −0.048 | |
| (2.21) | (3.54) | (2.23) | (0.116) | (0.202) | (0.119) | (0.033) | (0.051) | (0.033) | |
| Main effects | |||||||||
| County FE | X | X | X | X | X | X | X | X | X |
| Year FE | X | X | X | X | X | X | X | X | X |
| Additional controls Pre-BIPA payment × year FE | X | X | X | ||||||
| Urban × year FE | X | X | X | ||||||
| Pre-BIPA mean of dependent variable | 67.5 | 67.5 | 67.5 | 2.39 | 2.39 | 2.39 | 0.57 | 0.57 | 0.57 |
| 0.86 | 0.86 | 0.86 | 0.70 | 0.69 | 0.70 | 0.73 | 0.72 | 0.73 | |
Notes: Table shows coefficients on distance-to-floor × year interactions from difference-in-differences regressions. Although the estimation includes distance-to-floor interactions for all the years in our sample, we display coefficients for the post-reform years (2001–2003) above for brevity. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. Coefficients are scaled to reflect the impact of a $50 increase in monthly payments. The dependent variables are indicator for at least one plan (columns 1 to 3), number of plans conditional on at least one plan (columns 4 to 6), and Herfindahl-Hirschman Index (HHI) with a scale of 0 to 1 (columns 7 to 9). The sample in columns 1 to 3 is the balanced panel of county-years with nonmissing information on base rates and Medicare beneficiaries during 1997 to 2003. This sample includes 21,504 of 22,001 counties and more than 99.9 percent of all Medicare beneficiaries. The sample in columns 4 to 9 is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Year 2000, which is the year prior to BIPA implementation, is the omitted category. Controls are identical to those in Table 3. All monetary values are inflation adjusted to 2000 using the CPI-U. Robust standard errors clustered at the county level are reported in parentheses.
Panel A of Figure 7 shows the effect of a $50 increase in payments on the percentage of counties with at least one plan. For this analysis, we use the entire balanced panel of county-years with non-missing information on base rates and Medicare beneficiaries during 1997 to 2003. This sample includes 21,504 of 22,001 county-years and more than 99.9 percent of all Medicare beneficiaries. The plot shows no evidence of an effect on the percentage of counties with at least one plan. The parameter estimates, shown in columns 1 to 3 of Table 6, are similar across alternative specifications.
One potential reason for this lack of an extensive margin effect is that BIPA had only a minor effect on the total revenue that could be earned in marginal counties, mainly because of the small number of Medicare beneficiaries in these areas. In particular, the average county with zero plans in year 2001 had only 4,278 Medicare beneficiaries, compared to an average of 32,172 in counties with at least one plan. This means that although BIPA raised payments by an average $33 per month in these zero-plan counties, a plan capturing 5 percent of the Medicare beneficiaries would experience a total revenue increase of only $84,704, which might not be enough to cause a detectable effect on entry or exit.
While these results are interesting in their own right, the plan existence results also offer reassurance that the identifying variation is not systematically related to entry and exit from our sample. The pattern of the coefficients in panel A of Figure 7 indicates that changes to the number of counties with an MA plan are unlikely to be a source of bias in our main estimates. However, as a robustness test, we replicate all our analyses using a balanced sample of counties with an MA plan in each year between 1997 and 2003. These estimates, shown in online Appendix A.8, are very similar and confirm that selection is not biasing the results.
The increase in payments may have also influenced market concentration within the set of counties that had at least one plan. Panel B of Figure 7 shows the effect of a $50 increase in payments on the number of plans in each county conditional on there being at least one plan.38 Panel C shows the effect on the Herfindahl-Hirschman Index (HHI) for the number of plans in each county, again conditional on there being at least one plan. The HHI is the standard measure of market power used for antitrust analysis and is similar to our other dependent variables in weighting plans based on their enrollment shares. These plots show no evidence of an effect of the increased payments in 2001 on these different measures, though the pre-BIPA trends are not completely flat. In contrast, the extensive margin of plan participation in a county (at least one plan) that defines our premium analysis sample is a robust and precisely estimated zero, with flat pre-trends across all specifications. Overall, these results indicate that BIPA did not have a meaningful impact on market concentration, consistent with Duggan, Starc, and Vabson (2016), who show that their variation in payments is unrelated to insurer HHI.
IV. Model of Pass-Through
In the previous section, we showed that Medicare Advantage (MA) plans pass through approximately one-half of the increased capitation payments in the form of lower premiums and more generous benefits. In this section, we show that incomplete pass-through can possibly be explained by (i) advantageous selection into MA and (ii) market power among MA insurers and medical providers. To build intuition, we start by presenting figures that illustrate these potential mechanisms. We then present a model that, under assumptions on the nature of selection and competition, allows us to generate quantitative predictions on the relationship between pass-through and these underlying mechanisms. The model provides a framework for interpreting the empirical evidence that follows.
A. Graphical Analysis
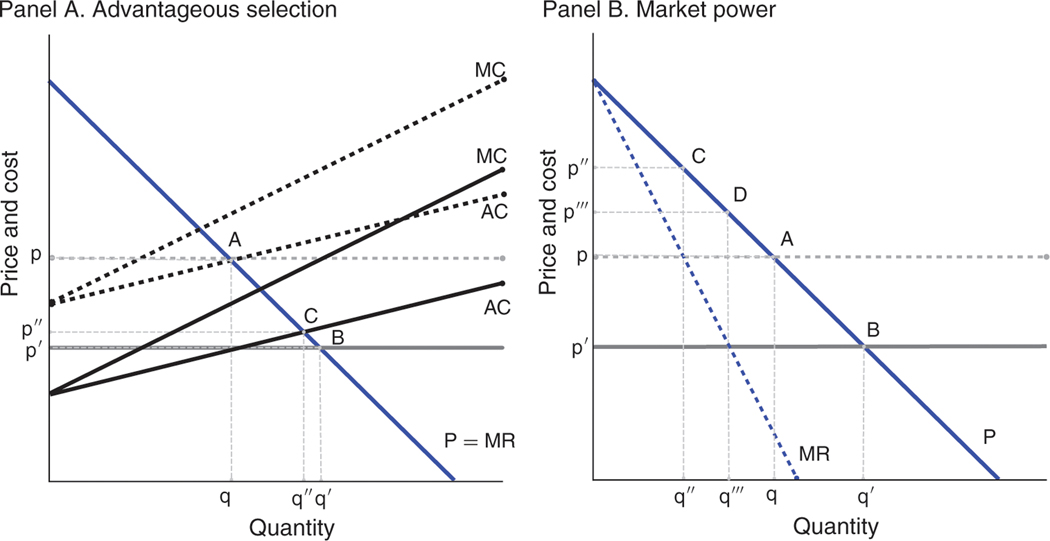
Figure 8 presents this graphical analysis. We model demand for MA as linear, and we define the marginal cost of providing an MA plan to an individual as the expected cost of providing medical care net of the capitation payment from Medicare. Within this framework, we can depict the increase in capitation payments under BIPA as a downward shift of the marginal cost curve. Our graphical approach is closely related to that of Einav, Finkelstein, and Cullen (2010), who examine selection in a perfectly competitive environment, and Mahoney and Weyl (2017), who examine the interaction of imperfect competition and selection.
Figure 8. Determinants of Incomplete Pass-Through.
Notes: Figure shows the pass-though of an increase in monthly payments depicted by a decrease in (net) marginal costs. Panel A examines pass-through when there are perfectly competitive markets and either no selection or advantageous selection. With no selection (horizontal AC curve), a downward shift in costs translates one-for-one into a reduction in premiums, from point A to point B. With advantageous selection (upward-sloping AC curve), a downward shift in costs translates less than one-for-one into a reduction in premiums, from point A to point C. Panel B examines pass-through where there is no selection and either perfectly competitive markets or a monopolist. Points A and B are repeated from panel A. With monopolist pricing, a downward shift in costs translates less than one-for-one into a reduction in premiums, from point C to point D.
Panel A of Figure 8 examines the impact of selection on pass-through in a perfectly competitive market. In a perfectly competitive market, firms earn zero profits and the equilibrium is defined by the intersection of the demand and the average cost curves. When there is no selection, firms face a horizontal average cost curve, and a downward shift in the average cost curve translates one-for-one into a reduction in premiums, depicted by the transition from point A to point B in the figure. When there is advantageous selection, average costs are upward sloping as the marginal consumer is more expensive than the average. Panel A illustrates that under advantageous selection an identically sized downward shift in the average cost curve is not fully passed through as firms offset the higher costs of the marginal consumers with higher prices to maintain zero profits in equilibrium, depicted by the shift from point A to point C.
Panel B examines the impact of market power on pass-though in a market with no selection. To simplify the exposition, we consider the extremes of perfect competition and monopoly. As described above, when there is perfect competition and no selection, a downward shift in the marginal cost curve is fully passed through to consumers, moving the equilibrium from point A to point B. The monopolist sets the price such that marginal revenue is equal to marginal cost. With a linear demand curve, this leads to 50 percent pass-through, shifting the equilibrium from point C to point D in the figure. More generally, Bulow and Pfleiderer (1983) show that the pass-through of a small cost shock is determined by the ratio of the slope of the demand curve to the slope of the marginal revenue curve.
B. Model
We build on and generalize this graphical analysis by constructing a model of pass-through in imperfectly competitive selection markets, drawing upon previous work by Fabinger and Weyl (2013b) and Mahoney and Weyl (2017). We direct the reader to these papers for technical details and microfoundations that support the modeling choices.
Suppose individuals differ in their cost to firms, , demographic risk score, , and willingness to pay for insurance, . Assume that insurance firms provide symmetric, although possibly horizontally differentiated, insurance products. Firms cannot discriminate across consumers with respect to either premiums or plan benefits.39 At a symmetric equilibrium, all firms charge the same premium . Aggregate demand at this price is given by and represents the fraction of the market with MA coverage. In addition to the premium, firms receive a risk-adjusted capitation payment equal to , where is the county base payment. At a symmetric equilibrium, all plans receive enrollees with the same average risk adjustment factor so that average capitation payments to firms are , where , where is the inverse demand function.
In practice, risk adjustment is normalized by the regulator to average to one in the overall Medicare population and is close to one in the MA segment. To avoid carrying extra notation in the derivation, we temporarily consider the case of no risk adjustment (, ) but fully incorporate this term when presenting the final pass-through equation below.
Total costs for the industry are summarized by an aggregate cost function which is equal to the aggregate medical costs paid by MA plans when the prevailing premium is . This specification rules out firm-level economies or diseconomies of scale, including fixed costs at the firm level.40 Average costs for the industry are given by , and marginal costs are given by . Adverse selection at the industry level is indicated by decreasing marginal costs , and advantageous selection is indicated by increasing marginal costs . For the purposes of our discussion, we limit our attention to cases where and have the same sign.41
In a perfectly competitive equilibrium, firms earn zero profits and prices are equal to average costs net of payments from Medicare: . At the other extreme, a monopolist chooses the price to maximize profits:
| (6) |
Setting the first-order condition to zero yields the price-setting equation , where denotes the standard absolute markup term and is the marginal (net of capitation payment) cost.
To allow for intermediate levels of competition, Mahoney and Weyl (2017) Introduce a parameter that interpolates between the price-setting equations for perfect competition and monopoly:
| (7) |
The model nests the extremes of perfect competition and monopoly along with a number of standard models of imperfect competition. Cournot competition is given by , where is the number of firms. Mahoney and Weyl (2017) show that the model is a reduced-form representation of differentiated product Bertrand competition when , where is the aggregate diversion ratio, the share of consumers that firm diverts from rivals when it lowers its price.42
C. Pass-Through
We are interested in how much of an increase in payments is passed through into lower health insurance premiums. For a small change in payments, pass-through is defined as the negative of the total derivative of premiums with respect to the capitation payment: . We will say there is full pass-through when and no pass-through when .43
First, consider the case of perfect competition. Setting and differentiating equation (7) with respect to yields
| (8) |
where we have suppressed arguments for notational simplicity. Under advantageous selection, average costs are decreasing in price ( and ) and therefore pass-through is less than 1. Consistent with panel A of Figure 8, even in a perfectly competitive market, part of the increase in capitation payments must go to compensate insurers for costlier marginal enrollees, explaining the lack of full pass-through.
In practice, Medicare risk adjusts payments to partially compensate insurers for selection. Incorporating risk rating yields the pass-through equation
| (9) |
which adds two terms to equation (8) above. The term in the denominator measures selection net of any change in average risk adjustment payments. The numerator is scaled by to reflect the fact that a $1 increase in base payments does not translate into a $1 increase in payments if MA enrollees have non-representative demographic risk . MA enrollees have lower average demographic risk , which slightly lowers the predicted pass-through rate. See online Appendix A.10 for a derivation of this pass-through formula.
Our model also provides predictions for pass-through under the more realistic assumption of imperfect competition . Guided by our empirical results that payments have no effect on market structure, we assume that is constant.44 Fully differentiating the pass-through equation yields
| (10) |
Increasing market power (higher ) shifts optimal price-setting away from average cost pricing and toward marginal cost pricing, where both costs are net of risk adjustment. As in equation (9), the net cost terms in the denominator are negative under advantageous selection, decreasing the pass-through rate. When there is no selection, the cost terms are zero and the pass-through formula simplifies to and is decreasing in market power for many standard parameterizations of demand. For instance, linear demand implies and simplifies the pass-through equation to .45
V. Selection
The objective of this section is to quantify the extent to which advantageous selection can explain our estimates of pass-through. If Medicare Advantage (MA) is advantageously selected, net of risk adjustment, then lower premiums draw in higher cost enrollees, and even a perfectly competitive market cannot pass through the full increase in payments.
A. Conceptual Approach
We estimate the reduction in pass-through that could be explained by selection and risk adjustment in a perfectly competitive market. Perfect competition is a natural benchmark because it implies a pass-through rate of one if there were no selection and no risk adjustment. In online Appendix A.11 we show that under the assumptions of linear demand and cost curves, the main effects of selection and market power are proportionally separable. Thus, to a first-order approximation, we can think about advantageous selection as scaling down the predicted pass-through for any given level of market power.
As shown in Section IV, pass-through in a perfectly competitive MA market is given by
| (11) |
where is the average risk adjustment factor, is the base payment, and is the change in the average costs net of any change in average risk adjustment payments. The superscript is added to the risk adjustment and cost terms to clearly distinguish these from risk and costs in the Traditional Medicare (TM) population, which we also discuss below. During our study period, risk adjustment was based on demographics, but the same formula could accommodate risk adjustment of any form, including the currently implemented diagnosis-based system or the type of diagnosis and drug utilization-based system being considered by CMS for future implementation.
We observe the average risk adjustment factor for MA plans in the data and can calculate directly. Since we observe the risk adjustment factor, we can also estimate . To do so, we estimate the reduced-form effect of base payments on the average risk adjustment factor using our main difference-in-differences strategy and then divide by the effect of base payments on premiums from Section III. This yields the effect of a change in premiums on the average risk adjustment factor .
Estimating is more complicated because we do not observe data on MA costs. To overcome this issue, we follow the prior MA literature (e.g., Brown et al. 2014; Newhouse et al. 2012) and use TM costs to proxy for counterfactual costs under MA. Previous studies show that beneficiaries who switch from TM to MA and vice versa have low costs while in TM relative to other TM beneficiaries and interpret this fact as indicating that MA is advantageously selected. This “switcher” approach identifies selection in a relatively small sample of switchers and relies on the assumption that the choice of MA versus TM is exogenous to changes in health. In contrast, our strategy measures selection in a larger sample of beneficiaries that includes new enrollees, and our estimates are identified using plausibly exogenous variation. Since our identifying variation in payments affects premiums, we can use insights from Einav, Finkelstein, and Cullen (2010), described below, to trace out the cost curve facing insurers and directly quantify the degree selection into MA.
Let denote the fraction of the market with TM coverage, and let denote average TM costs. Assume (i) the costs of covering a given individual in MA and TM are proportionally constant so that , , and (ii) the market average cost curves for both TM and MA are linear in quantity and therefore have a constant slope. These assumptions imply that the slopes of MA and TM average cost curves are of opposite sign and proportional:46
| (12) |
This result, combined with the fact that a change in premiums has an equal and opposite effect on MA and TM quantity , implies that an increase in premiums has effects on TM and MA average costs that are of the same sign and proportional:47
| (13) |
Intuitively, advantageous selection into MA implies that marginal enrollees are high cost relative to the MA average and low cost relative to the TM average. Therefore, if a decrease in MA premiums draws more individuals into MA and increases average MA costs, then the same decrease in premiums must lower TM enrollment and raise average costs among those who remain in TM.
This result allows us estimate up to the scaling parameter, , using the TM cost data. As before, we estimate the reduced-form effect of base payments on average TM costs using our difference-in-differences strategy and then divide by our estimate of the effect of base payments on premiums from Section III. The effect of a change in premiums on average MA costs is therefore .48
For our baseline estimates, we make the conservative assumption that costs under MA and TM are equal . This provides us an upper bound on the explanatory power of advantageous selection. If instead we follow a large literature that finds that costs are proportionally lower in managed care plans than in fee-for-service coverage , our estimates of the explanatory power of selection would be reduced.49
B. Selection Estimates
Figure 9 presents the difference-in-differences estimates that allow us to recover the explanatory power of selection. The plots are identical to those that examine the effects on premiums Figure 4 except with different dependent variables. For ease of interpretation, we scale the coefficient on the distance-to-floor variable by $50, which is approximately 10 percent of the $511 mean base payment in place prior to the Benefits Improvement and Protection Act (BIPA), and normalize the coefficient on year 2000 to zero so we can interpret the effects relative to the year before BIPA came into effect. Panel A of Table 7 displays parameter estimates from the corresponding difference-in-differences regressions, and online Appendix Table A3 shows alternative specifications that isolate different subsets of the identifying variation.
Figure 9: Selection: Impact of $50 Increase in Monthly Payments.
Notes: Figure shows scaled coefficients on distance-to-floor × year interactions from difference-in-differences regressions. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. Coefficients are scaled to reflect the impact of a $50 increase in monthly payments. The dependent variables are MA enrollment (panel A), traditional Medicare costs (panel B), and mean demographic risk payments for MA enrollees (panel C). The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 1999 to 2003. This sample includes 2,892 of 15,715 possible county-years and 63 percent of all Medicare beneficiaries. Controls are identical to those in Figure 3. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. The horizontal dashed lines indicate zero effects.
Table 7—
Selection: Impact of $50 Increase in Monthly Payments
| MA enrollment (%) | TM costs ($) | MA risk adjustment payment ($) | Mean premiums* ($) | Implied pass-through with selection () | |
|---|---|---|---|---|---|
|
|
|||||
| (1) | (2) | (3) | (4) | (5) | |
|
| |||||
| Panel A. Yearly BIPA effect | |||||
| 0.86 | −3.05 | −1.36 | −0.32 | 1.07 | |
| (0.60) | (1.67) | (0.48) | (0.05) | (0.17) | |
| 3.32 | −0.88 | −2.42 | −0.48 | 0.90 | |
| (0.83) | (3.41) | (0.59) | (0.06) | (0.13) | |
| 4.74 | 3.54 | −3.43 | −0.43 | 0.72 | |
| (0.90) | (3.73) | (0.81) | (0.07) | (0.10) | |
| Panel B. Pooled post-BIPA effect | |||||
| × post-BIPA | 3.29 | −0.05 | −2.83 | −0.47 | 0.85 |
| (0.71) | (2.80) | (0.59) | (0.05) | (0.09) | |
| Panel C. Controls: all panels | |||||
| Main effects | |||||
| County fixed effects | X | X | X | X | |
| Year fixed effects | X | X | X | X | |
| Pre-BIPA mean of dependent variable | 30.19 | 483.32 | 484.25 | 12.38 | |
Notes: Columns 1 through 4 show coefficients on distance-to-floor × year interactions from difference-in-differences regressions. Although the estimation includes distance-to-floor interactions for all the available years in our sample, we display coefficients for the post-reform years (2001–2003) above for brevity. The first-stage results displayed in Table 3 indicate that a $1 change in distance-to-floor translates into a $1 change in the monthly payments, so we can interpret the coefficients as the effect of an increase in monthly payments on a dollar-for-dollar basis. In columns 1 to 3, the coefficient on distance-to-floor is scaled by $50. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. The sample is the unbalanced panel of county-years with at least one MA plan over years 1999 to 2003. This sample includes 2,892 of 15,715 possible county-years and 63 percent of all Medicare beneficiaries. Year 2000, which is the year prior to BIPA implementation, is the omitted category. Controls are identical to those in Table 3. All monetary values are inflation adjusted to 2000 using the CPI-U. Robust standard errors clustered at the county level are reported in parentheses. Column 5 reports the implied pass-through in a perfectly competitive market based on the estimates in the corresponding row (see Section V for more details). Standard errors for this implied pass-through estimate are calculated by the bootstrap method using 200 iterations.
Impact of $1 increase in monthly payments shown in column 4.
Panel A of Figure 9 shows the effect of a $50 increase in monthly payments on MA enrollment. In terms of estimating the degree of selection, the effect on quantity can be thought of as a first stage. If payments had no effect on MA enrollment, there would be no identifying variation that would allow us to estimate the degree of selection. MA enrollment is slow to respond to the decline in premiums, consistent with inertia or switching costs Handel 2012. However, by 2003 the first stage is large, with a $50 increase in payments raising enrollment by 4.7 percentage points on a pre-BIPA mean of 30.2 percent, and is highly significant with a -value < 0.01.
In addition to allowing us to estimate selection, the quantity effect is independently informative about the basic structure of the MA market. The 2003 estimate implies an enrollment elasticity with respect to payments of If we assume that base payments affect enrollment only through premiums, so that base payments are a valid instrument for premiums, then the 2003 estimate implies a semi-elasticity of demand with respect to premiums of where the denominator is the change in premiums implied by a $50 increase in the base payments. While this is a market-level elasticity, with individual firms facing more elastic residual demand curves, our low aggregate price elasticity estimate is similar to the −0.009 semi-elasticity estimate by Town and Liu (2003) and the −0.013 semi-elasticity estimate by Dunn (2010). The low elasticity is also consistent with work on limited premium transparency (Stockley et al. 2015) and large switching costs (Nosal 2012) in the MA market.
Panel B of Figure 9 shows the effect of a $50 increase in payments on TM costs. To interpret the magnitude of the estimates, it is useful to divide by the effect on enrollment, which provides an estimate of the slope of the average cost curve . The 2003 point estimate of $3.54, shown in column 2 of Table 7, divided by the 4.7 percent enrollment effect implies a $75 slope of the average cost curve. Since average costs are $483 per month, this indicates that individuals with the highest willingness-to-pay for MA only cost about 16 percent less than the population on average. We cannot rule out the null hypothesis that the slope of the average cost curve is zero, with a 95 percent confidence interval that runs from −$80 to $230.50 Online Appendix Section A.9 demonstrates that the selection estimates are qualitatively similar in specifications with alternative controls and specifications with alternative measures of utilization.
Panel C of Figure 9 shows the effects on MA risk adjustment payments, which is the MA demographic risk score scaled by the year 2000 base payment. Since MA plan payments are scaled by an individual’s risk score, increases in average demographic risk, holding costs fixed, result in greater pass-through. The plot shows evidence that demographic risk declines with MA penetration. While the magnitude is statistically significant, the estimate is small. Dividing the 2003 point estimate of $3.43, shown in column 3 of Table 7, by the enrollment effect indicates a slope of risk adjustment payments with respect to quantity of −$72. Combining this estimate with our 2003 cost estimate yields a slope for the average cost curve net of risk adjustment of $147.51 We cannot reject that there is no net selection on the margin as the 95 percent confidence interval on this estimate runs from $8 to $302.52
To calculate the explanatory power of selection, we combine these estimates with equation (11), where the numerator of equation (11), the average risk adjustment factor among MA beneficiaries , is equal to 0.955 in our sample.53 We calculate standard errors of the implied pass-through by bootstrapping over counties.54 We estimate pass-through for each of the post-BIPA years. To increase power, we also construct a pooled pass-through estimate, which is calculated using regressions that specify a single post-BIPA coefficient for enrollment, demographic risk, costs, and premiums. These pooled estimates are shown in panel B of Table 7. Column 5 of Table 7 shows the reduction in pass-through implied by our estimates of selection. The pooled estimates indicate that selection reduces pass-through to 85 percent. A 95 percent confidence interval allows us to rule out estimates lower than 0.73 or higher than 0.98. The yearly estimates similarly vary from 72 percent to 107 percent.55
Taken together, the results above indicate that selection is unable to explain our finding that only one-half of the increase in payments is passed through to consumers. We estimate that a perfectly competitive market would pass through $0.85 of each $1 in increased payments. Alternatively put, of the combined $0.46 in payments that is not passed through to consumers, our estimates indicate that selection can account for $0.15 or about one-third of the shortfall.56
VI. Market Power
In this section, we examine the extent to which insurer market power is a mechanism that can explain our estimates of incomplete pass-through. In Section IV, we discussed how a monopolist facing a linear demand curve would pass through only one-half of an increase in payments (panel B of Figure 8). More generally, we showed that for a range of functional form assumptions on the shape of the demand curve, pass-through in an imperfectly competitive market is declining in market power. In light of the evidence on limited selection, the model implies that much of the incomplete pass-through in our setting is due to market power.
We investigate the quantitative importance of insurer market power by splitting the sample by measures of insurer market power prior to the 2000 Benefits Improvement and Protection Act (BIPA) and estimating the pass-through rate separately in each sample.57 It is important to emphasize that we view the following analysis as suggestive, since our research design isolates variation in payments to plans, not variation in pre-reform market power.
Figure 10 shows estimates of pass-through into mean premiums for different levels of competition. Panel A splits the sample by the year 2000 county-level insurer Herfindahl-Hirschman Index (HHI), with the highest HHI tercile corresponding to the most concentrated markets and the lowest HHI tercile corresponding to the markets with the least market power.58 Panel B splits the sample by whether the county had one, two, or three or more separate Medicare Advantage (MA) insurers in year 2000. The regression specifications used to construct these figures are identical to those used to construct the baseline pass-through plot (panel A of Figure 4), applied to each subsample. We show coefficients for year 2003, which is the year with the largest pass-through of premiums, on average. Estimates for 2001 and 2002 are shown in online Appendix Figure A9. As before, the vertical axes measure pass-through of payments, with the dashed horizontal line at zero indicating no pass-through and the dashed horizontal line at −1 indicating full pass-through.
Figure 10. Pass-Through and Market Concentration.
Notes: Figure shows coefficients on distance-to-floor × year 2003 interactions from several difference-in-differences regressions. The dependent variable is the mean premium defined as in Figure 4. Each point represents a coefficient from a separate regression in which the estimation sample is stratified by market concentration in the pre-BIPA period. In panel A, counties are binned according to the tercile of insurer HHI in plan year 2000. In panel B, counties are binned according to the number of insurers operating in the county in plan year 2000. Competition increases to the right of both panels. The unit of observation is the county × year, and observations are weighted by the number of beneficiaries in the county. While the analysis is conducted on segments of the data, the underlying sample is the unbalanced panel of county-years with at least one MA plan over years 1997 to 2003. This sample includes 4,262 of 22,001 possible county-years and 64 percent of all Medicare beneficiary-years. Controls are identical to those in Figure 3. The capped vertical bars show 95 percent confidence intervals calculated using standard errors clustered at the county level. Horizontal dashed lines are plotted at the reference values of 0 and −1, where −1 corresponds to 100 percent pass-through.
Panel A of Figure 10 shows that the pass-through rate is monotonically decreasing in pre-BIPA insurer HHI. The pass-through rate is 13 percent in the most concentrated HHI tercile and 63 percent in the tercile with the lowest market power. Panel B shows that the pass-through rate is similarly increasing in the number of pre-BIPA insurers in the county. When there is a single insurer, pass-through is 13 percent. In counties with three or more firms, pass-through increases to 74 percent. This is consistent with our model, which predicts that pass-through is decreasing in market power for many standard parameterizations of demand.
Online Appendix Figure A9 shows the effects for each year in the post-BIPA period. The 2002 estimates are almost identical to the 2003 estimates and show that pass-through is monotonically increasing in both measures of competition. Consistent with the main results in Figure 4, pass-through rates are lower in 2001 and the relationship between pass-through and market power is less precise. The parameter estimates underlying these figures are shown in online Appendix Table A5. The table also reports coefficients from full-sample regressions that interact pre-BIPA market power with the distance-to-floor variable. These confirm the statistical significance of the pattern in which pass-through declines with market power.
The estimates of pass-through in the most competitive markets also provide us with an alternative approach to gauge the importance of selection as a mechanism for our findings. We estimate premium pass-through of 74 percent in markets with at least 3 plans. If we add in 9 percent benefits pass-through, then these results imply pass-through is at least 83 percent in the most competitive markets, and therefore advantageous selection can explain no more than 17 percent of the reduction in pass-through (the difference between 100 percent and 83 percent), which is similar to the directly estimated 15 percent selection parameter.
We conclude by noting that despite the growth in Medicare Advantage since our period of analysis, many MA markets remain highly concentrated today. As of 2014, 88 percent of Medicare Advantage markets had insurer HHI values in excess of 2,500, the Department of Justice standard for highly concentrated markets. Further, because MA market structure varies across geographic markets within a time period much more than in aggregate across time, it is likely that pass-through continues to be geographically heterogeneous in the current MA program.
VII. Conclusion
We examine the pass-through to consumers of payments in Medicare Advantage (MA) using difference-in-differences variation brought about by the Benefits Improvement and Protection Act (BIPA). We show that approximately one-half of the marginal spending on the MA program is passed through to beneficiaries in the form of lower premiums and more generous benefits. We find little evidence that selection of more costly beneficiaries into MA can account for this incomplete pass-through, suggesting the result is driven by supply-side market power. Consistent with this intuition, we find that the pass-through of payments varies greatly with insurer market concentration, with premium pass-through rates of 13 percent in the least competitive markets and 74 percent in the markets with the most competition.
Our estimates of pass-through are directly relevant for the $156 billion in MA payment reductions scheduled to take effect under the Affordable Care Act. Counter to claims made by some commentators, our results predict that the incidence of such payment reductions would fall only partially on Medicare beneficiaries, while a significant fraction of these cuts would be borne by the supply side of the market. Our study does not address the division of surplus among inframarginal MA consumers and therefore does not speak directly to the welfare effects of a more dramatic counterfactual, such as completely abolishing (or significantly expanding) Medicare Advantage.
Supplementary Material
Acknowledgments
This paper was accepted to the AER under the guidance of Hilary Hoynes, Coeditor. This paper was previously circulated under the title: “Does Privatized Health Insurance Benefit Patients or Producers? Evidence from Medicare Advantage.” We thank three anonymous referees, as wells as Jason Abaluck, Christopher Afendulis, Michael Chernew, Amy Finkelstein, Matthew Grennan, Jonathan Kolstad, Amanda Kowalski, Timothy Layton, Matthew Notowidigdo, Robert Town, and seminar participants at the 2014 AHEC meeting, Duke Microeconomics Jamboree, Harvard, 2015 HEC Montreal Summer IO Conference, MIT, 2015 NBER Insurance IO meeting, 2014 NBER Public Economics meeting, Penn State University, 2013 and 2014 RWJ Scholars in Health Policy Research Annual Meetings, UC Berkeley, UC Santa Barbara Health Economics Conference, UC Santa Cruz, University of Chicago, University of Texas at Austin, and Yale for helpful comments. We are grateful to Abhi Gupta, Mariel Schwartz, Yin Wei Soon, and Hanbin Yang for excellent research assistance. Mahoney acknowledges the George J. Stigler Center for the Economy and State for financial support. Geruso acknowledges the Robert Wood Johnson Foundation. The authors declare that they have no relevant or material financial interests that relate to the research described in this paper.
Footnotes
Go to https://doi.org/10.1257/aer.20151362 to visit the article page for additional materials and author disclosure statement(s).
During our sample period, this private option was called Medicare Part C or Medicare+Choice. Since the passage of the Medicare Modernization Act in 2003, these plans have been called Medicare Advantage. We use the current naming convention throughout the paper.
Our product characteristics data include information on physician and specialist copays and supplemental benefits such as drug, dental, vision, and hearing aid coverage. To ensure that our estimates capture pass-through on all relevant margins, we additionally analyze survey data from Medicare with subjective quality assessments of every Medicare Advantage plan. We estimate a precise zero effect on these subjective quality evaluations, indicating that there was no pass-through on unobservable plan quality.
As shown in Fabinger and Weyl (2013b), the incidence or ratio of consumer to producer surplus is given by where is the pass-through rate and is an index of market power. Our baseline estimate of allows us to bound the incidence between 0.54 and 1.17 and implies that consumers receive no more than approximately one-half of the marginal surplus from the market.
Our paper is also related to the broader literature on MA including Cawley, Chernew, and McLaughlin (2005), who investigate the impacts of MA payment changes in 1997 on MA plan availability; Song, Landrum, and Chernew (2012, 2013), who study the impacts of annual benchmark changes on MA plan bids; Gowrisankaran, Town, and Barrette (2011), who estimate the mortality effects of MA enrollment and MA drug coverage; and Duggan, Starc, and Vabson (2016), who use cross-sectional variation in capitation payments between urban and rural counties to examine pass-through of Medicare Advantage subsidies. While we do not specify microfoundations for consumer demand, our estimates of limited price sensitivity complement research by Stockley et al. (2015) on low premium transparency and Nosal (2012) on large switching costs in the MA market.
While the prior literature relies on the assumption that switching between MA and TM is unrelated to changes in health status, our study makes no such assumption as we rely on plausibly exogenous variation in prices to identify selection. Another advantage of the present study over the prior literature is that our design allows us to examine all enrollees, new and old. The prior switcher studies cannot examine new enrollees because effects can be estimated only among individuals that have at least one year of history in MA or TM prior to a switch in their coverage.
Despite the growth in Medicare Advantage since our period of analysis, many Medicare Advantage markets remain highly concentrated today. The typical MA market (county) during our time period was highly concentrated (with a mean insurer HHI of 5,800 in 2000) and this remains true today (with a mean insurer HHI of 4,800 in 2014). To put this in some perspective, the DOJ thresholds for moderately and highly concentrated markets are 1,500 and 2,500 respectively. As of 2014, 88 percent of Medicare Advantage markets had insurer HHI values in excess of 2,500.
For examples of opposition to the cuts on the basis that seniors bear the burden, see “Obama Administration Reverses Proposed Cut to Medicare Plans,” Jason Millman, Washington Post, April 4, 2014.
Prior to 1998, MA capitation payments were set at 95 percent of the Average Adjusted Per Capita Cost (AAPCC), which was an actuarial estimate intended to match expected TM expenditures in the county for the “national average beneficiary.” Beginning in 1998, county base payments were updated via a complex formula created by the Balanced Budget Act (BBA) of 1997. Specifically, plans were paid the maximum of (i) a weighted mix of the county rate and the national rate (“the blend”), (ii)a minimum base payment level implemented by BBA, and (iii) a 2 percent “minimum update” over the prior year’s rate, applying in 1998 to the 1997 AAPCC. See online Appendix A.1 for additional details.
The bill was introduced in the House in October 2000 in close to its final form and passed in December. According to Achman and Gold (2002), Congress passed BIPA in response to pressure from MA insurers to undo the cost-control provisions of BBA 1997, which constrained MA payment growth.
Counties are designated urban if they are associated with an MSA with a population of 250,000 or greater. Rural counties are those not associated with an MSA, or associated with an MSA below the threshold.
The purpose of this risk adjustment was not to correct for geographic variation in illness or utilization, which is fully captured in the local county average, but to address sorting between TM and MA. Following the prior literature, we focus solely on the demographic risk adjustment in our analysis.
The average risk score in our estimation sample is different than 1.0 for two primary reasons. First, our estimation sample excludes individuals that qualify for Medicare through Social Security Disability Insurance. Second, only a subset of the variables the regulator uses for calculating the demographic risk score are available to us in the administrative data. In particular, the regulator uses age, sex, Medicaid status, working status, and institutionalized status, and we do not have information on either working status or institutionalized status. Thus, we calculate demographic risk scores using information on age, sex, and Medicaid status, assuming individuals are non-institutionalized and non-working.
MMA 2003 changed the formula by which the base payment is calculated substantially. In addition, the act introduced meaningful risk adjustment applied on top of the base payment rate to calculate the overall capitation payment. Several prior papers examine the effects of various aspects of MMA 2003 reform including Brown et al. (2014), McWilliams, Hsu, and Newhouse (2012), and Woolston (2012).
Plan premium sources vary by year and include the Medicare Compare database, the Medicare Options Compare database, and an out-of-pocket cost database (OOPC Resources) provided by CMS.
These detailed descriptions of plan benefits are sometimes referred to as Landscape Files or Plan Services Files.
We accessed these data through the National Bureau of Economic Research. Pre-1999 data are not available through the data re-use agreement with CMS.
Relative to the entire Medicare program, our effective sample size is much larger than the number of counties alone would suggest because counties served by an MA plan are on average much larger than counties without an MA plan: counties served by an MA plan during our time period have 30.3 thousand Medicare beneficiaries on average while counties without an MA plan have 4.0 thousand Medicare beneficiaries on average. Throughout the analysis, we weight county-year observations by the number of Medicare beneficiaries represented by the observations.
In online Appendix Figure A1 we show an alternative version of the bottom panel of Figure 1, in which the county-level histogram is weighted by the size of the MA population in 2000, rather than by the MA-eligible (i.e., Medicare) population. The alternative version is very similar to the bottom panel of Figure 1.
In online Appendix Figure A2, we show that this variation spans counties of varying population sizes. Overall, 53.7 percent of counties with an MA plan received an increase in payments. The figure shows that the percentage of “treated” counties is fairly stable across the distribution of county sizes.
Online Appendix Figure A3 shows the baseline maps from Figure 2 along with an additional set of maps that conditions on the sample of counties with an MA plan in at least one year of the 1997–2003 study period.
Year 2001 is unique in that we observe both and , due to the implementation of the floors in March of that year. In our analysis, year 2001 always refers to the level of payments for March through December 2001. Since counties received an additional one-time 1 percent increase in March 2001, we define as inclusive of this increase.
There was an exception in the law for when medical inflation was particularly high, in which case the floors were updated by a larger amount. See online Appendix A.1 for full details.
In principle, perfectly isolating the variation due to urban status would require completely nonparametric pre-BIPA payment rate year fixed effect interactions. The choice of quartiles is a compromise between flexibility and over-parameterizing the model.
This alternative specification controls flexibly for differential trends in the outcome variable across urban and rural areas by the inclusion of both the year fixed effects and urban year fixed effects. These allow for fully non-parametric over-time differences in outcomes across urban and rural counties. In other words, the estimates from this specification come from isolating the variation within counties with the same urban or rural status.
County-level mean premiums are constructed from plan-level data by weighting by the number of enrollees in each plan.
MA was changed after our sample period to allow plans to offer “rebates” that in effect operate as negative premiums. Examining data from this time period, Stockley et al. (2015) argue that firms do not pass-through higher payments in the form of rebates because the Medicare Plan Finder website does not prominently display this information, reducing the salience of these premium rebates at the time of purchase.
After the passage of BIPA in December 2000, the regulator required plans to submit new premiums and benefits by January 18, 2001, with the new premiums and benefits effective beginning February 2001 (Committee on Ways and Means 2004). In online Appendix Figure A7, we display a monthly sequence of our difference-in-differences coefficient estimates for premiums. The monthly plot shows a sharp drop in premiums in February 2001, consistent with plans responding in premium-setting at the first opportunity. We discuss the timing in full detail in online Appendix A.2.
In addition to varying premiums, insurers in the MA market often vary plan benefits such as copays and drug coverage across the different geographic markets they serve. Online Appendix A.4 provides more details on the within-insurer geographic variation in benefits and premiums.
In the CARA specification that is used in much of the literature, there are no income effects, and we would therefore predict no change in plan generosity. Given that the premium changes are small relative to income, even in specifications with non-constant risk aversion, we might expect only small changes in plan generosity.
The number of provider visits is calculated using the 2000 Medical Expenditure Panel Survey (MEPS).
Gowrisankaran, Town, and Barrette (2011) find that higher MA payment rates increased the probability that plans offered drug coverage, using data spanning 1993, when drug coverage rates were low, through 2000. By our last pre-reform year, most plans had already adopted drug coverage, possibly accounting for our finding of no incremental effect of the reform in 2001.
In particular, we estimate category-specific coinsurance rates among those MEPS respondents that report supplemental coverage. We then multiply these category-specific rates by the unconditional total monthly spending in each category, generating actuarial values of coverage for each supplemental benefit.
By the envelope theorem, we can calculate the value to consumers of a small reduction in copayments without needing to account for any increase in medical utilization caused by the reduced cost-sharing. In addition, since medical utilization is relatively inelastic, any changes in utilization are likely to be small.
If the actuarial value of the increase in plan benefits is larger in high out-of-pocket spending states of the world (where the marginal utility of consumption is higher) than in low out-of-pocket spending states of the world (where the marginal utility of consumption is lower), then the pass-through into benefits might have additional consumption-smoothing value to consumers which is not captured by the baseline actuarial value estimate. Additional analysis in online Appendix A.6 illustrates that any additional consumption-smoothing value from the change in plan benefits is small in this setting (roughly $0.01 per $1).
This confidence interval is constructed by bootstrapping standard errors for the sum of our distance-to-floor coefficients from the premium and actuarial value of benefits regressions. The bootstrap calculation uses 200 random samples of counties drawn with replacement.
There was a possible change to the regulator’s reporting between 1999 and 2000 in terms of separating non-local plans in the enrollment files. Non-local plans are those purchased outside of the county in which the enrolled individual is observed, and these plans are characterized by very low enrollment in the county of observation. While unimportant for our main enrollment-weighted outcomes such as premiums, these may generate data artifacts in the pre-period trends of plan counts.
Online Appendix Figure A8 includes additional plots examining the effect of the reform on the probability of ≥2 MA plans among the sample of counties with ≥1 MA plan.
Insurers in our empirical setting cannot vary premiums or plan benefits across beneficiaries. Our framework can be applied to settings where insurers can vary premiums or plan benefits by individual risk or demographic characteristics. To do so, our framework would need to be applied separately to each “market,” where a market is defined at the level at which insurers can set plan features. See Geruso and Layton (2017) for a full discussion of this point in the context of selection and risk adjustment in the ACA Exchanges.
This assumption is widely used in the literature (e.g., Einav, Finkelstein, and Cullen (2010) and Bundorf, Levin, and Mahoney 2011) and broadly consistent with the structure of the industry. The model does allow for individual-specific loads related to the costs of administering the plan. In the next section, we calculate pass-through empirically restricting the cost of insuring an individual, , to be an affine transformation of claim costs that we observe in the data.
This restriction simply eases the discussion of selection. The derived pass-through equations are equally applicable if this restriction does not hold.
The differentiated product Bertrand representation also requires the symmetry assumption that all firms receive a representative sample of all consumers purchasing the product in terms of their cost and that a firm cutting its price steals consumers with a similarly representative distribution of costs from its competitors. See Mahoney and Weyl (2017) for details.
The model can accommodate pass-through greater than one under imperfect competition and some forms of demand.
Because our estimates suggest that BIPA had little effect on product characteristics and no effect on market structure, the model takes these factors as given. This allows for a richer treatment of premium pass-through without making the model unnecessarily complex. It is important to emphasize that the aim of our model is to investigate mechanisms behind pass-through in the context of capitation payment changes within the MA market. Broad counterfactuals, such as analyzing the effect of alternative policies aimed at influencing plan entry exit, are outside the scope of our analysis.
More specifically, pass-through is decreasing in market power when demand is log-concave since . When , the pass-through rate can be greater than 1 and is increasing in market power. Fabinger and Weyl 2013a prove that if demand is linear or if it is based on an underlying willingness-to-pay distribution that is normal, logistic, Type I Extreme Value logit, Laplace, Type III Extreme Value, or Weibull or Gamma with shape parameter . They show that if demand is based on a willingness-to-pay distribution that is Pareto (constant elasticity), Type II Extreme Value, or Weibull or Gamma with shape parameter . They show that switches from to for a log-normal distribution of willingness-to-pay.
A proof is provided in online Appendix A.12. Intuitively, the slopes of the MA and TM average cost curves are proportional because linearity implies that the slope of the average cost curves are one-half of the slope of the marginal cost curves, and marginal costs are assumed to be proportional between MA and TM.
The equality simply follows from the fact that .
We observe only claims costs. Although we cannot rule out that increasing unobservable administrative costs could be an additional mechanism contributing to incomplete pass-through, any such effects are likely small. Non-claims costs such as advertising, broker fees for customer acquisition, claims administration, and profits combined typically account for less than 15 percent of the full premiums paid in these markets.
We know from above that . Since and under advantageous selection into MA, implies and therefore that our estimates provide an upper bound on the explanatory power of advantageous selection.
This confidence interval is constructed by bootstrapping standard errors for the ratio . This bootstrap calculation relies on 200 random samples of counties drawn with replacement.
The slope of the average cost curve net of risk adjustment is larger than the slope of the average cost curve alone because our point estimates suggest that, on the margin, demographic risk adjustment reinforces rather than compensates for advantageous selection.
This confidence interval is constructed by bootstrapping standard errors for the term . This bootstrap calculation relies on 200 random samples of counties drawn with replacement.
As discussed in Section I, we conduct our risk adjustment analysis with demographic risk adjustment factors normalized to 1 over our sample population. These normalized risk adjustment factors reflect the relative demographic risk scores across the MA and TM samples, where the average MA normalized risk adjustment factor is 0.955 and the average TM normalized risk adjustment factor is 1.02.
We construct bootstrap standard errors by drawing a random sample of counties with replacement, estimating the effect on enrollment and costs for this sample, and using these estimates to construct a sample-specific pass-through rate. Our standard errors are based on calculating pass-through in this manner for 200 random samples.
In addition, we explore potential heterogeneity in the selection effect by pre-BIPA measures of insurer market power. Based on this analysis reported in online Appendix Table A4, we cannot reject the hypothesis that the selection effect is identical across markets with different pre-BIPA insurer market power.
Because we find advantageous selection has little role in explaining the incomplete pass-through we observe during our period of study, it is unlikely that more recent refinements in risk adjustment have meaningfully affected the takeaways from our paper.
While we do not find evidence that BIPA affected market structure, splitting the sample by pre-BIPA market power is appropriate because the increase in payments could, at least in principle, affect the number of firms in each county.
When stratify counties by HHI terciles, we do not weight by population. The reason is that there are a small number of urban counties (e.g., Miami-Dade) with very large populations and low HHI (because they have many plans). If we weighted by population, the lowest HHI tercile would not have enough counties to generate precise estimates.
Contributor Information
MARIKA CABRAL, Department of Economics, The University of Texas at Austin, 1 University Station, Austin, TX 78712.
MICHAEL GERUSO, Department of Economics, The University of Texas at Austin, 1 University Station, Austin, TX 78712.
NEALE MAHONEY, University of Chicago Booth School of Business, 5807 South Woodlawn Avenue, Chicago, IL 60637.
REFERENCES
- Achman Lori, and Gold Marsha. 2002. “Medicare+Choice 1999–2001: An Analysis of Managed Care Plan Withdrawals and Trends in Benefits and Premiums.” New York: Commonwealth Fund. [Google Scholar]
- Agarwal Sumit, Souphala Chomsisengphet, Mahoney Neale, and Stroebel Johannes. 2014. “A Simple Framework for Estimating the Consumer Benefits from Regulating Hidden Fees.” Journal of Legal Studies 43 (S2) : S239–52. [Google Scholar]
- Agarwal Sumit, Chomsisengphet Souphala, Mahoney Neale, and Stroebel Johannes. 2015. “Regulating Consumer Financial Products: Evidence from Credit Cards.” Quarterly Journal of Economics 130 (1): 111–64. [Google Scholar]
- Brown Jason, Duggan Mark, Kuziemko Ilyana, and Woolston William. 2014. “How Does Risk Selection Respond to Risk Adjustment? New Evidence from the Medicare Advantage Program.” American Economic Review 104 (10) : 3335–64. [DOI] [PubMed] [Google Scholar]
- Bulow Jeremy I, and Pfleiderer Paul. 1983. “A Note on the Effect of Cost Changes on Prices.” Journal of Political Economy 91 (1) : 182–85. [Google Scholar]
- Bundorf M Kate Jonathan Levin, and Mahoney Neale. 2011. “Pricing and Welfare in Health Plan Choice.” American Economic Review 102 (7) : 3214–48. [DOI] [PubMed] [Google Scholar]
- Cabral Marika, Geruso Michael, and Mahoney Neale. 2018. “Do Larger Health Insurance Subsidies Benefit Patients or Producers? Evidence from Medicare Advantage: Dataset.” American Economic Review. 10.1257/aer.20151362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carey Colleen. 2014. “Sharing the Burden of Subsidization: Evidence from a Payment Update in Medicare Part D.” Unpublished. [Google Scholar]
- Cawley John, Chernew Michael, and McLaughlin Catherine. 2005. “HMO Participation in Medicare+Choice.” Journal of Economics & Management Strategy 14 (3) : 543–74. [Google Scholar]
- Clemens Jeffrey, and Gottlieb Joshua D. 2017. “In the Shadow of a Giant: Medicare’s Influence on Private Physician Payments.” Journal of Political Economy 125 (1) : 1–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Committee on Ways and Means. 2004. “Background Material and Data on Programs within the Jurisdiction of the Committee on Ways and Means.” Green Book 2004. Washington, DC: US Government Publishing Office. [Google Scholar]
- Curto Vilsa, Einav Liran, Levin Jonathan, and Bhattacharya Jay. 2015. “Can Health Insurance Competition Work? Evidence from Medicare Advantage.” NBER Working Paper 20818. [Google Scholar]
- Dafny Leemore S. 2005. “How Do Hospitals Respond to Price Changes?” American Economic Review 95 (5) : 1525–47. [DOI] [PubMed] [Google Scholar]
- Dague Laura. 2014. “The Effect of Medicaid Premiums on Enrollment: A Regression Discontinuity Approach.” Journal of Health Economics 37: 1–12. [DOI] [PubMed] [Google Scholar]
- Duggan Mark, Starc Amanda, and Vabson Boris. 2016. “Who Benefits When the Government Pays More? Pass-Through in the Medicare Advantage Program.” Journal of Public Economics 141: 50–67. [Google Scholar]
- Dunn Abe. 2010. “The Value of Coverage in the Medicare Advantage Insurance Market.” Journal of Health Economics 29 (6) : 839–855. [DOI] [PubMed] [Google Scholar]
- Einav Liran, Finkelstein Amy, and Cullen Mark R. 2010. “Estimating Welfare in Insurance Markets Using Variation in Prices.” Quarterly Journal of Economics 125 (3) : 877–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabinger Michal, and Weyl E. Glen. 2013a. “Pass-Through and Demand Forms.” Unpublished. [Google Scholar]
- Fabinger Michal, and Glen Weyl E. 2013b. “Pass-Through as an Economic Tool: Principles of Incidence under Imperfect Competition.” Journal of Political Economy 121 (3) : 528–83. [Google Scholar]
- Finkelstein Amy, Gentzkow Matthew, and Williams Heidi. 2014. “Sources of Geographic Variation in Health Care: Evidence from Patient Migration.” Quarterly Journal of Economics 131 (4) : 1681–1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geruso Michael, and Layton Timothy J. 2017. “Selection in Insurance Markets and Its Policy Remedies.” Journal of Economic Perspectives 31 (4) : 23–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowrisankaran Gautam, Town Robert, and Barrette Eric. 2011. “Managed Care, Drug Benefits and Mortality: An Analysis of the Elderly.” B.E. Journal of Economic Analysis & Policy 11 (2). [Google Scholar]
- Hackmann Martin, Kolstad Jonathan T., and Kowalski Amanda E. 2015. “Adverse Selection and an Individual Mandate: When Theory Meets Practice.” American Economic Review 105 (3) : 1030–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel Benjamin R. 2012. “Adverse Selection and Inertia in Health Insurance Markets: When Nudging Hurts.” American Economic Review 103 (7) : 2643–82. [DOI] [PubMed] [Google Scholar]
- Lustig Josh. 2010. “Measuring Welfare Losses from Adverse Selection and Imperfect Competition in Privatized Medicare.” Unpublished. [Google Scholar]
- Mahoney Neale, and Weyl E. Glen. 2017. “Imperfect Competition in Selection Markets.” Review of Economics and Statistics 99 (4): 637–51. [Google Scholar]
- McWilliams J. Michael John Hsu, and Newhouse Joseph P. 2012. “New Risk-Adjustment System Was Associated with Reduced Favorable Selection in Medicare Advantage.” Health Affairs 31 (12) : 2630–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millman Jason. 2014. “Obama Administration Reverses Proposed Cut to Medicare Plans.” Washington Post, April 4, 2014. [Google Scholar]
- Newhouse Joseph P., Price Mary, Huang Jie, McWilliams J. Michael, and Hsu John. 2012. “Steps to Reduce Favorable Risk Selection in Medicare Advantage Largely Succeeded, Boding Well for Health Insurance Exchanges.” Health Affairs 31 (12) : 2618–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosal Kathleen. 2012. “Estimating Switching Costs for Medicare Advantage Plans.” Unpublished. [Google Scholar]
- Song Zirui, Landrum Mary Beth, and Chernew Michael E. 2012. “Competitive Bidding in Medicare: Who Benefits from Competition?” American Journal of Managed Care 18 (9): 546. [PMC free article] [PubMed] [Google Scholar]
- Song Zirui, Landrum Mary Beth, and Chernew Michael E. 2013. “Competitive Bidding in Medicare Advantage: Effect of Benchmark Changes on Plan Bids.” Journal of Health Economics 32 (6) : 1301–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockley Karen, McGuire Thomas, Afendulis Christopher, and Chernew Michael E. 2015. “Premium Transparency in the Medicare Advantage Market: Implications for Premiums, Benefits, and Efficiency.” NBER Working Paper 20208. [Google Scholar]
- Town Robert, and Liu Su. 2003. “The Welfare Impact of Medicare HMOs.” RAND Journal of Economics 34 (4) : 719–36. [PubMed] [Google Scholar]
- Woolston William Gui. 2012. “Selection and the Manipulation of Price Signals: Evidence from Private Medicare Plans.” Unpublished. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.