Tracking Joint Angles During Whole-Arm Movements Using Electromagnetic Sensors

Abstract

Electromagnetic (EM) motion tracking systems are suitable for many research and clinical applications, including in vivo measurements of whole-arm movements. Unfortunately, the methodology for in vivo measurements of whole-arm movements using EM sensors is not well described in the literature, making it difficult to perform new measurements and all but impossible to make meaningful comparisons between studies. The recommendations of the International Society of Biomechanics (ISB) have provided a great service, but by necessity they do not provide clear guidance or standardization on all required steps. The goal of this paper was to provide a comprehensive methodology for using EM sensors to measure whole-arm movements in vivo. We selected methodological details from past studies that were compatible with the ISB recommendations and suitable for measuring whole-arm movements using EM sensors, filling in gaps with recommendations from our own past experiments. The presented methodology includes recommendations for defining coordinate systems (CSs) and joint angles, placing sensors, performing sensor-to-body calibration, calculating rotation matrices from sensor data, and extracting unique joint angles from rotation matrices. We present this process, including all equations, for both the right and left upper limbs, models with nine or seven degrees-of-freedom (DOF), and two different calibration methods. Providing a detailed methodology for the entire process in one location promotes replicability of studies by allowing researchers to clearly define their experimental methods. It is hoped that this paper will simplify new investigations of whole-arm movement using EM sensors and facilitate comparison between studies.

1 Introduction

For some applications, electromagnetic (EM) motion capture sensors2 are a practical alternative to the more commonly used optoelectronic (OE) sensors. Although EM sensors have some disadvantages [1], including a small sensing volume [2] (a sphere with radius of the order of 4 ft) and susceptibility to electromagnetic interference from ferromagnetic materials [2–8] and electrical equipment [8], they have some advantages over optoelectronic sensors. EM sensors: do not require a direct line of sight; output six degrees-of-freedom (DOF) per sensor; sample at relatively high frequencies (between 40 and 360 samples/s); and are relatively low-cost. In addition, they have relatively high accuracy (1–5 mm for translation, 0.5–5 deg for rotation) and resolution (of the order of 0.05 mm for translation 0.001 deg for rotation). These characteristics make them well-suited for many short-range applications, including evaluation of upper-limb movement in research and clinical settings [1,9].

Unfortunately, the methodology for in vivo measurements of whole-arm movements using EM sensors is not well described in the literature. To clarify, the recommendations of the International Society of Biomechanics (ISB) [10] have provided a great service in clearly defining body coordinate systems (BCSs) for individual bones and joint coordinate systems (JCSs) between bones. However, by necessity, the ISB recommendations do not provide clear guidance or standardization on all steps required to measure joint angles. In particular, for measuring whole-arm movements in vivo using EM sensors, the following steps are not well defined: First, although the BCS and JCS are clearly defined for individual joints, they are not clearly defined for whole-arm movements. Simply concatenating the various JCS is ambiguous because JCS definitions sometimes differ for different limb regions.3 Similarly, although the ISB recommendations includes guidelines for adapting the JCS, originally defined for the right upper limb, to the left upper limb, the guidelines are not consistent among the joints of the upper limb.4 Second, some landmarks recommended for calibration are difficult or impossible to access in vivo.5 Third, the ISB recommendations do not include guidelines for the placement of EM sensors. Fourth, the ISB recommendations deliberately exclude the calibration process, leaving it “up to the individual researcher to relate the marker or other (e.g., electromagnetic) coordinate systems (CSs) to the defined anatomic system through digitization, calibration movements, or population-based anatomical relationships.” Fifth, the ISB recommendations do not include the inverse kinematics algorithms required to extract joint angles from EM sensor data.

Although some of these gaps have been filled in by individual studies, the added recommendations are usually specific to OE motion capture. Although similar, methods for tracking motion using EM sensors differ significantly from those for OE sensors in several aspects, including sensor placement and portions of the inverse kinematics process. Also, although motion analysis software packages are commercially available, they are likewise usually made for OE systems and do not recommend methodological details for EM sensors, nor do they provide the underlying equations necessary for customization (such as inclusion of soft-tissue artifact compensation). In addition, the few studies involving EM sensors often lack sufficient details in the description of their methods to enable replication. Finally, although a small number of these gaps are easily overcome, for in vivo measurements of whole-arm movements using EM sensors, these gaps are numerous, complex, and inter-related, making it difficult to choose the best course of action and all but impossible to make meaningful comparisons between studies.

In this paper, we describe in detail the process for using EM sensors to measure whole-arm movements in vivo and obtain upper limb joint angles defined as much as possible according to ISB recommendations. This process includes defining joint angles, placing sensors, calibrating the sensor system, calculating rotation matrices from sensor data, and extracting unique joint angles from rotation matrices. We present this process for both the right and left upper limbs using the landmark and postural calibration methods. Models with 9DOF (3 each at the shoulder, elbow/forearm, and wrist) and 7DOF (3 at the shoulder, 2 at the elbow/forearm, and 2 at the wrist) are presented. All equations required to complete the entire process are included in the appendices. Although this process is described for all major DOF of the upper limb, a subset of these descriptions can be used for any combination of upper-limb DOF.

2 Methods

2.1 Definitions: Body-Segment Coordinate Systems, Joint Coordinate Systems, and Joint Angles.

The ISB recommendations [10] define joint angles through the use of BCS and JCS. Each body segment is represented by a BCS that is fixed in, and rotates with, the body segment. Rotation of one BCS relative to an adjacent BCS constitutes a joint, which is defined by its JCS. The definition of a JCS includes both the axes of rotation and, because finite rotations do not commute, the sequence of rotation (e.g., rotate first about the first JCS axis by $\alpha$, then about the second JCS axis by $\beta$, and finally about the third JCS axis by $\gamma$). Angles $\alpha$, $\beta$, and $\gamma$, which are examples of Euler/Cardan angles,6 are the joint angles.

While the ISB recommendations focus mostly on describing rotation between two articulating bones, they can also be used to describe global motion caused by the aggregate rotation of multiple bones. This paper focuses on global limb motion and follows the ISB recommendations on global motion when specified in Ref. [10]. Specifically, we defined four body segments (from proximal to distal): thorax, upper arm, forearm, and hand (represented by the third metacarpal), which are represented by BCS $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, and $\mathrm{D}$, respectively (Fig. 1(a) and Table 1). These four body segments are connected by three joints (Table 2): the thorax and humerus are connected by the thoracohumeral joint, the humerus, and distal forearm articulate via the elbow (humeroulnar) joint and the forearm (radio ulnar) joint, grouped as one joint in this paper, and the distal forearm and hand segments are connected by the wrist joint. Here, the three joints are referred to as the shoulder, elbow-forearm, and wrist joints, all of which are examples of global motion. These JCS (Table 2) were taken from among the options proposed in the ISB recommendations.

Fig. 1.

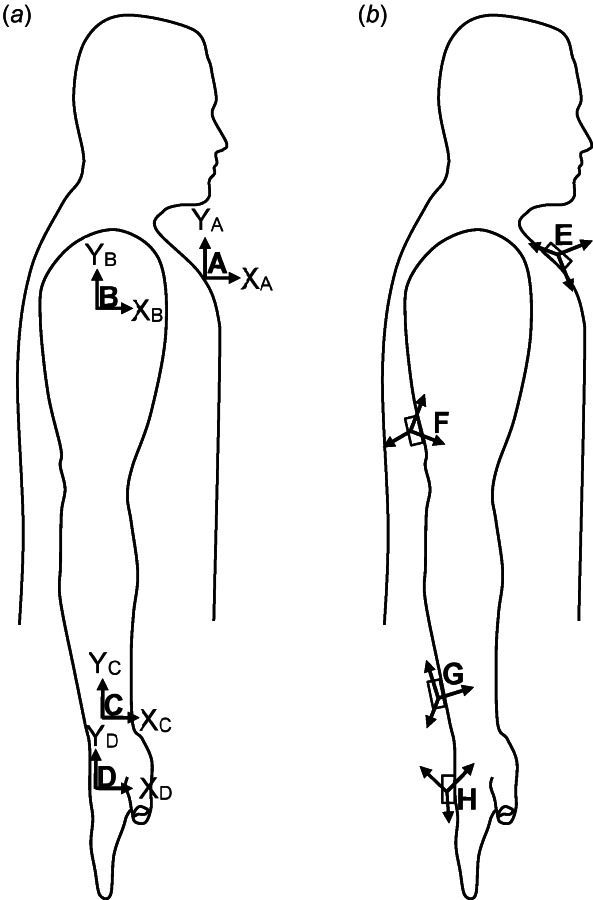
Body segment coordinate systems (BCS) and sensor coordinate systems (SCS) of the right arm are shown in (a) and (b), respectively. (a) The BCS of the thorax, upper arm, forearm, and hand align in anatomical position. (b) In general, the SCS are not aligned to each other or to their respective BCS.

Table 1.

Body coordinate systems and SCS suggested for in vivo measurements of whole-arm movements, chosen from among the multiple definitions advocated by the ISB recommendations [10]

Label	Description	Reference to ISB recommendation [10]
$\mathrm{A}$	BCS of thorax	2.3.1
$\mathrm{B}$	BCS of upper arm (humerus)	2.3.5 = 3.3.1
$\mathrm{C}$	BCS of forearm (distal forearm)	2.3.6 = 3.3.2
$\mathrm{D}$	BCS of hand (third metacarpal)	4.3.4
$\mathrm{E}$	SCS of sensor on thorax	N/A
$\mathrm{F}$	SCS of sensor on upper arm	N/A
$\mathrm{G}$	SCS of sensor on forearm	N/A
$\mathrm{H}$	SCS of sensor on hand	N/A
$\mathrm{U}$	Stationary frame of transmitter	N/A

Table 2.

Joint coordinate systems suggested for in vivo measurements of whole-arm movements, chosen from among the multiple definitions advocated by the ISB recommendations [10]

Joint	Axis	Angle	Description	Positive direction	Origin (0 deg)	ISB equivalent
Shoulder (humerus relative to thorax)	$Y\hspace{0.17em}\left(Y_A\right)$	${\alpha }_s$	Plane of elevation	(positive $Y$)	(anatomical position)	e1 of humerus rel. to thorax, ${\gamma }_h$ (2.4.7)
	$X^{\prime }\left(\mathrm{Int}.\right)$	${\beta }_s$	Elevation	(positive $X\prime$)	(anatomical position)	e2 of humerus rel. to thorax, ${\beta }_h$ (2.4.7)
	$Y^{″}\left(Y_B\right)$	${\gamma }_s$	Axial rotation	Internal rotation	(anatomical position)	e3 of humerus rel. to thorax, ${\left({\gamma }_h\right)}_2$ (2.4.7)
Elbow-forearm (forearm relative to humerus)	$Z\hspace{0.17em}\left(Z_B\right)$	${\alpha }_e$	Elbow flexion–extension	Flexion	Fully extended	e1 of elbow/forearm joint, ${\alpha }_{\text{HF}}$ (3.4.1)
	$X^{\prime }\left(\mathrm{Int}.\right)$	${\beta }_e$	Carrying angle	(positive $X\prime$)	$Y_C$ in $X_B-Y_B$ plane	e2 of elbow/forearm joint, ${\beta }_{\text{HF}}$ (3.4.1)
	$Y^{″}\left(Y_C\right)$	${\gamma }_e$	Forearm pronation–supination	Pronation	Fully supinated	e3 of elbow/forearm joint, ${\gamma }_{\text{HF}}$ (3.4.1)
Wrist (third metacarpal relative to forearm)	$Z\hspace{0.17em}\left(Z_C\right)$	${\alpha }_w$	Wrist flexion–extension	Flexion	third metacarpal parallel to line from US to EL-EM midpoint	e1 of wrist joint, $\alpha$ (4.4.1)
	$X^{\prime }\left(\mathrm{Int}.\right)$	${\beta }_w$	Wrist radial–ulnar deviation	Ulnar deviation		e2 of wrist joint, $\beta$ (4.4.1)
	$Y^{″}\left(Y_D\right)$	${\gamma }_w$	Wrist axial rotation	(positive $Y″$)	$X_D$ in $X_C-Y_C$ plane	e3 of wrist joint, $\gamma$ (4.4.1)

Each JCS is defined by axes of rotation, listed in order from first to third rotation axis. The rotation axes are given in terms of axes of the BCS of the distal segment and, in parentheses, in terms of axes embedded in the proximal and distal segments.8 Given are also the names of the angles of rotation used in this paper, along with their descriptions and explanations of which direction is positive and where the angle begins. Finally, the last column lists the equivalent axes and angles defined in the ISB recommendations (with references).

Some may be concerned that global definitions of joints may neglect the contributions of some bones. It is important to understand that even though the proposed model does not explicitly provide all of the information provided by more detailed models, the information it does provide is nonetheless equally accurate. For example, even though the proposed model does not explicitly parse rotation of the thoracohumeral joint into rotation at the sternoclavicular, acromioclavicular, and glenohumeral joints (GHs), the proposed model does include scapular and clavicular contributions. In fact, defining the thoracohumeral joint simply as the orientation of the humerus relative to the thorax forces it to include all contributions of the scapula and clavicle to rotation of the humerus relative to the thorax. Researchers interested in whole-arm movement often do not parse thoracohumeral rotation into rotations at the sternoclavicular, acromioclavicular, and glenohumeral joints, but instead group these joints into a single “shoulder joint.” Therefore, we present here the thoracohumeral joint as the “shoulder joint” as recommended by the ISB (section 2.4 of Ref. [10]). In our opinion, use of this global definition of shoulder motion is the safest way to promote accurate reports of shoulder motion during whole arm movements, albeit at the sacrifice of detail. Furthermore, researchers who wish to parse rotation of the thoracohumeral joint into rotation at the sternoclavicular, acromioclavicular, and glenohumeral joints can easily expand our procedures by including sensors on the scapula and clavicle. Recommendations for the BCS of the scapula and clavicle, and for the JCS of the sternoclavicular, acromioclavicular, and glenohumeral joints are given by the ISB [10]. Prior studies using EM sensors to investigate the shoulder complex include [7,14–16].

In addition to the shoulder JCS recommended by the ISB (Table 2), we provide an alternative shoulder JCS (Table 3) that does not suffer from gimbal lock in anatomical shoulder position. To clarify, gimbal lock is a mathematical singularity; when a joint is in gimbal lock, it is not possible to determine the first and third joint angles uniquely. In addition, close to gimbal lock, small changes in the actual orientation (in this case, the orientation of the upper arm) produce large changes in the first and third joint angles. Gimbal lock is an unavoidable property of Euler/Cardan angles—any JCS includes two orientations (180 deg apart) that suffer from gimbal lock. The only remedy is to choose a JCS whose two gimbal-lock orientations are as far as possible from the orientations of interest. The ISB recommends using a $YX\prime Y″$ rotation sequence for the shoulder, which suffers from gimbal lock when the shoulder is in neutral abduction–adduction (and 180 deg of abduction). This JCS definition is appropriate for studies that focus on movements with abduction angles around 90 deg, such as overhead tasks and some athletic tasks. In contrast, studies that focus on movements involving small abduction–adduction angles (i.e., when the upper arm is at the side of the thorax), which include many of the activities of daily living, are better off using a $ZX\prime Y″$ sequence (Table 3). This sequence places gimbal lock in 90 deg of abduction (and 90 deg of adduction, which is beyond the range of motion). Note that gimbal lock is not a problem for the elbow-forearm and wrist joints because gimbal lock would occur when the carrying angle and radial-ulnar deviation are at 90 deg, which is far beyond the range of motion in these DOF.

Table 3.

Alternative JCS for the shoulder ( $ZX\prime Y″$)

Joint	Axis	Angle	Description	Positive direction	Origin (0 deg)
Shoulder (humerus rel. to thorax)	$Z\hspace{0.17em}\left(Z_A\right)$	${\alpha }_s$	Shoulder flexion–extension	Flexion	(Anatomical position)
	$X^{\prime }\left(\mathrm{Int}.\right)$	${\beta }_s$	Shoulder abduction–adduction	Adduction	(Anatomical position)
	$Y^{″}\left(Y_B\right)$	${\gamma }_s$	Shoulder internal–external humeral rotation	Internal rotation	(Anatomical position)

This JCS exhibits gimbal lock in 90 deg of shoulder abduction instead of anatomical position (0 deg of abduction).

2.2 Sensor Placement.

Attached to each body segment is an EM motion capture sensor (a receiver) with its own sensor coordinate system (SCS), labeled (proximal to distal) as $\mathrm{E}$, $\mathrm{F}$, $\mathrm{G}$, and $\mathrm{H}$, respectively (Fig. 1(b) and Table 1). Theoretically, each sensor can be attached to its respective limb segment at any location and in any orientation. However, judicious placement can minimize the effects of soft-tissue artifact, especially for longitudinal rotations such as humeral internal–external rotation and forearm pronation–supination [17]. Because humeral rotation causes the skin of the distal portion of the upper arm to rotate more than the skin of the proximal portion, it is recommended that the upper arm sensor be attached to the distal portion of the upper arm. Similarly, because the calculation of forearm pronation–supination relies on the sensor attached to the forearm, and the distal portion of the forearm rotates much more than the proximal portion, it is recommended that the forearm sensor be attached to the distal portion of the forearm, just proximal to the wrist joint [17]. Attaching the hand sensor to the dorsal aspect of the hand in such a way that it straddles the third and fourth metacarpals makes it particularly stable. The thorax sensor is attached to the sternum [14]. EM systems typically include a stationary transmitter, whose coordinate frame of the transmitter, $U$, is fixed in space and serves as the universal frame for describing the orientation of all other frames.

2.3 Calibration.

Because the sensors can be affixed to the limb segment in any orientation and are therefore not generally aligned with the BCS of the corresponding body segment, a calibration is required to determine the orientation of each BCS relative to the corresponding SCS.7 This calibration can take one of three forms [18]: (1) using an instrumented stylus to define a number of anatomical landmarks [7,9], (2) placing the limb in a calibration posture in which all joint angles are known [19], or (3) performing functional movements to define functional axes [20]. The first method is the landmark calibration method and is recommended by ISB [10], but the second method, the postural calibration method, is simpler and common, especially for in vivo experiments. Therefore, we present both the landmark and postural calibration methods below (with equations in Appendix B).

2.3.1 Landmark Calibration.

The landmark calibration method determines the relationship between a BCS and its corresponding SCS through the use of landmarks and therefore requires that the experimenter determine the position of a number of landmarks on the subject (Table 4, Fig. 2(a)). The landmarks on the thorax, upper arm, and forearm included here are identical to those recommended by ISB [10], but the landmarks on the hand were altered for in vivo use. To clarify, the third metacarpal was used to represent the orientation of the hand, as suggested in 4.3.4 of the ISB recommendations. However, instead of using the centers of the head and base of the third metacarpal to determine its long axis ( $y_D$), which are not easily accessed in living subjects, we used the projections of those centers onto the dorsum of the hand, i.e., the dorsal-most point of the head and base of the third metacarpal. The base of the third metacarpal can be palpated on the dorsum of the hand by moving proximally along the length of the third metacarpal. Also, instead of using the plane of symmetry of the bone to determine the other two axes (because it is difficult to identify in vivo), we used the dorsal projections of the heads of the second and fourth metacarpals. These two landmarks and $y_D$ form a plane that defines $x_D$, from which $z_D$ can be calculated. We suggest that these landmarks on the hand be located when the fingers are in a relaxed position (neither fully extended nor fully flexed).

Table 4.

Anatomical landmarks used in the landmark calibration method

Abbreviation	Description
C7	Processus Spinosus (spinous process) of the seventh cervical vertebra
T8	Processus Spinosus (spinous process) of the eighth thoracic vertebra
IJ	Deepest point of Incisura Jugularis (suprasternal notch)
PX	Processus Xiphoideus (xiphoid process), most caudal point on the sternum
GH	Glenohumeral rotation center, estimated by motion recordings
EL	Most caudal point on lateral epicondyle
EM	Most caudal point on medial epicondyle
RS	Most caudal-lateral point on the radial styloid
US	Most caudal-medial point on the ulnar styloida
MC2Hd	Dorsal projection of midpoint of head of second metacarpalb
MC3Hd	Dorsal projection of midpoint of head of third metacarpalb
MC4Hd	Dorsal projection of midpoint of head of fourth metacarpalb
MC3Bd	Dorsal projection of midpoint of base of third metacarpalb

Note: The descriptions of landmarks C7 through US are taken directly from the ISB recommendations [10], but landmarks for the hand (MC2Hd through MC3Bd) were altered for in vivo use.

^aAccording to 2.3.5 of the ISB recommendations, this landmark must be located when the elbow is flexed 90 deg and the forearm is fully pronated.

^bThe fingers should be in a relaxed position.

Fig. 2.

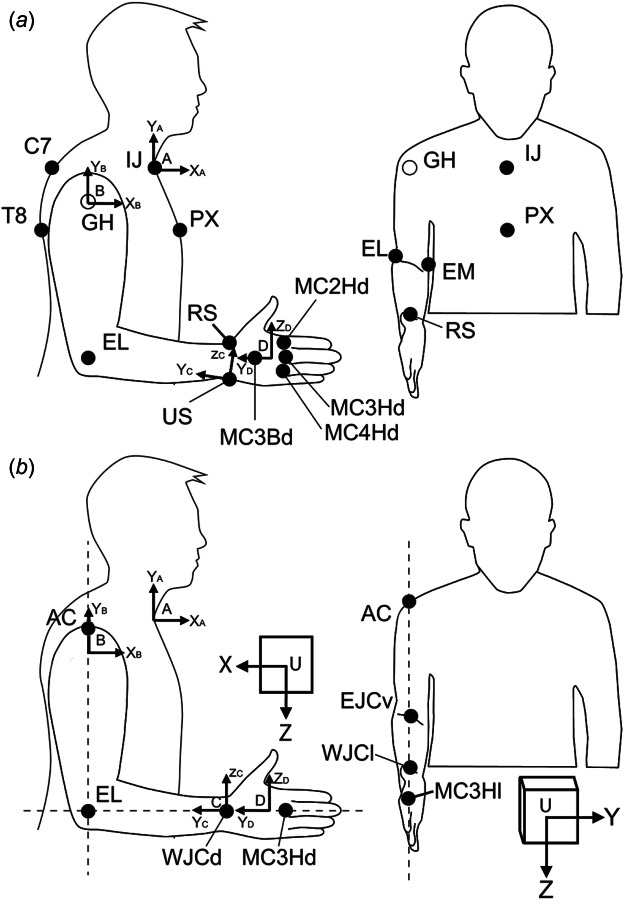
Landmarks needed for Landmark calibration method (a) and postural calibration method (b). (a) In the landmark method, the landmarks given by solid circles are localized with the help of the stylus. The center of the glenohumeral joint (GH, open circle) cannot be palpated and is estimated from shoulder movements. Note that some landmarks, such as the ulnar styloid, should be located in a different posture (see above). (b) In the postural method, the illustrated landmarks are aligned parallel to the axes of the universal frame of the transmitter (U). Laser levels used to aid in this process are depicted as dashed lines. Abbreviations in A and B are defined in Tables 4 and 5, respectively.

With the exception of the center of rotation of the glenohumeral joint (see below), the positions of these landmarks can be recorded with the help of a stylus, which is available in some EM systems or is, alternatively, easily constructed by attaching an EM sensor to the end of a long slender object [7]. The location of the tip of the stylus relative to the SCS of the EM sensor can be determined experimentally by calculating the pivot point of the instantaneous helical axes, analogous to determining the center of rotation of the glenohumeral joint (see below).

The center of rotation of the glenohumeral joint is one of the landmarks required for landmark calibration (Table 4), but it cannot be palpated. The ISB recommendations suggest estimating it by calculating the pivot point of the instantaneous helical axes following [21,22] (see also Ref. [23]), who implemented the method described in Ref. [24]. This method requires a sensor on the scapula and a sensor on the upper arm. The sensor on the scapula is only needed to find the center of rotation of the glenohumeral joint and may be removed immediately afterward since the center of rotation will be recorded relative to the sensor on the upper arm. Subjects are asked to make a number of shoulder rotations from which the center of rotation of the glenohumeral joint can be estimated as described in Appendix B.1.1.

Once the landmarks are localized, one can calculate the relationship between each SCS and its associated BCS following the process outlined in Appendix B.1.

2.3.2 Postural Calibration.

The postural calibration method is meant to be a simple and quick approximation of the landmark calibration method; it does not require the use of a stylus or determination of the center of rotation of the GH. According to this method, the subject assumes a posture in which his/her BCS frames have a known orientation with respect to the transmitter frame $U$. The orientation of each SCS is recorded in this posture, from which the relationships between the BCS and SCS can be determined. This approach only requires a single posture, which is often the posture shown in Fig. 2, referred to as neutral position. This posture is preferred over anatomical posture because anatomical posture places the elbow and forearm at or near the end of the range of motion, which varies between subjects.

Aligning the BCS frames to the transmitter frame is accomplished with the use of landmarks that are marked on the skin (e.g., with a pen) and aligned in the parasagittal, frontal, and transverse planes, as shown in Fig. 2. A variety of landmarks have been used in the literature. We present here landmarks (Table 5) that are as close as possible to those suggested in the ISB recommendations [10] but do not require the use of a stylus or determination of GH. The acromion approximates the position of GH in the anteroposterior and mediolateral directions (the position of GH in the superior–inferior direction is not required). Note that the forearm and hand are aligned when the lateral epicondyle, wrist joint center, and head of the third metacarpal are collinear. To allow easy alignment of all BCS frames at once, this suggested alignment differs from the ISB standard, which defines the long axis of the forearm as passing through the ulnar styloid (as opposed to the wrist joint center). Finally, the head of the second metacarpal is visible in the parasagittal plane and approximates the position of the head of the third metacarpal in that plane.

Table 5.

Anatomical landmarks used in the postural calibration method

Abbreviation	Description
AC	Acromion
EL	Most caudal point on lateral epicondyle
EJCv	Ventral projection of elbow joint center (EJC) into antecubital fossa, where EJC is assumed midway between EL and EM
WJCd	Dorsal projection of wrist joint center (WJC), where WJC is assumed midway between RS and US
WJCl	Lateral projection of wrist joint center (WJCL = RS)
MC3Hd	Dorsal projection of midpoint of head of third metacarpal
MC2Hl	Lateral projection of midpoint of head of second metacarpal

Aligning this many landmarks at once can be accomplished with the use of three laser levels that project lines onto the subject's upper limb (Fig. 2). If the laser-level lines are parallel to the axes of the transmitter frame, then aligning the landmarks to the laser levels will place the BCS frames in a known orientation relative to the transmitter frame. Once the subject is in the correct position, one can calculate the relationship between each SCS and its associated BCS following the process outlined in Appendix B.2.

2.4 Inverse Kinematics.

The process of calculating joint angles from sensor angles requires four steps, represented by the columns of blocks in Fig. 3.

Fig. 3.

Schematic of the inverse kinematics process for whole-arm movements. Inputs include angles $\left[a,e,r\right]$ (representing azimuth, elevation, and roll) of each sensor ( $\mathrm{E}$– $\mathrm{H}$) and the rotation matrices between each sensor and its BCS ( $\mathrm{A}$– $\mathrm{D}$) established during calibration. The output consists of the three joint angles ( $\left[\alpha ,\beta ,\gamma \right]$) for each of the shoulder ( $s$), elbow-forearm ( $e$), and wrist ( $w$) joints. The inverse kinematics process includes the four steps described above, each represented by a column of boxes: (1) $\mathit{aer}\to R_{\text{SCS}}$ converts sensor angles into rotation matrices describing the orientation of each SCS with respect to the universal frame, (2) $R_{\text{SCS}}\to R_{\text{BCS}}$ multiplies each SCS rotation matrix by its calibration matrix, yielding the rotation matrices describing the orientation of each BCS related to the universal frame, (3) $R_{\text{BCS}}\to R_{\text{JCS}}$ multiplies the rotation matrices of adjacent BCS to obtain JCS rotation matrices, and (4) $R_{\text{JCS}}\to \alpha \beta \gamma$ extracts joint angles from each JCS rotation matrix. The leading superscript and subscript of rotation matrices indicate the original and final CS; for example, ${}_B{}^{A}R$ is the rotation matrix that describes $B$ relative to $A$ (see Appendix A for more detail).

Step 1: The set of angles $\left[a,e,r\right]$ describing the orientation (azimuth, elevation, and roll) of each SCS relative to the transmitter frame $U$ is converted to a rotation matrix.

Step 2: These rotation matrices are multiplied with the rotation matrices describing the orientation of each SCS relative to its associated BCS (determined during calibration) to determine the orientation of each BCS relative to $U.$

Step 3: The rotation matrices (describing the orientation of each BCS relative to $U$) of adjacent BCS are multiplied to calculate the orientation of one BCS relative to its adjacent BCS (which gives the JCS rotation matrix).

Step 4: The joint angles are extracted from the JCS rotation matrices.

Though the second and third steps in this process involve only simple matrix multiplications, defining the proper rotation matrices (in step 1 and during calibration) and extracting joint angles can be challenging. All of the equations needed to perform each of these steps are provided in Appendix C.

2.5 Seven-Degrees-of-Freedom Model.

The upper limb is often modeled as having 7DOF (instead of 9DOF) by assuming that the carrying angle of the elbow ( ${\beta }_e$) and the amount of axial rotation at the wrist ( ${\gamma }_w$) are constant. These assumptions simplify the extraction of joint angles from rotation matrices (Appendix C.4).

2.6 Left Arm.

For clinical motions of the left limb to have the same sign convention as those for the right limb (e.g., wrist flexion is positive, wrist extension is negative), the BCS of the left limb must be defined differently than the BCS of the right limb. In anatomical posture, the BCS frames of the left limb and thorax must have y-axes that point distally and x-axes that point dorsally, with z-axes completing the right-handed triad as shown in Fig. 4 (compare to Fig. 1). Using the postural calibration method to calibrate the left arm requires additional care (see Appendix B.2.2).

Fig. 4.

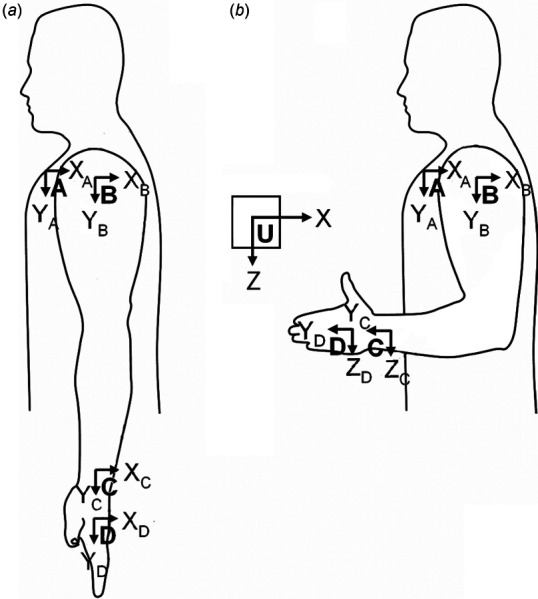
Body‐coordinate systems are defined differently for the left arm, shown here in anatomical position (a) and neutral position (b)

3 Discussion

In vivo measurement of joint angles during whole-arm movements requires many steps, including body and joint coordinate system definitions, sensor placement, calibration, and inverse-kinematics algorithms. Some of these steps are not well defined in the literature, particularly for EM sensors. Important details are often omitted, spread across many different sources, incompatible across sources (sometimes even across joints within the same source), or under-constrained. A small number of such gaps are easily overcome by the individual researcher. Unfortunately, the number, complexity and inter-relatedness of these gaps become almost intractable for in vivo measurements of whole-arm movements using EM sensors, rendering it difficult to choose the best course of action and compare results between studies. Therefore, the purpose of this paper was to provide a comprehensive methodology for using EM motion capture to track joint angles of the whole arm in vivo.

3.1 Comparison to International Society of Biomechanics Recommendations

3.1.1 Conformance.

The method presented in this paper is based as closely as possible on the ISB recommendations and the studies that formed the basis for the ISB recommendations. BCS definitions for all four limb segments (Table 1) were selected following ISB recommendations for global limb motion. JCS definitions also followed ISB recommendations for global motion (Table 2). We used global definitions because they are more common in the disciplines of motor control, clinical evaluation, rehabilitation, and occupational therapy.

The ISB recommendations do not include guidelines for calibration but states that “it is up to the individual researcher to relate the marker or other (e.g., electromagnetic) coordinate systems to the defined anatomic system” [10]. The landmark calibration method described in this paper uses an anatomical system that follows the ISB landmarks used to define BCS as closely as possible (minor adaptation for third metacarpal).

3.1.2 Differences.

In select instances, the methods presented in this paper deviated from the ISB standards. These specific deviations include the landmarks of the third metacarpal and the BCS definitions of the left limb. The landmarks used to define the third metacarpal in the landmark method were altered from those specified by the ISB, which are not accessible in vivo. We chose landmarks that, in addition to being accessible in vivo, would result in a similar calibration as the inaccessible landmarks. The BCS frames for the left limb are defined such that right and left limb motion follow the same sign convention. This follows the ISB recommendations for the left elbow-forearm and wrist, but differs from the ISB recommendations for the left shoulder, which suggests mirroring marker data with respect to the XY plane. Since this practice creates inconsistencies between the joints of the same limb and is not directly applicable to EM sensors (which output sensor orientation directly instead of just marker position), we provided explicit BCS definitions for EM motion capture of the left shoulder that are compatible with the other methods presented here.

3.1.3 Additions.

Some information provided in this paper is not addressed in the ISB recommendations but is still necessary for in vivo measurement of whole-arm movements. Examples include proper sensor placement, explanations of gimbal lock for specific rotation sequences, adaptations for a 7DOF model, and the process and accompanying equations needed to estimate the center of rotation for the glenohumeral joint. Likewise, the equations and algorithms needed to perform inverse kinematics on EM data are presented in full.

In addition to the landmark calibration method, we also presented the postural calibration method. It differs slightly from the ISB guidelines (in its definition of the long axis of the forearm) but provides a quick and simple approximation of the landmark method and is commonly used in the disciplines mentioned above.

We also provided the equations for a shoulder angle sequence ( $ZX\prime Y″$) that does not suffer from gimbal lock in anatomical position like the ISB-recommended $YX\prime Y″$ sequence. Studies focusing on large abduction angles should use the $Y{X}^{\prime }{Y}^{″}$ sequence, which places gimbal lock in neutral abduction–adduction, whereas studies focusing on small shoulder abduction angles are better off using the $ZX\prime Y\prime$ sequence, which places gimbal lock at 90 deg of abduction (see Sec. 2.1 for more details).

3.2 Implementation.

The methods presented here have been tested and successfully implemented in a whole-arm study of tremor [25,26]. We are currently working on a quantitative comparison of postural versus landmark calibration methods to allow for more informed comparison between studies.

3.3 Limitations.

The methodology given in this paper has two noteworthy limitations in the inverse kinematics process: the inverse kinematics algorithms do not (1) take advantage of the position information of the sensors or (2) compensate for the effects of soft-tissue artifact. It is possible to use the partially redundant nature of the position and orientation data from the sensors to minimize errors [20] or compensate for soft-tissue artifact. Soft-tissue artifact refers to the error in calculated joint angle caused by movement of the skin (and the sensor placed on the skin) relative to the underlying skeletal structures. This error is especially large in axial rotation of the humerus and in forearm pronation–supination. During axial rotation of the humerus, for example, the tissues close to the glenohumeral joint remain mostly static, whereas tissues close to the elbow joint rotate, with varying amounts of movement in between. It is clear that sensors placed at different locations on the upper arm will detect different amounts of rotation, resulting in errors of the order of 20–50% of the axial rotation of the humerus [27–29]. Multiple methods have been developed to compensate for soft-tissue artifact [27,28,30–34], but with the exception of Ref. [28], these methods were developed for optoelectric motion capture systems and cannot be directly applied to electromagnetic motion capture systems because the algorithms take advantage of the individual markers used in optoelectronic systems. The first step in developing soft-tissue artifact compensation methods for electromagnetic systems is to establish a self-consistent framework for calibration and inverse kinematics, which is the focus of this paper. We are currently working on extending the inverse kinematics presented here to include soft-tissue artifact compensation.

3.4 Additional Methodological Considerations.

This paper focuses on the steps necessary for tracking joint angles: defining joint angles, placing sensors, calibrating the sensor system, calculating rotation matrices from sensor data, and extracting unique joint angles from rotation matrices. However, there are additional considerations that must be taken into account when using EM sensors. Yaniv et al. described a broad set of factors influencing the utility of EM motion capture systems in clinical settings [1]. Here, we discuss briefly some of these and other factors.

One of the chief concerns is accuracy; it is important to verify the instrument's accuracy within one's own testing environment. This can be accomplished in a variety of ways. Some studies have placed sensors at known distances to the transmitter or to each other, often using assessment phantoms such as grid boards [1–4,6,8,35]. Other studies have characterized the accuracy of EM systems by comparing EM measurements to a standard, such as a robot [36] or materials testing device [8], optoelectronic motion capture system [5,36,37], inclinometer [15], pendulum potentiometer [38], inertial-ultrasound hybrid motion capture system [39], or linkage digitizer [7].

Factors affecting accuracy include transmitter–receiver separation distance, distortion of the electromagnetic field, and limitations in dynamic response.

Transmitter–receiver separation. In EM systems, the signal drops off with the third power of transmitter–sensor separation, so errors are reduced by keeping the sensor(s) as close as possible to the transmitter [2]. The effect of distance from the transmitter can be assessed by measuring the distance and relative orientation between two sensors fixed relative to each other as the sensors are moved throughout the testing environment. If it is known that the sensor will remain within a certain distance from the transmitter, it is possible in some EM systems to increase the resolution by decreasing the range of the analog-to-digital conversion.

Distortion of electromagnetic field. Since EM motion capture systems use an electromagnetic field to measure the position and orientation of the sensors, distortions of this field cause measurement errors. Many studies have investigated the magnitude of such errors due to ferromagnetic materials or electrical equipment (power lines, monitors, accelerometers) close to the motion capture system [1–4,6–8,35], or in specialized environments such as clinical suites [1,3,8,40], specialized laboratories [41], and virtual-reality environments [39]. These studies have made it clear that the most direct approach for decreasing such errors is to increase the distance between ferromagnetic materials and the transmitter and/or sensor, since metal effects decrease as the third power of transmitter-metal separation and sensor-metal separation, and as the sixth power of separation of metal from both transmitter and sensor [2]. Interference from electrical equipment can be reduced with appropriate sampling synchronization and filtering [2]. Further reductions in errors may be possible by applying correcting algorithms [5,37] or choosing the sampling rate based on the type of metal [6].

Limitations in dynamic response. For applications in which fast dynamic response is required (e.g., visual feedback in virtual-reality environments), one may have to take additional factors into account. Adelstein et al. characterized the latency, gain, and noise of two EM systems at a variety of frequencies spanning the bandwidth of volitional human movement [42].

There are, of course, additional considerations specific to each application. For example, in their study on using EM systems to localize electrodes and natural landmarks on the head, Engels et al. found that skin and hair softness and head movements affected the localization precision [4].

3.5 Conclusion.

The purpose of this paper was to provide a detailed methodology for in vivo measurements of whole-arm movements using EM sensors, following the ISB recommendations [10] as much as possible. This methodology includes consistent definitions of joint angles for global motions of the whole arm, recommendations for placing sensors, processes required for calibration, and complete equations for performing inverse-kinematics. We present this methodology for both the right and left upper limbs and for the landmark and postural calibration methods. Although presented here for the entire upper limb (9 or 7 DOF), the methodology can be adapted to a subset of upper-limb joints. It is hoped that this paper will simplify new investigations of whole-arm movement using EM sensors and facilitate comparison between studies.

Published Code

Accompanying code and instructions can be found online.9

Appendix A. Notation

In this paper, we use the following common notation described in more detail in Ref. [11]. The unit vectors defining a coordinate system (CS) are labeled with the name of the CS as a trailing subscript. For example, CS $\mathrm{B}$ is defined by unit vectors ${\widehat{\mathbf{x}}}_B$, ${\widehat{\mathbf{y}}}_B$, and ${\widehat{\mathbf{z}}}_B$. Vectors can be expressed in (i.e., decomposed into the unit vectors of) any CS, and the preceding superscript indicates the CS in which a vector is expressed. For example, ${}_{\hspace{0.17em}}{}^A\widehat{\mathbf{x}}_B$, ${}_{\hspace{0.17em}}{}^A\widehat{\mathbf{y}}_B$, and ${}_{\hspace{0.17em}}{}^A\widehat{\mathbf{z}}_B$ are the unit vectors of CS $\mathrm{B}$, expressed in CS $\mathrm{A}$. Rotation matrices, which describe the orientation of one CS relative to another, have a leading superscript and subscript that indicate the original and final CS. For example, ${}_B{}^{A}R$ is the rotation matrix that describes $\mathrm{B}$ relative to $\mathrm{A}$, i.e., ${}_B{}^{A}R=\left[\begin{array}{ccc}{}_{\hspace{0.17em}}{}^A\widehat{\mathbf{x}}_B& {}_{\hspace{0.17em}}{}^A\widehat{\mathbf{y}}_B& {}_{\hspace{0.17em}}{}^A\widehat{\mathbf{z}}_B\end{array}\right]$. The product ${}_B{}^{A}R=R_Y\left(\alpha \right)\hspace{0.17em}{R}_{X^{\prime }}\left(\beta \right){\hspace{0.17em}R}_{Y^{″}}\left(\gamma \right)$ means that ${}_B{}^{A}R$ is the rotation matrix describing a sequence of three rotations: first about the $Y$-axis by $\alpha$, then about the once-rotated $X\prime$-axis by $\beta$, then about the twice-rotated $Y$′′-axis by $\gamma$. In general, rotation matrices vary with time, and ${}_B{}^{A}R\left(t\right)$ denotes the rotation matrix at some time t, whereas ${}_B{}^{A}R\left(0\right)$ denotes the rotation matrix established during calibration. The symbol $\times$ represents the cross-product operation, and $\left|\mathbf{a}\right|$ represents the magnitude (L² norm) of vector $\mathbf{a}$.

Appendix B. Calibration

Step 2 of the inverse kinematics process (Fig. 3) requires the rotation matrices describing the orientation of each SCS relative to its associated BCS $({}_A{}^{E}R,\hspace{0.17em}{}_B{}^{F}R,\hspace{0.17em}{}_C{}^{G}R,\hspace{0.17em}{}_D{}^{H}R)$. We provide here the equations necessary to obtain these rotation matrices using two methods: landmark calibration and postural calibration.

B.1 Landmark Calibration

The landmark calibration method requires the positions of the landmarks listed in Table 4, which can be obtained using a stylus (see 2.3.1). Here, we use the following notation: ${}_{\hspace{0.17em}}{}^E\mathbf{p}_{C7}$ represents the vector location of the C7 landmark in the frame of Sensor E at the time C7 was located with the stylus; ${}_U{}^E{R}_{C7}$ represents the rotation matrix describing the SCS frame E with respect to the universal frame at the time C7 was located with the stylus; and ${}_{\hspace{0.17em}}{}^E\mathbf{y}_A$ is a vector pointing along the y-axis of BCS A, expressed in SCS E (but unlike ${}_{\hspace{0.17em}}{}^E\widehat{\mathbf{y}}_A$, ${}_{\hspace{0.17em}}{}^E\mathbf{y}_A$ does not generally have unit length). Rotation matrices ${}_A{}^{E}R$, ${}_B{}^{F}R$, ${}_C{}^{G}R$, and ${}_D{}^{H}R$ can be obtained as follows:

Matrix ${}_A{}^{E}R$

$${}_{\hspace{0.17em}}{}^E\mathbf{p}_{C7}={}_U{}^{E}R_{C7}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{C7}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_E)$$

$${}_{\hspace{0.17em}}{}^E\mathbf{p}_{T8}={}_U{}^{E}R_{T8}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{T8}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_E)$$

$${}_{\hspace{0.17em}}{}^E\mathbf{p}_{IJ}={}_U{}^{E}R_{IJ}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{IJ}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_E)$$

$${}_{\hspace{0.17em}}{}^E\mathbf{p}_{PX}={}_U{}^{E}R_{PX}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{PX}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_E)$$

$${}_{\hspace{0.17em}}{}^E\mathbf{y}_A=\frac{{}^E{\mathbf{p}}_{IJ}+{}^E{\mathbf{p}}_{C7}}{2}-\frac{{}^E{\mathbf{p}}_{PX}+{}^E{\mathbf{p}}_{T8}}{2}$$

$${}_{\hspace{0.17em}}{}^E\widehat{\mathbf{y}}_A=\frac{{}_{\hspace{0.17em}}{}^E\mathbf{y}_A}{\left|{}_{\hspace{0.17em}}{}^E\mathbf{y}_A\right|}$$

$${}_{\hspace{0.17em}}{}^E\mathbf{z}_A={}_{\hspace{0.17em}}{}^E\widehat{\mathbf{y}}_A\times ({}_{\hspace{0.17em}}{}^E\mathbf{p}_{C7}-{}_{\hspace{0.17em}}{}^E\mathbf{p}_{IJ})$$

$${}_{\hspace{0.17em}}{}^E\widehat{\mathbf{z}}_A=\frac{{}_{\hspace{0.17em}}{}^E\mathbf{z}_A}{\left|{}_{\hspace{0.17em}}{}^E\mathbf{z}_A\right|}$$

$${}_{\hspace{0.17em}}{}^E\widehat{\mathbf{x}}_A={}_{\hspace{0.17em}}{}^E\widehat{\mathbf{y}}_A\times {}_{\hspace{0.17em}}{}^E\widehat{\mathbf{z}}_A$$

$${}_A{}^{E}R=\left[\begin{array}{ccc}{}_{\hspace{0.17em}}{}^E\widehat{\mathbf{x}}_A& {}_{\hspace{0.17em}}{}^E\widehat{\mathbf{y}}_A& {}_{\hspace{0.17em}}{}^E\widehat{\mathbf{z}}_A\end{array}\right]$$

Matrix ${}_C{}^{G}R$ (must be calculated before ${}_B{}^{F}R$ because ${}_B{}^{F}R$ requires ${\widehat{\mathbf{y}}}_C$)

$${}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{EL}}={}_U{}^{G}R_{\text{EL}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{EL}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_G)$$

$${}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{EM}}={}_U{}^{G}R_{\text{EM}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{EM}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_G)$$

$${}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{RS}}={}_U{}^{G}R_{\text{RS}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{RS}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_G)$$

$${}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{US}}={}_U{}^{G}R_{\text{US}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{US}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_G)$$

$${}_{\hspace{0.17em}}{}^G\mathbf{y}_C=\frac{{}^G{\mathbf{p}}_{\text{EL}}+{}^G{\mathbf{p}}_{\text{EM}}}{2}-{}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{US}}$$

$${}_{\hspace{0.17em}}{}^G\widehat{\mathbf{y}}_C=\frac{{}_{\hspace{0.17em}}{}^G\mathbf{y}_C}{\left|{}_{\hspace{0.17em}}{}^G\mathbf{y}_C\right|}$$

$${}_{\hspace{0.17em}}{}^G\mathbf{x}_C={}_{\hspace{0.17em}}{}^G\widehat{\mathbf{y}}_C\times ({}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{RS}}-{}_{\hspace{0.17em}}{}^G\mathbf{p}_{\text{US}})$$

$${}_{\hspace{0.17em}}{}^G\widehat{\mathbf{x}}_C=\frac{{}_{\hspace{0.17em}}{}^G\mathbf{x}_C}{\left|{}_{\hspace{0.17em}}{}^G\mathbf{x}_C\right|}$$

$${}_{\hspace{0.17em}}{}^G\widehat{\mathbf{z}}_C={}_{\hspace{0.17em}}{}^G\widehat{\mathbf{x}}_C\times {}_{\hspace{0.17em}}{}^G\widehat{\mathbf{y}}_C$$

$${}_C{}^{G}R=\left[\begin{array}{ccc}{}_{\hspace{0.17em}}{}^G\widehat{\mathbf{x}}_C& {}_{\hspace{0.17em}}{}^G\widehat{\mathbf{y}}_C& {}_{\hspace{0.17em}}{}^G\widehat{\mathbf{z}}_C\end{array}\right]$$

Matrix ${}_B{}^{F}R$

${}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{GH}}$ (calculated as described in Appendix B.1.1)

$${}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{EL}}={}_U{}^{F}R_{\text{EL}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{EL}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_F)$$

$${}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{EM}}={}_U{}^{F}R_{\text{EM}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{EM}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_F)$$

$${}_{\hspace{0.17em}}{}^F\mathbf{y}_B={}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{GH}}-\frac{{}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{EL}}+{}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{EM}}}{2}$$

$${}_{\hspace{0.17em}}{}^F\widehat{\mathbf{y}}_B=\frac{{}_{\hspace{0.17em}}{}^F\mathbf{y}_B}{\left|{}_{\hspace{0.17em}}{}^F\mathbf{y}_B\right|}$$

$${}_{\hspace{0.17em}}{}^F\widehat{\mathbf{y}}_C={}_U{}^{F}R_{\text{US}}\hspace{0.17em}{}_G{}^{U}R_{\text{US}}{}_{\hspace{0.17em}}{}^G\widehat{\mathbf{y}}_C$$

$${}_{\hspace{0.17em}}{}^F\mathbf{z}_B={\widehat{\mathbf{y}}}_B\times {\widehat{\mathbf{y}}}_C$$

$${}_{\hspace{0.17em}}{}^F\widehat{z}_B=\frac{{}_{\hspace{0.17em}}{}^F\mathbf{z}_B}{\left|{}_{\hspace{0.17em}}{}^F\mathbf{z}_B\right|}$$

$${}_{\hspace{0.17em}}{}^F\widehat{\mathbf{x}}_B={}_{\hspace{0.17em}}{}^F\widehat{\mathbf{y}}_B\times {}_{\hspace{0.17em}}{}^F\widehat{\mathbf{z}}_B$$

$${}_B{}^{F}R=\left[\begin{array}{ccc}{}_{\hspace{0.17em}}{}^F\widehat{\mathbf{x}}_B& {}_{\hspace{0.17em}}{}^F\widehat{\mathbf{y}}_B& {}_{\hspace{0.17em}}{}^F\widehat{\mathbf{z}}_B\end{array}\right]$$

Matrix ${}_D{}^{H}R$

$${}_{\hspace{0.17em}}{}^H\mathbf{p}_{\mathrm{M}\mathrm{C}2\mathrm{H}\mathrm{d}}={}_U{}^{H}R_{\mathrm{M}\mathrm{C}2\mathrm{H}\mathrm{d}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\mathrm{M}\mathrm{C}2\mathrm{H}\mathrm{d}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_H)$$

$${}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC3Hd}}={}_U{}^{H}R_{\text{MC3Hd}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{MC3Hd}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_H)$$

$${}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC4Hd}}={}_U{}^{H}R_{\text{MC4Hd}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{MC4Hd}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_H)$$

$${}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC3Bd}}={}_U{}^{H}R_{\text{MC3Bd}}\hspace{0.17em}({}_{\hspace{0.17em}}{}^U\mathbf{p}_{\text{MC3Bd}}-{}_{\hspace{0.17em}}{}^U\mathbf{p}_H)$$

$${}_{\hspace{0.17em}}{}^H\mathbf{y}_D={}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC3Bd}}-{}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC3Hd}}$$

$${}_{\hspace{0.17em}}{}^H\widehat{\mathbf{y}}_D=\frac{{}_{\hspace{0.17em}}{}^H\mathbf{y}_D}{\left|{}_{\hspace{0.17em}}{}^H\mathbf{y}_D\right|}$$

$${}_{\hspace{0.17em}}{}^H\mathbf{x}_D={}_{\hspace{0.17em}}{}^H\widehat{\mathbf{y}}_D\times ({}_{\hspace{0.17em}}{}^H\mathbf{p}_{\mathrm{M}\mathrm{C}2\mathrm{H}\mathrm{d}}-{}_{\hspace{0.17em}}{}^H\mathbf{p}_{\text{MC4Hd}})$$

$${}_{\hspace{0.17em}}{}^H\widehat{\mathbf{x}}_D=\frac{{}_{\hspace{0.17em}}{}^H\mathbf{x}_D}{\left|{}_{\hspace{0.17em}}{}^H\mathbf{x}_D\right|}$$

$${}_{\hspace{0.17em}}{}^H\widehat{\mathbf{z}}_D={}_{\hspace{0.17em}}{}^H\widehat{\mathbf{x}}_D\times {}_{\hspace{0.17em}}{}^H\widehat{\mathbf{y}}_D$$

$${}_D{}^{H}R=\left[\begin{array}{ccc}{}_{\hspace{0.17em}}{}^H\widehat{\mathbf{x}}_D& {}_{\hspace{0.17em}}{}^H\widehat{\mathbf{y}}_D& {}_{\hspace{0.17em}}{}^H\widehat{\mathbf{z}}_D\end{array}\right]$$

B.1.1 Estimating the Center of Rotation of the Glenohumeral Joint (Adapted From Ref. [21]).

To estimate the location of the GH used in the landmark calibration method, subjects are asked to make a number of shoulder rotations involving flexion–extension, abduction–adduction, and internal–external humeral rotation. Given the position and orientation of the upper arm sensor relative to the transmitter ( ${}_{\hspace{0.17em}}{}^U\mathbf{p}_{F,U}\left(t\right)$ and ${}_F{}^{U}R\left(t\right)$, respectively), and the position and orientation of the scapular sensor relative to the transmitter ( ${}_{\hspace{0.17em}}{}^U\mathbf{p}_{S,U}\left(t\right)$ and ${}_S{}^{U}R\left(t\right)$), we can express the position and orientation of the scapular sensor relative to the upper arm sensor

$${}_{\hspace{0.17em}}{}^F\mathbf{p}_S\left(t\right)={}_U{}^{F}R\left(t\right)\left[{}_{\hspace{0.17em}}{}^U\mathbf{p}_S\left(t\right)-{}_{\hspace{0.17em}}{}^U\mathbf{p}_F\left(t\right)\right]$$

$${}_S{}^{F}R\left(t\right)={}_U{}^{F}R\left(t\right){}_S{}^{U}R\left(t\right)$$

The rotation of the scapula relative to the humerus is described by the instantaneous helical axis (IHA), whose direction is given by the angular velocity vector $\mathbf{\omega }\left(t\right)={[{\omega }_x,{\omega }_y,{\omega }_z]}^T$ (superscript $T$ denotes the transpose). The elements of ${}_{\hspace{0.17em}}{}^F\mathbf{\omega }\left(t\right)$ (expressed in terms of frame $F$) can be determined from the rotation matrix and its derivative [24]

$$\left[\begin{array}{ccc}0& -{\omega }_z\left(t\right)& {\omega }_y\left(t\right)\\ {\omega }_z\left(t\right)& 0& -{\omega }_x\left(t\right)\\ -{\omega }_y\left(t\right)& {\omega }_x\left(t\right)& 0\end{array}\right]=\frac{d\left[{}_S{}^{F}R\left(t\right)\right]}{dt}{\left[{}_S{}^{F}R\left(t\right)\right]}^T$$

The position of the IHA at any time $t$ is expressed in terms of frame $F$ as

$${}^F{\mathbf{p}}_{\text{IHA}}\left(t\right)={}^F{\mathbf{p}}_S\left(t\right)+\frac{{}^F{\mathbf{\omega }}_{\left(t\right)}\times {}^F{\dot{\mathbf{p}}}_S\left(t\right)}{{\left|\mathbf{\omega }\left(t\right)\right|}^2}$$

The center of rotation over time is the mean “pivot” closest to all IHA. For a set of $n$ IHA with positions ${\left({}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{IHA}}\right)}_i$ and angular velocity vectors ${}_{\hspace{0.17em}}{}^F\mathbf{\omega }_i$, the optimal position (in the least-squared sense) of the center of rotation of the glenohumeral joint is

$${}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{GH}}=Q^{-1}\frac{1}{n}\sum _{i=1}^n{Q}_i\hspace{0.17em}{\left({}_{\hspace{0.17em}}{}^F\mathbf{p}_{\text{IHA}}\right)}_i$$

with

$$Q=\frac{1}{n}\sum _{i=1}^n{Q}_i\text{and}{Q}_i=I-{}_{\hspace{0.17em}}{}^F{\stackrel{\rightharpoonup }{n}}_i\hspace{0.17em}{{}_{\hspace{0.17em}}{}^F{\stackrel{\rightharpoonup }{n}}_i}^T$$

where $I$ is the 3-by-3 identity matrix and ${\mathbf{n}}_i$ is the unit vector along ${\stackrel{\rightharpoonup }{\omega }}_i$, i.e., ${}_{\hspace{0.17em}}{}^F\mathbf{n}_i=\frac{{}_{\hspace{0.17em}}{}^F\mathbf{\omega }_i}{\left|{}_{\hspace{0.17em}}{}^F\mathbf{\omega }_i\right|}$. Because this method is sensitive to low angular velocities, Stokdijk et al. excluded from the calculation samples with angular velocity below 0.25 rad/s [21].

B.2 Postural Calibration

In the postural calibration method, the subject assumes a posture in which his/her BCS frames have a known orientation with respect to the transmitter frame $U$ (see 2.3.2). Since the BCS

frames are different for the right and left arms (see Secs. 2.1 and 2.6), we present the process separately for the right and left arms.

B.2.1 Right Arm.

With the right upper limb and transmitter positioned as shown in Fig. 2(b), the rotation matrices describing the orientation of the BCS relative to the universal frame are

$${}_A{}^{U}R\left(0\right)={}_B{}^{U}R\left(0\right)=\left[\begin{array}{ccc}-1& 0& 0\\ 0& 0& -1\\ 0& -1& 0\end{array}\right]\text{and}{}_C{}^{U}R\left(0\right)={}_D{}^{U}R\left(0\right)=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& -1\end{array}\right]$$

where we made explicit that rotation matrices are functions of time $t$, i.e., ${}_A{}^{U}R\left(t\right)$, with $t=0$ representing the moment of calibration (when landmarks were aligned). From the orientation of the SCS at the moment all landmarks are aligned $\left({}_E{}^{U}R\right(0)$, ${}_F{}^{U}R\left(0\right)$, ${}_G{}^{U}R\left(0\right)$, and ${}_H{}^{U}R\left(0\right))$, the relationship between the BCS and SCS can be calculated as

$${}_E{}^{A}R={}_U{}^{A}R\left(0\right)\hspace{0.17em}{}_E{}^{U}R\left(0\right),{}_F{}^{B}R={}_U{}^{B}R\left(0\right)\hspace{0.17em}{}_F{}^{U}R\left(0\right),{}_G{}^{C}R={}_U{}^{C}R\left(0\right)\hspace{0.17em}{}_G{}^{U}R\left(0\right),\text{and}{}_H{}^{D}R={}_U{}^{D}R\left(0\right)\hspace{0.17em}{}_H{}^{U}R\left(0\right)$$

The relationship between an SCS and its corresponding BCS was approximated as constant over time, i.e., ${}_E{}^{A}R={}_E{}^{A}R\left(t\right)={}_E{}^{A}R\left(0\right)$. For more detail, see the Limitations section of the Discussion.

B.2.2 Left Arm.

With the left upper limb and transmitter positioned as shown in Fig. 4(b), the orientations of the BCS frames relative to the transmitter frame are

$${}_A{}^{U}R\left(0\right)={}_B{}^{U}R\left(0\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right]\text{and}{}_C{}^{U}R\left(0\right)={}_D{}^{U}R\left(0\right)=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$$

From the orientation of the SCS at the moment, all landmarks are aligned ( ${}_E{}^{U}R\left(0\right)$, ${}_F{}^{U}R\left(0\right)$, ${}_G{}^{U}R\left(0\right)$, and ${}_H{}^{U}R\left(0\right)$), the relationship between the BCS and SCS can be calculated with the same equations used for the right upper limb

$${}_E{}^{A}R={}_U{}^{A}R\left(0\right)\hspace{0.17em}{}_E{}^{U}R\left(0\right),{}_F{}^{B}R={}_U{}^{B}R\left(0\right)\hspace{0.17em}{}_F{}^{U}R\left(0\right),{}_G{}^{C}R={}_U{}^{C}R\left(0\right)\hspace{0.17em}{}_G{}^{U}R\left(0\right),\text{and}{}_H{}^{D}R={}_U{}^{D}R\left(0\right)\hspace{0.17em}{}_H{}^{U}R\left(0\right)$$

Appendix C. Inverse Kinematics

As described in Sec. 2.4, the process of calculating joint angles from sensor angles requires four steps (Fig. 3).

C.1 Step 1: Calculating Rotation Matrices From Sensor Angles

Most electromagnetic motion tracking systems provide the orientation of each sensor as a set of Euler angles or as a rotation matrix (between transmitter and sensor). If the output is given as a rotation matrix, step 1 can be skipped, but before moving on to step 2, one should ensure that the rotation matrix describes the SCS relative to the universal frame and not the universal frame relative to the SCS (e.g., ${}_E{}^{U}R$ instead of ${}_U{}^{E}R$). If the output is given as the rotation of the universal frame relative to the SCS, one can obtain its inverse by simply transposing the matrix (e.g., ${}_E{}^{U}R={}_U{}^E{R}^{-1}={}_U{}^E{R}^T$).

If the sensor orientation is given in terms of angles (e.g., azimuth, elevation, and roll), the rotation matrices must be calculated before moving on to step 2. Calculating the rotation matrices requires knowledge of the Euler angle axes and sequence used by the system. For example, for trakSTAR, the Euler angles are defined as follows: rotation about $z$ by $a$, followed by rotation about $y\prime$ by $e$, followed by rotation about $x″$ by $r$, where $a$, $e$, and $r$ are the angles of azimuth (yaw), elevation (pitch), and roll, respectively, and $z$, $y\prime$, $x″$ are axes of the rotating sensor frame. From this, the rotation matrix can be calculated. For example, ${}_E{}^{U}R$ can be calculated from the $\left[a,e,r\right]$ angles associated with sensor E as

$${}_E{}^{U}R=R_z\left(a\right)\hspace{0.17em}{R}_{y^{\prime }}\left(e\right){\hspace{0.17em}R}_{x^{\prime \prime }}\left(r\right)$$

$${}_E{}^{U}R=\left[\begin{array}{ccc}\text{ca}& -\text{sa}& 0\\ \text{sa}& \text{ca}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\text{ce}& 0& \text{se}\\ 0& 1& 0\\ -\text{se}& 0& \text{ce}\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& cr& -sr\\ 0& sr& cr\end{array}\right]$$

$${}_E{}^{U}R=\left[\begin{array}{ccc}c\mathit{ace}& c\mathit{asesr}-\mathit{sacr}& c\mathit{asecr}+\mathit{sasr}\\ s\mathit{ace}& s\mathit{asesr}+\mathit{cacr}& s\mathit{asecr}-\mathit{casr}\\ -\text{se}& c\mathit{esr}& c\mathit{ecr}\end{array}\right]$$

where $c$ ≡ cos and $s$ ≡ sin. The same equations can be used to calculate ${}_F{}^{U}R$, ${}_G{}^{U}R$, and ${}_H{}^{U}R$. Using angles $a$, $e$, and $r$ at time $t$, this equation can be used to calculate ${}_E{}^{U}R\left(t\right)$, ${}_F{}^{U}R\left(t\right)$, ${}_G{}^{U}R\left(t\right)$, and ${}_H{}^{U}R\left(t\right)$. Alternatively, using angles $a$, $e$, and $r$ obtained during calibration, this equation can be used to calculate ${}_E{}^{U}R\left(0\right)$, ${}_F{}^{U}R\left(0\right)$, ${}_G{}^{U}R\left(0\right)$, and ${}_H{}^{U}R\left(0\right)$.

C.2 Step 2: Obtaining Body Coordinate System Orientation in Universal Frame

The rotation matrices found in Step 1, which describe the orientations of the SCS relative to $U$, are multiplied with the rotation matrices describing the orientation of each SCS relative to its associated BCS (determined during calibration). The resulting product is the orientation of each BCS relative to $U$

$${}_{\mathit{A}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{E}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)\hspace{0.17em}{}_{\mathit{A}}{}^{\mathit{E}}\mathit{R}\left(0\right),\hspace{0.17em}{}_{\mathit{B}}{}^{\mathit{U}}R\left(\mathit{t}\right)={}_{\mathit{F}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)\hspace{0.17em}{}_{\mathit{B}}{}^{\mathit{F}}\mathit{R}\left(0\right),\hspace{0.17em}{}_{\mathit{C}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{G}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right){}_{\mathit{C}}{}^{\mathit{G}}\mathit{R}\left(0\right),\hspace{0.17em}\mathrm{and}{}_{\mathit{D}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{H}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)\hspace{0.17em}{}_{\mathit{D}}{}^{\mathit{H}}\mathit{R}\left(0\right)$$

C.3 Step 3: Obtaining Joint Coordinate Systems Rotation Matrices

The rotation matrices describing the orientation of each BCS relative to $U$ found in Step 2 are then used to calculate the JCS rotation matrices. More specifically, adjacent BCS are multiplied to obtain the JCS rotation matrices describing the orientation of one BCS relative to its adjacent BCS

$${}_{\mathit{B}}{}^{\mathit{A}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{U}}{}^{\mathit{A}}\mathit{R}\left(\mathit{t}\right){}_{\mathit{B}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right),\hspace{0.17em}{}_{\mathit{C}}{}^{\mathit{B}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{U}}{}^{\mathit{B}}\mathit{R}\left(\mathit{t}\right)\hspace{0.17em}{}_{\mathit{C}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right),\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}{}_{\mathit{D}}{}^{\mathit{C}}\mathit{R}\left(\mathit{t}\right)={}_{\mathit{U}}{}^{\mathit{C}}\mathit{R}\left(\mathit{t}\right)\hspace{0.17em}{}_{\mathit{D}}{}^{\mathit{U}}\mathit{R}\left(\mathit{t}\right)$$

C.4 Step 4: Extracting Joint Angles From Rotation Matrices

The final step in the inverse kinematics process is to extract joint angles from the rotation matrix associated with each JCS ( ${}_B{}^{A}R,\hspace{0.17em}{}_C{}^{B}R,$ and ${}_D{}^{C}R$). The relationship between the joint angles and rotation matrix associated with a JCS is prescribed by the rotation sequence of that JCS. Consequently, different algorithms must be used for different JCS. The 9DOF case is presented first, with simplifications for the 7DOF case presented afterwards.

C.4.1 Nine-Degrees-of-Freedom Model

Shoulder

$YX\prime Y″$. According to the ISB recommendations [10], the rotation sequence associated with the JCS of the thoracohumeral joint is $YX\prime Y″$, so its rotation matrix is

$${}_B{}^{A}R=R_Y\left({\alpha }_s\right)\hspace{0.17em}{R}_{X^{\prime }}\left({\beta }_s\right){\hspace{0.17em}R}_{Y^{\prime \prime }}\left({\gamma }_s\right)$$

$${}_B{}^{A}R=\left[\begin{array}{ccc}c{\alpha }_s& 0& s{\alpha }_s\\ 0& 1& 0\\ -s{\alpha }_s& 0& c{\alpha }_s\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c{\beta }_s& -s{\beta }_s\\ 0& s{\beta }_s& c{\beta }_s\end{array}\right]\left[\begin{array}{ccc}c{\gamma }_s& 0& s{\gamma }_s\\ 0& 1& 0\\ -s{\gamma }_s& 0& c{\gamma }_s\end{array}\right]$$

$${}_B{}^{A}R=\left[\begin{array}{ccc}-s{\alpha }_{s}c{\beta }_{s}s{\gamma }_s+c{\alpha }_{s}c{\gamma }_s& s{\alpha }_{s}s{\beta }_s& s{\alpha }_{s}c{\beta }_{s}c{\gamma }_s+c{\alpha }_{s}s{\gamma }_s\\ s{\beta }_{s}s{\gamma }_s& c{\beta }_s& -s{\beta }_{s}c{\gamma }_s\\ -c{\alpha }_{s}c{\beta }_{s}s{\gamma }_s-s{\alpha }_{s}c{\gamma }_s& c{\alpha }_{s}s{\beta }_s& c{\alpha }_{s}c{\beta }_{s}c{\gamma }_s-s{\alpha }_{s}s{\gamma }_s\end{array}\right]$$

where $c$ ≡ cos and $s$ ≡ sin. The elements of ${}_B{}^{A}R$ must equal the numeric values of the elements of ${}_B{}^{A}R$ calculated through steps 1–3 of the inverse kinematics process, resulting in 9 equations and 3 unknowns. Unfortunately, these nine equations do not contain enough information to determine a unique solution; there are two sets of joint angles ( ${\left[{\alpha }_s,{\beta }_s,{\gamma }_s\right]}_1$ and ${\left[{\alpha }_s,{\beta }_s,{\gamma }_s\right]}_2$) that satisfy these nine equations. Which set is correct? They are both correct in the sense that both sets produce the same joint configuration (i.e., the same orientation of the distal limb segment relative to the proximal limb segment); therefore, mathematically it does not matter which set is chosen as long as one consistently chooses the same set to avoid discontinuities in joint angles from one sample to the next. That said, for ease of interpretation it may be useful to choose the set that is within the range of motion of the joint, as follows. The cosine of ${\beta }_s$ is given in ${}_B{}^{A}R\left(2,2\right)$, and the sine of ${\beta }_s$ can be calculated from ${}_B{}^{A}R\left(2,1\right)$ and ${}_B{}^{A}R\left(2,3\right)$ as $\pm \sqrt{{\left[{}_B{}^{A}R\left(2,1\right)\right]}^2+{\left[{}_B{}^{A}R\left(2,3\right)\right]}^2}$. Therefore, ${\beta }_s$ can be computed as

$${\beta }_s=\mathrm{a}\text{tan}2\left\{\pm \sqrt{{\left[{}_B{}^{A}R(2,1)\right]}^2+{\left[{}_B{}^{A}R(2,3)\right]}^2},\hspace{0.17em}{}_B{}^{A}R(2,2)\right\}$$

where atan2 is the four-quadrant inverse tangent function. Choosing the negative square root as the first argument of atan2 (as opposed to the positive square root) forces ${\beta }_s$ to be in the range ${-180\hspace{0.17em}\mathrm{deg}\le \beta }_s\le 0\hspace{0.17em}\mathrm{deg}$, which is appropriate for shoulder abduction–adduction (abduction is negative according to the ISB convention). Having chosen this range for ${\beta }_s$, one can find unique solutions for the other two angles

$${\alpha }_s=\mathrm{a}\text{tan}2\{\frac{{}_B{}^{A}R(1,2)}{\text{sin}{\beta }_s},\hspace{0.17em}\frac{{}_B{}^{A}R(3,2)}{\text{sin}{\beta }_s}\}$$

$${\gamma }_s=\mathrm{a}\text{tan}2\{\frac{{}_B{}^{A}R(2,1)}{\text{sin}{\beta }_s},\hspace{0.17em}\frac{-{}_B{}^{A}R(2,3)}{\text{sin}{\beta }_s}\}$$

These equations work well unless ${\beta }_s=0$ or ${\beta }_s=180\hspace{0.17em}\mathrm{deg}$, resulting in division by zero. In these configurations, the joint is in gimbal lock, and it is not possible to differentiate between ${\alpha }_s$ and ${\gamma }_s$ because their axes ( $Y$ and $Y″$) are parallel (or antiparallel). To clarify, after a rotation about $Y$ by ${\alpha }_s$, then a “rotation” about $X\prime$ by ${\beta }_s=0$, and finally a rotation about $Y^{″}=Y$ by ${\gamma }_s$, it is not possible to determine how much of the total rotation came from the first rotation versus the last rotation. However, it also does not matter since the final joint orientation will be the same no matter how much of the rotation is assigned to ${\alpha }_s$ versus ${\gamma }_s$. Therefore, one may choose the proportions to assign to each angle. It is common to set ${\alpha }_s=0$, assigning all of the rotation to ${\gamma }_s$. In this case ( ${\alpha }_s={\beta }_s=0$), the rotation matrix degenerates to

$${}_B{}^{A}R=\left[\begin{array}{ccc}c{\gamma }_s& 0& s{\gamma }_s\\ 0& 1& 0\\ -s{\gamma }_s& 0& c{\gamma }_s\end{array}\right]$$

and ${\gamma }_s$ can be uniquely determined as

$${\gamma }_s=\mathrm{a}\text{tan}2\left\{{}_B{}^{A}R(1,3),{}_B{}^{A}R(1,1)\right\}$$

Although the calculation of ${\alpha }_s$ and ${\gamma }_s$ results in division by zero only when ${\beta }_s$ exactly equals 0 or 180 deg, effects of gimbal lock are felt in the vicinity of ${\beta }_s=0$ and ${\beta }_s=180\hspace{0.17em}\mathrm{deg}$. More specifically, close to gimbal lock, small changes in limb orientation may cause very large changes in joint angles. While the resulting joint angles may not be easily interpreted, they are nonetheless correct in the sense that they represent the correct joint configuration.

Shoulder $ZX\prime Y″$. If one uses the $ZX\prime Y″$ sequence to describe the shoulder (see Sec. 2.1), the rotation matrix is

$${}_B{}^{A}R=R_Z\left({\alpha }_s\right)\hspace{0.17em}{R}_{X^{\prime }}\left({\beta }_s\right){\hspace{0.17em}R}_{Y^{\prime \prime }}\left({\gamma }_s\right)$$

$${}_B{}^{A}R=\left[\begin{array}{ccc}c{\alpha }_s& -s{\alpha }_s& 0\\ s{\alpha }_s& c{\alpha }_s& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c{\beta }_s& -s{\beta }_s\\ 0& s{\beta }_s& c{\beta }_s\end{array}\right]\left[\begin{array}{ccc}c{\gamma }_s& 0& s{\gamma }_s\\ 0& 1& 0\\ -s{\gamma }_s& 0& c{\gamma }_s\end{array}\right]$$

$${}_B{}^{A}R=\left[\begin{array}{ccc}-s{\alpha }_{s}s{\beta }_{s}s{\gamma }_s+c{\alpha }_{s}c{\gamma }_s& -s{\alpha }_{s}c{\beta }_s& s{\alpha }_{s}s{\beta }_{s}c{\gamma }_s+c{\alpha }_{s}s{\gamma }_s\\ c{\alpha }_{s}s{\beta }_{s}s{\gamma }_s+s{\alpha }_{s}c{\gamma }_s& c{\alpha }_{s}c{\beta }_s& -c{\alpha }_{s}s{\beta }_{s}c{\gamma }_s+s{\alpha }_{s}s{\gamma }_s\\ -c{\beta }_{s}s{\gamma }_s& s{\beta }_s& c{\beta }_{s}c{\gamma }_s\end{array}\right]$$

where $c$ ≡ cos and $s$ ≡ sin. Analogous to the derivation above, ${\beta }_s$ can be calculated as

$${\beta }_s=\mathrm{a}\text{tan}2\left\{{}_B{}^{A}R(3,2),\pm \sqrt{{\left[{}_B{}^{A}R(3,1)\right]}^2+{\left[{}_B{}^{A}R(3,3)\right]}^2}\right\}$$

Choosing the positive square root for the second argument of atan2 forces ${\beta }_s$ to lie in the range $-90\hspace{0.17em}\mathrm{deg}\le {\beta }_s\le 90\hspace{0.17em}\mathrm{deg}$ and results in a unique set of joint angles

$${\alpha }_s=\mathrm{a}\text{tan}2\{\frac{-{}_B{}^{A}R(1,2)}{\text{cos}{\beta }_s},\hspace{0.17em}\frac{{}_B{}^{A}R(2,2)}{\text{cos}{\beta }_s}\}$$

$${\gamma }_s=\mathrm{a}\text{tan}2\{\frac{-{}_B{}^{A}R(3,1)}{\text{cos}{\beta }_s},\hspace{0.17em}\frac{{}_B{}^{A}R(3,3)}{\text{cos}{\beta }_s}\}$$

Positive values of ${\beta }_s$ represent adduction beyond neutral position and are generally outside the range of motion of the shoulder. However, ${\beta }_s$ will be positive when the joint is in extreme positions, e.g., when the shoulder is abducted beyond 90 deg. Although it may be difficult to interpret such extreme joint angles as clinical motions, they nonetheless are mathematically correct in the sense that they produce the correct joint configuration.

For this rotation sequence ( $ZX\prime Y″$), gimbal lock occurs when ${\beta }_s=-90\hspace{0.17em}\mathrm{deg}$ (arm abducted into the horizontal plane) or ${\beta }_s=90\hspace{0.17em}\mathrm{deg}$ (not physically possible). As for the $YX\prime Y″$, in gimbal lock the first and third axes are parallel, and it is not possible to determine how much of the rotation should be assigned to the first versus third axis; it is common to set ${\alpha }_s=0$, assigning all of the rotation to ${\gamma }_s$. In this case ( ${\alpha }_s=0\hspace{0.17em}\mathrm{deg}$ and ${\beta }_s=90\hspace{0.17em}\mathrm{deg}$), the rotation matrix degenerates to

$${}_B{}^{A}R=\left[\begin{array}{ccc}c{\gamma }_s& 0& s{\gamma }_s\\ s{\gamma }_s& 0& -c{\gamma }_s\\ 0& 1& 0\end{array}\right]$$

and ${\gamma }_s$ can be uniquely determined as

$${\gamma }_s=\mathrm{a}\text{tan}2\left\{{}_B{}^{A}R(1,3),{}_B{}^{A}R(1,1)\right\}$$

Elbow-forearm.

In accordance with the ISB guidelines, we used the $ZX\prime Y″$ rotation sequence for the elbow-forearm joint. The derivation of the rotation matrix is identical to that of the shoulder when using the $ZX\prime Y″$ sequence

$${}_C{}^{B}R=R_Z\left({\alpha }_e\right)\hspace{0.17em}{R}_{X^{\prime }}\left({\beta }_e\right){\hspace{0.17em}R}_{Y^{\prime \prime }}\left({\gamma }_e\right)$$

$${}_C{}^{B}R=\left[\begin{array}{ccc}c{\alpha }_e& -s{\alpha }_e& 0\\ s{\alpha }_e& c{\alpha }_e& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c{\beta }_e& -s{\beta }_e\\ 0& s{\beta }_e& c{\beta }_e\end{array}\right]\left[\begin{array}{ccc}c{\gamma }_e& 0& s{\gamma }_e\\ 0& 1& 0\\ -s{\gamma }_e& 0& c{\gamma }_e\end{array}\right]$$

$${}_C{}^{B}R=\left[\begin{array}{ccc}-s{\alpha }_{e}s{\beta }_{e}s{\gamma }_e+c{\alpha }_{e}c{\gamma }_e& -s{\alpha }_{e}c{\beta }_e& s{\alpha }_{e}s{\beta }_{e}c{\gamma }_e+c{\alpha }_{e}s{\gamma }_e\\ c{\alpha }_{e}s{\beta }_{e}s{\gamma }_e+s{\alpha }_{e}c{\gamma }_e& c{\alpha }_{e}c{\beta }_e& -c{\alpha }_{e}s{\beta }_{e}c{\gamma }_e+s{\alpha }_{e}s{\gamma }_e\\ -c{\beta }_{e}s{\gamma }_e& s{\beta }_e& c{\beta }_{e}c{\gamma }_e\end{array}\right]$$

where $c$ ≡ cos and $s$ ≡ sin. Extraction of the joint angles is analogous to the shoulder joint; the elements of ${}_C{}^{B}R$ must equal the numeric values of the elements of ${}_C{}^{B}R$ calculated through steps 1–3 of the inverse kinematics process, resulting in 9 equations and 3 unknowns, which are satisfied by two sets of joint angles: ${\left[{\alpha }_e,{\beta }_e,{\gamma }_e\right]}_1$, and ${\left[{\alpha }_e,{\beta }_e,{\gamma }_e\right]}_2.$ The two ${\beta }_e$ angles are

$${\beta }_e=\mathrm{a}\text{tan}2\left\{{}_C{}^{B}R(3,2),\pm \sqrt{{\left[{}_C{}^{B}R(3,1)\right]}^2+{\left[{}_C{}^{B}R(3,3)\right]}^2}\right\}$$

In this case, the physical limitations of the range of motion of ${\beta }_e$ (i.e., carrying angle) make the choice between ${\beta }_{e1}$ and ${\beta }_{e2}$ obvious. The carrying angle will always be well within the range: $-90\hspace{0.17em}\mathrm{deg}\le {\beta }_e\le 90\hspace{0.17em}\mathrm{deg}$, therefore the positive square root will always yield clinically interpretable joint angles. Having selected ${\beta }_{e1}$, ${\alpha }_{e1}$ and ${\gamma }_{e1}$ can be found as

$${\alpha }_e=\mathrm{a}\text{tan}2\{\frac{-{}_C{}^{B}R(1,2)}{c\mathrm{o}s{\beta }_e},\hspace{0.17em}\frac{{}_C{}^{B}R(2,2)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e}\}$$

$${\gamma }_e=\mathrm{a}\text{tan}2\{\frac{-{}_C{}^{B}R(3,1)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e},\hspace{0.17em}\frac{{}_C{}^{B}R(3,3)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e}\}$$

For the elbow-forearm joint, gimbal lock occurs when ${\beta }_e=-90\hspace{0.17em}\mathrm{deg}$ or ${\beta }_e=90\hspace{0.17em}\mathrm{deg}$ (i.e., carrying angle =  $\pm 90\hspace{0.17em}\mathrm{deg}$). Neither of these orientations is physically possible, so gimbal lock is not a problem for the elbow.

Wrist.

In accordance with the ISB guidelines, we defined the wrist joint using the $ZX\prime Y″$ rotation sequence. The derivation of the rotation matrix is identical to that of the elbow

$${}_D{}^{C}R=R_Z\left({\alpha }_w\right)\hspace{0.17em}{R}_{X^{\prime }}\left({\beta }_w\right){\hspace{0.17em}R}_{Y^{\prime \prime }}\left({\gamma }_w\right)$$

$${}_D{}^{C}R=\left[\begin{array}{ccc}c{\alpha }_w& -s{\alpha }_w& 0\\ s{\alpha }_w& c{\alpha }_w& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c{\beta }_w& -s{\beta }_w\\ 0& s{\beta }_w& c{\beta }_w\end{array}\right]\left[\begin{array}{ccc}c{\gamma }_w& 0& s{\gamma }_w\\ 0& 1& 0\\ -s{\gamma }_w& 0& c{\gamma }_w\end{array}\right]$$

$${}_D{}^{C}R=\left[\begin{array}{ccc}-s{\alpha }_{w}s{\beta }_{w}s{\gamma }_w+c{\alpha }_{w}c{\gamma }_w& -s{\alpha }_{w}c{\beta }_w& s{\alpha }_{w}s{\beta }_{w}c{\gamma }_w+c{\alpha }_{w}s{\gamma }_w\\ c{\alpha }_{w}s{\beta }_{w}s{\gamma }_w+s{\alpha }_{w}c{\gamma }_w& c{\alpha }_{w}c{\beta }_w& -c{\alpha }_{w}s{\beta }_{w}c{\gamma }_w+s{\alpha }_{\mathrm{w}}s{\gamma }_w\\ -c{\beta }_{w}s{\gamma }_w& s{\beta }_w& c{\beta }_{w}c{\gamma }_w\end{array}\right]$$

where $c$ ≡ cos and $s$ ≡ sin. Extraction of the joint angles is analogous to the elbow-forearm joint. The elements of ${}_D{}^{C}R$ must equal the numeric values of the elements of ${}_D{}^{C}R$ calculated through steps 1–3 of the inverse kinematics process, resulting in 9 equations and 3 unknowns. Again, these equations yield two sets of joint angles: ${\left[{\alpha }_w,{\beta }_w,{\gamma }_w\right]}_1$, and ${\left[{\alpha }_w,{\beta }_w,{\gamma }_w\right]}_2.$

Calculating ${\beta }_{w1}$ and ${\beta }_{w2}$ involves the same equation as the elbow-forearm joint

$${\beta }_w=\mathrm{a}\text{tan}2\left\{{}_D{}^{C}R(3,2),\pm \sqrt{{\left[{}_D{}^{C}R(3,1)\right]}^2+{\left[{}_D{}^{C}R(3,3)\right]}^2}\right\}$$

In this case, the physical limitations of ${\beta }_w$ (i.e., radial/ulnar deviation) also make the choice between ${\beta }_{w1}$ and ${\beta }_{w2}$ obvious. The wrist will never deviate radially or ulnarly beyond the range $-90\hspace{0.17em}\mathrm{deg}\le {\beta }_w\le 90\hspace{0.17em}\mathrm{deg}$, therefore the positive square root will always yield clinically interpretable joint angle values. Having selected ${\beta }_{w1}$, ${\alpha }_{w1}$ and ${\gamma }_{w1}$ can be found as

$${\alpha }_w=\mathrm{a}\text{tan}2\{\frac{-{}_D{}^{C}R(1,2)}{\text{cos}{\beta }_w},\hspace{0.17em}\frac{{}_D{}^{C}R(2,2)}{\text{cos}{\beta }_w}\}$$

$${\gamma }_w=\mathrm{a}\text{tan}2\{\frac{-{}_D{}^{C}R(3,1)}{\text{cos}{\beta }_w},\hspace{0.17em}\frac{{}_D{}^{C}R(3,3)}{\text{cos}{\beta }_w}\}$$

For the wrist joint, gimbal lock occurs when ${\beta }_w=-90\hspace{0.17em}\mathrm{deg}$ or ${\beta }_w=90\hspace{0.17em}\mathrm{deg}$ (i.e., radial deviation of 90 $\hspace{0.17em}\mathrm{deg}\hspace{0.17em}$ or ulnar deviation of 90 $\hspace{0.17em}\mathrm{deg}$, respectively). Neither of these orientations is physically possible, so gimbal lock is not a problem for the wrist.

C.4.2 Seven-Degrees-of-Freedom Model.

The 7DOF model of the arm is a simplification that assumes the elbow carrying angle ( ${\beta }_e$) and wrist axial rotation ( ${\gamma }_w$) to be constant (see Table 2). The wrist experiences only small amounts of axial rotation, so one may wish to approximate ${\gamma }_w$ as zero. The carrying angle has been measured to be of the order of 5–15 deg for men and 10–25 deg for women [17]. Depending on the application, one may wish to approximate the carrying angle as zero or as a constant value in the measured range. Alternatively, the carrying angle could be measured for individual subjects as the angle between the ulna and the extension of the humerus when the arm is in anatomical position (Fig. 1) [17]

$${\beta }_e=\mathrm{a}\text{cos}({\widehat{y}}_B·{\widehat{y}}_C)$$

where $\left[·\right]$ denotes the dot product. Unit vectors ${\widehat{y}}_B$ and ${\widehat{y}}_C$ must be expressed in the same frame. Choosing frame B,

$${\beta }_e=\mathrm{a}\text{cos}\left[{}_{\hspace{0.17em}}{}^B\widehat{y}_B·({}_C{}^{B}R\hspace{0.17em}{}_{\hspace{0.17em}}{}^C\widehat{y}_C)\right]$$

where ${}_{\hspace{0.17em}}{}^B{\widehat{y}}_B={}_{\hspace{0.17em}}{}^C{\widehat{y}}_C={\left[0,\hspace{0.17em}1,\hspace{0.17em}0\right]}^T$ and ${}_C{}^{B}R$ describes the orientation of C relative to B when the arm is in anatomical position.

Having chosen a value for ${\beta }_e$, one can calculate ${\alpha }_e$ and ${\gamma }_e$ directly using the equations in Appendix C.4.1

$${\alpha }_e=\mathrm{a}\text{tan}2\{\frac{-{}_C{}^{B}R(1,2)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e},\hspace{0.17em}\frac{{}_C{}^{B}R(2,2)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e}\}$$

$${\gamma }_e=\mathrm{a}\text{tan}2\{\frac{-{}_C{}^{B}R(3,1)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e},\hspace{0.17em}\frac{{}_C{}^{B}R(3,3)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_e}\}$$

Since ${\alpha }_e$ and ${\gamma }_e$ depend on ${\beta }_e$, all three joint angles will differ from those calculated with the 9DOF model. In contrast, choosing a value for ${\gamma }_w$ does not affect ${\beta }_w$ and ${\alpha }_w$ (see Appendix C.4.1)

$${\beta }_w=\mathrm{a}\text{tan}2\left\{{}_D{}^{C}R(3,2),\sqrt{{\left[{}_D{}^{C}R(3,1)\right]}^2+{\left[{}_D{}^{C}R(3,3)\right]}^2}\right\}$$

$${\alpha }_w=\mathrm{a}\text{tan}2\{\frac{-{}_D{}^{C}R(1,2)}{\text{cos}{\beta }_w},\hspace{0.17em}\frac{{}_D{}^{C}R(2,2)}{\text{cos}{\beta }_w}\}$$

Note that the simplicity associated with the 7DOF model comes at a cost: the resulting joint angles no longer satisfy the rotation matrices perfectly.

Funding Data

• NSF (Grant No. 1806056; Funder ID: 10.13039/100000001).

• CBET (Funder ID: 10.13039/100000146).