Effect of Articular Surface Compression on Cartilage Extracellular Matrix Deformation

Abstract

Early stage osteoarthritis is characterized by disruption of the superficial zone (SZ) of articular cartilage, including collagen damage and proteoglycan loss, resulting in “mechanical softening” of the extracellular matrix (ECM). The role of the SZ in controlling fluid exudation and imbibition during loading and unloading, respectively, was studied using confined creep compression tests. Bovine osteochondral (OC) plugs were subjected to either a static (88 kPa) or cyclic (0–125 kPa at 1 Hz) compressive stress for five minutes, and the cartilage deformation and recovery were measured during tissue loading and unloading, respectively. During unloading, the articular surface of the cartilage was either loaded with a small 1% tare load (∼1 kPa) applied through a porous load platen (covered), or completely unloaded (uncovered). Then the SZ (∼10%) of the cartilage was removed and the creep tests were repeated. Randomized tests were performed on each OC specimen to assess variability within and between plugs. Static creep strain was always greater than cyclic creep strain except at the beginning of loading (10–20 cycles). Uncovering the articular surface after creep deformation resulted in faster thickness recovery compared to the covered recovery. Removal of the SZ resulted in increased static and cyclic creep strains, as well as an increase in the cyclic peak-to-peak strain envelope. Our results indicate that an intact SZ is essential for normal cartilage mechanical function during joint motion by controlling fluid exudation and imbibition, and concomitantly ECM deformation and recovery, when loaded and unloaded, respectively.

1 Introduction

1.1 Physical Properties of Articular Cartilage.

A key feature of early stage osteoarthritis in humans and animal models is the disruption and fibrillation of the surfaces of the articular cartilage lining the boney ends of joints [1–5]. The damage to the articular surface is attributed to both mechanical breakdown (wear, injury) and biological degradation (enzymatic cleavage) of the extracellular matrix (ECM), resulting in denatured and damaged collagen and loss of the proteoglycan (PG) macromolecules. Initial damage is located at and just below the articular surface, progressing further into the ECM as the disease progresses. The role of the articular surface has been extensively studied in joint lubrication (reviewed by Refs. [6] and [7]), while its role in ECM deformation has not been as widely studied [8–12]. Here we explored the role of the articular surface for controlling interstitial fluid motion in and out of the tissue's ECM, as well as the concomitant deformation and recovery of the ECM.

During normal physical activities, movable joints are subjected to a wide range of varying loads, whether the joint is weight bearing, such as in the lower extremities (e.g., hip, knee, and ankle), or force bearing as in the upper extremities (e.g., shoulder, elbow, and wrist). The type or pattern of the loads can also be quite variable, ranging from static, dead-weight loads (e.g., standing), to repetitive cyclic loads (e.g., gait, running), and even random loadings (e.g., during multitasking activities and sports). These joint loads are resisted by the articular cartilage covering the opposing boney surfaces of the joints, resulting in the continuous deformation and recovery of the cartilage's ECM over millions of loading cycles. The contact mechanics and tribology of joints, and the mechanical response of the articular cartilage, have been extensively studied using experimental and theoretical models [4,13,14].

It is well known that adult (mature) articular cartilage is inhomogeneous and transversely anisotropic. The water, proteoglycan, collagen, and cell (chondrocyte) contents all vary with depth from the articular surface to the underlying subchondral bone. The superficial zone (SZ) is the region below the articular surface (∼10 to 20% of the total cartilage thickness), and it is comprised of the uppermost lamina splendens (LS, ∼5 to 10 μm) and superficial tangential zone (STZ, ∼100 to 200 μm) (Fig. 1(a)). The LS is a thin acellular gel composed of phospholipids and hyaluronan, and densely packed collagen fibrils running parallel to the articular surface (Fig. 1(b)) [15,16]. The content of the STZ is high in water (∼85%), collagen, cells, and the small PG molecule, superficial zone proteoglycan (SZP, also known as PRG4 or lubricin); it also has less PG (macromolecules and aggrecan) than in the middle and deep zones where the PG content is significantly higher [17–21]. The structure of the STZ is also unique, the collagen and cells are both aligned parallel to the articular surface, (Fig. 1(b)) [17,21]. Of importance to the mechanical properties and function of the ECM is that the collagen's fibril arrangement changes with depth; the collagen fibrils are tightly packed and aligned parallel to the articular surface in the STZ and then bend (rotate) through the middle zone into the deep zone (i.e., Benninghoff's arcades), where they become perpendicular and embedded into the subchondral bone (Fig. 1(a)) [22–24]. This novel anatomically layered, heterogeneous composition and morphologically distinct structure provides articular cartilage with unique nonlinear, poroviscoelastic mechanical properties to resist the varying types of applied joint loads.

Fig. 1.

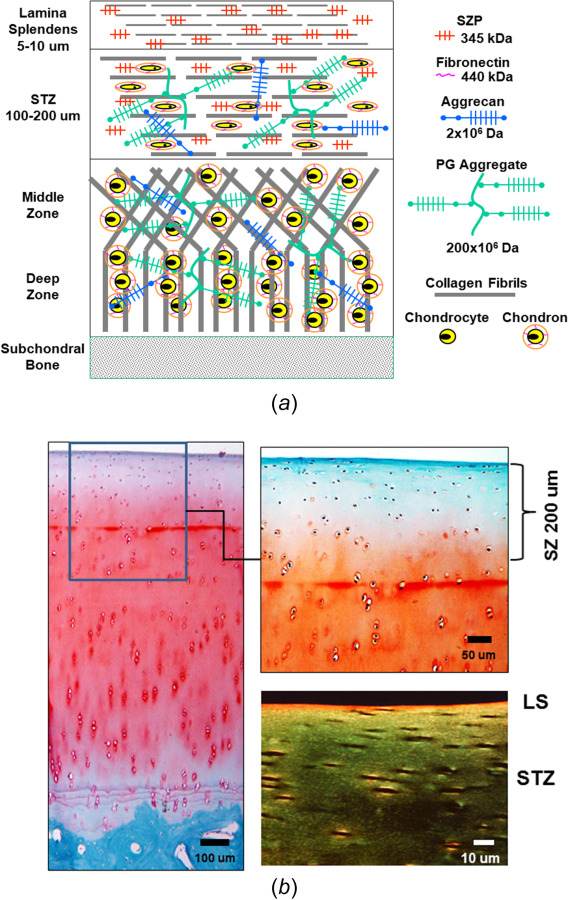
Schematic representation of the structure (composition, location, and orientation) of adult articular cartilage (not to scale; color version online): (a) diagram of articular cartilage illustrating different regions and components. The superficial zone (SZ, 10–20% of full thickness) is comprised of the LS and superficial tangential zone (STZ), with collagen and cells aligned parallel to the articular surface. Cells and collagen in the middle zone (MZ) are more randomly distributed, while in the deep zone (DZ) the collagen and cells are perpendicular to the articular surface. The SZ has the highest collagen and water contents and lowest proteoglycan content. (b) Microscopic histology of mature bovine knee cartilage (left and top right) stained with safarin-O for proteoglycan and fast-green for collagen (online, red and blue-green, respectively). Polarized light microscopy (bottom right) shows aligned collagen fibers in the SZ (LS and STZ). Cartilage thickness = 1.2 mm.

1.2 Creep Response of Articular Cartilage.

In compression, cartilage exudes its interstitial fluid, the efflux of which is dependent upon the amount of ECM strain (volume decrease). Both the tissue's creep and relaxation responses result in strain distributions that are nonlinear throughout the tissue thickness [25], with the highest strain occurring in the STZ where the compressive modulus is lowest [26]. As has been previously demonstrated [27], increasing tissue strain results in decreased tissue permeability. This is an important mechanism for controlling fluid flow and tissue deformation, especially at the articular surface. Higginson et al. [28] used a simple numerical approach to model the static (steady or dead weight) and cyclic (sinusoidal) creep response of cartilage. They found less creep deformation and fluid flow at each cycle compared to an equivalent static load. In a later experiment, Higginson and Snaith [29] applied a cyclic load (1 Hz) superimposed on a static load to study bovine and human cartilage response in confined compression; the dynamic response to the cyclic load was near linearly elastic, with an elastic modulus order of magnitude higher than previously reported. In 1983, we performed a similar experimental study to measure the fluid transport in adult bovine articular cartilage subjected to a static (1.25 MPa) or cyclic (0–1.25 MPa) compressive load [8]. Loads were applied to osteochondral (OC) specimens in confined compression so that the interstitial fluid movement occurred only across the articular surface through the SZ. We found that for the same time intervals, the resulting net efflux of interstitial fluid was greater for the static load compared to the cyclic load. More importantly, we found that during deformation recovery when a small load was applied to the articular surface, the fluid influx was significantly decreased compared to no load. Even though we did not measure the creep and recovery deformations, the findings allowed us to postulate that when loaded the collagen fibril network in the SZ would collapse, causing a decrease in the porosity and permeability of the SZ, and thus restrict the exudation and imbibition of interstitial fluid from the middle and deep zones during loading and unloading, respectively (see Fig. 2). Evidence exists for this mechanism from uniaxial confined compression tests [30,31].

Fig. 2.

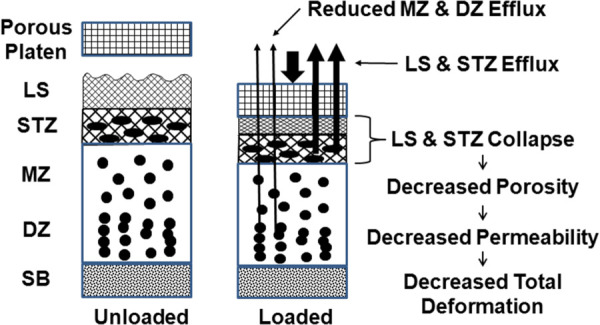
Schematic illustration of superficial zone (SZ) mechanical function. Loading the articular surface collapses the SZ (LS+STZ) as water is exuded, decreasing SZ porosity and permeability. This restricts interstitial fluid transport from the middle zone (DZ) and deep zone (DZ), thus decreasing extracellular matrix deformation.

Later experimental and theoretical studies confirmed some of these earlier findings.

Several in vitro and in vivo studies reported less cartilage creep deformation from cyclic loads compared to static loads [32–34]. Athanasiou et al. [35] found the rate of static creep strain was much faster compared to deformation recovery and suggested that a small load applied during recovery may have collapsed the SZ to restrict fluid imbibition. A similar conclusion was reported by Barker and Seedhom [36] when a continuously applied small tare load (1% of maximum load) was applied during the unloading cycle of cyclic creep, resulting in decreased SZ permeability and blocking fluid influx, drastically increasing the creep time to steady-state. Later Zhang et al. [37] developed a biphasic, large deformation, nonlinear poroelastic model of cyclic cartilage creep, based on the Barker and Seedhom [36] experiments, including strain-dependent tissue properties (modulus and permeability). They found that the volumetric strain was greatest in the SZ, causing reduced ECM cyclic creep strain due to decreased SZ permeability which inhibited fluid exudation and imbibition. Guo et al. [12] used a similar model to study static creep in cartilage and found that the permeability in the STZ decreased by 88% during ramp loading, then becoming constant until creep equilibrium.

Other studies have found that at higher cyclic frequencies, greater than ∼0.1 Hz, the compressive modulus and strain are primarily independent of fluid flow, exhibiting an almost purely elastic response [38–40]. At very low frequencies the ECM has a very large cyclic strain amplitude (envelope), the ECM being fully compressible and fully recoverable. As the frequency increases, the envelope and the creep rate decrease until steady-state equilibrium is reached [39,41]. This response has been attributed to the collapse of the SZ in the early stages of creep [12,39].

1.3 Effect of Superficial Zone Removal.

In our previous study using one adult bovine OC specimen [42], the ECM deformations were measured for similar static and cyclic creep loads. The static strains were always found greater than the cyclic strains. When the static load was changed to a cyclic load after 60 min of static creep deformation, the cyclic strain slowly decreased over 60 min to that of the cyclic creep. After the test was performed, the uppermost ∼100 um (∼7%) of the SZ was removed and the cyclic test was repeated. The intact and SZ removed specimens had a net efflux of interstitial fluid during creep deformation; however, the SZ removed strain envelope (12%–10%, efflux-influx, respectively) was much greater than the intact strain envelope (6%–4%). Both strain envelopes decreased until the efflux equaled the influx at creep equilibrium, ∼30 min. This preliminary experiment demonstrated good agreement with our proposed model for the role of the SZ in controlling fluid transport across the articular surface when mechanically loaded and unload (Fig. 2; see also Fig. 2 [42]).

Some of the most important studies to understand the role of the SZ in controlling fluid transport across the articular surface have used confined creep experiments with SZ removal. Setton et al. [9] compared the static creep responses of a group of intact bovine cartilage specimens to another group of cartilage specimens having ∼30% of the surface removed (∼400 μm). Removal of the SZ increased the rate of creep for early times but decreased the rate to equilibrium at larger times. The aggregate modulus did not change between the two groups; however, the SZ removed group's permeability increased >twofold. In intact cartilage, large SZ strains were predicted within the first 100 s of creep, indicating that fluid exudation was faster through the ECM without the SZ. In a later study using relaxation tests [10], removal of ∼25% (∼600 um) of the surface resulted in a decrease of ∼25% in the cyclic dynamic modulus and an increase of ∼50% in the aggregate equilibrium modulus, both indications that the SZ is the softest zone with significantly decreased permeability when mechanically loaded. These experimental studies concluded that removal of the SZ opens the surface to increased fluid transport and matrix deformation. Several theoretical models provided further validation for this mechanism [12,43,44]. Finite element analyses were used to compare ECM deformation and fluid flow in intact and SZ removed models. Similar results were found; SZ removal increased the permeability, resulting in an increase in the rate of creep deformation and fluid flow efflux.

In an in vivo animal study, static and cyclic creep tests were performed on the articular cartilage from an anterior cruciate ligament injury model with progressive loss of the SZ [45]. The static creep rate and instantaneous modulus, and the dynamic (cyclic) modulus all decreased by ∼fivefold with SZ degradation (thinning, softening), concomitant with significant changes in STZ collagen organization. They concluded that loss of the mechanical properties of the cartilage's SZ was one of the earliest changes occurring in osteoarthritis. Finally, using an in vitro model of osteoarthritis, in which the SZ was subjected to enzyme degradation, the creep deformation significantly increased compared to the predegradation intact SZ [46], and when the articular surface was repaired the creep deformation decreased to that of the intact creep deformation [47]. These later studies demonstrated the importance of an intact SZ for articular cartilage mechanical function.

1.4 Role of Superficial Zone in Mechanical Response of Extracellular Matrix.

A significant limitation of these previous in vitro [9,10] and in vivo [45,46] studies was, respectively, the removal of an excessive portion of the articular surface, much greater than the SZ, and the uncontrolled and undocumented amount of SZ removal. In addition, to the best of our knowledge, no studies have compared the static and cyclic creep responses of intact and SZ removed articular cartilage, nor the effect of a small tare load on the articular surface during the unloading recovery phase of ECM swelling.

The objectives of this study were (1) to compare the ECM deformation during static and cyclic creep compressive loading, and (2) characterize the role of the SZ in controlling the ECM deformation and recovery during and after static and cyclic creep, the later when the compressive load is removed. First, we hypothesized that a lower static creep stress, the equivalent root-mean-square (RMS) value of the cyclic stress, would result in static creep strains similar to that of the cyclic creep strains. Our second hypothesis was that collapse of the SZ, specifically within the STZ, would cause a decrease in the SZ permeability to restrict fluid exudation and imbibition during loading and unloading, respectively, and concomitantly decrease matrix deformation and recovery. Conversely, removal of the SZ would increase fluid exudation and imbibition during loading and unloading, and increase matrix deformation and recovery, respectively. Finally, we hypothesized that a very small compressive load (termed “tare loads”), as little as 1% of the applied deforming, when applied to the articular surface during creep recovery would be sufficient to collapse the SZ and restrict fluid influx and tissue recovery. To test these hypotheses we monitored tissue deformation during the loading (static and cyclic) and unloading (recovery) phases in a series of mechanical creep-recovery tests on intact specimens, with tissue recovery performed with and without the presence of a small tare load. These tests were then repeated on the same specimens after having their articular surface removed, again with and without the presence of the tare load. We found that the static RMS creep strains were significantly greater than the cyclic creep strains, SZ removal significantly increased static and cyclic matrix deformation, and a small tare load significantly reduce fluid influx during recovery.

2 Methods

2.1 Materials and Specimen Preparations.

As previously described, four mature male bovine knees (ages 2, 2, 4, and 7 years old) were obtained within four hours of death, placed in a media solution of Hanks balanced salt solution + protease inhibitors + antibacterial, and frozen until tested [8]. At the time of testing, the knees were thawed at room temperature and 10 mm outer diameter (o.d.) osteochondral plugs of articular cartilage with underlying subchondral bone were removed from the medial (N = 3) and lateral femoral (N = 1) condyles, femoral intercondylar notches (N = 8), and the patellae (N = 1), using a sharpened, metal cylindrical 10 mm inner diameter (i.d.) punch. Plugs were always cut so that the articular surface was aligned perpendicular to the long axis of the plug. The tissue thickness h was measured by averaging six readings around the perimeter using a dissecting microscope. Tissue thickness was later used to convert the surface displacement to average tissue strain.

At the time of testing, the OC plug was inserted into a 10 mm diameter (i.d.) metal chamber mounted onto a servocontrolled materials test system (MTS Systems, Eden Prairie, MN) (Fig. 3(a)). A height adjuster was used to raise the articular surface of the plug to just below the top of the metal chamber, and the surface of the plug bathed in incubation media at room temperature. This protocol provided for a tight fit of the cartilage and bone within the chamber, which avoided cartilage lateral swelling before and lateral expansion after load application.

Fig. 3.

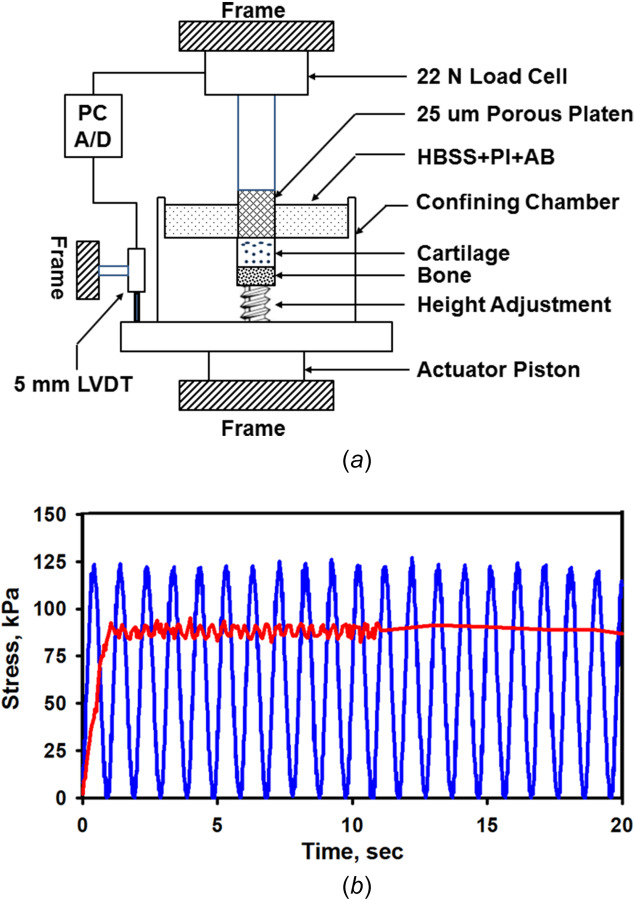
Mechanical confined creep test system for applying static and cyclic compressive loads: (a) osteochondral specimens are held in a confining chamber and the articular surface of the cartilage is loaded with a rigid porous platen and (b) the articular cartilage surface was loaded with a static (0.707 kg) or cyclic (1.0 kg at 1 Hz) load for 300 s (equivalent stresses of 88 kPa and 125 kPa, respectively), superimposed on a small constant tare load (∼1% of applied load). Shown are the static and cyclic applied stress waveforms (online version, red and blue, respectively) for one specimen (#28-05); static = 87.8±2.8 kPa and cyclic = 119.5±19.5 kPa (mean ± standard deviation).

2.2 Creep Testing Protocol.

Confined creep compression tests (static and cyclic) were performed by loading the articular surface using a cylindrical (9.6 mm o.d.), porous plane-ended bronze platen of 25-μm porosity (Fig. 3(a)). The load was measured using a 22 N load cell (model 34, Honeywell Sensotec, Inc. Columbus, OH; resolution ∼ 1 gm) and the platen displacement using a 5-mm linear variable differential transducer (Honeywell Sensotec; resolution ∼ 1 μm). Before each test, the cartilage surface was loaded three times with a 1 kg load (stress, σ = 125 kPa at 1 s cycles), and then allowed to recover unloaded for 20 min. The platen was then slowly lowered until it just contacted the articular surface. A small tare load of 7–10 gms (1% of applied load, 0.9–1.3 kPa) was applied for 15 min to flatten the articular surface and ensure uniform tissue-platen contact (Figs. 4(a) and 4(b)). In addition to the tare load, the cartilage plug was then loaded for 5 min (300 s) with either a constant load of 707 gms (σ = 88 kPa) applied over 1 s, termed static creep or a cyclic peak-to-peak (P–P) sinusoidal load of 0–1 kg (σ = 0–125 kPa) applied at 1 Hz, termed cyclic creep (Figs. 3(b) and 4). The maximum applied stresses used for both creep tests were chosen to limit the total creep strain to ∼25 to 30%.

Fig. 4.

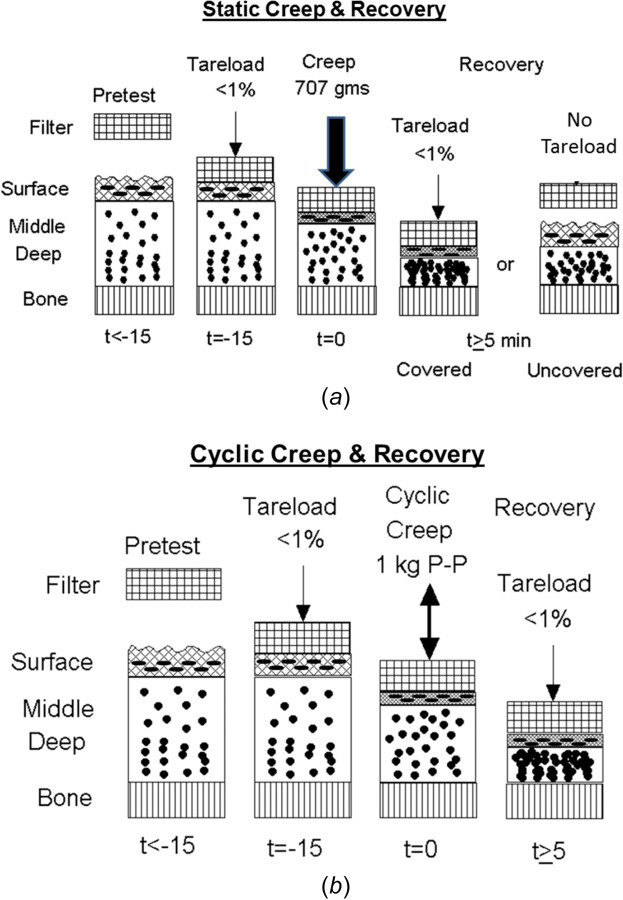
Protocols for (a) static and (b) cyclic creep loading, and unloading covered and uncovered recovery tests. Osteochondral specimens are unloaded for 15 min (pretest) and then loaded with a 1% tare load for an additional 15 min. (a) For static creep testing, a constant load is applied for 5 min, followed by either unloading the articular surface to the 1% tare load (covered recovery) or completely unloading the surface (uncovered recovery), both monitored until the cartilage recovers its initial thickness. (b) For cyclic creep testing, a sinusoidal cyclic load is applied for 5 min, followed by covered recovery.

The static and cyclic creep loads and platen displacements were recorded using a computer data acquisition system at the following rates: static creep at 20 Hz for 15 s, then 0.5 Hz for 285 s, and cyclic creep at 50 Hz for 300 s. After five minutes of tissue compression, the surface was unloaded and allowed to recover (swell) until regaining its initial thickness (usually ∼90 min). Two different methods were used for the recovery phase (Figs. 4 and 5). In covered recovery, the applied creep load was reduced to the value of the initial tare load (1%), and the surface deformation was continuously recorded at 20 Hz for 15 s and then at 0.2 Hz for 90 min (5400 s) or until the initial platen position (i.e., cartilage thickness) was obtained. In uncovered recovery, the load was completely removed by lifting the platen of the articular surface. To record tissue deformation during recovery, the platen was slowly lowered, at 1-min intervals, until it just made contact with the articular surface (load < tare load) and was then immediately retracted, recording the contact load and platen displacement. This was repeated for 90 min or until regaining original cartilage thickness. Covered and uncovered recovery were performed for static creep, while the only covered recovery was performed for cyclic creep.

Fig. 5.

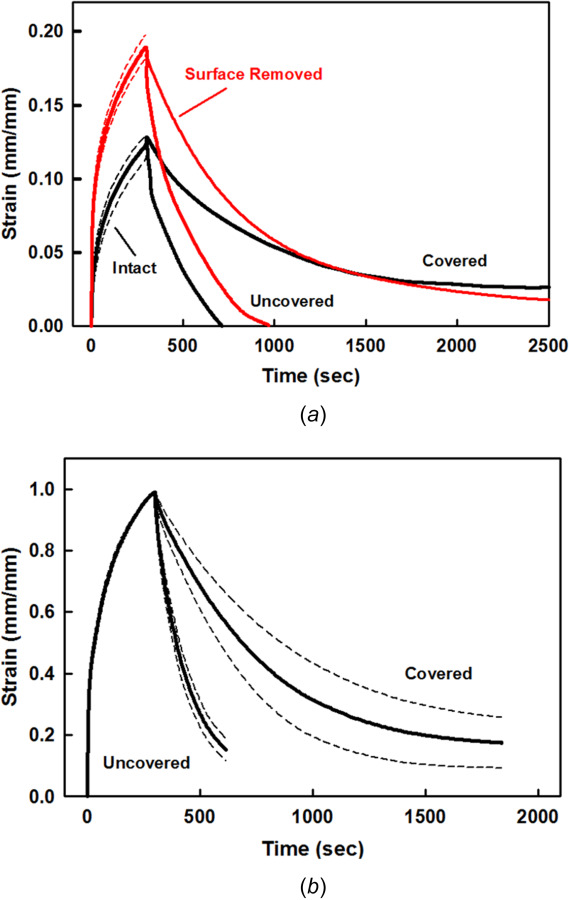
Intact specimens for static creep strain and covered and uncovered recovery. (a) Single specimen (#25-01) with repeated tests for static creep (n = 5) and covered (n = 3) and uncovered (n = 2) recovery. Thickness h = 1.20 mm, water content β = 78.7%, and PG content = 2.9%. (b) Multiple specimens (N = 4) with repeated tests for static creep (n = 19) and covered (n = 10) and uncovered (n = 9) recovery. h = 1.26±0.23 mm, β = 77.1±1.2%, and PG = 3.2±0.7%. Mean (solid) ± SEM (dashed).

After the tissue regained its initial thickness h, the test was stopped and the specimen was allowed to recover for an additional 1-h period. The static and cyclic creep tests were then repeated on the same specimen, using randomization for either covered or uncovered recovery tests. Finally, after testing each intact specimen the plug was removed from the fixture, mounted on a Bailey freezing stage (−20 °C) attached to a Leitz 1300 Sledge Microtome (E. Leitz, New York), and the uppermost Δh ∼ 100 to 200 μm of the articular surface was removed parallel to the articular surface. The static and cyclic creep and recovery tests were then repeated as described above.

2.3 Proteoglycan and Water Content.

Proteoglycan and water contents of the articular cartilage were determined for each specimen. Using a scalpel, the cartilage was removed from the subchondral bone and combined with the slices removed from the articular surface. The cartilage wet (W_wet) and dry (W_dry) weights were measured using a Cahn 25 Electromicrobalance (resolution ±1 pgm), before and after 24 h of lyophilization drying, respectively, and the percent fluid content β was calculated as β = 100 × (W_wet−W_dry)/W_wet. The cartilage was then digested in 0.5 mg/ml proteinase K (MP Biomedicals LLC, Solon, OH) solution containing 30 nM Tris HCl (pH = 8.0) in 60 °C water bath overnight. PG content was determined from the amount of sulfated-glycosaminoclycans in each digest using the dimethylmethylene blue method [48] and a standard curve of chondroitin 6-sulfate (Sigma-Aldrich, St. Louis, MO). Specimens were quantified spectrophotometrically at 535 nm using a Tecan SpectraFluor Plus plate-reader (Tecan Group, Durham, NC). PG content was normalized by the cartilage wet weight (PG/WW) and given as a percent wet weight (%WW).

2.4 Data and Statistical Analyses.

Tissue deformations were converted to nominal strain (ε = ECM deformation/tested thickness) to account for differences in plug thickness before (h) and after surface removal (h − Δh). In order to combine (average) the different specimen's static and cyclic creep and recovery responses strains ε were normalized to the peak intact static creep strain at 300 s (ε_peak), given as ε /ε_peak (the normalized intact static creep strain ε /ε_peak = 1). The number of plugs tested is given as “N” while the number of repeated tests on an individual plug is given as “n”. Averages are given as mean ± standard deviation of N plugs tested or n repeated tests. In graphical figures, line plots are given as the mean ± standard error of the mean (SEM; solid line ± dashed line, respectively; online version, intact in black and surface removed in red). The cyclic maximum and minimum P-P creep strains are shown for each cycle with upper (ε_max) and lower (ε_min) lines, respectively, where the maximum strain (ε_max) is at the loaded peak (1 kg + 1% tare) and the minimum strain (ε_min) at the unloaded peak (1% tare). In addition, plots of the cyclic strain envelope are shown as upper (ε_out) and lower (ε_in) P-P lines; the efflux strain (ε_{out =} |ε_min − ε_max|) and influx strain (ε_{in =} |ε_max − ε_min|) representing the ECM strains for interstitial fluid efflux and influx during cyclic loading and unloading, respectively. For N combined cyclic specimens, the cyclic strain envelope was also normalized by the intact static creep strain at 300 s, given as ε/ε_peak. Finally, statistical differences in material properties were calculated using Student-t tests, with significant p-values at a level of 0.05; analyses were performed using Excel 2010 (Microsoft) and SigmaPlot 10 (Systat, Inc.) software. Statistical differences between the creep and recover responses (line plots) for the intact and surfaced removed specimens were determined by comparing the mean ±95% confidence intervals of the responses (data not shown).

3 Results

A total of 13 OC plugs were removed from adult bovine knees and were subjected to static (N = 8) and cyclic (N = 5) confined compression creep testing. Application of static stress of 88 kPa (RMS of cyclic stress) or cyclic stress of 125 kPa produced tissue strains in the intact and surface-removed specimens ranging from 15% to 25% after 5 min of compression. In order to determine the repeatability of the creep tests, each static and cyclic creep and recovery test, on intact and surface-removed specimens, was repeated between 2 and 12 times. Repeated tests on individual specimens produced similar tissue deformation and recovery patterns and strains, with little variation (see below).

The overall mean cartilage thickness was 1.51±0.26 mm, with no significant difference (p = 0.396) between the static (1.46±0.31 mm) and cyclic (1.59±0.15 mm) cartilage thicknesses. The overall mean cartilage PG content was 3.16±0.83%/WW, also with no significant difference (p = 0.811) between the static (3.12±0.74%/WW) and cyclic (3.24±1.06%/WW) tested plugs. The overall mean cartilage fluid content was 76.9±3.0%; however, the mean fluid content of the static tested plugs (77.3±1.3%) was significantly higher (p = 0.038) compared to the cyclic tested plugs (73.9±3.9%). This small difference (<5%) was due to greater wet weight for the cyclic plugs compared to the static plugs (106.1±32.6 mg versus 89.7±24.1 mg, respectively, p = 0.001), while the dry weights were not different (20.5±6.3 mg versus 28.4±11.8 mg, respectively, p = 0.316). Even though there was a small difference in fluid content, this was not considered to have a significant effect on any of the creep test comparisons. Finally, the overall thickness removed from the articular surface was 142±20 um (10.1±2.5% of full thickness), with no significant difference (p = 0.396) between the static (142±23 um or 10.6±2.9%) and cyclic (140±17 um or 9.0±0.6%) tested plugs.

3.1 Static Creep Responses, Covered and Uncovered.

Static creep confined compression tests were performed on intact cartilage plugs for 300 s, and then the load was either removed from the articular surface (uncovered) or reduced to a 1% tare load (covered) (Fig. 5). Upon load application there was a rapid increase in ECM strain, followed by a slower increase in ECM strain over the 300 s of loading, characteristic of the nonlinear, biphasic, and poroelastic response of adult articular cartilage (response for one plug, with repeated testing, is shown in Fig. 5(a); the average response for four plugs is shown in Fig. 5(b)). Immediately after load removal (unloading), the uncovered specimens rapidly regained their initial shape in about 10–15 min, which was slower than the five minutes of creep deformation. As compared to the uncovered specimens, the covered specimens required more than 2–3 times the recovery time, as much as one hour or more.

3.2 Static Creep Response, Articular Surface Removed.

After static creep tests were performed on intact cartilage plugs, including repeated tests, the tests were repeated after removal of the uppermost superficial zone, also with repeated testing (Figs. 6(a) and 6(b), single specimen with repeated tests). Surface removal resulted in a significant increase in ECM deformation during the loading phase as compared to the intact specimen. ECM strains were ∼25% to 50% higher for the surface-removed specimens after 300 s. After performing the static creep tests (intact and surface removed), ECM deformation recovery was performed for covered and uncovered unloading (Fig. 6(b) single specimen with repeats, and Fig. 6(c), the average response of three specimens). Similar to the intact specimens, the surface-removed specimens rapidly regained their initial thickness in about 10–15 min when the load was completely removed (uncovered), while the covered specimens required substantially longer times. Except for differences in strain magnitude, the recovery time responses were similar between the intact and surface-removed specimens.

Fig. 6.

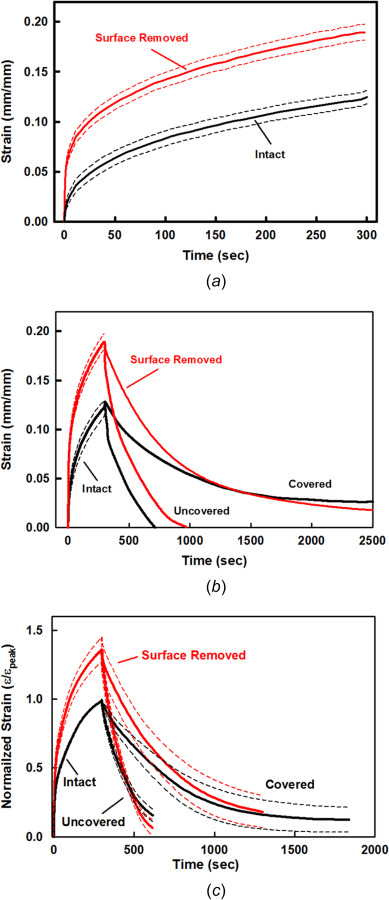
Intact and surface-removed specimens for static creep strain and covered and uncovered recovery. Single specimen (#28-03) with repeated tests for (a) intact (n = 2) and surface removed (n = 4) static creep strain, and (b) covered (n = 2 and 1) and uncovered (n = 1 and 2) recovery. Insert (a) shows static and cyclic maximum strain ε_max for 0–20 s. h = 1.50 mm, β = 76.2%, and PG = 2.3%, surface removed Δh = 139 μm (7.3%). (c) Normalized creep strain for paired intact and surface-removed specimens (N = 3) with repeated tests (n = 9 and 6),and covered (n = 4 and 3) and uncovered (n = 4 and 3) recovery. h = 1.28 ± 0.28 mm, β = 76.5 ± 0.6%, PG = 3.3 ± 0.9%, and Δh = 130 ± 46 μm (10.7 ± 3.6%). Mean (solid) ± SEM (dashed).

3.3 Cyclic and Static Creep Responses.

Static and cyclic compression creep tests were performed on intact specimens applying either a constant RMS stress of 88 kPa or cyclic peak-to-peak stress of 0 to ∼125 kPa, respectively, both superimposed on a static 1% tare stress, for 300 s. Then, the cartilage was allowed to fully recover to its initial thickness with the articular surface covered by the porous platen (σ = 1% tare). The test was then repeated but with the alternate loading type, either the cyclic or constant RMS stress, respectively. This sequence of alternating static and cyclic creep tests followed by covered recovery, was repeated several times on each of five individual specimens to evaluate reproducibility within each specimen (n = 2–6) (Fig. 7(a)) and between specimens (Fig. 7(b)). Repeated tests on individual specimens showed good repeatability, as did tests between different specimens.

Fig. 7.

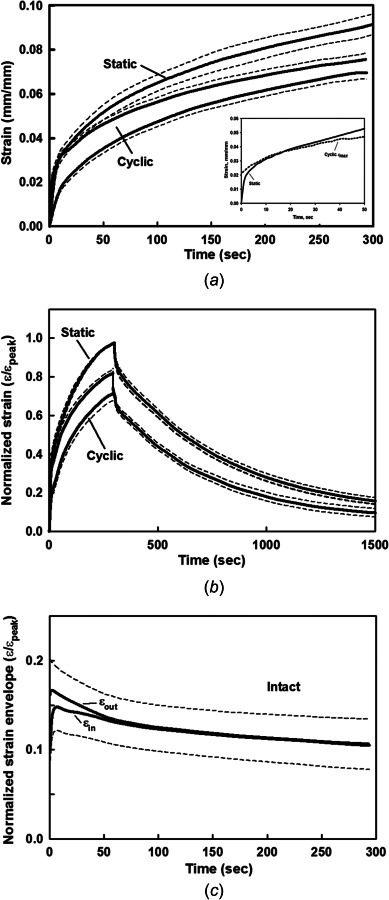
Intact specimens for static and cyclic creep strain and covered recovery. (a) single specimen (#28-05) with repeated tests (n = 3) for static and cyclic creep strain. h = 1.77 mm, β = 71.5%, and PG = 4.0% (b) Static and cyclic normalized creep strain and covered recovery for paired specimens (N = 5) withrepeated tests (n = 13 and 14). h = 1.59±0.15 mm, β = 73.9 ± 3.9%, and PG = 3.2 ± 1.1%. (c) Normalized strain envelope for the loading (ε_out) and unloading (ε_in) strains during each cycle of cyclic creep in (b). Cyclic strain envelope is indicated by superimposed sinusoidal waveform. Mean (solid) ± SEM (dashed).

In each specimen, the cyclic stress (125 kPa) resulted in a higher creep strain compared to the static stress (88 kPa) creep strain, but only at the start of loading (insert, Fig. 7(a)). The static strain increased faster than the cyclic creep strain, which became greater after ∼10 to 20 s. The static strain continued to increase faster until the end of creep loading. The width of the cyclic creep strain envelope for each cycle (ε_out–ε_in) continually decreased with increasing creep time (cycles) (Fig. 7(c)), indicating a decrease in the net loss of interstitial fluid through the articular surface as the cyclic creep strain slowly increased. Finally, there was no difference in the covered recovery of the cartilage thickness between the static and cyclic loading tests (Fig. 7(b)), both of which took ∼1 h.

3.4 Static and Cyclic Creep Responses, Intact and Surface Removed.

In the final sequences of testing, two intact specimens were first subjected to static and cyclic creep testing, the SZ was then removed, and the specimens were retested in static and cyclic creep tests, all specimens having covered recovery and multiple within specimen repeated tests (n = 2–3 each). The mean of the repeated responses (static, cyclic, recovery) for the two specimens was averaged (N = 2) and the normalized strains and strain envelopes were plotted for all four conditions, the surface removed strains based on the reduced thickness h–Δh (Fig. 8). Comparisons between the cyclic and static creep strains were similar to those reported above, with larger strains for the RMS static applied stress compared to the cyclic applied stress, both of which increased with surface removal (Figs. 8(a) and 8(b)). Surface removal did not affect the cyclic or static-covered recoveries, the intact and surface removed recoveries all taking almost 60 min. Compared to the intact cyclic creep strains, removal of the surface region (∼9%) resulted in an increase in the cyclic creep strain while also increasing the cyclic strain envelope (Figs. 8(b) and 8(c)).

Fig. 8.

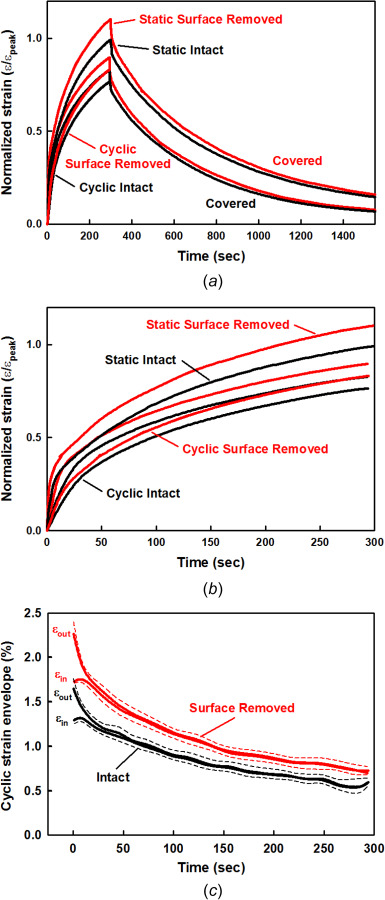
Intact and surface-removed specimens for static and cyclic creep strain and covered recovery. (a) Mean static and cyclic normalized creep strain and covered recovery for intact and surface-removed specimens (N = 2, n = 2–6 for each test).h = 1.56 ± 0.30 mm, β = 73.4 ± 2.7%, PG = 1.6 ± 0.2%, and Δh = 136 ± 26 μm (8.7 ± 0.3%). (b) Normalized static and cyclic creep strains during creep loading. (c) Normalized strain envelope for the loading (ε_out) and unloading (ε_in) strains during each cycle of cyclic creep in (b).

4 Discussion

In this study, the articular cartilage surface of intact osteochondral plugs was loaded in confined creep compression with static and cyclic stress using a porous rigid platen. The cartilage surface was then unloaded to recover its initial shape, with the articular surface covered by the load platen with small, applied stress (1% of maximum) or with the load platen completely removed. Then the uppermost layer of cartilage, the superficial zone, was removed and the static and cyclic creep and recovery tests were repeated. The results from these tests, together with those from a previous publication [42], are schematically summarized in Fig. 9.

Fig. 9.

Schematic illustration of the different creep responses for intact and surface removed articular cartilage during static (RMS) and cyclic (P–P) creep loading. The width of the cyclic creep envelope represents the net loss of interstitial fluid on each cycle (efflux–influx > 0). Surface removal increases the efflux of interstitial fluid and static and cyclic ECM deformation. Completely removing the load from the articular surface (uncovered) increases the rate of tissue swelling compared to that of covering the surface (covered) for both the static and cyclic recovery. Included are the results from a previous study [42] for the cyclic recovery response when a static (RMS) creep load was replaced by a cyclic (P–P) load; note that the cyclic recovery strain (swelling) reaches that of the cyclic creep strain.

It is well known that each constituent within each zone of articular cartilage has a unique mechanical role during tissue loading and unloading. When cartilage is at rest and unloaded, the PG macromolecules swell, imbibing water and stretching the collagen fibers. When loaded the ECM will compress, forcing out interstitial fluid and compacting the PG macromolecules, the later exerting increasing osmotic resistance (internal stress) against further compaction. Tissue deformation will proceed at a rate proportional to the fluid loss from the ECM, as the fluid moves through the PG-collagen matrix and out the articular surface (shown schematically in Fig. 2). As the tissue's compressive strain increases, the matrix porosity will decrease, as well as the ECM's permeability, thereby decreasing fluid movement and tissue deformation. The results from our experiments indicate that the uppermost articular surface layer (i.e., SZ), comprising the LS and STZ, of about 100–200 μm in thickness, is unable to resist even the small compressive loads applied in our tests, resulting in the SZ collapsing and decreasing surface permeability and ECM fluid efflux. This structural collapse is probably due to the absence of significant amounts of compressive resisting elements in the STZ, which is high in tangentially aligned collagen fibrils and small molecular weight SZP molecules (345 kDa), with negligible amounts of the much larger aggrecan (2 MDa) and PG (∼200 MDa) molecules (Fig. 1) [49,50]. SZP molecules have been postulated to act primarily as a lubricant for boundary lubrication during joint articulation [51,52]); however, removal of the SZ does not increase cartilage's coefficient of friction [53]. Our results suggest that the small SZP's presence in the SZ is more likely there to provide some minimal resistance to compressive loads in order to avoid complete closure of the SZ, especially during cyclic loading and unloading where fluid efflux and influx occurs.

4.1 Creep During Static and Cyclic Loading.

In our previous study [42] using a single OC specimen, cartilage was loaded in confined compression using high cyclic stress (σ_cyclic = 1.25 MPa), then unloaded (uncovered) until the cartilage regained its initial thickness, and again loaded with high static stress (σ_static = 1.25 MPa) for another hour. The static stress resulted in a greater creep strain compared to the cyclic creep stress, a similar result found in several other studies which used different tests and loading conditions [28,32,34]. Based on these studies, we hypothesized that a lower static creep stress, the equivalent RMS value of the cyclic stress, would result in static creep strains equivalent to that of the cyclic creep strains. To test this hypothesis we applied an RMS static stress (σ_static = 88 kPa) and cyclic stress (σ_cyclic = 125 kPa), both of which were smaller than previously used to restrict the creep strains to within the linear biphasic response [30]. We found that the RMS static creep strains were still much higher than the cyclic creep strains, disproving our hypothesis (Fig. 9, static and cyclic creep). The one exception was for the first 10–20 cycles at the start of the cyclic creep test, where the cyclic peak strains (ε_max) were slightly greater than the RMS static strains (Fig. 7(a)), a result clearly due to the higher applied maximum P-P stress (σ_cyclic > σ_static). Shortly thereafter the static creep strains became increasingly greater than those of the cyclic creep strains. Thus, the RMS static stress was not equivalent to the cyclic P-P stress.

The RMS value of a sinusoidal waveform is defined as the equivalent constant or static value to give the same amount of energy, heat, or power in one cycle (e.g., alternating current (AC) and direct current (DC)). In our case, the static RMS stress (σ_rms = 0.707 × σ_cyclic) results in a significantly higher creep strain compared to that of the cyclic creep strain (Figs. 7(a) and 7(b)). At fast loading rates (τ1 s), cartilage behaves mechanically like an elastic material [54]. Thus, based on the amount of stored energy during static loading W_static = σε/2) and cyclic loading (half cycle, W_cyclic = σε/8), we can estimate the static stress for the equivalent strain to be ∼31 kPa (σ_static = σ_cyclic/4). Whether the equivalent static creep strain would occur with this lower static stress will need to be tested.

An interesting finding from our previous study [42] was when the cartilage was first cyclically loaded for one hour, unloaded (uncovered) to fully recover its initial thickness, loaded with static stress for one hour, where static creep strain ≫ cyclic creep strain, and then the static stress changed to cyclic stress for another one hour. The resulting cyclic creep strain decreased to that of the previous cyclic creep strain, termed cyclic recovery and shown in Fig. 9 (cyclic recovery and cyclic creep). While we did not perform this sequence in this study, this finding is of interest and should be studied further, for intact and surface-removed specimens, and covered and uncovered cyclic recovery.

4.2 Effect of Surface Zone Removal on Creep Strain and Recovery.

The mechanism of the structural collapse of the SZ under compressive loads, resulting in decreased surface permeability, fluid efflux, and ECM deformation (Fig. 2), was found in both the static and cyclic creep tests performed in our study. Removal of the uppermost surface layer, ∼150 μm thick, eliminated this mechanical barrier during compression, resulting in significantly increased static creep strains, as well as increased cyclic creep strains and strain envelopes (Figs. 6, 7, and 9). Similar results for the importance of an intact SZ in restricting cartilage compression were reported from experimental tests [9,10,45] and theoretical models [12,43,44]. It may be possible that at sufficiently high static and cyclic stresses, the SZ could completely close and inhibit interstitial fluid exudation and imbibition, before as well as when creep strain equilibrium is reached.

Possibly more important is that the SZ structural collapse mechanism was also present during the covered recovery phase, following load removal when a small 1% tare load was applied to the articular surface by the porous platen (Fig. 4). Covered recovery was significantly slower as compared to uncovered recovery when the platen was completely removed (Figs. 5, 6, and 9). Fully uncovering the surface allowed the superficial layer to quickly expand (i.e., swell), increasing surface permeability, fluid influx, and ECM thickness. However, even a small surface load was sufficient to collapse the surface layer and significantly restrict fluid influx and tissue thickness recovery.

Of some surprise was that the removal of the SZ layer did not increase the rate of strain (thickness) recovered during covered or uncovered recovery after static (Figs. 6(b) and 6(c)) or cyclic (Figs. 7(b), 8(a), and 8(d)) creep, even though it did have a significant effect during the creep phase. We can postulate that this phenomenon is most likely due to the amount of internal stored strain energy available for fluid influx through the collapsed SZ layer. During intact static and cyclic loading, high interstitial fluid pressures will be generated within the tissue, increasing during the creep phase as the SZ collapses and traps the fluid within the ECM. The high interstitial fluid pressure is still sufficient to produce some fluid exudation through the SZ, even with surface collapse, at least until creep strain equilibrium is reached and the SZ is completely closed to fluid efflux. Removal of the SZ layer removes this barrier for increased fluid efflux across the articular surface during creep loading and thus increased ECM strain. When the intact articular surface is completely unloaded (uncovered recovery), the SZ opens and the internal strain energy stored within the compressed tissue matrix is sufficient to expand the ECM and draw fluid through the unloaded surface layer (imbibition) for rapid thickness recovery. However, any load applied to the intact articular surface during unloading (covered recovery) will continue to sufficiently collapse the SZ and slow fluid imbibition and thickness recovery. In our study, removing ∼10% (142±20 μm, N = 13) of the articular surface increased creep strain, but it did not change the strain recovery between uncovered and covered unloading. We conclude that while removing ∼10% of the SZ was sufficient to open the surface enough to allow increased fluid efflux during loading due to high interstitial fluid pressure, it was insufficient to completely eliminate the surface collapse and decreased surface permeability caused by the contacting porous load platen during covered unloading. This suggests that the stored internal energy generated during loading was not able to overcome the increased resistance to fluid influx through the collapsed SZ. On the other hand, it is possible that the full SZ thickness was not removed (SZ thickness in bovine knee ∼150 μm) [55], and any remaining tissue from the STZ could have influenced interstitial fluid transport (imbibition) across the articular surface. Increasing the thickness of the SZ removed might reverse this result.

4.3 Study Limitations.

There were several limitations in our study. To simulate early stage osteoarthritis, we removed between ∼100 and 200 μm of the superficial zone, such that we were not able to separate the role of the lamina splendens from that of the underlying superficial tangential zone. In addition, the average thickness removed, 142 μm, probably did not remove the entire STZ. Possibly an experiment setup where very thin slices, ∼10 um, are sequentially removed and the creep tests repeated could be used. In a previous study [46], enzyme degradation of the articular surface resulted in increased creep deformation, similar to what was found in this study with surface removal.

Our cyclic creep tests used low stress magnitudes and a simple sinusoidal waveform at a frequency of 1 Hz. More realistic in vivo stress magnitudes and patterns could be applied to simulate human gait, not only for the creep phase but also the recovery phase [33,37,56,57]. Our one-dimensional confined creep-recover test configuration was specifically used to limit interstitial fluid efflux-influx, respectively, through the superficial zone; however, other more complex (two-dimensional, three-dimensional) configurations need to be explored. For example, cyclic deep knee bends performed by human volunteers over 15 min resulted in patellar cartilage deformations from 2.4% to 8.6%, which required more than 90 min to recover [34]. In a recent study, Voinier et al. [58] reported an order of magnitude faster fluid covered recovery rates (tare = 34.7 Pa) following indentation creep (stress = 1.7 kPa) using a flat-ended nonporous indenter, compared to that of a curved cartilage-on-glass configuration. While these two test configurations are dramatically different, they do show the importance of contact geometry and porosity.

Finally, combining sequential surface removal, increased numbers of specimens in each test, and using mathematical models to describe the static and cyclic creep and recovery responses, with and without a tare load, would provide a larger database for statistical analyses of each factor, and provide for a better understanding of the mechanical function of the different zones of articular cartilage. While we did quantify each specimen's water and PG contents, we did not analyze the collagen content or orientation in the SZ, two important factors for fluid transport through the SZ [12].

5 Conclusions

Our results indicate that an intact articular surface, specifically the lamina splendens and collagen-rich superficial tangential zone (Fig. 1(a)), is essential for the health and function of articular cartilage during joint motion due to its ability to control tissue deformation and recovery. This is accomplished by controlling fluid movement through the superficial zone, exudation, and imbibition, as the superficial zone matrix is compressed when loaded and expanded when unloaded, respectively. Loss of this mechanism has two important consequences related to the initiation and progression of osteoarthritis. First, it could account for the depletion (loss or wash out) of PG and aggrecan macromolecules observed in the SZ of degenerative tissue, where surface disruption is evident in the early stages of osteoarthritis [2,3]. It may be possible that increased fluid exudation could effectively drag the macromolecular and smaller components (including link protein and hyaluronic acid) out of the tissue's ECM, even before PG aggregation occurs. Thus, an intact surface layer would not only control tissue deformation but also act to restrain ECM molecular component efflux [46,59]. Second, uncovering of the articular surface appears necessary to ensure rapid tissue swelling to regain its thickness by imbibing lost interstitial fluid. This mechanism would be especially significant during oscillating type movements, such as in gait, where the exudation and imbibition of fluid would aid in joint lubrication [6,60], or when attempting to repair injured tissue through a joint motion for nutrient transport [8,61].

To summarize our results, joint motion (loading and unloading) is one of the primary mechanisms for the formation, maintenance, degradation, and repair of the articular cartilage in all diarthrodial (movable) joints. All joints are reciprocating in that the articular contact surfaces are covered and uncovered during loading and unloading motion, respectively, and thus appear to be self-lubricating through interstitial fluid motion across the articular surfaces. Therefore, oscillating motion is essential for health and function through covering the articular surfaces during loading to limit fluid exudation and deformation, as well as through uncovering of the articular surface during unloading to enhance fluid imbibition and deformation recovery.

Funding Data

• National Institutes of Health (Grant No. AR28151; Funder ID: 10.13039/100000002).