Mechanical regulation of substrate adhesion and de-adhesion drives a cell-contractile wave during Drosophila tissue morphogenesis

Summary

During morphogenesis, mechanical forces induce large-scale deformations; yet, how forces emerge from cellular contractility and adhesion is unclear. In Drosophila embryos, a tissue-scale wave of actomyosin contractility coupled with adhesion to the surrounding vitelline membrane drives polarized tissue invagination. We show that this process emerges subcellularly from the mechanical coupling between myosin II activation and sequential adhesion/de-adhesion to the vitelline membrane. At the wavefront, integrin clusters anchor the actin cortex to the vitelline membrane and promote activation of myosin II, which in turn enhances adhesion in a positive feedback. Following cell detachment, cortex contraction and advective flow amplify myosin II. Prolonged contact with the vitelline membrane prolongs the integrin-myosin II feedback, increases integrin adhesion, and thus slows down cell detachment and wave propagation. The angle of cell detachment depends on adhesion strength and sets the tensile forces required for detachment. Thus, we document how the interplay between subcellular mechanochemical feedback and geometry drives tissue morphogenesis.

Graphical abstract

Highlights

• •A wave of MyoII activation propagates within cells of the dorsal epithelium
• •Integrins immobilize the cell apical cortex in contact with the vitelline membrane
• •Two mechanochemical feedbacks cause MyoII accumulation during wave propagation
• •The detachment angle depends on adhesion strength and tunes tensile detachment forces

Collinet et al. study a wave of tissue deformation in Drosophila involving adhesion to the vitelline membrane, actomyosin contractility, and de-adhesion. They show that this process originates at the subcellular scale from two sequential and spatially separated mechanochemical feedbacks. The system’s geometry ensures wave propagation by tuning de-adhesion forces.

Introduction

During development, active forces due to cell contractility and adhesion drive tissue shape changes.^1,2,3,4,5 Spatial and temporal control over the processes generating such forces is essential for robust morphogenesis, which additionally depends on the mechanical and geometrical environment of the tissue, such as its rigidity and the shape of its boundaries.⁶ Patterns of gene expression coordinate cell adhesion and contractility in space and time in many organisms.^6,7 For instance, the polarized recruitment of non-muscle myosin II (MyoII) at the medio-apical surface of epithelial cells induces tissue bending and invagination.^8,9,10,11 The restricted expression of specific transcription factors within the tissue regionalizes the activity of specific signaling pathways and culminates in the localized activation of MyoII.^{6,7,12,13,14,15,16,17} Similarly, planar polarized recruitment of MyoII and regulation of cell adhesion at cell-cell contacts depend on specific transcriptional patterns and lead to polarized cell intercalation driving tissue extension.^{6,18,19,20,21,22,23,24,25,26,27} However, cell contractility and adhesion also display remarkable interplay and self-organization. Many features of contractility, such as actomyosin pulses, flows, and waves, can only be explained by local stochastic interactions and mechanochemical feedback.^{8,10,28,29,30,31,32,33,34,35} These feedback interactions often involve adhesion molecules, such as E-cadherin (E-cad) and integrins, which regulate and are in turn regulated by actomyosin contractility.^2,36,37,38 Thus, the local interplay between adhesion and contractility can spatially orient forces. For instance, in Drosophila embryos anchorage to E-cad clusters has been shown to bias actomyosin flows and contractions.³⁹ In turn, the direction of the contractile forces applied to such clusters (producing tensile or shear stress) regulates E-cad levels at junctions.⁴⁰ At a larger scale, adhesion to fixed substrates such as the cuticle or the embryonic vitelline membrane, rigid structures enveloping the tissue, has been shown to play an important role in morphogenesis by spatially regulating forces and directing tissue flows.^{6,35,41,42,43} Thus, tissue dynamics during morphogenesis emerge from the interplay between contractile and adhesive forces whose spatial-temporal distribution is not only encoded genetically but also emerges as self-organized from local mechanochemical feedbacks and the system’s geometry. However, it is unclear how the large-scale forces directing tissue flows emerge locally from the interplay between contractility and adhesion. Here, we address this during morphogenesis of the posterior endoderm in Drosophila embryos, where a wave of actomyosin contractility is coupled to adhesion to the vitelline membrane and propagates in a self-replicating manner.³⁵

During gastrulation, the posterior endoderm invaginates and flows toward the anterior, thereby driving the initial phase of germband extension (Figure 1A, left). Here, a genetic program induces the initial apical recruitment of MyoII and tissue bending at the posterior of the embryo.³⁵ The recruitment of MyoII apically in this highly curved region leads to polarized tissue flow toward the flatter dorsal side of the embryo, where there is a lower cost to bending.⁴⁴ Thus, both genetic and geometric information underlie the onset of polarized flow.⁴⁴ After this initial phase, where an initial invagination is generated, polarized flow and invagination continue, driven by a tissue-level mechanochemical wave of Rho1/MyoII activation propagating from posterior to anterior from one cell to the next along the antero-posterior (AP) axis across the dorsal epithelium.³⁵ A tissue-level characterization of this process³⁵ emphasized its discrete nature. MyoII was reported to be activated with rapid kinetics across the entire apical surface of cells, and activation in a given cell at position n occurred only after invagination of the cell at position n − 1, suggesting a cell-to-cell relay mechanism. This mechanism was described by a cycle of 3D cell deformations consisting of 4 key steps (Figure 1A, right). First, cells anterior to the invaginating furrow are compressed basally and lifted upward, bringing them in contact with the overlaying vitelline membrane. Second, the cells spread their apico-lateral surface against the vitelline membrane and adhere via integrins.^35,42 Third, when cells reach the edge of the advancing furrow, they activate MyoII contractility in an integrin-dependent manner. Fourth, MyoII contractility detaches cells from the vitelline membrane and allows them to invaginate. This relays the cycle to the next round of cells causing the anterior propagation of MyoII activation and of the invaginating furrow. Thus, a wave of adhesion, MyoII activation, and detachment sustains the persistent movement of the posterior endoderm.³⁵

Figure 1.

MyoII recruitment in cells of the Drosophila posterior endoderm

(A) Left: a Drosophila embryo where the posterior endoderm is labeled in green and the lateral ectoderm in gray. Dashed box: the region of imaging. Red arrows: the directions of wave propagation and tissue invagination. Right: 3D cycle of cell deformation during wave propagation. In gray: three cells at different stages of the cycle. The numbers indicate the different steps of the cycle.

(B) High resolution image of MyoII during wave propagation. Top: a larger view of the propagation zone. Bottom: stills from a single cell over time. The boxed regions represent the approximate position of the cells at the bottom relative to the invaginating furrow. Yellow: the cell contours; white arrows: individual MyoII speckles typical of the slow recruitment phase. Scale bars, 5 μm.

(C) Time traces of MyoII mean intensity and cell area in cells of the propagation zone. Inset: a zoomed view of the MyoII time trace in the dashed box. Time 0 is the onset of rapid MyoII recruitment. Mean ± SEM, n = 37 cells, 3 embryos.

(D) Stills of a cell of the propagation zone at the stage of rapid MyoII recruitment. Scale bars, 5 μm.

(E) Kymograph of MyoII of the cell in (D). Scale bars, 5 μm and 1 min. Yellow arrows in (D) and (E), sequential events of MyoII recruitment just before local cortex detachment.

(F) Kymograph heatmap of MyoII mean intensity in cells during wave propagation. n = 37 cells, 3 embryos. Cells were registered in time as in (C) and in space by positioning their posterior boundary (P-boundary) at x = 0 at time t = 0 (see also Figure S1F).

Although this model explains how MyoII contractility is linked to anterior tissue flow, several questions remain unanswered. It is unclear how MyoII activation occurs in contact with the vitelline membrane and how integrins regulate this. It is also unclear how MyoII contractility interacts with integrin adhesion to the vitelline membrane to detach the cells and relay the cycle. To address these questions, here, we studied the detailed dynamics of MyoII and integrin recruitment in contact with the vitelline membrane and how the cycle of cell attachment/detachment to it mediates wave propagation.

Results

A subcellular wave of MyoII propagates within cells

To better characterize MyoII recruitment during wave propagation, we imaged cells of the Drosophila posterior endoderm at high spatial and temporal resolution. We used the actin-binding domain of utrophin (Utr-ABD) or Gap-43, to label F-actin or cell membranes, respectively, and visualized MyoII with a MyoII regulatory light chain (MRLC) fused to mCherry or EGFP. We observed two phases of MyoII recruitment in cells. First, at a 1–2 cell distance from the furrow when cells adhered to the vitelline membrane, we observed MyoII recruitment at low levels (Figures 1B, 1C, and S1A; Video S1). This phase was characterized by the appearance of transient MyoII pulses across the entire apical surface of the cell (Figures 1B and S1B; Video S1). Then, when cells were near the advancing border of the invaginating furrow, MyoII recruitment significantly accelerated (Figures 1C and S1A), accumulating in discrete bright clusters at the posterior of the cell just before local detachment from the vitelline membrane (Figures 1D and 1E; Video S2). Several clusters appeared per cell as the cell detached (Figures S1C and S1D), first near the cell posterior and then more anteriorly, indicating that high MyoII recruitment propagates inside the cell (Figures 1D and 1E; Video S2).

Video S1. High spatiotemporal resolution imaging of MyoII in cells of the propagation zone, related to Figure 1

Scale bar 5 μm. Time is in mm:ss.

Video S2. MyoII wave propagation inside cells of the posterior endoderm, related to Figure 1

Scale bar 5 μm. Time is in mm:ss.

We tracked and registered cells in time and space (see STAR Methods and Figures S1E–S1G) and plotted the local mean intensity of MyoII as a function of time and distance from the posterior cell boundary at time 0 (Figures 1F and S1F). Using this representation, we visualized the intracellular propagation of MyoII in the fixed reference frame of the embryo and estimated its velocity to ∼6 μm/min, similar to the velocity of the tissue-level wave in the same frame of reference.³⁵

Thus, MyoII accumulation and cell detachment propagate within cells as a wave with kinetics similar to those of the tissue-level wave, suggesting that similar mechanisms underlie both, with the latter being a larger-scale manifestation of the former. We further investigated the mechanism driving this subcellular wave.

Integrin adhesion to the vitelline membrane immobilizes the apical actin cortex

Previous work suggested that cells engage in apical frictional coupling and adhesion to the vitelline membrane before activating MyoII.^35,42 We thus tested whether the medio-apical actin cortex adhered to the overlying immobile vitelline membrane before propagation of the intracellular wave of MyoII. The Utr(ABD) probe labeled F-actin filaments and concentrated actin forming bright spots in the medio-apical cortex⁴⁵ (Figures 2A and 2B). We tracked their movement in cells during wave propagation using the Kanade-Lucas-Tomasi (KLT) feature tracker algorithm.^45,46,47 We found that before cell spreading onto the vitelline membrane, actin filaments and bright spots moved anteriorly together with cell boundaries (Figures 2A and 2C, upper part of the kymograph) and displayed an average positive velocity of 3.37 ± 0.04 SEM μm/min (Figure 2E). Subsequently, upon spreading onto the vitelline membrane and before cell detachment, actin filaments and bright spots significantly slowed down (Figures 2B and 2C, bottom part of the kymograph) and displayed an average velocity of 0.47 ± 0.05 SEM μm/min (Figure 2E), indicating an immobilization of the apical actin cortex. The intracellular wave of MyoII appeared after contact with the vitelline membrane and propagated across the immobilized actin cortex (Figure 2C).

Figure 2.

Actin cortex immobilization and integrin recruitment during wave propagation

(A and B) Apical actin cortex before (A) and after (B) spreading onto the vitelline membrane. Left: top and side views of a tracked cell. Yellow: cell contour. Bottom: snapshots of the boxed regions at 20-s intervals. Colored arrowheads: individual actin particles followed over time. Right: time projection over 80 s of the boxed regions. Semi-transparent colored lines: trajectories of the tracked actin particles. Scale bars: 5 μm in top views and max projections, 2 μm in side views, and 3 μm in the snapshots at the bottom.

(C and D) Kymographs of F-actin (in gray) and MyoII (in green) along the posterior-anterior (PA) axis in a WT (C) and a αPS3 RNAi-injected embryo (D). Yellow: A- and P-boundaries of the cell. White semi-transparent lines: traces of actin particles. Scale bars, 5 μm and 2 min.

(E and F) Heatmap kymographs of actin particle velocities for WT (E) and αPS3 RNAi-injected embryos (F). Particle velocities are measured in the referential of the embryo, and the data are plotted relative to the moving P-boundary of the cell. Dashed oval region: region where velocities are close to 0. n = 37 cells, 3 WT embryos, and 76 cells, 4 αPS3 RNAi embryos.

(G and H) Stills of βPS (G) and Talin (H) in the posterior endoderm during wave propagation. Top: larger scale view. Middle: stills on a single cell over time. Yellow: cell contours. White arrows: medio-apical puncta forming focal complexes. Bottom: kymographs along the PA axis of individual cells. White arrows: immobile puncta forming focal complexes (in white boxes). Yellow: the A- and P-boundaries of the cell. Scale bars: 5 μm in large views, 3 μm in bottom stills, and 5 μm and 2 min in kymographs.

(I and J) Time traces of cell area and the number of βPS puncta per cell (I) or their total integrated intensity (J). Mean ± SD. n = 25 cells, 2 embryos.

In (E), (F), (I), and (J), time 0 is the time of wave activation (rapid MyoII recruitment).

The immobilization of the actin cortex prior to MyoII recruitment is reminiscent of the formation and maturation of nascent adhesions by integrins during cell migration.³⁷ To test whether integrin-mediated adhesion to the vitelline membrane immobilized the apical cell cortex, we depleted by RNAi the αPS3 integrin, which is involved in the adhesion of the posterior endoderm to the vitelline membrane.^35,42 The pattern of cell movement (Figure 2D) and, consequently, of the actin particle velocities changed (Figure 2F). Consistent with previous findings,³⁵ in αPS3 RNAi embryos, cells first moved rapidly toward the anterior, failed to immobilize against the vitelline membrane, and eventually moved backward toward the invaginating furrow (Figures 2D and 2F). The actin filaments and bright spots moved together with the cell and displayed strong negative velocities (i.e., directed posteriorly), indicating that in the absence of αPS3, the cortex is not immobilized. We conclude that the actin cortex immobilization prior to propagation of the intracellular MyoII depends on integrin-mediated adhesion to the vitelline membrane.

We then analyzed the dynamics of integrins and of integrin-associated proteins (IAPs). In Drosophila, the βPS integrin is the main β-integrin and is the only one present in the embryo during gastrulation.⁴⁸ βPS forms complexes with all of the 5 α subunits present in the Drosophila genome.⁴⁹ In the embryo, βPS and Talin, an essential IAP present nearly at all stages of integrin adhesion formation and maturation,^37,38,50,51 are ubiquitous and deposited maternally^52,53 while only 3 of the 5 α subunits are expressed in restricted dorsal and ventral regions during gastrulation⁵² (Figure S2A). To visualize integrins, we used knockin lines of βPS and of Talin fused to EGFP⁵⁴ and Y-Pet,⁵⁵ respectively. We found that βPS accumulated in bright intracellular vesicles and at the plasma membrane in bright puncta, reminiscent of focal complexes,³⁷ only in a dorsal posterior region where αPS3 is expressed (Figure S2B). Elsewhere, βPS remained in faint intracellular structures resembling the endoplasmic reticulum (ER), suggesting that delivery to the cell surface is blocked, as expected from a missing α chain. Similarly, Talin showed a cortical accumulation in bright puncta only in cells of the same dorsal posterior region, while elsewhere it was found in the cytoplasm (Figure S2C). This suggests that during gastrulation, βPS forms functional integrin heterodimers involved in substrate adhesion only where αPS3 is expressed. Indeed, in αPS3 RNAi embryos, βPS lost its plasma membrane localization in puncta (Figure S2D). We conclude that αPS3 is necessary to form focal complexes in the posterior endoderm where the wave of MyoII and cell invagination propagates.

To quantitatively analyze focal complex dynamics during wave propagation, we imaged the apical planes of cells in contact with the vitelline membrane at high spatial and temporal resolution. We found that as cells spread their apical surface onto the vitelline membrane, they formed medio-apical puncta of βPS and Talin that were immobile in the referential of the vitelline membrane (Figures 2G and 2H; Video S3). The number of βPS puncta increased more than 10-fold over time before cell detachment (Figure 2I), while their average size and their average intensity increased less (2- to 3-fold, Figure S2E). Thus, the global increase in total integrated βPS intensity (Figure 2J) mostly stemmed from an increase in the number of puncta (Figures 2I and S2E).

Video S3. βPS and Talin accumulation in medio-apical focal complexes in cells of the propagation zone, related to Figure 2

Scale bar 5 μm. Time is in mm:ss.

We conclude that apical cell adhesion to the vitelline membrane is organized in focal complexes, whose number increases over time. This immobilizes the underlying actin cortex before activation of the intracellular wave of MyoII.

MyoII activation occurs in contact with the vitelline membrane and depends on integrins

To better understand how MyoII propagates as a wave inside cells, we analyzed how and when MyoII accumulates with respect to cortex adhesion to and detachment from the vitelline membrane. Qualitative observations from top and side views (Figure 3A) showed that during wave propagation MyoII clusters appeared in contact with the vitelline membrane and became brighter upon cell detachment (Figures 3A and S3B). This suggested that MyoII recruitment might be induced in contact and might further increase upon detachment from the vitelline membrane. A local change in MyoII concentration depends on two processes: (1) the transport by advective flows due to cortex contraction of MyoII mini-filaments bound to the actin cortex and (2) the net association/dissociation of MyoII mini-filaments to the actin cortex from the cytoplasmic pool (here called MyoII activation rate, R_MyoII, which captures turnover and Rho pathway-mediated recruitment). To disentangle the contribution of these two effects, we imaged F-actin together with MyoII. We locally measured the MyoII intensity and used KLT to determine the velocity of the actin cortex (see STAR Methods). These measurements allowed us to determine the local rates of MyoII concentration, MyoII advection, and R_MyoII, using mass conservation^34,56 (Figure 3B).

Figure 3.

Integrin-dependent MyoII activation in contact with the vitelline membrane

(A) Top and side views of MyoII propagation in a cell. White arrows: foci of MyoII initial recruitment in contact with the vitelline membrane. Yellow: cell contours. Scale bars, 5 μm.

(B) Equation of local mass balance for MyoII in a coarse-grained moving piece of cortex. The contributions of MyoII activation (R_MyoII) and advection are stated explicitly. The cartoons represent a change in MyoII local concentration by advection with cortex contraction (left) or by the turnover rate of MyoII mini-filaments binding to the cortex (right).

(C) Spatial profiles of MyoII rates with the distance of the apical cortex from the vitelline membrane in WT cells (cortex apico-basal position). Mean ± SD. n = 3 embryos (37 cells).

(D) Top and side view of MyoII during wave propagation in a cell. The zones in contact with and detachment from the vitelline membrane (VM) are indicated.

(E) Stills of MyoII and E-cad in a control (water injection) and a αPS3 RNAi embryo during wave propagation. Scale bars, 5 μm.

(F) Heatmap kymographs of MyoII mean intensity in the indicated conditions. Data are plotted relative to the moving P-boundary of the cells. n = 96 cells, 5 control (water injection) embryos and n = 76 cells, 4 αPS3 RNAi embryos.

(G and H) Spatial profile of MyoII rates with the distance of the apical cortex from the vitelline membrane, in grey (G) and actin cortex deformation rate (H) in the indicated conditions. In (H), a negative rate indicates local contraction. Mean ± SD. n = 5 embryos (96 cells) for control (water injection) and n = 4 embryos (76 cells) for αPS3 RNAi.

(I) Cartoon of the spatial distribution of the indicated MyoII rates in a cell during wave propagation. VM, vitelline membrane.

In (C), (G) and (H), dashed line, cortex detachment; gray box, region of cortex disappearance from the field of view where measurements are less reliable.

We mapped these quantities within cells during wave propagation and correlated their local distribution with the contact to the vitelline membrane (Figure 3C). We found that MyoII advection and activation spatially segregate and contribute to MyoII concentration in different regions of the cell. In more anterior regions, where the actin cortex is in contact with the vitelline membrane, R_MyoII dominated and contributed almost entirely to the rate of MyoII concentration (Figures 3C and 3D). More posteriorly, where the cortex was detached from the vitelline membrane, MyoII advection increased significantly and contributed to further increasing the MyoII concentration rate (Figures 3C and 3D) and MyoII levels (Figures S3A and S3B). This indicates that the MyoII wave propagates within the cell with a front that recruits new MyoII mini-filaments in contact with the vitelline membrane, followed by advection once the cortex detaches from it, which further increases MyoII concentration (Figure 3I). The time evolution of the MyoII rates in fixed regions of the cell cortex confirmed this. R_MyoII increased first when the cortex was still in contact with the vitelline membrane. Then, upon cortex detachment from the vitelline membrane, MyoII advection increased and further increased the rate of MyoII concentration (Figure S3E).

Since focal complexes respond to force^37,38,57 and regulate Rho signaling and MyoII contractility in other systems,^57,58,59 we next investigated how integrins regulate MyoII recruitment and the rates of advection/activation. As expected, depleting αPS3 by RNAi strongly reduced the levels of MyoII during wave propagation³⁵ (Figures 3E and 3F; Video S4), although to a lower extent compared with αPS3 null mutants (Figures S3F and S3G; Video S4), and did not increase cell-to-cell variability, compared with controls (see Figures S3H–S3J and STAR Methods). The rates of MyoII concentration, MyoII advection, and R_MyoII were also significantly reduced, compared with controls (Figure 3G). However, the rate of cortex deformation (the strain rate ∇v), which directly contributes to MyoII advection (−C_MyoII∇v, Figure 3B; STAR Methods), was not significantly different from that of controls (Figure 3H), indicating that the reduced MyoII advection and concentration rate stem from a lower initial recruitment of MyoII mini-filaments (which reduces C_MyoII and thus also MyoII advection and the concentration rate, Figure 3B). We thus conclude that depleting integrins primarily reduces R_MyoII in contact with the vitelline membrane.

Video S4. MyoII dynamics during wave propagation in αPS3 null mutants and RNAi-injected embryos, related to Figures 3 and S3

Scale bars 10 μm. Time is in mm:ss.

These results indicated that during wave propagation MyoII accumulation occurs by two distinct and spatially segregated mechanisms. First, integrins promote MyoII activation in contact with the vitelline membrane by a direct or an indirect mechanism (e.g., mechanical resistance to contraction or modulation of other mechanisms), and second, MyoII further accumulates by advection upon cortex detachment when the cortex contraction is no longer resisted by integrin adhesion (Figure 3I). Notably, upon cortex detachment, MyoII promotes its own accumulation in a positive feedback loop.³³

MyoII contractility controls focal complexes maturation and stability

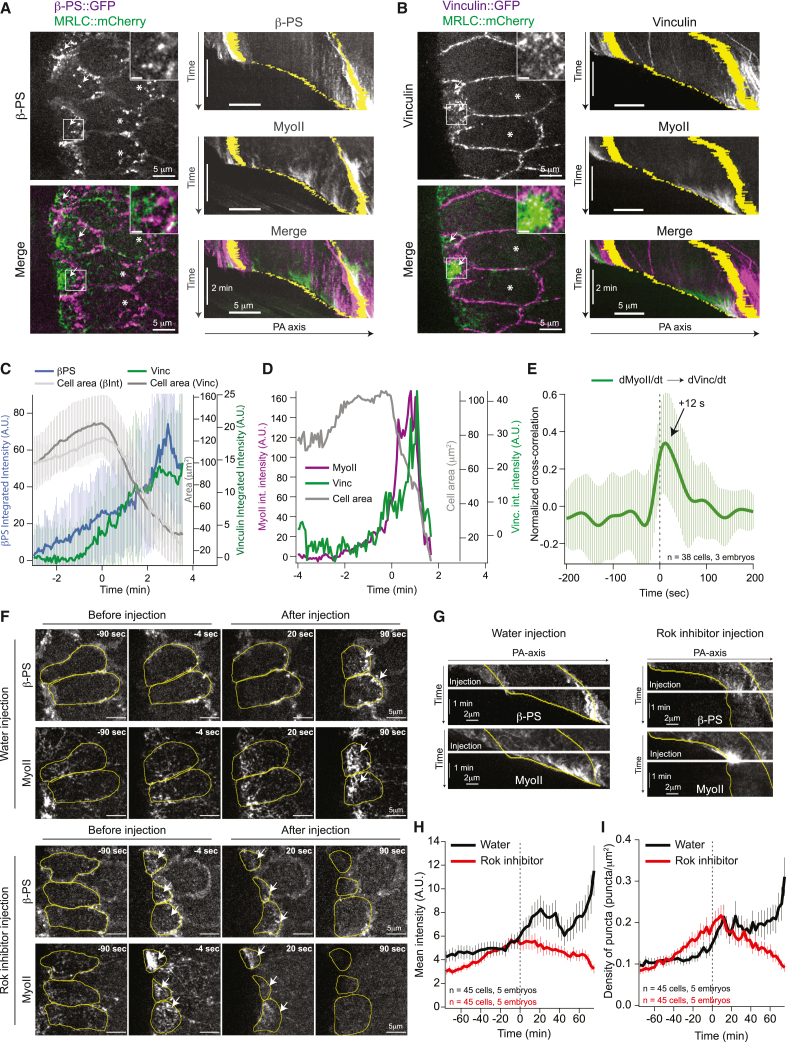
Since integrins respond to forces exerted by actomyosin contractility,^38,59,60 we next investigated whether MyoII contractility during wave propagation regulates focal complexes’ maturation and stability. We imaged MyoII, together with the βPS integrin, and observed that βPS accumulated in medio-apical puncta much earlier than the appearance of MyoII at high levels during intracellular wave propagation (Figures 4A, left and kymographs and S4A; Video S5, top). Interestingly, shortly before cortex detachment, MyoII clusters formed in proximity to βPS puncta and appeared connected to them, suggesting the MyoII clusters might be anchored to and might pull on the focal complexes (Figure 4A, inset; Video S5, top).

Figure 4.

MyoII contractility is required for integrin focal complex stabilization and maturation

(A and B) Stills (left) and kymographs (right) of βPS (A) and Vinculin (B) with MyoII during wave propagation. Left: grayscale (for βPS and Vinculin) and merge images; scale bars, 5 μm. Inset: zoom of the white box; scale bars, 1 μm. White arrows, cells at MyoII wave propagation stage. White asterisks, cells where MyoII increases slowly, and the intracellular wave has not yet been activated. Right: gray scale and merged kymographs. Yellow: A- and P-boundary of the cell. Scale bars, 5 μm and 2 min.

(C) Time traces of βPS (blue) and Vinculin (green) integrated intensity with their respective cell area (gray). Mean ± SD. For βPS, n = 25 cells (2 embryos) and for Vinculin, n = 42 cells (3 embryos).

(D) Time traces of the integrated intensity of MyoII (magenta) and Vinculin (green) with apical area (gray) in a cell.

(E) Average normalized cross-correlation between the time derivatives of the MyoII and Vinculin time traces. Mean ± SD. n = 38 cells (3 embryos).

(F) Stills of βPS and MyoII in cells of the posterior endoderm upon water and Rok inhibitor injection during wave propagation. Scale bars, 5 μm. Yellow, cell contours of selected cells; white arrows, accumulations of MyoII or integrin focal complexes.

(G) Kymographs along the PA axis of βPS and MyoII extracted from cells in (F). White line, time of injection; yellow lines, A- and P-boundaries of one cell. Scale bars, 2 μm and 1 min.

(H and I) Time traces of βPS mean intensity (H) and βPS density of puncta (I) in cells at wave propagation stage. Mean ± SEM, n = 45 cells (5 embryos) in both conditions.

In (C) and (D), time 0 is the onset of rapid MyoII recruitment. In (H) and (I), time 0 is the time of injection.

Video S5. Dynamics of βPS and Vinculin with MyoII in the medio-apical cortex during wave propagation, related to Figure 4

Scale bars 5 μm. Time is in mm:ss.

To test this possibility further, we imaged Vinculin, a protein recruited to focal complexes upon force during maturation to focal adhesions (FAs),^37,57,61,62 together with either βPS or MyoII. As expected, Vinculin labeled E-cad junctions,⁴⁰ but it also appeared in bright medio-apical puncta in contact with the vitelline membrane (Figure 4B; Video S5, bottom). These puncta represent bona fide Vinculin recruitment on pre-formed focal complexes under tension since, in contrast to βPS, their number and intensity increased only shortly before cell detachment at the time when MyoII appeared at high levels during intracellular wave propagation (Figures 4B, 4C, and S4B; Video S5, bottom), and they co-localized with βPS (Figure 4C). Furthermore, a positive cross-correlation of 0.34 ± 0.04 SEM between the rates of change of the total fluorescence intensity of Vinculin and MyoII with a time delay of ∼12 s indicated that a strong increase in Vinculin signal shortly followed a rapid increase in MyoII (Figures 4D and 4E).

These data suggest that MyoII contractility is required for focal complex maturation and stabilization. To test this directly, we blocked MyoII contractility by injecting a Rho kinase (Rok) inhibitor (H-1152) during wave propagation. This very rapidly reduced MyoII concentration at the cell cortex and arrested wave progression. It also affected the recruitment of βPS at focal complexes; βPS puncta faded away in both the cells at the edge of the furrow where the intracellular MyoII wave propagates (Figures 4F–4I; Video S6) and the more anterior cells where focal complexes form in contact with the vitelline membrane before the intracellular wave is activated (Figures S4D–S4F). We conclude that MyoII activity is required for the stabilization and maturation of focal complexes. Wave propagation is thus characterized by positive feedback between integrins and MyoII; integrins are required to activate MyoII, and in turn MyoII stabilizes integrin focal complexes. This positive feedback loop operates in contact with the vitelline membrane where MyoII contractility exerts shear stress on integrin complexes.

Video S6. Water and Rok inhibitor injection during wave propagation, related to Figures 4 and S4

Scale bar 5 μm. Time is in mm:ss.

Cortex detachment allows MyoII wavefront propagation and controls the duration of the integrin-MyoII feedback

Since the integrin-MyoII positive feedback operates in contact with the vitelline membrane, we next investigated whether the rate of detachment regulates the speed of the wave and the levels of MyoII and adhesion. We hypothesized that tensile forces, arising from cell contractility in the invagination, are transmitted to the anchoring point at the front of the invagination and promote cortex detachment (Figure 5A, left bottom diagram). We thus mechanically interfered with cell detachment in two ways. First, we mildly depleted α-catenin (α-Cat) in embryos by RNAi. This weakens the connections of the actomyosin cortex to E-cad junctions⁶³ and thus reduces force integration⁶⁴ and transmission to the anchoring point at the front of the furrow. Second, using laser-mediated tissue cauterizations,^65,66 we generated immobile mechanical fences 10–12 cells anterior to the moving furrow to introduce mechanical resistance to the movement of the furrow and to cell invagination.³⁵ In both cases, we observed a slower anterior progression of the invaginating front, compared with control embryos (Figures 5A and 5B; Video S7), associated with a slower detachment of the local cell cortex following local MyoII recruitment (Figures 5B, 5C, S5A, and S5B, gray curves). Interestingly, we observed that within single cells across different conditions the speed of cortex detachment highly correlated with the speed of the MyoII wave, as measured from kymographs (Figures 5B and 5D). This indicates that local detachment is required to propagate the MyoII wavefront within the cell, thus setting the pace of the wave.

Figure 5.

Reducing detachment speed reduces MyoII wavefront speed

(A) Top: tissue-level view of MyoII propagation in a WT (left), an α-Cat RNAi (middle), and an embryo with anterior fences (right). Bottom: illustrations of the forces involved in detachment of the cell at the front of the invaginating furrow in the conditions above. Green arrows, contractile forces; orange and blue arrows, adhesion and de-adhesion forces; black arrows, anterior movement; red arrows, resistive forces due to immobile fences; red dot, the point of cortex detachment. The dashed lines indicate a reduction of the speed of movement (black arrows) or force integration (green arrows), compared with WT.

(B) Kymographs along the PA axis of MyoII in a cell during wave propagation in the indicated conditions. Yellow, the A- and P-boundaries of the cell; white arrows, MyoII accumulations. The orange and cyan lines indicate the speed of the MyoII wavefront and the speed of cortex detachment, respectively. The yellow dashed line indicates the time of local cortex detachment following MyoII accumulation. Scale bars, 5 μm and 2 min.

(C) Local cortex detachment time following MyoII cluster accumulation. n = 161 events, 95 cells, 5 embryos for water injection; 185 events, 89 cells, 5 embryos for α-Cat RNAi; 113 events, 57 cells, 3 embryos for WT control; and 99 events, 45 cells, 3 embryos for anterior fence. ^∗∗∗p < 0.001 at a Mann-Whitney test.

(D) Scatterplot of the detachment vs. MyoII wavefront velocities measured as illustrated in (B). n = 116 cells (5 embryos) for water injection, 75 cells (5 embryos) for α-Cat RNAi, 57 cells (3 embryos) for WT control, and 45 cells (3 embryos) for anterior fence. The Pearson correlation coefficient is 0.85 with p < 0.001.

Video S7. MyoII wave propagation in α-Cat RNAi and embryos with anterior immobile fences, related to Figure 5

Scale bars 20 μm. Time is in mm:ss.

The increased time of contact with the vitelline membrane due to slower detachment is expected to prolong the activity of the integrin-MyoII positive feedback (Figure 6A). We then expected that in α-Cat RNAi and embryos with anterior fences, MyoII activation would be prolonged, leading to higher MyoII levels and increased accumulation of integrin in focal complexes. Consistent with a delayed detachment of the cortex (Figures 6B, S5A, and S5B, gray curves), we found that in both conditions R_MyoII, measured over time in a fixed region of the cortex, was similar to controls but remained positive for a longer time (Figures 6B, S5A, and S5B, green curves), explaining the observed higher levels of MyoII (Figures S5A and S5B). Importantly, this was integrin dependent, as depleting αPS3 by RNAi in both α-Cat RNAi-injected embryos (Figures 6C–6E; Video S8, left) and embryos with anterior fences (Figure S6; Video S8, right) significantly reduced the elevated levels of MyoII and R_MyoII to levels similar to those where only αPS3 was depleted (Figures 6C–6E and S6). We next tested if integrin accumulation in focal complexes also increased in α-Cat RNAi or embryos with anterior immobile fences. We imaged βPS together with MyoII, and we found that the local density of βPS and of the βPS-positive puncta increased (Figures 6F and 6G; Video S9). Interestingly, the average size and the average total intensity of the puncta also increased (Figures S5C and S5D), indicating that the focal complexes mature into larger structures reminiscent of FAs upon longer time of contact. This led to increased cell adhesion to the vitelline membrane as individual cells frequently resisted detachment inducing an irregular advancing furrow (Figure 6F; Video S9).

Figure 6.

Prolonging contact with the vitelline membrane increases the duration of the integrin-MyoII feedback

(A) Illustration of the integrin-MyoII positive feedback.

(B) Time evolution of the MyoII rates with the distance from the vitelline membrane (cortex AB position) in a fixed region of the cortex in the indicated conditions. n = 5 embryos (96 cells) for water injection, 5 embryos (89 cells) for α-Cat RNAi, and 3 embryos (47 cells) for anterior fence. Mean ± SEM.

(C) Stills of MyoII in the indicated conditions during wave propagation. Scale bars, 10 μm.

(D) Heatmap kymographs of MyoII mean intensity in the indicated conditions.

(E) Spatial profile of MyoII rates in the indicated conditions with the distance of the apical cortex from the vitelline membrane in grey (averaging time window 0–3 min for WT and αPS3 RNAi and 0–6 min for α-Cat and α-Cat + αPS3 RNAi). Dashed lines: cortex detachment. Gray boxes: region of cortex disappearance from the field of view where measurements are less reliable. In (D) and (E), data are plotted relative to the moving P-boundary of the cells. n = 96 cells, 5 control (water-injected) embryos; 76 cells, 4 αPS3 RNAi embryos; 89 cells, 5 α-Cat RNAi embryos; and 104 cells, 5 α-Cat + αPS3 RNAi embryos. In (E), mean ± SD.

(F) Stills of βPS and MyoII during wave propagation in the indicated conditions. Gray scale for βPS and merge images are shown. Dashed white line: the border of the invaginating furrow. Scale bars, 5 μm.

(G) Time traces of MyoII mean intensity (top), βPS mean intensity (middle), and the density of βPS puncta (bottom) in WT (light green and light orange) and embryos with anterior fences (AF, dark green and dark orange). n = 52 cells from 3 WT embryos and 49 cells from 5 embryos with anterior fences. Mean ± SD.

In (B), (D), and (G), time 0 is the time of wave activation (rapid MyoII recruitment).

Video S8. MyoII wave propagation in α-Cat RNAi or embryos with anterior fences depleted or not of αPS3, related to Figures 6 and S6

Scale bars 5 μm. Time is in mm:ss.

Video S9. βPS and MyoII propagation in α-Cat RNAi and embryos with anterior immobile fences, related to Figure 6

Scale bars 5 μm. Time is in mm:ss.

We conclude that local cortex detachment allows MyoII wavefront propagation and controls the duration of the integrin-MyoII feedback activation mechanism.

The angle of detachment changes according to the adhesion strength and modifies de-adhesion tensile forces

Cortex detachment plays a key role in wave propagation as it regulates the speed of the MyoII wavefront and the duration of the integrin-MyoII feedback. We thus investigated how detachment is controlled from the standpoint of the local forces causing integrin de-adhesion from the vitelline membrane and considered the role of tissue geometry (Figure 7A). At the apical surface in contact with the vitelline membrane, MyoII contractility exerts shear forces on integrins that reinforce focal complex formation and maturation^67,68 (Figure 7A). On the contrary, MyoII contractility in the furrow and the detached posterior part of the cell, which is at an angle θ from the vitelline membrane (Figure 7A), exerts tensile forces that might cause de-adhesion of integrins and, consequently, cell detachment. We speculate that only the normal component of the tensile forces exerted on integrins (F sin θ) induces de-adhesion. De-adhesion then occurs when these tensile forces exceed a threshold set by the strength of integrin adhesion. Assuming a constant contractile force, increasing or decreasing adhesion by integrins is expected to change the angle θ at which de-adhesion occurs (higher angle for stronger adhesion). To test this, we measured the detachment angle θ during wave propagation in conditions where we modulated adhesion to the vitelline membrane. αPS3 RNAi, which reduces adhesion, significantly reduced the detachment angle θ, compared with controls (Figures 7B and 7C). Conversely, α-Cat RNAi and anterior immobile fences, which increased the duration of the integrin/MyoII positive feedback and thereby adhesion (Figures 6F and 6G), significantly increased the angle θ relative to controls (Figures 7B and 7C). Furthermore, depleting αPS3 in α-Cat RNAi embryos significantly reduced the angle θ, compared with α-cat RNAi embryos, to levels similar to αPS3 RNAi alone (Figures 7B and 7C). Thus, the angle θ of detachment changes with the levels of adhesion to the substrate, indicating that tensile forces due to MyoII contractility in the invaginating furrow oppose integrin adhesion to the vitelline membrane to induce cortex detachment during wave propagation.

Figure 7.

The angle of detachment changes according to the adhesion strength

(A) Illustration of the forces acting at the site of detachment. Blue arrow, de-adhesion force due to MyoII contractility in the invaginated furrow and the detached side of the cell; red dot, the site of detachment; orange arrow, adhesion force. Inset: increasing the angle θ increases the vertical component F sin θ for a given de-adhesion force.

(B) Side views of cells during wave propagation in the indicated conditions. Labeling: F-actin. Yellow vertical lines: A- and P-cell boundaries as detected from cell segmentation of corresponding top views. Scale bars, 5 μm.

(C) Average detachment angle θ in the indicated conditions. n = 95 cells (5 embryos) for water injection control, 85 cells (5 embryos) for α-Cat RNAi, 76 cells (4 embryos) for αPS3 RNAi, 60 cells (5 embryos) for α-Cat + αPS3 RNAi, 98 cells (6 embryos) for WT control, and 47 cells (3 embryos) for anterior fence. ^∗∗∗p < 0.001 and n.s. p > 0.05 at a Mann-Whitney test.

(D) Side views from a time lapse of cell detachment in a WT embryo. Labeling: F-actin. Scale bars, 5 μm. The white dots and dashed line indicate the movement of the invaginated furrow. The orange dots and dashed line indicate the movement of the detachment point.

(E) Time traces of the angle θ (red) and the speed of the detachment point along the PA axis (black) of the cell in (D). The thick lines are smoothed time traces, and the thin semi-transparent lines are the actual measurements from time lapse.

(F) Average normalized cross-correlation between the time derivatives of the detachment speed and the angle θ time traces. Mean ± SD. n = 92 cells, 5 WT embryos.

(G) Apical view of the detaching invagination front in a WT embryo labeled with βPS::GFP. Scale bars, 5 μm. White dashed line: detachment front. Yellow horizontal line: example of horizontal line used to measure the speed of the detachment front and the local βPS intensity (see STAR Methods).

(H) Representative smoothed time traces of the local βPS mean intensity (red) and the detachment front velocity along the PA axis (black).

(I) Average normalized cross-correlation between the time derivatives of the detachment point speed and the local βPS intensity time traces. Mean ± SD. n = 24 lines, 5 WT embryos.

(J) Illustration of the mechanochemical feedbacks recruiting MyoII during wave propagation.

(K) Illustration of the change in the detachment angle θ according to different levels of adhesion force. Examples of the conditions showing these effects are listed.

We next studied how fluctuations in adhesion densities in the wild-type (WT) impacted the detachment angle θ during wave propagation. Since integrin adhesion is organized in discrete focal complexes where integrins concentrate, we expected that the detachment angle θ fluctuates and increases in front of sites of stronger adhesion (i.e., with more focal complexes). We measured the angle θ over time in WT embryos and found that it fluctuated during cell detachment (Figures 7D and 7E). θ increased when the local speed of detachment decreased, as shown by the negative cross-correlation of −0.30 ± 0.02 SEM between their time derivatives (Figure 7F). Although the detachment speed was on average similar to the speed of anterior motion of the basal furrow, it fluctuated more (Figures 7D and S7A–S7D), and transient mismatch between the two speeds highly correlated with the change in angle θ (Figures S7E and S7F). The difference in the fluctuations between these two velocities decreased when depleting αPS3 (αPS3 RNAi alone or together with α-Cat RNAi, Figure S7D), suggesting that variations in the speed of detachment might be linked to heterogeneities in integrin adhesion to the vitelline membrane. To test this directly, we measured the correlation between the local speed of detachment, measured as the speed of the furrow movement in the most apical sections in contact with the vitelline membrane, and the local βPS intensity, and we found that on average the speed of detachment decreased when the local βPS intensity increased (Figures 7G–7I).

We showed that the angle of cell detachment from the vitelline membrane changes according to experimentally induced or naturally occurring variations in the strength of integrin adhesion. Altogether, we conclude that tissue geometry, namely the angle of the furrow at the point of contact with the vitelline membrane, is a tuning parameter that allows cell detachment to occur for a large range of adhesion strength, thereby sustaining wave propagation.

Discussion

Tissue morphogenesis results from both deterministic mechanisms and self-organized dynamics through feedbacks and local interactions.⁶ This is well illustrated by the morphogenetic wave of tissue invagination in the Drosophila embryo.³⁵ Initiation of the wave is determined by a genetically controlled invagination in the endoderm primordium³⁵ and by its interplay with egg curvature that gives rise to a polarized flow.⁴⁴ Instead, wave propagation is self-organized and involves a mechanochemical feedback and interactions with the vitelline membrane.^35,42 However, how tissue-level wave propagation emerges from the local interaction between MyoII contractility and adhesion to the vitelline membrane and how cell detachment is regulated were unclear. We now characterized the detailed subcellular mechanisms underlying the tissue-scale wave and reveal a tight interplay between MyoII contractility, integrin adhesion, and apical membrane geometry in this process.

We found that MyoII contractility and cell detachment from the vitelline membrane propagate as coupled waves within cells and not simply from one cell to the next within the tissue, as previously reported.³⁵ Thus, the tissue-scale wave originates from a subcellular mechanochemical process that occurs within the cell cortex and propagates to the next cell as it does within the cortex of a given cell. As such, compartmentalization into cells is not key to understanding this process and a continuum mechanical description suffices, as for other processes in the embryo.⁶⁹ Within the cell, two distinct mechanochemical feedback mechanisms regulate the MyoII wave (Figure 7J). A first mechanism operates at the wavefront in contact with the vitelline membrane and leads to recruitment of new MyoII mini-filaments in an integrin-dependent manner (Figure 3). In turn, MyoII contractility stabilizes integrin focal complexes (Figure 4), thus forming a positive feedback loop that amplifies MyoII activation and adhesion. This is similar to the mutual regulation between integrins and actomyosin contractility in mammals, where integrins regulate Rho signaling and MyoII^57,58,59 and in turn respond to shear forces exerted by actomyosin contractility.^{38,59,60,67,68} However, it also presents some key differences. In vertebrates the FA kinase (FAK) is critical for FA maturation and mediates signal transduction from integrins, which modulates Rho signaling and actomyosin contractility.^58,70,71 Instead, Drosophila fak null mutants are viable and show only minor defects.^72,73,74 Thus, in Drosophila, FAs mature differently and integrins might promote MyoII activation via different mechanisms, such as regulation of other signaling pathways⁵² or mechanical feedback involving the coupling with the cortical actomyosin network.⁷⁵ After cortex detachment, MyoII further concentrates by advection with the contracting actin cortex. Since MyoII drives cortex contraction and its own advection with the upstream regulators Rho1 and Rok,³³ a second positive feedback loop operates after cortex detachment, which further accumulates MyoII. Interestingly, these two feedback mechanisms are spatially and temporally segregated, reflecting sequential adhesion to (first positive feedback) and de-adhesion from (second positive feedback) the vitelline membrane during wave propagation (Figure 7J).

Our results also illustrate the impact of the system’s geometry on wave propagation. First, the state of contact with the vitelline membrane (in contact or not) defines whether MyoII locally accumulates by recruitment of new mini-filaments or by cortex advection (Figure 7J). Thus, the local geometry (in contact or not with the vitelline membrane) instructs the local mechanochemistry of MyoII accumulation. Second, the rate of cell detachment defines the overall levels of MyoII and adhesion to the substrate by defining the duration of the integrin-MyoII feedback. Notably the rate of wave propagation relies on the strength of adhesion to the vitelline membrane. Too strong adhesion slows down detachment and generates a vicious cycle by prolonging the duration of the integrin-MyoII feedback, which could stall wave propagation. Too weak adhesion fails to sustain the anterior movement of the invaginating furrow and to activate sufficient levels of MyoII. In WT Drosophila embryos, intermediate levels of integrin adhesion allow for persistent anterior propagation of the invagination wave at an optimal rate. Interestingly, this is different from Tribolium where very strong adhesion to the vitelline membrane leads to a fixed anchorage point and no wave propagation.⁴² Third, we propose that the tissue geometry offers another level of control through the local angle of detachment and the tensile de-adhesion forces (Figure 7K). Changes of the angle in front of sites of strong/weak adhesion allows for modulating the detachment force, thus sustaining wave propagation in spite of fluctuating levels of integrins due to the discrete nature of FAs. Altogether, our results illustrate how mechanochemical and geometrical feedbacks integrate locally to regulate cell and tissue dynamics.

Our work also sheds light on the role of integrin adhesion in morphogenesis. Indeed, integrins are required for the morphogenetic wave in multiple ways. First, they facilitate initiation of the wave through the formation of a deep invagination. The frictional coupling to the vitelline membrane resists the initial anterior flow of the tissue that emerges from tissue curvature⁴⁴ and thereby contributes to the formation of an invagination by tissue buckling. Second, integrin adhesion sustains wave propagation directly by amplifying MyoII activation at the cell cortex through a mechanochemical feedback. The interplay between integrin adhesion and contractility in this morphogenetic process bears interesting similarities with cell motility. Indeed, cell motility and wave morphogenesis in Drosophila both require the cyclic interplay between adhesion, MyoII activation, and de-adhesion. However, in contrast to cell migration on 2D substrates, during wave propagation the retrograde actin flow is not due to actin nucleation at the front of the cells but rather it is a retrograde flow of cells (and of their actin cortex) due to a gradient of contractility that peaks in the posterior invagination. This is similar to retrograde actin flow in confined 3D amoeboid cell motility^76,77 but occurs at the scale of the tissue. In the absence of integrins, posterior contractility in the invagination drives a retrograde flow of cells and their apical actin cortex toward the posterior (Figure 2D), which cannot produce any anterior movement because of the absence of adhesion/friction. In the WT, integrin adhesion couples this tissue-level retrograde flow to the vitelline membrane and thereby causes forward movement. Importantly, the region of integrin-based adhesion to the vitelline membrane propagates also as a wave toward the anterior, due to the attachment/detachment cycle that we report here. If integrin adhesion was irreversible, forward movement would be stalled and wave propagation would be blocked. Sustained forward movement is thus ensured by the fact that adhesion itself is locally transient through cell detachment.

This study exemplifies how large-scale tissue dynamics emerge from the interplay of cell mechanochemical processes and cell geometry.

Limitations of the study

One limitation of our study is that it does not allow for determining whether integrins promote activation of MyoII by a chemical or mechanical mechanism. It is unlikely that they activate MyoII through a direct modulation of Rho signaling, as we do not find a strict spatiotemporal correspondence between the appearance of MyoII clusters with that of integrin focal complexes. Furthermore, in integrin null mutants, MyoII is still activated, although at low levels (Figures S3F and S3G). Other factors such as signaling from G protein-coupled receptors (GPCRs) might be involved in activating MyoII, and integrins might tune/amplify receptor surface availability or signaling activity during wave propagation. Further studies to dissect the respective roles and the interactions between integrins and other signaling modules will be required to elucidate this.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
H-1152 dihydrochloride	Enzo Lifesciences	ALX-270-423
Critical commercial assays
SureClean Plus	Bioline	BIO-37074
RiboMAX Large Scale RNA Production System	Promega	Cat #P1300
Experimental models: Organisms/strains
D.melanogaster: sqh-MRLC::mCherry[VK18]	Bailles and Collinet et al.35	N/A
D.melanogaster: sqh-MRLC::mCherry[VK27]	Garcia De Las Bayonas et al.78	N/A
D.melanogaster: sqh-MRLC::eGFP	Gift from R Karess, Institut Jacques Monod	N/A
D.melanogaster: sqh-Utr(ABD)::GFP	Dehapiot et al.45	N/A
D.melanogaster: UASp-Gap43::mCherry	Guillot and Lecuit80	N/A
D.melanogaster: E-cad::EGFPKin	Bloomington Drosophila Stock Center	BL_60584
D.melanogaster: mys::EGFPKin	Klapholz et al.54	N/A
D.melanogaster: rheaI-Ypet	Lemke et al.55	N/A
D.melanogaster: sGFP::Vinculin	Kale et al.40	N/A
D.melanogaster: mCherry::Vinculin	Kale et al.40	N/A
D.melanogaster: P{GAL4-nos.NGT}A	Bloomington Drosophila Stock Center	BL_32563
D.melanogaster: scabKO	This paper	N/A
Oligonucleotides
Primers for cloning and sequencing, see Table S2	This paper	N/A
Software and algorithms
ImageJ	National Institutes of Health	https://imagej.nih.gov/ij/, RRID: SCR_003070
Tissue Analyzer	Aigouy et al.84	https://github.com/baigouy/tissue_analyzer
Stack Focuser	Michael Umorin	https://imagej.nih.gov/ij/plugins/stack-focuser.html
Metamorph	Molecular Devices	https://www.moleculardevices.com, RRID: SCR_002368
Matlab	Mathworks	https://www.mathworks.com, RRID: SCR_001622
Ilastik (v. 1.3.3)	Berg et al.83	https://www.ilastik.org, RRID: SCR_015246
IgorPro (v6.3 or 9)	Wavemetrics	https://www.wavemetrics.com, RRID: SCR_000325
Custom Image analysis software	This paper	https://doi.org/10.5281/zenodo.10021680

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Thomas Lecuit (thomas.lecuit@univ-amu.fr).

Material availability

Plasmids, FASTA sequences and transgenic fly lines generated in this study are all available on request.

Data and code availability

All data supporting the findings of this study are available within the paper and the source data file (Data S1). Raw image data will be shared by the lead contact upon request. All original code to measure the MyoII rates and detect MyoII recruitment events is available at Zenodo. The DOI is listed in the key resources table.

Experimental model and study participants details

The experiments were performed on Drosophila melanogaster embryos. The adult flies were maintained under standard laboratory conditions in plastic vials at 18°C, 22°C or 25°C with standard fly food. Embryo collection was performed in fly cages with apple juice agar plates, supplemented with yeast paste. For technical reasons it was not possible to determine the sex of the analyzed embryos. Please refer to the key resources table for the details of the fly lines used.

Method Details

Fly strains

All fly insertions used in this study are listed in the key resources table. Fly lines carrying following insertions and alleles were used: live cell imaging of MyoII Regulatory Light Chain (MRLC) (encoded by the gene spaghetti-squash, sqh, FlyBase ID: FBgn0003514) was carried out using either sqh-MRLC::mCherry (either inserted on chromosome 2 at the VK18 [53B2] site³⁵ or inserted at the VK27 [89E11] site⁷⁸ on chromosome 3) or sqh-MRLC::EGFP on chromosome 2 (gift from R. Karess). F-actin was visualized using a sqh-Utr(ABD)::GFP insertion on chromosome 3.^45,79 Ubiquitous expression of a UASp-Gap43::mCherry insertion on chromosome 3 was used to visualize the plasma membrane⁸⁰ and was driven using a nanos-Gal4. E-cadherin (shg in Drosophila, FlyBase ID: FBgn0003391) was visualized using E-cad::EGFP^Kin, an EGFP knock-in allele at the locus generated by homologous recombination.⁸¹ β-PS is the main β-Integrin in Drosophila and it is encoded by the gene myospheroid (mys, FlyBase ID: FBgn0004657). Live imaging of β-PS was carried out using mys::EGFP^Kin an EGFP knock-in allele of myospheroid at the locus.⁵⁴ Talin is encoded by rhea (FlyBase ID: FBgn0260442) in Drosophila and a Y-Pet knock-in allele in exon 6 (Talin^I-Ypet)⁵⁵ was used for live imaging. Vinculin was visualized using an sGFP::Vinculin or an mCherry::Vinculin fosmid insertions on Chromosome 3 at the ATTp-2 landing site or Chromosome 2 at the ATTp-40 respectively.⁴⁰ The null mutant for αPS3 (scab, CG8095, FlyBase ID: FBgn0286785), scab^KO, was generated in this study.

All used fly strains are listed in Table S1.

RNA interference and drug injections

Embryos were collected from fresh agar plates in cages kept at 21-22°C and flies were allowed to lay eggs for 0.5-1h. Embryos were then dechorionated in bleach (3.2%), rinsed and aligned on coverslips covered with heptane-glue. After a few minutes of desiccation, embryos were covered with Halocarbon 200 oil and injected with dsRNAs, RNase-free water or chemical inhibitors. Post-injection embryos were stored at 22°C until live imaging. Injections were performed at 50–80% embryo length from the posterior and on the lateral side in all experiments in this paper.

dsRNA probes directed against αPS3 (scab, CG8095, FlyBase ID: FBgn0286785) and α-Catenin (aCat, CG17947, FlyBase ID: FBgn0010215) were made using PCR products containing the sequence of the T7 promoter (TAATACGACTCACTATAGGG) followed by 18-21 nucleotides specific to the gene. The dsRNA probes against scab and aCat target nucleotides 2652–3101 of the scab-RB, (Flybase ID: FBtr0087369) and nucleotides 101–828 of aCat-RA (Flybase ID: FBtr0070038) transcripts, respectively. The sequences of the primers used to generate the dsRNA probes are listed in Table S2. PCR products purified from gels were subsequently used as a template for the in vitro RNA synthesis with the T7 polymerase using Ribomax (Promega, P1300). The dsRNA probes were purified using Sure-Clean Plus (Bioline, BIO-37047) and were diluted in RNAase free water for injection at a final concentration of 5 μM in embryos less than 1 h old. Cell-to-cell and embryo-to-embryo variability in dsRNAs injected embryos (αPS3 RNAi) was measured and compared to control conditions (water injections, Figures S3H–S3J). We found that, for all RNAi injected embryos, the average MyoII levels (integrated intensity) after wave activation (averaging time window 0-3mins) were more than 3 folds below the average value of control embryos (water injection). In 84% of the cells from RNAi injected embryos MyoII levels were below the mean – 1SD of the water injected controls (Figure S3H). The standard deviation (SD) between cells within individual embryos was lower in αPS3 RNAi compared to water injection controls (Figure S3I) and the ratio of the SDs between cells and the SD between embryos was similar between RNAi and water injected controls (Figure S3J, p>0.05 at a Mann-Whitney test), indicating that the RNAi did not introduce significant additional difference between the cell-to-cell and the embryo-to-embryo variability.

The Rho kinase (Rok in Drosophila, FlyBase ID: FBgn0026181) inhibitor H-1152 (Enzo Lifesciences) was injected at a concentration of 40 mM in embryos at stage 7 during time lapse using an InjectMan4 micromanipulator and a FemtoJet 4i microinjector from Eppendorf directly installed on the microscope.

The dilution factor in the embryo is typically 1:50 so we expect a final concentration of 800 μM for the H-1152 inhibitor and 100 nM for the dsRNA probes.

Generation of the scab^KO allele

The scab^KO allele was generated by CRISPR/Cas9 gene editing (performed by Wellgenetics, Taiwan). The entire ORF and a part of the 5’ and 3’ UTRs were deleted (from -281 nt to +8,670 nt from ATG of the scab-RB transcript FlyBase ID: FBtr0087369) and replaced by an attP-3xP3-RFP selection marker cassette containing: forward attP (49bp) and a floxed 3xP3-RFP selection marker which has been flipped out by Cre recombinase in a second step. Deletion was verified by genomic PCR and Sanger sequencing. This scab^KO allele is a null allele of αPS3 and flies are not homozygous viable and maintained over CyO balancer.

For the comparison of αPS3 RNAi and αPS3 KO phenotypes (Figures S3F and S3G), embryos from heterozygote mothers; scab^KO, E-cad::EGFP^Kin, sqh-MRLC::mCherry;/Cyo crossed with males scab^KO/Cyo were injected with water and were compared to embryos from mothers; E-cad::EGFP^Kin, sqh-MRLC::mCherry;/+ crossed with males yw and injected with either water or dsRNAs against αPS3.

Live Imaging

For live imaging embryos were aligned on coverslips with heptane-glue and were covered with Halocarbon 200 oil, as described earlier.⁸² Embryos were imaged at stage 7 in the dorsal and posterior region (unless otherwise specified) for 12 to 15 min at room temperature (22°C) depending on the experiment. Dual color time lapse imaging was performed using simultaneous acquisition on a confocal spinning disc (CSU-X1, Yokogawa) Nikon Eclipse Ti inverted microscope equipped with 2 cameras (Rolera EM-C², QImaging or Kinetix, Photometrics) using a 100X/N.A 1.45 Plan Apo oil-immersion objective from Nikon.

For live imaging of F-Actin and MyoII z-stacks of 4 μm (8 planes, spacing 0.5 μm) from the vitelline membrane were acquired with a time interval 4s/stack. For live imaging of β-PS alone or together with MyoII or Vinculin and of Talin z-stacks of 1 μm (2 planes, spacing 0.5 μm) from the vitelline membrane were acquired with a time interval 3s/stack. For live imaging of Vinculin and MyoII z-stacks of 2 μm (4 planes, spacing 0.5 μm) from the vitelline membrane were acquired with a time interval 4s/stack. For live imaging of E-cad and MyoII (Figures 3E and S3F) z-stacks of 4-6 μm (8-12 planes, spacing 0.5 μm) from the vitelline membrane were acquired with a time interval 4-6s/stack. Time lapses of deeper stacks (10 μm) of MyoII (Figure 3A) were acquired by collecting 20 planes with a spacing of 0.5 μm every 10s. Deep z-stacks (9-10 μm) of β-PS and Talin (Figures S2B and S2C) were acquired in living embryos with a spacing of 0.5 μm.

In all cases, imaging conditions (exposure time and laser power) were optimized and kept constant between controls and perturbed embryos.

Immobile fences by tissue cauterizations

Tissue cauterizations to perturb the anterior movement of the dorsal epithelium were generated as previously described.³⁵ Briefly, a line cauterization of approximately 30 μm along the Medio-Lateral (ML) axis at ∼30% Embryo Length (EL) from the posterior was generated by focusing a near-infrared (NIR, 1030nm) laser with a 100X/N.A. 1.4 oil-immersion Plan Apo VC, Nikon objective on the apical side of the embryonic blastoderm (∼1–2 μm above adherens junctions) with an average power of 500 mW at the back aperture of the objective and moving the stage with a constant speed of 17-20 μm/s.

Image processing, cell tracking and segmentation

All image processing and data analysis were performed using ImageJ (1.53v), Matlab (2019b or 2014b) including Curve Fitting, Image Processing, Statistics and Machine Learning Toolboxes (Mathworks), Ilastik (v. 1.3.3) and IgorPro (v6.3 or 9, Wavemetrics). Graphs were produced with either Matlab or IgorPro and exported to Adobe Illustrator 2023 for final processing in figures.

Maximum intensity projections were used for measurements of fluorescence intensity and for cell segmentation. Before projection z-stacks were smoothed with a mean filter with a kernel of 0.5 pixels (0.03-0.04 μm) to increase the signal-to-noise ratio (SNR) in the projected images. Cell segmentation and tracking were performed as previously described⁶⁵ using Ilastik (v. 1.3.3)⁸³ and Tissue Analyzer.⁸⁴ Briefly, cell outlines were labelled with either E-cad::GFP or Utr::GFP. The 2D projections were first band-pass-filtered with cutoffs of 1 μm (low pass) and 8 μm (high pass) and then processed with Ilastik (output prediction) to generate image predictions of cell outlines. Cell segmentation was initially performed on the Ilastik image predictions and then manually corrected on the actual images before final image segmentation and cell tracking with Tissue Analyzer.

Side views along the AP-axis were generated by first registering cells along the y direction using the position of cell centroids to remove y drifts and by re-slicing the image 4D hyperstacks (x-, y-, z- and time dimensions) across a DV width of 2 μm (25 pixels) around the cell centroid. Side views were then generated with maximum intensity projection of the resliced planes. Kymographs along the AP-axis were obtained with a similar method but using maximum intensity projection time series (x-, y- and time dimensions) as input for re-slicing. Kymographs are either maximum intensity projections across a DV width of 2 μm around the cell centroid (Figures 1E, 2G, 2H, 4A, 4B, and 4G) or across the entire medio-apical region of the cell (Figure 5B).

The apico-basal position of the actin cortex was estimated using a custom ImageJ macro integrating the ‘stack focuser’ plugin from M. Umorin previously described.^35,65 The macro uses the ‘stack focuser’ plugin to define the most focused plane in all positions of the image. This information is stored in an heightmap image which is smoothed with a median filter using a radius of 1.2 μm (15 pixels). The smoothed images are then used as input to generate heatmap kymographs and spatial and temporal profiles of the apico-basal position of the cortex as described below.

All measurements of fluorescence were performed after local background subtraction as previously described.^35,65 Briefly, for all images background intensities were subtracted by masking out structures of interest (MyoII clusters, Integrin puncta etc.) and then subtracting residual intensities. The masks were generated using a manually defined intensity threshold on images pre-treated with the “background subtraction” function of ImageJ (using a radius of ∼4 μm (50 pixels) for MyoII and ∼0.4 μm (5 pixels) for βPS and Vinculin) to reduce the effects of uneven illumination of view field. Residual background images were smoothed with a gaussian blur filter with a radius of ∼0.3-0.6 μm (4-8 pixels) before subtraction.

Quantification and statistical analysis

Measurements of fluorescence intensity and focal complexes in cells

Measurements of fluorescence intensity were performed in the entire medio-apical region of cells (Figures 1C, 2J, 4C, 4D, 4H, 6G, S1A, S1D, S2E, S4A, S4B, and S4E) using an ROI obtained by automated segmentation and tracking that was shrunken by 10 pixels (0.8 μm) to remove junctional signal.

For measurements of focal complex puncta, a simple threshold-based image segmentation was performed to detect individual β-PS or Vinculin puncta and extract their size and intensity. First, a manually defined threshold was selected on images pre-treated with the “background subtraction” function of ImageJ (using a radius of ∼0.4 μm) to reduce the effects of uneven illumination of view field. Then images were binarized and particles were detected with the function “analyze particles” of ImageJ. The particles belonging to each cell were used to determine the total number of puncta per cell, their average size, mean intensity and integrated intensity. In Figures 4I, 6G, and S4F the density of puncta per cell was determined as N of puncta per cell / cell area. For β-PS a running average across 3 images of the time lapse was performed before particle detection to further reduce noise and fluctuations in particle detection.

Time registration of individual cells was always relative to the onset of the rapid MyoII recruitment phase and was performed on measurements of MyoII mean intensity across the entire cell. Time 0 was initially defined when MyoII mean intensity overcame a threshold and then was corrected manually based on cell area and MyoII integrated intensity measurements (this is also the time when the area of the cell starts decreasing due to its detachment from the vitelline membrane). The same time registration was used to register cells for the generation of heatmap kymographs (see below).

Feature tracking and measurement of velocity fields

Velocity fields of the F-actin network were obtained by tracking discrete apical F-actin structures with a Kanade-Lucas-Tomasi (KLT)^46,47 feature tracking algorithm coupled with an affine consistency test to minimize errors⁸⁵ implemented in the C programming language (Stan Birchfield https://cecas.clemson.edu/∼stb/klt) as previously described.⁴⁵ The KLT output is then post-processed using a custom Matlab routine. Trajectories were filtered to eliminate too short trajectories (less than 3 frames, i.e. 8 sec), those with unrealistic particle speeds (more than 0.24 μm/sec) and those crossing boundaries between two cells. From the particle trajectories, a velocity field is obtained by derivating the position of all the particles and interpolating the resulting velocities on a fixed grid of 0.64x0.64μm² (8x8 pixels²). We compared results obtained with KLT to Particle Image Velocimetry (PIV) and found that KLT is computationally faster and gives comparable results. In our case, since KLT tracks features, it has the advantage that the velocity field is not influenced by material coming into the field of view from other planes (reviewed also in Vig et al.⁸⁶).

MyoII rates and cortex deformation

MyoII rates were estimated using mass balance in the plane of the cortex. The evolution of MyoII concentration in a given volume of the cortex, here considered a 2D surface, is set by the MyoII bound to the actin cortex and being transported with it (by advection within the plane), and by the net balance of binding/unbinding of new MyoII minifilaments to the cortex (i.e. from the cytoplasmic pool). As previously described for actin concentration⁵⁶ and MyoII,³⁴ we use the mass balance equation:

$$\frac{Dc}{Dt}=\frac{\partial c}{\partial t}+\mathit{v}\nabla c=-c\nabla \cdot \mathit{v}+R_{MyoII}$$

Where $c$ is MyoII concentration, $\mathit{v}$ the velocity of the MyoII flow, and $R_{MyoII}$ is the effective rate of MyoII incorporation (net binding/unbinding rate of new MyoII minifilaments) into the actin cortex, and $\frac{Dc}{Dt}$ is the comoving derivative of the concentration. We infer the speed of MyoII within the plane from the velocity field of actin particles (see above) and the concentration of MyoII from the fluorescence intensity of MRLC::mCherry in the image (maximum intensity projections obtained as described above). Pixel intensities are averaged on a grid of 0.64x0.64μm² (8x8 pixels²). A rolling average across time is performed on both the averaged pixel intensities and the velocities, with a window of 3 frames (8 seconds). We then calculate spatial and temporal derivatives using respectively central differences and forward difference. We can thus deduce from the previous equation the effective reaction kinetics rate (R_MyoII) for each position of the grid at all time points:

$$R_{MyoII}\left(x,y,t\right)=\frac{\partial c}{\partial t}+v_x\frac{\partial c}{\partial x}+v_y\frac{\partial c}{\partial y}+c(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y})$$

We then average $R_{MyoII}$ in time with a rolling average of 3 frames (8 seconds).

The validity of our code was checked on simple simulations where we impose a homogeneous expansion rate of cells as hexagons, and keep ‘MyoII’ concentration constant. The average R_MyoII value found by the method above described, although noisy at the boundary of the MyoII domain, matched the expected value of R_MyoII.

Since we are interested in the time evolution of MyoII bound to a region of the actin cortex which can move by translations, in Figures 3C, 3G, 6B, 6E, S3E, S5A, S5B, S6C, and S6D we plotted the comoving time derivative of MyoII $\frac{Dc}{Dt}$. Indeed, our analysis being based on an Eulerian representation (fixed grid), the movement of the actin cortex between two arbitrarily defined neighboring boxes (e.g. from box 1 to box 2) causes corresponding changes of the concentration time derivative $\frac{\partial c}{\partial t}$ between the boxes (e.g. an increase in box 2 and a corresponding decrease in box 1). The term $v\nabla c$ accounts for this, such that comoving time derivative $\frac{Dc}{Dt}$ is not affected by simple movements between neighboring boxes, but only by concentration by advection with the contracting cortex ($-c\nabla \cdot v$) and net binding/unbinding rate of new MyoII minifilaments to the cortex ($R_{MyoII}$).

The cortex deformation rate in Figure 3H is the isotropic strain rate $\frac{1}{2}$∇⋅v, that is $\frac{1}{2}\left(\frac{{\partial v}_x}{\partial x}+\frac{{\partial v}_y}{\partial y}\right)$ as noted in the equations above, and was measured using the velocity fields of actin particles (see above).

Kymographs heatmaps and spatial and temporal profiles

Kymograph heatmaps of MyoII concentration, MyoII rates, local cortex deformation and of the F-actin particle speed were generated by mapping these parameters on a fixed grid of 0.64x0.64μm² (8x8 pixels²), as above. For each time point we attribute each box of the grid to a given cell using a cell mask from cell segmentation and tracking. The position of the boxes is then registered together with the cell. In time, cells are registered as described above using measurements of MyoII mean intensity in the entire cell. In space, cells are registered either by positioning their P-boundary at time 0 at the position x=0 as shown in Figure S1F or by defining x=0 the position of the cell P-boundary for all time points (moving P-boundary), as in Figure S1G. We then average (by the mean, except for the deformation rate where an averaging by the median was performed) in space (along the dorsoventral axis) and across different cells, to obtain the kymograph as in Figures 1F, 2E, 2F, 3F, 6D, S1F, S1G, S3A, S3C, and S6B.

Spatial and temporal profiles of the MyoII concentration, MyoII rates, local cortex deformation and of the cortex distance from the vitelline membrane were obtained for each embryo directly from heatmap kymographs of these parameters by computing the median across the y-axis (for spatial profiles) or the mean across the x-axis (for temporal profiles, as illustrated in Figures S3A and S3C). For spatial profiles, heatmap kymographs in the frame of reference of the cell moving P-boundaries were used. For temporal profiles, we used heatmap kymographs in the fixed frame of reference of the embryo (cell registration relative to position of the P-boundary at time 0). The spatial profile of each embryo was obtained by computing the median between 0-3 min (or 0-6 min for a-Cat, and α-Cat + αPS3 RNAi in Figure 6E and AF in water injection and AF in αPS3 RNAi in Figure S6C) at all x positions in the heatmap. The temporal profile of each embryo was obtained by computing the mean across a region of 5 μm (centered around x=4-7 μm depending on the embryo) for all y positions (time) in the heatmap. Profiles of the apico-basal position of the cortex were obtained with the same method using heightmap images obtained as described above as input for the analysis.

Measurements of the spatial intensity profile in Figure S3G were performed differently and did not involve cell segmentation and tracking nor the generation of heatmap kymographs. Briefly, for each embryo the position of the moving invaginating furrow was tracked manually over time and used to register image time series. Average time projections across 12 mins from the onset of tissue-level wave propagation were obtained and used to measure the fluorescence intensity along three 12 μm thick-horizontal lines along the AP-axis. For each embryo the average of these 3 lines was computed and mean profiles between embryos are plotted in Figure S3G.

Heatmap kymographs of MyoII concentration in the fixed frame of reference of the embryo were used to estimate the speed of the MyoII wave inside cells in Figure 1F. Similar to what previously described,³⁵ the mean heatmap kymograph across 3 embryos was first binarized and then a linear fit of the positions where MyoII concentration was higher than a threshold was performed as a function of time. Note that the speed extracted here was compared to the speed of the wave in the fixed frame of reference of the embryo as in Ext. Fig. 6j in Bailles et al.³⁵ and not the frame of reference of the tissue as in Fig. 1d of the same paper. In this former reference a correction for the elastic deformation of the cells due to their apical spreading to the vitelline membrane was applied.

Detection of MyoII recruitment events

The discrete events of MyoII recruitment during the propagation of the intracellular wave of MyoII were detected either manually or automatically and the two methods were compared (Figure S1C). For the manual detection we compared for each cell top views (max projections) of MyoII with corresponding time traces of the integrated fluorescence intensity. In general, events of MyoII recruitment were defined when the rate of MyoII integrated intensity in the cell was greater than 500 A.U/s (see Figure S1D for one example) and when such peaks were associated to visible recruitment of MyoII in the medio-apical cortex of the cell (87% of the events). As reference, 13% of the peaks of the MyoII integrated intensity above 500 A.U/s were rejected as not validated by the visual inspection of the images (e.g. associated to segmentation error or presence of chorion impurities in the images). In few cases (13% of the detections) clearly visible recruitment of MyoII in the medio-apical cortex upon visual inspection was associated to peaks of the rate of MyoII integrated intensity below 500 A.U/s. Finally, close peaks of the rate of MyoII integrated intensity were considered separate events of MyoII recruitment when MyoII appeared in separated clusters by at least 1μm distance. For automated detection, we developed a custom Matlab procedure based on the native "findpeaks" function. Prior to peak identification, the integrated MyoII intensity profiles were smoothed via a spline function with a smoothing parameter set at 0.1. The detection was then fine-tuned using the following built-in parameters: minimum height of 12000 A.U., minimum prominence of 2500 A.U., and minimum width of 20 seconds. Additionally, we imposed a minimum prominence-to-width ratio to filter out large, slowly assembling peaks that often arise from events unrelated to MyoII recruitment. For both methods the number of MyoII recruitment steps after the max in cell area (i.e. during intercellular wave propagation) is reported in Figure S1C.

We compared the two methods for a set of 95 cells in 5 WT embryos and we found that the two methods detected overall similar N of events of MyoII recruitment (150 and 116 events for the manual and automated detection respectively) with similar distributions of the number of MyoII recruitment events/cell (Figure S1C). The differences were mostly accounted for by missed events by the automated detection (22% of the manually detected events were missed by the automated detection and accounted for ∼80% of the total errors by automated detection). Events that were either split or fused by the automated detection method accounted for 3% of the manually detected events and ∼12% of the total errors while wrong detections (due for instance to segmentation errors or bright chorion spots in the field of view) for 2% of the manually detected events and ∼7% of the total errors. The manual method was considered more reliable and was used as the method of reference.

MyoII wavefront and detachment speed from kymographs

The measurements of the MyoII wavefront and detachment speed in Figure 5D were performed on kymographs of MyoII (Figure 5B) using the Velocity Measurement Tool (available at https://dev.mri.cnrs.fr/projects/imagej-macros/wiki/Velocity_Measurement_Tool). Kymographs of MyoII were produced as described above. For each cell, events of MyoII clusters accumulation detected as above were reported in the corresponding MyoII kymographs. A segmented line connecting the anterior front of such clusters accumulations was drawn manually and the average MyoII wavefront velocity was computed using the function “measure Velocities” of the Velocity Measurement Tool. The detachment speed was computed similarly by manually drawing a segmented line following the detaching P-boundary of the cell. The time of detachment in Figure 5C was computed by measuring the y distance (in seconds) between the two segmented lines at the center of MyoII clusters accumulations.

Angle θ and detachment point and furrow velocities

The detachment angle θ, and the velocities of the detachment point and the basal furrow were measured from reconstructed side views of F-actin obtained as described above. The detachment point was defined as the most posterior point of the cell still in contact with the vitelline membrane. The position of the basal furrow was defined as the most basal point at the posterior of the cell visible in our stacks. The position of these points was tracked manually along the AP-axis and instantaneous velocities were computed. The detachment angle θ at all time points was determined from the coordinates of these two points using the atan2 (arctangent) function with the ImageJ software.

Correlation of the local β-PS intensity with the detachment speed

To correlate the local intensity of β-PS to the local detachment speed (Figures 7H and 7I), we manually tracked, in top views, the point of detachment (defined as the most posterior point of the tissue anterior to the furrow) on a horizontal line along the AP-axis (yellow line Figure 7G) and we measured the β-PS intensity just anterior to this point. For each embryo we performed measurements along 4-5 horizontal lines. The instantaneous AP detachment velocity was calculated from the x coordinates of the tracked points. The local β-PS mean intensity was measured in an oval region with an aspect ratio of 0.66 and a major DV axis of 6 μm (75 pixels) positioned 0.4 μm (5 pixels) anterior to the point of detachment for each detachment point and for all time points.

Cross-correlation

Cross-correlation was performed as previously described.⁶⁵ Briefly, time traces were smoothed using a binomial algorithm using IgorPro software before derivation. The normalized cross-correlation was calculated with IgorPro software using the following formula:

$$C_N\left(\tau \right)=\frac{{\int }_0^T\left(f\left(t\right)-\overline{f}\right).\left(g\left(t+\tau \right)-\overline{g}\right)dt}{\sqrt{{\int }_0^T{\left(f\left(t\right)-\overline{f}\right)}^{2}dt}.\sqrt{{\int }_0^T{\left(g\left(t\right)-\overline{g}\right)}^{2}dt}}$$

where $t$ is the time, $T$ the total time of analysis, $\tau$ the lagtime. The mean cross-correlation function was calculated as the average of the cross-correlation functions of all cells (Figures 4E, 7F, and S7F) or lines (Figure 7I) and was used to estimate the peak correlation value and the corresponding time delay. The frame rate of the time lapses used for this analysis was 3 or 4 s/frame depending on the experiment.

Statistical analysis

For all experiments the number of samples (lines/cells/embryos) are indicated in the figure legend. All measurements were performed in 2-8 embryos. In experiments where embryos are not injected, we consider each embryo as an independent experiment. In drug and dsRNA injection experiments the number of independent experiments is defined as the number of independent injections. Data points from different lines/cells/embryos from at least 2 independent experiments were pooled to estimate the mean, S.D. and s.e.m. values plotted.

All p-values for individual experiments are calculated using a non-parametric Mann–Whitney test (Matlab statistic toolbox) and reported in the figure legends. p<0.05 indicates a significant result. No statistical method was used to predetermine sample size. The experiments were not randomized, and the investigators were not blinded to allocation during experiments and outcome assessment.

Published: December 15, 2023