Abstract
Laser speckle contrast imaging (LSCI) is applied in various biomedical applications for full-field characterization of blood flow and tissue perfusion. The accuracy of the contrast interpretation and its conversion to the blood flow index depends on specific parameters of the optical system and scattering media. One such parameter is the polarisation of detected light, which is often adjusted to minimize specular reflections and image artefacts. The polarisation’s effect on the detected light scattering dynamics and, therefore, the accuracy of LSCI data interpretation requires more detailed investigation. In this study, we used LSCI and Dynamic Light Scattering Imaging to evaluate the effects of the detected light polarisation when imaging perfusion in the mouse cortex. We found that cross-polarisation results in a shorter decorrelation time constant, a higher coherence degree and stronger dynamic scattering compared to the parallel-polarisation or no-polariser configurations. These results support the cross-polarisation configuration as the most optimal for brain cortex imaging and suggest against direct or calibrated comparisons between the contrast recordings made with different polarisation configurations.
1. Introduction
Laser speckle contrast imaging (LSCI) is a rapidly developing technology capable of dynamic characterisation of tissue perfusion with a high spatiotemporal resolution, which has found multiple applications in brain research [1–6]. It is based on characterising the speckle pattern generated by the coherent laser light scattered from a sample and recorded with a CMOS or CCD camera [7,8]. Moving scattering particles in the sample (e.g. red blood cells) cause intensity fluctuations in the speckle pattern, which appear as blurring when integrated over a sufficiently long exposure time. The blurring can be subsequently quantified in terms of spatial or temporal contrast:
| (1) |
where is the contrast, and are the mean and standard deviation of the intensity, respectively, is the exposure time, is the intensity autocorrelation function, and is the time lag. The intensity autocorrelation function is, in turn, related to the field correlation function and thus to the decorrelation time , a quantitative measure of the particles dynamics [8–10]. The most recent model, which includes static scattering as well as different dynamic regimes, is described as [11]:
| (2) |
where ; is the decorrelation time constant, reflects the coherence degree and averaging of speckle dynamics, represents the fraction of the dynamic scattering component, and is an offset caused by measurement noise. depends on the secondary type of dynamics with a value of 0.5 for multiple scattering from unordered motion [12,13] or 2 for single scattering from ordered motion [12,14], and , which takes values from 0 to 1 [11], represents the influence of the component compared to the single scattering from unordered or multiple scattering from ordered dynamics [7,12].
Values of the parameters described above are critical in establishing the relationship between contrast and the decorrelation time and, thus, perfusion. Generally, it is assumed that the coherence degree parameter accounts for the features of the optical system [8,11,15–17], for all possible noise-contributing factors [9,11,18], while , , and reflect the properties of the dynamic scattering media [9,11,18,19]. In the experimental settings, however, the effects of some optical features are entangled with the "tissue parameters" as well. One such feature is the polarisation of the detected light, the importance of which has been highlighted throughout the history of LSCI [8,15,20–24]. Polarisation of scattered light from a linearly polarised laser light source starts linearly polarised for single-scattered photons and becomes more unpolarised with more scattering events [20,21]. The unpolarised light can be further represented by an incoherent combination of vertical and horizontal linearly polarised light, which cannot form an interference pattern according to the 3rd Fresnel-Argo law. Introducing a linear polariser in the LSCI detection path removes one of the incoherent components and, therefore, should theoretically double the coherence degree and increase the contrast range. Furthermore, adjusting the polarisation angle makes it possible to achieve "cross"-polarisation and filter out the linearly polarised component that originated from single scattering. Traditionally, cross-polarisation is used to reduce specular reflection artefacts, but potentially, it may also change the dynamics regime and make LSCI more sensitive to deeper dynamics [11,23–25].
In the present study, we use LSCI combined with Dynamic Light Scattering Imaging (DLSI) to evaluate the effects of three different polarisation configurations ( - no-polariser, - linear polariser in the "parallel" orientation, and - linear polariser in the "cross" orientation) on the dynamic light scattering parameters and the contrast interpretation when imaging mouse cortex. We find the average contrast in the cross-polarisation configuration to be noticeably lower than for parallel-polarisation and demonstrate the underlying changes in the intensity autocorrelation function shape. We associate the shape differences with changes in the decorrelation time, static scattering and coherence degree parameters, measured with DLSI. Finally, we suggest possible explanations for such changes and discuss the potential consequences of our observations for LSCI applications.
2. Methods
Animal preparation and imaging
All experimental protocols were approved by the Danish National Animal Experiments Inspectorate and conducted according to the ARRIVE guidelines and guidelines from Directive 2010/63/EU of the European Parliament on the protection of animals used for scientific purposes. Five 14-week-old C57Bl6 mice with chronically installed optical windows in the somatosensory cortex area were used. The surgical procedure is standard and was described in detail in previous studies [3,26,27]. Briefly, a craniotomy and installation of an optically transparent 4 mm round glass and metal head plate were performed in anaesthetized mice (3% isoflurane in oxygen initial anaesthesia, reduced to 1.5% during the surgery). After surgery, mice were allowed to recover for 10 days before imaging, receiving medication (Bupremorphine, Carprofen, Ampicillin) intraperitoneally for four days following surgery. During surgery and imaging sessions, animals were placed on a homeothermic heating pad to maintain body temperature at . During the imaging sessions, the head plates were fixated in a custom-made mount, and 1.5% isoflurane was delivered to the animals via a non-tight mask at a level just enough to maintain the anaesthetized condition.
Laser Speckle Contrast Imaging and Dynamic Light Scattering Imaging were performed to assess brain perfusion in each mouse using a custom-made imaging system. The light from a fibre-coupled volume holographic grating stabilized laser diode (785 nm, Thorlabs FPV785P), controlled with a laser driver (Thorlabs LDC210C) and temperature controller (Thorlabs TED200C) was delivered on the cranial window from the side at . The back-scattered light collected by the objective (Leica N PLAN 2.5x, NA=0.07) passed through a variable neutral density filter and a linear polariser (Thorlabs LPNIRB100). The polariser was adjusted to "cross" or "parallel" orientations when collecting the and data or removed when recording the data. The neutral density filter was adjusted accordingly to maintain approximately the same average intensity over the field of view for all polarisation conditions. The resulting speckle patterns were recorded for 4 seconds, using a high-speed CMOS camera (Photron Nova S6, ), operating at a frame rate of 30000 frames (512×384 pixels, ≈ 3×2.25 mm field of view) per second and exposure time . The speckle-to-pixel size ratio of the system was estimated to be , which, according to our most recent study [28], should provide an excellent signal-to-noise ratio but a reduced value of the coherence degree parameter [8,28]. A static phantom was used to estimate the value of the coherence degree parameter, which was found to be . As in our previous studies [11,16], the static scattering phantom was a rough (non-glossy) white paper that ensures a fully developed speckle pattern and a speckle contrast of 1 at .
Data analysis
Both LSCI and DLSI data processing were described in detail in previous studies [8,11], and therefore, we only provide a concise overview. For LSCI analysis, frames with exposure time T=5 ms were produced by averaging 151 raw intensity frames. The contrast was calculated as , where and are the standard deviation and the mean of intensity, which were calculated over 5x5 pixels neighbourhood or over 25 frames for spatial and temporal contrast ( and ), respectively [8,28,29]. For the DLSI analysis, we calculated normalized intensity autocorrelation function as:
| (3) |
where is the intensity recorded at a specific pixel, is the time corresponding to the current frame, and is the time lag value ranging from 0 to 33ms. For the follow-up comparison and DLSI fitting, we identified 3 different types of regions of interest (ROIs): 1) relatively large vessels (2nd branch of the middle cerebral artery, N=1 per animal), 2) small vessels (on the scale of 5th branch of the middle cerebral artery, N=5 per animal) and 3) parenchyma (all pixels not belonging to visible vessels). The ROIs were selected using semi-manual segmentation based on adaptive thresholding of the average temporal contrast images. Average was calculated for each ROI type in each animal and fitted using the DLSI model (Eq. (2)). For visualisation purposes, parameters and were combined in parameter ranging from 0 to 2, where represents multiple scattering unordered motion, - single scattering unordered motion or multiple scattering ordered motion and - single scattering ordered motion. Statistical analysis was performed using paired t-test where relevant, with exact -values being reported. For data averaged across animals, mean and standard deviation values are reported.
3. Results
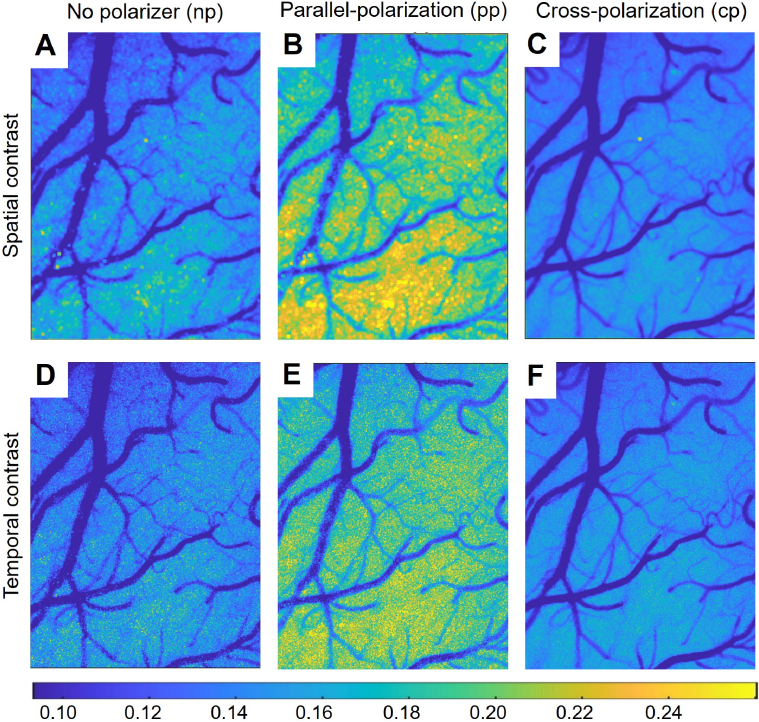
Examples of laser speckle contrast images for different polarisation modes are shown in Fig. 1. Averaged across animals and the field of view, the configuration results in the highest contrast and . The configuration has a significantly lower contrast with and . For , the contrast has further decreased to and , being significantly lower than the contrast in the ( and ) but not in the ( and ) configurations. The difference between and is expected - the coherence degree decreases because non-polarised light contains two incoherent components, thus resulting in lower contrast for the configuration. For cross-polarisation, however, no reduction in the coherence degree is expected. Therefore, being similar to , but significantly lower than can only be explained by cross-polarisation changing the scattering media parameters, such as the decorrelation time constant or the degree of dynamic scattering.
Fig. 1.
Examples of laser speckle contrast images for the no-polariser (A, D), parallel-polarisation (B, E) and cross-polarisation (C, F) configurations. The images show that for spatial (A-C) and temporal (D-F) analysis, and result in much lower contrast values than , implying differences in the dynamic light scattering parameters.
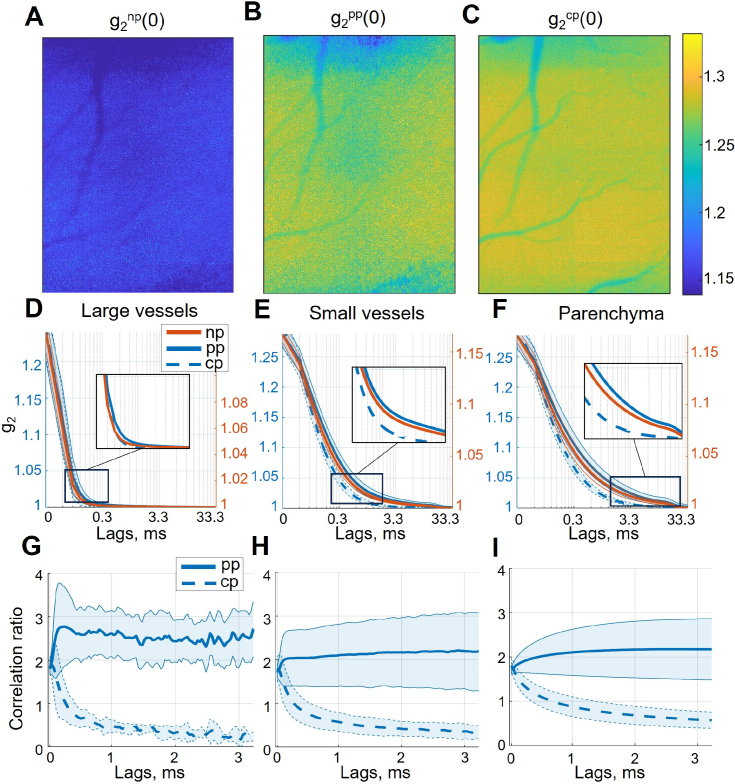
To understand the underlying dynamic light scattering differences, we performed DLSI recordings and analysis. Exemplary images of the intensity autocorrelation function at the zero time-lag are shown in Fig 2, A-C. Average is the highest in the with , followed by the and then by the configuration . The being significantly lower than and ( and respectively) is expected due to the coherence degree being reduced in the presence of both incoherent components of the unpolarised light. At the same time, being larger than implies that the coherence degree and or the degree of dynamic scattering is higher for cross-polarisation. Neither, however, can explain the contrast decrease in the configuration. On the contrary, more dynamic scattering would result in a higher , while a higher coherence degree will increase both and . Consequently, the decrease in contrast caused by cross-polarisation can only be explained by differences in the shape of , which decorrelates noticeably faster for the than the and configurations (Fig. 2, D-F). The difference is less noticeable for large vessels, becomes more pronounced in small vessels and is most prominent in the parenchyma. It becomes even more evident when the correlation ratio, calculated as or , is examined (Fig. 2, G-I). The parallel-polarisation correlation ratio fluctuates around 2 with little time-lag dependency, which fits well with the coherence degree being the primary difference compared to the configuration. However, for the configuration, the ratio decreases below 1, despite starting at the highest point, implying a shorter decorrelation time constant and changes in other parameters responsible for the shape of the intensity autocorrelation function. A possible explanation for such difference would be that the detected photons in the configuration are mostly multiple-scattered, reaching deeper layers of the parenchyma rather than single-scattered photons from the less perfused superficial layers. Additionally of interest, a "plateau" can be observed in the parenchymal and , lasting from . Such shape inconsistency might reflect the presence of other dynamics (e.g. cellular motility) much slower than the motion of red blood cells, which is expected to decorrelate within 5 ms [11,18,30].
Fig. 2.
Intensity autocorrelation function for different polarisations and regions of interest. A-C, examples of per-pixel for , and polarisation configurations respectively. The maximum is noticeably below the theoretical value of 2 due to the reduced coherence degree and small speckle-to-pixel size ratio (according to the static scattering phantom measurements is , see Methods section). D-F, corresponding to large vessels, small vessels and parenchymal regions of interest. Please note that were calculated over a sufficient number of time lags to reach , but to keep the axis limits the same between subplots, only the first 33.3 ms were shown. G-H, correlation ratio for and in comparison to , corresponding to large vessels, small vessels and parenchymal regions of interest.
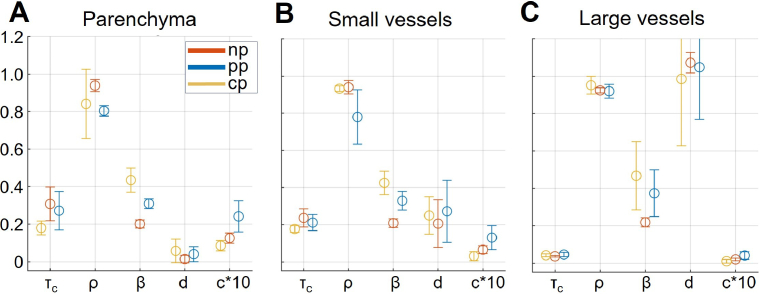
Results of the DLSI model (Eq. 2) fitting for the respective regions of interest are summarised in Fig. 3. Polaraiser in "cross"-orientation, on average, resulted in a shorter decorrelation time and higher coherence degree , matching well observations made based on Fig. 2. The coherence degree also closely matches the calibration with static phantom . The lower coherence degree in the configuration could be explained by the same pixel integrating non-interfering multiple (originally unpolarized) and single-scattered light. For other parameters, however, the fitting results are less consistent and challenging to explain. In particular, the dynamic scattering component appears to be the lowest in the , followed by the and only then the configuration. Such an order is unexpected - considering the ratios between the multiple- and single-scattered light and assuming that the latter comes from the surface layers with more static scattering, one would expect the contribution of dynamic scattering for the to lie between the respective values for the and configuration. Likewise, one would expect parameter to be the lowest in the and the highest in the configuration. The fitting results, however, appear to be inconsistent with such an assumption. The mismatch between the expectations and the fitted values of and can possibly be attributed to the fitting error. The error is primarily caused by fitting a limited number of meaningful data points (≈10 for large vessels, ≈100-200 for parenchyma) using a model with five parameters, some of which have minuscule differences in their effects.
Fig. 3.
Results of the DLSI model (Eq. 2) fitting for different polarisations, corresponding to the three regions of interest - parenchyma (A), small vessels (B) and large vessels (C). Please note that parameter is reported multiplied by 10 for visualisation purposes.
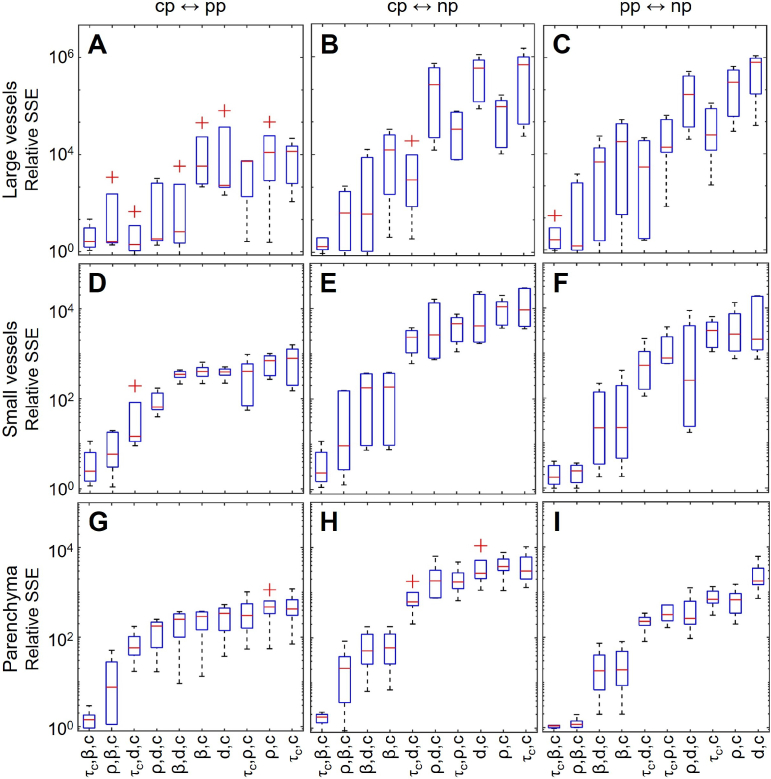
To address the problem of the fitting quality and identify parameters most likely responsible for the observed differences in the shape of , we attempted fitting with a reduced number of active parameters. More specifically, we fixed all of the parameters at values obtained for a specific regime (e.g. ) and attempted to fit the data from the other two configurations by sequentially removing the constraint, first from pairs of parameters ( ; ; ; ) and then triplets of parameters ( ; ; ; ; ; ; ). Parameter was always included as it defines constant offset and, therefore, is required for adequate fitting and produces little interference on other parameters. In total, the fitting was performed for all 9 pairs of configurations (including e.g. both to and to ). The resulting sum of squares due to error (SSE), relative to the one obtained with 5-parameters fit, is shown in Fig. 4. Overall, the combination of , and parameters demonstrated the best performance, achieving SSE only 1.5 times larger than the 5-parameters fit when averaged across all regions of interest and configurations. The corresponding average parameters ratios were as follows: , , and . The second-best combination ( , , ) and the third-best combination ( , , ) resulted in the average SSE 12 and 99 times larger than the 5-parameters fit, respectively. With the other parameters restricted, the dynamic scattering component in the second-best combination was largest in the and lowest in the configuration with the ratio well matching our assumptions described above.
Fig. 4.
The sum of squares due to error (SSE) obtained for different pairs or triplets of fitting parameters relative to SSE obtained using the 5-parameters model. Rows correspond to different regions of interest - large vessels (A-C), small vessels (D-F) and parenchyma (G-I). Columns reflect configuration pairs with respect to the fitting process. Relative SSE getting closer to 1, means that fitting with a respective limited model (e.g. only with , and ) gets more comparable in quality to the complete model with five active parameters, and therefore, that the respective subset of the parameters is sufficient to explain the difference between the polarisation configurations.
4. Conclusion
In the present study, we have explored the effects of detected light polarisation on dynamic light scattering parameters and how it should be accounted for when interpreting LSCI data. We found that cross-polarisation results in similar contrast values as no-polariser configuration, both significantly lower than the contrast obtained with parallel-polarisation. Our in-depth DLSI analysis suggests that the differences between the polarisation configurations can be primarily explained by changes in the coherence degree, decorrelation time constant and, possibly, the degree of dynamic scattering contribution. The coherence degree increased by 85% in the and by 130% in the compared to the configuration. Two factors can explain such a difference: 1) in the configuration, both incoherent components of unpolarised light are present, reducing the coherence degree by half, and 2) in the and configurations, non-interfering single-scattered and multiple-scattered photons are integrated on the sensor, further reducing the coherence degree. The decorrelation time constant is increased by 52% in the but decreased by 15% in the , compared to the configuration. It corresponds to the underlying dynamics in being 18% faster than in and 79% faster than in the configuration and can be explained by multiple-scattered photons sampling dynamics from deeper, more perfused regions. Likewise, it would explain why, with the decorrelation time being fixed, the degree of the dynamic scattering contribution is decreased by 6% in the and increased by 9% in the compared to the configuration. Contrary to our expectations, the dynamics regime parameter was not significantly affected and did not appear to be a key parameter in explaining the difference between the configurations (Fig. 4). Given these points, however, it is essential to note the limitations of fitting the complete DLSI model with 5 parameters when studying minor alterations in the shape of the intensity autocorrelation function. To address this problem, we have attempted fitting various sets of 2 and 3 parameters, identifying the ones producing the minimal error. Despite this, the actual parameters’ values and the respective ratios might differ slightly from those we have obtained, as, e.g. both and are expected to change simultaneously.
Furthermore, as we note from Fig. 2, and configurations appear to contain additional dynamics decorrelating at , much slower than expected for the red blood cells motion. Studying slow dynamics might be an unexpected benefit of using parallel-polarisation and should be explored further, which would, however, require introducing multiple decorrelation times in the DLSI model. Except for the slow dynamics, our results show that cross-polarisation is likely the most optimal choice for mouse cortex imaging, as it 1) allows the highest coherence degree, 2) is least affected by the static scattering, and 3) should be capable of characterising the perfusion at deeper cortex regions. The coherence degree fitted for the configuration - in the parenchyma (Fig. 2) is also the closest to estimated using static phantom, making it easier to calibrate. Cross-polarisation is also expected to be the most beneficial regime for trans-cranial studies [31], as it allows deeper penetration and reduces specular reflections. Conversely, the coherence degree of and regimes is more challenging to estimate, as it is also affected by the single- and multiple-scattered photons integration. Considering differences in measured dynamics, comparing the contrast obtained using different polarisation configurations is highly inadvisable and should be avoided even for relative measurements.
Funding
Lundbeck Foundation10.13039/501100003554 (R345-2020-1782).
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Dunn A. K., Bolay H., Moskowitz M. A., et al. , “Dynamic imaging of cerebral blood flow using laser speckle,” J. Cereb. Blood Flow Metab. 21(3), 195–201 (2001). 10.1097/00004647-200103000-00002 [DOI] [PubMed] [Google Scholar]
- 2.Bolay H., Reuter U., Dunn A. K., et al. , “Intrinsic brain activity triggers trigeminal meningeal afferents in a migraine model,” Nat. Med. 8(2), 136–142 (2002). 10.1038/nm0202-136 [DOI] [PubMed] [Google Scholar]
- 3.Sunil S., Erdener S. E., Lee B. S., et al. , “Awake chronic mouse model of targeted pial vessel occlusion via photothrombosis,” Neurophotonics 7(01), 1 (2020). 10.1117/1.NPh.7.1.015005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bergonzi K. M., Bauer A. Q., Wright P. W., et al. , “Mapping functional connectivity using cerebral blood flow in the mouse brain,” J. Cereb. Blood Flow Metab. 35(3), 367–370 (2015). 10.1038/jcbfm.2014.211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu Q., Chen S., Soetikno B., et al. , “Monitoring acute stroke in mouse model using laser speckle imaging-guided visible-light optical coherence tomography,” IEEE Trans. Biomed. Eng. 65(10), 2136–2142 (2018). 10.1109/TBME.2017.2706976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Karatas H., Erdener S. E., Gursoy-Ozdemir Y., et al. , “Thrombotic distal middle cerebral artery occlusion produced by topical fecl3 application: a novel model suitable for intravital microscopy and thrombolysis studies,” J. Cereb. Blood Flow Metab. 31(6), 1452–1460 (2011). 10.1038/jcbfm.2011.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fercher A., Briers J. D., “Flow visualization by means of single-exposure speckle photography,” Opt. Commun. 37(5), 326–330 (1981). 10.1016/0030-4018(81)90428-4 [DOI] [Google Scholar]
- 8.Boas D. A., Dunn A. K., “Laser speckle contrast imaging in biomedical optics,” J. Biomed. Opt. 15(1), 011109 (2010). 10.1117/1.3285504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Parthasarathy A. B., Tom W. J., Gopal A., et al. , “Robust flow measurement with multi-exposure speckle imaging,” Opt. Express 16(3), 1975–1989 (2008). 10.1364/OE.16.001975 [DOI] [PubMed] [Google Scholar]
- 10.Liu C., Kılıç K., Erdener S. E., et al. , “Choosing a model for laser speckle contrast imaging,” Biomed. Opt. Express 12(6), 3571–3583 (2021). 10.1364/BOE.426521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Postnov D. D., Tang J., Erdener S. E., et al. , “Dynamic light scattering imaging,” Sci. Adv. 6(45), eabc4628 (2020). 10.1126/sciadv.abc4628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Davis M. A., Gagnon L., Boas D. A., et al. , “Sensitivity of laser speckle contrast imaging to flow perturbations in the cortex,” Biomed. Opt. Express 7(3), 759–775 (2016). 10.1364/BOE.7.000759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Boas D. A., Sakadžić S., Selb J. J., et al. , “Establishing the diffuse correlation spectroscopy signal relationship with blood flow,” Neurophotonics 3(3), 031412 (2016). 10.1117/1.NPh.3.3.031412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Duncan D. D., Kirkpatrick S. J., “Can laser speckle flowmetry be made a quantitative tool?” J. Opt. Soc. Am. A 25(8), 2088–2094 (2008). 10.1364/JOSAA.25.002088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kirkpatrick S. J., Duncan D. D., Wells-Gray E. M., “Detrimental effects of speckle-pixel size matching in laser speckle contrast imaging,” Opt. Lett. 33(24), 2886–2888 (2008). 10.1364/OL.33.002886 [DOI] [PubMed] [Google Scholar]
- 16.Postnov D. D., Cheng X., Erdener S. E., et al. , “Choosing a laser for laser speckle contrast imaging,” Sci. Rep. 9(1), 2542 (2019). 10.1038/s41598-019-39137-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zheng S., Mertz J., “Correcting sampling bias in speckle contrast imaging,” Opt. Lett. 47(24), 6333–6336 (2022). 10.1364/OL.474604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Parthasarathy A. B., Kazmi S. S., Dunn A. K., “Quantitative imaging of ischemic stroke through thinned skull in mice with multi exposure speckle imaging,” Biomed. Opt. Express 1(1), 246–259 (2010). 10.1364/BOE.1.000246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zheng S., Mertz J., “Direct characterization of tissue dynamics with laser speckle contrast imaging,” Biomed. Opt. Express 13(8), 4118–4133 (2022). 10.1364/BOE.462913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goodman J. W., “Statistical properties of laser speckle patterns,” in Laser Speckle and Related Phenomena , (Springer, 1975), pp. 9–75. [Google Scholar]
- 21.Li J., Yao G., Wang L. V., “Degree of polarization in laser speckles from turbid media: Implications in tissue optics,” J. Biomed. Opt. 7(3), 307–312 (2002). 10.1117/1.1483313 [DOI] [PubMed] [Google Scholar]
- 22.Tong Z., Chen X., “Speckle contrast for superposed speckle patterns created by rotating the orientation of laser polarization,” J. Opt. Soc. Am. A 29(10), 2074–2079 (2012). 10.1364/JOSAA.29.002074 [DOI] [PubMed] [Google Scholar]
- 23.Colin E., Plyer A., Golzio M., et al. , “Imaging of the skin microvascularization using spatially depolarized dynamic speckle,” J. Biomed. Opt. 27(04), 046003 (2022). 10.1117/1.JBO.27.4.046003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li D.-Y., Xia Q., Yu T.-T., et al. , “Transmissive-detected laser speckle contrast imaging for blood flow monitoring in thick tissue: from monte carlo simulation to experimental demonstration,” Light: Sci. Appl. 10(1), 241 (2021). 10.1038/s41377-021-00682-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Postnov D., Marsh D. J., Cupples W. A., et al. , “Synchronization in renal microcirculation unveiled with high-resolution blood flow imaging,” eLife 11, e75284 (2022). 10.7554/eLife.75284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holtmaat A., Bonhoeffer T., Chow D. K., et al. , “Long-term, high-resolution imaging in the mouse neocortex through a chronic cranial window,” Nat. Protoc. 4(8), 1128–1144 (2009). 10.1038/nprot.2009.89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shaw K., Bell L., Boyd K., et al. , “Neurovascular coupling and oxygenation are decreased in hippocampus compared to neocortex because of microvascular differences,” Nat. Commun. 12(1), 3190 (2021). 10.1038/s41467-021-23508-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.González Olmos A., Zilpelwar S., Sunil S., et al. , “Optimizing the precision of laser speckle contrast imaging,” Sci. Rep. 13(1), 17970 (2023). 10.1038/s41598-023-45303-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Briers D., Duncan D. D., Hirst E., et al. , “Laser speckle contrast imaging: theoretical and practical limitations,” J. Biomed. Opt. 18(6), 066018 (2013). 10.1117/1.JBO.18.6.066018 [DOI] [PubMed] [Google Scholar]
- 30.Yuan S., Devor A., Boas D. A., et al. , “Determination of optimal exposure time for imaging of blood flow changes with laser speckle contrast imaging,” Appl. Opt. 44(10), 1823–1830 (2005). 10.1364/AO.44.001823 [DOI] [PubMed] [Google Scholar]
- 31.Sdobnov A., Bykov A., Molodij G., et al. , “Speckle dynamics under ergodicity breaking,” J. Phys. D: Appl. Phys. 51(15), 155401 (2018). 10.1088/1361-6463/aab404 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.