Abstract
One of the significant challenges to designing an emulsion transportation system is predicting frictional pressure losses with confidence. The state-of-the-art method for enhancing reliability in prediction is to employ artificial intelligence (AI) based on various machine learning (ML) tools. Six traditional and tree-based ML algorithms were analyzed for the prediction in the current study. A rigorous feature importance study using RFECV method and relevant statistical analysis was conducted to identify the parameters that significantly contributed to the prediction. Among 16 input variables, the fluid velocity, mass flow rate, and pipe diameter were evaluated as the top predictors to estimate the frictional pressure losses. The significance of the contributing parameters was further validated by estimation error trend analyses. A comprehensive assessment of the regression models demonstrated an ensemble of the top three regressors to excel over all other ML and theoretical models. The ensemble regressor showcased exceptional performance, as evidenced by its high R2 value of 99.7 % and an AUC-ROC score of 98 %. These results were statistically significant, as there was a noticeable difference (within a 95 % confidence interval) compared to the estimations of the three base models. In terms of estimation error, the ensemble model outperformed the top base regressor by demonstrating improvements of 6.6 %, 11.1 %, and 12.75 % for the RMSE, MAE, and CV_MSE evaluation metrics, respectively. The precise and robust estimations achieved by the best regression model in this study further highlight the effectiveness of AI in the field of pipeline engineering.
Keywords: Artificial intelligence, regression model, Friction, experimental data, statistical analysis
1. Introduction
1.1. Background
Emulsion refers to a specific two-phase mixture that involves continuous and dispersed phases of immiscible liquids, such as oil and water. If oil or water constitutes the continuous phase, the mixture is categorized as oil-in-water (O/W) (Fig. 1A) or water-in-oil (W/O) emulsion (Fig. 1B). The dispersed phase is usually comprised of spherical bubbles. The size distribution of the bubbles may vary over an extensive range. The stability of emulsions is ensured with surfactants, which have an affinity to the immiscible phases and can reduce surface tension. Even though emulsions are significant fluids in various industries including food, cosmetics, pharmaceuticals, agrochemicals, and the petroleum industry, the large-scale pipeline transportation of emulsions is most important in the petroleum industry [[1], [2], [3], [4], [5], [6], [7]]. One of the key parameters while designing or operating a pipeline is the frictional pressure losses or pressure gradient. Process engineers need a clear understanding of the piecewise and comprehensive friction losses in the pipeline network to ensure the uninterrupted transportation of fluids. The knowledge of pressure drops helps them select the respective sizes of the pumps, motors, and pipes as well as the construction materials. The methodology of estimating friction losses for single-phase flow is well established; however, the development of a similar method for emulsion transportation is still at a nascent stage.
Fig. 1.
Schematic presentation of types of emulsions: (A) O/W; (B) W/O.
1.2. Theory-based traditional models
The frictional pressure losses (ΔP/L) were modeled with Fanning friction factor (f) as follows (Eq. (1)) provided that the emulsion can be considered a Newtonian fluid [4,7]:
| (1) |
where is the emulsion density [kg/m3], (V) is the average velocity [m/s], and (D) is the pipe diameter [m]. The following correlations were suggested for (f):
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
In the above-mentioned equations (Eqs. (2)–(6)), is the equivalent sand-grain roughness of a rough pipe-wall [m], is the relative roughness of a pipe [−], Re is the Reynolds number [−], and is the emulsion's dynamic viscosity [Pa.s]. The values of can be correlated to the flow conditions as shown below [5,[8], [9], [10], [11]]:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
In Eqs. 7–11, is the continuous phase viscosity [Pa.s], is the dispersed phase viscosity [Pa.s], (Ca) is the Capillary number [−], (Vc)is the average velocity of the continuous phase [m/s], is the interfacial tension [N/m], (R) is the average droplet radius of the dispersed phase [m], is the dispersed phase volume fraction [−], and is the maximum packing volume fraction of undeformed droplets of dispersed phase [−]. The value of varies with the type of packing arrangement of droplets. It is 0.52 for simple cubic packing of uniform spheres, 0.64 for random close packing, and 0.74 for hexagonal close packing of uniform hard spheres. A modified version of this model was also suggested in case the emulsion behaves as a shear-thinning non-Newtonian fluid that follows a power-law model [7]:
| (12) |
| (13) |
| (14) |
| (15) |
In Eqs. 12–15, is shear stress [Pa], is shear rate [s−1], is consistency index [Pa.sn], and ( is the flow index [−]. On the other hand, Hoshyargar and Ashrafizadeh [2] investigated the rheological properties of crude oil-in-water emulsions and the factors affecting the rheology of the O/W emulsions stabilized by surfactants were also investigated. They found the crude oil to be a Newtonian fluid with a viscosity of 0.3–11 Pa s; however, the rheological behavior of the O/W emulsions could be explained with the complex Herschel−Bulkley model:
| (16) |
In Eq. (16), the yield stress [Pa]. Considering the emulsions as non-Newtonian Herschel−Bulkley fluids, they modeled the friction losses with the following set of correlations:
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
In Eqs. 17–24, is a generalized Reynolds number [−] and is the Hedstrome number [−].
Inkson et al. [3] investigated the application of computational fluid dynamics (CFD) in predicting the pressure losses for the pipeline transportation of emulsions. They treated an emulsion as a suspension that does not reach the maximum packing of particles but undergoes a phase inversion at a critical dispersed volume fraction. For the computational modeling, they combined the suspension stress model proposed by Morris and Boulay [12] with the Eulerian multiphase model. The emulsion viscosity was defined with Eqs. 25 and 26 in terms of two components, relative viscosity () and normal relative viscosity ():
| (25) |
| (26) |
The overall solution was controlled with Semi-Implicit Method for Pressure Linked Equations or SIMPLE algorithm, which is a numerical procedure of solving Navier–Stokes equations. The constitutive relations were solved to simulate the data obtained using low flow rates on the commercial CFD platform of STAR-CCM+. A similar platform was used by Plasencia et al. [6] for simulating the pipeline transportation of emulsions under laminar and turbulent flow conditions. Unlike Inkson et al. [3], they used a modified version of the model suggested by Krieger and Dougherty [13] to estimate emulsion viscosity. The constitutive discrete equations were solved based on the finite volume method and Phase-Coupled SIMPLE algorithm. The emulsion turbulence was simulated with the Elliptic Blend model, which resolves transport equations for the reduced wall-normal stress component and the elliptic blending factor in addition to the turbulent kinetic energy per unit mass of the velocity fluctuations () and the turbulent dissipation rate (). The uncertainties related to predictions of pressure gradients were estimated about two times the standard deviation of the measurements; the uncertainties increased with the flow rates in the laminar flow zone and appeared to be much higher in the transition or turbulent region.
1.3. Modeling with artificial intelligence
The ranges of applicability of the previously proposed empirical or computational models limit their applications. In addition to the complexity of applying the models, they are also known to involve a significant degree of uncertainty. One of the solutions for the reliable prediction of pressure losses is employing artificial intelligence (AI)-based machine learning (ML). Compared to traditional models, this kind of soft computational approach exhibits superior performance as they are formulated with highly accurate hypothesis functions. Further, the ML models are able to learn the linear and/or non-linear interactions among the features and the outcomes in the data. The hyperparameters of the algorithms are tuned so that these parameters can best explain the relationships of the feature attributes to the outcome variables in the form of a hypothesis function. On the other hand, the traditional models are not necessarily developed to exploit the inherent association between the feature attributes and the corresponding outcomes from the perspective of data science. Rather, the traditional models are usually developed based on the physical observations of a specific set of experiments. Even though these models have scientific value, they fail to accurately estimate the pressure gradient outcomes on new sets of experimental data.
In the realm of multiphase flow, AI-based tools have been widely utilized for prediction and classification purposes [[14], [15], [16], [17], [18]]. However, when it comes to predicting pressure losses specifically for stable emulsion transportation using ML, there is a striking absence of substantial attempts or studies in the existing literature. The application of ML techniques to accurately forecast friction losses in the context of emulsion transportation via pipelines has been largely overlooked or neglected by researchers. Only a few studies obliquely addressed the issue. The most relevant studies are discussed as follows.
Aljubran et al. [19] investigated the application of machine learning algorithms such as artificial neural network (ANN), logistic regression (LR), and extremely randomized trees (ERT) on a data set of 6878 points to predict a set of water-based drilling fluids’ properties: density, yield stress, plastic viscosity, gel strength, filtration fluid loss, and pH. They found ERT to be capable of accurately predicting the measurements on the holdout test set with a coefficient of determination (R2) of 91.07 ± 6.35 %. Wahid et al. [20] developed and evaluated ML algorithms for accurately predicting pressure gradients (PGs) in various oil-water flow patterns (FPs) in horizontal wellbores. Nine FPs including emulsion were considered, and 1100 experimental data points were used to train the models. The evaluated algorithms included Support Vector Machine (SVM), Gaussian Process (GP), Random Forest (RF), ANN, k-Nearest Neighbor (kNN), and their fusions. Seven predictor variables were identified as important for accurate predictions, including oil and water velocities, flow pattern, input diameter, oil and water densities, and oil viscosity. The GP had the highest prediction accuracy, outperforming other algorithms except for the model fusions. Cross-validation analysis demonstrated the superior performance of GP compared to ANN. The study highlighted the potential of ML models for designing energy-efficient transportation systems in the petroleum industry for liquid-liquid flow in wellbores. The performance of ML algorithms in classifying nine oil-water FPs in horizontal pipes using liquid and pipe geometric properties was also investigated [21]. The ML algorithms tested include SVM, Ensemble Learning, RF, Multilayer Perceptron Neural Network (MLPNN), kNN, and weighted Majority Voting (wMV). Experimental data points for the nine FPs were extracted from the literature, and the dataset was balanced using the synthetic minority over-sampling technique. The ML models were evaluated using various metrics such as accuracy, sensitivity, specificity, precision, F1-score, and Matthews Correlation Coefficient. The results showed that the wMV achieved an accuracy of 93.03 % in classifying the oil-water FPs, with seven out of nine FPs having accuracies above 93 %. Statistical analysis indicated that the accuracy of FPs using wMV was significantly higher than using the ML models individually. Recently, a hybrid ML scheme to simultaneously predict FP and PG for oil-water two-phase flow was proposed [22]. They used the GP [20] for predicting PGs and the wMV [21] for predicting the FPs. The researchers used a dataset of 1637 experimental data points for oil-water two-phase flows in horizontal and inclined pipes. They employed the modified Binary Grey Wolf Optimization Particle Swarm Optimization (BGWOPSO) algorithm to identify important features in the dataset. The performance of the ML models was evaluated based on the metrics used in Refs. [20,21]. Cross-validation was performed using a repeated train-test split strategy. The overall FP classification accuracy exceeded 91 %, with 90.61 % sensitivity and 98.53 % specificity using a wMV approach. Using GP regression, the evaluation metrics for PG prediction yielded a MAPE of 10.65 %, a root mean square error of 86.26 Pa/m, and an adjusted R2 of 0.96.
Thus, predicting friction losses in emulsion pipelines using ML tools is an underexplored area. While AI has been widely used in multiphase flow, there is a lack of models that have been specifically designed for predicting pressure losses in stable emulsion flow. This research gap highlights the need for further exploration of ML-based approaches to improve prediction accuracy and optimize emulsion transport systems. The main contributions of the current study include exploring and tailoring ML techniques for predicting pressure gradients in emulsion pipelines. This study serves as a starting point for further research and offers insights that can enhance the efficiency of emulsion transport systems in various industries. The main research contributions of the current study are highlighted below.
-
1.
Several state-of-the-art ML regression models were optimized and evaluated for estimating the pressure gradients for emulsion flows in different pipelines.
-
2.
Recursive Feature Elimination (RFE) algorithm was employed to identify the most relevant set of features.
-
3.
Different evaluation metrics and other analytical tools were used for the comparative analysis of the performances of the regression models in predicting the frictional pressure losses.
-
4.
The top-performing ML algorithm's pressure loss estimations were compared with those of the relevant theoretical model.
-
5.
A comprehensive ML-based modeling methodology was developed for the pressure losses during the pipeline transportation of emulsions.
2. Methods and materials
2.1. Dataset
A database consisting of 7029 measurements of pressure gradients was used for the current study. The data were collected from Ref. [7]. Both O/W and W/O emulsions were pumped through five different pipes while measuring the friction losses. The viscosity, pressure drop, and flow rate were measured using calibrated devices. The emulsions were prepared with three different oils and water in a mixing tank that was equipped with three baffles, a heating/cooling coil, and a temperature controller. The types of emulsions were identified as W/O and O/W with an in-line conductance cell, which was used to measure the electrical conductance of the emulsions continuously. The effects of three polymeric additives and a surfactant on the pressure losses were also investigated. The additives promoted emulsion stability. All experiments were performed at 25 °C. Table 1 presents the dataset with its statistical details. A standard deviation of zero (0) or the similarity of maximum, average, and minimum indicates the constant value of an input parameter. Table 2 shows the distribution of the data points based on the types of emulsions used for the flow experiments.
Table 1.
Statistical presentation of the current database.
| Type | Parameter (Unit) | Maximum | Average | Minimum | Standard Deviation |
|---|---|---|---|---|---|
| Input (Controlled Variable) | Pipe diameter (m) | 0.0265 | 0.01798 | 0.0089 | 0.01 |
| Oil Fraction (−) | 0.95 | 0.67 | 0.2 | 0.18 | |
| Water Fraction (−) | 0.8 | 0.33 | 0.05 | 0.19 | |
| Oil Density (kg/m3) | 816 | 769 | 753 | 25 | |
| Oil Viscosity (Pa.s) | 0.00600 | 0.00350 | 0.00250 | 0.00147 | |
| Oil Surface Tension (N/m) | 0.0405 | 0.0345 | 0.0113 | 0.0114 | |
| Polymer Fraction (−) | 0.010 | 0.007 | 0.001 | 0.004 | |
| Polymer Molecular Weight (−) | 7000000 | 5091192 | 700000 | 2591302 | |
| Surfactant Fraction (−) | 0.020 | 0.015 | 0.001 | 0.007 | |
| Mass Flow Rate (kg/s) | 5712.00 | 8.36 | 0.01 | 188.53 | |
| Velocity (m/s) | 12.31 | 2.94 | 0.05 | 1.95 | |
| Water Density (kg/m3) | 997 | 997 | 997 | 0 | |
| Water Surface Tension (N/m) | 0.0720 | 0.0720 | 0.0720 | 0 | |
| Water Viscosity (Pa.s) | 0.00089 | 0.00089 | 0.00089 | 0 | |
| Surfactant Viscosity (Pa.s) | 0.23 | 0.23 | 0.23 | 0 | |
| Hydrophile-Lipophile Balance (−) | 2.1 | 2.1 | 2.1 | 0 | |
| Output (Measured Variable) | Pressure Gradient (Pa/m) | 60698 | 10320 | 3 | 12850 |
Table 2.
Distribution of data points based on emulsion types.
| Types of Emulsions | Number of Data Points |
|---|---|
| W/O | 3517 |
| W/O + Polymer | 386 |
| W/O + Surfactant | 1675 |
| O/W + Surfactant | 1451 |
2.2. Computational framework
As a computational framework, we used a Google Colab Python interface for dataset processing, analyses, ML model training, evaluation, and validation. Different libraries and functions that are available in Python 3 were used for conducting statistical analyses and producing visualization plots.
2.3. Data preprocessing
2.3.1. Noise removal
In order to remove any existing noise in the dataset, the data columns were checked for invalid values. All the ‘NaN’ (i.e. Not a Number) values in the data columns were replaced by the mean value of that corresponding column. Also, the possible outliers in the dataset were identified using the LocalOutliersFactor algorithm available in the Python package. The number of total data points was reduced to 7002 after the noise removal steps.
2.3.2. Feature normalization
Feature normalization is an important pre-processing step of applying ML algorithms. A z-score standardization technique was applied to normalize all feature values. The objective was to achieve a uniform numerical range for different types of features with various ranges. Each feature column was transformed to a normalized range with mean as zero (0) and standard deviation as one (1), using , where, is the transformed normalized value, is the original value, is the mean over the column features, and is the standard deviation over the column features. A positive standardized z-score indicates the value is above the average, whereas a negative score indicates the corresponding value is below the average.
2.3.3. Feature importance analysis
It is critical to identify the features having the most predictive power or contributing most to predicting the output before applying any ML algorithms. In general, these important features substantially take part in forecasting the outcome through the hypothesis function. The remaining less relevant features can be eliminated in the subsequent stages such as model training and testing due to their lower impacts on the outcome. It usually helps in simplifying the model and accelerating the processes of training and prediction. For the current study, the most relevant features in the context of predicting pressure gradients were selected using the recursive feature elimination by cross-validation (RFECV) method. The RFECV algorithm identifies the most important features by eliminating the lesser relevant or unnecessary features in steps along with cross-validation (CV). It chooses the optimal subset of features to retain based on the CV score of the external estimator model. In the present work, the random forest regressor was used as an external estimator in a 5-fold CV framework in the RFECV algorithm. Fig. 2 shows the CV scores for the features used to train the model. The optimal number of features was found as 12 among a set of 17 features, which is manifested in the graph. The CV score hit the highest value and became constant once the number of selected features reached 12. The ascending order ranking of the 12 most important features is depicted in Fig. 3. These relevant features were used in the model hyperparameter optimization and training stage.
Fig. 2.
RFECV reported CV scores while using selected number of features during feature selection.
Fig. 3.
RFE selected 12 (twelve) important features and their corresponding importance scores.
2.3.4. Feature correlation and interactions
We analyzed the relationships between the important features and the outcome using Pearson's correlation coefficient method. The heatmap analysis of the correlation matrix is shown in Figure A1. The matrix depicts the correlation between the important variables and the outcome (the last column). In terms of the relationship with the outcome, velocity shows the strongest correlation while the pipe diameter stands out as the second highest correlated variable.
Regression-plot, as an exploratory data analytics tool, generally helps to understand the interactions between features and the outcome. We randomly selected 1000 samples to perform the regression plot analysis to understand the non-linear relationships between the top five (5) features. A polynomial function order of two (2) was used to model the relationships between the attributes and the outcome. In Figure A2, the upper and lower diagonals depict the relationships between each pair of attribute columns in the context of the ‘Pressure Loss’ outcome. On the other hand, the univariate distribution for each attribute is shown as a histogram in the main-diagonal subplots. This regression-plot analysis indicates that the relationship between the features and the outcome needs to be modeled as either a higher-order polynomial or other complex non-linear function involving the relevant features.
2.4. ML algorithms
In the current research, six supervised regression models were selected to estimate the real-valued pressure gradients using the twelve most relevant features. The models are Random Forest Regressor (RFR), Extreme Gradient Boosting Regressor (XgBR), Cat Boost Regressor (CBR), Mulit-layer Perceptron Regressor (MLPR), K-Nearest Neighbor Regressor (KNNR), and Decision Tree Regressor (DTR). These constitute a set of recent state-of-the-art ML algorithms that are known to efficiently handle non-linear regression learning problems. An ‘Ensemble Model’ that combines the estimates of the best three models was also used for the current study. This kind of ensemble modeling is developed based on the actual concept of ensemble learning which focuses on making more accurate predictions using an average model, instead of a single model. A brief description of each ML algorithm is provided as follows.
2.4.1. RFR
The RFR is a regression algorithm that is developed based on the random forest ensemble technique. It works as a meta-estimator, which combines multiple randomly drawn decision trees from the data and provides the output of a new estimation as the average. As an ensemble regressor, the RFR produces a stronger model by combining multiple decision tree models. It uses a bootstrapping technique that randomly samples subsets of a dataset over a number of iterations using the required number of features to build each decision tree estimator [23].
2.4.2. CBR
CBR is a decision tree-based gradient-boosting model for supervised regression problems. It is based on the main idea of boosting which is to sequentially fit multiple weak models, which are slightly better estimators than random choices. While fitting, the models continually learn from the mistakes of former models, and the process is continued until any arbitrary differentiable loss function, i.e., the difference between the estimation and actual values is no longer minimized. The minimization of the loss function is performed using a gradient descent optimization algorithm that gives the technique the name of ‘gradient boosting’ [24].
2.4.3. XgBR
The XgBR is an efficient implementation of a gradient-boosting algorithm for regression-based predictive modeling. As mentioned previously, boosting refers to a technique in which several decision trees are added one at a time to an ensemble ML model and fit to rectify the estimation errors made by prior models. The XgBR is designed to be both computationally efficient and highly effective in terms of faster execution and prediction performance [25].
2.4.4. MLPR
MLPR implements a multi-layer perceptron algorithm that is trained using backpropagation in a neural network architecture consisting of several non-linear hidden layers, input, and output layers. The MLPR model is able to learn a non-linear function approximation for any regression problem from the training observations [26].
2.4.5. KNNR
The KNNR is a non-parametric regression method that can be used for regression modeling. In general, the KNNR algorithm uses the concept of ‘feature proximity’ to estimate the continuous values of any new observation. In this technique, any new observation is assigned a value depending on how closely it resembles the observations in a neighborhood in the training set. The K-value in the KNNR model indicates the number of neighbors that needs to take into consideration. The proximity between continuous variables is calculated using distance methods like Euclidean and Manhattan distance [27].
2.4.6. DTR
The DTR is the simplest regression technique that builds the regression model in the form of a tree structure. It splits the dataset into smaller subsets while developing an incremental associated decision tree. Finally, a single tree is produced with the decision and leaf nodes. The decision nodes represent the values of the feature attributes used to build the model, whereas the leaf nodes represent an estimation of the continuous target values. The root node represents the best feature predictor as well as the topmost decision node in a tree [27].
2.4.7. Average regression model
The average regression (AvgR) model that was used for the current study combines the prediction of the top three regression models and produces an ensemble output. Specifically, it runs three best regression models, calculates the average of the three real-valued estimates, and reports that as the final outcome. The ensemble model calculates the output using the following formula.
| (27) |
In Eq. (27), is the estimation of i-th regression model and n is the number of the regression model. The average ensemble model is scalable to any value of n. For the current study, n = 3. The conceptual diagram of our ensemble regressor model is depicted in Fig. 4.
Fig. 4.
The concept of the ensemble (average) regression model: X indicates the input vector consisting of (m) experimental parameters, whereas Model 1, Model 2, and Model 3 represent the top three regression models selected for producing the ensemble model; the combination module averages the individual model estimations, , , and in order to produce the final estimation as .
2.5. ML model training
The training process was initiated after selecting the set of suitable ML algorithms for the current regression problem. The model training involved multiple steps including splitting the datasets into training and hold-out testing, tuning the hyperparameters of the ML model on the training dataset using a suitable technique, fitting the model using the optimal hyperparameters on the training data, and, finally, evaluating the models on hold-out test data using appropriate evaluation metrics. The dataset was split into 80 % of training and 20 % of independent test data. The fit of the ML models included tuning the hyperparameters of the ML algorithms on the training data in a k-fold CV framework. The objective was to find the optimal values of the hyperparameters resulting in the lowest estimation error for the current regression problem. During the k-fold cross-validation, the training data points were divided into k-folds, and the ML model was trained, i.e., its hyperparameters were tuned on (k-1) folds while validating the model with the remaining fold. The process was iterated k-times until each fold was used as a validation set for model evaluation. In the current study, a cross-validated grid search method was used to tune the hyperparameters of the regression models on the training dataset. The grid search method uses various combinations of the specified hyperparameters with corresponding values and measures the mean squared error (MSE) of the model for each combination on the validation dataset. The amalgamation of hyperparameters for which the best performances (i.e., lowest average MSE) had been obtained was reported as the optimal hyperparameters for a particular ML model. The 5-fold cross-validated grid search-based hyperparameter tuning is demonstrated as an algorithmic pseudocode in Fig. 5. Finally, the ML model was trained using the optimal hyperparameters on all the training data. The complete process of ML model training and evaluation is depicted in Fig. 6.
Fig. 5.
Algorithmic pseudocode explaining hyperparameter tuning using 5-fold CV.
Fig. 6.
A flowchart elucidating the complete ML model training and evaluation process.
2.6. Evaluation metrics
A set of evaluation metrics was selected for assessing the ML models and identifying the best-performing model for the current regression problem [[20], [21], [22]]. The metrics are described in the following paragraphs.
2.6.1. Coefficient of determination
Coefficient of determination (R2) is a regression performance score, which represents the amount of variance in the response variables that can be explained by the feature parameters. The value of R2 score usually varies between 0 and 1; R2 = 1.0 if the model can predict with 100 % accuracy. Any negative value of R2 indicates an arbitrarily worse model. The mathematical formula for R2 score is defined as follows,
| (28) |
| (29) |
In Eqs. 28 and 29 is the estimation, is actual value, is the mean actual value, and is the total number of data points.
2.6.2. Mean absolute error
The mean absolute error (MAE) measures the average of the absolute differences between the actual and estimated values. This score expresses the magnitude of error between the estimation (model output) of an observation and the experimentally measured value of that observation. The MAE score is defined using Eq. (30):
| (30) |
2.6.3. Median absolute error
The median absolute error (MDAE) score is a regression performance measure that is able to calculate the variability of the true and estimated values of a sample dataset. This evaluation metric is useful as it is robust to outliers. The error is calculated by taking the median of all absolute differences between the actual and estimated values. The MDAE score is calculated using Eq. (31):
| (31) |
2.6.3.1. Mean squared error
The mean squared error (MSE) is a regression score to measure the average of the squared differences between the actual and estimated values. MSE is also considered the expected value of the squared error loss. This metric is strictly a positive value that decreases as the estimation error approaches zero. The correlation to calculate the MSE score is presented below with Eq. (32):
| (32) |
2.6.4. Root mean squared error
The root mean squared error (RMSE) represents the square root of the mean squared deviations between the model estimations and true values of the observations. It is a popular measure to evaluate regression models which aggregates the magnitude of the estimation errors for a set of data points into a single measure of estimation power. RMSD is a non-negative value and a value of zero indicates a perfect fit of the model to the data points. The lower the RMSD, the better the model's performance is. The RMSE is calculated with Eq. (33):
| (33) |
2.6.5. Coefficient of variation of mean squared error
The coefficient of variation of MSE (CV-MSE) score is a measure that calculates the ratio of the mean squared error and the mean of the dependent variables () in a set of observations. It is a relative measure of the model's variability that calculates the size of the mean square deviation of its estimations in relation to the mean actual values. The lower the value of CV-MSE, the lesser the variability is. The following Eq. (34) is used to calculate the CV-MSE score:
| (34) |
2.6.6. Explained variance score
The explained variance score is a measure that captures the model's ability to explain the variance of the dataset. The score represents the fraction of the variation being explained by the model. Usually, a high explained variance score indicates the model's superior estimation power. If the estimation error of a model is unbiased, the explained variance and R2 scores will be identical. The explained variance is defined as follows (Eq. (35)):
| (35) |
2.6.7. Max error
The max error score is simply the maximum of the absolute deviation between actual and estimated values. This score shows the highest estimation error made by each of the regressor models. The max error is defined using the following Eq. (36):
| (36) |
2.6.8. Regression AUC-ROC score
The AUC-ROC score represents the area under the receiver operating characteristic curve from prediction scores. In the regression scenario, it is calculated based on the fundamental concept of finding the probability that a classifier will rank a randomly chosen larger-valued instance higher than a randomly chosen lower-valued one. It is equal to the probability that the regression model actually ranks o1 higher than o2 when considering any two observations, o1 and o2, such that o1 > o2 in terms of continuous real values.
3. Results and discussion
3.1. Hyperparameter tuning
The hyperparameter optimization of the ML algorithms was performed using the grid search method via a 5-fold CV framework. We chose a set of important parameters for each algorithm to optimize on the training data, which is a common practice (see, for example, [18,21]). A range or a list of values was specified for each parameter during the grid search with MSE as the evaluation metric. The values of parameters for which the lowest MSE value was obtained for each regression model were reported as the optimal parameter values. The names of the parameters along with the range and the optimized value of each parameter of the six regression models are shown in Table 3. The GridSearchCV method in the ‘sklearn’ package was used for hyperparameter optimization for the current study. For the tree-based models, the most common hyperparameter to tune is the ‘n_estimators’ (‘iterations’ in the case of RFR), which indicates the number of trees in the forest of the model. Interestingly, the XgBR model requires a larger number of trees for constructing an optimal forest of the model compared to CBR and RFR, which was evident in the longer training time in the case of XgBR modeling. The optimal ‘depth’ for both CBR and DTR models was found as comparable. The best error criterion for the DTR model was ‘squared error’. The optimal value for ‘alpha’ or the regularization parameter in MLPR resulted as 0.05 for 1000 training iterations, which indicates a penalty needed to be imposed on the coefficient size to avoid model overfitting. For the KNNR (k-nearest neighbors regressor) model, the 'weight' parameter plays a crucial role in determining the influence of neighboring samples on the current sample's prediction. In this study, the optimal value for the 'weight' parameter was found to be 'distance'. This setting implies that neighbors with smaller distances to the current sample will have a larger weight associated with them, while neighbors with larger distances will have a relatively smaller weight.
Table 3.
The optimized hyperparameter values and the corresponding ranges for an optimal parameter grid search.
| Model | Hyperparameters | Range | Optimal Parameter Value |
|---|---|---|---|
| CBR | depth | (10, 18) | 16 |
| learning_rate | (0.01, 0.1) | 0.1 | |
| iterations | (30, 50, 100) | 100 | |
| RFR | n_estimators | (30, 50, 100, 150) | 150 |
| min_samples_split | (0.6, 2, 3) | 2 | |
| max_features | (‘sqrt’, ‘log2’, 0.6,1.0) | log2 | |
| XgBR | learning_rate | (0.05, 0.20) | 0.20 |
| n_estimators | (500, 1500, 2000) | 2000 | |
| KNNR | n_neighbors | (3, 10, 1) | 6 |
| weights | (‘uniform’, ‘distance’) | ‘distance’ | |
| MLPR | max_iter | (1000, 2000) | 1000 |
| hidden_layer_sizes | ((150,100,50),(200,150,100)) | (200,150,100) | |
| alpha | (0.05, 0.001) | 0.05 | |
| DTR | criterion | ('squared_error', 'friedman_mse', 'absolute_error', 'poisson') | 'squared_error' |
| max_depth | (5, 20) | 17 |
3.2. Model performance on test data
The performance of the regression models (AvgR, CBR, RFR, XgBR, MLPR, KNNR, and DTR) along with that of the theoretical model on the independent test data is presented in Table 4. Even though RF, CBR, and XgBR demonstrated highly accurate performance, the best results were obtained by using the average regressor. Indeed, a paired t-test revealed that the comparative differences between the performance of the AvgR model and that of the top three models (RF, CBR, and XgBR) were statistically significant as p < 0.005 with a 95 % confidence interval. In fact, the AvgR was distinctively the top-performing model in terms of all regression metrics. Among the six base ML models considered in the study, the tree-based models (RFR, CBR, and XgBR) demonstrated superior performance compared to traditional models like MLPR and KNNR across all evaluation metrics. However, it is worth noting that KNNR exhibited lower error trends than MLPR in terms of all error metrics, including MAE, RMSE, CV_MSE, and Max Error, indicating its relatively better performance in terms of prediction accuracy. The DTR model, characterized by its simple decision tree logic, exhibited the lowest performance among all the ML models. This outcome is understandable due to the limited complexity of the decision tree model compared to other ML algorithms. In contrast, the theoretical model performed significantly worse in comparison to the ML models. This disparity in performance was expected, primarily because the theoretical model relies on heuristic equations to estimate the output, which may not fully capture the complexities of the dataset. Interestingly, even the relatively underperforming DTR model produced more reliable predictions than the theoretical model for the current dataset. This highlights the potential of ML models, even those with lower performance, to provide more accurate predictions compared to traditional theoretical models in this context.
Table 4.
The performance assessment of six regressors, the average regressor, and the theoretical model on independent test data using different evaluation metrics (the best performance of the AvgR is shown in bold while the worst performance of the theoretical model is displayed in italics).
| Model |
R2 |
AUC-ROC Score |
MAE |
MDAE |
MSE |
RMSE |
CV_MSE |
Explained Variance Score |
Max Error |
|---|---|---|---|---|---|---|---|---|---|
| AvgR | 0.997 | 0.983 | 377 | 170.93 | 479260 | 692.29 | 46.33 | 0.997 | 5465 |
| RFR | 0.996 | 0.983 | 417 | 180.75 | 644242 | 802.65 | 62.29 | 0.996 | 6843 |
| CBR | 0.997 | 0.980 | 424 | 224.34 | 549249 | 741.11 | 53.10 | 0.997 | 6943 |
| XgBR | 0.996 | 0.975 | 473 | 265.82 | 602523 | 776.22 | 58.25 | 0.996 | 6572 |
| MLPR | 0.995 | 0.976 | 496 | 244.09 | 867594 | 931.45 | 83.87 | 0.995 | 8822 |
| KNNR | 0.995 | 0.979 | 462 | 208.22 | 752476 | 867.45 | 72.74 | 0.995 | 7859 |
| DTR | 0.992 | 0.972 | 577 | 249.38 | 1270870 | 1127.33 | 122.85 | 0.992 | 11371 |
| Theoretical model | 0.916 | 0.939 | 1995 | 811.30 | 13516294 | 3676.45 | 1306.61 | 0.922 | 23125 |
3.3. Prediction error trend analysis with an increasing number of features
We analyzed the estimation error trends of the best model, AvgR on the independent test data using several evaluation metrics including MDAE, MAE, and CV_MSE. For this set of experiments, prediction errors were estimated by increasing the number of features for training. The degree of errors continued reducing up to twelve (12) features. Using more features did not decrease the prediction error any further. In Fig. 7, the error curves are drawn against the number of features exploited during training. The error trend is particularly visible for the CV_MSE metric in the figure. The outcome of this experiment corroborates that one of the best-performing ML models shows no further improvements in estimating the pressure losses for an increasing number of features beyond 12. In addition, it validates the feature importance experiments that also demonstrated the optimal number of features as 12.
Fig. 7.
Presentation of the prediction error trends with respect to the number of features used for training in the case of the AvgR regression model.
3.4. Comparison of models’ performances
A detailed performance analysis was carried out for all models using various visualization plots including scatter diagrams, prediction error plots, and boxplots. The scatter plot in Fig. 8 shows the estimations from seven regression models for the test data, in which the X-axis represents the measured values of pressure losses and the Y-axis stands for its estimated values. In the case of perfect modeling, all the data points lie exactly on the ideal regression line, which is the diagonal. On the other hand, the imperfect model's estimations show a higher deviation from the diagonal line. As can be seen in Fig. 8, the AvgR estimations (red points) lie very close to the perfect regression line indicating a close agreement between measured and estimated values with the R2 value of 0.997, while other ML models exhibit comparatively higher deviations from the ideal regression line.
Fig. 8.
Comparative performances of six regression models against the average model in predicting pressure losses on test data.
As mentioned previously, a few models were developed earlier on the theoretical framework to estimate the pressure losses associated with the pipeline transportation of emulsions. The author of the current dataset also developed a theoretical model based on similar models available in the literature [7]. The model was validated with the experimental measurements. Our best regression model responses on the independent test data were compared with the corresponding predictions of the theoretical model. Fig. 9 illustrates the scatter distribution plot of the models’ responses. As shown in the figure, the theoretical model predictions (blue dots) show significantly higher deviations compared to the AvgR (red dots). In terms of the R2-score, the theoretical estimations achieved only 91 %, whereas ML estimations reached as high as 99.7 %. Note that the theoretical model consists of equations that exploit a heuristic combination of the experimental parameters based on physics. Unlike ML, there was no attempt of learning the parametric weights from the training data.
Fig. 9.
Scatter plot illustrating a comparison of the estimations obtained with the theoretical model and the average regressor for the independent test data.
3.5. Estimation error analysis for ML and theoretical models
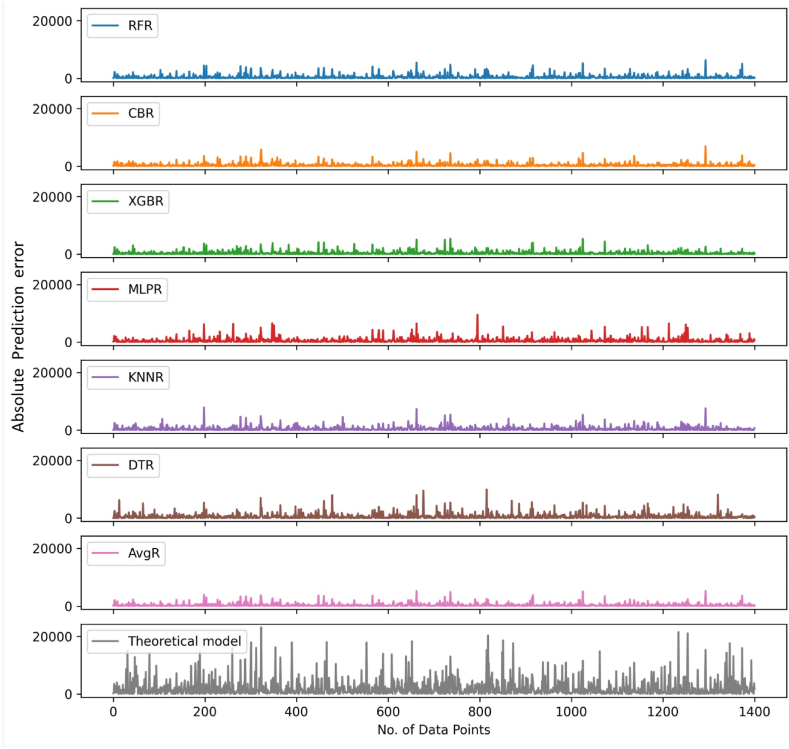
The absolute prediction error plots of the regressors and the theoretical model are illustrated in Fig. 10. This kind of visualization plot is useful in realizing the error trends over individual data points. As shown in the figure, the absolute error trends for the best three regressors are lower than other models. In the case of the AvgR model, the error peaks are smoothed when averaging over the three responses. Consequently, the corresponding error distribution contains comparatively smaller error peaks. On the other hand, the theoretical model's estimation error plot consists of more and higher error peaks when compared to any ML model. The maximum error was more than 20,000 units for the theoretical model, whereas the highest error observed for any of the ML models was less than 9000 units.
Fig. 10.
The estimation errors in the predicted pressure losses on independent test data by using ML and theoretical models.
Further analysis of the various error distributions of the ML models for independent test data was carried out over 100 iterations with randomly generated (i.e. shuffled) training and test sets in each iteration. This experiment was conducted to assess the consistency of the predictive performances of the ML regression models. Specifically, the MSE, CV_RMSE, and MDAE error value ranges in the iterations were explained by placing those into boxplots for each of the seven models. The middle horizontal line in a boxplot indicates the median value of the estimation errors for each method. The distance from the top edge to the bottom edge of the box refers to the interquartile range (IQR). The values shown as circles outside the whiskers represent the outliers for a specific method. In the case of CV_RMSE boxplots (Fig. 11), the median quartile lines are found almost exactly in the middle of the IQR for the top-performing models (RFR, CBR, XgBR, and AvgR). This trend indicates that errors are equally distributed in the upper and lower quartile areas. The CV_RMSE error ranges of these four models did not exceed 100 units for 100 % of test data points. On the other hand, the top three models show a higher range of errors in the case of the MAE boxplot analysis (Figure A3). Whereas approximately 80 % of errors lie below 450 units of error of the top three models, the average regressor has the MAE ranges below 400 units for all cases. Specifically, more than 50 % of MAE errors fall below 350 units for the best-performing AvgR model. For these two types of errors, the lower and upper whiskers stretch over a smaller range of scores that includes the errors outside the median quartile range. The MDAE analysis using boxplots shows a wider range of error distribution for all four models of interest (Figure A4). The lower and upper whisker ranges are wider, which indicates that more errors fall outside the median quartile line. Even with these error trends, the AvgR model shows the best performance compared to other regression models. All four quartiles of the AvgR model boxplot fall below 200 units of MDAE. The current boxplot analysis clearly demonstrates the superiority of the AvgR model while showing the following two trends.
-
1.
Compared to the other regression models, the AvgR model shows either no or a few outliers for all evaluation metrics;
-
2.
The IQR for the AvgR boxplots is either the smallest among all models or comparable to those of the top three models.
Fig. 11.
Boxplot analysis for CV_RMSE prediction error of different ML algorithms on independent test data using 100 iterations.
These results indicate the robustness of the AvgR model as it invariably produces the least amount of estimation errors.
3.6. Applications and future research
The best-performing ML model, AvgR is directly applicable in its current form to predict the pressure losses for the pipeline transportation of emulsions at a given set of process conditions. Values of twelve design or operational parameters are required as input from the user. These input parameters are treated as predictors to provide the output of the pressure gradient. An overview of how to implement the ML model is shown in Fig. 12 with a block diagram. This kind of user-friendly automated system is developed with the implementation of a decision support system (DSS). A DSS expedites the process of comparing a set of engineering scenarios, significantly reducing the time to make decisions based on the predictions. It is especially important when the relationship between input(s) and output is non-linear and complex. A DSS also helps to address the following human limitations: (a) manual data analysis and interpretation usually introduce bias into predictions; (b) ML modeling can be complex as it requires programming skills and deep AI knowledge. It can provide an estimation of the pressure gradient for pipeline transportation of emulsions to any end-user, such as a general pipeline engineer or management personnel who does not necessarily have in-depth knowledge in the fields of emulsion mechanics, computer programming, artificial intelligence, or data science. Thereby, a DSS can contribute directly by improving the efficiency of engineering design, optimization, and project management processes related to emulsion pipelines. Accurate estimation of the pressure gradient is important in determining the flow rate and overall efficiency of such systems. Using the DSS to predict pressure gradients under various flow conditions, such as laminar/turbulent flow and emulsion composition, engineers can select optimal pipe diameters, pressure losses, and pump sizes to improve efficiency, reduce energy consumption, and minimize costs for long-distance transportation of emulsion. However, more research is necessary to develop a user-friendly DSS based on the current AvgR model to estimate the pressure losses for emulsion transportation.
Fig. 12.
Presentation of the working methodology for the AvgR-based automated system that can be used to predict the pressure gradient for the pipeline transportation of emulsion.
It should be noted that four steel pipes with nominal diameters of ¼ inch, ½ inch, ¾ inch, and 1 inch as well as a 1-inch PVC pipe were used for generating the current dataset. However, industrial-scale operations may involve pipes as large as 30 inches. More data should be produced using larger pipes with varying surface roughness so that the current model can be validated prior to its industrial-scale applications. The database, as demonstrated in Fig. 12, can always be updated with new data to improve prediction accuracy. It makes the DSS-based application of an ML model robust.
4. Conclusion
The current research presents an ML-based method to estimate the pressure losses for emulsion flows in pipelines. A set of six state-of-the-art regression models are trained and evaluated on an emulsion flow dataset consisting of more than 7000 data points. In addition, an ensemble regression model, AvgR is developed by computing the mean of the top three model estimations. It demonstrates superiority over all other models when rigorously evaluated using nine evaluation metrics on the independent test set. Furthermore, a comparative analysis between the physics-based theoretical model and the AvgR regression model distinctly exhibits the superior accuracy of the AI-based estimations of the pressure losses. The outstanding performance of the ML model manifests its extreme utility in the engineering design, operation, and maintenance of emulsion pipelines. The main findings of the present study are described below.
-
1.
The feature interaction analyses suggest non-linear interactions between experimental features and the pressure gradient outcome.
-
2.
Out of 17 available experimental parameters, the feature importance study reveals a set of 12 significant variables that contribute most towards estimating the pressure losses.
-
3.
With a 99.70 % of R2 and Explained Variance scores, the AvgR model estimations show the highest agreement with the measured values of pressure losses among all regression models.
-
4.
The AvgR demonstrates considerably superior performance with respect to the key regression metrics as its error is orders of magnitude less than that of the theoretical model.
5. Data Availability Statement
The data utilized in this study were obtained from a PhD research [7]. The complete document can be accessed online at the provided link: https://uwspace.uwaterloo.ca/bitstream/handle/10012/4890/Thesis%203.pdf?sequence=1. The experimental procedures necessary for collecting the data were performed in Professor Pal's laboratory, which is situated at the University of Waterloo in Canada.
CRediT authorship contribution statement
Noor Hafsa: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Sayeed Rushd: Writing – review & editing, Writing – original draft, Validation, Supervision, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Hadeel Alzoubi: Writing – review & editing, Visualization, Software, Resources, Investigation. Majdi Al-Faiad: Writing – review & editing, Writing – original draft, Data curation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The current research was supported through the Annual Funding track by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. 3353]. We would also like to acknowledge the patronage of the College of Engineering and the College of Computer Science and Information Technology at King Faisal University.
Appendix.
Fig. A1.
Presentation of the correlation analysis among the most relevant features and outcomes.
Fig. A2.
Regression analysis of relationships between top five (5) features and outcome for sample data points.
Fig. A3.
Boxplot analysis for MAE prediction error of different ML algorithms on independent test data using 100 iterations
Fig. A4.
Boxplot analysis for MDAE prediction error of different ML algorithms on independent test data using 100 iterations.
References
- 1.Al-Yaari M., Hussein I.A., Al-Sarkhi A. Pressure drop reduction of stable water-in-oil emulsions using organoclays. Appl. Clay Sci. 2014;95:303–309. doi: 10.1016/j.clay.2014.04.029. [DOI] [Google Scholar]
- 2.Hoshyargar V., Ashrafizadeh S.N. Optimization of flow parameters of heavy crude oil-in-water emulsions through pipelines. Ind. Eng. Chem. Res. 2013;52(4):1600–1611. doi: 10.1021/ie302993m. [DOI] [Google Scholar]
- 3.Inkson N.J., Plasencia J., Lo S. Metallurgical and Process Industries, In: CFD2014; 2014. Predicting emulsion pressure drop in pipes through CFD multiphase rheology models; pp. 453–458. (10th International Conference on CFD in Oil & Gas). [Google Scholar]
- 4.Omer A., Pal R. Pipeline flow behavior of water‐in‐oil emulsions with and without a polymeric additive in the aqueous phase. Chem. Eng. Technol.: Industrial Chemistry‐Plant Equipment‐Process Engineering‐Biotechnology. 2010;33(6):983–992. doi: 10.1002/ceat.200900297. [DOI] [Google Scholar]
- 5.Pal R. Viscous behavior of concentrated emulsions of two immiscible Newtonian fluids with interfacial tension. J. Colloid Interface Sci. 2003;263(1):296–305. doi: 10.1016/S0021-9797(03)00125-5. [DOI] [PubMed] [Google Scholar]
- 6.Plasencia J., Inkson N., Nydal O.J. Research on the viscosity of stabilized emulsions in different pipe diameters using pressure drop and phase inversion. Experimental and Computational Multiphase Flow. 2021:1–23. doi: 10.1007/s42757-020-0102-2. [DOI] [Google Scholar]
- 7.Omer A. Ph.D. Dissertation, University of Waterloo; Ontario: 2009. Pipeline Flow Behavior of Water-In-Oil Emulsions.https://uwspace.uwaterloo.ca/bitstream/handle/10012/4890/Thesis%203.pdf?sequence=1 [Google Scholar]
- 8.Pal R. Rheology of polymer‐thickened emulsions. J. Rheol. 1992;36(7):1245–1259. doi: 10.1122/1.550310. [DOI] [Google Scholar]
- 9.Pal R. Shear viscosity behavior of emulsions of two immiscible liquids. J. Colloid Interface Sci. 2000;225(2):359–366. doi: 10.1006/jcis.2000.6776. [DOI] [PubMed] [Google Scholar]
- 10.Pal R. Evaluation of theoretical viscosity models for concentrated emulsions at low capillary numbers. Chem. Eng. J. 2001;81(1–3):15–21. doi: 10.1016/S1385-8947(00)00174-1. [DOI] [Google Scholar]
- 11.Pal R., Rhodes E. Viscosity/concentration relationships for emulsions. J. Rheol. 1989;33(7):1021–1045. doi: 10.1122/1.550044. [DOI] [Google Scholar]
- 12.Morris J.F., Boulay F. Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 1999;43(5):1213–1237. doi: 10.1122/1.551021. [DOI] [Google Scholar]
- 13.Krieger I.M., Dougherty T.J. A mechanism for non‐Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959;3(1):137–152. doi: 10.1122/1.548848. [DOI] [Google Scholar]
- 14.Shaban H., Tavoularis S. Measurement of gas and liquid flow rates in two-phase pipe flows by the application of machine learning techniques to differential pressure signals. Int. J. Multiphas. Flow. 2014;67:106–117. doi: 10.1016/j.ijmultiphaseflow.2014.08.012. [DOI] [Google Scholar]
- 15.Zhang Y., Azman A.N., Xu K.W., Kang C., Kim H.B. Two-phase flow regime identification based on the liquid-phase velocity information and machine learning. Exp. Fluid. 2020;61:1–16. doi: 10.1007/s00348-020-03046-x. [DOI] [Google Scholar]
- 16.Khamehchi E., Bemani A. Prediction of pressure in different two-phase flow conditions: machine learning applications. Measurement. 2021;173 doi: 10.1016/j.measurement.2020.108665. [DOI] [Google Scholar]
- 17.Rushd S., Gazder U., Qureshi H.J., Arifuzzaman M. Advanced machine learning applications to viscous oil-water multi-phase flow. Appl. Sci. 2022;12(10):4871. doi: 10.3390/app12104871. [DOI] [Google Scholar]
- 18.Hafsa N., Rushd S., Yousuf H. Comparative performance of machine-learning and deep-learning algorithms in predicting gas–liquid flow regimes. Processes. 2023;11(1):177. doi: 10.3390/pr11010177. [DOI] [Google Scholar]
- 19.Aljubran M.J., AlBahrani H.I., Ramasamy J., Magana-Mora A. Drilling fluid properties prediction: a machine learning approach to automate laboratory experiments. Research Square, preprint. 2022 doi: 10.21203/rs.3.rs-1407939/v1. [DOI] [Google Scholar]
- 20.Wahid M.F., Tafreshi R., Khan Z., Retnanto A. Prediction of pressure gradient for oil-water flow: a comprehensive analysis on the performance of machine learning algorithms. J. Petrol. Sci. Eng. 2022;208 doi: 10.1016/j.petrol.2021.109265. [DOI] [Google Scholar]
- 21.Wahid M.F., Tafreshi R., Khan Z., Retnanto A. Automated flow pattern recognition for liquid–liquid flow in horizontal pipes using machine-learning algorithms and weighted majority voting. ASME. Letters Dyn. Sys. Control. 2023;3(1) doi: 10.1115/1.4056903. [DOI] [Google Scholar]
- 22.Wahid M.F., Tafreshi R., Khan Z., Retnanto A. A hybrid model to predict the pressure gradient for the liquid-liquid flow in both horizontal and inclined pipes for unknown flow patterns. Heliyon. 2023;9(4) doi: 10.1016/j.heliyon.2023.e14977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Svetnik V., Liaw A., Tong C., Culberson J.C., Sheridan R.P., Feuston B.P. Random forest: a classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003;43(6):1947–1958. doi: 10.1021/ci034160g. [DOI] [PubMed] [Google Scholar]
- 24.Hancock J.T., Khoshgoftaar T.M. CatBoost for big data: an interdisciplinary review. Journal of big data. 2020;7(1):1–45. doi: 10.1186/s40537-020-00369-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chen T., Guestrin C. Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining. 2016. Xgboost: a scalable tree boosting system; pp. 785–794. [DOI] [Google Scholar]
- 26.Murtagh F. Multilayer perceptrons for classification and regression. Neurocomputing. 1991;2(5–6):183–197. doi: 10.1016/0925-2312(91)90023-5. [DOI] [Google Scholar]
- 27.Hastie T., Tibshirani R., Friedman J.H., Friedman J.H. second ed. Springer; New York: 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data utilized in this study were obtained from a PhD research [7]. The complete document can be accessed online at the provided link: https://uwspace.uwaterloo.ca/bitstream/handle/10012/4890/Thesis%203.pdf?sequence=1. The experimental procedures necessary for collecting the data were performed in Professor Pal's laboratory, which is situated at the University of Waterloo in Canada.