Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Dec 18;9(1):1389–1397. doi: 10.1021/acsomega.3c07773

Computational Discovery of High-Temperature Ferromagnetic Semiconductor Monolayer H–MnN2

Hua Chen 1, Ling Yan 1, Xu-li Wang 1, Jing-jing Xie 1, Jin Lv 1,*, Hai-shun Wu 1,*
PMCID: PMC10785093  PMID: 38222525

Abstract

graphic file with name ao3c07773_0007.jpg

In the past few years, two-dimensional (2D) high-temperature ferromagnetic semiconductor (FMS) materials with novelty and excellent properties have attracted much attention due to their potential in spintronics applications. In this work, using first-principles calculations, we predict that the H–MnN2 monolayer with the H–MoS2-type structure is a stable intrinsic FMS with an indirect band gap of 0.79 eV and a high Curie temperature (Tc) of 380 K. The monolayer also has a considerable in-plane magnetic anisotropy energy (IMAE) of 1005.70 μeV/atom, including a magnetic shape anisotropy energy induced by the dipole–dipole interaction (shape-MAE) of 168.37 μeV/atom and a magnetic crystalline anisotropy energy resulting from spin–orbit coupling (SOC-MAE) of 837.33 μeV/atom. Further, based on the second-order perturbation theory, its in-plane SOC-MAE of 837.33 μeV/atom is revealed to mainly derive from the couplings of Mn-dxz,dyz and Mn-dx2–y2,dxy orbitals through Lz in the same spin channel. In addition, the biaxial strain and carrier doping can effectively tune the monolayer’s magnetic and electronic properties. Such as, under the hole and few electrons doping, the transition from semiconductor to half-metal can be realized, and its Tc can go up to 520 and 620 K under 5% tensile strain and 0.3 hole doping, respectively. Therefore, our research will provide a new, promising 2D FMS for spintronics devices.

1. Introduction

Spintronics has aroused broad concern on account of the advantages of good nonvolatile properties, long-term high speed, low power dissipation, and high integrity,1,2 and two-dimensional (2D) magnetic materials with unique physical and chemical properties have been widely used in spintronics. However, although many 2D materials have been realized since graphene was successfully stripped in an experiment, most of them lack intrinsic ferromagnetism (FM), and Curie temperatures (Tc) are far below room temperature, which greatly limits their practical application.3−7 In fact, the excellent and effective spintronics materials usually have low dimension, high spin polarization, long-range. FM and high Tc. So, it is urgent to find novel intrinsic 2D FM materials with high spin polarization, good high temperature resistance, and long spin life.

Recently, the experimentally successful synthesis of MoN2 bulk with van der Waals layered structure has attracted many researchers’ interests in transition metal dinitride (TMN2) materials.8,9 Obviously, bulk MoN2 and MoS2 have similar structure,10,11 so refer to the studies of MoS2 monolayers,12−14 many 2H-phase and 1T-phase transition metal dinitride (H-TMN2 and T-TMN2) monolayers were considered and studied. Such as Frapper and Ding et al. predicted that H–MoN2 is a ferromagnetic metal with a high Curie temperature of 420 K, and after hydrogenation, the transition from H–MoN2 to T-MoN2 will happen, and the latter will possess an anisotropic Dirac cone at the off-symmetry reciprocal site.15,16 In addition, Zhao et al. showed that the T-YN2 monolayer is a new type of P-state Dirac half-metal with a Curie temperature of more than 332 K, and its ferromagnetic ground state can be well maintained under carrier doping or external strain.17 Meanwhile, Kan et al. calculated that H-YN2 exhibits ferromagnetic half-metal properties.8 Furthermore, Liu et al. found that T-TaN2 has a robust FM half-metal state and a high Curie temperature (339 K) due to the strong Np–Np direct exchange interaction, and its half-metal gap of 0.72 eV is sufficient to prevent spin-flip transitions. Both T-NbN2 and T-MnN2 are intrinsic ferromagnetic half-metals.18 Besides, Chen et al. used a high-throughput system to study 87 possible H, T, and novel configurations of TMN2, and by means of the density functional theory (DFT), the properties and dynamical, thermodynamical, and mechanical stabilities of some of them were calculated in detail. Among them, T-MnN2 exhibits ferromagnetic half-metallicity with a Curie temperature (360 K) and out-of-plane magnetic anisotropy.19 All these studies indicate that TMN2 materials have great application prospects in spintronic devices.20−26 However, there is still a dearth of reports on H–MnN2. Here, therefore, we are interested in studying the electronic and magnetic properties of H–MnN2.

In this paper, we study the mechanical, dynamical, and thermal stabilities and the electronic and magnetic properties of the H–MnN2 monolayer. Further, we also apply strain and carrier doping to regulate them. The results show that the H–MnN2 monolayer is an intrinsic high-temperature FM semiconductor. Moreover, its FM state and semiconductor properties can be almost well preserved under strain, and Tc shows an increasing trend. For carrier doping, however, the ferromagnetism is also basically maintained very well, but monolayer H–MnN2 will transform from the semiconductor into metal or half-metal. Moreover, using second-order perturbation theory, we analyze the physical origin of the magnetic anisotropy energy (MAE) as well. This study opens the way for the practical application of monolayer H–MnN2 in spintronics.

2. Computational Details

All first-principles calculations were based on the DFT of generalized gradient approximation in the form of Perdew–Burke–Ernzerhof27 inclusion with the help of the VASP28 code. The projector-augmented-wave (PAW)29 method was used to describe the electron–ion interaction. Combined with previous research, the effective Hubbard Ueff = 4.0 eV was added according to Dudarev’s method for the Mn-d orbitals in our work.25,26,30 The cutoff of plane-wave kinetic energy was set to be 500 eV, and a vacuum layer of 20 Å was applied along the z direction to avoid interlayer interactions. The force and total energy convergence criteria were set to 0.01 eV/Å and 10–5 eV. Meanwhile, the 13 × 13 × 1 and 7 × 7 × 1 Monkhorst–Pack k-point grid31 were used for the unit cell and 2 × 2 × 1 supercell calculations, respectively.

Besides, Monte Carlo simulation was used to simulate the Curie temperature of the H–MnN2 monolayer based on the Heisenberg model, and the spin Hamiltonian can be expressed as

2. 1

where ⟨ij⟩ represents all adjacent Mn atomic sites, J represents the magnetic exchange coupling parameters between adjacent Mn atoms, Si/Sj represents the spin vector of magnetic atoms, and A is the magnetic anisotropy parameter of a single atom.32,33

3. Results and Discussion

3.1. Structure and Stability

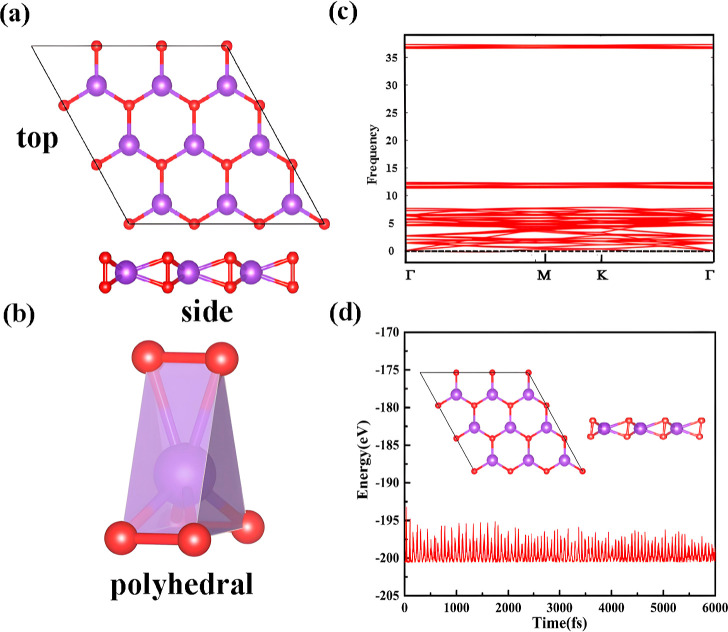
Similar to the H–MoS2 monolayer, the H–MnN2 monolayer also has a hexagonal symmetry structure, composed of one Mn atom layer sandwiched by two same N atom layers on two sides, and the optimal lattice constant is 3.49 Å, as illustrated in Figure 1a,b. Then, as we all know, the stability of 2D materials is very important for experimental synthesis and practical applications in the future. So, we first test the chemical stability of the H–MnN2 monolayer by calculating its cohesive energy, which is defined as follows

3.1. 2

where EMnN2 is the energy of the MnN2 monolayer, and EMn and EN are the energies of the isolated Mn atom and N atom, respectively. By energy calculation, the Ec of the H–MnN2 monolayer is −3.64 eV. The negative cohesive energy obviously indicates that the process is an exothermic chemical reaction and clearly signifies the monolayer’s chemical stability. Next, the elastic constants (Cij) are considered because they can provide a critical message about the mechanical stability of a monolayer.34 The corresponding key parameters are C11 = 300.19 N·m–1, C12 = 160.76 N·m–1, C22 = 292.12 N·m–1, and C66 = 2.52 N·m–1, according to the Born elastic stability criteria of the hexagonal crystal system (C11 > 0, C11·C22 > C122, C66 > 0); the H–MnN2 monolayer is mechanically stable. Further, the Young’s modulus is 214.10 N·m–1 calculated by using E2D = (C112 – C122)/C11, which is much smaller than that of graphene (340 N·m–1),35 but larger than that of 1T-TaN2 (102 N·m–1),18 1T-YN2 (49.20 N·m–1),17 and silicene (62 N·m–1),36−38 etc. This verifies that the H–MnN2 monolayer is a mechanically rigid material as well.

Figure 1.

Figure 1

Open in a new tab

(a,b) Geometric structure, (c) phonon spectrum, and (d) AIMD for a 3 × 3 × 1 supercell of monolayer H–MnN2. The purple and red balls represent Mn and N atoms, respectively.

In addition, we also calculate the phonon spectrum of monolayer H–MnN2 based on the density functional perturbation theory embedded in phonon software to evaluate its dynamic stability. It can be seen from Figure 1c that there is no imaginary frequency in the entire Brillouin zone of phonon spectra, indicating that the H–MnN2 monolayer is dynamically stable. At the same time, as shown in Figure 1d, based on the canonical ensemble (NVT) with a Nose’ thermostat for temperature control, 3 × 3 × 1 supercell of H–MnN2 is put at 300 K with a total of 6 ps at 1 fs per step for molecular dynamics simulation (AIMD). Obviously, the energy fluctuates within a very small range, and the final structure is also well preserved during the whole simulation, confirming its thermal stability.

3.2. Magnetic and Electronic Properties

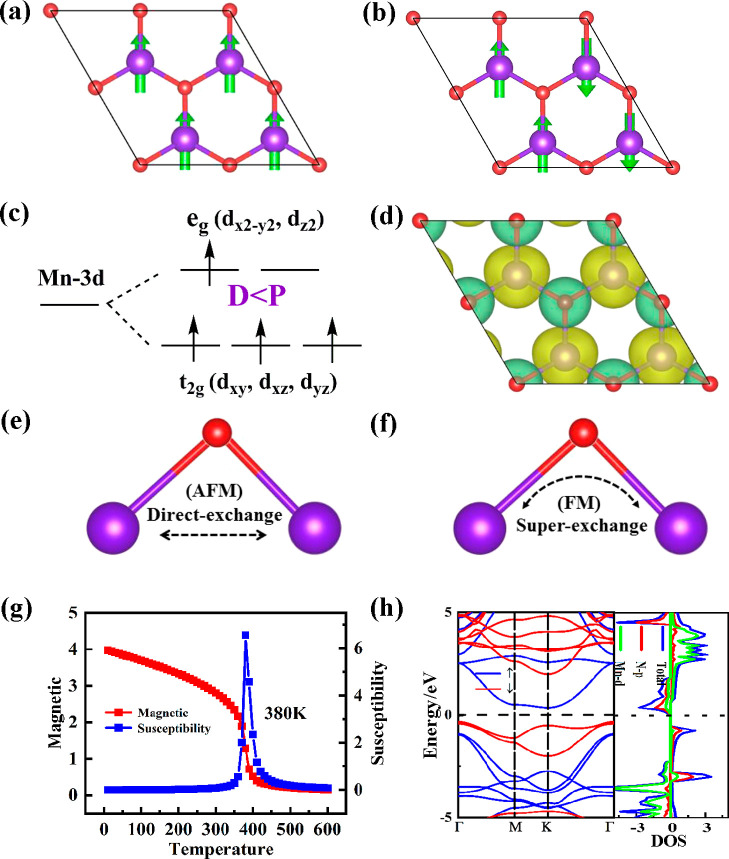
After confirming the stability of the monolayer, we next study the magnetic properties of the H–MnN2 monolayer. To begin with, in order to determine the magnetic ground state of the H–MnN2 monolayer, two magnetic configurations are designed in a 2 × 2 × 1 supercell (Figure 2a,b). The energy calculations show that the energy difference between the FM configuration and the antiferromagnetic (AFM) configuration is 102.48 meV per unit cell, and the FM configuration has lower energy, indicating that the Mn atoms prefer the ferromagnetic couple. Meanwhile, we also find the total magnetic moment per unit cell of the H–MnN2 monolayer is 3.26 μB, which is mostly contributed by Mn atoms (4.07 μB) because that per N atom only provides an opposite magnetic moment of 0.41 μB. The reason may be that the d orbital of the Mn atom causes a small crystal field split due to the ligand effect of the N atoms; the Mn atom appears in a high spin state, as shown in Figure 2c. Then, by qualitatively analyzing, four d electrons of the Mn atom occupy spin-up dxy, dxz, dyz, and dz2 orbitals, presenting four spin single electrons. In order to more clearly understand the specific charge transfer of electrons inside the material, we calculate the monolayer’s charge transfers based on the Bader charge analysis as well and reveal that each Mn atom denotes 1.293 e charge and each N atom can get 0.646 e charge from the Mn atom. Plus, the spin-polarized charge density displayed in Figure 2d obviously reflects the existence of FM coupling between magnetic atoms as well. Finally, we infer that the ferromagnetic coupling mechanism of the H–MnN2 monolayer may result from the existence of superexchange FM interaction mediated by nonmagnetic N atoms between adjacent magnetic Mn atoms, and its effect is stronger than the direct exchange AFM interaction between adjacent Mn atoms, as depicted in Figure 2e,f.

Figure 2.

Figure 2

Open in a new tab

Different magnetic configurations in the H–MnN2 monolayer: (a) FM and (b) AFM. (c) Splitting of the 3d orbital of the Mn atom in a small crystal field split; the P and D represent the pairing and splitting energies of the d orbitals, respectively. (d) Spin polarized charge density, the yellow area indicates spin up, and the green area indicates spin down. (e,f) Illustrations of the direct exchange and superexchange interactions between the two Mn atoms. (g) Tc of the H–MnN2 unit cell and (h) spin-polarized band structure and the density of states.

As we all know, the Mermin–Wagner theorem indicates that magnetic anisotropy is one of the key factors for the stable existence of two-dimensional intrinsic ferromagnetic materials. Because thermal perturbations can easily destroy the two-dimensional magnetism in Heisenberg’s isotropic model at finite temperatures, magnetic anisotropy can remove this limitation, thus allowing the existence of an intrinsic long-range ferromagnetic sequence. So, a lot of experiments and calculations have been devoted to finding more low-dimensional materials with large MAE to make them more suitable for spintronics.39−41 Usually, MAE is mainly derived from the contributions of magnetocrystalline anisotropy energy resulting from spin–orbit coupling (SOC-MAE) and magnetic shape anisotropy energy induced by the dipole–dipole interaction (shape-MAE) (see the Supporting Information for more details). Therefore, based on the correlative theory, we calculate that the H–MnN2 monolayer possesses a considerable IMAE of 1005.70 μeV/atom, including a shape-MAE of 168.37 μeV/atom and a SOC-MAE of 837.33 μeV/atom. The easy magnetization axis is the y axis. To gain insight into the physical origin of SOC-MAE, the orbital-resolved SOC-MAE and partial density of states (PDOS) of the different Mn-d and N-p orbits are plotted in Figure 3. Directly, we can observe that the contribution of the Mn-d orbital to SOC-MAE is much greater than that of the N-p orbital. For the Mn-d orbitals, in the same spin channel, dx2–y2/dxy and dxz/dyz provide larger positive SOC-MAE (IMAE) through Lz coupling, while dz2/dyz provides an obviously negative SOC-MAE (PMAE) through Lx coupling. Ultimately, the IMAE is partially canceled out by PMAE, and the H–MnN2 monolayer presents an in-plane SOC-MAE (837.33 μeV/Mn).

Figure 3.

Figure 3

Open in a new tab

(a–d) Orbital-resolved MAE and the PDOS of Mn-d and N-p orbitals.

Besides, Curie temperature is an important parameter to measure the practical application of materials.42,43 So, here, considering that the bond lengths of dMn–Mn of the next-nearest- and next–next-nearest neighbor are slightly larger and can be ignored, and in order to simplify the problem of solving J, according to the ferromagnetic and antiferromagnetic configuration of H–MnN2 in Figure 2a,b, we only calculate the nearest-neighbor magnetic exchange coupling parameters J by the following formula.

3.2. 3
3.2. 4

where E0 represents the energy of the nonmagnetic state, the S value of the Mn atom is 2, and A is the single-site magnetic anisotropy parameter, which is numerically equal to MAE/S2. So, the calculated J is 6.04 meV for the H–MnN2 monolayer. Then, using the Monte Carlo simulation based on the Heisenberg model, in which the dual effects of magnetic exchange coupling interaction J and single ion magnetic anisotropy A need to be considered, a supercell of 50 × 50 was used, 105 steps were simulated at each temperature, and all spins were flipped randomly. Finally, it can be seen from Figure 2g that the magnetic susceptibility reaches its maximum at 380 K and the magnetic moment decreases to zero, meaning that the Curie temperature of the H–MnN2 monolayer is 380 K. This is higher than many two-dimensional magnetic materials that have been reported.4−6 It also shows that monolayer H–MnN2 has good prospects in the practical application of spin devices.

In the end, we also understand the electronic properties of monolayers. As shown in Figure 2h, the band calculation shows that the H–MnN2 monolayer is an indirect bandgap of 0.79 eV semiconductor, with the valence band maximum from the spin-down states at the Γ point and the conduction band minimum from the spin-up states at the K point. Further, from the density of states, we can see that the spin states near the Fermi level are mainly contributed by the d orbital of the Mn atom and the p orbital of the N atom, but their contributions to spin up and spin down states are very asymmetrical, which results in the H–MnN2 monolayer having a semiconductor property and exhibiting significant spin polarization.

3.3. Biaxial Strain Modulation

Exploring the influence of external stimuli on the magnetic and electronic properties of materials can enrich and broaden their practical applications. As such, many studies have shown that lattice mismatch will directly occur in the structures of monolayer materials under biaxial strain, resulting in changes in their physical and chemical properties, as well as their magnetic and electronic properties.41,44−46 So, here, we apply a biaxial strain of −5 to 5% to the H–MnN2 monolayer to investigate the changes of its electronic and magnetic properties, and the biaxial strain is defined as

3.3. 5

where a and a0 represent the lattice parameters with and without strain regulation, respectively. Positive and negative values of ε represent tensile and compressive strains, respectively.

First, we survey the effects of strain on the magnetism of the H–MnN2 monolayer. As shown in Figure 4a, intuitively, the energy difference ΔEex (ΔEex = EAFM – EFM) under biaxial strains from −5 to 5% increases almost monotonically over the entire stress range and eventually can rise to 170.82 meV/per unit cell at the 5% tensile strain. The nearly linear curve shows that the biaxial tensile strain has a good regulation effect on the magnetism of the H–MnN2 monolayer, which suggests that the FM states are well maintained and indicates that the ferromagnetic properties of the monolayer would be continuously improved under the larger tensile strain. The increases of the local magnetic moment of the Mn atom (listed in Table S1) from 3.86μB to 4.20μB (5% tensile strain) also confirm the result. At the same time, we also need to pay attention to the large compressive strain that will lead to a phase transition, such as a H–MnN2 monolayer performing an AFM ground state at −5% strain. The reason may be that the strain directly affects the structure of the monolayer and the strength of direct exchange. AFM interaction and superexchange FM interaction are closely related to the bond distance between two adjacent magnetic atoms (dMn1–Mn2) and the bond angle between them and N atom (θMn1–N–Mn2).41,47,49 That is, the larger the dMn1–Mn2, the weaker the direct exchange AFM interaction, and the more the θMn1–N–Mn2 deviates from 90°, the weaker the superexchange FM interaction.41 Therefore, we explore the structural changes of the whole strain, and the results have been presented in Figure S1. Careful analysis reveals that, under compressive stress, the enhancement of the AFM interaction is stronger than that of the FM interaction, so the AFM ground state appears finally. However, under tensile stress, the weakening degree of the AFM interaction gradually increases compared with the weakening degree of the FM interaction, so that the FM state of the monolayer will gradually stabilize and improve under tensile strain. Here, we also calculate the charge transfers between the Mn atom and N atom under the various biaxial strains by using the Bader charge analysis, and the results are shown in Table S2. Obviously, compared to the original charge transfer, the larger compressive strain will increase the number of electrons transferred between the Mn atom and the N atom, and the larger tensile strain will reduce the number of electrons transferred between them. This result is consistent with the magnetic analysis above. As the compressive strain increases, the of FM superexchange interaction gradually weakens, meaning that the exchange of electrons between Mn–N–Mn atoms can be weakened, so the electrons are more inclined to be localized on each atom and the ionic bond of Mn–N is stronger; that is, the number of electrons on the Mn atom and the N atom and the number of electron transfers between them increase. This result is also consistent with the gradual shortening of the bond lengths of dMn–N shown in Table S2 and the gradual reduction of the magnetic moment of the Mn atom shown in Table S1. Of course, the tensile strains finally give the opposite result. Besides, the effect of biaxial strain on the IMAE of the monolayer is completely opposite. As shown in Figure 4b, the monolayer’s IMAE decreases linearly and drops to 0.70 meV/cell at last. Later, based on the Heisenberg model and using Monte Carlo methods, we simulate the Tc of the monolayer under different stresses, and the results are presented in Figure 4c. Clearly, Tc almost exhibits the same trend as ΔEex and can reach a maximum of 520 K at 5% tensile strain. By analyzing the changes of the corresponding influencing factors J and A in Figure S2a, we found that the reason why Tc has such a change is mainly due to the dominant role of the change of J, except for the case of 3% compressive strain, which is mainly affected by A. This also proves that the FM state of the H–MnN2 monolayer can be well regulated under tensile stress.

Figure 4.

Figure 4

Open in a new tab

(a) Exchange energy difference ΔEex of the H–MnN2 monolayer under −5 to 5% biaxial strain. (b) Monolayer’s MAE of biaxial strain and carrier doping, (c) Tc’s change in biaxial strain. (d) Band gaps of the monolayer under −5 to 5% strain, (e) Exchange energy difference ΔEex of the monolayer under 0.5 hole to 0.5 electron doping. (f) Tc of the H–MnN2 monolayer under carrier doping.

Then, the effects of biaxial strain on electronic properties are studied and shown in Figures 5 and S3. Looking at the band structures, we can find that the semiconductor property of the H–MnN2 monolayer is kept under any strain. Further observations show that under the tensile stress, only the spin-up band of the valence band moves down slightly, while under the compression stress, not only the spin-up band of the valence band moves up, but the spin-up band of the conduction band also moves down. However, they do not pass through the Fermi level (Ef) in the end, so the semiconductor properties are still maintained, and their corresponding band gaps are shown in Figure 4d. Then, upon observation of the projected density of states, the same result is given. Besides, we can find that the contribution of the Mn-d orbital near Ef increases with the increase of tensile strain but decreases with the increase of compressive stress.

Figure 5.

Figure 5

Open in a new tab

Spin-polarized band structures of the H–MnN2 monolayer under −5 to 5% biaxial strain, respectively.

3.4. Carrier Doping Modulation

In addition to the biaxial strain, carrier doping may influence the magnetic coupling of systems as well because it would affect the electron transition probability and the magnetic order arrangement of the nearest neighbor metal ions. Furthermore, some previous works have confirmed that carrier doping can achieve the transformation of materials from metal/semiconductor to semimetal and half-metal materials, which can achieve 100% spin polarization, which is beneficial to the practical application of materials.47−52 So, here, we also discuss the influence of carrier doping from 0.5 hole to 0.5 e on magnetism and the electronic properties of this monolayer.

Similarly, the effects of carrier doping on the magnetism of the H–MnN2 monolayer are investigated first. For the magnetic moments, as listed in Table S3, we find that the total magnetic moment of a monolayer can increase both with hole doping and electron doping, and this is mainly because the opposite magnetic moment provided by the N atom decreases significantly with the increase of doping concentration, while the magnetic moment of the Mn atom only increases slightly. Then, combining with the results depicted in Figure 4e, although there is a phase transition in large hole doping, such as when the monolayer shows the AFM ground state when the 0.5 hole is doped, the ΔEex of carrier doping from 0.5 hole to 0.5 e increases almost monotonically, indicating the good modulation effects on magnetism of the H–MnN2 monolayer will appear in large electron doping. While there is a significant energy jump (200.10 meV/per unit cell) occurring at 0.3 hole doping, this may be due to the fact that when this concentration of holes is introduced, the electron transfer number and ferromagnetic sequence between adjacent magnetic atoms appear to change, and then the monolayer’s FM is enhanced. Meanwhile, the MAE of the monolayer should also be considered. As shown in Figure 4b, for electron doping, the IMAE is basically unchanged. However, for the hole doping, its MAE value is significantly enlarged. Finally, based on the Heisenberg model and using the Monte Carlo methods as well, the Tc of every doping case is simulated and basically exhibits an increasing trend, but realizes a maximum of 620 K at 0.3 hole doping, as shown in Figure 4f. Similarly, after comprehensive analysis of the changes of the corresponding influencing factors J and A in Figure S2b, the change of Tc is also mainly affected by the change of J, while the change of A is almost negligible.

Next, as shown in Figures 6 and S4, the influences of carrier doping on electronic properties are also observed by using the band structures and projected density of states. Surprisingly, when doped with 0.1–0.2 electrons, the spin-up bands of the conduction band move down rapidly and then pass through Ef to make the monolayer half-metallic. Then, as more electrons are doped, the spin-down bands of the conduction band also move down quickly and pass through Ef, causing metallicity to appear. While for hole doping, only the spin-down bands of the valence band move up quickly and pass through the Fermi level (Ef) in the end, making the H–MnN2 monolayer half-metallic, except that the AFM H–MnN2 monolayer is metallic under 0.5 hole doping. What’s more, the projected density of states also shows the same results. Here, the realization of half-metal is very important for its application in spintronics.

Figure 6.

Figure 6

Open in a new tab

Spin-polarized band structures of the H–MnN2 monolayer under 0.5 hole–0.5 electronic doping, respectively.

4. Conclusions

In conclusion, with the help of DFT, the electronic structure and magnetic properties of the H–MnN2 monolayer have been investigated comprehensively. We have found that the H–MnN2 monolayer is an intrinsic ferromagnetic semiconductor with a room temperature Tc of 380 K and a considerable IMAE of 1005.70 μeV/atom, including a shape-MAE of 168.37 μeV/atom and a SOC-MAE of 837.33 μeV/atom. Meanwhile, we have also disclosed that the SOC-MAE of 837.33 μeV/atom mainly derives from the couplings of Mn-dxz,dxy and Mn-dx2–y2,dxy orbitals through Lz in the same spin channel. In addition, the two nearly linear curves of ΔEex show the good modulation effect of biaxial tension strain and larger electronic doping on the magnetism of the H–MnN2 monolayer, suggesting that the ferromagnetic properties of this monolayer can be continuously improved by them. Moreover, under the hole and small electronic doping, the transition from semiconductor to half-metal will be realized. So, such a novel monolayer of H–MnN2 with excellent properties and strong regulatory properties is a potential new generation material for spintronics.

Acknowledgments

This work is supported by the Natural Science Foundation of Shanxi province (no. 20210302123336). The authors acknowledge that Jin-lan Wang’s group from Southeast University provides the Monte Carlo simulation software package.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c07773.

  • Theoretical details of MAE simulation; bond angle θMn–N–Mn and bond distance dMn–Mn as a function of applied strain; total magnetic moment (Mtot) of unit cell and magnetic moment of Mn and N atoms under various strains; results of the Bader charge transfer and the changes of the bond length between Mn atom and N atom (dMn–N) of the H–MnN2 monolayer under the various biaxial strains; total magnetic moment (Mtot) of the unit cell and the magnetic moment of Mn and N atoms under various charge doping; changes of the corresponding influencing factors J and A of the H–MnN2 monolayer under the biaxial strains and carrier doping; DOS of biaxial strain modulation, and DOS of carrier doping modulation (PDF)

Author Contributions

† H.C. and L.Y. contributed equally to this study.

The authors declare no competing financial interest.

Supplementary Material

ao3c07773_si_001.pdf (634.4KB, pdf)

References

  1. Lin Y. M.; Dimitrakopoulos C.; Jenkins K. A.; Farmer D. B.; Chiu H. Y.; Grill A.; Avouris Ph. 100-GHz Transistors from Wafer-Scale Epitaxial Graphene. Science 2010, 327, 662. 10.1126/science.1184289. [DOI] [PubMed] [Google Scholar]
  2. Liu M.; Yin X. B.; Ulin-Avila E.; Geng B. S.; Zentgraf T.; Ju L.; Wang F.; Zhang X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. 10.1038/nature10067. [DOI] [PubMed] [Google Scholar]
  3. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  4. Huang B. B.; Clark G.; Navarro-Moratalla E.; Klein D. R.; Cheng R.; Seyler K. L.; Zhong D.; Schmidgall E.; McGuire M. A.; Cobden D. H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
  5. Gong C.; Li L.; Li Z.; Ji H.; Stern A.; Xia Y.; Cao T.; Bao W.; Wang C.; Wang Y.; Qiu Z. Q.; Cava R. J.; Louie S. G.; Xia J.; Zhang X. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. 10.1038/nature22060. [DOI] [PubMed] [Google Scholar]
  6. Liu J. Y.; Sun Q.; Kawazoe Y.; Jena P. Exfoliating biocompatible ferromagnetic Cr-trihalide monolayers. Phys. Chem. Chem. Phys. 2016, 18, 8777–8784. 10.1039/c5cp04835d. [DOI] [PubMed] [Google Scholar]
  7. Zhuo Z. W.; Wu X. J.; Yang J. L. Two-Dimensional Phosphorus Porous Polymorphs with Tunable Band Gaps. J. Am. Chem. Soc. 2016, 138 (22), 7091–7098. 10.1021/jacs.6b02964. [DOI] [PubMed] [Google Scholar]
  8. Wu F.; Huang C. X.; Wu H. P.; Lee C. H.; Deng K. M.; Kan E. J.; Jena P. Atomically Thin Transition-Metal Dinitrides: High-Temperature Ferromagnetism and Half-Metallicity. Nano Lett. 2015, 15, 8277–8281. 10.1021/acs.nanolett.5b03835. [DOI] [PubMed] [Google Scholar]
  9. Wang S. M.; Ge H.; Sun S. L.; Zhang J. Z.; Liu F. M.; Wen X. D.; Yu X. H.; Wang L.; Zhang Y.; Xu H. W.; Neuefeind J. C.; Qin Z. F.; Chen C. F.; Jin C. Q.; Li Y. W.; He D. W.; Zhao Y. S. A New Molybdenum Nitride Catalyst with Rhombohedral MoS2 Structure for Hydrogenation Applications. J. Am. Chem. Soc. 2015, 137, 4815–4822. 10.1021/jacs.5b01446. [DOI] [PubMed] [Google Scholar]
  10. Yu Z. H.; Pan Y. M.; Shen Y. T.; Wang Z. L.; Ong Z. Y.; Xu T.; Xin R.; Pan L. J.; Wang B. G.; Sun L. T.; Wang J. L.; Zhang G.; Zhang Y. W.; Shi Y.; Wang X. R. Towards intrinsic charge transport in monolayer molybdenum disulfide by defect and interface engineering. Nat. Commun. 2014, 5, 5290. 10.1038/ncomms6290. [DOI] [PubMed] [Google Scholar]
  11. Pan H.; Zhang Y. W. Edge-dependent structural, electronic and magnetic properties of MoS2 nanoribbons. J. Mater. Chem. 2012, 22, 7280. 10.1039/c2jm15906f. [DOI] [Google Scholar]
  12. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  13. Economou S. E. High-fidelity quantum gates via analytically solvable pulses. Phys. Rev. B 2012, 85, 241401. 10.1103/PhysRevB.85.241401. [DOI] [Google Scholar]
  14. Liu X. G.; Li Z. Y. Electric Field and Strain Effect on Graphene-MoS2 Hybrid Structure:Ab Initio Calculations. J. Phys. Chem. Lett. 2015, 6, 3269–3275. 10.1021/acs.jpclett.5b01233. [DOI] [Google Scholar]
  15. Yu S. Y.; Huang B. W.; Jia X. J.; Zeng Q. F.; Oganov A. R.; Zhang L. T.; Frapper G. Exploring the Real Ground-State Structures of Molybdenum Dinitride. J. Phys. Chem. C 2016, 120, 11060–11067. 10.1021/acs.jpcc.6b00665. [DOI] [Google Scholar]
  16. Wang Y. L.; Ding Y. The hydrogen-induced structural stability and promising electronic properties of molybdenum and tungsten dinitride nanosheets: a first-principles study. J. Mater. Chem. C 2016, 4, 7485–7493. 10.1039/C6TC02161A. [DOI] [Google Scholar]
  17. Liu Z. F.; Liu J. Y.; Zhao J. J. YN2 monolayer: Novel p-state Dirac half metal for high-speed spintronics. Nano Res. 2017, 10 (6), 1972–1979. 10.1007/s12274-016-1384-3. [DOI] [Google Scholar]
  18. Liu J. Y.; Liu Z. F.; Song T. L.; Cui X. Computational search for two-dimensional intrinsic half-metals in transition-metal dinitrides. J. Mater. Chem. C 2017, 5, 727–732. 10.1039/C6TC04490E. [DOI] [Google Scholar]
  19. Ding J. F.; Yao Q. S.; Sun H. S.; Chen S. B.; Wu F.; Huang C. X.; Kan E. J. High-throughput calculations of spintronic tetra-phase transition metal dinitrides. J. Mater. Chem. C 2021, 9, 14401–14407. 10.1039/D1TC03700E. [DOI] [Google Scholar]
  20. Xu J.; Wang D. S.; Liu Y. H.; Lian R. Q.; Gao X. Y.; Chen G.; Wei Y. J. Theoretical prediction and atomic-scale investigation of a tetra-VN2 monolayer as a high energy alkali ion storage material for rechargeable batteries. J. Mater. Chem. A 2019, 7, 26858–26866. 10.1039/C9TA08580G. [DOI] [Google Scholar]
  21. Sheng X.-F.; Chen S.; Kang W. B.; Fang W. Y. Monolayer XN2 (X = Ti, Zr, Hf): novel 2D materials with high stability, simultaneously high electron and hole mobilities from density functional theory. Mater. Today Commun. 2022, 31, 103313. 10.1016/j.mtcomm.2022.103313. [DOI] [Google Scholar]
  22. Zhang C. Z.; Sun Q. A. Honeycomb BeN2 Sheet with a Desirable Direct Band Gap and High Carrier Mobility. J. Phys. Chem. Lett. 2016, 7, 2664–2670. 10.1021/acs.jpclett.6b01291. [DOI] [PubMed] [Google Scholar]
  23. Wang Y. L.; Ding Y. Uncovering a Stable Phase in Group V Transition-metal Dinitride (MN2, M = Ta, Nb, V) Nanosheets and Their Electronic Properties via First-principles Investigations. J. Phys. Chem. C 2018, 122, 26748–26755. 10.1021/acs.jpcc.8b08885. [DOI] [Google Scholar]
  24. Gao Y.; Pan H. G.; Zhou B. Z. Bilayer hexagonal structure MnN2 nanosheets with room-temperature ferromagnetic half-metal behavior and a tunable electronic structure. Phys. Chem. Chem. Phys. 2023, 25, 23728–23737. 10.1039/D3CP01588B. [DOI] [PubMed] [Google Scholar]
  25. Xu C. Y.; Zhang J.; Tu H. R.; Guo Z. X.; Yuan X. X.; Tian Y. Biaxial strain tuned magnetic anisotropy of ferromagnetic penta-MnN2 monolayer. Solid State Sci. 2021, 117, 106634. 10.1016/j.solidstatesciences.2021.106634. [DOI] [Google Scholar]
  26. Zhao K. X.; Wang Q. High Curie temperature ferromagnetism in penta-MnN2 monolayer. Appl. Surf. Sci. 2020, 505, 144620. 10.1016/j.apsusc.2019.144620. [DOI] [Google Scholar]
  27. Perdew J. P.; Burke K. E. M.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  28. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  29. Blochl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  30. Wang L.; Maxisch T.; Ceder G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 2006, 73, 195107. 10.1103/PhysRevB.73.195107. [DOI] [Google Scholar]
  31. Chadi D. J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. 10.1103/PhysRevB.16.1746. [DOI] [Google Scholar]
  32. Zhang Y. H.; Wang B.; Guo Y. L.; Li Q.; Wang J. L. A universal framework for metropolis Monte Carlo simulation of magnetic Curie temperature. Comput. Mater. Sci. 2021, 197, 110638. 10.1016/j.commatsci.2021.110638. [DOI] [Google Scholar]
  33. Mermin N. D.; Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133–1136. 10.1103/PhysRevLett.17.1133. [DOI] [Google Scholar]
  34. Mouhat F.; Coudert F. X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
  35. Lee C.; Wei X. D.; Kysar J. W.; Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  36. Ding Y.; Wang Y. L. Density Functional Theory Study of the Silicene-like SiX and XSi3 (X = B, C, N, Al, P) Honeycomb Lattices: The Various Buckled Structures and Versatile Electronic Properties. J. Phys. Chem. C 2013, 117, 18266–18278. 10.1021/jp407666m. [DOI] [Google Scholar]
  37. Zhao T. S.; Zhou J.; Wang Q.; Kawazoe Y.; Jena P. Ferromagnetic and Half-Metallic FeC2 Monolayer Containing C2 Dimers. Appl. Mater. Interfaces 2016, 8, 26207–26212. 10.1021/acsami.6b07482. [DOI] [PubMed] [Google Scholar]
  38. Zhang Y.; Kang J.; Zheng F.; Gao P. F.; Zhang S. L.; Wang L. W. Borophosphene: A New Anisotropic Dirac Cone Monolayer with a High Fermi Velocity and a Unique Self-Doping Feature. J. Phys. Chem. Lett. 2019, 10, 6656–6663. 10.1021/acs.jpclett.9b02599. [DOI] [PubMed] [Google Scholar]
  39. Zhang J. M.; Yang B. S.; Zheng H. L.; Han X. F.; Yan Y. Large magnetic anisotropy and strain induced enhancement of magnetic anisotropy in monolayer TaTe2. Phys. Chem. Chem. Phys. 2017, 19, 24341–24347. 10.1039/C7CP04445C. [DOI] [PubMed] [Google Scholar]
  40. Gong C.; Kim E. M.; Wang Y.; Lee G.; Zhang X. Multiferroicity in atomic van der Waals Heterostructures. Nat. Commun. 2019, 10, 2657. 10.1038/s41467-019-10693-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wang X. L.; Guo H. M.; Chen H.; Yan L.; Xie J. J.; Zhang Y.; Lv J.; Wu H. Intrinsic ferromagnetic half-metal: Non-equivalent alloying compounds CrMnI6 monolayer. Appl. Surf. Sci. 2023, 623, 157084. 10.1016/j.apsusc.2023.157084. [DOI] [Google Scholar]
  42. Anderson P. W. New Approach to the Theory of Superexchange Interactions. Phys. Rev. 1959, 115, 2–13. 10.1103/PhysRev.115.2. [DOI] [Google Scholar]
  43. Bhattacharyya G.; Choudhuri I.; Bhauriyal P.; Garg P.; Pathak B. Ferromagnetism in magnesium chloride monolayer with an unusually large spin-up gap. Nanoscale 2018, 10, 22280–22292. 10.1039/C8NR07429A. [DOI] [PubMed] [Google Scholar]
  44. Dong X. J.; You J. Y.; Gu B.; Su G. Strain-Induced Room-Temperature Ferromagnetic Semiconductors with Large Anomalous Hall Conductivity in Two-Dimensional Cr2Ge2Se6. Phys. Rev. Appl. 2019, 12, 014020. 10.1103/PhysRevApplied.12.014020. [DOI] [Google Scholar]
  45. Xu Z.; Zhu H. Two-dimensional manganese nitride monolayer with room temperature rigid ferromagnetism under strain. J. Phys. Chem. C 2018, 122, 14918–14927. 10.1021/acs.jpcc.8b02323. [DOI] [Google Scholar]
  46. Guan Z. Y.; Ni S. Strain-Controllable High Curie Temperature and Magnetic Crystal Anisotropy in a 2D Ferromagnetic Semiconductive FeI3 Monolayer. Appl. Electron. Mater. 2021, 3, 3147–3157. 10.1021/acsaelm.1c00363. [DOI] [PubMed] [Google Scholar]
  47. Kanamori J. Crystal Distortion in Magnetic Compounds. J. Appl. Phys. 1960, 31, S14–S23. 10.1063/1.1984590. [DOI] [Google Scholar]
  48. Zhang W. B.; Qu Q.; Zhu P.; Lam C. H. Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides. J. Mater. Chem. C 2015, 3, 12457–12468. 10.1039/C5TC02840J. [DOI] [Google Scholar]
  49. Guo Y. L.; Yuan S. J.; Wang B.; Shi L.; Wang J. L. Half-metallicity and enhanced ferromagnetism in Li-adsorbed ultrathin chromium triiodide. J. Mater. Chem. C 2018, 6, 5716–5720. 10.1039/C8TC01302K. [DOI] [Google Scholar]
  50. Zhang J. Y.; Zhao B.; Ma C. L.; Yang Z. Q. Bipolar ferromagnetic semiconductors and doping-tuned room-temperature half-metallicity in monolayer MoX3 (X = Cl, Br, I): An HSE06 study. Phys. Rev. B 2021, 103, 075433. 10.1103/PhysRevB.103.075433. [DOI] [Google Scholar]
  51. Xie J. J.; Wang X. L.; Yan L.; Chen H.; Lv J.; Wu H. S. First-principles prediction of room-temperature half-metallicity in strain- and 2 carrier-tunable monolayer Mn2Sn2Te6. Phys. E 2023, 150, 115704. 10.1016/j.physe.2023.115704. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c07773_si_001.pdf (634.4KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES