Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Dec 26;146(1):1053–1061. doi: 10.1021/jacs.3c12008

Proof-of-Concept Quantum Simulator Based on Molecular Spin Qudits

Simone Chicco †,‡, Giuseppe Allodi †, Alessandro Chiesa †,‡,§, Elena Garlatti †,‡,§, Christian D Buch ∥, Paolo Santini †,‡,§,*, Roberto De Renzi †,*, Stergios Piligkos ∥,*, Stefano Carretta †,‡,§,*
PMCID: PMC10785809  PMID: 38147824

Abstract

graphic file with name ja3c12008_0005.jpg

The use of d-level qudits instead of two-level qubits can largely increase the power of quantum logic for many applications, ranging from quantum simulations to quantum error correction. Magnetic molecules are ideal spin systems to realize these large-dimensional qudits. Indeed, their Hamiltonian can be engineered to an unparalleled extent and can yield a spectrum with many low-energy states. In particular, in the past decade, intense theoretical, experimental, and synthesis efforts have been devoted to develop quantum simulators based on molecular qubits and qudits. However, this remarkable potential is practically unexpressed, because no quantum simulation has ever been experimentally demonstrated with these systems. Here, we show the first prototype quantum simulator based on an ensemble of molecular qudits and a radiofrequency broadband spectrometer. To demonstrate the operativity of the device, we have simulated quantum tunneling of the magnetization and the transverse-field Ising model, representative of two different classes of problems. These results represent an important step toward the actual use of molecular spin qudits in quantum technologies.

Introduction

Magnetic molecules, whose magnetic core is typically made of one or few exchange coupled magnetic ions, have provided an ideal playground to investigate fundamental phenomena, ranging from quantum tunneling of the magnetization in isolated molecules1,2 to hysteresis at 60–80 K of single-molecule origin3,4 or decoherence.5,6 A strength point of this class of materials is that their complex single-molecule spin dynamics can be accessed even by bulk measurements.7,8 Nevertheless, coherent manipulation and readout of a single TbPc2 molecule was shown in a single-molecule transistor.9,10

Being controllable quantum objects, magnetic molecules have attracted considerable attention as molecular qubits,11−13 thanks to the remarkable possibilities of engineering their Hamiltonian14 and the long coherence times (from hundreds of μs to ms) reported in Cu15 or VO complexes.16−18 Moreover, the possibility of controlling their quantum state by electric fields19−22 and the blueprint of a magnetic quantum processor23 have been recently shown. These results are very interesting, but what makes magnetic molecules really potentially disruptive for quantum technologies is the fact that they naturally provide multilevel quantum systems, i.e., qudits with large number of states.24−27 Indeed, the use of qudits as elementary units of computation28−31 can simplify or improve quantum algorithms32−37 and quantum sensing protocols.38 For instance, qudit encoding can significantly reduce the number of two-body gates and thus improve the implementation of quantum algorithms.37,39 Moreover, by enconding a protected qubit into a single multilevel object, quantum error correction could be implemented without the large overhead of resources required by qubit-based codes.25,40−44

In the past decade, many efforts have been focused on using molecular qudits as quantum simulators (QSs).45−49 QSs are controllable quantum systems whose dynamics is externally driven to calculate the ground state50 or to mimic the time evolution51 of the “target” Hamiltonian, i.e., the Hamiltonian of the model that needs to be simulated. QSs made of molecular qudits would be very interesting, because problems involving quantum objects with many degrees of freedom can be solved more efficiently by going beyond the binary qubit logic. For instance, nuclear52 or bosonic48 Hamiltonians can be naturally mapped to the higher dimensional qudit Hilbert space, avoiding the large growth of qubits53 or complex gates54 typical of multiqubit encodings. Moreover, a QS based on molecular qudits could embed quantum error correction. However, in spite of more than a decade of efforts, an experimental realization of a QS based on MQs was still lacking, thus leaving their striking potential completely unexpressed.13

Here, we show the first realization of a working proof-of-concept quantum simulator based on an ensemble of 173Yb(trensal) qudits,55 and we demonstrate its operation by implementing the quantum simulation of models representative of two different classes of problems: an integer spin >1/2 subject to quantum tunneling of the magnetization (QTM) and a pair of spins 1/2 coupled by Ising interaction in the presence of a transverse field (transverse field Ising model, TIM). In both cases, our QS reproduces the correct physical behavior, and the results are in good agreement with calculations.

Results and Discussion

Quantum Hardware

The core of the quantum simulator consists of a crystal containing isotopically enriched 173Yb(trensal), doped at 1% into its diamagnetic [Lu(trensal)] isostructural analogue (see Experimental Section). Due to the large crystal field splitting of Yb(III), each molecule behaves as an electronic spin qubit (effective spin S = 1/2) coupled to a 6-levels nuclear spin qudit I = 5/2, providing 2 × 6 states. The corresponding spin Hamiltonian is given by

graphic file with name ja3c12008_m001.jpg 1

where the first two terms represent the strong axial hyperfine interaction (A∥ = −898 MHz, A⊥ = −615 MHz), the third one describes the nuclear quadrupolar coupling (p = −66 MHz) and the last two are the electronic (gx = gy = 2.9, gz = 4.3) and nuclear (gI = −0.2592) Zeeman terms. These parameters, determined in previous works55,56 (see Supporting Information, Figure S1), provide sufficient energy separation of the nuclear transitions for the selective manipulation of each energy gap, while being close enough for addressing multiple transitions within our broad multifrequency setup. Static fields B0 between 0.12 and 0.22 T are applied orthogonal to the molecular C3 symmetry axis (Figure 1a). At these fields, the electronic Zeeman energy is the leading term in eq 1, thus the eigenstates are almost factorized and are labeled by the dominant electronic and nuclear spin components along B0, |mS, mI⟩. Here, we focus on states |mS = 1/2, mI⟩, with mI = 1/2, −1/2, −3/2, −5/2 and use the simplified notation |0⟩, |1⟩, |2⟩, |3⟩, as shown in Figure 1b. The corresponding transition frequencies are f1 (|0⟩ ↔ |1⟩, red), f2 (|1⟩ ↔ |2⟩, yellow), and f3 (|2⟩ ↔ |3⟩, blue).

Figure 1.

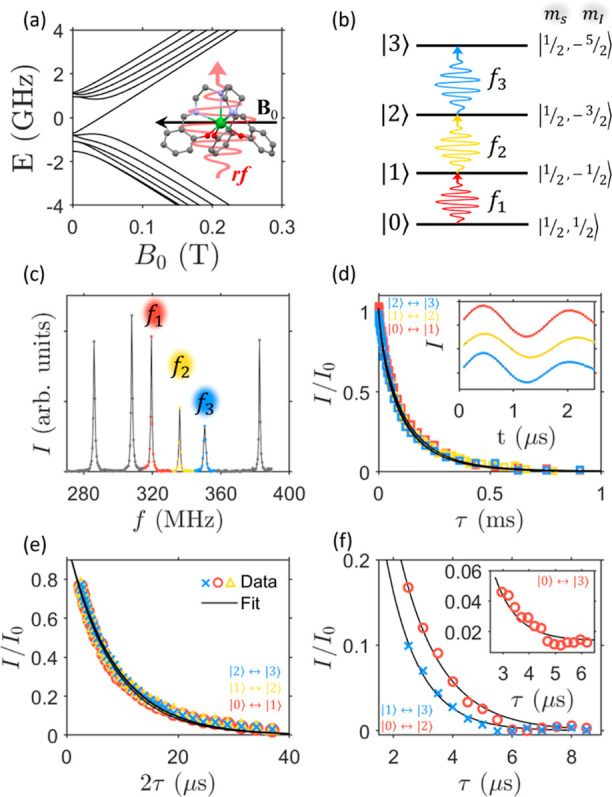
Figure 1

Open in a new tab

Calibration of the quantum hardware. (a) Calculated energy level diagram of 173Yb(trensal) with the static field B0 perpendicular to the molecular C3 axis. The molecule and the direction of the static (black) and driving (red) fields are shown as inset. (b) Scheme of the nuclear qudit subspace targeted in this work, with states labeled as |0⟩, |1⟩, |2⟩, and |3⟩ and transition frequencies as f1, f2, and f3 in the ascending order. (c) Example of the NMR spectrum of the 173Yb(trensal) qudit at B0 = 0.12 T and T = 1.4 K, with the peaks representing the nuclear transitions within the computational subspace highlighted in colors. (d) Relaxation times Tη1 measured (dots) on each of the nuclear transitions with the multifrequency protocol, with B0 = 0.22 T and T = 1.4 K. Inset: some examples of coherent Rabi manipulation of the transitions indicated in panel (b) (labeled in color-code), demonstrating universal qudit control. (e) Phase memory time Tη2 measured for each transition marked in panel (c), at B0 = 0.22 T and T = 1.4 K. (f) Double (main) and triple (inset) quantum coherence times. Error bars are within the size of the symbols.

The use of an ordered ensemble of identical qudits as QS has the advantage of yielding the expectation values with high statistics directly in a single run. Full control of the qudits is achieved by addressing each energy gap using a flexible broadband NMR spectrometer equipped with a tailored multifrequency probe spanning the frequency range ∼200–450 MHz. The driving Hamiltonian is

graphic file with name ja3c12008_m002.jpg 2

where Θ is the Heaviside step function and the sum runs over different pulses of amplitude B1j (parallel to the c axis), duration τj, center t0j, frequency ωj/2π, and phase ϕj addressing consecutive (ΔmI = ±1) transitions (i.e., ωj = fη × 2π, with η = 1, 2, 3). The simulator operates at 1.4 K, a temperature at which all the eigenstates are populated. Hence, we prepare an initial pseudopure state by proper sequences of pulses (see subsection on Quantum Tunneling and Experimental Section).

Calibration

We first need to show that a universal set of gates can be implemented in the QS and calibrate it. The NMR spectrum is reported in Figure 1c, with the transition frequencies f1 = 319.5 MHz, f2 = 336.0 MHz, and f3 = 350.5 MHz at B0 = 0.12 T (f1 = 333.7 MHz, f2 = 362.4 MHz, and f3 = 386.2 MHz at B0 = 0.22 T, see Supporting Information, Figure S1), highlighted in the corresponding color code. 173Yb(trensal) has sharp spectral lines (fwhm ∼ 0.5 MHz), ensuring the possibility of individually addressing the transitions (see Figures 1b and S2, Supporting Information). To demonstrate full coherent control, we performed transient nutation experiments to induce ΔmI = ±1 Rabi oscillations with arbitrary phases between all the selected nuclear states (inset of Figure 1d). These operations are the basic gates building up our quantum simulation sequences. Rabi experiments were also exploited to set the duration of the pulses to be nearly the same, by calibrating the driving fields used for the QS (see Supporting Information, Table S1).

Relaxation times much longer than the time needed to perform the full gate sequence and sufficiently long coherence times are required to perform a reliable quantum simulation. Thus, we measured all the relevant characteristic times Tη1 and Tη2 in the experimental conditions exploited in the quantum simulations. First, the relaxation times Tη1 of the three selected transitions were probed by exploiting a double-frequency method. The signal decay is profiled by probing the transition fη between states |η – 1⟩ and |η⟩ after an out-of-equilibrium surplus population is induced by an excitation pulse on the transition fη±1, to investigate the relaxation toward thermal equilibrium of diagonal elements of the density matrix (see Experimental Section). The results obtained at the applied static field B0 = 0.22 T are reported in Figure 1d, yielding Tη1 values of the order of 100 μs for all the transitions. Similar results were obtained at B0 = 0.12 T (see Supporting Information, Figure S3).

Single-quantum coherence times Tη2 (of superpositions between states with ΔmI = 1) were measured by a standard Hahn-echo pulse sequence and are shown in Figure 1e (see also Supporting Information, Figure S4). The three transitions fη (η = 1, 2, and 3) show very similar Tη2 ∼ 8 μs, significantly longer than simulation times. Additional key pieces of information for qudit-based architectures are the coherence times of superpositions involving ΔmI > 1 states, the so-called multiple-quantum coherences. These superpositions are in fact created during quantum simulations, and their characterization is therefore important for the design of optimized sequences. In order to extract multiple-quantum coherences, we first created the desired ΔmI > 1 superposition exploiting π-pulses for state swaps (see Experimental Section). After a variable delay, we used π pulses to back swap the states and employ a 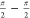Inline graphic sequence for detecting the decay of these coherences. Results for double- and triple-quantum coherences between the selected nuclear states are reported in Figure 1f (main panel and inset, respectively). Since multiple-quantum superpositions involve states which are magnetically more different from each other, we found shorter coherence times with respect to single coherences (∼1.2 μs for ΔmI = 2 and ∼0.7 μs for ΔmI = 3). However, because of the chosen encoding, the system is placed into superpositions of multiple states only for time intervals much shorter than the full sequence duration. Thus, these coherences are shown not to affect significantly the quantum simulation (see Supporting Information, Figure S5).

As shown later in the article, these values permit the QS to capture the physics of the target models.

Quantum Simulations

The versatility of the QS is demonstrated by performing two different quantum simulations exploiting the multilevel structure of the molecular qudit: (i) the quantum tunneling of the magnetization of a single S = 1 spin, where the 2S + 1 states of the target system are mapped onto the hardware levels and the unitary evolution is exactly decomposed into transitions between neighboring levels (see subsection on Quantum Tunneling). (ii) The time dependence of the magnetization and of the correlation function for two spins 1/2 in a transverse magnetic field in two different regimes: either noninteracting or with an Ising coupling. Here, the two-spin Hilbert space is mapped onto the single qudit energy levels and the unitary evolution induced by the target Hamiltonian is decomposed into a sequence of elementary steps by using the Suzuki–Trotter approximation. This explores the possibility of encoding several spins into single qudits (see subsection on the Transverse Field Ising Model).

Quantum Tunneling

We consider an S = 1 target system characterized by the Hamiltonian (with D > 0)

graphic file with name ja3c12008_m004.jpg 3

For E = 0, this corresponds to the double-well potential sketched in Figure 2a, where the ground state is a degenerate doublet with maximum absolute value of the magnetization (arrows in Figure 2a), i.e., M = ±S. A small rhombic anisotropy term E in 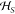Inline graphic activates quantum tunneling through the barrier and hence a system prepared in one of the two wells oscillates between states with opposite magnetization.

Figure 2.

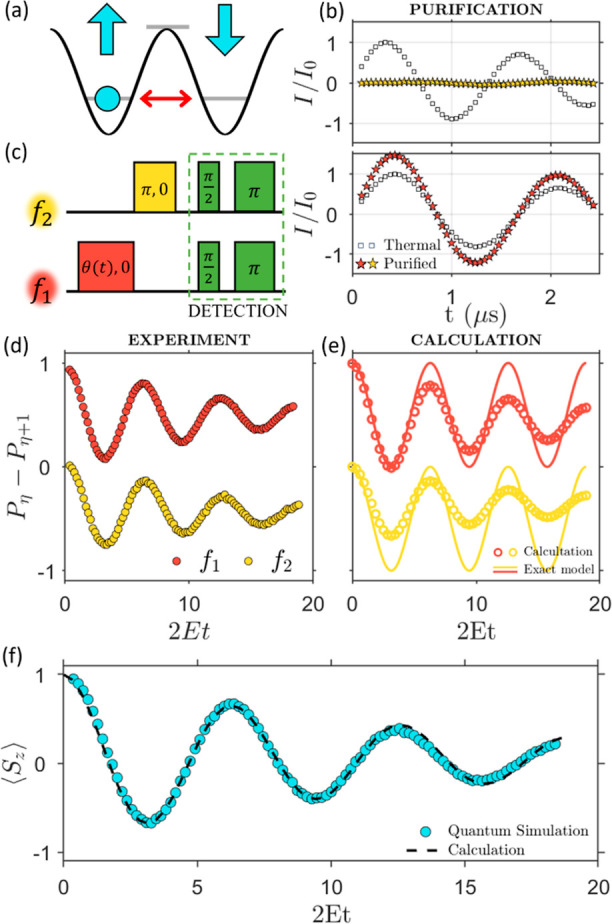
Figure 2

Open in a new tab

Simulation of quantum tunneling of the magnetization. (a) Sketch of the double-well axial crystal field potential acting on a spin S = 1 system prepared in M = 1 (circle) and subject to quantum tunneling activated by rhombic anisotropic terms (red double-arrow). (b) Test of the purification protocol by sending pulses at frequency f2 (top) and f1 (bottom), respectively addressing |1⟩ ↔ |2⟩ and |0⟩ ↔ |1⟩ transitions, and comparing the driven dynamics before and after purification. (c) 2-Frequency pulse sequence consisting of a pulse of length θ(t) = Et at frequency f1, followed by a π pulse at frequency f2 and concluded by Hahn-echo detection. (d) Difference of populations between consecutive levels |0⟩ ↔ |1⟩ (red) and |1⟩ ↔ |2⟩ (yellow), measured at B0 = 0.12 T and T = 1.4 K by Hahn-echo sequences at frequencies f1 and f2, respectively, at the end of the quantum simulation. (e) Corresponding noiseless calculations (lines) or including measured single- and double-quantum Tη2, as well as additional dephasing due to inhomogeneities of the driving field (circles). (f) Measured (blue circles) and calculated (dashed line) expectation value of the magnetization of the target system. Error bars are within the size of the symbols.

To simulate the phenomenon, the three levels of the S = 1 target system are mapped onto the hardware states |0⟩, |1⟩, and |2⟩ of Figure 1b, which are initially in a thermal mixture because our experiment is not at T = 0. Therefore, we prepare the initial pseudopure state in this subspace by first applying a π/2 pulse at frequency f2 which creates a superposition between states |1⟩ and |2⟩ with equal amplitudes. This is followed by a waiting time ∼2.5T22 to let the relative coherence decay. The resulting density matrix in the {|0⟩, |1⟩, |2⟩} subspace is therefore of the form ρ0–2 = ϵ|0⟩⟨0| + (p1 + p2)/2(|0⟩⟨0| + |1⟩⟨1| + |2⟩⟨2|), with ϵ = p0 – (p1 + p2)/2 and pη the initial Boltzmann population of the energy states. Apart from normalization, this state is equivalent for quantum simulation to the pure density matrix ρ0–2 = |0⟩⟨0|. Indeed, the part of ρ0–2 proportional to the identity in the considered subspace does not produce any signal in our experiment. To check the “purification” procedure, we compare in Figure 2b Rabi oscillations addressing transitions |1⟩ ↔ |2⟩ (top) and |0⟩ ↔ |1⟩ (bottom) before and after the sequence. Without purification (i.e., with thermal populations), a pulse of variable length at frequency f2 induces oscillations between states |1⟩ and |2⟩. Conversely, after the purification sequence states |1⟩ and |2⟩ start with equal populations and hence Rabi oscillations are not observed (Figure 2b, top), as it would occur at T = 0. Concerning the transition |0⟩ ↔ |1⟩, the purification protocol enhances by about 50% their population difference, resulting in an amplification of Rabi oscillations (Figure 2b, bottom). In addition, we verified that coherences are lost after the waiting time (see Experimental Section and Supporting Information, Figure S6).

Having tested that the prepared state is spectroscopically equivalent to the pure state |0⟩, we illustrate the simulation of the tunneling dynamics as a function of the simulation time t. The optimized sequence57 is shown in Figure 2c, ending with Hahn echo sequences at frequencies f1 and f2 to access differences between the populations of neighboring levels of the hardware Pη – Pη+1.

Results are shown in Figure 2d, in excellent agreement with calculations (Figure 2e) including decoherence in Lindblad formalism (see Experimental Section) and an additional decay ascribed to inhomogeneity of the driving field.55,58 From these population differences we can extract the target observable ⟨Sz⟩ = P0 – P2, i.e., the magnetization of the simulated system (see Figure 2f). This displays the expected quantum oscillation at frequency E/π, in very good agreement with calculations.

Transverse Field Ising Model

We now consider a different problem, represented by a target system of two spins 1/2, interacting via the Hamiltonian

graphic file with name ja3c12008_m006.jpg 4

where sαi are spin 1/2 operators and we set b = J. The quantum simulation of the corresponding time evolution Inline graphic requires to decompose U(t) into elementary operations which can be implemented on the hardware. In most qubit-based processors, this implies separately simulating one- and two-body terms in eq 4 and then applying a Suzuki–Trotter (ST) approximation to U(t), i.e.

graphic file with name ja3c12008_m008.jpg 5

Such an approximation becomes exact for a large number of Trotter steps n, at the price of an increasing number of noisy gates. Nevertheless, a proper trade-off can be found to reproduce the correct dynamics at not too large simulated times with a rather small n, thus limiting decoherence.

Here, the four states of the target two-spin system {|↑↑⟩, |↑↓⟩, |↓↑⟩, |↓↓⟩} are mapped onto the qudit subspace {|0⟩, |1⟩, |2⟩, |3⟩}. Hence, each one-body unitary gate in eq 5 is simulated by a pair of pulses of the same length θ = bt/n at frequencies f1 and f3, simultaneously addressing |0⟩ ↔ |1⟩ and |2⟩ ↔ |3⟩ transitions. This directly implements a rotation of the second qubit, i.e., exp[−isy2bt/n].59 The same pulses, preceded and followed by a π state-swap at frequency f2, implement a rotation of the first qubit exp[−isy1bt/n]. The resulting sequence yields the exact quantum simulation of Inline graphic for the noninteracting (J = 0) case, and it also corresponds to the first Trotter step of the interacting case (Figure 3a, left). The simulation of the two-body term exp[−isz1sz2Jt] on a qubit hardware would require controlled-phase gates at the end of each Trotter step. In our qudit architecture, this entangling error-prone gate can be rewritten in terms of single-qudit operations, simply adjusting the phases of the pulses addressing consecutive |0⟩ ↔ |1⟩ and |2⟩ ↔ |3⟩ transitions, as shown in Figure 3a (for the second Trotter step).

Figure 3.

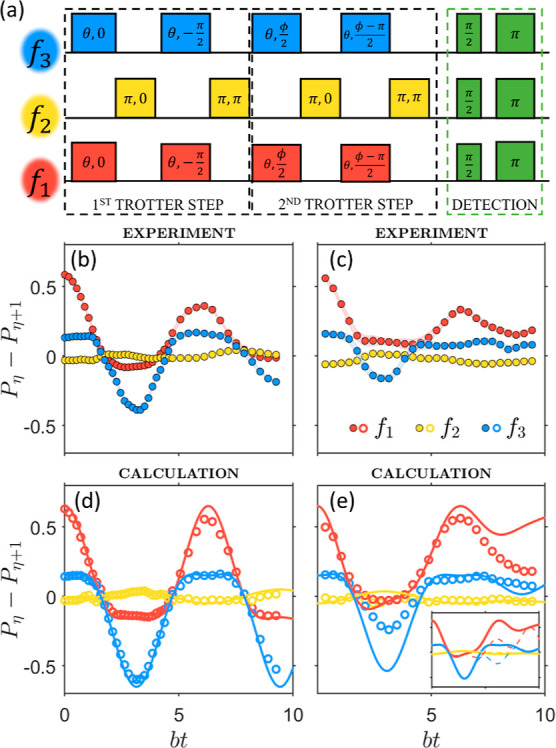
Figure 3

Open in a new tab

Simulation of the transverse Ising model. (a) 3-Frequency pulse sequence to implement the quantum simulation of the transverse-field Ising model on 4 levels of the hardware qudit and to detect the final output. (b,c) Difference of populations between neighboring levels, measured at B0 = 0.22 T and T = 1.4 K by echo-sequences at the three driving frequencies f1 (red), f2 (yellow), and f3 (blue) for the non-interacting (b) and interacting (c) cases. The shaded areas represent the estimated experimental uncertainties in the amplitude determination. (d,e) Corresponding calculations for n = 2 with the inclusion of the incoherent Lindblad dynamics induced by the measured single-, double-, and triple-quantum coherence times. Inset of panel (e): results for n = 2 Suzuki–Trotter decomposition compared with the exact evolution induced by the target Hamiltonian (dashed lines).

An extension of the purification protocol illustrated above is used also in this second experiment to prepare the initial state (see Experimental Section and Supporting Information, Figures S7 and S8). Detection of the output state is accomplished again by Hahn echo sequences at the frequencies f1, f2 and f3.

Population differences measured at the end of the quantum simulation are reported in Figure 3 in noninteracting (b) and interacting (c) regimes, while corresponding observables are shown in Figure 4. Whereas for J = 0 the simulation is exact, for J ≠ 0, two Trotter steps are sufficient to capture the dynamics for bt ≲ 5 (inset of Figure 3e). Nevertheless, we have explored also longer simulation times to make a more stringent demonstration of our capability of controlling the quantum hardware in the presence of the complex dynamics induced by this sequence. Several of the pulses for the J ≠ 0 case have been applied in parallel (Figure 3a) to make the duration of the sequences similar in the two cases and hence less dependent on decoherence. The simulation could be extended to longer times by an exact decomposition in planar rotations, which however requires a significantly longer pulse sequence.

Figure 4.

Figure 4

Open in a new tab

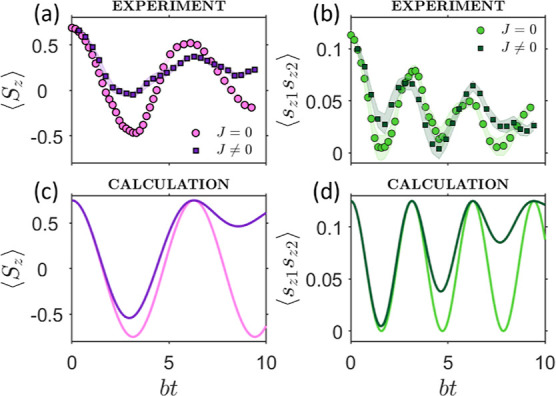
Observables for the transverse-field Ising model. Comparison between (a) total magnetization Sz = sz1 + sz2 and (b) equal-time cross-correlation function ⟨sz1sz2⟩ for the examined two-spin model without (J = 0) and with (J = b) Ising spin–spin coupling. Error bars represent the estimated uncertainties propagated from the experimental amplitudes of Figure 3b,c. They are more important for ⟨sz1sz2⟩, where the signal results from a subtraction of experimental data. (c,d) Corresponding noiseless calculations (lines) for n = 2.

From Figure 3b–e, we note a good agreement between experimental results (b,c) and calculations for n = 2 (d,e), where the measured coherence times are included in a Lindblad formalism (circles). Pure dephasing here induces a damping of the oscillations of Pη – Pη+1 (dashed lines), but the nontrivial time dependence induced by the target Hamiltonian is well reproduced. Hence, our quantum simulator is able to catch the correct physical behavior of the target system. In particular, the total magnetization Sz = sz1 + sz2 and the equal-time correlation ⟨sz1sz2⟩ simulated by the QS are reported in Figure 4a,b and compared with exact calculations for n = 2 (c,d). The QS predicts the oscillation frequency to be larger in the correlation than in the total magnetization, in good agreement with calculations. This agreement is remarkable especially for correlations, which are difficult to simulate because they are obtained from the difference of measured quantities (see Experimental Section). In addition, the differences in the time-dependence between the interacting and noninteracting cases in the magnetization are captured by the QS.

Conclusions and Perspectives

We have demonstrated a proof-of-concept quantum hardware which explicitly makes use of the multilevel structure of molecular qudits as a key resource for quantum simulation. This is done by following two different approaches, targeting different classes of problems:

  • (1)

    the dynamics of a single multilevel system is directly mapped onto the energy levels of the qudit. This scheme can be extended from S > 1/2 problems to bosonic or Fermionic degrees of freedom, which are of crucial interest but require complex encodings on multiqubit platforms.48,52−54

  • (2)

    we have considered a multispin system whose Hilbert space is encoded into a single-qudit.13 This approach is important for the scalability of the platform in the near future. By encoding several spins of the target Hamiltonian into the same qudit, we significantly reduce the number of two-body gates, which are usually the most error-prone operations. Then, one can exploit a register consisting of several molecular (nuclear) qudits interacting via their electronic spins,47 to implement gates between different qudits. This can be still done in an ordered ensemble like a magnetically diluted crystal.

To further increase the scalability, the electronic spins can be used to activate an effective communication between distant qudits mediated by photons in superconducting resonators,23 after having swapped quantum information from the nuclear spins. This is made possible by the specific choice of molecular qudits as elementary units.

The presence of metal ions whose spins are strongly coupled to nuclear ones provides specific features which make this architecture different from standard liquid-state NMR quantum computing (NMR-QC).51 Indeed, besides being an important resource for scalability, this coupling can play a key role in specific protocols such as quantum-error correction.25,43 Moreover, it leads to large splittings between nuclear levels, making the thermal initialization in a pure state possible at mK temperatures. Finally, the unparalleled degree of tailoring of the spin Hamiltonian of magnetic molecules60 is a crucial advantage with respect to standard NMR-QC systems.

The next steps will involve the addition of higher-frequency pulses to control also electronic degrees of freedom, e.g., to mimic the interaction with a heat bath and then simulating open quantum systems.49,61 Moreover, the use of more levels and/or multispin molecules will largely extend the class of Hamiltonians addressable by our quantum simulator.

Experimental Section

Synthesis

A single crystal of isotopically enriched 173Yb(trensal) diluted at 1% into the isotructural Lu(trensal) was grown according to a published method for Er(trensal),62 where instead of using Er(OTf)3·9H2O as in the published method, 173Yb(OTf)3·9H2O and Lu(OTf)3·9H2O in the molar ratio 1:99 were used. Both Ln salts were synthesized according to a literature procedure, where the corresponding Ln2O3 was dissolved in boiling dilute triflic acid, and the Ln salt was obtained by slow evaporation of the corresponding solution.63 Isotopically enriched 173Yb2O3 was obtained from Neonest AB. Inductively coupled plasma mass spectrometry (ICP–MS) was used to determine the dilution of 173Yb(trensal) in Lu(trensal). ICP–MS was performed at the Department of Chemistry, University of Copenhagen on a Bruker Aurora Elite. Small crystals of 173Yb0.01Lu0.99(trensal) grown in the same tube as the one used for the experiments in the main text were dissolved in boiling nitric acid (14%). The nitric acid was prepared by diluting TraceSelect grade conc. nitric acid with Milli-Q water. The solution was then diluted with TraceSelect grade nitric acid (2%) until the concentration of 173Yb and Lu were within the calibration range of the instrument (1–50 ng/mL). Prior to determining the concentrations of 173Yb and Lu, the ICP–MS instrument was tuned using six standard solutions with concentrations of Yb and Lu spanning the range 0–50 ng/mL. These standard solutions were prepared by diluting a reference solution from Inorganic Ventures using TraceSelect grade nitric acid (2%). For the measurements of the Yb concentration, the instrument was programmed only to detect the 173Yb isotope. The ICP–MS measurement afforded a ratio of 9:991 173Yb/Lu.

Apparatus

The experimental apparatus for the characterization and control of the nuclear qudit has been specifically designed by combining the potentialities of the homemade broadband NMR spectrometer “HyReSpect”64 with a fast state-of-the-art arbitrary waveform generator (Arb Rider AWG-5062D, hereafter AWG) from Active Technologies. The multifrequency pulse sequences for the coherent manipulation of the nuclear qudit were in fact generated by the AWG externally triggered by the spectrometer, while the spectrometer was devoted to the final state detection. The characteristics of the experimental setup are particularly suitable for the present experiment: a flat response over a wide frequency span, very short dead times (<1.3 μs) to make echo-detection compatible with the qudit phase memory time, fast RF switching, a broadband receiver stage, and fast signal averaging.

The high sensitivity of the technique, enhanced by the strong hyperfine interactions of 173Yb(trensal), allows for the use of a NMR probe covering a wide frequency range (±30 MHz in our experiments), which can be attained by inserting a parallel resistor in the LC circuit. The loss in sensitivity 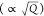Inline graphic due to the diminished Q-factor of the probe was compensated by the isotopic enrichment of the target 173Yb species.

Calibration

Rabi nutation experiments on each transition fη were performed by implementing a (θ(t))η – (π)η echo sequence, where the first pulse of variable length induces the nutation of the spin system in the rotating frame, while the refocusing is generated by the π-pulse. The decay observed in the intensity of Rabi oscillation (see inset of Figure 1d) is dominated by the inhomogeneity of the driving field B1, which adds to the 1/Tη2 rate.

Relaxation times Tη1 between each pair of levels were measured by exploiting a double-frequency sequence generated by the AWG, of the type 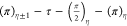Inline graphic. Indeed, the sequence to measure the time Tη1 (corresponding to the transition fη: |η – 1⟩ ↔ |η⟩) consists of (i) a population transfer to one of the two targeted nuclear states induced by π-pulse on a neighboring transition fη±1 and (ii) the detection of the increment of the Hanh-echo signal on fη due to the induced out-of-equilibrium surplus population. The variable delay τ enables the determination of time required for the recovery of the thermal state populations on the targeted nuclear states |η – 1⟩ and |η⟩, i.e., Tη1. The Tη1 decays are then subtracted by the Hahn-echo initial amplitude of the transition used for the detection. Studying the relaxation of a nuclear state population transferred to a nearby state under these conditions is different from the standard inversion-recovery method, since here the effect of the relaxation is probed on a transition not directly affected by the first excitation pulse. This provides a lower bound to the relaxation time of each pair of nuclear spin levels.

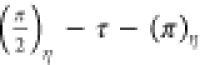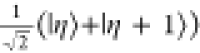Single-quantum coherence times Tη2 were measured by a standard Inline graphic Hanh-echo sequence, exploiting the standard spectrometer setup. The measurement of the multiple-quantum coherences required instead a multifrequency pulse sequence generated by the AWG, for the preparation of the desired double- or triple-coherent superposition of states by addressing only consecutive transitions. The sequence for generating the double-quantum coherences can be written as (π/2)η+1 – (π)η+2 – τ – (−π)η+2. 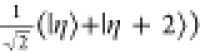First, a coherent superposition Inline graphic is created between consecutive states by addressing the transition fη+1. 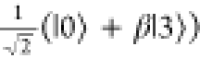A π-pulse on fη+2 is then used to implement a state-swap between |η + 1⟩ and |η + 2⟩, yielding the desired double-quantum coherent superposition Inline graphic. After a variable delay τ to follow the coherence decay, a (−π) pulse on fη+2 is implemented to back-swap the states. This final step recovers the now-decayed single-quantum coherent superposition on fη+1, which can be detected by the spectrometer. For triple-quantum coherences, an additional (π)3 pulse (together with the corresponding back-swap (−π)3 one) is needed in order to prepare the Inline graphic coherent superposition.

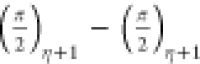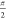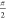Multiple-quantum coherences were then measured by exploiting a Inline graphic detection sequence, where the first pulse was generated by the AWG and the last one by the spectrometer (hence only the latter was phase-coherent with the detection reference). The spin coherence induced by the first Inline graphic pulse, which would appear in principle as a (not observable) spin echo, is also encoded by this pulse into population differences. 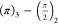Such a longitudinally encoded frozen-in replica of the phase coherence present after the first pulse is then turned into transverse coherence by the second Inline graphic pulse and then detected by the spectrometer as a spin echoa. The same detection method was used to measure the decay of the coherences induced by the pseudopurification sequences, to check that they are completely lost after the waiting time ∼2.5Tη2 before starting the quantum simulation (see Figures S5 and S7). 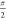For the quantum simulation of the transverse field Ising model, the pseudopure state was prepared with a Inline graphic sequence. The first π pulse induces a state-swap between |2⟩ and |3⟩, followed by the Inline graphic on f2 creating a superposition between states |1⟩ and |2⟩ with equal amplitudes. Given the very similar Boltzmann population differences of the three involved levels, this sequence yields (apart from a contribution proportional to identity and a scale factor) a dominant population in |0⟩ (0.75), small populations in |1⟩ (0.11) and |2⟩ (0.14). This enabled us to test the simulation starting from a non-trivial initial state.

Quantum simulations were performed with an oscillating field B1 ∼ 1 G and B1 ∼ 5 G for the QTM Hamiltonian and for the TIM model, respectively. In the latter case, we have used shorter pulses (larger B1) because the pulse sequence is much longer. Moreover, the pulse duration has been tuned independently for each transition, in order to match their durations and compensate the effects of the broad-resonance of the NMR probe. A higher static field (B0 = 0.22 T) has been chosen for the TIM model quantum simulation to amplify the coherence time, given the much longer duration of the pulse sequence.

All the detected echoes were then Fourier-transformed, phase-corrected, and analyzed in the frequency domain by picking the spectral amplitude of the echo at a fixed frequency shift.

Observables

The Hahn echo sequences at the end of the quantum simulations measure the differences between the populations of neighboring levels of the hardware Pη – Pη+1. From these quantities, it is possible to extract physical observables, mapped on the hardware state population.

For the QTM problem, the target magnetization of the spin S = 1 is given by ⟨Sz⟩ = P1 – P–1. By mapping the target states |M = 1⟩, |M = 0⟩, |M = −1⟩ into the hardware states |0⟩, |1⟩, |2⟩, the observable becomes ⟨Sz⟩ = P0 – P2. Since the only accessible quantities are the population difference between neighbor nuclear states, the magnetization of the simulated system (Figure 2f) can be rewritten in terms of quantities that can be directly extracted from the experiment

graphic file with name ja3c12008_m021.jpg 6

For the TIM model, the target magnetization of the two-spin system is analogously defined as ⟨Sz⟩ = P↑↑ – P↓↓. Again, by mapping the target states |↑↑⟩, |↑↓⟩, |↓↑⟩, |↓↓⟩ into the hardware states |0⟩, |1⟩, |2⟩, |3⟩, the observable becomes ⟨Sz⟩ = P0 – P3. Thus, the magnetization of the simulated system (Figure 4a), in terms of experimentally accessible quantities, becomes

graphic file with name ja3c12008_m022.jpg 7

For this Hamiltonian, we have also extracted the equal-time correlation ⟨sz1sz2⟩. This can be extracted by exploiting completeness relations as follows

graphic file with name ja3c12008_m023.jpg 8

where we have labeled by |m⟩ = |0⟩, |1⟩, |2⟩, |3⟩ the hardware eigenstates and exploited the fact that the target observables sz1 and sz2 are diagonal on this basis. By finally noting that

graphic file with name ja3c12008_m024.jpg 9

and rewriting |⟨ψ|m⟩|2 = Pm, we get

graphic file with name ja3c12008_m025.jpg 10

Numerical Calculation

Numerical calculations to reproduce the implemented quantum simulations have been performed by solving the Lindbald master equation

graphic file with name ja3c12008_m026.jpg 11

where ρ is the system density matrix in the eigenbasis, ρ = ∑ηη′ρηη′|η⟩⟨η′|, H = H0 + H1(t) is the system Hamiltonian (including time-dependent pulses), and γηη′ are pure dephasing rates of each specific superposition between eigenstates |η⟩ and |η′⟩. In the reported experiments, |η⟩ ≈ |mS, mI⟩ and we have focused on the subspace with fixed mS = 1/2. Hence, rates γηη′ between states with different mI correspond to the inverse of the single and multiple-quantum coherence times discussed in the main text. Additional mechanisms depending on the details of the setup, like inhomogeneities of the driving fields, could contribute to γηη′. These additional dephasing rates have been determined in the quantum tunneling experiment from the observed damping of the oscillations and included in the corresponding calculations. Conversely, to pinpoint the effect of decoherence in the complex dynamics associated with the TIM model, only the measured Tη2 (single- and multiquantum) have been included in the calculations. The detection procedure has also been simulated. We have found that here pure dephasing acts practically as an overall scaling factor on the measured signal. Hence, we have rescaled both signal and calculations to the known value at t = 0.

Sequence Optimization

The quantum simulation of the TIM model [target Hamiltonian 4] involves a Suzuki–Trotter decomposition, in which rotations of the target qubits are alternated to an entangling ZZ evolution UZZ(Jτ) = exp[−isz1sz2Jτ], τ = t/n. In order to reduce the number of pulses to be subsequently implemented, we have exploited the following identity

graphic file with name ja3c12008_m027.jpg 12

where R(i)y(β) = exp[−isyiβ], R(1)c(β) = R(1)α(β) ⊗ |0⟩⟨0| + R(1)–α(β) ⊗ |1⟩⟨1| and Rα(β) = exp[−i(cos αsy – sin αsx)β]. Analogous expressions hold for R(2)c(β). In practice, this corresponds to including UZZ in the subsequent planar rotation. The rotation axis in the plane (α) corresponds to the phase factor of the pulse. Note that the effect of the entangling UZZ gate is still present, because R(i)c are conditional (entangling) gates in the two-qubit basis of the target system.

Acknowledgments

This work received financial support from the European Union—NextGenerationEU, PNRR MUR project PE0000023-NQSTI, from the European Union’s Horizon 2020 program under grant agreement no. 862893 (FET-OPEN project FATMOLS), from the Novo Nordisk foundation under grant NNF21OC0070832 in the call “Exploratory Interdisciplinary Synergy Programme 2021” and from Fondazione Cariparma.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c12008.

  • NMR spectra, calibration results, and additional measurements of relaxation and coherence times (PDF)

Author Contributions

⊥ G.A., A.C., and E.G. contributed equally to this paper.

The authors declare no competing financial interest.

Footnotes

a

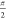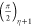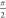This process is referred to in the NMR literature as a “stimulated echo”,65 whose textbook sequence consists of three Inline graphic pulses: the first Inline graphic pulse creating the coherence between |η⟩ and |η + 1⟩ and the other two Inline graphic pulses representing the detection sequence, where the last pulse “stimulates” an extra spin echo. 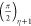We stress that, in our experiment, the detected signal cannot be due to either the trivial Hahn echo of the two Inline graphic pulses themselves, nor any other combination of pulses generated by the AWG alone. Since the spectrometer and the AWG are mutually incoherent, such spin echoes would average out on signal accumulation. On the contrary, reciprocal coherence of the two instruments is not needed if spin coherence is first encoded in populations, as sketched in the main text.

Supplementary Material

ja3c12008_si_001.pdf (605.2KB, pdf)

References

  1. Mannini M.; Pineider F.; Danieli C.; Totti F.; Sorace L.; Sainctavit P.; Arrio M.-A.; Otero E.; Joly L.; Cezar J. C.; Cornia A.; Sessoli R. Quantum tunnelling of the magnetization in a monolayer of oriented single-molecule magnets. Nature 2010, 468, 417–421. 10.1038/nature09478. [DOI] [PubMed] [Google Scholar]
  2. Wernsdorfer W.; Sessoli R. Quantum Phase Interference and Parity Effects in Magnetic Molecular Clusters. Science 1999, 284, 133–135. 10.1126/science.284.5411.133. [DOI] [PubMed] [Google Scholar]
  3. Goodwin C. A. P.; Ortu F.; Reta D.; Chilton N. F.; Mills D. P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. 10.1038/nature23447. [DOI] [PubMed] [Google Scholar]
  4. Guo F.-S.; Day B. M.; Chen Y.-C.; Tong M.-L.; Mansikkamäki A.; Layfield R. A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. 10.1126/science.aav0652. [DOI] [PubMed] [Google Scholar]
  5. Shiddiq M.; Komijani D.; Duan Y.; Gaita-Ariño A.; Coronado E.; Hill S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
  6. Takahashi S.; Tupitsyn I. S.; van Tol J.; Beedle C. C.; Hendrickson D. N.; Stamp P. C. E. Decoherence in crystals of quantum molecular magnets. Nature 2011, 476, 76–79. 10.1038/nature10314. [DOI] [PubMed] [Google Scholar]
  7. Baker M. L.; Guidi T.; Carretta S.; Ollivier J.; Mutka H.; Güdel H. U.; Timco G. A.; McInnes E. J. L.; Amoretti G.; Winpenny R. E. P.; Santini P. Spin dynamics of molecular nanomagnets unravelled at atomic scale by four-dimensional inelastic neutron scattering. Nat. Phys. 2012, 8, 906–911. 10.1038/nphys2431. [DOI] [Google Scholar]
  8. Chiesa A.; Guidi T.; Carretta S.; Ansbro S.; Timco G. A.; Vitorica-Yrezabal I.; Garlatti E.; Amoretti G.; Winpenny R. E. P.; Santini P. Magnetic Exchange Interactions in the Molecular Nanomagnet Mn12. Phys. Rev. Lett. 2017, 119, 217202. 10.1103/PhysRevLett.119.217202. [DOI] [PubMed] [Google Scholar]
  9. Thiele S.; Balestro F.; Ballou R.; Klyatskaya S.; Ruben M.; Wernsdorfer W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. 10.1126/science.1249802. [DOI] [PubMed] [Google Scholar]
  10. Godfrin C.; Ferhat A.; Ballou R.; Klyatskaya S.; Ruben M.; Wernsdorfer W.; Balestro F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm. Phys. Rev. Lett. 2017, 119, 187702. 10.1103/PhysRevLett.119.187702. [DOI] [PubMed] [Google Scholar]
  11. Gaita-Ariño A.; Luis F.; Hill S.; Coronado E. Molecular spins for quantum computation. Nat. Chem. 2019, 11, 301–309. 10.1038/s41557-019-0232-y. [DOI] [PubMed] [Google Scholar]
  12. Atzori M.; Sessoli R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. 10.1021/jacs.9b00984. [DOI] [PubMed] [Google Scholar]
  13. Carretta S.; Zueco D.; Chiesa A.; Gómez-León Á.; Luis F. A perspective on scaling up quantum computation with molecular spins. Appl. Phys. Lett. 2021, 118, 240501. 10.1063/5.0053378. [DOI] [Google Scholar]
  14. Timco G. A.; Carretta S.; Troiani F.; Tuna F.; Pritchard R. J.; Muryn C. A.; McInnes E. J. L.; Ghirri A.; Candini A.; Santini P.; Amoretti G.; Affronte M.; Winpenny R. E. P. Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 2009, 4, 173–178. 10.1038/nnano.2008.404. [DOI] [PubMed] [Google Scholar]
  15. Bader K.; Dengler D.; Lenz S.; Endeward B.; Jiang S.-D.; Neugebauer P.; van Slageren J. Room Temperature Quantum Coherence in a Potential Molecular Qubit. Nat. Commun. 2014, 5, 5304. 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
  16. Zadrozny J. M.; Niklas J.; Poluektov O. G.; Freedman D. E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. 10.1021/acscentsci.5b00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Atzori M.; Tesi L.; Morra E.; Chiesa M.; Sorace L.; Sessoli R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. 10.1021/jacs.5b13408. [DOI] [PubMed] [Google Scholar]
  18. Ding Y.-S.; Deng Y.-F.; Zheng Y.-Z. The Rise of Single-Ion Magnets as Spin Qubits. Magnetochem 2016, 2, 40. 10.3390/magnetochemistry2040040. [DOI] [Google Scholar]
  19. Fittipaldi M.; Cini A.; Annino G.; Vindigni A.; Caneschi A.; Sessoli R. Electric field modulation of magnetic exchange in molecular helices. Nat. Mater. 2019, 18, 329–334. 10.1038/s41563-019-0288-5. [DOI] [PubMed] [Google Scholar]
  20. Liu J.; Mrozek J.; Ullah A.; Duan Y.; Baldoví J. J.; Coronado E.; Gaita-Ariño A.; Ardavan A. Quantum coherent spin–electric control in a molecular nanomagnet at clock transitions. Nat. Phys. 2021, 17, 1205–1209. 10.1038/s41567-021-01355-4. [DOI] [Google Scholar]
  21. Liu Z.; Wang Y.-X.; Fang Y.-H.; Qin S.-X.; Wang Z.-M.; Jiang S.-D.; Gao S. Electric field manipulation enhanced by strong spin-orbit coupling: promoting rare-earth ions as qubits. Natl. Sci. Rev. 2020, 7, 1557–1563. 10.1093/nsr/nwaa148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fang Y.-H.; Liu Z.; Zhou S.; Fu P.-X.; Wang Y.-X.; Wang Z.-Y.; Wang Z.-M.; Gao S.; Jiang S.-D. Spin-Electric Coupling with Anisotropy-Induced Vanishment and Enhancement in Molecular Ferroelectrics. J. Am. Chem. Soc. 2022, 144, 8605–8612. 10.1021/jacs.2c00484. [DOI] [PubMed] [Google Scholar]
  23. Chiesa A.; Roca S.; Chicco S.; de Ory M.; Gómez-León A.; Gomez A.; Zueco D.; Luis F.; Carretta S. Blueprint for a Molecular-Spin Quantum Processor. Phys. Rev. Appl. 2023, 19, 064060. 10.1103/PhysRevApplied.19.064060. [DOI] [Google Scholar]
  24. Moreno-Pineda E.; Wernsdorfer W. Measuring molecular magnets for quantum technologies. Nat. Rev. Phys. 2021, 3, 645–659. 10.1038/s42254-021-00340-3. [DOI] [Google Scholar]
  25. Chiesa A.; Macaluso E.; Petiziol F.; Wimberger S.; Santini P.; Carretta S. Molecular Nanomagnets as Qubits with Embedded Quantum-Error Correction. J. Phys. Chem. Lett. 2020, 11, 8610–8615. 10.1021/acs.jpclett.0c02213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Biard H.; Moreno-Pineda E.; Ruben M.; Bonet E.; Wernsdorfer W.; Balestro F. Increasing the Hilbert space dimension using a single coupled molecular spin. Nat. Commun. 2021, 12, 4443. 10.1038/s41467-021-24693-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Moreno-Pineda E.; Godfrin C.; Balestro F.; Wernsdorfer W.; Ruben M. Molecular spin qudits for quantum algorithms. Chem. Soc. Rev. 2018, 47, 501–513. 10.1039/C5CS00933B. [DOI] [PubMed] [Google Scholar]
  28. Bullock S. S.; O’Leary D. P.; Brennen G. K. Asymptotically Optimal Quantum Circuits for d-Level Systems. Phys. Rev. Lett. 2005, 94, 230502. 10.1103/PhysRevLett.94.230502. [DOI] [PubMed] [Google Scholar]
  29. Anderson B. E.; Sosa-Martinez H.; Riofrío C.; Deutsch I. H.; Jessen P. S. Accurate and Robust Unitary Transformations of a High-Dimensional Quantum System. Phys. Rev. Lett. 2015, 114, 240401. 10.1103/PhysRevLett.114.240401. [DOI] [PubMed] [Google Scholar]
  30. Morvan A.; Ramasesh V. V.; Blok M. S.; Kreikebaum J. M.; O’Brien K.; Chen L.; Mitchell B. K.; Naik R. K.; Santiago D. I.; Siddiqi I. Qutrit Randomized Benchmarking. Phys. Rev. Lett. 2021, 126, 210504. 10.1103/PhysRevLett.126.210504. [DOI] [PubMed] [Google Scholar]
  31. Asaad S.; Mourik V.; Joecker B.; Johnson M. A. I.; Baczewski A. D.; Firgau H. R.; Mądzik M. T.; Schmitt V.; Pla J. J.; Hudson F. E.; Itoh K. M.; McCallum J. C.; Dzurak A. S.; Laucht A.; Morello A. Coherent electrical control of a single high-spin nucleus in silicon. Nature 2020, 579, 205–209. 10.1038/s41586-020-2057-7. [DOI] [PubMed] [Google Scholar]
  32. Campbell E. T. Enhanced Fault-Tolerant Quantum Computing in d-Level Systems. Phys. Rev. Lett. 2014, 113, 230501. 10.1103/PhysRevLett.113.230501. [DOI] [PubMed] [Google Scholar]
  33. Lanyon B. P.; Barbieri M.; Almeida M. P.; Jennewein T.; Ralph T. C.; Resch K. J.; Pryde G. J.; O’Brien J. L.; Gilchrist A.; White A. G. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 2009, 5, 134–140. 10.1038/nphys1150. [DOI] [Google Scholar]
  34. Wang Y.; Hu Z.; Sanders B. C.; Kais S. Qudits and High-Dimensional Quantum Computing. Front. Phys. 2020, 8, 479. 10.3389/fphy.2020.589504. [DOI] [Google Scholar]
  35. Hu X.-M.; Guo Y.; Liu B.-H.; Huang Y.-F.; Li C.-F.; Guo G.-C. Beating the channel capacity limit for superdense coding with entangled ququarts. Sci. Adv. 2018, 4, eaat9304 10.1126/sciadv.aat9304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Weggemans J. R.; Urech A.; Rausch A.; Spreeuw R.; Boucherie R.; Schreck F.; Schoutens K.; Minář J.; Speelman F. Solving correlation clustering with QAOA and a Rydberg qudit system: a full-stack approach. Quantum 2022, 6, 687. 10.22331/q-2022-04-13-687. [DOI] [Google Scholar]
  37. Fischer L. E.; Chiesa A.; Tacchino F.; Egger D. J.; Carretta S.; Tavernelli I. Universal Qudit Gate Synthesis for Transmons. PRX Quantum 2023, 4, 030327. 10.1103/PRXQuantum.4.030327. [DOI] [Google Scholar]
  38. Kristen M.; Schneider A.; Stehli A.; Wolz T.; Danilin S.; Ku H. S.; Long J.; Wu X.; Lake R.; Pappas D. P.; Ustinov A. V.; Weides M. Amplitude and frequency sensing of microwave fields with a superconducting transmon qudit. npj Quantum Inf. 2020, 6, 57. 10.1038/s41534-020-00287-w. [DOI] [Google Scholar]
  39. Gao X.; Appel P.; Friis N.; Ringbauer M.; Huber M. On the role of entanglement in qudit-based circuit compression. Quantum 2023, 7, 1141. 10.22331/q-2023-10-16-1141. [DOI] [Google Scholar]
  40. Pirandola S.; Mancini S.; Braunstein S. L.; Vitali D. Minimal qudit code for a qubit in the phase-damping channel. Phys. Rev. A 2008, 77, 032309. 10.1103/PhysRevA.77.032309. [DOI] [Google Scholar]
  41. Michael M. H.; Silveri M.; Brierley R.; Albert V. V.; Salmilehto J.; Jiang L.; Girvin S. M. New Class of Quantum Error-Correcting Codes for a Bosonic Mode. Phys. Rev. X 2016, 6, 031006. 10.1103/PhysRevX.6.031006. [DOI] [Google Scholar]
  42. Hu L.; Ma Y.; Cai W.; Mu X.; Xu Y.; Wang W.; Wu Y.; Wang H.; Song Y. P.; Zou C.-L.; Girvin S. M.; Duan L.-M.; Sun L. Quantum error correction and universal gate set operation on a binomial bosonic logical qubit. Nat. Phys. 2019, 15, 503–508. 10.1038/s41567-018-0414-3. [DOI] [Google Scholar]
  43. Petiziol F.; Chiesa A.; Wimberger S.; Santini P.; Carretta S. Counteracting dephasing in Molecular Nanomagnets by optimized qudit encodings. npj Quantum Inf. 2021, 7, 133. 10.1038/s41534-021-00466-3. [DOI] [Google Scholar]
  44. Mezzadri M.; Chiesa A.; Lepori L.; Carretta S. Fault-Tolerant Computing with Single Qudit Encoding. arXiv 2023, arXiv:2307.10761. 10.48550/arXiv.2307.10761. [DOI] [PubMed] [Google Scholar]; quant-ph, submission date: July 29, 2023 (accessed Nov 30, 2023)
  45. Santini P.; Carretta S.; Troiani F.; Amoretti G. Molecular Nanomagnets as Quantum Simulators. Phys. Rev. Lett. 2011, 107, 230502. 10.1103/PhysRevLett.107.230502. [DOI] [PubMed] [Google Scholar]
  46. Chiesa A.; Whitehead G. F. S.; Carretta S.; Carthy L.; Timco G. A.; Teat S. J.; Amoretti G.; Pavarini E.; Winpenny R. E. P.; Santini P. Molecular nanomagnets with switchable coupling for quantum simulation. Sci. Rep. 2014, 4, 7423. 10.1038/srep07423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Atzori M.; Chiesa A.; Morra E.; Chiesa M.; Sorace L.; Carretta S.; Sessoli R. A two-qubit molecular architecture for electronmediated nuclear quantum simulation. Chem. Sci. 2018, 9, 6183–6192. 10.1039/C8SC01695J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Tacchino F.; Chiesa A.; Sessoli R.; Tavernelli I.; Carretta S. A proposal for using molecular spin qudits as quantum simulators of light–matter interactions. J. Mater. Chem. C 2021, 9, 10266–10275. 10.1039/D1TC00851J. [DOI] [Google Scholar]
  49. Lockyer S. J.; Chiesa A.; Brookfield A.; Timco G. A.; Whitehead G. F. S.; McInnes E. J. L.; Carretta S.; Winpenny R. E. P. Five-Spin Supramolecule for Simulating Quantum Decoherence of Bell States. J. Am. Chem. Soc. 2022, 144, 16086–16092. 10.1021/jacs.2c06384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Du J.; Xu N.; Peng X.; Wang P.; Wu S.; Lu D. NMR Implementation of a Molecular Hydrogen Quantum Simulation with Adiabatic State Preparation. Phys. Rev. Lett. 2010, 104, 030502. 10.1103/PhysRevLett.104.030502. [DOI] [PubMed] [Google Scholar]
  51. Georgescu I. M.; Ashhab S.; Nori F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. 10.1103/RevModPhys.86.153. [DOI] [Google Scholar]
  52. Rico E.; Dalmonte M.; Zoller P.; Banerjee D.; Bögli M.; Stebler P.; Wiese U.-J. SO(3) “Nuclear Physics” with ultracold Gases. Ann. Phys. 2018, 393, 466–483. 10.1016/j.aop.2018.03.020. [DOI] [Google Scholar]
  53. Di Paolo A.; Barkoutsos P. K.; Tavernelli I.; Blais A. Variational quantum simulation of ultrastrong light-matter coupling. Phys. Rev. Res. 2020, 2, 033364. 10.1103/PhysRevResearch.2.033364. [DOI] [Google Scholar]
  54. Sawaya N. P. D.; Menke T.; Kyaw T. H.; Johri S.; Aspuru-Guzik A.; Guerreschi G. G. Resource-efficient digital quantum simulation of d-level systems for photonic, vibrational, and spin-s Hamiltonians. npj Quantum Inf. 2020, 6, 49. 10.1038/s41534-020-0278-0. [DOI] [Google Scholar]
  55. Hussain R.; Allodi G.; Chiesa A.; Garlatti E.; Mitcov D.; Konstantatos A.; Pedersen K.; De Renzi R.; Piligkos S.; Carretta S. Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit. J. Am. Chem. Soc. 2018, 140, 9814–9818. 10.1021/jacs.8b05934. [DOI] [PubMed] [Google Scholar]
  56. Rollano V.; de Ory M. C.; Buch C. D.; Rubín-Osanz M.; Zueco D.; Sánchez-Azqueta C.; Chiesa A.; Granados D.; Carretta S.; Gomez A.; Piligkos S.; Luis F. High cooperativity coupling to nuclear spins on a circuit quantum electrodynamics architecture. Commun. Phys. 2022, 5, 246. 10.1038/s42005-022-01017-8. [DOI] [Google Scholar]
  57. The sequence is optimized for the quantum simulation of the tunneling of a S = 1 spin starting from a M = 1 state.
  58. Nellutla S.; Choi K.-Y.; Pati M.; van Tol J.; Chiorescu I.; Dalal N. S. Coherent Manipulation of Electron Spins up to Ambient Temperatures in Cr5+(S = 1/2) Doped K3NbO8. Phys. Rev. Lett. 2007, 99, 137601. 10.1103/PhysRevLett.99.137601. [DOI] [PubMed] [Google Scholar]
  59. The rotation axis in the xy plane is set by the phase ϕm of the pulse in eq 2. ϕm = 0 implements a rotation about y.
  60. Ferrando-Soria J.; Moreno-Pineda E.; Chiesa A.; Fernandez A.; Magee S. A.; Carretta S.; Santini P.; Vitorica-Yrezabal I.; Tuna F.; Timco G. A.; McInnes E. J.; et al. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 2016, 7, 11377. 10.1038/ncomms11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Rogers C. J.; Asthana D.; Brookfield A.; Chiesa A.; Timco G. A.; Collison D.; Natrajan L. S.; Carretta S.; Winpenny R. E. P.; Bowen A. M. Modelling Conformational Flexibility in a Spectrally Addressable Molecular Multi-Qubit Model System. Angew. Chem., Int. Ed. 2022, 61, e202207947 10.1002/anie.202207947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Pedersen K. S.; Ungur L.; Sigrist M.; Sundt A.; Schau-Magnussen M.; Vieru V.; Mutka H.; Rols S.; Weihe H.; Waldmann O.; Chibotaru L. F.; Bendix J.; Dreiser J. Modifying the properties of 4f single-ion magnets by peripheral ligand functionalisation. Chem. Sci. 2014, 5, 1650–1660. 10.1039/C3SC53044B. [DOI] [Google Scholar]
  63. Vesborg P. C. K.; Chorkendorff I.; Brock-Nannestad T.; Dethlefsen J. R.; Bendix J. Note: Simple means for selective removal of the 365 nm line from the Hg spectrum using Dy. Rev. Sci. Instrum. 2011, 82, 096102. 10.1063/1.3639128. [DOI] [PubMed] [Google Scholar]
  64. Allodi G.; Banderini A.; De Renzi R.; Vignali C. HyReSpect: A broadband fast-averaging spectrometer for nuclear magnetic resonance of magnetic materials. Rev. Sci. Instrum. 2005, 76, 083911. 10.1063/1.2009868. [DOI] [Google Scholar]
  65. Hahn E. L. Spin Echoes. Phys. Rev. 1950, 80, 580–594. 10.1103/PhysRev.80.580. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja3c12008_si_001.pdf (605.2KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES