Improving machine learning with ensemble learning on observational healthcare data

Abstract

Ensemble learning is a powerful technique for improving the accuracy and reliability of prediction models, especially in scenarios where individual models may not perform well. However, combining models with varying accuracies may not always improve the final prediction results, as models with lower accuracies may obscure the results of models with higher accuracies. This paper addresses this issue and answers the question of when an ensemble approach outperforms individual models for prediction. As a result, we propose an ensemble model for predicting patients at risk of postoperative prolonged opioid. The model incorporates two machine learning models that are trained using different covariates, resulting in high precision and recall. Our study, which employs five different machine learning algorithms, shows that the proposed approach significantly improves the final prediction results in terms of AUROC and AUPRC.

Introduction

Ensemble learning is a machine learning paradigm that employs multiple machine learning algorithms to train several models (so-called weak classifiers). These models are based on features extracted from a variety of data projections, and their results are combined using different voting strategies to produce superior results compared to any individual algorithm used alone¹. Ensemble methods have been widely used to develop predictive models for a wide range of clinical applications, such as Alzheimer’s disease diagnosis², predicting diabetes mellitus³, acute kidney injury⁴, spinal curvature type⁵, gastric cancer cell line classification⁶, and more. The success of an ensemble method depends on multiple factors, including the sampling, training, and combination of base models. Different techniques have been proposed for ensemble classification models: Bagging⁷, in which weak classifiers are trained based on different random subsets; AdaBoost⁸, which is trained based on adjusting weights of samples previously misclassified; Random forest⁹, which is trained based on different sample dimensions and feature dimensions; Gradient boosting¹⁰, which is trained on random subsets to reduce the residuals generated by previous classifiers. The hypothesis of these methods is that each classifier learns different aspects of the problem based on a different subset of data and different feature sets, resulting in the best decision when the results are combined.

Unlike these methods, some studies proposed ensembling strong classifiers. For instance, Talukder et al.¹¹ in 2022 proposed ensemble learning for colon and lung cancer diagnosis based on six prediction models, including support vector machine (SVM), logistic regression (LR), multilayer perceptron (MLP), random forest (RF), extreme gradient boosting (XGB), and light gradient boosting (LGB). However, they only improved the base model results by combining three of the best-performing models, which had almost identical accuracy: SVM, MLP, and LR. The problem with their approach is that all these classifiers were trained with deep learning features obtained from transfer learning, resulting in high accuracy but high variance. Therefore, the ensemble of all models with relatively high and low accuracy yields an average result that may or may not outperform all base models. We addressed this issue and demonstrated that ensembling multiple machine learning (ML) models with high variance can improve the final prediction.

Our hypothesis is to develop an ensemble of two distinct models with high recall and precision. As a result of the ensemble process, the final prediction will be moderated in such a way that the false-positive cases obtained from the first model with high recall will be regulated by the second model with high precision. This idea is comparable to the boosting ensemble approach, in which misclassified cases receive high weights when passing to the subsequent models to be correctly fitted. The difference is that in the boosting approach, there is no control over the recall and precision of the models, and all subsequent models only focus on fitting the misclassified cases.

To investigate our hypothesis, we employed our approach to develop a machine learning model for identifying patients at risk of postoperative prolonged opioid use. Opioids are currently the first-line treatment for postoperative pain, regardless of prior opioid-related problems^12,13. Most surgical patients receive opioids, regardless of co-morbidities, prior opioid-related issues, or potential drug-drug interactions, and perioperative opioid exposure may be a gateway to opioid misuse and addiction^14,15. Previous research has shown that even for low-risk surgeries, opioid-naive surgical patients may continue to request opioids one year after discharge¹⁵. Therefore, the prediction of prolonged opioid use has significant impacts on the quality of pain management, patient outcomes, healthcare costs, and the opioid epidemic.

Methods

Data heterogeneity is one of the major challenges in clinical machine learning because data varies widely in terms of quality, format, and completeness, making it difficult to develop models that are robust across diverse data sources. On the other hand, studies on postoperative prolonged opioid use have utilized limited predictive features, using non-standardized data from various sources, limiting their generalizability and reliability across populations. We addressed these issues by developing our models using the Observational Medical Outcomes Partnership (OMOP) Common Data Model (CDM), which not only allows researchers to validate our proposed models in different OMOP databases but also allows them to apply our approach to different clinical use cases. The OMOP CDM standardizes the format of observational healthcare data, allowing the code to be directly shared with other researchers working with different OMOP datasets.

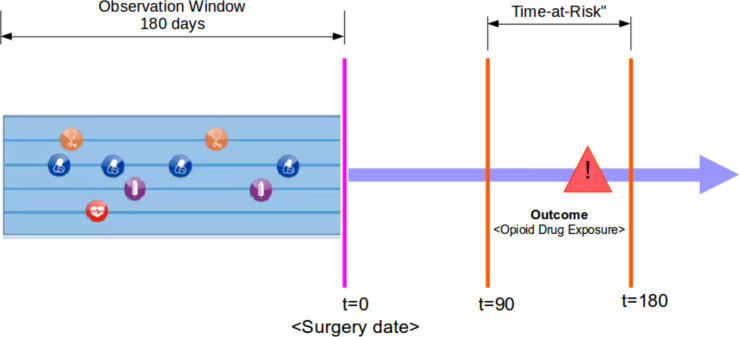
Study design and source data: This study is a retrospective analysis of observational health data that has received approval from the Institutional Review Board (IRB) at Stanford University. The analysis and prediction models were implemented using OHDSI’s standardized R packages, and all source codes and settings are available in the GitHub repository at https://github.com/su-boussard-lab/ESPOUSE. We have used the STARR-OMOP dataset, which is electronic health record data from two hospitals deidentified and mapped to the OMOP CDM. As illustrated in Figure 1, the prediction problem is defined as predicting any opioid drug exposure within 90-180 days after surgery (Time-at-Risk) based on the 180-day observation period prior to surgery.

Figure 1.

Prediction definition.

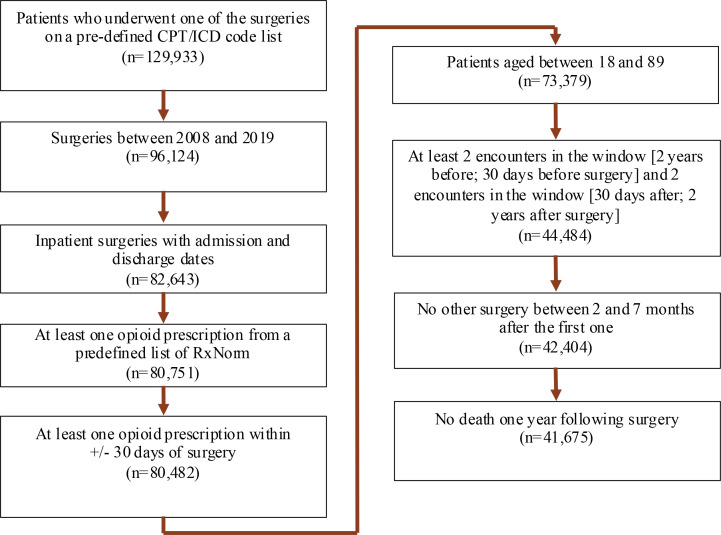
Cohort study: The target cohort includes patients between the ages of 18 and 89 who underwent inpatient surgery between 2008 and 2019 and received at least one opioid prescription 30 days before or after the surgery. Patients were included in the cohort if they had at least two visits, from two years to 30 days before surgery and from 30 days to two years after surgery. We also excluded patients who underwent secondary surgery between two and seven months following the index surgery, as well as those who died within one year after the index surgery. Our definition of prolonged opioid use (i.e., outcome cohort) is any opioid exposure between 90 and 180 days after surgery. In the cohort selection, nine groups of RxNorm opioid drug ingredients, such as codeine, fentanyl, hydrocodone, hydromorphone, morphine, meperidine, methadone, oxycodone, and tramadol, were used to identify opioid prescriptions, and seventeen key groups of surgeries were considered to identify target procedures. Figure 2 depicts the cohort selection criteria as well as the number of patients obtained from each one.

Figure 2.

Cohort selection flowchart.

Covariate setting and feature selection: We defined our covariate setting based on (1) demographic features, including gender, age group, race, and ethnicity; (2) clinical occurrence features, including drug exposure, condition, procedure, and measurement; (3) clinical count features, including drug count, condition count, procedure count, and measurement count; and (4) drug-era occurrence features.

We extracted all covariates using OHDSI’s feature extraction R package and calculated their distribution across prolonged and non-prolonged opioid users. As a result of feature extraction, we achieved 35,864 district covariates. We evaluated all these covariates using the Positive-Negative Frequency (PNF)¹⁶ metric and selected all the most relevant features with respect to prolonged opioid use. PNF is a feature evaluation metric that calculates the relevance degree of two categorical variables in imbalanced circumstances. We calculated the relevance degree of covariate c with respect to outcome o, prolonged opioid use, as follows:

$$\begin{array}{l}PNF(c,o)=1+\frac{P(c|o)-P(c|\overline{o})}{P(c|o)+P(c|\overline{o})}\\ \end{array}$$ Equation 1

In Equation 1, P(c|o) and P(c|ō) indicate the occurrence probability of covariate c in a random patient that does and does not belong to prolonged opioid use, respectively. As PNF produces values between 0 and 2, we chose all covariates whose PNF values were greater than 1.5, indicating a more positive correlation with prolonged opioid use. As a result, we acquired 3,418 relevant covariates, representing 9.5% of all covariates. The performance of the PNF metric in feature evaluation has already been evaluated and compared to other metrics, such as odds ratio, chi-square, and information gain, in the imbalanced classification problem, demonstrating its superiority to others¹⁷. As a result, we built our base models on the full and relevant set of covariates selected by the PNF metric.

Base model development: We developed five base models, including Lasso Logistic Regression (LR), Random Forest (RF), AdaBoost (AB), Extreme Gradient Boosting (GB), and Naive Bayes (NB), using OHDSI’s PatientLevelPrediction¹⁸ R package version 6.0.4, available at https://github.com/OHDSI/PatientLevelPrediction. The dataset was divided into train (80%) and test (20%) sets using a stratified random sampling method. We used 5-fold cross-validation on the train set with a grid search strategy to select the best hyperparameters. We also removed infrequent covariates with less than 0.001 frequency from our feature set. We trained two models for each algorithm using full and relevant covariates.

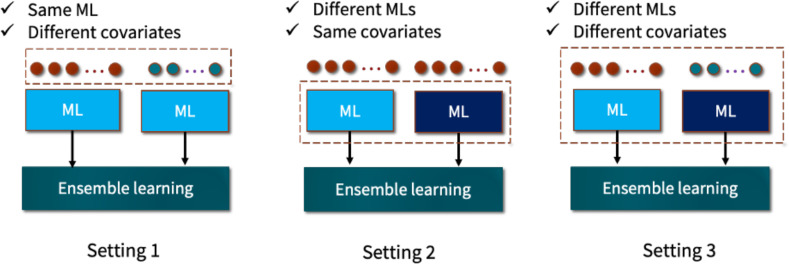
Ensemble model development: Based on the settings shown in Figure 3, we developed three types of ensemble models using OHDSI’s EnsemblePatientLevelPrediction R package. In the first setting, we combined the predictions of two base models that were trained using the same algorithm but with different sets of features: all features and the most relevant features predictive of prolonged opioid use. As a result of this setting, five ensemble models were generated. The second type of ensemble model was developed by combining the predictions of the five ML models that were trained on the same feature set. Because there are two feature sets, the second setting resulted in two ensemble models.

Figure 3.

Ensemble learning settings.

Finally, we built another ensemble model using the ensemble of all base models trained with full and relevant features. The final prediction in this model was derived from the predictions of 10 ML models.

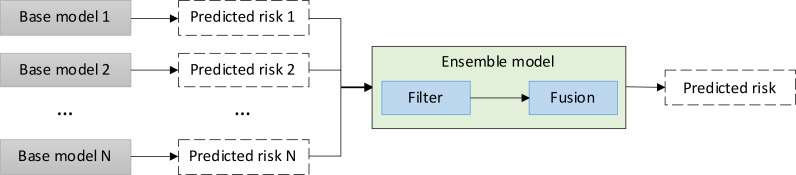
In general, ensemble models are built in two steps: filtering and fusion. The filtering step is used to eliminate models with significantly lower accuracy than the others, resulting in an increase in the variance of prediction outcomes throughout the ensemble learning process. We did not filter any of the base models because our hypothesis is to demonstrate the ensemble of base models, which are trained to learn specific aspects of the problem. Therefore, the performance disparity may have no effect on the final prediction because each of the base models will play a complementary role in the ensemble model. The second step is fusion, which is used to combine the prediction outcomes of the base models. Three main approaches are used in the literature: bagging, boosting, and stacking. While the bagging approach combines individual predictions uniformly by averaging the output values, the boosting approach combines the model outputs using a weighted average. In contrast to these two approaches, the stacking method uses another model to train the final prediction based on the predictions of the base models. Figure 4 depicts the risk prediction schema in an ensemble model. To investigate our hypothesis, we used the bagging approach in the development of three types of ensemble models.

Figure 4.

Risk prediction schema in an ensemble model.

Model evaluation: To measure model discrimination, we used two threshold-independent metrics, area under the receiver operating characteristic curve (AUROC) and area under the precision-recall curve (AUPRC), as well as a calibration plot to evaluate the calibration of the model outputs in predicting the risk of prolonged opioid use. While AUROC represents a harmonic mean of sensitivity and specificity, AUPRC represents a mean of precision and recall. As a result, using both metrics in model evaluation can reveal different aspects of the models’ performance. To compare AUROC values, we calculated the 95% confidence interval (CI) using 2000 stratified bootstrap replicates¹⁹.

Results

Cohort characterization: The cohort included 41,675 patients, of whom 6,071 (14.6%) were prolonged opioid users. We characterized the target cohort based on the demographic covariates we used in model development, including gender, race, ethnicity, and age groups, which had a p-value < 0.001. Table 1 summarizes the distribution of these covariates among prolonged and non-prolonged users. We also explored the age statistics of the target cohort, stratified by prolonged and non-prolonged opioid use. While the average and median ages for prolonged users were 56.65 and 58, respectively, they were 57.48 and 60 for non-prolonged users, which was not statistically significant (p=0.22628).

Table 1.

Target cohort characterization. All covariates listed had a p-value < 0.001

Covariate	Value	Total		Prolonged		Non-prolonged
		Count	Percent	Count	Percent	Count	Percent
Gender	Female	23,173	55.60%	3,539	58.29%	19,634	55.14%
	Male	18,502	44.39%	2,532	41.71%	15,970	44.85%
Race	White	27,085	64.99%	3,899	64.22%	23,186	65.12%
	Asian	5,508	13.22%	733	12.07%	4,775	13.41%
	Black	1,475	3.54%	320	5.27%	1,155	3.24%
	Other/Unknown	7,607	18.25%	1119	18.43%	6,488	18.22%
Ethnicity	Hispanic or Latino	5,634	13.52%	932	15.35%	4,702	13.21%
	Non-Hispanic or Latino	35,366	84.86%	5,090	83.84%	30,276	85.04%
Age group	15 - 19	554	1.33%	57	0.94%	497	1.40%
	20 - 24	1,150	2.76%	144	2.37%	1,006	2.83%
	25 - 29	1,243	2.98%	178	2.93%	1,065	2.99%
	30 - 34	1,679	4.03%	259	4.27%	1,420	3.99%
	35 - 39	2,103	5.05%	314	5.17%	1,789	5.02%
	40 - 44	2,441	5.86%	377	6.21%	2,064	5.80%
	45 - 49	3,139	7.53%	492	8.10%	2,647	7.43%
	50 - 54	4,009	9.62%	668	11.00%	3,341	9.38%
	55 - 59	4,561	10.94%	753	12.40%	3,808	10.70%
	60 - 64	4,816	11.56%	777	12.80%	4,039	11.34%
	65 - 69	5,347	12.83%	747	12.30%	4,600	12.92%
	70 - 74	4,551	10.92%	540	8.89%	4,011	11.27%
	75 - 79	3,245	7.79%	423	6.97%	2,822	7.93%
	80 - 84	1,915	4.59%	230	3.79%	1,685	4.73%
	85 - 89	922	2.21%	112	1.84%	810	2.28%

Prediction results: Table 2 provides a summary of the AUROC values of ten base models trained using five ML algorithms, along with ensemble models resulting from the three settings described earlier. The last row shows the results of ensemble models achieved by combining two ML models with two feature sets (setting 1), and the last column shows the ensemble results achieved by combining five ML models with the same feature set (setting 2). The bottom right cell shows the ensemble model obtained by combining all ten base models (setting 3). The AUROC values demonstrated that all the ensemble models obtained from Setting 1 outperformed the base models, among which lasso logistic regression achieved the best ensemble AUROC value. All improvements were significant at p<0.05, except for NB. We also observed that ensemble models obtained from Setting 2 were unable to outperform all base models. Finally, while the ensemble model obtained from Setting 3 outperformed all individual base models, the models obtained from Setting 1 performed the best.

Table 2.

AUROC of base and ensemble models with 95% confidence interval.

Covariate setting	Base machine learning models					Ensemble Setting 2
	LR	RF	GB	AB	NB
All	0.749 (0.734-0.765)	0.734 (0.717-0.75)	0.747 (0.732-0.763)	0.736 (0.720-0.752)	0.675 (0.659-0.690)	0.744 (0.729-0.759)
Relevant	0.704 (0.684-0.723)	0.709 (0.690-0.728)	0.709 (0.691-0.728)	0.707 (0.689-0.726)	0.678 (0.660-0.696)	0.707 (0.689-0.726)
Ensemble Setting 1	0.784 (0.769-0.800)	0.773 (0.757-0.789)	0.783 (0.767-0.798)	0.773 (0.757-0.788)	0.693 (0.676-0.710)	Setting 3 0.770 (0.755-0.785)

We reported AUPRC values for the same experiment in Table 3. Unlike AUROC, which showed the superiority of the base models with all covariates, AUPRC indicated the superiority of the models with relevant covariates. According to the paired t-test, the results achieved from the two feature sets were significant at p < 0.01. As a result, we observed that the ensemble models obtained from the ML algorithms with two different feature sets (Setting 1) outperformed the base models and achieved the highest AUPRC values.

Table 3.

AUPRC of base and ensemble models.

Covariate setting	Base machine learning models					Ensemble Setting 2
	LR	RF	GB	AB	NB
All	0.3703	0.3634	0.3766	0.3529	0.2468	0.3648
Relevant	0.4743	0.4614	0.4622	0.4615	0.2801	0.4252
Ensemble Setting 1	0.5037	0.4693	0.4875	0.4854	0.2810	Setting 3 0.4343

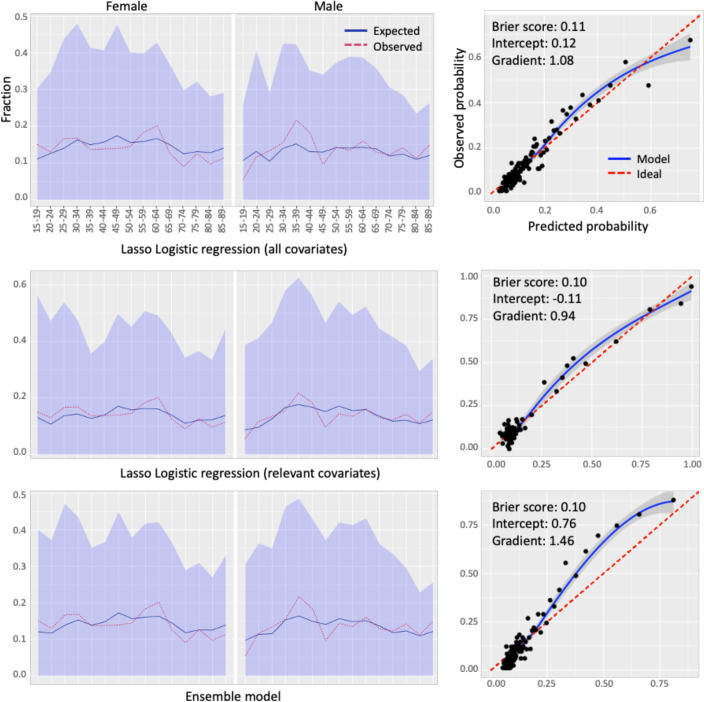
Calibration results: To show the impact of ensemble learning on the output of the ML models, we reported the calibration plots in Figure 5 for the best-performing ensemble model achieved from two base models using lasso logistic regression with two different feature sets. According to the calibration plots, while the two base models produce more calibrated risk probabilities, the ensemble model slightly underestimates the risk probability. Nevertheless, the Brier score of the ensemble model, which calculates the mean squared error between predicted probabilities and the observed values, is very similar to that of the base models, indicating that the predictions produced by the base and ensemble models are equally accurate. We also observed that the second base model trained with the relevant covariates produces more calibrated risk probabilities for males and females across different age groups than the first trained with all covariates. This is also evident in the ensemble model, which has a higher Brier score than the first base model. Furthermore, demographic calibration results revealed that model calibration varies between males and females over specific age groups. For instance, while the difference between observed and predicted risk is slightly higher in females aged 55 to 65, it is higher for males aged 30 to 45.

Figure 5.

Calibration plots on the test set stratified by demographic covariates with a Brier score, weak calibration intercept, and gradient for the ensemble model obtained from two base models using lasso logistic regression with two different feature sets.

Discussion

Ensemble learning is a machine learning technique that combines multiple models to improve prediction accuracy and reliability. However, when there is a high variance in accuracy among base models, combining them can be challenging. To address this issue, studies filter base models before fusion to eliminate models with lower accuracy. In this study, we addressed this issue and proposed an ensemble model for predicting patients at risk of prolonged opioid use, incorporating two types of base models regardless of performance disparities to improve overall prediction. The approach involves training ML models with all covariates and those relevant to prolonged opioid use, resulting in two types with high AUROC and AUPRC. The first model, using all covariates, has a high AUROC but high false-positive rates, resulting in low precision. To deal with this issue, we ensembled it with models trained on only predictive features of prolonged opioid use, reducing false-positive cases and achieving high precision.

Our results in Table 2 showed that the ensemble of two models outperformed the overall prediction, despite significant differences in AUROC. In this approach, two models trained with two different covariates produce two distinct misclassification errors. The majority of errors in the model trained with all covariates are related to false-positive cases, while in the model trained with relevant covariates, they are false-negative. Therefore, the combination of these models moderates the error region, resulting in higher AUROC and AUPRC.

Ensembling multiple models using different algorithms with the same feature set (Setting 2 in Table 2) leads to an overall prediction range between the best and worst models. This suggests that ensemble learning cannot significantly impact overall prediction if all base models have the same misclassification attitude. On the other hand, combining multiple models with different feature sets and algorithms (Setting 3 in Table 2) can improve overall AUROC but may not be significant when compared to base models with all covariates. In terms of AUPRC, most of the base models with relevant covariates performed better than the ensemble models with Settings 2 and 3. This demonstrates that ensemble learning performance decreases when base models make similar predictions, and increasing the number of base models cannot improve overall AUROC and AUPRC simultaneously.

The impact of using two different feature sets was evident in the performance of ensemble models using the same ML algorithms. In the study, the majority of patients belong to the negative class, causing ML models with all covariates to tend towards negative cases because all misclassification errors have the same impact on the loss function of models. In contrast, when a model is trained using a relevant feature set, it may be more accurate in identifying positive cases while paying less attention to negative ones. At this point, the PNF metric plays an important role because it assesses the degree of relevance of features based on the imbalanced distribution of patients between the prolonged and non-prolonged classes. The impact of the PNF metric on the imbalanced classification problem has been recently investigated and compared to that of deep feature extraction methods²⁰, showing the PNF metric produces comparable results in combination with ML models compared to deep learning models. Therefore, using different feature sets with the same ML algorithm helps learn various aspects of a problem, particularly in clinical applications like opioid use prediction. This approach offers a better trade-off between AUROC and AUPRC, making it more relevant in these applications.

The calibration of ML models is crucial for risk stratification in clinical applications. We assessed the calibration of the ensemble model achieved from our best-performing model, lasso logistic regression, using two different feature sets. The calibration result supported our hypothesis, as we wanted to moderate the risk probabilities of the first model with all covariates by using the second one, which was trained over relevant features. The second model reduced the false-positive cases for which the first model calculated high risk scores, resulting in an underestimation of the ensemble model. This is because we did not calibrate the output of the ensemble model, and the calibration plot reflects the impact of using the bagging approach on the model output. This suggests the calibration of the ensemble model based on the validation database.

Overall, this study addressed a significant challenge in using ML for clinical applications where a single model was unable to provide a trade-off between precision and recall. Although we still need more accurate models to be used in clinical practice, this approach provides a vision for developing decision support systems that involve multiple models with different characteristics. Identifying prolonged opioid users is one of the examples that can benefit from such decision-support systems. Early identification of patients at risk can allow healthcare providers to implement alternative pain management strategies and minimize the risk of opioid-related adverse outcomes such as misuse and addiction. Prolonged opioid use can also lead to increased healthcare utilization and costs, particularly if patients develop opioid use disorder or other complications. Together, this highlights the impact of ensemble learning, which makes ML models more accountable and actionable in clinical practice. This approach divides the main prediction problem into sub-prediction tasks, training multiple models with relevant features. An ensemble model generates a decision support system for predicting the main problem, considering the outputs of each subtask. This approach offers a better trade-off between precision and recall and is more understandable to clinicians by generating a transparent ensemble process that displays the output of base models on various subtasks of the main problem.

Our study had some limitations in terms of patient population and model development. We created models based on a single institution’s database, which limits the diversity of the patients and the models’ generalizability. To overcome this limitation, we developed our models using OMOP data and OHDSI’s standardized tools and methods libraries. As a result, all developed models are deployable and validatable on various OMOP databases, and we intend to evaluate the generalizability of ensemble models in our feature work. Another limitation of this study was the use of binary features in model development, which are obtained from individual CDM concepts for each patient over a fixed period of time. This limits our models’ ability to identify modifiable risks associated with prolonged opioid use. Although this limitation affects the performance of individual ML models, it may not have a major impact on the conclusion of our study, in which ensemble learning is used to improve the overall model prediction. However, more research is required to investigate the impact of the combination of different types of features on the performance of the base and ensemble models.

Conclusion

This study developed and investigated three ensemble models for identifying patients at risk of prolonged opioid use using machine learning models trained on two different feature sets. The results showed that ensemble learning significantly improves overall prediction accuracy when the base models do not share a large common error region. Combining two base models with high variance in accuracy did not diminish overall prediction accuracy but also enhanced it. Our findings indicated that ensemble models derived from two different feature sets using the same ML algorithm outperform other ensemble approaches and base models. The study highlights the potential of ensemble learning to improve machine learning performance by allowing a trade-off between model precision and recall when capturing different aspects of the prediction problem with a minimal common margin of error. This provides a vision for developing decision support systems that combine multiple models focusing on different aspects of the prediction rather than developing a single model covering all of them. Future work could include developing decision support systems incorporating modifiable risk factors by using base models trained on temporal covariates.