Tailoring chemical bonds to design unconventional glasses

Significance

Glasses and the corresponding crystals usually share a similar local order and comparable properties. We explain these similarities by quantifying chemical bonding. Using quantum chemical bonding descriptors (electrons transferred and shared between atoms), we demonstrate that in common glasses like SiO₂, GeSe₂, and GeSe, chemical bonding in the glass and the corresponding crystal hardly differ. To the contrary, for crystals only found in a distinct region of the map, spanned by the two bonding descriptors, unconventional glasses are obtained, which differ in both local order and optical properties. This region contains crystals of GeTe, Sb₂Te₃, and GeSb₂Te₄, which employ metavalent bonding. Hence, we can design unconventional glasses by identifying those crystals, which employ theses peculiar bonds.

Abstract

Glasses are commonly described as disordered counterparts of the corresponding crystals; both usually share the same short-range order, but glasses lack long-range order. Here, a quantification of chemical bonding in a series of glasses and their corresponding crystals is performed, employing two quantum-chemical bonding descriptors, the number of electrons transferred and shared between adjacent atoms. For popular glasses like SiO₂, GeSe₂, and GeSe, the quantum-chemical bonding descriptors of the glass and the corresponding crystal hardly differ. This explains why these glasses possess a similar short-range order as their crystals. Unconventional glasses, which differ significantly in their short-range order and optical properties from the corresponding crystals are only found in a distinct region of the map spanned by the two bonding descriptors. This region contains crystals of GeTe, Sb₂Te₃, and GeSb₂Te₄, which employ metavalent bonding. Hence, unconventional glasses are only obtained for solids, whose crystals employ theses peculiar bonds.

Crystallization and vitrification are important processes to produce solids with tailored properties. Protein crystallization demonstrates which large efforts scientists have undertaken to unravel the atomic arrangement in protein molecules. Glasses, on the other hand, attract with their ability to be shaped at ease above the glass transition temperature. Hence, crystals and glasses are the two most important states of solid matter. Scientists have early on pondered about the differences in atomic arrangement and material properties between glasses and the corresponding crystals. The similarity of many properties of simple oxides between the glassy and crystalline phase led Zachariasen to state a very practical rule: The short-range order in the glass should be essentially the same as in the crystal, since “the atoms are held together by the same forces” (1). Today, we would possibly replace the word “forces” by “bonding mechanism.” Zachariasen continued by discussing some simple rules, which help to identify and predict those oxides that can easily form glasses.

Indeed, short-range order has been measured in many glasses since that time and it was shown to be close (with minor distance and angular fluctuations and few coordination defects) to that of the corresponding crystal. Such glasses are also denoted as Zachariasen glasses or glassy covalent networks. Now, one can wonder whether it is possible to break this rule and design functional glasses that are unconventional in the sense that they do not bear the same short-range order and opto-electronic properties as their crystal. A first indication that this will be possible is given by phase change materials (PCMs), which are utilized to store data (2) and realize active metasurfaces as well as nanophotonic switches (3) and neuromorphic computers (4). In these, the atomic arrangement differs considerably between the glass-like (amorphous) material and the corresponding crystal (5–8). Furthermore, good phase change materials crystallize very quickly, a necessity to rapidly switch between the glassy/amorphous and crystalline state in memory applications (9–11). Pronounced differences between the glass and the crystalline state are also observed for several characteristic properties such as the optical dielectric constant ɛ_∞ (a measure of the electronic polarizability), the Born effective charge Z* (a measure of the chemical bond polarizability), or the effective coordination number (ECoN) (a measure of the atomic arrangement) (12). The difference in optical and electrical properties, in conjunction with the ability to switch rapidly between both states is responsible for a range of applications of phase change materials, including optical and electronic data storage, as well as photonic devices (3, 13). Hence, PCMs reveal the characteristic property portfolio of quantum materials, i.e., a distinct change of properties upon external stimuli (14).

This raises the question which mechanism is responsible for the pronounced deviation of properties and the differences in atomic arrangement between the glass and the crystalline state. We will answer this question by employing recently developed concepts to analyze chemical bonding utilizing quantum-chemical tools (15–19). This will enable us to challenge Zachariasen’s conjecture. Does the bonding in glassy compounds always correspond to their crystalline counterparts? At least for phase change materials, we will present compelling evidence for the contrary. We will generalize that the functional nature of these unconventional glasses arises from rather unusual chemical bonding in the crystalline state.

Results and Discussion

Before quantifying the chemical bonding in glassy phase change materials, we will explore the bonding in glassy SiO₂, the prime example of a network-forming glass already discussed by Zachariasen in 1932. To this end, Fig. 1A displays the number of electrons shared between adjacent atoms as a function of the interatomic spacing for SiO₂ in the crystal and in the glass. The number of electrons shared (ES) between adjacent atoms is twice the delocalization index (DI), the number of electron pairs formed between two atoms. This quantity is determined from the quantum mechanical wavefunction, in particular from the non-classical part (the electron exchange contribution) of the electron pair density (see SI Appendix for more details) (15).

Fig. 1.

Comparison of chemical bonding and atomic arrangement in glassy and crystalline SiO₂ (A) and GeTe (B). For SiO₂, the atomic arrangement in the crystal (indicated by bars) and the glass is very similar; the glass only shows a small variation in bond length (Zachariasen glass). Interestingly, the quantum chemical bonding descriptor, the number of electrons shared between adjacent atoms is very similar for both phases, too. This is fundamentally different for GeTe, where the distribution functions for both the Ge-Te distances as well as the number of electrons shared (ES = 2 * DI) between adjacent atoms differ significantly between the two phases. GeTe hence forms a non-Zachariasen glass. The relative distance is the interatomic distance divided by the first neighbor distance in the crystal.

Ionic bonds typically only share less than an electron (ES < 1), while standard 2 center–2 electron (2c-2e) covalent bonds tend to share an electron pair, i.e. have an ES value close to 2. The ES value of SiO₂ is only 0.72, since each oxygen atom receives 0.8 electrons from two neighboring Si atoms, in agreement with the high polar character of the Si–O bond. Fig. 1A compares the atomic arrangement in crystalline and glassy SiO₂, analyzing more than 1,000 bond distances in the latter. It confirms that the atomic arrangement in crystalline and glassy SiO₂ can be hardly distinguished (see ref. 20), at least as far as the short-range order is concerned. Interestingly, Fig. 1A also shows the reason for this similarity. An analysis of the number of electrons shared between adjacent atoms shows an almost identical situation for glassy and crystalline SiO₂, i.e., the bonding in both phases hardly differs. This corroborates the conjecture that oxide glasses like SiO₂ have the same short-range order as the crystal, since the chemical bonding is very similar. In GeTe, instead (Fig. 1B), a very different situation is encountered. The atomic arrangement in the glassy phase is characterized by a much larger difference between shorter and longer bonds and a wide distribution of atomic distances. This can be attributed to pronounced differences in chemical bonding, in striking contrast to a view expressed recently [(21), see SI Appendix]. Glassy GeTe hence forms a non-Zachariasen glass. It can be observed that, in any glass, when the distance (and chemical order) is equal to that of the crystal (SI Appendix, Fig. S1), the number of shared electrons is similar. In the particular case of GeTe, aligned bonds are longer (about 3 Å) than those in the crystal and share about 1 electron, indicative of 3c-2e bonding. As expected, the electron sharing is decreasing with increasing atomic separation and decreasing covalent character of the bond. This quantifies the common belief that the bond length scales with the bond strength. A similar behavior was reported (21) for a number of chemical-bonding indicator data, calculated at the bond critical points (BCPs) in simulated models of amorphous and crystalline GST. It is not a surprise that the properties of bonds in amorphous and crystalline structures are similar when they are evaluated at a common geometry. This is merely a consequence of the local character of the properties being examined. Those properties considered in ref. 21 are local in nature since they refer to a precise point, the BCP, taken as the most representative point along the bond path joining two adjacent nuclei. The DIs, despite being the result of an integration of the exchange correlation density over the two atomic basins of these atoms, are known to be also fundamentally local in character. It is therefore not surprising that the same (local) atomic arrangement in the glass and the crystal is accompanied by the same chemical bonding descriptors. This is the essence of the Zachariasen conjecture, the similarity of chemical bonding in the glass and the crystal leads to a similarity in atomic arrangement.

In the supplement, the comparison of the atomic arrangement and chemical bonding is presented for several solids. Some of them closely match SiO₂, i.e., they show the same bonding descriptors and atomic arrangement as in the crystalline state. This holds for GeSe₂ but also to a good approximation for GeSe. Yet, there are compounds where the glass and the crystal have significant differences in their atomic arrangement (5–8). Besides GeTe, this also holds for GeSb₂Te₄ (22), a prototypical phase change material, and Sb₂Te₃. Apparently, GeSb₂Te₄, Sb₂Te₃ (23), and GeTe form non-Zachariasen glasses (NZG), where the atomic arrangement and chemical bonding differs significantly between the glass and the crystal.

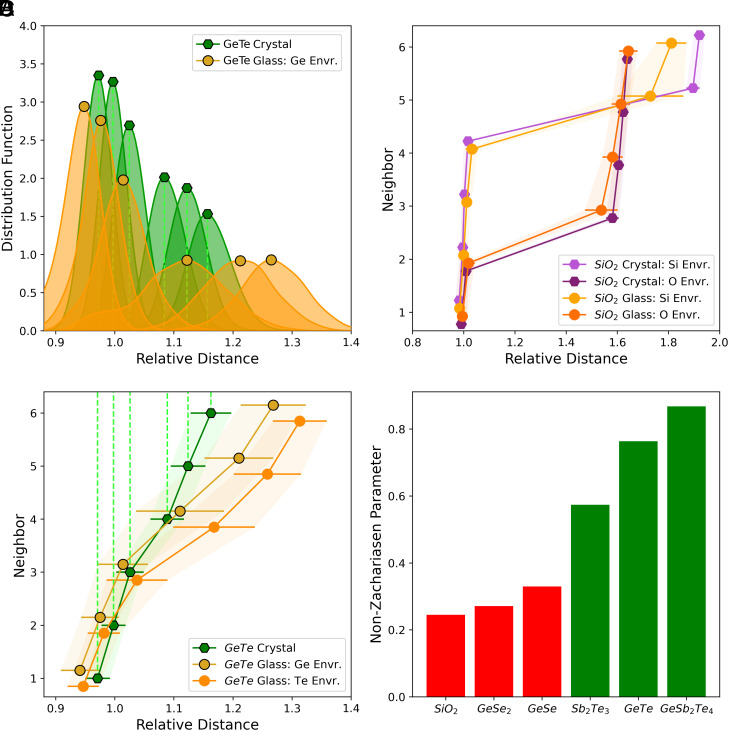
To quantify the departure from the Zachariasen conjecture in different glasses, we define a local order parameter based on the analysis of the local environment of each atom. To this end, configurations for the glass and the crystal are generated by DFT-based Molecular Dynamics at finite temperature (300 K). Hence, even in the crystal, a distribution of atomic distances is found. We consider the distributions of the first N_b neighbors surrounding each atom, averaged for each species, as previously used in ref. 24. These distributions overlap (Fig. 2A) and, for each species, their averages (Fig. 2 B and C) can be used to define the order parameter NZ as the difference between the first neighbor distances in the crystal and the glass, properly weighted to treat all species on an equal footing (SI Appendix).

Fig. 2.

Comparison of the atomic arrangement in glassy and crystalline GeTe (Left), SiO₂, and other glasses (Right). (A) Distributions of the six normalized distances between the first Ge neighbors of glassy (orange) and crystalline α-GeTe (green), from which the average distances (B) are calculated. (B) Averaged, normalized first neighbor distances for crystalline and glassy GeTe (see ref. 24). d₀ = 2.86 Å is the short GeTe neighbor distance in α-GeTe. There is only one (green) line for the crystal since Ge and Te atoms are equivalent. The atomic arrangement in glassy GeTe differs significantly from crystalline GeTe. Data for Ge and Te neighbors are shown since the formation of a small number of tetrahedral Ge sites, caused by some homopolar bonds, leads to a small asymmetry of the distribution function. (C) d_i/d₀ for crystalline and glassy Sio₂. d₀ = 1.63 Å is the Si–O distance. The local environments for the glass and the crystal are very similar. In panels (B) and (C), the error bars are the SDs of the distributions. (D) Non Zachariasen (NZ) parameter measuring the difference between the local atomic arrangements in crystal and glasses for selected compounds. While GeTe, Sb₂Te₃, and GeSb₂Te₄ show pronounced differences between glass and crystal, only small differences for SiO₂, GeSe₂, and GeSe are found.

In crystalline SiO₂ (Fig. 2B), the first four distances around Si are equivalent, hence d_i are aligned, while the first six distances in crystalline GeTe displayed in Fig. 2A are not, revealing the slight Peierls distortion of the crystal at 300 K. In glassy GeTe, the much larger splitting of the distance distribution is a signature of a markedly different atomic arrangement around Ge and Te atoms. Comparing panels Fig. 2 B and C reveals that this difference, quantified by the NZ parameter, is large for GeTe and very small for SiO₂. As displayed in Fig. 2D, SiO₂ (0.25), GeSe₂ (0.27), and GeSe (0.33) have low NZ values because their local orders in crystalline and glassy states are very similar. On the contrary, the four GeTe structures tested, which differ by their decreasing amount of quasialigned bonds (6), Sb₂Te₃ and the two GeSb₂Te₄ structures have significantly larger NZ values, in the 0.57 to 0.92 range. The local order in these glassy phase change materials structures is different from that of their crystalline counterpart. They are prototypes of NZG and their bonding mechanism, characterized using advanced quantum mechanical tools is also different.

The pronounced differences in the atomic arrangement between the different glasses and crystals compared in Fig. 2D raise the question how the properties of both phases differ for the different solids (see SI Appendix, Table S4 for all property values). This is depicted in Fig. 3 for six different properties including the optical dielectric constant ɛ_∞, the effective coordination number (ECoN), the Born effective charge Z*, the maximum height of the absorption peak ɛ₂^Max, and its energy E(ɛ₂^Max), as well as the maximum vibration frequency v_max. This last quantity hardly differs between the glass and the crystal for any of the materials studied. For the other quantities, especially those which are related to chemical bonding, like the optical properties and the chemical bond polarizability Z*, some materials show striking differences between glass and crystal, while others do not. Fig. 3 reveals that only for those solids, where the atomic arrangement differs significantly between the glassy and the crystalline phase, pronounced changes of properties accompany crystallization of the glassy phase.

Fig. 3.

Comparison of the properties of six different glasses (red) and their crystalline counterparts (blue). Six different quantities are depicted to show the differences between glass and crystal; the effective coordination number (ECoN), the optical dielectric constant ɛ∞, the maximum vibration frequency v_max, the maximum height of the absorption peak ɛ₂^max, and its energy E(ɛ₂^max), as well as the (cation) Born effective charge Z*. Pronounced changes of properties upon crystallization are only observed for the three non-Zachariasen glasses Sb₂Te₃, GeTe, and GeSb₂Te₄ (100% scale is ECoN = 6, ɛ∞ = 80, v_max =40 THz, E(ɛ₂^max) =10 eV, ɛ₂^max = 100 and Z* = 12 e).

Zachariasen has argued that the atomic arrangement in oxide glasses would be the same as in the corresponding crystal, since the chemical bonding is the same in both phases. This conjecture can now be verified with the quantum chemical bonding analysis already shown for GeTe and SiO₂ in Fig. 1. All solids studied here have been depicted in the map displayed in Fig. 4. This map is spanned by two different quantum-chemical bonding descriptors, the number of electrons transferred, and the number of electrons shared between adjacent atoms. The map separates different bonding mechanisms rather well. Ionic bonding is characterized by pronounced electron transfer between adjacent atoms, while in covalent bonding pronounced electron sharing (electron pair formation) prevails. The large number of nearest neighbors in metals leads to a small number of electrons shared between adjacent atoms. In conjunction with moderate charge transfer, this locates solids which employ metallic bonding in the lower left corner of the map. Between covalent and metallic bonding, another bonding mechanism is located, which is characterized by a characteristic property portfolio including large values of the Born effective charge Z *, the optical dielectric constant ɛ∞ Solids which are characterized by these properties have been denoted as “metavalent” solids or incipient metals (12). Crystalline GeTe, Sb₂Te₃, and GeSb₂Te₄ fall into this category.

Fig. 4.

2D map classifying chemical bonding in crystals and glasses. The map is spanned by the number of electrons shared (Left y-axis) between adjacent atoms and the electron transfer renormalized by the formal oxidation state (x-axis). Different colors characterize different material properties and have been related to different types of bonds. The glasses of three solids are characterized by a bonding mechanism which closely resembles the crystal (GeSe₂, SiO₂, and GeSe). On the contrary, for GeTe, Sb₂Te₃, and GeSb₂Te₄, pronounced changes in bonding occur upon crystallization. While crystalline GeTe, Sb₂Te₃, and GeSb₂Te₄ employ metavalent bonding, their glasses are covalently bonded. Metavalent crystals show characteristic features of quantum materials, i.e., they show a pronounced change of properties upon external stimuli like pressure or temperature. These materials change their bonding mechanism upon vitrification, while this is not the case for any other bonding mechanism in solids.

With the quantum chemical bonding descriptors, one can now compare the glassy and crystalline phases of solids. This comparison shows that for all solids, where the atomic arrangement and properties of the glass and the crystal barely differ (SiO₂, GeSe, and GeSe₂), the chemical bonding descriptors also hardly change. All of these glasses hence fulfill the Zachariasen conjecture, that the close similarity of atomic arrangement in both phases is due to the similarity in chemical bonding. Yet, there are also NZGs (GeTe, Sb₂Te₃, and GeSb₂Te₄). These are glasses, which are formed upon vitrification of incipient metals. Such metavalent crystals are characterized by a competition of electron delocalization (as in metallic bonding) and electron localization (as in covalent or ionic bonding). This leads to pronounced changes upon external stimuli, characterizing these solids as quantum materials.

Glass formation in these chalcogenide-based quantum materials leads to pronounced changes of atomic arrangement, turning the bonding more covalent. Hence, only such materials which form metavalent crystalline solids, reveal a pronounced change of bonding upon crystallization. It is possibly no surprise that Zachariasen could not yet envision in 1932 the advent of such quantum materials and their unconventional property portfolio we witness today. The property changes of these materials upon crystallization are exploited in different applications such as phase change materials for optical and electronic data storage as well as neuromorphic computing. Fig. 4 reveals that metavalent solids are prime candidates as phase change materials since they offer the desired pronounced property contrast between the glassy and the crystalline phase. Yet, Fig. 4 offers additional insights. The quantum chemical bonding descriptors which span the map in this figure are also excellent property predictors. As shown recently, there is a close relationship between the position of the map and the resulting band gap as well as the dielectric function ɛ₂(w) (19). It has even been demonstrated that the crystallization kinetics is closely related to the position of the map in the metavalent regime. Compounds closer to the green dashed line crystallize (switch) much more rapidly than metavalent solids which are located closer to the border between metavalent and covalent bonding (25).

At the same time, the findings presented here also lead to several interesting questions and should motivate relevant follow-up studies. First of all, it would be rewarding to increase the number of glasses that are depicted in Fig. 4. It could be for instance very interesting to further explore solids, whose crystals are located right above the upper edge of metavalent solids. In this region, p-bonded compounds are found, such as Sb₂Se₃ or Sb₂S₃, which offer larger band gaps than metavalent crystals, beneficial for photonic applications in the visible. The present design rule and the corresponding map can help to identify such photonic materials.

Finally, the most interesting questions seem related to the border between metavalent and metallic bonding. First studies have shown that there are even plasmonic phase change materials, i.e., crystalline phases that have metallic-like (plasmonic) optical properties. In₃SbTe₂ is one of these materials, which has a glassy phase with a band gap of about 0.7 eV (26). Hence, one can switch between a metallic-like crystalline phase and an infrared-transparent covalent glass, providing interesting application opportunities (27). It seems very rewarding to look for additional plasmonic phase change materials at the border between metallic and metavalent bonding. Finally, one can ponder whether there are any other crystalline metals which have unconventional phases when rapidly quenched from the melt. For instance, chiral metals like AlPt (28) are potential candidates in this search for such unconventional non-crystalline phases. It will be interesting to locate such metals in Fig. 4, as well. The generality of the method makes it directly applicable to quantify the possible bonding origin of the changes observed in glassy MOF (29) and hybrid perovskites (30), for which metavalent bonding has been shown to prevail in a number of crystalline phases (31).

To briefly conclude, we have shown that upon vitrification crystals with the peculiar metavalent bonding turn into glasses, leading to significant changes in terms of bonding, short-range order, and opto-electronic properties. This finding provides a clear design rule, how to find unconventional glasses, i.e., those with opto-electronic properties which change significantly upon crystallization. Upon inversion of this argument, it is now also easy to understand why ordinary glasses have similar optical properties to their crystalline counterpart, since in these solids the bonding hardly changes during crystallization.

Materials and Methods

Six different glasses compositions (SiO2, GeSe, GeSe₂, Sb₂Te₃, GeSb₂Te₄, and GeTe) are studied using density functional theory (32) and molecular dynamics. Amorphous/glassy configurations with 189 to 249 atoms have been generated by melt–quench technique with VASP (33) using PBE exchange correlation functional (34) together with PAW potentials (35, 36).

The systems are cooled down from 3,000 K in several steps, first slightly above and below the experimental melting temperature, then by 100 degrees intervals down to 300 K. At each temperature plateau, the density is adjusted to obtain negligible residual stress.

For each system, the crystal was also simulated with MD at 300 K with gamma point sampling and supercells counting 140 to 216 atoms. For GeTe, GeSb₂Te₄, and Sb₂Te₃, further annealing and data acquisition at 300 K were performed using self-consistent DF2 van der Waals functional (37) and fixed volume, as in ref. 6.

The Born effective charge and static dielectric constant have been computed using Density Functional Perturbation Theory including local field effects (38) whereas the frequency-dependent imaginary dielectric function was computed using a sum over DFT states. Finally, the vibrational frequencies have been computed using finite differences on fully relaxed structures.

To quantify the impact of aging on bonding, we computed four different GeTe structures with different total energies (see ref. 6) as well as two GeSb₂Te₄ models.

Computations.

PAW SCF wave function calculations for all the systems for which LIs and DIs have been calculated were performed with the pw.x module of the Quantum Espresso (QE) package (39). The all-electron density is used to determine the QTAIM atomic basins by Critic2 (40, 41). PAW wave functions are then transformed into Maximally Localized Wannier Functions through the Wannier90 code (42). These are used by the Critic2 code to compute the localization and delocalization indices (DI and LI). The convergence of the final DI and LI values was checked on the crystal phase calculations.

Averaged DI using the Effective Coordination Number ECON.

To compute an average value for the number of electrons shared (twice the delocalization index), we weighted the DI contributions according to the EcoN definition (43).

This prevents the use of any distance cutoff to define the coordination number in the disordered system. In order to provide a direct comparison, the DI have been averaged in this same way for the crystalline phases. For crystalline GeTe, Sb₂Te₃, and GeSb₂Te₄, the ECON values (averaged over the species) equal 5.58, 5.84, and 4.45, respectively.

For any given atom i, an effective average interatomic distance r_avg is defined as:

$$r_{\mathit{avg}}=\frac{{\sum }_{j=1,N;j\ne i}{r_{\mathit{ij}}e}^{1-{\left(r_{\mathit{ij}}/r_1\right)}^6}}{{\sum }_{j=1,N;j\ne i}{e}^{1-{\left(r_{\mathit{ij}}/r_1\right)}^6}}.$$

r_ij being the interatomic distance between atom i and j and r₁ the shortest distance among these. The effective coordination number and effective delocalization index are then obtained with

$$ECoN=\sum _{j=1,N;j\ne i}{e}^{1-{\left(r_{\mathit{ij}}/r_{\mathit{avg}}\right)}^6},$$

$${\mathit{DI}}_{\mathit{avg}}=\frac{1}{\mathit{ECoN}}\sum _{j=1,N;j\ne i}{{\mathit{DI}}_{\mathit{ij}}e}^{1-{\left(r_{\mathit{ij}}/r_1\right)}^6}.$$

DI_ij being the delocalization index between the Bader basins of atoms i and j.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.