Unbiased construction of constitutive relations for soft materials from experiments via rheology-informed neural networks

Significance

Development of phenomenological constitutive relations that describe the stress response of soft materials to an imposed deformation is commonly associated with generalizations and idealized assumptions (biases). Thus, science-based data-driven methods capable of describing the physical dynamical behavior of soft materials from limited experiments can create a new paradigm in how constitutive models are constructed in general, and in new fundamental physics discovery. In this work, through a concerted theoretical, experimental, and data-driven approach, rheology-informed neural networks are developed for unbiased construction of rheologically relevant constitutive models, without compromising rigor or foundational sciences. The platform developed here is general enough that it can be extended to areas well beyond complex fluids or soft matter physics and across other disciplines as well.

Abstract

The ability to concisely describe the dynamical behavior of soft materials through closed-form constitutive relations holds the key to accelerated and informed design of materials and processes. The conventional approach is to construct constitutive relations through simplifying assumptions and approximating the time- and rate-dependent stress response of a complex fluid to an imposed deformation. While traditional frameworks have been foundational to our current understanding of soft materials, they often face a twofold existential limitation: i) Constructed on ideal and generalized assumptions, precise recovery of material-specific details is usually serendipitous, if possible, and ii) inherent biases that are involved by making those assumptions commonly come at the cost of new physical insight. This work introduces an approach by leveraging recent advances in scientific machine learning methodologies to discover the governing constitutive equation from experimental data for complex fluids. Our rheology-informed neural network framework is found capable of learning the hidden rheology of a complex fluid through a limited number of experiments. This is followed by construction of an unbiased material-specific constitutive relation that accurately describes a wide range of bulk dynamical behavior of the material. While extremely efficient in closed-form model discovery for a real-world complex system, the model also provides insight into the underpinning physics of the material.

Soft materials in general, and more specifically complex and structured fluids, commonly exhibit a rich and diverse set of responses to applied deformations. These responses can include the emergence of a yield stress, below which the material shows solid-like behavior (1), and above which the system exhibits viscoplastic flow with complex dynamics (2, 3). Additionally, soft systems can show strong thermokinematic memory of the history of flow, a phenomenon commonly referred to as thixotropy (4–6). Whether the goal is to understand biological flows (7–10), to design advanced manufacturing processes for complex fluids with targeted properties (11), or to describe natural geophysical flows (12, 13), the first essential step is to describe the complex stress responses to different flowing conditions through closed-form mathematical expressions. The quest to discover the constitutive relations made from kinematic variables for different classes of complex fluids is as old as the science of rheology itself. Conventionally, these governing equations are derived from knowledge-based phenomenological models that describe the stress response of a complex fluid to an applied deformation. In its crude form, different combinations of mechanical analogues, such as springs, dashpots, and sliding blocks can be combined in different arrangements to represent the elastic, viscous, and plastic characteristics of the fluid. Ultimately, a set of coupled ordinary differential equations (ODEs) are used to represent the rheological constitutive equations for such complex fluids. As the fluid’s response to a specific flow becomes more complex, so too must the model that can describe the behavior. For instance, while the steady-state rate-dependent viscosity of a fluid can be described through a simple empirical relation with a few parameters, accurately accounting for the time-dependent response of a thixotropic elasto-visco-plastic (TEVP) materials to an applied deformation dramatically increases the number of parameters involved (5, 6, 14, 15). While it is extremely important and central to our understanding of complex fluids, this conventional phenomenological approach to constitutive modeling has three main limitations: i) As the complexity of the phenomenon under question increases, the number of model parameters required to describe it becomes difficult to ascertain, and commonly one has to resort to ad hoc parameters with minimal physical relevance; ii) since these models are built in a bottom-up manner using different elements, they commonly represent so-called ideal behavior and do not accurately describe the behavior of the real fluids under investigation; and iii) these models are inherently biased to their fundamental construction. For example, a viscoelastic constitutive relation, and a thixotropic one can be virtually identical with respect to their stress responses (4, 16), but the choice of model strongly biases the implied physics. Thus, model construction frameworks that are unbiased, versatile, and compact in their form can be potentially transformative in our understanding of soft materials by mitigating virtually all of the limitations listed above.

Using data to identify the underlying governing constitutive relation can greatly enhance and alter our modeling, simulation, and comprehension of complex physical systems in a variety of scientific and engineering applications. Recent improvements in processing power, data availability, and machine learning theories have stoked significant interest in data-driven discovery of physical principles and governing equations (17–22). For example, a sparsity-promoting method called sparse identification of nonlinear dynamics (SINDy) (23) can be used to pick dominant candidate functions from a high-dimensional nonlinear function space based on sparse regression to identify parsimonious governing equations. The sequential threshold ridge regression (STRidge) approach can obtain the sparsity, which iteratively calculates the sparse solution subjected to hard thresholds to produce a simple governing equation by balancing the accuracy and complexity of identified models (18). For the past few years, SINDy has received a lot of interest and different techniques have been developed with various applications to find projected low-dimensional surrogate models in the form of ODEs and PDEs (24–31). Nonetheless, the numerical differentiation in SINDy is highly dependent on the quality as well as the quantity of the data at hand, making it a less-than-ideal framework for problems with limited or noisy datasets. Nonetheless, these limitations can be alleviated by employing automatic differentiation (AD) (32).

Data-driven models and machine learning (ML) algorithms have become inextricably linked tools for analyzing and predicting various phenomena (33–38). Nonetheless, traditional ML frameworks have a strictly statistical foundation and rely on exhaustively large amounts of data to produce accurate predictions. Additionally, ML algorithms in general are agnostic to the physical underpinnings of the system. Such ML frameworks are also constrained to predictions in the range of the training data and are generally incapable of making out-of-range predictions. Therefore, there has been an increasing effort to develop methods that function well on small datasets, as well as embedding the essential physics of a given problem into the ML algorithms (39–42). Physics-based ML frameworks provide a platform for the inclusion of the physical underpinnings of a system into the algorithm either implicitly or explicitly (43).

Recently, a series of different rheology-informed neural networks have been developed by embedding the appropriate rheological understanding of the system within the ML platform (44–49). Here, we extend the RhINNs framework with conspicuous features of interpretability and generalizability, to construct governing ODEs of complex fluids from a limited sparse experimental data. The goal is to automatically detect and construct rheologically relevant, unbiased, and robust constitutive models from the experimental data that can be later used to predict the complex response and behavior of the material to flow protocols that differ from the ones used to construct the model.

Materials and Methods

Experiments.

We study the stress response of a soft polymer microgel, an aqueous suspension of Carbopol 980, to a series of rheological tests. The choice of this system allows for rigorous benchmarking against other experimental reports and models, as it has been shown to be a simple yield stress fluid with no dependence on shear history (50). The 1 wt % Carbopol formulation used in this study was prepared as described in a prior study (51). Rheological measurements were made with a Modular Compact Rheometer (MCR) 702 from Anton Paar, using 50 mm parallel plate geometry with a gap of 1 mm. To avoid wall slip, 240-grit waterproof sandpaper was attached to the geometry using double-sided tape. The amplitude sweep data was collected at angular frequencies of 1, 0.562, and 0.316 rad/s. The strain amplitude was varied from 0.00562 to 10 strain units for all the angular frequencies tested. The steady shear startup data were collected at rates over the range 0.01 to 31.6 1/s until steady state was reached.

Data-Driven Model Construction Framework.

We consider the constitutive equation governing the Carbopol system to be given by Eq. 1, in which σ is the latent solution of the system and $\gamma$ is the applied strain. $\mathcal{G}(.)$ is a general nonlinear form of the constitutive equation consisting of the stress response of the material as well as the applied strain with their temporal derivatives parameterized by $\mathbf{\Lambda }$.

$$\begin{array}{c}\hfill \mathcal{G}[\sigma ,\gamma ,\dot{\sigma },...,\dot{\gamma },\ddot{\gamma },...,\sigma \gamma ,\sigma \dot{\gamma },\dot{\sigma }\gamma ,...;\mathbf{\Lambda }]=0.\end{array}$$ [1]

We assume that the physical law can be approximated by sparse regression using a small number of key terms that can be chosen from a vast library of candidate functions. This library can include any functional form or the variables that are believed to be of any significance. To make sure that our approach is unbiased to our previous understanding of the system, we include many variations of the shear stress, shear strain, and their first and second derivatives in the candidate function library. Subsequently, Eq. 1 can be reformulated in the form of Eq. 2, in which $\mathbf{\Phi }$ is given as a row vector defined as $\mathbf{\Phi }=[1,\sigma ,\gamma ,\dot{\gamma },\ddot{\gamma },...,\sigma \gamma ,\sigma \dot{\gamma },\dot{\sigma }\gamma ,...]$ and $\mathbf{\Lambda }$ is a sparse coefficient vector with the same size as $\mathbf{\Phi }$.

$$\begin{array}{c}\hfill \dot{\sigma }=\mathbf{\Lambda }\mathbf{\Phi }.\end{array}$$ [2]

This formulation re-structures the problem to be that of discovery, in which the goal is to find the sparse $\mathbf{\Lambda }$ given the temporal measurement data of $\sigma$.

Rheology-Informed Neural Network.

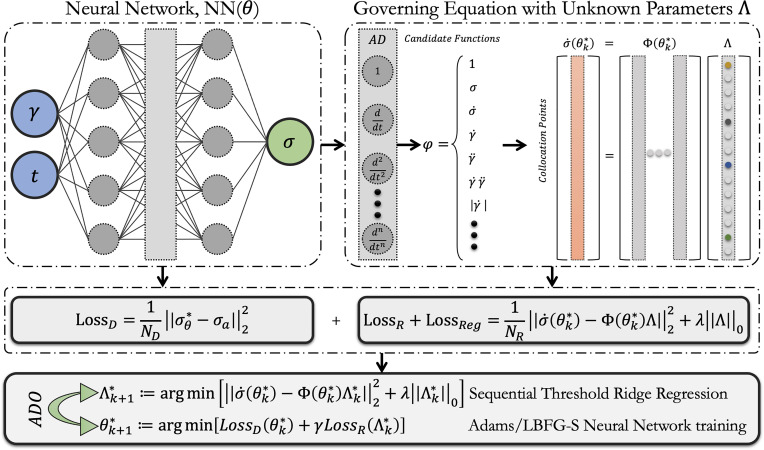
We model the system response and identify the parsimonious closed form of the governing ODE at the same time. Fig. 1 shows a schematic description of our framework.

Fig. 1.

Schematic view of the model construction framework. A neural network with trainable parameters $\theta$ with two inputs of time and deformation (strain), and one output of shear stress. Assembling the candidate function vector using automatic differentiation (AD) for the sparse regression. Calculating the total loss value based on three components of data, equation residual, and regularization term. Implementing alternating direction optimization (ADO) to optimize the neural network trainable parameters as well as the model parameter to achieve a close-form ODE. In the ADO process, the significantly contributing candidate functions are selected based on the Ridge regression method. The hyperparameters of the neural network are also tuned using a combination of Adam and L-BFGS methods. The process is iterated until an acceptable accuracy is obtained.

The neural network is used to approximate the latent solution based on the experimental data by adjusting its trainable hyperparameters, namely the weights and biases. With recent developments in automatic differentiation (AD), we can calculate the temporal derivative of the latent solution to generate the candidate functions in $\mathbf{\Phi }$. Thus, the sparse representation of the reconstructed ODE can be written in a residual form as $Los{s}_R=\dot{\sigma }-\mathbf{\Lambda }\mathbf{\Phi }$. This residual is valuated on a large number of collocation points that are synthetically generated throughout the temporal domain. The fundamental idea is to modify both the ODE coefficients and the neural network trainable parameters in a way that the neural network can adapt to the measured experimental data while adhering to the constraints established by the underlying ODE. The total loss that is used to train both the neural network hyperparameters as well as the ODE coefficients is shown in Eq. 3.

$$\begin{array}{c}\hfill Los{s}_t=Los{s}_D+\gamma Los{s}_R+{\lambda ||\mathbf{\Lambda }||}_0.\end{array}$$ [3]

This equation is composed of three parts: $Los{s}_D$ which is defined as the discrepancies between the neural network predictions and the experimental data; $Los{s}_R$ that is the physical residual loss modified by the relative weight value of $\gamma$; and a regularization term for the constructed ODE coefficients based on the $L_0$ norm and relative weight value of $\lambda$. By minimizing the total loss shown in Eq. 3, the neural network can provide a data-driven full-field system response as well as uncovering the parsimonious closed-form ODE. To properly optimize such high-dimensional problems, an alternating direction optimization (ADO) algorithm is employed to learn the trainable parameters by breaking the overall optimization process into a number of digestible sub-problems, as shown in Eq. 4.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\lambda }_{k+1}^{\ast }:=argmin[||\dot{\sigma }({\theta }_k^{\ast })-\mathbf{\Phi }({\theta }_k^{\ast }){\mathbf{\Lambda }||}_2^2+{\lambda ||\mathbf{\Lambda }||}_0]\hfill \\ {\theta }_{k+1}^{\ast }:=argmin[Los{s}_D({\theta }_k^{\ast })+\gamma Los{s}_R({\lambda }_k^{\ast })]\hfill \end{array}\right..\end{array}$$ [4]

In each step of the ADO algorithm, the neural network is first trained on the experimental data to find the best latent solution as well as its derivatives to calculate the candidate functions. Afterward, sequential threshold ridge regression (52) is used on the collocation points to eliminate non-significant terms in the candidate function library and create the close-form ODE. This process is iterated until an acceptable accuracy is achieved. A combined use of neural networks and sparse regression leads to two results: 1) a neural network framework that can accurately model the latent solution and its derivatives to form the candidate functions; and 2) a sparse regression that can constrain the candidate function with respect to the experimental data leading to a closed-form ODE to describe the system.

The architecture of the neural network, in particular the number of layers as well as the number of neurons per layer, has a substantial impact on the accuracy of the predictions as well as the algorithm’s performance. In this study, the relative absolute error (RAE) is chosen as the measure of accuracy to investigate and optimize the role of network hyperparameters and settings. The depths of the NNs were changed from 1 to 10 layers, and the widths from 10 to 100 neurons per layer. Widths ranging between 25 and 50, and depths ranging between 4 and 8 were found to yield the best levels of accuracy while avoiding overfitting. The loss function is optimized using a combination of Adam optimizer with a learning rate of 1e-3 and L-BFGS method together with Xavier’s initialization method, while the hyperbolic tangent function is employed as the activation function.

Results and Discussion

The ultimate goal is to develop reliable machine learning frameworks to provide robust and accurate closed-form constitutive relations for complex fluids. The experimental behavior of the system (shown in Figs. 2, 3, and 4) clearly indicate a complex elasto-visco-plastic response that can be described through separation of the deformation into recoverable and unrecoverable strains (53). Here, we use the experimental data from two oscillatory flow protocols in the large and small amplitude oscillatory shear (LAOS and SAOS) regimes to recover the closed-form ODE governing the system. The number of recovered candidate functions can change depending on the complexity of the observed data. Here, when applied to data strictly in the SAOS regime, or alternatively in the LAOS regime, only a limited number of candidate functions are identified to be the contributing factors for each condition, which is not a representative of the entire behavior of the system. All the dominant modes are correctly identified only when a combination of both SAOS and LAOS experimental data (regardless of amplitude or frequency) is used during the training. This is somewhat expected, as the shear stress response in different regimes is dominated by different physical characteristics of the fluid. For instance, small perturbations about the equilibrium position in the SAOS regime naturally cannot probe the plastic nature of the fluid.

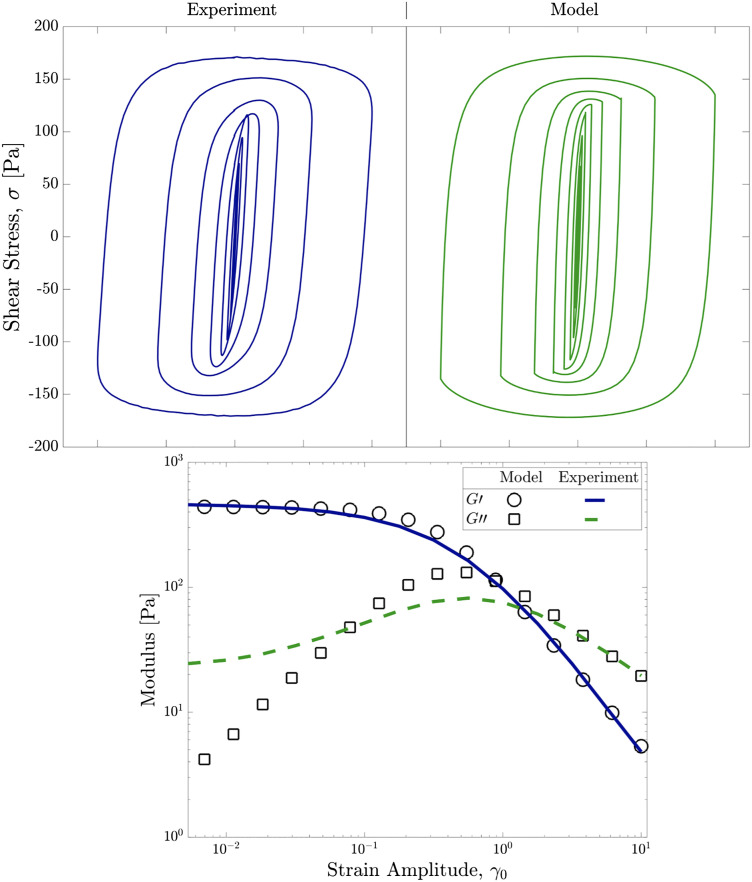
Fig. 2.

(Top) SAOS to LAOS stress response, and (Bottom) Storage, $G^{\prime }$, and loss, $G"$, moduli of Carbopol measured experimentally, and benchmarked against the predictions of discovered constitutive model at the frequencies of 1.0 rad/s for the applied shear strains of 0.0056 to 10.0 [-].

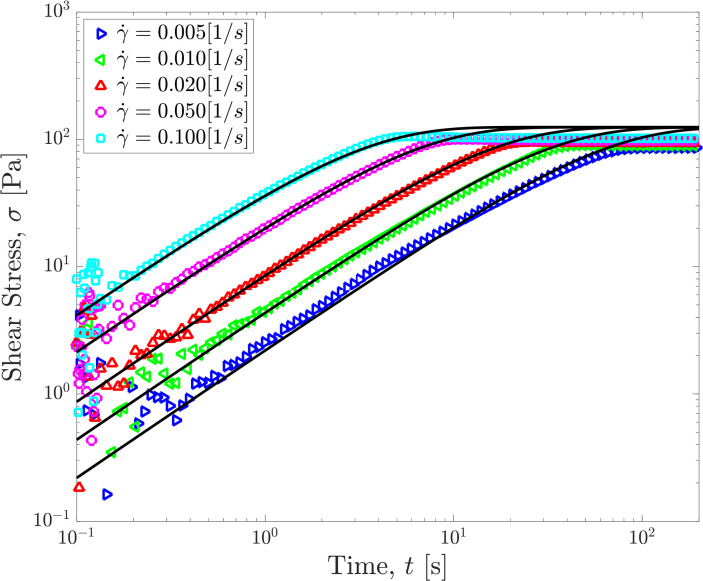
Fig. 3.

Stress response of the elasto-visco-plastic fluid to a start-up of shear experiment, benchmarked against the prediction of recovered/constructed constitutive model for applied shear rates of $\dot{\gamma }$ = 0.001 to 0.1 [s${}^{-1}$]. The symbols represent the experimental measurements and solid lines represent the model predictions.

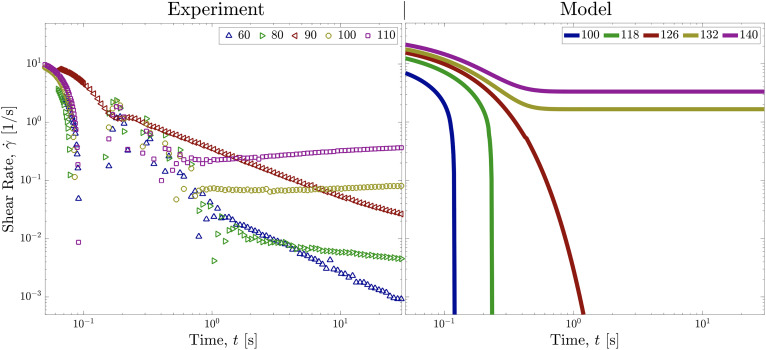
Fig. 4.

Strain rate response of the elasto-visco-plastic fluid in a creep experiment, benchmarked against the prediction of recovered/constructed constitutive model, with different applied shear stresses. Scattered data on the Left represent the experimental measurements and solid lines on the Right represent the model predictions.

The dynamical behavior of elasto-visco-plastic (EVP) materials is typically modeled at the continuum level in terms of a critical stress, below which it is assumed that no plastic flow occurs. Early efforts to develop models for the rheology of yield stress fluids, including those of Bingham, Herschel and Bulkley, and Casson, concentrated on establishing descriptions of the state of steady flow that matched experimental data (54–57). These models contained no information regarding the yielding process, and assumed the pre-yielding behavior was that of an infinitely rigid solid. They therefore only captured the viscoplastic behavior. Data recorded from transient experiments indicated that there was a measurable elastic modulus below the yield stress that was not accounted for by the viscoplastic-only models. Oldroyd extended the early attempts by explicitly accounting for both the viscoplastic flow regime above the yield stress (58), as well as the viscoelastic solid behavior below the yield stress. This two-regime behavior is currently referred to as the Oldroyd–Prager formalism (58, 59). Despite capturing the viscoelastic solid and viscoplastic flow behaviors, models that follow the Oldroyd–Prager formalism predict instantaneous yielding that manifests as abrupt changes in the rheology that are not observed experimentally. Recently, a couple of models have been proposed that go beyond the Oldroyd–Prager formalism and account for yielding as a continuous process (53, 60). Efforts to improve upon these models continue, as advanced applications require all aspects of material behavior to be accurately captured.

Alternatively, a library of candidate functions consisting of twenty (20) terms such as $\dot{\gamma }$, $\ddot{\gamma }$, $\sigma$, and their products and variations is evaluated to construct the ODE describing the shear stress responses. It should be noted that the list of candidate functions can be arbitrarily extensive. In this work, we performed a series of preliminary tests and found that consideration of the main variables (deformation rate, and shear stress) and their products and variations will suffice, including common candidate functions observed in phenomenologically derived rheological constitutive models will suffice inefficient construction of a new model. The training efforts are performed in eight iterations of ADO including 5,000 iterations of Adam optimizer and 100 iterations of STRidge optimizer, followed by a final L-BFGS optimizer. Two sets of oscillatory experimental data, one from SAOS and another from the LAOS region, at an angular frequency of 1 rad/s are used simultaneously to recover the model. The discovered ODE for our material is shown in Eqs. 5 and 6 with the coefficients shown in Table 1.

$$\begin{array}{c}\hfill \dot{\sigma }=\frac{C_1|\dot{\gamma }|\sigma +C_2\dot{\gamma }+C_3\ddot{\gamma }+C_4\dot{\gamma }|\dot{\gamma }|+C_5\ddot{\gamma }|\dot{\gamma }|}{1+C_6|\dot{\gamma }|}.\end{array}$$ [5]

$$\begin{array}{cc}\hfill \dot{\sigma }\left(1+C_6|\dot{\gamma }|\right)-\sigma \left(C_1|\dot{\gamma }|\right)=& \dot{\gamma }\left(C_2+C_4|\dot{\gamma }|\right)\hfill \\ \hfill & +\ddot{\gamma }\left(C_3+C_5|\dot{\gamma }|\right).\hfill \end{array}$$ [6]

Table 1.

Numerical values of the constructed model coefficients (Eq. 5)

C1	C2	C3	C4	C5	C6
−3.576	444.0	−1.0	17.2	19.0	0.481

The discovered model, as expressed in these equations, contains terms proportional to the stress and stress rate, and the strain rate and its derivative, with each term having a prefactor that is dependent on the magnitude of the shear rate. $C_1$ is unitless, $C_2$ has stress units of [Pa], $C_3$ and $C_4$ have viscosity units of [Pa s], and $C_5$ has units of [Pa s${}^2$]. Parameters like $C_5$ are usually not observed in similar constitutive equations. However, the product of the first and second derivatives of the shear strain was found to be an important candidate function. The second derivative of the strain by itself is a parameter that features in many common constitutive relations for complex fluids such as the Oldroyd-B and Giesekus models and relates to retardation effects that limit how quickly a system is able to acquire strain upon application of stress. The product of the first and second derivatives is not in common use and may point toward new physics. Last, $C_6$ has time units of [s], which commonly corresponds to an intrinsic timescale within the material’s stress response such as a relaxation or retardation time. For any constitutive model to be further used in describing a fluid’s rheological behavior, it must first be shown consistent with respect to the second law of thermodynamic (61). The new constructed model shown in Eq. 5 does not violate Planck’s statement of entropy production during a flow reversal experiment, and hence is thermodynamically consistent.

The case of steady-state shearing helps us discern physical meaning from many of the parameters. At steady state, $\dot{\sigma }=$$\ddot{\gamma }=0$, and the model simplifies to

$$\begin{array}{c}\hfill \sigma =\frac{-C_2}{C_1}\text{sign}(\dot{\gamma })-\frac{C_4}{C_1}\dot{\gamma },\end{array}$$ [7]

which is equivalent to the Bingham model for yield stress fluids with a yield stress of $\frac{-C_2}{C_1}$ and a Bingham plastic viscosity of $\frac{-C_4}{C_1}$. Further, the model accurately represents the physics by requiring the sign of the shear rate as a multiplier of the yield stress. This ensures that application of a negative shear rate will give the right stress, a statement that is often left out of the Bingham model when only uni-directional shearing is expected. Of the two viscosities contained in the model, only $C_4$ affects the steady-state behavior, which means that $C_3$ must therefore represent a viscoelastic solid viscosity that more strongly influences the pre-yielded state, and gives rise to retardation behaviors.

Immediately after a step-strain is applied to the model, $\dot{\gamma }=\ddot{\gamma }=0$ and we see that $\dot{\sigma }=0$, meaning that the model represents a yield stress fluid that does not relax stress when flow is ceased. The presence, however, of $C_6$ shows that the model has a rate-dependent relaxation time that allows it to relax stress while being sheared, a physical phenomenon only recently observed and predicted (53, 62).

A closer inspection of Eqs. 5 and 6 reveals that the LAOS flow protocol is an ideal experimental protocol for recovering all the candidate functions. Other protocols that elicit nonlinear behaviors could also be used, but LAOS has particular strengths that make its use more efficient at discovery. Large step strain experiments could be used, but in such experiments, the strain remains constant for the interval where the stress is recorded, immediately after the initial application. The strain rate and its derivative also remain at zero for the interval where stress is measured. Candidate functions involving those terms could not be found with step strain training data. If training is based instead on steady shear startup data, the strain changes at a constant rate and the strain rate functions would be discoverable. However, the functions with the second derivative of strain cannot be recovered. Similarly, if training only uses creep data where the applied stress is constant, functions with stress rate terms cannot be recovered. Large amplitude oscillatory shear experiments are therefore ideally suited to gathering information for the construction of accurate constitutive relations because they provide access to information from the stress and strain rates, as well as their derivatives. The widest possible set of candidate functions can therefore be identified. It is perhaps not surprising that recent studies that have advanced our understanding of transient nonlinear rheology have used LAOS protocols (53, 63).

Having the closed-form equation as well as the material constants, we can now evaluate its predictions of the stress response of the gel under a series of different flow protocols and deformation rates. To this end, start-up of flow at various deformation rates and oscillatory shear experiments at other frequencies are performed and benchmarked against the model’s predictions. We show in Fig. 2, Top the comparison between the experimentally measured stress response and the predictions made by the closed-form ODE recovered from the two initial oscillatory experiments at a frequency of 1 rad/s. Results for two other frequencies, entirely unseen by the neural network, are also provided in SI Appendix, Fig. S1. From the amplitude sweep results in Fig. 2, Bottom it is evident that the discovered model describes the storage and loss moduli of the Carbopol system accurately over a wide range of deformations. It should be noted that the new model’s predictions are significantly more accurate compared to classical phenomenological models’ best description of the same material. For instance, our newly constructed model predictions are compared against elasto-visco-plastic model of Saramito (64) in SI Appendix, Fig. S2.

While the intricate details of the stress response at different frequencies unseen by the neural network become more complicated, the data-driven discovered model of Eqs. 5 and 6 consistently tracks the observed experimental measurements. This suggests that the model includes the essential physics required to describe the system. While this is promising, the applicability of the constructed model to other flow protocols should also be tested to assess the versatility of the candidate functions realized. In other words, any model constructed or discovered has to be generalizable to all rheologically relevant flow protocols. To check this condition, the comparison of the model and the experimental measurements during a series of start-up flow experiments with applied deformation rates varying by more than a factor of 20, from 0.005 [1/s] to 0.1 [1/s] is shown in Fig. 3. The discovered model is found to closely track the experimentally measured shear stresses regardless of the applied deformation rate, with an accurate initial elastic modulus, and an accurate prediction of the critical shear strain at which the stress approaches its quasi-steady state value.

To truly test the applicability of the model in predicting the behavior of the material under question, an inverse solution of the constitutive model is considered. In this case, the inverse solution comes in the form of creep experiments, in which a shear stress is applied and rate of deformation is solved for. Results in Fig. 4 show the experimental measurements of the creep response (scattered data) benchmarked against the predictions of our discovered model (solid lines). A hallmark of these elasto-visco-plastic materials is the phenomenon of viscosity bifurcation, where the viscosity remains measurable and finite above the yield stress and diverges below it (65, 66). A bifurcation in the viscosity is also a bifurcation in the shear rate, which we show in Fig. 4. At larger applied shear stresses, a transient decay to a terminal but quasi-steady measurable deformation rate is usually observed. Although quantitatively at different critical applied stresses for the bifurcation (126 Pa for the model and 96 Pa for the experiments), Fig. 4 indicates that our model successfully predicts the viscosity bifurcation phenomenon.

Conclusion

In this work, we introduced a framework for data-driven informed discovery and construction of rheologically relevant constitutive models for soft materials. By leveraging the advances in automatic differentiation, and different dimension reduction algorithms, an automatic and unbiased model construction and identification platform has been developed. This framework allows for automatic sensitivity analysis of a vast number of candidate functions (modes) to be included in a test library. Through a multi-step process, the most dominant modes within the candidate function library are automatically identified and a model is constructed using those functions. To benchmark and validate our discovered model for a test elasto-visco-plastic fluid, a series of different rheological experiments were performed. Our six-parameter model was found to recover a variety of different rheological tests closely, with no further adjustment of the parameters, and only from two sets of initial experiments. While applicability of the full model was presented, removal of any of the six components within the model will result in loss of accuracy. In particular, removal of the product of the first and second strain derivatives yields predictions that differ qualitatively and quantitatively from observed experiments (SI Appendix, Fig. S3). This further suggests that the neural network indeed recovers the essential functions to describe a physical behavior. More importantly, the model was found to be capable of predicting the material’s behavior in flow protocols that significantly differ from the ones used in the discovery step, suggesting that the platform truly discovers the most effective and compact form of the constitutive relation with a minimal number of experimental inputs. However, in the model discovery stage, additional care should be taken in ensuring that different regimes of a material’s response are provided. Training and discovery based only on SAOS or LAOS data were found to result in an incomplete model construction with limited predictability.

The general methodology and the framework developed here offer a series of significant advances that compliment conventional approaches to constitutive modeling in mechanics or rheology: i) The model discovery/construction is efficiently performed using a very limited number of experiments; ii) model parameters are strictly limited to those that are truly dominant modes within the candidate functions, preventing redundant parameter additions that do not necessarily contribute to a specific system’s response to an applied deformation; and iii) unbiased and exhaustive search of the candidate functions can lead to discovery of new physics. In our work, we found that the product of the first and second derivatives of the shear strain plays a key role in the total stress response of the elasto-visco-plastic fluid. This is unexpected, and not a common term in classical constitutive equations in the rheology literature. As such, the methodology/platform proposed here could potentially enable a leap forward in our fundamental understanding of complex fluids in general, and more particularly in how we perceive their constitutive modeling. While the proposed methodology was tested and validated in a series of rheological tests for a soft material, the general approach can be easily adapted to other material characterization techniques and mechanical probes as well, with applications far beyond rheology. It should be noted that for the constitutive model developed here to be directly used in place of any similarly formulated constitutive model of interest, and combined with conservation equations to describe actual complex fluid flows beyond viscometric ones, a tensorial description with frame-invariance is a necessity. The current model developed here solely focuses on the shear stress (a single component of the stress tensor) and as such is unable to describe normal stresses that are essential in recovery of a realistic flow. However, by extension of the current model and adaptation of frameworks such as one introduced by Lennon et al. (67), frame-invariant tensorial constitutive models can be developed. Finally, similar to any data-driven approach, there are important practical limitations to the applicability of our approach beyond which this general methodology may not result in an accurate model construction. Beyond practical choice within the candidate function library and training process, perhaps the most important limitation of data-driven model construction and physics discovery is with regard to the physical behavior of the material itself. In particular, the number of measurable/observable parameters of the system must strictly follow the number of dependent variables in the model. For instance, in describing thixotropy, inclusion of a microstructure parameter and its time evolution equation within the constitutive model is commonly required. However, this microstructural parameter is not directly measurable, and as such no data can be made available to construct a model for it. Similarly, exposing the neural network to a full range of physical behavior is necessary in constructing an accurate model.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data presented in the manuscript are available in the Mendeley Data repository (68).